Analysis of Airflow Dynamics and Instability in Closed Spaces Ventilated by Opposed Jets Using Large Eddy Simulations
Abstract
1. Introduction
2. Experimental Setup
3. Case Set
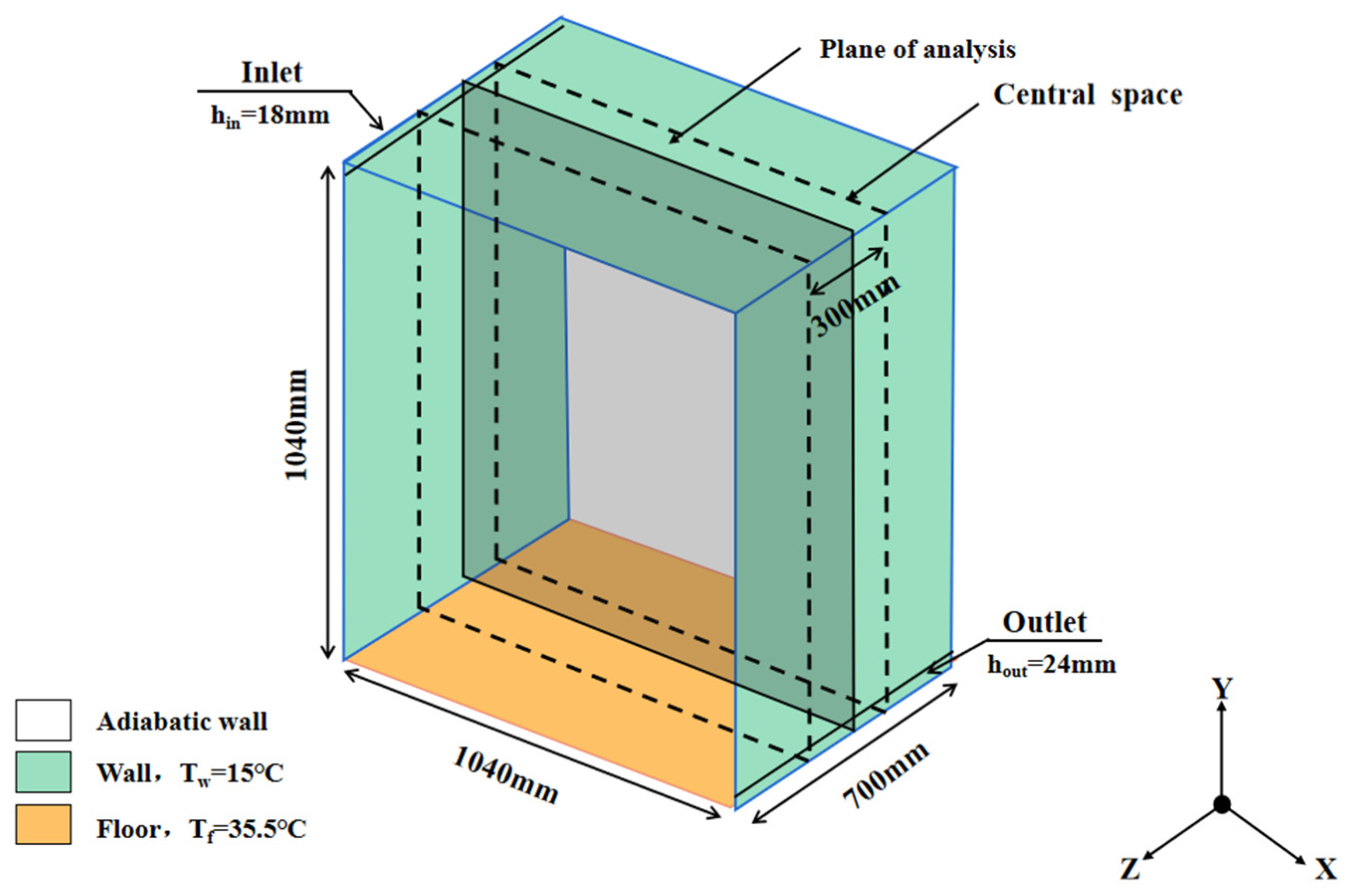
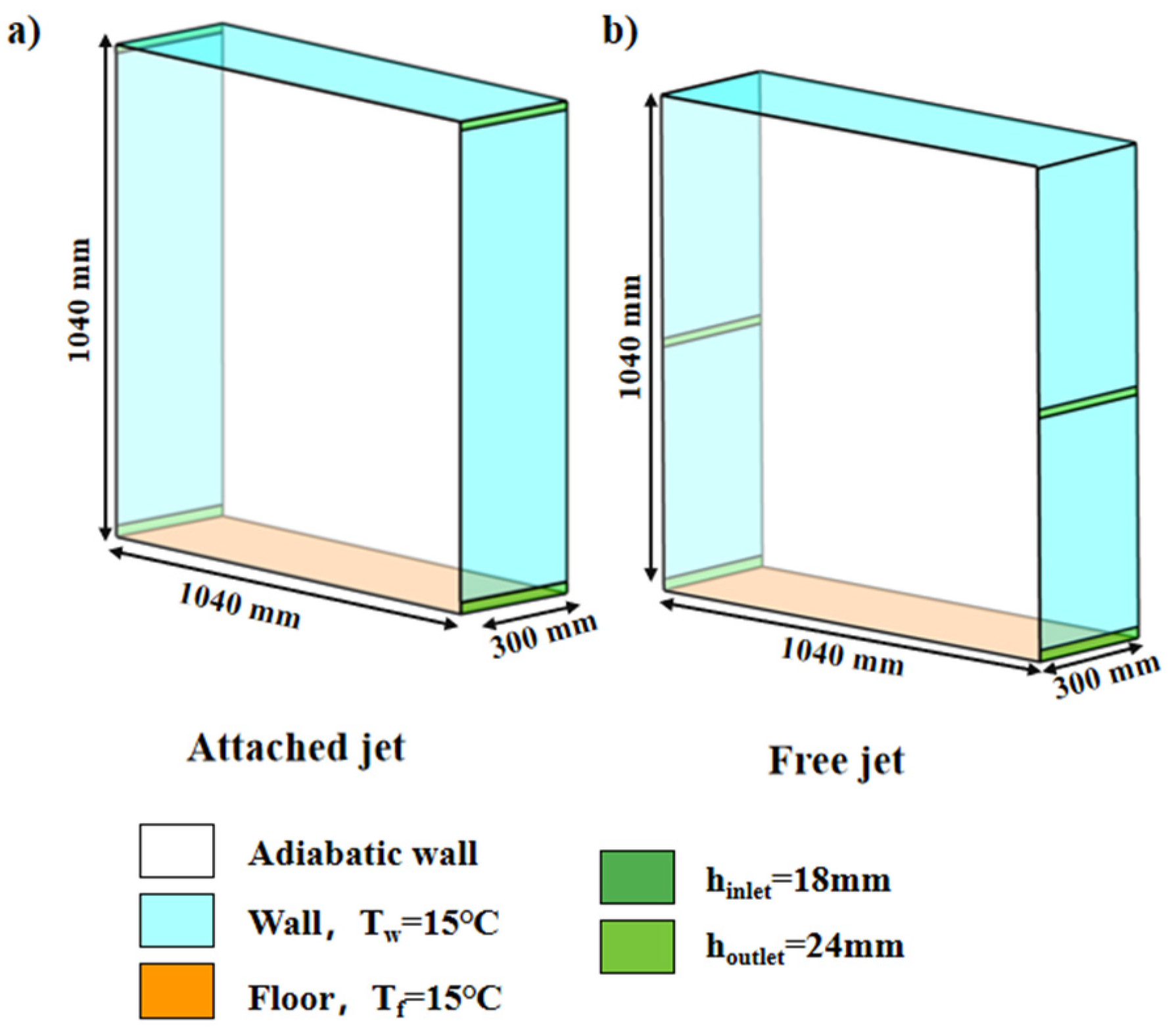
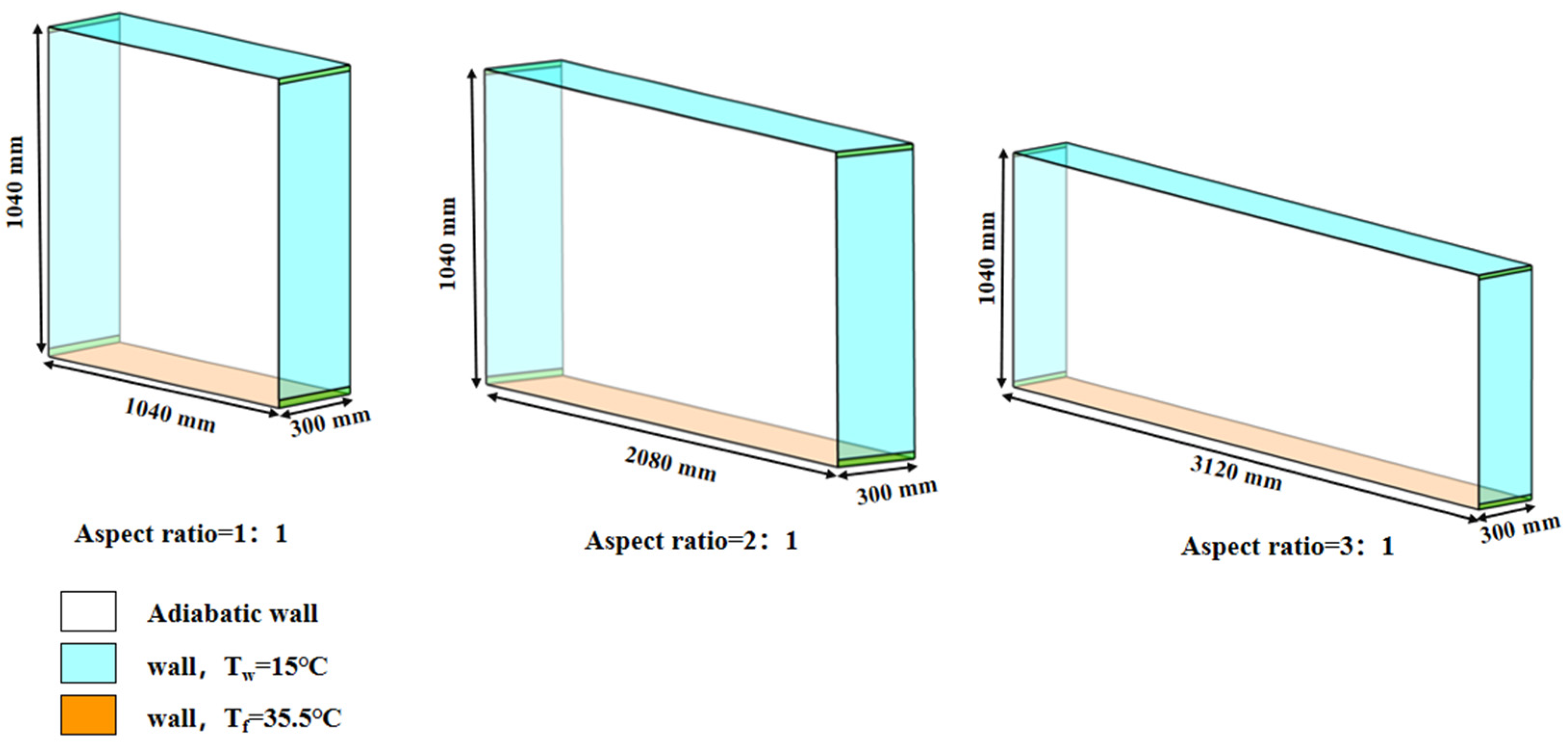
3.1. Geometric Model
3.2. Boundary Conditions
3.3. Solver Settings
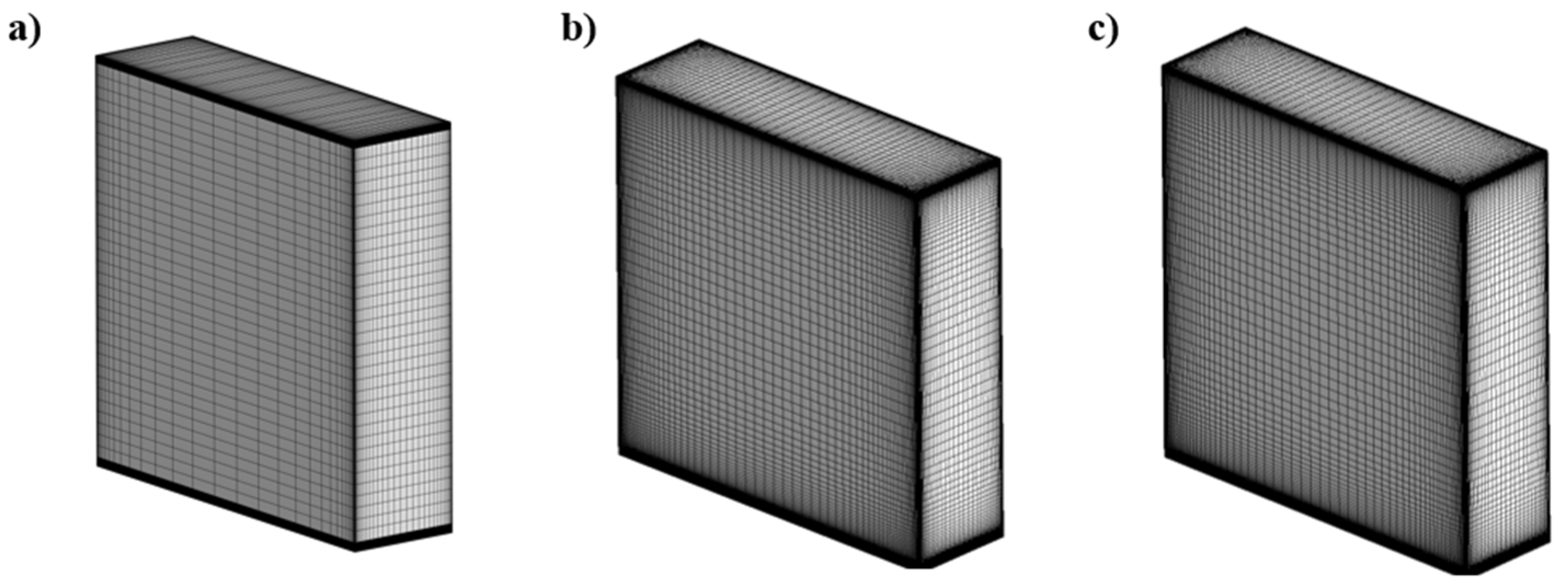
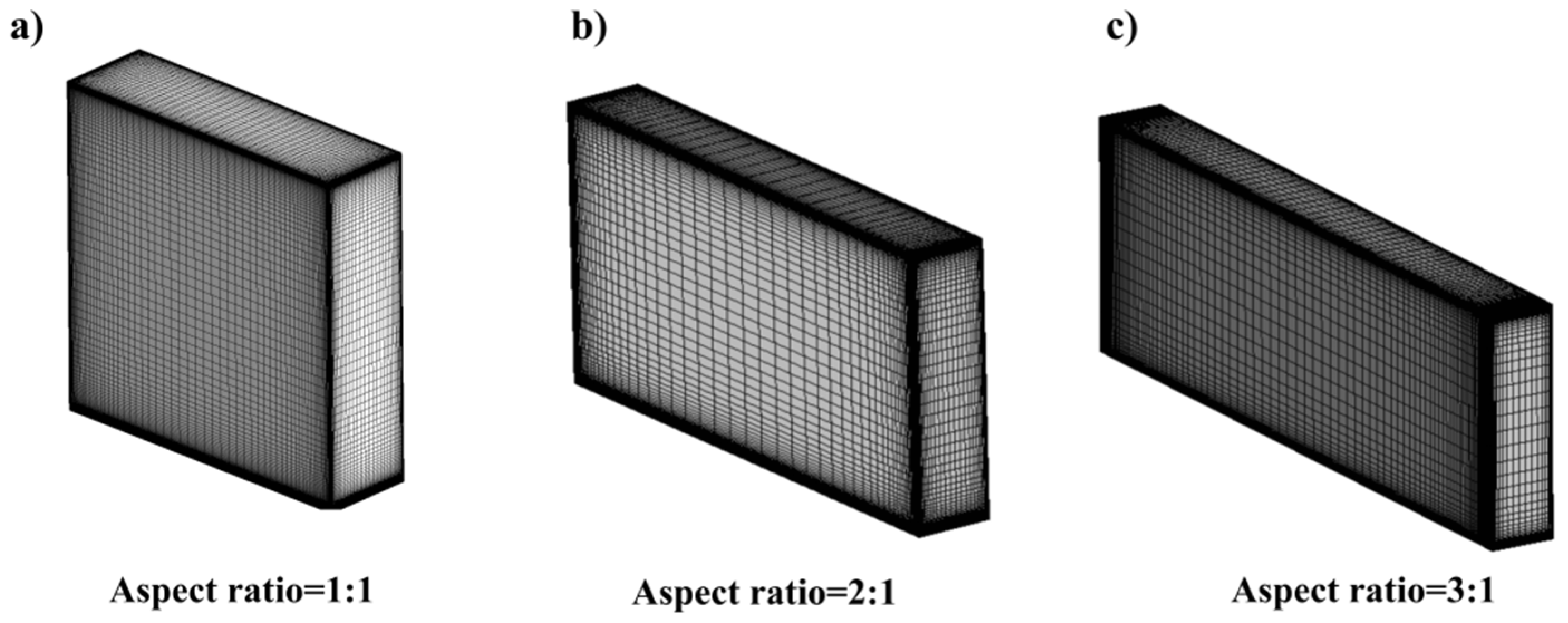
3.4. Grid
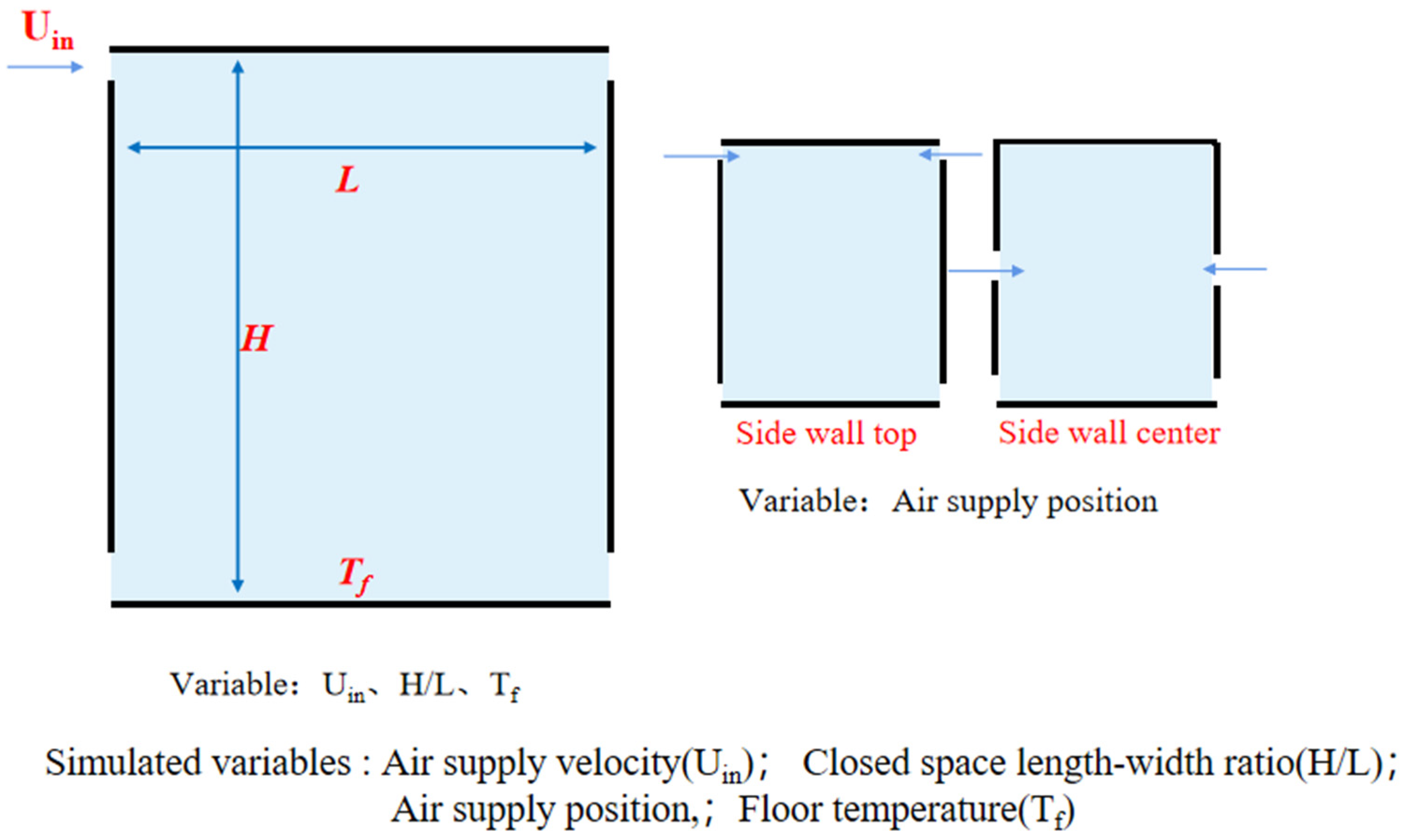
3.5. Numerical Case Setup
4. Result Analysis
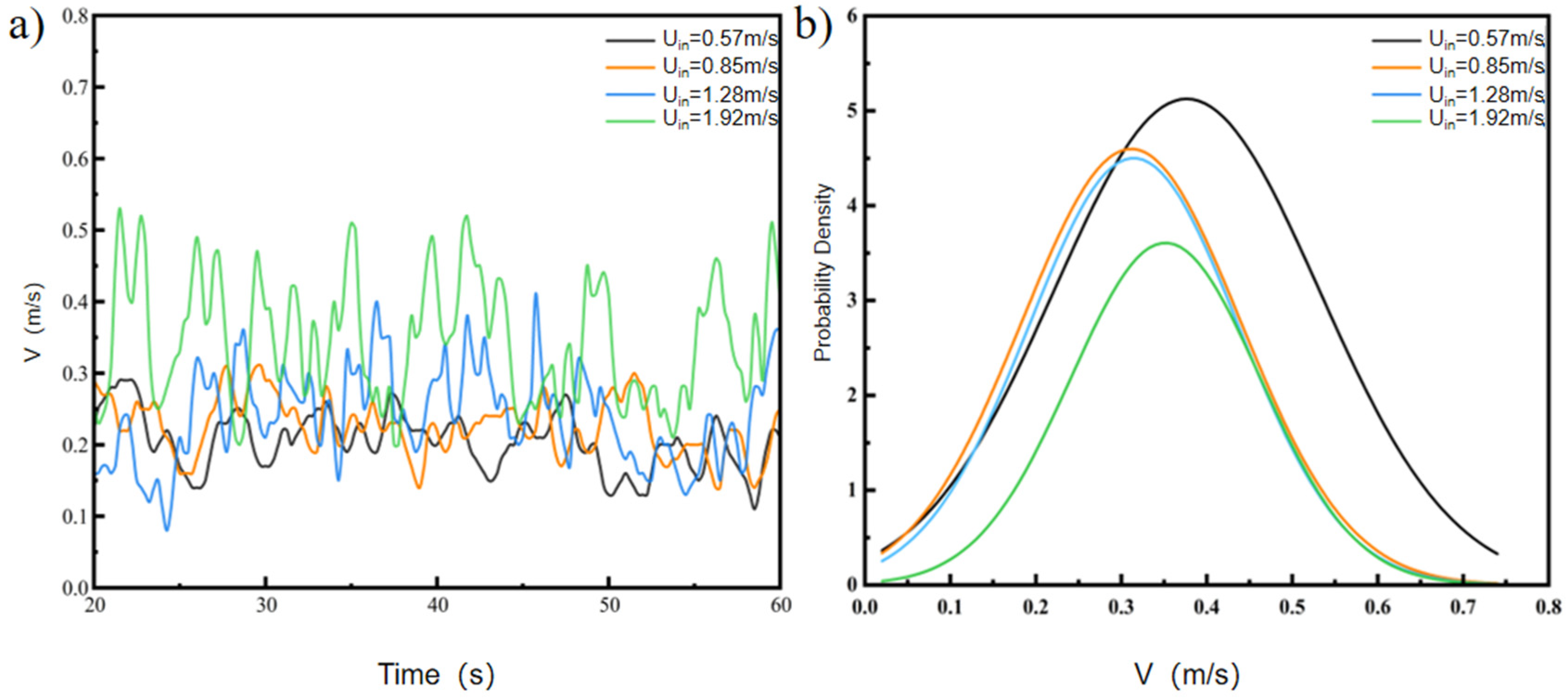
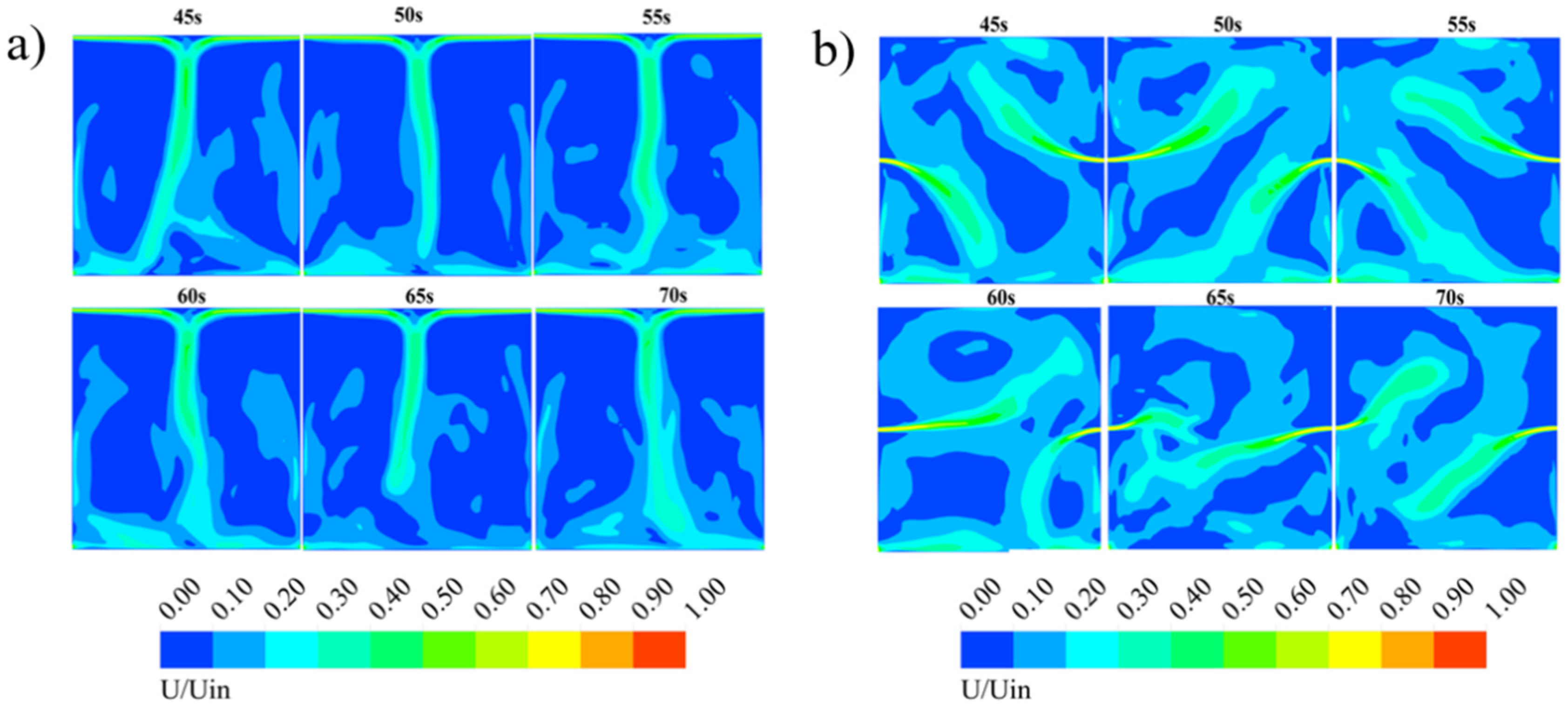
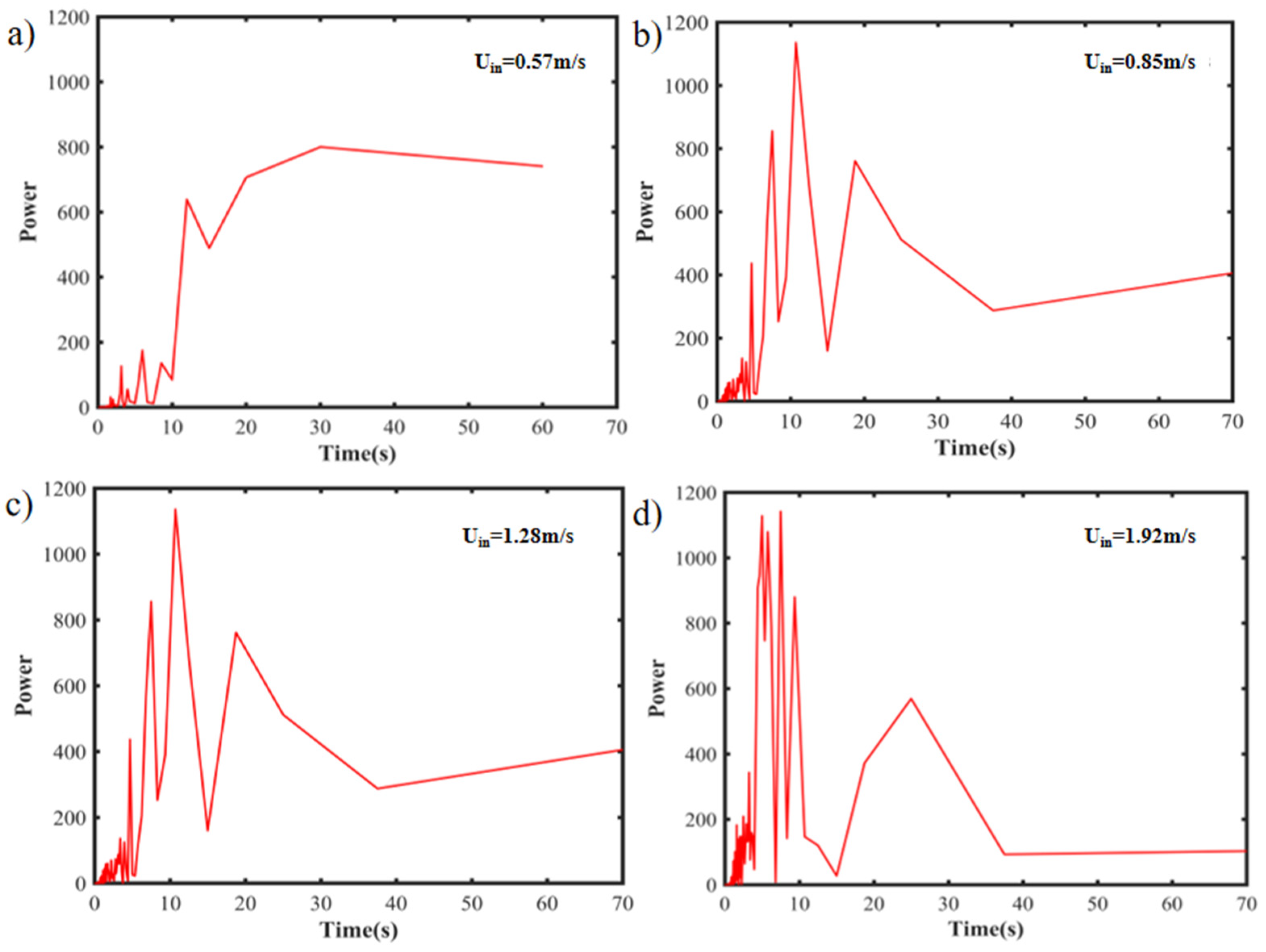
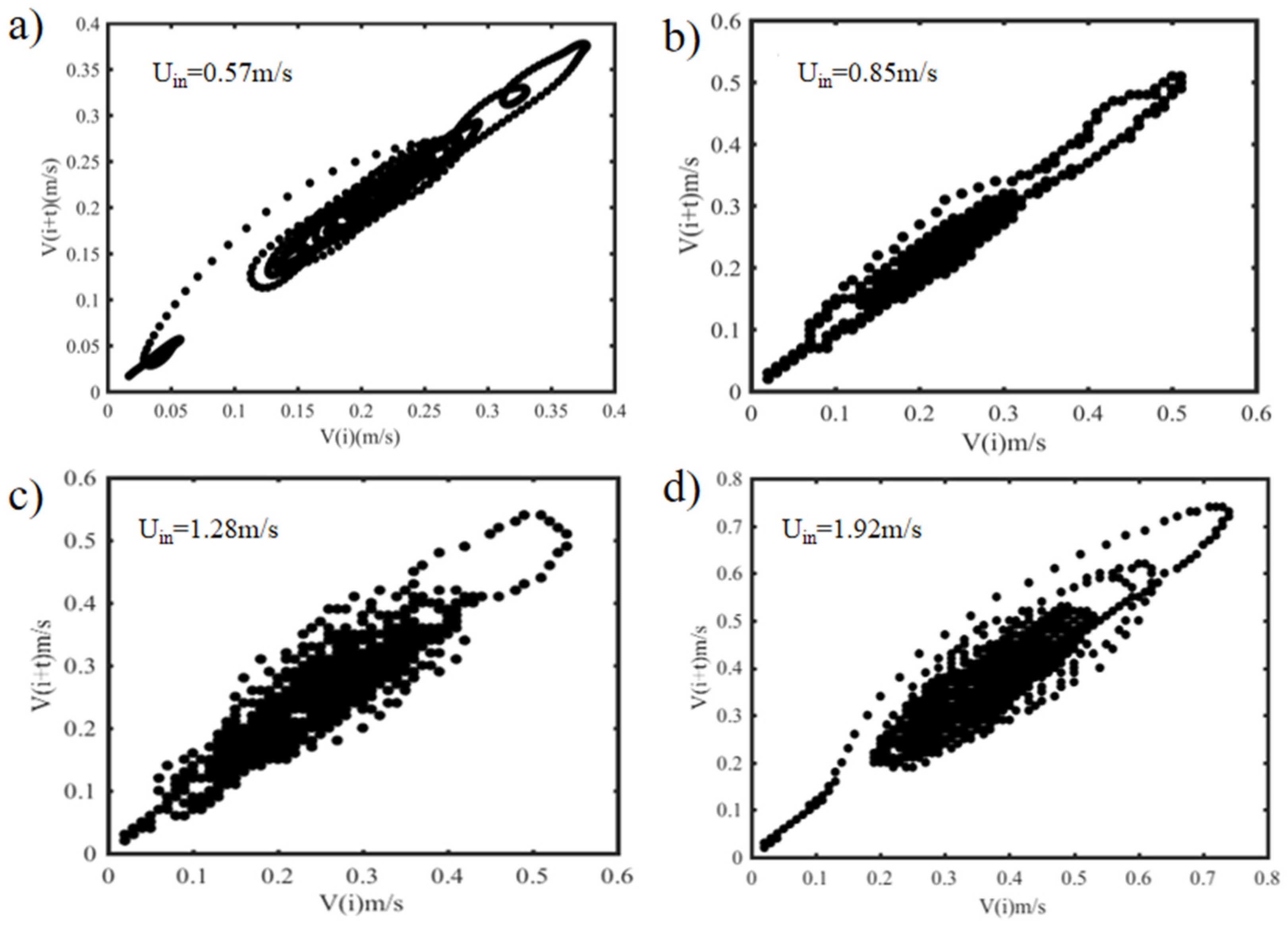
4.1. Different Air Supply Velocities
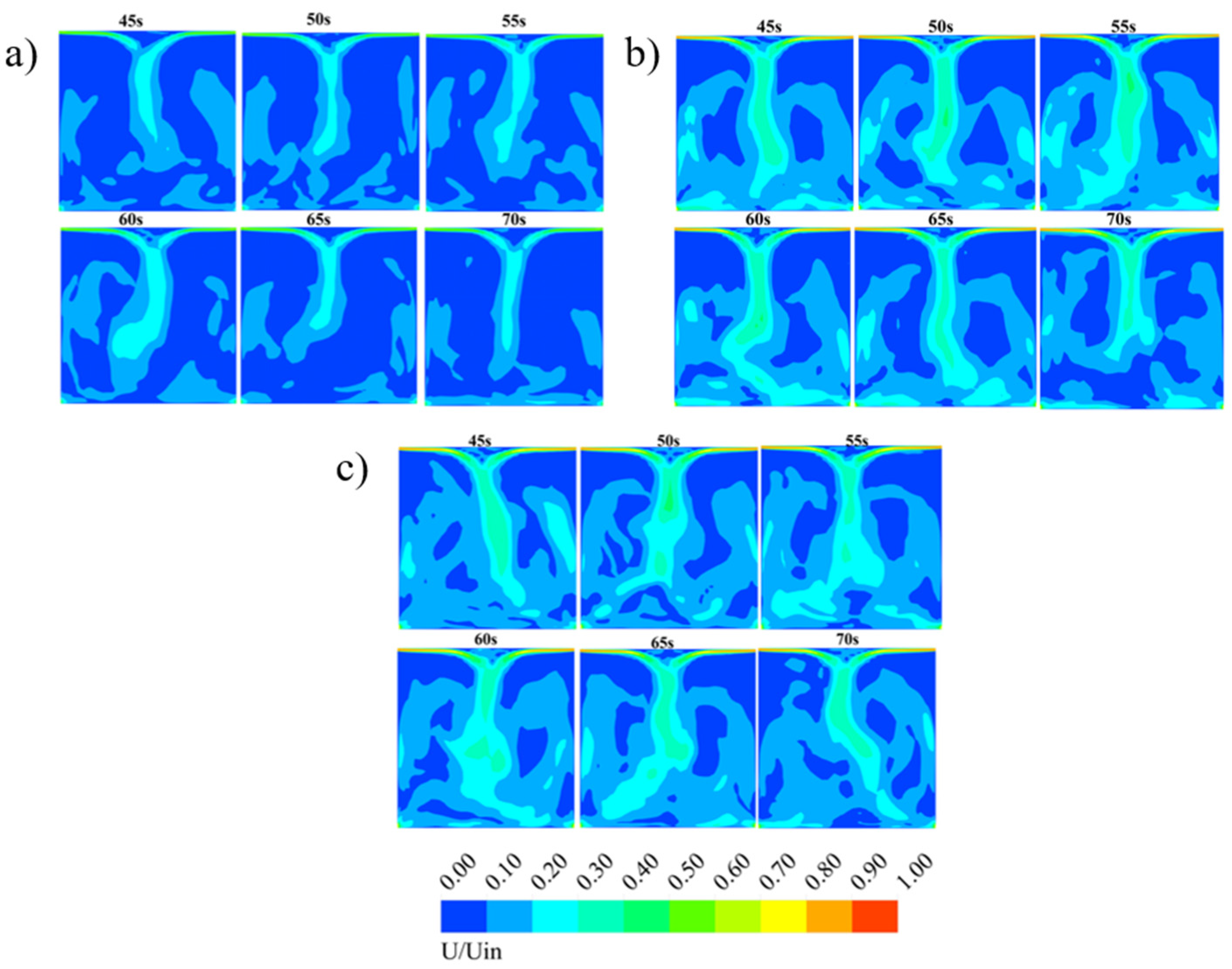
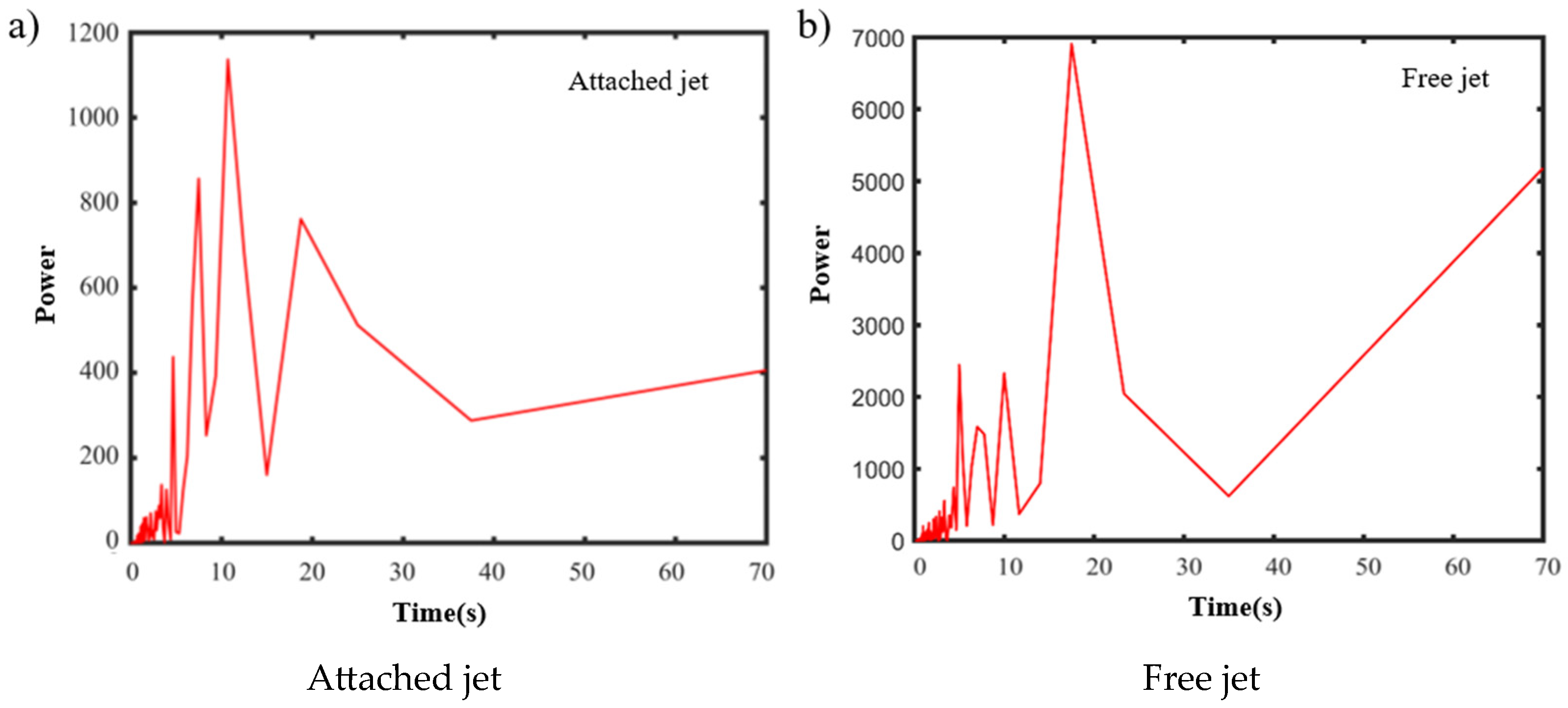
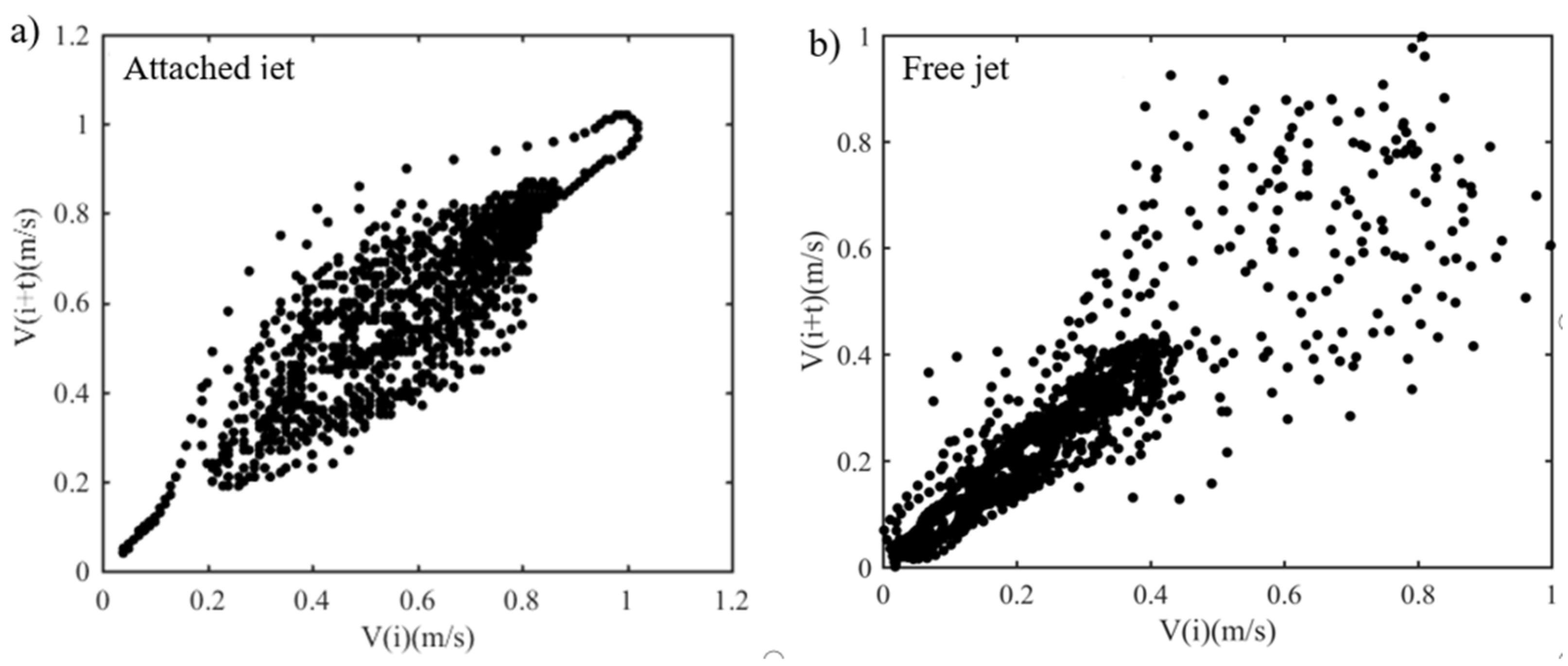
4.2. Impact of Air Supply Positions
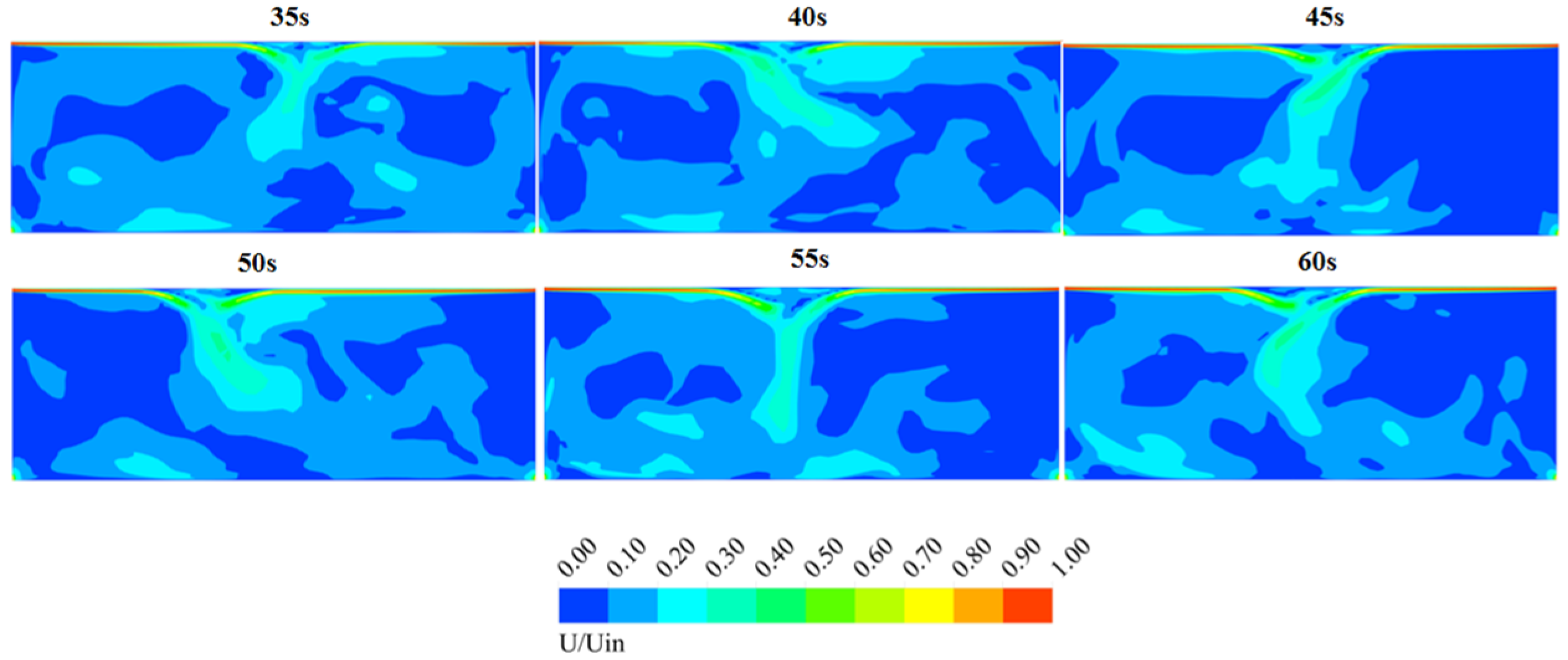
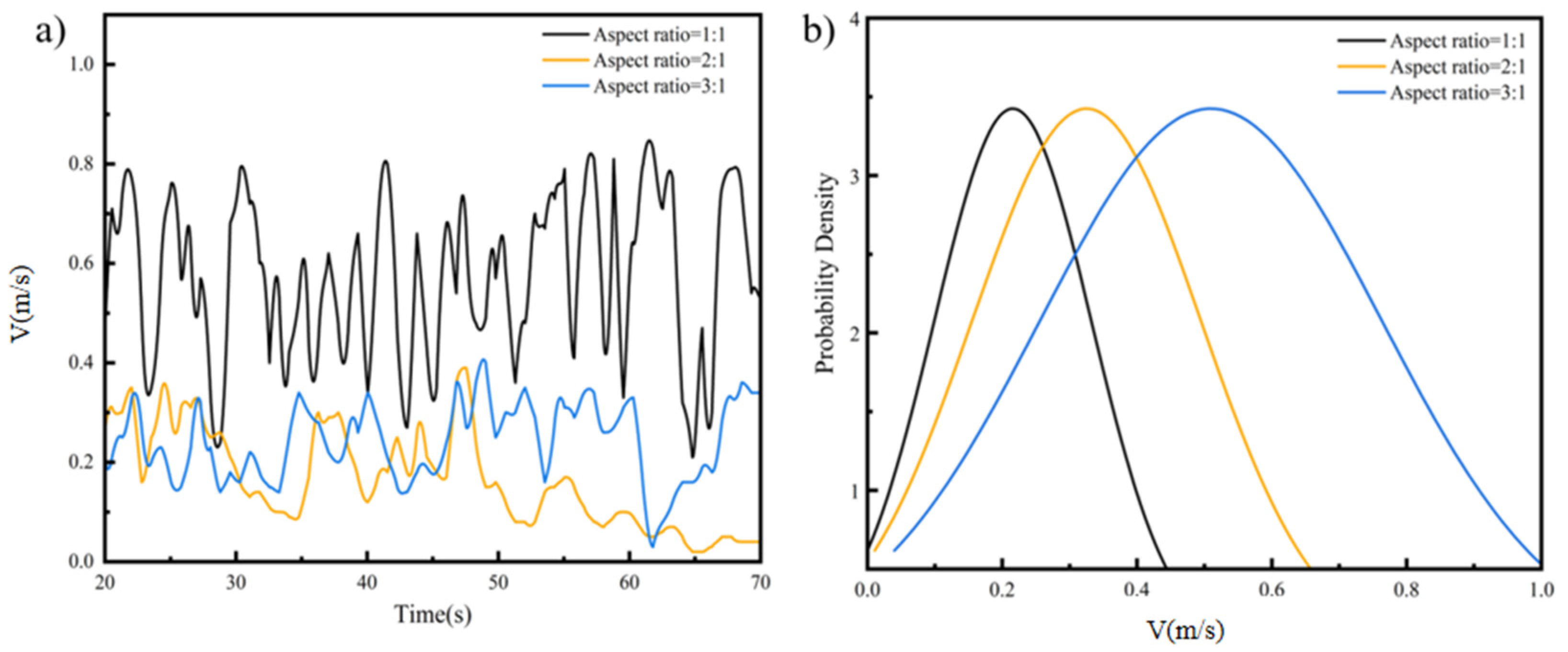
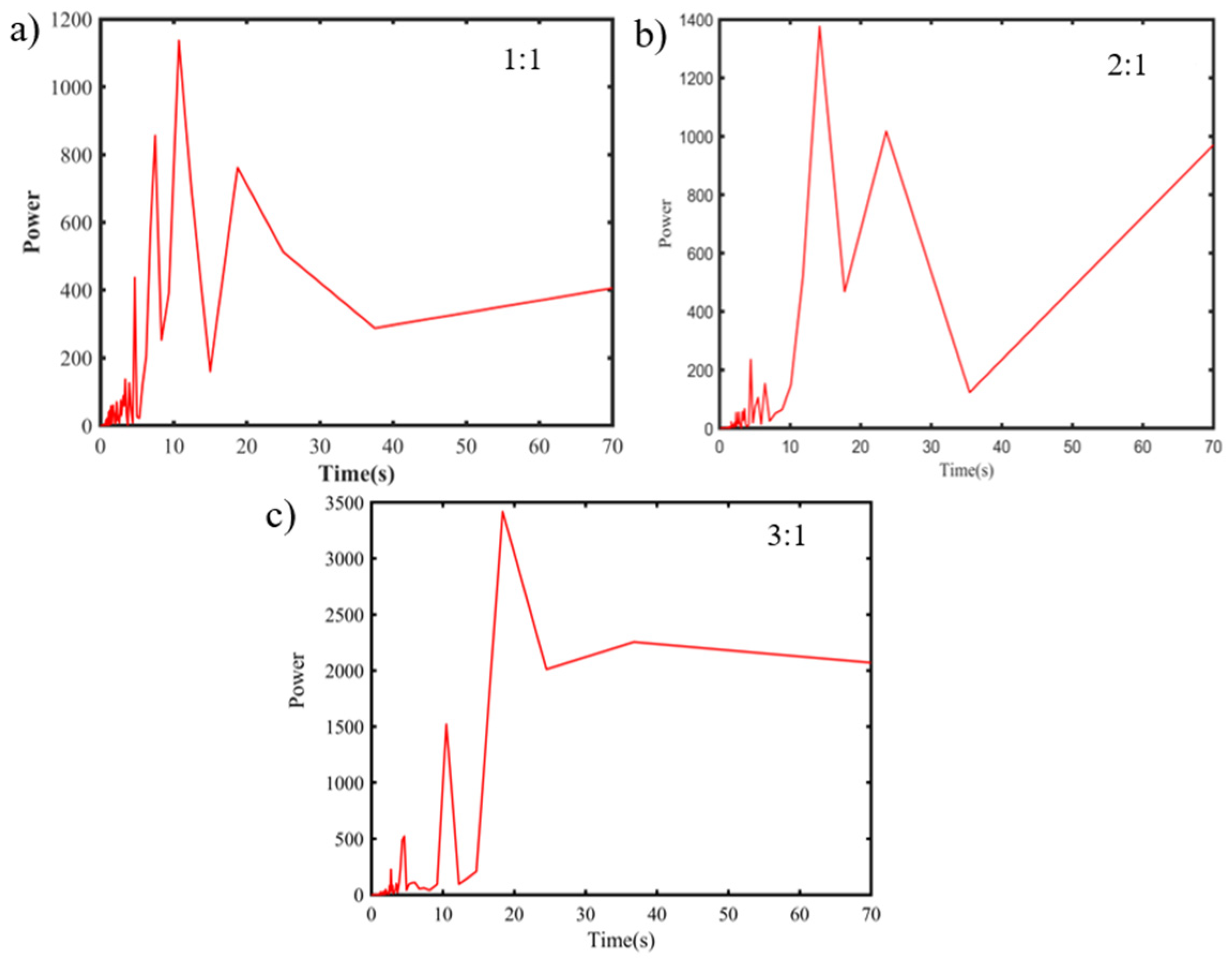
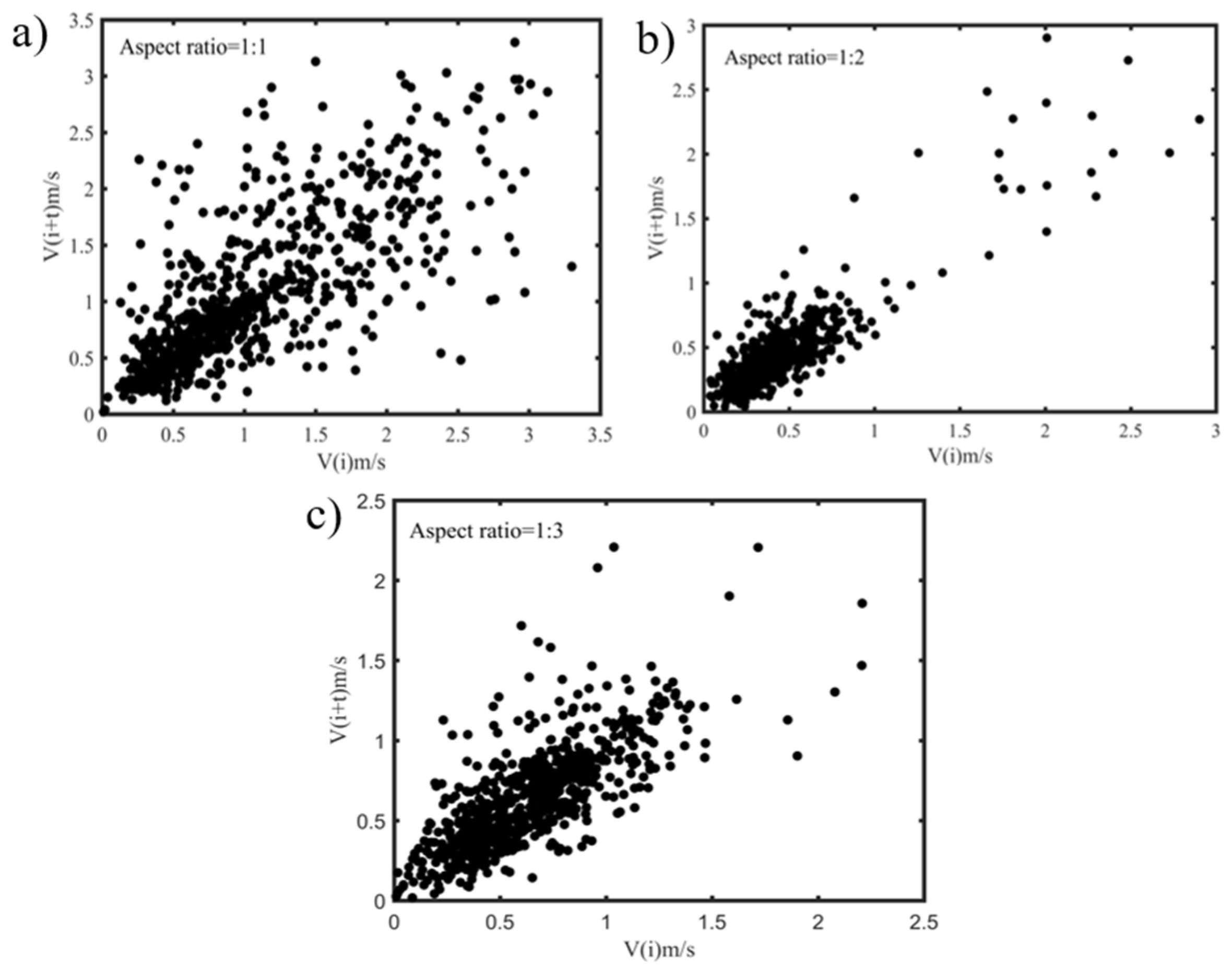
4.3. Impact of the Aspect Ratio
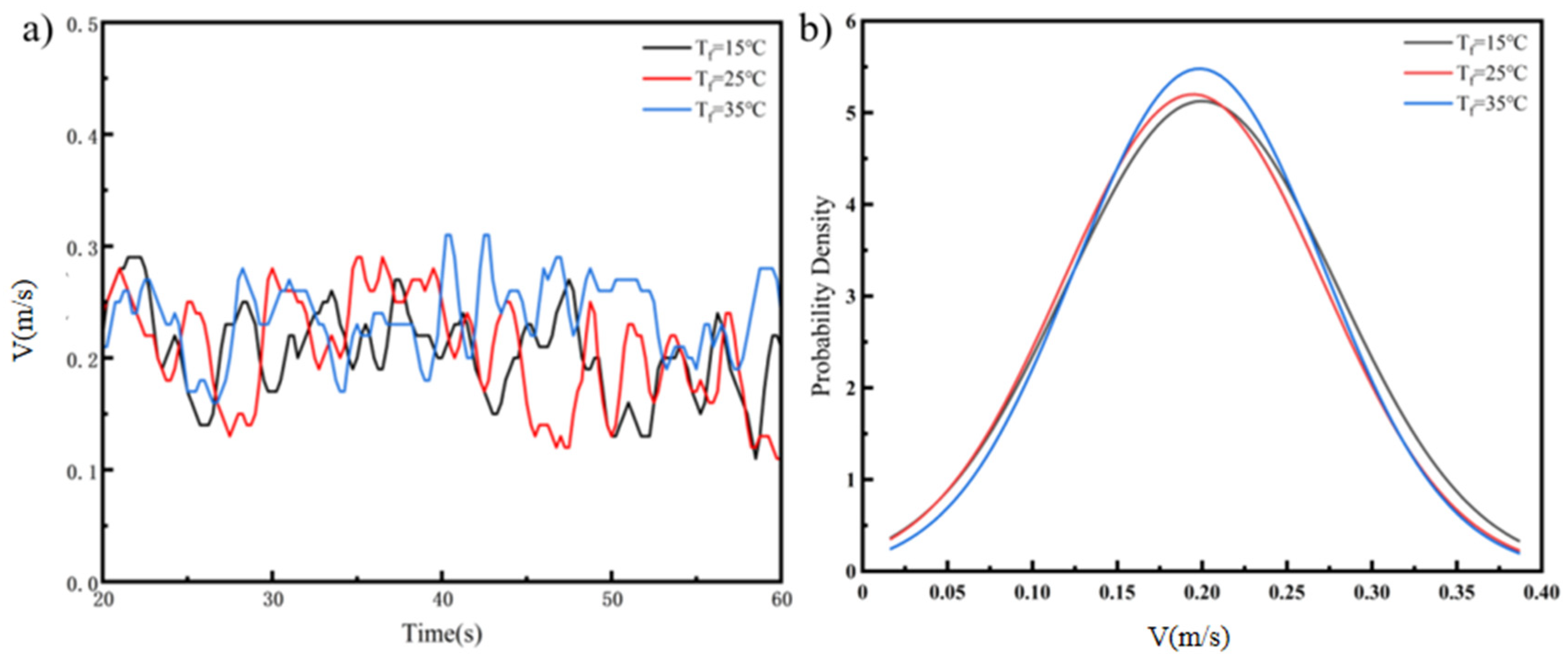
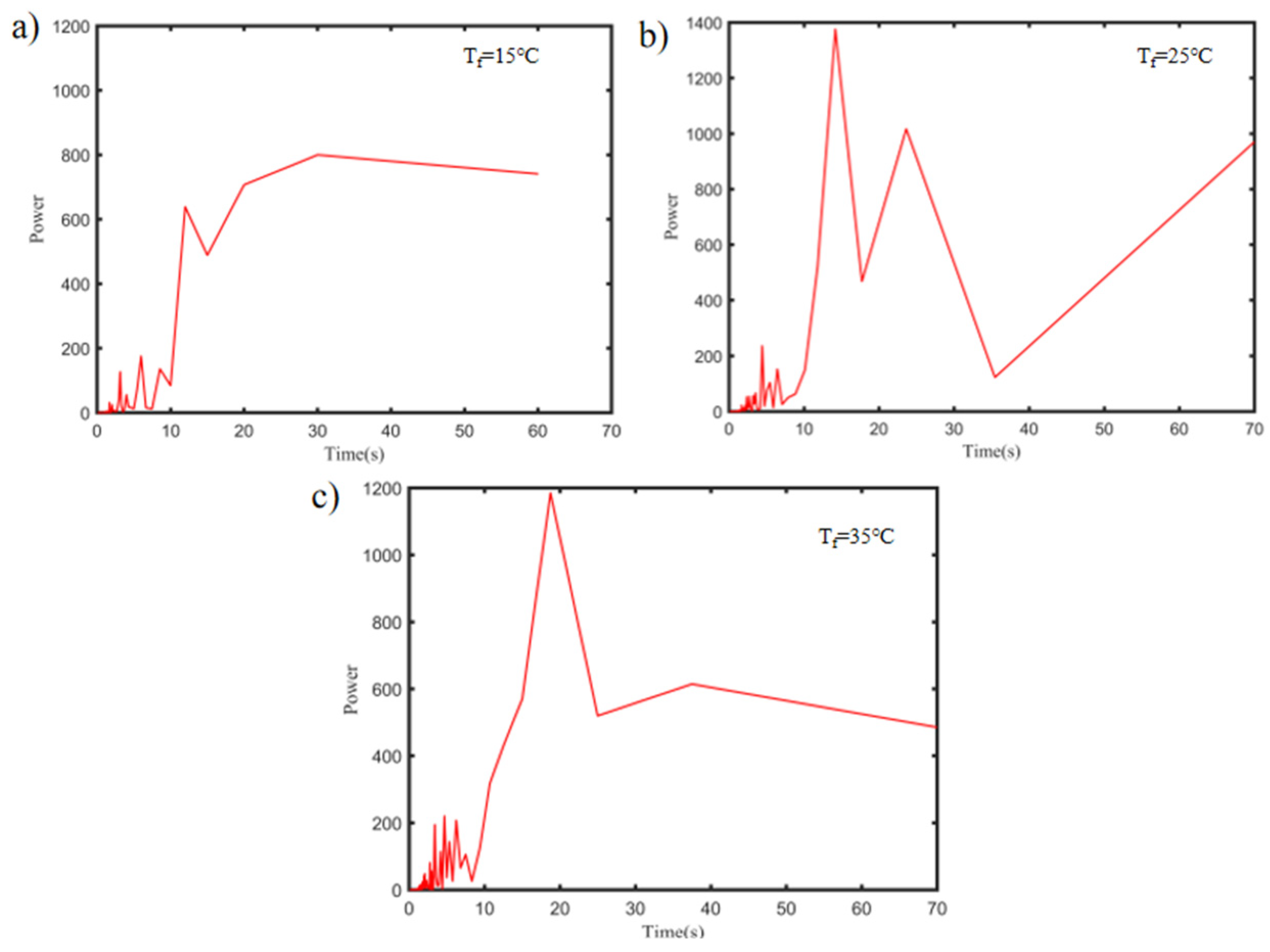
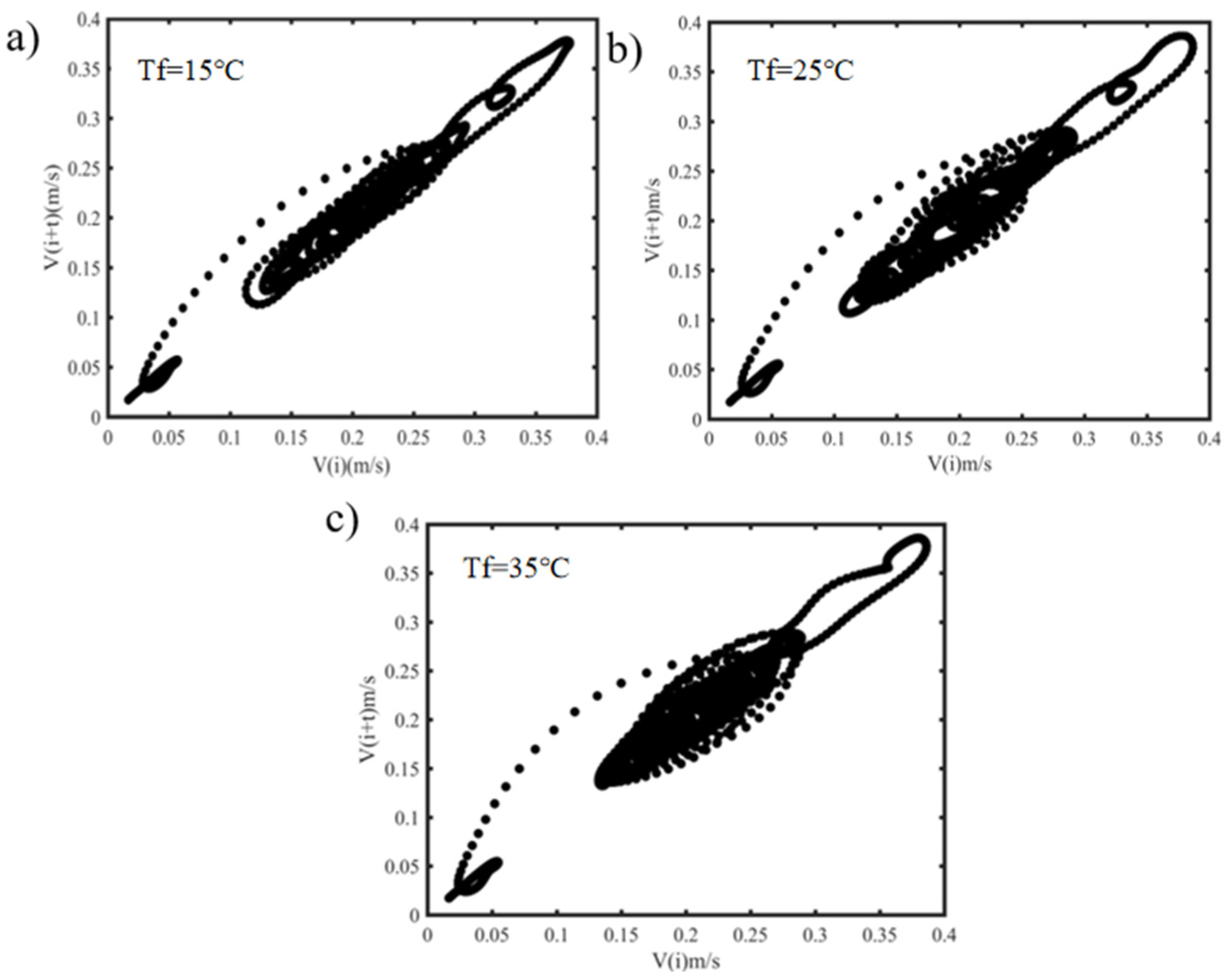
4.4. Impact of Floor Temperature
4.5. Periodicity Analysis
4.6. Phase Space Reconstruction Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- World Health Organization. Modes of Transmission of Virus Causing COVID-19: Implications for IPC Precaution Recommendations: Scientific Brief 29 March 2020; World Health Organization: Geneva, Switzerland, 2020.
- Allan, M.; Lièvre, M.; Laurenson-Schafer, H.; De Barros, S.; Jinnai, Y.; Andrews, S.; Stricker, T.; Formigo, J.P.; Schultz, C.; Perrocheau, A.; et al. The world health organization COVID-19 surveillance database. Int. J. Equity Health 2022, 21 (Suppl. S3), 167. [Google Scholar] [CrossRef] [PubMed]
- National Health Commission. Novel Coronavirus Pneumonia Diagnosis and Treatment Plan (Trial Version 9). Available online: http://www.gov.cn/zhengce/zhengceku/2022-03/15/content_5679257 (accessed on 15 March 2022).
- Tang, J.W.; Marr, L.C.; Li, Y.; Dancer, S.J. COVID-19 has redefined airborne transmission. BMJ 2021, 373, n913. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.; Zhao, B. Movement and transmission of human exhaled droplets/droplet nuclei. Kexue Tongbao/Chin. Sci. Bull. 2021, 66, 493–500. [Google Scholar] [CrossRef]
- Cao, G.; Awbi, H.; Yao, R.; Fan, Y.; Sirén, K.; Kosonen, R.; Zhang, J.J. A review of the performance of different ventilation and airflow distribution systems in buildings. Build. Environ. 2014, 73, 171–186. [Google Scholar] [CrossRef]
- Xu, C.; Yu, C.W.F. Prevention and control of COVID-19 transmission in the indoor environment. Indoor Built Environ. 2022, 31, 1159–1160. [Google Scholar] [CrossRef]
- Nielsen, P.V.; Restivo, A.; Whitelaw, J.H. The velocity characteristics of ventilated rooms. J. Fluids Eng. 1978, 100, 291–298. [Google Scholar] [CrossRef]
- Moureh, J.; Flick, D. Wall air–jet characteristics and airflow patterns within a slot ventilated enclosure. Int. J. Therm. Sci. 2003, 42, 703–711. [Google Scholar] [CrossRef]
- Moureh, J.; Flick, D. Airflow characteristics within a slot-ventilated enclosure. Int. J. Heat Fluid Flow 2005, 26, 12–24. [Google Scholar] [CrossRef]
- Li, W.F.; Huang, G.F.; Tu, G.Y.; Liu, H.F.; Wang, F.C. Experimental study of planar opposed jets with acoustic excitation. Phys. Fluids 2013, 25, 014108. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, J.; Chao, J.; Yang, C.; Chen, H. Evaluation of dynamic airflow structures in a single-aisle aircraft cabin mockup based on numerical simulation. Indoor Built Environ. 2022, 31, 398–413. [Google Scholar] [CrossRef]
- Denshchikov, V.A.; Kondrat’Ev, V.N.; Romashov, A.N.; Chubarov, V.M. Auto-oscillations of planar colliding jets. Fluid Dyn. 1983, 18, 460–462. [Google Scholar] [CrossRef]
- Rolon, J.C.; Veynante, D.; Martin, J.P.; Durst, F. Counter jet stagnation flows. Exp. Fluids 1991, 11, 313–324. [Google Scholar] [CrossRef]
- Champion, M.; Libby, P.A. Reynolds stress description of opposed and impinging turbulent jets. Part I: Closely spaced opposed jets. Phys. Fluids A Fluid Dyn. 1993, 5, 203–216. [Google Scholar] [CrossRef]
- Weersink, R. Experimental Study of the Oscillatory Interaction Between Two Free Opposed Turbulent Round Jets. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2010. [Google Scholar]
- Li, W.F.; Yao, T.L.; Liu, H.F.; Wang, F.C. Experimental investigation of flow regimes of axisymmetric and planar opposed jets. AIChE J. 2011, 57, 1434–1445. [Google Scholar] [CrossRef]
- Hassaballa, M.; Ziada, S. Self-excited oscillations of two opposing planar air jets. Phys. Fluids 2015, 27, 014109. [Google Scholar] [CrossRef]
- Ansari, A.; Chen, K.K.; Burrell, R.R.; Egolfopoulos, F.N. Effects of confinement, geometry, inlet velocity profile, and Reynolds number on the asymmetry of opposed-jet flows. Theor. Comput. Fluid Dyn. 2018, 32, 349–369. [Google Scholar] [CrossRef]
- Zhao, Y.; Brodkey, R.S. Averaged and time-resolved, full-field (three-dimensional), measurements of unsteady opposed jets. Can. J. Chem. Eng. 1998, 76, 536–545. [Google Scholar] [CrossRef]
- Johnson, D.A. Experimental and numerical examination of confined laminar opposed jets part I. Momentum imbalance. Int. Commun. Heat Mass Transf. 2000, 27, 443–445. [Google Scholar] [CrossRef]
- Pawlowski, R.P.; Salinger, A.G.; Shadid, J.N.; Mountziaris, T.J. Bifurcation and stability analysis of laminar isothermal counterflowing jets. J. Fluid Mech. 2006, 551, 117–139. [Google Scholar] [CrossRef]
- Kind, R.J.; Suthanthiran, K. The interaction of two opposing plane turbulent wall jets. J. Fluid Mech. 1973, 58, 389–402. [Google Scholar] [CrossRef]
- Wood, P.; Hrymak, A.; Yeo, R.; Johnson, D.; Tyagi, A. Experimental and computational studies of the fluid mechanics in an opposed jet mixing head. Phys. Fluids A Fluid Dyn. 1991, 3, 1362–1368. [Google Scholar] [CrossRef]
- Srisamran, C.; Devahastin, S. Numerical simulation of flow and mixing behavior of impinging streams of shear-thinning fluids. Chem. Eng. Sci. 2006, 61, 4884–4892. [Google Scholar] [CrossRef]
- Wu, Q.G.; Liang, X.G.; Chen, Z.J.; Ren, J.X. Numerical study on the bifurcation phenomenon of convective heat transfer in square cavity oblique inlet. J. Tsinghua Univ. Nat. Sci. Ed. 2000, 40, 102–105. [Google Scholar]
- Zou, K.; Yang, M.; Zhang, H.Y. Numerical study of mixed convection heat transfer in square space. J. Eng. Thermophys. 2001, 22, 207–210. [Google Scholar]
- Zheng, Z.H.; Zhang, J.L. Characteristics and numerical simulation of ventilation and air conditioning in manned spacecraft cabin. Build. Therm. Vent. Air Cond. 2005, 24, 86–90. [Google Scholar]
- Zhao, F.Y.; Liu, D.; Tang, G.F. Multiple steady fluid flows in a slot-ventilated enclosure. Int. J. Heat Fluid Flow 2008, 29, 1295–1308. [Google Scholar] [CrossRef]
- Liu, D.; Zhao, F.Y.; Tang, G.F. Nonunique convection in a three-dimensional slot-vented cavity with opposed jets. Int. J. Heat Mass Transf. 2010, 53, 1044–1056. [Google Scholar] [CrossRef]
- Zhao, M.; Yang, M.; Lu, M.; Zhang, Y. Evolution to chaotic mixed convection in a multiple ventilated cavity. Int. J. Therm. Sci. 2011, 50, 2464–2472. [Google Scholar] [CrossRef]
- Shishkina, O.; Wagner, C. A numerical study of turbulent mixed convection in an enclosure with heated rectangular elements. J. Turbul. 2012, 13, N22. [Google Scholar] [CrossRef]
- Körner, M.; Shishkina, O.; Wagner, C.; Thess, A. Properties of large-scale flow structures in an isothermal ventilated room. Build. Environ. 2013, 59, 563–574. [Google Scholar] [CrossRef]
- Yang, C.; Zhang, X.; Cao, X.; Liu, J.; He, F. Numerical simulations of the instantaneous flow fields in a generic aircraft cabin with various categories turbulence models. Procedia Eng. 2015, 121, 1827–1835. [Google Scholar] [CrossRef]
- Kandzia, C.; Mueller, D. Flow structures and Reynolds number effects in a simplified ventilated room experiment. Int. J. Vent. 2016, 15, 31–44. [Google Scholar] [CrossRef]
- Kandzia, C.; Mueller, D. Stability of large room airflow structures in a ventilated room. Int. J. Vent. 2018, 17, 1–16. [Google Scholar] [CrossRef]
- Thysen, J.H.; van Hooff, T.; Blocken, B.; Van Heijst, G.J.F. CFD simulations of two opposing plane wall jets in a generic empty airplane cabin: Comparison of RANS and LES. Build. Environ. 2021, 205, 108174. [Google Scholar] [CrossRef]
- Thysen, J.H.; van Hooff, T.; Blocken, B.; van Heijst, G. PIV measurements of opposing-jet ventilation flow in a reduced-scale simplified empty airplane cabin. Eur. J. Mech.-B/Fluids 2022, 94, 212–227. [Google Scholar] [CrossRef]
- Thysen, J.H.; van Hooff, T.; Blocken, B.; van Heijst, G.J.F. Instantaneous characteristics of interacting opposing plane jets in a generic enclosure measured with PIV. Exp. Fluids 2023, 64, 19. [Google Scholar] [CrossRef]
- Blay, D. Confined turbulent mixed convection in the presence of horizontal buoyant wall jet. In Fundamentals of Mixed Convection; HTD-Vol. 213; ASME: New York, NY, USA, 1992. [Google Scholar]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence, Warwick 1980: Proceedings of a Symposium Held at the University of Warwick 1979/80; Springer: Berlin/Heidelberg, Germany, 2006; pp. 366–381. [Google Scholar]
- Packard, N.H.; Crutchfield, J.P.; Farmer, J.D.; Shaw, R.S. Geometry from a time series. Phys. Rev. Lett. 1980, 45, 712. [Google Scholar] [CrossRef]
- Hara, T.; Shimizu, M.; Iguchi, K.; Odagiri, G. Chaotic fluctuation in natural wind and its application to thermal amenity. Nonlinear Anal. Theory Methods Appl. 1997, 30, 2803–2813. [Google Scholar] [CrossRef]
- Davidson, L.; Nielsen, P.V. Large eddy simulations of the flow in a three-dimensional ventilated room. Dep. Build. Technol. Struct. Eng. Indoor Environ. Technol. 1996, R9651, 59. [Google Scholar]
- Ezzouhri, R.; Joubert, P.; Penot, F.; Mergui, S. Large Eddy simulation of turbulent mixed convection in a 3D ventilated cavity: Comparison with existing data. Int. J. Therm. Sci. 2009, 48, 2017–2024. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, Q. Large eddy simulation of natural and mixed convection airflow indoors with two simple filtered dynamic subgrid scale models. Numer. Heat Transf. Part A Appl. 2000, 37, 447–463. [Google Scholar]







| Case | Supply Air | Air Velocity (m/s) | Aspect Ratio of the Enclosed Space | Ground Temperature (°C) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Attached jet | Free jet | 0.57 | 0.85 | 1.28 | 1.92 | 1:1 | 1:2 | 1:3 | 15 | 25 | 35 | |
| Case 1 | √ | √ | √ | √ | √ | √ | √ | |||||
| Case 2 | √ | √ | √ | √ | √ | |||||||
| Case 3 | √ | √ | √ | √ | √ | √ | ||||||
| Case 4 | √ | √ | √ | √ | √ | √ | ||||||
| Grid | |||
|---|---|---|---|
| Y+ | Coarse | Basic | Fine |
| Maximum | 5.1 | 3.4 | 2.8 |
| Average | 1.6 | 1.0 | 0.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Li, Y.; Ding, P.; Chen, H.; Zhang, Y.; Xing, Y. Analysis of Airflow Dynamics and Instability in Closed Spaces Ventilated by Opposed Jets Using Large Eddy Simulations. Buildings 2025, 15, 1707. https://doi.org/10.3390/buildings15101707
Wang C, Li Y, Ding P, Chen H, Zhang Y, Xing Y. Analysis of Airflow Dynamics and Instability in Closed Spaces Ventilated by Opposed Jets Using Large Eddy Simulations. Buildings. 2025; 15(10):1707. https://doi.org/10.3390/buildings15101707
Chicago/Turabian StyleWang, Congcong, Yu Li, Pengchao Ding, Hongbing Chen, Yan Zhang, and Yongjie Xing. 2025. "Analysis of Airflow Dynamics and Instability in Closed Spaces Ventilated by Opposed Jets Using Large Eddy Simulations" Buildings 15, no. 10: 1707. https://doi.org/10.3390/buildings15101707
APA StyleWang, C., Li, Y., Ding, P., Chen, H., Zhang, Y., & Xing, Y. (2025). Analysis of Airflow Dynamics and Instability in Closed Spaces Ventilated by Opposed Jets Using Large Eddy Simulations. Buildings, 15(10), 1707. https://doi.org/10.3390/buildings15101707






