Investigation on the Buckling Behavior of Normal Steel CHS Beam–Columns: A Revised Design Approach with Reliability Analysis

Abstract

This paper focuses on the buckling behavior of circular hollow section (CHS) beam–columns. The literature review highlights the need for further investigations to improve the accuracy of structural performance predictions and optimize the design guidelines for CHS beam–columns. A comprehensive parametric study was conducted using the developed finite element model, which included a total of 1400 simulations, including sections made from cold-formed and hot-finished steel. An assessment of the existing design provisions in Eurocode 3 is presented. Based on the results, a revised buckling design approach is proposed. The existing design provisions in Eurocode 3 provide conservative predictions on the buckling resistance of CHS beam–columns for both cold-formed and hot-finished sections. The proposed design approach demonstrated improved accuracy in predicting the buckling resistance, with mean predicted-to-test ratios and RMSE values of 0.99 and 8.1 kN for Class 1–2 sections, and 1.00 and 6.4 kN for Class 3–4 sections. Finally, a reliability analysis was conducted to assess the safety and reliability of the proposed design approach, resulting in a partial safety factor of 1.12 compared to 1.14 for Eurocode 3, indicating slightly reduced conservatism, while maintaining adequate safety levels.

1. Introduction

The use of circular hollow sections (CHSs) has increased considerably in recent years, largely due to their distinct aesthetic qualities and favorable mechanical characteristics. These attributes include outstanding performance under compressive forces, excellent resistance to bi-axial bending, and improved torsional rigidity [1,2,3]. CHSs are commonly employed in a range of structural applications, including columns, beams, arches, trusses, and wind turbine towers [4,5,6,7,8]. Their manufacturing process typically involves either cold-forming or hot-rolling techniques. Cold-formed CHSs display a continuous rounded stress–strain behavior, as a result of the cold-working effects introduced during their formation [9,10,11,12,13]. Conversely, hot-finished CHSs exhibit an initial linear elastic response, followed by a well-defined yield plateau and moderate strain hardening [14,15,16,17,18]. This research investigates the performance of beam–columns constructed from both cold-formed and hot-finished CHSs.

The design provisions for conventional carbon steel cross-sections are specified in EN 1993-1-1 [19], which classifies cross-sections based on their most slender element and employs the effective width method to account for local instability in the structural design [19,20,21]. According to these guidelines, Class 1 and 2 cross-sections are designed to resist loads up to their full plastic capacity, whereas Class 3 (semi-compact) cross-sections are limited according to their elastic resistance due to early local buckling. Class 4 sections have a lower capacity than the elastic cross-sectional capacity, because they are prone to local buckling before reaching the elastic resistance of the cross-section. This results in a discontinuity in the resistance function at the transition between Class 2 and Class 3 sections, leading to an underestimation of the load-carrying capacity for Class 3 sections, particularly when their local slenderness is close to the Class 2 threshold [22]. This limitation is especially significant for CHSs, as their high shape factor exacerbates the issue; therefore, the behavior of CHSs is the focus of this paper.

The behavior of circular hollow section (CHS) stub columns has been widely investigated, including sections made from hot-rolled [23,24,25,26,27] and cold-formed [28,29,30,31,32] steel. Additionally, there are several studies that have examined CHS beam members produced through the use of hot-rolling [33,34,35,36] and cold-forming [37,38,39,40] techniques. Research attention has also been paid to CHS beam–columns, particularly those fabricated from normal-strength steel [41,42,43,44,45,46] and high-strength steel [47,48,49,50,51,52,53], with a focus on their cross-sectional capacity. However, research on the buckling resistance of CHS beam–columns remains limited, with a notable scarcity of studies focusing on both high-strength steel [54,55,56] and normal-strength steel [57,58,59]. This literature review underscores the need for further investigations to improve the accuracy of structural performance predictions and optimize the design guidelines for CHS beam–columns, especially those made from normal-strength steel (i.e., with a yield strength below 460 N/mm²).

In this context, the present study aims to investigate the buckling resistance of normal-strength steel CHS beam–columns. Therefore, a finite element model is developed and validated using experimental data from previous studies. This model is then employed to perform a comprehensive parametric study. A total of 1400 simulations are developed, including both cold-formed and hot-finished sections. Furthermore, a revised buckling design approach is proposed to enhance the predictive accuracy of CHS member resistance. The results for the proposed method and the design provisions in prEN 1993-1-1 [19] are compared with those obtained from the finite element model. The safety of the proposed design approach is evaluated using reliability analysis.

2. Buckling Resistance of CHS Beam–Columns

2.1. The prEN 1993-1-1 Design Provisions

The design rules for the buckling resistance of CHS beam–columns in prEN 1993-1-1 [19] are discussed in this section. The classification limits in prEN 1993-1-1 [19] are 50, 70, and 90 for Class 1, Class 2, and Class 3 sections, respectively, as presented in Equation (1). In which, ${\mathrm{d}}_{\mathrm{e}}$ is the outer diameter of the section, $\mathrm{t}$ is the section thickness, and ${\mathrm{f}}_{\mathrm{y}}$ is the yield strength. The characteristic resistance for compression (${\mathrm{N}}_{\mathrm{R}\mathrm{k}}$) is equal to $\mathrm{A}\times {\mathrm{f}}_{\mathrm{y}}$, where $\mathrm{A}$ is the cross-sectional area for Class 1–3 sections or the effective cross-sectional area for Class 4 sections. The characteristic bending resistance (${\mathrm{M}}_{\mathrm{R}\mathrm{k}}$) is determined using the section modulus, specifically the plastic (${\mathrm{W}}_{\mathrm{p}\mathrm{l}}$), elastic (${\mathrm{W}}_{\mathrm{e}\mathrm{l}}$), and effective (${\mathrm{W}}_{\mathrm{e}\mathrm{f}\mathrm{f}}$) section modulus for Class 1–2, Class 3, and Class 4 sections, respectively.

$${\displaystyle \frac{{\mathrm{d}}_{\mathrm{e}}}{\mathrm{t}\frac{235}{{\mathrm{f}}_{\mathrm{y}}}}}$$

(1)

The designed buckling resistance for CHS beam–columns subjected to compression (${\mathrm{N}}_{\mathrm{E}\mathrm{d}}$) and bending (${\mathrm{M}}_{\mathrm{E}\mathrm{d}}$) is obtained using the interaction relationship, presented in Equation (2).

$${\displaystyle \frac{{\mathrm{N}}_{\mathrm{E}\mathrm{d}}}{{\mathrm{\chi }}_{\mathrm{c}}\frac{{\mathrm{N}}_{\mathrm{R}\mathrm{k}}}{{\mathrm{\gamma }}_{\mathrm{M}1}}}}+{\mathrm{k}}_{\mathrm{y}\mathrm{y}}{\displaystyle \frac{{\mathrm{M}}_{\mathrm{E}\mathrm{d}}}{\frac{{\mathrm{M}}_{\mathrm{R}\mathrm{k}}}{{\mathrm{\gamma }}_{\mathrm{M}1}}}}\le 1.0$$

(2)

$${\mathrm{\chi }}_{\mathrm{c}}={\displaystyle \frac{1}{\mathrm{\varnothing }+\sqrt{{\mathrm{\varnothing }}^2-{\mathrm{\lambda }}_{\mathrm{c}}^2}}}\le 1.0$$

(3)

$$\mathrm{\varnothing }=0.5\left[1+\mathrm{\alpha }\left({\mathrm{\lambda }}_{\mathrm{c}}-0.2\right)+{\mathrm{\lambda }}_{\mathrm{c}}^2\right]$$

(4)

$${\mathrm{\lambda }}_{\mathrm{c}}=\sqrt{{\displaystyle \frac{{\mathrm{N}}_{\mathrm{R}\mathrm{k}}}{{\mathrm{N}}_{\mathrm{c}\mathrm{r}}}}}$$

(5)

where ${\mathrm{\chi }}_{\mathrm{c}}$ is the flexural buckling reduction factor, ${\mathrm{\lambda }}_{\mathrm{c}}$ is the member’s relative slenderness, ${\mathrm{N}}_{\mathrm{c}\mathrm{r}}$ is the Euler buckling load, and $\mathrm{\alpha }$ represents the imperfection factor for the CHS taken to be equal to 0.13 for hot-finished and 0.49 for cold-formed steel. Moreover, ${\mathrm{\gamma }}_{\mathrm{M}1}$ is the partial safety factor and is taken as the unity for carbon steel [19].

The interaction factor (${\mathrm{k}}_{\mathrm{y}\mathrm{y}}$) for the CHS is determined, the details of which are shown in

Table 1. Interaction factors, ($k_{yy}$), given in prEN 1993-1-1 [19].

Class	${\mathit{\lambda }}_{\mathit{c}} < 1$	${\mathit{\lambda }}_{\mathit{c}} \ge 1$
Class 1–2	$k_{yy}=C_m\left[1+\left({\lambda }_c-0.20\right)n_y\right]$	$k_{yy}=C_m\left[1+0.8n_y\right]$
Class 3–4	$k_{yy}=C_m\left[1+0.6{\lambda }_c{n}_y\right]$	$k_{yy}=C_m\left[1+0.6n_y\right]$

. The equivalent uniform moment parameter (${\mathrm{C}}_{\mathrm{m}}$) is assumed to be 1 for uniform bending. Moreover, ${\mathrm{n}}_{\mathrm{y}}$ represents the ratio of the design-to-characteristic flexural compression load, calculated as shown in Equation (6).

$${\mathrm{n}}_{\mathrm{y}}={\displaystyle \frac{{\mathrm{N}}_{\mathrm{E}\mathrm{d}}}{{\mathrm{\chi }}_{\mathrm{c}}\frac{{\mathrm{N}}_{\mathrm{R}\mathrm{k}}}{{\mathrm{\gamma }}_{\mathrm{M}1}}}}$$

(6)

2.2. Revised Buckling Design Approach

Following the analysis and discussion presented in Section 4, a revised buckling design approach for CHS beam–columns is proposed. This approach incorporates two primary improvements: (a) a revised imperfection factor ($k_{yy}$) and (b) an extended plateau length in terms of the design parameter, ${\mathrm{\varnothing }}_{\mathrm{m}\mathrm{o}\mathrm{d}}$. These modifications are detailed in

Table 2. Proposed interaction factors ($k_{yy}$).

Class	${\mathit{\lambda }}_{\mathit{c}} < 1$	${\mathit{\lambda }}_{\mathit{c}} \ge 1$
Class 1–2	$k_{yy}=C_m\left[1+1.5\left({\lambda }_c-0.3\right)n_y\right]$	$k_{yy}=C_m\left[1+0.7n_y\right]$
Class 3–4	$k_{yy}=C_m\left[1+0.1{\lambda }_c{n}_y\right]$	$k_{yy}=C_m\left[1+0.1n_y\right]$

, with the corresponding expressions provided in Equation (7). The coefficients employed in the revised design approach were determined through statistical optimization, aiming to minimize prediction errors and enhance the accuracy of the model’s outcomes. It is indicated that the revised buckling design approach outperforms the current EC3 approach in regard to both cold-formed and hot-finished sections.

$${\mathrm{\varnothing }}_{\mathrm{m}\mathrm{o}\mathrm{d}}=0.5\left[1+\mathrm{\alpha }\left({\mathrm{\lambda }}_{\mathrm{c}}-0.4\right)+{\mathrm{\lambda }}_{\mathrm{c}}^2\right] \mathrm{for} \mathrm{Class} 1–4$$

(7)

3. Finite Element Model

3.1. Development

To examine the behavior of CHS beam–columns, a finite element (FE) model was developed using Abaqus software 2016 [60]. The model is based on the approach that was successfully validated by Meng and Gardner [61], which showed a high level of accuracy in capturing the response of CHS beam–columns in terms of their ultimate capacity, load–deflection response, and buckling behavior [61]. The model was created using a Riks solver solution, available in the Abaqus software [60], which is suitable for geometrically and materially nonlinear analyses. The element was modeled using a four-noded shell element, with reduced integration (S4R) [61,62]. A finer mesh was applied at the mid-span to accurately capture the buckling response [61]. Symmetrical boundary conditions were applied to the longitudinal plane and mid-cross-sectional plane. A full-length finite element model was used for validation to capture potential asymmetric buckling behavior, whereas a quarter model was employed in the parametric study to enhance the computational efficiency by exploiting the symmetry of the geometry and loading. The initial imperfections were based on test measurements, with additional imperfection amplitudes introduced parametrically to evaluate their effect on the structural response, as shown in

Table 3. A comparison of the FE model’s ultimate load capacity and the test results in [61].

	NFE/Ntest
	Measured ωg	ωg = Lcr/500	ωg = Lcr/1000	ωg = Lcr/2000
Mean	0.982	0.956	0.970	0.980
CoV	0.027	0.034	0.030	0.026

. The steel material was modeled using an elastic–perfectly plastic stress–strain relationship, based on Eurocode 3 [19]. A more detailed description of the FE model development process can be found in [61].

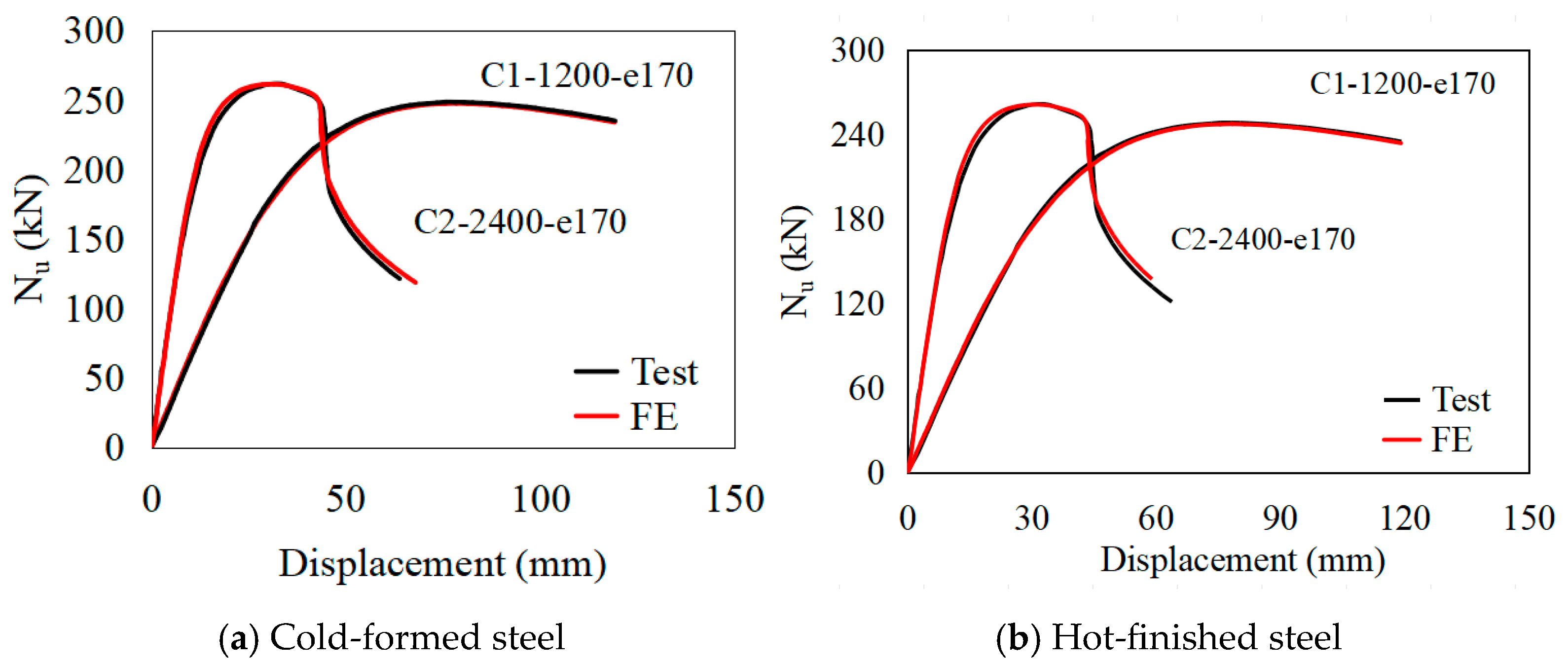
3.2. Validation

The FE models were validated by comparing the load–deflection relationship, the ultimate bearing capacity, and the failure modes with experimental data. Detailed geometric information on the experimental specimens used in the validation process can be found in [61]. Figure 1 presents a comparison of the numerical and experimental load–mid-height lateral displacement curves for a selected specimen. It is important to note that the four specimens presented in Figure 1, two with cold-formed steel and two with hot-rolled steel, are only representative examples; additional specimens were also utilized during the model validation process to ensure broader reliability and robustness. The comparison between the finite element (FE) predictions and the experimental results, as illustrated in the figure, demonstrates strong agreement in regard to the key response characteristics. The initial stiffness observed in both the test and the FE curves is well-matched, indicating that the model captures the early elastic behavior of the specimens effectively. Moreover, the FE model accurately replicates the ultimate buckling resistance, with only minor deviations in the peak load values. Notably, the FE simulation also captures the post-peak softening behavior and the associated reduction in axial capacity, reflecting the realistic progression of failure. The consistency in the displacement trends and peak strength between the two curves validates the robustness of the model. These results confirm that the developed FE model is reliable in simulating both the load–displacement response and the failure mode, providing a useful tool for predicting structural performance under similar conditions.

As illustrated in Figure 2, the failure mode captured by the FE simulation closely resembles the experimental observation. Both the physical test (Figure 2a) and the numerical model (Figure 2b) exhibit a pronounced global buckling pattern, with a clear curvature concentrated near the mid-height of the member. The similarity in the deformation shape and buckling location indicates that the FE model accurately simulates the instability behavior of the tested specimen. This agreement not only validates the effectiveness of the material modeling and boundary conditions applied in the simulation, but also reinforces the FE model’s ability to predict realistic failure mechanisms.

In addition, the accuracy of the ultimate capacity was assessed by incorporating four different global geometric imperfection amplitudes (ω_g), through a comparative analysis between the numerical results (N_FE) and the corresponding values from the experimental tests (N_test), as presented in Table 3. The geometric imperfection with a critical length of (Lcr)/1000 provided accurate predictions, while also minimizing the computational time [61]. There is an excellent level of agreement with the corresponding experimental values, with the mean value and coefficient of variation (CoV) values of the N_u,FE/N_u,test ratio being 0.97 and 0.03, respectively. In summary, the FE model is found to be efficient and reliable in regard to predicting the buckling resistance of CHS beam–columns.

3.3. Parametric Studies

A total of 1400 numerical models were constructed to generate extensive data on the buckling resistance of cold-formed (694) and hot-finished (706) CHS beam–columns. This study examined a wide range of influential parameters, including the eccentricity (e), diameter-to-thickness ratio, effective length, and yield stress, as key factors in the design of CHS beam–columns (e.g., [43,61]). The buckling behavior of structural members is influenced by several key parameters, including the D_e/t ratio, yield strength (f_y), critical length (L_cr), and eccentricity (e). Each of these factors plays a distinct role in determining the ultimate buckling capacity of a section. For instance, a higher D_e/t ratio indicates thinner walls relative to the diameter, making the section more prone to local buckling under axial loads, due to its reduced stiffness and stability. Conversely, a lower D_e/t ratio suggests a stockier, more compact section, with greater resistance to local deformation and buckling. In addition, a higher yield strength generally increases the buckling capacity, as the material can resist higher stresses before yielding. However, in slender sections, a higher yield strength can sometimes amplify local buckling effects, especially if not accompanied by sufficient stiffness (i.e., a low D_e/t). Moreover, longer members have greater slenderness and are, therefore, more susceptible to global buckling under axial loads. Finally, eccentric loading introduces bending moments, in addition to axial compression, increasing the potential combined buckling failure.

Table 4. The range of key parameters used in the parametric study.

	De/t	Lcr (mm)	fy (MPa)	e (mm)
Mean	34.9	2894.7	355	55.16
Maximum	84.9	5311.6	355	344.93
Minimum	10.0	522.0	355	2.70

summarizes the range of parameters used in this study. The parametric study employed is discussed in the subsequent section to evaluate the accuracy of the revised buckling design approach and the design provisions in the EC3 design rules [19].

4. Results and Discussion

The modified buckling design approach proposed, along with the design rules in prEN 1993-1-4 (EC3) [19], is evaluated by comparing the predicted resistances with the corresponding values from the FE model. In order to present an accurate comparison with the results from the FE model, the analysis is performed based on the characteristic resistance. Various statistical metrics are used, including the mean ratio of the predicted-to-FEM buckling resistance (N_u/N_FEM), standard deviation (SD), coefficient of variation (CoV), root mean square error (RMSE), and the maximum and the minimum relative errors, as shown in

Table 5. Statistical analysis of the predicted ultimate buckling resistance in comparison with the corresponding FE results.

	EC3		Proposed
	Class 1–2	Class 3–4	Class 1–2	Class 3–4
Mean	0.98	0.91	0.99	1.00
SD	0.05	0.07	0.04	0.09
CoV	0.05	0.08	0.04	0.09
RMSE	11.82	8.39	8.11	6.39
Max relative error (%)	6.61	1.41	7.6	11.3
Min relative error (%)	−17.42	−29.7	−13.5	−28.1

. As shown in the table, the absolute value of the minimum relative error is consistently greater than that of the maximum relative error, which reflects the conservative nature of the proposed design method. The modified buckling design approach provides more accurate and consistent predictions of buckling resistance compared to the EC3 rules. It is acknowledged that the revised design equations may, in some cases, slightly overestimate the buckling resistance. This limitation has been noted to ensure appropriate application of the proposed method, despite its overall improved accuracy and consistency, as demonstrated by the statistical evaluation. A more detailed analysis of cold-formed and hot-finished sections is presented separately, in the following sections.

4.1. Cold-Formed Sections

Figure 3 presents a comparison between the predicted ultimate buckling capacities (N_u) from the proposed design model and the corresponding FE simulation results (N_FEM), for all four cross-section classes. The data show that the proposed model maintains a high level of agreement with the FE results across all the classes, with most predictions falling within the ±10% bounds, indicating strong predictive accuracy. In contrast, the EC3 predictions tend to underestimate the buckling capacity, especially for Classes 1 and 2, wherein the proposed model clearly outperforms the EC3predictions in terms of both accuracy and consistency. The reduced scatter and tighter clustering around the ideal diagonal line further confirm the robustness of the proposed formulation. This demonstrates that the proposed model provides a reliable and improved alternative to the EC3 rules for predicting the ultimate buckling resistance of stainless steel members.

The findings indicate that both methods yield conservative predictions. For EC3, the mean N_u/N_FEM values are 0.95 for Class 1–2 sections and 0.89 for Class 3–4 sections, whereas the modified approach improves these predictions to 0.97 and 0.99, respectively. The statistical measures for EC3 are as follows: for Class 1–2 sections, the standard deviation (SD), coefficient of variation (CoV), root mean square error (RMSE), and the maximum and minimum relative errors are 0.05, 0.06, 15.2 kN, 5.6%, and −22.6%, respectively. For Class 3–4 sections, these values are 0.08, 0.09, 10.7 kN, −1.8%, and −33%.

For the modified approach, the corresponding values are 0.04, 0.04, 9.0 kN, 7.6%, and −17.7% for Class 1–2 sections, and 0.1, 0.1, 7.6 kN, 9.3%, and −30.6% for Class 3–4 sections. These results highlight that the revised approach significantly improves the accuracy of the predicted buckling resistance, while maintaining a conservative estimation.

4.2. Hot-Finished Sections

Figure 4 presents a comparison of the predicted ultimate buckling capacities obtained using the proposed method and Eurocode 3 (EC3) with the finite element model (FEM) results for hot-finished sections, classified into section Classes 1 through to 4. The plots show the relationship between the FEM results (x-axis) and the predicted capacities (y-axis), with the diagonal line representing perfect agreement and dashed lines indicating ±10% and ±20% deviations. In all classes, the proposed method exhibits closer alignment with the FEM results than EC3, which tends to slightly underestimate the capacity, particularly in regard to Classes 3 and 4. The clustering of the data points for the proposed method within the ±10% margin highlights its improved accuracy and consistency across all the section classes. Overall, the results suggest that the proposed method is more reliable than EC3 for predicting the buckling performance of hot-finished structural sections.

In general, conservative predictions are observed for both the EC3 and the revised buckling design approach. With the mean value of the N_u/N_FEM for EC3 being 1.01 and 0.92 for Class 1–2 and Class 3–4 sections, respectively, whereas the modified approach improves these values to 1.00 and 1.01 for Class 1–2 and Class 3–4 sections, respectively.

The statistical measures for EC3 are as follows: for Class 1–2 sections, the standard deviation (SD), coefficient of variation (CoV), root mean square error (RMSE), and the maximum and minimum relative errors are 0.04, 0.04, 8.5 kN, 7.7%, and −12.3%. For Class 3–4 sections, these values are 0.07, 0.07, 6.0 kN, 4.6%, and −26.4%. For the modified approach, the corresponding values are 0.03, 0.03, 7.2 kN, 7.6%, and −9.2% for Class 1–2 sections, and 0.09, 0.08, 5.2 kN, 13.3%, and −25.5% for Class 3–4 sections. These results indicate that the modified approach provides excellent predictions on the buckling resistance of hot-finished sections, achieving greater accuracy than EC3.

5. Reliability Analysis

This section presents the reliability analysis, conducted using the First Order Reliability Method (FORM), in accordance with Annex D of EN 1990 [63], in order to evaluate the reliability of the proposed buckling design approach and the design rules in prEN 1993-1-4 [19].

Table 6. Reliability analysis results.

Resistance Model	$\stackrel{-}{\mathbf{b}}$	${\mathbf{k}}_{\mathbf{d},\mathbf{n}}$	${\mathbf{k}}_{\mathbf{n}}$	Vr	${\mathsf{\gamma }}_{\mathbf{M}1}$
EC3	1.031	3.04	1.64	0.092	1.138
Revised buckling design approach	0.996	3.04	1.64	0.082	1.121

provides a summary of the key statistical parameters considered in this analysis, including the design fractile factor for the ultimate limit state (${\mathrm{k}}_{\mathrm{d},\mathrm{n}}$); the characteristic fractile factor (${\mathrm{k}}_{\mathrm{n}}$); the combined coefficient of variation, which accounts for the resistance model and basic variable uncertainties ${\mathrm{V}}_{\mathrm{r}}$; the mean ratio of the test results to the resistance model predictions obtained through least squares fitting ($\overline{\mathrm{b}}$); and the partial safety factor for resistance, ${\mathrm{\gamma }}_{\mathrm{M}1}$. The coefficient of variation (CoV) for the cross-sectional area and yield stress f_y are taken to be 0.025 and 0.035, respectively [61]. A qualitative sensitivity assessment was also conducted, indicating that variations in the key parameters, particularly the coefficient of variation of the yield strength and cross-sectional area, can significantly affect the calculated reliability index, β. For instance, increasing the CoV of the yield strength from 0.035 to 0.05 resulted in a noticeable reduction in β, highlighting the importance of accurately characterizing the material properties when applying the proposed design approach. To enhance the reliability assessment, a simple perturbation-based sensitivity analysis was carried out by individually varying the key input parameters by ±10%. It was found that the coefficient of variation of the cross-sectional area had the most significant impact on the reliability index (β), followed by the CoV of the yield strength. This highlights the critical importance of geometric accuracy in reliability-based design applications.

The partial safety factor (${\mathrm{\gamma }}_{\mathrm{M}1}$) is determined as follows:

$${\mathrm{\gamma }}_{\mathrm{M}1}={\displaystyle \frac{{\mathrm{r}}_{\mathrm{k}}}{{\mathrm{r}}_{\mathrm{d}}}}$$

(8)

$${\mathrm{r}}_{\mathrm{d}}=\mathrm{b}{\mathrm{g}}_{\mathrm{r}\mathrm{t}}\left(\underset{\_}{{\mathrm{X}}_{\mathrm{m}}}\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\mathrm{k}}_{\mathrm{d},\mathrm{\infty }}\mathrm{Q}-0.5{\mathrm{Q}}^2\right)$$

(9)

$${\mathrm{r}}_{\mathrm{k}}=\mathrm{b}{\mathrm{g}}_{\mathrm{r}\mathrm{t}}\left(\underset{\_}{{\mathrm{X}}_{\mathrm{m}}}\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-{\mathrm{k}}_{\mathrm{\infty }}\mathrm{Q}-0.5{\mathrm{Q}}^2\right)$$

(10)

$$\mathrm{Q}=\sqrt{\mathrm{l}\mathrm{n}\left({\mathrm{V}}_{\mathrm{r}}^2+1\right)}$$

(11)

$${\mathrm{V}}_{\mathrm{r}}^2=\left({\mathrm{V}}_{\mathrm{\delta }}^2+1\right)\left[\prod _{\mathrm{i}=1}^{\mathrm{j}}\left({\mathrm{V}}_{\mathrm{X}\mathrm{i}}^2+1\right)\right]-1$$

(12)

$${\mathrm{V}}_{\mathrm{r}\mathrm{t}}^2=\sum _{\mathrm{i}}^{\mathrm{j}}{\mathrm{V}}_{\mathrm{X}\mathrm{i}}^2$$

(13)

In these expressions, r_k and r_d represent the characteristic and design resistance,${\mathrm{V}}_{\mathrm{x}\mathrm{i}}$ is the CoV for the yield stress and the geometric dimensions of the CHS. The value of the parameter, ${\mathrm{k}}_{\mathrm{\infty }}$, is taken as 1.64 for r_k and 3.04 for r_d.

Table 6 presents the derived partial safety factors (${\mathrm{\gamma }}_{\mathrm{M}1}$) for both the EC3 and the revised buckling design approach. The partial safety factor required for the modified buckling design approach and the EC3 is 1.121 and 1.138, respectively. The slightly lower value of the safety factor suggests less conservatism in the resistance predictions. The performed reliability analysis confirms that the proposed buckling design approach is a safe and reliable design tool for resistance predictions for CHS beam–columns.

6. Conclusions

The present study investigates the buckling resistance of CHS beam–columns produced using cold-formed and hot-rolled steel. An extensive parametric study was conducted using the developed finite element model, with a total of 1400 simulations. A comparative analysis was conducted to assess the performance of the proposed buckling design approach, along with the existing design provisions in Eurocode 3. Based on the FE data collected in this study, the findings demonstrate that the modified buckling design approach provides a more reliable and efficient method for predicting the buckling resistance of CHS beam–columns. Additionally, the safety and effectiveness of the proposed approach was confirmed using reliability analysis. The key results and observations are as follows:

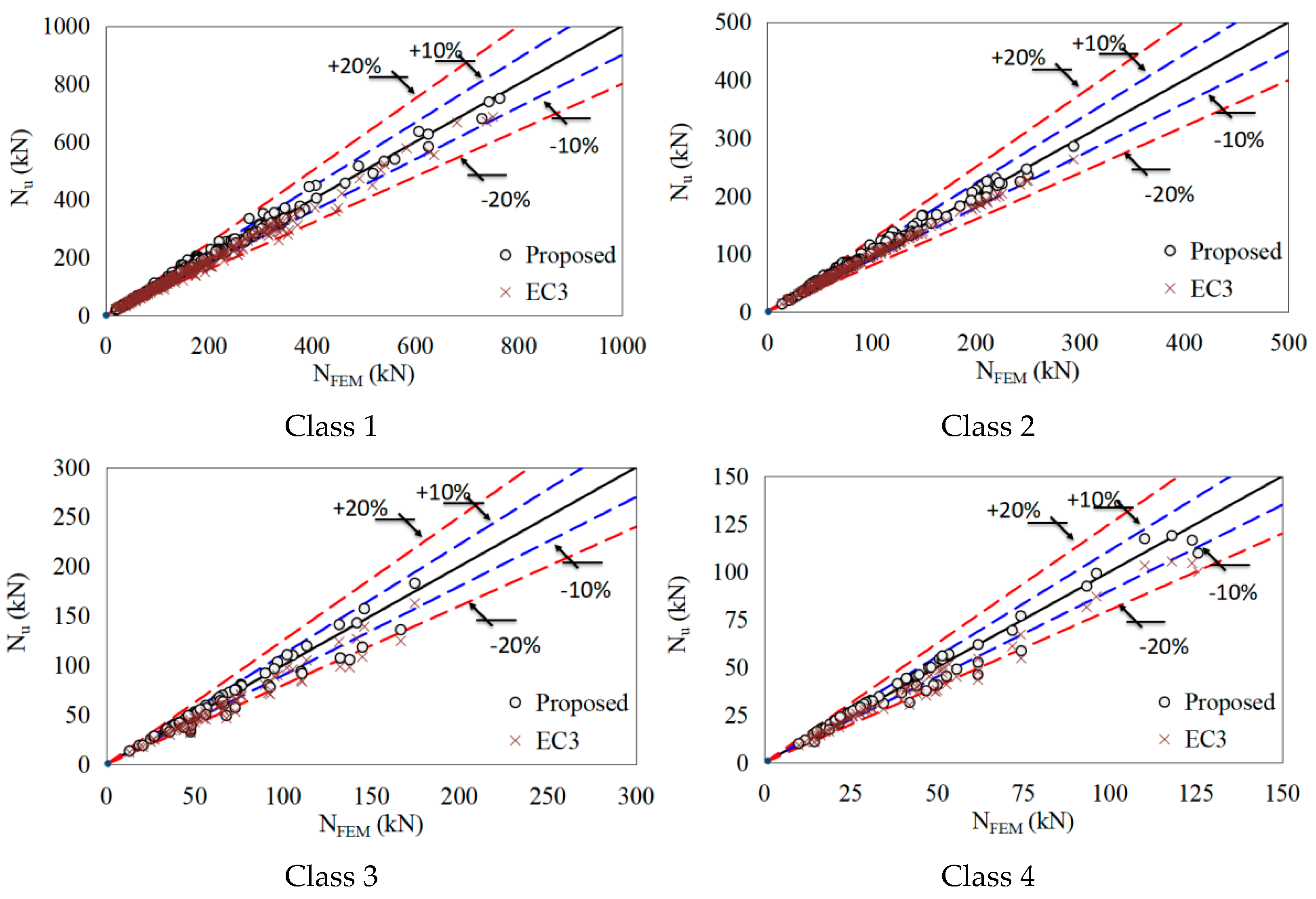
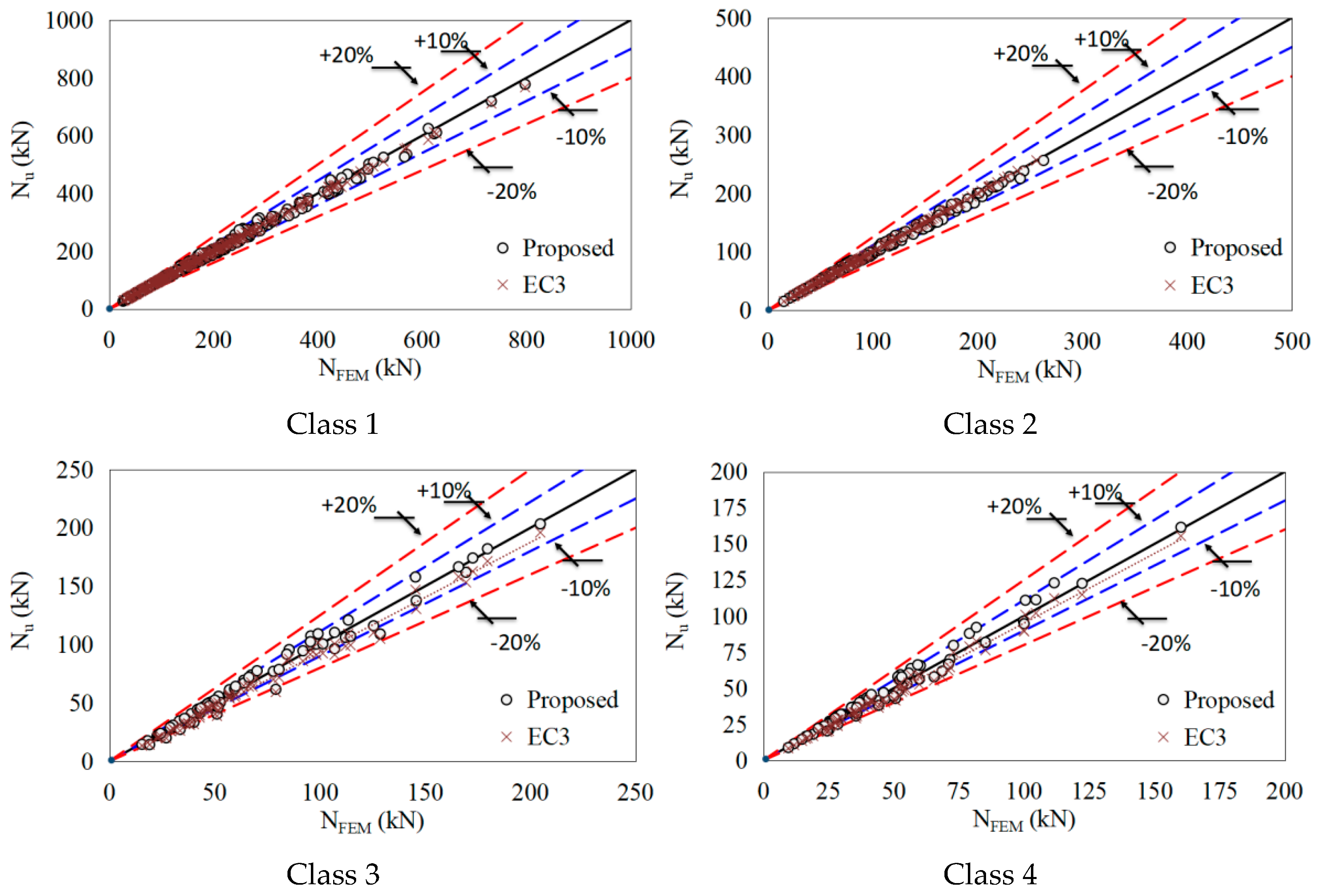
• The existing design provisions in Eurocode 3 clearly underestimate the buckling resistance of CHS beam–columns, with an acceptable level of accuracy for both cold-formed and hot-finished sections. On the other hand, the proposed buckling design approach provides more accurate and consistent resistance predictions compared with Eurocode 3;
• For Eurocode 3, the mean predicted-to-design ratio and RMSE are 0.98 and 11.8 kN for Class 1–2 sections, and 0.91 and 8.4 kN for Class 3–4 sections, respectively;
• For the proposed approach, these values are 0.99 and 8.1 kN for Class 1–2 sections and 1.00 and 6.4 kN for Class 3–4 sections, respectively;
• The reliability analysis suggests a partial safety factor of 1.138 for Eurocode 3 and a slightly lower value of 1.121 for the proposed approach, providing less conservatism in the prediction of the buckling resistance of CHS beam–columns.