Multi-Project Staff Scheduling Optimization Considering Employee Welfare in Construction Projects

Abstract

Multi-project staff scheduling optimization is a critical challenge in engineering management. However, traditional methods often overlook employee welfare, resulting in scheduling solutions that lack a people-centered approach. This study develops a multi-objective model that incorporates employee welfare to balance project performance and staff well-being. A mixed-integer programming model is proposed, integrating task allocation, resource scheduling, income growth, and workload balance as core optimization objectives. An improved Spider Wasp Optimization Algorithm (SWOIM) is employed to solve this model. The experimental results demonstrate that SWOIM outperforms conventional optimization algorithms in convergence speed, stability, and solution quality. It enhances staff scheduling efficiency while ensuring fair compensation and balanced workload distribution. A case study further validates the practical applicability of the proposed approach, showing that the optimized schedule not only improves task allocation but also enhances employee satisfaction and overall organizational performance. This study presents a people-centered scheduling framework aligned with sustainable workforce management principles and offers practical insights for improving multi-project coordination.

1. Introduction

Engineering projects are growing in scale and complexity due to the rapid global expansion of infrastructure development. The success or failure of these projects hinges not only on advanced technologies and effective resource allocation but also on personnel matching and management efficiency. In current engineering practice, team formation and staff scheduling face numerous challenges, including uncertainty in project demands, mismatches between talent supply and demand, reliance on empirical decision-making in traditional scheduling approaches, and inefficiencies in workforce allocation. A critical limitation of the existing methods is their neglect of individual employee characteristics, such as skill level, accumulated experience, work preferences, and career development needs. This oversight often leads to irrational task assignments, diminishing project execution efficiency, and undermining employee satisfaction and retention. Consequently, developing a scientifically grounded scheduling model that accounts for individual employee attributes has become essential for enhancing organizational efficiency and overall project performance.

In multi-project management practice, optimizing staff scheduling is widely recognized as a core strategy for enhancing corporate competitiveness. Traditional models typically focus on objectives such as time, cost, and resource utilization, employing linear programming or heuristic algorithms to maximize efficiency. However, a critical factor—employee welfare—is often overlooked [1]. Research has shown that job satisfaction, psychological workload, and opportunities for career development significantly influence the quality of project execution [2]. While intensive scheduling may reduce project duration, it frequently leads to employee burnout, diminished collaborative efficiency, and heightened risks of hidden costs and staff turnover [3]. Driven by the principle of “human-centeredness”, leading enterprises, such as Google and Toyota, have begun integrating employee well-being into scheduling decisions, using flexible work arrangements and real-time feedback mechanisms to enhance project stability and employee motivation.

Nevertheless, such practices often lack systematic theoretical foundations, with the existing studies tending to examine isolated dimensions of well-being [4,5,6]. A comprehensive framework is still absent—one that can quantify the synergistic relationship between the multidimensional aspects of employee welfare (e.g., workload balance, compensation, and incentives) and project performance. Moreover, this category of scheduling problems falls under NP-hard problems. As the scale of the problem grows, traditional mathematical approaches like integer programming struggle to deliver satisfactory solutions efficiently [7]. Metaheuristic algorithms have emerged as effective methods for tackling complex optimization challenges marked by high dimensionality and intricate variable interdependencies [8,9]. These algorithms leverage stochastic mechanisms and population-based search techniques to navigate the solution space, enabling the discovery of near-optimal solutions within acceptable computation times. Consequently, they are widely utilized across diverse fields. For instance, Song et al. developed the Adaptive Particle Swarm Optimization (APSO/DU) algorithm for portfolio optimization tasks [10]; Majumder et al. employed the Teaching–Learning-Based Optimization (TLBO) algorithm to solve trajectory planning problems for industrial robots [11]; and K. Li et al. presented a Spider Wasp Optimizer (SWO) enhanced by Support Vector Machines (SVMs) for diagnosing transformer faults [12]. Although metaheuristic algorithms, like Non-dominated Sorting Genetic Algorithm-II (NSGA-II) and Multi-Objective Particle Swarm Optimization (MOPSO), have demonstrated strong capabilities in multi-objective optimization, they still face challenges such as dynamically tuning objective weights and handling complex constraints in practical applications [13].

To address these research gaps, this study proposes a multi-project staff scheduling optimization method that integrates multidimensional employee welfare factors to optimize project execution efficiency and well-being. First, a mixed-integer programming model is developed to balance efficiency and welfare, designing a rational and human-centered scheduling plan without relying on predefined corporate welfare systems. The optimization objectives encompass workload balance, salary increments, and employee benefits, ultimately enhancing job satisfaction and teamwork efficiency while creating a multi-win scenario for individuals, organizations, and society [14]. Second, an improved Spider Wasp Optimization Algorithm (SWOIM) is introduced. It incorporates a simulated annealing mechanism and a Cauchy–Gaussian hybrid variational strategy to enhance its global search capability. Through a dynamic weight adjustment technique, the algorithm achieves the synergistic optimization of efficiency and welfare objectives. Finally, numerical experiments and comparative analyses confirm the effectiveness and applicability of the proposed approach. This research supports the United Nations’ Sustainable Development Goal 8 (“Decent Work and Economic Growth”). It advocates a shift in scheduling theory from a traditional “efficiency-first” model to a “human–efficiency symbiotic” framework. The findings offer novel perspectives and methodologies for engineering management, providing enterprises with optimized scheduling strategies that enhance organizational performance and competitiveness.

The technical roadmap of this paper is shown in Figure 1.

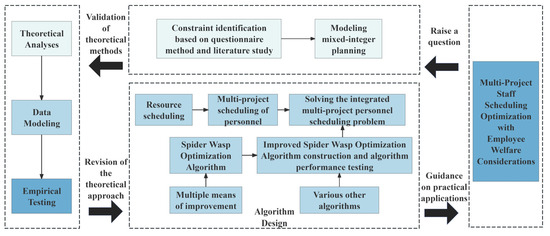
Figure 1. Technical roadmap.

2. Literature Review

2.1. Literature Review on Resource Scheduling Issues

Resource scheduling is a core strategy in parallel project management aimed at optimizing the allocation and control of limited resources (e.g., workforce, equipment, funds) to ensure timely and high-quality project delivery. Given the complexity of resource allocation, researchers have proposed various innovative approaches to address this challenge. Maenhout and Vanhoucke were among the first to introduce precise algorithms to optimize staffing under resource constraints to minimize total cost [15]. Nearchou et al. expanded this work by studying multi-site scenarios and analyzing the impact of staffing on both price and duration, proposing optimization strategies to reduce total and transfer costs [16]. Peng and Liu combined inverse optimization methods, two-layer nested genetic algorithms, and nonlinear programming to explore manual scheduling scenarios, achieving very short durations at the lowest possible cost [17].

In recent years, research on resource scheduling has continued to evolve. Jingjing Wang and Liu focused on prefabricated component production, optimizing both resource scheduling and equipment maintenance co-management to enhance production efficiency [18]. Qin proposed a scheduling approach for human resources under multi-project and multi-objective conditions, utilizing an improved genetic algorithm to address the problem. This offered new insights into handling resource distribution in complex environments [19]. L. Zhang and Yang proposed a dynamic human resource scheduling algorithm adapted to regional demands through simulation optimization [20]. Hafezi Zadeh et al. employed a simulated annealing algorithm to optimize human resource scheduling, providing fresh perspectives in the field [21].

Expanding the scope of resource scheduling.In cloud computing, Wei et al. combined Hidden Markov Models (HMMs) with a Stackelberg game strategy to construct a practical model to optimize the cloud resource distribution [22]. Rostami and Bagherpour studied multi-project scheduling problems with decentralized resource constraints, optimizing project duration and facility siting costs [23]. Li et al. proposed a layered scheduling strategy integrating an improved ant colony algorithm with deep Q-networks to boost task execution performance based on user requirements [24]. Jing Wang leveraged deep learning techniques to construct a real-time optimization framework for scheduling industrial and commercial resources, supporting engineers in making smarter decisions [25]. Lastly, Du and Chen optimized resource node combinations based on an improved ant colony algorithm to minimize response time in cloud computing resource allocation [26].

Various optimization methods have demonstrated excellent performance in addressing the multi-objective resource scheduling problem (MSRCPSP). Wang et al. designed a knowledge-based Multi-objective Fruit Fly Optimization Algorithm (MOFOA) aimed at simultaneously minimizing project timelines and expenditures [27]. Tirkolaee et al. applied nonlinear programming methods to address multi-objective and multi-modal resource scheduling in payment planning, targeting an enhancement in net present value while shortening project duration [28]. Uysal et al. introduced a GPU-based Genetic Algorithm (GA) to reduce project portfolio duration while ensuring that resource constraints and prioritization relationships are satisfied [29]. Zhang applied an ant colony algorithm to address the Multi-mode Resource Constrained Project Scheduling Problem (MRCPSP), focusing on minimizing project duration [30].

Despite the significant progress made in time and cost minimization in the studies mentioned above, multi-project resource scheduling still faces a key challenge: achieving rational allocation among projects to maximize overall benefits in a resource-limited and competitive environment. Furthermore, the current research has largely overlooked the role of employee welfare factors in resource scheduling optimization, which is crucial for sustainable management and will be an important focus of future studies. Additionally, while exact and heuristic algorithms can uncover problem characteristics and provide optimal solutions, they face the challenge of “combinatorial explosion” as project complexity increases, limiting their applicability in multi-project staff scheduling. Therefore, future research should focus on balancing project benefits with employee welfare to achieve a win–win situation and explore more efficient algorithms to enhance the intelligence and optimization of engineering management practices.

2.2. Literature Review on Employee Benefit Issues

In reviewing the extant literature about employee well-being factors, most studies underscore the paramount significance of employee well-being. As an illustrative case, Cox, leveraging thematic analysis and constant comparative modeling, insightfully uncovered the pressing necessity for millennial employees to be offered diverse benefits that foster work–life balance, thereby enhancing job satisfaction [31]. Peng et al. emphasized that incorporating psychological support for workers and fostering a strong safety culture are key elements in managing construction site safety [32]. Jaworski et al. further underscored the significance of practical training approaches—such as on-the-job learning and job shadowing—in enhancing training satisfaction. Moreover, factors like the ability to select benefits and incentives and satisfaction with training influenced employee commitment [33]. In a quantitative study, Boudreaux convincingly demonstrated that new firms that offer stable benefits experience reduced employee turnover rates and increased profitability, directly optimizing firm performance [34].

Subsequently, the research perspective has shifted to explore the multidimensional aspects influencing employee well-being. Němečková suggested that, given the individualized nature of employee well-being, firms should avoid one-size-fits-all benefits packages since employees have different preferences and place varying values on specific benefits [35]. Shahzad et al. investigated the impacts of capacity development, interest alignment, and management backing on employee performance, identifying employee retention as a moderating variable in these relationships [36]. Tuzovic and Kabadayi established a comprehensive analytical framework and proposed a research agenda to assess how social distancing policies affect employee well-being [37]. Additionally, Ilies et al. expanded the perspective by proposing the inclusion of interpersonal and intrapersonal need satisfaction to more comprehensively assess the benefits of employee well-being, providing an in-depth understanding of how employees’ perceptions of work triggers influence their attitudes and behaviors [38]. Su and Swanson proposed that organizations adopting Corporate Social Responsibility (CSR) practices can generate positive effects at multiple levels—enhancing employee well-being, promoting environmentally responsible behavior, and strengthening trust and commitment in employee–employer relationships [39].

Notably, despite the substantial findings from the aforementioned studies on employee benefits, few have systematically integrated and analyzed the comprehensive project and employee benefits within engineering management. Despite elucidating a significant relationship between leadership, work motivation [40], and performance, the study by Joseph-Armstrong did not delve into the core topic of employee well-being and project effectiveness in parallel with engineering management. Consequently, future research endeavors should delve deeper into achieving a balance and optimizing project effectiveness and employee welfare in engineering management, thereby fostering a win–win scenario.

2.3. Research Gaps and Contributions

The existing research provides meaningful guidance for implementing multi-project personnel scheduling, particularly in reducing cost and duration. However, unlike conventional resource scheduling methods, the approach proposed in this paper integrates essential aspects of workforce planning. A thorough literature analysis reveals a notable research gap—comprehensive scheduling models that factor in employee welfare are mainly absent from traditional resource scheduling studies.

This study adopts the SWOIM algorithm as the primary solution technique. As a heuristic optimization method, SWOIM features strong global search ability and minimal parameter tuning requirements. Despite its potential, applications of SWOIM in integrated personnel scheduling remain limited in the current literature. This paper introduces improvements, such as simulated annealing-based acceptance mechanisms and stochastic Cauchy perturbations, to enhance its efficiency and accuracy. It offers a more robust approach to solving complex scheduling problems. Based on the above analysis, this paper contributes to the field in the following ways:

(1) Practical Applications:

This study constructs a mixed-integer programming model to optimize multi-project staff scheduling, focusing on employee welfare. By incorporating workers’ preferences and well-being into the scheduling process, organizations can establish more human-centered work plans. This enhances job satisfaction and organizational loyalty and effectively mitigates employee turnover, contributing to long-term business stability.

(2) Theoretical Contributions:

This paper theoretically addresses a research gap by embedding employee welfare considerations into multi-project personnel scheduling, thereby advancing the theoretical framework of resource allocation. Additionally, this study broadens the practical scope of SWOIM by applying it to scheduling problems, promoting a transition from purely project-centric planning to a dual-focus model that values organizational efficiency and employee well-being.

(3) Algorithmic Improvements:

Regarding algorithmic design, this research presents an upgraded version of SWOIM, incorporating mechanisms such as simulated annealing acceptance, periodic removal of duplicate solutions (every 50 generations), Cauchy-based random perturbations, binary tournament selection, shuffled crossover, and Gaussian mutation. These refinements enhance the algorithm’s global search capability and help avoid premature convergence. Comparative experiments demonstrate that the improved SWOIM consistently outperforms alternative algorithms in terms of solution quality and convergence speed.

3. Model Construction

3.1. Problem Description

This research focuses on the efficient and rational assembly of project teams within a multi-project context, considering key factors such as workload distribution, base salary, and benefit increases. The objective is to enhance overall project performance while boosting employee satisfaction and improving team collaboration. This presents a multifaceted optimization challenge, balancing multiple goals and constraints. To tackle this, we propose a mixed-integer programming model that optimizes project outcomes and employee well-being. By incorporating welfare-related elements into the scheduling process, the proposed approach generates more effective, employee-friendly, and flexible scheduling solutions.

3.2. Parameter Settings

The model parameters are set as shown in Table 1.

Table 1. Related parameters and their implications.

Parameters	Parameter Meaning
I	Project collection, i1, i2∈I
H	Set of personnel, h∈H
J	Set of tasks, j1, j2∈J
K	Set of skills, k∈K
$T_{i,j}^h$	The time required for task j of project i to be completed by personnel h
$C_{i,j}^h$	The cost associated with task j of project i being serviced by person h
$S_{h,k}$	The proficiency of personnel h in skill k
$R_{i,j}^h$	The number of resources required to service task j of project i by person h
$B_{i,j}^h$	The incremental welfare of task j of project i for person h
$V_{i,j}^k$	Proficiency requirements for skill k for task j of item i
$P_h$	The basic pay for personnel h
${\omega }_{j1,j2}^i$	Whether task j1 in project i is the immediately preceding task of task j2: 1 if yes; 0 otherwise
$\alpha$	The maximum budget
$M{t}_i$	The maximum duration of project i
$\beta$	The maximum number of resources
${\varphi }_i$	The weighting of item i in terms of duration
$M{p}^{+}$	The maximum income from personnel
$M{p}^{-}$	The minimum income for personnel
$E{t}^{+}$	The maximum time for personnel to perform
$E{t}^{-}$	The minimum time for personnel to perform
$w_1,w_2,w_3$	The weighting of time, cost, and resources
${\varpi }_1,{\varpi }_2,{\varpi }_3$	The weighting of income, time, and equilibrium
${\psi }_1,{\psi }_2$	The weighting of projects and employees
$X_{i,j}^h$	Whether task j of item i is serviced by person h: 1 if yes; 0 otherwise
$T{a}_{i,j}$	Time of the start of execution of task j for project i
$T{b}_{i,j}$	The time at which task j of item i ends its execution

3.3. Research Hypothesis

(1) To ensure the validity and consistency of the scheduling model, several assumptions are made in this study: all employees are presumed to possess the essential skills required for their assigned tasks; they adhere to the schedule without delays; tasks are clearly defined, mutually exclusive, and non-overlapping; and employees exhibit stable behavior and consistent work performance. This model does not account for external disruptions, fluctuations in behavior, or existing internal welfare systems.

(2) Ensure that each task is assigned to only one employee per project.

(3) Employee benefits and combined program benefits are quantifiable.

3.4. Mixed-Integer Programming Modeling

Mixed-integer programming models involve defining decision variables, an objective function, and constraints. The primary aim is to determine an optimal resource allocation strategy that maximizes the objective function, considering cost, time, efficiency, and other relevant parameters.

In this study, decision variables represent whether a specific task in a project is assigned to a particular employee. The objective function reflects the total project benefit, incorporating employee welfare. The constraints include limits on task assignments, resource usage, skill requirements, time constraints, cost restrictions, and welfare increment conditions. To address project performance and employee welfare, the multi-objective optimization problem is transformed into a single-objective problem using a weighting method, simplifying the identification of the optimal scheduling solution.

The objective function is as follows:

$$f_1={\displaystyle \sum _{i\in I}{\varphi }_{i}Max\left\{T{b}_{i,j}|j\in J\right\}}$$

(1)

$$f_2={\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{\displaystyle \sum _{h\in H}{C}_{i,j}^h{X}_{i,j}^h}}}$$

(2)

$$f_3={\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{\displaystyle \sum _{h\in H}{R}_{i,j}^h{X}_{i,j}^h}}}$$

(3)

$$f_4={\displaystyle \sum _{h\in H}\left(P_h+{\displaystyle \sum _{i\in I}{\displaystyle \sum _{i\in J}{X}_{i,j}^h{B}_{i,j}^h}}\right)}$$

(4)

$$f_5={\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{\displaystyle \sum _{h\in H}{X}_{i,j}^h{T}_{i,j}^h}}}$$

(5)

$$\begin{array}{l}{f}_6=1-0.5{\displaystyle \frac{Max\left\{{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{X}_{i,j}^h{T}_{i,j}^h|h\in H}}\right\}-Min\left\{{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{X}_{i,j}^h{T}_{i,j}^h|h\in H}}\right\}}{Max\left\{{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{X}_{i,j}^h{T}_{i,j}^h|h\in H}}\right\}}}-\\ 0.5{\displaystyle \frac{Max\left\{P_h+{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{X}_{i,j}^h{B}_{i,j}^h|h\in H}}\right\}-Min\left\{P_h+{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{X}_{i,j}^h{B}_{i,j}^h|h\in H}}\right\}}{Max\left\{P_h+{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{X}_{i,j}^h{B}_{i,j}^h|h\in H}}\right\}}}\end{array}$$

(6)

$$Max(F_1)=w_1{\displaystyle \frac{{\displaystyle \sum _{i\in I}{\varphi }_{i}M{t}_i-f_1}}{{\displaystyle \sum _{i\in I}{\varphi }_{i}M{t}_i}}}+w_2{\displaystyle \frac{\alpha -f_2}{\alpha }}+w_3{\displaystyle \frac{\beta -f_3}{\beta }}$$

(7)

$$Max(F_2)={\varpi }_1{\displaystyle \frac{f_4-M{p}^{-}}{M{p}^{+}-M{p}^{-}}}+{\varpi }_2{\displaystyle \frac{E{t}^{+}-f_5}{E{t}^{+}-E{t}^{-}}}+{\varpi }_3{f}_6$$

(8)

$$Max(F)={\psi }_1{F}_1+{\psi }_2{F}_2$$

(9)

Equation (1) represents the latest completion time for all tasks in the project, adjusted by weighting. Equation (2) denotes the total cost required for project completion. Equation (3) reflects the total resource usage during the project’s execution. Equation (4) accounts for all employees’ total salary and benefit expenses. Equation (5) quantifies the total working hours of all employees. Equation (6) measures the balance of task distribution among employees. Equations (1)–(6) define the sub-objective functions of the model. In Equation (7), $f_1$, $f_2$, and $f_3$ represent the normalized values of three efficiency-related sub-objectives, i.e., project duration, total cost, and overall resource consumption, with $w_1$, $w_2$, and $w_3$ as their respective weights. Since these sub-objectives are cost-related (i.e., lower values are preferable), reverse normalization is applied so that smaller raw values correspond to higher normalized values, aligning them with the maximization goal. This objective function optimizes project efficiency by balancing time, cost, and resource usage. In Equation (8), $f_4$, $f_5$, and $f_6$ represent the normalized values of three welfare-related sub-objectives, i.e., income fairness, working time balance, and task allocation equity, with corresponding weights ${\varpi }_1$, ${\varpi }_2$, and ${\varpi }_3$. This function aims to maximize employee welfare by improving fairness in task assignments, work hours, and compensation, thereby enhancing satisfaction and rationality in the scheduling process. Finally, the combined objective function is formulated in Equation (9) by integrating Equations (7) and (8) using a weighted-sum approach. This unified objective function optimizes project outcomes and employee welfare, supporting a dual-objective optimization strategy that balances individual fairness with overall project efficiency. It advances a people-centered approach to multi-project staff scheduling.

The constraints are as follows:

$$\begin{array}{l}\forall i\in I,j\in J\\ {\displaystyle \sum _{h\in H}{X}_{i.j}^h}=1\end{array}$$

(10)

$$\begin{array}{l}\forall i\in I,j\in J,k\in K,h\in H\\ S_{h,k}{X}_{i.j}^h\ge X_{i,j}^h{V}_{i,j}^k\end{array}$$

(11)

$$\begin{array}{l}\forall i\in I,j1,j2\in J,j1\ne j2\\ {\omega }_{j1.j2}^{i}T{a}_{i,j2}\ge {\omega }_{j1.j2}^{i}T{b}_{i,j1}\end{array}$$

(12)

$$\begin{array}{l}\forall i1,i2\in I,j1,j2\in J,h\in H\\ (i1\ne i2)or(j1\ne j2),X_{i1,j1}^h+X_{i2,j2}^h=2\\ Min(T{b}_{i1,j1},T{b}_{i2,j2})\le Max(T{a}_{i1,j1},T{a}_{i2,j2})\end{array}$$

(13)

$$\begin{array}{l}M{p}^{-}={\displaystyle \sum _{h\in H}{P}_h}+{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}Min\left\{B_{i,j}^h|h\in H\right\}}}\\ M{p}^{+}={\displaystyle \sum _{h\in H}{P}_h}+{\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}Max\left\{B_{i,j}^h|h\in H\right\}}}\\ E{t}^{-}={\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}Min\left\{T_{i,j}^h|h\in H\right\}}}\\ E{t}^{+}={\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}Max\left\{T_{i,j}^h|h\in H\right\}}}\end{array}$$

(14)

$$\begin{array}{l}\forall i\in I,j\in J\\ T{b}_{i,j}=T{a}_{i,j}+{\displaystyle \sum _{h\in H}{T}_{i,j}^h{X}_{i,j}^h}\end{array}$$

(15)

$$\begin{array}{l}\forall i\in I\\ Max\left\{T{b}_{i,j}|j\in J\right\}\le M{t}_i\end{array}$$

(16)

$${\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{\displaystyle \sum _{h\in H}{C}_{i.j}^h{X}_{i,j}^h}}}\le \alpha$$

(17)

$${\displaystyle \sum _{i\in I}{\displaystyle \sum _{j\in J}{\displaystyle \sum _{h\in H}{R}_{i,j}^h{X}_{i,j}^h}}}\le \beta$$

(18)

Equation (10) ensures that each task is assigned to a single individual, simplifying the scheduling and optimization process. Equation (11) enforces skill requirements, guaranteeing that the assigned personnel possess the qualifications for each task. Equation (12) dictates the task execution sequence based on precedence relationships, preventing resource conflicts and inefficiencies. Equation (13) limits each employee to one task at a time, optimizing work efficiency and quality. Equation (14) introduces a min-max function to balance employee benefits, promoting fairness. Equation (15) defines each task’s start and end times, while Equation (16) imposes duration constraints to ensure the project is completed within the allotted timeframe. Equation (17) sets a budget constraint to cap the total project cost. Finally, Equation (18) limits resource usage to the available supply.

4. Algorithm Design

The model introduced in this study is a mixed-integer programming model, classified as an NP-hard problem, inherently making it challenging to obtain optimal solutions. Due to the multiple objectives and constraints, exact algorithms often struggle to provide satisfactory solutions within a reasonable time frame, typically resulting in locally optimal or near-optimal solutions. The SWO algorithm has demonstrated superior performance compared to nine well-established metaheuristic algorithms, including the Slime Mold Algorithm (SMA), the Marine Predators Algorithm (MPA), the Equilibrium Optimizer (EO), the Gorilla Troops Optimizer (GTO), the African Vultures Optimization Algorithm (AVOA), the Grey Wolf Optimizer (GWO), the Whale Optimization Algorithm (WOA), Successive Convex Approximation (SCA), and Red Fox Optimization (RFO). It is known for its fast search capabilities and high solution accuracy, with flexible updating strategies that effectively balance exploration and exploitation [13,41]. However, the original SWO algorithm suffers from limited convergence accuracy, slower convergence speed, and a tendency to get trapped in local optima. To address these issues, this study presents an enhanced version, SWOIM, which incorporates several improvements: a simulated annealing acceptance mechanism, periodic elimination of duplicate solutions (every 50 generations), random perturbation using Cauchy variants, and the use of binary tournament selection, shuffled crossover, and Gaussian mutations. These enhancements boost the global search capacity, accelerate convergence speed, and reduce the likelihood of the algorithm becoming stuck in local optima.

4.1. Basic Spider Wasp Optimization Algorithm

The SWO algorithm is inspired by the natural behaviors of female spider wasps, especially their hunting, nesting, and mating behaviors [13]. The algorithm’s optimization process is organized into two main phases: one that mimics hunting and nesting activities and another that simulates mating behaviors.

4.1.1. Scenario Generation and Targeting

In the SWO algorithm, the female spider wasp starts with an initial phase called the “exploration operator”, during which it searches for potential targets. When a suitable prey is located, the process moves to the “exploitation operator”, simulating the approach and capture stages.

Search Stage (Exploration Operator)

As previously mentioned, the female spider wasp initiates this operation to identify its preferred prey at the start of the search. This behavior can be represented mathematically by the following expression:

$$\overrightarrow{x_i^{t+1}}=\overrightarrow{x_i^t}+u_1\ast (\overrightarrow{x_a^t}-\overrightarrow{x_b^t})$$

(19)

Random numbers $\overrightarrow{x_a^t}$ and $\overrightarrow{x_b^t}$ are two solutions randomly chosen from the current population. The constant forward speed of the female wasp is determined using an adaptive factor, represented as $u_1$, and is mathematically defined by the following equation:

$$u_1=\left|rn\right|\ast r_1$$

(20)

where $r_1$ is a random number between 0 and 1 and $rn$ is a random number sampled from a normal distribution. If the female wasp fails to capture the prey falling from the sphere, she may lose it. To recover the lost prey, the female wasp uses various exploration strategies, which are mathematically defined as follows:

$$\overrightarrow{x_i^{t+1}}=\overrightarrow{x_c^t}+u_2\ast (\overrightarrow{L}+\overrightarrow{r_2}\ast (\overrightarrow{H}-\overrightarrow{L}))$$

(21)

$$u_2=B\ast \cos (2\pi l)$$

(22)

$$B={\displaystyle \frac{1}{1+e^l}}$$

(23)

where $\overrightarrow{x_c^t}$ is a randomly selected solution from the current population representing the location of the dropped prey and $\overrightarrow{L}$ and $\overrightarrow{H}$ denote the lower and upper bounds, respectively. Rrr is a vector of random values generated within the interval [0, 1], and $l$ is a random number between −1 and −2. Finally, as described below, the decision between Equations (19) and (21) is made when determining the next position of the female wasp:

$$\overrightarrow{x_i^{t+1}}=\left\{\begin{array}{l}\mathrm{Equation} (19) r_3<r_4\\ \mathrm{Equation} (21) otherwise\end{array}\right.$$

(24)

where $r_3$ and $r_4$ are two arbitrary numbers between 0 and 1.

Following and Escaping Stage (Exploration and Exploitation Operator)

Spider wasps calculate their new position relative to the spider using the following formula in order to capture it at that location:

$$\overrightarrow{x_i^{t+1}}=\overrightarrow{x_i^t}+C\ast \left|2\ast \overrightarrow{r_5}\ast \overrightarrow{x_a^t}-\overrightarrow{x_i^t}\right|$$

(25)

$$C=\left(2-2\ast ({\displaystyle \frac{t}{t_{\max }}})\right)\ast r_6$$

(26)

where $t$ and $t_{\max }$ represent the current and maximum function values sought, respectively. $\overrightarrow{r_5}$ is a vector of values ranging from 0 to 1, generated randomly using a uniform distribution. $r_6$ is a random value created between 0 and 1, also based on a uniform distribution. However, it is possible that the spiders may flee from the female wasps, causing the distance between them to increase over time. To model this behavior in the SWO algorithm, the following equations are used:

$$\overrightarrow{x_i^{t+1}}=\overrightarrow{x_i^t}\ast \overrightarrow{vc}$$

(27)

where $\overrightarrow{vc}$ is a vector of values generated arbitrarily between $k$ and $-k$ using a normal distribution. $k$ is created by applying the following equation:

$$\begin{array}{l}k=1-1\ast ({\displaystyle \frac{t}{t_{\max }}})\end{array}$$

(28)

The following equation can be used to obtain an acceptable compromise between Equations (22) and (24):

$$\overrightarrow{x_i^{t+1}}=\left\{\begin{array}{l}\mathrm{Equation} (25) r_3<r_4\\ \mathrm{Equation} (27) otherwise\end{array}\right.$$

(29)

In SWO, the following equation is used to trade off between (24) and (29):

$$\overrightarrow{x_i^{t+1}}=\left\{\begin{array}{l}\mathrm{Equation} \left(24\right) p<k\\ \mathrm{Equation} \left(29\right) otherwise\end{array}\right.$$

(30)

where $p$ is a randomly selected number within [0, 1] based on the characteristics of a uniform distribution.

Nesting Behavior (Exploitation Operator)

Female wasps drag immobilized spiders into their nests. Spider wasps demonstrate diverse nesting behaviors, including digging and forming cells in the soil, building mud nests on leaves or rocks, and utilizing existing nests or cavities. To model these various nesting behaviors, SWO employs two equations. The first equation simulates attracting spiders to an optimal location, constructing a nest for a stationary spider, and laying eggs on its abdomen, as outlined in the following equation. The formula below is then used to calculate the new position of a spider wasp relative to the spider in order to capture it:

$$\overrightarrow{x_i^{t+1}}=\overrightarrow{x^{*}}+\cos (2\pi l)\ast (\overrightarrow{x^{*}}-\overrightarrow{x_i^t})$$

(31)

where $\overrightarrow{x^{*}}$ denotes the optimal solution found so far. The second equation models the process of constructing nests at locations randomly selected from the female spider population. An additional step size is included to prevent the creation of two nests at the same location. This equation is mathematically expressed as follows:

$$\overrightarrow{x_i^{t+1}}=\overrightarrow{x_a^t}+r_3\ast \left|\gamma \right|\ast (\overrightarrow{x_a^t}-\overrightarrow{x_i^t})+(1-r_3)\ast \overrightarrow{U}\ast (\overrightarrow{x_b^t}-\overrightarrow{x_c^t})$$

(32)

where $\gamma$ is a random value selected based on the taxing flight and $\overrightarrow{U}$ is a vector of binary values used to decide whether an additional step is applied during the update process. The decision to apply the extra step size can be determined by the factors outlined below:

$$\overrightarrow{U}=\left\{\begin{array}{l}1 \overrightarrow{r_4}<\overrightarrow{r_5}\\ 0 otherwise\end{array}\right.$$

(33)

where $\overrightarrow{r_4}$ and $\overrightarrow{r_5}$ are two random vectors generated from a uniform distribution, with values ranging between 0 and 1. To update each solution during the optimization process, Equations (28) and (29) are randomly swapped according to the following equation:

$$\overrightarrow{x_i^{t+1}}=\left\{\begin{array}{l}\mathrm{Equation} (31) r_3<r_4\\ \mathrm{Equation} (32) otherwise\end{array}\right.$$

(34)

Finally, during the SWO process, the trapping behavior defined by Equation (30) is replaced with the nesting behavior described by Equation (33) using the following equations:

$$\overrightarrow{x_i^{t+1}}=\left\{\begin{array}{l}\mathrm{Equation} (30) i<N\ast k\\ \mathrm{Equation} (34) otherwise\end{array}\right.$$

(35)

4.1.2. Mating Behavior

The SWO method for generating new solutions, or spider wasp eggs, is mathematically expressed as follows:

$$\overrightarrow{x_i^{t+1}}=Crossover(\overrightarrow{x_i^t},\overrightarrow{x_m^t},Cr)$$

(36)

In SWO, where $\overrightarrow{x_m^t}$ and $\overrightarrow{x_i^t}$ represent the vectors of female and male spider wasps, respectively, and $Crossover$ denotes the uniform crossover operator applied to $\overrightarrow{x_m^t}$ and $\overrightarrow{x_i^t}$ with a crossover probability of $Cr$, the following equation is used to differentiate between male and female spider wasps:

$$\overrightarrow{x_m^{t+1}}=\overrightarrow{x_i^t}+e^l\ast \left|\beta \right|\ast \overrightarrow{v_1}+(1-e^l)\ast \left|{\beta }_1\right|\ast \overrightarrow{v_2}$$

(37)

where $\beta$ and ${\beta }_1$ are two numbers randomly selected from a normal distribution and $\overrightarrow{v_1}$ with $\overrightarrow{v_2}$ are two vectors generated by the following equation:

$$\overrightarrow{v_1}=\left\{\begin{array}{l}\overrightarrow{x_a}-\overrightarrow{x_i} f(\overrightarrow{x_a})<f(\overrightarrow{x_i})\\ \overrightarrow{x_i}-\overrightarrow{x_a} otherwise\end{array}\right.$$

(38)

$$\overrightarrow{v_2}=\left\{\begin{array}{l}\overrightarrow{x_b}-\overrightarrow{x_c} f(\overrightarrow{x_b})<f(\overrightarrow{x_c})\\ \overrightarrow{x_c}-\overrightarrow{x_b} otherwise\end{array}\right.$$

(39)

The factor $TR$ controls the balance between Equations (35) and (36).

4.1.3. Population Reduction and Memory Saving

After the female spider wasp lays eggs on the host’s abdomen, she seals the nest and moves to a more isolated location. This represents the completion of the female wasp’s role in the optimization process, allowing other wasps to take over and potentially yield better results by finishing the remaining functional evaluations. A portion of the population is removed to accelerate convergence, increasing the functional evaluations performed by the remaining wasps. Throughout the optimization, the population size is dynamically adjusted according to the following formula:

$$N=N_{\min }+(N-N_{\min })\times k$$

(40)

where $N$ represents the population size and $N_{\min }$ denotes the minimum population size required to prevent the optimization process from converging to local minima. Additionally, SWO incorporates memory retention techniques to transfer the best-performing solution from each wasp to the next generation. Essentially, each wasp’s proposed new position is compared with its current one, and it is replaced if the current solution is suboptimal.

4.2. Improved Spider Wasp Optimization Algorithm

4.2.1. Enhancement of the Global Search Strategy

To enhance the efficiency and accuracy of SWOIM in its global search phase, this study introduces the Metropolis acceptance criterion, random perturbation–Cauchy’s variation, and a mechanism to remove duplicate solutions every 50 generations. Perturbation is applied during each iteration using a specified probability and mutation method, outlined as follows:

(1) The Metropolis Acceptance Criterion.

1. In each iteration, generate a random number $r_1$, where $r_1$ is a number randomly chosen from a uniform distribution between 0 and 1.

2. Accept the objective function value of a new solution $r_1$ if it is below the preset acceptance threshold, even if it leads to a worse objective function. This strategy helps the algorithm avoid becoming trapped in local optima by permitting the acceptance of some suboptimal solutions. The process can be outlined as follows:

a. Initialize the temperature $T$ and define a cooling factor $\alpha$.

b. At the beginning of each iteration, update the current temperature $T=\alpha \times T$.

c. For the generated random number $r_1$, compute the acceptance probability $P=e^{-\Delta E/T}$, where $\Delta E$ represents the difference in objective function values between the current solution and the new solution.

d. If $r_1<P$, accept the new solution; otherwise, retain the current solution.

This approach helps avoid convergence to local optima during the optimization process, while preserving the breadth and flexibility of the search.

(2) Random Perturbation—Cauchy Variation.

When a new solution is accepted according to the Metropolis acceptance criterion, the Cauchy distribution is applied for variation. This helps the algorithm avoid local optima by introducing a wide range of random perturbations. The specific steps are as follows:

a. For each dimension of each individual $x_i$, generate a Cauchy-distributed random number ${\delta }_i$.

b. Update the individuals $x_i=x_i+{\delta }_i$.

c. Use the formula for generating random numbers from the Cauchy distribution, i.e., ${\delta }_i=\gamma \cdot \tan (\pi \cdot (r-0.5))$, where $\gamma$ is the scale parameter and $r$ is a uniform random number between 0 and 1.

Random perturbation–Cauchy variation improves the algorithm’s ability to find the global optimal solution by introducing stochastic perturbations. This allows the algorithm to escape local optima and explore a broader search space, significantly enhancing its global search capability.

(3) Remove Duplicate Solutions Every 50 Generations.

To maintain population diversity and prevent premature convergence, duplicate solutions are removed from the population every 50 generations. The specific steps are as follows:

a. Check the iteration count, where the algorithm performs a deletion operation if the current iteration count is a multiple of 50 (i.e., the 50th, 100th, 150th generation, etc.).

b. Iterate through the current population using a hash table or set to record individuals that have appeared.

c. If duplicates are found, mark and remove them to ensure the population contains unique individuals.

This approach prevents the algorithm from stagnating in later stages and helps maintain population diversity.

4.2.2. Enhancement of the Local Search Strategy

In the local search phase, this study introduces improvements to the selection, crossover (intersection), and mutation strategies to explore promising regions of the solution space and avoid stagnation. The enhancements are detailed as follows:

(1) Binary Tournament Selection.

In each selection operation, employ the binary tournament selection method, following these specific steps:

a. Randomly select two individuals, labeled as $x_1$ and $x_2$, from the population.

b. Compare the objective function values of these two individuals and select the superior one for advancement to the next generation.

c. Repeat the aforementioned steps until the population of the new generation is complete.

This method ensures a higher proportion of high-quality individuals selected in each operation, thereby enhancing the algorithm’s convergence speed.

(2) Shuffling Crossover.

For the selected individuals, implement the shuffling crossover operation using the following specific steps:

a. Concatenate the gene sequences of two parental individuals into a new gene sequence.

b. Randomly shuffle this gene sequence to generate new offspring.

Through shuffling crossover, the genes of the parent individuals can be recombined, increasing population diversity and preventing premature algorithm convergence.

(3) Gaussian Mutation.

In the mutation operation, employ the Gaussian mutation method using the following specific steps:

a. For each gene $x_i$ of every individual, generate a random number ${\in }_i$ that follows a Gaussian distribution.

b. Update the gene $x_i=x_i+{\in }_i$ of the individual.

c. Use the formula for generating random numbers from a Gaussian distribution, i.e., ${\in }_i\sim N\left(0,{\sigma }^2\right)$, where $\sigma$ represents the standard deviation.

Gaussian mutation allows for a fine-grained search within a narrow range, enhancing solution accuracy and diversity.

Through these improvement measures, SWOIM can better maintain population diversity, avoid premature convergence, enhance global search capability, and improve optimization effectiveness, demonstrating stronger search capabilities and higher optimization precision in complex optimization problems.

The flowchart of SWOIM is depicted in Figure 2.

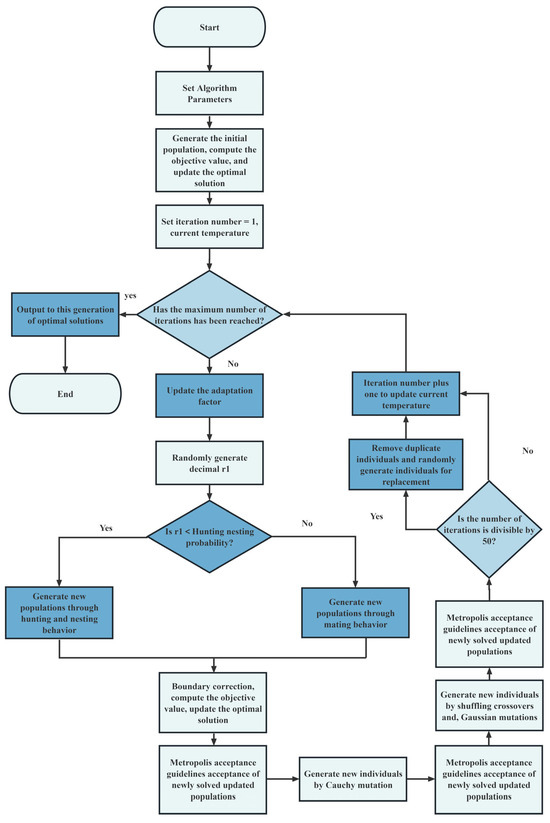
Figure 2. Algorithm flow diagram.

5. Algorithm Testing

5.1. Test Case Generation

To assess the effectiveness of the proposed improved algorithm, this study conducted comparative experiments involving six different algorithms: the Chicken Swarm Algorithm (CSO), Basic Particle Swarm Optimization (PSO), SWO, SMA, GWO, and the improved version, SWOIM. Although PSPLIB is a widely recognized benchmark library for project scheduling, it does not include test cases tailored to the specific requirements of this research. Therefore, customized multi-project personnel scheduling scenarios were developed, and the solution performance of each algorithm was evaluated using these tailored cases as benchmarks.

5.2. Algorithm Parameter Setting

To demonstrate the algorithms’ superiority in solution quality and convergence efficiency, all six algorithms were coded and executed using MATLAB R2022a on a standard commercial PC (Windows 11 OS, Intel(R) Core(TM) i5-8300H CPU @ 2.30 GHz, 8 GB RAM). Each algorithm was independently run 500 times, preserving the best solution at each generational update. The algorithm-specific parameters, shown in Table 2, were refined through iterative testing, empirical tuning, and multiple rounds of adjustment.

Table 2. Algorithm parameters.

Algorithm Name		Parameter Configuration
CSO	Population size	Number of iterations	G	Percentage of roosters	Proportion of hens
	100	500	10	0.15	0.7
PSO	Population size	Number of iterations	cc	Particle velocity range	Inertial weighting
	100	500	[1.5, 1.5]	[−0.5, 0.5]	0.8
SWO	Population size	Number of iterations
	100	500
SMA	Population size	Number of iterations
	100	500
GWO	Population size	Number of iterations	A
	100	500	2
SWOIM	Population size	Number of iterations
	100	500

5.3. Test Results and Discussion

The performance outcomes of the multiple independent runs across different problem scales are illustrated in Table 3 and Figure 3, Figure 4 and Figure 5. As shown in Table 3, SWOIM consistently delivers the best results with minimal standard deviation across all test instances, highlighting its superior robustness. In comparison, algorithms such as PSO and CSO show greater variability, indicating less consistency in their outputs. Figure 3, Figure 4 and Figure 5 depict the convergence behaviors of the tested algorithms across the three datasets. These plots demonstrate that SWOIM quickly minimizes the objective function value in the initial iterations and reaches near-optimal solutions with fewer evaluations, reflecting its efficient convergence. This advantage can be attributed to integrating the simulated annealing-based acceptance mechanism and Cauchy-distributed perturbations, which enhance global search effectiveness early on while ensuring reliable convergence later in the process. Overall, SWOIM performs better than the other approaches in addressing the optimization task.

Table 3. Comparison of experimental results of multiple algorithms running independently.

Case Scale (Number of Projects, Number of Assignments, Number of Personnel)	Algorithm Name	Optimum Value	Average Value	Standard Deviation
(4,10,6)	CSO	−223,400	−256,160	13,885
	PSO	−245,300	−298,480	19,080
	SWO	−211,300	−220,710	5295
	SMA	−211,100	−222,990	7721
	GWO	−226,000	−255,670	11,273
	SWOIM	−211,100	−211,100	0
(2,10,6)	CSO	0.6261	0.5945	0.0123
	PSO	0.6187	0.5608	0.0210
	SWO	0.6216	0.5958	0.0105
	SMA	0.6313	0.5905	0.0180
	GWO	0.6313	0.5959	0.0165
	SWOIM	0.6324	0.6098	0.0123
(2,10,10)	CSO	0.5989	0.5629	0.0141
	PSO	0.5804	0.5283	0.0201
	SWO	0.6046	0.5682	0.0111
	SMA	0.5922	0.5547	0.0136
	GWO	0.5829	0.5500	0.0116
	SWOIM	0.6132	0.5908	0.0108

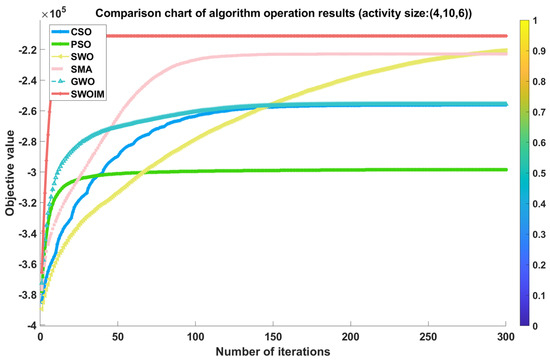
Figure 3. Comparison of convergence curves (4,10,6).

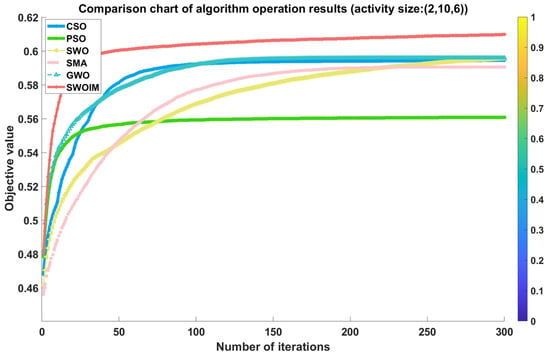
Figure 4. Comparison of convergence curves (2,10,6).

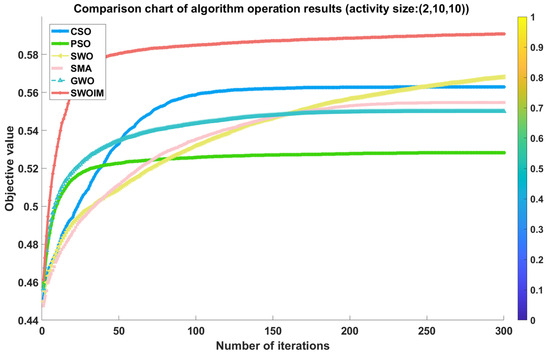
Figure 5. Comparison of convergence curves (2,10,10).

6. Example Analysis

6.1. Case Study Introduction

To validate the applicability of the proposed scheduling model and algorithms, this study presents a practice-oriented case study based on a real-world construction management scenario in a medium-sized construction enterprise. The enterprise concurrently executes two separate projects—one focused on residential construction and the other on municipal infrastructure renovation—each comprising ten tasks assigned to a shared pool of six technicians. This setup captures the inherent complexity of task overlap, shared human resources, and skill-based task allocation, which are characteristic challenges in multi-project management within the construction industry.

Multiple factors, including budget limitations, resource availability, task urgency, and employees’ skill levels, constrain the execution of construction projects. To better reflect real-world construction practices, the proposed model incorporates employee welfare considerations—such as workload equalization, income enhancement, and task fairness—capturing the scheduling challenges associated with high-intensity operations and workforce mobility on construction sites. Drawing on managerial experience from the construction industry, this study assigns a weight of 0.6 to the time objective (highlighting the critical importance of on-time project delivery) and weights of 0.2 each to cost and resource utilization. For the employee welfare objective, the weights are 0.5 for workload balance, 0.3 for working hours, and 0.2 for income growth. The overall optimization balances project performance and employee welfare equally, with a combined target weight of 0.5 for each, aiming to achieve a win–win outcome in scheduling. This case is employed to evaluate the applicability and effectiveness of the proposed SWOIM algorithm in real-world multi-project scheduling scenarios in the construction sector.

Therefore, in this case, the duration of Project one is ${\varphi }_1=0.6$, and the duration of Project two is ${\varphi }_2=0.4$. The project sub-objectives for time $w_1$, cost $w_2$, and resources $w_3$ are weighted at 0.6, 0.2, and 0.2, respectively. The employee sub-objectives for income ${\omega }_1$, time ${\omega }_2$, and equilibrium ${\omega }_3$ are weighted at 0.2, 0.3, and 0.5, respectively. To balance the comprehensive benefits of the project and the welfare of the employees, a weight of 0.5 is applied to both. Some of the data for this case are presented in Table 4, Table 5 and Table 6.

Table 4. Increased benefits for employee completing their assignments.

Project Number	Task Number	Employee Number 1	Employee Number 2	Employee Number 3	Employee Number 4	Employee Number 5	Employee Number 6
1	1	92	90	115	86	65	50
	2	103	67	102	116	112	108
	3	86	103	73	117	93	69
	4	72	86	76	90	91	64
	5	105	78	60	99	103	94
	6	118	71	86	52	52	114
	7	116	82	67	53	67	56
	8	107	52	99	79	75	56
	9	118	111	62	96	54	52
	10	75	51	62	66	71	96
2	1	87	101	70	77	93	87
	2	50	101	86	65	91	57
	3	108	61	69	115	65	73
	4	82	120	53	91	59	85
	5	92	80	108	59	118	75
	6	93	105	72	51	53	110
	7	66	100	103	105	107	107
	8	69	59	55	76	117	107
	9	78	91	69	68	69	95
	10	110	101	100	99	104	53

Table 5. Immediate relationships between the tasks of the project.

Project Number	Preceding Operation	Subsequent Operation
1	1	3
	4	7
	6	8
	8	10
2	2	5
	3	5
	4	8
	8	10

Table 6. Basic pay for personnel.

	Basic Salary
Employee number 1	6267
Employee number 2	6128
Employee number 3	6159
Employee number 4	5966
Employee number 5	6208
Employee number 6	6134

Other specific experimental data are shown in Appendix A.

6.2. Algorithm Operation Results and Analysis

6.2.1. Results of Running the Improved Spider Wasp Optimization Algorithm

Figure 6 illustrates the outcomes generated by the SWOIM algorithm under various constraints, including task distribution, resource allocation, skill matching, scheduling time, budget limits, and employee welfare enhancement (note that the algorithm settings remain consistent with the previous performance evaluation). The findings indicate a uniform increase in staff compensation, reflecting a more equitable income distribution. This outcome suggests that the scheduling strategy strengthens organizational efficiency and boosts employee morale and commitment. Such a compensation growth pattern demonstrates strong potential for promoting the enterprise’s long-term stability and further confirms the algorithm’s practical value.

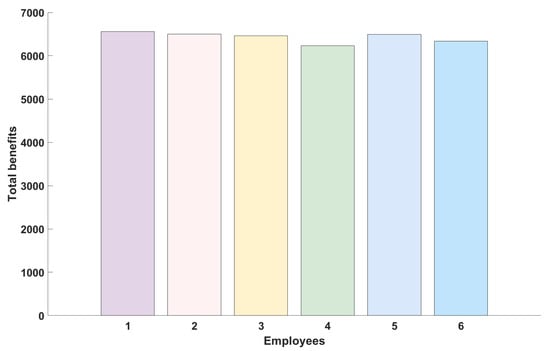
Figure 6. Total employee benefits (each color represents a different employee).

6.2.2. Scheduling Optimization Results and Analysis

This case study applies the SWOIM framework, which integrates considerations such as task prioritization, limitations in resources and time, required skill sets, budget restrictions, and employee welfare targets. The findings confirm that the method efficiently produces practical and well-optimized staff assignment plans for both projects. As illustrated in Figure 6, all six employees’ cumulative incomes and benefits improved post-optimization, with the increases distributed relatively evenly. This reflects the model’s ability to support equitable task distribution and balanced workloads, enhancing employee morale and perceived fairness within the organization. Such fairness is particularly vital in the construction sector, where workforce stability and motivation directly impact project progress and on-site safety. Figure 7 presents the refined task scheduling for each employee across both projects. For example, in sequence, Employee 1 is scheduled to complete Task 4 on Project 2 and Tasks 8 and 2 on Project 1. This structured task arrangement reduces downtime, avoids overlaps, and aligns with real-world construction workflow requirements. Figure 8 shows each staff member’s total number of working days, revealing that all six employees were assigned between 27 and 29 working days. This outcome suggests a well-managed distribution of labor, avoiding the concentration of tasks on a few individuals and mitigating the risks of staff underutilization, both critical in labor-dependent construction environments.

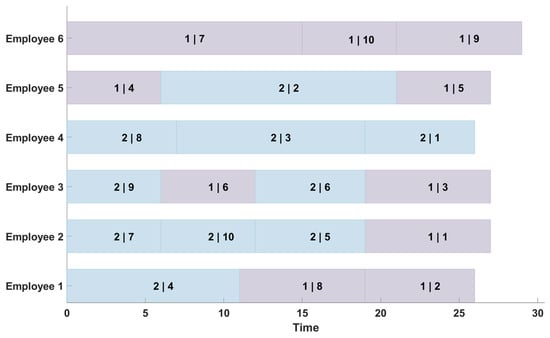
Figure 7. Employee task scheduling across two projects, with colors indicating project affiliation (blue for Project 1, purple for Project 2).

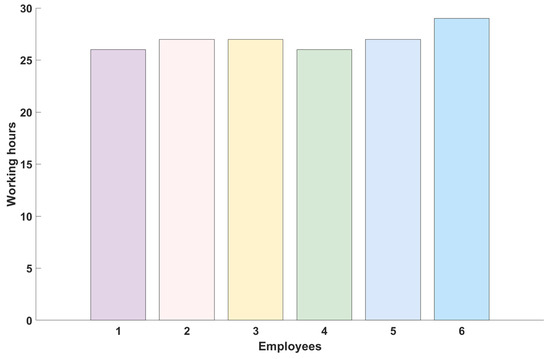
Figure 8. Employee working hours (each color represents a different employee).

It is important to emphasize that while this section mainly highlights optimization results concerning employee welfare, such as increases in income, improved task distribution, and more balanced working hours, these metrics indirectly indicate enhanced organizational performance, particularly in project implementation. By fostering fair workload allocation and ensuring a reasonable distribution of working time, the model boosts employee morale and efficiency and motivates staff through increased earnings [2]. These improvements collectively lead to shorter project timelines, more effective cost management, and optimized resource deployment, reinforcing the objective of improving overall project execution efficiency.

In summary, the scheduling method proposed in this paper optimizes the comprehensive benefits of multi-project scheduling by integrating employee welfare factors. It constructs a more reasonable and human-centered scheduling scheme through SWOIM.

6.3. Management Recommendations

Based on this study, we propose the following management recommendations to help managers improve staff scheduling in a multi-project environment while enhancing employee welfare:

(1) Emphasize Employee Welfare: Integrate employee welfare into scheduling decisions by balancing work intensity with salary rewards, fostering employee loyalty, and reducing turnover. Regularly conduct employee satisfaction surveys, adjust scheduling plans to align with employee needs, and minimize excessive overtime and unreasonable task allocations.

(2) Optimize Resource Allocation: Effectively allocate project resources to prevent conflicts and resource wastage. Use intelligent optimization algorithms to improve the scientific and rational approach to personnel scheduling, ensuring the appropriate distribution of resources and reducing redundancy.

(3) Adopt Adaptive Optimization: By incorporating adaptive weight adjustment and feedback mechanisms, context-sensitive scheduling strategies can be developed and evolve in response to increasing project complexity and workforce feedback.

These findings emphasize that a well-being-oriented scheduling approach can simultaneously enhance project performance and employee well-being, offering construction companies a pathway to more sustainable and innovative workforce management.

7. Conclusions

This study explores the challenge of personnel scheduling across multiple projects with particular emphasis on employee welfare. After outlining the problem, key constraints—including task assignment, resource availability, skill requirements, time limits, cost restrictions, and welfare growth—are incorporated within a framework that seeks to maximize project performance and employee well-being. A multi-objective mixed-integer programming model is developed, and to facilitate efficient computation, the model is converted into a single-objective form using a weighted approach. To solve this NP-hard problem with complex decision variables, SWOIM is introduced. Two sets of experiments are conducted to assess the algorithm’s effectiveness and advantages: the first compares multiple algorithms across varying test scales to evaluate robustness and performance, while the second applies the enhanced algorithm to a real-world case for practical validation. The results confirm that the proposed method delivers strong performance, producing tailored personnel allocation strategies for employee welfare in multi-project settings. The optimized approach boosts resource use and project delivery efficiency and better supports staff needs, strengthening organizational competitiveness and sustainability. Ultimately, the model achieves the dual goals of enhancing overall project outcomes and workforce welfare.

Compared to traditional algorithms, the algorithm developed in this study demonstrates significant superiority in managing multi-project staff scheduling. Furthermore, this paper analyzes and designs a mixed-integer planning model centered on employee welfare, integrating considerations of project management efficiency and employee welfare needs. The model addresses multiple objectives and constraints comprehensively and thoroughly accounts for practical complexities, thereby enriching the theory of resource scheduling. This promotes a paradigm shift in scheduling models from solely project-benefit-oriented to a balanced approach that integrates employee welfare and project benefit considerations.

The limitations of this study and directions for future research include the following: Firstly, the current model assumes that employee behavior remains consistent and that there is complete adherence to the scheduled plan. However, in real-world scenarios, variations in individual performance and deviations from the set schedule are often observed, which could reduce the overall effectiveness of the scheduling system. Secondly, the welfare criteria used in this research are limited to task distribution, fairness, and monetary rewards without considering broader factors like psychological well-being, career growth, and work–life balance. Thirdly, the model is based on a static scheduling system and does not account for real-time adjustments or the dynamic reallocation of tasks. Future studies could explore incorporating behavioral response models or applying robust optimization techniques to address these challenges better and accommodate fluctuations in employee behavior. Furthermore, the welfare assessment could be enriched by including a wider range of indicators based on employee satisfaction surveys. Lastly, integrating real-time feedback with dynamic scheduling could significantly improve the model’s applicability and adaptability in fluctuating project conditions.