Impact of Multi-Defect Coupling Effects on the Safety of Shield Tunnels and Cross Passages
Abstract
1. Introduction
2. Engineering Background
2.1. Project Overview
2.2. Engineering Pathologies and Defect Manifestations
- (1)
- Structural cracking conditions
- (2)
- Segment offset conditions
- (3)
- Tunnel deformation conditions
- (4)
- Cavity conditions behind the lining
3. Characteristics and Intrinsic Causes of Engineering Defects
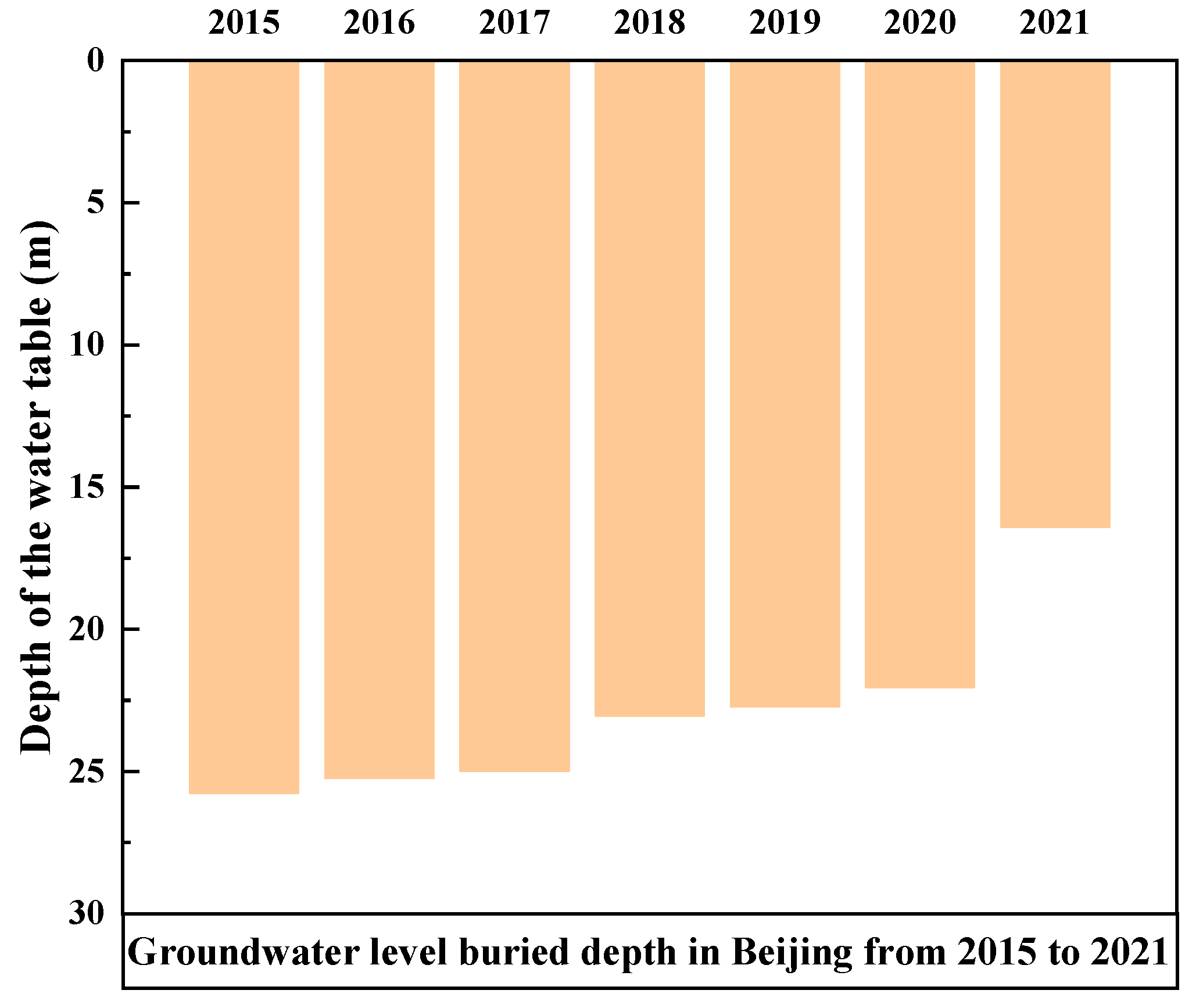
- (1)
- Environmental exposure factors
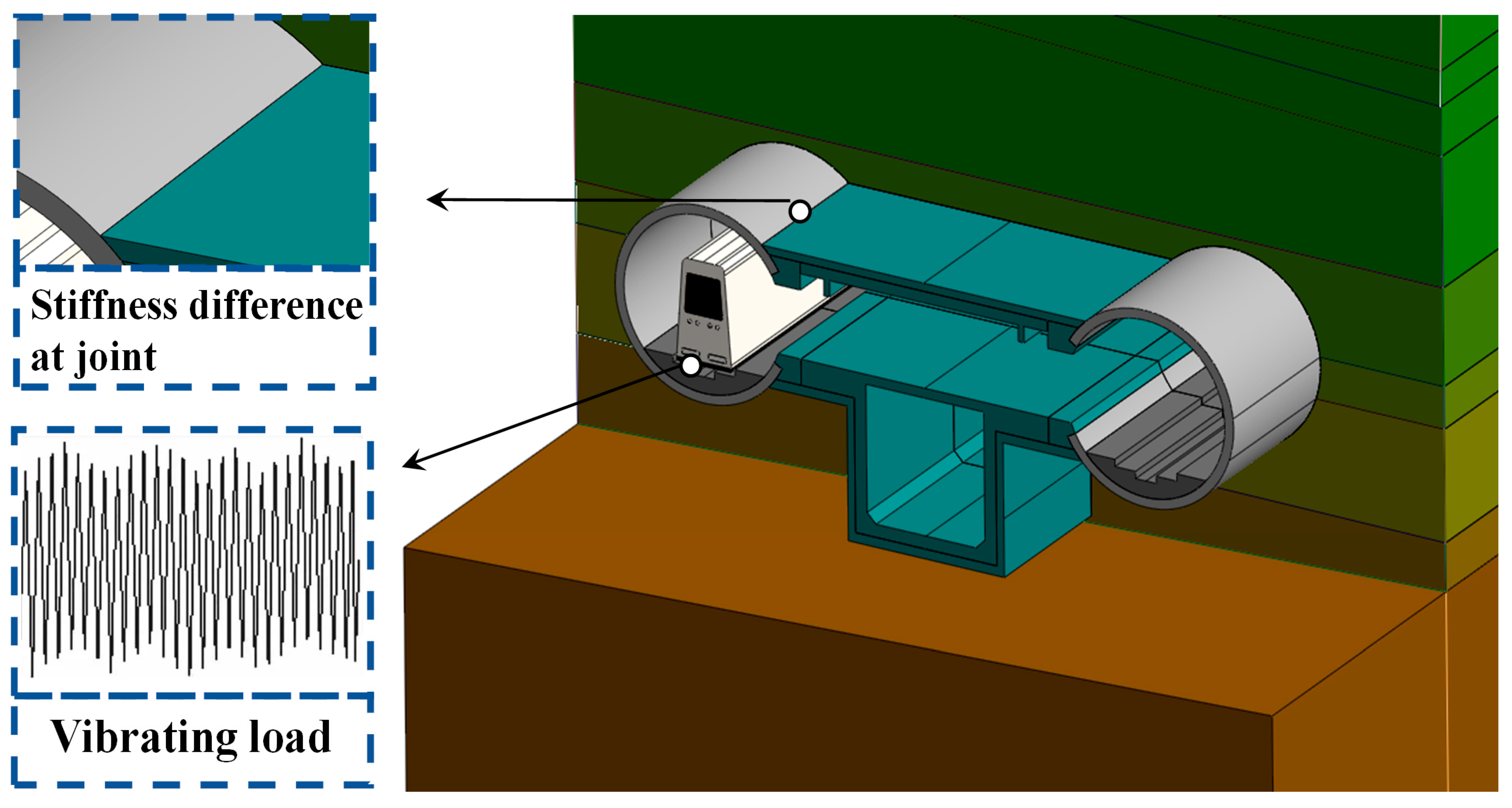
- (2)
- Structural intrinsic factors
4. Structural Mechanical Response of Tunnel and Connecting Passage Under Coupled Effects of Multiple Defects
4.1. Numerical Model
4.1.1. Model and Material Parameters
4.1.2. Boundary Conditions
4.1.3. Numerical Calculation Process
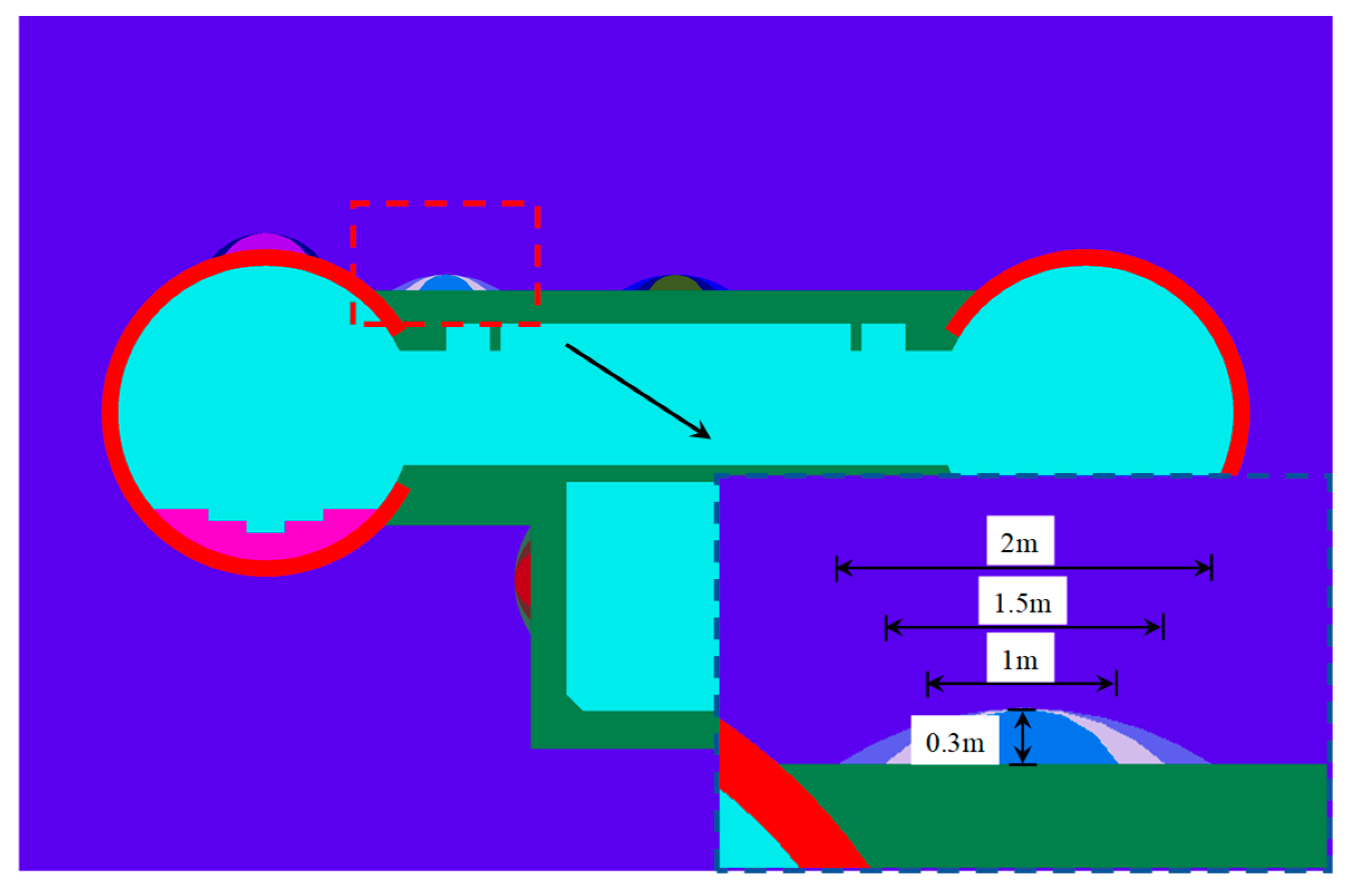
4.2. Calculation Cases
4.3. Analysis of Numerical Calculation Results
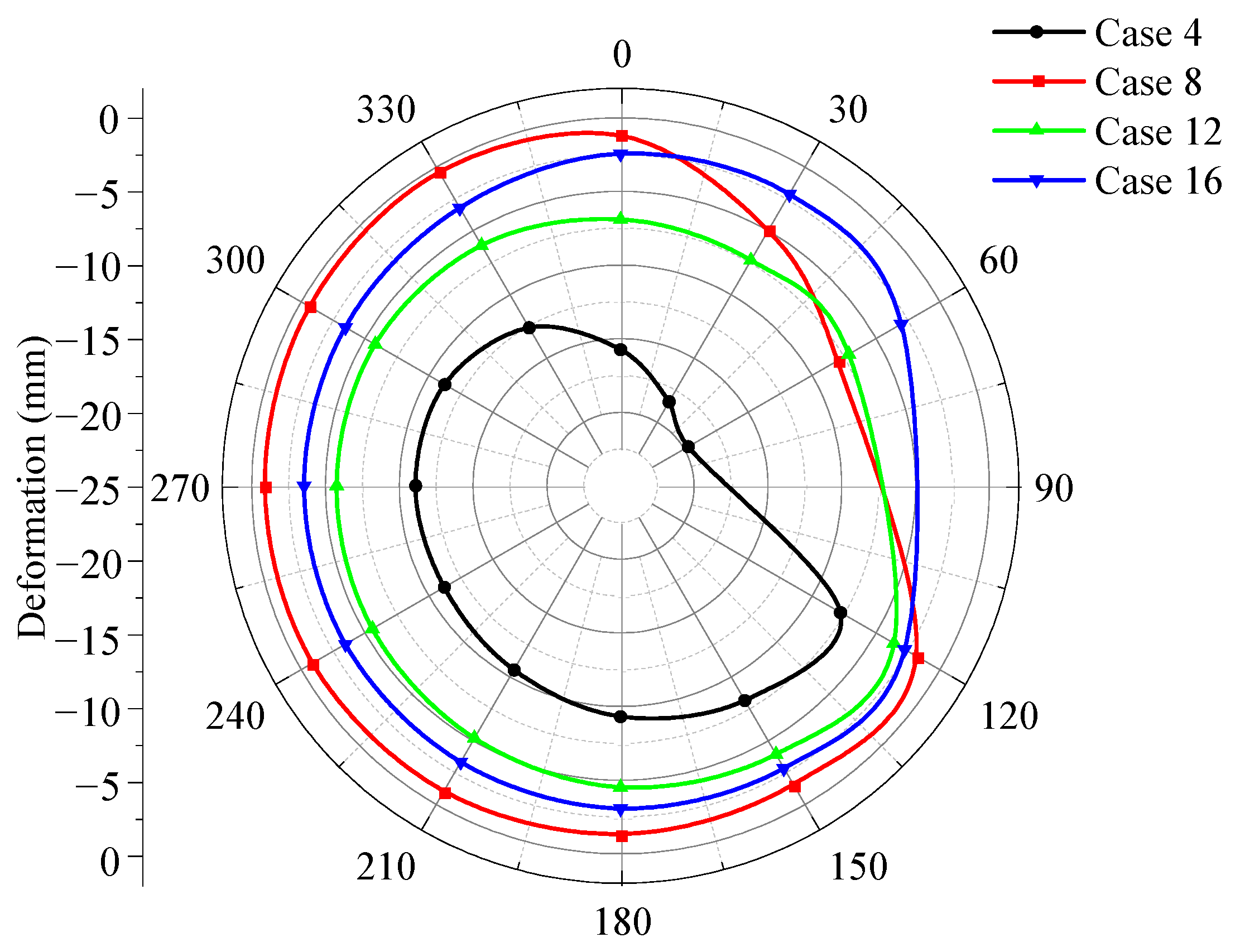
4.3.1. Influence Patterns of Defect Locations on Structural
4.3.2. Influence Patterns of Defect Severity on Structural Response
- (1)
- Influence patterns of leakage intensity on structural response
- (2)
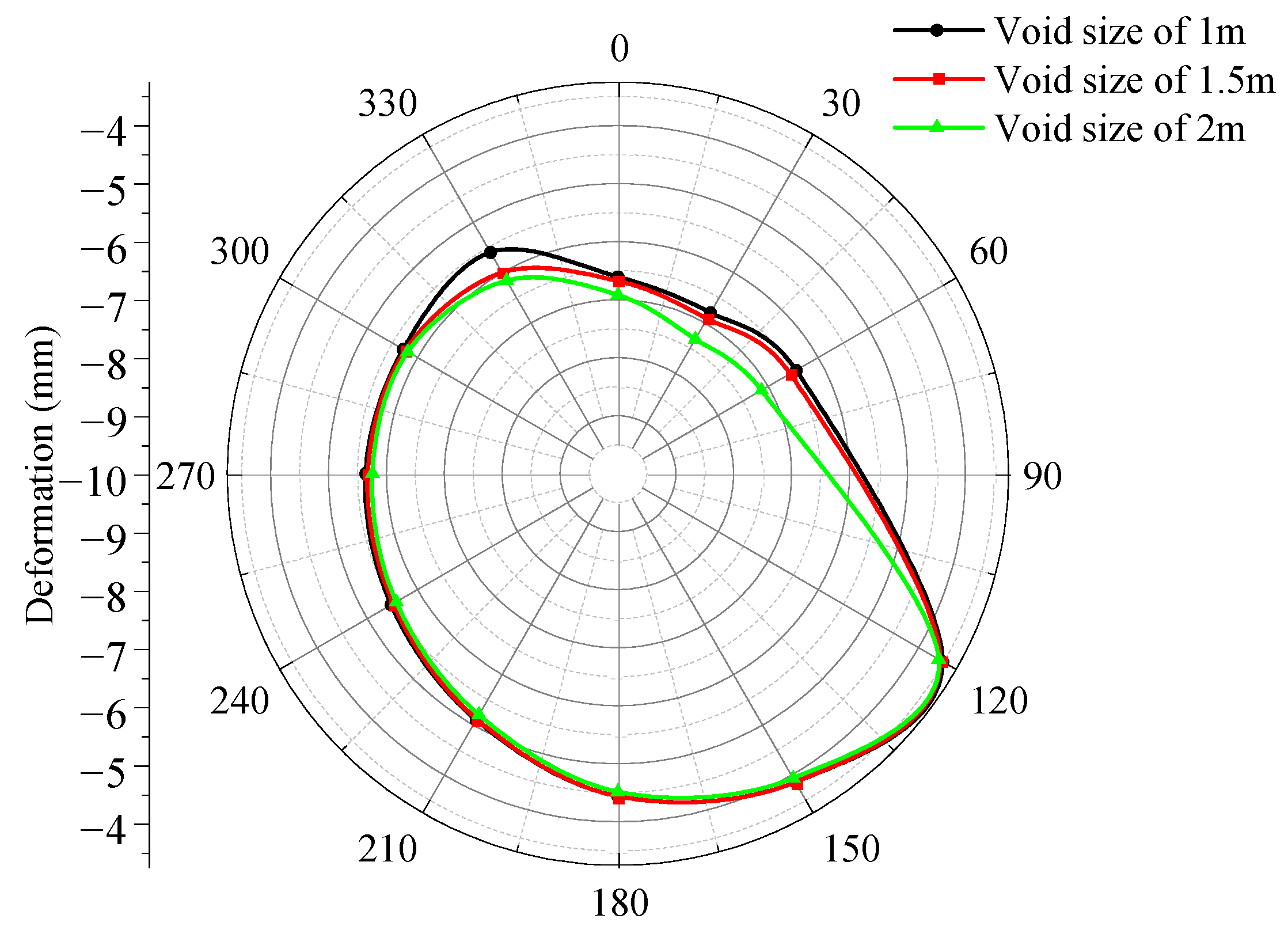
- Influence patterns of void size on structural response
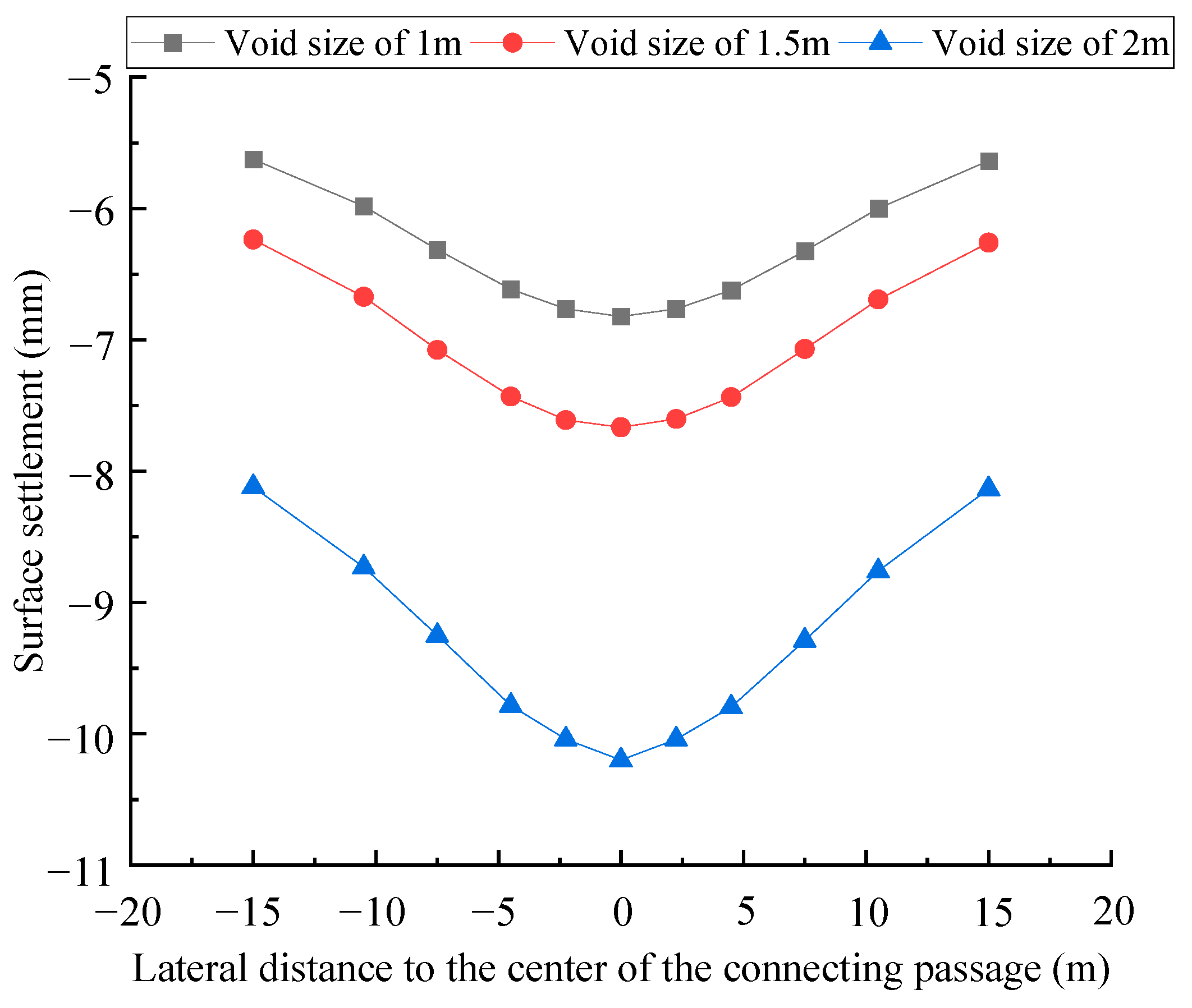
- (3)
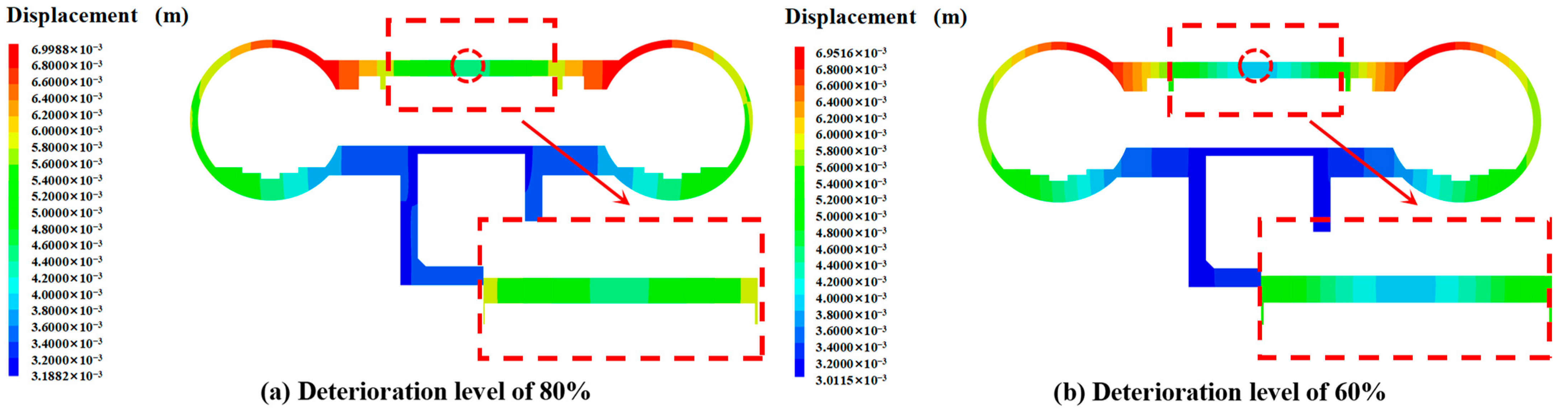
- Influence Patterns of Structural Deterioration Level
5. Bayesian Network-Based Safety Risk Assessment Method for Shield Tunnels and Connecting Passages
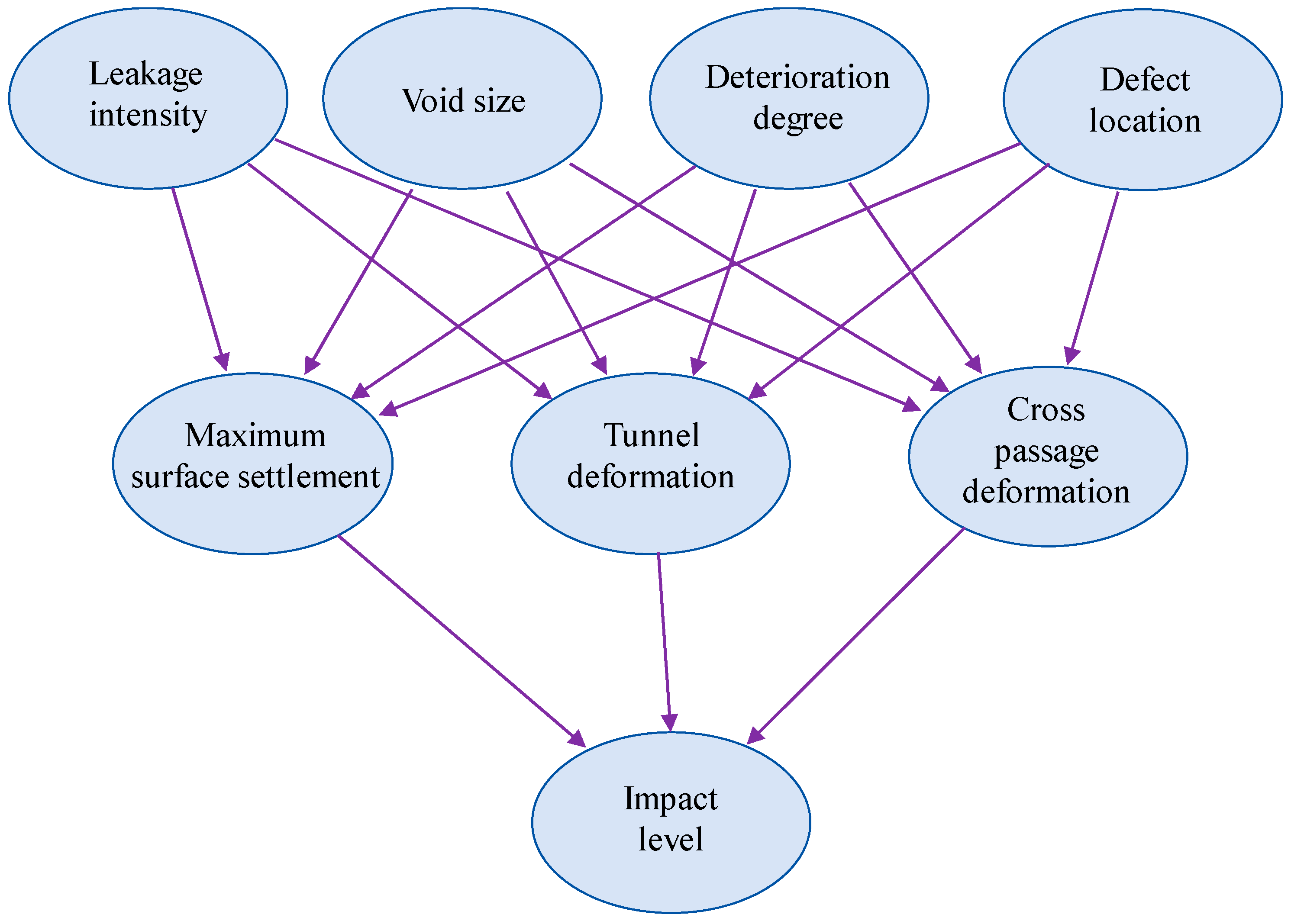
5.1. Establishment of Bayesian Network Model
5.2. Analysis of Safety Risk Factors
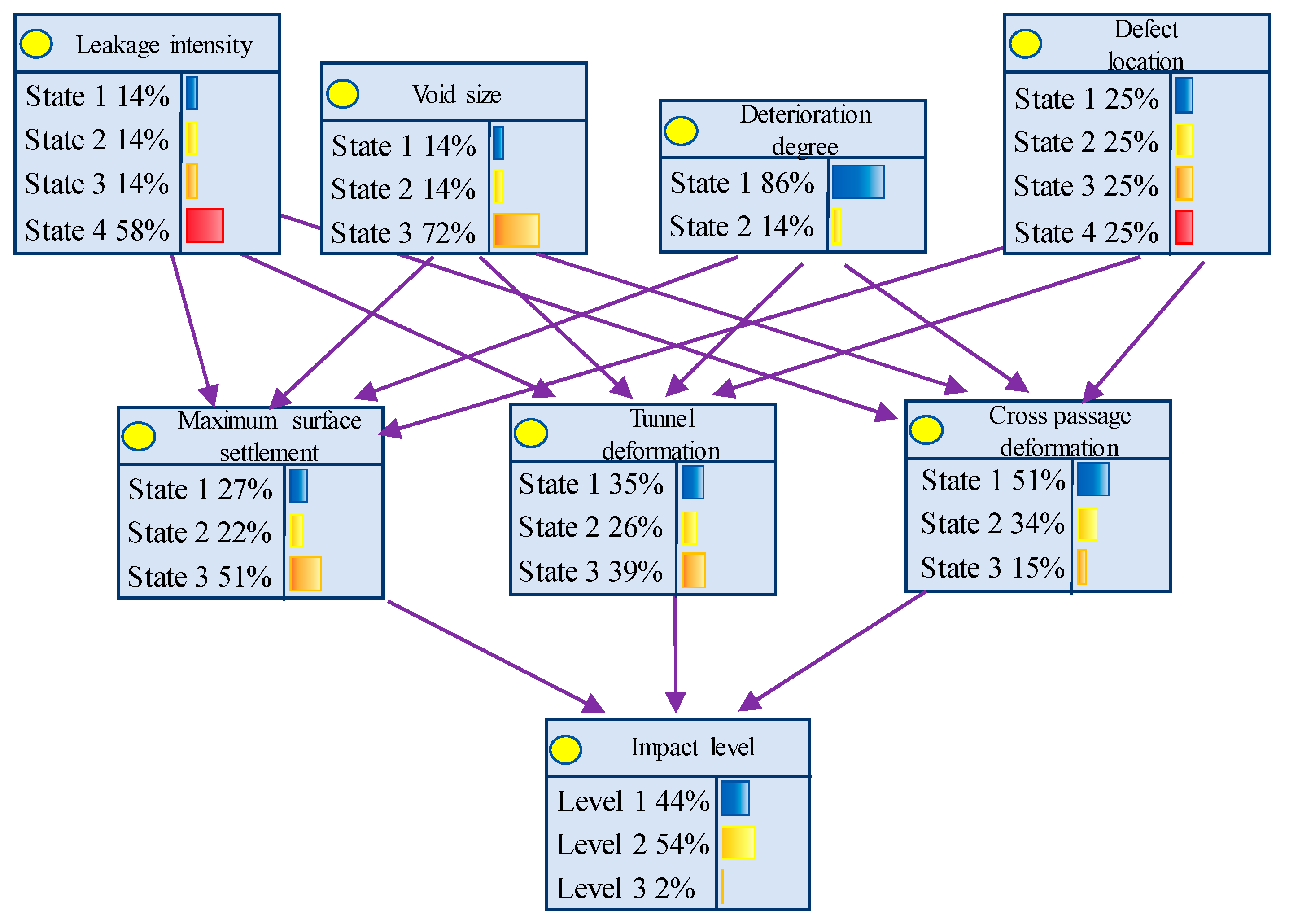
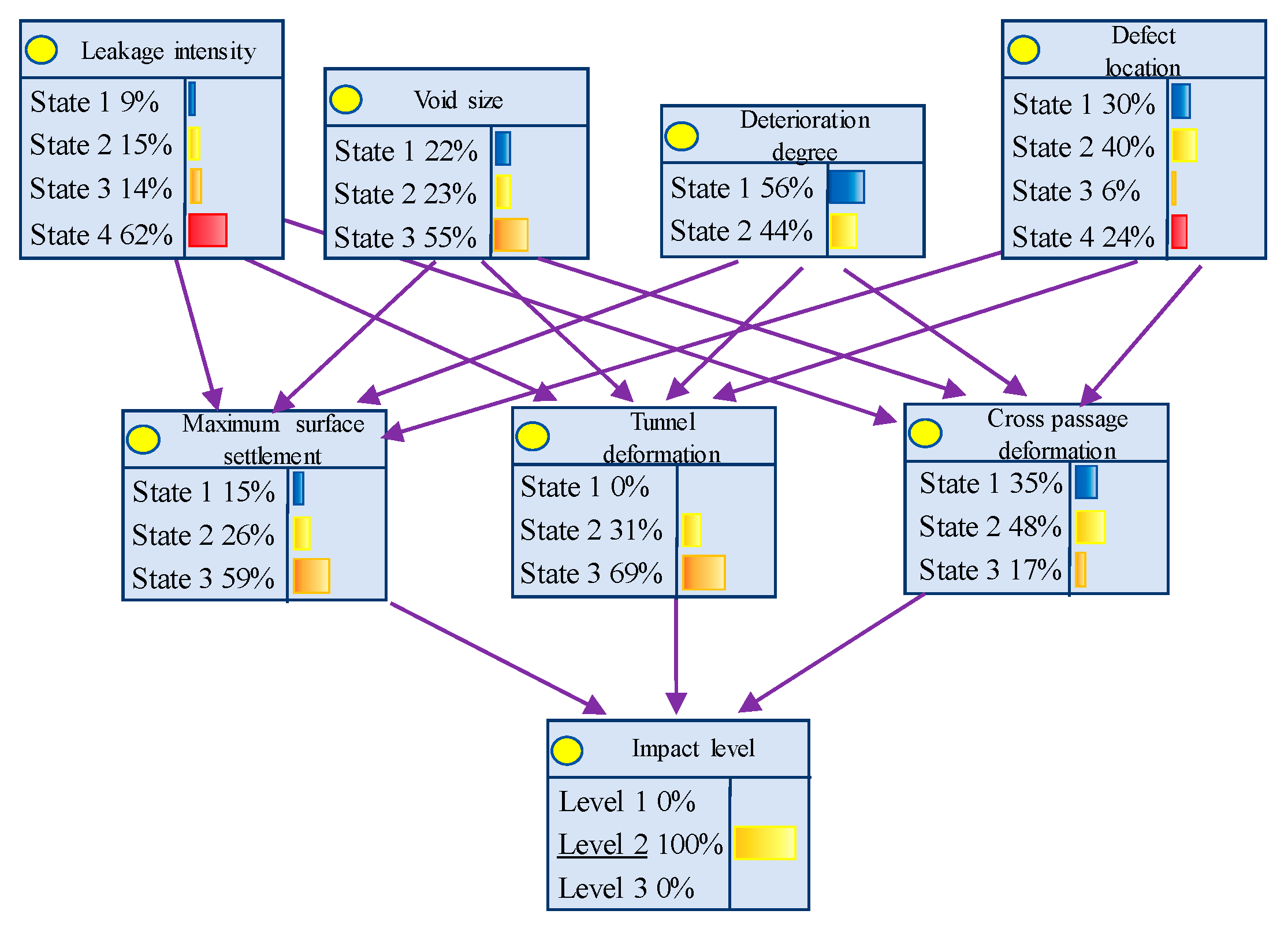
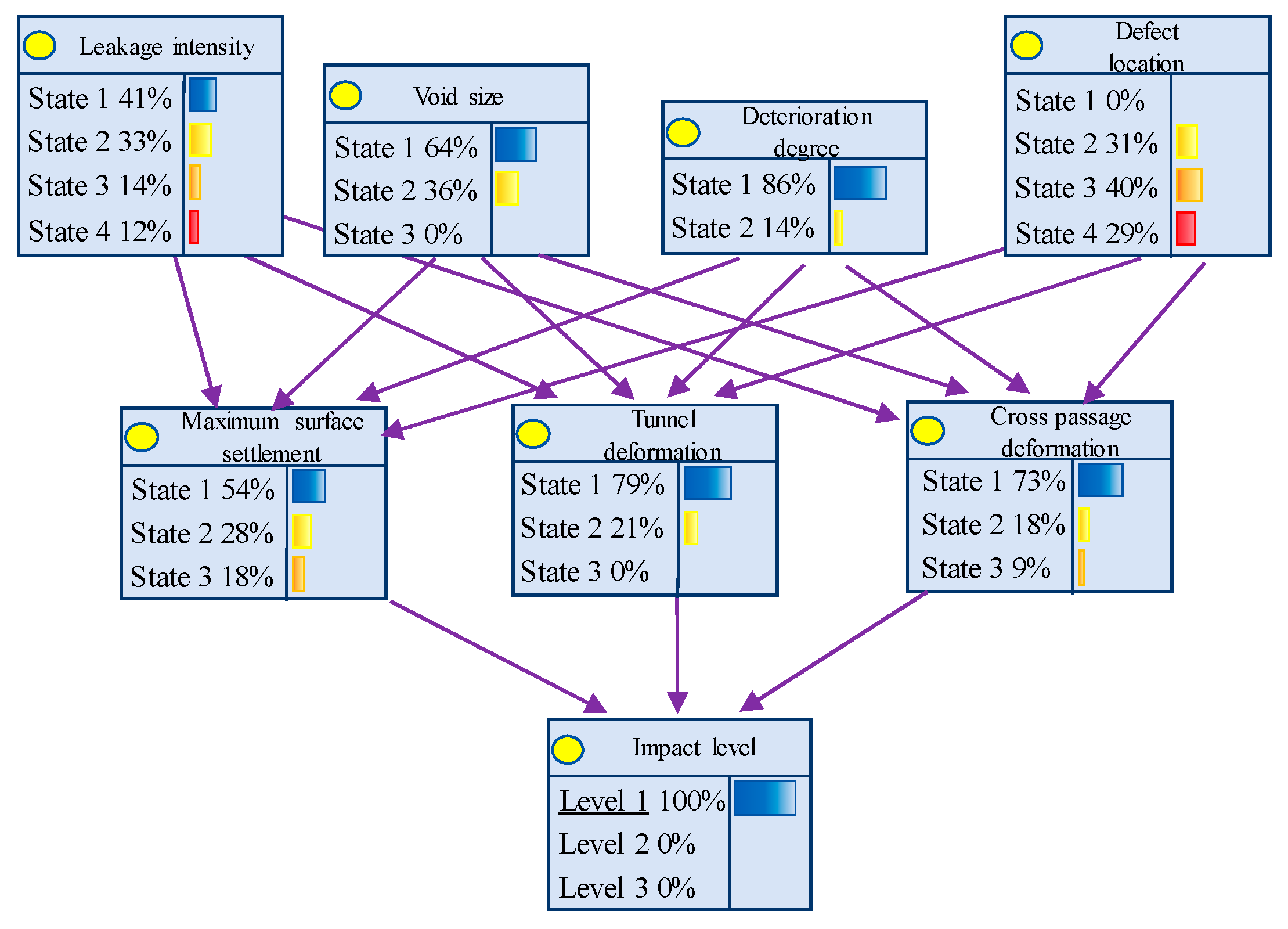
5.3. Safety Risk Prediction for Shield Tunnels and Connecting Passages
6. Conclusions
- (1)
- Statistical analysis indicates that the primary potential hazards in the section include leakage caused by missing drainage pipes in the pump room of the connecting passage located in the middle section, as well as partial leakage in the lower-layer foundational concrete structure of the track bed, voids, and tunnel deformation. Through comprehensive analysis, the core factors contributing to structural defects are non-uniform deformation at segment joints and train vibration effects. The rise in groundwater levels forming water-rich zones serves as the primary source of tunnel defects, and the deterioration of structural defects exacerbates structural damage.
- (2)
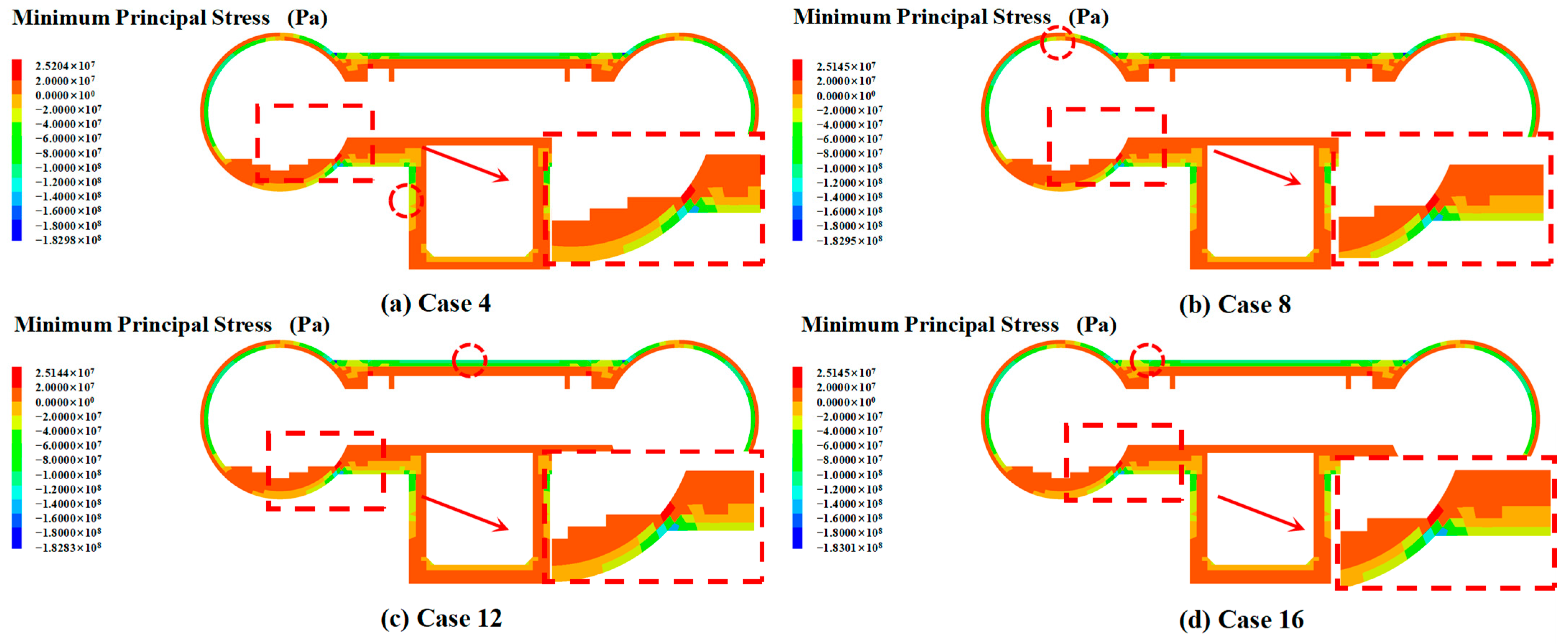
- Numerical simulations were conducted to investigate the impacts of multi-defect coupling effects on shield tunnels and connecting passages. The results demonstrate that when structural defects are closer to the bottom, the dissipation values of pore water pressure in the stratum near leakage areas increase, the volume of affected soil expands, and cumulative surface settlement values escalate, leading to more pronounced ground and structural deformations. Peak principal stresses and the most significant stress variations occur at the connection zones between twin tunnels and the connecting passage, indicating that special attention should be paid to stress states at these locations during defect prevention and control.
- (3)
- Under multi-defect coupling conditions, void size variations exert the most significant influence on structural stress states. Due to the loss of surrounding rock constraints in lining void areas, the lining exhibits compressive deformation toward void cavities in both longitudinal and circumferential directions, with deformation trends becoming more pronounced as void sizes increase. Larger voids notably widen and deepen surface settlement troughs.
- (4)
- The established Bayesian network model enables safety risk diagnosis for existing defects. Analysis reveals that structural safety negatively correlates with leakage degree, void size, deterioration level, and burial depth of defect locations. Void size emerges as a critical influencing factor for safety, where increased void dimensions elevate safety risks, necessitating timely monitoring and protective measures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, X.; Sun, Q.H. Analysis of progressive collapse characteristics of shield tunnels. Tunn. Constr. 2021, 41, 913–922. [Google Scholar]
- Liu, Y.J. Research on Structural Safety and Dynamic Characteristics of Beijing Metro Shield Tunnels Under Defect Conditions. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2019. [Google Scholar]
- Guo, Y.X. Study on treatment methods for segment damage and defects in shield tunnels. Mod. Urban Transit 2020, 5, 55–60. [Google Scholar]
- Huang, J.; Zhang, D.L.; Liang, W.H.; Dong, F.; Li, A.; Zhao, G.; Yang, K.; Niu, X.K. Review of safety control technologies for tunnel structures during service period. Railw. Stand. Des. 2024, 68, 1–19. [Google Scholar]
- Dong, F.; Fang, Q.; Zhang, D.L. Analysis of defect conditions in Beijing Metro operational tunnels. China Civ. Eng. J. 2017, 50, 104–113. [Google Scholar]
- Ministry of Railways Maintenance Bureau. Railway Maintenance Technical Manual (Tunnels); China Railway Publishing House: Beijing, China, 1997. [Google Scholar]
- Asakura, T.; Kojima, Y. Tunnel maintenance in Japan. Tunn. Undergr. Space Technol. 2003, 18, 161–169. [Google Scholar] [CrossRef]
- Lee, W.F.; Ishihara, K. Piping failure of a metro tunnel construction. In Proceedings of the International Conference on Forensic Geotechnical Engineering, Mumbai, India, 10–12 December 2015; Springer: New Delhi, India, 2016; pp. 123–140. [Google Scholar]
- Huang, C.; Chen, W.J.; Su, D.; Lei, G.P. Review on causes of subway tunnel structural defects and fault tree models. Mod. Tunn. Technol. 2020, 57, 264–272. [Google Scholar]
- Zhang, Z.G.; Mao, M.D.; Pan, Y.T.; Zhang, M.; Ma, S.; Cheng, Z.; Wu, Z. Experimental study for joint leakage process of tunnel lining and particle flow numerical simulation. Eng. Fail. Anal. 2022, 141, 106715. [Google Scholar] [CrossRef]
- Wu, C.X.; Wang, M.W.; Zeng, R.K.; Li, Y.L.; Lu, P.; Zhang, Y.L. Zoning of surrounding rock settlement during joint leakage of underwater shallow-buried shield tunnels. Railw. Eng. 2023, 63, 94–98. [Google Scholar]
- Li, R.; Lei, H.; Ma, C.; Liu, Y.; Liu, N. The development of sand erosion induced by shield-tunnel joint leakage. Eng. Fail. Anal. 2023, 153, 107560. [Google Scholar] [CrossRef]
- Liu, Y.K.; Wu, Y.; Li, W.H.; Zhang, Q.-S.; Liu, R.T.; Bai, J.-W. Development of a water leakage model test system and investigation of the water leakage behavior in subsea shield tunnels during operation. Measurement 2024, 233, 114723. [Google Scholar] [CrossRef]
- Zhang, C.P.; Feng, G.; Zhang, X.; Han, K.H.; Zhang, D.L. Safety state analysis of tunnel structures under the influence of dual voids behind linings. Chin. J. Geotech. Eng. 2015, 37, 487–493. [Google Scholar]
- Ding, Z.D.; Ji, X.F.; Li, X.Q.; Ren, Z.; Zhang, S. Influence of symmetric and asymmetric voids on mechanical behaviors of tunnel linings: Model tests and numerical simulations. Symmetry 2019, 11, 774. [Google Scholar] [CrossRef]
- Wang, S.H.; Wang, P.Y.; Liu, Y.; Zhu, B.Q. Experimental study on failure modes of tunnels under void conditions at different locations. J. Northeast. Univ. (Nat. Sci.) 2020, 41, 863–869. [Google Scholar]
- Shi, Y.; Chen, Z.; Wei, D.; Zhang, T.; Zhou, X.; Zhao, X.; Hu, J.; Zhou, Y. Analysis of structural response of subway shield tunnel lining under the influence of cavities. Adv. Civ. Eng. 2021, 2021, 6682283. [Google Scholar] [CrossRef]
- Li, F.H.; Li, R.; Jiang, Y.L.; Gao, H.; Wang, Y.B.; Wang, P.X. Experimental study on the influence of void grouting behind secondary lining with formwork on lining mechanical behavior. Mod. Tunn. Technol. 2021, 58, 147–158. [Google Scholar]
- Li, J.C.; Wang, Z.Y.; Tan, Y.; Cao, Y.-C. Failure evolution and mechanism of ground collapse due to exfiltration of shallowly buried water pipeline. Eng. Fail. Anal. 2024, 162, 108342. [Google Scholar] [CrossRef]
- Li, Y.; Yu, G.; He, L.; Cui, Y. Microscopic investigation of the occurring process of contact erosion. Soils Found. 2025, 65, 101234. [Google Scholar] [CrossRef]
- Liang, Y.N.; Yuan, Y.S. Effects of sulfate erosion environmental factors on concrete performance degradation. J. China Univ. Min. Technol. 2005, 34, 452–457. [Google Scholar]
- Nie, L.; Xu, J.; Bai, E. Dynamic stress-strain relationship of concrete subjected to chloride and sulfate attack. Constr. Build. Mater. 2018, 165, 232–240. [Google Scholar] [CrossRef]
- Rusati, P.K.; Song, K.I. Magnesium chloride and sulfate attacks on gravel-sand-cement inorganic binder mixture. Constr. Build. Mater. 2018, 187, 565–571. [Google Scholar] [CrossRef]
- Wang, H.; Huang, X.; Jin, G.L. Evolution of physical and mechanical properties of concrete specimens under acid corrosion. Hazard Control Tunn. Undergr. Eng. 2023, 5, 57–64. [Google Scholar]
- Cao, S.Y.; Zhu, B.L. Properties of corroded concrete and reinforced concrete. J. Tongji Univ. 1990, 18, 239–242. [Google Scholar]
- Rahman, M.M.; Bassuoni, M.T. Thaumasite sulfate attack on concrete: Mechanisms, influential factors and mitigation. Constr. Build. Mater. 2014, 73, 652–662. [Google Scholar] [CrossRef]
- Shin, J.H.; Kim, S.H.; Shin, Y.S. Long-term mechanical and hydraulic interaction and leakage evaluation of segmented tunnels. Soils Found. 2012, 52, 38–48. [Google Scholar] [CrossRef]
- Zhang, D.M.; Ma, L.X.; Zhang, J.; Hicher, P.; Juang, C. Ground and tunnel responses induced by partial leakage in saturated clay with anisotropic permeability. Eng. Geol. 2015, 189, 104–115. [Google Scholar] [CrossRef]
- Wu, H.N.; Shen, S.L.; Chen, R.P.; Zhou, A. Three-dimensional numerical modelling on localized leakage in segmental lining of shield tunnels. Comput. Geotech. 2020, 122, 103549. [Google Scholar] [CrossRef]
- Li, Q.T. Numerical simulation and analysis of structural defects in soft soil metro shield tunnels. Railw. Stand. Des. 2021, 65, 95–103. [Google Scholar]
- Zhang, X. Study on the Influence of Joint Leakage and Soil Permeability Anisotropy on Shield Tunnel Seepage. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2022. [Google Scholar]
- Gong, C.; Wang, Y.; Peng, Y.H.; Ding, W.; Lei, M.; Da, Z.; Shi, C. Three-dimensional coupled hydromechanical analysis of localized joint leakage in segmental tunnel linings. Tunn. Undergr. Space Technol. 2022, 130, 104742. [Google Scholar] [CrossRef]
- Liu, Y.J.; Yang, J.; Yin, Z.Y. Numerical analysis of the impact of internal erosion on underground structures: Application to tunnel leakage. Rock Soil Mech. 2022, 43, 1383–1390. [Google Scholar]
- Zhang, X.; Zhou, J.; Jiang, Y.C.; Horris, K.N. Numerical simulation of the influence of joint leakage and soil permeability anisotropy on shield tunnel seepage. J. Cent. South Univ. (Nat. Sci. Ed.) 2023, 54, 1012–1022. [Google Scholar]
- Park, D. Numerical investigation on the effect of water leakage on the ground surface settlement and tunnel stability. Tunn. Undergr. Space Technol. 2024, 146, 105621. [Google Scholar] [CrossRef]
- Qin, X.; Zhang, G.; Ge, R. Effect of erosion void on segmental tunnel lining: 2D numerical investigation. Transp. Geotech. 2022, 37, 100846. [Google Scholar] [CrossRef]
- Ye, Z.J.; Yang, Y.D. Three-dimensional effects of multiple voids behind lining on the mechanical behavior of tunnel structure. Ain Shams Eng. J. 2022, 13, 101732. [Google Scholar] [CrossRef]
- Qiao, J.; Sun, Y.; Hu, J.; Zhang, W. Mechanical behavior of secondary lining vault void and mold grouting repair considering contact effect. Structures 2023, 56, 105003. [Google Scholar] [CrossRef]
- Wang, D.K.; Luo, J.J.; Wang, G.Q.; Li, F.L.; Hou, Y.J. Dynamic response of heavy-haul railway tunnels under conditions of water-rich surrounding rock and voids at tunnel bottom. J. Harbin Inst. Technol. 2023, 55, 33–42. [Google Scholar]
- Zhang, H.Q.; Ding, Z.D.; Yuan, H. Seismic vulnerability study of highway tunnels considering lining thinning and voids. J. Nat. Disasters 2024, 33, 164–174. [Google Scholar]
- Tian, C.; Huang, L.; Liang, Y. Longitudinal deformation mechanism of shield tunnels caused by erosion voids in the underlying soil. Tunn. Undergr. Space Technol. 2025, 157, 105890. [Google Scholar] [CrossRef]
- Yasuda, N.; Tsukada, K.; Asakura, T. Elastic solutions for circular tunnel with void behind lining. Tunn. Undergr. Space Technol. 2017, 70, 274–285. [Google Scholar] [CrossRef]
- Shao, S.; Wu, Y.M.; Fu, H.L. Modified calculation model for internal forces of tunnel vault voids with insufficient thickness based on load-structure method. Mod. Tunn. Technol. 2022, 59, 188–196. [Google Scholar]
- Xie, S.L.; Hu, A.F.; Xiao, Z.R.; Wang, M.-H.; Hu, X.-J.; Della Vecchia, G.; Mariani, S. Analysis of two-dimensional consolidation behavior of soils under cyclic loading considering exacerbated tunnel leakage. Comput. Geotech. 2024, 174, 106124. [Google Scholar] [CrossRef]
- Luo, T.X.; Zhou, Y.F.; Zheng, Q.Z.; Hou, F.; Lin, C. Lightweight deep learning model for identifying tunnel lining defects based on GPR data. Autom. Constr. 2024, 165, 105506. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, S.; Yan, L.; Zhang, J.; Zheng, Y.; Yang, H. Intelligent recognition of tunnel lining defects based on deep learning: Methods, challenges and prospects. Eng. Fail. Anal. 2025, 170, 109332. [Google Scholar] [CrossRef]
- Dou, H.; Lv, Y.; Sun, X.; Liu, X.; Li, Z. Research on health evaluation method of single ring segment of subway shield tunnel under multi-defect coupling. Railw. Stand. Des. 2025, 69, 11–19. [Google Scholar]
- Fu, S. Research on the Evaluation of Safety Status of Tube Sheet Structure of Metro Shield Tunnel. Master’s Thesis, Xi’an University of Architecture and Technology, Xi’an, China, 2024. [Google Scholar]
- Tu, S.Q.; Li, W.; Zhang, C.P.; Liu, T.X.; Wang, L.B.; Jin, Z.X. Model test and discrete element method simulation of tunnel face stability in sand-gravel inclined layered stratum. Comput. Geotech. 2024, 172, 106456. [Google Scholar] [CrossRef]
- Tu, S.Q.; Li, W.; Zhang, C.P.; Chen, W. Effect of inclined layered soils on face stability in shield tunneling based on limit analysis. Tunn. Undergr. Space Technol. 2023, 131, 104773. [Google Scholar] [CrossRef]
- Jin, Z.X.; Zhang, C.P.; Li, W.; Tu, S.Q.; Wang, L.B.; Wang, S.X. Stability analysis for excavation in frictional soils based on upper bound method. Comput. Geotech. 2024, 165, 105916. [Google Scholar] [CrossRef]
- Liu, T.X.; Zhang, C.P.; Li, W.; Tu, S.Q.; Wang, L.B.; Jin, Z.X. Face failure mechanism of fault tunnels under high-temperature and high-pressure conditions using the discrete element method. Comput. Geotech. 2025, 179, 107059. [Google Scholar]
- GB 50446-2017; Code for Construction and Acceptance of Shield Tunneling Method. China Architecture & Building Press: Beijing, China, 2017.
- DB11/685-2021; Code for Design of Stormwater Management and Harvest Engineering in Sponge City Construction. Beijing Municipal Government Publications: Beijing, China, 2021.
- Zhong, X.C.; Zhang, J.R.; Qin, J.S.; Zhu, W. Simplified calculation model and influencing factors analysis of equivalent longitudinal bending stiffness for shield tunnels. Rock Soil Mech. 2011, 32, 132–136. [Google Scholar]
- Huang, H.W.; Xu, L.; Yan, J.L. Study on transverse rigidity efficiency of shield tunnels. Chin. J. Geotech. Eng. 2006, 28, 11–18. [Google Scholar]
- Zhang, Y.; Lu, H.F.; Yao, D.X. Study on Deformation and Failure Characteristics of Roof and Floor Mining Based on FLAC3D Model Ubiquitous. Mine Eng. 2020, 08, 361–367. [Google Scholar] [CrossRef]
- Xue, S.Z. Waterproofing Technology for Underground Buildings, 1st ed.; China Architecture & Building Press: Beijing, China, 2003. [Google Scholar]
- GB 50108-2008; Technical Code for Waterproofing of Underground Works. China Planning Press: Beijing, China, 2008.
- Liu, H.J. Research on Computational Models for Health Diagnosis of Highway Tunnels. Ph.D. Thesis, Tongji University, Shanghai, China, 2003. [Google Scholar]
- Liu, H.R.; Zhong, Z.L. Influence of vault voids on stability of tunnel surrounding rock and primary support structure. Chin. J. Undergr. Space Eng. 2014, 10, 619–623. [Google Scholar]
- Wang, T.; Liao, B.C.; Ma, X. Bayesian network-based probabilistic assessment method for construction safety risks. China Civ. Eng. J. 2010, 43, 384–391. [Google Scholar]
- Zhang, L.M. Safety Risk Management of Buildings Induced by Subway Shield Under Uncertain Conditions. Ph.D. Thesis, Huazhong University of Science and Technology, Wuhan, China, 2014. [Google Scholar]
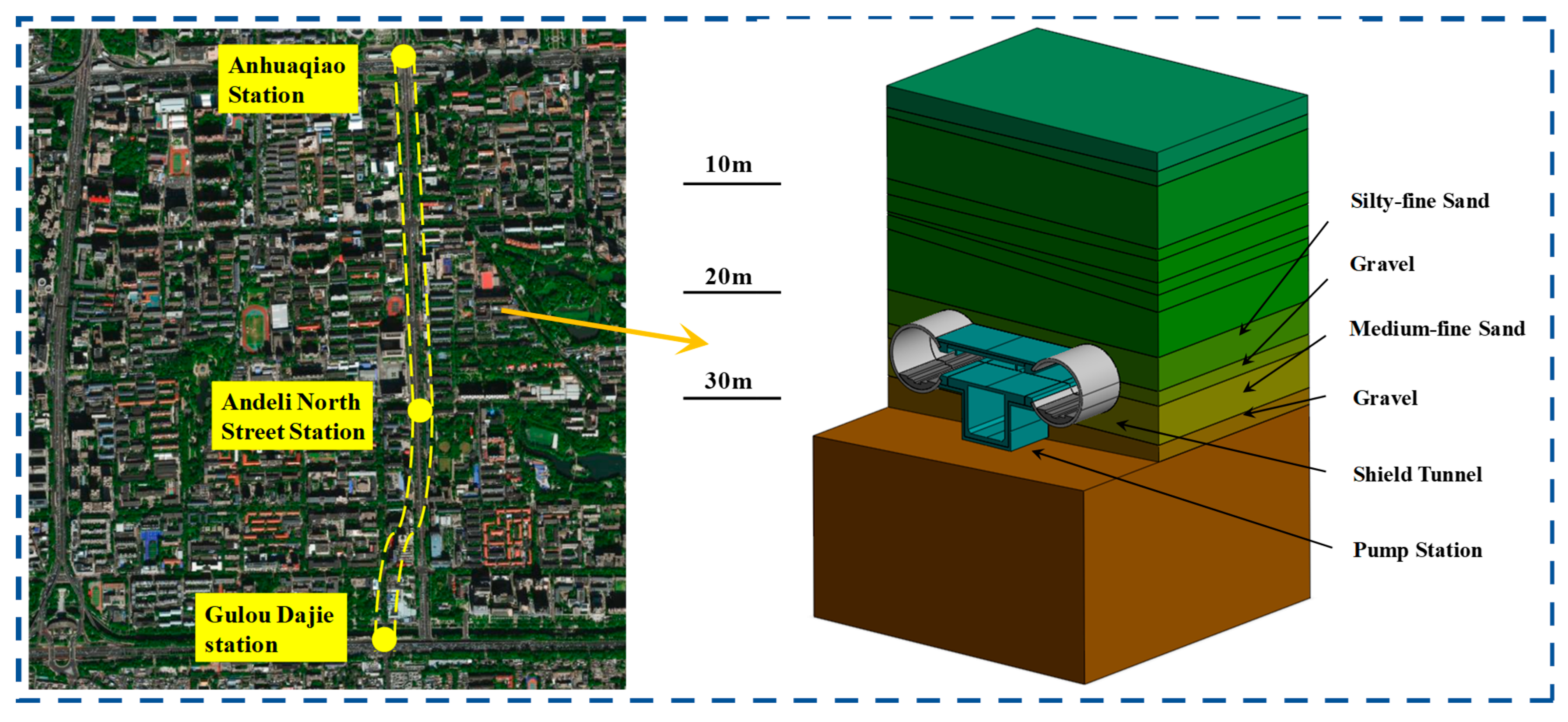

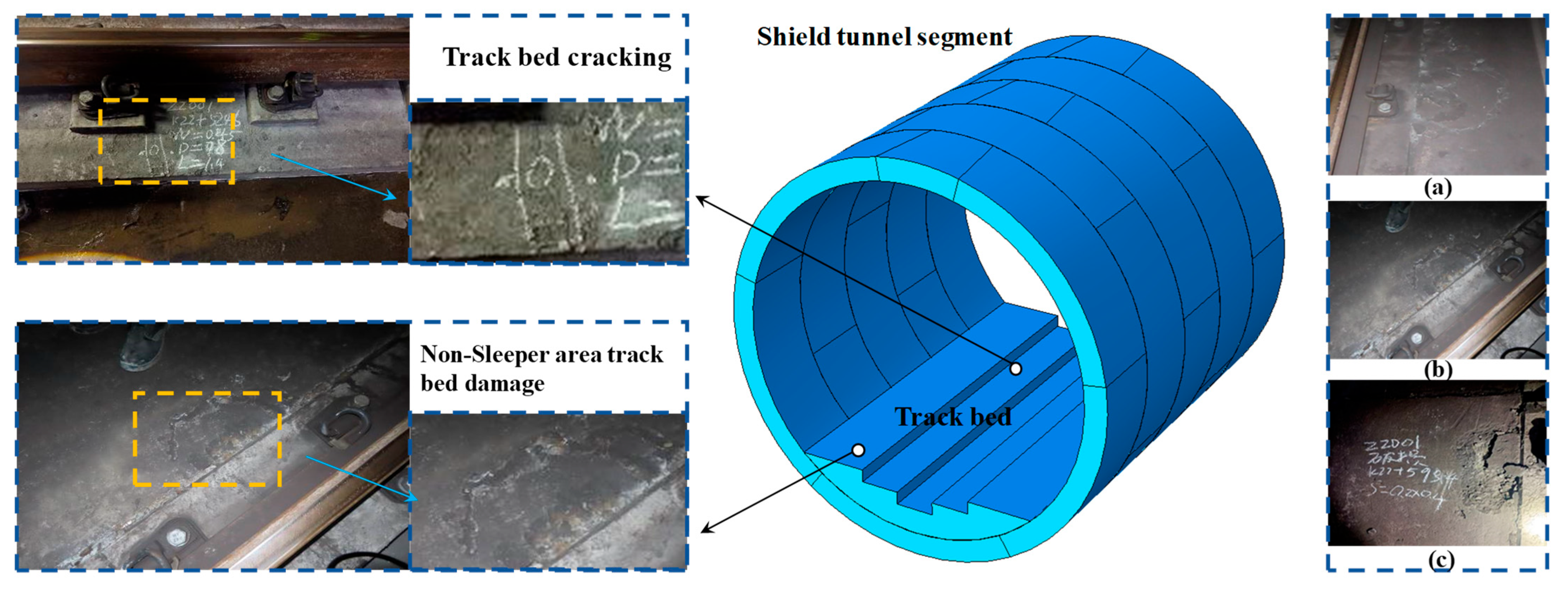



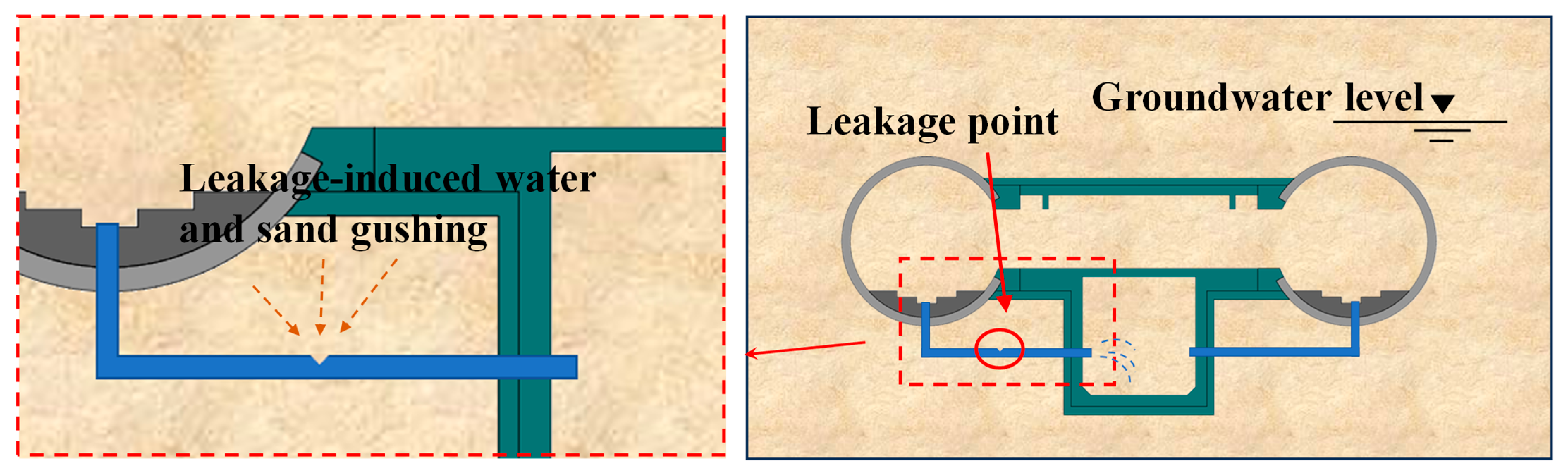
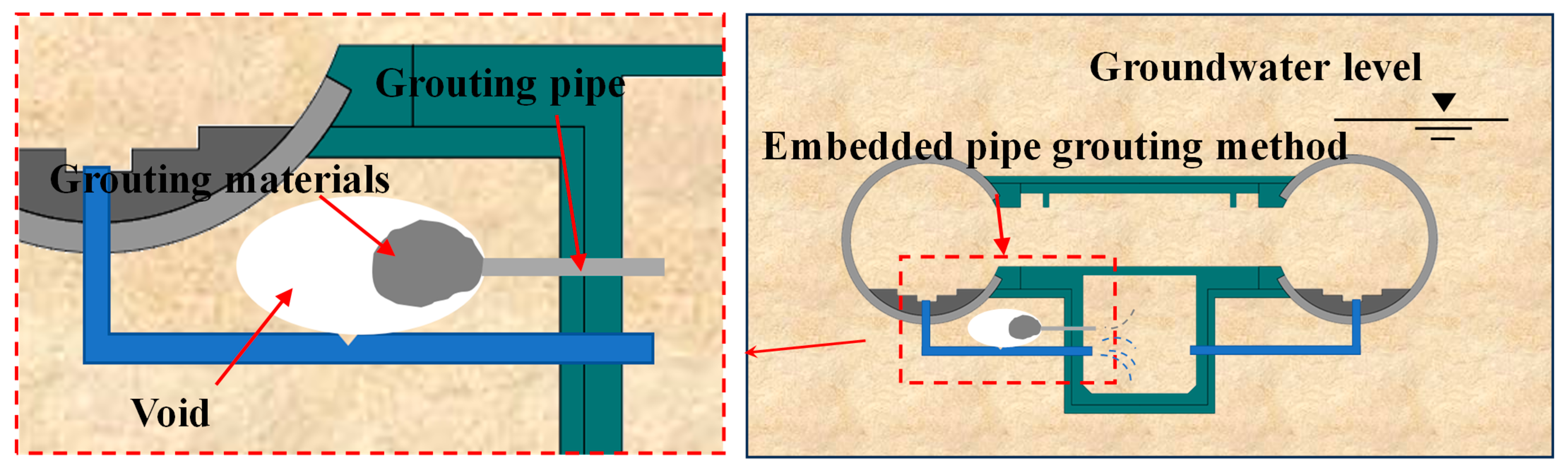
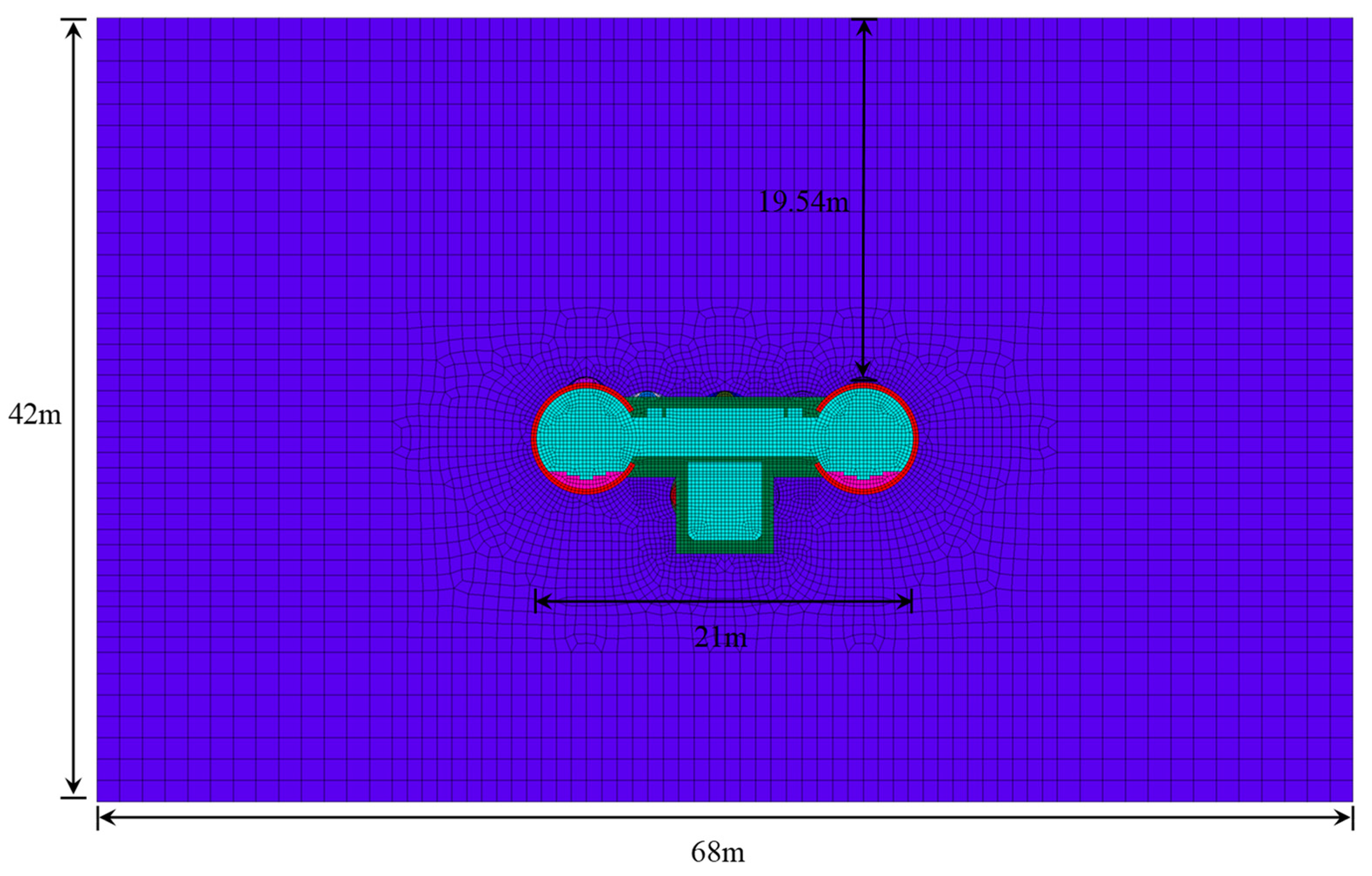
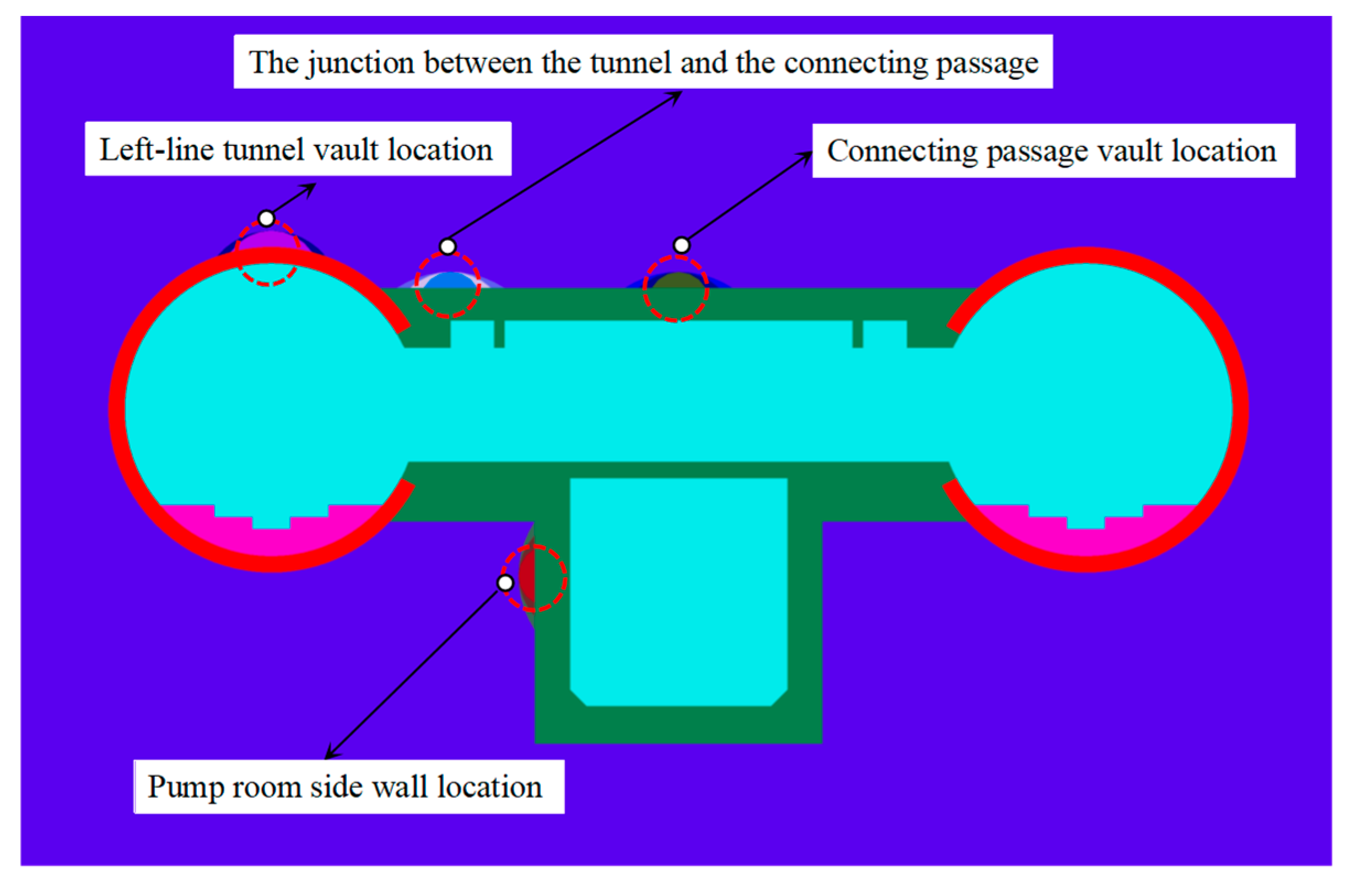











| Types of Defects | Location of Defects | Characterization of Defects |
|---|---|---|
| Structural cracking | Right-side wall of Left Line (YK22+523.9) | Segment cracking: Width = 0.24 mm, length = 0.4 m, depth = 98 mm |
| Right-side wall of Left Line (ZK22+528.2) | Grouting hole leakage | |
| Left-side track bed (non-sleeper area) of Right Line (YK22+576.4) | Concrete spalling | |
| Left-side track bed (non-sleeper area) of Right Line (YK22+561.4) | Concrete spalling | |
| Left-side track bed (non-sleeper area) of Left Line (ZK22+593.4) | Concrete spalling | |
| Track bed of Left Line | Total 15 cracks: Crack widths range from 0.27 mm to 1.40 mm. The maximum width (1.40 mm) is located at ZK22+547.0. | |
| Track bed of Right Line | Total 2 cracks: Crack widths range from 1.07 mm to 1.37 mm. The maximum width (1.37 mm) is located at YK22+524.4. | |
| Segment offset | Segments of Left Line | Maximum inter-ring offset = 13 mm, maximum intra-ring offset = 6 mm |
| Segments of Right Line | Maximum inter-ring offset = 14 mm, maximum intra-ring offset = 5 mm | |
| Tunnel deformation | Left Line | Initial structural clearance convergence measurements: 5.3500 m to 5.4148 m |
| Right Line | The initial measurement results of structural clearance convergence in the Right Line tunnel range from 5.3723 m to 5.4076 m; the maximum ovality is 9.9‰, exceeding the allowable deviation requirement of 6‰ specified in the code. | |
| Void behind the lining | ZK22+504.8(YK22+482.4)~ ZK22+604.8(YK22+582.4) | A total of 6 loose zones, 5 water-rich zones, and 4 delamination locations between the track bed and tunnel invert have been identified. |
| Parameter | Material Type | Density (kg/m3) | Elastic Modulus (GPa) | Poisson’s Ratio | Internal Friction Angle | Cohesion (kPa) |
|---|---|---|---|---|---|---|
| Soil mass | Sandy soil | 2000 | 0.025 | 0.35 | 32 | 0.1 |
| Shield tunnel segment | C50 concrete | 2500 | 34.5 | 0.16 | - | - |
| Connecting passage and pump room | C40 concrete | 2500 | 30.0 | 0.18 | - | - |
| Cases | Coupled Multiple Defect Locations | Leakage Intensity | Void Size | Deterioration Level | Objective |
|---|---|---|---|---|---|
| 1 | Pump room side wall location | Damp stain | 2 m | 80% | Investigate the influence patterns of leakage intensity, void size, and structural deterioration level on the structural behavior of shield tunnels and cross passages. |
| 2 | Dripping leakage | ||||
| 3 | Linear seepage | ||||
| 4 | Water gushing | ||||
| 5 | Left-line tunnel vault location | Damp stain | 2 m | 80% | |
| 6 | Dripping leakage | ||||
| 7 | Linear seepage | ||||
| 8 | Water gushing | ||||
| 9 | Connecting passage vault location | Damp stain | 2 m | 80% | |
| 10 | Dripping leakage | ||||
| 11 | Linear seepage | ||||
| 12 | Water gushing | ||||
| 13 | The junction between the tunnel and the connecting passage | Damp stain | 2 m | 80% | |
| 14 | Dripping leakage | ||||
| 15 | Linear seepage | ||||
| 16 | Water gushing | ||||
| 17 | Pump room side wall location | Water gushing | 1 m | 80% | |
| 18 | Water gushing | 1.5 m | 80% | ||
| 19 | Left-line tunnel vault location | Water gushing | 1 m | 80% | |
| 20 | Water gushing | 1.5 m | 80% | ||
| 21 | Connecting passage vault location | Water gushing | 1 m | 80% | |
| 22 | Water gushing | 1.5 m | 80% | ||
| 23 | The junction between the tunnel and the connecting passage | Water gushing | 1 m | 80% | |
| 24 | Water gushing | 1.5 m | 80% | ||
| 25 | Pump room side wall location | Water gushing | 2 m | 60% | |
| 26 | Left-line tunnel vault location | Water gushing | 2 m | 60% | |
| 27 | Connecting passage vault location | Water gushing | 2 m | 60% | |
| 28 | The junction between the tunnel and the connecting passage | Water gushing | 2 m | 60% |
| Parameter Variable | Level Classification | Parameter Variables | Level Classification |
|---|---|---|---|
| Leakage severity X1 | 1: Damp stain 2: Dripping leakage 3: Linear seepage 4: Water gushing | Maximum surface settlement A1 | 1: A1 < 10 mm 2: 10 mm ≤ A1 < 15 mm 3: 15 mm ≤ A1 |
| Void size X2 | 1: 1 m 2: 1.5 m 3: 2 m | Tunnel deformation A2 | 1: A2 < 5 mm 2: 5 mm ≤ A2 < 10 mm 3: 10 mm ≤ A2 |
| Deterioration severity X3 | 1: 80% 2: 60% | Cross passage deformation A3 | 1: A3 < 5 mm 2: 5 mm ≤ A3 < 10 mm 3: 10 mm ≤ A3 |
| Defect location X4 | 1: Pump room side wall location 2: Left-line tunnel vault location 3: Connecting passage vault location 4: The junction between the tunnel and the connecting passage3: 4.5 m | Impact level T | 1: 1 ≤ T < 2 2: 2 ≤ T < 3 3: 3 ≤ T < 4 |
| Risk Contributors | Probability of Impact Levels |
|---|---|
| Leakage severity X1 = Water gushing | Level 1: 32%; Level 2: 33%; Level 3: 35% |
| Void size X2 = 2 m | Level 1: 16%; Level 2: 31%; Level 3: 53% |
| Deterioration severity X3 = 60% | Level 1: 25%; Level 2: 35%; Level 3: 40% |
| Defect location X4 = Pump room sidewall location | Level 1: 19%; Level 2: 19%; Level 3: 62% |
| No. | Known Influencing Factors | Impact Level Probability Distribution | |||||
|---|---|---|---|---|---|---|---|
| Leakage Severity | Void Size/m | Deterioration Level | Defect Location | Level 1 | Level 2 | Level 3 | |
| 1 | Damp stain | 1 | 80% | Left-line tunnel vault location | 90% | 10% | 0 |
| 2 | Linear seepage | 1.5 | 60% | Connecting passage vault location | 0 | 43% | 57% |
| 3 | Dripping leakage | 2 | 80% | Pump room side wall location | 0 | 26% | 74% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, X.; Xing, H.; Li, W.; Song, W.; Xie, Z. Impact of Multi-Defect Coupling Effects on the Safety of Shield Tunnels and Cross Passages. Buildings 2025, 15, 1696. https://doi.org/10.3390/buildings15101696
Niu X, Xing H, Li W, Song W, Xie Z. Impact of Multi-Defect Coupling Effects on the Safety of Shield Tunnels and Cross Passages. Buildings. 2025; 15(10):1696. https://doi.org/10.3390/buildings15101696
Chicago/Turabian StyleNiu, Xiaokai, Hongchuan Xing, Wei Li, Wei Song, and Zhitian Xie. 2025. "Impact of Multi-Defect Coupling Effects on the Safety of Shield Tunnels and Cross Passages" Buildings 15, no. 10: 1696. https://doi.org/10.3390/buildings15101696
APA StyleNiu, X., Xing, H., Li, W., Song, W., & Xie, Z. (2025). Impact of Multi-Defect Coupling Effects on the Safety of Shield Tunnels and Cross Passages. Buildings, 15(10), 1696. https://doi.org/10.3390/buildings15101696







