Numerical Study on Hydraulic Coupling and Surrounding Rock Deformation for Tunnel Excavation Beneath Reservoirs
Abstract
1. Introduction
2. Numerical Simulation and Methods
2.1. Governing Equations
2.2. Modeling Process and Geometry
2.3. Initial and Boundary Conditions
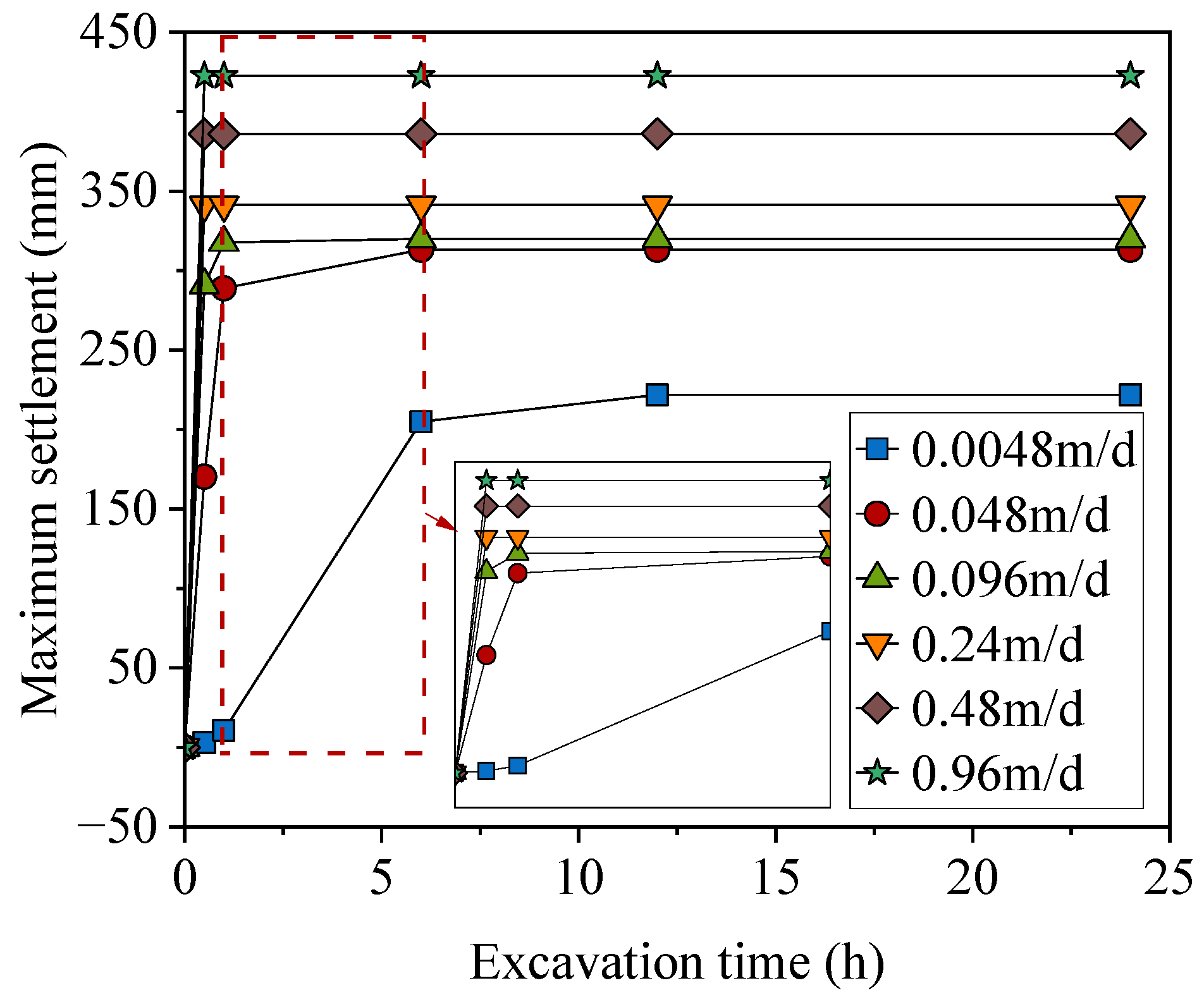
2.4. Grid Validation and Model Validation
2.5. Parametric Analysis
3. Results and Discussion
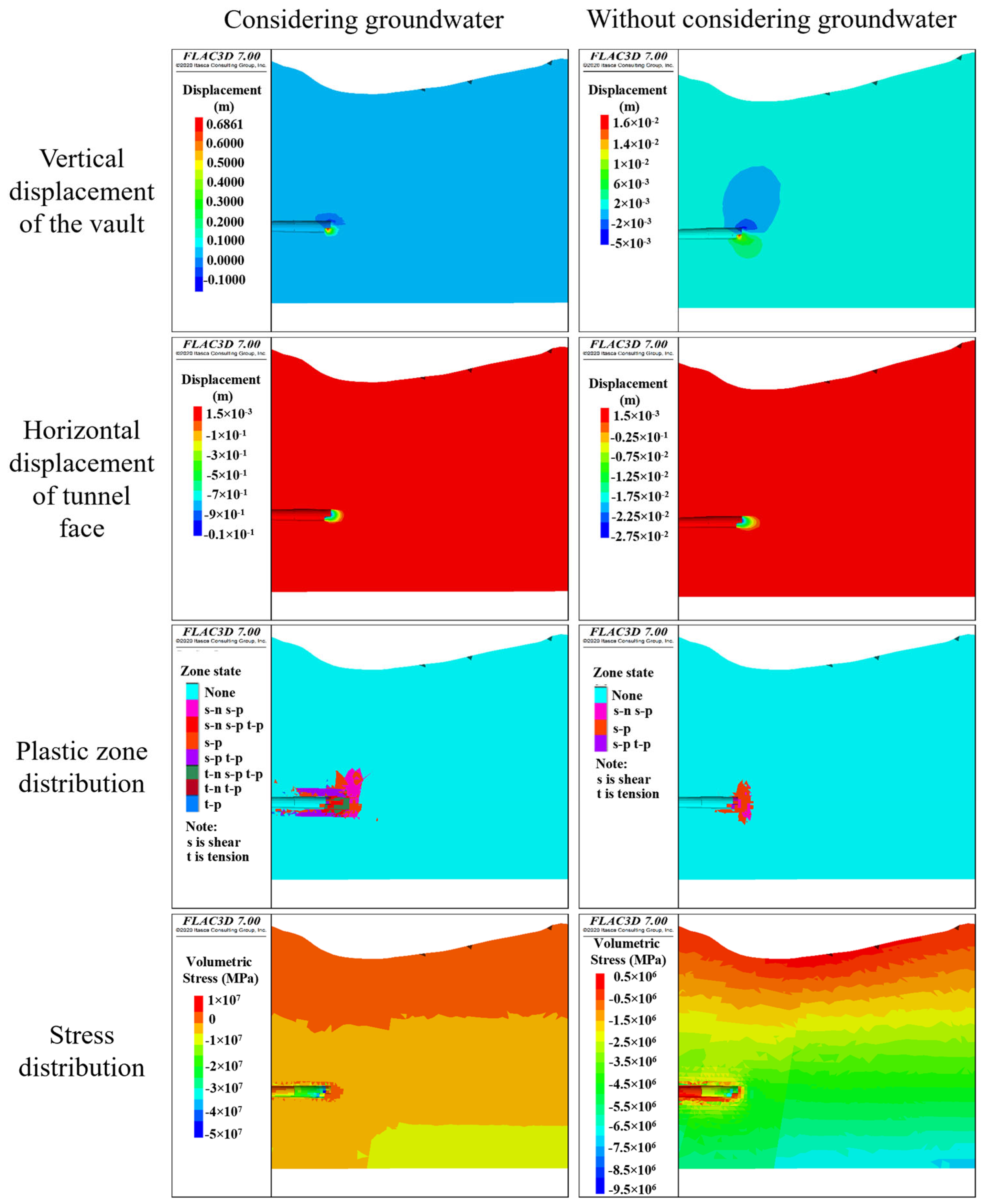
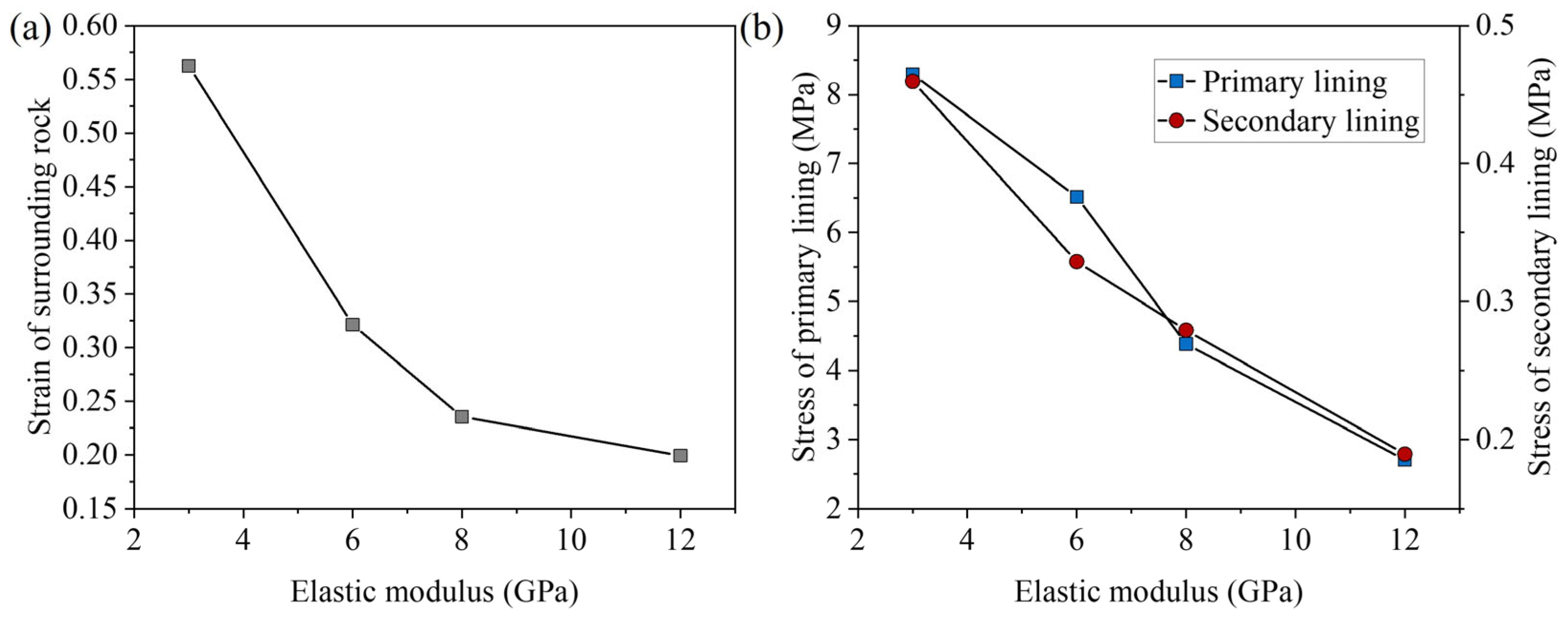
3.1. Deformation and Stress Analysis of Surrounding Rock Induced by Tunnel Excavation and Drainage
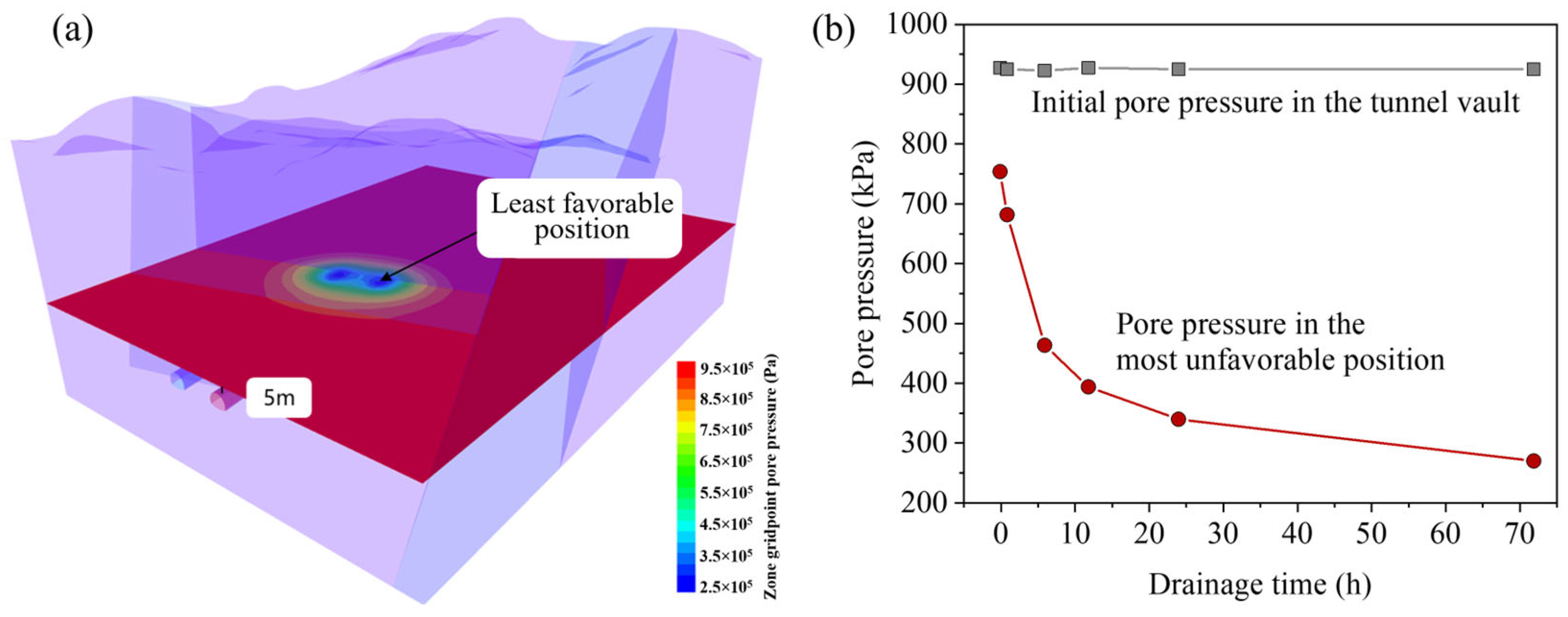
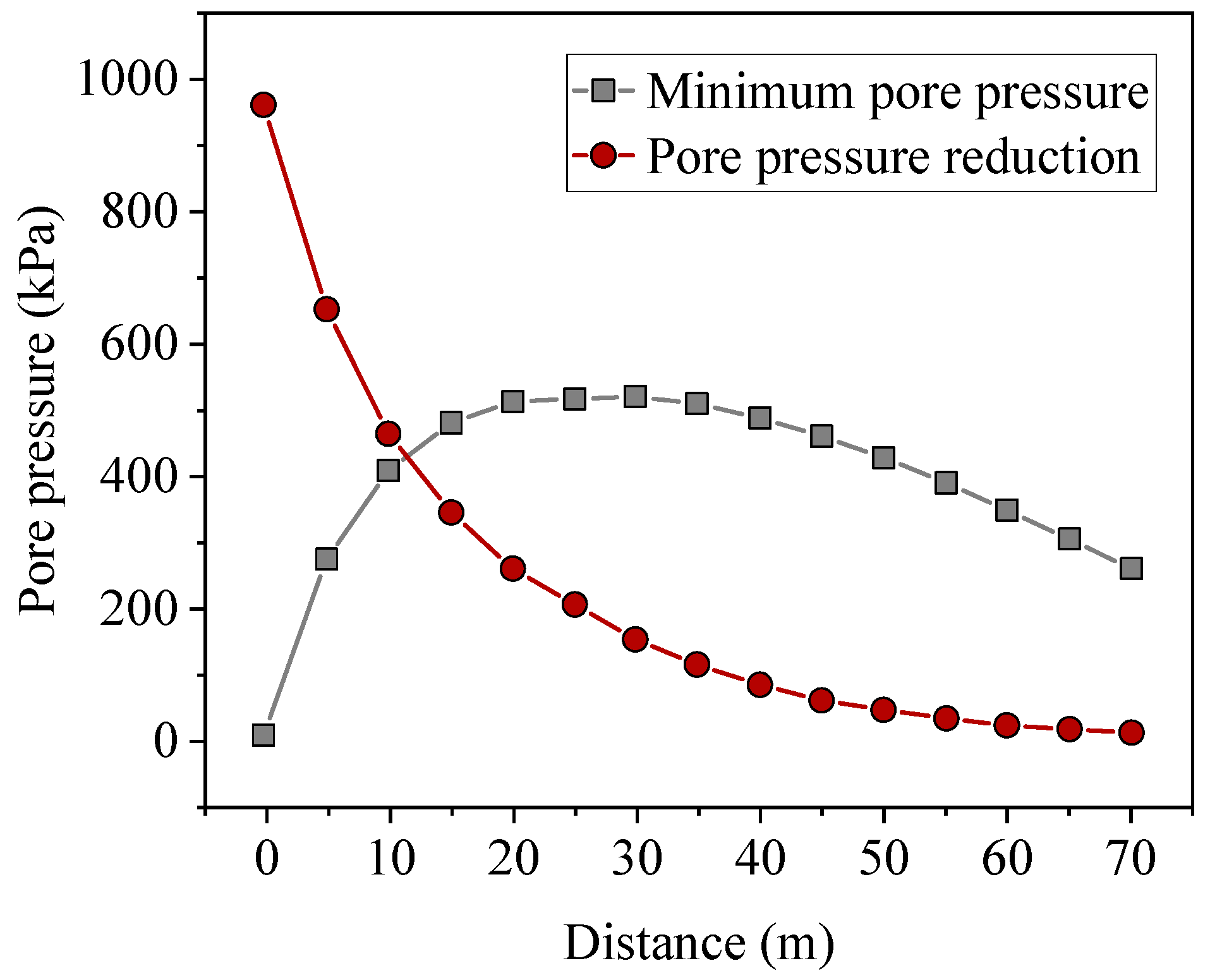
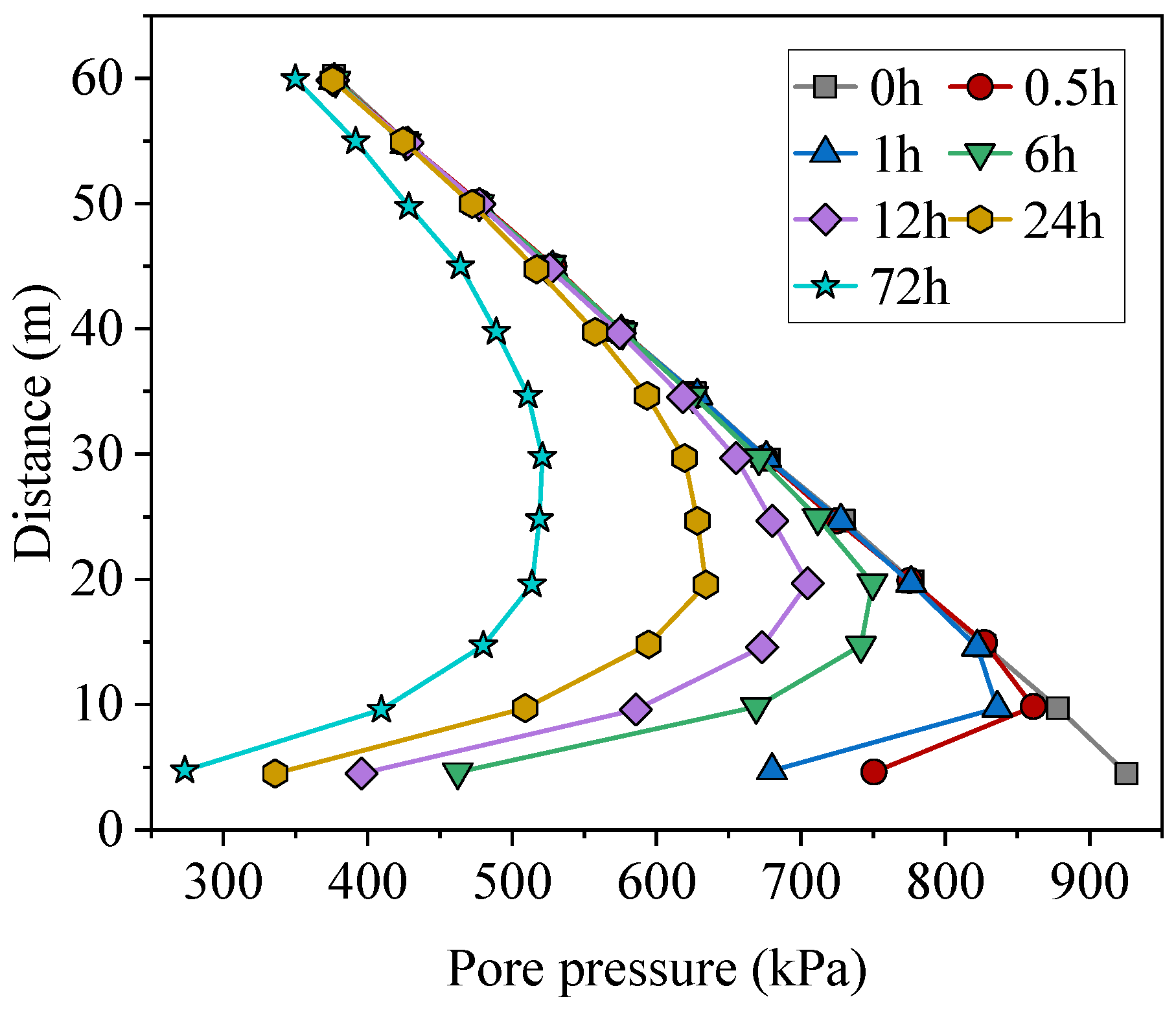
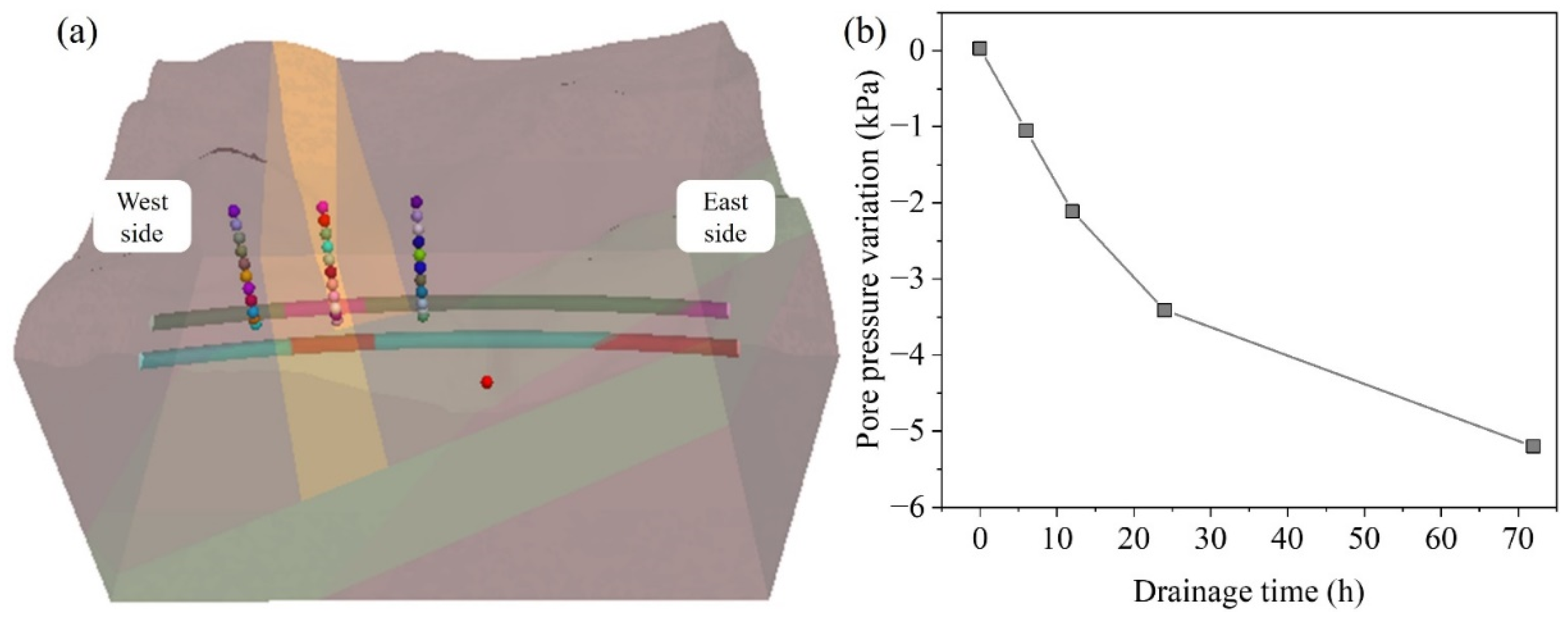
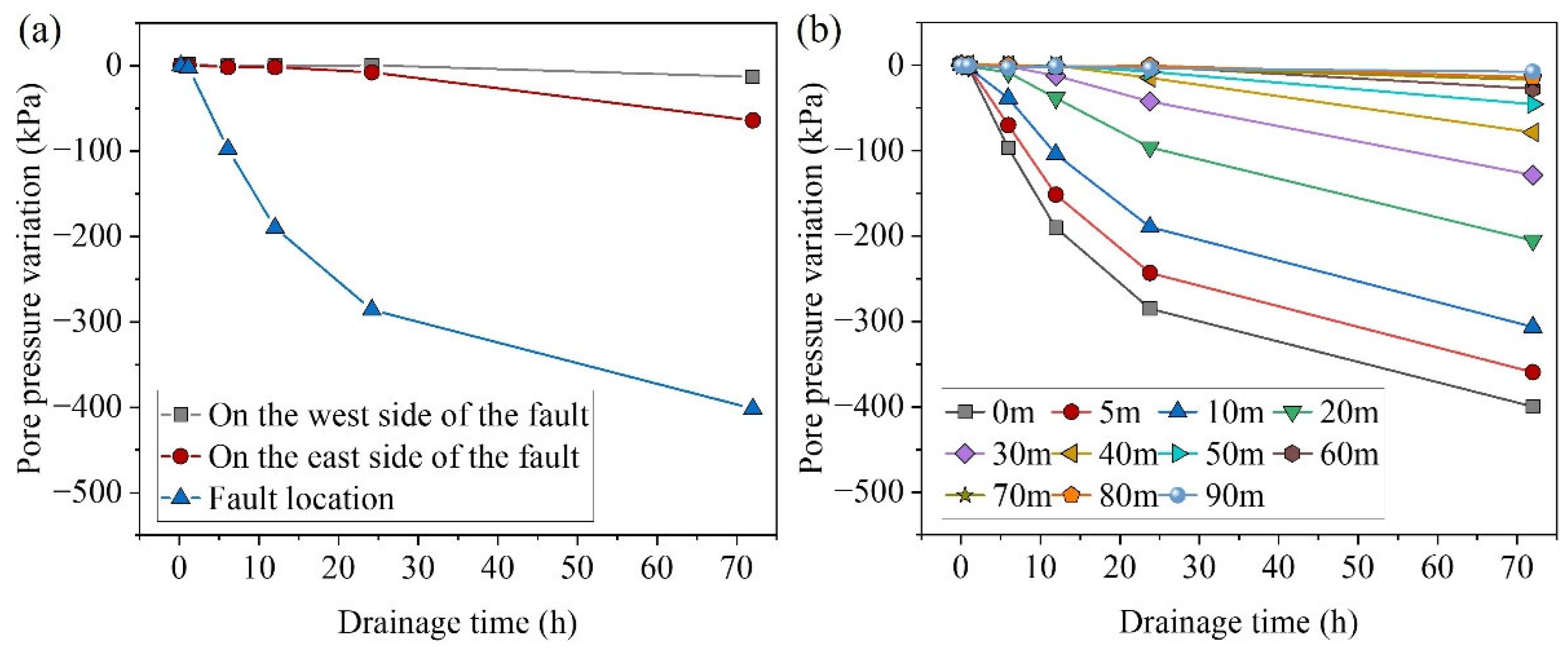
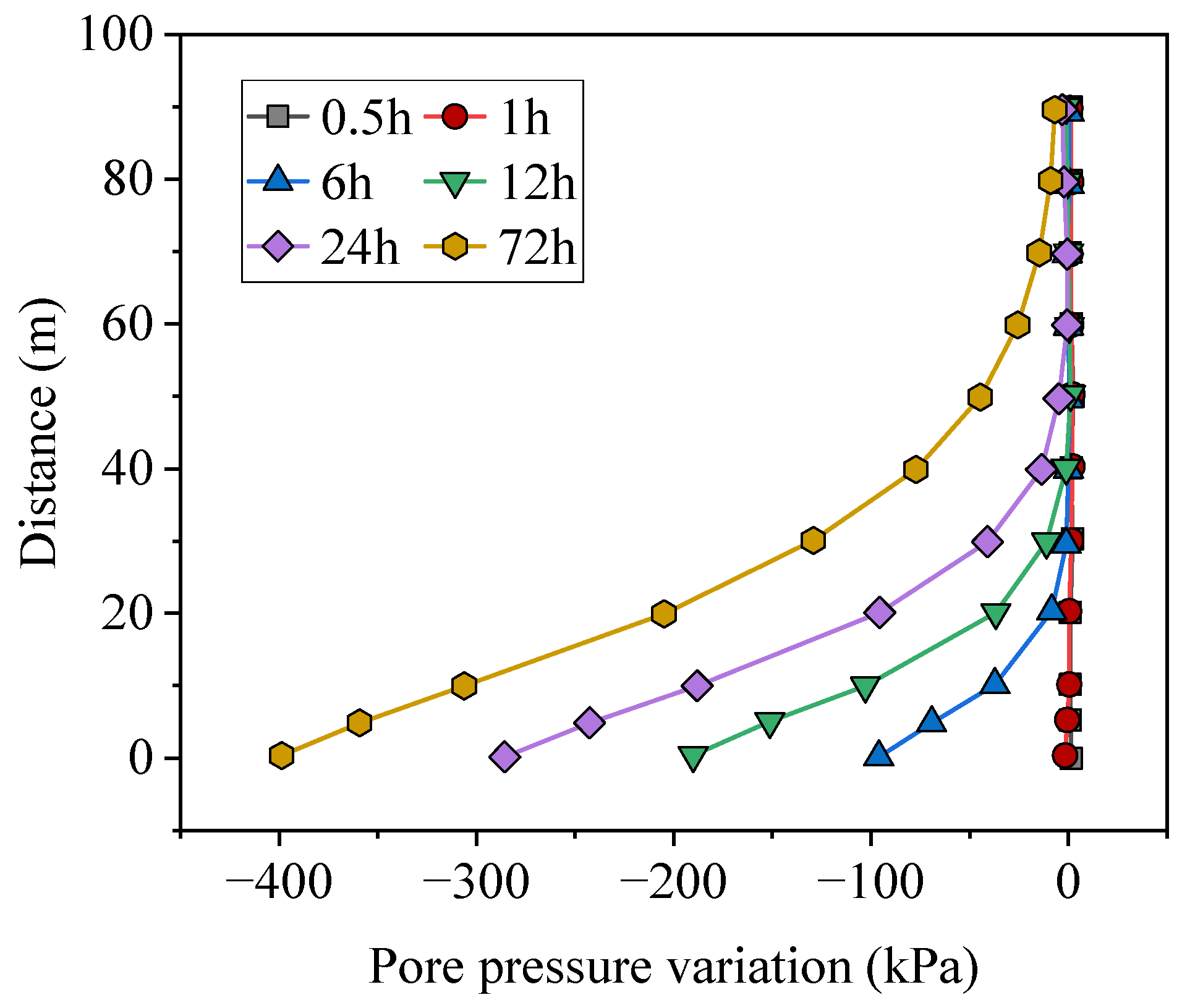
3.2. Pore Pressure Variation in the Surrounding Rock Due to Tunnel Excavation and Drainage
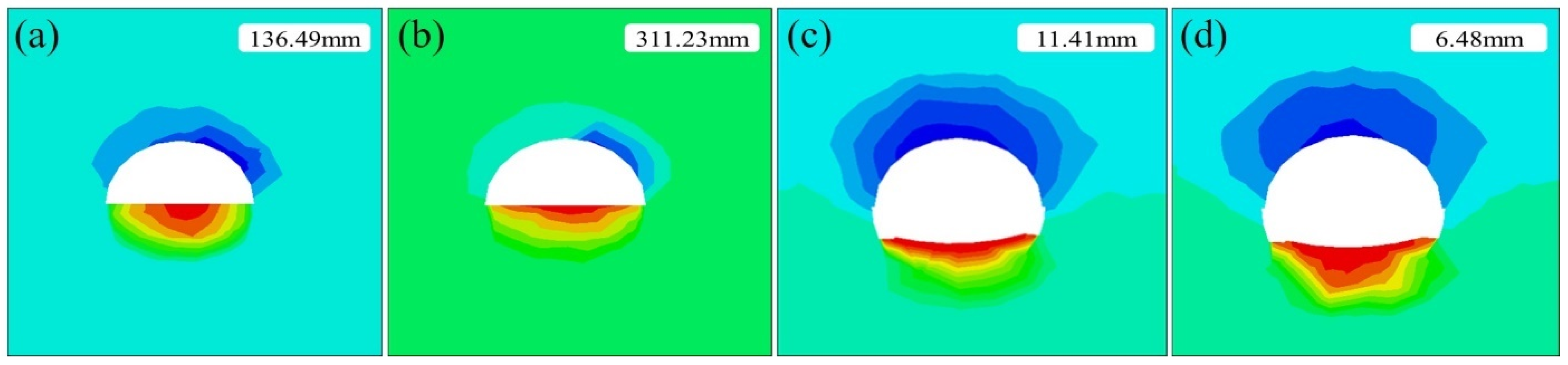
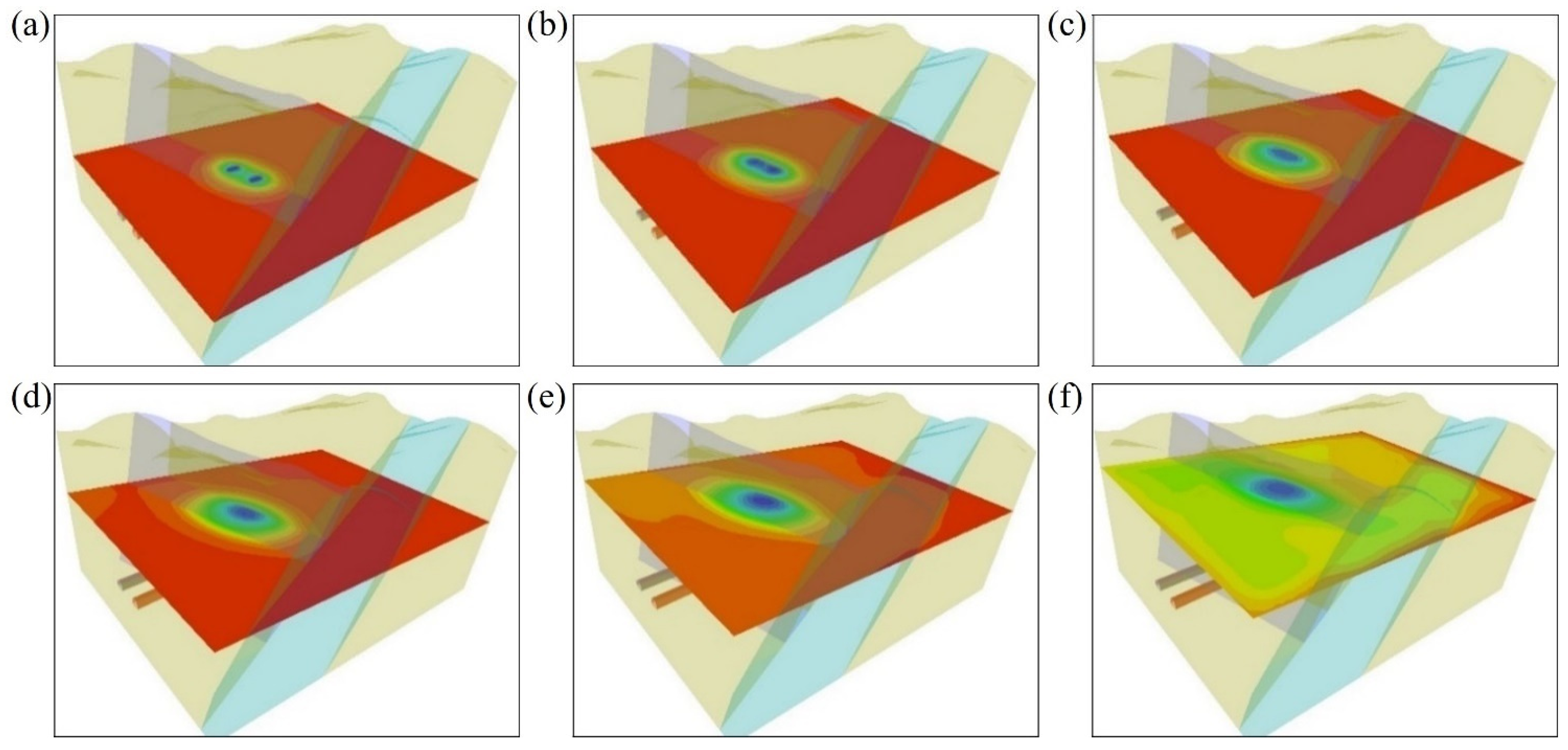
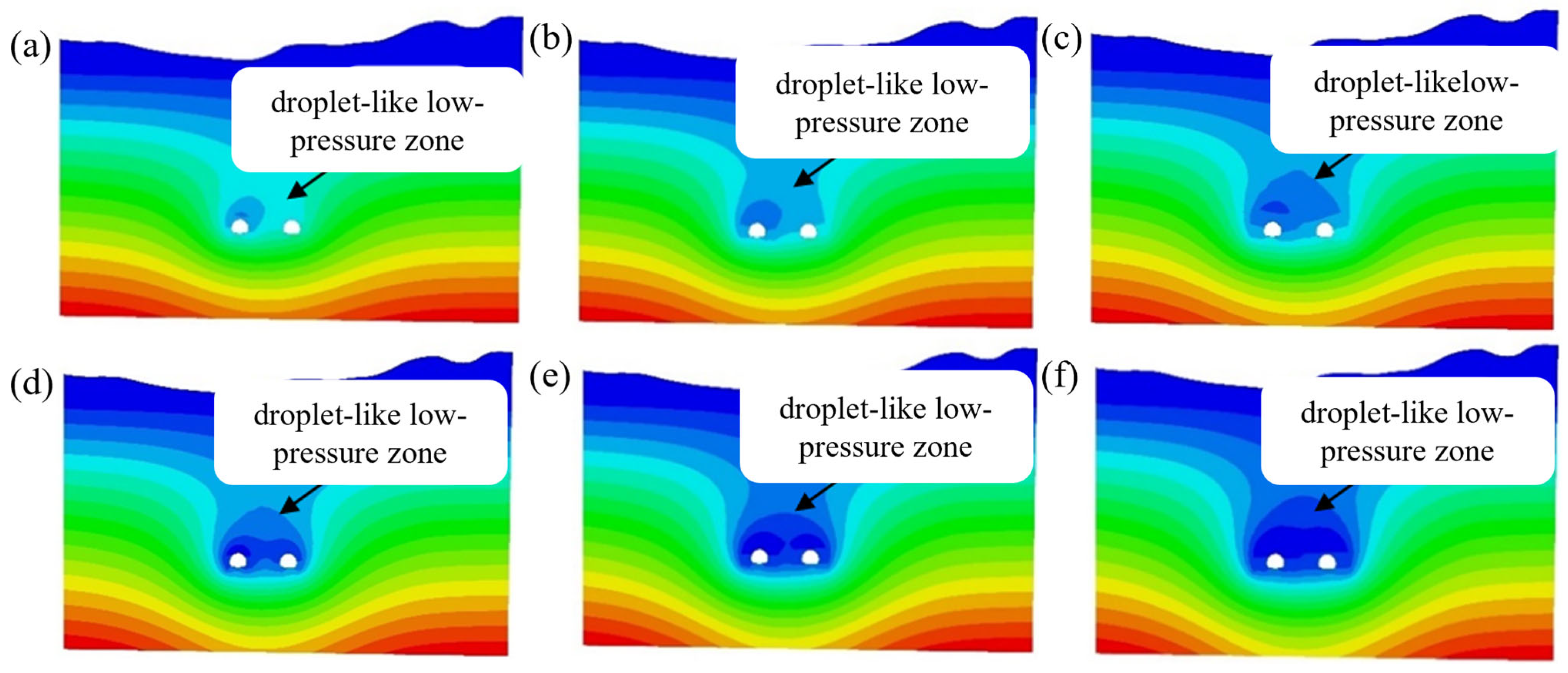
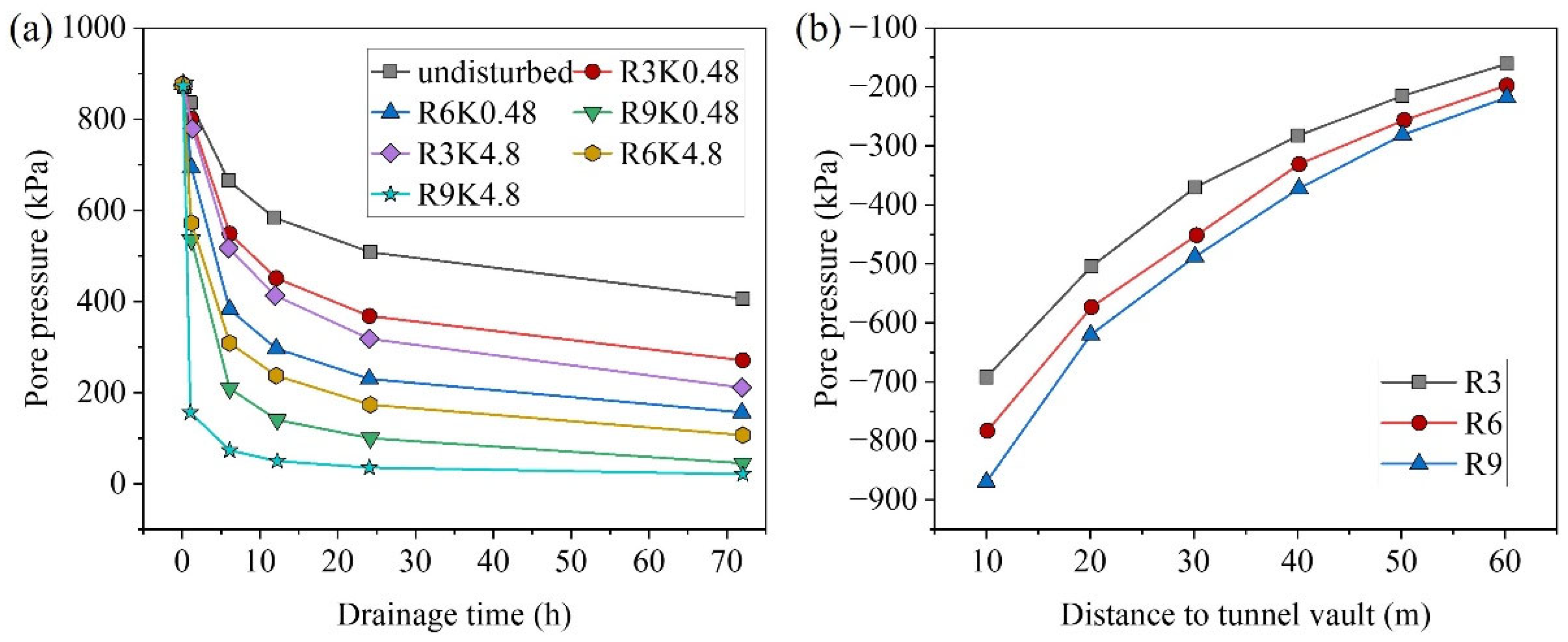
3.3. Pore Pressure Analysis Considering Excavation Disturbance
4. Conclusions
- (1)
- Excavating tunnels in geological conditions with abundant groundwater increases the likelihood of accidents. A decrease in the elastic modulus of the surrounding rock and an increase in the permeability coefficient will raise the pressure on the tunnel lining and heighten the risk of sudden, severe deformation of the surrounding rock, thereby increasing the likelihood of collapse.
- (2)
- The influence of pore pressure increases with longer drainage durations. As tunnel excavation progresses, the pore pressure at the bottom of the Tianzhuhu reservoir gradually decreases. Continuous monitoring of the water level and bottom pore pressure in the Tianzhuhu reservoir is recommended during excavation to prevent fracture penetration caused by blasting and excavation, thereby ensuring the safe operation of the reservoir and construction safety.
- (3)
- Excavation-induced disturbances significantly affect the permeability of the surrounding rock, notably altering the distribution of pore pressure. During excavation, it is crucial to closely monitor the impact of these disturbances on rock permeability and, if necessary, promptly implement grouting measures to reduce permeability and enhance stability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, X.; Zhao, Y. Comment on construction of railway tunnels in China by statistical data. Mod. Tunn. Technol. 2006, 43, 7–17, 22. [Google Scholar]
- Zhao, Y.; Li, P. A Statistical analysis of China’s traffic tunnel development data. Engineering 2018, 4, 3–5. [Google Scholar] [CrossRef]
- Jiang, S. Quality and technical countermeasures in highway tunnel engineering. Mod. Tunn. Technol. 2017, 54, 1–12. [Google Scholar]
- Yu, T.; Ying, K.; Wang, J.; Yao, Z.; Fang, Y. Stability evaluation of the sequential excavation method of large-section double-arch tunnel in fly ash accumulation stratum through physical model. Tunn. Undergr. Space Technol. 2025, 158, 106391. [Google Scholar] [CrossRef]
- Yang, W.; Boldini, D.; Zhang, D. Practical implementation of Bi-Elliptical displacement-controlled method in analysing shallow and large tunnel excavation impact. Tunn. Undergr. Space Technol. 2025, 158, 106266. [Google Scholar] [CrossRef]
- Meng, F.; Qiao, S. Study on the deformation of existing tunnel under the combined effect of pit excavation and dewatering based on the Kerr foundation model. Tunn. Undergr. Space Technol. 2025, 158, 106382. [Google Scholar] [CrossRef]
- Zhao, Y.; Feng, S.; Zhang, X.; Zheng, Q.; Cao, B. Fully coupled hydromechanical study of tunnel excavation considering leachate leakage from a high water-level landfill. Comput. Geotech. 2024, 175, 106696. [Google Scholar] [CrossRef]
- Guo, S. Numerical Simulation and Analysis of Excavation Disturbance for a Super-Large Diameter Shield Tunnel Crossing Yangtze River in Wuhu; Hefei University of Technology: Hefei, China, 2022. [Google Scholar]
- Geng, Y. Study on Mechanism of Hydraulic Coupling Failure and Water Inrush Disaster Under TBM Excavation Disturbance; Shandong University: Jinan, China, 2021. [Google Scholar]
- Li, L. Study on Construction Technology of Duanjiawu Tunnel Passing Through Xinyantang Reservoir; Chongqing Jiaotong University: Chongqing, China, 2020. [Google Scholar]
- Terzaghi, K. Theoretical Soil Mechanics (Translated by Xu Zhiying); Geological Publishing House: Beijing, China, 1996. [Google Scholar]
- Biot, M. The general three-dimensional consolidation theory. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Witherspoon, P.A.; Tsang, Y.W.; Long, J.C.; Noorishad, J. New approaches to problems of fluid flow in fractured-rock masses. In Proceedings of the ARMA US Rock Mechanics/Geomechanics Symposium, Cambridge, MA, USA, 29 June–2 July 1981. [Google Scholar]
- Zhuo, J.; Zhang, Q. Interface Element Method for Mechanics Problems of Discontinuous Media; Science Press: Beijing, China, 2000. [Google Scholar]
- Huyakorn, P.; Lester, B.; Faust, C. Finite element techniques for modeling groundwater flow in fractured aquifers. Water Resour. Res. 1983, 19, 1019–1035. [Google Scholar] [CrossRef]
- Yang, T. Study on Infiltrate Character and Coupling Analysis of Seepage and Stress in Rock Failure Process; Northeastern University: Shengyang, China, 2001. [Google Scholar]
- Li, S.; Wu, D. Effect of confining pressure, pore pressure and specimen dimension on permeability of Yinzhuang sandstone. Int. J. Rock Mech. Min. Sci. 1997, 34, 435–441. [Google Scholar] [CrossRef]
- Tang, C.A.; Yang, W.T.; Fu, Y.F.; Xu, X.H. A new approach to numerical method of modelling geological processes and rock engineering problems—Continuum to discontinuum and linearity to nonlinearity. Eng. Geol. 1998, 49, 207–214. [Google Scholar] [CrossRef]
- Yang, T.; Tham, L.; Tang, C. Influence of heterogeneity of mechanical properties on hydraulic fracturing in permeable rocks. Rock Mech. Rock Eng. 2004, 37, 251–275. [Google Scholar] [CrossRef]
- Yang, T.; Liu, J.; Tang, C. A coupled flow-stress-damage model for groundwater outbursts from an underlying aquifer into mining excavations. Int. J. Rock Mech. Min. Sci. 2007, 44, 87–97. [Google Scholar] [CrossRef]
- Yang, T.; Zhu, W.; Yu, Q.; Liu, H. The role of pore pressure during hydraulic fracturing and implications for groundwater outbursts in mining and tunneling. Hydrogeol. J. 2011, 19, 995–1008. [Google Scholar] [CrossRef]
- Kong, F. Research on reinforcing technology for surrounding rock undercrossing the reservoir of Xiuning tunnel along the Guangdong-Kunming railway. Urban Geol. 2017, 12, 35–39. [Google Scholar]
- Peng, W.; Su, M.; Gao, K. Design and research on lining structure of Dayao Mountains No.1 Tunnel undercrossing reservoir. Highway 2017, 62, 243–247. [Google Scholar]
- Hou, W.; Wu, Y.; He, L. The analysis of effects of reservoir under the high water head upon tunnel seepage flow based on GEO-SLOPE. J. Xi’an Univ. Technol. 2006, 02, 171–174. [Google Scholar]
- Yang, F.-R.; Lee, C.-H.; Kung, W.-J.; Yeh, H.-F. The impact of tunneling construction on the hydrogeological environment of “Tseng-Wen Reservoir Transbasin Diversion Project” in Taiwan. Eng. Geol. 2009, 103, 39–58. [Google Scholar] [CrossRef]
- Mao, R.; Liu, S.; Ma, F.; Li, Z.; Zhang, X. The numerical simulation analysis of ground settlement of around tunnel under ground-water seepage. In Proceedings of the Conference on Environmental Science and Information Application Technology, Wuhan, China, 17–18 July 2010. [Google Scholar]
- Zhang, C.; Shang, Y.; Li, W. Limit analysis of face stability of special-shaped shield tunnels considering solid-fluid coupling effect. China J. Highw. Transp. 2023, 36, 345–357. [Google Scholar]
- Jin, X.; Li, X.; Zhang, Y. Seepage stress coupling analysis of river crossing tunnel excavating. Hydrogeol. Eng. Geol. 2010, 37, 62–67. [Google Scholar]
- Yu, Z.; Zhang, G.; Cui, H.; Wang, Z.; Cao, Z. A cross season antifreeze system utilizing tunnel lining GHEs and solar energy: Performance and effect mechanism at various environment parameters. Renew. Energy 2025, 242, 122428. [Google Scholar] [CrossRef]
- Yu, Z.; Zhang, G.; Li, C.; Cao, Z. Numerical investigation on work performance of the anti-freezing drainage system of tunnel utilizing TPCT. Appl. Therm. Eng. 2024, 253, 123849. [Google Scholar] [CrossRef]
- Wei, T.; Wang, C.; Zhao, Y.; Bi, J.; Zhang, Y. A new semi–Analytical method for elastic–strain softening circular tunnel with hydraulic–mechanical coupling. Eng. Geol. 2025, 344, 107826. [Google Scholar] [CrossRef]
- Xiao, F.; Chen, X.; Zhu, Y.; Xie, P.; Salimzadeh, S.; Zhang, Q.-B. Multi-LoD BIM integrated design framework for pressurised tunnel: Hydro-mechanical coupling simulation and sustainability assessment. Tunn. Undergr. Space Technol. 2025, 158, 106404. [Google Scholar] [CrossRef]
- Zaheri, M.; Ranjbarnia, M. An analytical–numerical method for the hydraulic–mechanical coupling analysis of time-dependent behavior of pressurized tunnels: Impact of an excavation damaged zone. Comput. Geotech. 2024, 170, 106299. [Google Scholar] [CrossRef]
- Yang, M.; Zhao, X. Single pile analysis method in layered soil. J. Tongji Univ. (Nat. Sci.) 1992, 04, 421–428. [Google Scholar]
- GB 50911; Code for Monitoring Measurement of Urban Rail Transit Engineering. China Architecture and Building Press: Beijing, China, 2013. (In Chinese)

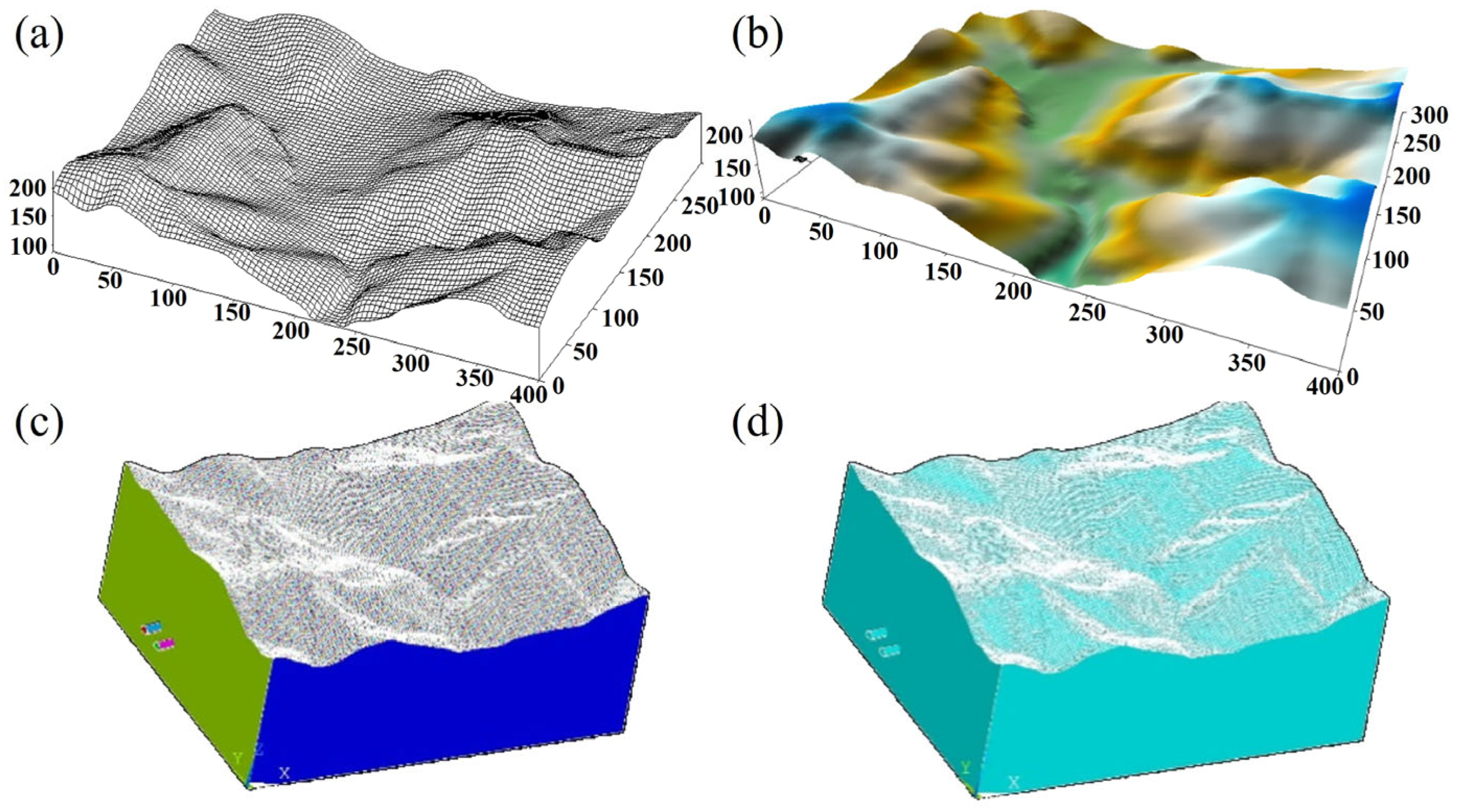
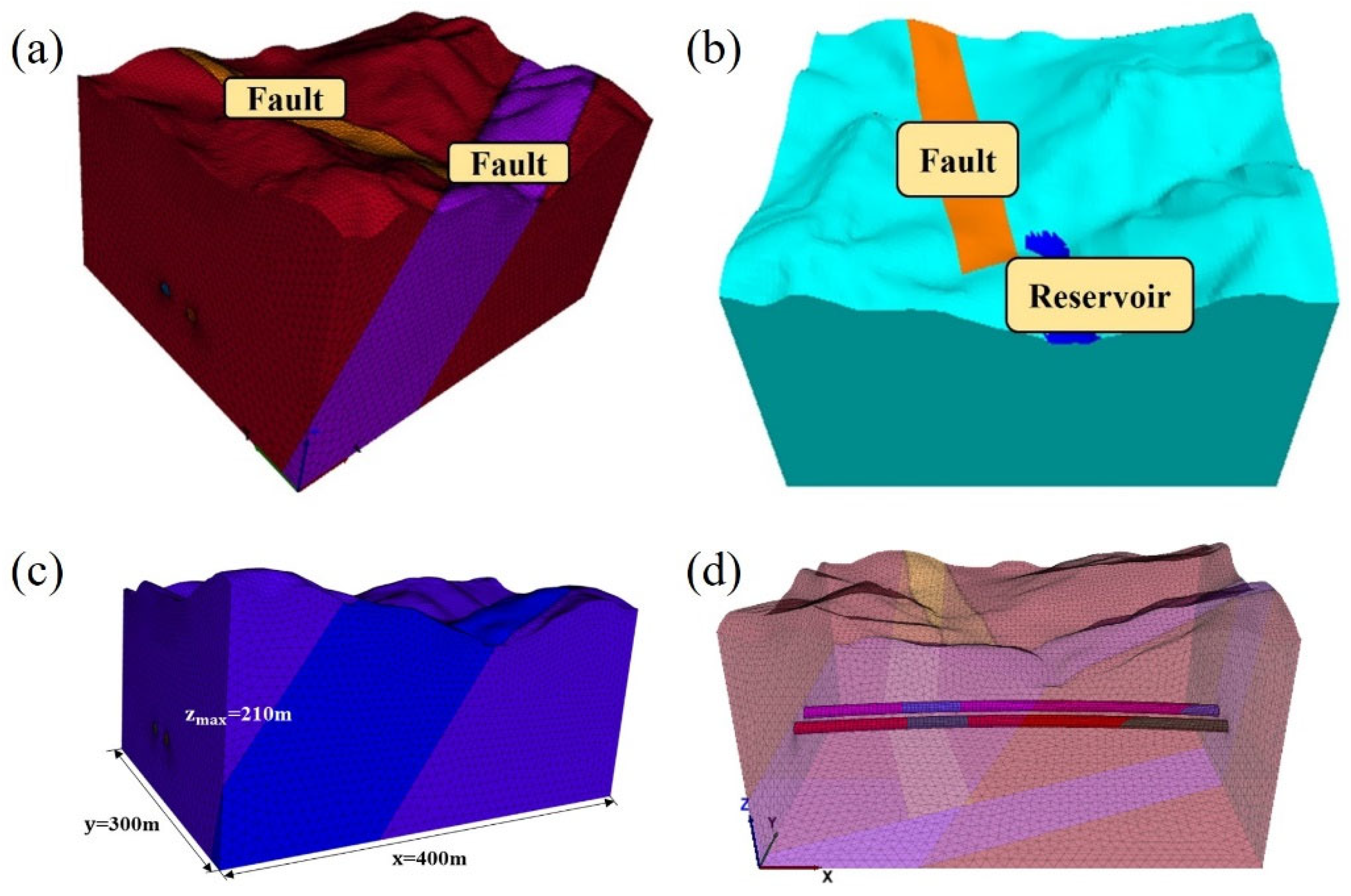



| Parameter | Unit | Value |
|---|---|---|
| Theoretical value | m3/d | 0.72 |
| Test value (not considering silt) | m3/d | 0.88 |
| Test value (considering silt) | m3/d | 0.69 |
| Type | Elastic Modulus (MPa) | Poisson’s Ratio | Volumetric Weight (kN/m3) | Internal Friction Angle (°) | Cohesion (kPa) |
|---|---|---|---|---|---|
| Slope residual deposits of silty clay, gravels | 12 | 0.33 | 18 | 20 | 20 |
| 6-1 Fully weathered granite | 24 | 0.32 | 19 | 11 | 30 |
| 6-2 Strongly weathered granite | 120 | 0.31 | 19.5 | 12 | 18 |
| 6-3 Clastic and strongly weathered granite | 180 | 0.30 | 20.5 | 26 | 70 |
| Fault zone | 8000 | 0.26 | 22 | 33 | 380 |
| 6-4 Medium weathered granite | 12,000 | 0.22 | 24 | 37 | 450 |
| Type | Permeability Coefficient (m/d) | Porosity (%) | Saturation (%) |
|---|---|---|---|
| Slope residual deposits of silty clay, gravels | 0.002 | 55 | 50 |
| 6-1 Fully weathered granite | 0.065 | 55 | 60 |
| 6-2 Strongly weathered granite | 0.06 | 50 | 100 |
| 6-3 Clastic and strongly weathered granite | 0.055 | 50 | 100 |
| Fault zone | 0.048 | 40 | 100 |
| 6-4 Medium weathered granite | 0.013 | 25 | 100 |
| Type | Elastic Modulus (MPa) | Poisson’s Ratio | Heaviness (kN/m3) |
|---|---|---|---|
| Primary lining | 20 | 0.2 | 24 |
| Secondary lining | 30 | 0.2 | 25 |
| Grouting area | 15 | 0.25 | 24 |
| Working Condition | Fractured Surrounding Rock | Non-Fractured Surrounding Rock | |
|---|---|---|---|
| Group 1 | Elastic modulus (MPa) | 3 | 4 |
| Poisson’s ratio | 0.30 | 0.26 | |
| Group 2 | Elastic modulus (MPa) | 6 | 8 |
| Poisson’s ratio | 0.28 | 0.24 | |
| Group 3 | Elastic modulus (MPa) | 8 | 12 |
| Poisson’s ratio | 0.26 | 0.22 | |
| Group 4 | Elastic modulus (MPa) | 12 | 16 |
| Poisson’s ratio | 0.24 | 0.20 | |
| Excavation Time | 3 GPa (Working Condition 1) | 6 GPa (Working Condition 2) | 9 GPa (Working Condition 3) | 12 GPa (Working Condition 4) |
|---|---|---|---|---|
| 0.5 h | 646 | 415 | 170.6 | 2.5 |
| 1 h | 785 | 468 | 290 | 10.8 |
| 6 h | 816 | 470 | 314.8 | 25 |
| 12 h | 816 | 470 | 314.8 | 26 |
| 24 h | 816 | 470 | 314.8 | 26 |
| Working Condition ID | Disturbance Range (m) | Surrounding Rock Permeability Coefficient (m/d) | |
|---|---|---|---|
| Fault Location | Non-Fault Location | ||
| R3K0.48 | 3 | 0.48 | 0.13 |
| R6K0.48 | 6 | 0.48 | 0.13 |
| R9K0.48 | 9 | 0.48 | 0.13 |
| R3K4.8 | 3 | 4.8 | 1.3 |
| R6K4.8 | 6 | 4.8 | 1.3 |
| R9K4.8 | 9 | 4.8 | 1.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhang, G.; Yu, Z.; Ya, Z. Numerical Study on Hydraulic Coupling and Surrounding Rock Deformation for Tunnel Excavation Beneath Reservoirs. Buildings 2025, 15, 1693. https://doi.org/10.3390/buildings15101693
Wang S, Zhang G, Yu Z, Ya Z. Numerical Study on Hydraulic Coupling and Surrounding Rock Deformation for Tunnel Excavation Beneath Reservoirs. Buildings. 2025; 15(10):1693. https://doi.org/10.3390/buildings15101693
Chicago/Turabian StyleWang, Shaodan, Guozhu Zhang, Zihao Yu, and Zhou Ya. 2025. "Numerical Study on Hydraulic Coupling and Surrounding Rock Deformation for Tunnel Excavation Beneath Reservoirs" Buildings 15, no. 10: 1693. https://doi.org/10.3390/buildings15101693
APA StyleWang, S., Zhang, G., Yu, Z., & Ya, Z. (2025). Numerical Study on Hydraulic Coupling and Surrounding Rock Deformation for Tunnel Excavation Beneath Reservoirs. Buildings, 15(10), 1693. https://doi.org/10.3390/buildings15101693







