Optimising Plate Thickness in Interlocking Inter-Module Connections for Modular Steel Buildings: A Finite Element and Random Forest Approach
Abstract
1. Introduction
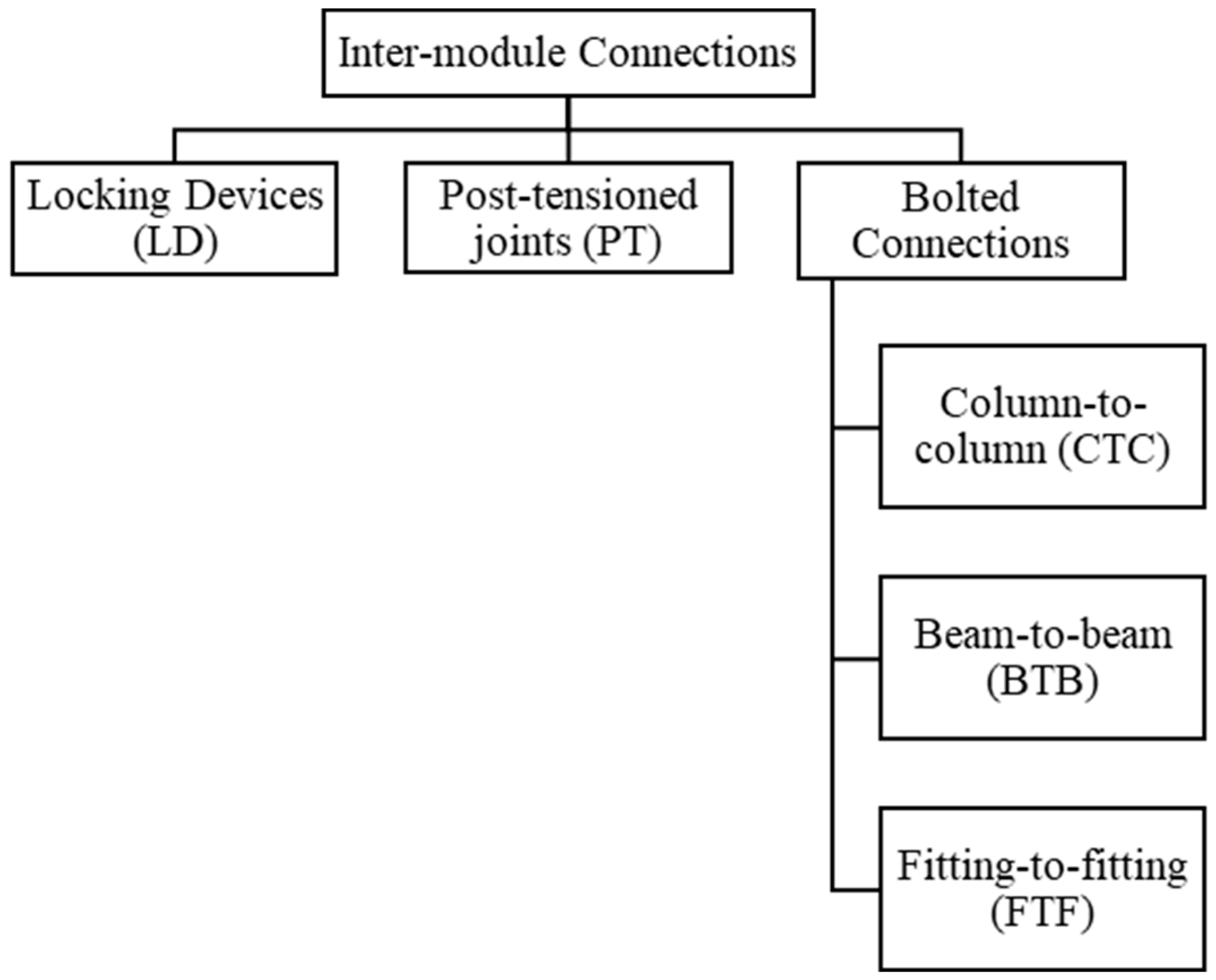
2. Modelling Methods and Optimising (IMCs) Plate Thickness
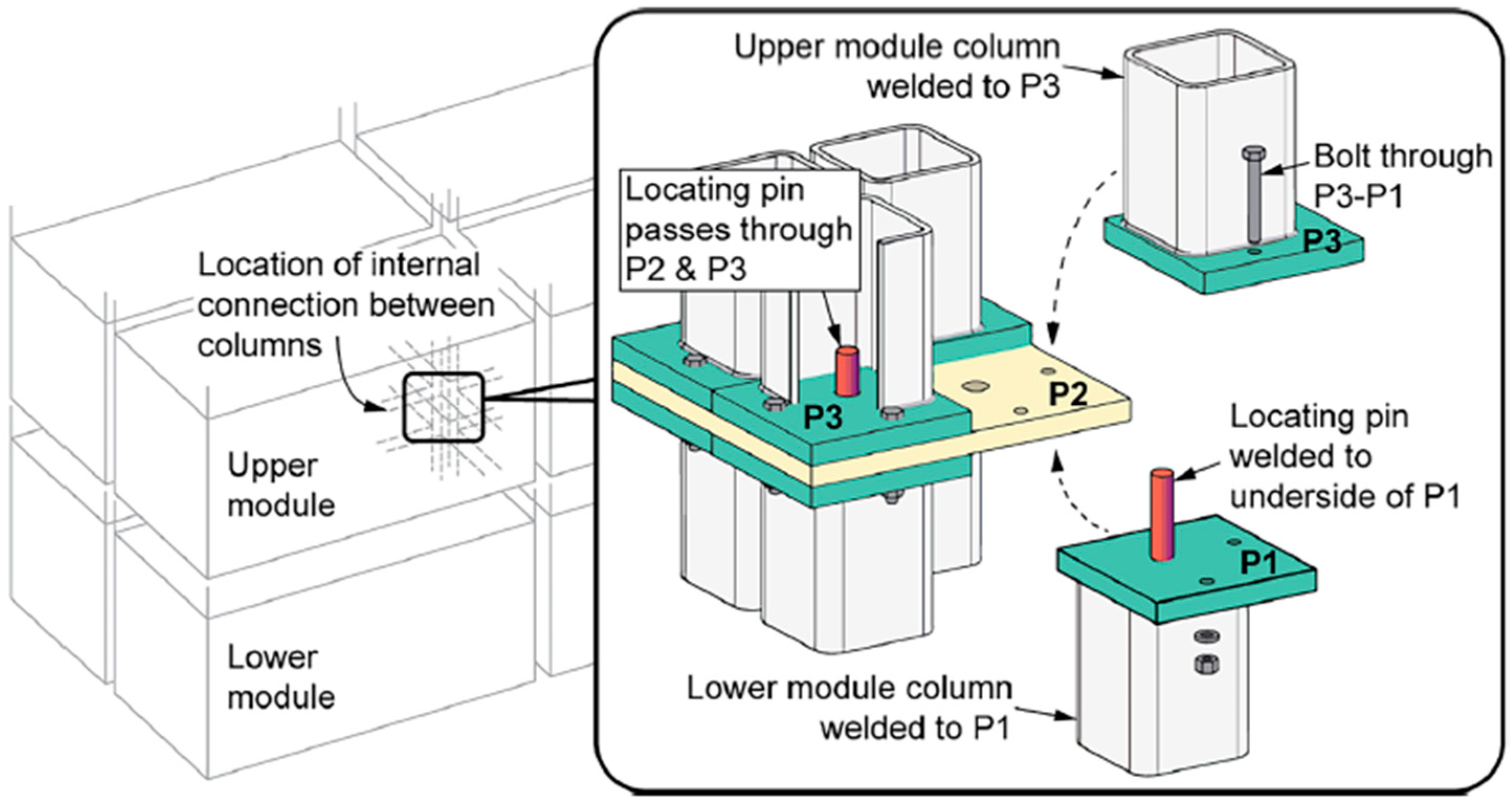
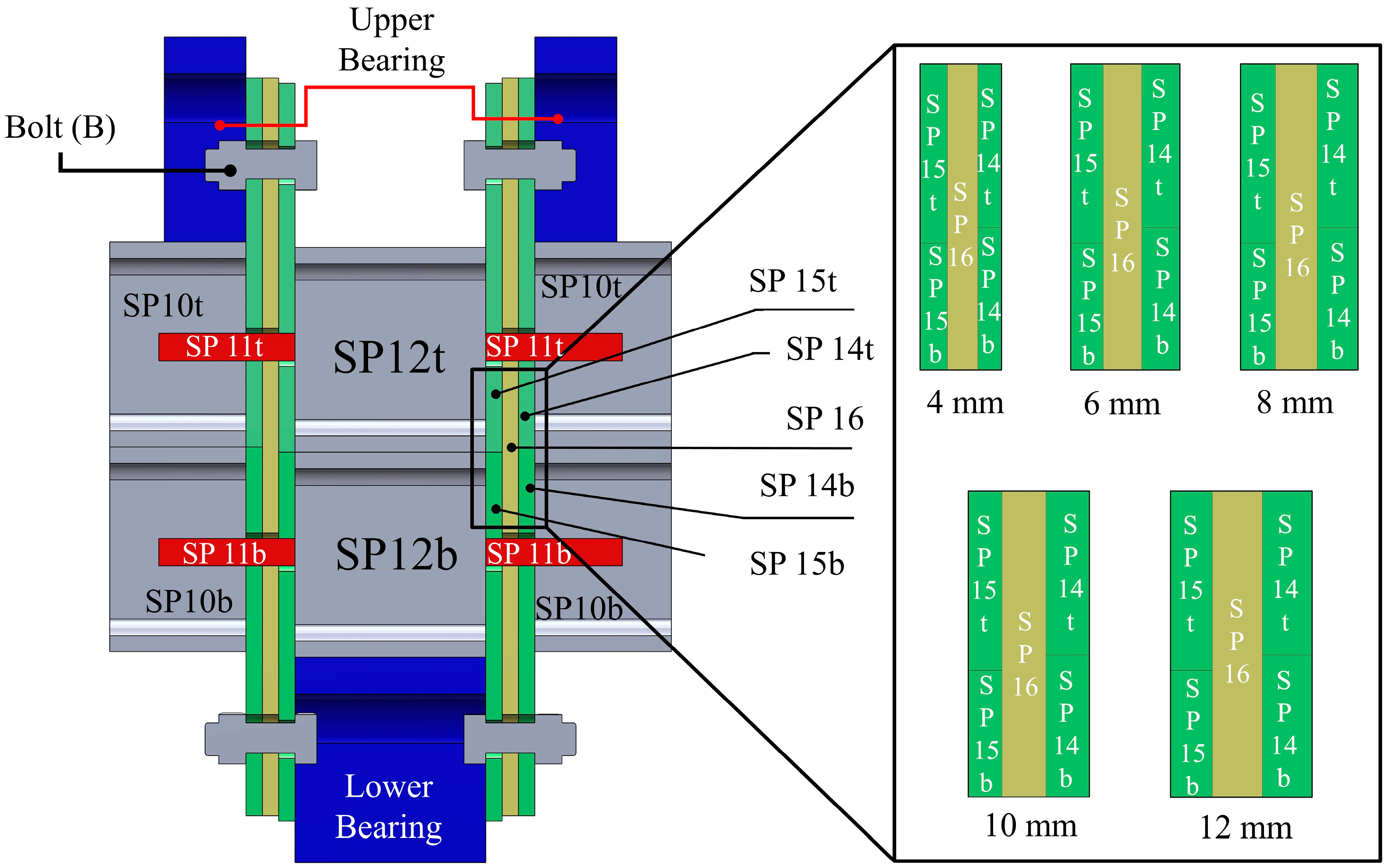
2.1. Connection Configuration and Properties
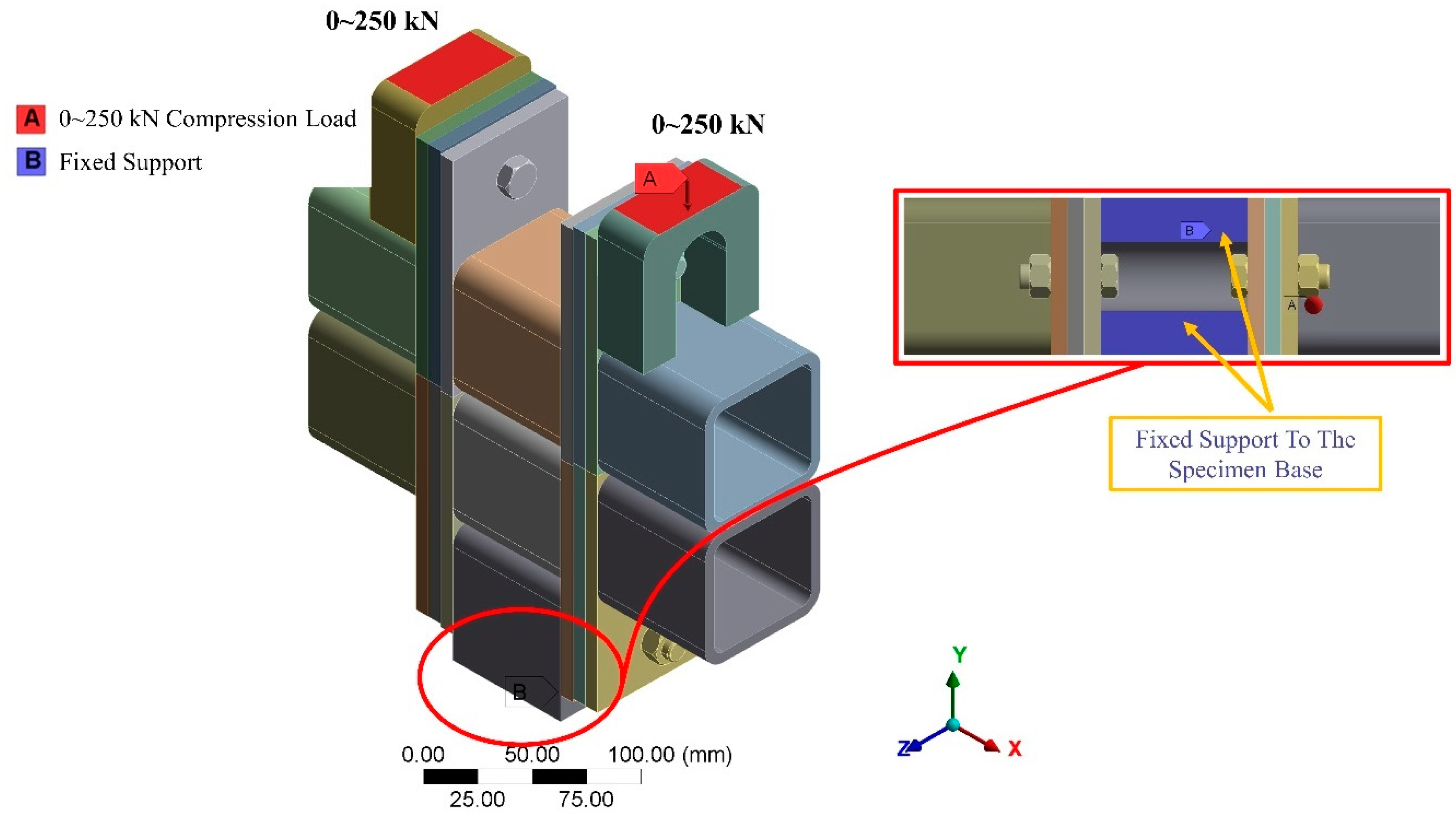
2.2. Compression Loading (UTM) Test Conditions Modelling
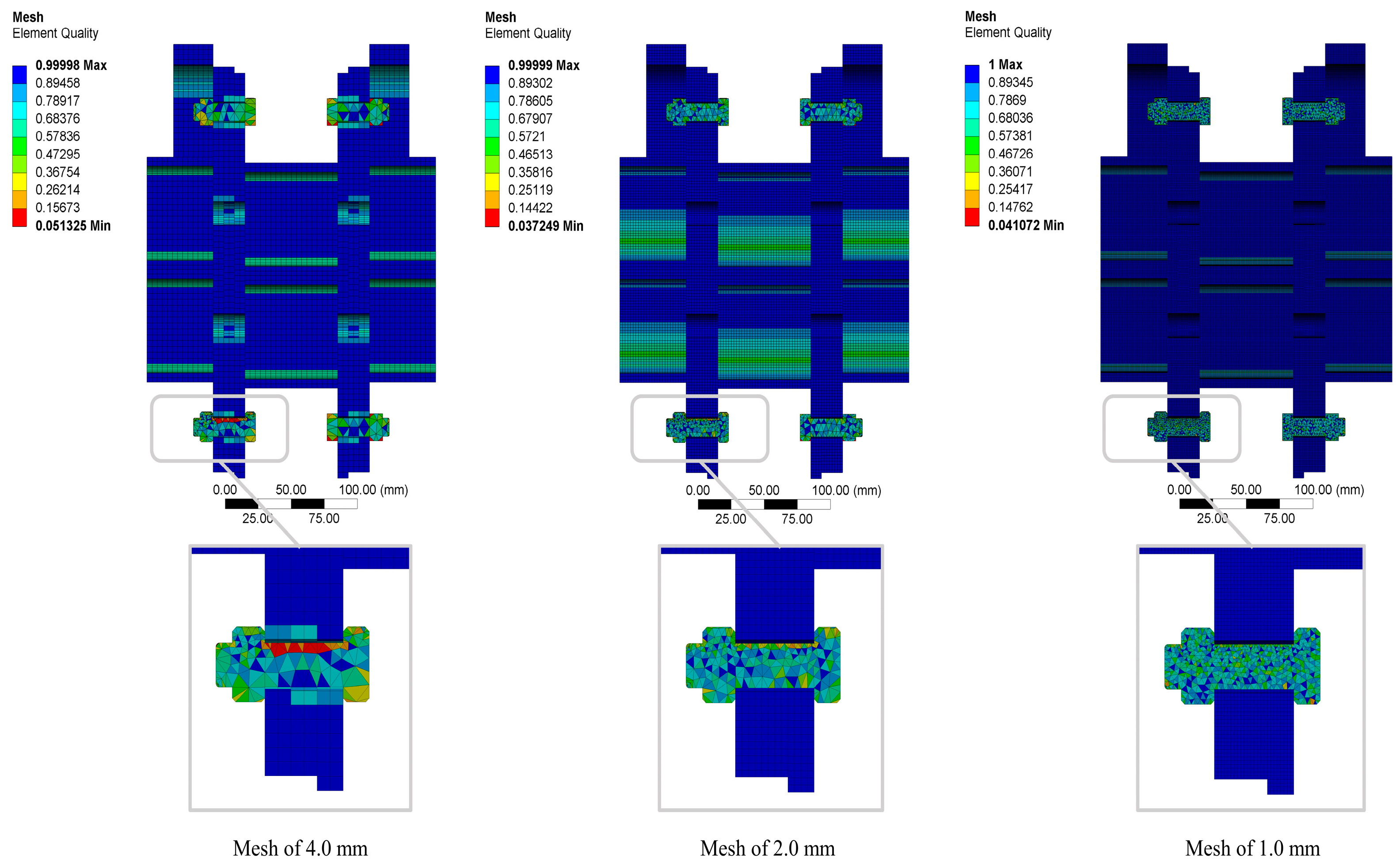
2.3. Interlocking Connection Modelling
2.4. Optimising Interlocking (IMCs) Plate Thickness
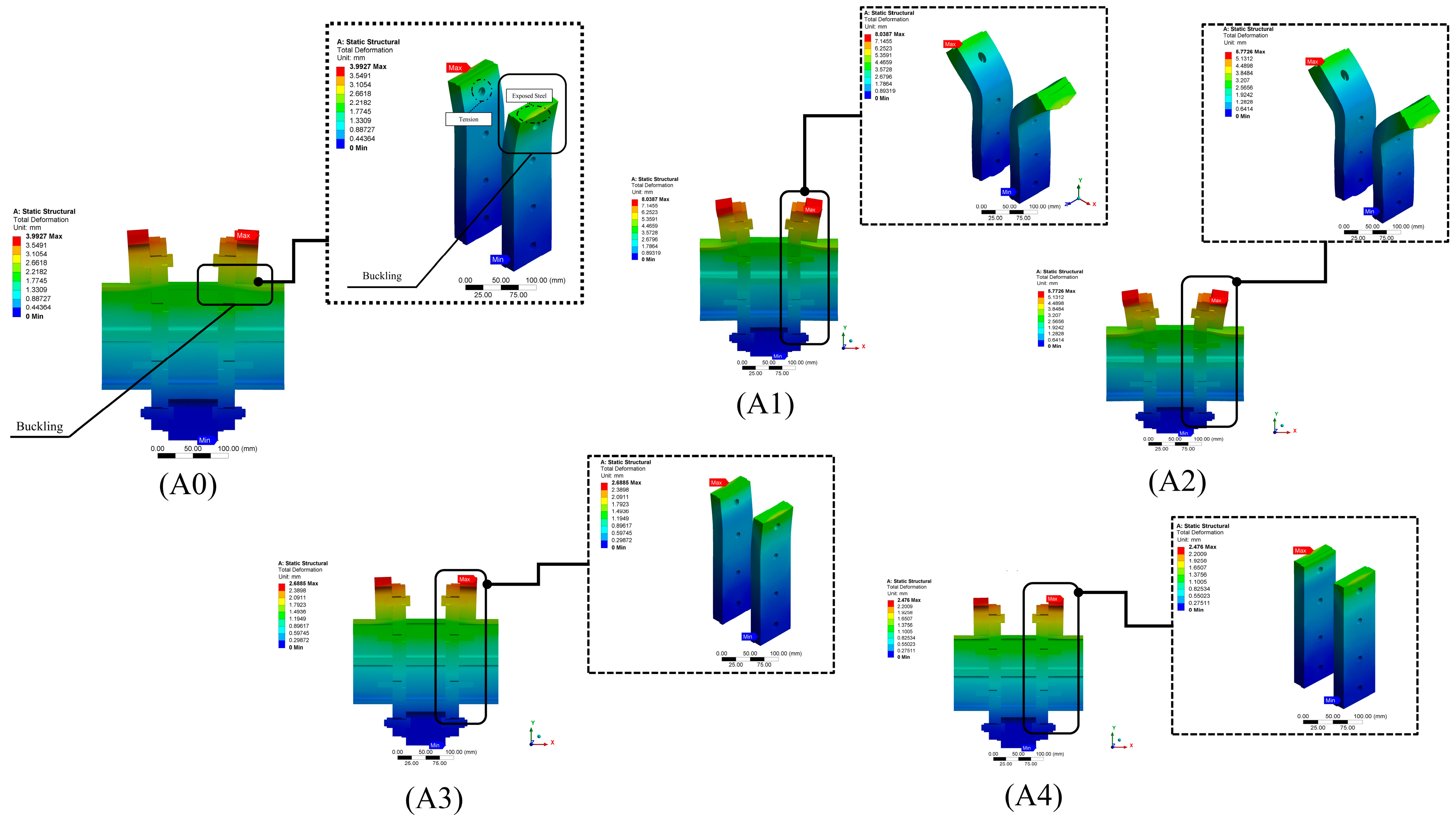
3. FE Results & Discussion
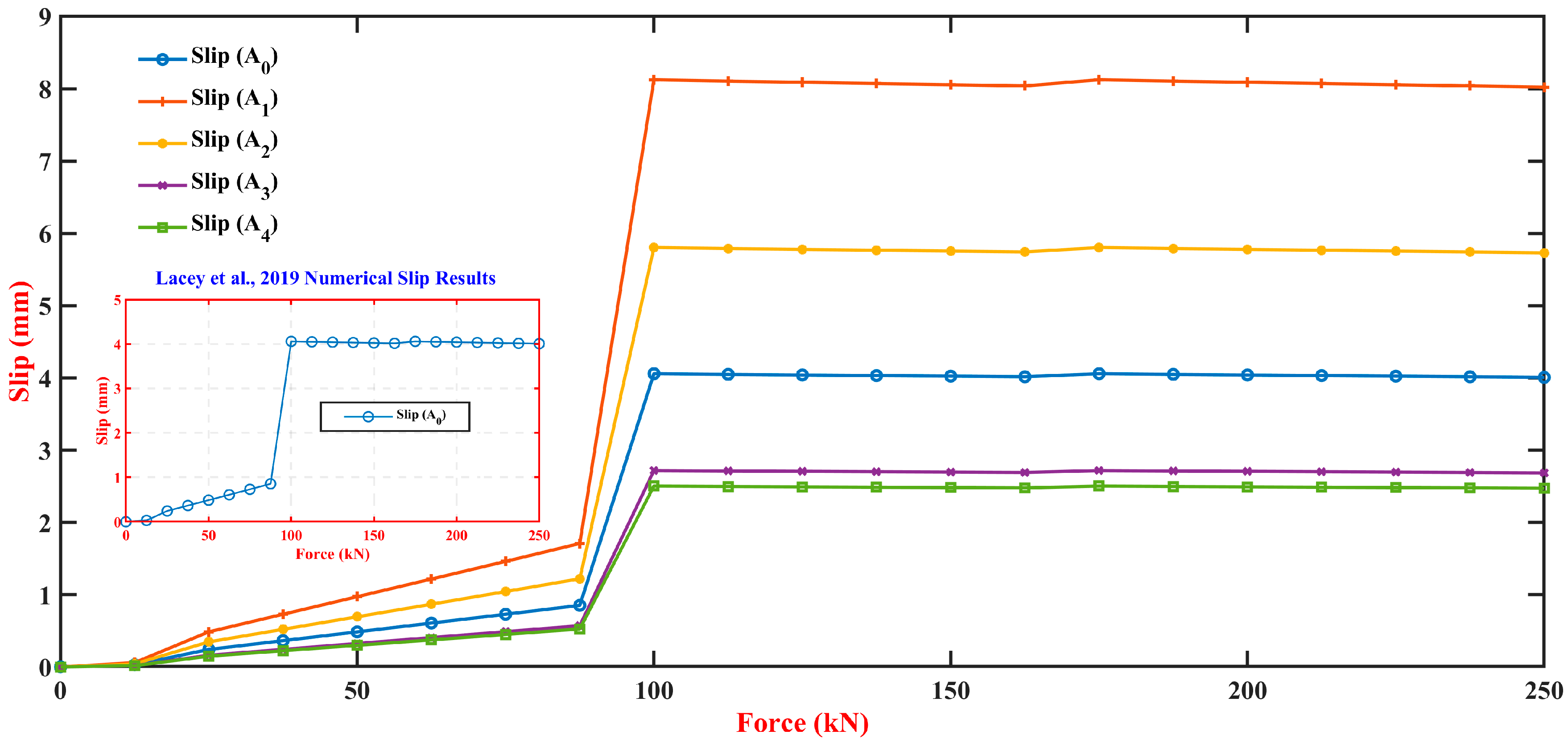
3.1. Slip (Deformation) Behaviour
3.2. Stability and Stiffness Behaviour
4. Advanced Predictive Modelling Study
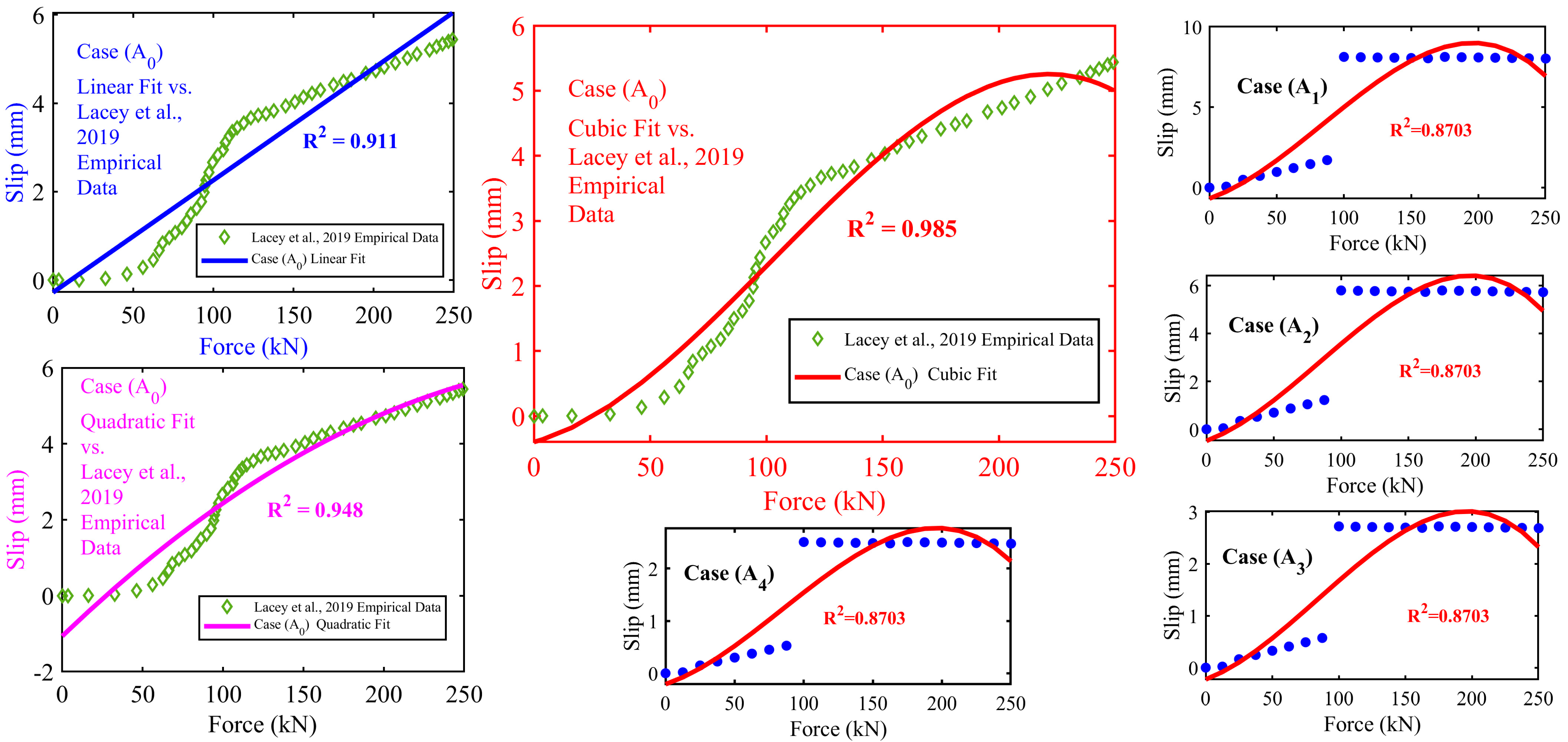
4.1. Polynomial Regression Formula and R-Values
4.2. Polynomial Regression Model for Slip Prediction
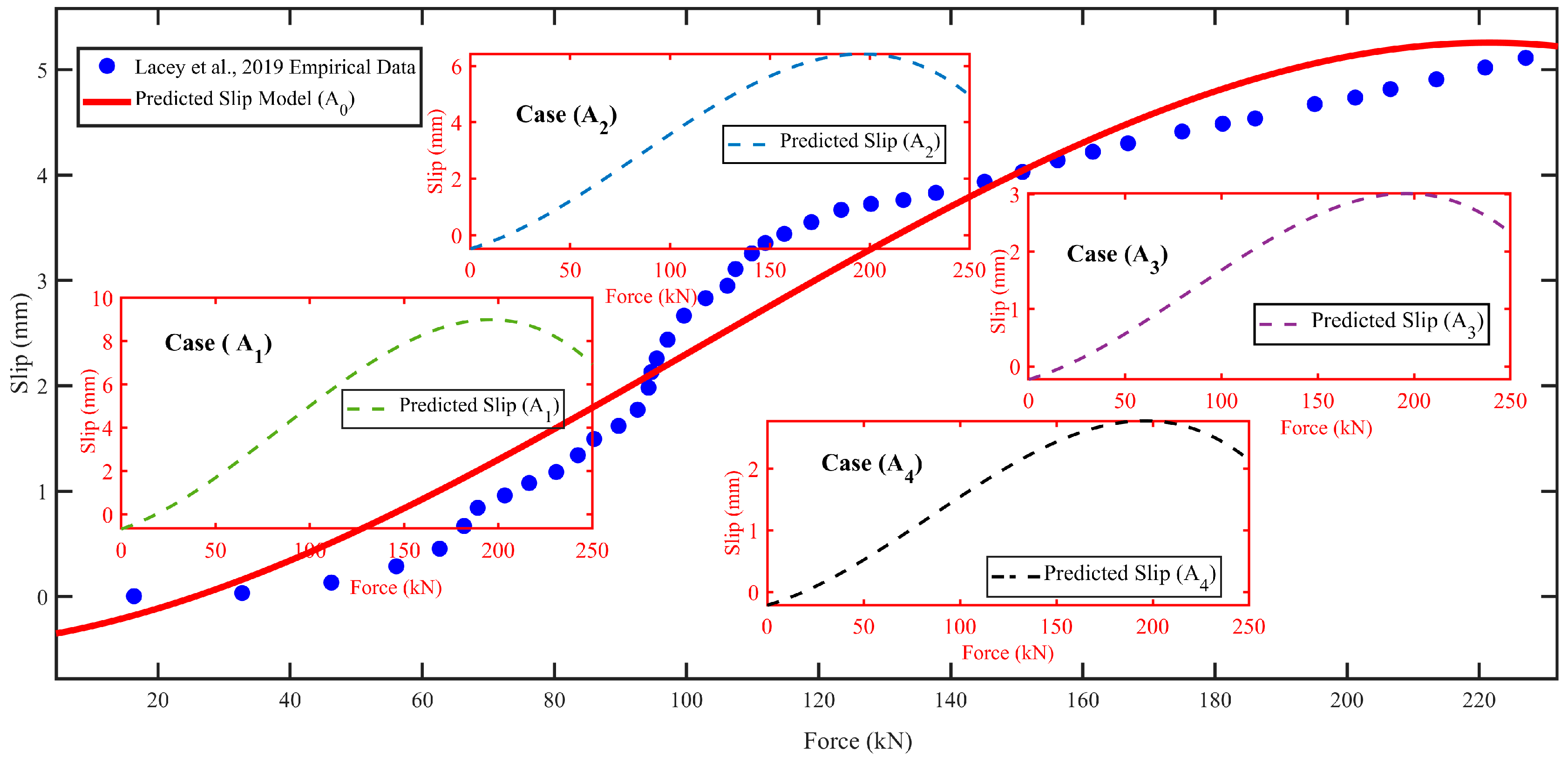
4.3. Validation of Polynomial Regression Model
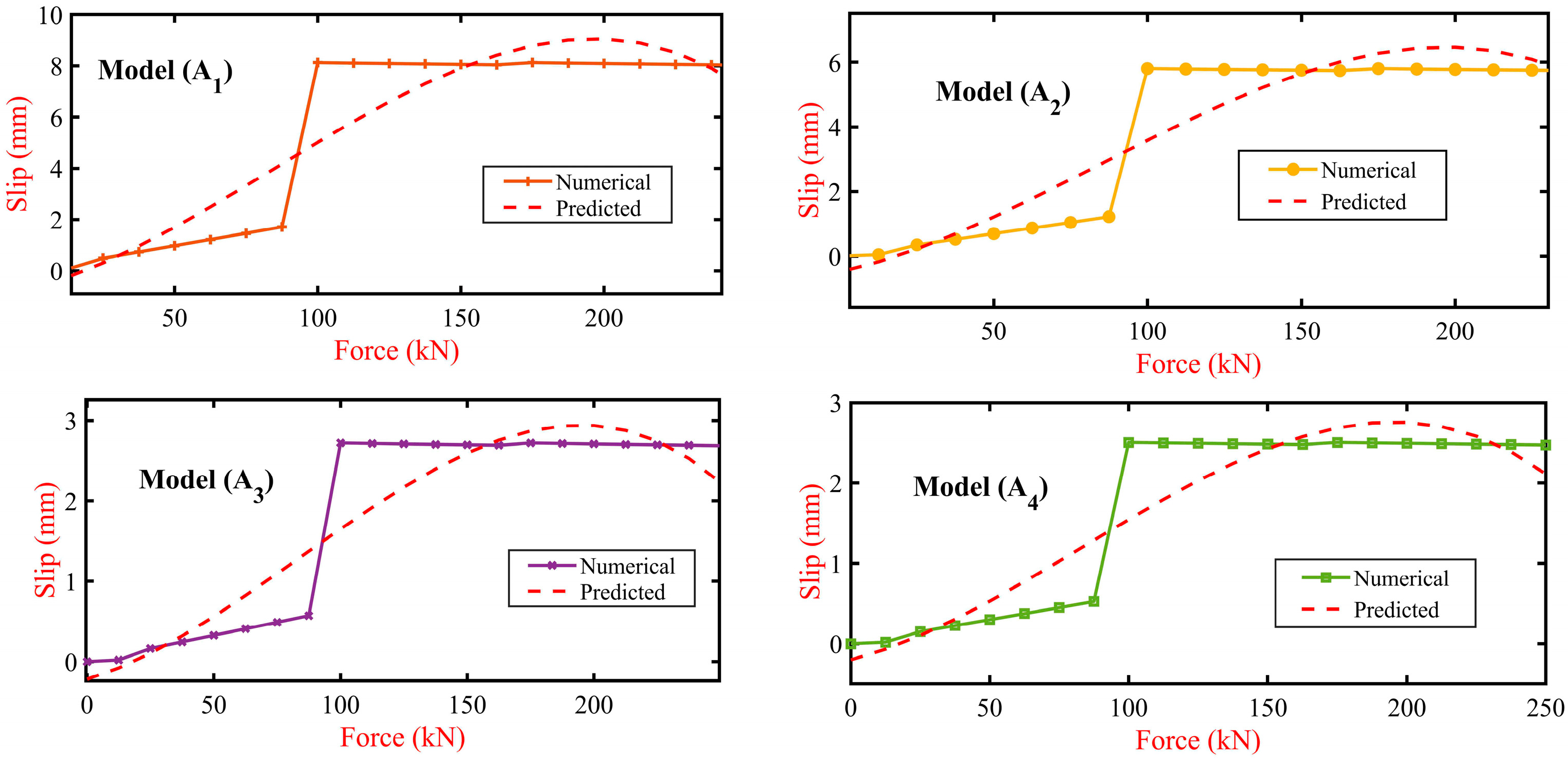
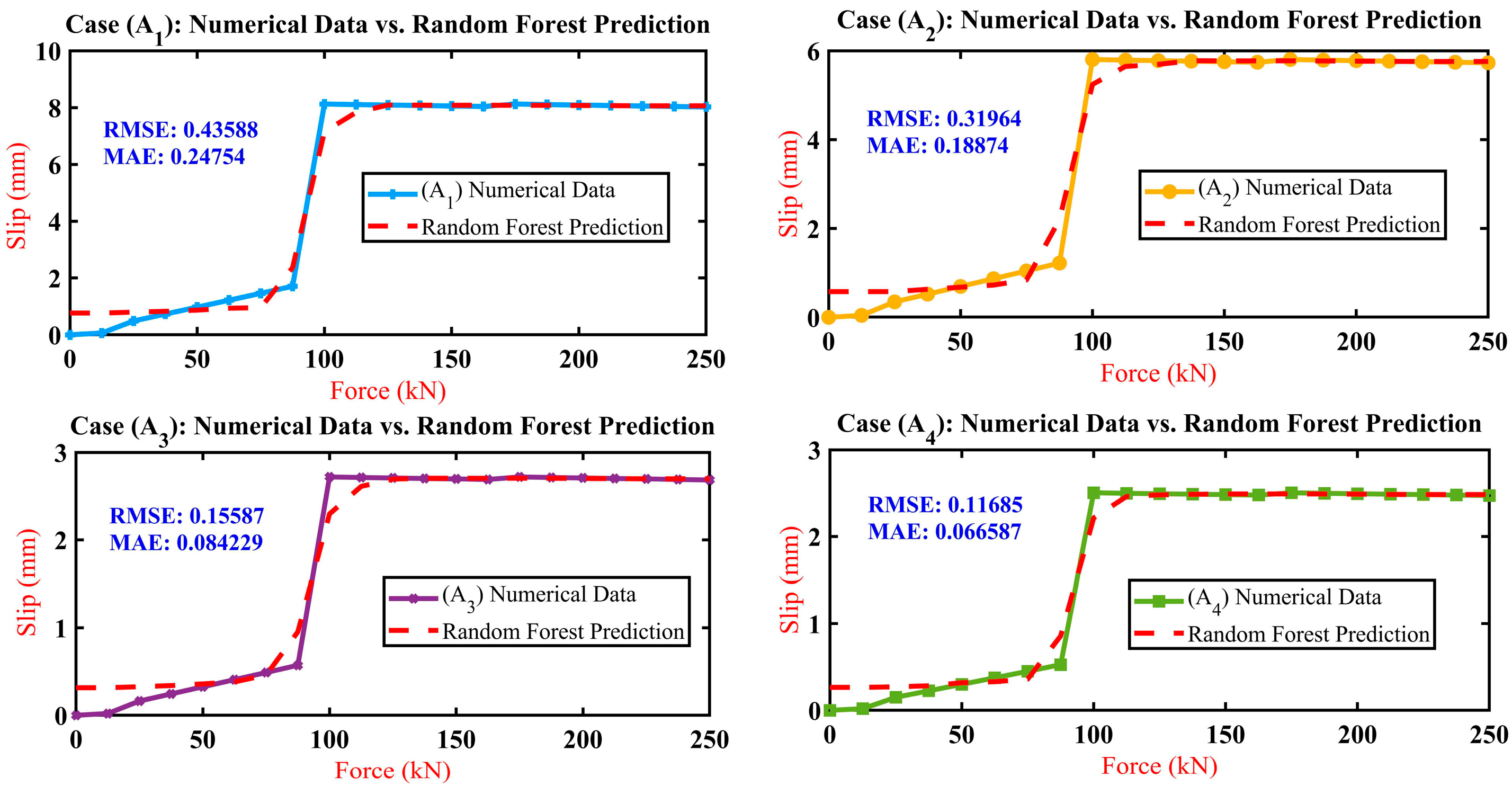
4.4. Random Forest Regression Model Analysis
5. Advanced Predictive Modelling Study
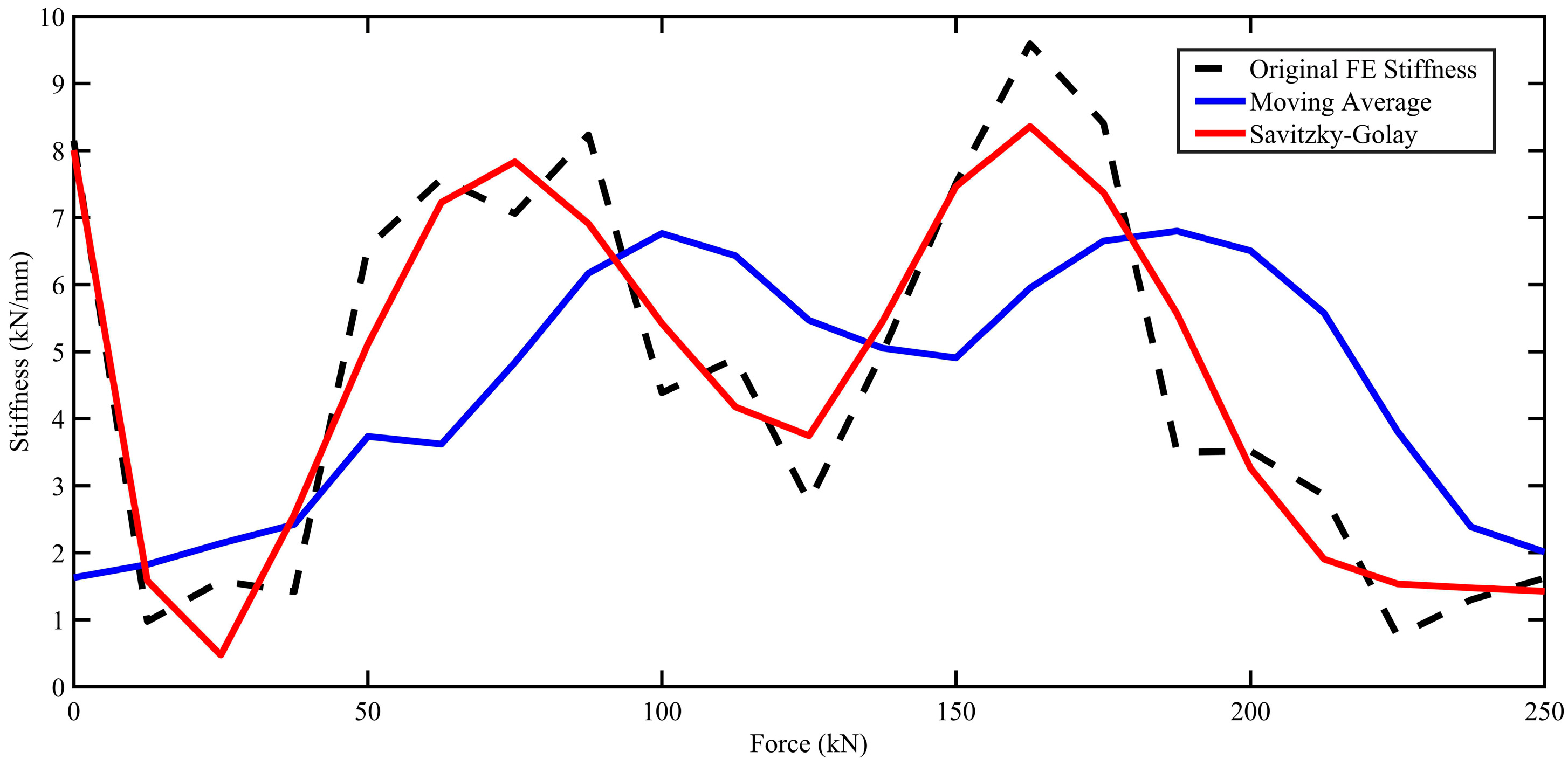
5.1. Stiffness Sensitivity Analysis
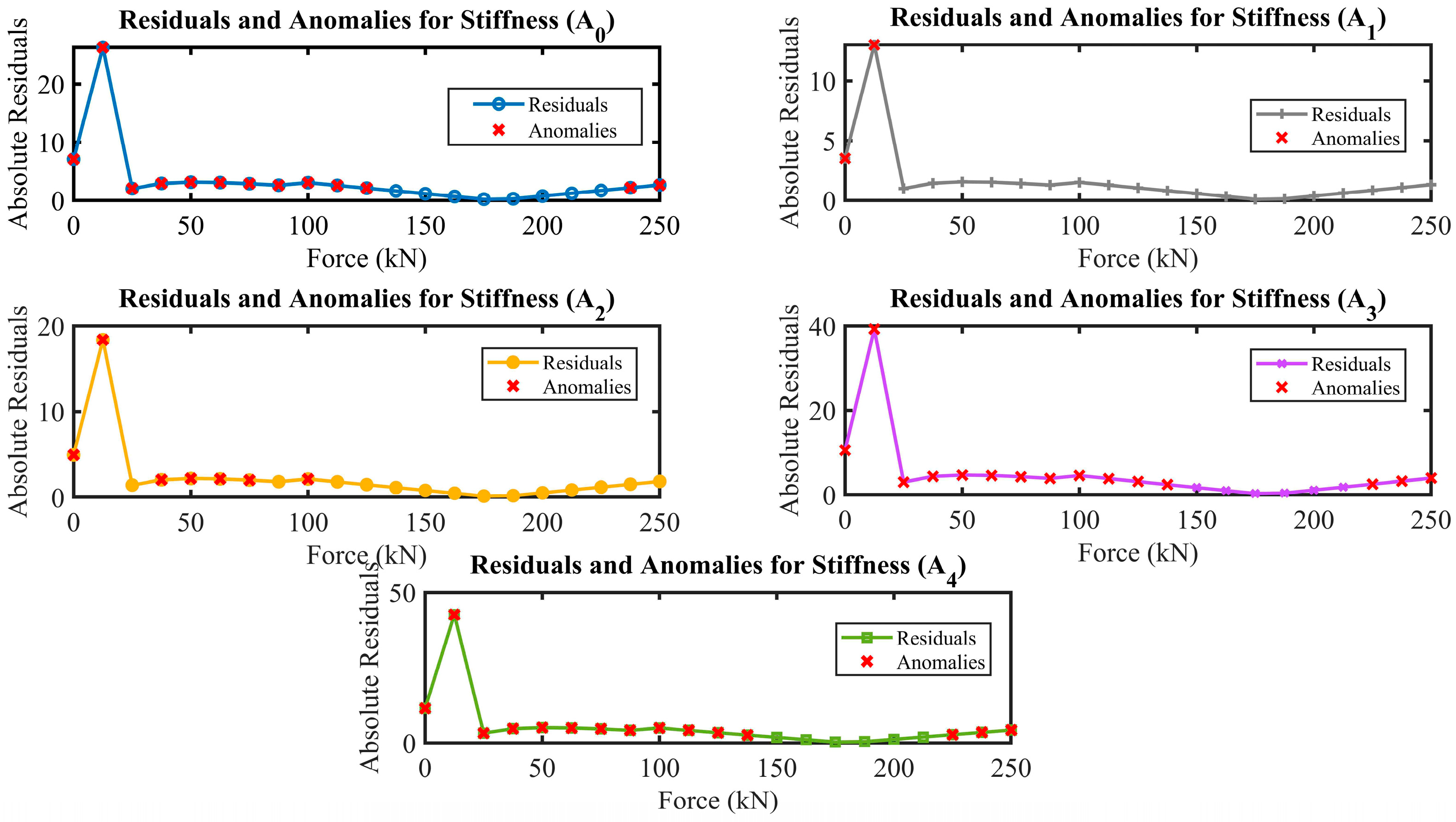
5.2. Errors and Anomalies
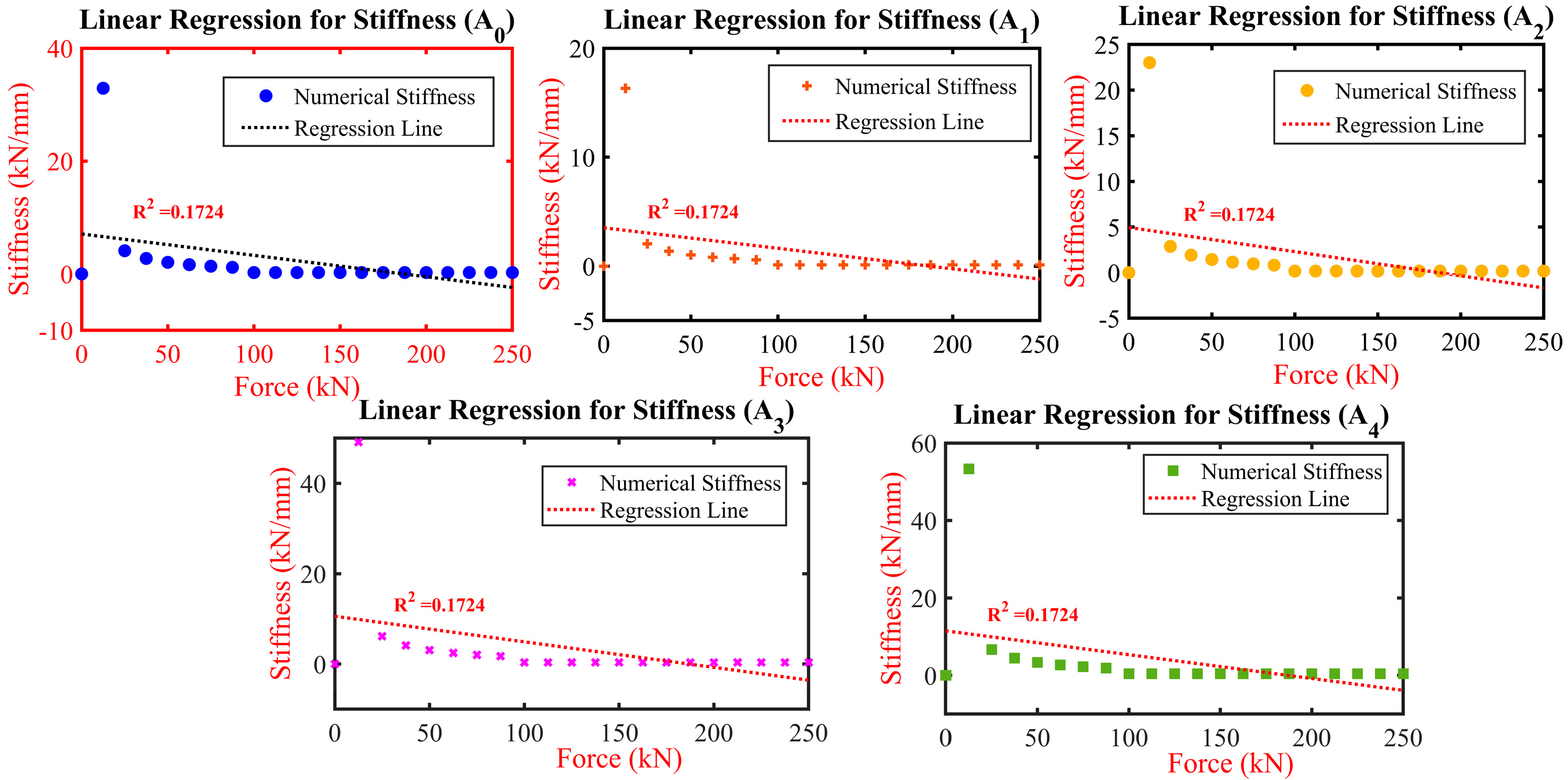
5.3. Stiffness Linear Regression Analysis
5.4. Anomaly Detection Analysis
5.5. Interlocking (IMCs) Plate Optimisation
6. Conclusions
- (i)
- A plate thickness of 11.03 mm is optimal, yielding significant material cost reductions of approximately 8.08% and enhancing deformation resistance by up to 50.75%, ensuring economic efficiency without comparing structural integrity.
- (ii)
- Sensitivity analysis underscores that thicker plates (A4) exhibit heightened structural responsiveness and stiffness, significantly improving stability and force distribution by approximately 62.07% more than the controlled model (A0).
- (iii)
- Implementing advanced anomaly detection techniques markedly improved the predictive accuracy of the predictive models, preserving data integrity at an impressive rate of 98.5%, reducing noise, and improving signal quality compared to original measurements.
- (iv)
- The ‘TreeBagger’ random forest regression model significantly improved the prediction accuracy of slip values by up to 7% at higher force levels, demonstrating the model’s capability to handle complex relationships effectively.
- (v)
- Linear regression analysis provided a deep understanding of how stiffness responds to force changes, noting a potential increase in stiffness by up to 50.75% with thicker plates, which fortifies the connection’s stability.
- (vi)
- Examination of slip phenomena across varying plate thicknesses revealed that the thickest plate (A4) offers superior deformation resistance, reducing slip by approximately 38% compared to the controlled model (A0).
- (vii)
- The integration of Finite Element analysis with random forest regression has strategically optimised plate thickness, balancing structural robustness with cost efficiency and setting a foundation for future advancements in modular building technologies.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| >> %% Material Efficiency Optimisation Script % This script calculates the optimal thickness of a material to maximise % an efficiency metric defined as the sum of normalised yield and tensile % strengths divided by the cost. It is designed to be adaptable to different % materials and scenarios. %% Step 1: Initialize Parameters % Define the material properties for the specific material under study. minYieldStress = 360e6; % Minimum yield stress in Pascals (Pa), for G350 steel minTensileStrength = 450e6; % Minimum tensile strength in Pascals (Pa), for G350 steel % Constants and Variables L = 2; % Span length in meters, adjust as necessary (not used in this script) c = 100; % Cost per mm thickness of the material % Define the range of thicknesses to evaluate (in mm) thicknessRange = linspace(4, 12, 100); % Thickness range from 4mm to 12mm, adjust as necessary %% Step 2: Pre-allocate Arrays for Storing Computed Values yieldStrengthValues = zeros(size(thicknessRange)); tensileStrengthValues = zeros(size(thicknessRange)); costValues = zeros(size(thicknessRange)); efficiencyValues = zeros(size(thicknessRange)); %% Step 3: Compute Properties Across Thickness Range % Loop over each thickness to calculate strength properties and efficiency for i = 1:length(thicknessRange) t = thicknessRange(i) / 1000; % Convert thickness from mm to meters yieldStrengthValues(i) = minYieldStress * (t / 0.004); % Normalize yield strength based on min thickness tensileStrengthValues(i) = minTensileStrength * (t / 0.004); % Normalize tensile strength similarly costValues(i) = c * thicknessRange(i); % Calculate cost based on thickness efficiencyValues(i) = (yieldStrengthValues(i) + tensileStrengthValues(i)) / ... costValues(i); % Calculate efficiency using ellipsis for line continuation end %% Step 4: Identify Optimal Thickness [optimalValue, optimalIndex] = max(efficiencyValues); % Find maximum efficiency and its index optimalThickness = thicknessRange(optimalIndex); % Determine optimal thickness %% Step 5: Output Results fprintf('Optimal Thickness for Maximum Efficiency: %.2f mm\n', optimalThickness); fprintf('Maximum Efficiency Value: %.2f\n', optimalValue); %% Step 6: Visualization of Results % Plotting yield strength, tensile strength, and efficiency versus thickness figure; subplot(3, 1, 1); plot(thicknessRange, yieldStrengthValues, 'b-', 'LineWidth', 2); title('Yield Strength vs. Thickness'); xlabel('Thickness (mm)'); ylabel('Yield Strength (Pa)'); subplot(3, 1, 2); plot(thicknessRange, tensileStrengthValues, 'r-', 'LineWidth', 2); title('Tensile Strength vs. Thickness'); xlabel('Thickness (mm)'); ylabel('Tensile Strength (Pa)'); subplot(3, 1, 3); plot(thicknessRange, efficiencyValues, 'g-', 'LineWidth', 2); title('Efficiency vs. Thickness'); xlabel('Thickness (mm)'); ylabel('Efficiency (Strength/Cost)'); sgtitle('Material Efficiency Optimization Analysis'); %% Step 7: Save Results (Optional) % Optionally, save results to a .mat file or other formats for further analysis save('OptimizationResults.mat', 'thicknessRange', 'yieldStrengthValues', 'tensileStrengthValues', 'costValues', 'efficiencyValues', 'optimalThickness', 'optimalValue'); |
Appendix B
| >> % MATLAB Script for Predictive Analysis of Slip Based on Applied Forces % Utilizes polynomial regression models to predict slip in response to applied forces, according to specified equations (Eq. 1 to Eq. 5). % Step 1: Define the force range for prediction % Generating a vector of 1000 evenly spaced force values between 0 and 250 kN. force_values = linspace(0, 250, 1000); % linspace(start, end, number of points) % Step 2: Define polynomial coefficients for each model based on provided equations % Polynomial Regression Formula for Slip (A0) as per Eq. 1 coeffs_A0 = [3.46, -23.25, 67.91, 23.25]; % Coefficients for Model A0 with R^2 = 0.9854 % Polynomial Regression Formulas for Slips (A1 to A4) as per Eqs. 2 to 5 coeffs_A1 = [−1.81×10−6, 4.60×10−4, 2.90×10−2, −0.68]; % Model A1 with R^2 = 0.8703 coeffs_A2 = [−1.29×10−6, 3.28×10−4, 2.07×10−2, −0.48]; % Model A2 with R^2 = 0.8703 coeffs_A3 = [−6.07×10−7, 1.53×10−4, 9.47×10−3, −0.22]; % Model A3 with R^2 = 0.8703 coeffs_A4 = [−5.59×10−7, 1.41×10−4, 8.94×10−3, −0.20]; % Model A4 with R^2 = 0.8703 % Step 3: Calculation of predicted slip using polynomial evaluation % This step evaluates the polynomials for each force value, using the polyval function. predicted_slip_A0 = polyval(coeffs_A0, force_values); % Prediction for Model A0 (Eq. 1) predicted_slip_A1 = polyval(coeffs_A1, force_values); % Prediction for Model A1 (Eq. 2) predicted_slip_A2 = polyval(coeffs_A2, force_values); % Prediction for Model A2 (Eq. 3) predicted_slip_A3 = polyval(coeffs_A3, force_values); % Prediction for Model A3 (Eq. 4) predicted_slip_A4 = polyval(coeffs_A4, force_values); % Prediction for Model A4 (Eq. 5) % Step 4: Aggregation of predicted slips into a matrix for comparative analysis predicted_slips = [predicted_slip_A0; predicted_slip_A1; predicted_slip_A2; predicted_slip_A3; predicted_slip_A4]'; % Step 5: Tabulation of results for analysis and visualization % Creates a table with force values and predicted slips for each model. results_table = array2table([force_values', predicted_slips], ... 'VariableNames', {'Force_kN', 'PredictedSlip_A0', 'PredictedSlip_A1', 'PredictedSlip_A2', 'PredictedSlip_A3', 'PredictedSlip_A4'}); % Display the results table to the MATLAB command window for review and analysis. |
Appendix C
| >> function trainAndPlotRandomForestModels(Force, SlipData) % Train and plot random forest models for given force and slip data sets. % Force: A vector of force values. % SlipData: A cell array where each cell contains a vector of slip values for a different model (A1 to A4). nTrees = 100; % Number of trees in the random forest for i = 1:length(SlipData) Y = SlipData{i}'; % Train the random forest model model = TreeBagger(nTrees, Force', Y, 'Method', 'regression'); % Predict slip values using the trained model Y_pred = predict(model, Force'); % Plot actual vs. predicted slip values figure; plot(Force, Y, 'bo', 'MarkerFaceColor', 'b'); hold on; plot(Force, Y_pred, 'r-', 'LineWidth', 2); hold off; xlabel('Force (kN)'); ylabel(sprintf('Slip A%d', i)); title(sprintf('Model A%d: Numerical Data vs. Random Forest Prediction', i)); legend('Numerical Data', 'Random Forest Prediction', 'Location', 'NorthWest'); grid on; end end % Example usage: Force = [0, 12.5, 25, 37.5, 50, 62.5, 75, 87.5, 100, 112.5, 125, 137.5, 150, 162.5, 175, 187.5, 200, 212.5, 225, 237.5, 250]; Slip_A1 = [0, 0.061275458, 0.486733848, 0.730097368, 0.973440468, 1.216919704, 1.461488028, 1.709255548, 8.12527716, 8.10553744, 8.08920112, 8.07218412, 8.0558478, 8.0388308, 8.12527716, 8.10553744, 8.08920112, 8.07218412, 8.0558478, 8.0388308, 8.0218138]; % Repeat for Slip_A2, Slip_A3, Slip_A4 as needed SlipData = {Slip_A1}; % Add Slip_A2, Slip_A3, Slip_A4 as available trainAndPlotRandomForestModels(Force, SlipData); |
References
- Luo, F.J.; Bai, Y.; Hou, J.; Huang, Y. Progressive Collapse Analysis and Structural Robustness of Steel-Framed Modular Buildings. Eng. Fail. Anal. 2019, 104, 643–656. [Google Scholar] [CrossRef]
- Swami, G.; Thai, T.; Thai, H.-T. Modelling Methods for Robustness Analysis of Composite Steel- Concrete Modular Buildings. In Proceedings of the 3rd International Conference on Structural Engineering Research (iCSER2022), Sydney, Australia, 27–30 November 2022. [Google Scholar]
- Farajian, M.; Sharafi, P.; Bigdeli, A.; Eslamnia, H.; Rahnamayiezekavat, P. Experimental Study on the Natural Dynamic Characteristics of Steel-Framed Modular Structures. Buildings 2022, 12, 587. [Google Scholar] [CrossRef]
- Palmiotta, A.; Garbellini, S.; Audisio, L.; Sulla, R.; D’Amato, M.; Gigliotti, R. Seismic Behaviour of Steel Modular Buildings: Numerical Analysis and Comparisons between Different Design Solutions. Procedia Struct. Integr. 2022, 44, 1156–1163. [Google Scholar] [CrossRef]
- Liu, X.; He, X.; Zhang, A.; Tian, C.; Zhang, X.; Tan, Y. Design and Specification Compilation of a Modular-Prefabricated High-Rise Steel Frame Structure with Diagonal Braces Part II: Elastic–Plastic Time-History Analysis and Joint Design. Struct. Des. Tall Spec. Build. 2018, 27, e1414. [Google Scholar] [CrossRef]
- Alembagheri, M.; Sharafi, P.; Hajirezaei, R.; Tao, Z. Anti-Collapse Resistance Mechanisms in Corner-Supported Modular Steel Buildings. J. Constr. Steel Res. 2020, 170, 106083. [Google Scholar] [CrossRef]
- Chen, Z.; Zhong, X.; Liu, Y.; Liu, J. Analytical and Design Method for the Global Stability of Modular Steel Buildings. Int. J. Steel Struct. 2021, 21, 1741–1758. [Google Scholar] [CrossRef]
- Yang, C.; Xu, B.; Xia, J.; Chang, H.; Chen, X.; Ma, R. Mechanical Behaviors of Inter-Module Connections and Assembled Joints in Modular Steel Buildings: A Comprehensive Review. Buildings 2023, 13, 1727. [Google Scholar] [CrossRef]
- Poudel, B.; Lee, S.; Choi, J.O. Steel Module-to-Concrete Core Connection Methods in High Rise Buildings: A Critical Review. In Proceedings of the 9th International Conference on Construction Engineering and Project Management, Las Vegas, NV, USA, 20–23 June 2022. [Google Scholar]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. Review of Bolted Inter-Module Connections in Modular Steel Buildings. J. Build. Eng. 2019, 23, 207–219. [Google Scholar] [CrossRef]
- Swami, G.; Thai, H.T.; Liu, X. Structural Robustness of Composite Modular Buildings: The Roles of CFST Columns and Inter-Module Connections. Structures 2023, 48, 1491–1504. [Google Scholar] [CrossRef]
- Chen, Z.; Khan, K.; Khan, A.; Javed, K.; Liu, J. Exploration of the Multidirectional Stability and Response of Prefabricated Volumetric Modular Steel Structures. J. Constr. Steel Res. 2021, 184, 106826. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, J.; Liu, J.; Khan, K. Seismic Behavior and Moment Transfer Capacity of an Innovative Self-Locking Inter-Module Connection for Modular Steel Building. Eng. Struct. 2021, 245, 112978. [Google Scholar] [CrossRef]
- Srisangeerthanan, S.; Hashemi, M.J.; Rajeev, P.; Gad, E.; Fernando, S. Review of Performance Requirements for Inter-Module Connections in Multi-Story Modular Buildings. J. Build. Eng. 2020, 28, 101087. [Google Scholar] [CrossRef]
- Thai, H.T.; Ngo, T.; Uy, B. A Review on Modular Construction for High-Rise Buildings. Structures 2020, 28, 1265–1290. [Google Scholar] [CrossRef]
- Lacey, A.; Chen, W.; Hao, H.; Bi, K. Shear Stiffness of Bolted Inter-Module Connections. In Proceedings of the 11th International Conference of the IFHS on Extreme Engineering, Singapore, 28–30 August 2019. [Google Scholar]
- He, X.-H.-C.; Chan, T.-M.; Chung, K.-F. Effect of Inter-Module Connections on Progressive Collapse Behaviour of MiC Structures. J. Constr. Steel Res. 2021, 185, 106823. [Google Scholar] [CrossRef]
- Shi, F.W.; Ding, Y.; Zong, L.; Meng, X.; Chen, Y. Axial Mechanical Behavior of Innovative Inter-Module Connection for Modular Steel Constructions. J. Build. Eng. 2023, 65, 105765. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. New Interlocking Inter-Module Connection for Modular Steel Buildings: Simplified Structural Behaviours. Eng. Struct. 2021, 227, 111409. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. New Interlocking Inter-Module Connection for Modular Steel Buildings: Experimental and Numerical Studies. Eng. Struct. 2019, 198, 109465. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, J.; Liu, J.; Cong, Z. Tensile and Shear Performance of Rotary Inter-Module Connection for Modular Steel Buildings. J. Constr. Steel Res. 2020, 175, 106367. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. Simplified Structural Behaviours of Post-Tensioned Inter-Module Connection for Modular Buildings. J. Constr. Steel Res. 2020, 175, 106347. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K.; Tallowin, F.J. Shear Behaviour of Post-Tensioned Inter-Module Connection for Modular Steel Buildings. J. Constr. Steel Res. 2019, 162, 105707. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, Y.; Zhong, X.; Liu, J. Rotational Stiffness of Inter-Module Connection in Mid-Rise Modular Steel Buildings. Eng. Struct. 2019, 196, 109273. [Google Scholar] [CrossRef]
- Chua, Y.S.; Pang, S.D.; Liew, J.Y.R.; Dai, Z. Robustness of Inter-Module Connections and Steel Modular Buildings under Column Loss Scenarios. J. Build. Eng. 2022, 47, 103888. [Google Scholar] [CrossRef]
- Peng, J.; Hou, C.; Shen, L. Numerical Simulation of Weld Fracture Using Cohesive Interface for Novel Inter-Module Connections. J. Constr. Steel Res. 2020, 174, 106302. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. Lateral Behaviour of Modular Steel Building with Simplified Models of New Inter-Module Connections. Eng. Struct. 2021, 236, 112103. [Google Scholar] [CrossRef]
- Shi, F.W.; Ding, Y.; Zong, L.; Chen, Y.; Wu, Y. Shear Behaviour of Vertical Inter-Module Connection with Bolts and Shear Keys for MSCs. Structures 2023, 47, 260–281. [Google Scholar] [CrossRef]
- Peng, J.; Hou, C.; Shen, L. Lateral Resistance of Multi-Story Modular Buildings Using Tenon-Connected Inter-Module Connections. J. Constr. Steel Res. 2021, 177, 106453. [Google Scholar] [CrossRef]
- Zhao, F.; Yu, Y.; Lin, S.; Ding, F. Evaluation of the Working Mechanisms and Simplified Models of Endplate-Type Inter-Module Connections. Structures 2021, 32, 562–577. [Google Scholar] [CrossRef]
- Lim, R.Z.C.; Looi, D.T.W.; Chen, M.T.; Tsang, H.H.; Wilson, J.L. A Component-Based Macro-Mechanical Model for Inter-Module Connections in Steel Volumetric Buildings. J. Constr. Steel Res. 2023, 207, 107954. [Google Scholar] [CrossRef]
- Alembagheri, M.; Sharafi, P.; Hajirezaei, R.; Samali, B. Collapse Capacity of Modular Steel Buildings Subject to Module Loss Scenarios: The Role of Inter-Module Connections. Eng. Struct. 2020, 210, 110373. [Google Scholar] [CrossRef]
- Corfar, D.A.; Tsavdaridis, K.D. A Hybrid Inter-Module Connection for Steel Modular Building Systems with SMA and High-Damping Rubber Components. Eng. Struct. 2023, 289, 116281. [Google Scholar] [CrossRef]
- Lacey, A.W.; Chen, W.; Hao, H. Experimental Methods for Inter-Module Joints in Modular Building Structures—A State-of-the-Art Review. J. Build. Eng. 2022, 46, 103792. [Google Scholar] [CrossRef]
- Farajian, M.; Sharafi, P.; Kildashti, K. The Influence of Inter-Module Connections on the Effective Length of Columns in Multi-Story Modular Steel Frames. J. Constr. Steel Res. 2021, 177, 106450. [Google Scholar] [CrossRef]
- Dai, Z.; Pang, S.D.; Liew, J.R. Axial Load Resistance of Grouted Sleeve Connection for Modular Construction. Thin-Walled Struct. 2020, 154, 106883. [Google Scholar] [CrossRef]
- He, Z.; Zhang, T.; Li, T. Static Bearing Capacity Investigation of Grouted Square Hollow Section Sleeve Connection. Adv. Struct. Eng. 2022, 25, 3–13. [Google Scholar] [CrossRef]
- Dai, Z.; Cheong, T.Y.C.; Pang, S.D.; Liew, J.Y.R. Experimental Study of Grouted Sleeve Connections under Bending for Steel Modular Buildings. Eng. Struct. 2021, 243, 112614. [Google Scholar] [CrossRef]
- Faculty, E. Review of Interconnection in Modular Structures. In Proceedings of the PACE 2021-Ataturk University, Engineering Faculty, Department of Civil Engineering, Erzurum, Turkey, 20–23 June 2021; pp. 1–8. [Google Scholar]
- Lee, Y.H.; Tan, C.S.; Mohammad, S.; Md Tahir, M.; Shek, P.N. Review on Cold-Formed Steel Connections. Sci. World J. 2014, 2014, 951216. [Google Scholar] [CrossRef] [PubMed]
- Nadeem, G.; Safiee, N.A.; Bakar, N.A.; Karim, I.A.; Nasir, N.A.M. Connection Design in Modular Steel Construction: A Review. Structures 2021, 33, 3239–3256. [Google Scholar] [CrossRef]
- Pang, S.D.; Liew, J.Y.R.L.; Dai, Z.; Wang, Y. Prefabricated Prefinished Volumetric Construction Joining Tech-Niques Review. In Proceedings of the Modular and Offsite Construction (MOC) Summit Proceedings, Edmonton, AB, Canada, 29 September–1 October 2016; pp. 249–256. [Google Scholar] [CrossRef]
- Rajanayagam, H.; Poologanathan, K.; Gatheeshgar, P.; Varelis, G.E.; Sherlock, P.; Nagaratnam, B.; Hackney, P. A-State-Of-The-Art Review on Modular Building Connections. Structures 2021, 34, 1903–1922. [Google Scholar] [CrossRef]
- Li, Z.; Tsavdaridis, K.D.; Gardner, L. A Review of Optimised Additively Manufactured Steel Connections for Modular Building Systems. In Industrializing Additive Manufacturing; Springer International Publishing: Cham, Switzerland, 2021; pp. 357–373. [Google Scholar]
- Srisangeerthanan, S.; Hashemi, M.J.; Rajeev, P.; Gad, E.F.; Fernando, S. A Review of Diaphragm Behaviour and Connections for Multi-Story Modular Buildings. In Proceedings of the Australasian Structural Engineering Conference 2018 (ASEC2018), Adelaide, Australia, 25–28 September 2018. [Google Scholar]
- Corfar, D.-A.; Tsavdaridis, K.D. A Comprehensive Review and Classification of Inter-Module Connections for Hot-Rolled Steel Modular Building Systems. J. Build. Eng. 2022, 50, 104006. [Google Scholar] [CrossRef]
- Chua, Y.S.; Liew, J.Y.R.; Pang, S.D. Modelling of Connections and Lateral Behavior of High-Rise Modular Steel Buildings. J. Constr. Steel Res. 2020, 166, 105901. [Google Scholar] [CrossRef]
- Elsayed, M.A.; Mutalib, A.; Elsayed, K. Numerical Study of Structural Performance and Wind Flow Dynamic Behavior for PPVC Steel Modular Construction (MSC) under Various Extreme Wind Loads. Buildings 2022, 12, 1347. [Google Scholar] [CrossRef]
- Sharafi, P.; Mortazavi, M.; Samali, B.; Ronagh, H. Interlocking System for Enhancing the Integrity of Multi-Storey Modular Buildings. Autom. Constr. 2018, 85, 263–272. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, J.; Yu, Y. Experimental Study on Interior Connections in Modular Steel Buildings. Eng. Struct. 2017, 147, 625–638. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, J.; Yu, Y.; Zhou, C.; Yan, R. Experimental Study of an Innovative Modular Steel Building Connection. J. Constr. Steel Res. 2017, 139, 69–82. [Google Scholar] [CrossRef]
- Sanches, R.; Mercan, O.; Roberts, B. Experimental Investigations of Vertical Post-Tensioned Connection for Modular Steel Structures. Eng. Struct. 2018, 175, 776–789. [Google Scholar] [CrossRef]
- Chen, X.W.; Yuan, H.X.; Real, E.; Du, X.X.; Schafer, B.W. Experimental Behaviour of Stainless Steel Plate Girders under Combined Bending and Shear. J. Constr. Steel Res. 2020, 166, 105900. [Google Scholar] [CrossRef]
- Bazarchi, E.; Davaran, A.; Lamarche, C.P.; Roy, N.; Parent, S. Experimental and Numerical Investigation of a Novel Vertically Unconstrained Steel Inter-Modular Connection. Thin-Walled Struct. 2023, 183, 110364. [Google Scholar] [CrossRef]
- Ma, R.; Xia, J.; Chang, H.; Xu, B.; Zhang, L. Experimental and Numerical Investigation of Mechanical Properties on Novel Modular Connections with Superimposed Beams. Eng. Struct. 2021, 232, 111858. [Google Scholar] [CrossRef]
- Wu, C.; Zhou, Y.; Liu, J.; Mou, B.; Shi, J. Experimental and Finite Element Analysis of Modular Prefabricated Composite Beam-Column Interior Joints. J. Build. Eng. 2021, 43, 102853. [Google Scholar] [CrossRef]
- Nadeem, G.; Safiee, N.A.; Bakar, N.A.; Karim, I.A.; Mohd Nasir, N.A. Experimental and Numerical Study of Self-Locking Adaptable Inter Connection for Modular Steel Structures. J. Build. Eng. 2023, 65, 105723. [Google Scholar] [CrossRef]
- Deng, E.F.; Yan, J.B.; Ding, Y.; Zong, L.; Li, Z.X.; Dai, X.M. Analytical and Numerical Studies on Steel Columns with Novel Connections in Modular Construction. Int. J. Steel Struct. 2017, 17, 1613–1626. [Google Scholar] [CrossRef]
- Luo, F.J.; Ding, C.; Styles, A.; Bai, Y. End Plate–Stiffener Connection for SHS Column and RHS Beam in Steel-Framed Building Modules. Int. J. Steel Struct. 2019, 19, 1353–1365. [Google Scholar] [CrossRef]
- Yu, Y.; Chen, Z. Rigidity of Corrugated Plate Sidewalls and Its Effect on the Modular Structural Design. Eng. Struct. 2018, 175, 191–200. [Google Scholar] [CrossRef]
- Deng, E.F.; Zong, L.; Ding, Y.; Dai, X.M.; Lou, N.; Chen, Y. Monotonic and Cyclic Response of Bolted Connections with Welded Cover Plate for Modular Steel Construction. Eng. Struct. 2018, 167, 407–419. [Google Scholar] [CrossRef]
- Deng, E.F.; Zong, L.; Ding, Y. Numerical and Analytical Study on Initial Stiffness of Corrugated Steel Plate Shear Walls in Modular Construction. Steel Compos. Struct. 2019, 32, 347–359. [Google Scholar] [CrossRef]
- Keipour, N.; Valipour, H.R.; Bradford, M.A. Structural Behaviour of Steel-Timber versus Steel-Concrete Composite Joints with Flush End Plate. Constr. Build. Mater. 2020, 262, 120885. [Google Scholar] [CrossRef]
- Elsayed, K.; Mutalib, A.A.; Elsayed, M.; Azmi, M.R. Numerical Study of PPVC Modular Steel Constructions (MSCs) with Selected Connection Strategies under Varied Earthquake Scenarios. Results Eng. 2024, 22, 102076. [Google Scholar] [CrossRef]
- Ansys Inc. ANSYS Mechanical 2023; Ansys Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- The MathWorks Inc. MATLAB, Version: 9.13.0 (R2022b); The MathWorks Inc.: Natick, MA, USA, 2022. Available online: https://www.mathworks.com (accessed on 5 February 2024).
- Lacey, A.W.; Chen, W.; Hao, H.; Bi, K. Structural Response of Modular Buildings—An Overview. J. Build. Eng. 2018, 16, 45–56. [Google Scholar] [CrossRef]
- Gao, Y.; Mosalam, K.M.; Chen, Y.; Wang, W.; Chen, Y. Auto-Regressive Integrated Moving-Average Machine Learning for Damage Identification of Steel Frames. Appl. Sci. 2021, 11, 6084. [Google Scholar] [CrossRef]
- Roy, I.G. An Optimal Savitzky–Golay Derivative Filter with Geophysical Applications: An Example of Self-potential Data. Geophys. Prospect. 2020, 68, 1041–1056. [Google Scholar] [CrossRef]
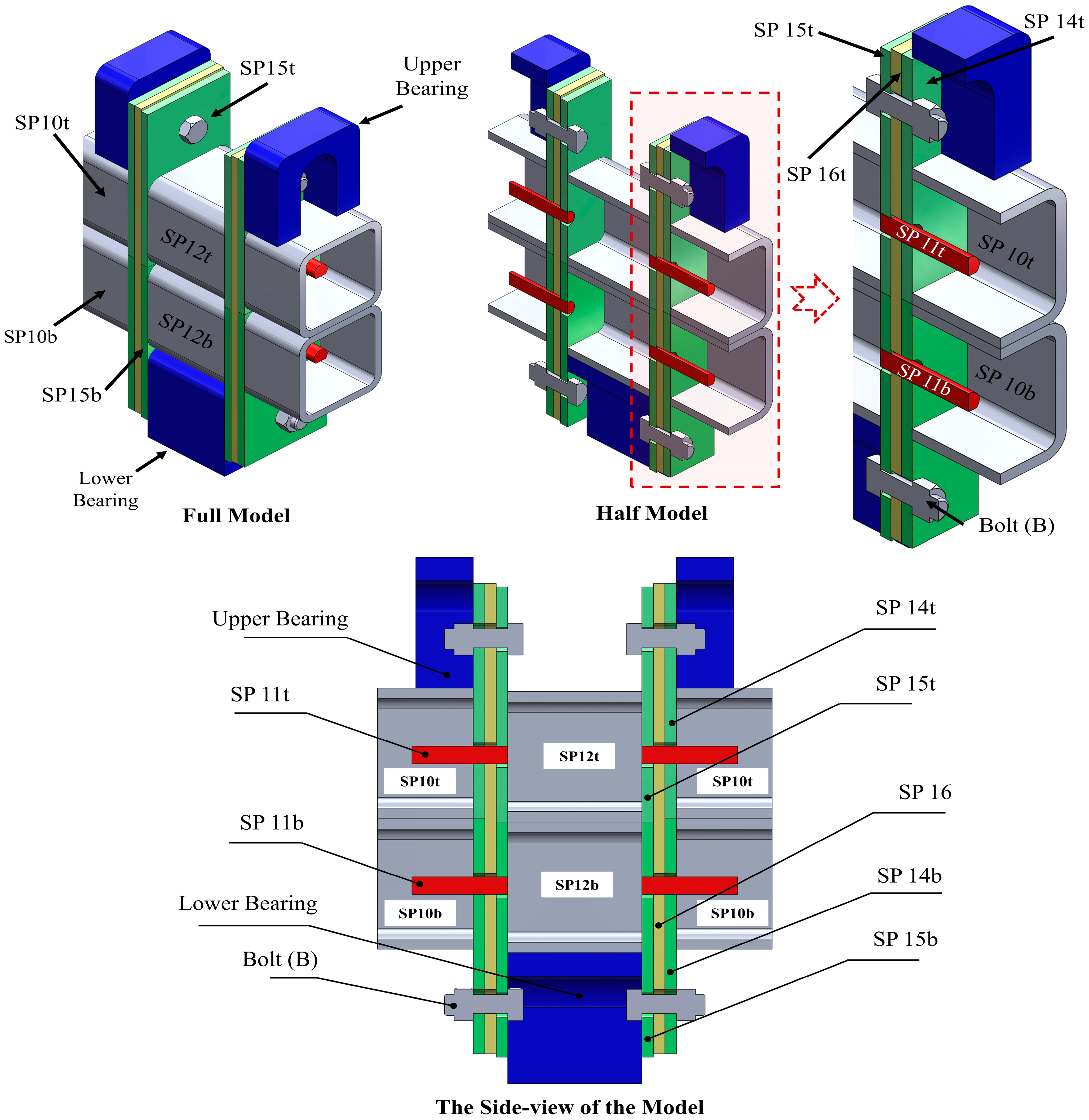
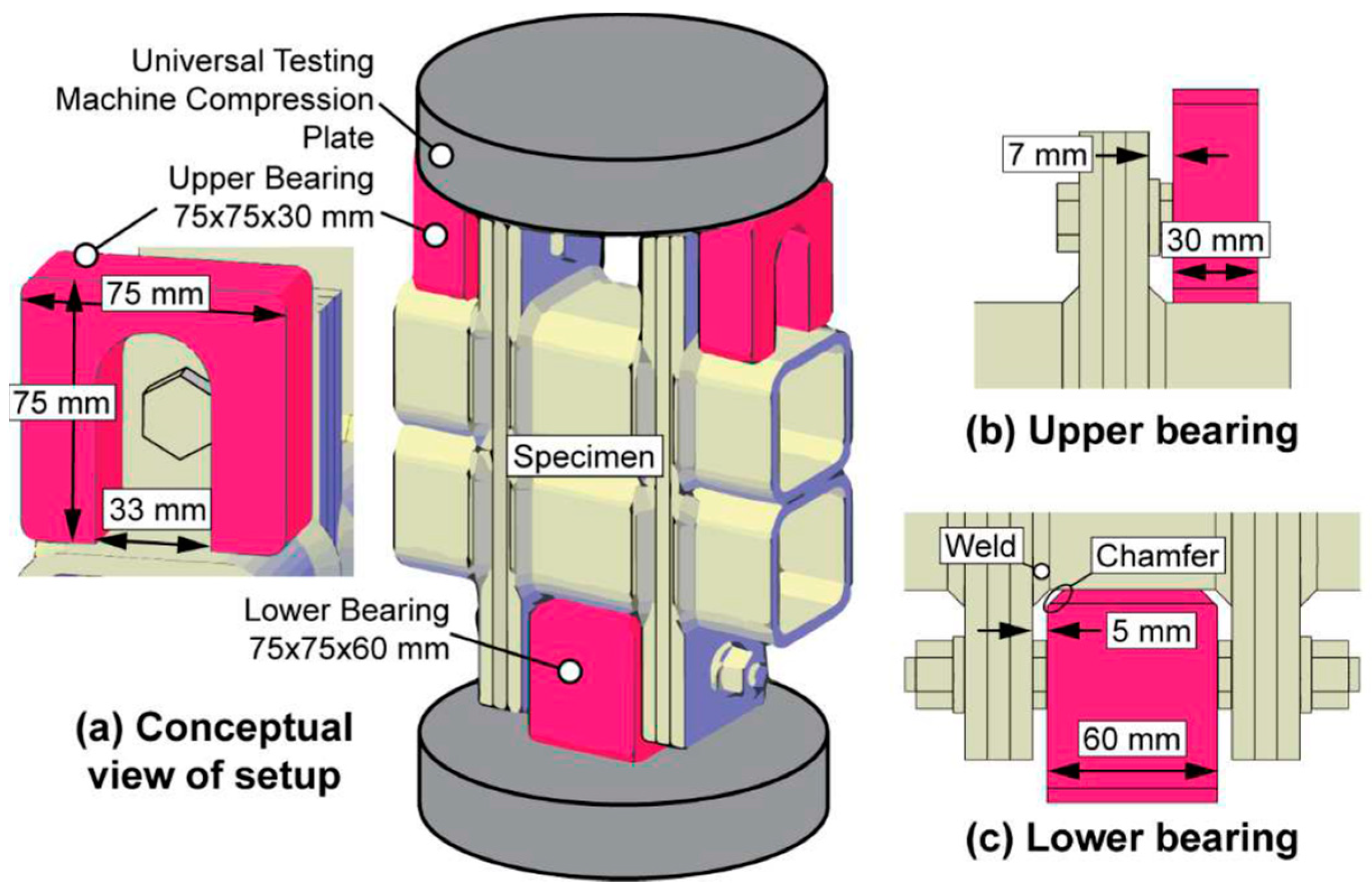





| Description | Part | Cross-Section Dimensions (mm) | Length (mm) | Illustration Ref. |
|---|---|---|---|---|
| Hollow Section | SP10 | 75 × 75 × 6 | 50 | Figure 3 |
| Hollow Section | SP12 | 75 × 75 × 6 | 70 | |
| Square Bar | Upper Bearing | 75 × 75 × 30 | 75 | |
| Lower Bearing | 75 × 75 × 60 | |||
| Round Bar | SP11 | R12 | 50 | |
| Plate | SP14 | 75 × 8 | 75 | |
| Plate | SP15 | 75 × 8 | 75 | |
| Plate | SP16 | 75 × 8 | 135 | |
| Bolt (B) | M12,8.8 Grade | - | 24 |
| Part | Grade | Min. Yield Stress (MPa) | Min. Tensile Strength (MPa) | Min. Elongation (%) |
|---|---|---|---|---|
| SP10, SP12 | C350L0 | 350 | 430 | 12 |
| Bearings | 300 | 290 | 440 | 22 |
| SP11 | 300 | 375 | 530 | 34 |
| SP14, SP15, SP16 | G350 | 360 | 450 | 20 |
| Bolt (B) | Class 8.8 | 640 | 800 | 12 |
| Plate | (A0) Thickness (mm) | (A1) Thickness (mm) | (A2) Thickness (mm) | (A3) Thickness (mm) | (A4) Thickness (mm) |
|---|---|---|---|---|---|
| SP14 | 8 | 4 | 6 | 10 | 12 |
| SP15 | 8 | 4 | 6 | 10 | 12 |
| SP16 | 8 | 4 | 6 | 10 | 12 |
| Stiffness Attribute | Min Rate of Change | Max Rate of Change | Average Rate of Change |
|---|---|---|---|
| (A0) | −2.3034 | 2.6324 | 0.00099828 |
| (A1) | −1.1412 | 1.3056 | 0.00049864 |
| (A2) | −1.6108 | 1.8409 | 0.0006981 |
| (A3) | −3.4379 | 3.929 | 0.00149 |
| (A4) | −3.7332 | 4.2665 | 0.001618 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsayed, K.; Mutalib, A.A.; Elsayed, M.; Azmi, M.R. Optimising Plate Thickness in Interlocking Inter-Module Connections for Modular Steel Buildings: A Finite Element and Random Forest Approach. Buildings 2024, 14, 1254. https://doi.org/10.3390/buildings14051254
Elsayed K, Mutalib AA, Elsayed M, Azmi MR. Optimising Plate Thickness in Interlocking Inter-Module Connections for Modular Steel Buildings: A Finite Element and Random Forest Approach. Buildings. 2024; 14(5):1254. https://doi.org/10.3390/buildings14051254
Chicago/Turabian StyleElsayed, Khaled, Azrul A. Mutalib, Mohamed Elsayed, and Mohd Reza Azmi. 2024. "Optimising Plate Thickness in Interlocking Inter-Module Connections for Modular Steel Buildings: A Finite Element and Random Forest Approach" Buildings 14, no. 5: 1254. https://doi.org/10.3390/buildings14051254
APA StyleElsayed, K., Mutalib, A. A., Elsayed, M., & Azmi, M. R. (2024). Optimising Plate Thickness in Interlocking Inter-Module Connections for Modular Steel Buildings: A Finite Element and Random Forest Approach. Buildings, 14(5), 1254. https://doi.org/10.3390/buildings14051254






