A Multiscale Method to Develop Three-Dimensional Anisotropic Constitutive Model for Soils
Abstract
1. Introduction
2. Inherent Anisotropy
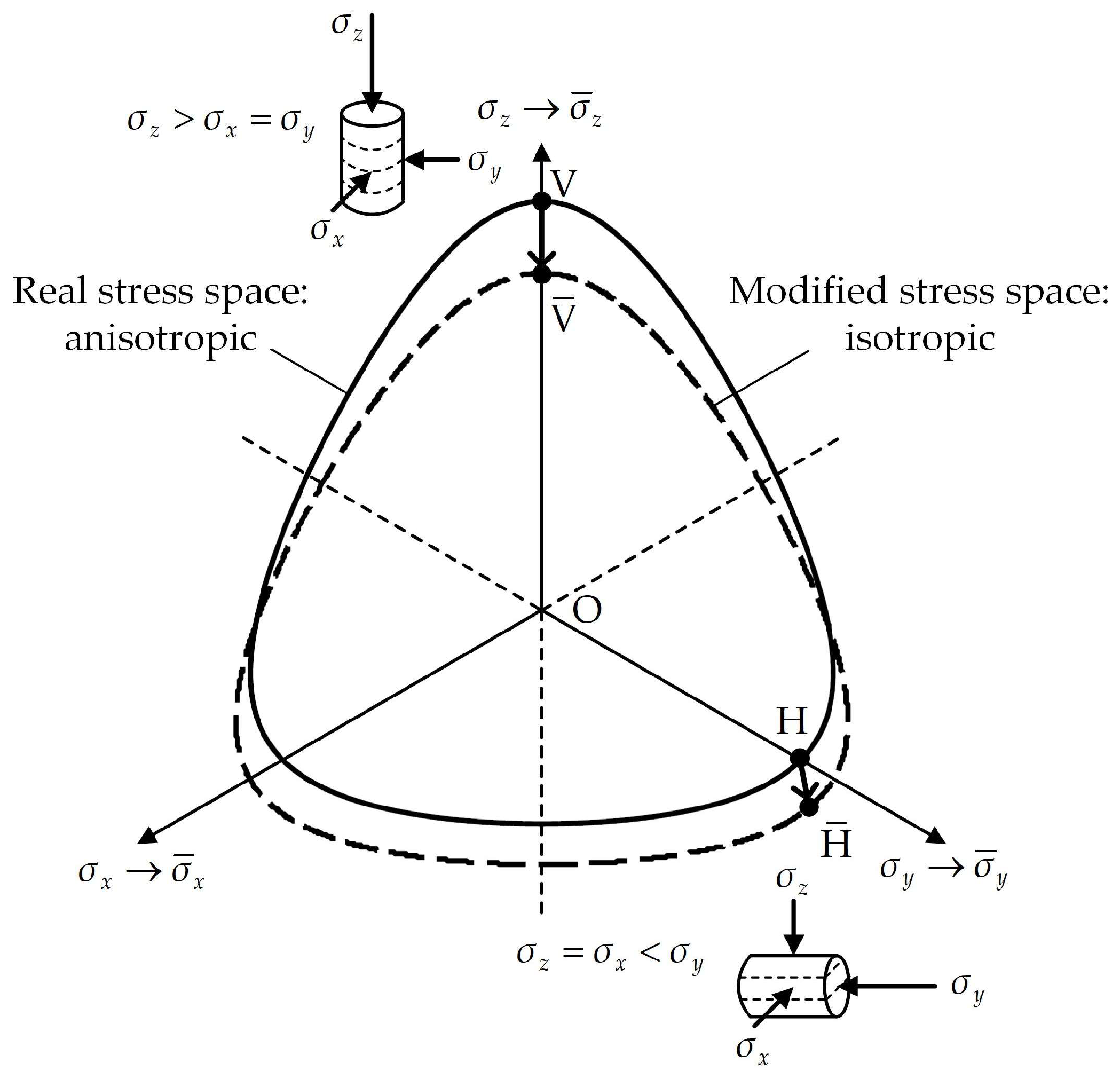
2.1. Modified Stress Tensor
2.1.1. Basic Idea
2.1.2. Formula
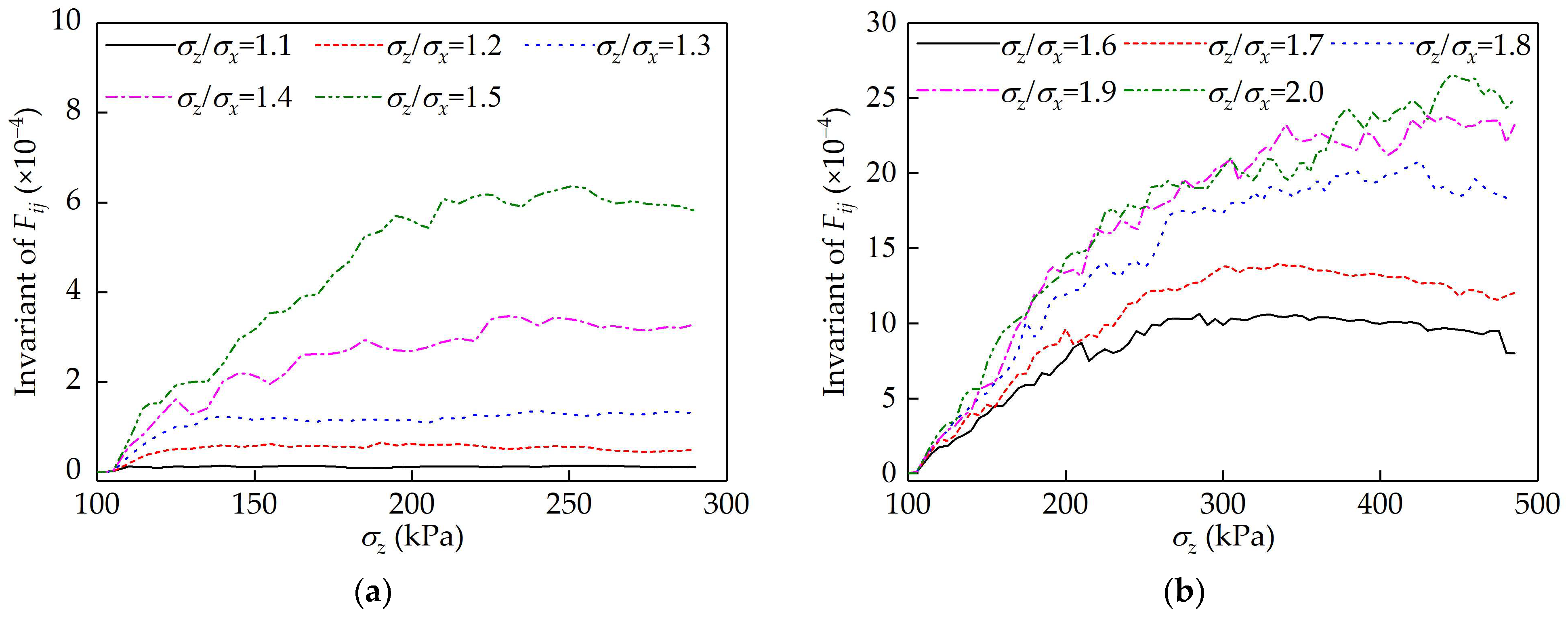
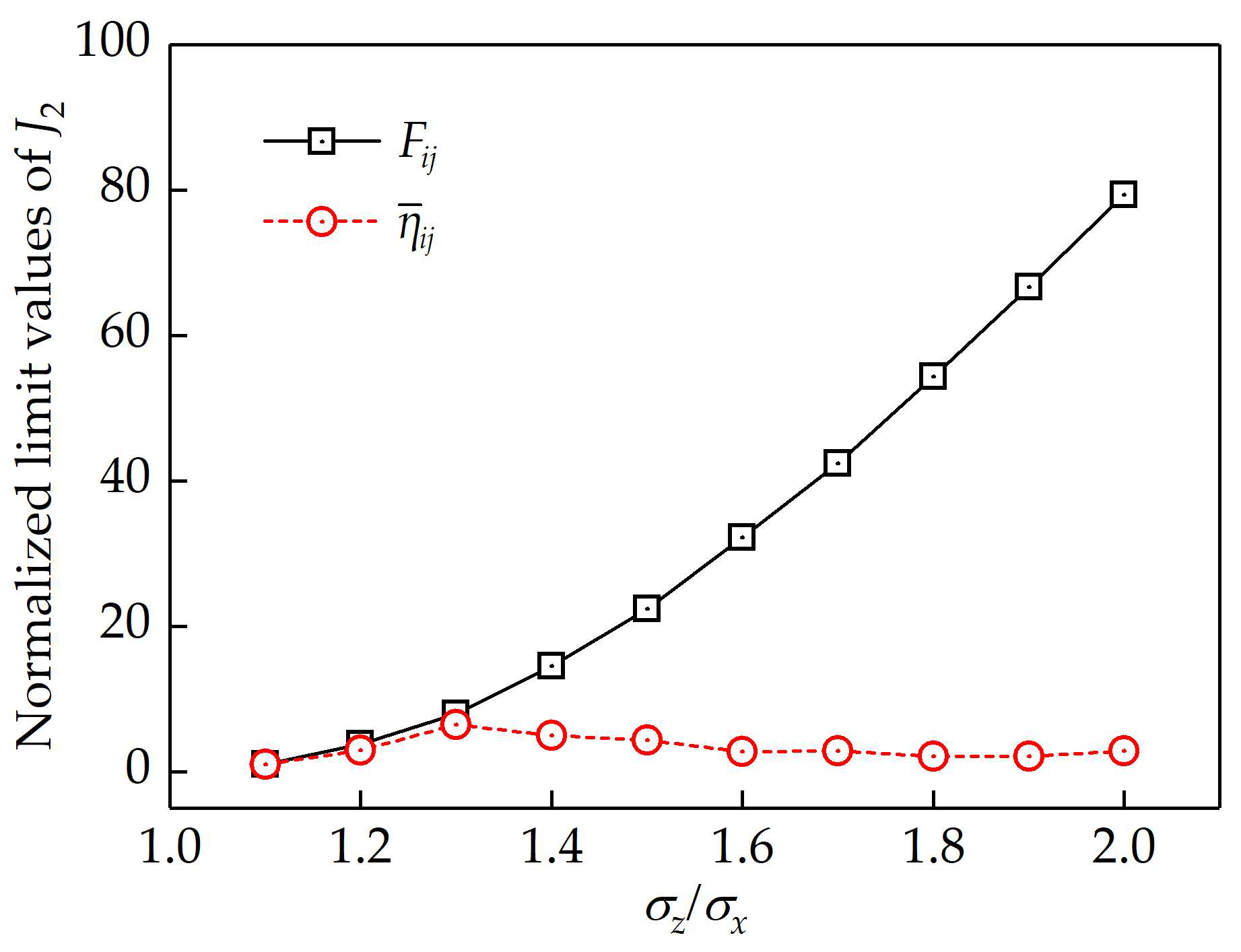
2.1.3. A Simple DEM Verification
2.2. Transformed Stress Tensor
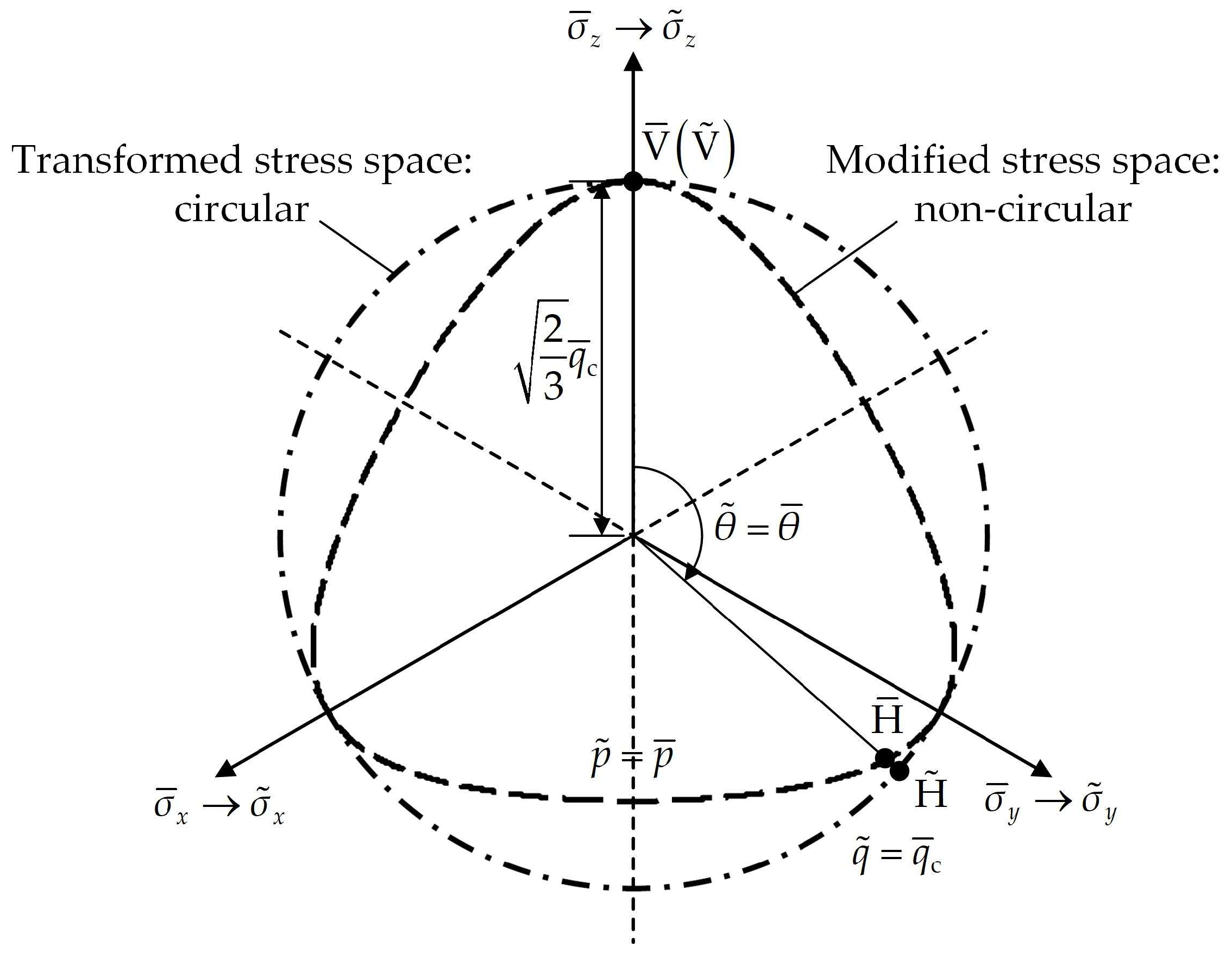
2.2.1. Basic Idea
2.2.2. Formula
2.3. Brief Summary
3. Anisotropic Yield Surface
3.1. In 3D Stress Space
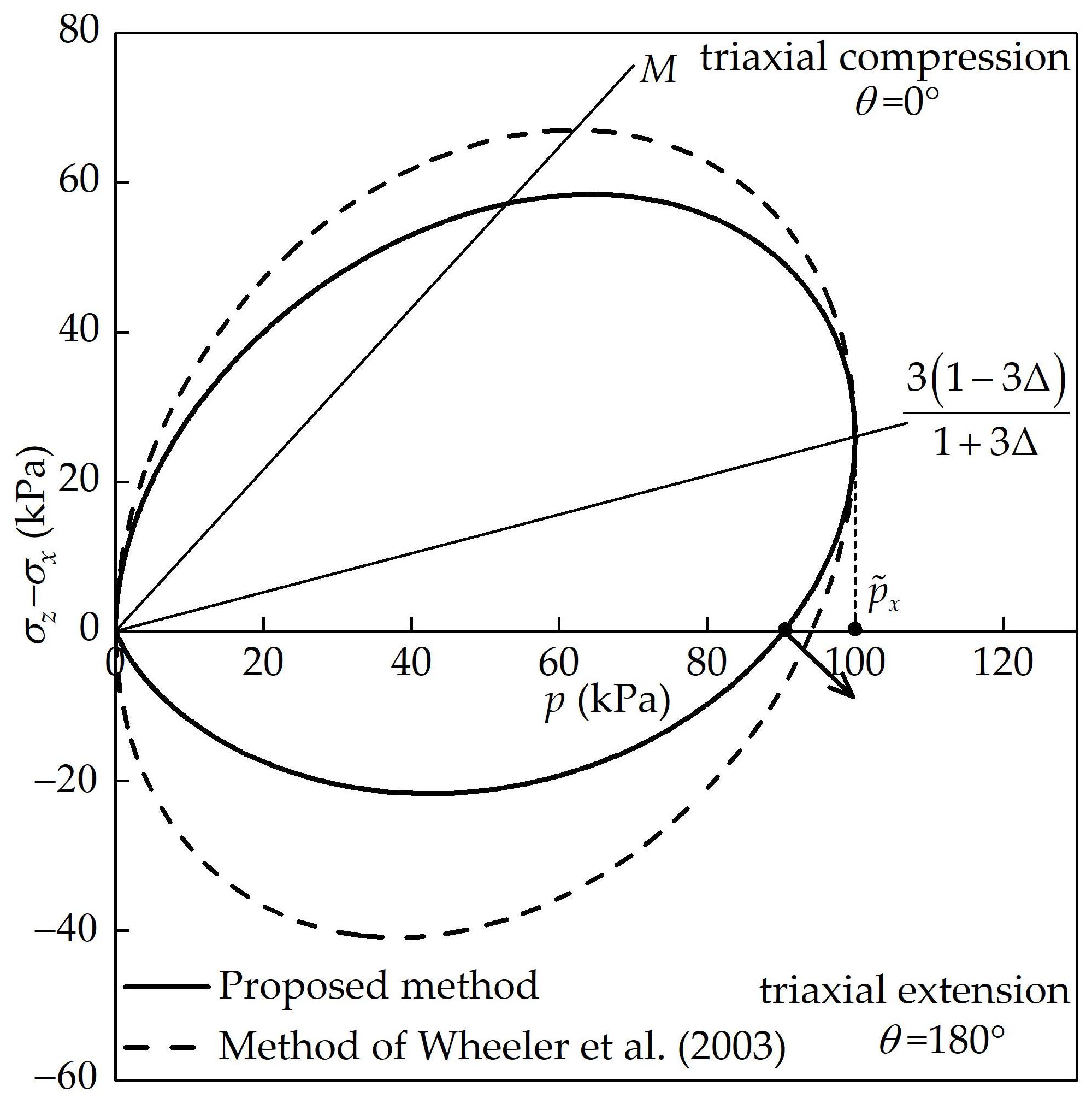
3.2. On the Triaxial Meridian Plane
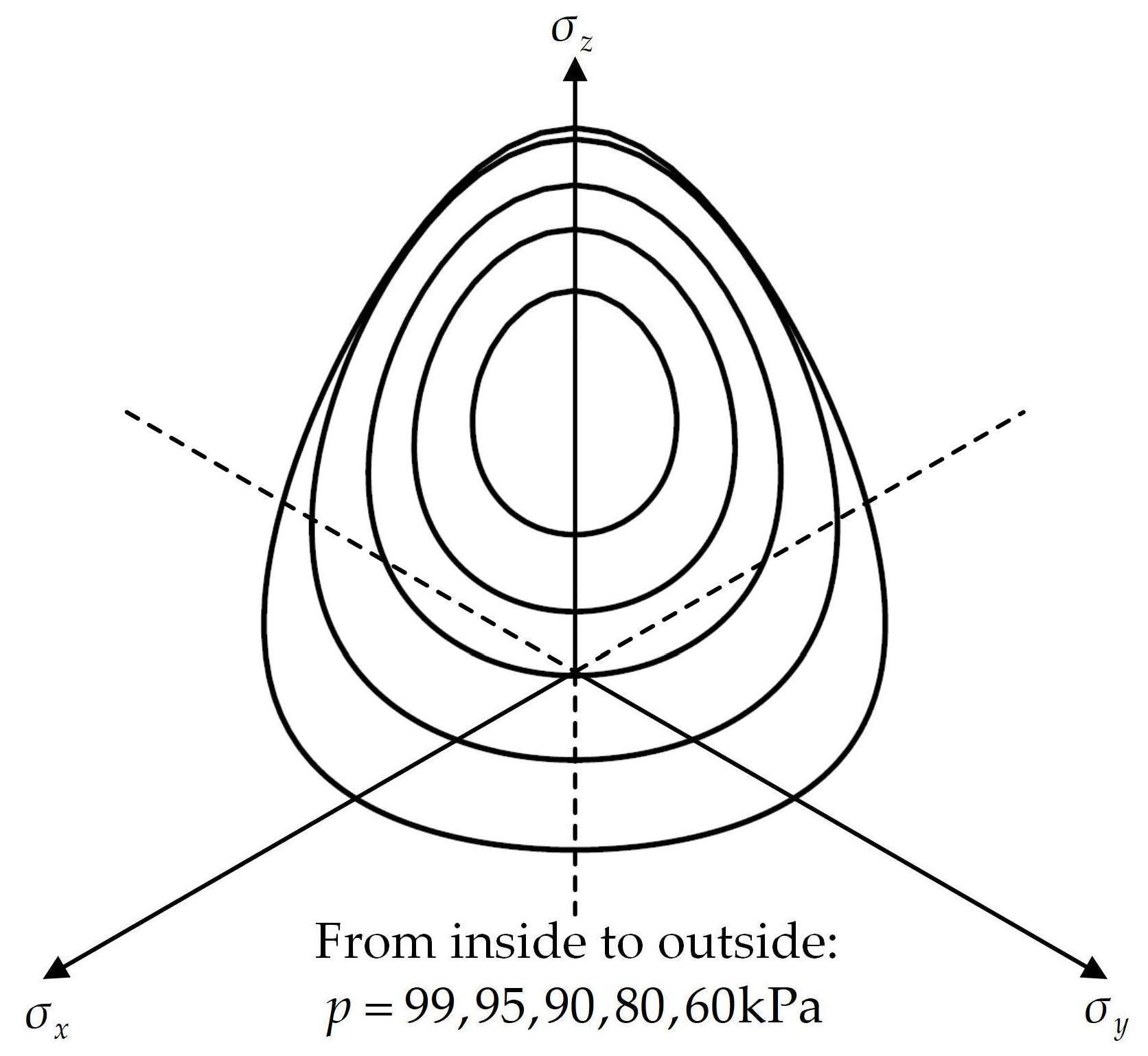
3.3. On the Deviatoric Plane
4. Induced Anisotropy
5. Anisotropic MCC Model
5.1. Plastic Flow Rule
5.2. Hardening Law
5.3. Elastic Stiffness Matrix
5.4. Elastoplastic Stiffness Matrix
5.5. Comparison between the Isotropic and Anisotropic MCC Models
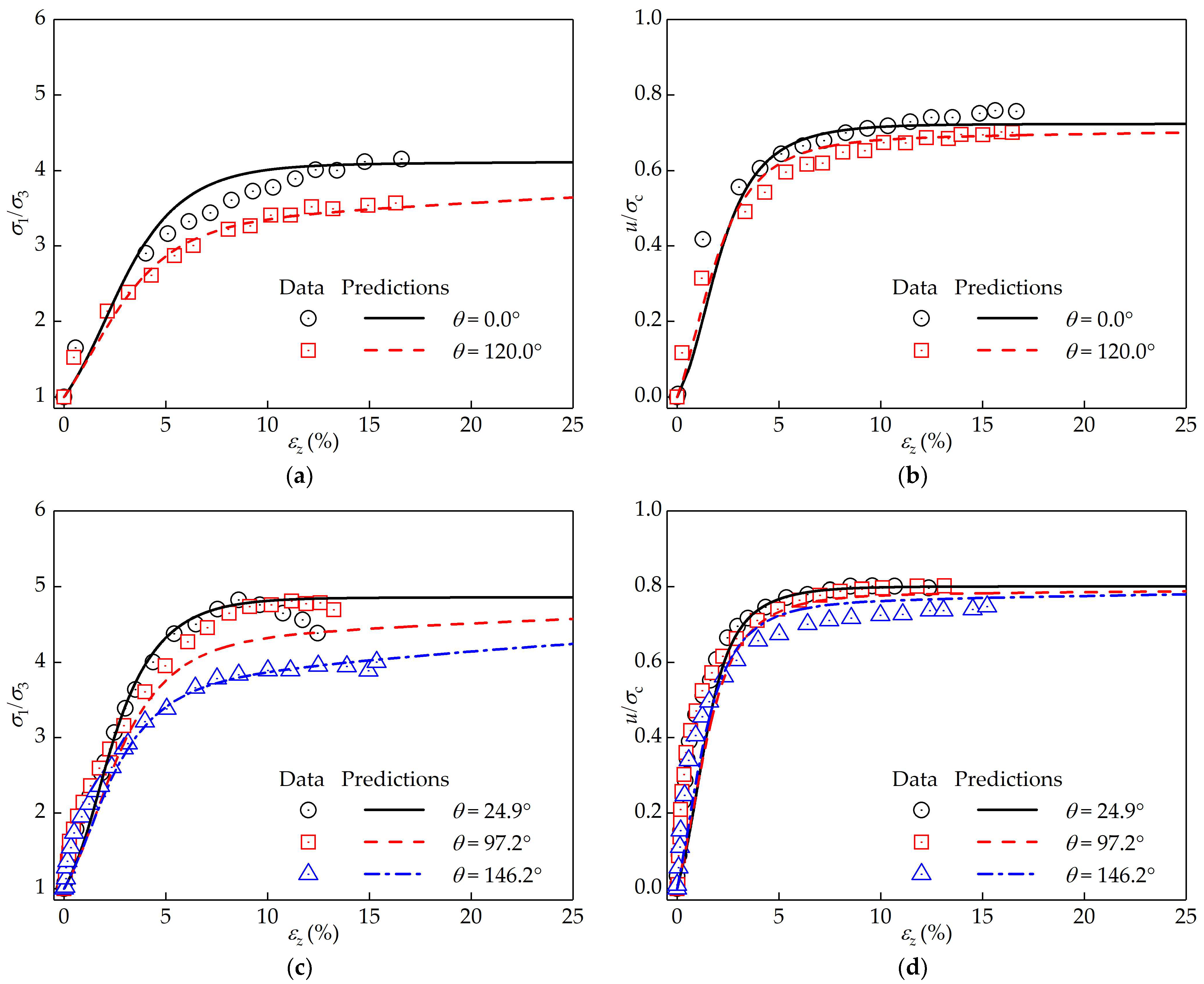
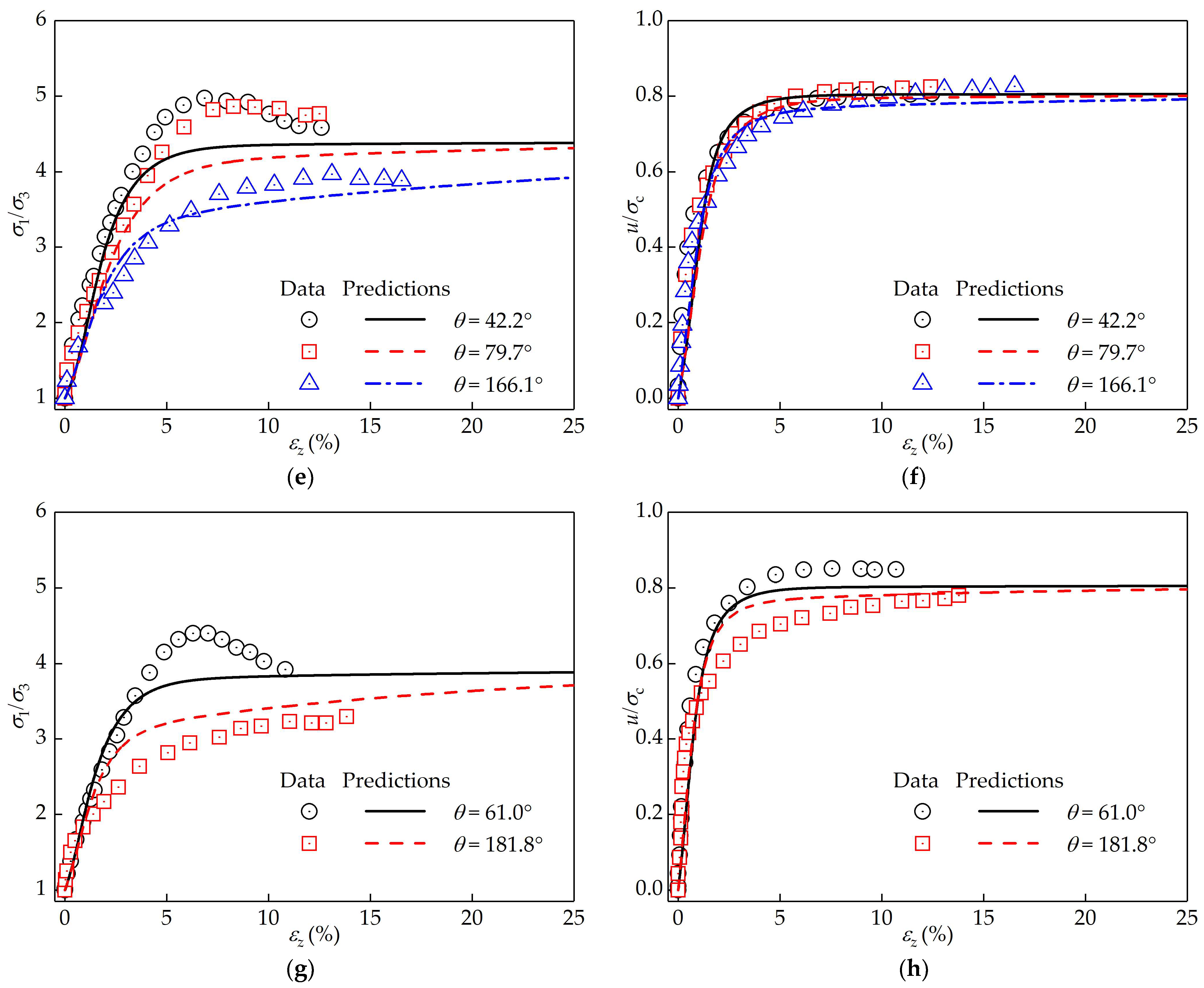
6. Verification of the Proposed Method
7. Conclusions
- The inherent anisotropy is considered using two steps of stress mapping. From to , anisotropic soil is equivalent to isotropic soil; from to , the true triaxial yield/failure behaviors are similar to those of triaxial compression.
- The induced anisotropy is represented by a fabric evolution law, which plays the same role as the rotational hardening law but can capture the microscopic mechanism behind soil deformation.
- Based on an isotropic constitutive model, , the anisotropic model can be easily developed to predict the stress–strain relation of anisotropic soil in a three-dimensional stress state.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lai, V.Q.; Shiau, J.; Keawsawasvong, S.; Seehavong, S.; Cabangon, L.T. Undrained stability of unsupported rectangular excavations: Anisotropy and non-homogeneity in 3D. Buildings 2022, 12, 1425. [Google Scholar] [CrossRef]
- Ng, C.W.W.; Qu, C.X.; Ni, J.J.; Guo, H.W. Three-dimensional reliability analysis of unsaturated soil slope considering permeability rotated anisotropy random fields. Comput. Geotech. 2022, 151, 104944. [Google Scholar] [CrossRef]
- Fang, Y.; Cui, J.; Wanatowski, D.; Nikitas, N.; Yuan, R.; He, Y. Subsurface settlements of shield tunneling predicted by 2D and 3D constitutive models considering non-coaxiality and soil anisotropy: A case study. Can. Geotech. J. 2022, 59, 424–440. [Google Scholar] [CrossRef]
- Sekiguchi, H.; Ohta, H. Induced anisotropy and time dependency in clays. In Proceedings of the 9th International Conference on Soil Mechanics and Foundation Engineering, Tokyo, Japan, 10–15 July 1977; pp. 229–238. [Google Scholar]
- Pestana, J.M.; Whittle, A.J. Formulation of a unified constitutive model for clays and sands. Int. J. Numer. Anal. Methods Geomech. 1999, 23, 1215–1243. [Google Scholar] [CrossRef]
- Wheeler, S.J.; Näätänen, A.; Karstunen, M.; Lojander, M. An anisotropic elastoplastic model for soft clays. Can. Geotech. J. 2003, 40, 403–418. [Google Scholar] [CrossRef]
- Niu, Y.Q.; Chang, D.; Wang, X.; Liao, M.K. Anisotropic constitutive model of frozen silty clay capturing ice cementation degradation under high mean stresses. J. Mater. Res. Technol.-JMRT 2023, 27, 1461–1472. [Google Scholar] [CrossRef]
- Shi, Z.H.; Hambleton, J.P.; Buscarnera, G. Bounding surface elasto-viscoplasticity: A general constitutive framework for rate-dependent geomaterials. J. Eng. Mech. 2019, 145, 04019002. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Lai, Y.M.; Pei, W.S.; Yu, F. An anisotropic bounding surface elastoplastic constitutive model for frozen sulfate saline silty clay under cyclic loading. Int. J. Plast. 2020, 129, 102668. [Google Scholar] [CrossRef]
- Zhang, A.; Dafalias, Y.F.; Jiang, M.J. A bounding surface plasticity model for cemented sand under monotonic and cyclic loading. Géotechnique 2023, 73, 44–61. [Google Scholar] [CrossRef]
- Dafalias, Y.F.; Manzari, M.T. Simple plasticity sand model accounting for fabric change effects. J. Eng. Mech. 2004, 130, 622–634. [Google Scholar] [CrossRef]
- Zhang, F.; Ye, B.; Noda, T.; Nakano, M.; Nakai, K. Explanation of cyclic mobility of soils: Approach by stress-induced anisotropy. Soils Found. 2007, 47, 635–648. [Google Scholar] [CrossRef]
- Anastasopoulos, I.; Gelagoti, F.; Kourkoulis, R.; Gazetas, G. Simplified constitutive model for simulation of cyclic response of shallow foundations: Validation against laboratory tests. J. Geotech. Geoenviron. Eng. 2011, 137, 1154–1168. [Google Scholar] [CrossRef]
- Seidalinov, G.; Taiebat, M. Bounding surface SANICLAY plasticity model for cyclic clay behavior. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 702–724. [Google Scholar] [CrossRef]
- Hong, P.Y.; Pereira, J.M.; Cui, Y.J.; Tang, A.M.; Collin, F.; Li, X.L. An elastoplastic model with combined isotropic-kinematic hardening to predict the cyclic behavior of stiff clays. Comput. Geotech. 2014, 62, 193–202. [Google Scholar] [CrossRef]
- Shirmohammadi, A.; Hajialilue-Bonab, M. Simulation of the behavior of structured clay using nonassociated constitutive model with and without anisotropic fabric at critical state. J. Eng. Mech. 2023, 149, 04022115. [Google Scholar] [CrossRef]
- Dejaloud, H.; Rezania, M. Double image stress point bounding surface model for monotonic and cyclic loading on anisotropic clays. Acta Geotech. 2023, 18, 2427–2456. [Google Scholar] [CrossRef]
- Macias, A.L.; Rotta Loria, A.F. SANISAND-C*: Simple ANIsotropic constitutive model for SAND with Cementation. Int. J. Numer. Anal. Methods Geomech. 2023, 47, 2815–2847. [Google Scholar] [CrossRef]
- Corti, R.; Diambra, A.; Wood, D.M.; Escribano, D.E.; Nash, D.F.T. Memory surface hardening model for granular soils under repeated loading conditions. J. Eng. Mech. 2016, 142, 04016102. [Google Scholar] [CrossRef]
- Zhang, J.M.; Wang, G. Large post-liquefaction deformation of sand, part I: Physical mechanism, constitutive description and numerical algorithm. Acta Geotech. 2012, 7, 69–113. [Google Scholar] [CrossRef]
- Liu, X.Y.; Zhang, X.W.; Kong, L.W.; Yin, S.; Xu, Y.Q. Shear strength anisotropy of natural granite residual soil. J. Geotech. Geoenviron. Eng. 2022, 148, 04021168. [Google Scholar] [CrossRef]
- Karimzadeh, A.A.; Leung, A.K.; Gao, Z.W. Shear strength anisotropy of rooted soils. Géotechnique, 2022; ahead of print. [Google Scholar] [CrossRef]
- Fakharian, K.; Kaviani-Hamedani, F.; Imam, S.M.R. Influences of initial anisotropy and principal stress rotation on the undrained monotonic behavior of a loose silica sand. Can. Geotech. J. 2022, 59, 847–862. [Google Scholar] [CrossRef]
- Tobita, Y.; Yanagisawa, E. Modified stress tensors for anisotropic behavior of granular materials. Soils Found. 1992, 32, 85–99. [Google Scholar] [CrossRef][Green Version]
- Yao, Y.; Tian, Y.; Gao, Z. Anisotropic UH model for soils based on a simple transformed stress method. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 54–78. [Google Scholar] [CrossRef]
- Li, X.S.; Dafalias, Y.F. Anisotropic critical state theory: Role of fabric. J. Eng. Mech. 2012, 138, 263–275. [Google Scholar] [CrossRef]
- Wang, R.; Dafalias, Y.F.; Fu, P.C.; Zhang, J.M. Fabric evolution and dilatancy within anisotropic critical state theory guided and validated by DEM. Int. J. Solids Struct. 2020, 188, 210–222. [Google Scholar] [CrossRef]
- Deng, N.; Wautier, A.; Thiery, Y.; Yin, Z.Y.; Hicher, P.Y.; Nicot, F. On the attraction power of critical state in granular materials. J. Mech. Phys. Solids 2021, 149, 104300. [Google Scholar] [CrossRef]
- Yao, Y.P.; Wang, N.D. Transformed stress method for generalizing soil constitutive models. J. Eng. Mech. 2013, 140, 614–629. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Wang, H.N.; Jiang, M.J. Strength criteria at anisotropic principal directions expressed in closed form by interparticle parameters for elliptical particle assembly. Granul. Matter 2023, 25, 1. [Google Scholar] [CrossRef]
- Gao, Z.W.; Zhao, J.D. A non-coaxial critical-state model for sand accounting for fabric anisotropy and fabric evolution. Int. J. Solids Struct. 2017, 106, 200–212. [Google Scholar] [CrossRef]
- Yuan, R.; Yu, H.S.; Hu, N.; He, Y. Non-coaxial soil model with an anisotropic yield criterion and its application to the analysis of strip footing problems. Comput. Geotech. 2018, 99, 80–92. [Google Scholar] [CrossRef]
- Xie, Y.; Cao, Z.; Yu, J. Effect of soil anisotropy on ground motion characteristics. Buildings 2023, 13, 3017. [Google Scholar] [CrossRef]
- Tian, D.S.; Zheng, H. A three-dimensional elastoplastic constitutive model for geomaterials. Appl. Sci. 2023, 13, 5746. [Google Scholar] [CrossRef]
- Du, Z.B.; Shi, Z.H.; Qian, J.G.; Huang, M.S.; Guo, Y.C. Constitutive modeling of three-dimensional non-coaxial characteristics of clay. Acta Geotech. 2022, 17, 2157–2172. [Google Scholar] [CrossRef]
- Xue, L.; Yu, J.K.; Pan, J.H.; Wang, R.; Zhang, J.M. Three-dimensional anisotropic plasticity model for sand subjected to principal stress value change and axes rotation. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 353–381. [Google Scholar] [CrossRef]
- Lade, P.V.; Abelev, A.V. Characterization of cross-anisotropic soil deposits from isotropic compression tests. Soils Found. 2005, 45, 89–102. [Google Scholar] [CrossRef]
- Zhao, C.F.; Kruyt, N.P. An evolution law for fabric anisotropy and its application in micromechanical modelling of granular materials. Int. J. Solids Struct. 2020, 196, 53–66. [Google Scholar] [CrossRef]
- Wen, Y.X.; Zhang, Y.D. Evidence of a unique critical fabric surface for granular soils. Géotechnique 2023, 73, 439–454. [Google Scholar] [CrossRef]
- Wang, R.; Fu, P.C.; Zhang, J.M.; Dafalias, Y.F. Evolution of various fabric tensors for granular media toward the critical state. J. Eng. Mech. 2017, 143, 04017117. [Google Scholar] [CrossRef]
- Sufian, A.; Artigaut, M.; Shire, T.; O’Sullivan, C. Influence of fabric on stress distribution in gap-graded soil. J. Geotech. Geoenviron. Eng. 2021, 147, 04021016. [Google Scholar] [CrossRef]
- Kirkgard, M.M.; Lade, P.V. Anisotropic three-dimensional behavior of a normally consolidated clay. Can. Geotech. J. 1993, 30, 848–858. [Google Scholar] [CrossRef]

| Reference | Anisotropic Yield Function | Rotational Hardening Law |
|---|---|---|
| Sekiguchi and Ohta [4] | / | |
| Wheeler et al. [6] | ||
| Dafalias and Manzari [11] | ||
| Zhang et al. [12] | where | |
| Anastasopoulos et al. [13] | ||
| Seidalinov and Taiebat [14] | ||
| Hong et al. [15] | ||
| Shirmohammadi and Hajialilue-Bonab [16] | ||
| Dejaloud and Rezania [17] | ||
| Macias and Rotta Loria [18] |
| Isotropic MCC Model | Anisotropic MCC Model | |
|---|---|---|
| Stress tensor | ||
| Yield function | ||
| Plastic flow rule | ||
| Hardening law | ||
| Elastic stiffness matrix | ||
| Elastoplastic stiffness matrix | ||
| Parameters | M, λ, κ, and ν | M, λ, κ, ν, Δ, C, and β |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, Y.; Chen, H.; Yao, Z.; Fang, Y. A Multiscale Method to Develop Three-Dimensional Anisotropic Constitutive Model for Soils. Buildings 2024, 14, 307. https://doi.org/10.3390/buildings14020307
Tian Y, Chen H, Yao Z, Fang Y. A Multiscale Method to Develop Three-Dimensional Anisotropic Constitutive Model for Soils. Buildings. 2024; 14(2):307. https://doi.org/10.3390/buildings14020307
Chicago/Turabian StyleTian, Yu, Hao Chen, Zijun Yao, and Yufei Fang. 2024. "A Multiscale Method to Develop Three-Dimensional Anisotropic Constitutive Model for Soils" Buildings 14, no. 2: 307. https://doi.org/10.3390/buildings14020307
APA StyleTian, Y., Chen, H., Yao, Z., & Fang, Y. (2024). A Multiscale Method to Develop Three-Dimensional Anisotropic Constitutive Model for Soils. Buildings, 14(2), 307. https://doi.org/10.3390/buildings14020307






