Analysis on Flexural Performance of Prestressed Steel-Reinforced UHPC Beams
Abstract
1. Introduction
2. Establishment of Finite Element Model
2.1. Constitutive Relationship of Materials
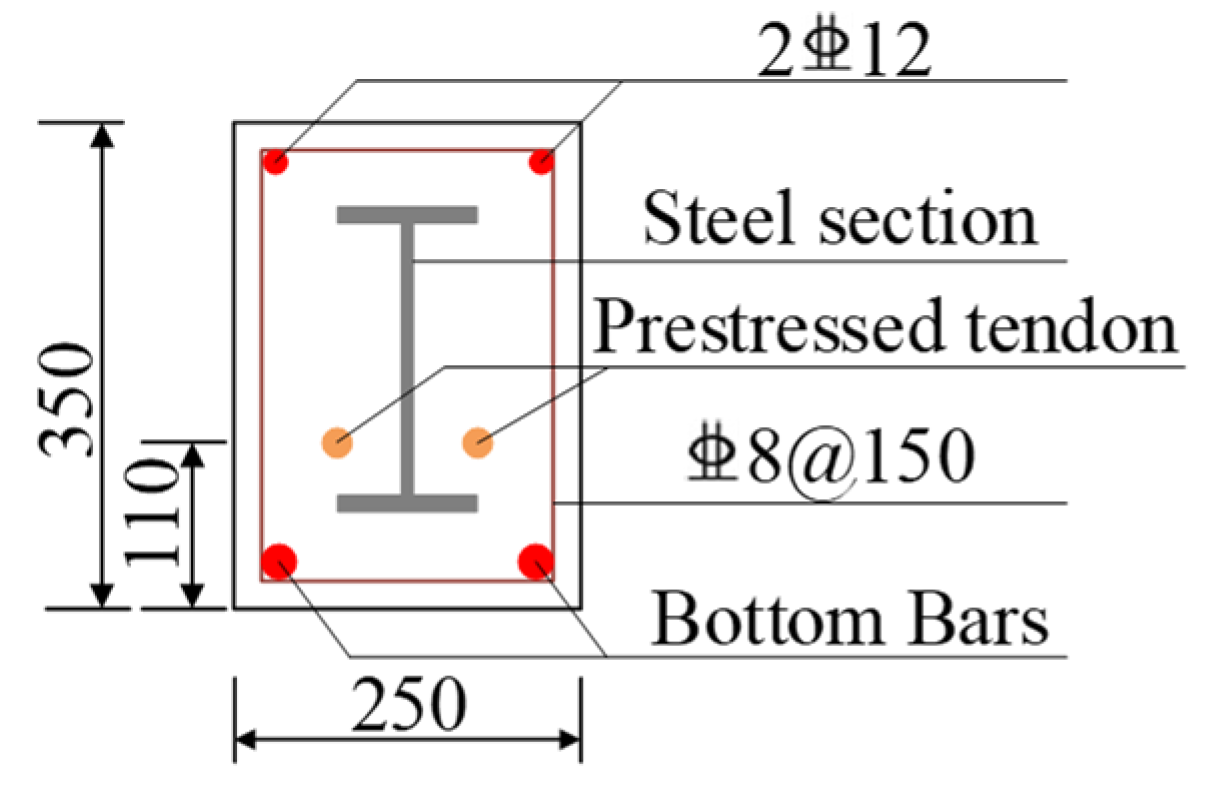
2.2. Model Design
2.3. Application of Prestress
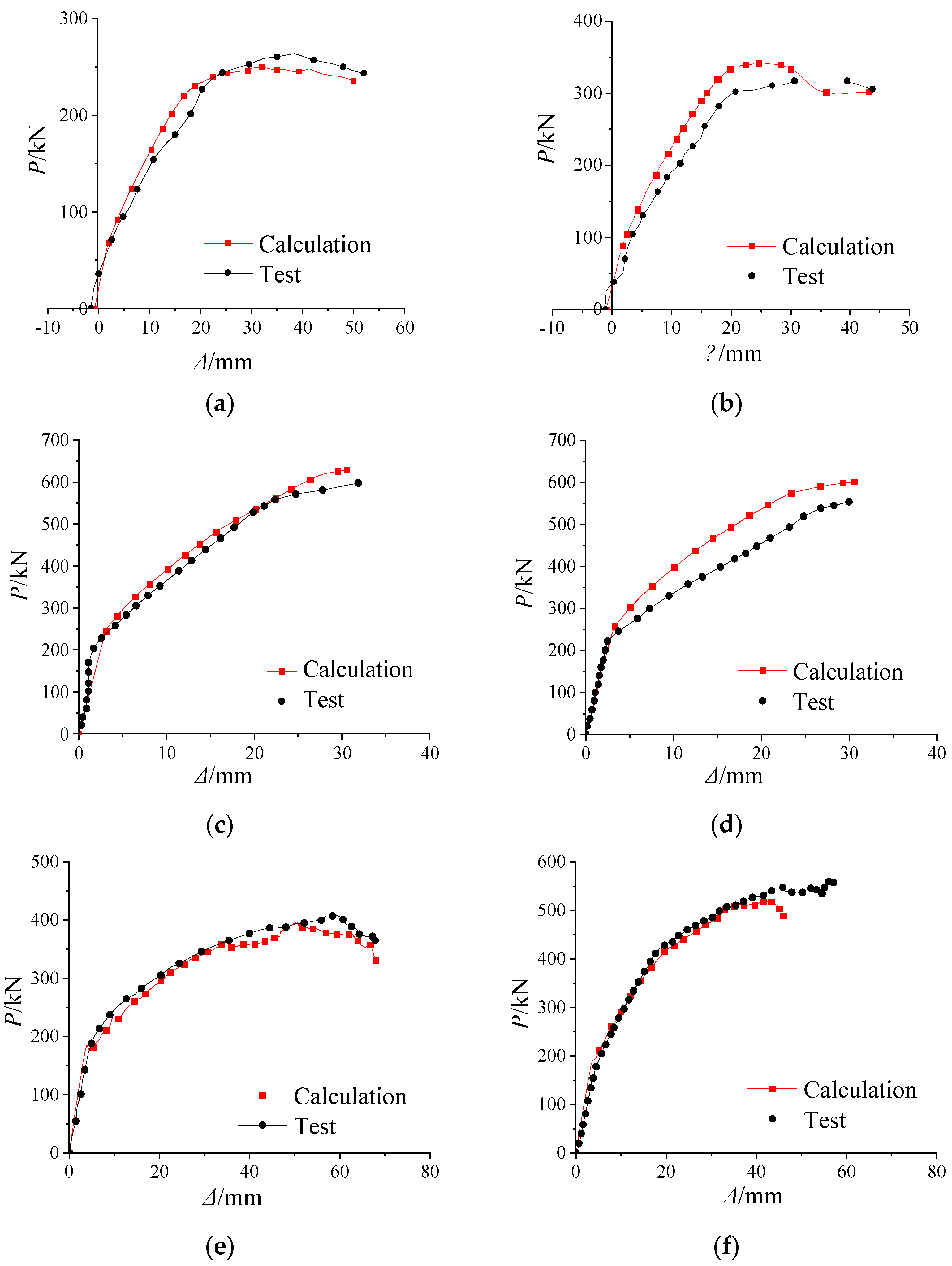
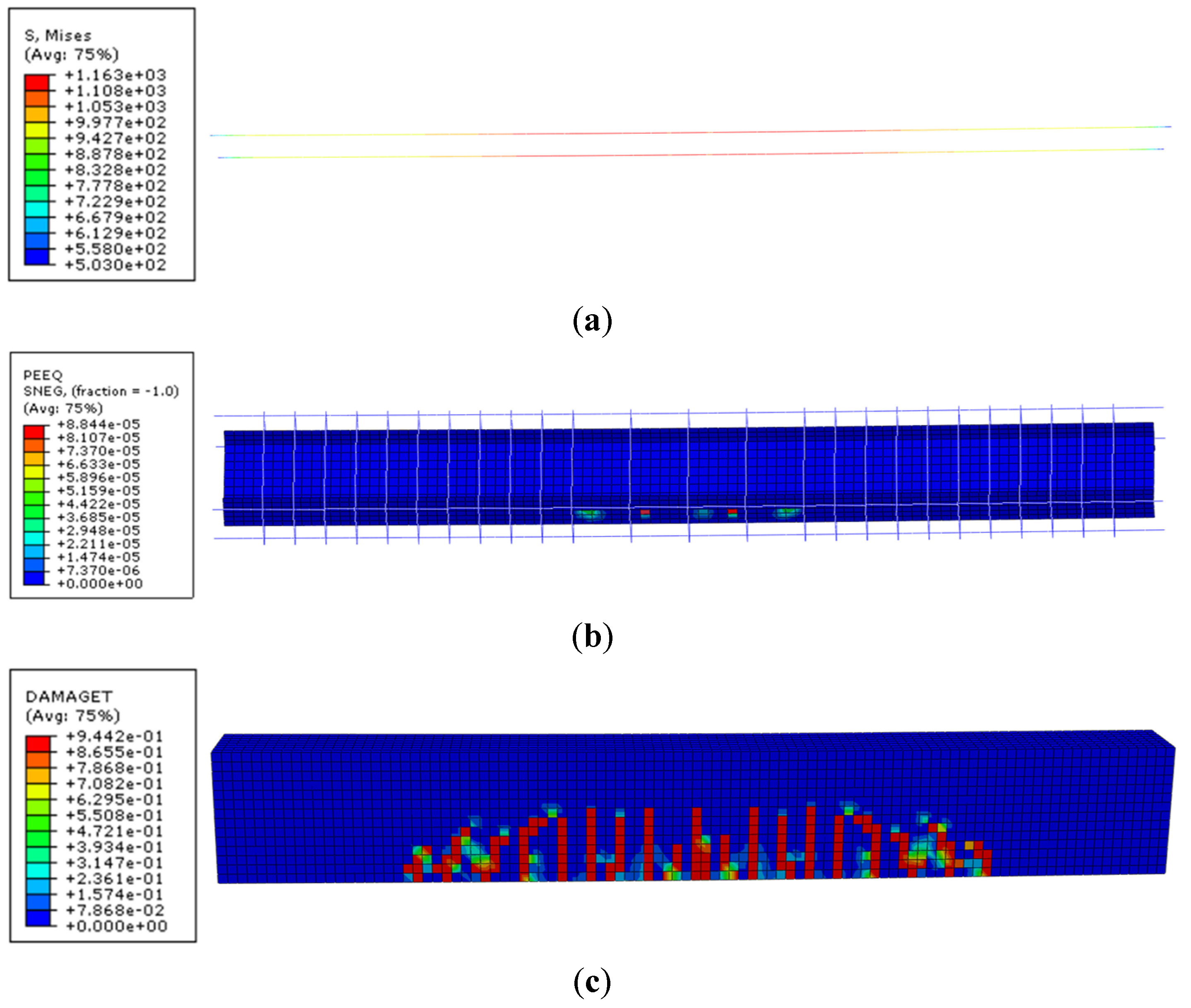
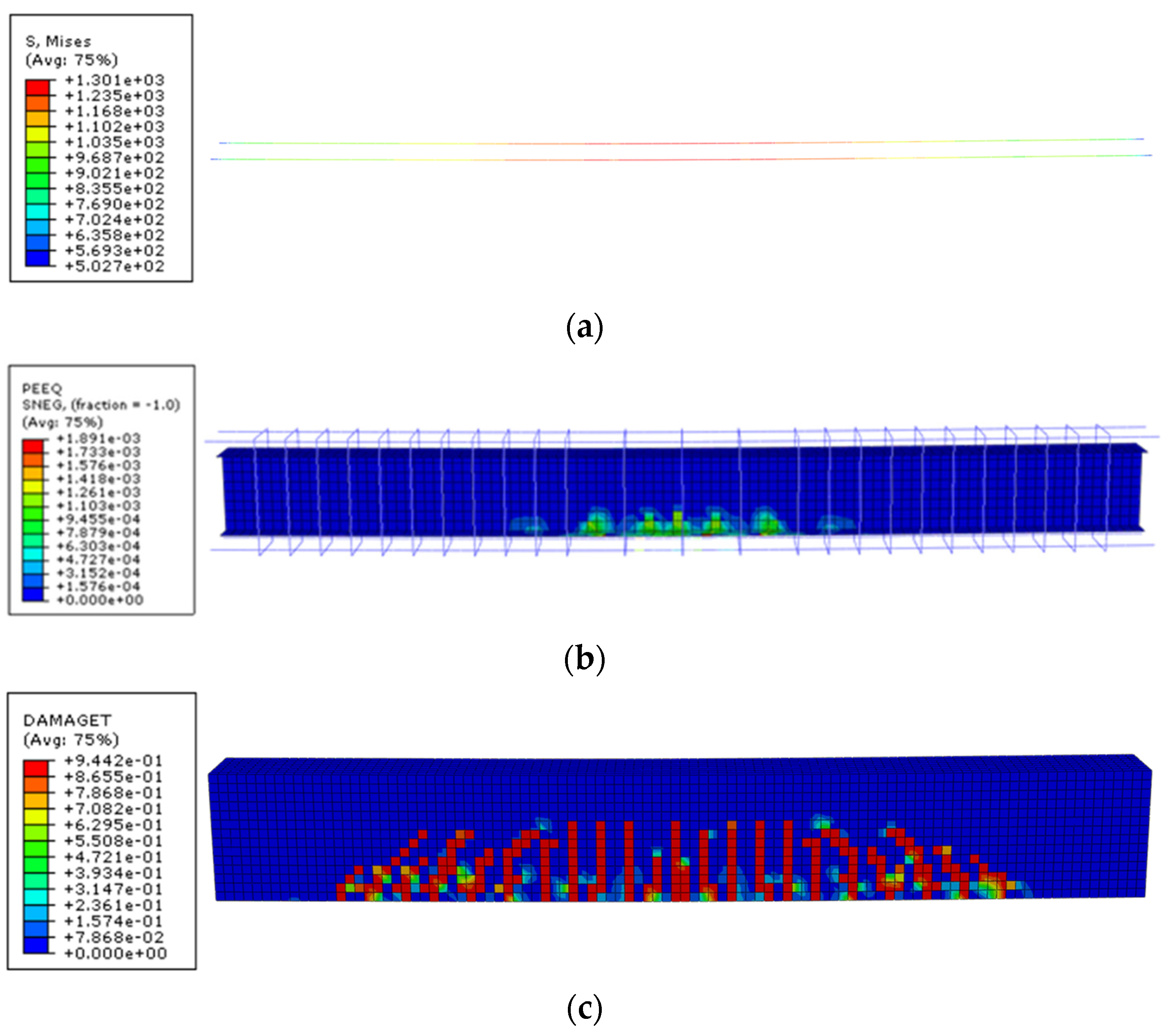
3. Validation of the Developed Model for Prestress Concrete Beams
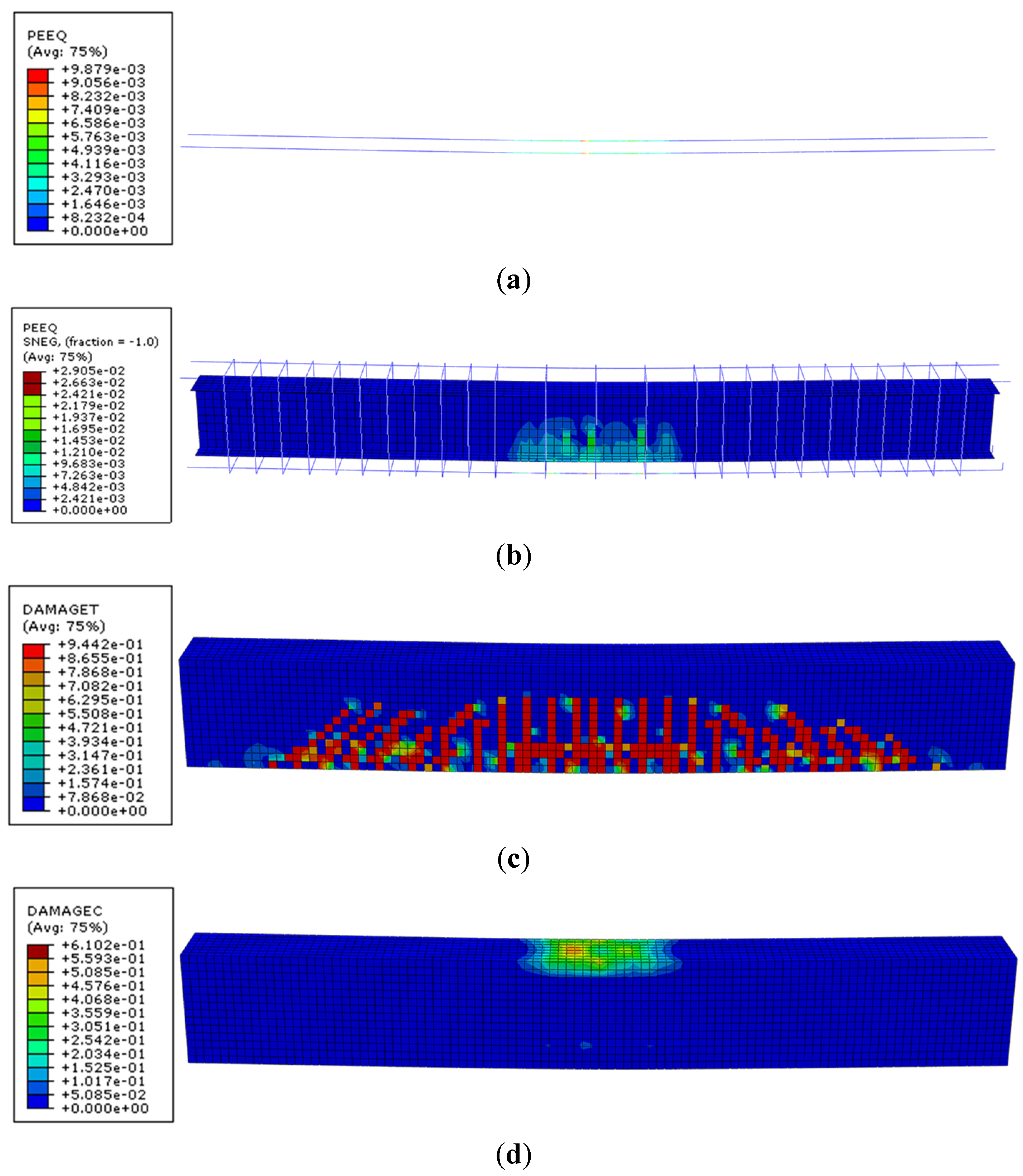
4. Nonlinear Analysis of Prestressed Steel-Reinforced UHPC Beams
4.1. Calculated Results and Analysis
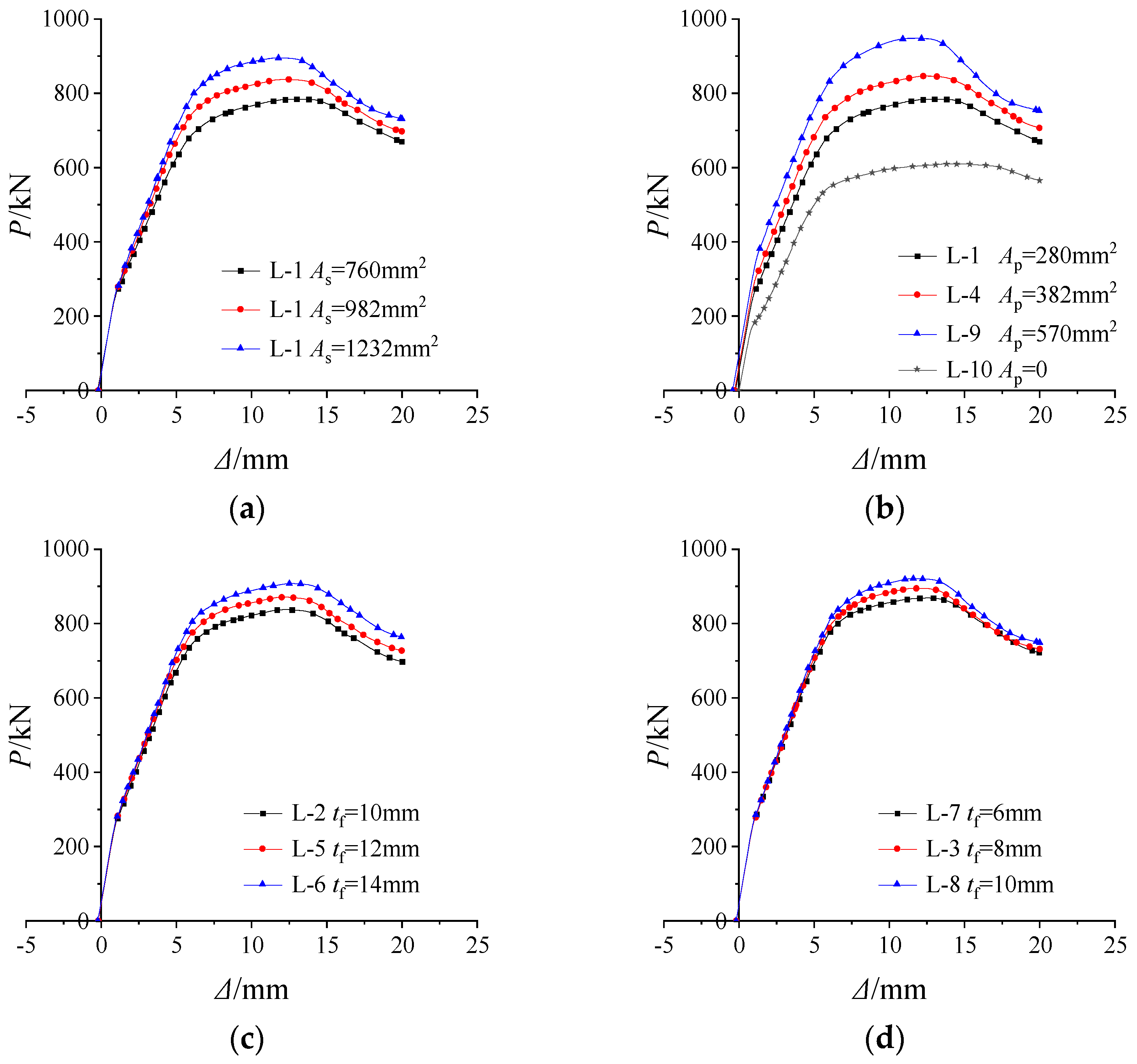
4.1.1. Load–Deflection Curves
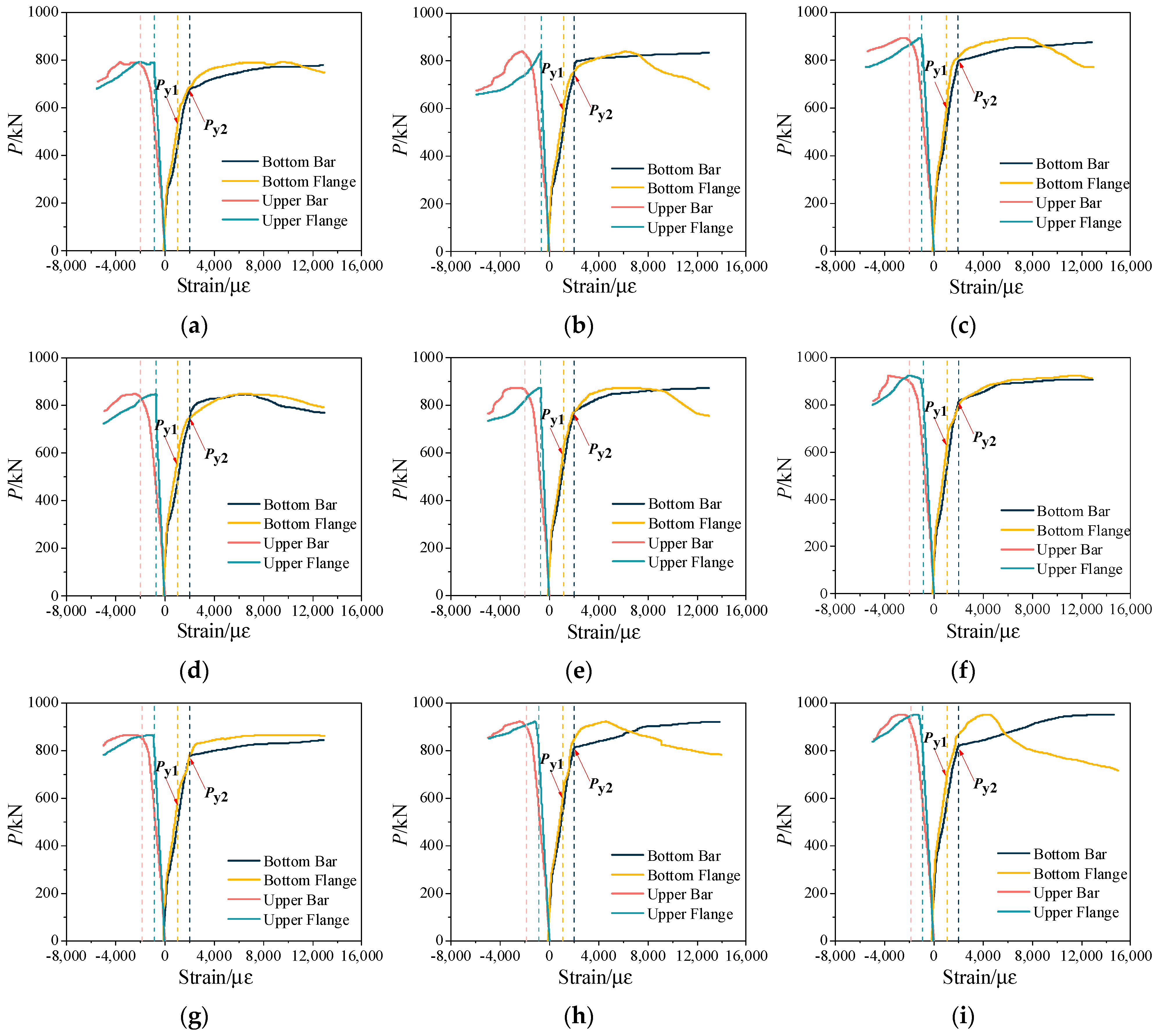
4.1.2. Load–Strain Curve
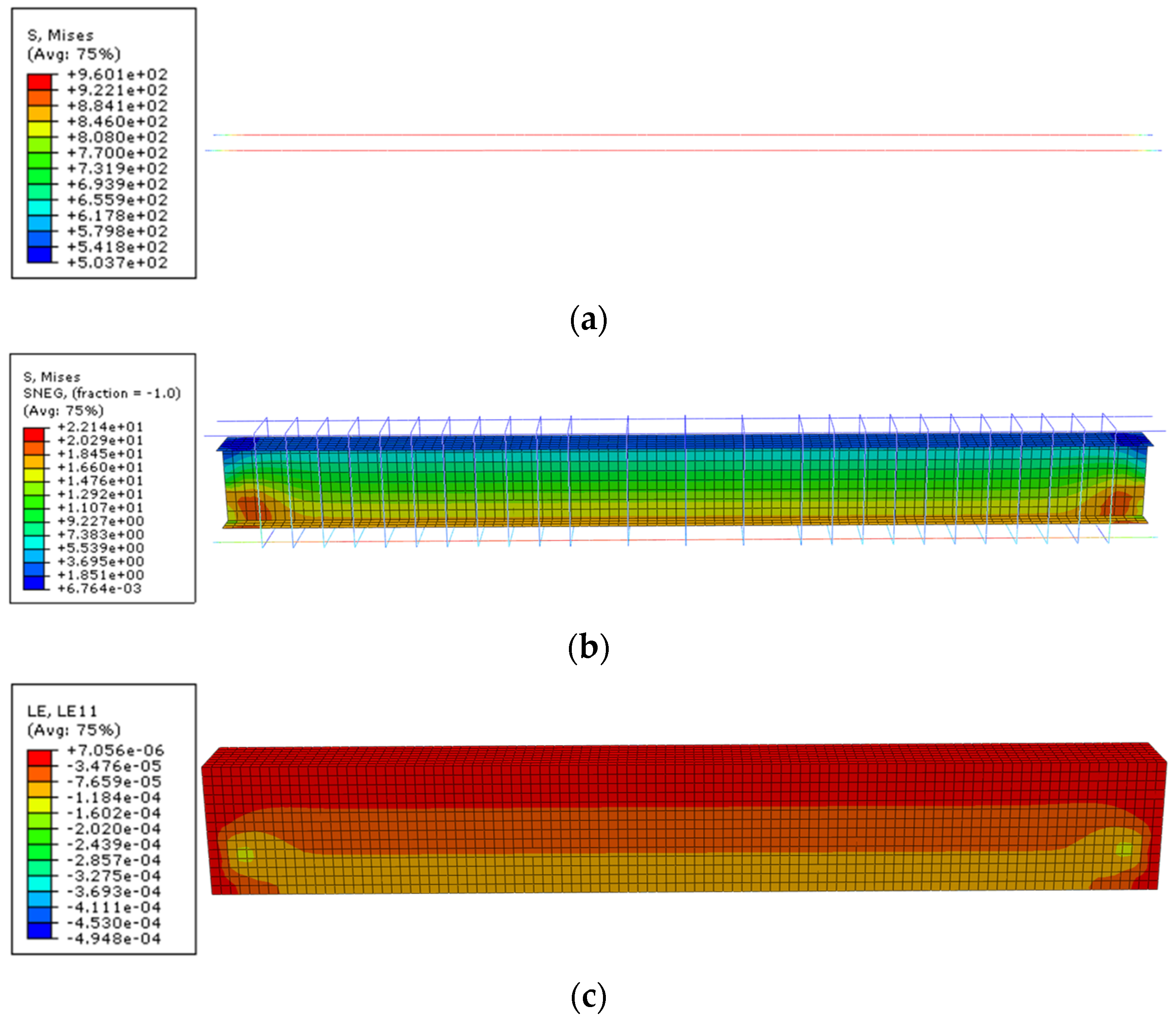
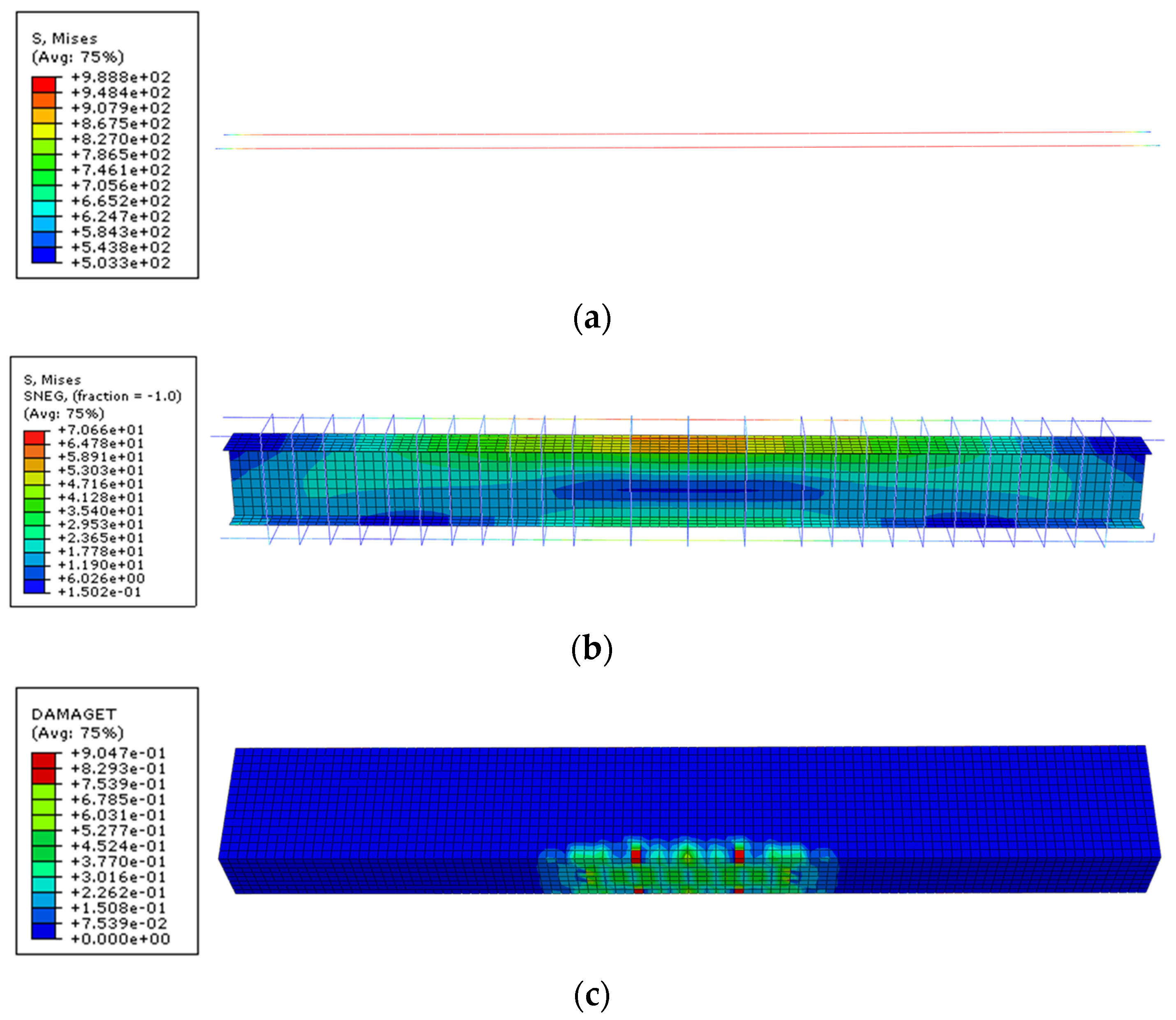
4.1.3. Analysis of the Whole Loading Process
Application of Prestress
Initial Cracking
Steel Section Yielding
Bottom Bar Yielding
Crushing
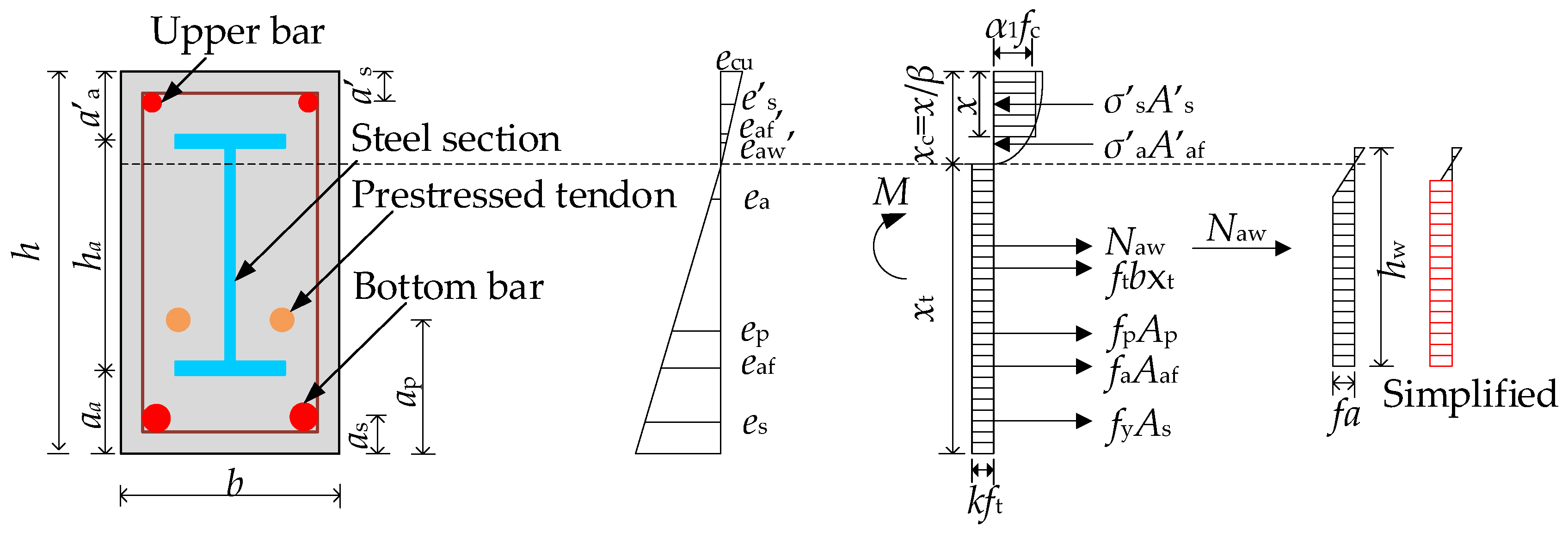
5. Calculation Method for the Flexural Capacity of the Cross-Section
5.1. Fundamental Principles
5.2. Calculation Method
5.3. Calculation Results
6. Discussion
7. Conclusions
- (1)
- The developed FE models accurately simulate the flexural behavior and ultimate bearing capacity of prestressed concrete beams, as confirmed by comparisons with experimental results. The average ratio of predicted to experimentally measured ultimate load Pu was 1.000, with a mean square deviation of 0.014 and a coefficient of variation of 0.014, indicating the high reliability of the FE models in predicting structural responses.
- (2)
- The flexural performance of prestressed steel-reinforced UHPC beams is significantly influenced by design parameters such as reinforcement ratio, prestressing level, web thickness, and flange thickness. When the reinforcement ratio increased from 1.17% to 1.90%, the ultimate load increased by 12.05%, while increasing the prestress level from 0.61 to 0.76 resulted in a 53.73% increase in ultimate load. Similarly, the flange thickness variations led to an increase in ultimate load of up to 9.67%, demonstrating that prestress and geometric parameters play a vital role in optimizing flexural capacity.
- (3)
- Prestressed steel-reinforced UHPC beams exhibit high stiffness, excellent ductility, and significant resistance to cracking. The addition of prestress increased the initial cracking load by 114.88% compared to non-prestressed beams, indicating substantial enhancement in the early-stage stiffness and durability. The beams maintained high load-bearing capacity in the plastic stage, achieving a maximum ultimate load of 967.98 kN, with good ductility and strong inelastic deformation capacity.
- (4)
- A predictive formula for the flexural capacity of prestressed steel-reinforced UHPC beams is proposed, with the tensile strength equivalent coefficient k recommended as 0.25. The calculated results show strong agreement with the FE simulations, with an average deviation of less than 3% between the predicted and simulated ultimate loads, indicating that the derived formulas are reliable for practical engineering applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Carmo, R.N.F.; Júlio, E. New trends for reinforced concrete structures: Some results of exploratory studies. Infrastructures 2017, 2, 17. [Google Scholar] [CrossRef]
- Reddy, C.D.; Rajkumar, R.; Umamaheswari, N. Behavior of composite rectangular RC beams encased with steel I-section under flexure. AIP Conf. Proc. 2022, 2460, 020017. [Google Scholar]
- Tuma, N.H.; Aziz, M.R. Flexural performance of composite ultra-high-performance concrete-encased steel hollow beams. Civ. Eng. J. 2019, 5, 1289–1304. [Google Scholar] [CrossRef]
- Musha, H.; Ohkuma, H.; Kitamura, T. Innovative UFC structures in Japan. In Proceedings of the International Symposium on Ultra-High Performance Fibre-Reinforced Concrete, Marseille, France, 1–3 October 2013; pp. 17–26. [Google Scholar]
- Yoo, D.Y.; Yoon, Y.S. A review on structural behavior, design, and application of ultra-high-performance fiber-reinforced concrete. Int. J. Concr. Struct. Mater. 2016, 10, 125–142. [Google Scholar] [CrossRef]
- Fayed, S.; Madenci, E.; Özkiliç, Y.O.; Basha, A. The flexural behaviour of multi-layered steel fiber reinforced or ultra-high performance-normal concrete composite ground slabs. J. Build. Eng. 2024, 95, 109901. [Google Scholar] [CrossRef]
- Lakavath, C.; Prakash, S.S.; Dirar, S. Experimental and numerical studies on shear behaviour of macro-synthetic fibre reinforced prestressed concrete beams. Constr. Build. Mater. 2021, 291, 123313. [Google Scholar] [CrossRef]
- Kueres, S.; Will, N.; Hegger, J. Shear strength of prestressed FRP reinforced concrete beams with shear reinforcement. Eng. Struct. 2020, 206, 110088. [Google Scholar] [CrossRef]
- Hou, W.; Lin, G.; Chen, B.; Guo, Z. Cyclic behavior and analysis of steel plate reinforced concrete coupling beams with a span-to-depth ratio of 2.5. Soil Dyn. Earthq. Eng. 2021, 148, 106817. [Google Scholar] [CrossRef]
- Xu, C.; Cao, P.Z.; Wu, K.; Lin, S.-Q.; Yang, D.G. Experimental investigation of the behavior composite steel-concrete composite beams containing different amounts of steel fibres and conventional reinforcement. Constr. Build. Mater. 2019, 202, 23–36. [Google Scholar] [CrossRef]
- Chen, C.; Lin, K.; Chen, Y. Behavior and shear strength of steel shape reinforced concrete deep beams. Eng. Struct. 2018, 175, 425–435. [Google Scholar] [CrossRef]
- Weng, C.; Yen, S.; Jiang, M. Experimental Study on Shear Splitting Failure of Full-Scale Composite Concrete Encased Steel Beams. J. Struct. Eng. 2002, 128, 1186–1194. [Google Scholar] [CrossRef]
- Yao, D.; Jia, J.; Wu, F.; Yu, F. Shear performance of prestressed ultra high strength concrete encased steel beams. Constr. Build. Mater. 2014, 52, 194–201. [Google Scholar] [CrossRef]
- Yang, I.H.; Joh, C.; Kim, B.S. Structural behavior of ultra high performance concrete beams subjected to bending. Eng. Struct. 2010, 32, 3478–3487. [Google Scholar] [CrossRef]
- Singh, M.; Sheikh, A.H.; Ali, M.M.; Visintin, P.; Griffith, M.C. Experimental and numerical study of the flexural behaviour of ultra-high performance fibre reinforced concrete beams. Constr. Build. Mater. 2017, 138, 12–25. [Google Scholar] [CrossRef]
- Wang, J.Y.; Gu, J.B.; Liu, C.; Huang, Y.H.; Xiao, R.C.; Ma, B. Flexural behavior of ultra high performance concrete beams reinforced with high strength steel. Struct. Eng. Mech. Int’l J. 2022, 81, 539–550. [Google Scholar]
- Dong, S.; Zhou, D.; Ashour, A.; Han, B.; Ou, J. Flexural toughness and calculation model of super-fine stainless wire reinforced reactive powder concrete. Cem. Concr. Compos. 2019, 104, 103367. [Google Scholar] [CrossRef]
- Yoo, D.; Yoon, Y. Structural performance of ultra-high-performance concrete beams with different steel fibers. Eng. Struct. 2015, 102, 409–423. [Google Scholar] [CrossRef]
- Cho, J.S.; Lundy, J.; Chao, S.H. Shear strength of steel fiber reinforced prestressed concrete beams. In Proceedings of the Structures Congress 2009, Don’t Mess with Structural Engineers: Expanding Our Role, Austin, TX, USA, 30 April–2 May 2009; pp. 1–9. [Google Scholar]
- Fu, C.; Li, Y.; Liang, S. Experimental study on flexural behavior of prestressed steel reinforced concrete simply supported beams. J. Build. Struct. 2007, 28, 62–73. (In Chinese) [Google Scholar]
- Fang, Z.; Tian, X.; Peng, F. Flexural strength of prestressed Ultra-High-Performance concrete beams. Eng. Struct. 2023, 279, 115612. [Google Scholar] [CrossRef]
- Zhan, Y.; Zhao, R.; Ma, Z.J.; Xu, T.; Song, R. Behavior of prestressed concrete-filled steel tube (CFST) beam. Eng. Struct. 2016, 122, 144–155. [Google Scholar] [CrossRef]
- Li, S.; Chen, W.; Zhang, Y. Flexural behavior of precast, prestressed, lightweight aggregate concrete-conventional concrete composite beams. Constr. Build. Mater. 2021, 274, 121926. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y.; Chen, W. Bending performance of unbonded prestressed basalt fiber recycled concrete beams. Eng. Struct. 2020, 221, 110937. [Google Scholar] [CrossRef]
- Guo, Z. Strength and Deformation of Concrete-Experimental Basis and Constitutive Relation; Tsinghua University Publishing House: Beijing, China, 1997. (In Chinese) [Google Scholar]
- Zheng, W.; Li, L.; Lu, S. Experimental study on mechanical behavior of normal section of reinforced powder concrete simply supported beam. J. Build. Struct. 2011, 32, 125–134. (In Chinese) [Google Scholar]
- Yu, T.; Teng, J.G.; Wong, Y.L.; Dong, S.L. Finite element modeling of confined concrete-II: Plastic-damage model. Eng. Struct. 2010, 32, 680–691. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, H.; Jiang, L.; Zhang, Y.; Yuan, Z.; Zhang, Z.; Chu, X.; Li, B. Seismic Behaviors of Novel Steel-Reinforced Concrete Composite Frames Prestressed with Bonding Tendons. Buildings 2023, 13, 2124. [Google Scholar] [CrossRef]
- Aksoylu, C.; Özkılıç, Y.O.; Çeledir, E.; Başaran, B.; Arslan, M.H. Experimental and numerical investigation of bending performance of prestressed purlins having different longitudinal web opening. Structures 2024, 60, 105839. [Google Scholar] [CrossRef]
- Chen, X. Study on Flexural Behavior and Finite Element Simulation of Partially Prestressed Concrete Beams with High-Strength Steel Bars. Master’s Thesis, Hebei University of Technology, Tianjin, China, 2018. (In Chinese). [Google Scholar]
- Xu, H. Study on Mechanical Properties of HRB500 Reinforced Prestressed Ultra-High Performance Concrete Beams. Ph.D. Thesis, Beijing University of Technology, Beijing, China, 2015. (In Chinese). [Google Scholar]
- JGJ 138-2016.2016; Code for Design of Composite Structures. China Architecture & Building Press: Beijing, China, 2016. (In Chinese)
- JTG/T 3650-2020; Technical Specifications for Construction of Highway Bridges and Culverts. Ministry of Transport of the People’s Republic of China: Beijing, China, 2020. (In Chinese)
- DBJ 43/T 325-2017; Technical Specification for Reactive Powder Concrete Structures. China Architecture & Building Press: Beijing, China, 2017. (In Chinese)
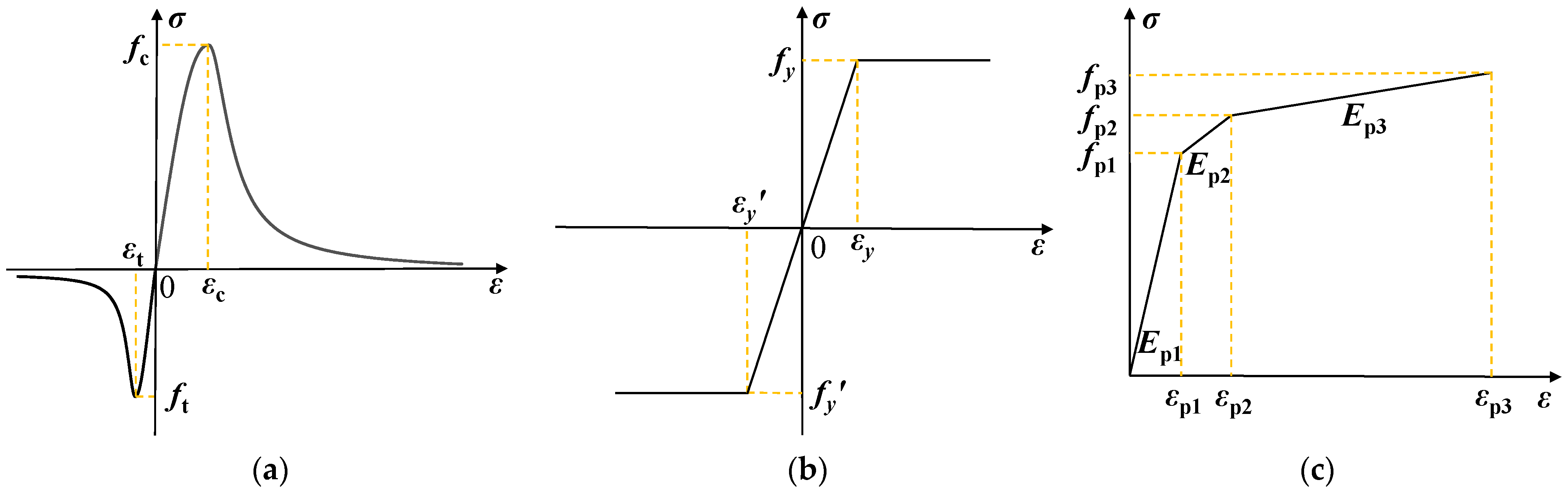

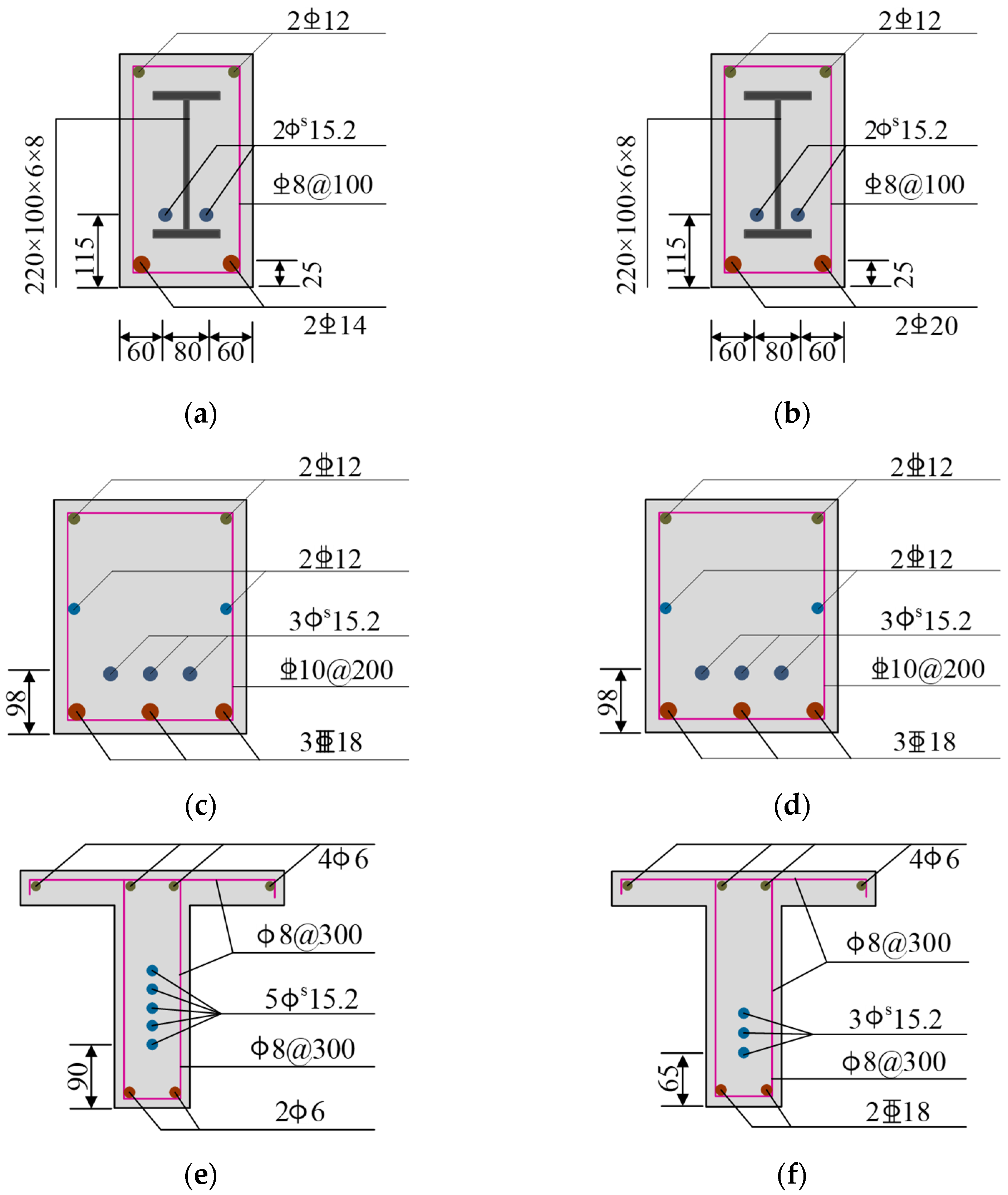


| Specimen | Concrete Strength /N·mm−2 | Elastic Modulus of Concrete/MPa | Bottom Bars | Strength of Bottom Bars /N·mm−2 | Effective Strength/kN |
|---|---|---|---|---|---|
| PSRCB-1 | 50.60 | 3.51 × 104 | 2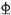 14 14 | 365.0 | 139.81 |
| PSRCB-4 | 50.60 | 3.51 × 104 | 2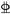 20 20 | 365.0 | 130.89 |
| YL-1 | 54.26 | 3.53 × 104 | 3 18 18 | 654.3 | 151.51 |
| YL-2 | 54.26 | 3.53 × 104 | 3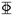 18 18 | 551.3 | 156.97 |
| PB-1 | 128.00 | 4.82 × 104 | 2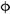 6 6 | 245.2 | 82.97 |
| PB-3 | 134.00 | 4.90 × 104 | 2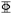 18 18 | 536.0 | 85.91 |
| Number | Put/kN | PuFE/kN | Put/PuFE |
|---|---|---|---|
| PSRB-1 | 265.51 | 249.93 | 1.06 |
| PSRB-4 | 311.51 | 341.55 | 0.91 |
| YL-1 | 598.11 | 629.30 | 0.95 |
| YL-2 | 553.76 | 601.37 | 0.92 |
| PB-1 | 408.22 | 390.98 | 1.04 |
| PB-3 | 545.87 | 518.20 | 1.05 |
| Specimen | Size of Steel Section (H × B × tw × tf) | Bottom Bars | Prestressed Tendon |
|---|---|---|---|
| L-1 | 220 × 100 × 8 × 10 | 2 22 22 | 2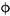 s15.2 s15.2 |
| L-2 | 220 × 100 × 8 × 10 | 2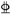 25 25 | 2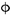 s15.2 s15.2 |
| L-3 | 220 × 100 × 8 × 10 | 2 28 28 | 2 s15.2 s15.2 |
| L-4 | 220 × 100 × 8 × 10 | 2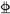 22 22 | 2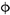 s17.8 s17.8 |
| L-5 | 220 × 100 × 8 × 12 | 2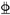 25 25 | 2 s15.2 s15.2 |
| L-6 | 220 × 100 × 8 × 14 | 2 25 25 | 2 s15.2 s15.2 |
| L-7 | 220 × 100 × 6 × 10 | 2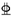 28 28 | 2 s15.2 s15.2 |
| L-8 | 220 × 100 × 10 × 10 | 2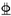 28 28 | 2 s15.2 s15.2 |
| L-9 | 220 × 100 × 8 × 10 | 2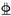 22 22 | 2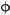 s21.6 s21.6 |
| L-10 | 220 × 100 × 8 × 10 | 2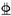 22 22 | 0 |
| Specimen | PuP/kN | PuFE/kN | PuP/PuFE |
|---|---|---|---|
| L-1 | 784.10 | 784.55 | 0.999 |
| L-2 | 838.85 | 837.71 | 1.001 |
| L-3 | 899.50 | 895.14 | 1.005 |
| L-4 | 850.00 | 846.67 | 1.004 |
| L-5 | 861.38 | 871.37 | 0.989 |
| L-6 | 883.78 | 908.11 | 0.973 |
| L-7 | 879.85 | 869.18 | 1.012 |
| L-8 | 917.55 | 921.20 | 0.996 |
| L-9 | 967.98 | 948.20 | 1.021 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Shi, T.; Zhu, Y.; Zhu, Z.; Wang, K. Analysis on Flexural Performance of Prestressed Steel-Reinforced UHPC Beams. Buildings 2024, 14, 4029. https://doi.org/10.3390/buildings14124029
Zhu Y, Shi T, Zhu Y, Zhu Z, Wang K. Analysis on Flexural Performance of Prestressed Steel-Reinforced UHPC Beams. Buildings. 2024; 14(12):4029. https://doi.org/10.3390/buildings14124029
Chicago/Turabian StyleZhu, Ye, Tianyu Shi, Yanzhu Zhu, Zhiyu Zhu, and Kun Wang. 2024. "Analysis on Flexural Performance of Prestressed Steel-Reinforced UHPC Beams" Buildings 14, no. 12: 4029. https://doi.org/10.3390/buildings14124029
APA StyleZhu, Y., Shi, T., Zhu, Y., Zhu, Z., & Wang, K. (2024). Analysis on Flexural Performance of Prestressed Steel-Reinforced UHPC Beams. Buildings, 14(12), 4029. https://doi.org/10.3390/buildings14124029




