An Efficient Construction Method of the 3D Random Asphalt Concrete Model Based on the Background Grid and the Moving-and-Densifying Algorithm
Abstract
1. Introduction
2. Generation of 3D Random Model
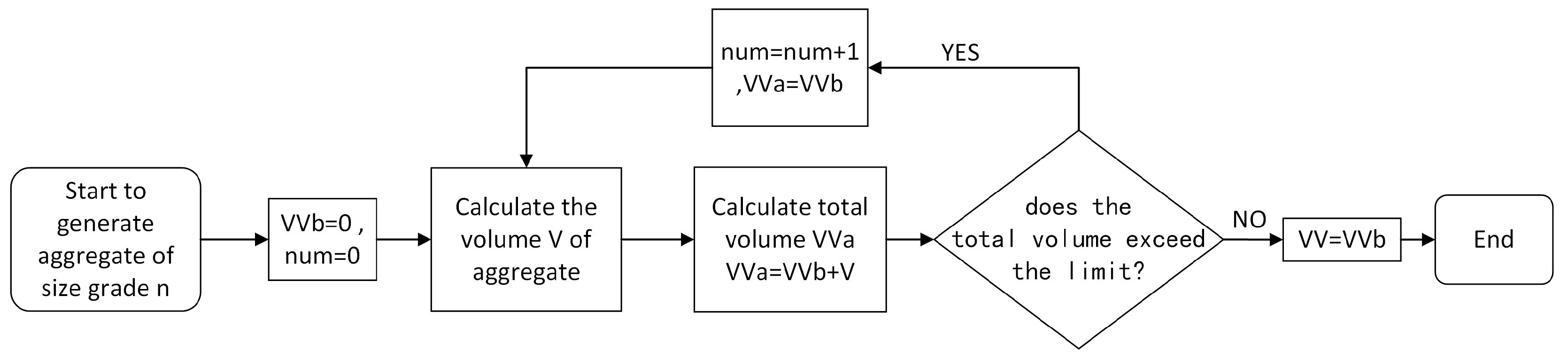
2.1. The Aggregates Target Volume for Model Generation
2.2. Aggregate Generation
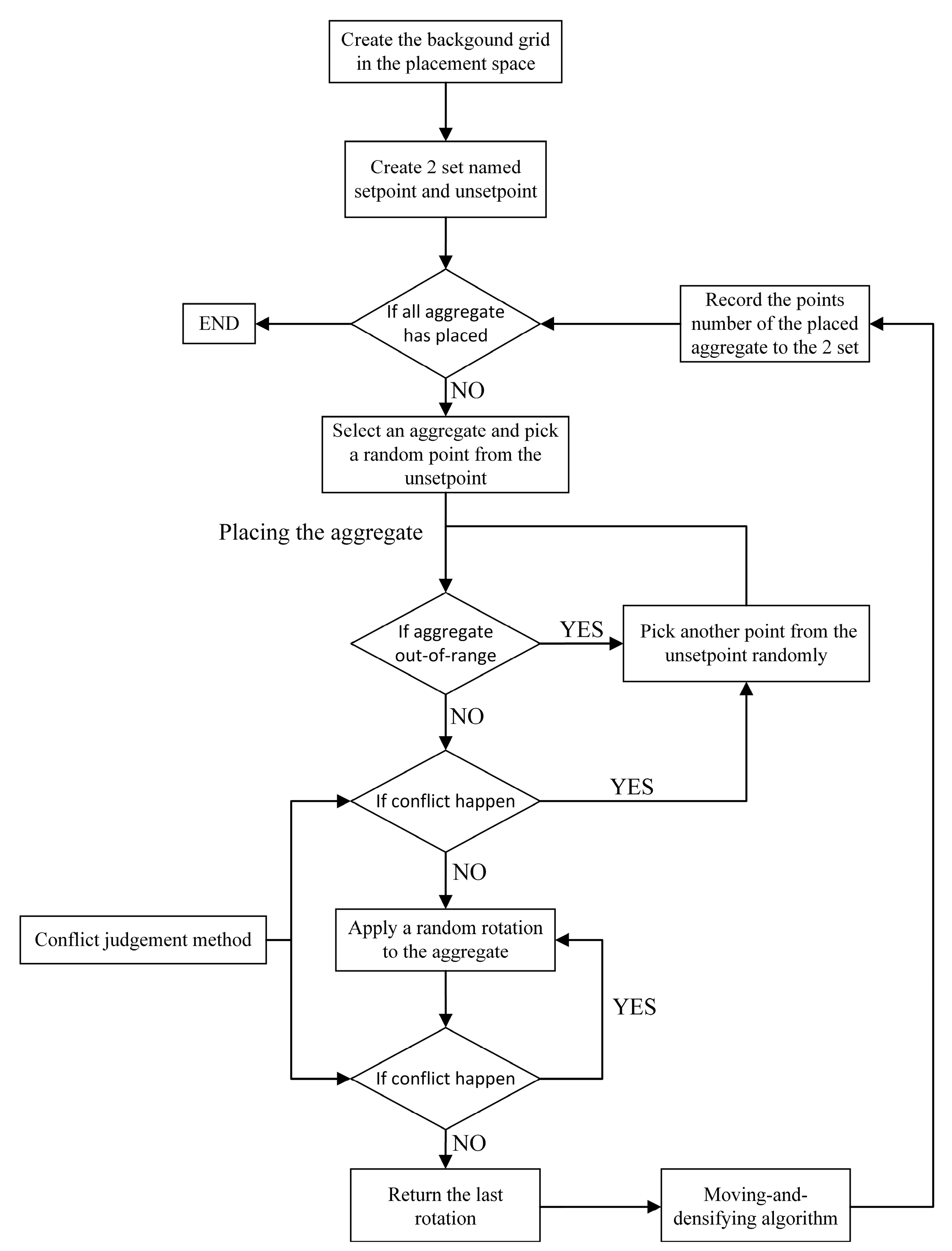
2.3. Packing of Aggregates
3. Construction of the Thermal Conductivity Predicting Model
3.1. Method Selection
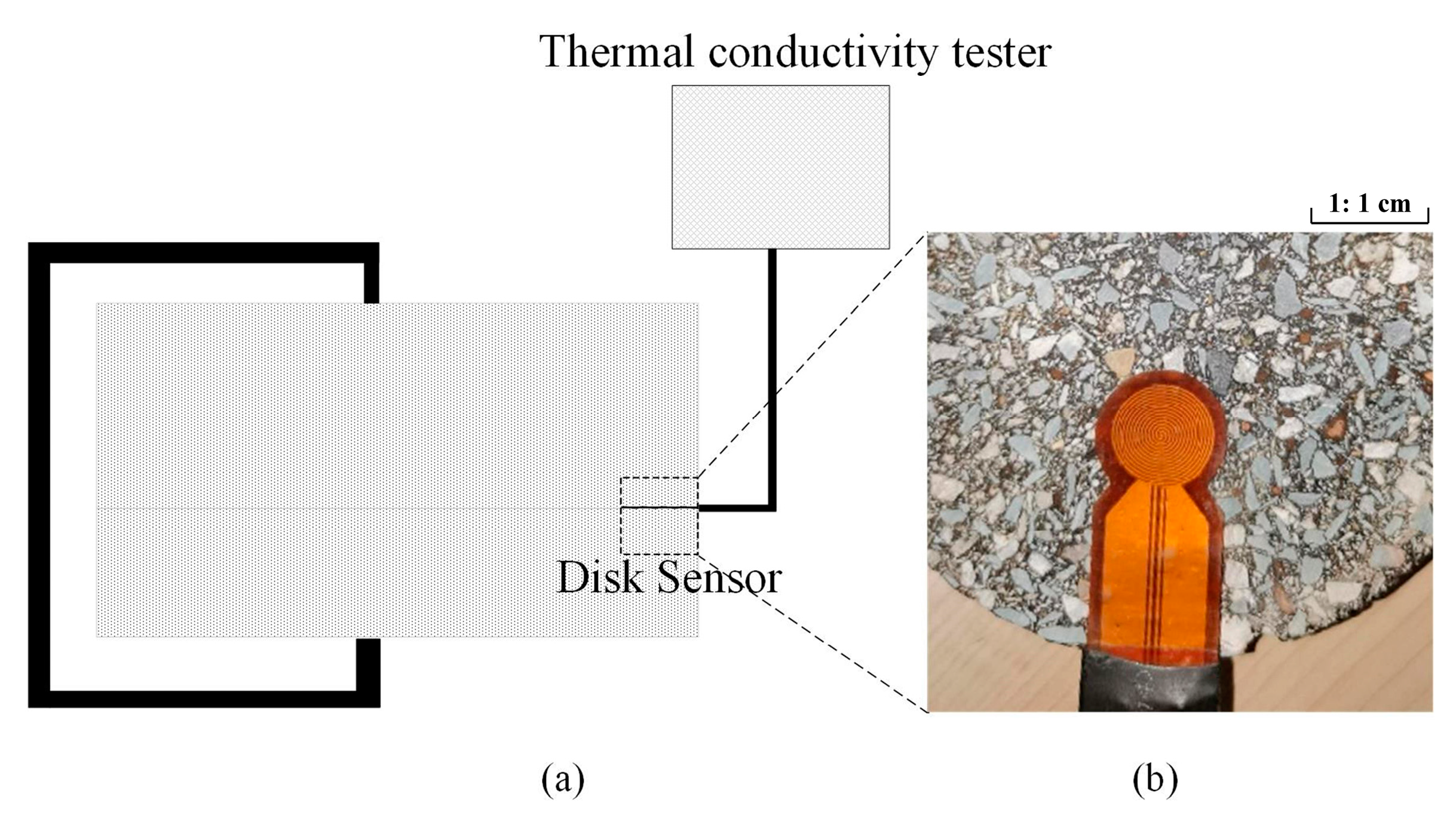
3.2. Determination of Thermal Conductivity
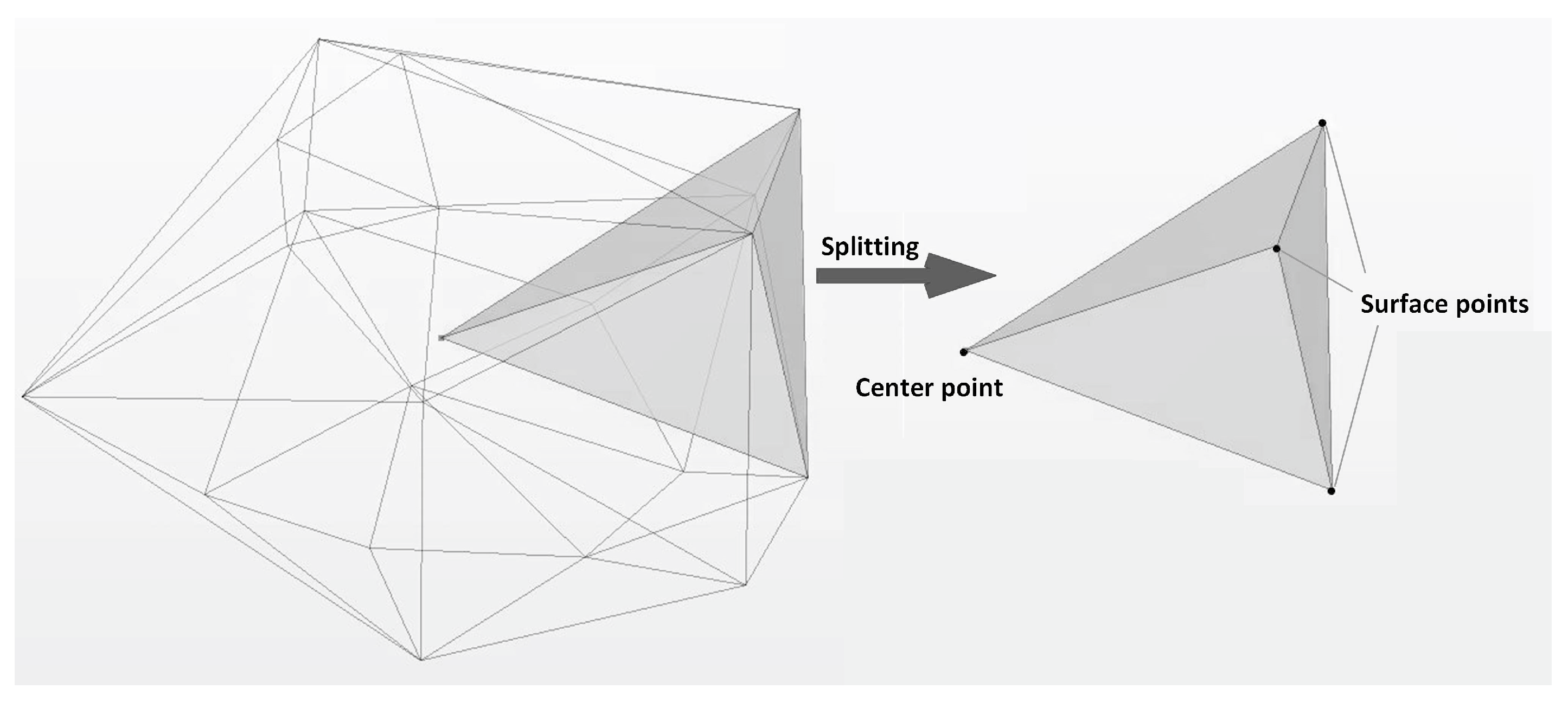
3.3. Construction of the Element Model
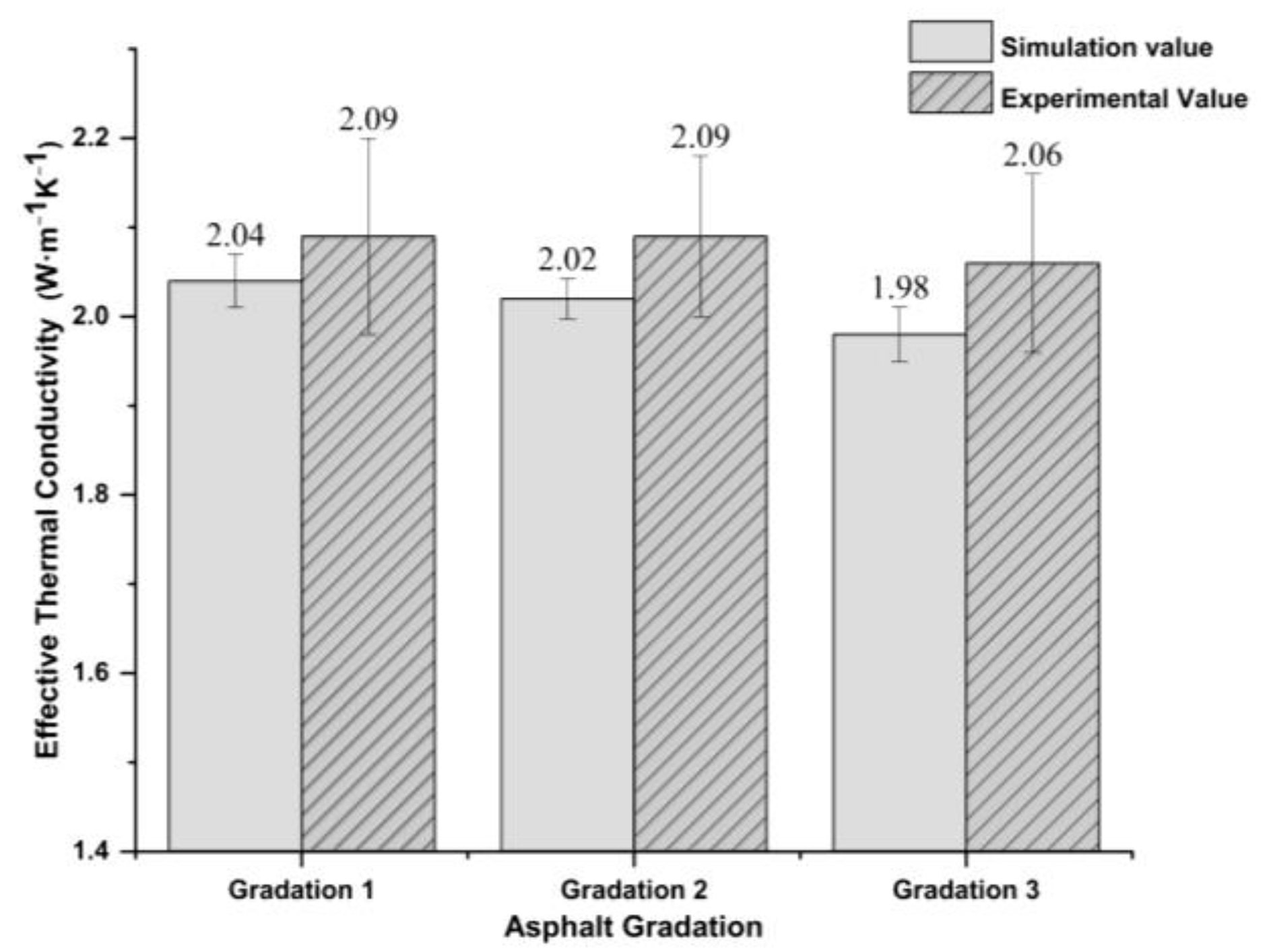
4. Prediction Results and Validation
5. Discussions
5.1. Restricted of Geometry Random Factors Based on the Stability
5.2. Efficiency Improvement of the Packing Algorithm
5.2.1. Efficiency Improvement of the Improved Take-and-Place Method
5.2.2. Efficiency Improvement by Minimizing the Calculation Area
6. Conclusions
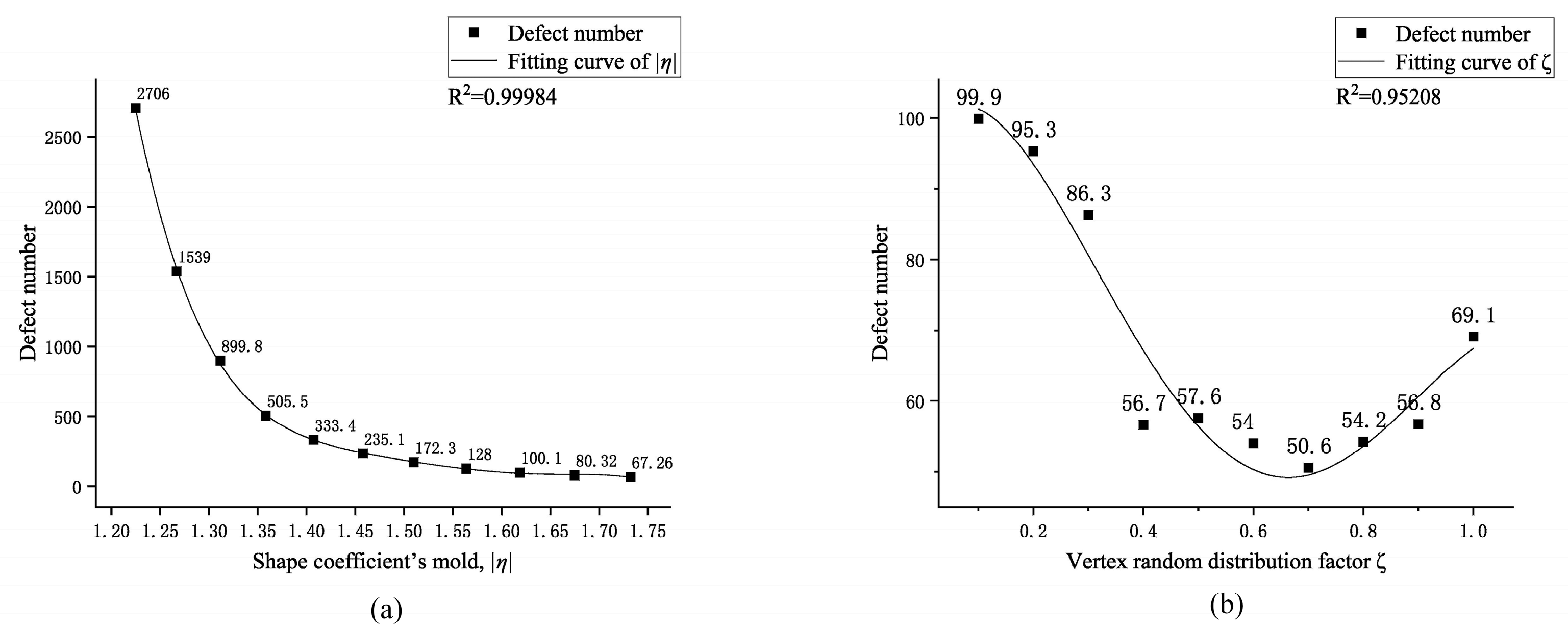
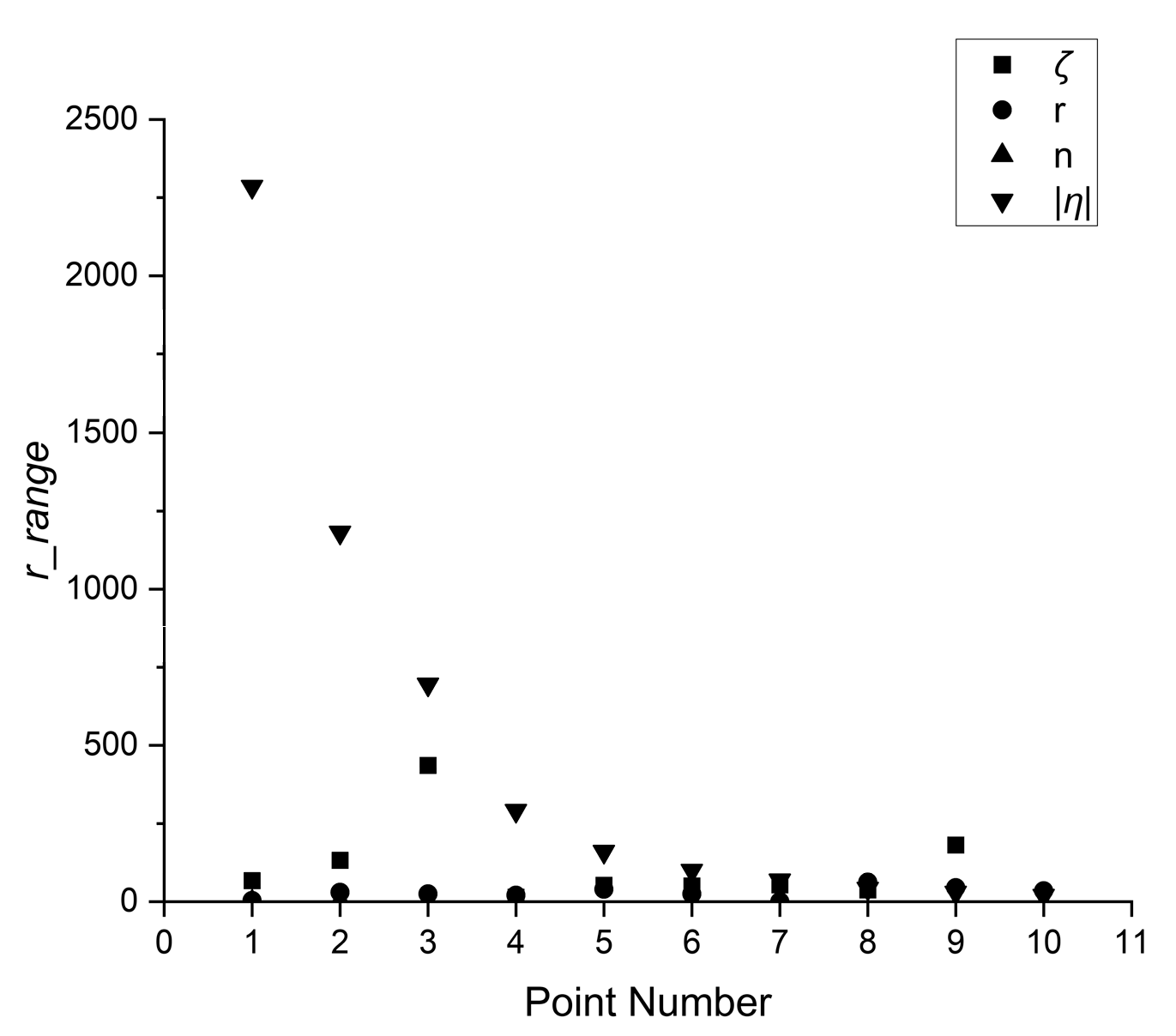
- A four-random-factors aggregate generation method was proposed, and the key factors in the four random factors were confirmed with the index of defect number. In this case, the key factors include the mold of the shape coefficient |η| and the vertex random distribution factor ζ. By restricting the value range of the key factors, the relative variation ranges of the stability index were reduced by 70.52% and 99.50%, respectively, and the averages were reduced by 80.71% and 18.70%, respectively.
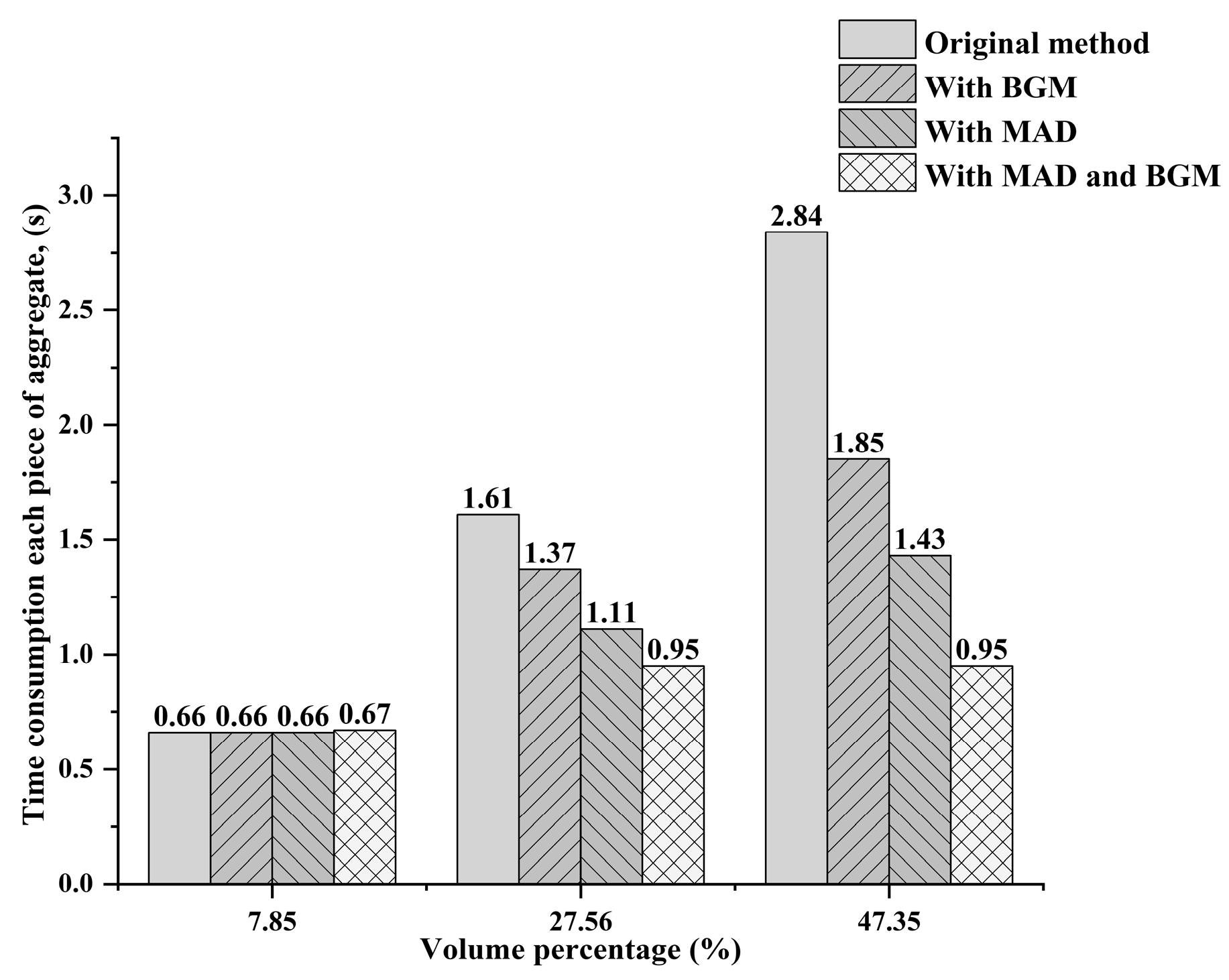
- The take-and-place method was improved by the BGM and the MAD algorithms, respectively, and the packing efficiency of both methods increased with the increase in the aggregate volume percentage. When the volume percentage of aggregates reached 47.35%, the packing efficiency of the take-and-place method with the MAD algorithm was 98.65% higher than that of the original take-and-place method, the take-and-place method with the BGM improved packing efficiency by 53.5%, and the packing efficiency of the improved method with the BGM and MAD algorithms was 198.98% higher than that of the original take-and-place method.
- A conflict judgment method for convex polyhedral aggregates was proposed. Additionally, the increase in computational efficiency for conflict judgment reached 27.13% by minimizing the calculation area.
- The thermal conductivity of the asphalt concrete model was simulated by the steady-state plate method. Compared with the experimental measurements, the maximum prediction error of the 3D random models was 3.88%, and the average was 3.21%. The 3D random model showed a smaller prediction error range (less than 5%) than the 2D models (more than 10%) and was more accurate than the 2D prediction model.
- It is important to adjust the developed model for use in real cases; although packing efficiency was greatly improved by this construction method the two-phase structure ignored the impact of the pore in the asphalt concrete which should be studied in further work. Further, the aggregate generation method can be replaced with a more efficient or real method to meet the requirement of the application. Additionally, further studies should investigate the application of the random models in other properties of asphalt concrete.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wang, D.; Ding, X.; Gu, L.; Ma, T. Assessment Model and Virtual Simulation for Fatigue Damage Evolution of Asphalt Mortar and Mixture. Adv. Mater. Sci. Eng. 2018, 59, 4807. [Google Scholar] [CrossRef]
- Du, C.; Liu, P.; Sun, Y.; Chen, J.; Liu, Q.; Oeser, M. Characterizing asphalt mixtures with random aggregate gradations based on the three-dimensional locally homogeneous model. Comput.-Aided Civ. Infrastruct. Eng. 2022, 37, 1687–1702. [Google Scholar] [CrossRef]
- Szydlowski, C.; Gorski, J.; Stienss, M.; Smakosz, L. Numerical Simulation of Asphalt Mixtures Fracture Using Continuum Models. In Proceedings of the 22nd International Conference on Computer Methods in Mechanics (CMM), Lublin University of Technology, Lublin, Poland, 13–16 September 2017. [Google Scholar] [CrossRef]
- Chen, J.; Wang, H.; Dan, H.; Xie, Y. Random Modeling of Three-Dimensional Heterogeneous Microstructure of Asphalt Concrete for Mechanical Analysis. J. Eng. Mech. 2018, 144, 2505. [Google Scholar] [CrossRef]
- Han, D.; Liu, G.; Zhao, Y.; Pan, Y.; Yang, T. Research on thermal properties and heat transfer of asphalt mixture based on 3D random reconstruction technique. Constr. Build. Mater. 2021, 270, 121393. [Google Scholar] [CrossRef]
- Xu, J.; Zheng, C. Random generation of asphalt mixture mesostructure and thermal-mechanical coupling analysis at low temperature. Constr. Build. Mater. 2021, 280, 122537. [Google Scholar] [CrossRef]
- Mu, K.; Chen, J.; Mu, Q.; Garg, A.; Gao, Z.; Li, Y. Development of a microstructure-based numerical approach for analyzing heat transfer within the asphalt mixture. Constr. Build. Mater. 2020, 260, 119890. [Google Scholar] [CrossRef]
- Sun, Y.; Du, C.; Gong, H.; Li, Y.; Chen, J. Effect of temperature field on damage initiation in asphalt pavement: A microstructure-based multiscale finite element method. Mech. Mater. 2020, 144, 103367. [Google Scholar] [CrossRef]
- Yang, W. Finite element model of concrete material based on CT image processing technology. J. Vis. Commun. Image Represent. 2019, 64, 102631. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Z.; Gong, H.; Zhou, C.; Chen, J.; Huang, B. 3D Multiscale Modeling of Asphalt Pavement Responses under Coupled Temperature-Stress Fields. J. Eng. Mech. 2022, 148, 2089. [Google Scholar] [CrossRef]
- Mora, C.F.; Kwan, A.K.H. Sphericity, shape factor, and convexity measurement of coarse aggregate for concrete using digital image processing. Cem. Concr. Res. 2000, 30, 351–358. [Google Scholar] [CrossRef]
- Ye, Y.; Sun, Y.; Gao, L.; Ma, Z.; Xue, X. Study On Creep Behavior Of Asphalt Mixture Based On Discrete Element Method. Balt. J. Road Bridge Eng. 2020, 15, 174–195. [Google Scholar] [CrossRef]
- Castillo, D.; Caro, S.; Darabi, M.; Masad, E. Influence of aggregate morphology on the mechanical performance of asphalt mixtures. Road Mater. Pavement Des. 2018, 19, 972–991. [Google Scholar] [CrossRef]
- Salemi, M.; Wang, H. Image-aided random aggregate packing for computational modeling of asphalt concrete microstructure. Constr. Build. Mater. 2018, 177, 467–476. [Google Scholar] [CrossRef]
- Yan, P.; Zhang, J.; Fang, Q.; Zhang, Y.; Fan, J. 3D numerical modelling of solid particles with randomness in shape considering convexity and concavity. Powder Technol. 2016, 301, 131–140. [Google Scholar] [CrossRef]
- Holla, V.; Vu, G.; Timothy, J.J.; Diewald, F.; Gehlen, C.; Meschke, G. Computational Generation of Virtual Concrete Mesostructures. Materials 2021, 14, 3782. [Google Scholar] [CrossRef]
- Du, C.; Sun, L.; Jiang, S.; Ying, Z. Numerical Simulation of Aggregate Shapes of Three-Dimensional Concrete and Its Applications. J. Aerosp. Eng. 2013, 26, 515–527. [Google Scholar] [CrossRef]
- Cao, P.; Jin, F.; Feng, D.; Zhou, C.; Hu, W. Prediction on dynamic modulus of asphalt concrete with random aggregate modeling methods and virtual physics engine. Constr. Build. Mater. 2016, 125, 987–997. [Google Scholar] [CrossRef]
- Huang, S.; Huang, L.; Lai, Z. An extension of the Fourier series-based particle model to the GJK-based contact detection and resolution framework for DEM. Comput. Part. Mech. 2022, 9, 381–391. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, S.; Huang, D.; Wang, X.; Zhang, Y. 3D shape quantification and random packing simulation of rock aggregates using photogrammetry-based reconstruction and discrete element method. Constr. Build. Mater. 2020, 262, 119986. [Google Scholar] [CrossRef]
- Yang, S.F.; Yang, X.H.; Yin, A.Y.; Jiang, W. Three-dimensional numerical evaluation of influence factors of mechanical properties of asphalt mixture. J. Mech. 2012, 28, 569–578. [Google Scholar] [CrossRef]
- Yin, A.; Yang, X.; Zeng, G.; Gao, H. Fracture simulation of pre-cracked heterogeneous asphalt mixture beam with movable three-point bending load. Constr. Build. Mater. 2014, 65, 232–242. [Google Scholar] [CrossRef]
- Ouyang, H.; Chen, X. 3D meso-scale modeling of concrete with a local background grid method. Constr. Build. Mater. 2020, 257, 119382. [Google Scholar] [CrossRef]
- Zhou, R.; Song, Z.; Lu, Y. 3D mesoscale finite element modelling of concrete. Comput. Struct. 2017, 192, 96–113. [Google Scholar] [CrossRef]
- Zhang, Z.; Song, X.; Liu, Y.; Wu, D.; Song, C. Three-dimensional mesoscale modelling of concrete composites by using random walking algorithm. Compos. Sci. Technol. 2017, 149, 235–245. [Google Scholar] [CrossRef]
- Muecke, E. Quickhull: Computing convex hulls quickly. Comput. Sci. Eng. 2009, 11, 54–56. [Google Scholar] [CrossRef]
- Weingrill, H.; Hohenauer, W.; Resch-Fauster, K.; Zauner, C. Analyzing Thermal Conductivity of Polyethylene-Based Compounds Filled with Copper. Macromol. Mater. Eng. 2019, 304, 1800644. [Google Scholar] [CrossRef]
- Yan, X.; Chen, L.; You, Q.; Fu, Q. Experimental analysis of thermal conductivity of semi-rigid base asphalt pavement. Road Mater. Pavement Des. 2019, 20, 1215–1227. [Google Scholar] [CrossRef]
- Anjum, F.; Rasool, F.; Mohyudin, F.; Ameen, A. Study of effect of moisture and temperature on thermal and physical properties of limestone using a transient plane source technique. In Proceedings of the 5th UTP-UMP-UAF Symposium on Energy Systems (SES), Kuantan, Malaysia, 1–2 October 2019. [Google Scholar] [CrossRef]
- Balkan, E.; Erkan, K.; Salk, M. Thermal conductivity of major rock types in western and central Anatolia regions, Turkey. J. Geophys. Eng. 2017, 14, 909–919. [Google Scholar] [CrossRef]
- Tang, B.; Zhu, C.; Xu, M.; Chen, T.; Hu, S. Thermal conductivity of sedimentary rocks in the Sichuan basin, Southwest China. Energy Explor. Exploit. 2019, 37, 691–720. [Google Scholar] [CrossRef]
- Zou, L.; Zheng, N.; Li, W.; Ji, X.; Zhang, W. Specific heat capacity test of asphalt mixture based on heat balance principle. J. Jiangsu Univ. 2016, 37, 347–351. [Google Scholar] [CrossRef]
- Mirzanamadi, R.; Johansson, P.; Grammatikos, S.A. Thermal properties of asphalt concrete: A numerical and experimental study. Constr. Build. Mater. 2018, 158, 774–785. [Google Scholar] [CrossRef]
- Chen, J.; Wang, H.; Li, L. Determination of Effective Thermal Conductivity of Asphalt Concrete with Random Aggregate Microstructure. J. Mater. Civ. Eng. 2015, 27, 1313. [Google Scholar] [CrossRef]






| References | Asphalt Mortar | Limestone [29,30,31] | Gradation 1# | Gradation 2# | Gradation 3# |
|---|---|---|---|---|---|
| Thermal conductivity (W/(m·K)) | 1.90 | 2.58 | 2.09 | 2.09 | 2.06 |
| Standard deviation. (W/(m·K)) | 0.07 | 0.45 | 0.09 | 0.07 | 0.08 |
| Specific heat capacity (J/(kg·K) | 862 | 850 | 856 | 856 | 856 |
| Reference | Max RE | Min RE | Avg RE |
|---|---|---|---|
| Mirzanamadi et al. [33] | 10.40 | 1.44 | 4.32 |
| Jiaqi Chen et al. [34] | 16.59 | 4.73 | 11.45 |
| KeMu et al. [7] | - | - | 9.00 |
| Random Factor | Lower Limit | Upper Limit |
|---|---|---|
| Vertex random distribution factor ζ | −1 | 1 |
| Sphere radius r | 0.5 dmin | 0.5 dmax |
| Vertex number N | 16 | 20 |
| Mold of shape coefficient |η| | 1.21 | 1.73 |
| Random Factor | Max | Min | P | Mean | r_range | Mean Decrease | r_range Increment |
|---|---|---|---|---|---|---|---|
| |η| | 1.46 | 1.73 | 54.07 | 130.51 | 128.60 | 546.13 | 300.39 |
| ζ | 0.40 | 0.90 | 50.00 | 54.94 | 0.36 | 13.08 | 72.09 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Chen, H.; Zhao, Y. An Efficient Construction Method of the 3D Random Asphalt Concrete Model Based on the Background Grid and the Moving-and-Densifying Algorithm. Buildings 2023, 13, 990. https://doi.org/10.3390/buildings13040990
Liu X, Chen H, Zhao Y. An Efficient Construction Method of the 3D Random Asphalt Concrete Model Based on the Background Grid and the Moving-and-Densifying Algorithm. Buildings. 2023; 13(4):990. https://doi.org/10.3390/buildings13040990
Chicago/Turabian StyleLiu, Xiaoming, Huaan Chen, and Yu Zhao. 2023. "An Efficient Construction Method of the 3D Random Asphalt Concrete Model Based on the Background Grid and the Moving-and-Densifying Algorithm" Buildings 13, no. 4: 990. https://doi.org/10.3390/buildings13040990
APA StyleLiu, X., Chen, H., & Zhao, Y. (2023). An Efficient Construction Method of the 3D Random Asphalt Concrete Model Based on the Background Grid and the Moving-and-Densifying Algorithm. Buildings, 13(4), 990. https://doi.org/10.3390/buildings13040990







