Failure Analysis of Transmission Tower in Full-Scale Tests

Xiuyun Gao; Rong Yi; Lingquan Zhang; Xiao Jiang; Jiaxiang Li

doi:10.3390/buildings12040389

,

and

¹

Economic and Technological Research Institute of State Grid Heilongjiang Electric Power Co., Ltd., Harbin 150036, China

²

Department of Civil Engineering, Northeastern University, Shenyang 110819, China

^*

Author to whom correspondence should be addressed.

Buildings2022, 12(4), 389;https://doi.org/10.3390/buildings12040389

This article belongs to the Special Issue Structural Health Monitoring

Version Notes

Order Reprints

Abstract

With the rapid development of Ultra-High Voltage (UHV) transmission lines, it is necessary to study the performance of UHV transmission towers. First, we performed full-scale tests on a transmission tower under seven loading patterns. Then, the test results were compared with the calculation results of the Chinese tower design software Transmission Tower Analysis Program (TTA), and the failure location of the tower and the stress characteristics of the key parts were studied. Finally, we discuss the influence of bolt slippage and a new joint on the tower performance, and propose some design proposals for the current Chinese code, based on the test results. The results show that a bolt slip will significantly increase the displacement of the transmission tower, but the residual displacement can correct it. The new joint design has good mechanical performance. The bracing member at the bottom of the tower leg is located at the connection of the tower leg and the foundation, and there is a significant sudden change in stiffness, which we recommend designing according to 4% of the axial force of the main members.

Keywords:

transmission tower; full-scale test; joint slip; tower failure; design code

1. Introduction

Recently, Ultra-High Voltage (UHV) lines for long-distance power transmission have been developing rapidly. As an essential part of UHV lines, UHV transmission towers need to bear larger line loads than high-voltage lines, and the consequences will be more serious once damaged. To reduce the damage to the transmission tower, caused by accidents, the existing design should be improved to make it more reasonable. With the rapid development of computer technology, numerical simulation has also become an important tool to study the performance of transmission towers under different cases. Albermani et al. [1,2] proposed a numerical simulation method, considering the transmission tower’s material and geometric nonlinearity, and studied the transmission tower’s static and dynamic failure. Tian et al. [3,4,5] studied the seismic response of the transmission tower, proposed a damper to reduce the seismic responses of the transmission tower, and verified its effectiveness through numerical simulation. Ji et al. [6] introduced the ice-shedding criterion to study the vibration of the transmission tower, caused by the conductor breakage. The results showed that the ice shedding caused by the vibration could not be ignored, in order to obtain the accurate responses of the transmission tower. The stress situation of the joint of the transmission tower is very complex, and the simulation of the transmission tower is a difficult problem. Joints are often simplified to rigid or hinged, but this is inaccurate. The bolt slip of the joint will cause the actual displacement of the transmission tower to be much larger than the calculated value. Yang et al. [7] studied the influence of different parameters on bolt slip through experiment and simulation. Gan et al. [8] proposed a simplified slip model and verified its accuracy through tests. An et al. [9] presented a general node element to describe the bolt slip effect by tension test. Ma et al. [10] studied the hysteretic characteristics of bolted joints under cyclic loads. Jiang et al. [11,12] studied the bolt slip and introduced the bolt slip model into the overall modeling of the transmission tower and investigated the performance of the tower, under different working conditions, through numerical simulation. The effect of joint slip on the bearing capacity of the tower is related to the load mode. Compared to numerical simulation, full-scale testing is a more reliable method to study the performance of towers because the assumptions in numerical simulation make it different from the actual situation, such as joint simplification and eccentric connection of members, but in full-scale tests, all of the above factors can be considered. Prasad et al. [13,14,15] studied the failure characteristics and influencing factors of transmission towers through full-scale tests and suggested that the slenderness ratio of the bracing member should not exceed 170. Moreover, full-scale experiments can also provide essential references for numerical simulations. Tian et al. [16,17] validated their member constitutive model through full-scale experiments. Fu et al. [18,19] considered the uncertainty of geometric parameters and material properties. They proposed a method to calculate the potential failure mode of the transmission tower through numerical simulation, which was also verified by full-scale tests. Li et al. [20] compared the design of towers in current principal international codes and proposed some suggestions for improving the design of transmission towers. At present, there are few full-scale test studies on UHV transmission towers, and the effectiveness of the new design joint needs to be verified by a full-scale test. This paper studies areas for improvement in the current Chinese design codes of transmission towers through full-scale tests and discusses the influences of bolted joints on transmission towers. Section 2 introduces the situation of the transmission tower test. Section 3 presents a finite element model of the tower. Section 4 discusses and analyzes the results, and Section 5 summarizes the full text.

2. Full-Scale Test

The employed tower is a suspension tower in a heavy icing area in China, with 30 mm design ice. The height is 54.5 m and the base size is 12.08 × 12.08 m. Q345 and Q420 steels are used for main members, and Q235 is used for the diagonal member. The main members of the tower body are listed in Figure 1. The model of the six-bundle conductor is JLHA4/G2A-900/75; the model of the ground wire is JLB20A-240.

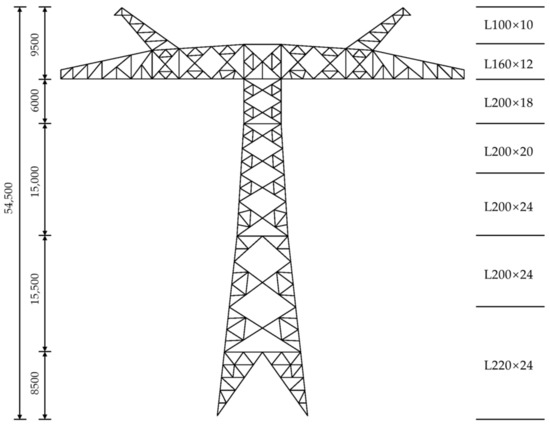
Figure 1. Tower dimensions (unit: mm).

Seven load cases were performed in the full-scale tests, as listed in Table 1. Case 5 and Case 7 are overload cases. For Cases 1–4 and Case 6, the loads are applied in the following steps: 0% → 50% → 75% → 90% → 95% → 100% → 50% → 0%. For Case 5, the loads are applied as 0% → 50% → 75% → 90% → 95% → 100% → 105% → 110% → 115% → 120% → 125% → 130% → 135% → 140% → 145% → 150% → 155% → 100% → 50% →0%. For Case 7, the loads are applied as 0% → 50% → 75% → 90% → 95% → 100% → 105% → 110% → 115% → 120% → 125% → 130% → 135% → 140% → 145%→ 150% → 100% → 50% → 0%. Figure 2 shows the full-scale test facility and loading point diagram.

Table 1. Scenarios of the full-scale test.

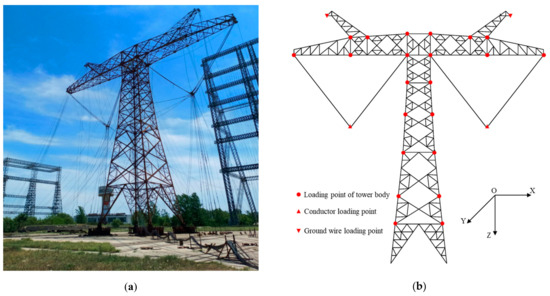
Figure 2. Schematic of experimental facilities and loading points. (a) Photo of the loading test; (b) Loading point.

Total stations were installed on the front and sides of the tower to observe the displacement of the measuring points on the tower. The selected displacement measuring point should reflect the overall deflection curve of the tower and the maximum displacement of the test tower. The displacement observation points are shown in Figure 3. The strain gauges were used to obtain the strain of the members, and the strain gauges were mainly arranged in the following positions: the important components of the tower, such as the tower body, tower legs, and the cross arm, the member with the larger stress value under each case during the tower calculation, and parts near the joints. The layout of strain gauges is shown in Figure 4. The strain gauges adopt different sticking methods, according to the member specifications and stress characteristics. Generally, for the brace member and the members with less stress, the gauges are placed along the core line on the connecting limb or two limbs. For members with large bending moments, the number of strain gauges should be increased. When there are two or more strain gauges at one strain measuring point, the strain gauges should be placed on the same cross-section of the member.

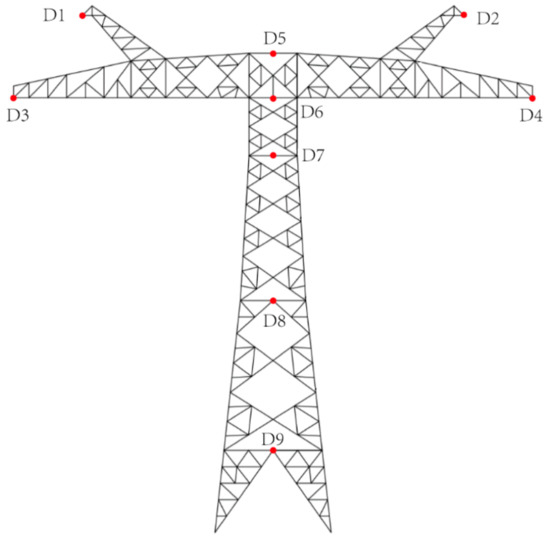
Figure 3. Displacement observation point layout.

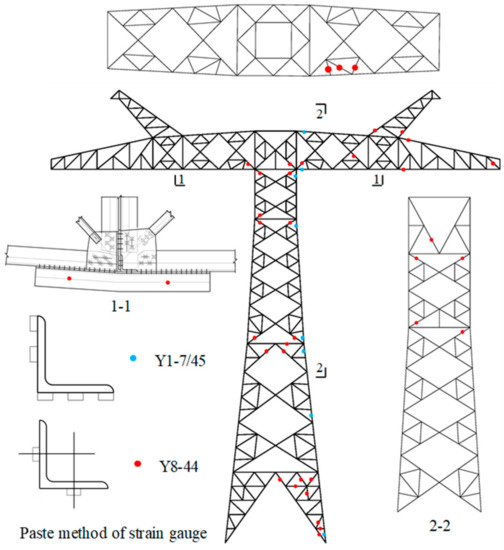
Figure 4. Layout of strain gauges.

For strain observation, the strains were read after each loading was stable for 1 min; when a loading case was over, each member was carefully checked for damage, making sure no damage occurred, and then the next test case was carried out. The key observation parts, corresponding to each load case, are shown in Figure 5.

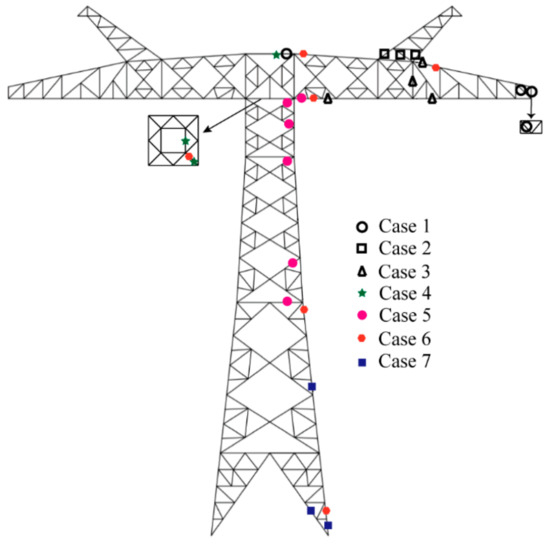
Figure 5. Key observation parts of each load case.

3. Finite Element Model of the Tower

Only the displacement and strain of a limited number of observation points could be obtained by the full-scale test. For numerical simulation, the stress and displacement distribution of the whole employed tower can be obtained, but the numerical results should be verified by comparing with the test results. In this paper, ANSYS was used to establish the numerical model of the tower. It should be noted that bolt slip was ignored in the modeling, and the BEAM188 element was used to model the transmission tower members. The established numerical model is shown in Figure 6. The calculation results in ANSYS were compared with the calculation results of the current domestic transmission tower design software Transmission Tower Analysis Program (TTA), and the limitations of the current Chinese tower design will be discussed.

Figure 6. The finite model of the tower.

4. Results and Discussion

4.1. Overload Case for Uneven Ice

The current tower design software in China is TTA, in which truss elements are used to simulate the tower member, ignoring the torsion and warping of the members. Under the torsion condition of the tower, the torsional stiffness and warping stiffness of the large-sized angle steel cannot be ignored, and the actual torsion angle of the tower is much smaller than the torsion angle calculated by TTA. Therefore, the actual axial force of the diagonals, due to torsional conditions, is much smaller than that calculated by TTA. The actual force is only one-third of that calculated by TTA. When the load reaches 155%, the comparison between the measured and calculated stress results of members in Case 5 is shown in Table 2, and the stress ratio is in brackets. In order to verify the difference between experiment and theory, we carried out manual calculation, and the process is shown in Appendix A.

Table 2. Results comparison.

However, the test results show that in Case 5 the force of the main member of the bottom tower leg, obtained by the test, is close to the calculation result of TTA.

4.2. Key Parts of the Transmission Tower

4.2.1. Tower Legs

The tower legs bear a relatively large load, which is a common damage position. In this full-scale test, the damage occurs in the tower legs. The strain observation point number for the tower leg is shown in Figure 7, and the test result of the tower legs is listed in Table 3. In Case 5 and Case 6, the axial force of the member, where the No. 40 measuring point is located, accounts for 3.7% and 0.8% of the axial force of the main material member of the tower leg, where the No. 7 measuring point is located, respectively. The force of the bracing member is about 3.7% of the axial force of the supporting main member, which is slightly higher than the 3% specified in the specification.

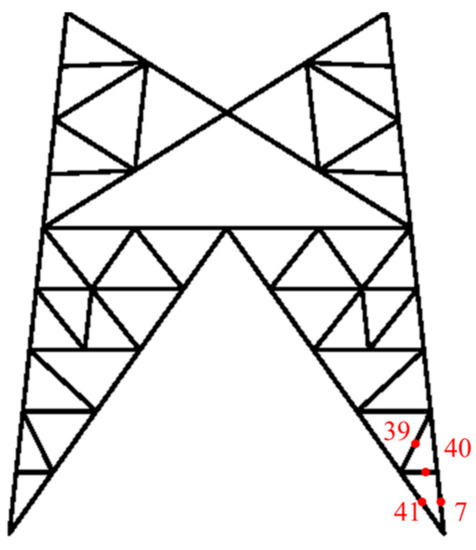
Figure 7. Strain observation point number.

Table 3. Test results of tower legs.

4.2.2. Diagonal Members under the Tower Head

The connection between the tower head and the tower body of the transmission tower is the key member to control the damage of the transmission tower in Case 5. When the design load is applied, the calculated stress ratio reaches 99%. When the load reaches 155%, the calculated stress ratio reaches 153%. However, in the full-scale test, the stress corresponding to 100% of the design load is 109 MPa, which is much smaller than the design strength of 310 MPa. When the load reaches 155%, the stress of the main members under the first diagonal members and the cross arm are 158.8 MPa and 305.5 MPa, respectively; both of these are in the elastic stage. At the same time, the tower leg is at 257.7 MPa, reaching 72% of the design strength, which is an increase of 10.7% over the calculated stress. The axial force obtained by the test is shown in Table 2.

Because TTA uses truss element to simulate the tower member, it ignores the torsion and warping of the member, with a total of four degrees of freedom. As a result, under the torsion condition, the actual torsion angle of the tower is much smaller than the torsion angle calculated by TTA. Therefore, the actual axial force of the diagonal of the tower body, due to the torsion condition, is much smaller than that calculated by TTA, and the actual force is only 0.33 times the calculated value. When the design load reaches 155%, the calculated axial force of the first cross inclined member is 779 kN, the measured axial force is 471 kN, and the relative deviation is 65%. It should be noted that the actual force of the main member is relatively close to the calculation.

4.2.3. The Connection between the Cross-Arm and Tower Body

Figure 8 shows the layout of strain gauges on the short angle steel at the outer back, between the cross arm and the tower body, and the test results of members are shown in Table 4. The applied loads are 100% design loads.

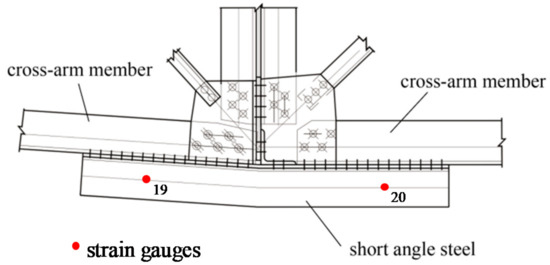
Figure 8. The layout diagram of measuring points.

Table 4. The test results of members.

By comparison, in Case 5, the outer back angle steel at the root of the cross-arm is subjected to a greater force, which plays a role in strengthening the root of the cross-arm, while the strengthening effect is not obvious under the maximum bending condition. In addition, under the working conditions, the measured axial force of the cross-arm at the root is 2014.6 kN, and the force transmission of the short angle steel is about 11.3%. In Case 6, the measured axial force of the cross-arm at the root is 1764.1 kN, and the force transmission by the short angle steel is about 3.1%. From the test results, the short angle steel can increase the stiffness of the joint; in Case 6, the short angle steel deforms more, and the axial force is also greater.

4.3. Displacement Analysis of the Transmission Tower

The measured displacement in the test is larger than the calculated displacement, especially in the two overload conditions (Case 5 and Case 7). The maximum displacements of Cases 5 and 7 in the test exceed 145% and 175% of the displacements calculated by TTA. This is mainly caused by the bolt slippage of the joints in the tower. The tower is connected by bolts, the diameter of the screw hole is at least 1.5 mm larger than the diameter of the screw, and the relative displacement of the bolt and the screw hole will occur during the test, resulting in calculation deviation. The angle steel tower is connected by many bolts, and the displacement is accumulated continuously, resulting in a relatively large difference between the measured displacement of the tower and the theoretically calculated displacement. This phenomenon existed in the previous tower tests.

By observing the displacement of the tower after unloading and correcting the measured displacement value, the influence of bolt slip can be minimized. Table 5 uses this method to correct the measured displacement value and compare it with the theoretically calculated value. The corrected deviation is much smaller. The deviation of the former three cases is within 10%, while the deviation of Case 5 and Case 6 is 16.0% and 13.4%, respectively, which means that the residual value is caused by the slippage of the transmission tower bolts and has a certain relationship with the sequence of the loading condition.

Table 5. Maximum displacements comparison between the tests and calculation.

4.4. Tower Failure Analysis

Two overload scenarios were carried out in this paper. In Case 7, the test tower was damaged, and the damaged position was the main member of the second section at the upper part of the tower leg (No. 701 member), as shown in Figure 9. The failure load is 118% of the design load. According to China’s current Steel Structure Design Standard (GB50017-2017), the theoretical value of failure load is 120% of the design load, which is very close to the test failure load. And the manual calculation process is shown in Appendix A. It should be noted that the test tower was overloaded with the maximum torsion of non-uniform ice (Case 5), and there were serious initial geometric defects and residual stresses in each member, which reduce the actual bearing capacity of the employed tower. Secondly, due to the calculation of Steel Structure Design Standard (GB50017-2017), it is assumed that the tower member is under axial compression. In fact, the main members of the transmission line tower appeared to show large eccentricity when transferring load, due to the changes in specifications and connection. In addition, the bolt slip could also decrease the bearing capacity of the tower. Therefore, after the tower failure, some tower members were tested in metal material experiments. The results are shown in Table 6.

Figure 9. Tower failure.

Table 6. Material tests.

It can be seen from the table that the actual yield strength of Q420B steel for the main member of the tower is, at most, 2% lower than the theoretical yield strength, and the actual yield strength increases by about 10–12% compared with the design value. The strength of the angle steel is not up to the standard, which is also the reason for the failure of the transmission tower and the failure load being less than calculated.

4.5. Tower Force Analysis

Table 7 shows the comparison between the measured axial force and the theoretically calculated axial force of the main force-bearing members under the control conditions. From the table, it can be seen that the theoretical calculation values of the axial force of the main members are close to the actual test values. The measured axial force of the main material of the ground wire bracket is slightly larger than the calculated axial force under Case 2, and the relative error is 2.4%. A certain allowance should be reserved for the ground wire support in the design process, and the calculated axial force differential stress ratio can be controlled within 95%. The measured axial force of the main member of the wire cross-arm is relatively large, within 17.8%. According to the above, the axial force of the member, shared by the short angle steel on the outer back of the cross-arm root, is about 11.3%, indicating that the effect of the reinforcing angle steel is more prominent. The measured axial forces of the main members of the tower body and the main members of the tower legs are relatively close to the calculated axial forces, indicating that when the tower is bent, the calculation model is relatively close to the actual force state, which verifies the accuracy of the calculation model.

Table 7. Comparison of the axial force of tower members with 100% loading.

5. Conclusions

In this paper, the performance of a UHV tower, under various typical working conditions, was studied through a full-scale test, and the design limit, the joint slip, and the failure of the tower were discussed. The following conclusions are drawn:

(1): The deviation of the measured displacement data of the tower under various working conditions and the calculated displacement value is within 16%, and the calculation stress of most members, by design on the tower, is close to the measured value. Therefore, the performance of the tower is good.
(2): Under the condition of torsion, the actual axial force of the diagonal is far less than the axial force calculated by TTA, which is only one-third of the calculated value of TTA.
(3): Compared with the calculation results of TTA and ANSYS, introducing the beam-truss hybrid calculation model in the Chinese tower design software, which can ensure the accuracy of the calculation, is suggested.
(4): The short angle steel on the outer back of the cross-arm root can effectively increase the stiffness of the joint under the condition of torsion, while the strengthening effect is not obvious under the maximum bending condition.
(5): Due to the bolt slippage, the measured displacement in the test is greater than the theoretical displacement value; however, the influence of bolt slip can be reduced by observing the displacement of the tower after unloading and correcting the measured displacement value.
(6): According to the calculation of the tower, it is reasonable that the failure position of the tower first occurred on the main member of the second section, at the upper part of the tower leg, which is consistent with the predicted position.
(7): The bracing member at the bottom of the tower leg is located at the connection of the tower leg and the foundation, and there is a sudden large change in stiffness. It is recommended to design according to 4% of the axial force of the main member.

Author Contributions

Conceptualization, X.G. and R.Y.; methodology, L.Z. and X.J.; software, R.Y. and J.L.; investigation, X.G.; data curation, L.Z. and X.J.; writing—original draft preparation, X.G.; writing—review and editing, R.Y. and L.Z.; supervision, X.J. and J.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by State Grid Heilongjiang Electric Power Co., Ltd. science and technology project (Grant 522448200018).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

No data were used to support this study.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

(a): Table 2 shows that the calculation results of the first diagonals below the tower head are obviously different from the experimental results. Therefore, the American standard ASCE10-15 is used for manual calculation. The calculation results are as follows:

\frac{w}{t} = \frac{160 - 14 - 16}{14} = 9.28

{(\frac{w}{t})}_{\lim} = \frac{80 Ψ}{\sqrt{F_{y}}} = \frac{80 \times 2.62}{\sqrt{345}} = 11.28

\frac{w}{t} < {(\frac{w}{t})}_{\lim}

C_{c} = π \sqrt{\frac{2 E}{F_{y}}} = 3.14 \times \sqrt{\frac{2 \times 206000}{345}} = 108.5

0 \leq \frac{L}{r} = \max (0.55 \times 5831 / 49.2, 0.275 \times 5831 / 31.6) = 65.18 \leq 120

\frac{K L}{r} = 60 + 0.5 \times \frac{L}{r} = 92.6 \leq C_{c}

F_{a} = [1 - \frac{1}{2} {(\frac{K L / r}{C_{c}})}^{2}] \times F_{y} = 219.42 M P a

\frac{F}{F_{a}} = \frac{277.79}{219.42} = 1.27

where w = flat width; t = thickness of leg;

Ψ

= 2.62 for F_y in MPa; F_y = minimum guaranteed yield stress; C_c = column slenderness ratio separating elastic and inelastic buckling; E = modulus of elasticity; L = unbraced length; r = radius of gyration; K = effective length coefficient.

The results show that the stress ratio, calculated according to American Standard ASCE10-15, is 1.27, which is still quite different from the test. This situation also shows that the current calculation method is different from the actual situation.

(b): In Section 4.4, according to the Chinese steel structure design standard GB50017-2017, the overload condition is calculated. The theoretical value of the failure load is 120% of the design load and the reason has been mentioned in the paper. The calculation process is as follows:

λ_{\min} = \frac{l}{i_{0}} = \frac{1543}{39} = 39.65

\frac{λ_{\min}}{ε_{k}} = \frac{39.56}{\sqrt{235 / 420}} = 52.89

φ = 0.842

N_{u} = φ A f = 0.842 \times 9066 \times 355 = 2709.92 k N

\frac{N_{u}}{N} = \frac{2709.92}{2260.3} = 1.20

where

λ_{\min}

= slenderness ratio; l = length; i₀ = radius of gyration;

ε_{k}

= steel number correction factor;

φ

= Stability coefficient of axially compressed members; A = sectional area; f = design value of tensile strength of steel; N_u = calculated load; N = design load.

References

Albermani, F.; Kitipornchai, S.; Chan, R. Failure analysis of transmission towers. Eng. Fail. Anal. 2009, 16, 1922–1928. [Google Scholar] [CrossRef]
Alminhana, F.; Mason, M.; Albermani, F. A compact nonlinear dynamic analysis technique for transmission line cascades. Eng. Struct. 2018, 158, 164–174. [Google Scholar] [CrossRef]
Zhang, J.; Li, H.; Li, C.; Tian, L. Seismic response analyses of transmission towers under multidimensional ground motions with rocking and torsion components. J. Aerosp. Eng. 2020, 33, 04020082. [Google Scholar] [CrossRef]
Tian, L.; Rong, K.; Zhang, P.; Liu, Y. Vibration control of a power transmission tower with pounding tuned mass damper under multi-component seismic excitations. Appl. Sci. 2017, 7, 477. [Google Scholar] [CrossRef]
Tian, L.; Ma, R.; Pan, H.; Qiu, C.; Li, W. Progressive collapse analysis of long-span transmission tower-line system under multi-component seismic excitations. Adv. Struct. Eng. 2017, 20, 1920–1932. [Google Scholar] [CrossRef]
Ji, K.; Rui, X.; Li, L.; Yang, F.; McClure, G. Dynamic response of iced overhead electric transmission Lines following cable rupture shock and induced ice shedding. IEEE Trans. Power Deliv. 2016, 31, 2215–2222. [Google Scholar] [CrossRef]
Yang, F.; Zhu, B.; Xing, H. THE slip characteristics and parametric study of bolted connections for transmission towers. Eng. Mech. 2017, 34, 116–127. [Google Scholar]
Gan, Y.; Deng, H.; Li, C. Simplified joint-slippage model of bolted joint in lattice transmission tower. Structures 2021, 32, 1192–1206. [Google Scholar] [CrossRef]
An, L.; Wu, J.; Jiang, W. Experimental and numerical study of the axial stiffness of bolted joints in steel lattice transmission tower legs. Eng. Struct. 2019, 187, 490–503. [Google Scholar] [CrossRef]
Ma, L.; Bocchini, P. Hysteretic model of single-bolted angle connections for lattice steel towers. J. Eng. Mech. 2019, 145, 04019052. [Google Scholar] [CrossRef]
Jiang, W.; Wang, Z.; McClure, G.; Wang, G.; Geng, J. Accurate modeling of joint effects in lattice transmission towers. Eng. Struct. 2011, 33, 1817–1827. [Google Scholar] [CrossRef]
Jiang, W.; Liu, Y.; Chan, S.; Wang, Z. Direct analysis of an ultrahigh-voltage lattice transmission tower considering joint effects. J. Struct. Eng. 2017, 143, 04017009. [Google Scholar] [CrossRef]
Prasad Rao, N.; Samuel Knight, G.; Lakshmanan, N.; Iyer, N. Investigation of transmission line tower failures. Eng. Fail. Anal. 2010, 17, 1127–1141. [Google Scholar] [CrossRef]
Prasad Rao, N.; Samuel Knight, G.; Seetharaman, S.; Lakshmanan, N.; Iyer, N. Failure analysis of transmission line towers. J. Perform. Constr. Facil. 2011, 25, 231–240. [Google Scholar] [CrossRef]
Prasad Rao, N.; Samuel Knight, G.; Mohan, S.; Lakshmanan, N. Studies on failure of transmission line towers in testing. Eng. Struct. 2012, 35, 55–70. [Google Scholar] [CrossRef]
Tian, L.; Pan, H.; Ma, R.; Zhang, L.; Liu, Z. Full-scale test and numerical failure analysis of a latticed steel tubular transmission tower. Eng. Struct. 2020, 208, 109919. [Google Scholar] [CrossRef]
Tian, L.; Guo, L.; Ma, R.; Gai, X.; Wang, W. Full-scale tests and numerical simulations of failure mechanism of power transmission towers. Int. J. Struct. Stab. Dyn. 2018, 18, 1850109. [Google Scholar] [CrossRef]
Fu, X.; Li, H. Uncertainty analysis of the strength capacity and failure path for a transmission tower under a wind load. J. Wind. Eng. Ind. Aerodyn. 2018, 173, 147–155. [Google Scholar] [CrossRef]
Fu, X.; Wang, J.; Li, H.; Li, J.; Yang, L. Full-scale test and its numerical simulation of a transmission tower under extreme wind loads. J. Wind. Eng. Ind. Aerodyn. 2019, 190, 119–133. [Google Scholar] [CrossRef]
Li, J.; McClure, G.; Wang, S. Ensuring the structural safety of overhead transmission lines by design. J. Aerosp. Eng. 2021, 34, 04021010. [Google Scholar] [CrossRef]

Figure 1. Tower dimensions (unit: mm).

Figure 2. Schematic of experimental facilities and loading points. (a) Photo of the loading test; (b) Loading point.

Figure 3. Displacement observation point layout.

Figure 4. Layout of strain gauges.

Figure 5. Key observation parts of each load case.

Figure 6. The finite model of the tower.

Figure 7. Strain observation point number.

Figure 8. The layout diagram of measuring points.

Figure 9. Tower failure.

Table 1. Scenarios of the full-scale test.

Case No.	Load Description
Case 1	Anchor right conductor, while the ground wires and left conductor anchored
Case 2	Right ground wire breakage
Case 3	Right conductor breakage
Case 4	Ice load
Case 5	Uneven ice, maximum torsion (overload)
Case 6	Uneven ice, maximum moment
Case 7	High intensity wind 45° (overload)

Table 2. Results comparison.

Location	Test (MPa)	TTA (MPa)	ANSYS (MPa)
The first diagonals below the tower head	158.8 (0.51)	474.3 (1.53)	140 (0.45)
Connection between the tower body and cross-arm	305.5 (0.85)	503 (1.4)	507 (1.4)
Main member of bottom tower leg	257.7 (0.72)	232.5 (0.65)	236 (0.66)

Table 3. Test results of tower legs.

Case No.	Strain No.	Member Specs	Test Internal Force (kN)
Case 5	39 (bracing member)	Q345 L80 × 7	46.3
	40 (bracing member)	Q345 L80 × 7	69.6
	41(main member)	Q345 L180 × 14	241.7
	7 (main member)	Q420 L220 × 22	1886.2
Case 6	39 (bracing member)	Q345 L80 × 7	5.6
	40 (bracing member)	Q345 L80 × 7	16.8
	41 (main member)	Q345 L180 × 14	254.8
	7 (main member)	Q420 L220 × 22	2195

Table 4. The test results of members.

Case No.	Strain No.	Member Specs	Test Internal Force (kN)
Case 5	19	Q420 L250 × 22	227.4
Case 5	20	Q420 L250 × 22	148.7
Case 6	19	Q420 L250 × 22	48.2
Case 6	20	Q420 L250 × 22	54.4

Table 5. Maximum displacements comparison between the tests and calculation.

Case No.	Displacement Observation Point No.	Position	Direction	D1	D2	D3	CV	RD	AD
Case 1	4	cross-arm	vertical	61	7	54	51	5.6%	19.6%
Case 2	2	ground wire bracket	longitudinal	206	21	185	182	1.6%	13.2%
Case 3	4	cross-arm	longitudinal	849	479	370	379	−2.4%	124%
Case 4	3	cross-arm	vertical	265	61	204	187	8.30%	41.7%
Case 5	3	cross-arm	longitudinal	1736	892	844	708	16.0%	145%
Case 6	3	cross-arm	longitudinal	483	192	291	252	13.4%	91.6%
Case 7	3	cross-arm	longitudinal	567	-	-	206	-	175.2%

Note: D1-test value, D2-residual value, D3-correction value, CV-calculation value, RD-relative deviation (deviation between corrected value and calculated value), AD-absolute deviation (deviation between test value and calculated value).

Table 6. Material tests.

Location	Member Specs	Test Yield Strength (MPa)	Theoretical Yield Strength (MPa)	Design Strength (MPa)	Test Value/Theoretical Value	Test Value/Design Strength
Main member 1	Q420 L220 × 24	398	400	355	0.995	1.121
Main member 2	Q420 L220 × 24	394	400	355	0.985	1.110
Main member 3	Q420 L200 × 24	392	400	355	0.980	1.104

Table 7. Comparison of the axial force of tower members with 100% loading.

Description	Member Specs	Case No.	Test Value (kN)	Calculated Value (kN)	Deviation
Ground support member	Q345 L110 × 10	Case 2	397.3	388.1	−2.4%
Cross-arm member	Q420 L220 × 2	Case 5	2014.6	2451.2	17.80%
Main member of the tower body	Q420 L200 × 24	Case 7	2094.8	2131.5	1.8%
Main member of the tower leg	Q420 L220 × 24	Case 7	2590.9	2740.0	5.4%

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Failure Analysis of Transmission Tower in Full-Scale Tests

Abstract

1. Introduction

2. Full-Scale Test

3. Finite Element Model of the Tower

4. Results and Discussion

4.1. Overload Case for Uneven Ice

4.2. Key Parts of the Transmission Tower

4.2.1. Tower Legs

4.2.2. Diagonal Members under the Tower Head

4.2.3. The Connection between the Cross-Arm and Tower Body

4.3. Displacement Analysis of the Transmission Tower

4.4. Tower Failure Analysis

4.5. Tower Force Analysis

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

Appendix A

References

Article Metrics

Citations

Article Access Statistics