Abstract
It has been recognized that one of the key issues in designing museums is the interaction between the layout of space and the layout of objects, and spatial configurations are strongly related to didactic narratives, social implications, and curatorial intentions. However, it has not yet been examined thoroughly how museums work from a spatial perspective. Apart from the layout of objects, spatial configurations play an important role in creating various walking sequences, ranging from main routes to auxiliary paths. Art museums in particular can be characterized by such deviations generated by the auxiliary path, but they are hardly understood from this aspect. Therefore, this study aims to explore the auxiliary paths and examine how they work through in-depth theoretical analysis based on space syntax. By analyzing four art museums in terms of isovist attributes, syntactic measures, spatial sequences, and possible trails, it has been concluded that in the cases of the Uffizi Gallery and the Moderna Museet, spatial sequences work conservatively, so that auxiliary paths are channeled back to the gathering space. This is because the walking experience is strongly correlated with visual syntactic features such as connectivity, integration, and intelligibility. Conversely, walking sequences in the case of the Centre Pompidou and the Alte Pinakothek work generatively, and auxiliary paths are rarely related to the gathering space because the walking experience is strongly concerned with visual geometric properties such as isovist area/perimeter and occlusivity.
1. Introduction
According to Macdonald, “collecting is fundamental to the idea of the museum,” and “the idea of the museum has become fundamental to collecting practices” (p. 81, [1]). Collecting is a kind of social activity of re-contextualizing objects; therefore, museums play a role in regulating, forming, or creating some kind of meaningful “whole.” On the basis of this conception, museum research has been conducted to identify types of collecting, analyze different motivations, examine collecting types in relation to social attributes, and explore the interaction between display layout and building morphology.
In terms of a museum’s morphological features, according to Pevsner, there has been an important change: collecting was usually displayed in either “centrally planned rooms” or “long galleries” until the 17th century, but from the 18th century, there was a strong tendency to set out collections in a spatial layout (p. 113, [2]): that is, the trend to “separate the types of items.” For example, L.C. Sturm suggested that an ideal museum is where “there are rooms for objects of natural history as well as one room on the top floor for small paintings, drawings and sculpture” (p. 114, [2]).
Regarding including and separating the types of items, one of the stereotyped museums was suggested through a series of museum competitions, such as the museums designed by Guy de Gisors and J.-F. Delannoy in 1778–79, E.-L. Boullée’s museum in 1783, or J.-M.-L. Durand’s design in 1802–09. These museums generally comprise a large square and set into the square is a Greek cross with four courtyards, with the four arms stretching out from a central “Pantheon rotunda” for works of art, natural history, a print room, and a library, etc. (pp. 118–123, [2]).
On the other hand, another stereotyped spatial morphology developed throughout museum history includes the Alte Pinakothek, designed by Leo von Klenze. The museum building is composed of a loggia, interfacing a series of many small rooms for displaying artworks on the one side, and leading outside to areas such as streets or gardens on the other side. Interestingly, the loggia provides access to all the small rooms, and it is somewhat limited for visitors to generate their own paths. This means that their movement is generated and controlled by the loggia. This may be termed as a lineally structured museum.
On the basis of this aspect, studies on museum architecture have focused on understanding museum space as a device for enhancing social interaction, shaping knowledge by classifying and arranging things, or creating a chronological sequence throughout the overall spatial organization [3,4]. Moreover, the space syntax community has focused on identifying the main dimensions of the variability of spatial layout and display strategies, proposing that both building and display layouts are intentionally designed not only to convey “a pre-given meaning” and reproduce “information” but also to create “possible meaning” and generate “a richer spatial structure” [5,6,7,8]. These theoretical aspects stress that there is a strong interaction between physical museum buildings and the process of collecting.
Thinking about the morphological features in terms of the walking experience, it has been suggested that a museum with traditional enfilades, such as Durand’s Museum, offers several equal alternatives for continuing the visitor’s route and, particularly, this spatial layout is often applied to museums that comprise different types of items or functions and deliver diverse themes. Thus, this type of museum does not need to have a long, narrow corridor. By contrast, a lineally structured museum, such as the Uffizi Gallery, the Alte Pinakothek, or the Moderna Museet, where spaces are rarely linked to one another but mostly adjoin with the loggia or corridor, creates a viewing order of items or themes, so that visitors might experience a single sequence along the loggia or corridor.
Brawne, however, has made an interesting point regarding the lineally structured museum: it provides auxiliary paths derived from the single main route [4]. This means that although the overall movement pattern is guided and even controlled by that single sequence at a global level, we can experience meaningful deviations in terms of walking sequences at a local level. Spatial experiences in this museum building could vary in terms of such auxiliary paths, and therefore such experiences could be a cumulative understanding of the form of the auxiliary paths.
However, it is not clear yet in what way those auxiliary paths form, how they are related to the main route, nor to what degree they are different from each other. Hence, this study particularly focuses on exploring and examining the auxiliary paths in lineally structured museums through in-depth theoretical analysis by using the space syntax technique; especially prominent art museums were analyzed to answer these questions.
2. Museum Studies
It has been recognized that one of the key issues in designing museums is the way the layout of space interacts with the layout of the objects [5] and, consequently, many researchers suggest that the spatial configuration provides “a structure of the exploitation of the collections and buildings by visitors” [9,10]. Others go even further to say that a visitor’s experience in the museum is closely related to three elements: “didactic narratives, the ambient experience of the wealth of a collection including the richness of its architectural exposition, and the opportunities for social interaction afforded by the environment” [11].
Huang also suggested two key ideas in understanding museum buildings: “organized walking” (i.e., spatial sequences), which can lead to the process of constructing disciplinary knowledge throughout the plan and “a gathering space”. By studying modern museums in Europe, he contends that there is “an underlying genotypical conflict between the need to congregate people and the need to organize their movement,” and this genotypical conflict works as a bias in characterizing “the spatial types of the modern museum” [6].
Duncan and Wallach, conversely, highlighted the significance of totality in the museum experience, created by installations, the layout of exhibition rooms, and the sequence of collections. Particularly, they thought that the totality of art and architectural form makes visitors organize their museum experience as an “architectural script” [7].
Regarding the importance of spatial arrangement in museum architecture, Brawne stressed intelligibility, which means clarity and a sense of the order of the spatial layout [4]. In museums, spatial experiences tend to be determined by viewing images in sequence. This means that the museum experience is very similar to the experience elsewhere in a building or a town, and, in this perspective, Brawne transposed Lynch’s five elements (paths, edges, districts, nodes, and landmarks) into a way of comprehending spatial experiences.
Psarra and Grajewski raised a fundamental question of how visitors understand museum buildings through movement, and defined museum buildings as systems of spaces that are seen sequentially through movement, and also as overall conceptual patterns that can be grasped at once. Based on these definitions, they suggested that experiencing buildings involve both levels of understanding: the architectural promenade and the conceptual structure [12]. In addition, Psarra, Wineman, Xu, and Kaynar argued that built space is understood as a relational pattern: a pattern of “distinctions, separations, interfaces, and connections”, and a pattern that “integrates, segregates, or differentiates its parts in relation to each other” [13].
Salgamcioglu and Cabadak questioned whether the type of space, particularly a permanent or temporary one, affects a visitor’s behavior in relation to objects and spatial configuration, and found a substantial distinction between permanent and temporary museum spaces: in permanent exhibitions, the visitor’s behavior is influenced by the interfacing between interior and exterior space, whereas in temporary cases, artworks are a crucial parameter, affecting the behavior [14].
Hence, it can be said that museums, especially in the layout of space, provide somewhat different and distinct experiences by utilizing spatial arrangements, and it might be argued that, apart from the idea of the strong relationship between spatial layout and display layout, spatial arrangements themselves play a decisive role in structuring the museum experience. However, it has not yet been examined in what way and how distinctly the spatial arrangements work. Thus, this paper specifically aims to explore and discover substantial answers to these theoretical questions.
3. Research Methodologies and Cases
3.1. Research Methodologies
With these questions, the cases were analyzed by the following methodologies: visibility graph analysis (VGA), spatial sequence generated by c-sequence length and c-sequence depth, spatial choice by d-ring, and possible trails.
Visibility graph analysis, as one of the primary techniques in space syntax, has been derived from Benedikt’s isovist and developed by the space syntax community. An isovist is defined as “the set of all points visible from a given vantage point in space” (p. 47, [15]), but it is not appropriate to assess the whole spatial layout of buildings because its geometric properties, such as the isovist area, perimeter, or shape, are purely local features of the viewpoint. Additionally, those properties miss the relationship between the viewpoint and the whole spatial environment. To overcome these problems, the space syntax community suggests VGA, which first sets out a grid (normally 0.6 or 1.0 m) throughout the spatial layout, and each one of the grid points is used as a viewpoint. After having completed this step, the VGA analyzes the relationship between a certain point and the others in both a geometric and a syntactic way using the depthmap X program (depthmapX-0.8.0_win64 version).
Geometrically, the isovist area is a measure of how much space can be seen from a given viewpoint and, conversely, how much the viewpoint can be seen from it; the perimeter is the perimeter of the isovist polygon; the compactness is a measure of the shape of the isovist (i.e., simple or complex, symmetrical or asymmetrical), so that the closer the isovist is to a circle, the more its compactness approaches a maximum value of 1; the occlusivity refers the occlusivity of the isovists, by measuring the length of the occluding radial boundary based on the perimeter of the isovists, and indicating “the depth to which environmental surfaces are partially covering each other as seen from the vantage point” (p. 53, [15]); and, lastly, the area/perimeter is obtained by the area to perimeter ratio, and it can be described as an adjective measure of “how ‘spiky’ or conversely how ‘rounded’ an isovist is” (p. 154, [16]).
In space syntax theory, spaces can be represented in two ways: depths and rings. Depth is the idea of how deep or shallow a given spatial structure is, and this conception is explained by connectivity, integration, and mean depth. The connectivity is meant to be the total number of direct connections to the other elements from a certain one at a local level; the integration, unlike the connectivity, is a measure of how many elements are related to the whole; and the visual mean depth is the average distance from each element to all elements within the spatial structure. Syntactically, therefore, VGA analyzes the visual connectivity as a local property, the integration as a global feature, and the mean depth. Additionally, we can identify how intelligible or understandable the spatial layout is by the correlation between visual connectivity and integration.
Contrary to the depths, the idea of rings is derived from two kinds of behavior: “occupation,” which happens in a convex way, and “movement,” which, conversely, occurs linearly. With these conceptions, spaces are defined as four different types (Figure 1a): an a-space is a space with a single link, and a b-space is one with more than one link, but it should be a part of “a connected sub-complex in which the number of links is one less than the number of spaces”, so that it is “on the way to (and back from) at least one dead-end space”; a c-space is one with “more than one link which form a part of sub-complex” containing neither a-space nor b-space, and it should lie on a single ring. Lastly, a d-space is the space with “more than two links,” which form a part of complexes containing neither a-space nor b-space, and it must lie on at least two rings (pp. 250–251, [17]).
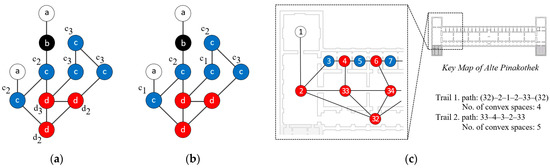
Figure 1.
(a) example of c-sequence length and d-ring with space types of a-space (white), b-space (black), c-space (blue), and d-space (red); (b) example of c-sequence depth with space types; (c) example of possible trails in the Alte Pinakothek Museum.
Considering these four types of space, it is certain that a-space and b-space are strongly related to occupational activities, whereas c-space and d-space are involved in the overall movement patterns (pp. 296–298, [8]). Theoretically, it can be said that c-spaces are concerned with specifying sequences and producing structured movement patterns, so that this kind of spatial layout works conservatively. Hence, from the conception of the c-spaces, it can be possible to explore how strongly spaces are framed with “the degree of sequence which is constructed by the pattern of c-spaces” ([5,8,18]). The length of the sequence is numerically indexed and described by the c-sequence length (Total) and c-sequence depth (Total). First, the value of the c-sequence length (Total) tells us “how many spaces form the c-sequence”, while the number of the c-sequence depth (Total) indicates “the depth into the c-sequence” ([5,18]). For example, there are five c-spaces in Figure 1a. Two of them are placed on one ring, constituting two c-spaces and two d-spaces. On this ring, people should pass through two c-spaces in order to finish their journey, so these c-spaces are labelled ‘c2’; that is, a sequence of two spaces without choice on the path. Similarly, the other c-spaces on the other ring are labelled ‘c3’, meaning a sequence of three spaces without choice. When we add all c-spaces together, we can account for the c-ness in this layout (i.e., the c-sequence length (Total): 13; c-sequence length (Mean): 2.6 = 13/5). In a similar way, we can also calculate the c-sequence depth (Total). For example, the two c-spaces in the ring are labelled ‘c1’ and ‘c2’ (Figure 1b). On the other ring, the c-spaces are labelled ‘c1’, ‘c2’, and ‘c3’. When we add the number of the c-spaces together, we can determine the depth of the c-sequence in this layout (i.e., the c-sequence depth (Total): 9; the c-sequence depth (Mean): 1.8 = 9/5).
On the other hand, d-spaces minimize those sequences, leading to the creation of many different paths, so that this layout acts in a generative way. With the idea of d-spaces, it can be examined “to what degree the spatial system allows us to take alternative routes”, and, thus, the choices are measured by the pattern of d-spaces. Similar to the c-sequence, we can index d-spaces according to the number of rings they are on. For example, there are three d-spaces in Figure 1a: one of them has three rings, and it can be labelled ‘d3, while the others have two rings, so that they are labelled ‘d2’. When adding the numbers together, we can determine the amount of rings (i.e., the d-ring (Total): 7; the d-ring (Mean): 2.3 = 7/3).
With these conceptions, the spatial sequence of a layout can be described by the c-sequence length and the c-sequence depth, whereas the choice of the layout can be illustrated by the d-ring. It should be noted that the terms of spatial sequence and choice used here are not actual but theoretical.
The possible trails, according to the previous methodology, are created with the following rules. All trails should start from d-spaces, pass through a-/b-/c-spaces, and end at d-spaces where the trails begin. The trail should form a single ring. In Figure 1c, for example, two possible trails can be drawn from the case of the Alte Pinakothek. Trail 1 starts from 32, representing the loggia; passes through 2, 1, 2, and 33, and then ends at 32 so that the path of Trail 1 is 32-2-1-2-33-32. Trail 2, however, starts from 33, passes through 4, 3, and 2, and then returns to 33. After having constructed the trails, each trail is calculated by the average VGA values in a geometric (e.g., the isovist area, perimeter, compactness, occlusivity, and area/perimeter) and a syntactic way (e.g., connectivity, integration, and mean depth).
The reason for constructing these possible trails is to explore how many trails starting from the d-spaces can be constructed, to identify to what extent they are distinct in terms of walking sequence and walking choice, and finally in what way the galleries are spatially distinct.
3.2. Cases
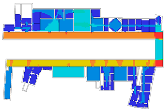
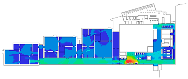
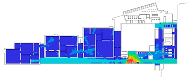
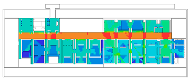
Four galleries were chosen as case studies: the Uffizi Gallery, the Alte Pinakothek, the Museum of Modern Art at level 5 of the Centre Pompidou, and the Moderna Museet. (Figure 2). The Uffizi Gallery, designed by Giorgio Vasari and then developed by Alfonso Parigi and Bernado Buontalenti, was originally designed to be an administrative office, but it was gradually transformed into a museum to house the Medici family’s art collections. One interesting point is that its edges against the adjacent buildings are very irregular. However, the loggia, which is the most dominant gathering space in this building, presents a powerful geometric shape, and it leads to gallery spaces in different shapes such as square, rectangle, octagon, oval, and polyhedron. Another interesting point is the arrangement of gallery spaces: for example, some galleries are arranged linearly so that visitors can cross the thresholds between gallery halls without going back to the loggia, but some others return visitors to the loggia.
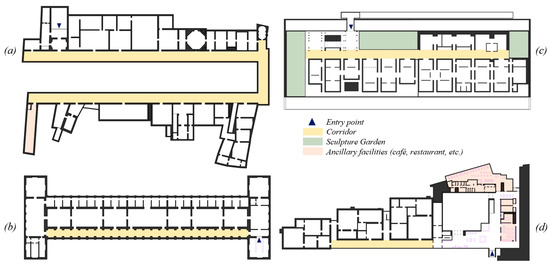
Figure 2.
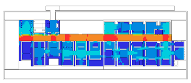
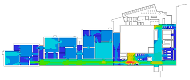
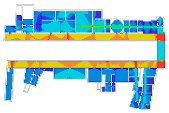
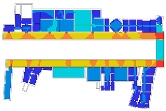
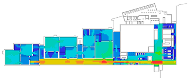
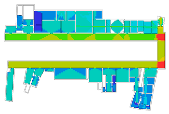
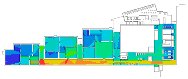
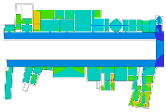
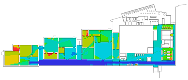
Cases: (a) second floor plan of the Uffizi Gallery in 2018, Italy; (b) second floor plan of the Alte Pinakothek in 1836, Germany; (c) fourth floor plan of the Centre Pompidou in 1977, France; (d) third floor plan of the Moderna Museet in 1998, Sweden.
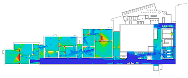
The Alte Pinakothek, designed by Leo von Klenze and opened to the public in 1836, was built for displaying pictures only in Berlin. One of the remarkable features of this gallery, as we can see in the Uffizi Gallery, is the loggia, which plays an important role in providing and controlling access to the middle gallery halls for large paintings, and also to the twenty-five cabinets located in the northern part of this building to hang small paintings on the wall (pp. 129–130, [2]).
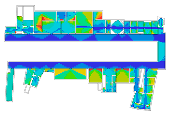
The Museum of Modern Art is located in the Centre Pompidou, designed by Richard Rogers and Renzo Piano. With the architectural conceptions of flexibility, transparency, and openness, any architectural elements or utilities are intentionally absent, and consequently, the interior space does not have any partitions or other vertical interruptions. However, the grand space had to be articulated by movable panels, placed in clusters, or dispersed in space. Particularly, the first transformation in 1974 was performed by the director of the museum, P. Hulton, to create “a spatial structure that resembles a city, with interlocking spaces, squares, paths and dead-ends” (p. 253, [5]). In 1985, the second transformation was introduced by G. Aulenti, with the idea of placing “the longitudinal and the transversal axes” across the floor plan and creating “room-like spaces that referred to the spatial conditions where the art of the first half of the twentieth century was conceived and to the domestic setting of private collections” (p. 256, [5]). One of the fascinating things from the transformations is that the long corridor leads us to such diverse urban-like elements. This space plays a role in providing access to gallery spaces, integrating spatial movements, and overlooks the outside of the building. More interestingly, the gallery spaces are grouped in several distinct ways and, as a result, substantial auxiliary paths are formed, although the movable panels are regularly placed.
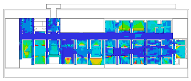
Lastly, the Moderna Museet, designed by Rafael Moneo and opened in 1998, is located on the island of Skeppsholmen in Stockholm. The museum brings together different collections in the building, such as Swedish artworks, the traditional avant-garde pieces, and the outstanding works of the classical modern period and later on of the New York school. One of the interesting characteristics is found in its spatial layout: an over 100-m-long corridor forms “the spine of the whole complex” and provides access to “the three clusters of museum galleries” and a temporary exhibition room near the main entrance (p. 69, [19]). This corridor plays a pivotal role in giving visitors a chance of choosing one of the clusters and in comprehending the spatial structure as a whole. The other particular characteristic is the clusters. There are three clusters, and each one is composed of six to seven gallery rooms that vary in size. Interestingly, all clusters have dead-end small gallery rooms similar to cabinets, so that it is possible for visitors to gain distinct experiences, not only through the serial gallery rooms, but also the clusters.
As we have discussed, these museums are understood to be representative of linearly structured museums: The Uffizi Gallery has a relatively long history as an art museum, and the outer edges in particular are irregular in form because of the adjacent buildings, but the loggia acts as an integral gathering space and provides access to the entire gallery space. We assumed that the spatial layout of the Alte Pinakothek might have been influenced by that of the Uffizi Gallery, as it has the same spatial structure, meaning that the loggia controls the overall accessibility to large gallery halls, but the halls, conversely, provide additional spatial sequences, leading to the cabinets located in the deepest part. The Museum of Modern Art in the Centre Pompidou, originally designed as an open multipurpose space, has been transformed into subdivided gallery spaces by placing partitions, but one of the interesting things is that the corridor, like a loggia, controls all access to the subdivided spaces and, unexpectedly, some extra sequences are discovered. The Moderna Museet also has a corridor giving access to three clusters, but the clusters do not lead to other spatial sequences.
4. Syntactic Analyses and Discussions
In this chapter, the cases have been explored quantitatively by space syntax techniques such as space types, spatial sequence and choice, isovist geometric features, and isovist syntactic properties. Then, possible trails derived from the cases have been theoretically examined to understand in what way the spatial configurations work distinctly and to what degree they are different.
4.1. Space Types, Walking Sequence, and Walking Choice
Table 1 shows the basic profiles of the four galleries. The Uffizi Gallery (UG) is composed of 53 convex spaces in total, and 41 are gallery halls (Figure 3). Regarding space type, the most prominent one is c-space (ratio: 0.55), and the others are a-space (0.19), d-space (0.17), and b-space (0.09) in sequence. In the Alte Pinakothek (AP), there are 39 convex spaces in total, and most of them (37 out of 39) are used as gallery halls. Concerning space type, the ratio of c-space (0.46) is very close to the ratio of d-space (0.44), and the others are a-space (0.08) and b-space (0.03). The Museum of Modern Art in the Centre Pompidou (CP) has a total of 67 convex spaces, which are defined, and 44 of them are designed for gallery space. Similar to the AP, both c-space and d-space are salient, 0.39 and 0.30, respectively, and the others are a-space (0.28) and b-space (0.03). Finally, in the Moderna Museet (MM), there are 36 convex spaces in total, and 20 spaces are used for exhibiting artworks. In this layout, the ratio of c-space is 0.44; a-space is 0.25; d-space is 0.17; and b-space is 0.14.

Table 1.
Summary of basic profiles, space types, c-sequence length, c-sequence depth, and d-ring of the cases.
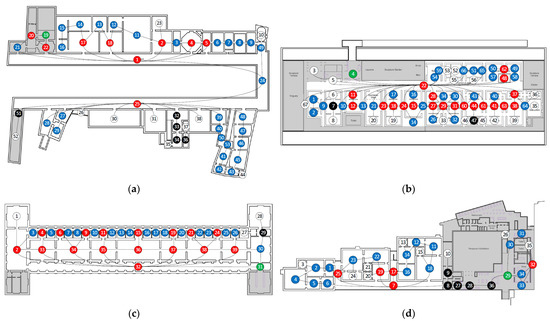
Figure 3.
Space type analysis of the cases, and numbers indicate convex spaces: (a) Uffizi Gallery; (b) Alte Pinakothek; (c) Centre Pompidou; (d) Moderna Museet.
Let us look into where these spaces are placed across the plans. In the UG, except for the ancillary facilities, d-spaces are discovered in the loggia (e.g., Nos. 1 and 25) and five gallery spaces (e.g., Nos. 17, 18, 2, 4, and 5). The others are a-/b-/c-spaces. Interestingly, some a- spaces (e.g., Nos. 26, 30, 31, and 38) are directly connected to the loggia. In the AP, the spaces placed in two southern strips (i.e., the loggia and the large gallery halls) are d-spaces. By contrast, the northern strip has mostly c-spaces. Only the two wings on both sides marginally have a-/b-spaces. Unlike the case of the UG, a-spaces are placed in the most remote area from the loggia. In the CP, spaces are arranged similarly: the main corridor (i.e., No. 22) is a d-space; the gallery spaces located on the southern side are c-/d-spaces; similar to the AP, a-spaces are placed along the southern edge of the plan, whereas some a-spaces on the northern side have a direct connection to the main corridor. The MM seems to be similar in that the main corridor (i.e., No. 7), comprising three convex spaces (i.e., Nos. 7, 17, and 25), is defined as a d-space; the clusters are combined with mainly c-spaces and occasionally a-spaces and a d-space.
Considering these basic profiles and arrangements of space type across the plans, we go further and look into the ratios of c-space and d-space, which are simply obtained by dividing the ratio (or the total number) of c-space by that of d-space. In Table 1, the UG has the highest ratio: 3.22, whereas the AP has the lowest ratio: 1.06. Regarding walking sequence and choice, as expected, two extremes can be defined from the cases: the values of c-sequence length (M) and c-sequence depth (M) in the UG (6.37 and 3.68, respectively) and the MM (3.87 and 2.43) are higher than those in the AP (2.11 and 1.55, respectively) and CP (1.76 and 1.38). Particularly, the UG’s length of the spatial sequence is two to three times longer than the others, and its depth is most three times deeper.
This tendency appears in a contrasting way on spatial choice: the value of the d-ring (M) of the AP (3.17) and the CP (2.85) are higher than those of the UG (2.42) and the MM (2.33). However, this result is not quite as great as that of the spatial sequence. This means that although the UG seems to have a strong linear spatial structure, it provides a small number of auxiliary paths starting from gallery spaces Nos. 17, 18, 2, 4, and 5.
From these results, it could be argued that gathering spaces such as loggias and corridors play an essential role in constituting the main sequences throughout spatial layouts. However, the two cases of the AP and the CP show distinctive features in that the halls, placed one step deeper from loggia and corridor, act as extra gathering spaces. This means that they work as key spaces for auxiliary paths at a local level within the main sequence. This characteristic has an impact on those two cases. However, the gathering spaces in both the UG and the MM work as the most powerful spaces constituting and controlling the whole sequences.
Unlike the cases of the AP, the CP, and the MM, the gathering spaces in the UG are connected directly to all different space types: for instance, No. 1 connects to c-spaces and d-spaces, and No. 25 connects to a-spaces, b-spaces, and c-spaces. Such connectivity to various space types leads us to unexpected walking sequences: sometimes the sequence ends in a single convex space (e.g., 25-30, 25-31, or 25-38), it lies on a relatively long sequence (e.g., 25-48-47-46-45-43-42-41-53-50-40-39-25), it provides an auxiliary path (e.g., 1-2-11-13-18-1 or 1-2-3-4-1), or it creates a backward sequence (e.g., 25-32-33-34-35-34-33-32-25). This can be discovered in the case of the CP, but it does not extend to the whole spatial layout. Thus, it can be argued that although the spatial layout of the UG seems to work conservatively due to the high value in c-sequence length (M), it provides diverse spatial experiences such as new paths or strongly ordered paths, dead ends, and enclosed spaces.
4.2. Visibility Graph Analysis
4.2.1. Visibility Graph Analysis in Terms of Geometric Measures
To what degree, then, are those spatial experiences regarding spatial sequence and choice differentiated from each other? To answer this question, we focus on looking into the geometric and syntactic results of VGAs (Table 2).

Table 2.
Syntactical result of VGAs of the cases.
As one of its geometric properties, the UG has the highest value of isovist areas (mean value of 395.65), whereas the CP has the lowest (296.20). Looking at the result of the isovist perimeter, however, the UG has the lowest value (mean value of 160.63), whereas the AP has the highest (190.75). The reason that the UG has contrasting results concerning isovist area and perimeter can be understood by noting that the u-shaped loggia, compared with the gallery halls, is composed of three huge convex spaces and a great number of viewpoints can be constructed. This means that the viewpoints in such simple and large convex spaces are easily visible. However, when looking at the isovist perimeter, one of the significant points of difference between the UG and the AP is the fact that cross-visibility in the UG hardly takes place between the loggia and the gallery halls and between the gallery halls, but in the latter case, it occurs quite easily, not only across the three parallel strips but also between the gallery halls, especially when the longest perimeters of the isovist polygon are measured along with the straight doorways in the strips.
Next, concerning the compactness of the isovist, as expected, there is a strong pattern in terms of shape: the a-/b-space is simpler and more symmetrical because its isovist polygon forms in a compact way, whereas the c-/d-space is more complex and asymmetrical because it has at least three links or, at most, a huge number of links, and these links make the isovist shape more complex, similar to a star shape. Thus, the compactness value of the isovist in the case of the UG (mean value of 0.25), where the a-/b-space is adjacent to the gathering space is higher than the others. Conversely, the AP and the CP, in which it is placed far from the gathering space, have a low mean isovist compactness value (both mean values of 0.17).
It might be said that the isovist occlusivity is one of the most fascinating measures in the geometric analysis because, as mentioned before, it tells us how previously unseen space, covered by any environmental elements, is discovered during movement ([18]). From the occlusivity analysis, it is quite obvious that the UG has the lowest value (mean value of 34.55), but the AP has the highest (123.42). The others, the CP (83.46) and the MM (83.23), are positioned in the middle of them. However, when we look closely at the result again, it is quite surprising that occlusive patterns are identified in the UG; for instance, the occlusive edges form in different ways: some of them at around Nos. 17 and 18 are configured diagonally; some galleries, Nos. 2, 3, 4, 5, 6, 7, 8, and 9, construct the occlusive edges linearly; or galleries such as Nos. 39, 40, 50, 53, 41, 42, 48, 47, 46, 45, and 43 have edges perpendicular to the loggia. Conversely, in the CP, the edges, particularly in the room-like spaces, are formed diagonally. However, the result of the MM is comparatively different from that of the CP, although the average value of the isovist occlusivity is quite similar to that of the CP. This is because the highest values are primarily found in the main corridor of the MM, but the occlusive edges do not extend to the gallery halls. This means that it is hard to expect dramatic visual changes in the clusters.
4.2.2. Visibility Graph Analysis in Terms of Syntactic Measures
Now we move on to the syntactic analysis of the VGA. In terms of connectivity as a local property, the UG shows, comparatively, the greatest mean value (396.31), whereas the MM has the least mean value (280.36). Regarding integration as a global feature, the UG has the lowest mean value (9.93), whereas the AP has the highest (6.34). From these two measures, it should be pointed out that a significant visibility shift is discovered in the case of the AP: the highly visible viewpoints at the local level are found in the loggia at the local level; however, the highly integrated viewpoints at the global level are in the large gallery halls in the middle strip. This means that the loggia in the UG works very well locally, but it does not make visitors comprehend the whole system globally. Conversely, the long lines of sight, which derive from the aligned doorways of the large gallery halls in the AP, make the whole spatial system more comprehensible and readable, although the loggia is intentionally designed to provide access to the gallery halls. In the other cases, concerning the CP and the MM, the main corridors work globally and locally as well.
Regarding mean depth, it is found that the UG has the highest mean depth value (a mean value of 3.70 and a maximum value of 6.79), but the AP has the lowest one (a mean value of 2.52 and a maximum value of 3.63).
4.2.3. Correlation between Space Types, Walking Sequence and Geometric Measures
Is there any possible correlation between the result of space types and the VGAs? If there is, what kinds of space types are strongly correlated with the geometric and syntactic properties? For this, a correlation analysis was performed. The data used in the correlation analysis are the basic profiles of the cases, such as the ratio of a-/b-/c-/d-space, the c-/d-space ratio, c-sequence length (M), c-sequence depth (M), and d-ring (M) defined in Table 1. Geometric measures of VGA analysis such as the mean value of the isovist area, perimeter, compactness, and occlusivity, and syntactic values of VGA, such as the mean value of the visual connectivity, integration, and mean depth are described in Table 2. It should be noted that the reason for carrying out the correlation analysis is to explore the relationships between space types, c-sequence, d-ring, geometric attributes, and syntactic features of the cases, and statistically explain how much the cases are different.
In Table 3, strong relationships can be seen between spatial sequences, choices, and the geometric measures of isovists. The isovist area is related to the values regarding c-space: for example, the r2 value of the area to c-space ratio is 0.875, to a c-sequence length (M) of 0.811, and a c-sequence depth (M) of 0.811. The isovist compactness is even more strongly related to these values: the correlation of the compactness with a c-/d-space ratio, which has an r2 value of 0.983, with a c-sequence length (M) of 0.999, and with a c-sequence depth (M) of 0.999.

Table 3.
Correlation matrix between space types, c-sequence length, c-sequence depth, d-ring, and VGA.
However, the other two geometric measures are opposed: in terms of the perimeter, they are correlated with d-space ratio and d-ring (M), r2 values of 0.757 and 0.735, respectively. Moreover, the isovist occlusivity is likely correlated with a d-space ratio with an r2 value of 0.775, but there are negatively related with the occlusivity and the c-/d-space ratio, with an r2 value of −0.812, a c-sequence length (M) of −0.724, and a c-sequence depth (M) of −0.726.
From those contrasting correlation results, the higher the ratio of c-space and c-/d-space, the greater the value of isovist area and compactness are. At the same time, the higher the ratio of d-space, the greater the value of isovist perimeter and occlusivity will be. Thus, a spatial layout where d-spaces are mainly occupied means that we are able to achieve not only open spatial relationships, but also rich cross-visibility through spaces that are particularly spiky, allowing “glimpses of other spaces past occluding surfaces” (p. 158, [19]).
These analyses once again strongly support the contention that both c-space and d-space play a decisive role in determining in what way spaces are related to each other, to what degree they are differentiated from one another, how strong or weak the spatial sequence is, and how distinctive spatial configurations are experienced globally or locally.
4.2.4. Correlation between Space Types, Spatial Sequence and Syntactic Measures
When we correlate syntactic values (e.g., visual connectivity, integration, and mean depth) with the types of space (Table 3), it is quite clear that the spatial layout of the UG, representing the highest ratio of c-space and the lowest of d-space, has a strong relationship between the visual connectivity and c-space ratio, c-sequence length (M), and c-sequence depth (M) with r2 values of 0.746, 0.658, and 0.659, respectively. By contrast, in the case of the AP, described by the highest ratio of d-space and the lowest c-/d-space ratio, there are strong relations between the visual integration and the d-space ratio (r2 value of 0.990) and the d-ring (0.947). There are meaningful correlations between the integration and the spatial sequence, but these are negatively related to c-sequence length (M), with an r2 value of −0.573, and to c-sequence depth (M), with that of −0.574.
Another strong relationship exists between the visual mean depth and the values regarding d-space: c-/d-space ratio with an r2 value of 0.817, c-sequence length (M) with 0.685, and c-sequence depth (M) of 0.687. Interestingly, the value of the c-space ratio is not likely to be related to the mean depth. To the values regarding d-space, the relationships are negatively related to the visual mean depth: −0.991 for the d-space ratio and −0.910 for the d-ring (M).
These syntactic measures, contrary to the geometric ones, are not properties of an individual isovist, but they are properties of the isovist’s relation to all other isovists in the spatial system, so that the syntactic measures explain the overall structure of the building. From this conception, it can be suggested that c-space creates locally rich spatial sequences but leads to a less integrated spatial system; d-space, however, provides fewer spatial sequences but allows generating different movements, and consequently, it minimizes depths and makes the spatial system more integrated.
4.3. Examining Possible Paths
As mentioned before, possible trails based on the conception of walking sequence and choice were suggested to determine in what way the galleries are differentiated from each other and how distinctive spatial configurations are experienced. For this, possible trails were generated, starting from and ending at one of the gathering d-spaces allowing the possibility of different paths.
In the UG, a total of 13 trails are defined (Table 4) and they can be divided into two groups. The first group is the one that the trail starts from and ends at convex space No. 1: for example, trail 1 consists of a total of six convex spaces, excluding gathering convex space No. 1, with the string of (1)-18-12-11-2-23-2-(1); Trail 2 consists of three convex spaces, (1)-2-23-2-3-4-(1); trail 3 consists of two convex spaces, (1)-4-5-(1); trail 4 consists of five convex spaces, (1)-5-6-8-9-49-24-(1); trail 5 consists of three convex spaces, (1)-18-13-17-(1); and trail 6 consists of five convex spaces, (1)-17-14-15-16-17-(1). At the same time, the second group is the trails that set out from convex space No. 25, running parallel to convex space No. 1. Trail 7 is composed of 13 convex spaces with the string of (25)-48-47-46-45-43-44-43-42-41-53-50-40-39-(25); trail 8 consists of one convex space, (25)-38-(25); trail 9 consists of 11 convex spaces, (25)-32-33-34-36-37-36-34-35-34-33-32-(25); trail 10 is composed of one convex space, (25)-31-(25); trail 11 consists of one convex space, (25)-30-(25); trail 12 also consists of one convex space, (25)-26-(25); and trail 13 is composed of three convex space, (25)-27-29-28-(25). What is interesting in these defined possible trails in the case of the UG is the fact that convex space No. 1 leads to more or less moderate lengthy trails, but convex space No. 25 allows for extreme spatial sequences: simple experiences vs. lengthy and complex ones.

Table 4.
Possible Trails and syntactic properties in the Uffizi Gallery.
In the case of the AP, a total of 17 possible trails can be identified (Table 5). However, it should be noted that there is a significant difference between them. Having seen the trails, the first group of trails, Nos. 1–8, form one of the main sequences, meaning that the trail starts and ends in the gathering space so that these trails form the main sequences. By contrast, the other trails, such as Nos. 9–17, begin at one of the large gallery halls, such as convex spaces Nos. 33, 34, 35, 36, 37, and 38, instead of the gathering one, forming auxiliary paths. One of the distinctive characteristics of the main sequences compared with the auxiliary paths is the length of the spatial sequence.

Table 5.
Possible Trails and syntactic properties in the Alte Pinakothek.
Regarding the main sequences, for instance, the trails, except for Nos. 1 and 8, comprise two convex spaces. The others represent diverse stories: for example, trail 9 begins at one of the large gallery halls (i.e., convex space No. 33), passes through two cabinets (i.e., convex spaces Nos. 4 and 3), and then ends at the start; trails 10, 11, 12, 15, and 16 show identical sequences, starting from the large gallery halls, going through three cabinets and one large gallery hall, and ending at the start; trails 13 and 14, similarly, begin at one of the large halls, going through five cabinets, and returning to the starts; and trail 17 is somewhat different in that there is a retreat due to the dead-end a-space (i.e., convex space No. 27).
In the CP (Table 6), a total of 28 trails are produced. Similar to the case of the AP, the trails can be grouped according to whether the gathering space is included in spatial sequences or not. Hence, the first group is the one in which trails begin and end at the corridor, whereas the other is the one that begins at one of the d-spaces used for gallery halls. There is a total of 21 trails (i.e., trails 1–21) and all of them start from and end at the corridor through a series of gallery halls. In terms of the length of sequences, trails 1, 17, and 19 have the shortest length as they comprise a single convex space, except for the gathering space (i.e., convex space No. 22). By contrast, trails 3, 14, and 15 are explained comparatively as one of the longest trails. The others are sequenced in a series of two, three, four, or five convex spaces. Regarding auxiliary paths, a total of seven trails are defined. Interestingly, five of them are the ones that begin at the gallery spaces: for example, trail 22 starts from the convex space No. 41, continues through 42, 41, 40, and 63, and returns to the start; trails 24, 25, 26, and 27 begin and end at the convex space No. 29 via 26, 27, 30, 31, or 32. By contrast, the other two auxiliary paths trails (i.e., trails 23 and 28) start from and terminate in secondary corridors such as convex space Nos. 24 and 60, passing through galleries such as 14, 15, 25, 43, 44, 45, 46, or 47.

Table 6.
Possible trails and syntactic properties in the Centre Pompidou.
Lastly, in the case of the MM, three possible trails are defined, and all of them are rooted in the gathering space (Table 7). Specifically, trail 1 is made up of seven gallery spaces, excluding the spaces used for the gathering purpose, with the string of (7)-6-5-4-2-3-2-1-(25)-(7). The others, trails 2 and 3, are composed of nine galleries with the strings of (7)-(25)-23-24-23-22-21-22-19-20-19-(7), and (7)-18-15-18-11-12-14-13-14-16-(17)-(1).

Table 7.
Possible Trails and syntactic properties in the Moderna Museet.
5. Discussion
From these results, it is unclear if the trails are somehow related to particular spatial sequences or choices. For instance, although a total of 13 trails in the UG are conceived, it has a low ratio in d-space (0.17) and the highest ratio of both c-space and c-/d-space (0.55 and 3.22, respectively). The AP has the highest ratio of d-space (0.44) with the lowest c-/d-space ratio (1.06), and a total of 17 trails are defined. The CP, however, has a somewhat lower d-space ratio (0.30) with a moderately lower ratio of c-/d-space (1.30), but at 28 trails, the greatest numbers among the cases are identified. Lastly, the MM has a low d-space ratio (0.17) with a comparatively higher ratio of c-/d-space (2.67), but it only has three trails.
Nevertheless, there is one significant finding from the possible trails. That is, the trails delineated in both the UG and the MM are strongly related to one of the gathering spaces (i.e., the loggia in the UG and the main corridor in the MM), so that all trails are main sequences, meaning that spatial sequences are closely associated with the gathering spaces. Hence, it can be said that the gathering space plays an essential role in providing variant spatial sequences: sometimes the sequence is very short and simple such as in trails 8, 10, 11, and 12 in the UG, and at other times, it is very long and complex such as in trails 7 and 9 in the UG and the trails in the MM.
In both the AP and the CP, however, trails are categorized into two groups, namely, main sequences and auxiliary paths, indicating that trails begin not at the gathering space but at one of the d-space gallery halls. For instance, more than half of the trails in the AP (i.e., nine out of 17) belong to auxiliary paths, therefore the large gallery halls running along the middle “strip” play an additional role in providing unexpected paths leading to cabinets, which are situated in an area of the gallery that is furthest away from the gathering space. Similarly, seven auxiliary paths in the CP allow extra journeys, and convex space No. 29, in particular, acts as a nodal point for providing diagonal experiences.
The conception of the main sequence and auxiliary paths is strengthened by the result of visual mean depth. In Table 2, the average value of visual mean depth in both the UG and the MM is relatively higher than that of the AP and the CP. This means that the d-space gallery halls, which are placed a step away from the gathering space, provide unforeseen journeys and also decrease the depth.
In what way, then, do they differ? To answer that question, a box and whisker plot was constructed to investigate the trail’s differences in terms of the isovist area, isovist compactness, isovist occlusivity, isovist perimeter, isovist shape (area/perimeter), and visual mean depth (Figure 4). The findings are summarized as follows:
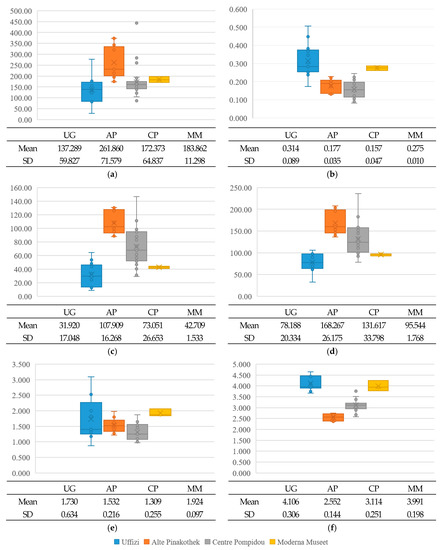
Figure 4.
Box and whisker plot for the possible trails: (a) isovist area; (b) isovist compactness; (c) isovist occlusivity; (d) isovist perimeter; (e) isovist area/perimeter; (f) isovist mean depth.
- Regarding the isovist area, it is certain that the values for the trails of the AP are significantly higher than the others, and they are also widely distributed: mean = 261.860, SD = 71.579, p < 0.001. By contrast, the values for the UG are lower than the others: mean = 137.289, SD = 59.827.
- In terms of the isovist compactness, the values for the trails of the UG (mean = 0.314, SD = 0.089, p < 0.001) are significantly higher than the others. By contrast, the values for the AP and the CP are lower. Hence, it can be explained that the shapes of isovists in the UG are comparatively simple and symmetrical, but in the cases of the AP and the CP, they are complex and asymmetrical.
- With the isovist occlusivity, the values for the trails of the AP (mean = 107.909, SD = 16.268, p < 0.001) are significantly higher than the others. However, when we look more closely into the values for the CP, it is quite interesting that the values of the trails are evenly distributed beyond the lower and upper quartiles. This means that the trails are strongly associated with the occlusive lines. Therefore, it can be said that, although the mean value of the CP is neither higher nor lower, the occlusivity is considered one of the key aspects in describing its configurational features.
- Considering the perimeter, it is definite that the values for the trails of the AP (mean = 168.267, SD = 26.175, p < 0.001) are significantly higher than the others. By contrast, the values for the UG are lower than the others.
- In terms of the isovist shape, defined with the division of the isovist area by the isovist perimeter, the values for the trails of the MM are significantly higher (mean = 1.924, SD = 0.097, p < 0.001), so it can be said that the isovist shape is likely rounded. By contrast, the values for the CP are lower (mean = 1.309, SD = 0.255, so the shape is more likely spiky.
- On the subject of the visual mean depth, the values for the trails of the UG are significantly higher (mean = 4.106, SD = 0.306, p < 0.001), but those for the AP are lower (mean = 2.552, SD = 0.144).
Taken together, it can be argued that from both geometric and syntactic perspectives, the trails of the UG are characterized as being symmetrical, compact, non-occlusive, rounded, non-cross-visible, and deep; the trails of the AP as asymmetrical, loose, occlusive, spiky, cross-visible, and shallow; the trails of the CP as asymmetrical, (partly) loose, (partly) occlusive, spiky, (partly) cross-visible, and shallow; and the trails of MM as symmetrical, compact, non-occlusive, rounded, non-cross-visible, and deep. It should be noted here that the characteristics of the CP’s trails are somewhat vague because of a great range of the isovist area and the isovist occlusivity. Despite the relatively lower mean values of these two measures, the values are running from the lowest to the highest.
6. Conclusions
This study aims to explore in what way linearly structured museums play a role in differentiating spatial configurations and spatial experiences and then to identify important underlying principles throughout with in-depth geometric and syntactic case studies, using space syntax techniques such as space type, spatial sequence and choice, isovist, and VGA. Particularly, possible trails, derived from the conception of space type and spatial sequence, are used to find out in what way spatial configurations work.
Through an in-depth investigation of four well-known art museums, namely, the Uffizi Gallery, the Alte Pinakothek, the Centre Pompidou, and the Moderna Museet, we have reached the following conclusions.
First, spatial sequence, leading to structured movement patterns, is strongly correlated with the isovist area and compactness but hardly corresponded to the isovist perimeter and occlusivity. Due to compressed and shortened features, the collection of visible surfaces (i.e., isovist) are simple, rounded, symmetric, and hard to discern, therefore working conservatively. This was discovered primarily in the cases of the UG and, partly, the MM. By contrast, spatial choice, enabling us to create our paths throughout the layout of space, is significantly related to isovist perimeter and occlusivity but not to the isovist area and compactness. Due to the lengthy and omnipresent properties, the collection of visible surfaces were asymmetric, complex, spiky, and easily seen, therefore working in a generative way. This was seen in the cases of the AP and partly in the CP.
Second, the spatial sequence is specifically defined as two types of sequences: the main sequence is derived from gathering space, yet with the auxiliary paths created from one of the gallery halls. The former is strongly associated with the gathering space, and it is mainly developed in the case of the UG and the MM. Here, we can argue that gathering space plays two roles: it provides syntactic information regarding gathering properties such as connectivity, integration, and intelligibility, and also leads us to return regularly to the same place (i.e., gathering space) after completing several distinct trails (e.g., a long journey composed of a series of c-spaces, a very short one made of only a single a-space, or the ones between them). Therefore, this spatial sequence is strongly correlated with visual syntactic features.
At the same time, the auxiliary paths are seldom related to gathering space. This means that it is independent of the main axis. For instance, the large gallery halls placed along the second strip in the AP work in articulating naïve trails via cabinets, and the galleries, located at the second row from the main corridor in the CP, organize a small walk. Particularly, this journey is strongly concerned with visual geometric properties such as occlusivity and the area/perimeter. Particularly, one should note that occlusivity is one significant attributes making the auxiliary paths distinctive. The AP is characterized by high values of occlusivity. This means that the occluding radial surfaces are longer than the other cases, so that the paths reflect perceptual uncertainty, although its spatial structure is powerfully linear. Additionally, the CP has relatively high values of occlusivity, and the auxiliary paths are quite unpredictable, which is also due to the occluding radial surfaces. On the other hand, the UG features low values of occlusivity, meaning that the occluding radial surfaces are shorter than the others, and, therefore, it can be said that the paths are quite predictable, in spite of a number of auxiliary paths.
Finally, we should note that space itself works in distinct ways: without a doubt, the gathering space provides access to all spaces across the floor plan and plays a role in generating different walking sequences that are mainly composed of c-spaces. These sequences are easily accessible and recognizable. However, when we look into the cases where d-spaces are the prominent space type, certain gallery halls play the same role of generating spatial sequences (i.e., auxiliary paths). Therefore, they perform two distinct functions: occupation and local movement. More importantly, local movement is facilitated by occlusive edges.
From these findings, it can be said that art museums work with distinctly different spatial sequences, and particularly, the auxiliary paths generated from the gathering spaces generate spatially different experiences. Thus, it might be argued that it seems that art museums work in the same way, while gallery spaces are configured in distinct ways. This is the reason that spatial experiences are substantially different from one another.
Author Contributions
Conceptualization, J.H.L. and Y.S.K.; methodology, J.H.L.; validation, J.H.L.; formal analysis, J.H.L. and Y.S.K.; investigation, J.H.L.; data preparation, J.H.L.; writing—original draft preparation, J.H.L.; writing—review and editing, J.H.L. and Y.S.K.; visualization, J.H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Macdonald, S. Collecting Practices. In A Companion to Museum Studies; Macdonald, S., Ed.; Wiley-Blackwell: West Sussex, UK, 2011; pp. 81–97. [Google Scholar]
- Pevsner, N. A History of Building Types; Princeton University Press: Princeton, NJ, USA, 1976. [Google Scholar]
- Brawne, M. The New Museum: Architecture and Display; Frederick A. Praeger: New York, NY, USA, 1965. [Google Scholar]
- Brawne, M. The Museum Interior: Temporary and Permanent Display Techniques; Thames and Hudson: London, UK, 1982. [Google Scholar]
- Tzortzi, K. The Interaction between Building Layout and Display Layout in Museums. Ph.D. Thesis, University College London, London, UK, 2007. [Google Scholar]
- Huang, H. The Spatialization of Knowledge and Social Relationships: A study on the Spatial Types of the Modern Museum. In Proceedings of the 3rd International Space Syntax Symposium, Atlanta, GA, USA, 7–11 May 2001. [Google Scholar]
- Duncan, C.; Wallach, A. The Museum of Modern Art as Late Capitalist Ritual: An Iconographic Analysis. Marx. Perspect. 1978, 1, 28–51. [Google Scholar]
- Hillier, B.; Tzortzi, K. Space Syntax: The Language of Museum Space. In A Companion to Museum Studies; Macdonald, S., Ed.; Wiley-Blackwell: West Sussex, UK, 2011; pp. 282–301. [Google Scholar]
- Choi, Y.K. The Morphology of Exploration and Encounter in Museum Layouts. Environ. Plan. B Plan. Des. 1999, 26, 241–250. [Google Scholar] [CrossRef]
- Peponis, J.; Dalton, R.C.; Wineman, J.; Dalton, N. Measuring the Effects of Layout upon Visitor’s Spatial Behaviours in Open Plan Exhibition Settings. Environ. Plan. B Plan. Des. 2004, 31, 454–473. [Google Scholar] [CrossRef]
- Penn, A.; Martinez, M.; Lemlij, M. Structure, Agency, and Space in the Emergence of Organisational Culture. In Proceedings of the 6th International Space Syntax Symposium, Istanbul, Turkey, 12–15 June 2007. [Google Scholar]
- Psarra, S.; Grajewski, T. Architecture, Narrative and Promenade in Bensen and Forsyth’s Museum of Scotland. Archit. Res. Q. 2000, 4, 122–136. [Google Scholar]
- Psarra, S.; Wineman, J.; Xu, Y.; Kaynar, I. Tracing the Modern: Space, Narrative and Exploration in the Museum of Modern Art, New York. In Proceedings of the 6th International Space Syntax Symposium, Istanbul, Turkey, 12–15 June 2007. [Google Scholar]
- Salgamcioglu, M.E.; Cabadak, D. Permanent and Temporary Museum Spaces: A Study on Human Behavior and Spatial Organization Relationship in Refunctioned Warehouse Spaces of Karakoy, Istanbul. In Proceedings of the 11th International Space Syntax Symposium, Lisbon, Portugal, 3–7 July 2017. [Google Scholar]
- Benedikt, M. To take hold of space: Isovists and isovist fields. Environ. Plan. B Plan. Des. 1979, 6, 47–65. [Google Scholar] [CrossRef]
- Conroy, R. Spatial Navigation in Immersive Virtual Environment. Ph.D. Thesis, University College London, London, UK, 2001. [Google Scholar]
- Hillier, B. Space is the Machine; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Lee, J.H. The Impact of Maps on Spatial Experience in Museum Architecture. Ph.D. Thesis, University College London, London, UK, 2014. [Google Scholar]
- Mack, G. Art Museums into the 21st Century; Birkhäuser: Basel, Swizerland, 1999. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).