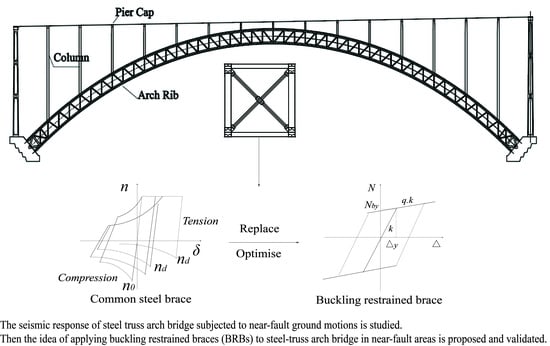
Application of BRB to Seismic Mitigation of Steel Truss Arch Bridge Subjected to Near-Fault Ground Motions
Abstract
:1. Introduction
2. Near-Fault Ground Motions
2.1. Selected Seismic Waves
2.2. Response Spectrum of Seismic Waves
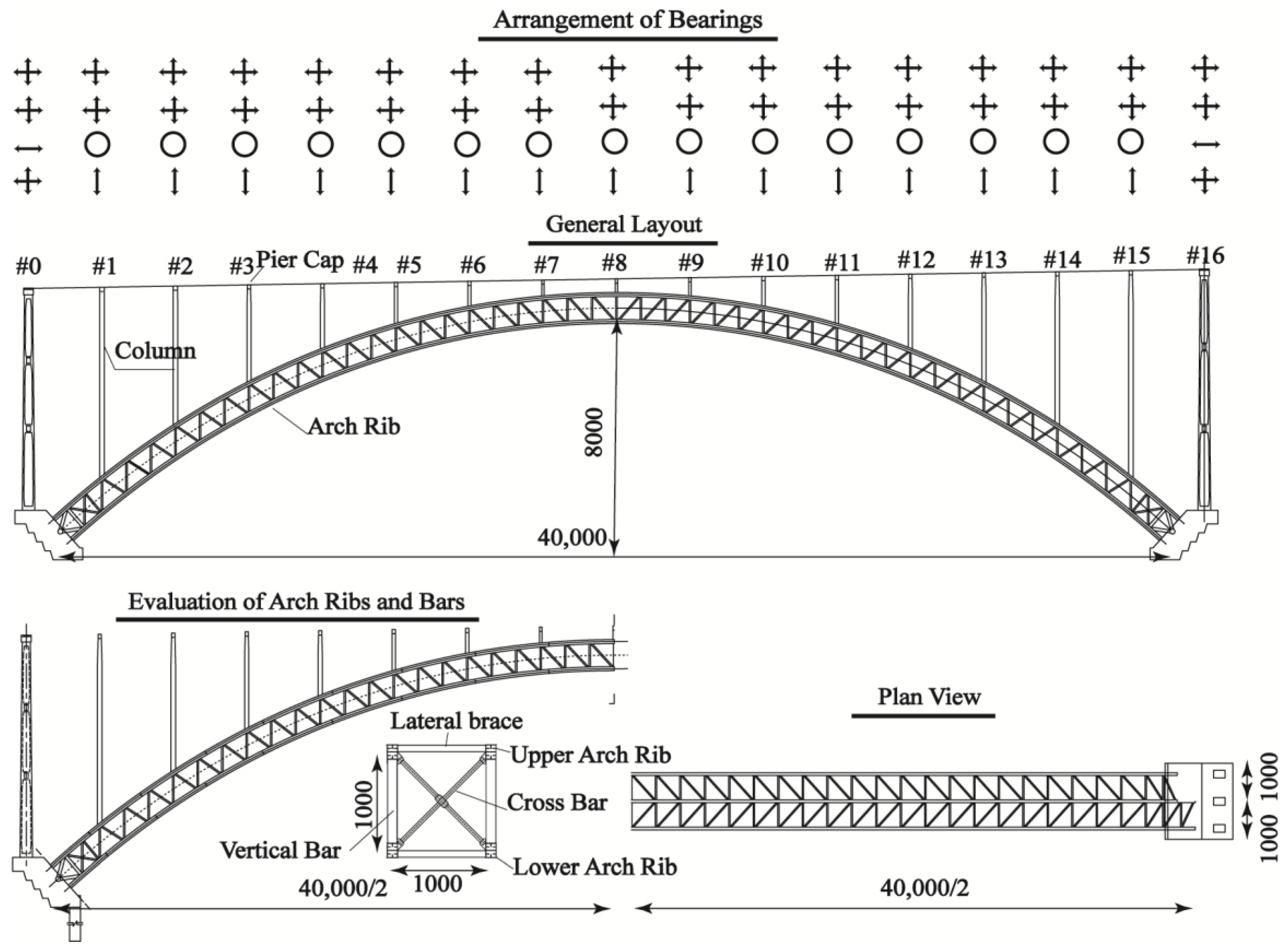
3. Bridge Prototype and Modelling
3.1. Case Study Bridge for System Response
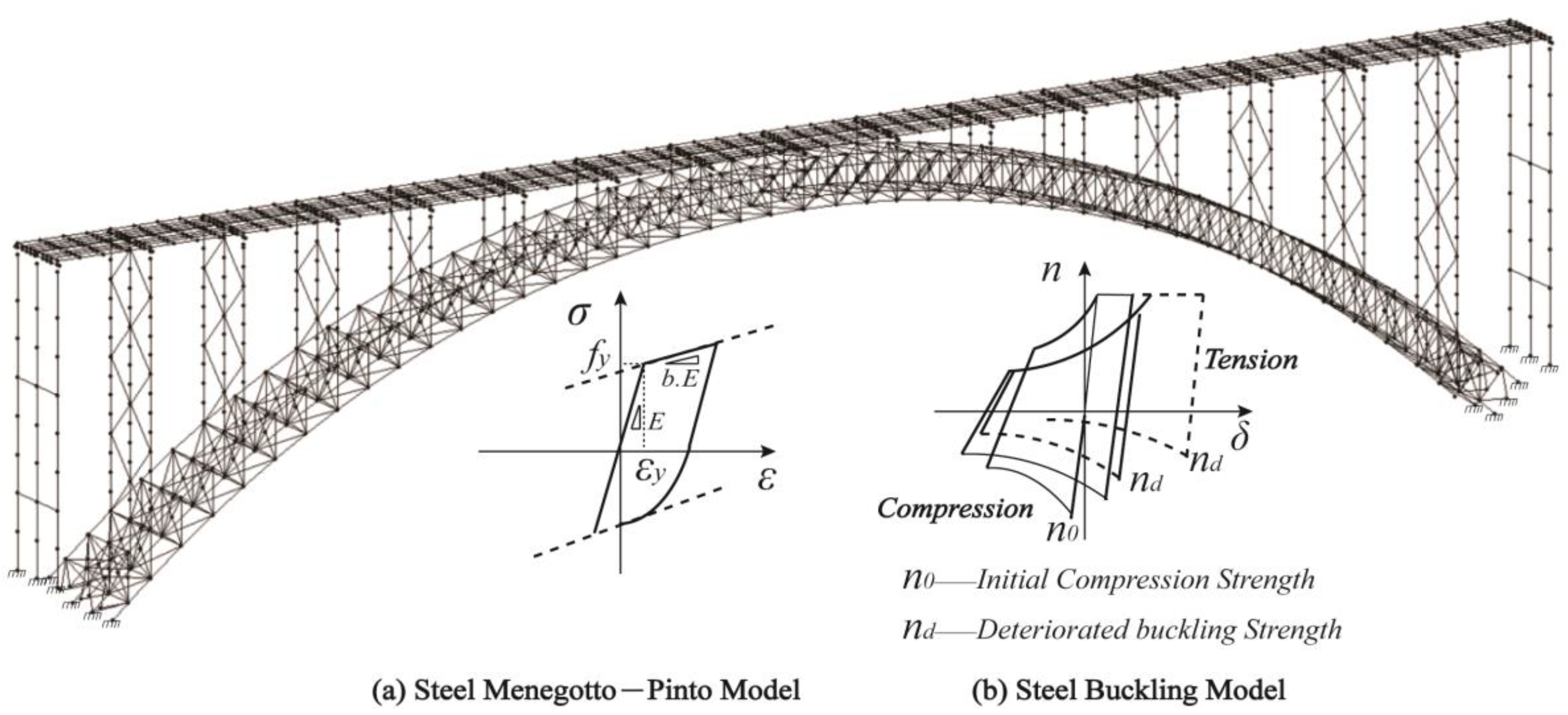
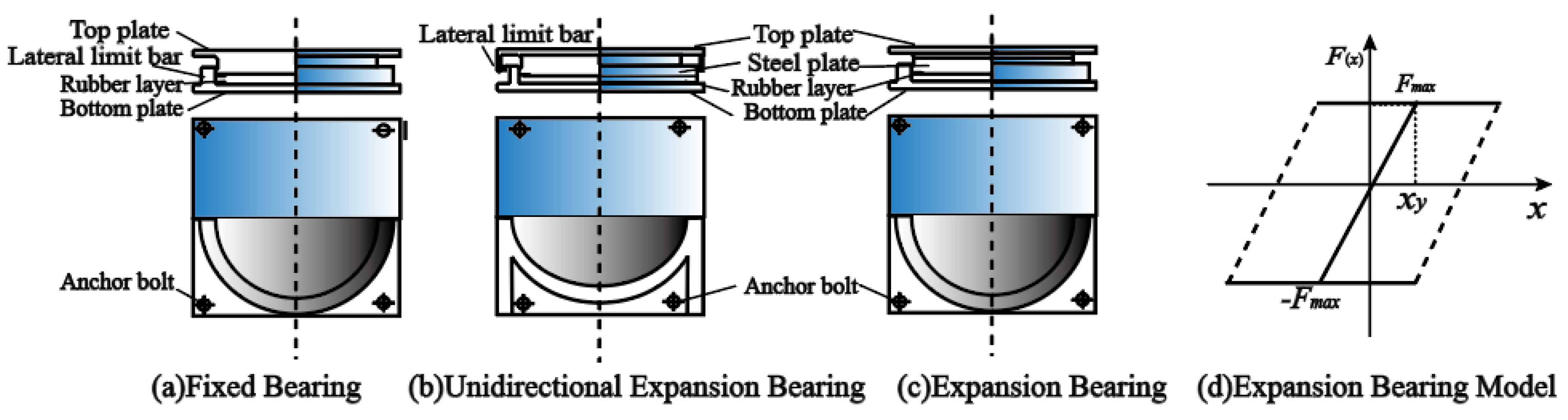
3.2. Finite Element Model
4. Bridge Response
4.1. Response of Arch Ribs
4.2. Buckling of Braces
5. Seismic Mitigation Scheme Using BRB
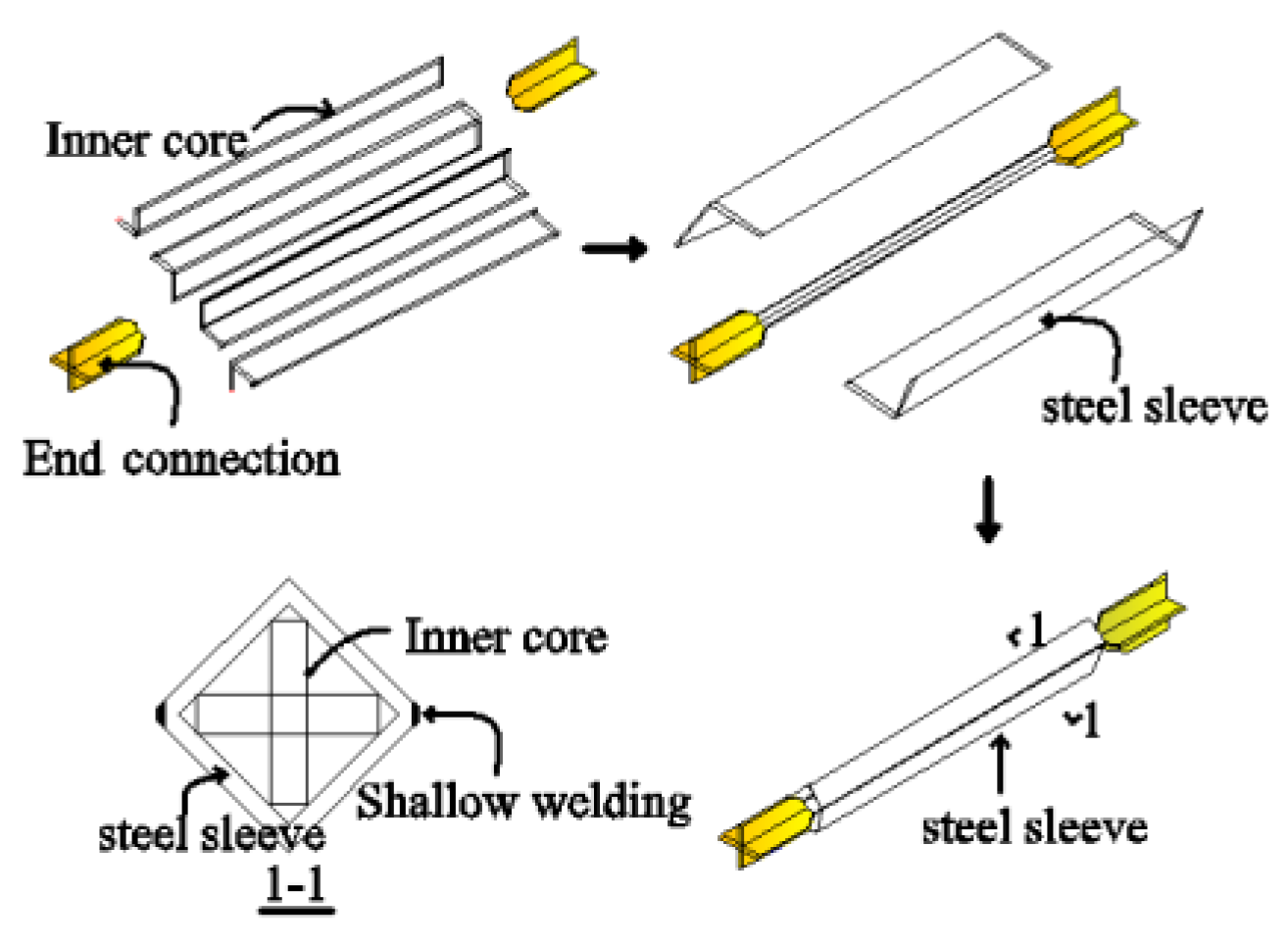
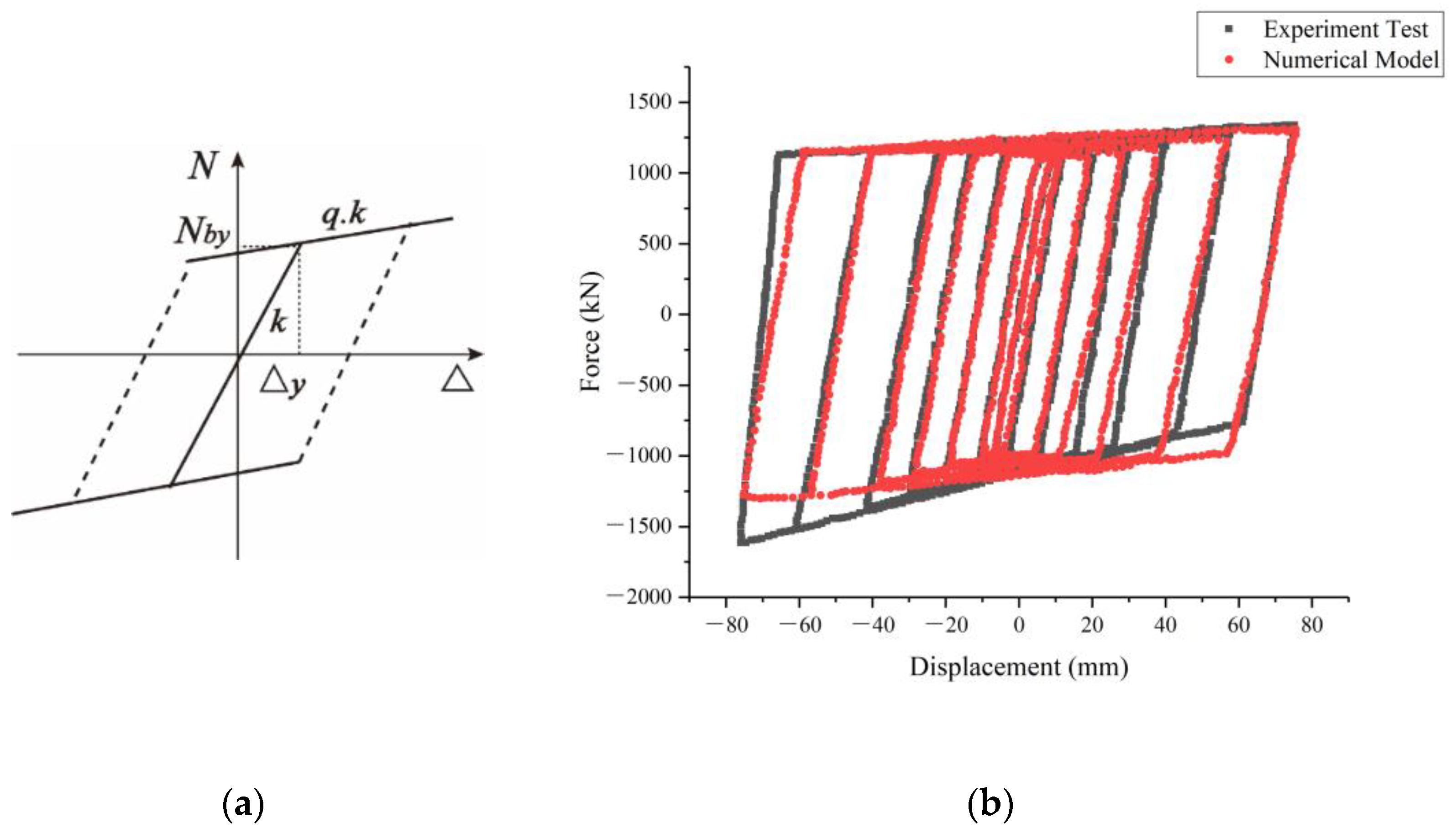
5.1. Design Parameters of BRB
5.2. Layout Scheme of BRBs
- (1)
- BRBs need to be arranged near sections with large force and relative displacement;
- (2)
- The layout of supports includes single diagonal bracing, V-shaped or herringbone form, but they should not be arranged in X-shaped cross form;
- (3)
- BRBs should be arranged in multiple directions of the structure, and it is expected to play a seismic mitigation role in multiple directions;
- (4)
- In order to reflect the seismic mitigation ratio of BRBs through comparative analysis, the study only replaces the original bridge braces with BRB members, without changing the number of braces;
- (5)
- The bearing capacity and dynamic characteristics of the bridge installed with BRB cannot be significantly changed.
5.3. The Seismic Mitigation Effect of BRBs on Bridges near Faults
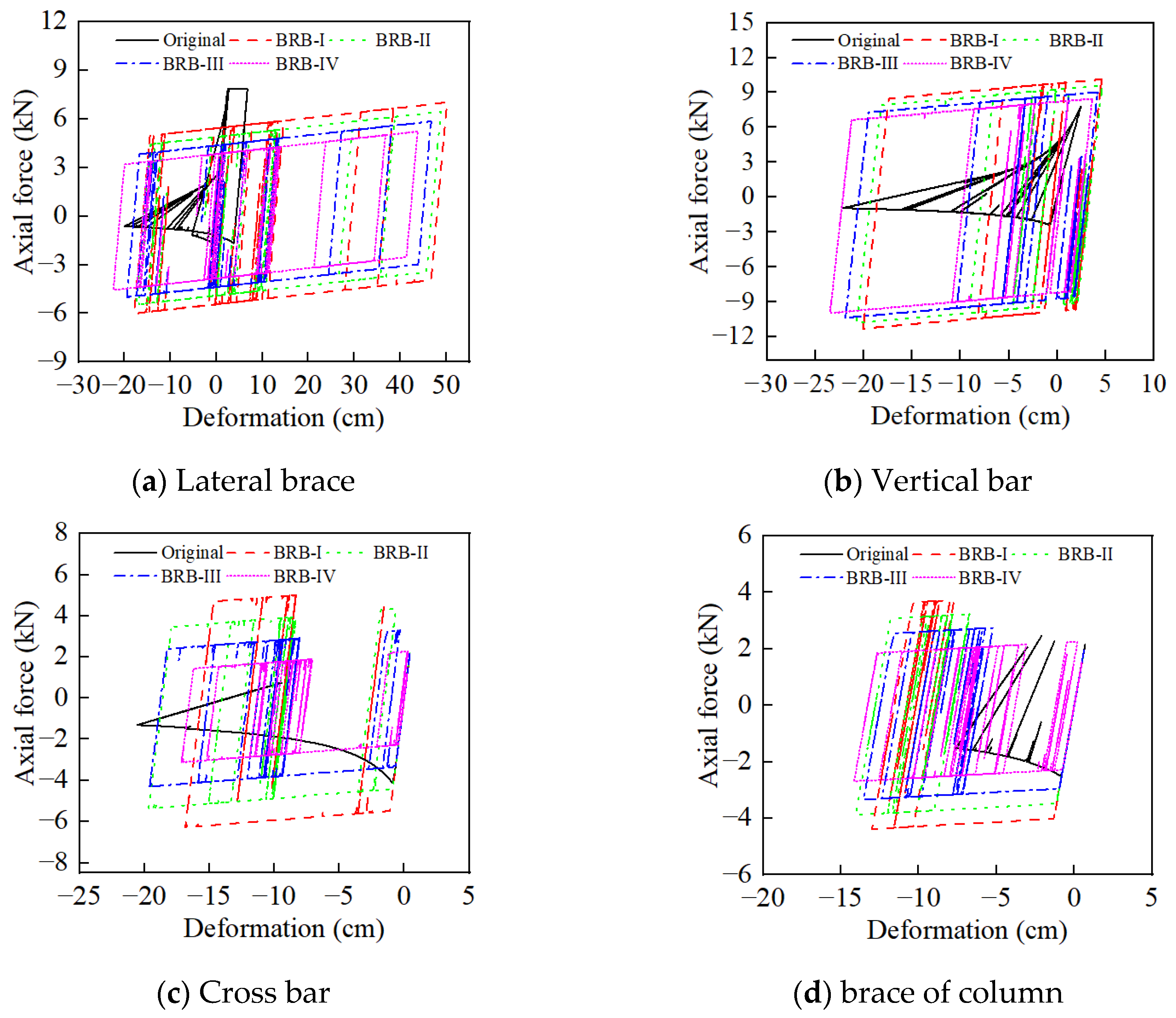
5.3.1. Comparison of Hysteresis Curves
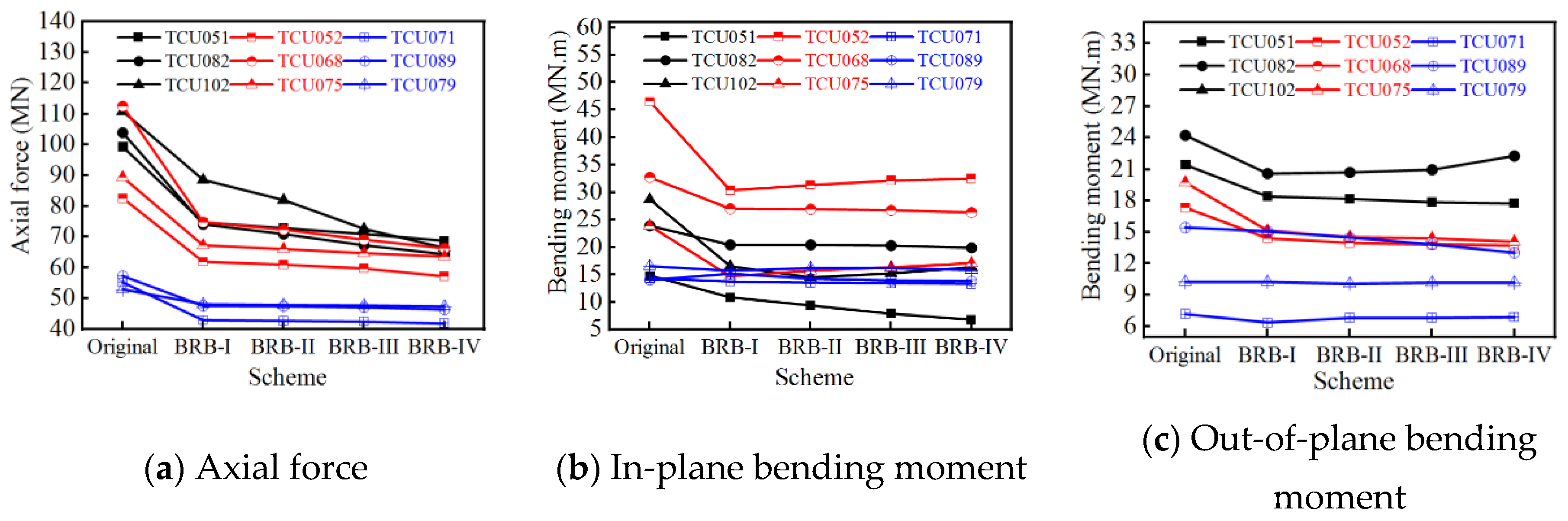
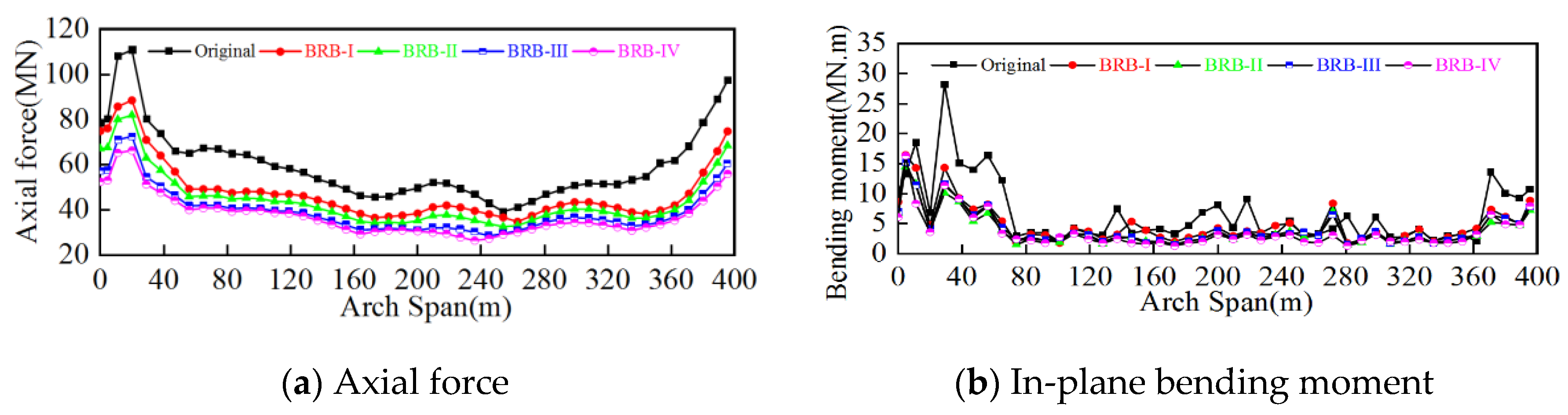
5.3.2. Effect of BRBs on Force and Displacement of Bridge
6. Conclusions
- (1)
- The low-frequency component of the pulsed ground motion in the near-fault zone significantly increases the displacement and internal force response of the bridge compared to the non-pulsed ground motion. The velocity pulses lead to more buckling damage of the braces and weakening of the bridge stiffness. In addition, the selected fling-step effect ground motions were more destructive than that of forward directivity effect.
- (2)
- Buckling restrained braces can function as fuses in arch bridge. In the prototype bridge, ordinary steel rods buckled under rare earthquakes and suffered a rapid loss of stiffness and capacity, resulting in a loss of function. A proportion of the plain steel supports could be replaced with BRBs without changing the quantity. Four BRB solutions were proposed, which differ in their yield strength. Since they have the same stiffness and are consistent with the original braces, the basic period of the structure remains the same. They can remain elastic under static conditions and frequent earthquakes and dissipate energy in rare earthquakes. Therefore, the axial force, in-plane bending moment, and transverse displacement of the arch rib can be significantly reduced, which is more prominent under the action of impulse ground motion.
- (3)
- The seismic mitigation rate of bridges under pulsed ground motions is much larger than that of ordinary non-pulse ground motion, which is particularly prominent in the axial force of arch foot and in-plane bending moment. This is because the pulsed ground motions cause more braces in the prototype bridge to buckle, and the role of buckling restrained braces in the optimized bridge is fully utilized.
- (4)
- There is a correlation between the seismic mitigation effect of buckling restrained braces and the design parameters, so the optimal scheme should be obtained through comparison. To a certain degree, reducing the strength of BRBs is helpful to improve the seismic mitigation effect of internal forces, but this should be adopted without reducing the stiffness of the prototype bridge.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- FEER Database. Available online: https://ngawest2.berkeley.edu (accessed on 1 July 2013).
- Somerville, P.G.; Smith, N.F.; Graves, R.W.; Abrahamson, N.A. Modification of Empirical Strong Ground Motion Attenuation Relations to Include the Amplitude and Duration Effects of Rupture Directivity. Seismol. Res. Lett. 1997, 68, 199–222. [Google Scholar] [CrossRef]
- Wu, G.; Zhai, C.; Li, S.; Xie, L. Effects of near-fault ground motions and equivalent pulses on Large Crossing Transmission Tower-line System. Eng. Struct. 2014, 77, 161–169. [Google Scholar] [CrossRef]
- Yang, D.; Zhou, J. A stochastic model and synthesis for near-fault impulsive ground motions. Earthq. Eng. Struct. Dyn. 2015, 44, 243–264. [Google Scholar] [CrossRef]
- Yan, G.; Chen, F. Seismic Performance of Midstory Isolated Structures under Near-Field Pulse-Like Ground Motion and Limiting Deformation of Isolation Layers. Shock Vib. 2015, 2015, 730612. [Google Scholar] [CrossRef] [Green Version]
- Chopra, A.K.; Chintanapakdee, C. Comparing response of SDF systems to near-fault and far-fault earthquake motions in the context of spectral regions. Earthq. Eng. Struct. Dyn. 2001, 30, 1769–1789. [Google Scholar] [CrossRef]
- Mavroeidis, G.P.; Papageorgiou, A.S. A mathematical representation of near-fault ground motions. Bull. Seismol. Soc. Am. 2003, 93, 1099–1131. [Google Scholar] [CrossRef]
- Ghahari, S.F.; Jahankhah, H.; Ghannad, M.A. Study on elastic response of structures to near-fault ground motions through record decomposition. Soil Dyn. Earthq. Eng. 2010, 30, 536–546. [Google Scholar] [CrossRef]
- Li, S.; Zhang, F.; Wang, J.-q.; Alam, M.S.; Zhang, J. Effects of Near-Fault Motions and Artificial Pulse-Type Ground Motions on Super-Span Cable-Stayed Bridge Systems. J. Bridge Eng. 2017, 22, 04016128. [Google Scholar] [CrossRef]
- Billah, A.H.M.M.; Alam, M.S.; Bhuiyan, M.A.R. Fragility Analysis of Retrofitted Multicolumn Bridge Bent Subjected to Near-Fault and Far-Field Ground Motion. J. Bridge Eng. 2013, 18, 992–1004. [Google Scholar] [CrossRef]
- Davoodi, M.; Jafari, M.K.; Hadiani, N. Seismic response of embankment dams under near-fault and far-field ground motion excitation. Eng. Geol. 2013, 158, 66–76. [Google Scholar] [CrossRef]
- Cui, Z.; Sheng, Q. Seismic response of underground rock cavern dominated by a large geological discontinuity subjected to near-fault and far-field ground motions. Chin. J. Rock Mech. Eng. 2017, 36, 53–67. [Google Scholar] [CrossRef]
- Losanno, D.; Hadad, H.A.; Serino, G. Seismic behavior of isolated bridges with additional damping under far-field and near fault ground motion. Earthq. Struct. 2017, 13, 119–130. [Google Scholar] [CrossRef]
- Chen, X.; Li, J.; Guan, Z. Influence of Ground Motion Characteristics on Higher-Mode Effects and Design Strategy for Tall Pier Bridges. J. Bridge Eng. 2022, 28, 04022126. [Google Scholar] [CrossRef]
- Yang, D.; Zhao, Y. Effects of rupture forward directivity and fling step of near-fault ground motions on seismic performance of base-isolated building structure. Acta Seismol. Sin. 2010, 32, 579–587. [Google Scholar] [CrossRef]
- Vui Van, C.; Ronagh, H.R. Correlation between parameters of pulse-type motions and damage of low-rise RC frames. Earthq. Struct. 2014, 7, 365–384. [Google Scholar] [CrossRef]
- Zaker Esteghamati, M.; Farzampour, A. Probabilistic seismic performance and loss evaluation of a multi-story steel building equipped with butterfly-shaped fuses. J. Constr. Steel Res. 2020, 172, 106187. [Google Scholar] [CrossRef]
- Upadhyay, A.; Pantelides, C.P.; Ibarra, L. Residual drift mitigation for bridges retrofitted with buckling restrained braces or self centering energy dissipation devices. Eng. Struct. 2019, 199, 109663. [Google Scholar] [CrossRef]
- Adanur, S.; Altunişik, A.C.; Bayraktar, A.; Akköse, M. Comparison of near-fault and far-fault ground motion effects on geometrically nonlinear earthquake behavior of suspension bridges. Nat. Hazards 2012, 64, 593–614. [Google Scholar] [CrossRef]
- Shrestha, B. Seismic response of long span cable-stayed bridge to near-fault vertical ground motions. KSCE J. Civ. Eng. 2015, 19, 180–187. [Google Scholar] [CrossRef]
- Lu, Z.H.; Usami, T.; Ge, H.B. Seismic performance evaluation of steel arch bridges against major earthquakes. Part 2: Simplified verification procedure. Earthq. Eng. Struct. Dyn. 2004, 33, 1355–1372. [Google Scholar] [CrossRef]
- Bai, F.-L.; Hao, H.; Li, H.-N. Seismic Response of a Steel Trussed Arch Structure to Spatially Varying Earthquake Ground Motions Including Site Effect. Adv. Struct. Eng. 2010, 13, 1089–1103. [Google Scholar] [CrossRef]
- Alvarez, J.J.; Aparicio, A.C.; Jara, J.M.; Jara, M. Seismic assessment of a long-span arch bridge considering the variation in axial forces induced by earthquakes. Eng. Struct. 2012, 34, 69–80. [Google Scholar] [CrossRef]
- Li, R.; Ge, H.; Maruyama, R. Assessment of post-earthquake serviceability for steel arch bridges with seismic dampers considering mainshock-aftershock sequences. Earthq. Struct. 2017, 13, 137–150. [Google Scholar] [CrossRef]
- Bazaez, R.; Dusicka, P. Cyclic loading for RC bridge columns considering subduction megathrust earthquakes. J. Bridge Eng. 2016, 21, 04016009. [Google Scholar] [CrossRef]
- Chen, X.; Ikago, K.; Guan, Z.; Li, J.; Wang, X. Lead-rubber-bearing with negative stiffness springs (LRB-NS) for base-isolation seismic design of resilient bridges: A theoretical feasibility study. Eng. Struct. 2022, 266, 114601. [Google Scholar] [CrossRef]
- Chen, X.; Xiang, N.; Guan, Z.; Li, J. Seismic vulnerability assessment of tall pier bridges under mainshock-aftershock-like earthquake sequences using vector-valued intensity measure. Eng. Struct. 2022, 253, 113732. [Google Scholar] [CrossRef]
- Chen, X.; Xiong, J. Seismic resilient design with base isolation device using friction pendulum bearing and viscous damper. Soil Dyn. Earthq. Eng. 2022, 153, 107073. [Google Scholar] [CrossRef]
- Alam, M.S.; Bhuiyan, M.A.R.; Billah, A.H.M.M. Seismic fragility assessment of SMA-bar restrained multi-span continuous highway bridge isolated by different laminated rubber bearings in medium to strong seismic risk zones. Bull. Earthq. Eng. 2012, 10, 1885–1909. [Google Scholar] [CrossRef]
- Dezfuli, F.H.; Alam, M.S. Performance-based assessment and design of FRP-based high damping rubber bearing incorporated with shape memory alloy wires. Eng. Struct. 2014, 61, 166–183. [Google Scholar] [CrossRef]
- Kim, J.K.; Choi, H.H. Behavior and design of structures with buckling-restrained braces. Eng. Struct. 2004, 26, 693–706. [Google Scholar] [CrossRef]
- Hoveidae, N.; Rafezy, B. Overall buckling behavior of all-steel buckling restrained braces. J. Constr. Steel Res. 2012, 79, 151–158. [Google Scholar] [CrossRef]
- Li, L.; Zhou, T.H.; Chen, J.W.; Chen, J.F. A New Buckling-Restrained Brace with a Variable Cross-Section Core. Adv. Civ. Eng. 2019, 2019, 4620430. [Google Scholar] [CrossRef] [Green Version]
- Xing, L.L.; Zhou, Y.; Huang, W. Seismic optimization analysis of high-rise buildings with a buckling-restrained brace outrigger system. Eng. Struct. 2020, 220, 110959. [Google Scholar] [CrossRef]
- Beiraghi, H.; Zhou, H. Dual-steel frame consisting of moment-resisting frame and shape memory alloy braces subjected to near-field earthquakes. Struct. Des. Tall Spec. Build. 2020, 29, e1784. [Google Scholar] [CrossRef]
- Wang, Y.; Ibarra, L.; Pantelides, C. Collapse capacity of reinforced concrete skewed bridges retrofitted with buckling-restrained braces. Eng. Struct. 2019, 184, 99–114. [Google Scholar] [CrossRef]
- Dong, H.H.; Du, X.L.; Han, Q.; Bi, K.M.; Hao, H. Hysteretic performance of RC double-column bridge piers with self-centering buckling-restrained braces. Bull. Earthq. Eng. 2019, 17, 3255–3281. [Google Scholar] [CrossRef]
- Sosorburam, P.; Yamaguchi, E. Seismic Retrofit of Steel Truss Bridge Using Buckling Restrained Damper. Appl. Sci. 2019, 9, 2791. [Google Scholar] [CrossRef] [Green Version]
- Xiang, N.; Alam, M.S.; Li, J. Effect of Multi-Story Brace Distribution on Seismic Performance of RC Tall Bridge Bents Retrofitted with Buckling Restrained Braces. J. Earthq. Eng. 2021, 26, 8688–8705. [Google Scholar] [CrossRef]
- Celik, O.C.; Bruneau, M. Seismic behavior of bidirectional-resistant ductile end diaphragms with buckling restrained braces in straight steel bridges. Eng. Struct. 2009, 31, 380–393. [Google Scholar] [CrossRef]
- Zaker Esteghamati, M. A Holistic Review of GM/IM Selection Methods from a Structural Performance-Based Perspective. Sustainability 2022, 14, 12994. [Google Scholar] [CrossRef]
- Carreño, R.; Lotfizadeh, K.H.; Conte, J.P.; Restrepo, J.I. Material model parameters for the Giuffrè-Menegotto-Pinto uniaxial steel stress-strain model. J. Struct. Eng. 2020, 146, 04019205. [Google Scholar] [CrossRef]
- JTG/T 2231-01; Specifications for Seismic Design of Highway Bridges. Ministry of Transport: Beijing, China, 2020.
- DBJ/CT105; Technical Specification for TJ Buckling Restrained Braces. Tongji University: Shanghai, China, 2011.
- Sun, F.F.; Li, G.Q.; Guo, X.K.; Hu, D.Z.; Hu, B.L. Development of new-type buckling-restrained braces and their application in aseismic steel frameworks. Adv. Struct. Eng. 2011, 14, 717–730. [Google Scholar] [CrossRef]









| Ground Motion Type | Earthquake | Rrup (km) | Tp (s) | PGA (cm/s2) | PGV (cm/s) | PGV/PGA (s) |
|---|---|---|---|---|---|---|
| Forward-directivity pulses | TCU-051 | 7.64 | 10.3 | 160 | 51.53 | 0.32 |
| TCU-082 | 5.16 | 8.1 | 226 | 51.54 | 0.23 | |
| TCU-102 | 1.19 | 9.6 | 304 | 87.16 | 0.29 | |
| Fling-step pulses | TCU-052 | 1.84 | 9.9 | 488 | 220.64 | 0.45 |
| TCU-068 | 0.32 | 12.3 | 365 | 291.94 | 0.76 | |
| TCU-075 | 3.38 | 5.5 | 332 | 116.05 | 0.35 | |
| Non-pulsed effect | TCU-071 | 4.88 | 1.5 | 528 | 69.83 | 0.13 |
| TCU-079 | 10.95 | 0.8 | 589 | 64.49 | 0.11 | |
| TCU-089 | 8.33 | 1.7 | 354 | 45.43 | 0.13 |
| Section |  Arch rib |  Lateral brace |  Vertical bar |  Cross bar |
| Geometric characteristics | A = 0.3184 m2 Iz = 0.081 m4 Iy = 0.0506 m4 Ix = 0.0744 m4 | A = 0.0239 m2 Iz = 0.0021 m4 Iy = 0.0003 m4 Ix = 0.175 × 10−5 m4 | A = 0.0392 m2 Iz = 0.0005 m4 Iy = 0.0066 m4 Ix = 0.483 × 10−5 m4 | A = 0.0392 m2 Iz = 0.0005 m4 Iy = 0.0066 m4 Ix = 0.483 × 10−5 m4 |
| Section |  Column |  Brace of column |  Pier cap |  Arch foot |
| Geometric characteristics | A = 0.1079 m2 Iz = 0.0432 m4 Iy = 0.0196 m4 Ix = 0.0359 m4 | A = 0.0228 m2 Iz = 0.0015 m4 Iy = 0.0003 m4 Ix = 0.196 × 10−5 m4 | A = 0.1304 m2 Iz = 0.0582 m4 Iy = 0.0337 m4 Ix = 0.0552 m4 | A = 0.3904 m2 Iz = 0.0870 m4 Iy = 0.0854 m4 Ix = 0.0751 m4 |
| Material | Elastic Modulus (Pa) | Poisson’s Ratio | Density (kg/m3) | Structural Member |
|---|---|---|---|---|
| Steel | 2.06 × 1011 | 0.3 | 7850 | Arch rib, lateral brace, vertical bar, cross bar, main beam |
| Concrete | 3.45 × 1010 | 0.166 | 2550 | Junction pier, bridge face plate |
| Types of Seismic Waves | P-D Pulsed Wave | P-S Pulsed Wave | Non-Pulsed Wave | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Seismic wave | TCU051 | TCU082 | TCU102 | TCU052 | TCU068 | TCU075 | TCU071 | TCU089 | TCU079 |
| Lateral brace | 45 | 46 | 91 | 84 | 78 | 82 | 18 | 34 | 36 |
| Vertical bar | 12 | 47 | 31 | 51 | 21 | 28 | 11 | 18 | 14 |
| Cross bar | 34 | 30 | 50 | 64 | 52 | 42 | 13 | 21 | 19 |
| Brace of column | 2 | 5 | 11 | 5 | 4 | 8 | 0 | 0 | 0 |
| Seismic Wave | TCU051 | TCU082 | TCU102 | TCU052 | TCU068 | TCU075 |
|---|---|---|---|---|---|---|
| Lateral brace | 2190.5 | 2722.9 | 2983.4 | 2234.5 | 2513.5 | 2794.7 |
| Vertical bar | 6477.7 | 5777.2 | 6466.4 | 6815.9 | 4725.7 | 6542.5 |
| Cross bar | 1262.5 | 1387.6 | 1340.2 | 1201.3 | 1185.5 | 1318.6 |
| Brace of column | 1079.8 | 904.6 | 990.9 | 1029.3 | 1092.1 | 1074.3 |
| Scheme No | Brace Type | Ae (mm2) | Fy (MPa) | Nb1 (kN) | Nb1/γre (kN) | N (kN) | Nby (kN) |
|---|---|---|---|---|---|---|---|
| I | Lateral brace | 20,500 | 235 | 4292.4 | 5723.2 | 2737.1 | 5484.7 |
| Vertical bar | 37,000 | 235 | 7747.2 | 10,329.7 | 6253.1 | 9899.3 | |
| Cross bar | 20,500 | 235 | 4292.4 | 5723.2 | 1273.0 | 5484.7 | |
| Brace of column | 15,000 | 235 | 3140.8 | 4187.7 | 1001.9 | 4013.2 | |
| II | Lateral brace | 18,500 | 235 | 3873.6 | 5164.8 | 2737.1 | 4949.6 |
| Vertical bar | 35,000 | 235 | 7328.5 | 9771.3 | 6253.1 | 9364.2 | |
| Cross bar | 16,500 | 235 | 3454.9 | 4606.5 | 1273.0 | 4414.5 | |
| Brace of column | 13,000 | 235 | 2722.0 | 3629.3 | 1001.9 | 3478.1 | |
| III | Lateral brace | 16,500 | 235 | 3454.9 | 4606.5 | 2737.1 | 4414.5 |
| Vertical bar | 33,000 | 235 | 6909.7 | 9212.9 | 6253.1 | 8829.1 | |
| Cross bar | 12,500 | 235 | 2617.3 | 3489.8 | 1273.0 | 3344.3 | |
| Brace of column | 11,000 | 235 | 2303.2 | 3071.0 | 1001.9 | 2943.0 | |
| IV | Lateral brace | 14,500 | 235 | 3036.1 | 4048.1 | 2737.1 | 3879.4 |
| Vertical bar | 31,000 | 235 | 6490.9 | 8654.6 | 6253.1 | 8294.0 | |
| Cross bar | 8500 | 235 | 1779.8 | 2373.0 | 1273.0 | 2274.2 | |
| Brace of column | 8500 | 235 | 1779.8 | 2373.0 | 1001.9 | 2274.2 |
| Brace Type | Arch Foot | Vault | 1/4 Arch Rib | Column#1&15 | Column#2&14 | Total |
|---|---|---|---|---|---|---|
| Lateral brace | 28 | 26 | 26 | 0 | 0 | 80 |
| Vertical bar | 20 | 15 | 15 | 0 | 0 | 50 |
| Cross bar | 20 | 15 | 15 | 0 | 0 | 50 |
| Brace of column | 0 | 0 | 0 | 4 | 4 | 8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Zhang, K.; Wu, X.; Liu, H.; Zhang, L. Application of BRB to Seismic Mitigation of Steel Truss Arch Bridge Subjected to Near-Fault Ground Motions. Buildings 2022, 12, 2147. https://doi.org/10.3390/buildings12122147
Gao H, Zhang K, Wu X, Liu H, Zhang L. Application of BRB to Seismic Mitigation of Steel Truss Arch Bridge Subjected to Near-Fault Ground Motions. Buildings. 2022; 12(12):2147. https://doi.org/10.3390/buildings12122147
Chicago/Turabian StyleGao, Haoyuan, Kun Zhang, Xinyu Wu, Hongjiang Liu, and Lianzhen Zhang. 2022. "Application of BRB to Seismic Mitigation of Steel Truss Arch Bridge Subjected to Near-Fault Ground Motions" Buildings 12, no. 12: 2147. https://doi.org/10.3390/buildings12122147
APA StyleGao, H., Zhang, K., Wu, X., Liu, H., & Zhang, L. (2022). Application of BRB to Seismic Mitigation of Steel Truss Arch Bridge Subjected to Near-Fault Ground Motions. Buildings, 12(12), 2147. https://doi.org/10.3390/buildings12122147