Shear Behavior of T-Shaped Concrete Beams Reinforced with FRP
Abstract
:1. Introduction
2. Experimental Procedure
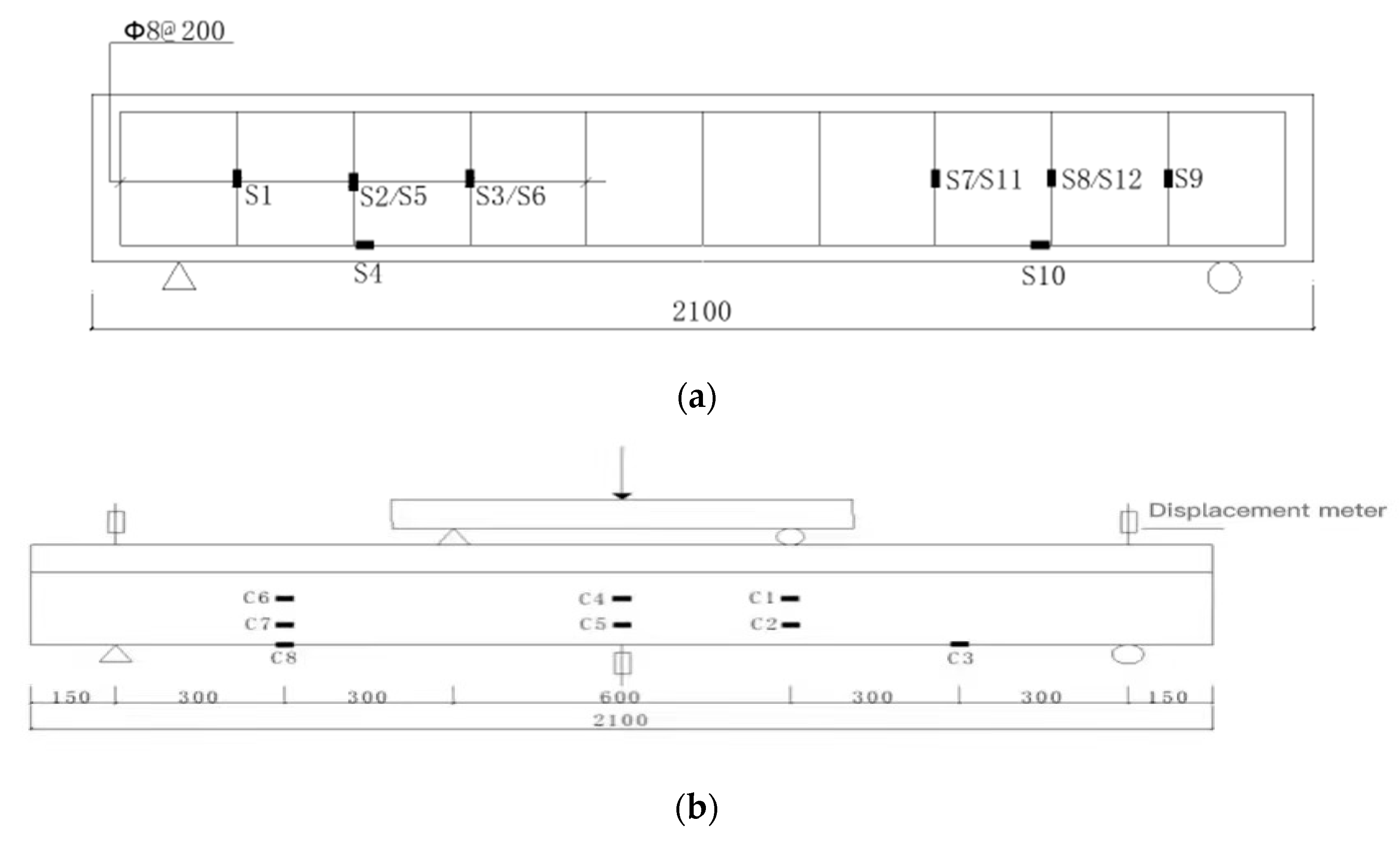
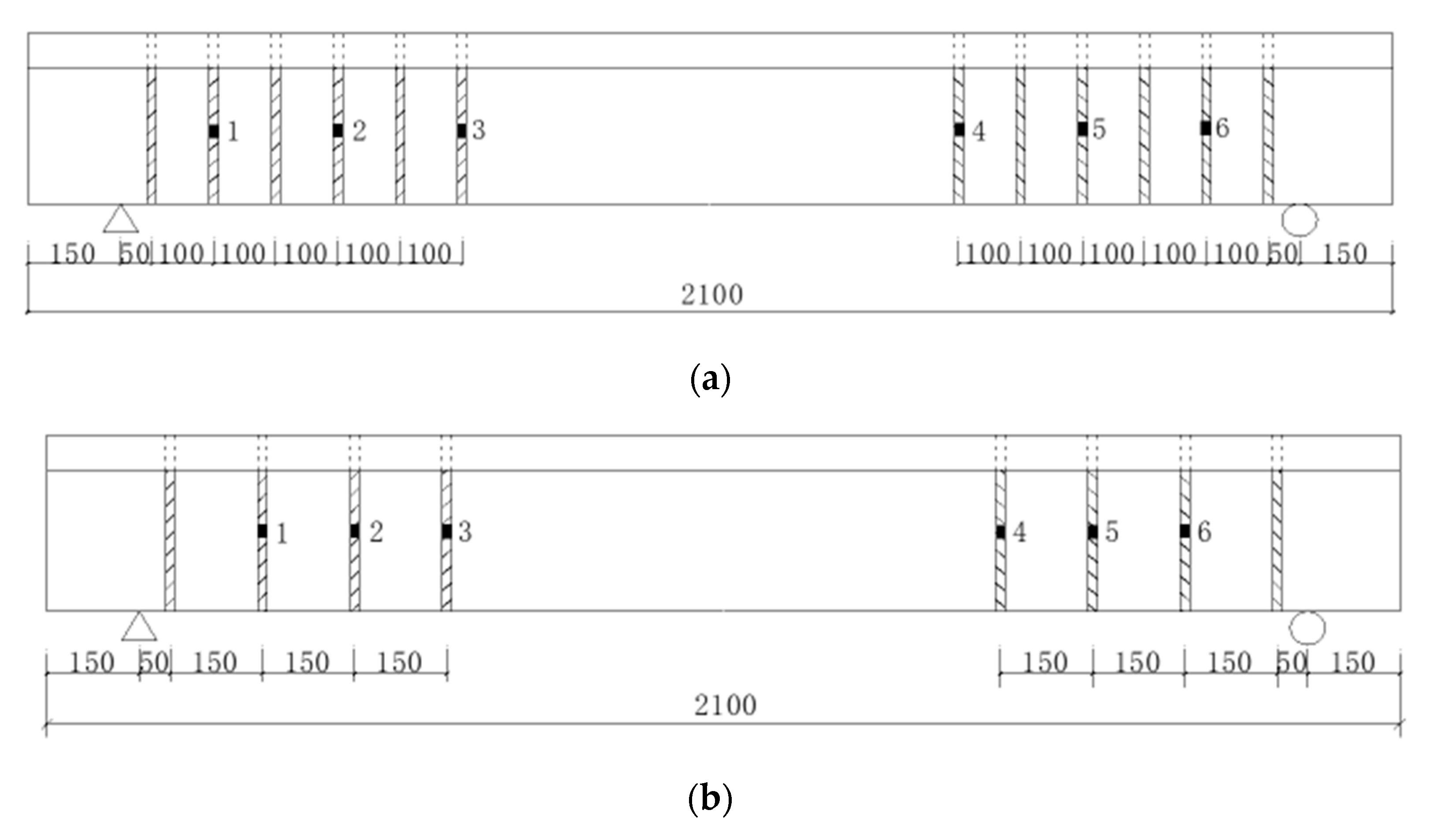
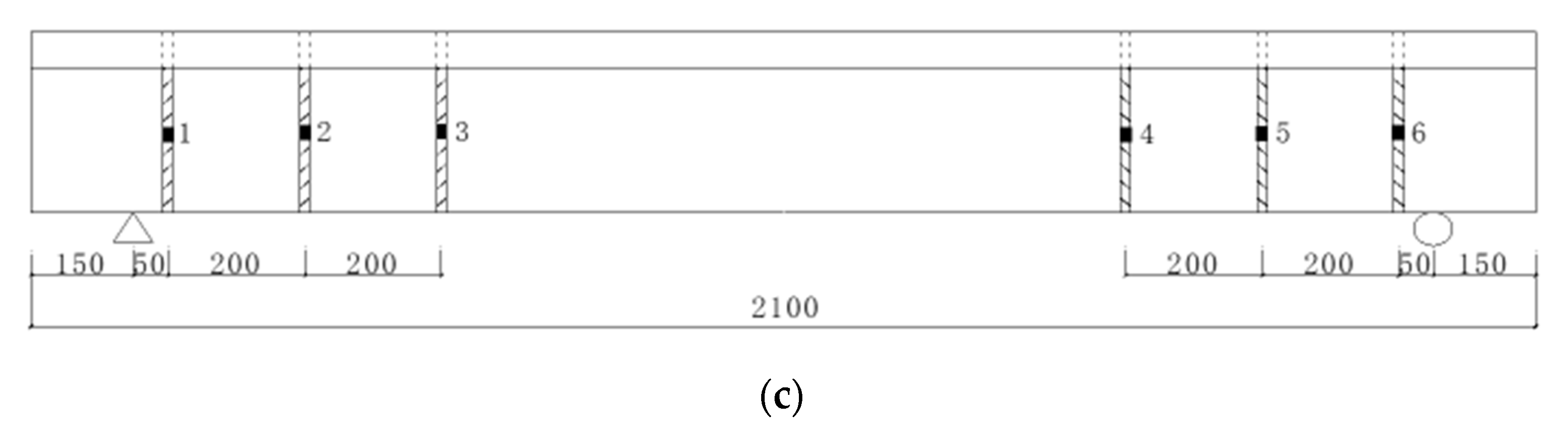
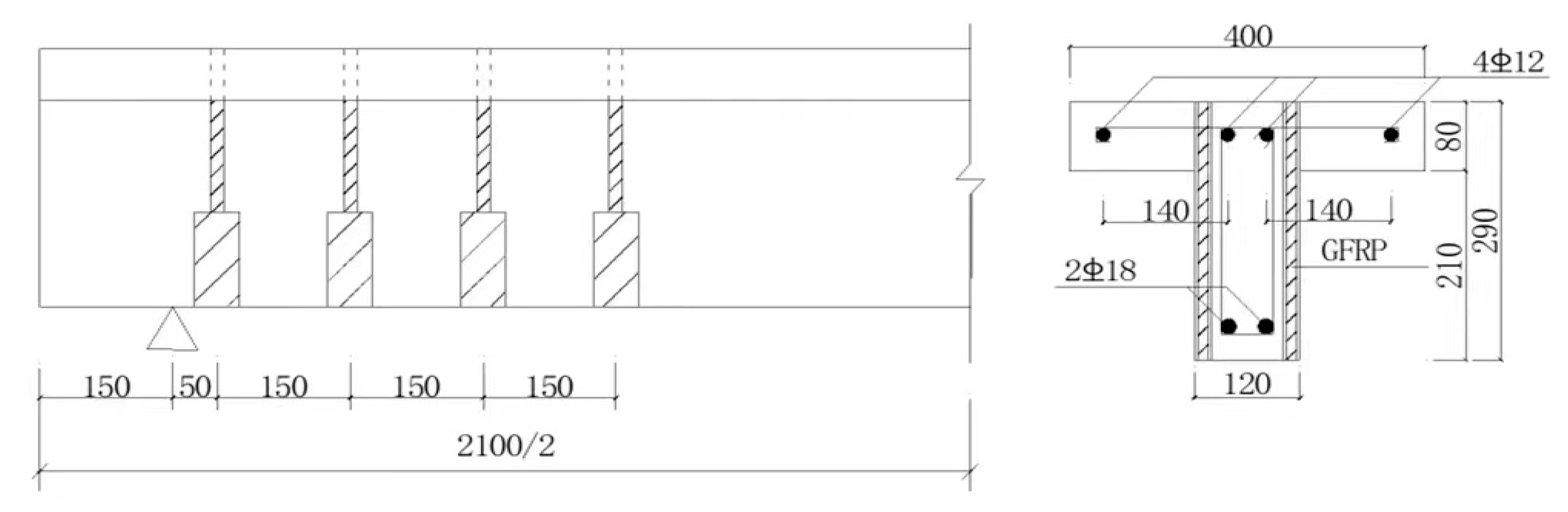
2.1. Specimen Making and Reinforcement
2.2. Test Setup and Process
2.3. Materials, Properties and Specimens
3. Experimental Test Results
3.1. Failure Modes
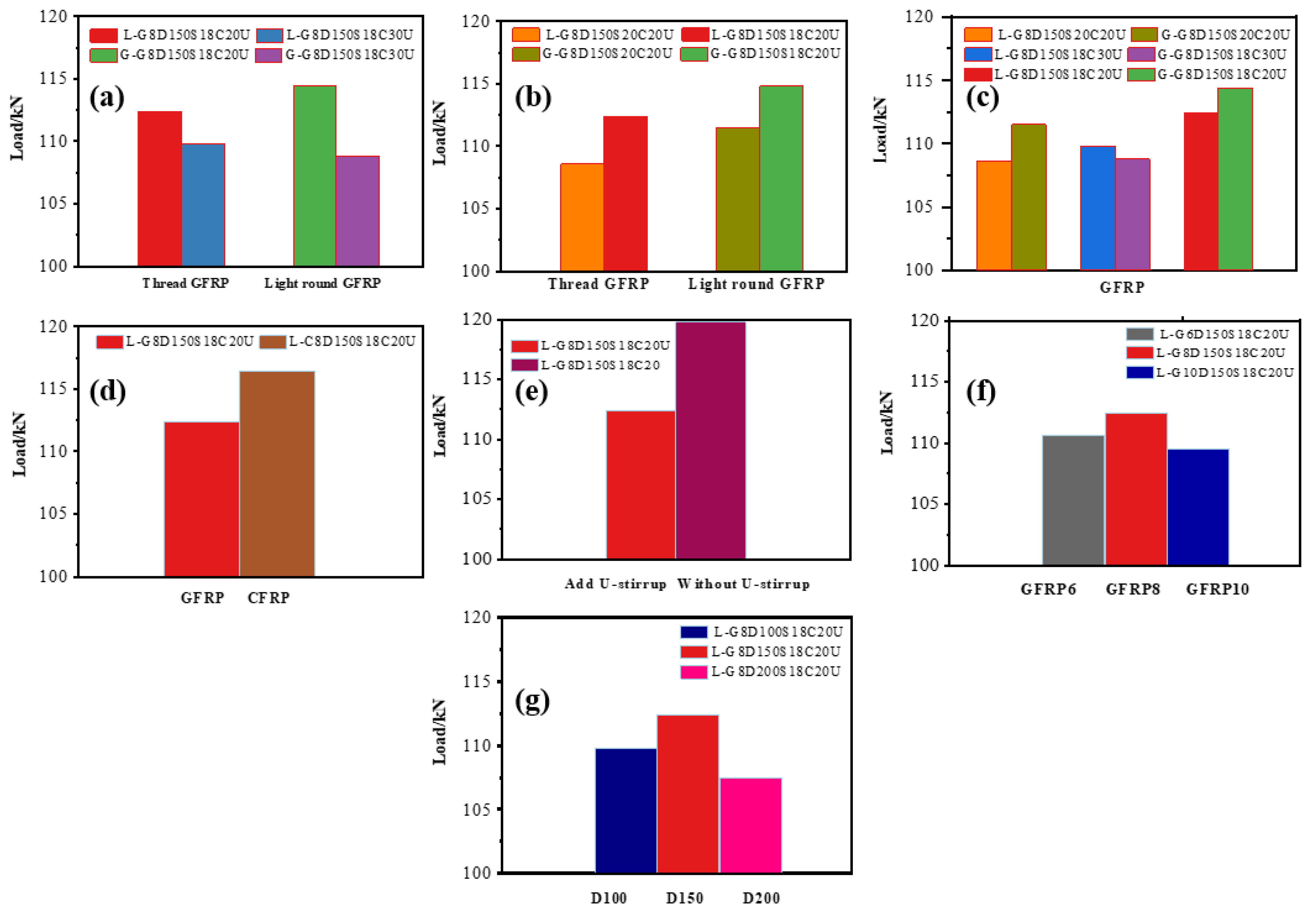
3.2. Bearing Capacity Analysis
3.3. Discussion of Test Parameters
3.3.1. Effect of Compressive Strength
3.3.2. Effect of Longitudinal Reinforcement Ratio
3.3.3. Effect of GFRP Surface Characteristics
3.3.4. Effect of FRP Types
3.3.5. Effect of Reinforcement Method
3.3.6. Effect of GFRP Diameter
3.3.7. Effect of GFRP Spacing
3.3.8. Effect of Shear Span Ratio
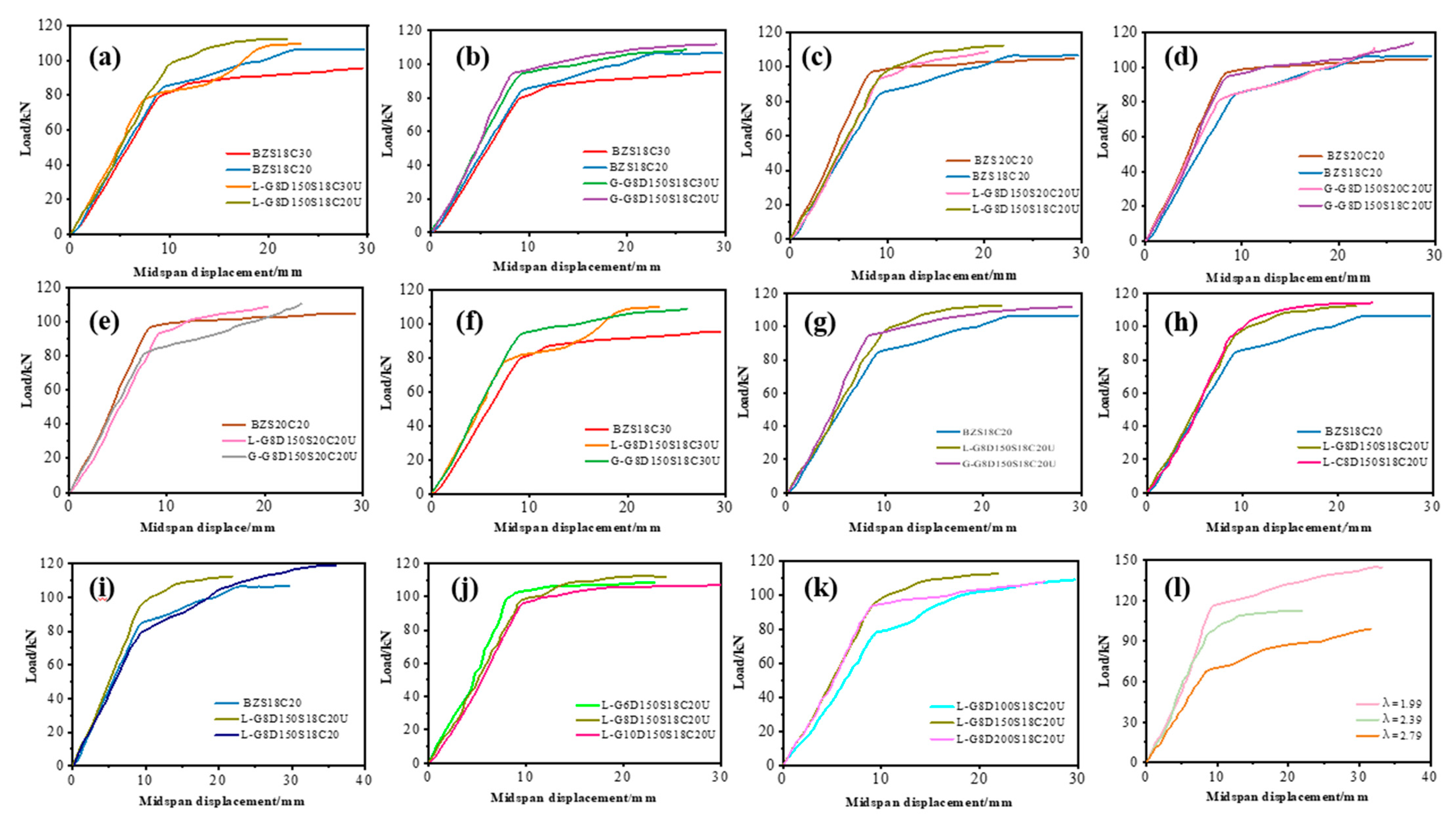
3.4. The Load-Deflection Relationships
3.5. Carrying Capacity Formula Correction
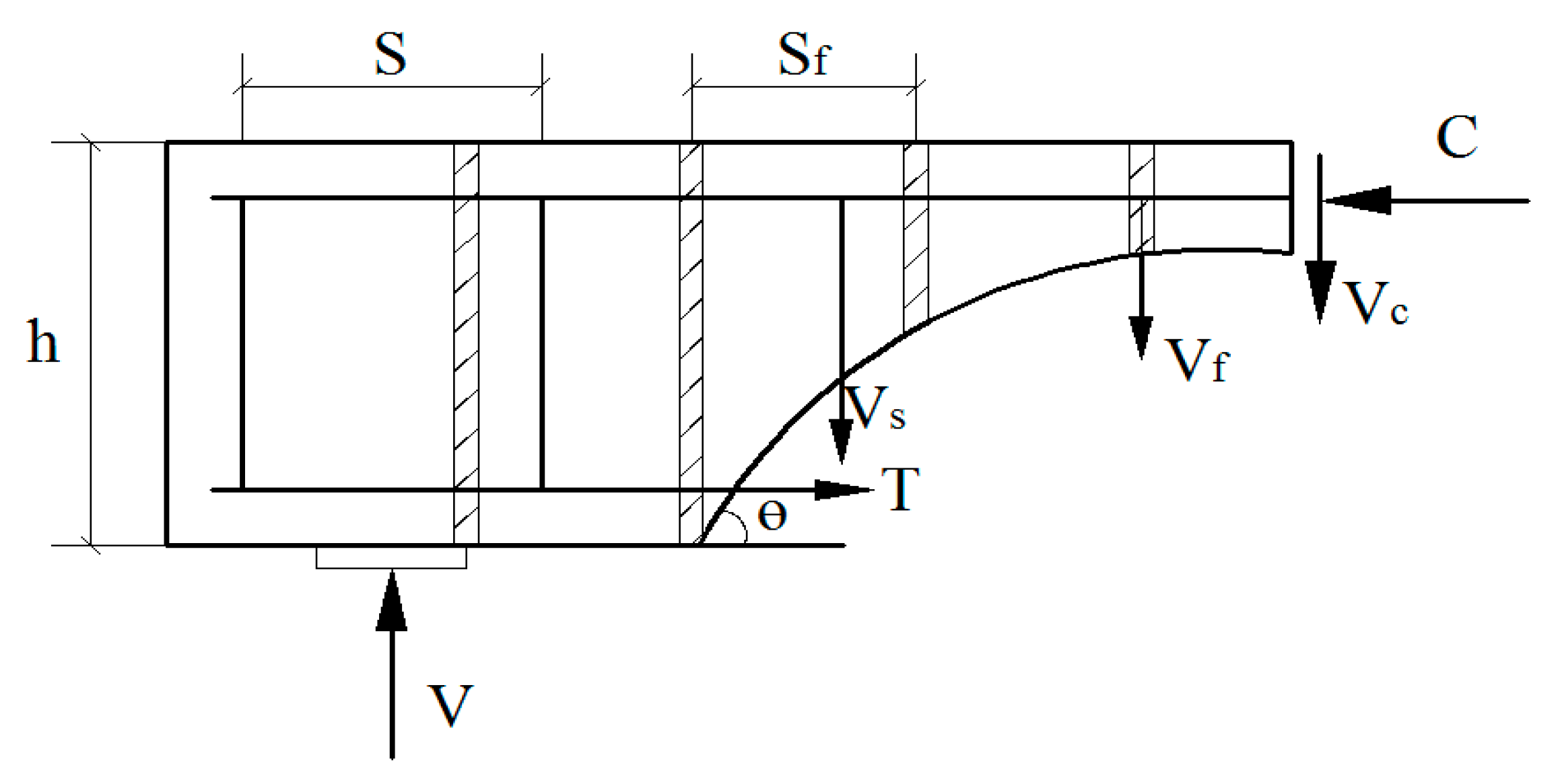
3.5.1. Calculation Formula of Shear Capacity
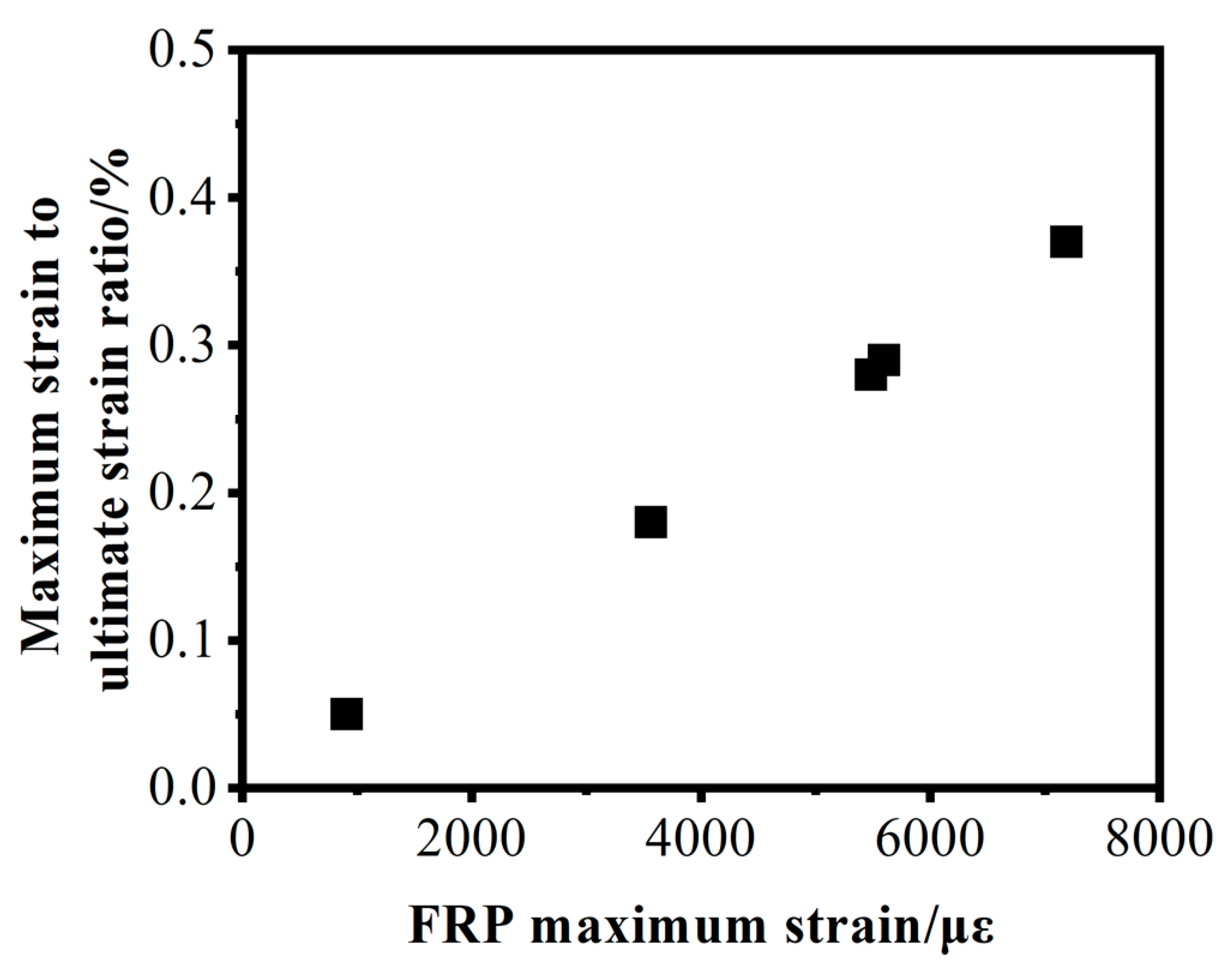
3.5.2. Determination of the Utilization Factor of FRP
3.5.3. Comparison of Experimental Values and Theoretical Values
4. Conclusions
- (1)
- The failure modes of the reinforced specimens are complex, including flexural failure and shear failure. Independent of failure mode, the stiffness degradation of the reinforced specimens is delayed and the displacement is reduced. The cracking load of the reinforced specimens in the pure flexural section did not increase, but the cracking load in the flexural section increased significantly, and the number and width of oblique cracks decreased significantly. Indeed, some cracks even stop developing when they encounter the FRP. The shear failure of the specimen strengthened by embedded optical circular GFRP bars is more likely than that by embedded thread GFRP bars. The bearing capacity of the reinforced specimen without the U-hoop is higher than that of the reinforced specimen with the U-hoop. However, since only one such specimen is designed, the dispersion of the results is large, and further verification is needed.
- (2)
- The concrete strength grade, longitudinal reinforcement ratio, surface characteristics, and the type and diameter of FRP bars have no effect on the mid-span displacement of the reinforced specimens. Conversely, the reinforcement method, FRP bar spacing, and shear span ratio of the specimens have a significant effect on the mid-span displacement of the reinforced specimens. The ultimate bearing capacity, stirrup strain and FRP bar strain of the strengthened specimens decrease with the increase in concrete strength grade and longitudinal reinforcement ratio. The increase rate of ultimate bearing capacity increases with the increase in concrete strength grade and decreases with the increase in longitudinal reinforcement ratio. The surface characteristics of FRP bars have a significant effect on the ultimate bearing capacity, ultimate bearing capacity increase rate, stirrup strain and FRP bar strain.
- (3)
- The shear failure mechanism of reinforced concrete beams strengthened with FRP embedded on the surface is similar to that of ordinary reinforced concrete beams, and the mechanism of FRP is similar to that of stirrups. Therefore, truss theory can be used for overall analysis. The test data show that using the method similar to that used for stirrups to calculate the shear capacity of FRP is also in line with the actual outcomes. According to the statistical results of the strain of FRP in the test and the results of data fitting, the utilization coefficient of FRP is determined to be 0.2.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pohoryles, D.A.; Melo, J.; Rossetto, T. Combined Flexural and Shear Strengthening of RC T-Beams with FRP and TRM: Experimental Study and Parametric Finite Element Analyses. Buildings 2021, 11, 520. [Google Scholar] [CrossRef]
- Colajanni, P.; Pagnotta, S.; Recupero, A.; Spinella, N. Shear resistance analytical evaluation for RC beams with transverse reinforcement with two different inclinations. Mater. Struct. 2020, 53, 18. [Google Scholar] [CrossRef]
- Colajanni, P.; Recupero, A.; Spinella, N. Shear strength degradation due to flexural ductility demand in circular RC columns. Bull. Earthq. Eng. 2015, 13, 1795–1807. [Google Scholar] [CrossRef]
- Lu, X.Z.; Chen, J.F.; Ye, L.P.; Teng, J.G.; Rotter, J.M. RC beams shear-strengthened with FRP: Stress distributions in the FRP reinforcement. Constr. Build. Mater. 2009, 23, 1544–1554. [Google Scholar] [CrossRef]
- Chen, J.-F.; Teng, J.G. Shear capacity of FRP-strengthened RC beams: FRP debonding. Constr. Build. Mater. 2003, 17, 27–41. [Google Scholar] [CrossRef]
- Koutas, L.N.; Tetta, Z.; Bournas, D.A.; Triantafillou, T.C. Strengthening of concrete structures with textile reinforced mortars: State-of-the-art review. J. Compos. Constr. 2019, 23, 03118001. [Google Scholar] [CrossRef]
- Deniaud, C.; Cheng, J.J.R. Reinforced concrete T-beams strengthened in shear with fiber reinforced polymer sheets. J. Compos. Constr. 2003, 7, 302–310. [Google Scholar] [CrossRef]
- Hawileh, R.A.; Nawaz, W.; Abdalla, J.A.; Saqan, E.I. Effect of flexural CFRP sheets on shear resistance of reinforced concrete beams. Compos. Struct. 2015, 122, 468–476. [Google Scholar] [CrossRef]
- Wegian, F.M.; Abdalla, H.A. Shear capacity of concrete beams reinforced with fiber reinforced polymers. Compos. Struct. 2005, 71, 130–138. [Google Scholar] [CrossRef]
- Hu, Z.; Zhou, X.; Guo, M.; Huang, X.; Hu, B. Enhancing the performance of CFRP shear-strengthened RC beams using “ductile” anchoring devices. Front. Mater. 2020, 7, 292. [Google Scholar] [CrossRef]
- Kotynia, R.; Oller, E.; Marí, A.; Kaszubska, M. Efficiency of shear strengthening of RC beams with externally bonded FRP materials–State-of-the-art in the experimental tests. Compos. Struct. 2021, 267, 113891. [Google Scholar] [CrossRef]
- Chen, G.M.; Li, S.W.; Fernando, D.; Liu, P.C.; Chen, J.F. Full-range FRP failure behaviour in RC beams shear-strengthened with FRP wraps. Int. J. Solids Struct. 2017, 125, 1–21. [Google Scholar] [CrossRef]
- Shahbazpanahi, S.; Ali, A.A.A.; Aznieta, F.N.; Kamgar, A.; Farzadnia, N. A Theoretical Method for Fracture Resistance of Shear-Strengthened RC Beams with FRP. Arab. J. Sci. Eng. 2014, 39, 3591–3597. [Google Scholar] [CrossRef]
- Belarbi, A.; Bae, S.-W.; Brancaccio, A. Behavior of full-scale RC T-beams strengthened in shear with externally bonded FRP sheets. Constr. Build. Mater. 2012, 32, 27–40. [Google Scholar] [CrossRef]
- Monti, G.; Liotta, M.A. Tests and design equations for FRP-strengthening in shear. Constr. Build. Mater. 2007, 21, 799–809. [Google Scholar] [CrossRef]
- Alam, M.S.; Hussein, A. Size effect on shear strength of FRP reinforced concrete beams without stirrups. J. Compos. Constr. 2013, 17, 507–516. [Google Scholar] [CrossRef]
- Ahmed, M.; Colajanni, P.; Pagnotta, S. Influence of Cross-Section Shape and FRP Reinforcement Layout on Shear Capacity of Strengthened RC Beams. Materials 2022, 15, 4545. [Google Scholar] [CrossRef] [PubMed]
- Pellegrino, C.; Modena, C. Fiber reinforced polymer shear strengthening of reinforced concrete beams with transverse steel reinforcement. J. Compos. Constr. 2002, 6, 104–111. [Google Scholar] [CrossRef]
- Bousselham, A.; Chaallal, O. Mechanisms of shear resistance of concrete beams strengthened in shear with externally bonded FRP. J. Compos. Constr. 2008, 12, 499–512. [Google Scholar] [CrossRef]
- CECS 146:2003; Technical Specification for Concrete Structures Strengthened with Carbon Fiber Sheets. China Plan Press: Beijing, China, 2003.




| Diameter d/mm | Power Level | Yield Strength fyk/MPa | Ultimate Tensile Strength fstk/MPa | Elongation δ/% |
|---|---|---|---|---|
| 8 | HPB235 | 307.5 | 537.5 | 30.5 |
| 12 | HRB335 | 365 | 550 | 28.5 |
| 18 | HRB335 | 375 | 625 | 29 |
| 20 | HRB335 | 355 | 520 | 28.5 |
| Concrete Strength Grade | Cube Compressive Strength/MPa | Axial Compressive Strength/MPa | Modulus of Elasticity/GPa |
|---|---|---|---|
| C20 | 21.4 | 14.3 | 26 |
| C30 | 31.5 | 21.1 | 31 |
| Adhesive | Splitting Tensile Strength/MPa | Bending Strength/MPa | Compressive Strength/MPa |
|---|---|---|---|
| JGN-type planting glue | 12.5 | 65.5 | 90.5 |
| FRP | Ultimate Tensile Strengthaverage/MPa | Modulus of Elasticity/GPa | Ultimate Tensile Strain/10-6 |
|---|---|---|---|
| GFRP | 1005 | 52 | 19,327 |
| CFRP | 2060 | 145 | 14,200 |
| Test Piece Number | Concrete Grade | Reinforcement Ratio | FRP Type | FRP Surface Characteristics | FRP Diameter | FRP Spacing | Shear Span Ratio | Reinforcement Method |
|---|---|---|---|---|---|---|---|---|
| BZS20C20 | C20 | 0.021 | — | — | — | — | 2.39 | — |
| BZS18C30 | C30 | 0.017 | — | — | — | — | 2.39 | — |
| BZS18C20 | C20 | 0.017 | — | — | — | — | 2.39 | — |
| L-G8D150S20C20U | C20 | 0.021 | GFRP | Thread | 8 | 150 | 2.39 | Add U-hoop |
| L-G8D150S18C30U | C30 | 0.017 | GFRP | Thread | 8 | 150 | 2.39 | Add U-hoop |
| L-G8D150S18C20U | C20 | 0.017 | GFRP | Thread | 8 | 150 | 2.39 | Add U-hoop |
| G-G8D150S20C20U | C20 | 0.021 | GFRP | Light circle | 8 | 150 | 2.39 | Add U-hoop |
| G-G8D150S18C30U | C30 | 0.017 | GFRP | Light circle | 8 | 150 | 2.39 | Add U-hoop |
| G-G8D150S18C20U | C20 | 0.017 | GFRP | Light circle | 8 | 150 | 2.39 | Add U-hoop |
| L-C8D150S18C20U | C20 | 0.017 | CFRP | Thread | 8 | 150 | 2.39 | Add U-hoop |
| L-G8D150S18C20 | C20 | 0.017 | GFRP | Thread | 8 | 150 | 2.39 | No U-hoop |
| L-G6D150S18C20U | C20 | 0.017 | GFRP | Thread | 6 | 150 | 2.39 | Add U-hoop |
| L-G10D150S18C20U | C20 | 0.017 | GFRP | Thread | 10 | 150 | 2.39 | Add U-hoop |
| L-G8D100S18C20U | C20 | 0.017 | GFRP | Thread | 8 | 100 | 2.39 | Add U-hoop |
| L-G8D200S18C20U | C20 | 0.017 | GFRP | Thread | 8 | 200 | 2.39 | Add U-hoop |
| L-G8D150S18C20U | C20 | 0.017 | GFRP | Thread | 8 | 150 | 2.79 | Add U-hoop |
| L-G8D150S18C20U | C20 | 0.017 | GFRP | Thread | 8 | 150 | 1.99 | Add U-hoop |
| Sample Number | Specimen Number | Failure Mode | Maximum Mid-Span Displacement (mm) | Diagonal Crack Width (mm) |
|---|---|---|---|---|
| 1 | BZS20C20 | Flexural failure | 29.87 | 4.40 |
| 2 | BZS18C30 | Flexural failure | 29.90 | 1.20 |
| 3 | BZS18C20 | Flexural failure | 28.37 | 1.48 |
| 4 | L-G8D150S20C20U | Flexural failure | 20.35 | 0.60 |
| 5 | L-G8D150S18C30U | Flexural failure | 23.23 | 0.48 |
| 6 | L-G8D150S18C20U | Flexural failure | 21.90 | 0.50 |
| 7 | G-G8D150S20C20U | Shear failure | 26.05 | – |
| 8 | G-G8D150S18C30U | Shear failure | 29.07 | – |
| 9 | G-G8D150S18C20U | Flexural failure | 23.71 | 0.90 |
| 10 | L-C8D150S18C20U | Flexural failure | 23.61 | 1.90 |
| 11 | L-G8D150S18C20 | Shear failure | 36.04 | 1.00 |
| 12 | L-G6D150S18C20U | Flexural failure | 22.38 | 0.40 |
| 13 | L-G10D150S18C20U | Flexural failure | 30.34 | 0.30 |
| 14 | L-G8D100S18C20U | Flexural failure | 29.66 | 9.40 |
| 15 | L-G8D200S18C20U | Shear failure | 26.64 | 0.35 |
| 16 | L-G8D150S18C20U (λ = 2.79) | Flexural failure | 26.60 | 0.50 |
| 17 | L-G8D150S18C20U (λ = 1.99) | Flexural failure | 32.29 | 0.90 |
| Test Piece Number | Pcr/kN | ΔPcr | Pcr1/kN | ΔPcr1 | Pu/kN | ΔPu | Stiffness/kN·mm−1 |
|---|---|---|---|---|---|---|---|
| BZS20C20 | 17 | — | 17.7 | — | 104.8 | — | 3.51 |
| BZS18C30 | 12.4 | — | 13.6 | — | 95.4 | — | 3.19 |
| BZS18C20 | 16.7 | — | 16.7 | — | 106.6 | — | 3.76 |
| L-G8D150S20C20U | 9.3 | −0.45 | 32.9 | 0.86 | 108.6 | 0.022 | 5.34 |
| L-G8D150S18C30U | 12.3 | −0.008 | 38 | 1.79 | 109.8 | 0.151 | 4.73 |
| L-G8D150S18C20U | 10.2 | −0.38 | 36 | 1.16 | 112.4 | 0.054 | 5.13 |
| G-G8D150S20C20U | 13.2 | −0.22 | 54 | 2.05 | 111.5 | 0.064 | 4.28 |
| G-G8D150S18C30U | 13.8 | 0.11 | 50 | 2.67 | 108.8 | 0.141 | 3.74 |
| G-G8D150S18C20U | 8.7 | −0.47 | 50 | 1.99 | 114.4 | 0.073 | 4.82 |
| L-C8D150S18C20U | 12 | −0.28 | 70 | 3.19 | 114.5 | 0.09 | 4.85 |
| L-G8D150S18C20 | 9.3 | −0.44 | 61 | 2.65 | 119.8 | 0.12 | 3.32 |
| L-G6D150S18C20U | 15.6 | −0.06 | 36 | 1.16 | 110.6 | 0.037 | 4.94 |
| L-G10D150S18C20U | 13.5 | −0.19 | 27.2 | 0.63 | 109.5 | 0.027 | 3.61 |
| L-G8D100S18C20U | 7.8 | −0.53 | 26 | 0.56 | 109.8 | 0.03 | 3.7 |
| L-G8D200S18C20U | 16.1 | −0.03 | 32 | 0.92 | 107.5 | 0.0084 | 4.04 |
| L-G8D150S18C20U (λ = 1.99) | 12.9 | — | 49.5 | — | 144.7 | — | 3.73 |
| L-G8D150S18C20U (λ = 2.79) | 13 | — | 40 | — | 99.2 | — | 4.48 |
| Test Piece Number | FRP Maximum Strain/με | Maximum Strain to Ultimate Strain Ratio |
|---|---|---|
| L-G8D150S18C30U | 7188 | 0.37 |
| G-G8D150S20C20U | 909 | 0.05 |
| G-G8D150S18C30U | 5597 | 0.29 |
| L-G8D150S18C20 | 5483 | 0.28 |
| L-G8D100S18C20U | 3562 | 0.18 |
| Test Piece Number | Main Crack Angle | ||
|---|---|---|---|
| L-G8D150S18C30U | 47° | 7.2 | 7.15 |
| G-G8D150S20C20U | 55° | 3.9 | 5.27 |
| G-G8D150S18C30U | 49° | 6.7 | 6.66 |
| L-G8D150S18C20 | 50° | 6.6 | 6.43 |
| L-G8D100S18C20U | 63° | 4.1 | 5.5 |
| Test Piece Number | |||
|---|---|---|---|
| L-G8D150S18C30U | 109.8 | 111.9 | 0.98 |
| G-G8D150S20C20U | 112.6 | 97.94 | 1.15 |
| G-G8D150S18C30U | 108.8 | 110.92 | 0.98 |
| L-G8D150S18C20 | 119.8 | 100.26 | 1.19 |
| L-G8D100S18C20U | 113.8 | 98.4 | 1.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Li, N.; Wang, Q.; Li, Z.; Qin, X. Shear Behavior of T-Shaped Concrete Beams Reinforced with FRP. Buildings 2022, 12, 2062. https://doi.org/10.3390/buildings12122062
Zhang Y, Li N, Wang Q, Li Z, Qin X. Shear Behavior of T-Shaped Concrete Beams Reinforced with FRP. Buildings. 2022; 12(12):2062. https://doi.org/10.3390/buildings12122062
Chicago/Turabian StyleZhang, Yannian, Ning Li, Qingjie Wang, Zhijun Li, and Xiaoyan Qin. 2022. "Shear Behavior of T-Shaped Concrete Beams Reinforced with FRP" Buildings 12, no. 12: 2062. https://doi.org/10.3390/buildings12122062
APA StyleZhang, Y., Li, N., Wang, Q., Li, Z., & Qin, X. (2022). Shear Behavior of T-Shaped Concrete Beams Reinforced with FRP. Buildings, 12(12), 2062. https://doi.org/10.3390/buildings12122062







