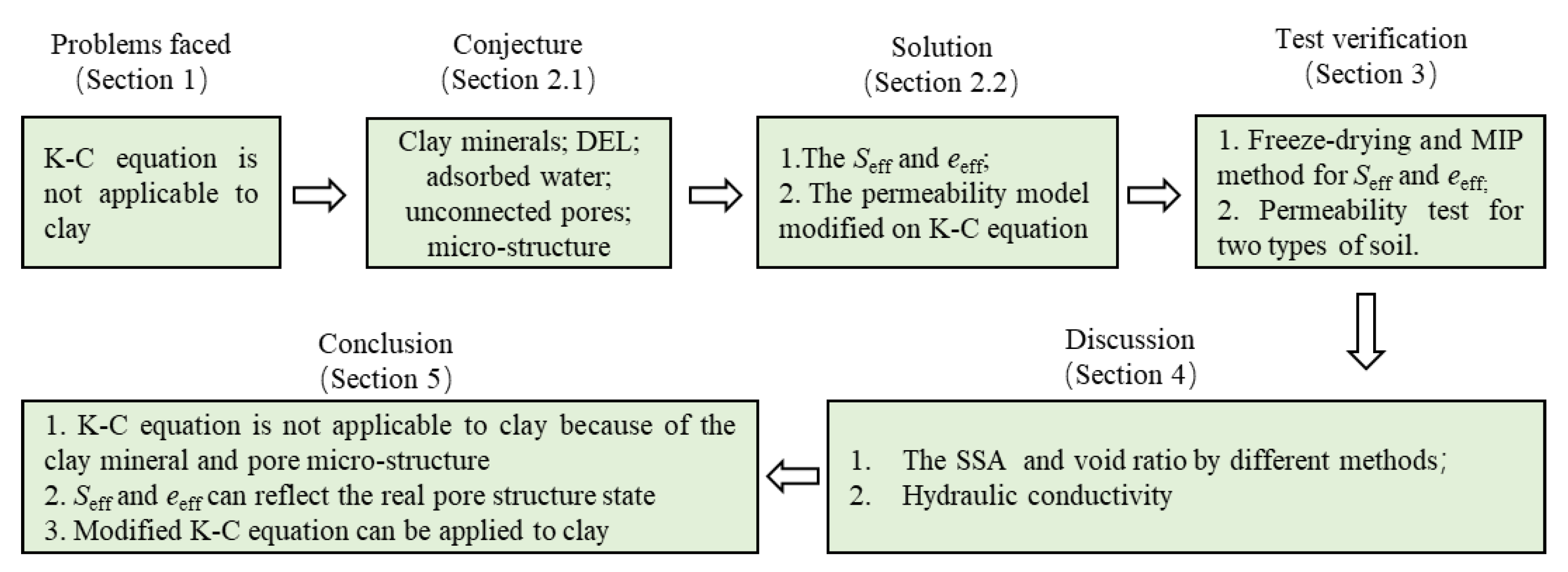
Permeability Prediction Model Modified on Kozeny-Carman for Building Foundation of Clay Soil
Abstract
1. Introduction
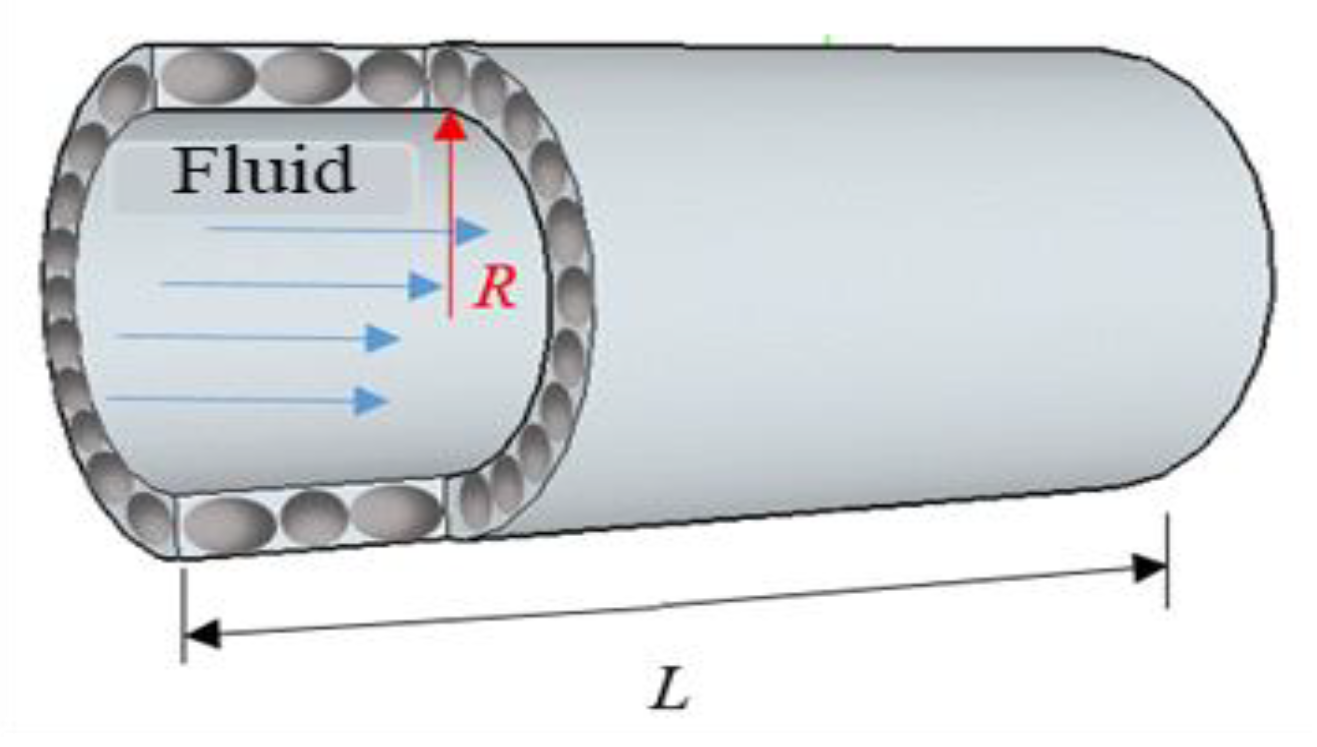
2. Effective Pores and the Permeability Prediction Model Modified on K-C Equation
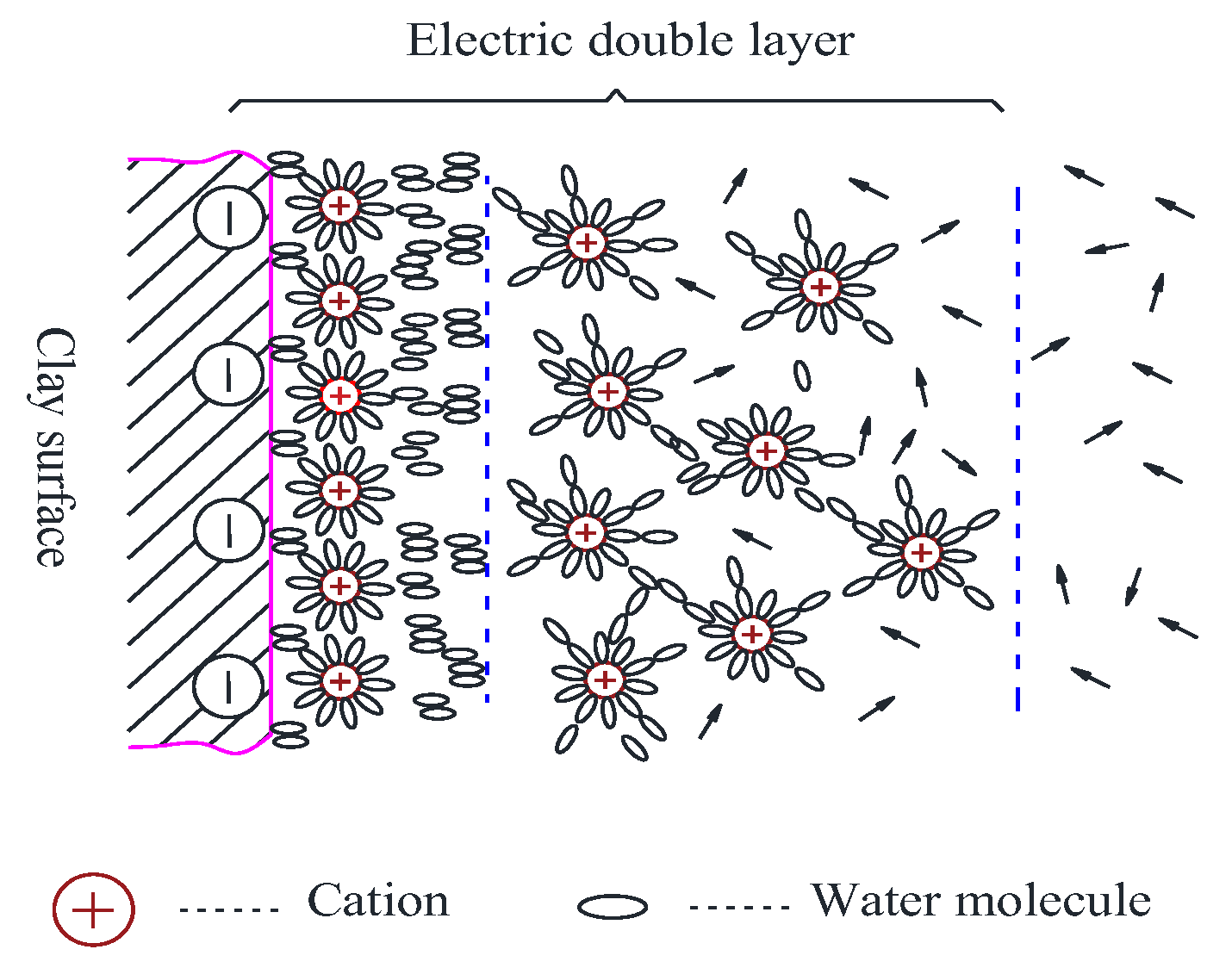
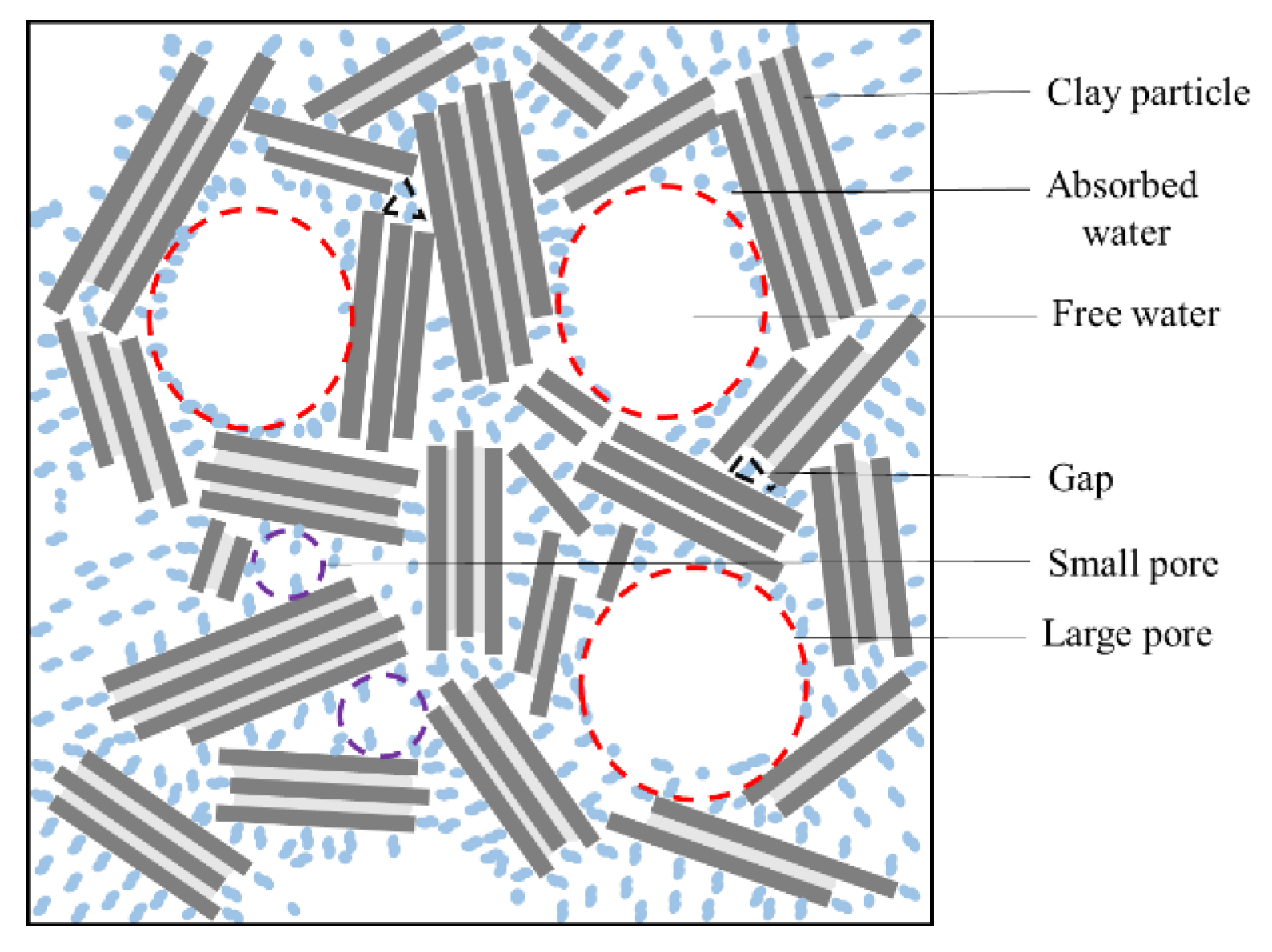
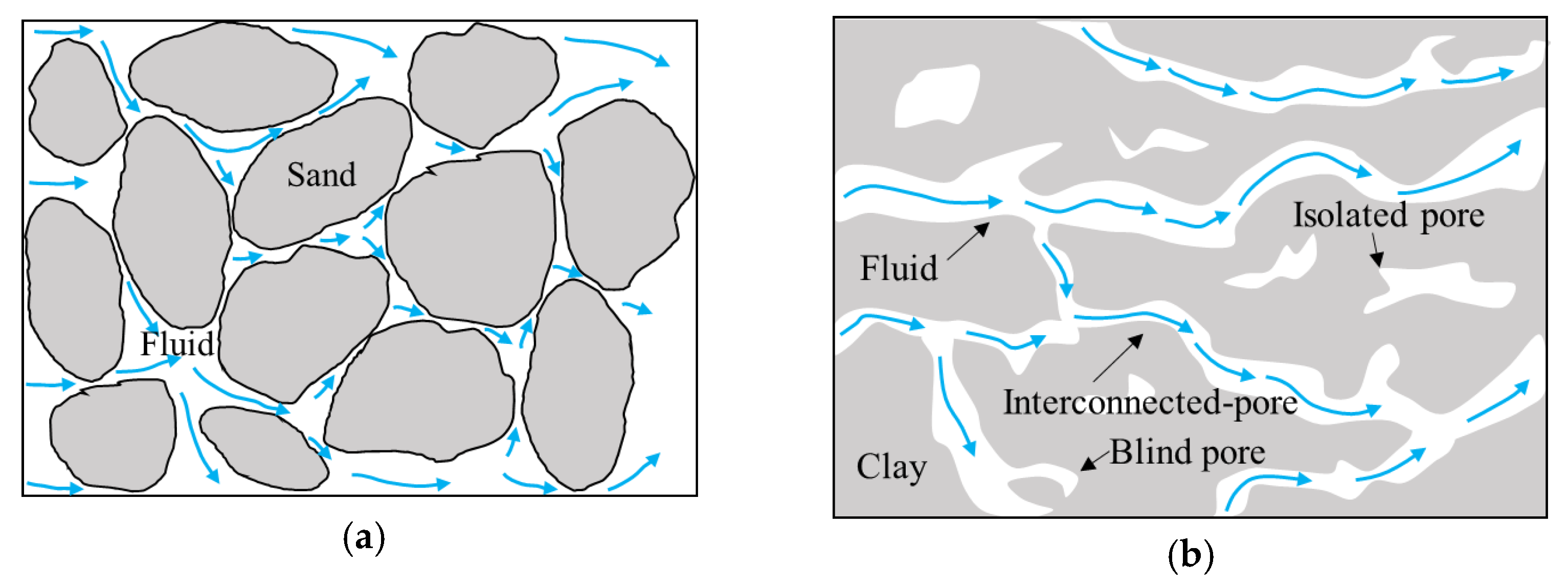
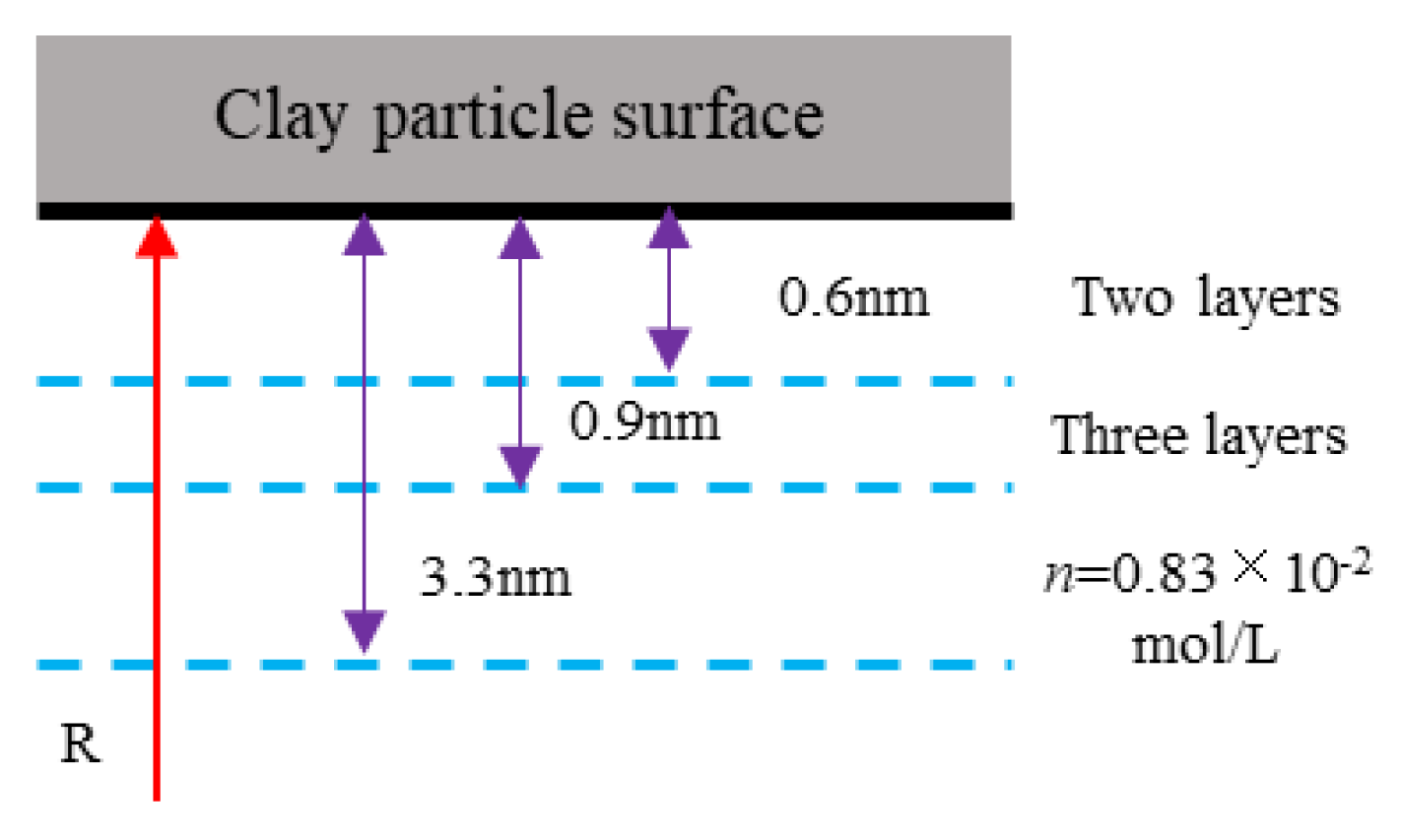
2.1. Effective Pores of Clay Seepage
2.2. The Permeability Prediction Model Modified on K-C Equation
3. Experimental Scheme and Result
3.1. Experimental Method and Scheme
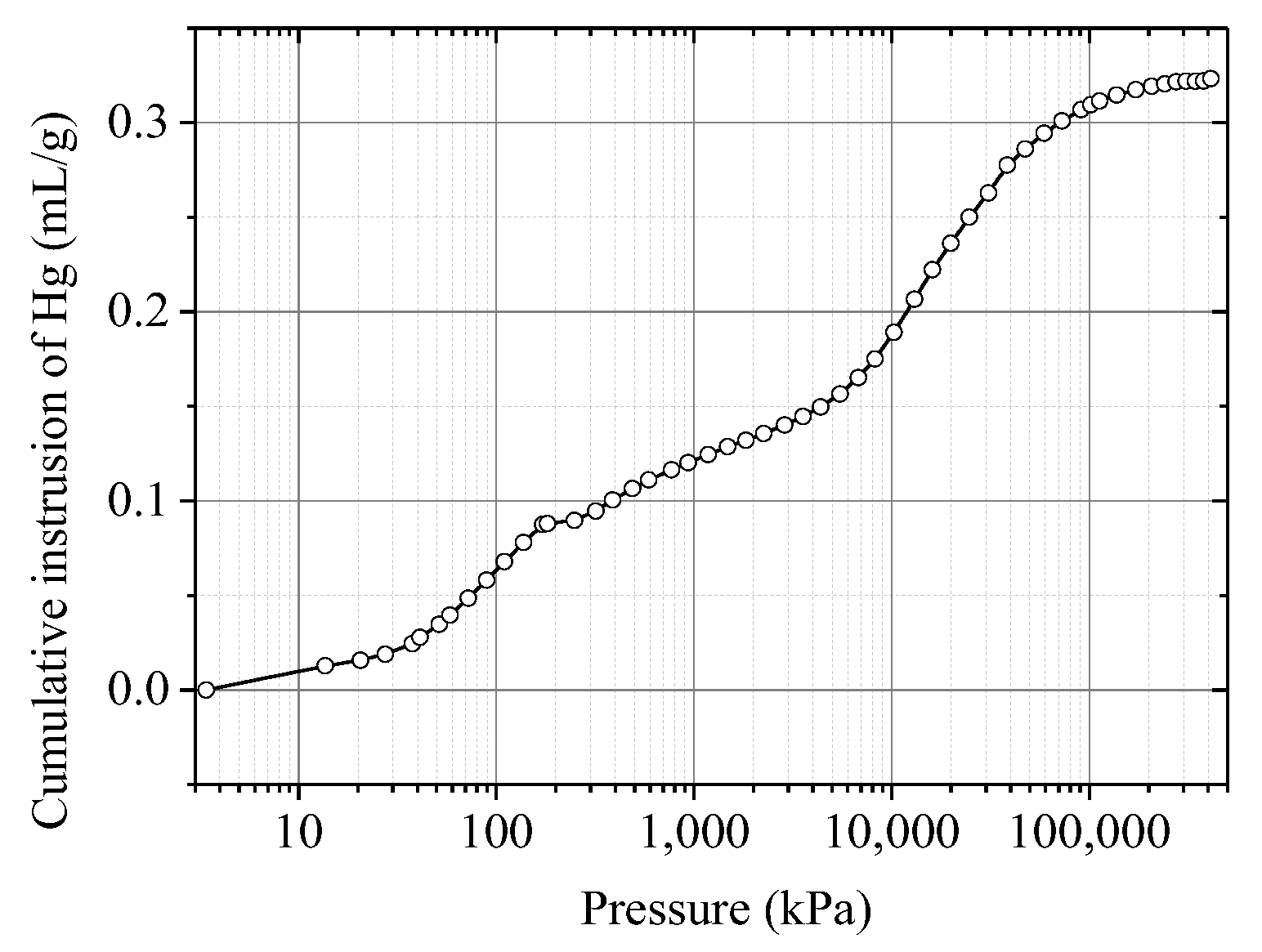
3.2. Experimental Results
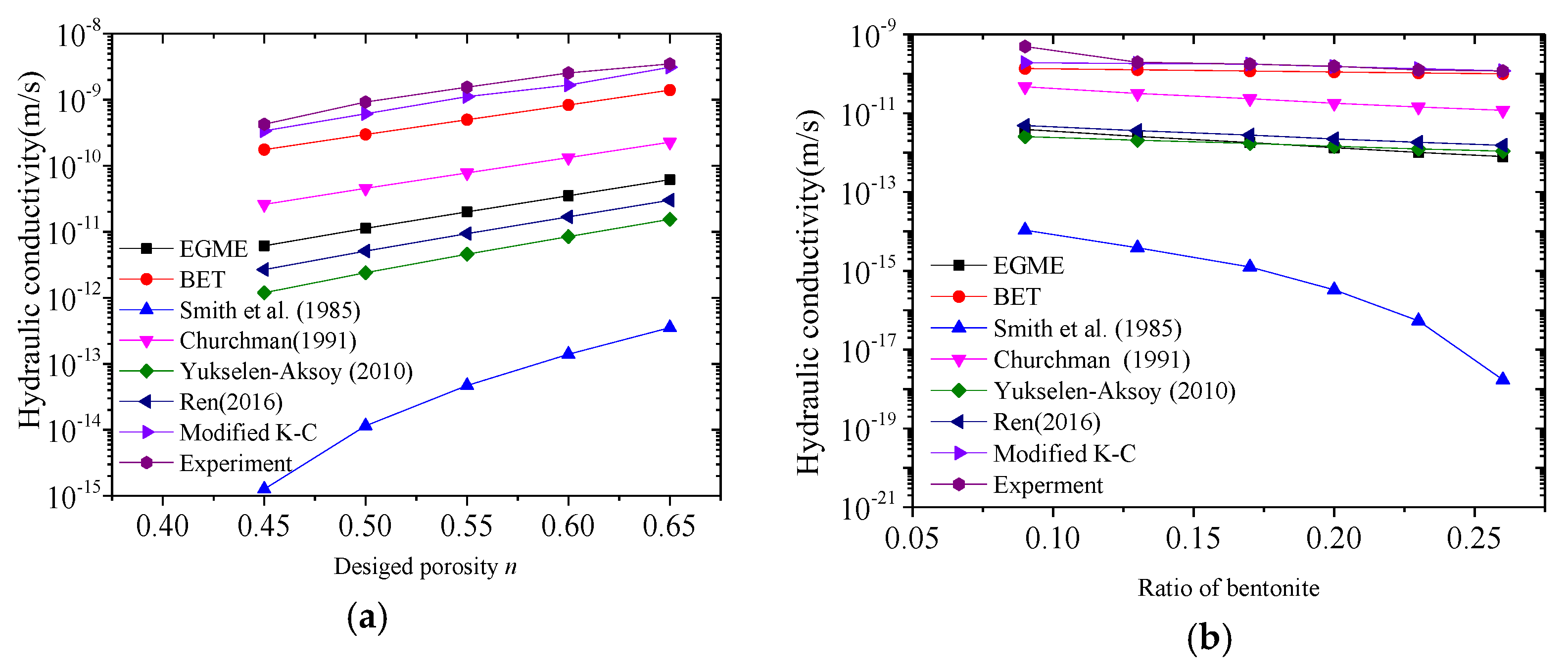
4. Discussion
4.1. The SSA and eeff by Different Methods
4.2. The Hydraulic Conductivity
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Chang, W.; Wang, P.; Wang, H.; Chai, S.; Yu, Y.; Xu, S. Simulation of the Q(2) loess slope with seepage fissure failure and seismic response via discrete element method. Bull. Eng. Geol. Environ. 2021, 80, 3495–3511. [Google Scholar] [CrossRef]
- Dong, H.; Huang, R.; Gao, Q. Rainfall infiltration performance and its relation to mesoscopic structural properties of a gravelly soil slope. Eng. Geol. 2017, 230, 1–10. [Google Scholar] [CrossRef]
- Jie, Y.X.; Jie, G.; Mao, Z.; Li, G. Seepage analysis based on boundary-fitted coordinate transformation method. Comput. Geotech. 2004, 31, 279–283. [Google Scholar] [CrossRef]
- Yao, Z.; Chen, Z.; Fang, X.; Wang, W.; Li, W.; Su, L. Elastoplastic damage seepage-consolidation coupled model of unsaturated undisturbed loess and its application. Acta Geotech. 2020, 15, 1637–1653. [Google Scholar] [CrossRef]
- Ba-Phu, N.; Kim, Y. An analytical solution for consolidation of PVD-installed deposit considering nonlinear distribution of hydraulic conductivity and compressibility. Eng. Comput. 2019, 36, 707–730. [Google Scholar]
- Pane, V.; Croce, P.; Znidarcic, D.; Ko, H.-Y.; Olsen, H.W.; Schiffman, R.L. Effects of consolidation on permeability measurements for soft clay. Géotechnique 1983, 33, 67–72. [Google Scholar] [CrossRef]
- Ren, X.; Zhao, Y.; Deng, Q.; Kang, J.; Li, D.; Wang, D. A relation of hydraulic conductivity—Void ratio for soils based on Kozeny-carman equation. Eng. Geol. 2016, 213, 89–97. [Google Scholar] [CrossRef]
- Chapuis, R.P. Predicting the saturated hydraulic conductivity of soils: A review. Bull. Eng. Geol. Environ. 2012, 71, 401–434. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, T.; Liu, F.; Peng, M.; Bate, B.; Wang, P. Hydro-mechanical coupled analysis of near-wellbore fines migration from unconsolidated reservoirs. Acta Geotech. 2022, 17, 3535–3551. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.; Xu, G.; Zheng, Y.; Kang, X. Improved model for predicting the hydraulic conductivity of soils based on the Kozeny–Carman equation. Hydrol. Res. 2021, 52, 719–733. [Google Scholar] [CrossRef]
- Hong, B.; Li, X.; Wang, L.; Li, L.; Xue, Q.; Meng, J. Using the effective void ratio and specific surface area in the Kozeny-Carman Equation to predict the hydraulic conductivity of loess. Water 2020, 12, 24. [Google Scholar] [CrossRef]
- Jang, J.; Narsilio, G.A.; Santamarina, J.C. Hydraulic conductivity in spatially varying media—A pore-scale investigation. Geophys. J. Int. 2015, 184, 1167–1179. [Google Scholar] [CrossRef]
- Chai, J.C.; Agung, P.M.A.; Hino, T.; Igaya, Y.; Carter, J.P. Estimating hydraulic conductivity from piezocone soundings. Geotechnique 2011, 8, 699–708. [Google Scholar] [CrossRef]
- Costa, A. Permeability-porosity relationship: A reexamination of Kozeny-Carman equation based on a fractal pore-space geometry assumption. Geophys. Res. Lett. 2006, 33, 87–94. [Google Scholar] [CrossRef]
- Asger, M.N.; Fridolin, O.; Henrik, B. Reexamination of Hagen-Poiseuille flow: Shape dependence of the hydraulic resistance in microchannels. Phys. Rev. E 2005, 71, 057301. [Google Scholar]
- Chapuis, R.P.; Legare, P.P. A simple method for determining the surface area of fine aggregates and fillers in bituminous mixtures. In Proceedings of the Effects of Aggregates and Mineral Fillers on Asphalt Mixture Performance, San Diego, CA, USA, 10 December 1991; pp. 177–186. [Google Scholar]
- Samarasinghe, A.M.; Huang, Y.H.; Drnevich, V.P. Permeability and consolidation of normally consolidated soils. J. Geotech. Eng. Div. 1982, 108, 835–850. [Google Scholar] [CrossRef]
- Childs, E.C. Dynamics of fluids in Porous Media. Eng. Geol. 1972, 7, 174–175. [Google Scholar] [CrossRef]
- Mesri, G.; Olson, R.E. Consolidation characteristics of montmorillonite. Geotechnique 1971, 4, 341–352. [Google Scholar] [CrossRef]
- Taylor, D.W. Fundamentals of soil mechanics. Soil Sci. 1948, 66, 161. [Google Scholar] [CrossRef]
- Carman, P.C. Permeability of saturated sands, soils and clays. J. Agric. Sci. 1939, 2, 12. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid flow through granular beds. Chem. Eng. Res. Des. 1937, 75, S32–S48. [Google Scholar] [CrossRef]
- Kozeny, J. Uber Kapillare Leitung des Wassers im Boden. Sitzungsber. Akad. Wiss. 1927, 136, 271–306. [Google Scholar]
- Li, M.; Chen, H.; Li, X.; Liu, L.; Lin, J. Permeability of granular media considering the effect of grain composition on tortuosity. Int. J. Eng. Sci. 2022, 174, 103658. [Google Scholar] [CrossRef]
- Xu, P.; Zhang, L.; Rao, B.; Qiu, S.; Shen, Y.; Wang, M. A fractal scaling law between tortuosity and porosity in porous media. Fractals 2020, 28, 2050025. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, W.; Zhang, X.; Long, G.; Fan, J.; Chen, H.; Deng, L. A novel fractal solution for permeability and Kozeny-Carman constant of fibrous porous media made up of solid particles and porous fibers. Powder Technol. 2019, 349, 92–98. [Google Scholar] [CrossRef]
- Bayesteh, H.; Mirghasemi, A.A. Numerical simulation of porosity and tortuosity effect on the permeability in clay: Microstructural approach. Soils Found. 2015, 55, 1158–1170. [Google Scholar] [CrossRef]
- Luo, L.; Yu, B.; Cai, J.; Zeng, X. Numerical simulation of tortuosity for fluid flow in two-dimensional pore fractal models of porous media. Fractals 2014, 22, 1450015. [Google Scholar] [CrossRef]
- Matyka, M.; Khalili, A.; Koza, Z. Tortuosity-porosity relation in porous media flow. Phys. Rev. E 2008, 78, 026306. [Google Scholar] [CrossRef]
- Scholes, O.N.; Clayton, S.A.; Hoadley, A.F.A.; Tiu, C. Permeability anisotropy due to consolidation of compressible porous media. Transp. Porous Media 2007, 68, 365–387. [Google Scholar] [CrossRef]
- Ichikawa, Y.; Kawamura, K.; Fujii, N.; Kitayama, K. Microstructure and micro/macro-diffusion behavior of tritium in bentonite. Appl. Clay Sci. 2004, 26, 75–90. [Google Scholar] [CrossRef]
- Mathavan, G.N.; Viraraghavan, T. Coalescence/filtration of an oil-in-water emulsion in a peat bed. Water Res. 1992, 26, 91–98. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Elsevier: New York, NY, USA, 1972. [Google Scholar]
- Ahuja, L.R.; Naney, J.W.; Williams, R.D. Estimating soil water characteristics from simpler properties or limited Data. Soil Sci. Soc. Am. J. 1985, 49, 1100–1105. [Google Scholar] [CrossRef]
- Ahuja, L.R.; Naney, J.W.; Green, R.E.; Nielsen, D.R. Macroporosity to characterize spatial variability of hydraulic conductivity and effects of land management. Soil Sci. Soc. Am. J. 1984, 48, 699. [Google Scholar] [CrossRef]
- Horton, R.; Thompson, M.L.; Mcbride, J.F. Estimating transit times of noninteracting pollutants through compacted soil materials. Soil Sci. Soc. Am. J. 1985, 51, 48–53. [Google Scholar] [CrossRef]
- Meegoda, N.J.; Knodel, P.C.; Gunasekera, S.D. A new method to measure the effective porosity of clays. ASTM Geotech. Test. J. 1992, 15, 12. [Google Scholar]
- Antognozzi, M.; Humphris, A.; Miles, M.J. Observation of molecular layering in a confined water film and study of the layers viscoelastic properties. Appl. Phys. Lett. 2001, 78, 300–302. [Google Scholar] [CrossRef]
- Dolinar, B.; Trcek, B. A new relationship between the mobile and the adsorbed water in fine-grained soils using an effective void-ratio estimation. Bull. Eng. Geol. Environ. 2019, 78, 4623–4631. [Google Scholar] [CrossRef]
- Koponen, A.; Kataja, M.; Timonen, J. Permeability and effective porosity of porous media. Phys. Rev. E 1997, 3, 3319–3325. [Google Scholar] [CrossRef]
- Singh, P.N.; Wallender, W.W. Effects of adsorbed water layer in predicting saturated hydraulic conductivity for clays with Kozeny–Carman equation. J. Geotech. Geoenvironmental Eng. 2008, 134, 829–836. [Google Scholar] [CrossRef]
- Urumović, K.; Urumović, S.K. The effective porosity and grain size relations in permeability functions. Hydrol. Earth Syst. Sci. Discuss. 2014, 11, 6675–6714. [Google Scholar]
- Sanzeni, A.; Colleselli, F.; Grazioli, D. Specific surface and hydraulic conductivity of fine-grained soils. J. Geotech. Geoenvironmental Eng. 2013, 139, 1828–1832. [Google Scholar] [CrossRef]
- Indraratna, B.; Trani, L. The use of particle size distribution by surface area method in predicting the saturated hydraulic conductivity of graded granular soils. Géotechnique 2010, 60, 957–962. [Google Scholar]
- Carrier, W.D., III. Goodbye, Hazen; Hello, Kozeny-Carman. J. Geotech. Geoenvironmental Eng. 2003, 129, 1054–1056. [Google Scholar] [CrossRef]
- Gregg, S.; Sing, K. Adsorption Surface Area and Porosity; Academic Press: London, UK, 1967. [Google Scholar]
- Santamarina, J.C.; Klein, K.A.; Wang, Y.H.; Prencke, E. Specific surface: Determination and relevance. Can. Geotech. J. 2002, 39, 233–241. [Google Scholar] [CrossRef]
- Phelps, G.W.; Harris, D.L. Specific surface and dry strength by methylene blue adsorption. Ceram. Bull. 1968, 12, 1146–1150. [Google Scholar]
- Churchman, G.J.; Burke, C.M.; Parfitt, R.L. Comparison of various methods for the determination of specific surfaces of sub soils. Eur. J. Soil Sci. 2010, 42, 449–461. [Google Scholar] [CrossRef]
- Cerato, A.B.; Lutenegger, A.J. Determination of surface area of fine-grained soils by the Ethylene Glycol Monoethyl Ether (EGME) method. Geotech. Test. J. 2002, 25, GTJ11087J. [Google Scholar]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Garzón, E.; Sánchez-Soto, P.J. An improved method for determining the external specific surface area and the plasticity index of clayey samples based on a simplified method for non-swelling fine-grained soils. Appl. Clay Sci. 2015, 115, 97–107. [Google Scholar] [CrossRef]
- Akin, I.D.; Likos, W. Single-point and multi-point water-sorption methods for specific surface areas of clay. Geotech. Test. J. 2016, 39, 20150117. [Google Scholar] [CrossRef]
- Locat, J.; Lefebvre, G.; Ballivy, G. Mineralogy, chemistry, and physical properties interrelationships of some sensitive clays from Eastern Canada. Can. Geotech. J. 1984, 21, 530–540. [Google Scholar] [CrossRef]
- Cerato, A. Influence of Specific Surface Area on Geotechnical Characteristics of Fine-Grained Soils. Master’s Thesis, Civil Engineering, College of Engineering, University of Massachusetts, Amherst, MA, USA, 2001. [Google Scholar]
- Macek, M.; Mauko, A.; Mladenovic, A.; Majes, B.; Petkovsek, A. A comparison of methods used to characterize the soil specific surface area of clays. Appl. Clay Sci. 2013, 83–84, 144–152. [Google Scholar] [CrossRef]
- Kobayashi, I.; Owada, H.; Ishii, T.; Iizuka, A. Evaluation of specific surface area of bentonite-engineered barriers for Kozeny-Carman law. Soils Found. 2017, 57, 683–697. [Google Scholar] [CrossRef]
- Ismeik, M.; Al-Rawi, O. Modeling soil specific surface area with artificial neural networks. Geotech. Test. J. 2021, 37, 20130146. [Google Scholar] [CrossRef]
- Sharma, A.; Hazra, B.; Spagnoli, G.; Sekharan, S. Probabilistic estimation of specific surface area and cation exchange capacity: A global multivariate distribution. Can. Geotech. J. 2021, 58, 1077–1094. [Google Scholar] [CrossRef]
- Meegoda, J.N.; Martin, L. In-situ determination of specific surface area of clays. Geotech. Geol. Eng. 2019, 37, 465–474. [Google Scholar] [CrossRef]
- Dolinar, B. Predicting the hydraulic conductivity of saturated clays using plasticity-value correlations. Appl. Clay Sci. 2009, 45, 90–94. [Google Scholar] [CrossRef]
- Dolinar, B.; Misic, M.; Trauner, L. Correlation between surface area and atterberg limits of fine-grained soils. Clays Clay Miner. 2007, 55, 519–523. [Google Scholar] [CrossRef]
- Yukselen-Aksoy, Y.; Kaya, A. Method dependency of relationships between specific surface area and soil physicochemical properties. Appl. Clay Sci. 2010, 50, 182–190. [Google Scholar] [CrossRef]
- Deng, Y.; Liu, Q.; Cui, Y.; Wang, Q.; Liu, S. Revisiting relationships among specific surface area, soil consistency limits, and group index of clays. J. Test. Eval. 2019, 47, 1392–1404. [Google Scholar] [CrossRef]
- Spagnoli, G.; Shimobe, S. A statistical reappraisal of the relationship between liquid limit and specific surface area, cation exchange capacity and activity of clays. J. Rock Mech. Geotech. Eng. 2019, 11, 874–881. [Google Scholar] [CrossRef]
- Mitchell, J.K.; Soga, K. Fundamentals of Soil Behavior, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Chen, J.; Fang, Y.; Gu, R.; Shu, H.; Ba, L.; Li, W. Study on pore size effect of low permeability clay seepage. Arab. J. Geosci. 2019, 12, 238. [Google Scholar] [CrossRef]
- GB/T 50123-2019; Standard for Geotechnical Testing Method. Ministry of Housing and Urban-Rural Development: Beijing, China, 2019.
- BS ISO 9277-2010; Determination of the Specific Surface Area of Solids by Gas Adsorption. BET Method. BSI Group: London, UK, 2010.
- ASTM D2434-68(2000); Standard Test Method for Permeability of Granular Soils (Constant Head). ASTM: West Conshohocken, PA, USA, 2000.
- Zeng, Z.; Cui, Y.J.; Talandier, J. Evaluating the influence of soil plasticity on hydraulic conductivity based on a general capillary model. Eng. Geol. 2020, 278, 105826. [Google Scholar] [CrossRef]
- Wang, Q.; Cui, Y.-J.; Tang, A.M.; Li, X.-L.; Ye, W.-M. Time- and density-dependent microstructure features of compacted bentonite. Soils Found. 2014, 54, 657–666. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, H.; Chen, P. Influence of hyper-alkaline solution infiltration on microscopic pore structure of compacted GMZ bentonite. J. Zhejiang Univ. Eng. Sci. 2013, 47, 602–608. [Google Scholar]
- Smith, C.W.; Hadas, A.; Dan, J.; Koyumdjisky, H. Shrinkage and Atterberg limits in relation to other properties of principal soil types in Israel. Geoderma 1985, 35, 47–65. [Google Scholar] [CrossRef]
- Churchaman, G.J.; Burke, C.M. Properties of sub soils in relation to various measures of surface area and water content. Eur. J. Soil Sci. 1991, 42, 463–478. [Google Scholar] [CrossRef]


| Sample No. | Quartz | Feldspar | Illite | Chlorite | Kaolinite | Others |
|---|---|---|---|---|---|---|
| N1 | 19.9 | 25.7 | 23.8 | 30.6 | ||
| N2 | 24.0 | 7.2 | 24.3 | 24.3 | 22.1 | |
| N3 | 25.8 | 27.8 | 23.8 | 22.6 | ||
| N4 | 24.8 | 23.4 | 26.3 | 23.3 | 2.2 | |
| N5 | 21.4 | 16.9 | 30.0 | 31.8 | ||
| N6 | 22.5 | 26.3 | 24.4 | 26.9 | ||
| N7 | 24.0 | 24.9 | 19.9 | 29.3 | 1.9 | |
| N8 | 22.2 | 27.4 | 25.9 | 24.5 | ||
| N9 | 19.7 | 19.0 | 30.0 | 31.3 | ||
| N10 | 23.2 | 26.5 | 25.3 | 23.2 | 1.9 |
| No. | Component | Porosity | Test Items | No. | Component | Porosity | Test Items |
|---|---|---|---|---|---|---|---|
| (mbent:mkao) | (mnatural:mbent) | ||||||
| S1 | bentonite+ kaolinite(0.134:1) | 0.45 | PL; Ip; e; SSA k | Y1 | 0.9:0.1 | 0.48 | PL; Ip; e; SSA k |
| S2 | 0.5 | Y2 | 0.85:0.15 | ||||
| S3 | 0.55 | Y3 | 0.8:0.2 | ||||
| S4 | 0.6 | Y4 | 0.75:0.25 | ||||
| S5 | 0.65 | Y5 | 0.7:0.3 | ||||
| Y6 | 0.65:0.35 |
| No. | n | Mass Ratio | EGME | BET | Smith et al. (1985) [74] | Churchman and Burke (1991) [75] | Yeliz Yukselen-Aksoy (2010) [63] | Ren (2016) [7] | Seff |
|---|---|---|---|---|---|---|---|---|---|
| S1 | 0.45 | 0.143:1 | 79.8 | 19.8 | 411.1 | 45.7 | 135.9 | 106.0 | 13.0 |
| S2 | 0.5 | 0.143:1 | 79. 8 | 19.8 | 411.1 | 45.7 | 135.9 | 106.0 | 12.5 |
| S3 | 0.55 | 0.143:1 | 79. 8 | 19.8 | 411.1 | 45.7 | 135.9 | 106.0 | 12.4 |
| S4 | 0.6 | 0.143:1 | 79. 8 | 19.8 | 411.1 | 45.7 | 135.9 | 106.0 | 12.2 |
| S5 | 0.65 | 0.143:1 | 79. 8 | 19.8 | 411.1 | 45.7 | 135.9 | 106.0 | 12.2 |
| Y1 | 0.48 | 0.1:1 | 108.2 | 26.1 | 388.2 | 41.7 | 124.1 | 100.2 | 21.5 |
| Y2 | 0.48 | 0.15:1 | 124.1 | 27.1 | 431.0 | 49.1 | 132.9 | 111.0 | 21.8 |
| Y3 | 0.48 | 0.2:1 | 138.7 | 21.4 | 470.3 | 55.9 | 140.9 | 121.0 | 22.0 |
| Y4 | 0.48 | 0.25:1 | 152.1 | 28.0 | 506.4 | 62.1 | 148.4 | 130.2 | 22.9 |
| Y5 | 0.48 | 0.3:1 | 164.5 | 29.5 | 539.8 | 67.8 | 155.2 | 138.6 | 23.6 |
| Y6 | 0.48 | 0.35:1 | 175.9 | 30.2 | 570.7 | 73.1 | 161.6 | 146.5 | 24.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Tong, H.; Yuan, J.; Fang, Y.; Gu, R. Permeability Prediction Model Modified on Kozeny-Carman for Building Foundation of Clay Soil. Buildings 2022, 12, 1798. https://doi.org/10.3390/buildings12111798
Chen J, Tong H, Yuan J, Fang Y, Gu R. Permeability Prediction Model Modified on Kozeny-Carman for Building Foundation of Clay Soil. Buildings. 2022; 12(11):1798. https://doi.org/10.3390/buildings12111798
Chicago/Turabian StyleChen, Jian, Huawei Tong, Jie Yuan, Yingguang Fang, and Renguo Gu. 2022. "Permeability Prediction Model Modified on Kozeny-Carman for Building Foundation of Clay Soil" Buildings 12, no. 11: 1798. https://doi.org/10.3390/buildings12111798
APA StyleChen, J., Tong, H., Yuan, J., Fang, Y., & Gu, R. (2022). Permeability Prediction Model Modified on Kozeny-Carman for Building Foundation of Clay Soil. Buildings, 12(11), 1798. https://doi.org/10.3390/buildings12111798








