Simplified Weather-Related Building Energy Disaggregation and Change-Point Regression: Heating and Cooling Energy Use Perspective
Abstract
1. Introduction
1.1. Background
1.2. Aims and Scope
- (Step 1) collection of the detailed hourly measurement dataset;
- (Step 2) aggregation of measured end-uses into energy sources and time resolution from hourly to monthly;
- (Step 3) disaggregation of each energy source into yearly heating and cooling energy uses again; and
- (Step 4) comparison of each group by ANOVA and correlation analysis to check causes of the largest estimation deviation.
2. Methods and Materials
2.1. Data Collection
- Space heating: energy consumption of the main heating systems. This includes central heating plants (boiler, etc.), heating-related water circulation pumps, and individual heating equipment (EHP, GHP, hot air heater, electric heating panel, etc.).
- Space cooling: energy consumption of the main cooling systems. This includes central cooling plants (chiller, cooling tower), cooling-related water circulation pump, and individual cooling equipment (EHP, GHP, PAC, etc.).
- Domestic hot water: energy consumption of the main hot water supply systems. This includes central hot water plants (boiler, etc.), water circulation pumps, and individual hot water supply equipment (electric water heater, gas water heater, etc.).
- Air movement: energy consumption of the fans of main air handling units (AHU, outdoor air conditioner, FCU, EHP, GHP, etc.). This includes air-moving processes by fans, such as heating, cooling, ventilation, and air circulation.
- Lighting: electricity consumption of lighting equipment branched from the distribution panel.
- Electric appliances: electricity consumption of the plug-load branched from the distribution panel.
- Indoor transportation: electricity consumption of elevators and escalators.
- Building auxiliary devices: electricity consumption of the water pumps except for heating and cooling use.
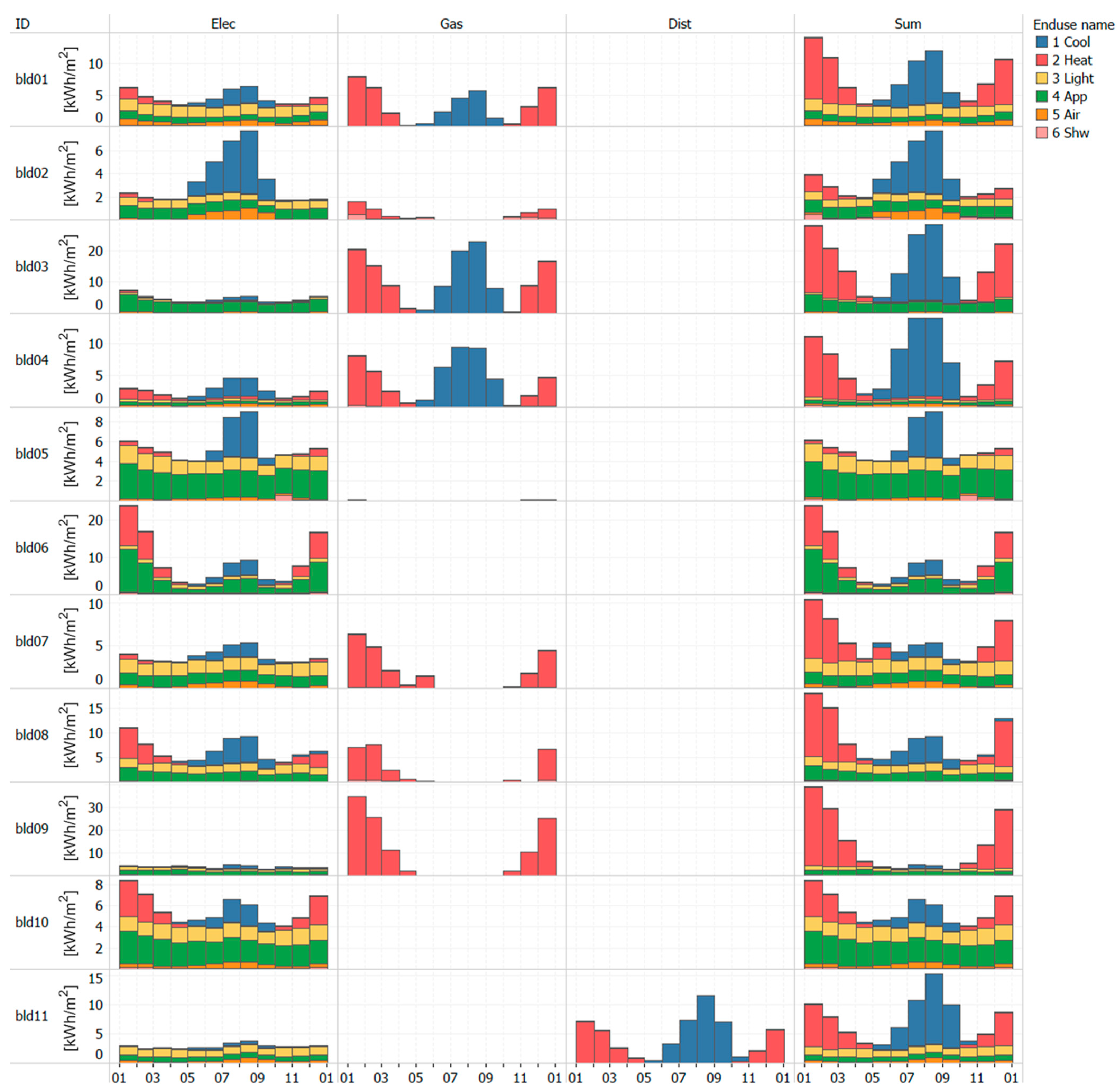
2.2. Energy Profiles of Target Buildings
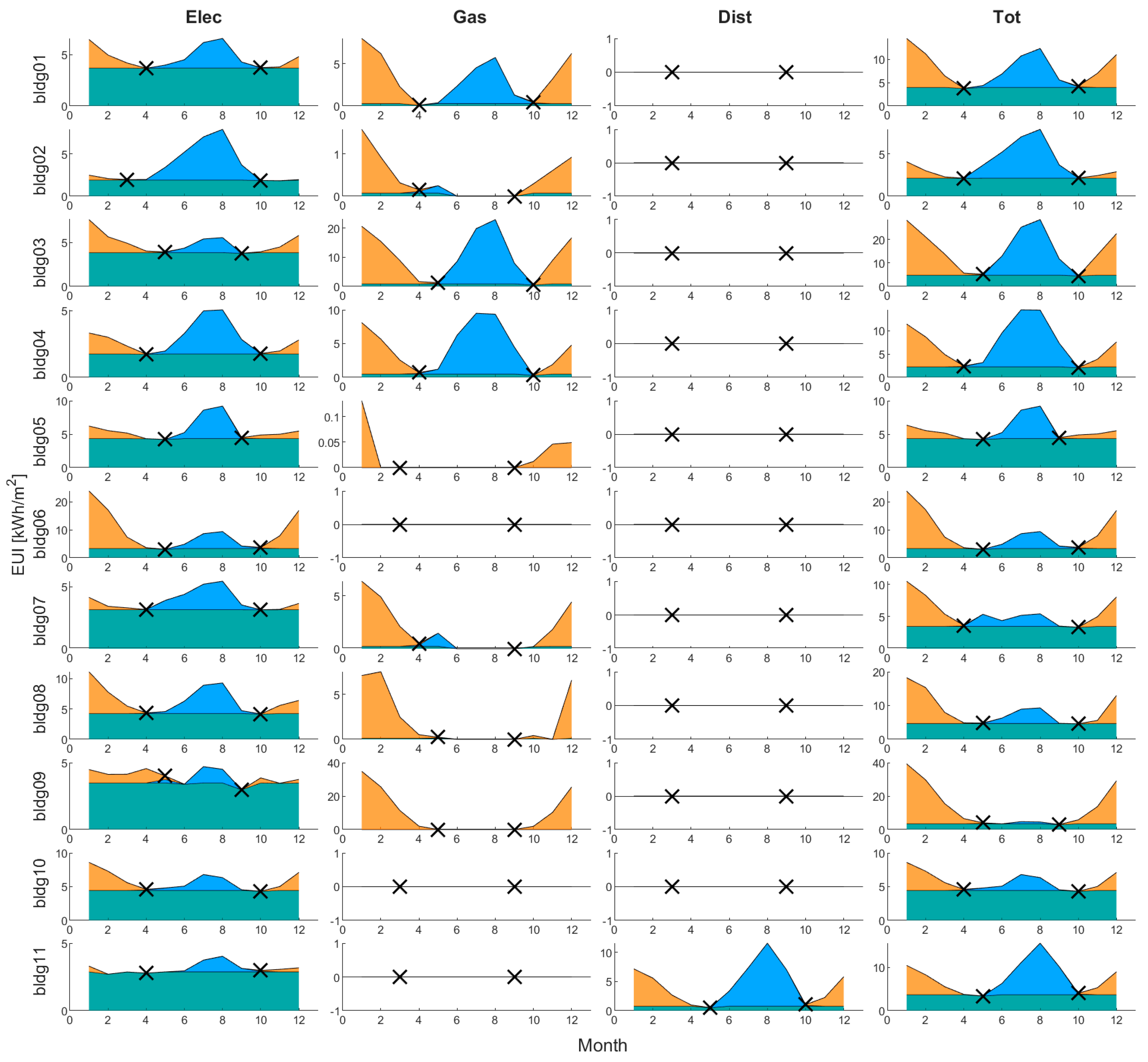
2.3. Simplified Weather-Sensitive Energy Disaggregation (SED) Approach
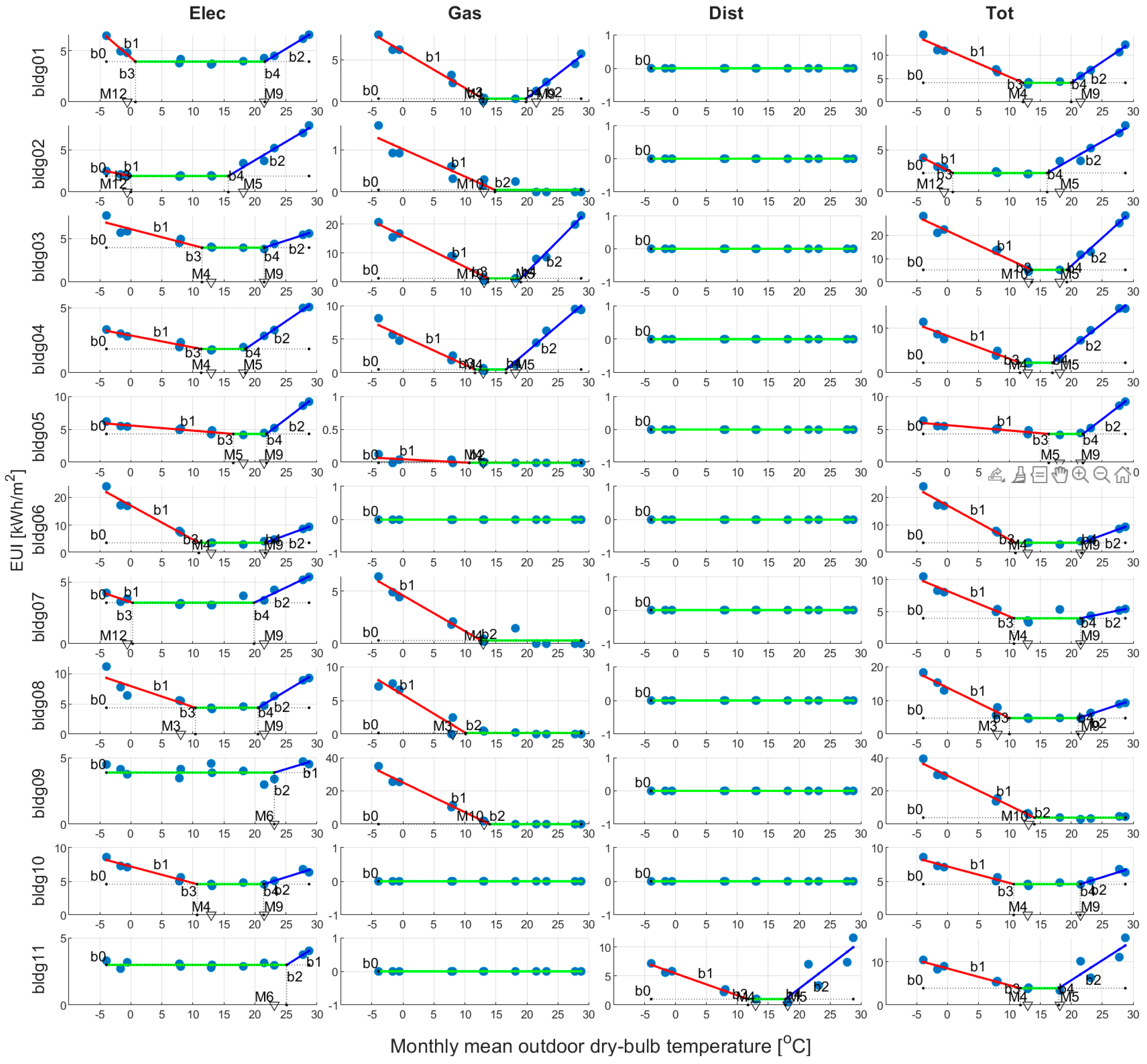
2.4. Change-Point Regression (CPR) Approach
- Step 1: constrained optimization is carried out to identify the best model coefficients () for each of the five different model types (k = 1,…,5). It comprises the constraint function for model coefficients () and the objective function for minimizing root-mean-squared error (RMSE) [16]. Constraints were set for each model coefficient to maintain its geometry.
- Step 2: the optimal model type with the lowest RMSE is chosen. By using the optimal model, heating and cooling energy consumption are predicted and summed to yearly values. All process is repeated at each energy source.
3. Results
3.1. SED Outputs
3.2. CPR Outputs
3.3. Group Difference in Approaches
3.4. Errors in Estimation
- Estimation in cooling-related energy: large PEs were observed for U- and B-shape buildings: bldg06, 07, 08, 09, and 10, regardless of SED and CPR. The absolute value of PE is in the range 18%–59%. This is significantly large compared to the W- and A-shape buildings (Figure 4), which have smaller PEs in the range between 3% and 14%. As mentioned in Section 2.2, such U- and B-shape types are weak by small fluctuations when estimating cooling energy use. The same is true for CPR: the largest PE was observed for U- and B-shape buildings. The absolute value of PE is in the range 3.1%–75.6%. Notably, the PE of bldg07 is small, but it seems that it happens by chance.
- Estimation in heating-related energy: as expected, the largest PE was observed for the A-shape building (bldg05). The absolute values of PE of SED and CPR are approximately 131% and 127.0%, respectively. Interestingly, bldg06, having a U-shape pattern, shows a relatively large error in SED and CPR (77.9% and 72.4%, respectively); the pattern of App shows seasonal variation, i.e., a W-shape as shown in Figure 4. One possible explanation is that the use of zone air conditioners or electric heaters was not fully controlled during the field measurement. The second reason is that energy end-uses of such zonal systems were mixed into “plug-load” branches and summed into the App category. This leads to seasonal fluctuations of the energy use of App, consequently leading to large errors. It should be noted that fully controlled measurement is difficult in practice; hence, it is necessary to analyze the results with these circumstances taken into account [36]. Since these measurement issues are outside the scope of this study, this was not addressed.
4. Discussion
4.1. Advantanges and Disadvantages of the Estimation Methods
- The processing algorithm for SED is light, can processes large datasets rapidly. Moreover, since it is a non-parametric approach, it can be implemented in Excel based on a simple calculation process. However, since the outdoor air temperature is not used, the correlation information between the outdoor air temperature and the energy consumption is lost. In addition, when it is necessary to compare the outputs between different climate regions, a weather normalization technique is needed. However, for CPR, such normalization is unnecessary because it already includes outdoor air temperature in the slope parameter.
- The advantage of the CPR method is that new information such as the balance temperature and slope parameter, and R2, can be obtained. Such information can be used to determine the heating and cooling energy performance. For example, based on the balance temperature, it is possible to guess the relative internal heat gain (e.g., equipment) intensity level or the comfort level [31]. In the case of R2, it is explanatory information for the outdoor temperature and, through this, the efficiency of operation of the building or the level of uncertainty in the behavior of occupants can be guessed. This information cannot be known through SED. In addition to the outdoor air temperature, other variables that affect energy consumption also can be considered. In other words, one of the primary benefits is that change-point multi-variable regression (CP-MVR) research has somewhat preceded it [20,26,31]. On the contrary, it requires an advanced analysis tool in which the optimization algorithm is run. As a result, the computation time may be relatively long. Another drawback is the finding that the optimal model process is sensitive to outliers. One or two outliers can lead to an upside-down shape, or a biased slope can be estimated [16]. To solve this problem, quantile regression [26] can be considered, but the complexity and difficulty increase. To use CPR more easily in practice, it is necessary to provide a special tool with increased usability in the government level. A representative example is the BETTER project [34].
4.2. Impact of Monthly Use Pattern in Estimation Error
4.3. Implication of Strong Correlation of Each Approaches in Relative Evaluation
5. Conclusions and Limitations
- Group differences. The ANOVA result showed that there was no significant difference among the three approaches of SED, CPR, and MEA. p-values were 0.821 and 0.980 for cooling and heating, respectively (Table 4).
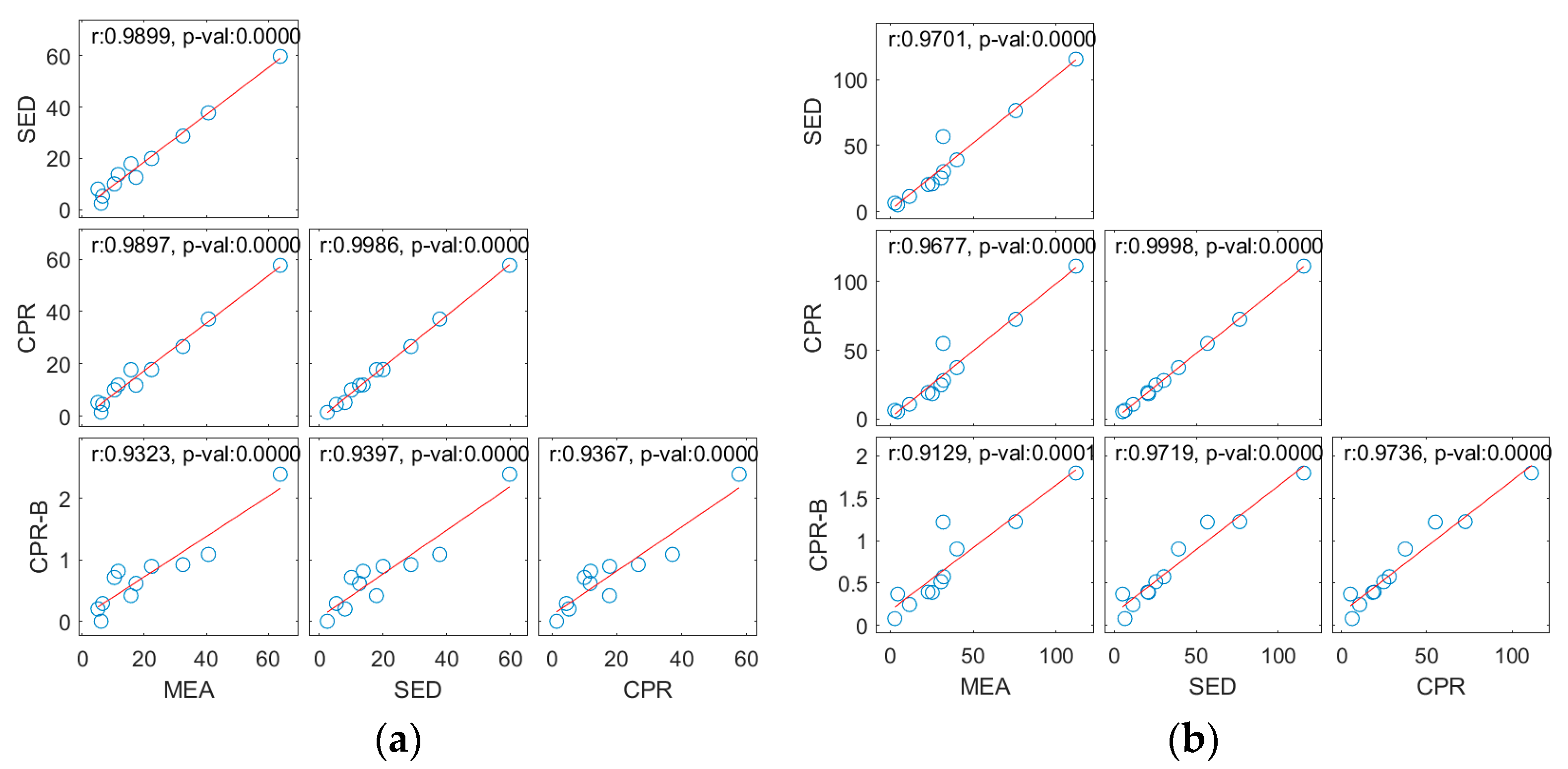
- Correlation. A strong correlation of r = 0.97 or higher was found when the four groups (SED, CPR, CPR-B, and MEA) were compared for cooling and heating (Figure 11). This implies the possibility of mutual complementarity.
- Estimation accuracy. The MPEs of both approaches were over- and under-estimated by roughly −5%–17% and 15%–11%, respectively (Table 6). The MAPEs for cooling and heating were both found to be at or below 30%. It was shown that both approaches produce marginally better results in cooling than heating quantity.
- Individual differences in estimation error. It was found that the four monthly use patterns (W, U, A, and B-shape) had a significant impact on the estimation accuracy of the SED and CPR when comparing differences between individual buildings. The stronger (weaker) the weather-sensitive energy, the smaller (larger) the estimation error. As mentioned in Section 4.2, however, this study did not provide classification criteria for the four shapes. Further study is needed for quantifying classification.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
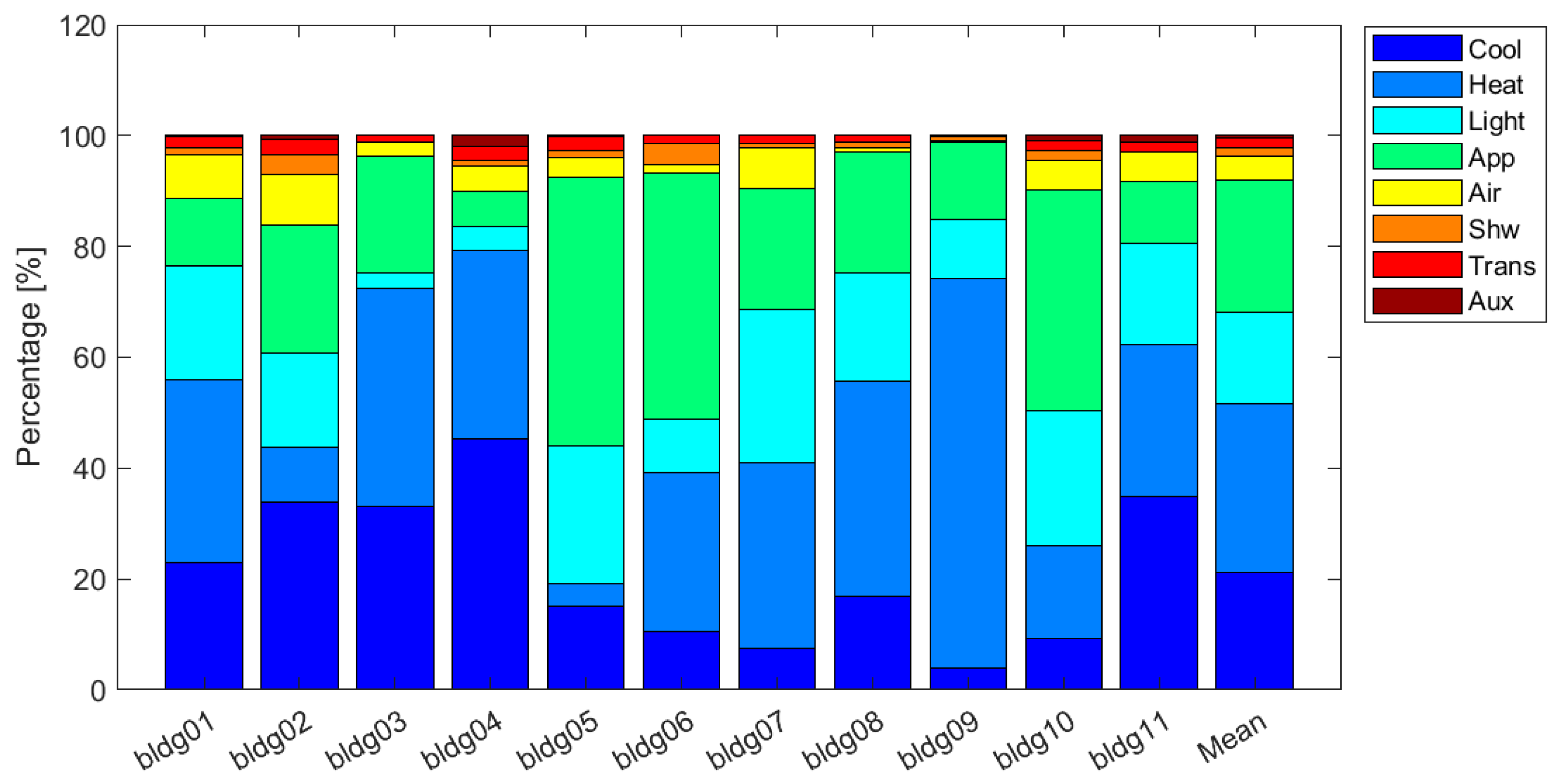
- On average, Cool is 21 kWh/m2 (21%), Heat is 35 kWh/m2 (31%), Light is 14 kWh/m2 (16%), App is 23 kWh/m2 (24%), Air is 4 kWh/m2 (4%), Shw is 1.6 kWh/m2 (2%), Trans is 1.6 kWh/m2 (2%), and Aux is 0.6 kWh/m2 (1%).
- The order of the largest average Cv is Heat, Aux, Cool, Shw, Air, App, Light, and Trans. The larger the Cv, the greater the monthly use pattern fluctuates (see Figure 4).
- In the case of bldg03 and bldg09, the gas consumption is more than double that of the electricity consumption.
- A certain group (bldg01, 03, 04, 07, and 11) that uses gas or district heating as cooling sources tends to have higher cooling energy consumption.
- The amount of the Shw, Trans, and Aux is negligible, less than 2%. Because of the low percentage, in some cases, field measurements were omitted to reduce costs (bldg03, 06, 07, 08, 09, and 11).
| ID | By Energy End-Uses | By Energy Sources | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cool | Heat | Light | App | Air | Shw | Trans | Aux | Tot. | Elec. | Gas | Dist. | |
| bldg01 | 22.4 | 32.2 | 20.3 | 11.7 | 7.7 | 1.4 | 1.8 | 0.3 | 97.7 | 57.2 | 40.6 | |
| bldg02 | 15.7 | 4.5 | 7.9 | 10.7 | 4.2 | 1.7 | 1.2 | 0.3 | 46.3 | 41.3 | 5.1 | |
| bldg03 | 63.9 | 75.6 | 5.7 | 40.3 | 5.2 | - | 2.2 | - | 192.9 | 59.6 | 133.3 | |
| bldg04 | 40.7 | 30.6 | 3.9 | 5.8 | 4.1 | 0.9 | 2.2 | 1.7 | 90.0 | 35.2 | 54.8 | |
| bldg05 | 10.4 | 2.8 | 17.0 | 33.2 | 2.4 | 1.0 | 1.6 | 0.2 | 68.5 | 68.3 | 0.2 | |
| bldg06 | 11.6 | 31.9 | 10.6 | 49.2 | 1.5 | 4.4 | 1.5 | - | 110.8 | 110.8 | ||
| bldg07 | 5.1 | 22.9 | 18.7 | 14.9 | 5.0 | 0.5 | 1.0 | - | 68.1 | 46.4 | 21.7 | |
| bldg08 | 17.4 | 40.2 | 20.4 | 22.6 | 0.6 | 1.3 | 1.1 | - | 103.6 | 78.8 | 24.8 | |
| bldg09 | 6.1 | 111.9 | 17.0 | 22.2 | 0.4 | 1.5 | - | 0.2 | 159.3 | 48.0 | 111.3 | |
| bldg10 | 6.6 | 11.7 | 17.1 | 27.9 | 3.7 | 1.3 | 1.3 | 0.6 | 70.1 | 70.1 | ||
| bldg11 | 32.5 | 25.4 | 17.1 | 10.2 | 5.0 | - | 1.7 | 1.0 | 93.0 | 37.6 | 55.4 | |
| Mean | 21.1 | 35.4 | 14.2 | 22.6 | 3.6 | 1.6 | 1.6 | 0.6 | 100.0 | 59.4 | 49.0 | 55.4 |
| Std. | 18.1 | 32.2 | 6.0 | 13.8 | 2.2 | 1.1 | 0.4 | 0.6 | 42.7 | 22.1 | 48.9 | n/a |
| Cv. | 0.86 | 0.91 | 0.42 | 0.61 | 0.61 | 0.72 | 0.27 | 0.91 | 0.43 | 0.37 | 1.00 | n/a |
| Min. | 5.1 | 2.8 | 3.9 | 5.8 | 0.4 | 0.5 | 1.0 | 0.2 | 46.3 | 35.2 | 0.2 | 55.4 |
| Max | 63.9 | 111.9 | 20.4 | 49.2 | 7.7 | 4.4 | 2.2 | 1.7 | 192.9 | 110.8 | 133.3 | 55.4 |
References
- Pérez-Lombard, L.; Ortiz, J.; González, R.; Maestre, I.R. A review of benchmarking, rating and labelling concepts within the framework of building energy certification schemes. Energy Build. 2009, 41, 272–278. [Google Scholar] [CrossRef]
- Borgstein, E.H.; Lamberts, R.; Hensen, J.L.M. Evaluating energy performance in non-domestic buildings: A review. Energy Build. 2016, 128, 734–755. [Google Scholar] [CrossRef]
- Mathew, P.; Mills, E.; Bourassa, N.; Brook, M. Action-oriented benchmarking: Using the CEUS database to benchmark commercial buildings in California. Energ. Eng. 2008, 105, 6–18. [Google Scholar] [CrossRef]
- Chung, W. Review of building energy-use performance benchmarking methodologies. Appl. Energy 2011, 88, 1470–1479. [Google Scholar] [CrossRef]
- Kim, D.W.; Kim, Y.M.; Lee, S.E. Development of an energy benchmarking database based on cost-effective energy performance indicators: Case study on public buildings in South Korea. Energy Build. 2019, 191, 104–116. [Google Scholar] [CrossRef]
- Zhai, Z.; Salazar, A. Assessing the implications of submetering with energy analytics to building energy savings. Energy Built Environ. 2020, 1, 27–35. [Google Scholar] [CrossRef]
- Wang, S.; Yan, C.; Xiao, F. Quantitative energy performance assessment methods for existing buildings. Energy Build. 2012, 55, 873–888. [Google Scholar] [CrossRef]
- Katipamula, S.; Underhill, R.M.; Goddard, J.K.; Taasevigen, D.J.; Piette, M.A.; Granderson, J.; Kuruganti, T. Small- and Medium-Sized Commercial Building Monitoring and Controls Needs: A Scoping Study (No. PNNL-22169, 1063081); Pacific Northwest National Laboratory (PNNL): Richland, WA, USA, 2012.
- Gov, n.d. About the Weatherization Assistance Program. Available online: https://www.energy.gov/eere/wap/about-weatherization-assistance-program (accessed on 16 June 2022).
- Sesana, M.M.; Salvalai, G. A review on building renovation passport: Potentialities and barriers on current initiatives. Energ. Build. 2018, 173, 195–205. [Google Scholar] [CrossRef]
- Sesana, M.M.; Rivallain, M.; Salvalai, G. Overview of the available knowledge for the data model definition of a building renovation passport for non-residential buildings: The ALDREN Project Experience. Sustainability 2020, 12, 642. [Google Scholar] [CrossRef]
- Ji, C.; Choi, M.; Hong, T.; Yeom, S.; Kim, H. Evaluation of the effect of a building energy efficiency certificate in reducing energy consumption in Korean apartments. Energy Build. 2021, 248, 111168. [Google Scholar] [CrossRef]
- Kissock, J.K.; Haberl, J.S.; Claridge, D.E. Development of a Toolkit for Calculating Linear, Change-Point Linear and Multiple-Linear Inverse Building Energy Analysis Models, ASHRAE Research Project 1050-RP [Final Report]; Energy Systems Laboratory, Texas A&M University: College Station, TX, USA, 2002. [Google Scholar]
- Pereira, L.; Nunes, N. Performance Evaluation in Non-Intrusive Load Monitoring: Datasets, Metrics, and Tools—A Review. WIREs Data Min. Knowl. Discov. 2018, 8, e1265. [Google Scholar] [CrossRef]
- Ahn, K.U.; Shin, H.S.; Park, C.S. Energy analysis of 4625 office buildings in South Korea. Energies 2019, 12, 1114. [Google Scholar] [CrossRef]
- Paulus, M.T.; Claridge, D.E.; Culp, C. Algorithm for automating the selection of a temperature dependent change point model. Energy Build. 2015, 87, 95–104. [Google Scholar] [CrossRef]
- ASHRAE. Handbook: Fundamentals 2017; American Society of Heating, Refrigerating and Air Conditioning Engineers: Atlanta, GA, USA, 2017. [Google Scholar]
- Ji, C.; Hong, T.; Kim, H.; Yeom, S. Effect of Building Energy Efficiency Certificate on Reducing Energy Consumption of Non-Residential Buildings in South Korea. Energy Build. 2022, 255, 111701. [Google Scholar] [CrossRef]
- Energy Auditor—Single Family 2.0: Utility Bill Analysis. Available online: https://www.energy.gov/eere/wap/downloads/energy-auditor-single-family-20-utility-bill-analysis (accessed on 29 September 2022).
- Haberl, J.S.; Cho, S. Literature Review of Uncertainty of Analysis Methods (Inverse Model Toolkit), Report to the Texas Commission on Environmental Quality; Energy Systems Laboratory, Texas A&M University: College Station, TX, USA, 2004. [Google Scholar]
- Oh, S.; Kim, K.H. Change-Point Modeling Analysis for Multi-Residential Buildings: A Case Study in South Korea. Energy Build. 2020, 214, 109901. [Google Scholar] [CrossRef]
- Prahl, D.; Beach, R. Analysis of Pre-Retrofit Building and Utility Data; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2014.
- Park, J.S.; Lee, S.J.; Kim, K.H.; Kwon, K.W.; Jeong, J.-W. Estimating Thermal Performance and Energy Saving Potential of Residential Buildings Using Utility Bills. Energy Build. 2016, 110, 23–30. [Google Scholar] [CrossRef]
- Eriksson, M.; Akander, J.; Moshfegh, B. Investigating Energy Use in a City District in Nordic Climate Using Energy Signature. Energies 2022, 15, 1907. [Google Scholar] [CrossRef]
- Aragon, V.; James, P.A.B.; Gauthier, S. The Influence of Weather on Heat Demand Profiles in UK Social Housing Tower Blocks. Build. Environ. 2022, 219, 109101. [Google Scholar] [CrossRef]
- Meng, Q.; Xiong, C.; Mourshed, M.; Wu, M.; Ren, X.; Wang, W.; Li, Y.; Song, H. Change-point multivariable quantile regression to explore effect of weather variables on building energy consumption and estimate base temperature range. Sustain. Cities Soc. 2020, 53, 101900. [Google Scholar] [CrossRef]
- Kissock, J.K.; Reddy, T.A.; Claridge, D.E. Ambient-temperature regression analysis for estimating retrofit savings in commercial buildings. J. Sol. Energy Eng. Trans. ASME 1998, 120, 168–176. [Google Scholar] [CrossRef]
- Ruch, D.; Claridge, D.E. A Four-Parameter Change-Point Model for Predicting Energy Consumption in Commercial Buildings. J. Sol. Energy Eng. 1992, 114, 77–83. [Google Scholar] [CrossRef]
- Burak Gunay, H.; Shen, W.; Newsham, G.; Ashouri, A. Detection and Interpretation of Anomalies in Building Energy Use through Inverse Modeling. Sci. Technol. Built Environ. 2019, 25, 488–503. [Google Scholar] [CrossRef]
- Kissock, J.; Seryak, J. Understanding Manufacturing Energy Use Through Statistical Analysis. In Proceedings of the Industrial Energy Technology Conference, Houston, TX, USA, 21–22 April 2004. [Google Scholar]
- Golden, A.; Woodbury, K.; Carpenter, J.; O’Neill, Z. Change Point and Degree Day Baseline Regression Models in Industrial Facilities. Energy Build. 2017, 144, 30–41. [Google Scholar] [CrossRef]
- Kissock, J.K.; Haberl, J.S.; Claridge, D.E. Inverse Modeling Toolkit: Numerical Algorithms, Ashrae KC-03-2-1(RP-1050); American Society of Heating, Refrigerating and Air Conditioning Engineers: Atlanta, GA, USA, 2003. [Google Scholar]
- Haberl, J.; Sreshthaputra, A.; Claridge, D.; Kissock, J. Inverse Model Toolkit: Application and Testing. KC-03-02-2(RP-1050); American Society of Heating, Refrigerating and Air Conditioning Engineers: Atlanta, GA, USA, 2003. [Google Scholar]
- Szum, C.; Zhou, N.; McQuillen, D.; Ding, C.; Li, H. Johnson Publishing Controls, Inc.: Han, & USDOE. (2021, July 27). In Building Efficiency Targeting Tool for Energy Retrofits (BETTER) Web Application (BETTER Web App) v.1.0; Computer Software; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2021. [Google Scholar] [CrossRef]
- Li, H.; Szum, C.; Nesler, C.; Lisauskas, S.; Snyder, S. Targeting Building Energy Efficiency Opportunities: An Open-Source Analytical and Benchmarking Tool. In Proceedings of the ASHRAE Winter Conference, Atlanta, GA, USA, 12–16 January 2019. [Google Scholar]
- Healy, W. Measurement Challenges in Achieving Energy Monitoring Systems in Buildings, Technical Note (NIST TN), National Institute of Standards and Technology, Gaithersburg, MD, [online]. 2010. Available online: https://tsapps.nist.gov/publication/get_pdf.cfm?pub_id=904372 (accessed on 14 September 2022).
- International Standard Organization (ISO). ISO12655; Energy Performance of Buildings—Presentation of Measured Energy Use of Buildings. International Organization for Standardization: Geneva, Switzerland, 2013.
- KIAEBS. Methods for Classification, Measurement and Normalization of Energy Consumption by End-Use in Office Buildings; Korean Institute of Architectural Sustainable Environment and Building Systems: Seoul, South Korea, 2016. [Google Scholar]
- Song, S.-Y.; Jin, H.-S.; Ha, S.-Y.; Kim, S.-I.; Kim, Y.-J.; Lee, S.-J.; Suh, I.-A. Detailed Office Building Energy Information Based on In Situ Measurements. Energies 2020, 13, 3050. [Google Scholar] [CrossRef]
- KMA Weather Data Service. Available online: https://data.kma.go.kr/resources/html/en/aowdp.html (accessed on 1 September 2022).
- Cho, M.S.; Le, D.Y. An Analysis of Residential Building Energy Consumption Using Building Energy Integrated Database—Focused on Building Uses, Regions, Scale and the Year of Construction Completion. J. Real Estate Anal. 2017, 3, 101–118. [Google Scholar] [CrossRef]
- Ji, C.-Y.; Choi, M.-S.; Gwon, O.-I.; Jung, H.-R.; Shin, S.-E. Greenhouse gas emissions from building sector based on national building energy database. J. Archi. Inst. Korea Struct. Constr. 2020, 36, 143–152. [Google Scholar]






| ID | Age | GFA [m2] | Number of Stories | HVAC System | Service Hot Water System |
|---|---|---|---|---|---|
| bldg01 | 1995 | 22,471 | 19F/B7 |
|
|
| bldg02 | 1983 | 10,517 | 10F/B2 |
|
|
| bldg03 | 1968 | 2482 | 7F/B1 |
|
|
| bldg04 | 2008 | 31,787 | 20F/B6 |
|
|
| bldg05 | 1990 | 1265 | 5F/B1 |
|
|
| bldg06 | 1971 | 4034 | 4F/B1 |
|
|
| bldg07 | 2006 | 29,547 | 21F/B5 |
|
|
| bldg08 | 2008 | 1633 | 5F/B1 |
|
|
| bldg09 | 1967 | 2408 | 4F/B2 |
|
|
| bldg10 | 1995 | 7124 | 11F/B4 |
|
|
| bldg11 | 2007 | 19,973 | 12F/B5 |
|
|
| Model Type | Form | Description |
|---|---|---|
| One-parameter (1P) | E = b0 | Non-weather-sensitive demand |
| Two-parameter (2P) | E = b0 + b1 T | |
| Three-parameter (3P) | ||
| for heating | E = b0 + b1 (b2 − T)+ | Seasonal weather-sensitive use (fuel in winter, electricity in summer for cooling) |
| for cooling | E = b0 + b1 (T − b2)+ | |
| Five-parameter (5P) | E = b0+ b1 (b3 − T)+ + b2 (T − b4)+ | Heating and cooling supplied by same meter |
| ID | Energy Source | CPR Type | b0a | b1b | b2c | b3d | b4e | R2 |
|---|---|---|---|---|---|---|---|---|
| bldg01 | Elec | 5p | 3.94 | 0.52 | 0.37 | 0.74 | 21.63 | 0.97 |
| Gas | 5p | 0.38 | 0.43 | 0.57 | 12.95 | 19.85 | 0.99 | |
| Tot | 5p | 4.11 | 0.58 | 0.90 | 12.19 | 19.99 | 0.98 | |
| bldg02 | Elec | 5p | 1.89 | 0.14 | 0.44 | 0.00 | 15.72 | 0.98 |
| Gas | 3p_h | 0.05 | 0.07 | 14.83 | n/a | n/a | 0.91 | |
| Tot | 5p | 2.25 | 0.37 | 0.42 | 0.83 | 16.10 | 0.97 | |
| bldg03 | Elec | 5p | 3.94 | 0.19 | 0.23 | 11.47 | 21.50 | 0.89 |
| Gas | 5p | 1.29 | 1.06 | 2.15 | 13.72 | 19.00 | 0.98 | |
| Tot | 5p | 5.22 | 1.22 | 2.40 | 13.59 | 19.28 | 0.98 | |
| bldg04 | Elec | 5p | 1.84 | 0.09 | 0.33 | 11.35 | 18.47 | 0.99 |
| Gas | 5p | 0.50 | 0.42 | 0.78 | 11.61 | 16.63 | 0.97 | |
| Tot | 5p | 2.27 | 0.52 | 1.09 | 11.70 | 16.95 | 0.98 | |
| bldg05 | Elec | 5p | 4.35 | 0.08 | 0.71 | 16.52 | 21.88 | 0.99 |
| Gas | 3p_h | 0.00 | 0.01 | 10.72 | n/a | n/a | 0.50 | |
| Tot | 5p | 4.35 | 0.08 | 0.71 | 16.36 | 21.88 | 0.98 | |
| bldg06 | Elec | 5p | 3.66 | 1.22 | 0.82 | 10.96 | 21.67 | 0.98 |
| Tot | 5p | 3.66 | 1.22 | 0.82 | 10.96 | 21.67 | 0.98 | |
| bldg07 | Elec | 5p | 3.33 | 0.17 | 0.24 | 0.28 | 19.86 | 0.91 |
| Gas | 3p_h | 0.31 | 0.34 | 12.59 | n/a | n/a | 0.96 | |
| Tot | 5p | 3.98 | 0.40 | 0.20 | 10.73 | 21.50 | 0.93 | |
| bldg08 | Elec | 5p | 4.37 | 0.34 | 0.62 | 10.41 | 20.51 | 0.87 |
| Gas | 3p_h | 0.17 | 0.56 | 10.11 | n/a | n/a | 0.95 | |
| Tot | 5p | 4.75 | 0.90 | 0.62 | 9.98 | 21.14 | 0.97 | |
| bldg09 | Elec | 3p_c | 3.88 | 0.14 | 23.14 | n/a | n/a | 0.27 |
| Gas | 3p_h | 0.00 | 1.79 | 13.97 | n/a | n/a | 0.99 | |
| Tot | 3p_h | 3.92 | 1.80 | 14.02 | n/a | n/a | 0.99 | |
| bldg10 | Elec | 5p | 4.58 | 0.25 | 0.29 | 10.68 | 21.43 | 0.95 |
| Tot | 5p | 4.58 | 0.25 | 0.29 | 10.68 | 21.43 | 0.95 | |
| bldg11 | Elec | 3p_c | 2.98 | 0.29 | 25.13 | n/a | n/a | 0.82 |
| Dist | 5p | 1.01 | 0.38 | 0.82 | 11.73 | 17.78 | 0.84 | |
| Tot | 5p | 3.89 | 0.39 | 0.92 | 11.77 | 17.98 | 0.85 |
| Variable | Sum of Squares | Df | Mean Square | F | Sig. | |
|---|---|---|---|---|---|---|
| Cooling-related | Between groups | 0.3406 | 2 | 0.1703 | 0.20 | 0.8212 |
| Within groups | 25.7693 | 30 | 0.8589 | |||
| Total | 26.1099 | 32 | ||||
| Heating-related | Between groups | 0.0040 | 2 | 0.0216 | 0.02 | 0.9807 |
| Within groups | 30.9801 | 30 | 1.0326 | |||
| Total | 31.0205 | 32 |
| Experiment | ID | EUI [kWh/m2·yr] | PE [%] | Pattern Type 3 | |||
|---|---|---|---|---|---|---|---|
| MEA | SED 1 | CPR 2 | SED vs. MEA | CPR vs. MEA | |||
| Cooling-related | bldg01 | 22.4 | 20.0 | 17.8 | −10.7 | −20.6 | W |
| bldg02 | 15.7 | 17.9 | 17.7 | 13.9 | 12.6 | A | |
| bldg03 | 63.9 | 59.7 | 57.7 | −6.6 | −9.7 | W | |
| bldg04 | 40.7 | 37.7 | 37.1 | −7.3 | −8.8 | W | |
| bldg05 | 10.4 | 10.1 | 10.0 | −3.1 | −3.8 | A | |
| bldg06 | 11.6 | 13.7 | 11.9 | 18.4 | 2.7 | U | |
| bldg07 | 5.1 | 8.0 | 5.2 | 59.1 | 3.1 | U | |
| bldg08 | 17.4 | 12.6 | 11.8 | −27.5 | −32.2 | U | |
| bldg09 | 6.1 | 2.5 | 1.4 | −59.2 | −76.6 | U | |
| bldg10 | 6.6 | 5.3 | 4.5 | −18.7 | −32.2 | B | |
| bldg11 | 32.5 | 28.7 | 26.6 | −11.5 | −18.1 | W | |
| Heating-related | bldg01 | 32.2 | 30.2 | 28.1 | −6.3 | −12.8 | W |
| bldg02 | 4.5 | 5.0 | 5.3 | 11.1 | 17.8 | A | |
| bldg03 | 75.6 | 76.5 | 72.5 | 1.1 | −4.1 | W | |
| bldg04 | 30.7 | 25.3 | 24.8 | −17.5 | −19.0 | W | |
| bldg05 | 2.8 | 6.4 | 6.3 | 131.1 | 127.0 | A | |
| bldg06 | 31.9 | 56.8 | 55.0 | 77.9 | 72.4 | U | |
| bldg07 | 22.9 | 20.5 | 19.3 | −10.7 | −15.9 | U | |
| bldg08 | 40.2 | 39.1 | 37.4 | −2.8 | −6.9 | U | |
| bldg09 | 111.9 | 115.5 | 111.3 | 3.2 | −0.6 | U | |
| bldg10 | 11.7 | 11.4 | 10.7 | −2.4 | −8.0 | B | |
| bldg11 | 25.4 | 20.9 | 18.4 | −17.9 | −27.5 | W | |
| Experiment | Metrics | SED vs. MEA | CPR vs. MEA |
|---|---|---|---|
| Cooling-related | MPE | −5% | −17% |
| MAPE | 21% | 20% | |
| Heating-related | MPE | 15% | 11% |
| MAPE | 26% | 28% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, D.-W.; Ahn, K.-U.; Shin, H.; Lee, S.-E. Simplified Weather-Related Building Energy Disaggregation and Change-Point Regression: Heating and Cooling Energy Use Perspective. Buildings 2022, 12, 1717. https://doi.org/10.3390/buildings12101717
Kim D-W, Ahn K-U, Shin H, Lee S-E. Simplified Weather-Related Building Energy Disaggregation and Change-Point Regression: Heating and Cooling Energy Use Perspective. Buildings. 2022; 12(10):1717. https://doi.org/10.3390/buildings12101717
Chicago/Turabian StyleKim, Deuk-Woo, Ki-Uhn Ahn, Hyery Shin, and Seung-Eon Lee. 2022. "Simplified Weather-Related Building Energy Disaggregation and Change-Point Regression: Heating and Cooling Energy Use Perspective" Buildings 12, no. 10: 1717. https://doi.org/10.3390/buildings12101717
APA StyleKim, D.-W., Ahn, K.-U., Shin, H., & Lee, S.-E. (2022). Simplified Weather-Related Building Energy Disaggregation and Change-Point Regression: Heating and Cooling Energy Use Perspective. Buildings, 12(10), 1717. https://doi.org/10.3390/buildings12101717






