Mechanical Steel Stitches: An Innovative Approach for Strengthening Shear Deficiency in Undamaged Reinforced Concrete Beams
Abstract
1. Introduction
2. Materials and Method
2.1. Preparation of Shear Beam
2.2. Strengthening Technic by Mechanical Steel Stitches (MSS)
2.3. Test Setup
3. Experimental Results and Discussion
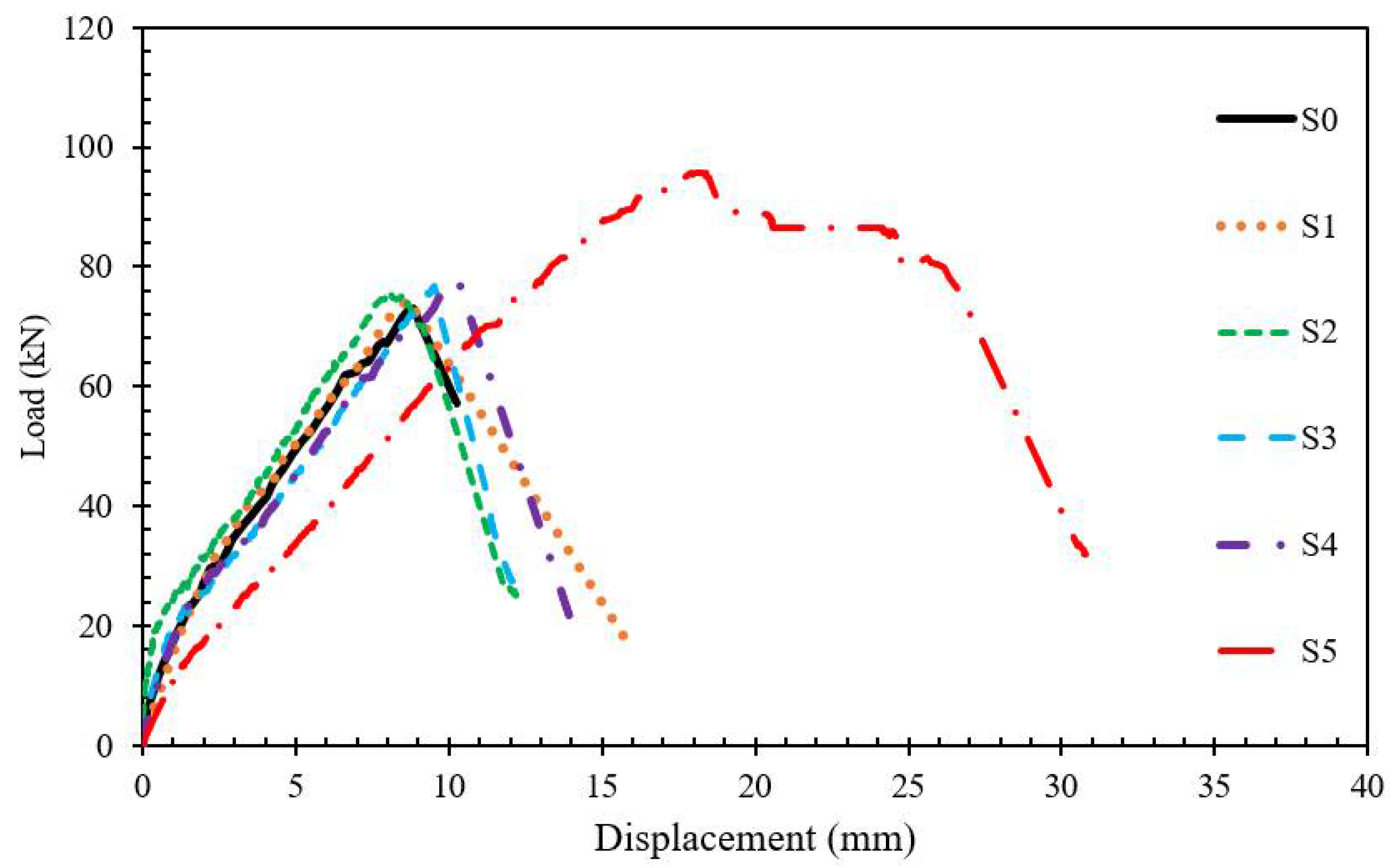
3.1. Reference Specimen: S0
3.2. Strengthened Specimens: S1, S2, S3, S4 and S5
4. Conclusions
- (1)
- As expected, shear failure occurred in the reference S0 beam. On the other hand, shear failure could not be prevented in S1, S2, S3 and S4 beams, where the MSS spacing gradually changes between d and d/2. It has been observed that the cracks formed in the range of 45°–60°. In the S5 specimen, where the MSS range was d/5 ((1%) MSS ratio), crack formation did not occur with this angle. Therefore, it can be concluded that tightening the spacing of MS would be helpful in preventing the shear fracture of the beams.
- (2)
- Since the MSs are attached to the existing reinforced concrete beam with anchors, some losses in section due to the drilling have occurred in the stiffness of the existing beams. For example, a 38% loss in initial stiffness occurred in S5 compared to S0. This situation slightly increased the amount of deflection occurring in the span of the beam. Especially in MSS application, micro-cracks formed during the drilling of existing beams merged due to the close proximity of the holes, and a damage mechanism similar to an adherence crack was observed.
- (3)
- While the capacity increase in S1, S2, S3 and S4 beams was limited compared to S0, a gain of nearly 31% occurred in the S-5 beam. However, a load carrying capacity increase depending on the d/s amount (s is spacing between MS) was not observed in the experiments. This situation is also related to the formation of cracks in the d to d/2 range without coinciding with the MSSs.
- (4)
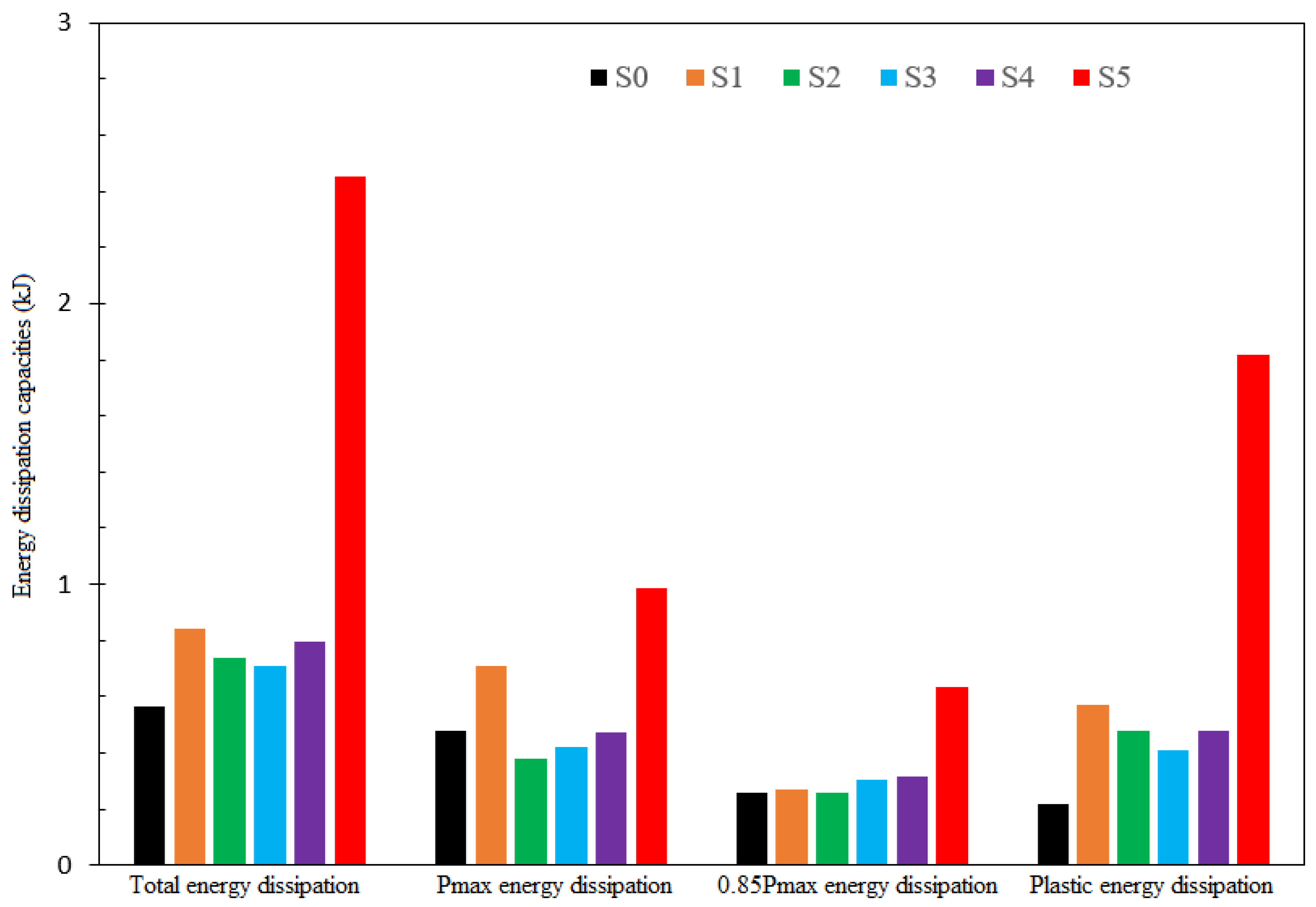
- The energy consumed (absorbed) by the beams S1, S2, S3 and S4 increased gradually compared to the reference beam S0. In addition, with the considerable increase in strength, the energy consumption of the S5 beam increased approximately 4 times compared to the S0 beam. The increase in displacement due to the decrease in stiffness of the S-5 beam had an effect on this increase.
- (5)
- Experimental results show that the RC beams strengthened with different MSS configurations as S1, S2, S3, and S4 have a modest increase in failure load. It would also seem that in terms of ductility the arrangement of the pins up to a spacing of 110 mm is negligible. On the other hand, the S5 MSS configuration allows a considerable increase in the ultimate load. Therefore, it is concluded that a certain level of spacing is quite critical in this novel external strengthening method.
- (6)
- It has been seen that the method proposed in this study can be used for strengthening purposes, especially in the RC members under the effect of shear, when traditional strengthening methods are not suitable in terms of cost, application, and time. Therefore, the outcomes of this study will be frontiers for new studies to be carried out for the optimum design of MSSs, which is not in the existing codes and is a fairly new retrofit/strengthening alternative for the literature.
- (7)
- In this study, MSSs applied angle, MS diameter, anchorage depth and mechanical properties were kept constant. Therefore, the effect of these parameters on the behavior of beams reinforced with MS should be investigated in future studies. Similarly, the mechanical properties of the beams, stirrups and longitudinal reinforcement amounts, beam’ geometric shapes, loading patterns, etc., are also waiting as an important research topic in MSS-reinforced beams.
- (8)
- In addition to the above-mentioned positive features, it is quite possible that MSSs will be exposed to corrosion over time due to their properties. For this, it is very important that the outside of the material is covered with a corrosion inhibitor in the strengthening to be made. In addition, in future studies, MSS applications can also be made with FRP materials. In this way, the corrosion situation is eliminated.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bousias, S.N.; Biskinis, D.; Fardis, M.N.; Spathis, A.-L. Strength, stiffness, and cyclic deformation capacity of concrete jacketed members. ACI Struct. J. 2007, 104, 521. [Google Scholar]
- Altun, F. An experimental study of the jacketed reinforced-concrete beams under bending. Constr. Build. Mater. 2004, 18, 611–618. [Google Scholar] [CrossRef]
- Bayülke, N. Structural Damage on 27 June 1998 Adana-Ceyhan Earthquake; General Directorate of Disaster Affairs, ERD: New Delhi, India, 1998. [Google Scholar]
- Korkmaz, H.H.; Dere, Y.; Özkılıç, Y.O.; Bozkurt, M.B.; Ecemiş, A.S.; Özdoner, N. Excessive snow induced steel roof failures in Turkey. Eng. Fail. Anal. 2022, 141, 106661. [Google Scholar] [CrossRef]
- Özkılıç, Y.O.; Aksoylu, C.; Arslan, M.H. Numerical evaluation of effects of shear span, stirrup spacing and angle of stirrup on reinforced concrete beam behaviour. Struct. Eng. Mech. Int’l. J. 2021, 79, 309–326. [Google Scholar]
- Gemi, L.; Madenci, E.; Özkılıç, Y.O.; Yazman, Ş.; Safonov, A. Effect of Fiber Wrapping on Bending Behavior of Reinforced Concrete Filled Pultruded GFRP Composite Hybrid Beams. Polymers 2022, 14, 3740. [Google Scholar] [CrossRef]
- Gemi, L.; Madenci, E.; Özkılıç, Y.O. Experimental, analytical and numerical investigation of pultruded GFRP composite beams infilled with hybrid FRP reinforced concrete. Eng. Struct. 2021, 244, 112790. [Google Scholar] [CrossRef]
- Özkılıç, Y.O.; Aksoylu, C.; Yazman, Ş.; Gemi, L.; Arslan, M.H. Behavior of CFRP-strengthened RC beams with circular web openings in shear zones: Numerical study. Structures 2022, 41, 1369–1389. [Google Scholar] [CrossRef]
- Arslan, M.H.; Yazman, Ş.; Hamad, A.A.; Aksoylu, C.; Özkılıç, Y.O.; Gemi, L. Shear strengthening of reinforced concrete T-beams with anchored and non-anchored CFRP fabrics. Structures 2022, 39, 527–542. [Google Scholar] [CrossRef]
- Özkılıç, Y.O.; Yazman, Ş.; Aksoylu, C.; Arslan, M.H.; Gemi, L. Numerical investigation of the parameters influencing the behavior of dapped end prefabricated concrete purlins with and without CFRP strengthening. Constr. Build. Mater. 2021, 275, 122173. [Google Scholar] [CrossRef]
- Gemi, L.; Aksoylu, C.; Yazman, Ş.; Özkılıç, Y.O.; Arslan, M.H. Experimental investigation of shear capacity and damage analysis of thinned end prefabricated concrete purlins strengthened by CFRP composite. Compos. Struct. 2019, 229, 111399. [Google Scholar] [CrossRef]
- Raza, S.; Khan, M.K.; Menegon, S.J.; Tsang, H.-H.; Wilson, J.L. Strengthening and repair of reinforced concrete columns by jacketing: State-of-the-art review. Sustainability 2019, 11, 3208. [Google Scholar] [CrossRef]
- More, R.U.; Kulkarni, D. Flexural behavioural study on RC beam with externally bonded aramid fiber reinforced polymer. Int. J. Res. Eng. Technol. 2014, 3, 316–321. [Google Scholar]
- Wu, B.; Zhang, S.; Liu, F.; Gan, T. Effects of salt solution on mechanical behaviors of aramid fiber–reinforced polymer (AFRP) sheets and AFRP-to-concrete joints. Adv. Struct. Eng. 2016, 19, 1855–1872. [Google Scholar] [CrossRef]
- Zhang, S.; Wu, B. Effects of salt solution on the mechanical behavior of concrete beams externally strengthened with AFRP. Constr. Build. Mater. 2019, 229, 117044. [Google Scholar] [CrossRef]
- Raval, C.; Shah, S.; Machhi, C. Experimental Study on Shear Behaviour of RC Beam Strengthened by AFRP Sheet. Int. J. All Res. Writ. 2020, 3, 62–68. [Google Scholar]
- Ma, C.-K.; Apandi, N.M.; Sofrie, C.S.Y.; Ng, J.H.; Lo, W.H.; Awang, A.Z.; Omar, W. Repair and rehabilitation of concrete structures using confinement: A review. Constr. Build. Mater. 2017, 133, 502–515. [Google Scholar] [CrossRef]
- Ma, G.; Li, H.; Yan, L.; Huang, L. Testing and analysis of basalt FRP-confined damaged concrete cylinders under axial compression loading. Constr. Build. Mater. 2018, 169, 762–774. [Google Scholar] [CrossRef]
- Qin, Z.; Tian, Y.; Li, G.; Liu, L. Study on bending behaviors of severely pre-cracked RC beams strengthened by BFRP sheets and steel plates. Constr. Build. Mater. 2019, 219, 131–143. [Google Scholar] [CrossRef]
- Duic, J.; Kenno, S.; Das, S. Flexural rehabilitation and strengthening of concrete beams with BFRP composite. J. Compos. Constr. 2018, 22, 04018016. [Google Scholar] [CrossRef]
- Joyklad, P.; Suparp, S.; Hussain, Q. Flexural response of JFRP and BFRP strengthened RC beams. Int. J. Eng. Technol. 2019, 11, 203–207. [Google Scholar] [CrossRef]
- Pham, T.M.; Chen, W.; Elchalakani, M.; Karrech, A.; Hao, H. Experimental investigation on lightweight rubberized concrete beams strengthened with BFRP sheets subjected to impact loads. Eng. Struct. 2020, 205, 110095. [Google Scholar] [CrossRef]
- Shen, D.; Li, M.; Kang, J.; Liu, C.; Li, C. Experimental studies on the seismic behavior of reinforced concrete beam-column joints strengthened with basalt fiber-reinforced polymer sheets. Constr. Build. Mater. 2021, 287, 122901. [Google Scholar] [CrossRef]
- Prado, D.M.; Araujo, I.D.G.; Haach, V.G.; Carrazedo, R. Assessment of shear damaged and NSM CFRP retrofitted reinforced concrete beams based on modal analysis. Eng. Struct. 2016, 129, 54–66. [Google Scholar] [CrossRef]
- Karzad, A.S.; Al Toubat, S.; Maalej, M.; Estephane, P. Repair of reinforced concrete beams using carbon fiber reinforced polymer. In Proceedings of the MATEC Web of Conferences: EDP Sciences 2017, Sharjah, United Arab Emirates, 18–20 April 2017; p. 01008. [Google Scholar]
- Karam, E.C.; Hawileh, R.A.; El Maaddawy, T.; Abdalla, J.A. Experimental investigations of repair of pre-damaged steel-concrete composite beams using CFRP laminates and mechanical anchors. Thin-Walled Struct. 2017, 112, 107–117. [Google Scholar] [CrossRef]
- Karzad, A.S.; Leblouba, M.; Al Toubat, S.; Maalej, M. Repair and strengthening of shear-deficient reinforced concrete beams using Carbon Fiber Reinforced Polymer. Compos. Struct. 2019, 223, 110963. [Google Scholar] [CrossRef]
- Yu, F.; Zhou, H.; Jiang, N.; Fang, Y.; Song, J.; Feng, C.; Guan, Y. Flexural experiment and capacity investigation of CFRP repaired RC beams under heavy pre-damaged level. Constr. Build. Mater. 2020, 230, 117030. [Google Scholar] [CrossRef]
- Yu, F.; Fang, Y.; Zhou, H.; Bai, R.; Xie, C. A Simplified Model for Crack Width Prediction of Flexural-Strengthened High Pre-Damaged Beams with CFRP Sheet. KSCE J. Civ. Eng. 2020, 24, 3746–3764. [Google Scholar] [CrossRef]
- Yu, F.; Fang, Y.; Guo, S.; Bai, R.; Yin, L.; Mansouri, I. A simple model for maximum diagonal crack width estimation of shear-strengthened pre-damaged beams with CFRP strips. J. Build. Eng. 2021, 41, 102716. [Google Scholar] [CrossRef]
- Bahij, S.; Omary, S.; Feugeas, F.; Faqiri, A. Structural Strengthening/Repair of Reinforced Concrete (RC) Beams by Different Fiber-Reinforced Cementitious Materials-A State-of-the-Art Review. J. Civ. Environ. Eng. 2020, 10. [Google Scholar] [CrossRef]
- Zaki, M.A.; Rasheed, H.A.; Alkhrdaji, T. Performance of CFRP-strengthened concrete beams fastened with distributed CFRP dowel and fiber anchors. Compos. Part B Eng. 2019, 176, 107117. [Google Scholar] [CrossRef]
- Aksoylu, C.; Özkılıç, Y.O.; Yazman, Ş.; Gemi, L.; Arslan, M.H. Experimental and Numerical Investigation of Load Bearing Capacity of Thinned End Precast Purlin Beams and Solution Proposals. Tek. Dergi 2021, 3, 10823–10858. [Google Scholar]
- Al-Khafaji, A.; Salim, H.; El-Sisi, A. Behavior of RC Beams Strengthened with CFRP Sheets under Sustained Loads; Elsevier: Amsterdam, The Netherlands, 2021; pp. 4690–4700. [Google Scholar]
- Kotynia, R.; Oller, E.; Marí, A.; Kaszubska, M. Efficiency of shear strengthening of RC beams with externally bonded FRP materials–State-of-the-art in the experimental tests. Compos. Struct. 2021, 267, 113891. [Google Scholar] [CrossRef]
- Abed, M.J.; Fayyadh, M.M.; Khaleel, O.R. Effect of web opening diameter on performance and failure mode of CFRP repaired RC beams. Mater. Today Proc. 2021, 42, 388–398. [Google Scholar] [CrossRef]
- Al-Fakih, A.; Hashim, M.H.M.; Alyousef, R.; Mutafi, A.; Sabah, S.H.A.; Tafsirojjaman, T. Cracking Behavior of Sea Sand RC Beam Bonded Externally with CFRP Plate; Elsevier: Amsterdam, The Netherlands, 2021; pp. 1578–1589. [Google Scholar]
- Jahami, A.; Temsah, Y.; Khatib, J.; Baalbaki, O.; Kenai, S. The behavior of CFRP strengthened RC beams subjected to blast loading. Mag. Civ. Eng. 2021, 3, 10309. [Google Scholar]
- Alhassan, M.; Al-Rousan, R.; Ababneh, A. Anchoring of the main CFRP sheets with transverse CFRP strips for optimum upgrade of RC Beams: Parametric experimental study. Constr. Build. Mater. 2021, 293, 123525. [Google Scholar] [CrossRef]
- Samb, N.; Chaallal, O.; El-Saikaly, G. Multilayer versus monolayer externally bonded CFRP sheets for shear strengthening of concrete T-Beams. J. Compos. Constr. 2021, 25, 04021025. [Google Scholar] [CrossRef]
- Mukhtar, F.M.; Shehadah, M.E. Shear behavior of flexural CFRP-strengthened RC beams with crack-induced delamination: Experimental investigation and strength model. Compos. Struct. 2021, 268, 113894. [Google Scholar] [CrossRef]
- Mansour, W. Numerical analysis of the shear behavior of FRP-strengthened continuous RC beams having web openings. Eng. Struct. 2021, 227, 111451. [Google Scholar] [CrossRef]
- Gemi, L.; Alsdudi, M.; Aksoylu, C.; Yazman, S.; Ozkilic, Y.O.; Arslan, M.H. Optimum amount of CFRP for strengthening shear deficient reinforced concrete beams. Steel Compos. Struct. 2022, 43, 735–757. [Google Scholar]
- Siddika, A.; Al Mamun, M.A.; Alyousef, R.; Amran, Y.M. Strengthening of reinforced concrete beams by using fiber-reinforced polymer composites: A review. J. Build. Eng. 2019, 25, 100798. [Google Scholar] [CrossRef]
- Capozucca, R.; Magagnini, E.; Vecchietti, M.V.; Khatir, S. RC beams damaged by cracking and strengthened with NSM CFRP/GFRP rods. Frat. Ed Integrità Strutt. 2021, 15, 386–401. [Google Scholar] [CrossRef]
- Panigrahi, A.K.; Biswal, K.; Barik, M. Strengthening of shear deficient RC T-beams with externally bonded GFRP sheets. Constr. Build. Mater. 2014, 57, 81–91. [Google Scholar] [CrossRef]
- Boumaaza, M.; Bezazi, A.; Bouchelaghem, H.; Benzennache, N.; Amziane, S.; Scarpa, F. Behavior of pre-cracked deep beams with composite materials repairs. Struct. Eng. Mech. 2017, 63, 575–583. [Google Scholar]
- Aksoylu, C. Experimental analysis of shear deficient reinforced concrete beams strengthened by glass fiber strip composites and mechanical stitches. Steel Compos. Struct. Int. J. 2021, 40, 267–285. [Google Scholar]
- Rahman, Z. Strength and ductility behaviour of FRC beams strengthened with externally bonded GFRP laminates. Mater. Today: Proc. 2021, 37, 2542–2546. [Google Scholar]
- Kumari, A.; Nayak, A. Strengthening of shear deficient RC deep beams using GFRP sheets and mechanical anchors. Can. J. Civ. Eng. 2021, 48, 1–15. [Google Scholar] [CrossRef]
- Ali, H.; Assih, J.; Li, A. Flexural capacity of continuous reinforced concrete beams strengthened or repaired by CFRP/GFRP sheets. Int. J. Adhes. Adhes. 2021, 104, 102759. [Google Scholar] [CrossRef]
- Abbass, M.; Medhlom, M.; Ali, I. Strength Capacity Cracks Propagations Deflection and Tensile Enhancement of Reinforced Concrete Beams Warped by Glass Fiber Reinforced Polymer Strips. Int. J. Eng. 2021, 34, 1094–1104. [Google Scholar]
- Miruthun, G.; Vivek, D.; Remya, P.; Elango, K.; Saravanakumar, R.; Venkatraman, S. Experimental investigation on strengthening of reinforced concrete beams using GFRP laminates. Mater. Today: Proc. 2021, 37, 27448. [Google Scholar] [CrossRef]
- Al-Shalif, S.A.; Akın, A.; Aksoylu, C.; Arslan, M.H. Strengthening of Shear-Critical Reinforced Concrete T-Beams with Anchored and Non-Anchored GFRP Fabrics Applications; Elsevier: Amsterdam, The Netherlands, 2022; pp. 809–827. [Google Scholar]
- Peng, J.; Tang, H.; Zhang, J. Structural behavior of corroded reinforced concrete beams strengthened with steel plate. J. Perform. Constr. Facil. 2017, 31, 04017013. [Google Scholar] [CrossRef]
- Kazem, H.; Rizkalla, S.; Kobayashi, A. Shear strengthening of steel plates using small-diameter CFRP strands. Compos. Struct. 2018, 184, 78–91. [Google Scholar] [CrossRef]
- Alam, M.A.; Onik, S.A.; Mustapha, K.N.B. Crack based bond strength model of externally bonded steel plate and CFRP laminate to predict debonding failure of shear strengthened RC beams. J. Build. Eng. 2020, 27, 100943. [Google Scholar] [CrossRef]
- Aykac, S.; Özbek, E. Strengthening of reinforced concrete T-beams with steel plates. Tek. Dergi 2011, 22. [Google Scholar]
- Acar, D. Çelik Levha ve Karbon Kumaşlarla Güçlendirilmiş Betonarme Kirişlerin Davranış ve Dayanımı. Master Thesis, Gazi University, Ankara, Turkey, 2014. [Google Scholar]
- Aykaç, B.; Acar, D. Betonarme Kirişlerin Dıştan Yapıştırılmış Karbon Kumaş Ve Çelik Levhalardan Oluşan Kompozit Malzemeyle Güçlendirilmesi. J. Fac. Eng. Archit. Gazi Univ. 2014, 29, 1. [Google Scholar] [CrossRef][Green Version]
- Abdul-Razzaq, K.S.; Ali, H.I.; Abdul-Kareem, M.M. A new strengthening technique for deep beam openings using steel plates. Int. J. Appl. Eng. Res. 2017, 12, 15935–15947. [Google Scholar]
- Demir, A.; Ercan, E.; Demir, D.D. Strengthening of reinforced concrete beams using external steel members. Steel Compos. Struct. 2018, 27, 453–464. [Google Scholar]
- Osman, B.H.; Wu, E.; Ji, B.; Abdulhameed, S.S. Repair of Pre-cracked Reinforced Concrete (RC) Beams with Openings Strengthened Using FRP Sheets Under Sustained Load. Int. J. Concr. Struct. Mater. 2017, 11, 171–183. [Google Scholar] [CrossRef]
- Xu, C.-X.; Peng, S.; Deng, J.; Wan, C. Study on seismic behavior of encased steel jacket-strengthened earthquake-damaged composite steel-concrete columns. J. Build. Eng. 2018, 17, 154–166. [Google Scholar] [CrossRef]
- Xu, C.C.X.; Sheng, P.S.; Wan, C.C. Experimental and Theoretical Research on Shear Strength of Seismic-Damaged SRC Frame Columns Strengthened with Enveloped Steel Jackets. Adv. Civ. Eng. 2019, 2019, 6401730. [Google Scholar] [CrossRef]
- Alshlash, S.; Aksoylu, C.; Erkan, I.H.; Arslan, M.H. Kesme Kapasitesi Yetersiz On Hasarli Betonarme Kirislerin “Dikis Demirleri” Ile Onarim/Guclendirilmesi”. In Proceedings of the IV International Scientific and Vocational Studies Congress—Engineering, Ankara, Turkey, 12–15 December 2019. [Google Scholar]
- Hamoush, S.; Ahmad, S. Concrete crack repair by stitches. Mater. Struct. 1997, 30, 418–423. [Google Scholar] [CrossRef]
- Altın, S.; Anıl, Ö.; Gökten, Y. Betonarme Kirişlerin Kesmeye Karşı Güçlendirilmesinde bir Kelepçe Uygulaması; Gazi Üniversitesi Mühendislik Mimarlık Fakültesi Dergisi: Ankara, Turkey, 2004; Volume 19, pp. 415–422. [Google Scholar]
- Rizal, A.R.; Wibowo, A.; Wijatmiko, I.; Remayanti, C. Effect of Repairing with Retrofit Method (Concrete Jacketing) Using Bamboo Reinforcement on Flexural Capacity of Reinforced Concrete Beam with Initial Damage Variation. Res. J. Adv. Eng. Sci. 2019, 4, 340–344. [Google Scholar]
- Chalioris, C.E.; Kytinou, V.K.; Voutetaki, M.E.; Papadopoulos, N.A. Repair of heavily damaged RC beams failing in shear using U-shaped mortar jackets. Buildings 2019, 9, 146. [Google Scholar] [CrossRef]
- Aldhafairi, F.; Hassan, A.; Abd-El-Hafez, L.M.; Abouelezz, A.E.Y. Different techniques of steel jacketing for retrofitting of different types of concrete beams after elevated temperature exposure. Structures 2020, 28, 713–725. [Google Scholar] [CrossRef]
- Di Trapani, F.; Malavisi, M.; Marano, G.C.; Sberna, A.P.; Greco, R. Optimal seismic retrofitting of reinforced concrete buildings by steel-jacketing using a genetic algorithm-based framework. Eng. Struct. 2020, 219, 110864. [Google Scholar] [CrossRef]
- Yuan, F.; Chen, M.; Pan, J. Flexural strengthening of reinforced concrete beams with high-strength steel wire and engineered cementitious composites. Constr. Build. Mater. 2020, 254, 119284. [Google Scholar] [CrossRef]
- Murthy, A.R.; Ganesh, P.; Sakthi Priya, G.N. Flexural Behaviour of Severely Damaged RC Beams Strengthened with Ultra-High Strength Concrete. In Recent Advances in Structural Engineering; Rao, A.R.M., Ramanjaneyulu, K., Eds.; Springer: Singapore, 2019; Volume 2, pp. 699–707. [Google Scholar]
- Hassan, A.; Baraghith, A.T.; Atta, A.M.; El-Shafiey, T.F. Retrofitting of shear-damaged RC T-beams using U-shaped SHCC jacket. Eng. Struct. 2021, 245, 112892. [Google Scholar] [CrossRef]
- Ganesh, P.; Ramachandra Murthy, A. Analytical model to predict the fatigue life of damaged RC beam strengthened with GGBS based UHPC. Structures 2021, 33, 2559–2569. [Google Scholar] [CrossRef]
- Chandrakar, J.; Singh, A.K. Retrofitting of Rcc Structral Members Using Concrete Jacketing. Int. J. Recent Dev. Civ. Environ. Eng. 2017, 2. ISSN 25814117. [Google Scholar]
- Rodrigues, H.; Pradhan, P.M.; Furtado, A.; Rocha, P.; Vila-Pouca, N. Structural Repair and Strengthening of RC Elements with Concrete Jacketing. In Strengthening and Retrofitting of Existing Structures; Costa, A., Arêde, A., Varum, H., Eds.; Springer: Singapore, 2018; pp. 181–198. [Google Scholar]
- TS500, Enstitü, T.S. TS 500 Betonarme Yapıların Tasarım ve Yapım Kuralları. Ankara, Türkiye. 2000. Available online: https://www.resmigazete.gov.tr/eskiler/2000/07/20000712M1-23.pdf (accessed on 25 August 2022).
- Özkılıç, Y.O.; Aksoylu, C.; Arslan, M.H. Experimental and numerical investigations of steel fiber reinforced concrete dapped-end purlins. J. Build. Eng. 2021, 36, 102119. [Google Scholar] [CrossRef]
- Aksoylu, C.; Özkılıç, Y.O.; Arslan, M.H. Damages on prefabricated concrete dapped-end purlins due to snow loads and a novel reinforcement detail. Eng. Struct. 2020, 225, 111225. [Google Scholar] [CrossRef]
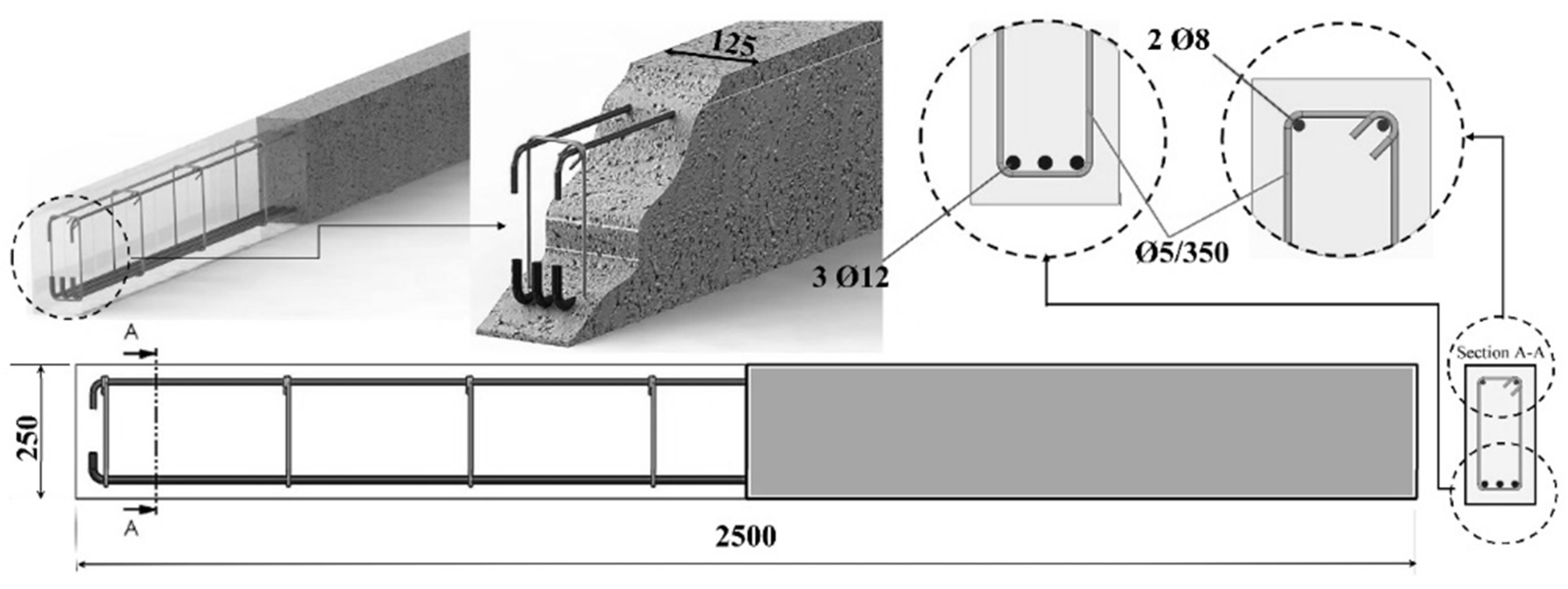










| Strengthening Type | Pre-Damaged Beams | Undamaged Beams | |
|---|---|---|---|
| FRP | AFRP * | Raza et al. (2019) [12] | More and Kulkarni (2014) [13]; Wu et al. (2016) [14]; Zhang and Wu (2019) [15]; Raval et al. (2020) [16]; |
| BFRP * | Ma et al. (2017) [17]; Ma et al. (2018) [18]; Qin et al. (2019) [19]; | Duic et al. (2018) [20]; Joyklad et al. (2019) [21]; Pham et al. (2020) [22]; Shen et al. (2021) [23] | |
| CFRP * | Prado et al. (2016) [24]; Karzad et al. (2017) [25]; Karam et al. (2017) [26]; Karzad et al. (2019) [27]; Yu et al. (2020) [28]; Yu et al. (2020) [29]; Yu et al. (2021) [30]; Bahij et al. (2020) [31] | Gemi et al. (2019) [11]; Zaki et al. (2019) [32]; Aksoylu et al. (2021) [33]; Al-Khafaji et al. (2021) [34]; Kotynia et al. (2021) [35]; Abed et al. (2021) [36]; Al-Fakih et al. (2021) [37]; Jahami et al. (2021) [38]; Alhassan et al. (2021) [39]; Samb et al. (2021) [40]; Mukhtar and Shehadah (2021) [41]; Mansour (2021) [42]; Gemi et al. (2022) [43]; | |
| GFRP * | Siddika et al. (2019) [44]; Capozucca et al. (2021) [45]; | Panigrahi et al. (2014) [46]; Boumaaza et al. (2017) [47]; Aksoylu (2021) [48]; Rahman (2021) [49]; Kumari ve Nayak (2021) [50]; Ali et al. (2021) [51]; Abbas et al. (2021) [52]; Miruthun et al. (2021) [53]; Al-Shalif et al. (2022) [54]; | |
| Steel Plate | Peng et al. (2017) [55]; Kazem (2018) [56]; Alam et al. (2020) [57] | Aykaç ve Özbek (2011) [58]; Acar (2014) [59]; Aykaç and Acar (2014) [60]; Abdul-Razzaq et al. (2017) [61]; Demir et al. (2018) [62] | |
| Mechanical Connections | Osman et al. (2017) [63]; Xu et al. (2018) [64]; Xu et al. (2019) [65]; Alshlash et al. (2019) [66] | Hamoush and Ahmad (1997) [67]; Altin et al. (2004) [68]; Rizal et al. (2019) [69]; Chalioris et al. (2019) [70]; Aldhafairi et al. (2020) [71]; Di Trapani et al. (2020) [72]; Yuan et al. (2020) [73]; | |
| Jacketing | Murthy et al. (2019) [74]; Hassan et al. (2021) [75]; Ganesh and Murthy (2021) [76] | Chandrakar ve Singh (2017) [77]; Rodrigues et al. (2018) [78] | |
| Specimen | MS Diameter (ϕ) (mm) | MS Number | MS Spacing (s) (mm) | MS Volumetric Ratio (ρMS) |
|---|---|---|---|---|
| S0 | - | - | - | --- |
| S1 | 6 | 4 | 220 | 0.0020 |
| S2 | 6 | 5 | 165 | 0.0027 |
| S3 | 6 | 6 | 130 | 0.0034 |
| S4 | 6 | 7 | 110 | 0.0041 |
| S5 | 6 | 15 | 45 | 0.0100 |
| Specimen No | First Crack | Beam Damage Type | MSS Damage Type | Special Cases | ||||
|---|---|---|---|---|---|---|---|---|
| Load (kN) | Design Type | Angle | Place | Load (kN) | Failure Type | |||
| S0 | 30 | Bending | 90° | Bending zone | 73.00 | Shear | --- | Experiment ended up shear failure on the left side |
| S1 | 10 | Bending | 90° | Bending zone | 74.59 | Shear | No damage observed on MS | Experiment ended up shear failure on the left side |
| S2 | 20 | Bending | 90° | Bending zone | 75.79 | Shear | No damage observed on MS | Experiment ended up shear failure on the right side |
| S3 | 20 | Bending | 90° | Bending zone | 76.90 | Shear | No damage observed on MS | Experiment ended up bending failure on the right side |
| S4 | 30 | Bending | 90° | Bending zone | 78.10 | Shear | No damage observed on MS | Experiment ended up bending failure on the right side |
| S5 | 20 | Bending | 90° | Bending zone | 95.74 | Shear | No damage observed on MS | Experiment ended up bending failure on the left side |
| Test Specimens | Pmax (kN) | Rate of Increase at Max Load (%) | Displacement at Maximum Load (mm) | Stiffness at Maximum Load (Pmax) (kN/mm) | Pu (0.85Pmax) (kN) | Displacement at Yield, δy (mm) | At Yield (0.85Pmax) Stiffness (kN/mm) | δu (mm) | Ductility Ratio |
|---|---|---|---|---|---|---|---|---|---|
| S0 | 73.00 | 1.00 | 8.83 | 8.26 | 62.00 | 6.62 | 9.36 | 9.83 | 1.49 |
| S1 | 74.59 | 2.17 | 8.67 | 8.60 | 63.40 | 7.02 | 9.02 | 10.06 | 1.43 |
| S2 | 75.79 | 3.82 | 8.07 | 9.39 | 64.42 | 6.45 | 9.98 | 9.49 | 1.47 |
| S3 | 76.90 | 5.34 | 9.53 | 8.06 | 65.36 | 7.87 | 8.30 | 10.02 | 1.27 |
| S4 | 78.10 | 6.98 | 10.17 | 7.68 | 66.38 | 8.07 | 8.22 | 11.02 | 1.36 |
| S5 | 95.74 | 31.15 | 17.89 | 5.35 | 81.38 | 14.00 | 5.81 | 25.66 | 1.83 |
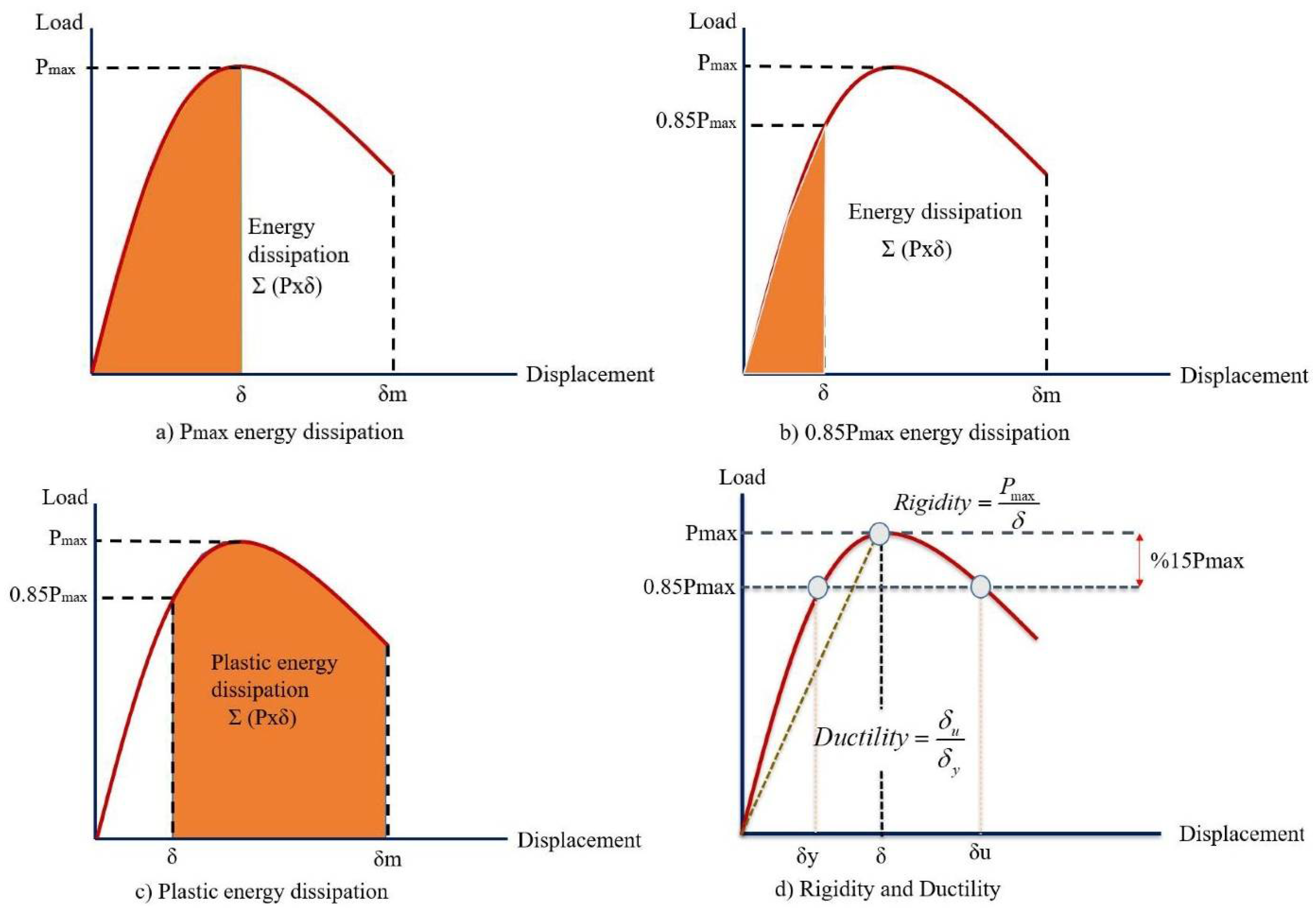
| Test Specimens | Maximum Displacement (mm) | Energy Dissipation at Pmax (kJ) | Energy Dissipation at 0.85Pmax (kJ) | Plastik Energy Dissipation (kJ) | Total Energy Dissipation (kJ) | Failure Type | Ductility Level |
|---|---|---|---|---|---|---|---|
| S0 | 10.26 | 0.47 | 0.26 | 0.21 | 0.56 | Shear | Deficient |
| S1 | 15.84 | 0.70 | 0.27 | 0.57 | 0.84 | Shear | Deficient |
| S2 | 12.21 | 0.37 | 0.26 | 0.47 | 0.73 | Shear | Deficient |
| S3 | 12.09 | 0.41 | 0.30 | 0.40 | 0.71 | Shear | Deficient |
| S4 | 14.01 | 0.47 | 0.31 | 0.47 | 0.794 | Shear | Deficient |
| S5 | 30.77 | 0.98 | 0.63 | 1.81 | 2.45 | Shear | Deficient |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aksoylu, C.; Özkılıç, Y.O.; Arslan, M.H. Mechanical Steel Stitches: An Innovative Approach for Strengthening Shear Deficiency in Undamaged Reinforced Concrete Beams. Buildings 2022, 12, 1501. https://doi.org/10.3390/buildings12101501
Aksoylu C, Özkılıç YO, Arslan MH. Mechanical Steel Stitches: An Innovative Approach for Strengthening Shear Deficiency in Undamaged Reinforced Concrete Beams. Buildings. 2022; 12(10):1501. https://doi.org/10.3390/buildings12101501
Chicago/Turabian StyleAksoylu, Ceyhun, Yasin Onuralp Özkılıç, and Musa Hakan Arslan. 2022. "Mechanical Steel Stitches: An Innovative Approach for Strengthening Shear Deficiency in Undamaged Reinforced Concrete Beams" Buildings 12, no. 10: 1501. https://doi.org/10.3390/buildings12101501
APA StyleAksoylu, C., Özkılıç, Y. O., & Arslan, M. H. (2022). Mechanical Steel Stitches: An Innovative Approach for Strengthening Shear Deficiency in Undamaged Reinforced Concrete Beams. Buildings, 12(10), 1501. https://doi.org/10.3390/buildings12101501









