Strain Hardening, Damage and Fracture Behavior of Al-Added High Mn TWIP Steels
Abstract
:1. Introduction
2. Materials and Experimental Methods
2.1. Materials Processing
2.2. Microstructure Characterization
2.2.1. Micro-Tensile Tests
2.2.2. Inclusions and Fracture Surface Analysis
2.3. Mechanical Tests
2.3.1. Macro-Tensile Tests with Digital Image Correlation (DIC)
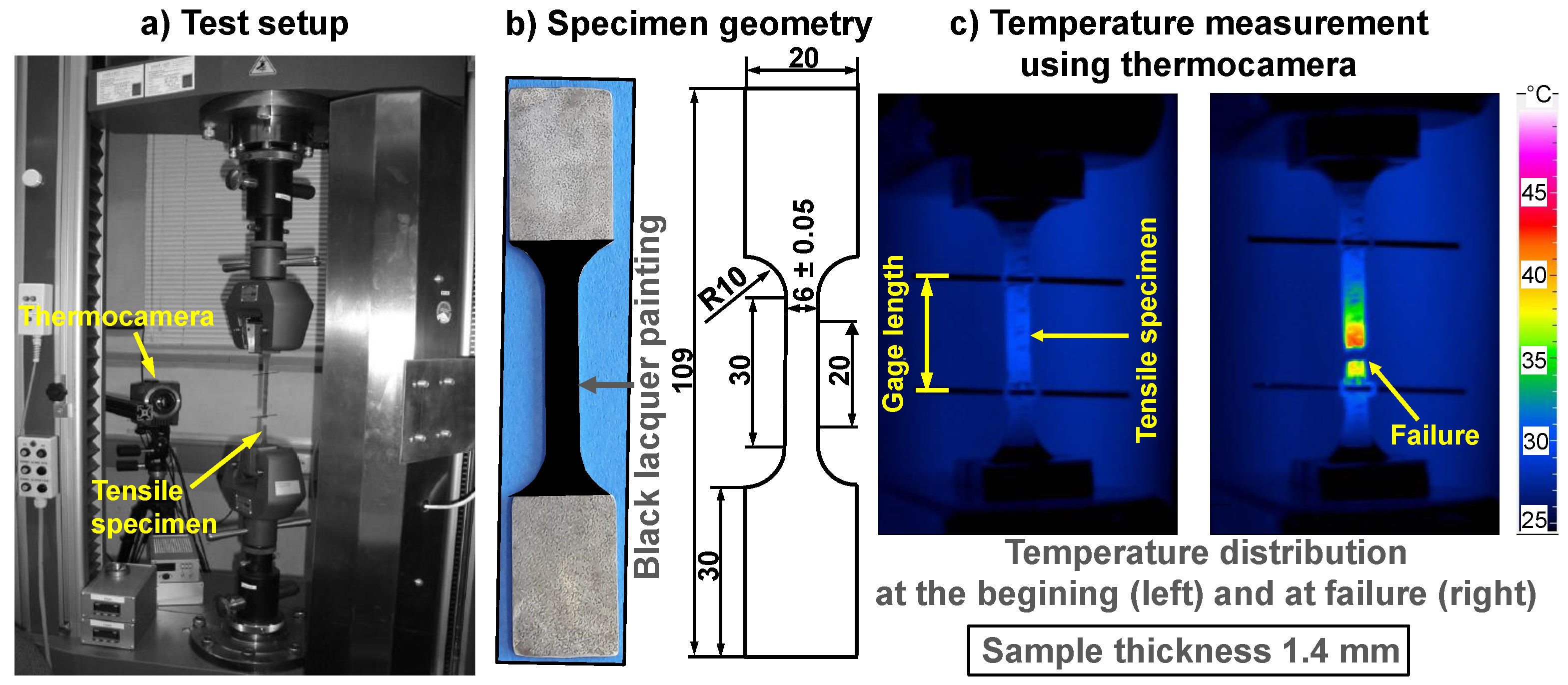
2.3.2. Macro-Tensile Tests with High-Speed Thermocamera
2.3.3. Elastic Constants Measurement
3. Results
3.1. Microstructure Analysis
3.2. Mechanical Properties
3.3. Deformation Mechanisms
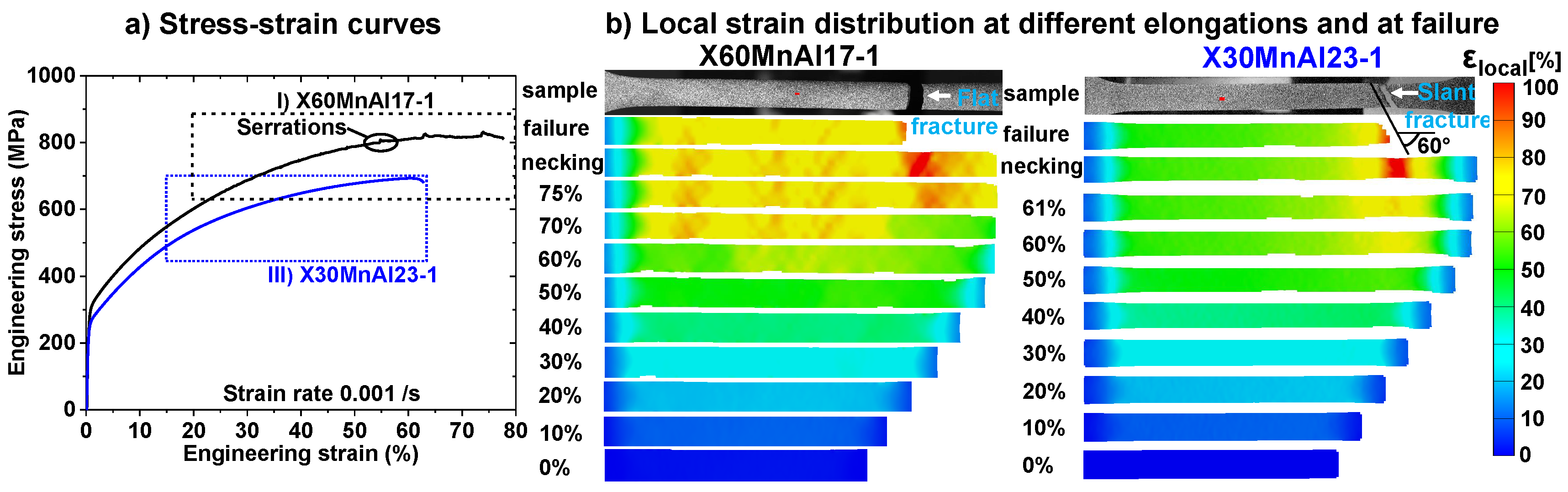
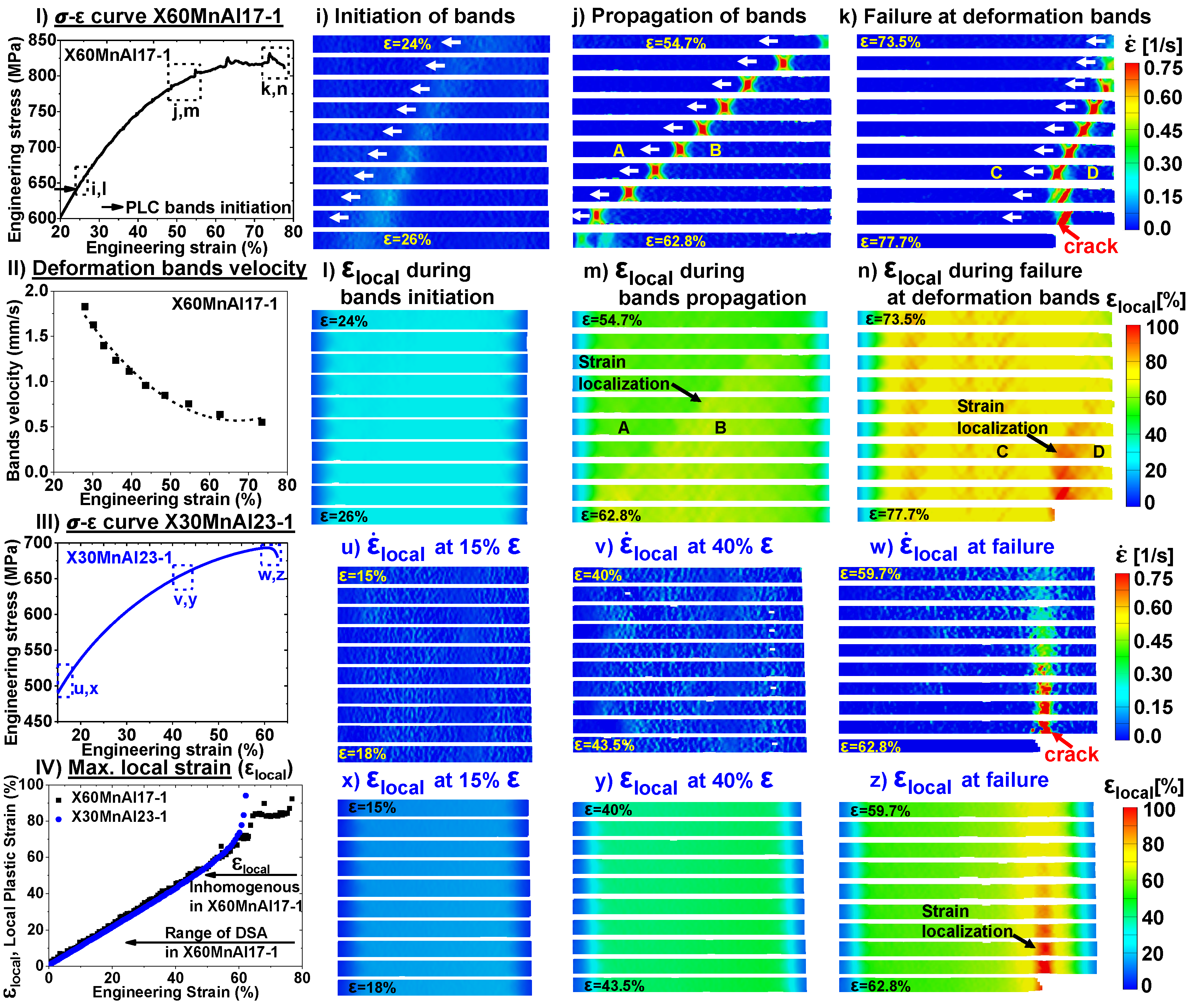
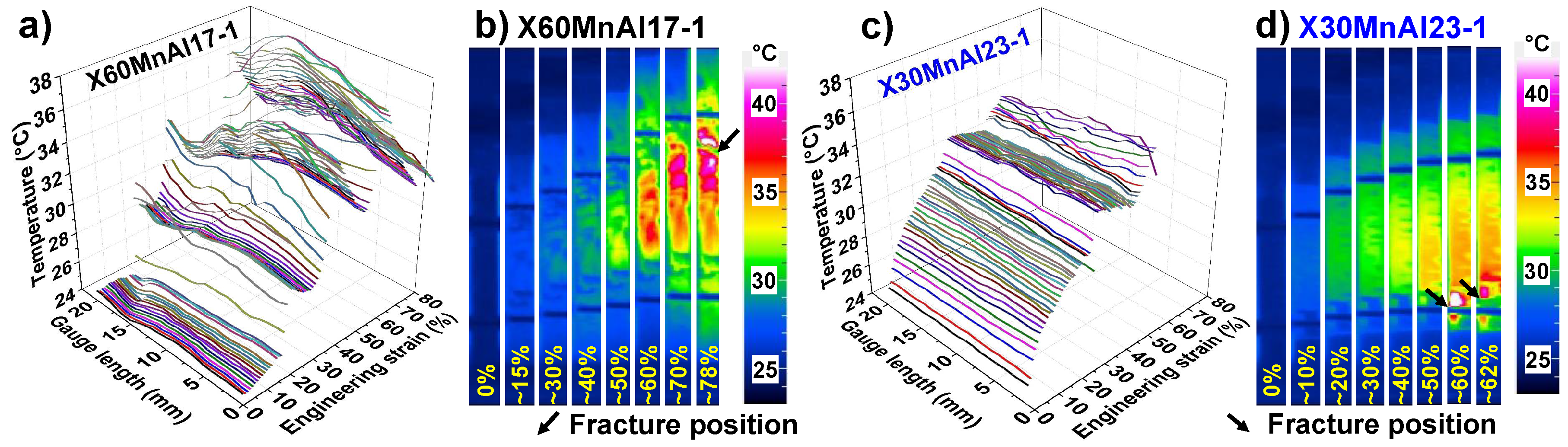
3.4. Local Deformation Behavior
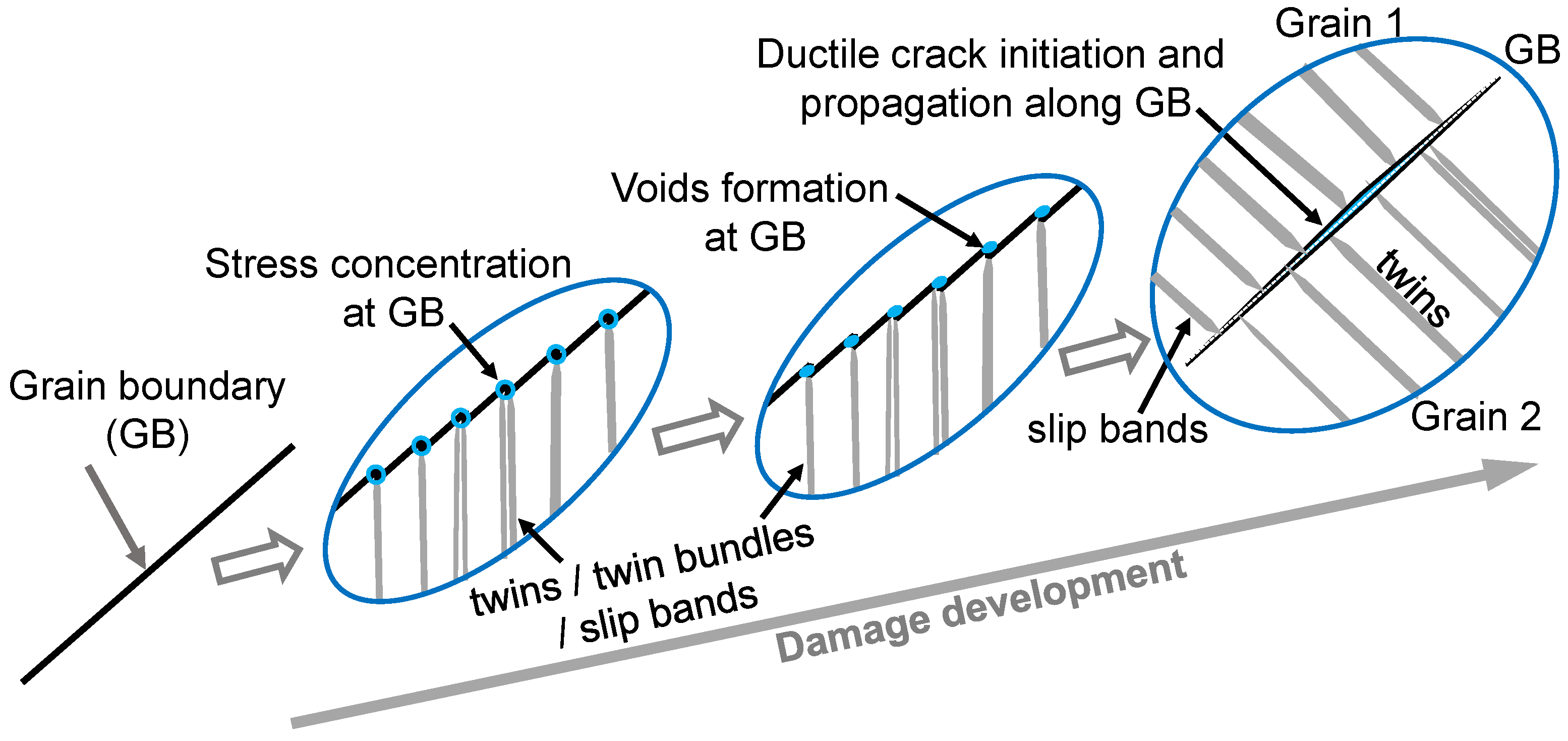
3.5. Mechanisms of Damage and Failure
4. Discussion
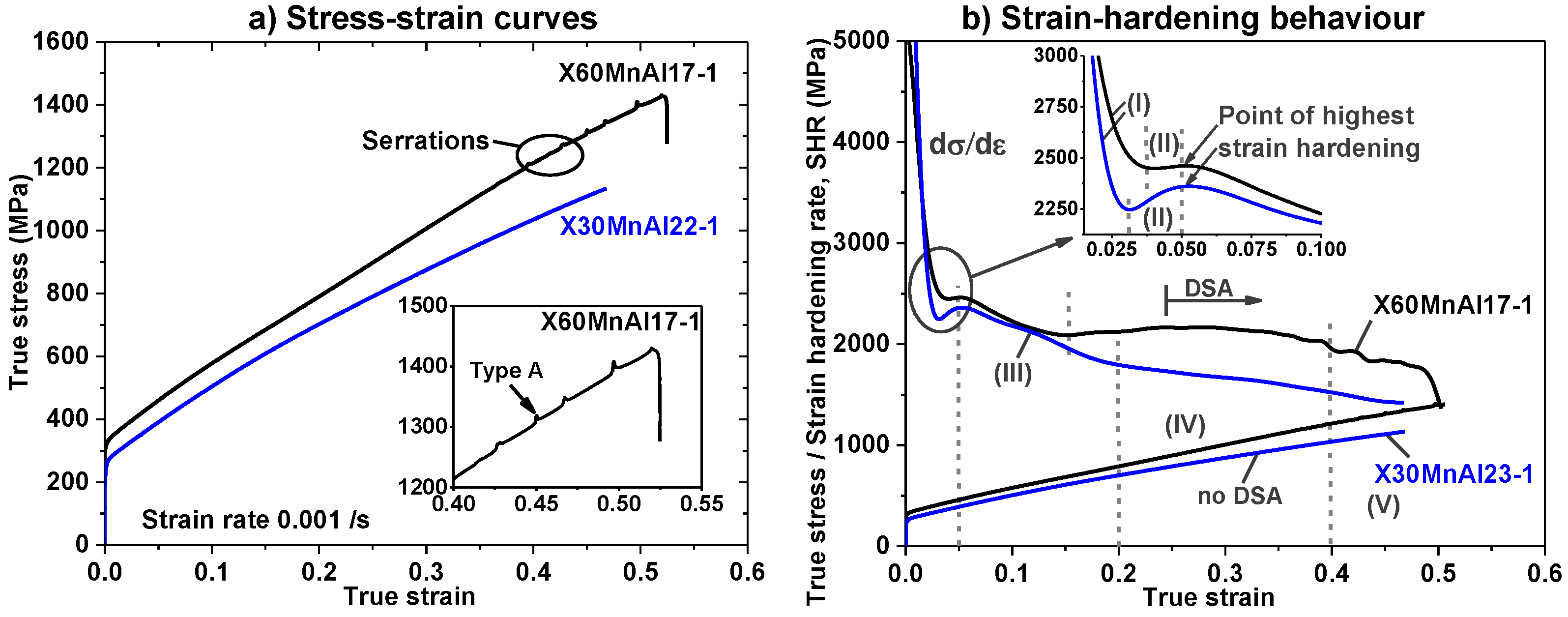
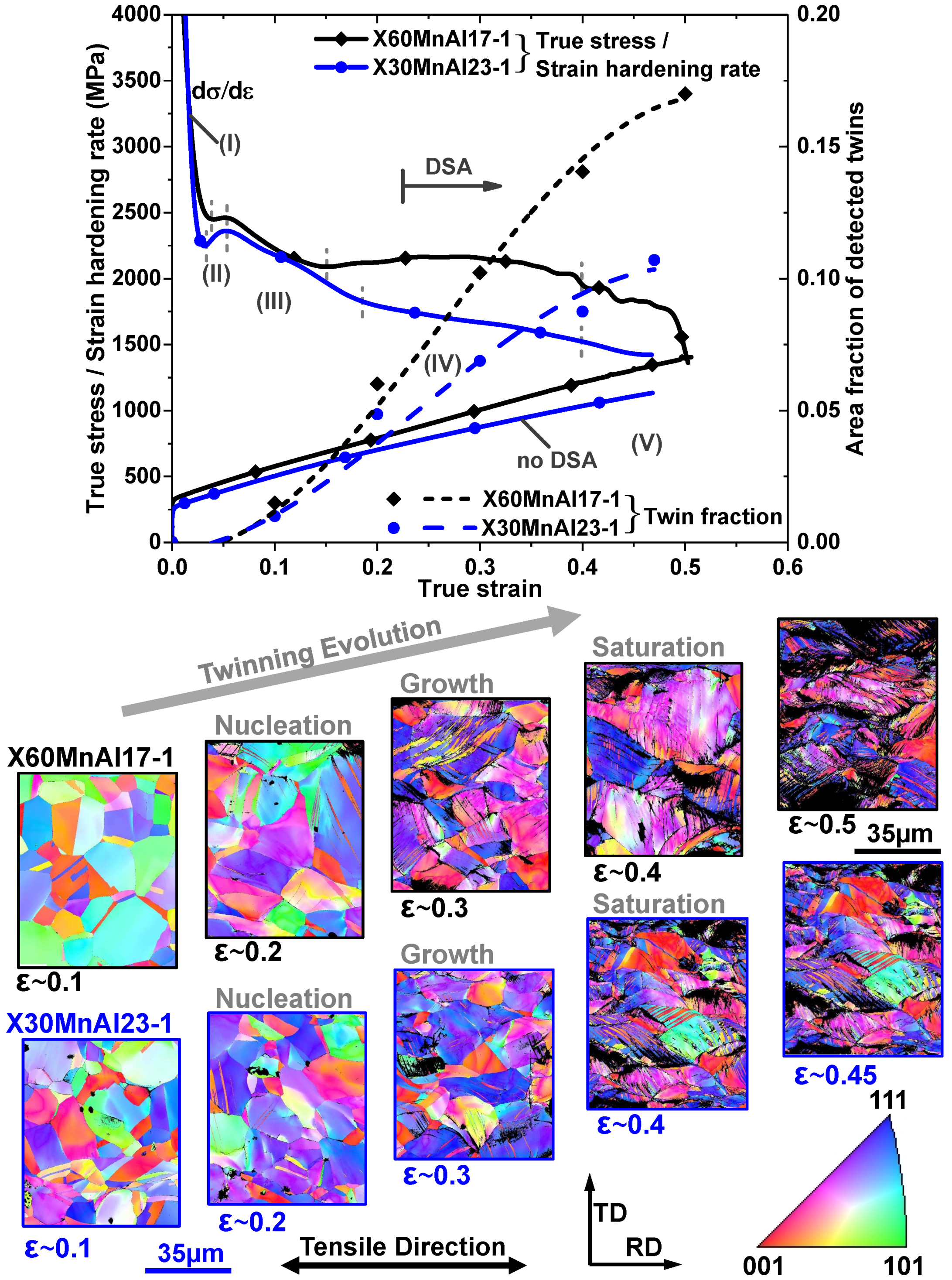
4.1. Serrated Flow and PLC Effect
4.2. Strain Hardening and Twinning Evolution
4.3. Damage and Fracture
5. Conclusions
- Strain hardening rate of an X60MnAl17-1 alloy is extraordinarily high compared to an X30MnAl23-1 alloy. An X60MnAl17-1 alloy showed higher yield strength, tensile strength and elongation compared to an X30MnAl23-1 alloy. The enhanced mechanical properties of the X60MnAl17-1 alloy is mainly due to the enhanced deformation twinning in addition to dislocation glide and also activation of dynamic strain aging (DSA). DSA is completely suppressed in an X30MnAl23-1 alloy at room temperature and quasi-static strain rate due to lower carbon content.
- Twining is the most predominant deformation mechanism occurred along with dislocation slip in both the alloys. The addition of Al has led to increased stacking fault energy thereby delaying nucleation of deformation twins and prolonged the saturation of twinning.
- Micro-cracks are observed at elongated MnS inclusions or at AlN inclusions at a relatively small strain of ∼2/3 of total strain. However, these micro-cracks showed no tendency to grow.
- Large heterogeneous deformation within the grains by twinning or dislocation slip has led to a high-stress concentration at grain boundaries (GBs) due to the interception of deformation twins and slip band extrusions at GBs. Hence micro-cracks in Al-added TWIP steels originated mainly at grain boundaries and triple junctions.
- In an X60MnAl17-1 alloy, the occurrence of DSA has led to inhomogeneous flow behavior due to the nucleation and propagation of deformation bands during deformation. This resulted in large strain localization within the deformation bands and the velocity of band motion decreased with increasing strain due to the intersection of two bands. The accumulation within the intersecting bands resulted in a macroscopic crack initiation close to the edges of the tensile specimen. In an X30MnAl23-1 alloy, homogenous distribution throughout the gauge length could be observed until the beginning of necking. Thereafter failure in the material occurred by classical necking and strain localization.
- The ductile failure mode is the most predominant mode of failure in Al-added TWIP steels, mainly characterized by the formation of very fine dimples with a crack propagation along GBs.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Macro-Tensile Tests Setup for the Local Strain Analysis Using Digital Image Correlation

Appendix B. Macro-Tensile Tests Setup for Temperature Measurement Using High Resolution Thermocamera
References
- Horvath, C.D. Advanced steels for lightweight automotive structures. In Materials, Design and Manufacturing for Lightweight Vehicles; Elsevier: Amsterdam, The Netherlands, 2010; pp. 35–78. [Google Scholar] [CrossRef]
- Hirsch, J. Aluminium in Innovative Light-Weight Car Design. Mater. Trans. 2011, 52, 818–824. [Google Scholar] [CrossRef]
- Hirsch, J.; Al-Samman, T. Superior light metals by texture engineering: Optimized aluminum and magnesium alloys for automotive applications. Acta Mater. 2013, 61, 818–843. [Google Scholar] [CrossRef]
- Sherman, A.M.; Sommer, C.J.; Froes, F.H. The use of titanium in production automobiles: Potential and challenges. JOM 1997, 49, 38–41. [Google Scholar] [CrossRef]
- Luo, A.; Sachdev, A. 12—Applications of magnesium alloys in automotive engineering. In Advances in Wrought Magnesium Alloys; Bettles, C., Barnett, M., Eds.; Woodhead Publishing Series in Metals and Surface Engineering; Woodhead Publishing: Cambridge, UK, 2012; pp. 393–426. [Google Scholar] [CrossRef]
- Kantanen, P.; Somani, M.; Kaijalainen, A.; Haiko, O.; Porter, D.; Kömi, J. Microstructural Characterization and Mechanical Properties of Direct Quenched and Partitioned High-Aluminum and High-Silicon Steels. Metals 2019, 9, 256. [Google Scholar] [CrossRef]
- Hall, J.N.; Fekete, J.R. Steels for auto bodies. In Automotive Steels: Design, Metallurgy, Processing and Applications; Woodhead Publishing: Cambridge, UK, 2017; pp. 19–45. [Google Scholar]
- Krauss, G. Physical metallurgy of steels. In Automotive Steels: Design, Metallurgy, Processing and Applications; Woodhead Publishing: Cambridge, UK, 2017; pp. 95–111. [Google Scholar]
- Grässel, O.; Krüger, L.; Frommeyer, G.; Meyer, L. High strength Fe–Mn–(Al, Si) TRIP/TWIP steels development–properties–application. Int. J. Plast. 2000, 16, 1391–1409. [Google Scholar] [CrossRef]
- Bouaziz, O.; Allain, S.; Scott, C.; Cugy, P.; Barbier, D. High manganese austenitic twinning induced plasticity steels: A review of the microstructure properties relationships. Curr. Opin. Solid State Mater. Sci. 2011, 15, 141–168. [Google Scholar] [CrossRef]
- Saeed-Akbari, A.; Mosecker, L.; Schwedt, A.; Bleck, W. Characterization and Prediction of Flow Behavior in High-Manganese Twinning Induced Plasticity Steels: Part I. Mechanism Maps and Work-Hardening Behavior. Metall. Mater. Trans. A 2012, 43, 1688–1704. [Google Scholar] [CrossRef]
- Lee, S.J.; Han, J.; Lee, S.; Kang, S.H.; Lee, S.M.; Lee, Y.K. Design for Fe-high Mn alloy with an improved combination of strength and ductility. Sci. Rep. 2017, 7, 3573. [Google Scholar] [CrossRef] [PubMed]
- De Cooman, B.C.; Estrin, Y.; Kim, S.K. Twinning-induced plasticity (TWIP) steels. Acta Mater. 2018, 142, 283–362. [Google Scholar] [CrossRef]
- Madivala, M.; Schwedt, A.; Prahl, U.; Bleck, W. Anisotropy and strain rate effects on the failure behavior of TWIP steel: A multiscale experimental study. Int. J. Plast. 2019, 115, 178–199. [Google Scholar] [CrossRef]
- Madivala, M.; Bleck, W. Strain Rate Dependent Mechanical Properties of TWIP Steel. JOM 2019, 71, 1291–1302. [Google Scholar] [CrossRef]
- Jung, I.C.; De Cooman, B.C. Temperature dependence of the flow stress of Fe–18Mn–0.6C–xAl twinning-induced plasticity steel. Acta Mater. 2013, 61, 6724–6735. [Google Scholar] [CrossRef]
- Pierce, D.T.; Jiménez, J.A.; Bentley, J.; Raabe, D.; Wittig, J.E. The influence of stacking fault energy on the microstructural and strain-hardening evolution of Fe–Mn–Al–Si steels during tensile deformation. Acta Mater. 2015, 100, 178–190. [Google Scholar] [CrossRef]
- Kim, J.K.; Kwon, M.H.; De Cooman, B.C. On the deformation twinning mechanisms in twinning-induced plasticity steel. Acta Mater. 2017, 141, 444–455. [Google Scholar] [CrossRef]
- Madivala, M.; Schwedt, A.; Wong, S.L.; Roters, F.; Prahl, U.; Bleck, W. Temperature dependent strain hardening and fracture behavior of TWIP steel. Int. J. Plast. 2018, 104, 80–103. [Google Scholar] [CrossRef]
- Chen, L.; Kim, H.S.; Kim, S.K.; De Cooman, B.C. Localized Deformation due to Portevin–LeChatelier Effect in 18Mn–0.6C TWIP Austenitic Steel. ISIJ Int. 2007, 47, 1804–1812. [Google Scholar] [CrossRef]
- Allain, S.; Cugy, P.; Scott, C.; Chateau, J.P.; Rusinek, A.; Deschamps, A. The influence of plastic instabilities on the mechanical properties of a high-manganese austenitic FeMnC steel. Int. J. Mater. Res. 2008, 99, 734–738. [Google Scholar] [CrossRef]
- Lee, S.J.; Kim, J.; Kane, S.N.; De Cooman, B.C. On the origin of dynamic strain aging in twinning-induced plasticity steels. Acta Mater. 2011, 59, 6809–6819. [Google Scholar] [CrossRef]
- Kang, M.; Shin, E.; Woo, W.; Lee, Y.K. Small-angle neutron scattering analysis of Mn–C clusters in high-manganese 18Mn–0.6C steel. Mater. Charact. 2014, 96, 40–45. [Google Scholar] [CrossRef]
- Song, W.; Houston, J. Local Deformation and Mn-C Short-Range Ordering in a High-Mn Fe-18Mn-0.6C Steel. Metals 2018, 8, 292. [Google Scholar] [CrossRef]
- Koyama, M.; Sawaguchi, T.; Tsuzaki, K. TWIP Effect and Plastic Instability Condition in an Fe-Mn-C Austenitic Steel. ISIJ Int. 2013, 53, 323–329. [Google Scholar] [CrossRef]
- Koyama, M.; Sawaguchi, T.; Tsuzaki, K. Overview of Dynamic Strain Aging and Associated Phenomena in Fe–Mn–C Austenitic Steels. ISIJ Int. 2018, 58, 1383–1395. [Google Scholar] [CrossRef]
- Kim, J.; Estrin, Y.; De Cooman, B.C. Application of a Dislocation Density-Based Constitutive Model to Al-Alloyed TWIP Steel. Metall. Mater. Trans. A 2013, 44, 4168–4182. [Google Scholar] [CrossRef]
- Kim, J.K.; De Cooman, B.C. Stacking fault energy and deformation mechanisms in Fe-xMn-0.6C-yAl TWIP steel. Mater. Sci. Eng. A 2016, 676, 216–231. [Google Scholar] [CrossRef]
- Yang, H.K.; Zhang, Z.J.; Dong, F.Y.; Duan, Q.Q.; Zhang, Z.F. Strain rate effects on tensile deformation behaviors for Fe–22Mn–0.6C–(1.5Al) twinning-induced plasticity steel. Mater. Sci. Eng. A 2014, 607, 551–558. [Google Scholar] [CrossRef]
- Yu, H.Y.; Lee, S.M.; Nam, J.H.; Lee, S.J.; Fabrègue, D.; Park, M.h.; Tsuji, N.; Lee, Y.K. Post-uniform elongation and tensile fracture mechanisms of Fe-18Mn-0.6C-xAl twinning-induced plasticity steels. Acta Mater. 2017, 131, 435–444. [Google Scholar] [CrossRef]
- Yang, C.L.; Zhang, Z.J.; Zhang, P.; Zhang, Z.F. The premature necking of twinning-induced plasticity steels. Acta Mater. 2017, 136, 1–10. [Google Scholar] [CrossRef]
- Fabrègue, D.; Landron, C.; Bouaziz, O.; Maire, E. Damage evolution in TWIP and standard austenitic steel by means of 3D X ray tomography. Mater. Sci. Eng. A 2013, 579, 92–98. [Google Scholar] [CrossRef]
- Lorthios, J.; Nguyen, F.; Gourgues, A.F.; Morgeneyer, T.F.; Cugy, P. Damage observation in a high-manganese austenitic TWIP steel by synchrotron radiation computed tomography. Scr. Mater. 2010, 63, 1220–1223. [Google Scholar] [CrossRef]
- Allain, S.; Chateau, J.P.; Bouaziz, O.; Migot, S.; Guelton, N. Correlations between the calculated stacking fault energy and the plasticity mechanisms in Fe–Mn–C alloys. Mater. Sci. Eng. A 2004, 387–389, 158–162. [Google Scholar] [CrossRef]
- Ledbetter, H.M.; Frederick, N.V.; Austin, M.W. Elastic–constant variability in stainless–steel 304. J. Appl. Phys. 1980, 51, 305–309. [Google Scholar] [CrossRef]
- Dastur, Y.N.; Leslie, W.C. Mechanism of work hardening in Hadfield manganese steel. Metall. Trans. A 1981, 12, 749–759. [Google Scholar] [CrossRef]
- Sevsek, S.; Brasche, F.; Haase, C.; Bleck, W. Combined deformation twinning and short-range ordering causes serrated flow in high-manganese steels. Mater. Sci. Eng. A 2019, 746, 434–442. [Google Scholar] [CrossRef]
- Shun, T.; Wan, C.M.; Byrne, J.G. A study of work hardening in austenitic Fe-Mn-C and Fe-Mn-Al-C alloys. Acta Metall. Mater. 1992, 40, 3407–3412. [Google Scholar] [CrossRef]
- Koyama, M.; Sawaguchi, T.; Tsuzaki, K. Deformation Twinning Behavior of Twinning-Induced Plasticity Steels with Different Carbon Concentrations. Tetsu-to-Hagane 2014, 100, 1253–1260. [Google Scholar] [CrossRef]
- Lebedkina, T.A.; Lebyodkin, M.A.; Chateau, J.P.; Jacques, A.; Allain, S. On the mechanism of unstable plastic flow in an austenitic FeMnC TWIP steel. Mater. Sci. Eng. A 2009, 519, 147–154. [Google Scholar] [CrossRef]
- Ogawa, T.; Koyama, M.; Tasan, C.C.; Tsuzaki, K.; Noguchi, H. Effects of martensitic transformability and dynamic strain age hardenability on plasticity in metastable austenitic steels containing carbon. J. Mater. Sci. 2017, 52, 7868–7882. [Google Scholar] [CrossRef]
- Song, W.; Bogdanovski, D.; Yildiz, A.; Houston, J.; Dronskowski, R.; Bleck, W. On the Mn–C Short-Range Ordering in a High-Strength High-Ductility Steel: Small Angle Neutron Scattering and Ab Initio Investigation. Metals 2018, 8, 44. [Google Scholar] [CrossRef]
- Wesselmecking, S.; Song, W.; Ma, Y.; Roesler, T.; Hofmann, H.; Bleck, W. Strain Aging Behavior of an Austenitic High-Mn Steel. Steel Res. Int. 2018, 88, 1700515. [Google Scholar] [CrossRef]
- Allain, S.; Bouaziz, O.; Lebedkina, T.; Lebyodkin, M. Relationship between relaxation mechanisms and strain aging in an austenitic FeMnC steel. Scr. Mater. 2011, 64, 741–744. [Google Scholar] [CrossRef]
- Gwon, H.; Kim, J.K.; Shin, S.; Cho, L.; De Cooman, B.C. The effect of vanadium micro-alloying on the microstructure and the tensile behavior of TWIP steel. Mater. Sci. Eng. A 2017, 696, 416–428. [Google Scholar] [CrossRef]
- Gutierrez-Urrutia, I.; Raabe, D. Grain size effect on strain hardening in twinning-induced plasticity steels. Scr. Mater. 2012, 66, 992–996. [Google Scholar] [CrossRef]








| Alloy | C | Si | Mn | P | S | Cr | Ni | Cu | Al | V | N | Fe | SFE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X60MnAl17-1 | 0.60 | 0.06 | 17.17 | <0.009 | <0.006 | 0.05 | 0.04 | 0.03 | 1.50 | 0.07 | 0.015 | Bal. | 29 |
| X30MnAl23-1 | 0.30 | 0.04 | 22.43 | <0.009 | <0.005 | 0.05 | 0.04 | 0.02 | 1.39 | 0.10 | 0.013 | Bal. | 24 |
| Alloy | Area Fraction (%) | Average Size (µm) | Largest Size (µm) |
|---|---|---|---|
| X60MnAl17-1 | 0.10 ± 0.01 | 1.23 ± 0.05 | 8.0 ± 1.5 |
| X30MnAl23-1 | 0.11 ± 0.02 | 1.50 ± 0.10 | 12.0 ± 2.0 |
| Alloy | YS | UTS | UE | TE | r-Value | n-Value | E | G | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Unit | MPa | MPa | % | % | - | - | kg/m | GPa | GPa | - |
| X60MnAl17-1 | 294 ± 10 | 844 ± 15 | 65 ± 5 | 70 ± 5 | 0.90 ± 0.01 | 0.35 ± 0.01 | 7700 ± 10 | 188 ± 2 | 75 ± 1 | 0.267 ± 0.01 |
| X30MnAl23-1 | 246 ± 10 | 693 ± 15 | 62 ± 2 | 63 ± 2 | 0.83 ± 0.01 | 0.37 ± 0.01 | 7715 ± 5 | 161 ± 1 | 63 ± 1 | 0.274 ± 0.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Madivala, M.; Schwedt, A.; Prahl, U.; Bleck, W. Strain Hardening, Damage and Fracture Behavior of Al-Added High Mn TWIP Steels. Metals 2019, 9, 367. https://doi.org/10.3390/met9030367
Madivala M, Schwedt A, Prahl U, Bleck W. Strain Hardening, Damage and Fracture Behavior of Al-Added High Mn TWIP Steels. Metals. 2019; 9(3):367. https://doi.org/10.3390/met9030367
Chicago/Turabian StyleMadivala, Manjunatha, Alexander Schwedt, Ulrich Prahl, and Wolfgang Bleck. 2019. "Strain Hardening, Damage and Fracture Behavior of Al-Added High Mn TWIP Steels" Metals 9, no. 3: 367. https://doi.org/10.3390/met9030367
APA StyleMadivala, M., Schwedt, A., Prahl, U., & Bleck, W. (2019). Strain Hardening, Damage and Fracture Behavior of Al-Added High Mn TWIP Steels. Metals, 9(3), 367. https://doi.org/10.3390/met9030367







