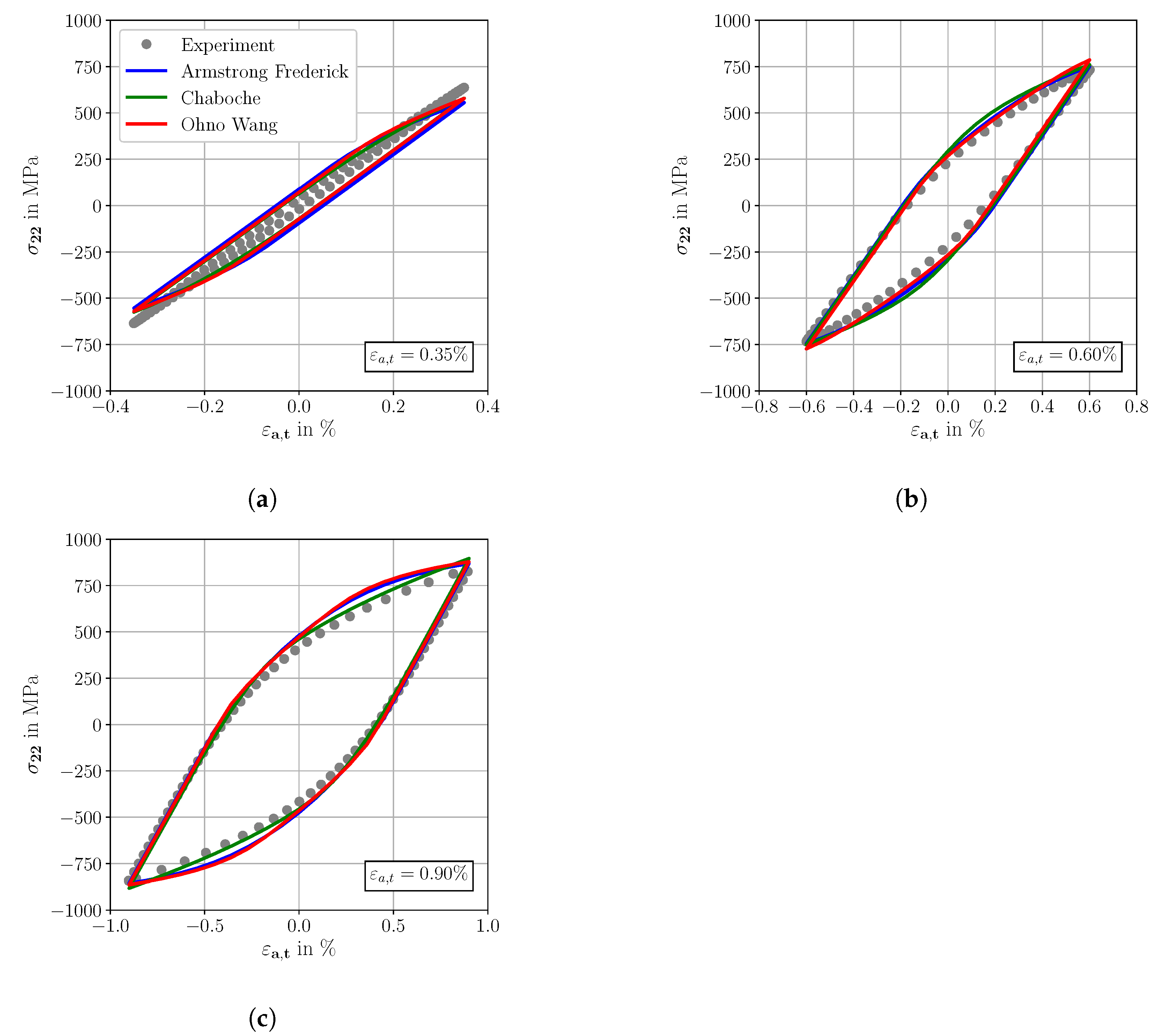Abstract
A fundamental prerequisite for the micromechanical simulation of fatigue is the appropriate modelling of the effective cyclic properties of the considered material. Therefore, kinematic hardening formulations on the slip system level are of crucial importance due to their fundamental relevance in cyclic material modelling. The focus of this study is the comparison of three different kinematic hardening models (Armstrong Frederick, Chaboche, and Ohno–Wang). In this work, investigations are performed on the modelling and prediction of the cyclic stress-strain behavior of the martensitic high-strength steel SAE 4150 for two different total strain ratios (R = −1 and R = 0). In the first step, a three-dimensional martensitic microstructure model is developed by using multiscale Voronoi tessellations. Based on this martensitic representative volume element, micromechanical simulations are performed by a crystal plasticity finite element model. For the constitutive model calibration, a new multi-objective calibration procedure incorporating a sensitivity analysis as well as an evolutionary algorithm is presented. The numerical results of different kinematic hardening models are compared to experimental data with respect to the appropriate modelling of the Bauschinger effect and the mean stress relaxation behavior at R = 0. It is concluded that the Ohno–Wang model is superior to the Armstrong Frederick and Chaboche kinematic hardening model at R = −1 as well as at R = 0.
1. Introduction
Martensitic high-strength steels are widely used as structural materials for highly loaded components in the automotive as well as in aerospace industry [1,2]. Among them, quenched and tempered SAE 4150 plays a pivotal role due to its excellent combination of strength and toughness [2]. Most of the breakdowns of these components are due to material fatigue representing the most dominant failure mechanism [3]. During service life, load spectra may exhibit varying load ratios whereby loading conditions unequal to R = −1 become important and influence fatigue life significantly as it is known from the Goodman relation [4].
Martensitic microstructures have been focused extensively in many experimental investigations [1,5,6,7]. There are two major martensitic morphologies in steels, known as lath and plate martensite. In low and medium carbon-alloyed steels such as the SAE 4150, lath martensite is formed during the diffussionless and shear transformation from austenite ( phase) to martensite ( phase) [2]. Lath martensite is characterized by its hierarchical morphology, comprising prior austenite grains (PAG), packets, blocks, and laths. An outstanding schematic representation of the morphological structure of martensite is given in Kitahara et al. [1]. Depending on the chemical composition, there can be formed up to 12 and 24 crystallographic variants from a single PAG with the Nishiyama–Wassermann (NW) and Kurdjumov–Sachs (KS) orientation relationship, respectively [1,5]. The PAGs are subdivided into several packets which contain parallel blocks with an identical habit plane. Blocks are collections of sub-blocks (groups of laths) which are separated by low angle misorientations [7]. The mechanical properties of the martensitic steels are significantly affected by the microstructural properties such as packet and block size [8,9]. Further strengthening mechanisms are high dislocation density and solid solution hardening by carbon [2].
Microstructure-sensitive approaches incorporating crystal plasticity constitutive models provide powerful techniques to investigate the cyclic deformation behavior of crystalline materials at the microscale. Within these frameworks, the investigated microstructure is modelled by a representative volume element (RVE) [10]. Numerous investigations on RVE modelling techniques have been made for non-hierarchical microstructures [11,12,13]. However, martensitic microstructures have been less-frequent subject of research. Studies about the modelling of martensitic RVEs as well as on appropriate multiscale tessellation techniques for martensitic microstructures have been performed, e.g., by Ghassemi-Armaki et al. [14], Altendorf et al. [15] and Sun et al. [16]. Sun et al. [16] proposed an RVE modelling approach for a hierarchical martensitic microstructure incorporating KS orientation relationship to perform investigations on the deformation behavior. In the present study, a comparable methodology as in Sun et al. [16] proposed is used to create the martensitic microstructures.
For realistic simulations of the cyclic material behavior, the use of appropriate constitutive models is also important in addition to adequate RVEs. Cyclic loading conditions including mean stresses require kinematic hardening (KH) models which are not only able to capture first order stress-strain hysteresis behavior but also higher order phenomena such as mean stress relaxation behavior [17]. It has been widely noted in literature for J plasticity that the Armstrong Frederick KH model failed to predict the mean stress evolution in cyclic loadings with non-zero mean stresses [18,19]. Hennessey et al. [17] reported for Al 7075-T6 a dramatically over prediction of the mean stress relaxation behavior also on crystal level in crystal plasticity simulations. Investigations on a polycrystalline IN718 superalloy by Cruzado et al. [20] show a good agreement between experimental and simulated mean stress relaxation behavior by using an Ohno–Wang KH model. Sweeney et al. [21] used a Chaboche KH model for micromechanical fatigue simulations with mean stresses of a L605 CoCr alloy and achieved also good agreements with experimental fatigue results. The Chaboche and Ohno–Wang models show the potential to capture complex evolutions of mean stress relaxation. However, these KH models result in an increased calibration effort. Trial and error approaches to determine the numerous constitutive parameters are not very efficient and time consuming [22]. To overcome this problem, genetic algorithms have been widely used to calibrate complex constitutive models [22,23,24]. Within the scope of this study, the applicability of these approaches to the martensitic steel SAE 4150 is also investigated.
Future sustainable resource-saving component developments require accurate lifetime prediction models incorporating the formation and early growth of small fatigue cracks. Micromechanical multiscale models are particularly suitable for these purposes. This is, because the fatigue crack initiation time is strongly linked to local stress and strain states as well as to the underlying microstructures in critical stressed regions [25]. Since fatigue properties are also strongly dependent on the cyclic deformation behavior, the primary objective of this study is the micromechanical modelling of the cyclic deformation behavior of the SAE 4150. A martensitic microstructure model, a comparison of different KH models capturing the cyclic stress-strain behavior for a wide range of applied strain amplitudes and strain ratios, and a multi-objective calibration procedure are presented in this study and validated by experiments.
This paper is structured as follows: first, in Section 2 the martensitic high-strength steel SAE 4150 is characterized with respect to microstructural properties as well as to the experimental cyclic stress-strain behavior. Next, the RVE multiscale modelling technique, the constitutive models and an appropriate multi-objective calibration procedure are described within Section 3. Results of the comparison between the Armstrong Frederick, Chaboche, and Ohno–Wang KH models are presented and discussed in Section 4. Finally, the main conclusions as well as the capabilities and limitations of the models are summarized in Section 5.
2. Material and Experiments
This section focuses on the experimentally determined properties of the quenched and tempered martensitic high-strength steel SAE 4150 (50CrMo4) with respect to microstructural properties and cyclic stress-strain behavior. The steel exhibits a hardness of 39 HRC and its chemical composition was determined by spark emission spectroscopy analysis. Table 1 shows the mean values of the corresponding alloying elements.

Table 1.
Chemical composition of the SAE 4150 in wt.%.
2.1. Microstructure Characterization
Scanning electron microscopy (SEM, Zeiss Merlin) observations including electron backscatter diffraction (EBSD) analyses were performed to characterize the microstructure with respect to grain morphology and crystallographic orientations. Therefore, multiple mechanically as well as electrically polished specimen were analyzed in the SEM and areas of approximately 100 × 100 µm were scanned with a constant sampling step size of 0.1 µm to capture the microstructural variety in detail.
The EBSD image quality (IQ) map as well as the corresponding EBSD orientation maps in inverse pole figure (IPF) color coding are shown in Figure 1a,b, respectively. Figure 1a reveals that the martensitic microstructure consists of multiple almost parallel crystallographic blocks forming morphological packets. According to the stereographic triangle in Figure 1b, the colors of the IPF correspond to the crystallographic directions normal to the investigated plane. The color coding of the EBSD map (Figure 1b) clearly reveals the characteristic morphology and the crystallographic properties of the lath martensite, in detail.

Figure 1.
Experimental analysis of the SAE 4150 microstructure: (a) EBSD image quality map (b) EBSD map in inverse pole figure color code.
The transformation from austenite into martensite can be described by the four possible major orientation relationships (OR): Bain [26], Kurdjumov–Sachs (KS) [27], Greninger-Troiano (GT) [28] and Nishiyama–Wassermann (NW) [29,30]. However, only the KS OR and the NW OR are focused on in the present study, since the Bain OR is rarely observed and the GT OR is in the middle of KS and NW OR [7,31]. The orientation relationships of KS and NW are listed in Table 2.

Table 2.
Kurdjumov–Sachs and Nishiyama–Wassermann orientation relationships for the transformation from a parent austenite grain into the corresponding martensitic variants [1,6,31].
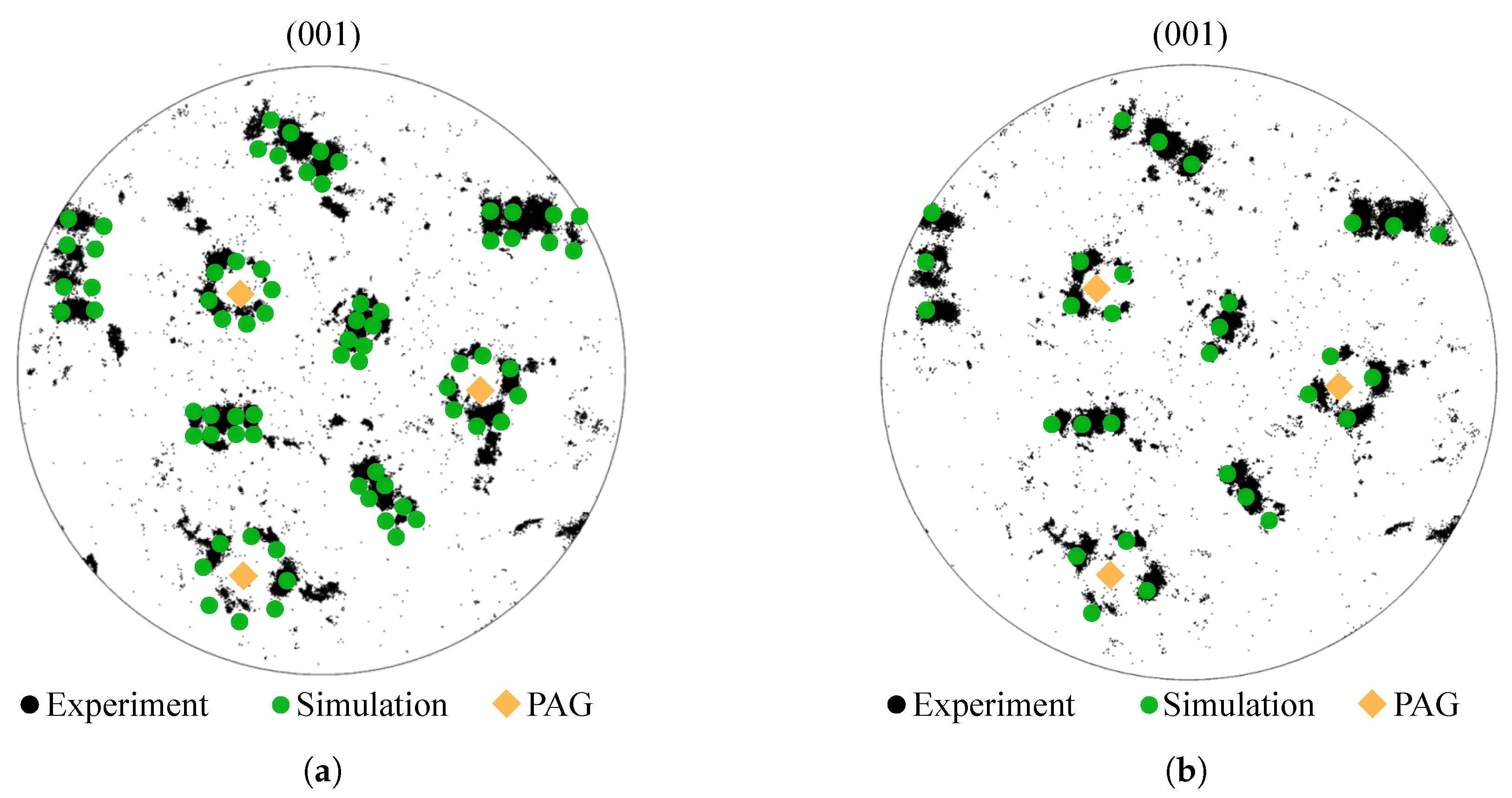
To identify the OR for the investigated lath martensite, (001) pole figures of experimental EBSD data are compared to calculated KS and NW data, Figure 2. The calculations of the KS and NW variants were performed by MTEX (version 5.1.1) [32] in MATLAB R2016b. The PAGs and the corresponding orientations are calculated from EBSD data by ARPGE (version 1.6) [33]. Experimental orientations are plotted by black dots representing the martensitic variants of the single PAG outlined in Figure 1b. Calculated martensitic variants based on the KS OR and NW OR are plotted by green dots in Figure 2a,b, respectively. The initial orientations of the PAG are highlighted in orange.
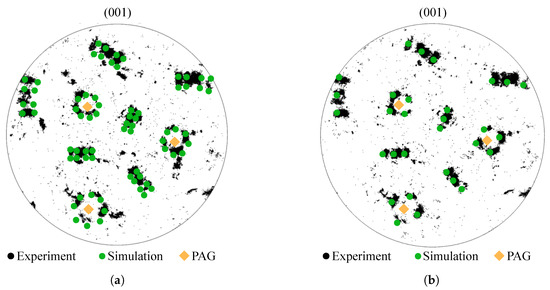
Figure 2.
(001) pole figures of experimental martensitic orientations within a single prior austenite grain, corresponding simulated martensitic orientations and the underlying prior austenite grain orientation: (a) with simulated Kurdjumov–Sachs OR (b) with simulated Nishiyama–Wassermann OR.
The qualitative comparison of Figure 2a,b indicates that the simulated NW OR shows a better agreement to the experimental orientations than the KS OR. Based on this qualitative result, the NW OR is used in this study.
2.2. Mechanical Cyclic Properties
From a macroscopic point of view, the cyclic deformation behavior of SAE 4150 plays a pivotal role regarding fatigue prediction and the calibration of the micromechanical model. The macroscopic deformation behavior in the low cycle fatigue (LCF)—regime is controlled by the collective elastic-plastic behavior of all grains. An assumption of the crystal plasticity fatigue modelling approach is that for macroscopic elastic loadings, the local hardening of individual critically oriented grains behaves in a similar manner as for a collective macroscopic elasto-plastic deformation in the LCF-regime [22,34]. By the adaptation of a crystal plasticity parameter set to stress-strain hystereses from LCF tests, whereby the grains collectively behave elasto-plastic, information of local hardening is gained which can be used for example in high cycle fatigue (HCF) simulations. Therefore, strain-controlled LCF experiments of the SAE 4150 were performed at room temperature to provide an experimental database for calibration and verification of the crystal plasticity model.
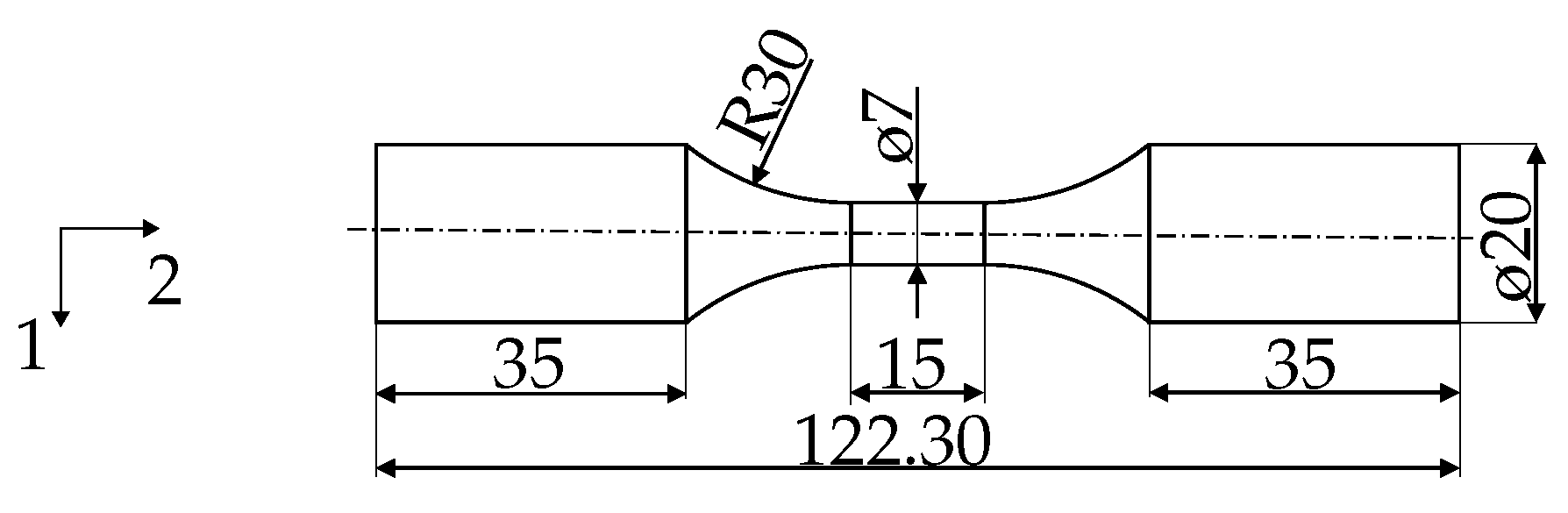
LCF tests were performed on a universal servo hydraulic test frame from MTS, according to the standards from ASTM E606 [35]. An extensometer from Sandner was mounted in the central zone of the unnotched fatigue specimen to precisely measure the axial displacements in the gauge section. Figure 3 shows the geometry and dimensions of the unnotched fatigue specimen. The tests were carried out for two different total strain ratios, R = −1 and R = 0. Multiple fully reversed tests were performed from 0.25% to 0.90%, whereby denotes the total strain amplitude. Four different total strain amplitudes ranging from 0.25% to 0.50% were investigated in the LCF tests at R = 0. A triangular waveform with a constant strain rate of 0.02 1/s was applied until fracture, with at least one specimen per strain amplitude.
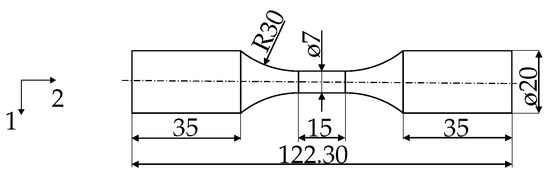
Figure 3.
Geometry and dimensions (in mm) of the unnotched low cycle fatigue test specimens.
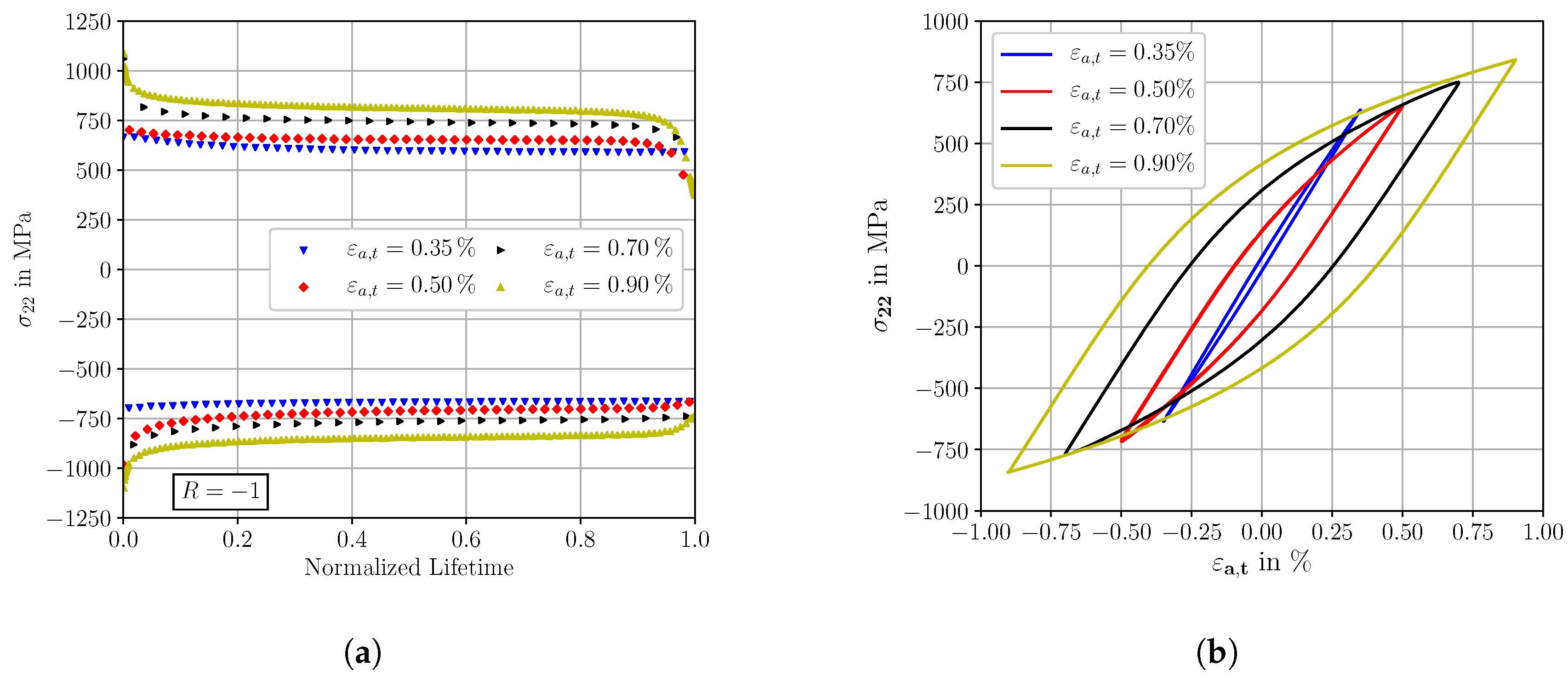
Figure 4a shows the evolution of the maximum and minimum stresses in loading direction vs. the normalized lifetime for the LCF tests at R = −1 with constant total strain amplitudes. Thereby, the characteristic behavior of heat-treated high-strength steels exhibiting an initial cyclic strain softening within the first number of cycles and a subsequent lifetime dominating part of cyclic stable conditions becomes visible [4,36]. The proportion of lifetime between the cyclic strain softening and the cyclic stable conditions is small and can, therefore, be neglected in the present study. According to Christ [36], the cyclic stable material conditions being represented by almost horizontal maximum and minimum stress curves in Figure 4a represent the dominating part of the material lifetime and the basis for fatigue calculations. The stabilized stress-strain hysteresis loops (at normalized lifetime = 0.5) of the different LCF experiments at R = −1 are shown in Figure 4b.
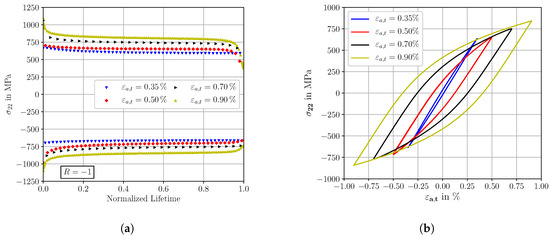
Figure 4.
Experimental low cycle fatigue test results: (a) Evolution of maximum and minimum stresses versus normalized lifetime at R = −1 for different strain amplitudes and (b) cyclic stress-strain behavior at R = −1, in cyclic stable material conditions (normalized lifetime = 0.5).
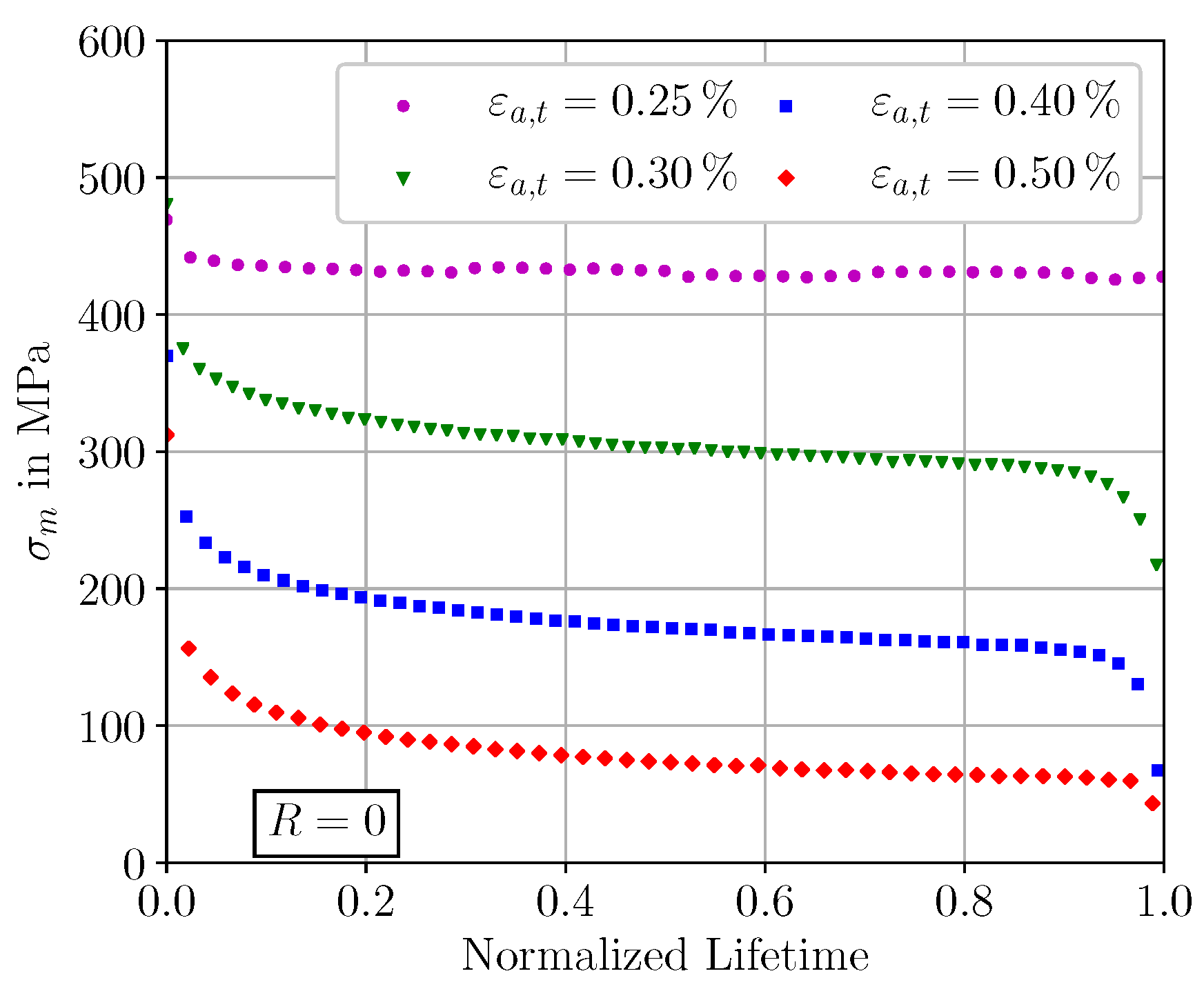
The different mean stress relaxation behavior for varying total strain amplitudes at R = 0 are shown in Figure 5. The results indicate that the rate of mean stress relaxation increases with the increase of total strain amplitude. This can be justified by the fact that the plastic strain amplitude represents a driving force for mean stress relaxation [37]. The mean stress relaxation behavior of the investigated SAE 4150 is comparable to other martensitic steels as reported by Wehner and Fatemi [38], Wu et al. [39] and Koh and Stephens [40].

Figure 5.
Experimental mean stress evolutions of SAE 4150 during cycling at different constant total strain amplitudes at R = 0.
3. Modelling Methodology and Constitutive Calibration Strategy
A micromechanical finite element model is developed for the experimentally investigated martensitic steel SAE 4150. Section 3.1 presents the generation and meshing approach for a three-dimensional lath martensitic RVE. To describe the plasticity behavior of lath martensitic microstructures at the crystal scale, an appropriate constitutive model with three different KH models is introduced in Section 3.2. Finally, a multi-objective parametrization procedure for the different constitutive models based on experimental LCF data is proposed in Section 3.3.
3.1. Generation of Representative Volume Elements
A Voronoi tessellation methodology is used to generate three-dimensional martensitic RVEs based on experimental SAE 4150 crystallographic characteristics. An idealized visualization of a multiscale martensitic microstructure is given in Kitahara et al. [1]. Thereby, the PAG represents the largest feature in the hierarchical three-scale microstructure. Each PAG can be subdivided into multiple packets and each packet is parallel to one of the four possible habit planes [6]. The individual packets are a collection of blocks with the same habit plane {111} [1,5,6,7].
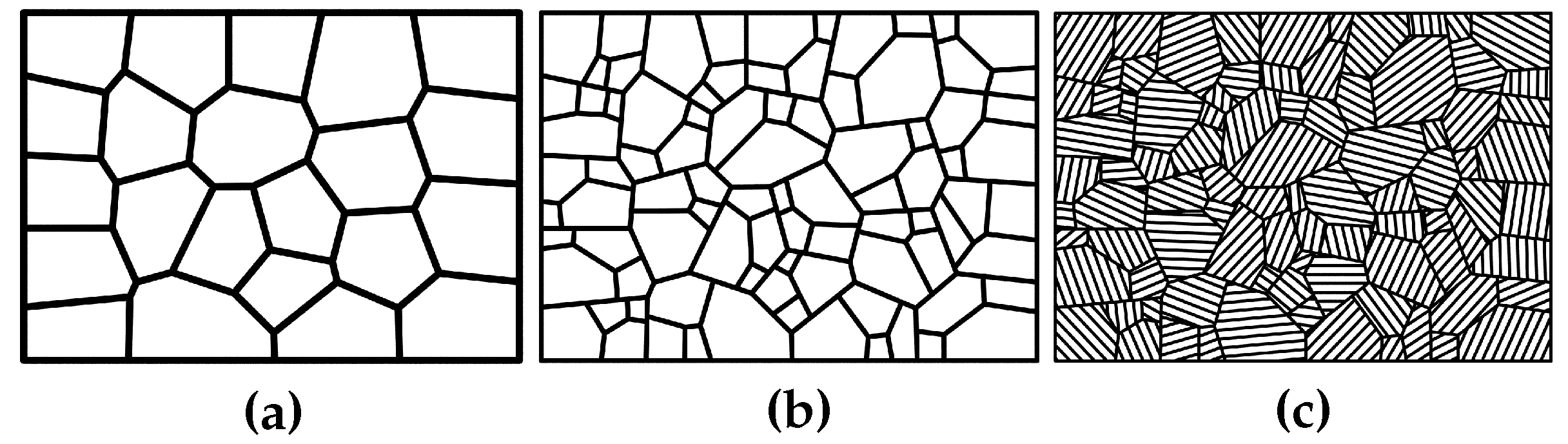
The multiscale Voronoi tessellations are performed by the C++ software library voro++ (version 0.4.6) [41] embedded in a python framework (version 2.7). The three-dimensional hierarchical martensitic grain structure is generated according to the following procedure which is shown schematically in a two-dimensional way in Figure 6. (i) First, the three-dimensional domain of the RVE is partitioned into multiple convex polygons representing the PAG structure. Thereby, the number of PAGs can be specified. Random crystallographic orientations in the form of Euler angles (in Bunge notation [42]) are assigned to the individual PAGs. (ii) In the second tessellation level, the individual PAGs are further divided into a predefined number of packets by the Voronoi tessellation. One of the four possible {111} habit planes is randomly assigned to each packet. (iii) Finally, block structures with a predefined width are generated within each packet parallel to the corresponding {111} habit plane. Using the NW OR, one of the three possible crystallographic variants is assigned to each block [7]. In reality, individual blocks are clusters of a variety of sub-blocks and laths. According to Morito et al. [7], misorientations between adjacent sub-blocks are typically . Thus, a further subdivision of the individual blocks into different martensitic laths was omitted and blocks are assumed as homogeneous entity. Thereby, martensitic blocks represent the smallest feature in the hierarchical three-scale microstructure, in the present study.
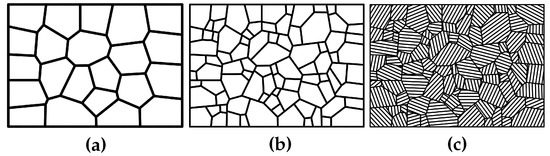
Figure 6.
Two-dimensional schematic procedure of the hierarchical modelling approach for lath martensitic microstructures of low carbon-alloyed steels. (a) Generation of prior austenite grains. (b) Partition of each prior austenite grain into packets. (c) Generation of blocks parallel to the corresponding habit plane within individual packets.
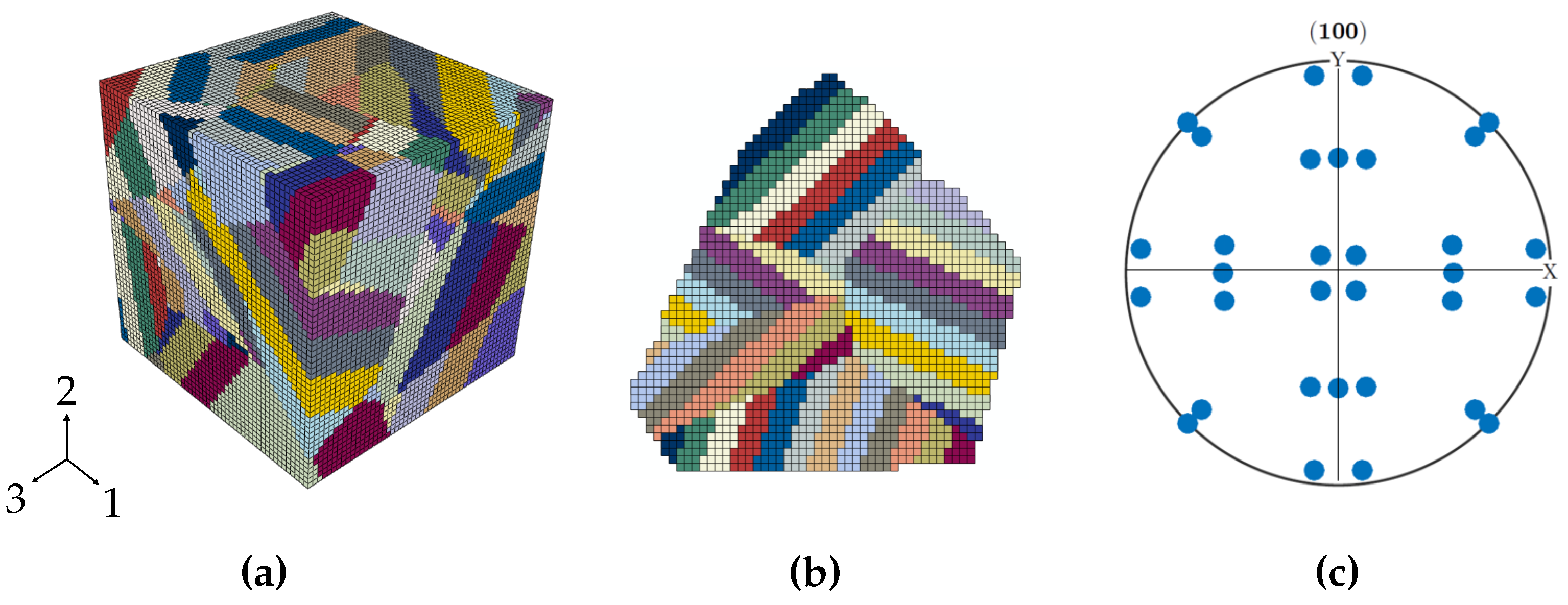
After the multiscale Voronoi tessellations, the information about the martensitic microstructure must be defined and incorporated into ABAQUS. This task is performed by a mesh generator written in python. The mesh generator initially creates a cubic regular mesh of 8-node linear brick elements (C3D8) and assigns the corresponding material property to each element according to its spatial position. Furthermore, periodic boundary conditions are applied on opposite faces of the RVE, in analogy to Smith’s [43] procedure. The loading direction of the RVE is represented by direction 2. Figure 7a shows a voxelated microstructure with 125,000 elements () mapping the martensitic microstructure and morphology in detail.
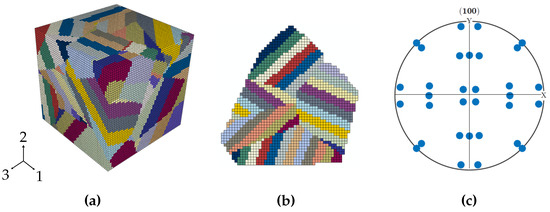
Figure 7.
Three-dimensional synthetic martensitic microstructure: (a) Representative volume element with 125,000 elements (b) two-dimensional representation of a transformed PAG with an initial orientation of (001)[100] (c) (100) pole figure of Figure 7b.
The correct implementation of the NW OR in the microstructure model is verified by the comparison between the (100) pole figure (Figure 7c) of a synthetically generated martensitic microstructure based on a PAG with an initial orientation of (001)[100] (Figure 7b) and the corresponding (100) reference pole figure which is shown in Kitahara et al. [6].
3.2. Constitutive Framework
To model the cyclic behavior of the considered martensitic high-strength steel SAE 4150, a crystal plasticity model which was introduced by Boeff et al. [13] is used and extended. In Section 3.2.1 the standard constitutive model on the crystal level is presented. The different phenomenological hardening evolution laws are given in Section 3.2.2.
3.2.1. Crystal Plasticity Model
A phenomenological local crystal plasticity model is used to determine the elastic and plastic cyclic response of the martensitic crystals, respectively. It is worth noting that the local crystal plasticity model is length scale independent [44]. Thereby, the model is not able to capture grain size effects such as the Hall-Petch effect [45,46].
The local crystal plasticity model is implemented in a finite strain framework and based on the multiplicative decomposition of the deformation gradient into elastic and plastic components,
In the intermediate (relaxed) configuration, it is assumed that plastic deformation occurs solely due to dislocation slip [47] on the 12 possible {110}<111> slip systems for BCC. Thereby, the plastic velocity gradient is determined by the superposition of crystallographic slips on the different slip systems via
where and represent the unit vectors in slip direction and normal to the slip plane in intermediate configuration equivalent to those from the reference configuration, respectively. By using the definition of the Green-Lagrange strain tensor, an elastic finite strain measure can be derived,
The second Piola-Kirchhoff stress representing the work conjugate stress measure is defined by
where represents the fourth-order elasticity tensor of the single crystal. The second Piola-Kirchhoff stress in the intermediate configuration can be used to approximate the resolved shear stress on each glide system,
since the elastic stretch is small for most metallic materials, according to Meissonnier et al. [48].
The magnitude of the shear rate on each glide system is related to the resolved shear stress via a phenomenological elasto-viscoplastic constitutive model. The original model was developed by Rice and Hutchinson [47,49,50] for monotonic loading.
The modification for cyclic loading was done by Cailletaud [51]:
where represents a reference shear rate, and are the individual resolved back stress and the critical resolved shear stress of each glide system . The elasto-viscoplastic formulation represents a power-law approach which is characterized by the inverse strain rate sensitivity exponent m.
3.2.2. Phenomenological Hardening Models
To capture isotropic as well as KH on crystal scale, different phenomenological hardening evolution laws are used. The isotropic hardening is considered by increasing the critical resolved shear stress on each slip system. The influence of any slip system on the fixed slip system with respect to isotropic hardening behavior is given by,
where represents the hardening matrix for interactions among slip systems [44]:
In this formulation, , a and represent the hardening parameter, hardening exponent, and the saturated shear stress, respectively.
KH and the resulting phenomenon called Bauschinger effect are captured by different non-linear KH models. From a micromechanical point of view, backstresses on slip systems result from dislocation slip irreversibility. A widely used evolution law for the backstress in phenomenological local crystal plasticity is the Armstrong Frederick (AF) [52] model representing an extension of the linear KH model proposed by Prager [53]. For the evolution of KH, the AF model assumes strain hardening and dynamic recovery, whereby the coefficients A and B represent the direct hardening and the dynamic recovery modulus, respectively [19]. From a mathematical point of view, the model is an ordinary first order differential equation with a recall term being called dynamic recovery:
A decomposed non-linear KH rule in J plasticity was proposed by Chaboche et al. [54]. Applied to micromechanical modelling, the model can be formulated by:
The proposed KH rule is a superposition of AF formulations. According to Chaboche [55], the superposition of the several hardening rules improves the transition between the elastic regime and the onset of plasticity. Initially, Chaboche [54] proposed to use three decomposed hardening rules with to improve the macroscopic simulation of cyclic stress-strain hysteresis and ratcheting behavior [18]. Therefore, in the present study, three decomposed hardening rules () are used.
An extension of the Chaboche KH model is the Ohno–Wang [19] KH model. The model formulation which was originally proposed for J plasticity can be written on the crystal level as [17,20]
The Ohno–Wang non-linear KH model is based on a strain hardening term minus a modified dynamic recovery term for an improved description of ratchetting and mean stress relaxation behavior. In Equation (11), the exponent M controls the non-linear character of the dynamic recovery term. The dynamic recovery term becomes active when the backstress reaches the saturation level A/B. In principle, several non-linear KH evolution laws of the Ohno–Wang model can also be superposed, as for example at the Chaboche model [17,19]. In this study, one non-linear KH evolution law of the Ohno–Wang model is used.
The presented crystal plasticity model is implemented as a user defined material (UMAT) subroutine in ABAQUS 2016.
3.3. Parametrization of the Crystal Plasticity Model
Systematically calibrated constitutive model parameters based on experimental input data are crucial for the prediction of fatigue crack initiation life. The calibration procedure exhibits a non-trivial effort due to the complexity of the mesoscale constitutive model, the numbers of KH coefficients and individual difficult accessible material parameters [22,24]. In the present case, few constitutive model parameters are taken from literature and others are calibrated to experimental LCF data by a multi-objective optimization procedure. In a first step, a numerically efficient RVE for the effective cyclic properties is generated to ensure an efficient optimization procedure. The multi-objective calibration strategy is then presented in detail.
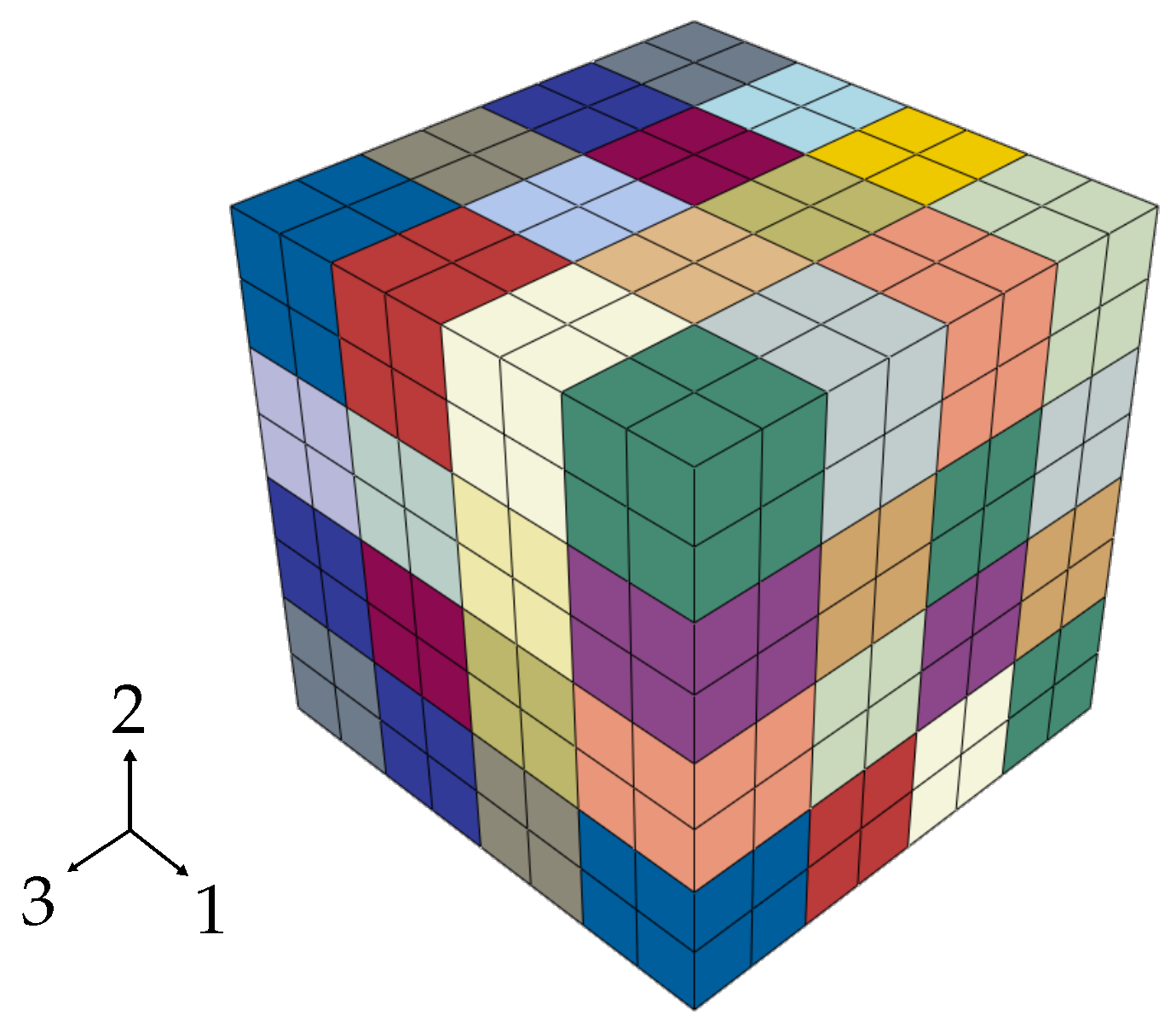
Based on the approach from Herrera-Solaz et al. [22,56], different representations of the microstructure were used to investigate the effective macroscopic cyclic properties with respect to accuracy and numerical efficiency. Therefore, two different RVE variants have been used to solely simulate the cyclic stress-strain hysteresis which will be used in the subsequent calibration procedure. The first variant V1 represents the RVE which contains a fully martensitic microstructure with the NW OR and 125,000 C3D8 elements, depicted in Figure 7a. The second variant V2, shown in Figure 8, denotes a simplified RVE with only 64 equiaxed grains and 512 C3D8 elements. It should be noted that fatigue crack initiation simulations cannot be carried out with the second reduced RVE realization because microstructural information is neglected; however, for the calibration process, the simplified microstructure is sufficiently accurate.
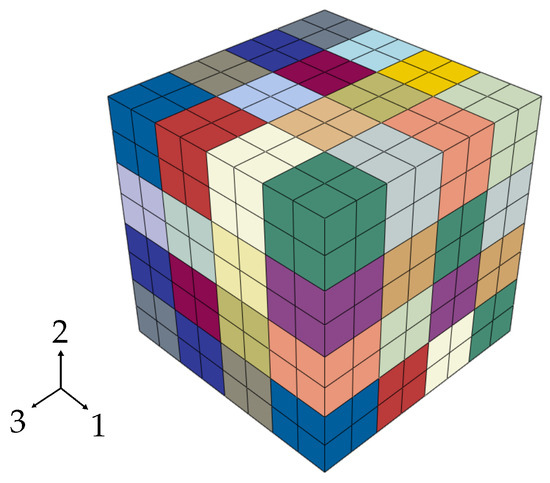
Figure 8.
RVE variant V2 with 512 elements for the simulation of effective cyclic properties.
According to Seguardo and Llorca [57], representations of RVEs with only one element per grain tend to be too stiff, due to the over constrained deformations within the individual grains. To overcome this problem, eight elements per grain have been used in variant V2 to represent single grains. A martensitic microstructure which includes multiple PAGs does not show any texture and exhibits isotropic material behavior, from a macroscopic point of view. This hypothesis can be confirmed by the three different pole figures, shown in Figure 9, which have been derived from the EBSD data of Figure 1b. Therefore, random orientations have been assigned to the individual grains by which the isotropy of the material can be taken into account.

Figure 9.
(100), (110) and (111) pole figures of the EBSD data from Figure 1b.
Strain-controlled micromechanical simulations of the effective cyclic properties indicate a small dependency between the discretization of the microstructure and the effective cyclic properties. In the present study, the maximum deviation in peak stress between the variants V1 and V2 is less than 1.0% for total strain ranges [0,1.0%]. Based on this observation, variant V2 with 512 C3D8 elements, random orientations and periodic boundary conditions on the RVE cell faces represents a good compromise between numerical efficiency and macroscopic accuracy for the simulation of effective cyclic properties which will be used in the numerical extensive multi-objective optimization procedure. However, for the final comparison of the different KH models and the evaluation of local microstructural quantities as well as for future fatigue simulations, the variant V1 with the fully martensitic microstructure will be used.
Calibration Strategy
The multi-objective calibration procedure is used to determine the constitutive model parameter sets for different KH models: AF, Chaboche (CH) and Ohno–Wang (OW). The cyclic stable experimental stress-strain hysteresis, with total strain amplitudes of , and , presented in Section 2 serve as reference for the calibration. The model parameters can be classified into four categories:
- a set of elastic constants of the crystal
- a set related to the flow rule
- a set related to the isotropic hardening
- a set related to the KH
The elastic stiffness tensor remains constant for the three different KH models. Elastic constants from an HSLA-50 steel provided by Xie et al. [24] were adopted. The values which are listed in Table 3 show a good agreement to experimental stress-strain curves within the elastic regime. The reference shear rate is set equal to 0.001 1/s for all models [13,17]. Due to the low macroscopic strain rate sensitivity of the considered SAE 4150 [58], the strain rate sensitivity exponent m is set equal to m = 100 to avoid any strain rate hardening [34]. It is worth noting that high strain rate sensitivity exponents make numerical convergence more difficult [17,34].

Table 3.
Elastic constants of the stiffness tensor , provided by Xie et al. [24].
According to Figure 4, the material of interest shows cyclic stable material behavior. Therefore, isotropic hardening is not considered in the present study. To do so, the set of parameters for isotropic hardening are set to zero.
The remaining constitutive parameters to be calibrated, such as the critical resolved shear stress and the KH parameters of the AF, CH, and OW KH model are strongly related to the stress-strain hysteresis loops. As a consequence of this, the calibration procedure implies the solution of multiple least-square minimization problems between the experimental and simulated stress-strain hysteresis loops, respectively. The three different models are fitted to the same fully reversed experimental stress-strain hysteresis loops determined for R = −1. The fitness function of the optimization problem for each hysteresis loop is defined as:
where represents the number of data points of each hysteresis, and the stresses measured in the LCF experiments and calculated in the micromechanical simulation, respectively.
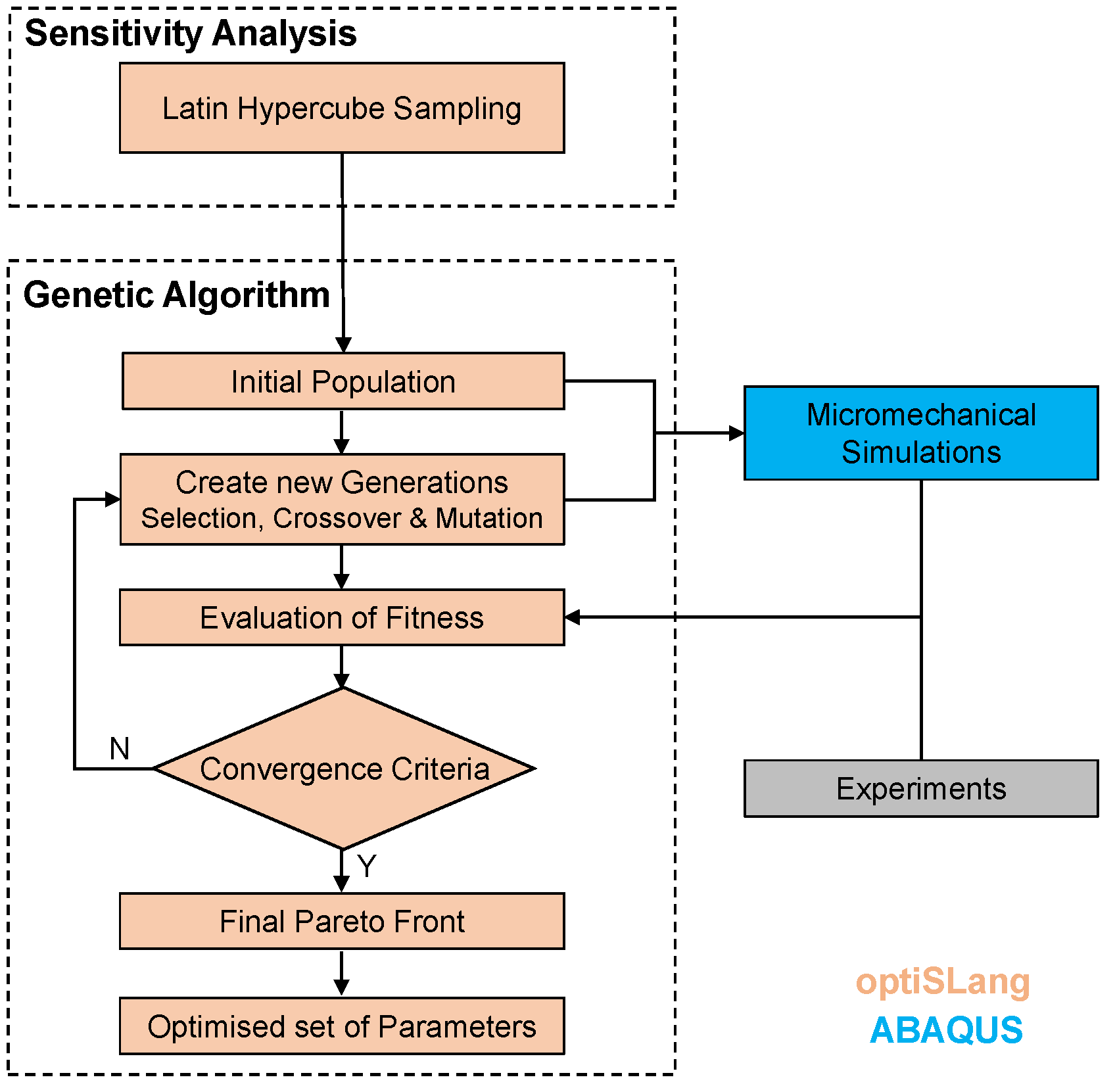
To treat the multi-objective optimization problem of each KH model adequately, a combined sensitivity analysis with an evolutionary algorithm (EA) is applied using OptiSlang [59] commercial software together with ABAQUS. Furthermore, the Pareto dominance criterion is applied due to the ability of the simultaneous consideration of multiple objectives [60]. Thereby, Pareto optimal crystal plasticity parameter sets are obtained which capture the cyclic stress-strain response for a wide range of applied strain amplitudes. Figure 10 shows the flow chart of the applied calibration procedure.
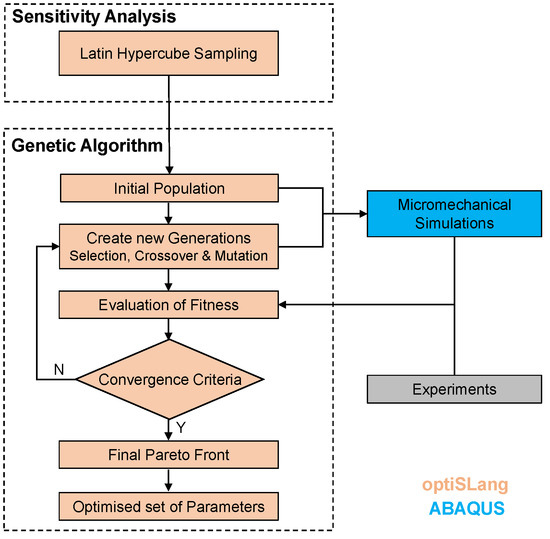
Figure 10.
Flow chart of the calibration procedure for the crystal plasticity parameters using a genetic algorithm.
The workflow starts with a stochastic-based sensitivity analysis to identify unimportant input parameters and for the verification of the fitness function and possible conflicts [59]. Thereby, a Latin hypercube (LHS) sampling technique is used. The main advantages of the LHS are the complete exploration of the input parameter space as well as the prevention of undesired correlations between the input parameters [61]. Multiple crystal plasticity simulations are performed for the constitutive model parameter sets defined by the LHS algorithm, within the sensitivity analysis. Therefore, at the end of the sensitivity analysis, multiple parameter sets can be compared in terms of fitness. The most suited parameter sets are then transferred to the multi-objective EA as an initial population. Instead of using a random initial population, the transfer of best designs out of the sensitivity analysis may significantly improve the efficiency of the multi-objective optimization [59].
For solving the multi-objective optimization problem, an EA which is based on the Strength Pareto Evolutionary Algorithm 2 [62] was used. The major benefit of this heuristic approach is the parallel search for a set of Pareto optimal solutions [59,60,63]. In the present study, the solutions have been selected in a way that the errors are equivalent for all three objectives.
4. Results and Discussion
The micromechanical model described in the previous section is used to model the cyclic effective properties of SAE 4150. First, the calibrated sets of crystal plasticity parameters for R = −1 are presented for the three KH models. Next, a prediction of the stress-strain hysteresis and the mean stress relaxation behavior for R = 0 is made and compared to the experimental data. Finally, these results are compared and discussed.
4.1. Calibration of the Constitutive Models
The KH model dependent Pareto optimal sets of the crystal plasticity parameters obtained by the multi-objective calibration procedure are shown in Table 4. Within the multi-objective calibration procedure, the numerical efficient RVE of Figure 8 was used for the numerous micromechanical simulations. Three experimental LCF stress-strain hysteresis at = 0.35%, = 0.60% and = 0.90%, have been required for the calibration of the KH constitutive models at R = −1.

Table 4.
Optimized parameter sets for different kinematic hardening models for quenched and tempered SAE4150 with 39 HRC.
4.2. Cyclic Deformation Behavior at R = −1—KH Model Comparison
The effective cyclic properties of the KH models are compared with the experimental stabilized stress-strain hysteresis at R = −1 within this section. Computational homogenization of the martensitic RVE of Figure 7a provides the effective cyclic properties from the numerical results. Figure 11 shows the comparison of the experimental stress-strain hystereses and the corresponding strain-controlled numerical results which were simulated with the parameter sets of Table 4 and the martensitic RVE of Figure 7a.
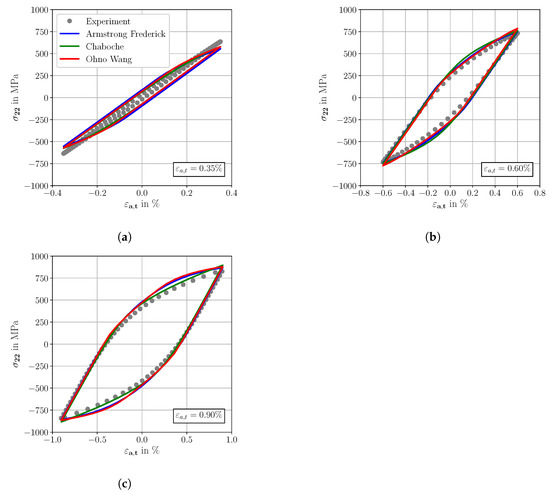
Figure 11.
Experimental and simulated stress-strain hysteresis loops of SAE 4150 at cyclic stable material conditions, for three different total strain amplitudes, (a) = 0.35%, (b) = 0.60% and (c) = 0.90%.
Based on the qualitative comparison of the cyclic stress-strain hysteresis in Figure 11, the AF, CH and OW models show in general a good agreement to the experimental results for R = −1. However, at the lowest strain amplitude = 0.35% all models predict slightly too high plastic strain ranges. There are only small differences between the different models for = 0.35% and = 0.60%. However, at = 0.90% the CH model shows a better agreement to experimental data than the AF and OW KH model.
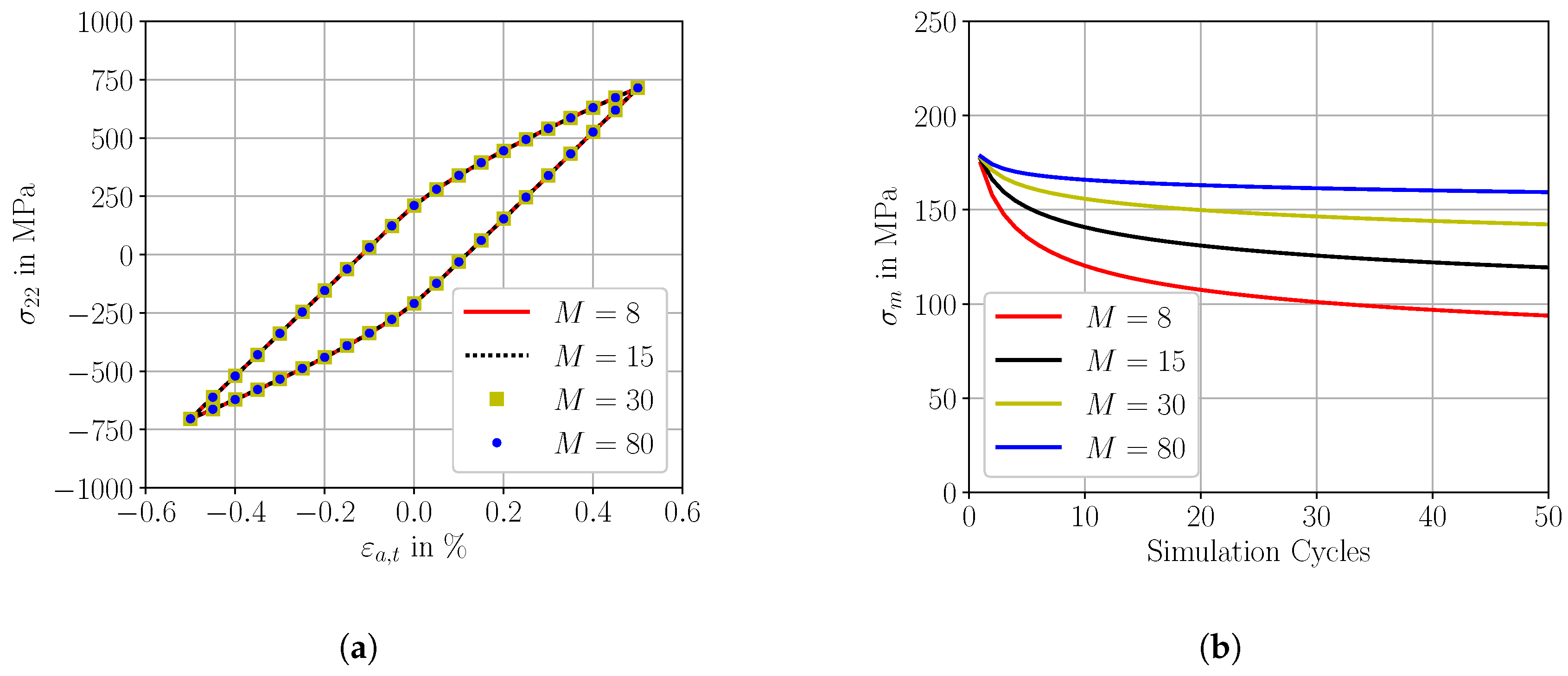
To quantify the influence of the exponent M of the OW model (defined in Equation (11)) on the effective cyclic properties at R = −1, multiple simulations at different total strain amplitudes were performed with varying exponents M in the range of M∈ [0;80]. For these micromechanical simulations, the martensitic RVE of Figure 7a was used. Figure 12a shows in a representative way the influence of the varying exponents M on the stress-strain hysteresis with a total strain amplitude of = 0.50%. These results reveal that the influence of the exponent M on the cyclic effective properties at zero mean stress is negligible. This observation agrees well with the results from Hennessey et al. [17]. However, the exponent M of the OW model significantly affects the mean stress relaxation rate. Figure 12b shows the mean stress relaxation behavior of a total strain amplitude of = 0.50% at R = 0 for 50 computational cycles depending on varying exponents M, whereby the simulations were based on the martensitic RVE of Figure 7a. This model feature enables the accurate modelling of the mean stress relaxation behavior by a specific selection of the exponent M.
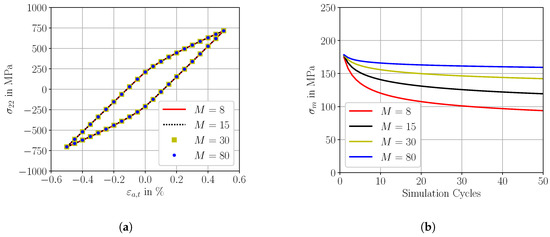
Figure 12.
Influence of the exponent M of the Ohno–Wang model, (a) on the effective cyclic properties at zero mean stress; (b) on the mean stress relaxation behavior at = 0.50% at R = 0.
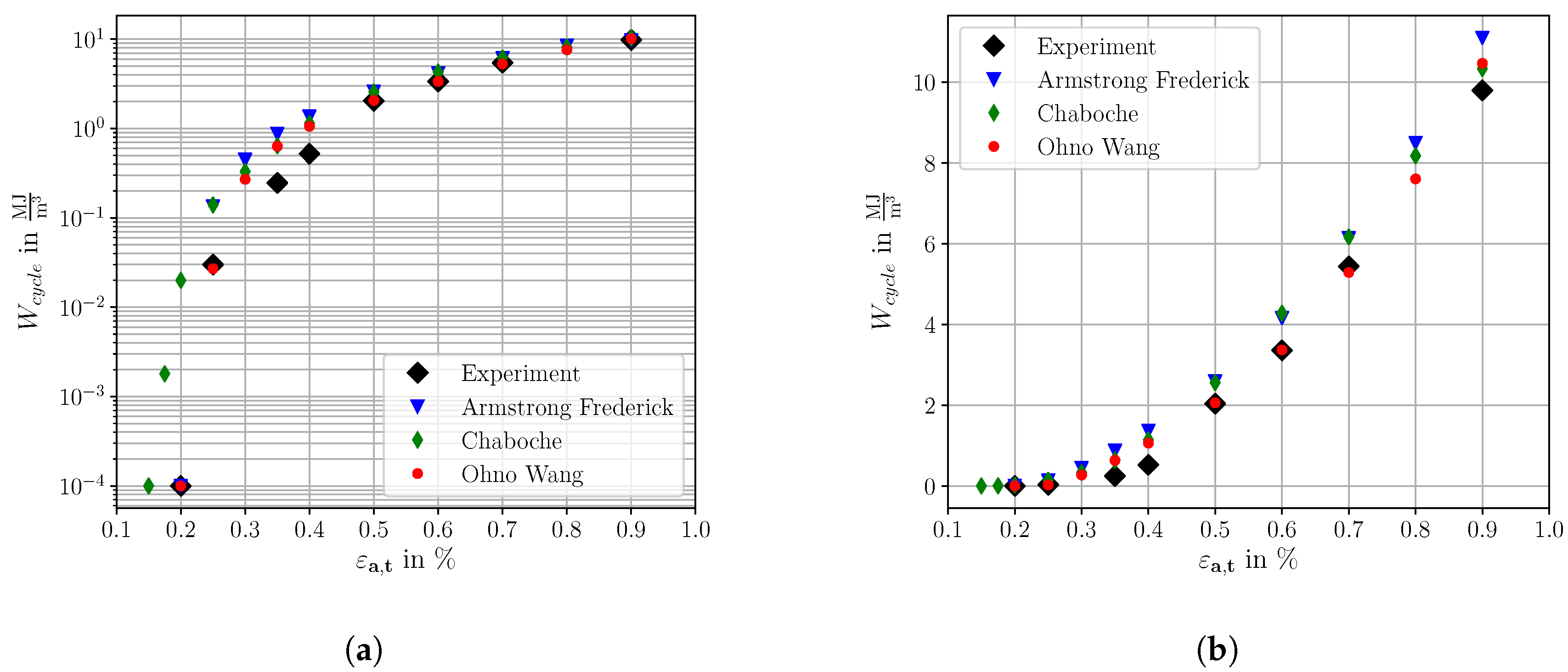
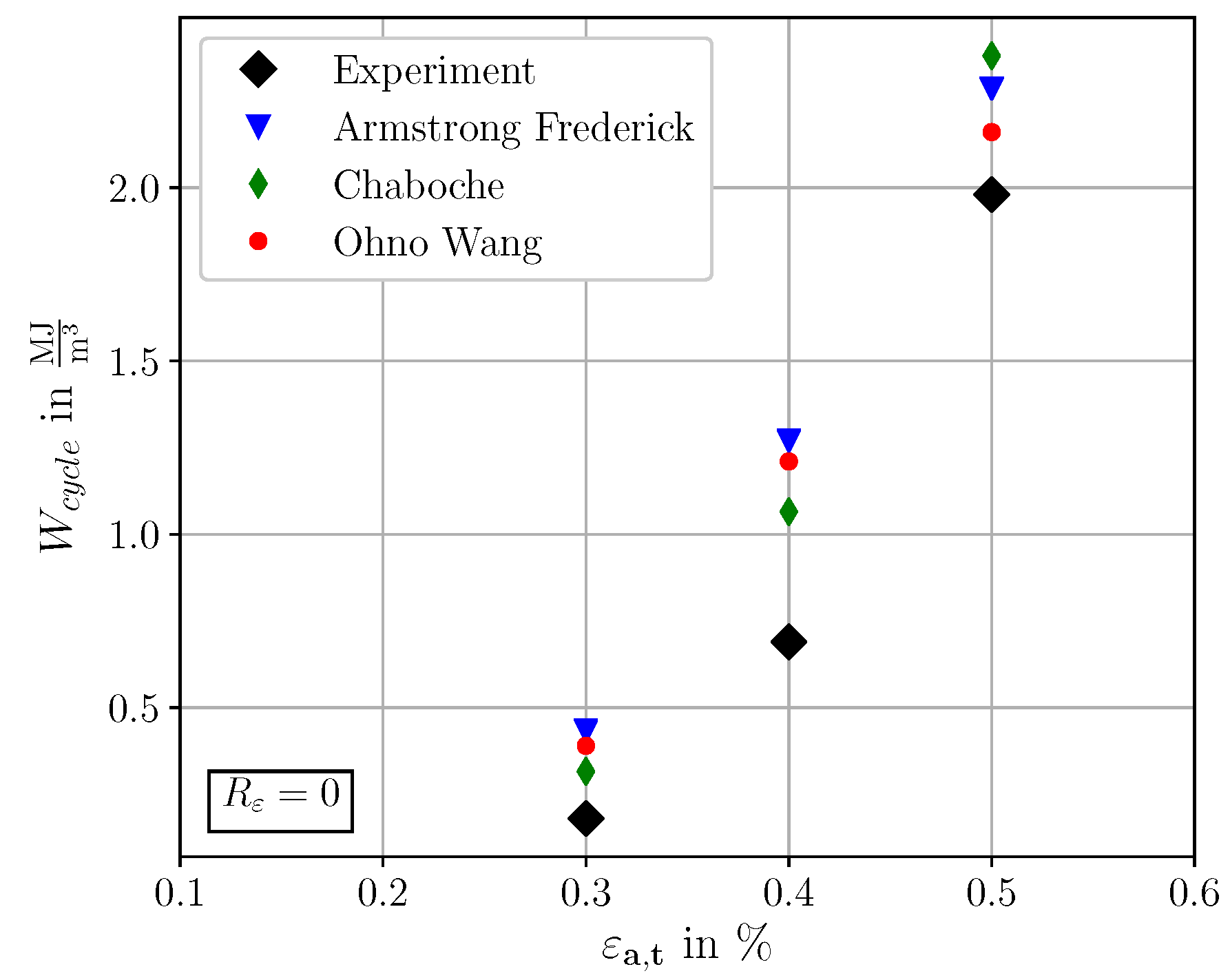
The qualitative comparison of the cyclic stress-stain curves indicates a good agreement between the three different KH models and the experimental data. However, to make a quantitative statement regarding the agreement of simulation and experiment, the plastic strain energy density is used in the following as an evaluation basis. The plastic strain energy density , defined in Equation (13), represents a fundamental quantity characterizing the level of fatigue loading. Plastic deformations result either in heat dissipation or in raising internal energy of the material. The increase of internal energy can be linked e.g., to formation of cracks, rearrangement of dislocations and formation of point defects [64]. Therefore, it is of particular importance to predict accurately the material specific characteristic in fatigue crack initiation simulations [65]. The characteristics depending on the three KH models were simulated with the martensitic RVE of Figure 7a. The applied strain rate for the cyclic simulations was set to 0.009 1/s. Due to the low applied strain rate, the rise of internal energy and temperature is assumed to be minimal since the dissipated plastic energy will be transported away by heat conduction. Figure 13a,b compare the simulated characteristics to experimental data of the SAE 4150 in a semi-log and linear representation, respectively.
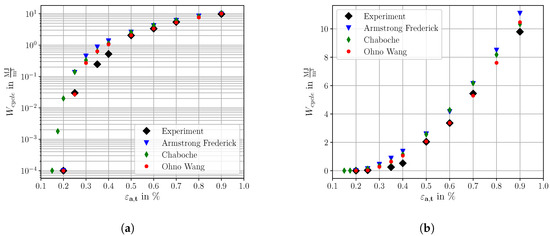
Figure 13.
Plastic strain energy density characteristics for three different kinematic hardening models and experimental data of SAE 4150 at R = −1; (a) with logarithmic y-axis (b) with linear y-axis.
The characteristics of the three KH models in Figure 13a reveal distinct differences for small applied total strain amplitudes. A good agreement with the experimental data shows the OW model, except for = 0.35% and = 0.40%. In contrast to this, the AF and CH model predict effective cyclic properties with slightly higher , in the present study. Especially the CH model reveals a lagged transition from the elastic-plastic to the complete elastic regime. This can potentially be traced back to the lower critical resolved shear stress of the CH model parameter set. The appropriate transition from the elastic-plastic to the fully elastic regime represents a fundamental prerequisite for an adequate modelling of fatigue damage under HCF loading, resulting in a preference for the OW model. Figure 13b is adequate for the evaluation of the characteristic for total strain amplitudes > 0.50%. In this regime of total strain amplitudes, the KH models do not show a significant difference with respect to cyclic effective properties. However, the AF model shows a slightly too high level of plasticity.
4.3. Cyclic Deformation Behavior at R = 0—KH Model Comparison
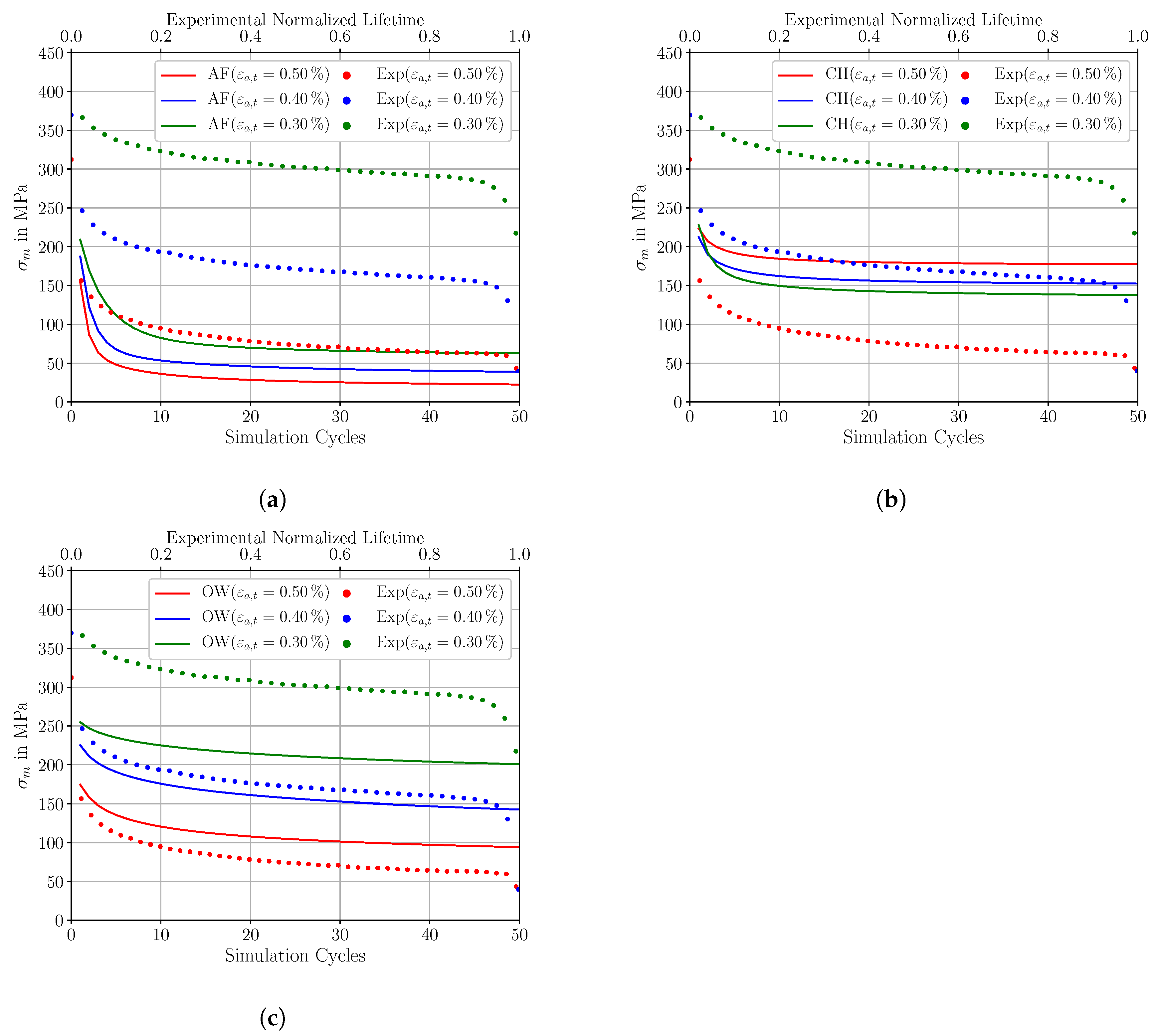
In the next step, predictions for a totally different strain ratio R = 0 are made using the calibrated constitutive parameters from R = −1. To characterize the mean stress relaxation behavior of the different KH models, simulations with the martensitic RVE of Figure 7a were performed for 50 loading cycles at a strain ratio of R = 0 with the equivalent numerical settings as in the previous section. The mean stress relaxation behavior of the AF, CH, and OW model is compared to experimental results in Figure 14a–c, respectively. Simulation results are shown as solid lines and the experimental references which are normalized with respect to lifetime are shown in a dotted form. The corresponding mean stress values at half normalized lifetime can be considered as experimental references due to the fact that also at R = −1 the stress-strain hysteresis is considered at half lifetime.
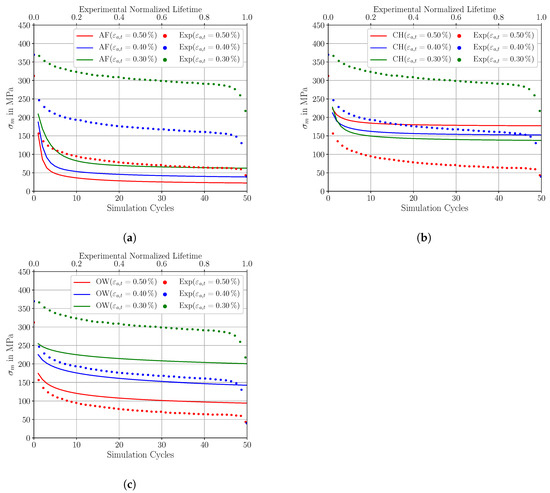
Figure 14.
Comparison of the mean stress relaxation behavior at R = 0 for three different total strain amplitudes = 0.30%, = 0.40% and = 0.50% between the micromechanical model prediction and the experimental results; (a) for the AF KH model (b) for the CH KH model and (c) for the OW KH model.
According to Figure 14a, the AF model is not able to capture any mean stress effects. The initial mean stresses are almost fully relaxed for all applied total strain amplitudes within the first 10 to 15 simulation cycles. The AF relaxation characteristic results in almost fully relaxed stress-strain hysteresis which are shown in Figure 16a–c. The plotted experimental stress-strain hysteresis is at half lifetime. In contrast to this, the predicted mean stresses by the Chaboche model, shown in Figure 14b, are only partially relaxed. However, the predicted mean stresses indicate inconsistent results. This is because the smallest applied strain amplitude = 0.30% shows the highest relaxation rates and consequently the lowest mean stresses. In general, there are increased relaxation rates at higher total strain amplitudes due to the presence of lager plastic strains which act as a driving force for mean stress relaxation [3,4,38,66]. Finally, the predicted mean stresses by the OW model are shown in Figure 14c. They are well consistent with the postulated relaxation theories. The three simulated mean stresses are all partially relaxed and the agreement with the experimental results is adequate for = 0.50%, = 0.40%. However, for the total strain amplitude of 0.30%, the agreement between the OW model and the experimental results at half normalized lifetime get worse, with absolute errors in excess of 90 MPa. These deviations can be attributed to the increased level of plasticity at the calibration of the KH models at R = −1 for small total strain amplitudes. Furthermore, transient effects may also contribute to mean stress deviations at small applied total strain amplitudes. Experimental relaxation data also indicate substantial declines in mean stress relaxation rates in the transition regime from the elastic-plastic to the elastic regime [3,66].
In analogy to the evaluation of the strain energy density characteristics for the fully reversed simulations in Section 4.2, Figure 15 shows the strain energy density characteristics for the simulations at R = 0. The three KH model dependent characteristics confirm that all KH models show an increased level of plasticity for the considered total strain amplitudes at R = 0. According to Figure 15, the strain energy density characteristic of the CH model shows the best agreement of the three KH models to the experimental strain energy densities for the total strain amplitudes of 0.30% and 0.40%. However, it is recalled that the CH model reveals an inconsistent mean stress relaxation behavior, according to Figure 14. Consequently, under consideration of the results from Figure 14 as well as Figure 15, the OW model is superior to the AF and CH model.
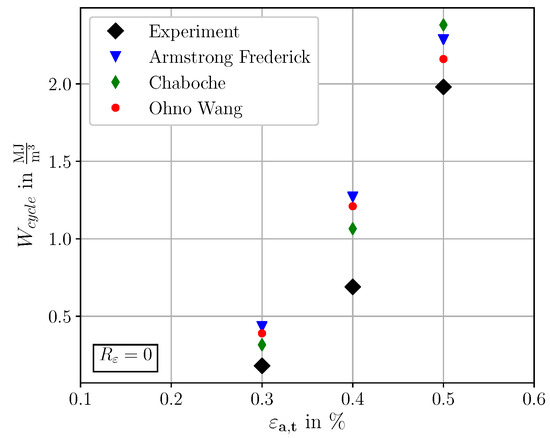
Figure 15.
Plastic strain energy density characteristics at R = 0, for the three different KH models in cycle stable conditions and the corresponding experimental data of SAE 4150 at half lifetime.
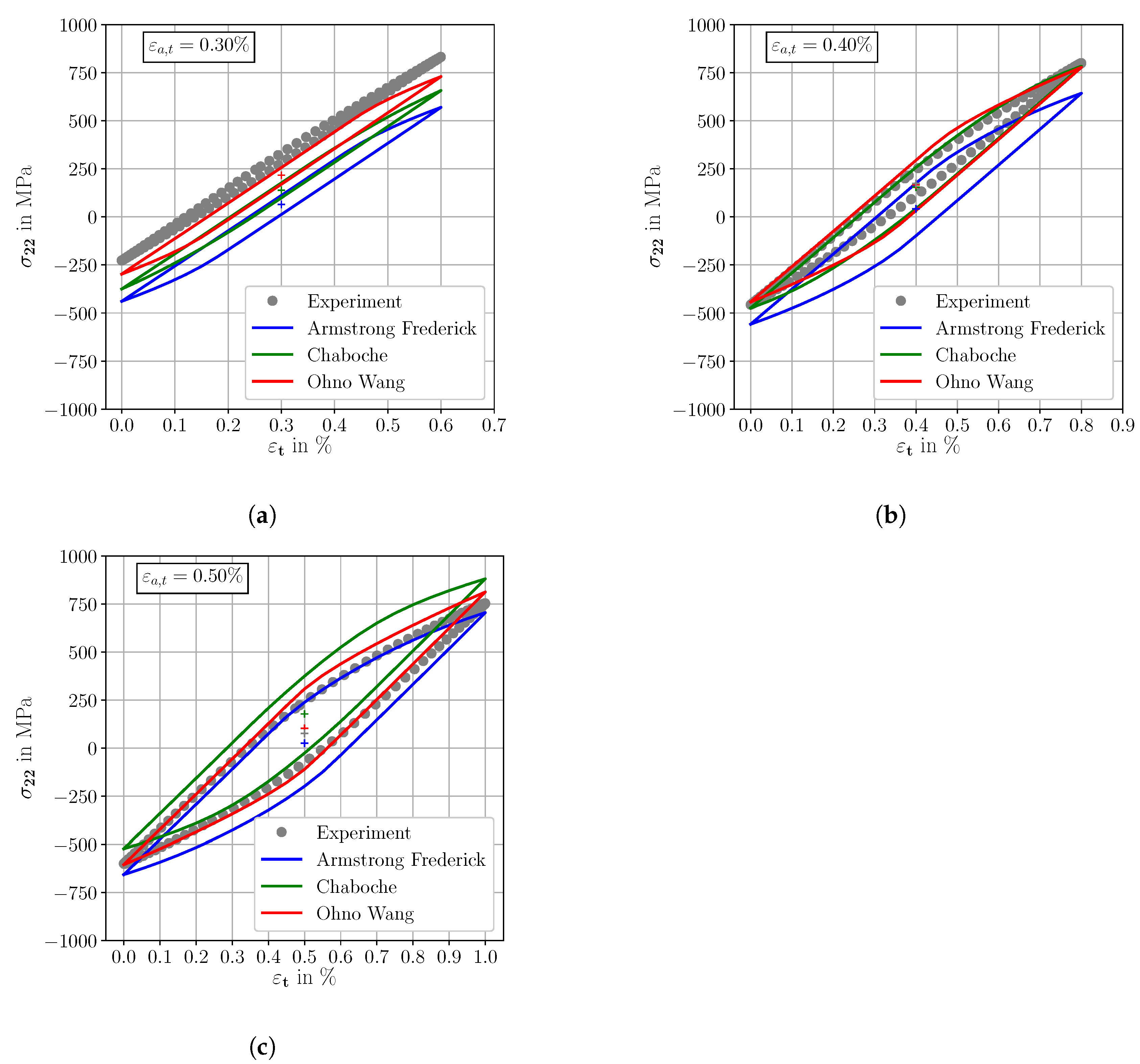
According to Figure 16b,c, the agreement of the predicted stress-strain hystereses by the OW model show an excellent agreement for = 0.40% and = 0.50% with the experimental results. Furthermore, the deviations for the hystereses at = 0.30% are still within acceptable ranges. The mean stress relaxation results of the OW model indicate a good transferability between different applied total strain amplitudes. This property is very important regarding the application of the micromechanical model to a wide variety of load cases.
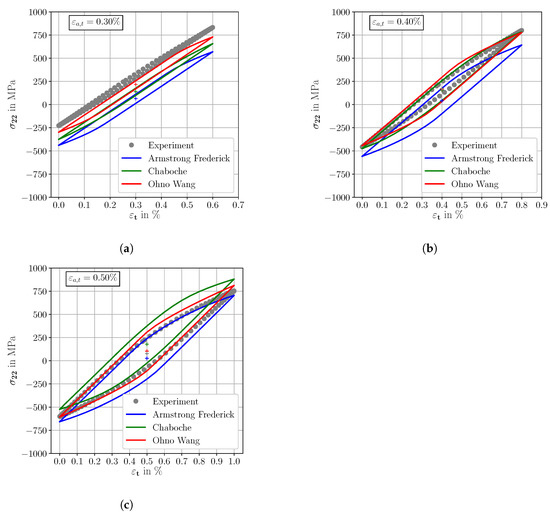
Figure 16.
Effective cyclic properties at R = 0, simulation and experimental results. The applied total strain amplitudes are (a) = 0.30%, (b) = 0.40% and (c) = 0.50%.
5. Conclusions
In the present study, a micromechanical framework has been developed to model the cyclic behavior of the martensitic high-strength steel SAE 4150 at different strain ratios. A multiscale martensitic microstructure model was developed and incorporated into the modelling framework. Furthermore, a phenomenological crystal plasticity model was used to perform micromechanical simulations and to evaluate different KH models with respect to mean stress relaxation behavior. To calibrate the different complex KH models in an efficient way, a multi-objective calibration procedure was developed and implemented. Three experimental cyclic stable stress-strain hystereses are required for the calibration procedure to capture the cyclic macroscopic deformation behavior of the considered SAE 4150 from [0,1.0%]. To identify an appropriate KH model for the cyclic deformation behavior under consideration of varying loading conditions, the calibration of the constitutive model must be performed for multiple strain ratios. A summary of the results is as follows:
- A comparison of experimental EBSD data and calculated OR indicates that the Nishiyama– Wassermann orientation relationship is well suited for representing the martensitic variants.
- A microstructure model for lath martensite incorporating the Nishiyama–Wassermann orientation relationship is proposed using a multiscale Voronoi tessellation technique.
- A multi-objective calibration procedure for the determination of the cyclic crystal plasticity constitutive parameters based on experimental LCF data is proposed. Thereby, a simplified numerical efficient RVE is used for the combined sensitivity analysis and the subsequent genetic algorithm. The simplified RVE shows macroscopically an almost equivalent stress-strain behavior than the most complex proposed martensitic RVE with deviations smaller than 1.0%.
- For fully reversed loadings (R = −1), the OW model shows an excellent agreement to experimental data, in particular for small applied total strain amplitudes. The agreement of the AF and Chaboche model to the experimental data are adequate, but with increasing errors. Consequently, the OW model is superior to the AF and Chaboche model for all applied total strain amplitudes, except for = 0.90% where the Chaboche model agrees better to experimental data than the OW model.
- Simulations of the KH model dependent mean stress relaxation behavior for (R = 0) indicate that the AF model is not able to capture mean stress effects. The mean stress relaxation predicted by the Chaboche model shows a non-consistent characteristic due to high mean stresses for large applied strain amplitudes and small mean stresses for small applied strain amplitudes. The OW model shows a good agreement to the experimental stress-strain hystereses at R = 0. Furthermore, the predicted mean stress relaxation characteristic by the OW model agrees well with the experimental characteristic with small deviations.
Author Contributions
Conceptualization, A.H., H.u.H., B.J.S. and P.S.-R.; methodology, B.J.S., X.S., A.H. and H.u.H.; investigation, B.J.S.; writing—original draft preparation, B.J.S.; visualization, B.J.S.; supervision, A.H. and P.S.-R.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kitahara, H.; Ueji, R.; Tsuji, N.; Minamino, Y. Crystallographic features of lath martensite in low-carbon steel. Acta Mater. 2006, 54, 1279–1288. [Google Scholar] [CrossRef]
- Krauss, G. Martensite in steel: Strength and Structure. Mater. Sci. Eng. A 1999, 273–275, 40–57. [Google Scholar] [CrossRef]
- Stephens, R.I.; Fatemi, A.; Stephens, R.R.; Fuchs, H. Metal Fatigue in Engineering, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2001. [Google Scholar]
- Shijve, J. Fatigue of Structures and Materials, 2nd ed.; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Morito, S.; Tanaka, H.; Konishi, R.; Furuhara, T.; Maki, T. The morphology and crystallography of lath martensite in Fe-C alloys. Acta Mater. 2003, 51, 1789–1799. [Google Scholar] [CrossRef]
- Kitahara, H.; Ueji, R.; Ueda, M.; Tsuji, N.; Minamino, Y. Crystallographic analysis of plate martensite in Fe–28.5 at. % Ni by FE-SEM/EBSD. Mater. Charact. 2005, 54, 378–386. [Google Scholar] [CrossRef]
- Morito, S.; Huang, X.; Furuhara, T.; Maki, T.; Hansen, N. The morphology and crystallography of lath martensite in alloy steels. Acta Mater. 2006, 54, 5323–5331. [Google Scholar] [CrossRef]
- Morito, S.; Yoshida, H.; Maki, T.; Huang, X. Effect of block size on the strength of lath martensite in low carbon steels. Mater. Sci. Eng. A 2006, 438–440, 237–240. [Google Scholar] [CrossRef]
- Swarr, T.; Krauss, G. The effect of structure on the deformation of as-quenched and tempered martensite in an Fe-0.2 % C-alloy. Metall. Trans. A 1976, 7, 41–48. [Google Scholar] [CrossRef]
- McDowell, D.; Dunne, F. Microstructure-sensitive computational modeling of fatigue crack formation. Int. J. Fatigue 2010, 32, 1521–1542. [Google Scholar] [CrossRef]
- Cruzado, A.; Gan, B.; Jiménez, M.; Barba, D.; Ostolaza, K.; Linaza, A.; Molina-Aldareguia, J.; Llorca, J.; Segurado, J. Multiscale modeling of the mechanical behavior of IN718 superalloy based on micropillar compression and computational homogenization. Acta Mater. 2015, 98, 242–253. [Google Scholar] [CrossRef]
- Wu, B.; Vajragupta, N.; Lian, J.; Hangen, U.; Wechsuwanmanee, P.; Münstermann, S. Prediction of plasticity and damage initiation behaviour of C45E+N steel by micromechanical modelling. Mater. Des. 2017, 121, 154–166. [Google Scholar] [CrossRef]
- Boeff, M.; Hassan, H.U.; Hartmaier, A. Micromechanical modeling of fatigue crack initiation in polycrystals. J. Mater. Res. 2017, 32, 4375–4386. [Google Scholar] [CrossRef]
- Ghassemi-Armaki, H.; Chen, P.; Bhat, S.; Sadagopan, S.; Kumar, S.; Bower, A. Microscale-calibrated modeling of the deformation response of low-carbon martensite. Acta Mater. 2013, 61, 3640–3652. [Google Scholar] [CrossRef]
- Altendorf, H.; Latourte, F.; Jeulin, D.; Faessel, M.; Saintoyant, L. 3D Reconstruction of a multiscale microstructure by anisotropic tessellation models. Image Anal. Stereol. 2014, 33, 121–130. [Google Scholar] [CrossRef]
- Sun, F.; Meade, E.D.; Dowd, N.P.O. Microscale modelling of the deformation of a martensitic steel using the Voronoi tessellation method. J. Mech. Phys. Solids 2018, 113, 35–55. [Google Scholar] [CrossRef]
- Hennessey, C.; Castelluccio, G.M.; McDowell, D.L. Sensitivity of polycrystal plasticity to slip system kinematic hardening laws for Al 7075-T6. Mater. Sci. Eng. A 2017, 687, 241–248. [Google Scholar] [CrossRef]
- Bari, S.; Hassan, T. Anatomy of coupled constitutive models for ratcheting simulation. Int. J. Plast. 2000, 16, 381–409. [Google Scholar] [CrossRef]
- Ohno, N.; Wang, J.D. Kinematic hardening rules with critical state of dynamic recovery, part I: Formulation and basic features for ratchetting behavior. Int. J. Plast. 1993, 9, 375–390. [Google Scholar] [CrossRef]
- Cruzado, A.; LLorca, J.; Segurado, J. Modeling cyclic deformation of inconel 718 superalloy by means of crystal plasticity and computational homogenization. Int. J. Solids Struct. 2017, 122–123, 148–161. [Google Scholar] [CrossRef]
- Sweeney, C.A.; Brien, B.O.; McHugh, P.E.; Leen, S.B. Experimental characterisation for micromechanical modelling of CoCr stent fatigue. Biomaterials 2014, 35, 36–48. [Google Scholar] [CrossRef] [PubMed]
- Herrera-Solaz, V.; Segurado, J.; LLorca, J. On the robustness of an inverse optimization approach based on the Levenberg–Marquardt method for the mechanical behavior of polycrystals. Eur. J. Mech. A Solids 2015, 53, 220–228. [Google Scholar] [CrossRef]
- Prithivirajan, V.; Sangid, M.D. The role of defects and critical pore size analysis in the fatigue response of additively manufactured IN718 via crystal plasticity. Mater. Des. 2018, 150, 139–153. [Google Scholar] [CrossRef]
- Xie, C.L.; Gosh, S.; Groeber, M. Modeling Cyclic Deformation of HSLA Steels Using Crystal Plasticity. J. Eng. Mater. Technol. 2004, 126, 339–352. [Google Scholar] [CrossRef]
- Krupp, U. Fatigue Crack Propagation in Metals and Alloys: Microstructural Aspects and Modelling Concepts; Wiley-VCH: Weinheim, Germany, 2007. [Google Scholar]
- Bain, E.C. The nature of martensite. Trans. Metall. Soc. AIME 1924, 70, 25–46. [Google Scholar]
- Kurdjumov, G.; Sachs, G. Über den Mechanismus der Stahlhärtung. Zeitschrift für Physik 1930, 64, 325–340. [Google Scholar] [CrossRef]
- Greninger, A.; Troiano, A. The mechanism of martensite formation. Trans. Metall. Soc. AIME 1949, 185, 590–598. [Google Scholar] [CrossRef]
- Nishiyama, Z. X-ray investigation of the mechanism of the transformation from face-centred cubic lattice to body-centred cubic. Sci. Rep. Tohoku Imp. Univ. Ser. 1 Math. Phys. Chem. 1934, 23, 637–664. [Google Scholar]
- Wassermann, G. Über den Mechanismus der alpha-gamma Umwandlung des Eisens. In Mitteilungen aus dem Kaiser-Wilhelm-Institut für Eisenforschung zu Düsseldorf; Verlag Stahleisen: Düsseldorf, Germany, 1935. [Google Scholar]
- Suikkanen, P.P.; Cayron, C.; DeArdo, A.J.; Karjalainen, L.P. Crystallographic Analysis of Martensite in 0.2C-2.0Mn-1.5Si-0.6Cr Steel using EBSD. J. Mater. Sci. Technol. 2011, 27, 920–930. [Google Scholar] [CrossRef]
- Bachmann, F.; Hielscher, R.; Schaeben, H. Texture Analysis with MTEX—Free and Open Source Software Toolbox. Solid State Phenom. 2010, 160, 63–68. [Google Scholar] [CrossRef]
- Cayron, C. ARPGE: A computer program to automatically reconstruct the parent grains from electron backscatter diffraction data. J. Appl. Crystallogr. 2007, 40, 1183–1188. [Google Scholar] [CrossRef] [PubMed]
- Gillner, K.; Münstermann, S. Numerically predicted high cycle fatigue properties through representative volume elements of the microstructure. Int. J. Fatigue 2017, 105, 219–234. [Google Scholar] [CrossRef]
- E606/E606M-12, A. Standard Test Method for Strain-Controlled Fatigue Testing; ASTM International: West Conshohocken, PA, USA, 2012. [Google Scholar]
- Christ, H.J. Wechselverformung von Metallen; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar]
- Totten, G.; Howes, M.; Inoue, T. (Eds.) Handbook of Residual Stress and Deformation of Steel, 1st ed.; ASM International: Materials Park, OH, USA, 2002. [Google Scholar]
- Wehner, T.; Fatemi, A. Effects of mean stress on fatigue behaviour of a hardened carbon steel. Int. J. Fatigue 1991, 13, 241–248. [Google Scholar] [CrossRef]
- Wu, D.L.; Xuan, F.Z.; Guo, S.J.; Zhao, P. Uniaxial mean stress relaxation of 9–12% Cr steel at high temperature: Experiments and viscoplastic constitutive modeling. Int. J. Plast. 2016, 77, 156–173. [Google Scholar] [CrossRef]
- Koh, S.K.; Stephens, R.I. Mean stress effects on low cycle fatigue for a high strength steel. Fatigue Fract. Eng. Mater. Struct. 1991, 14, 413–428. [Google Scholar] [CrossRef]
- Rycroft, C.H. Voro++: A Three-Dimensional Voronoi Cell Library in C++. Available online: http://math.lbl.gov/voro++/ (accessed on 1 February 2018).
- Engler, O.; Randle, V. Introduction to Texture Analysis: Macrotexture, Microtexture, and Orientation Mapping, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Smit, R.; Brekelmans, W.; Meijer, H. Prediction of the mechanical behavior of nonlinear heterogeneous systems by multi-level finite element modeling. Comput. Methods Appl. Mech. Eng. 1998, 155, 181–192. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.; Bieler, T.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Hall, E.O. The Deformation and Ageing of Mild Steel: II Characteristics of the Lüders Deformation. Proc. Phys. Soc. Sect. B 1951, 64, 742. [Google Scholar] [CrossRef]
- Petch, N.J. The Cleavage Strength of Polycrystals. J. Iron Steel Inst. 1953, 174, 25–28. [Google Scholar]
- Peirce, D.; Asaro, R.; Needleman, A. Material rate dependence and localized deformation in crystalline solids. Acta Metall. 1983, 31, 1951–1976. [Google Scholar] [CrossRef]
- Meissonnier, F.; Busso, E.; O’Dowd, N. Finite element implementation of a generalised non-local rate-dependent crystallographic formulation for finite strains. Int. J. Plast. 2001, 17, 601–640. [Google Scholar] [CrossRef]
- Rice, J. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1976, 348, 101–127. [Google Scholar] [CrossRef]
- Cailletaud, G. A micromechanical approach to inelastic behaviour of metals. Int. J. Plast. 1992, 8, 55–73. [Google Scholar] [CrossRef]
- Frederick, C.; Armstrong, P. A Mathematical Representation of the Multiaxial Bauschinger Effect; Technical report, Berkeley Nuclear Laboratories—CEGB Report RD/B/N731; Berkeley Nuclear Laboratories: Berkeley, CA, USA, 1966. [Google Scholar]
- Prager, W. Recent Developments in the Mathematical Theory of Plasticity. J. Appl. Phys. 1949, 20, 235–241. [Google Scholar] [CrossRef]
- Chaboche, J.L.; Dang, K.; Cordier, G. Modelization of the strain memory effect on the cyclic hardening of 316 stainless steel. Struct. Mech. React. Technol. 1979, 12, 1–10. [Google Scholar]
- Chaboche, J. A review of some plasticity and viscoplasticity constitutive theories. Int. J. Plast. 2008, 24, 1642–1693. [Google Scholar] [CrossRef]
- Herrera-Solaz, V.; LLorca, J.; Dogan, E.; Karaman, I.; Segurado, J. An inverse optimization strategy to determine single crystal mechanical behavior from polycrystal tests: Application to AZ31 Mg alloy. Int. J. Plast. 2014, 57, 1–15. [Google Scholar] [CrossRef]
- Segurado, J.; Llorca, J. Simulation of the deformation of polycrystalline nanostructured Ti by computational homogenization. Comput. Mater. Sci. 2013, 76, 3–11. [Google Scholar] [CrossRef]
- Schmid, S. Untersuchungen zum Ermüdungsverhalten von mittel- und hochfesten Stählen bei sehr hohen Lastspielzahlen unter Berücksichtigung von Schwingungsrisskorrosion infolge moderner Biokraftstoffe. Ph.D. Thesis, University Bremen, Bremen, Germany, 2013. [Google Scholar]
- Dynardo GmbH. optiSLang—The Optimizing Structural Language, version 6.2.0; Dynardo GmbH: Weimar, Germany, 2018.
- Konak, A.; Coit, D.W.; Smith, A.E. Multi-objective optimization using genetic algorithms: A tutorial. Reliab. Eng. Syst. Saf. 2006, 91, 992–1007. [Google Scholar] [CrossRef]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Zitzler, E.; Laumanns, M.; Thiele, L. SPEA2: Improving the Strength Pareto Evolutionary Algorithm; Technical Report 103; Computer Engineering and Networks Laboratory, Swiss Federal Institute of Technology (ETH): Zürich, Switzerland, 2001; Volume 103. [Google Scholar]
- Zitzler, E.; Thiele, L.; Deb, K. Comparison of Multiobjective Evolutionary Algorithms: Empirical Results. Evol. Comput. 2000, 8, 173–195. [Google Scholar] [CrossRef]
- Harvey, D.P.; Bonenberger, R.J.; Wolla, J.M. Effects of sequential cyclic and monotonic loadings on damage accumulation in nickel 270. Int. J. Fatigue 1998, 20, 291–300. [Google Scholar] [CrossRef]
- Ellyin, F.; Golos, K. Multiaxial Fatigue Damage Criterion. J. Eng. Mater. Technol. 1988, 110, 63–68. [Google Scholar] [CrossRef]
- Landgraf, R.W.; Chernenkoff, R.A. Residual Stress Effects on Fatigue of Surface Processed Steels. In Analytical and Experimental Methods for Residual Stress Effects in Fatigue; ASTM STP 1004; ASTM: West Conshohocken, PA, USA, 1988; pp. 1–12. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).