Hysteretic Behavior and Ultimate Energy Dissipation Capacity of Large Diameter Bars Made of Shape Memory Alloys under Seismic Loadings
Abstract
1. Introduction
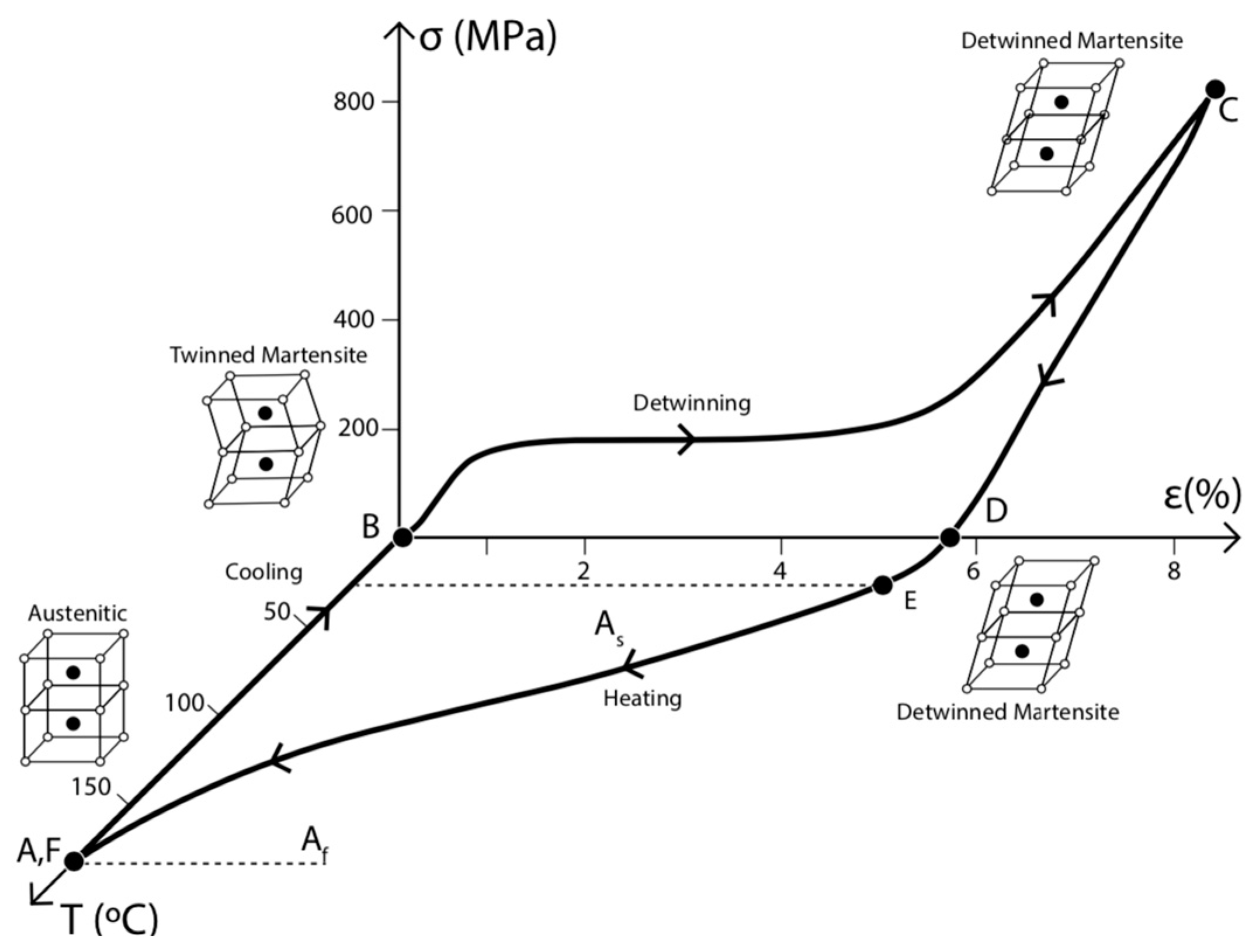
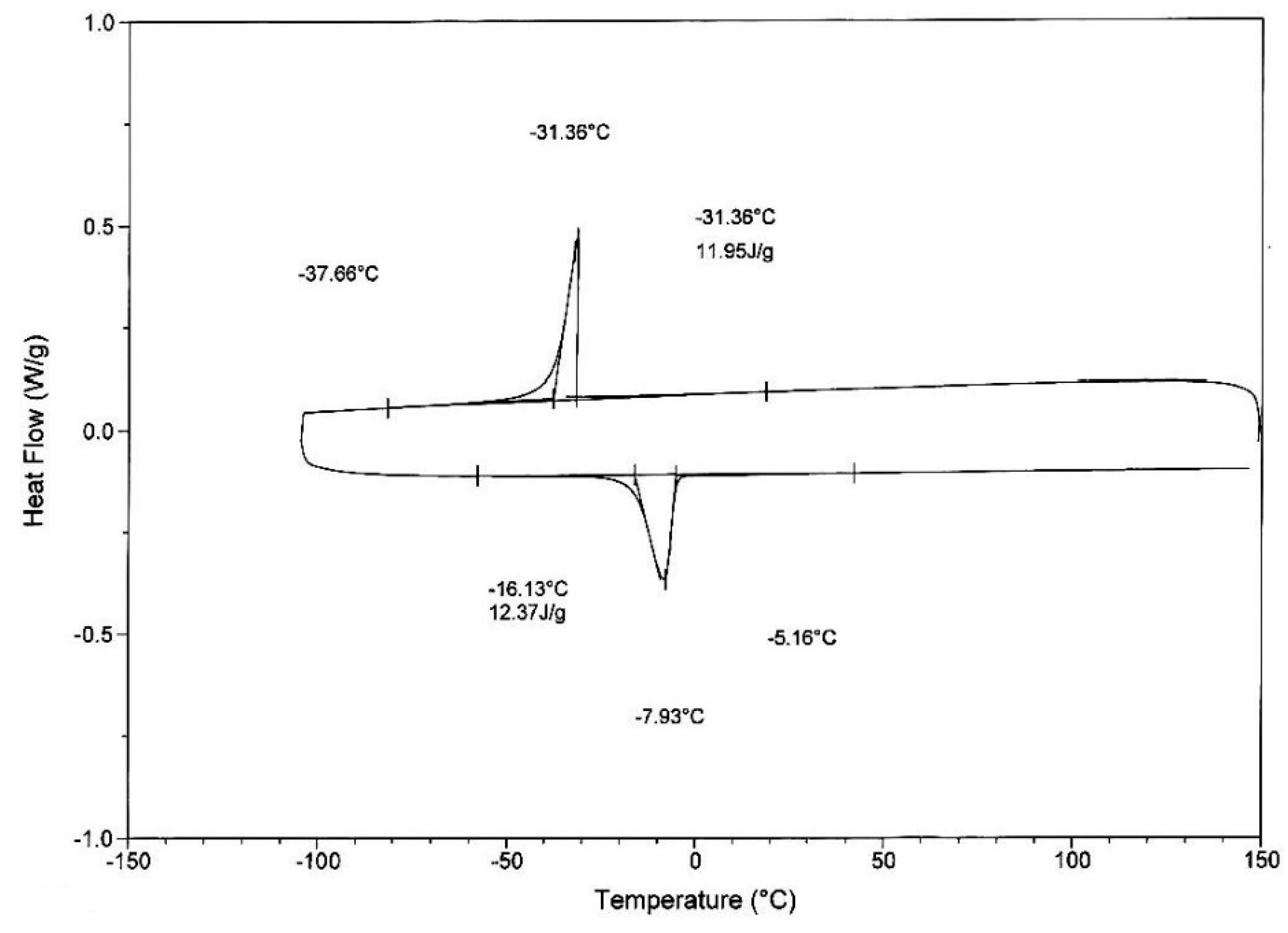
2. Cyclic Tests on NiTi Bars
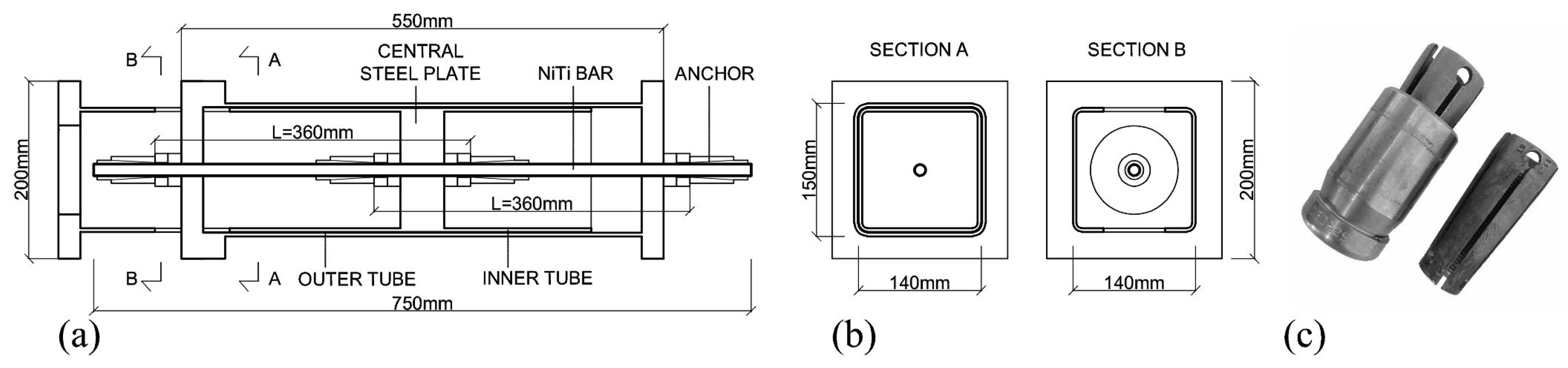
2.1. Test Specimens
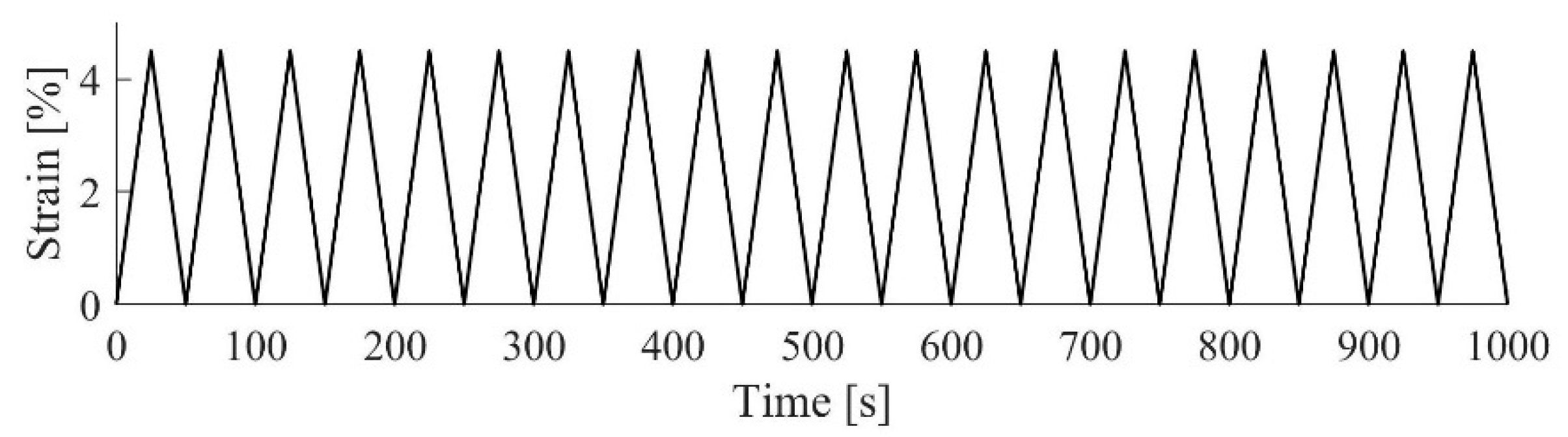
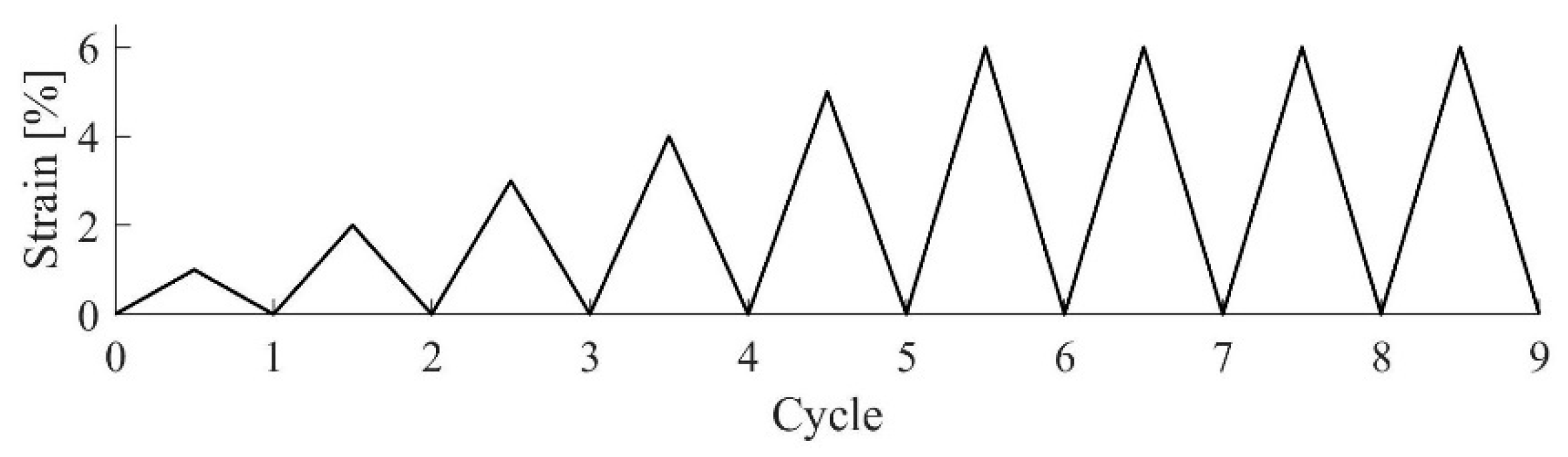
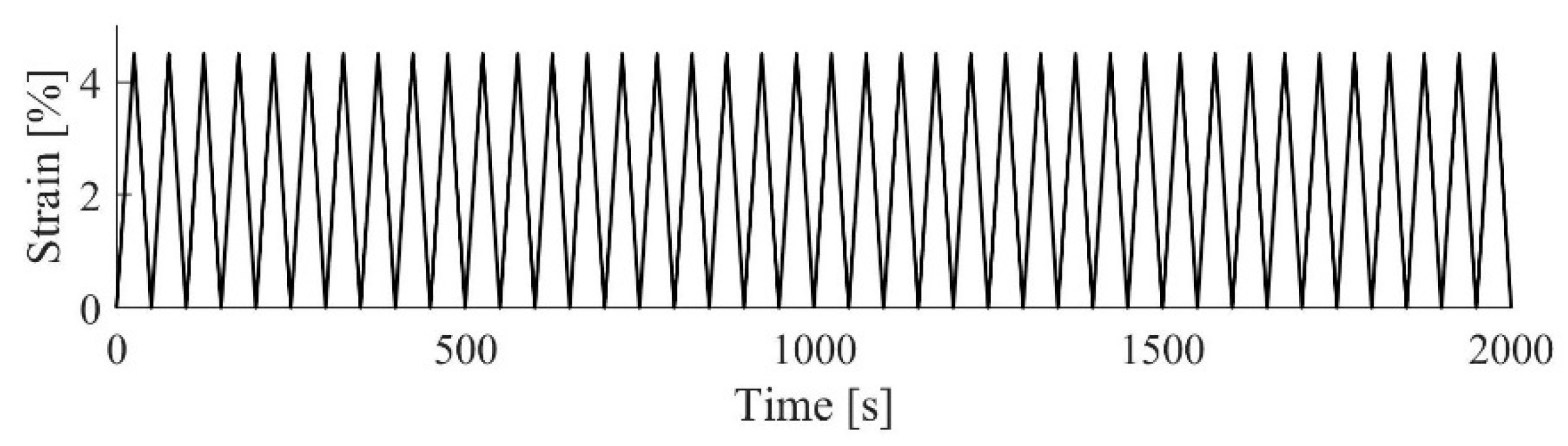
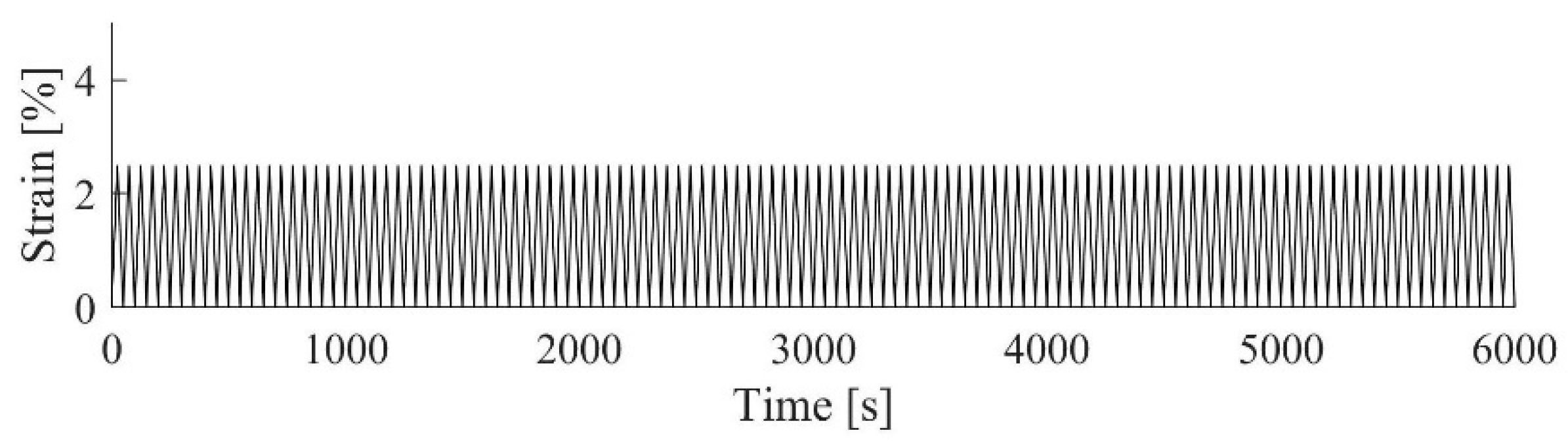
2.2. Loading Set up and Loading Protocol
2.2.1. Quasi-Static Cyclic Tests
2.2.2. Dynamic Cyclic Tests
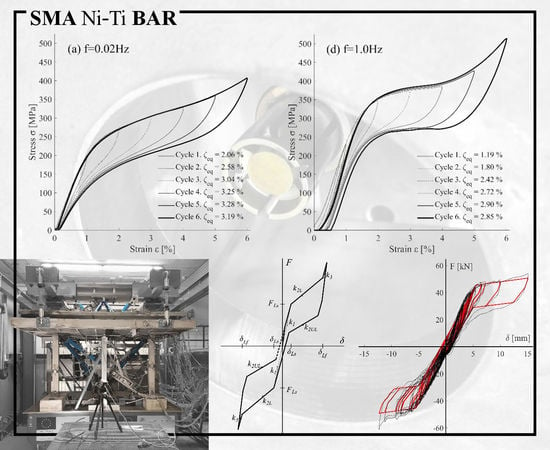
2.3. Test Results and Discussion
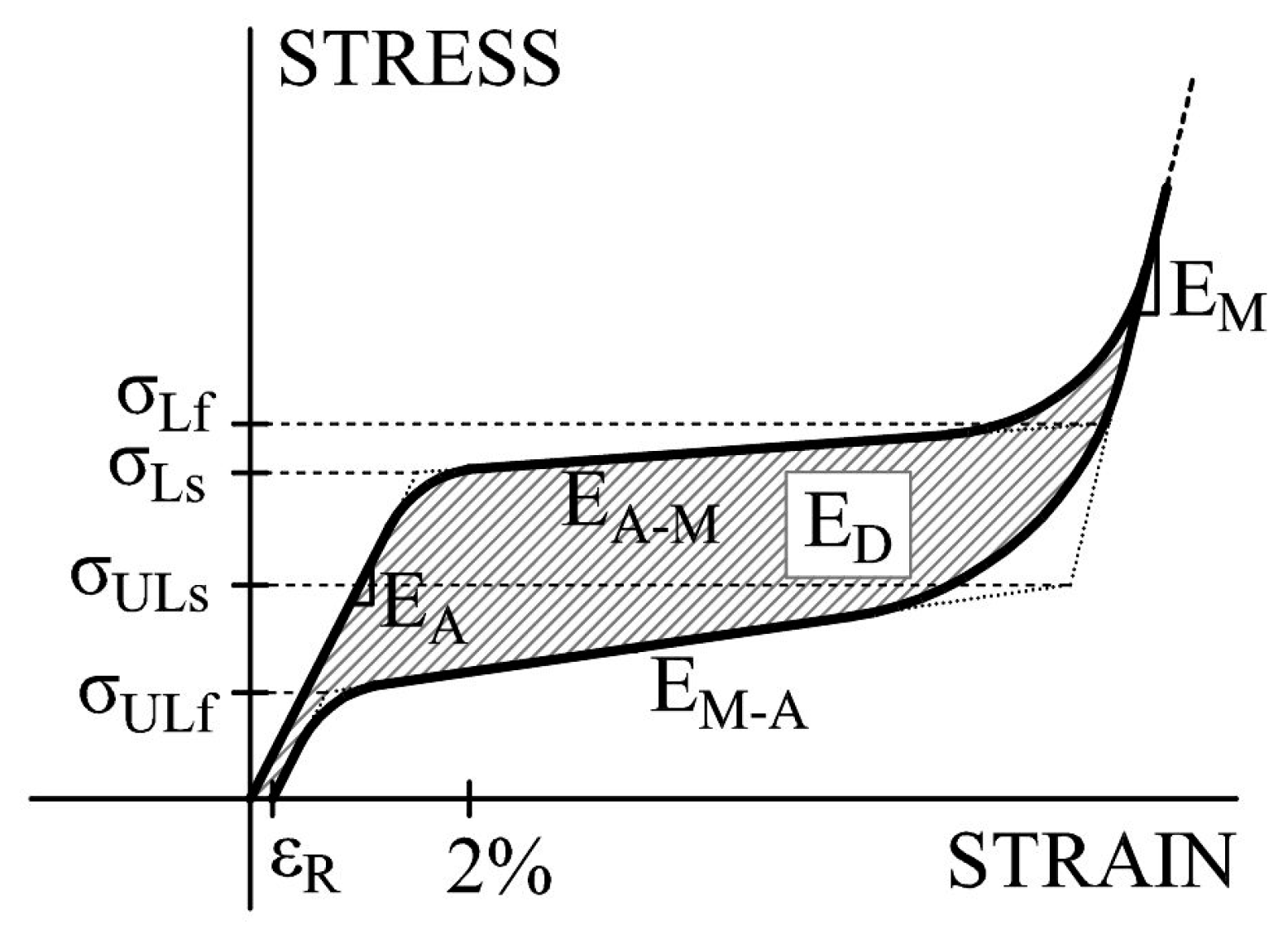
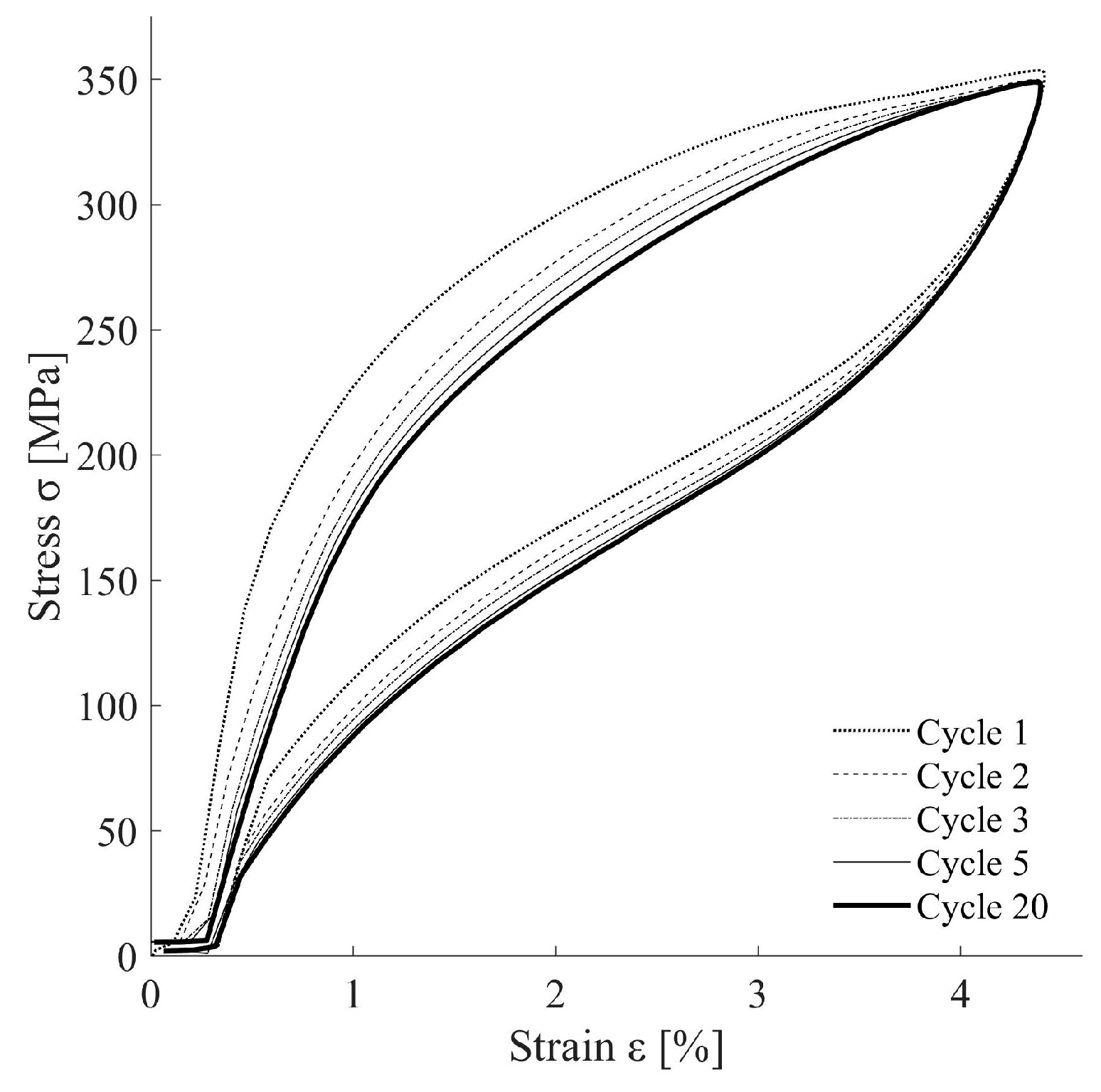
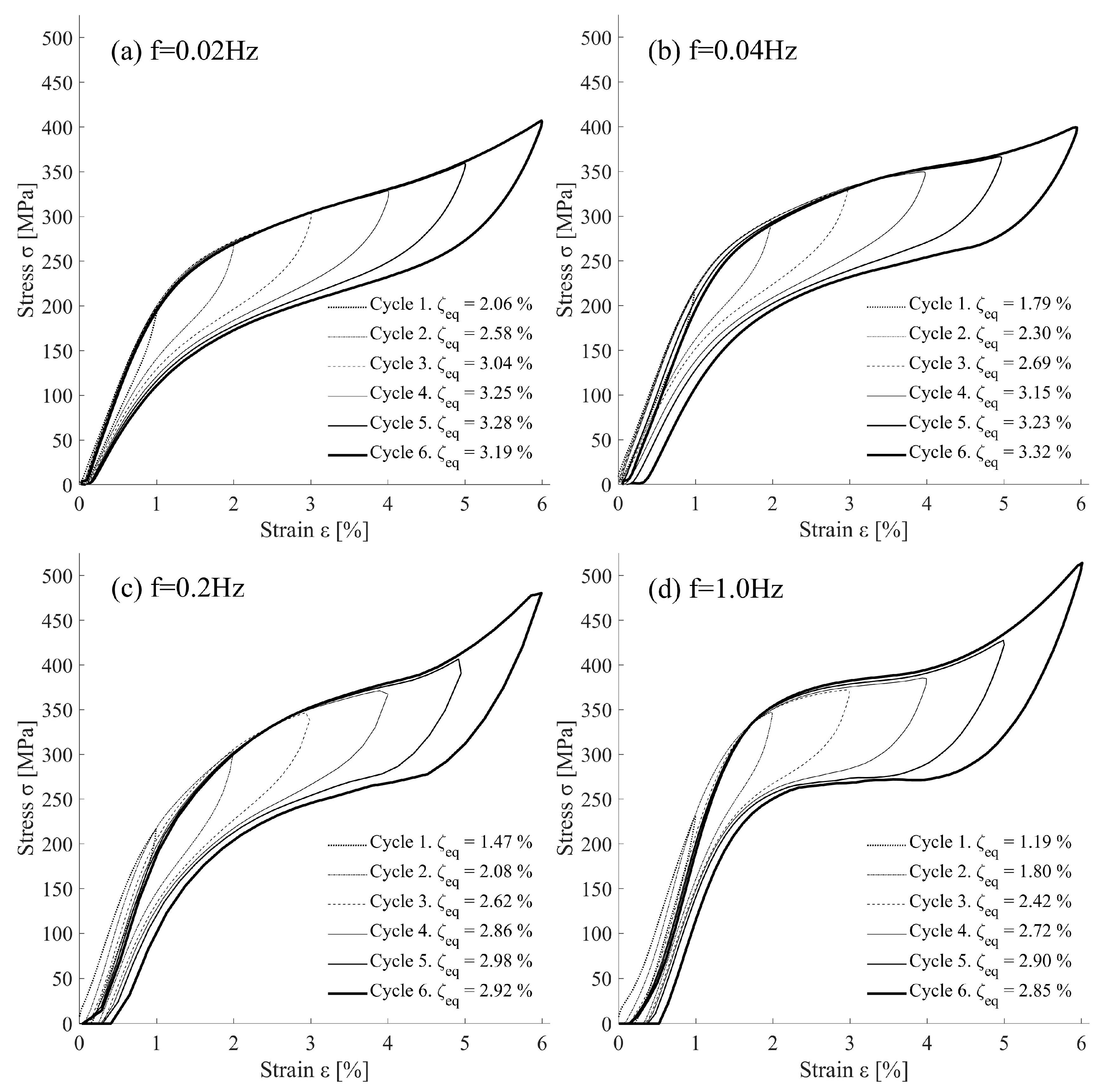
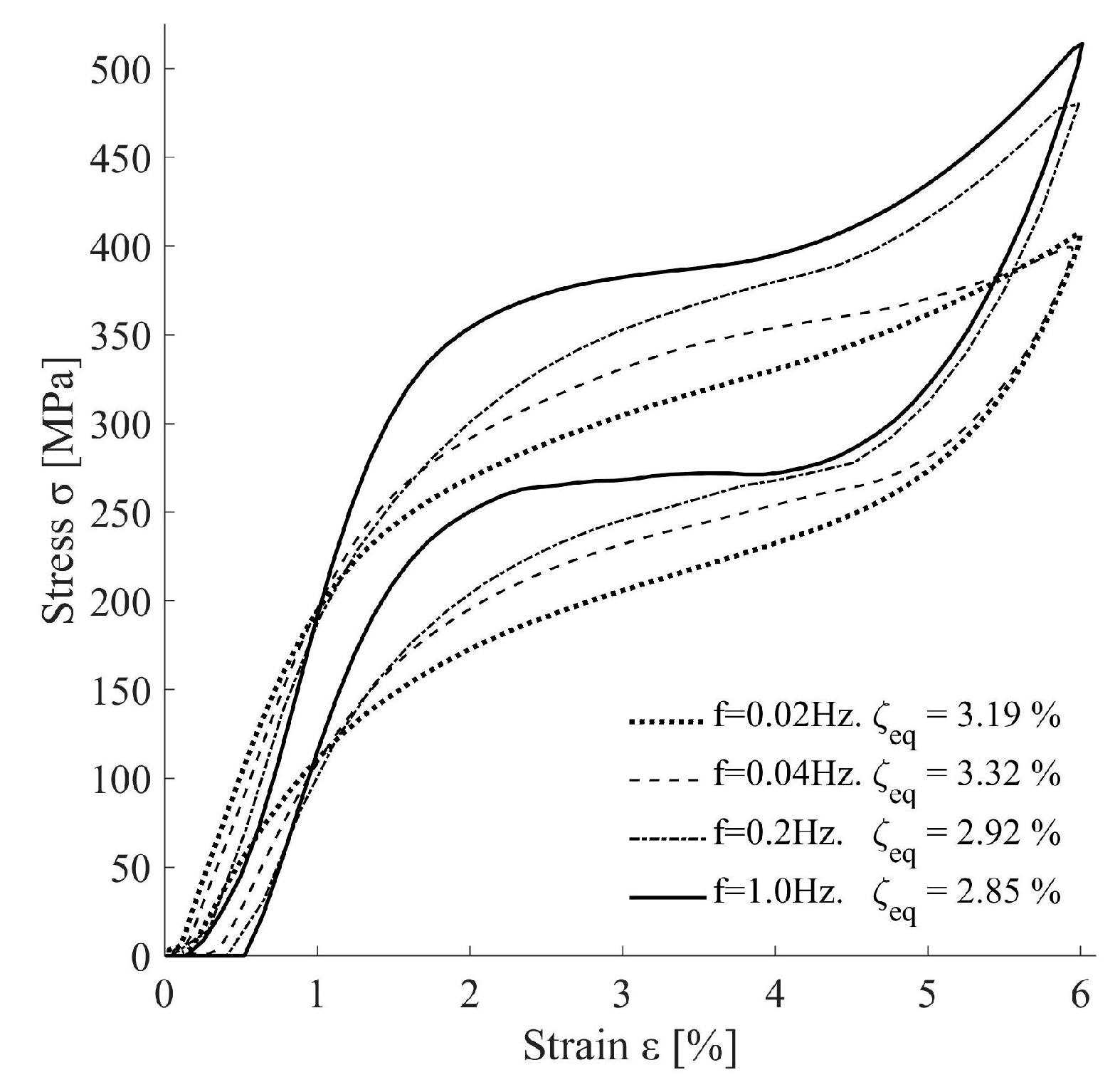
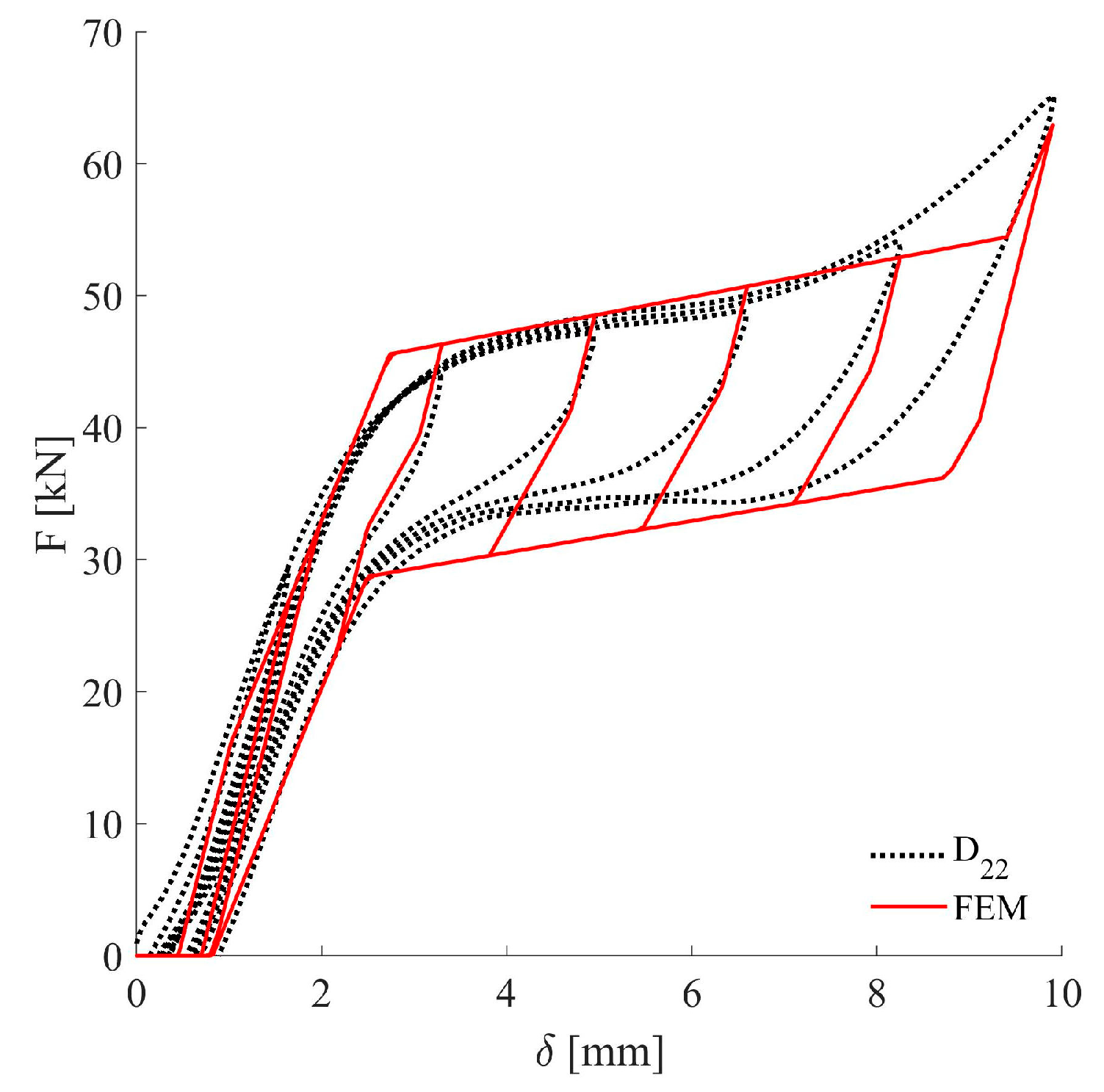
2.3.1. Hysteretic Behavior
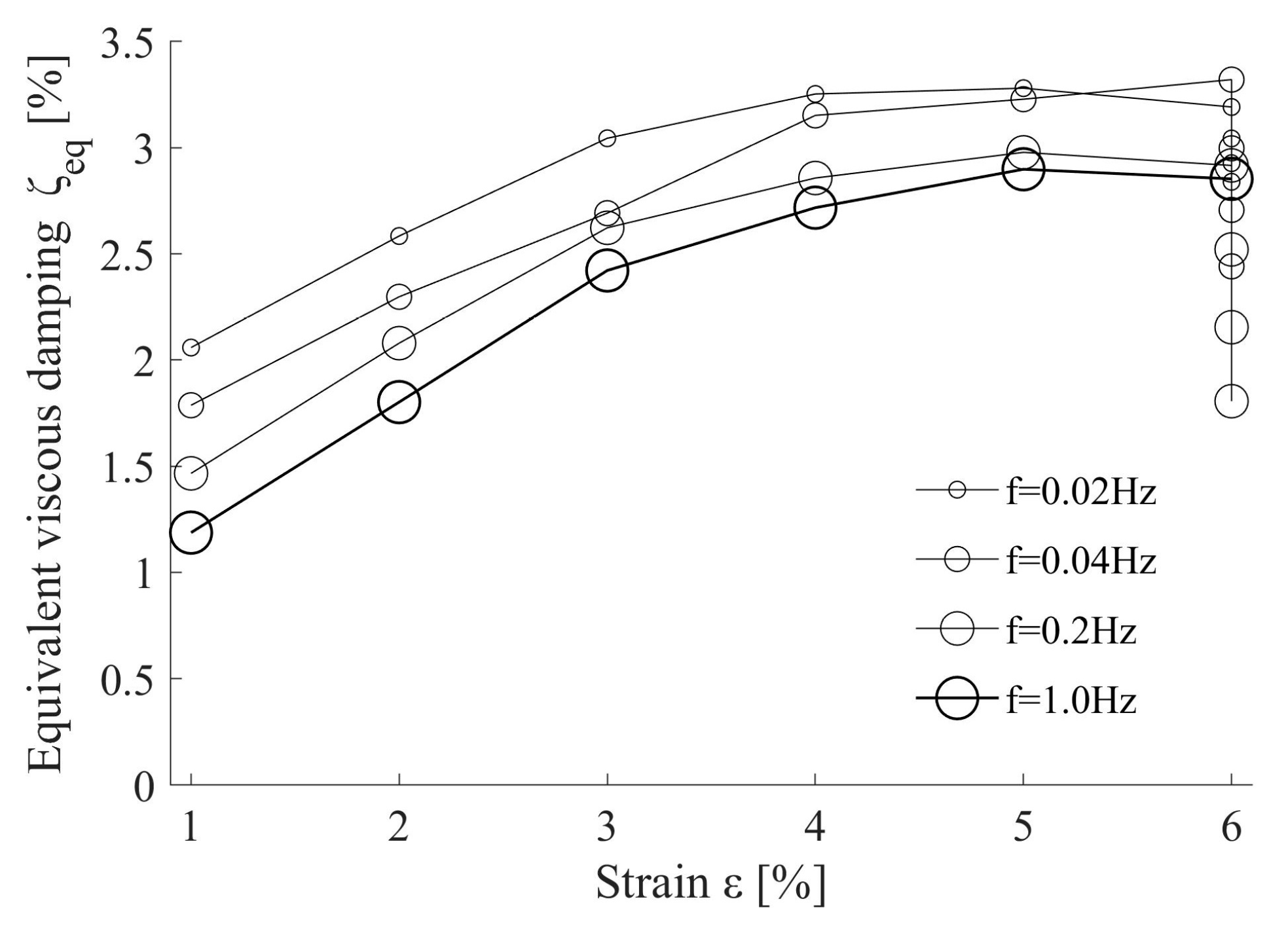
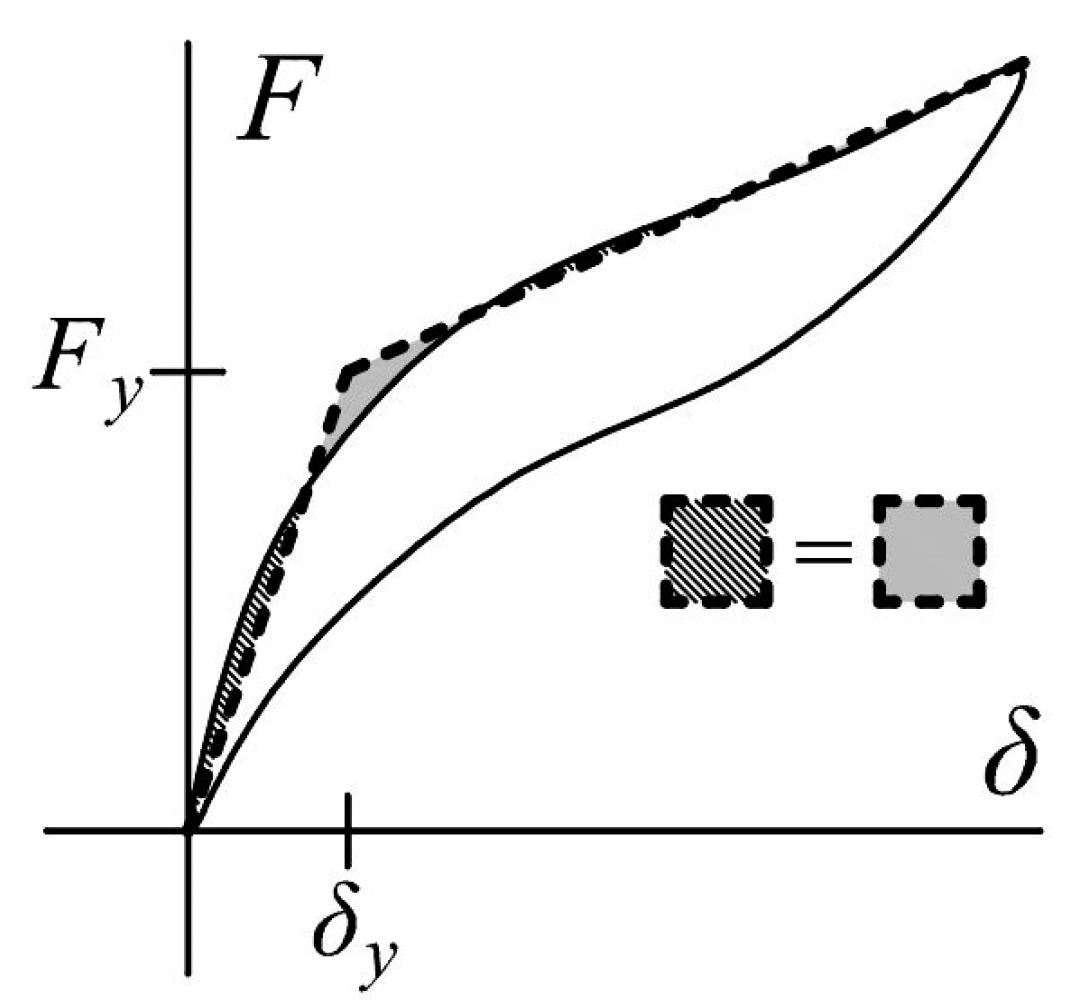
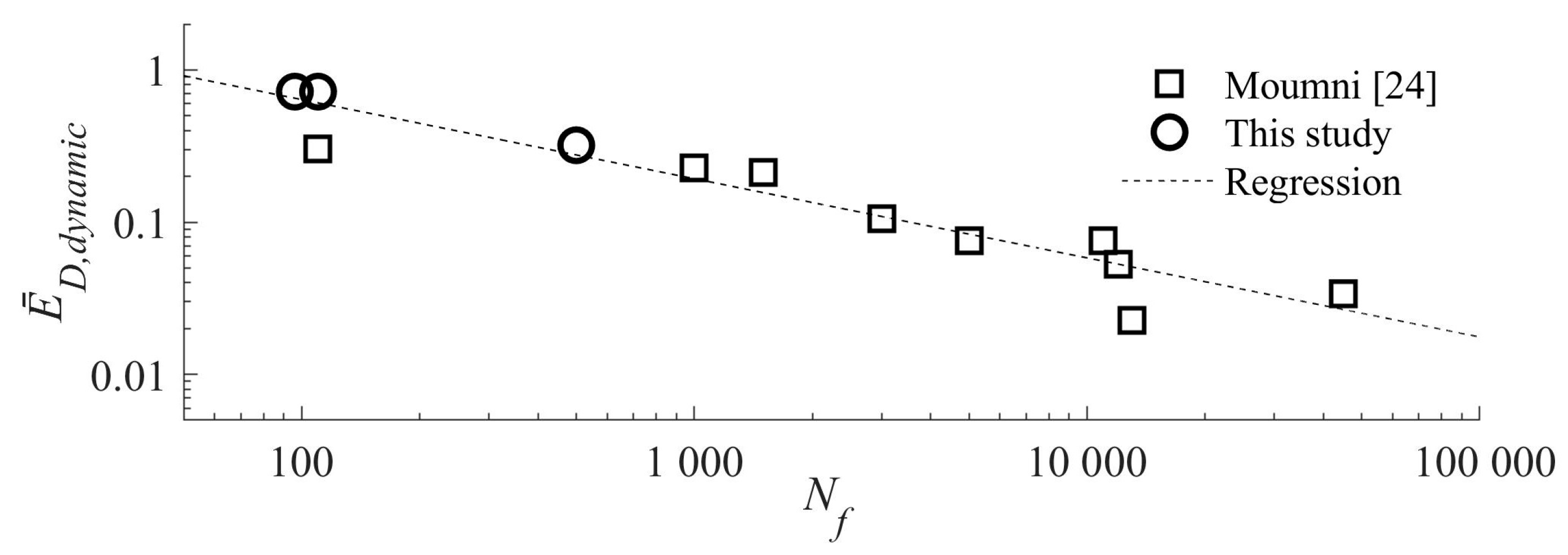
2.3.2. Ultimate Energy Dissipation Capacity
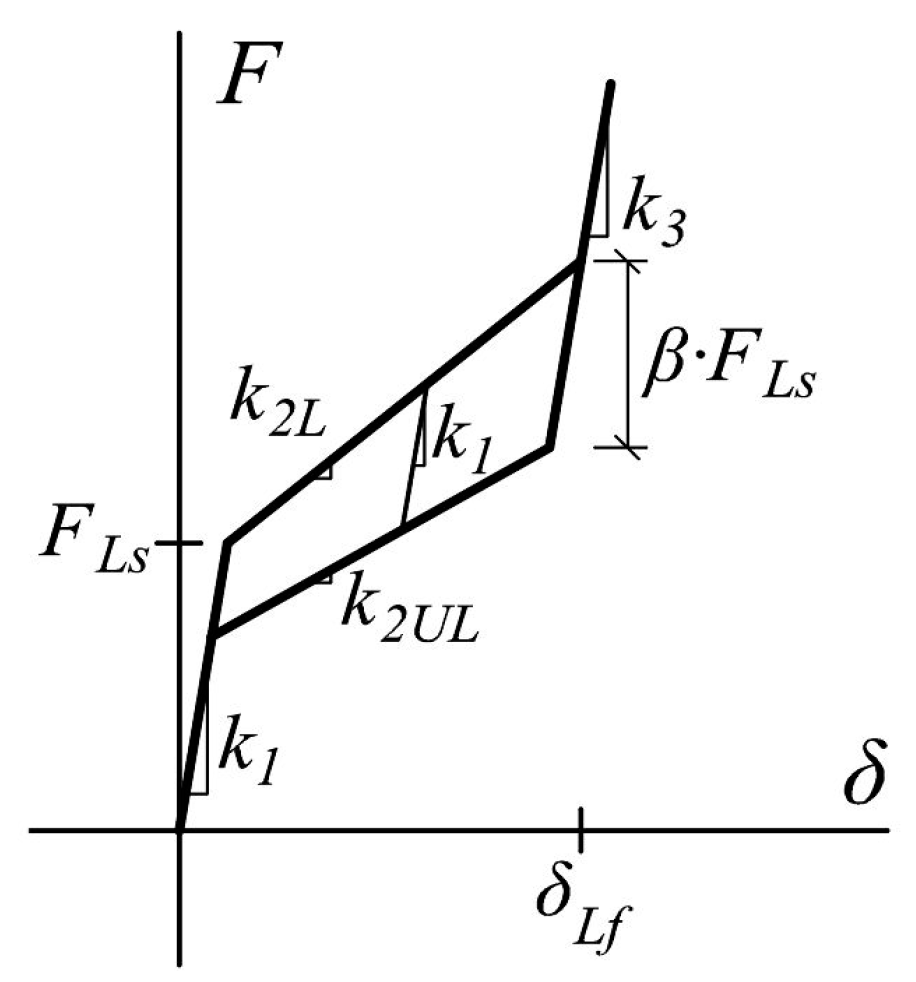
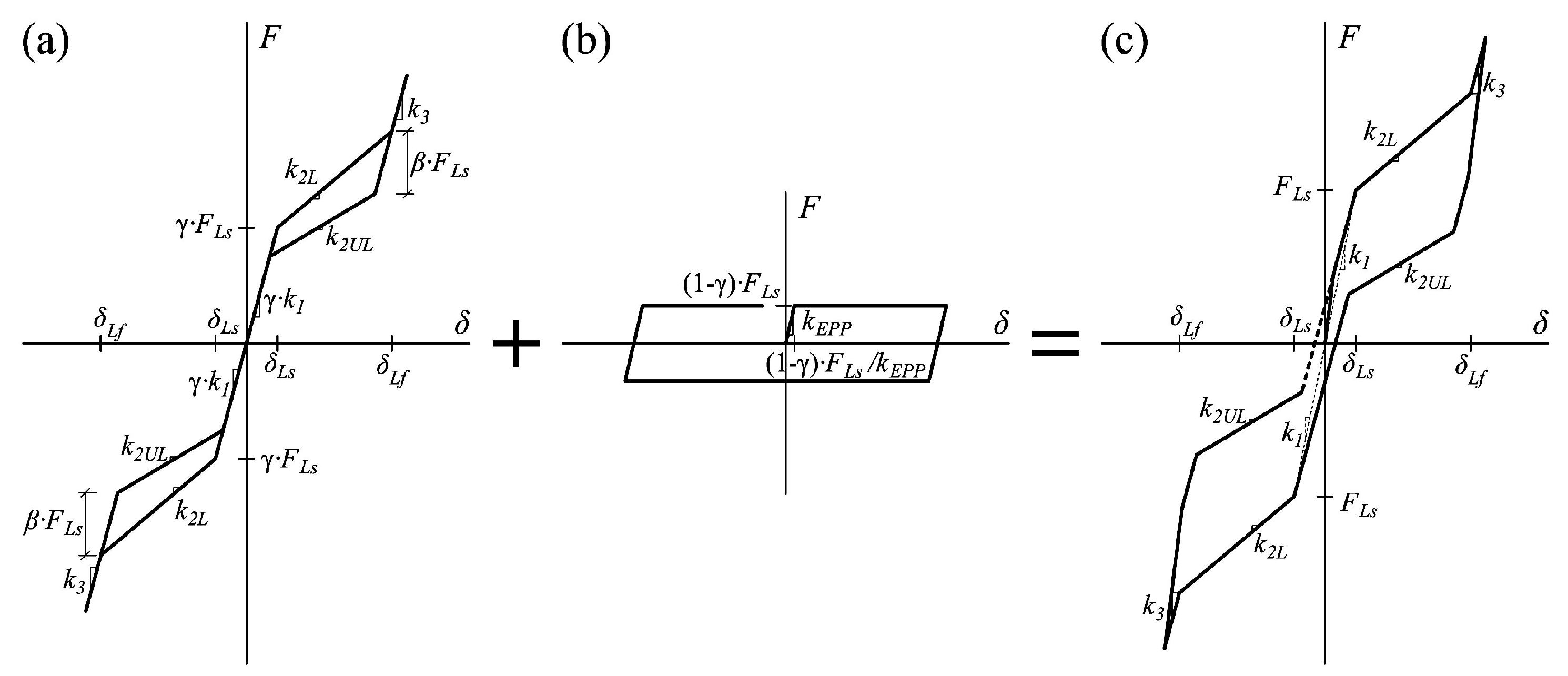
3. Numerical Characterization of the Hysteretic Behavior of NiTi Bars
4. Shake Table Tests of a Structure with NiTi Bars
4.1. Brace-Type NiTi Damper
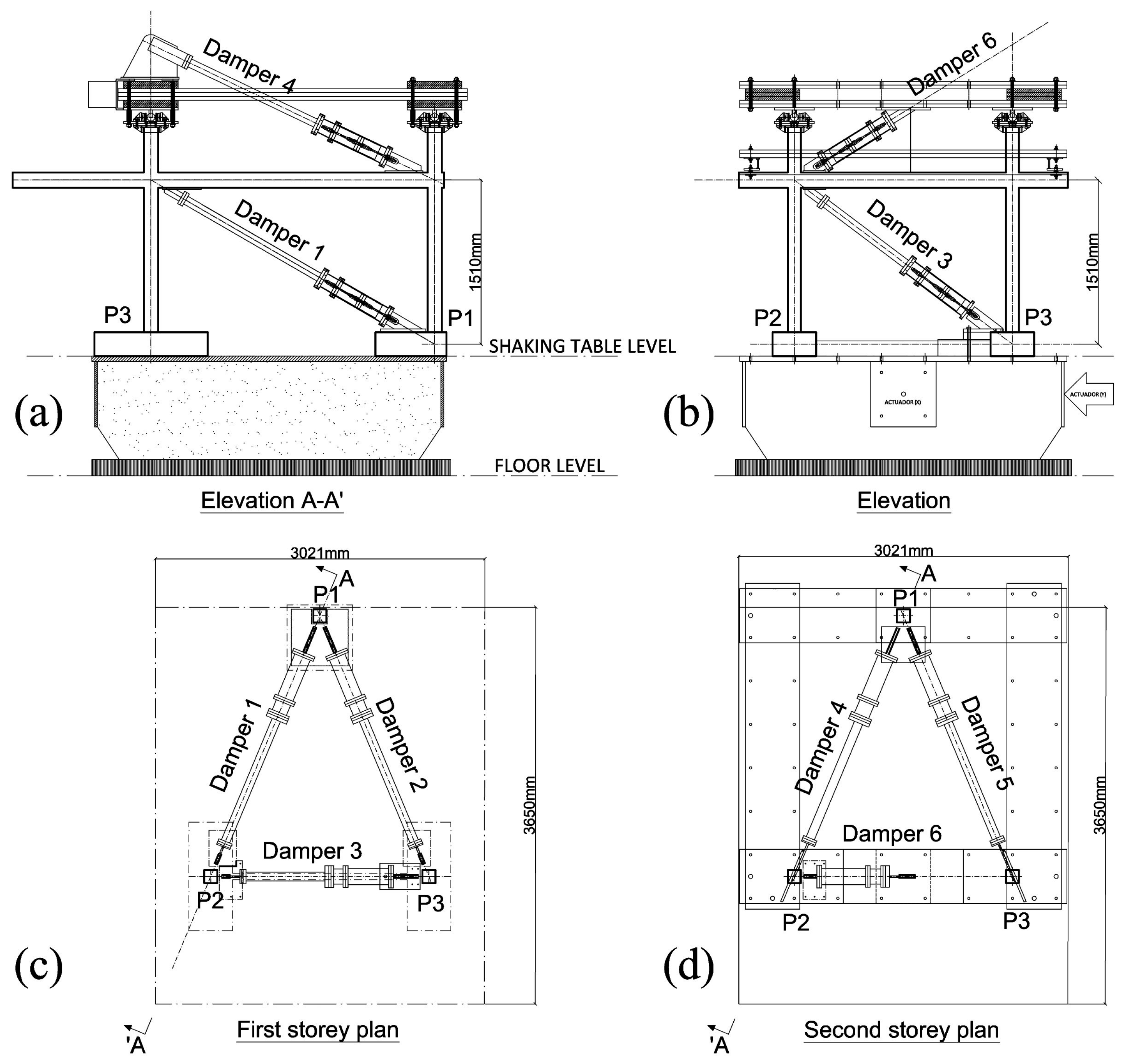
4.2. Test Specimen and Experimental Set up
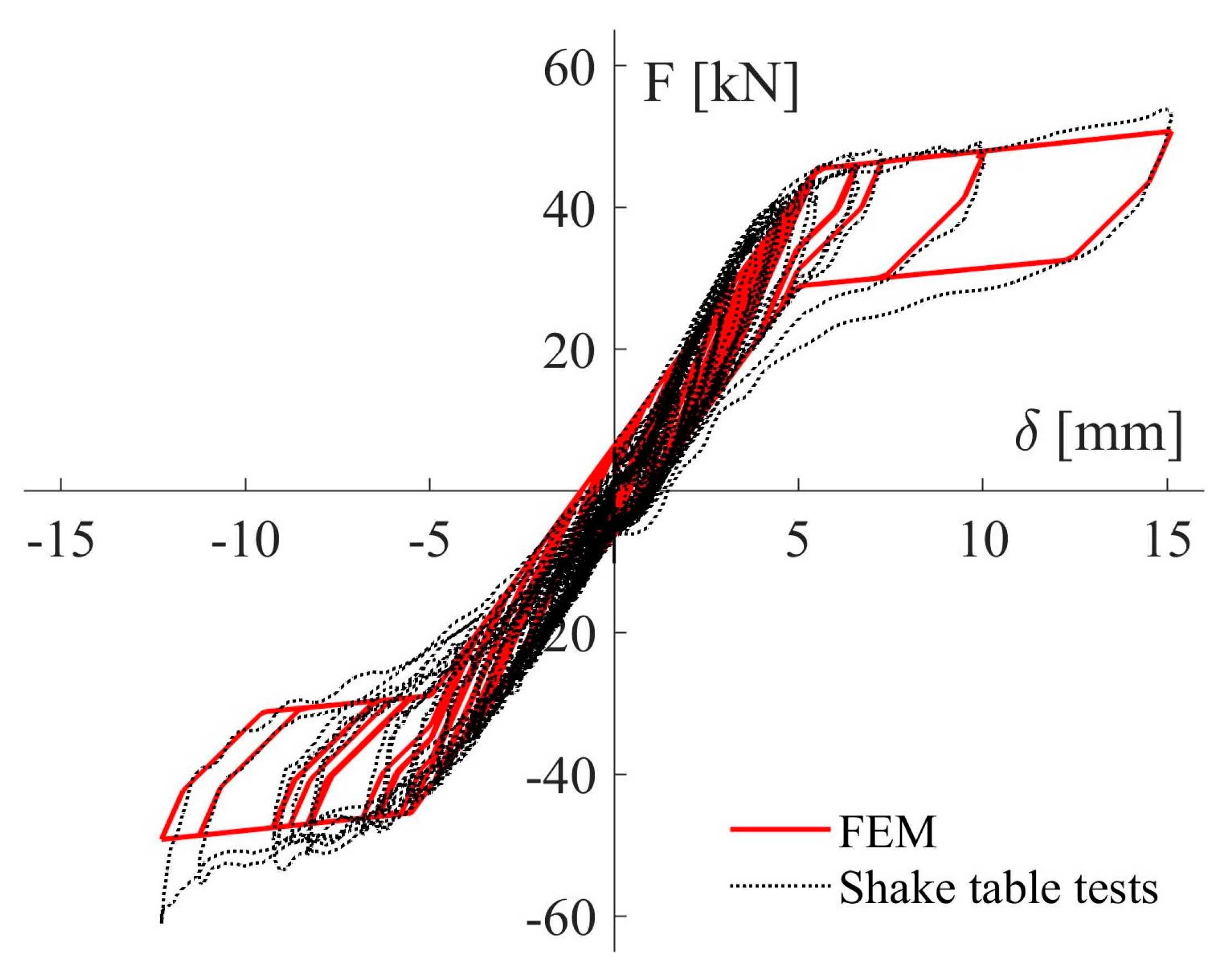
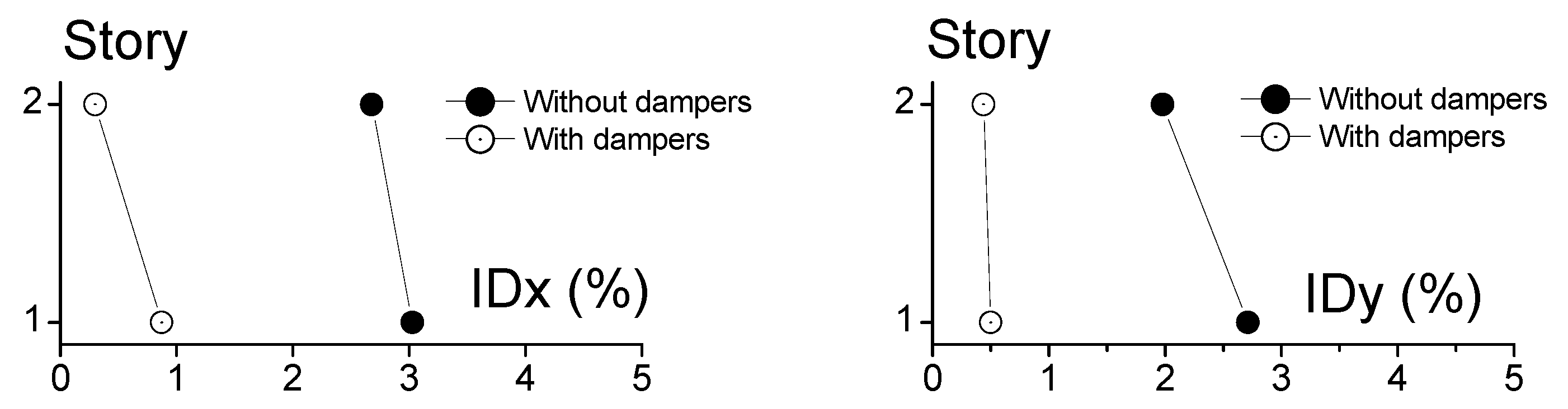
4.3. Seismic Tests and Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Dolce, M.; Cardone, D. Mechanical behaviour of shape memory alloys for seismic applications 1. Martensite and austenite NiTi bars subjected to torsion. Int. J. Mech. Sci. 2001, 43, 2631–2656. [Google Scholar] [CrossRef]
- Dolce, M.; Cardone, D. Mechanical behaviour of shape memory alloys for seismic applications 2. Austenite NiTi wires subjected to tension. Int. J. Mech. Sci. 2001, 43, 2657–2677. [Google Scholar] [CrossRef]
- DesRoches, R.; McCormick, J.; Delemont, M. Cyclic properties of superelastic shape memory alloy wires and bars. J. Struct. Eng.-ASCE 2004, 130, 38–46. [Google Scholar] [CrossRef]
- McCormick, J.; DesRoches, R.; Fugazza, D.; Auricchio, F. Seismic vibration control using superelastic shape memory alloys. J. Eng. Mater. Technol.-Trans. ASME. 2006, 128, 294–301. [Google Scholar] [CrossRef]
- McCormick, J.; Tyber, J.; DesRoches, R.; Gall, K.; Maier, H.J. Structural engineering with NiTi. II: Mechanical behavior and scaling. J. Eng. Mech.-ASCE 2007, 133, 1019–1029. [Google Scholar] [CrossRef]
- Tyber, J.; McCormick, J.; Gall, K.; DesRoches, R.; Maier, H.J.; Maksoud, A.E.A. Structural engineering with NiTi. 1: Basic materials characterization. J. Eng. Mech.-ASCE 2007, 133, 1009–1018. [Google Scholar] [CrossRef]
- Ozbulut, O.E.; Hurlebaus, S.; Desroches, R. Seismic response control using shape memory alloys: A review. J. Intell. Mater. Syst. Struct. 2011, 22, 1531–1549. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, H. High performance damage-resistant seismic resistant structural systems for sustainable and resilient city: A review. Shock Vibrat. 2018, 2018, 8703697. [Google Scholar] [CrossRef]
- Lagoudas, D.C. Shape Memory Alloys: Modeling and Engineering Applications; Springer: New York, NY, USA, 2008; pp. 6–7. [Google Scholar]
- Hartl, D.J.; Lagoudas, D.C. Aerospace applications of shape memory allows. J. Aerosp. Eng. 2007, 221, 535–552. [Google Scholar] [CrossRef]
- Chopra, A.K. Dynamics of Structures; Prentice Hall: Upper Saddle River, NJ, USA, 1995; Volume 3. [Google Scholar]
- Mahtabi, M.J.; Shamsaei, N.; Mitchell, M.R. Fatigue of nitinol: The state-of-the-art and ongoing challenges. J. Mech. Behav. Biomed. Mater. 2015, 50, 228–254. [Google Scholar] [CrossRef]
- Song, D.; Kang, G.; Kang, Q.; Yu, C.; Zhang, C. Experimental observations on uniaxial whole-life transformation ratchetting and low-cycle stress fatigue of super-elastic NiTi shape memory alloy micro-tubes. Smart Mater. Struct. 2015, 24, 075004. [Google Scholar] [CrossRef]
- Zhang, Y.; You, Y.; Moumni, Z.; Anlas, G.; Zhu, J.; Zhang, W. Experimental and theoretical investigation of the frequency effect on low cycle fatigue of shape memory alloys. Int. J. Plast. 2017, 90, 1–30. [Google Scholar] [CrossRef]
- Eggeler, G.; Hornbogen, E.; Yawny, A.; Heckmann, A.; Wagner, M. Structural and functional fatigue of NiTi shape memory alloys. Mater. Sci. Eng. A-Struct. Mater. Prop. Microstruct. Process. 2004, 378, 24–33. [Google Scholar] [CrossRef]
- Kimiecik, M.; Jones, J.W.; Daly, S. The effect of microstructure on stress-induced martensitic transformation under cyclic loading in the SMA nickel-titanium. J. Mech. Phys. Solids 2016, 89, 16–30. [Google Scholar] [CrossRef]
- Zhu, S.; Zhang, Y. Loading rate effect on superelastic SMA-based seismic response modification devices. Earthq. Struct. 2013, 4, 607–627. [Google Scholar] [CrossRef]
- Kan, Q.; Yu, C.; Kang, G.; Li, J.; Yan, W. Experimental observations on rate-dependent cyclic deformation of super-elastic NiTi shape memory alloy. Mech. Mater. 2016, 97, 48–58. [Google Scholar] [CrossRef]
- Ammar, O.; Haddar, N.; Dieng, L. Experimental investigation of the pseudoelastic behaviour of NiTi wires under strain- and stress-controlled cyclic tensile loadings. Intermetallics 2017, 81, 52–61. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Choi, J.-Y.; Guo, W.-G.; Isaacs, J.B. Very high strain-rate response of a NiTi shape-memory alloy. Mech. Mater. 2005, 37, 287–298. [Google Scholar] [CrossRef]
- Treadway, J.; Abolmaali, A.; Lu, F.; Aswath, P. Tensile and fatigue behavior of superelastic shape memory rods. Mater. Des. 2015, 86, 105–113. [Google Scholar] [CrossRef]
- Kang, G.; Song, D. Review on structural fatigue of NiTi shape memory alloys: Pure mechanical and thermo-mechanical ones. Theor. Appl. Mech. Lett. 2015, 5, 245–254. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, J.; Moumni, Z.; Van Herpen, A.; Zhang, W. Energy-based fatigue model for shape memory alloys including thermomechanical coupling. Smart Mater. Struct. 2016, 25, 035042. [Google Scholar] [CrossRef]
- Moumni, Z.; Van Herpen, A.; Riberty, P. Fatigue analysis of shape memory alloys: Energy approach. Smart Mater. Struct. 2005, 14, S287–S292. [Google Scholar] [CrossRef]
- Ikeda, T.; Nae, F.A.; Naito, H.; Matsuzaki, Y. Constitutive model of shape memory alloys for unidirectional loading considering inner hysteresis loops. Smart Mater. Struct. 2004, 13, 916–925. [Google Scholar] [CrossRef]
- Saleeb, A.F.; Padula II, S.A.; Kumar, A. A multi-axial, multimechanism based constitutive model for the comprehensive representation of the evolutionary response of SMAs under general thermomechanical loading conditions. Int. J. Plast. 2011, 27, 655–687. [Google Scholar] [CrossRef]
- Karakalas, A.A.; Machairas, T.T.; Solomou, A.G.; Saravanos, D.A. Modeling of partial transformation cycles of SMAs with a modified hardening function. Smart Mater. Struct. 2019, 28, 1–20. [Google Scholar] [CrossRef]
- Benavent-Climent, A.; Galé-Lamuela, D.; Donaire-Avila, J. Energy capacity and seismic performance of RC waffle-flat plate structures under two components of far-field ground motions: Shake table tests. Earthquake Eng. Struct. Dyn. 2019, 48, 949–969. [Google Scholar] [CrossRef]

| Reference | Frequency (Hz): ϕ (mm) | σy (MPa) | εy (%) | EA (MPa) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.02 | 1.0 | 0.02 | 1.0 | 0.02 | 1.0 | 0.02 | 1.0 | |||
| McCormick [4] | 0.25 | 504 | 553 | 1.83 | 1.79 | 275 | 309 | 1.12 | 1.00 | 0.89 |
| Zhu [17] | 0.58 | 305 | 309 | 1.22 | 1.12 | 250 | 275 | 2.10 | 1.48 | 0.71 |
| Dolce [2] | 1.84 | 390 | 415 | 1.40 | 1.25 | 279 | 332 | 1.00 | 0.83 | 0.84 |
| DesRoches [3] | 7.10 | 315 | 374 | 1.33 | 1.40 | 237 | 267 | 1.67 | 0.71 | 0.42 |
| McCormick [4] | 12.70 | 328 | 414 | 1.33 | 1.54 | 247 | 269 | 1.41 | 0.78 | 0.56 |
| This study | 12.70 | 245 | 359 | 1.12 | 1.39 | 219 | 258 | 1.78 | 1.11 | 0.62 |
| ε (%) | Nf | |||
|---|---|---|---|---|
| 4.0 | 124 | 1.17 | 106 | 0.73 |
| 4.0 | 112 | 1.17 | 96 | 0.73 |
| 2.5 | 260 | 0.52 | 500 | 0.32 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
González-Sanz, G.; Galé-Lamuela, D.; Escolano-Margarit, D.; Benavent-Climent, A. Hysteretic Behavior and Ultimate Energy Dissipation Capacity of Large Diameter Bars Made of Shape Memory Alloys under Seismic Loadings. Metals 2019, 9, 1099. https://doi.org/10.3390/met9101099
González-Sanz G, Galé-Lamuela D, Escolano-Margarit D, Benavent-Climent A. Hysteretic Behavior and Ultimate Energy Dissipation Capacity of Large Diameter Bars Made of Shape Memory Alloys under Seismic Loadings. Metals. 2019; 9(10):1099. https://doi.org/10.3390/met9101099
Chicago/Turabian StyleGonzález-Sanz, Guillermo, David Galé-Lamuela, David Escolano-Margarit, and Amadeo Benavent-Climent. 2019. "Hysteretic Behavior and Ultimate Energy Dissipation Capacity of Large Diameter Bars Made of Shape Memory Alloys under Seismic Loadings" Metals 9, no. 10: 1099. https://doi.org/10.3390/met9101099
APA StyleGonzález-Sanz, G., Galé-Lamuela, D., Escolano-Margarit, D., & Benavent-Climent, A. (2019). Hysteretic Behavior and Ultimate Energy Dissipation Capacity of Large Diameter Bars Made of Shape Memory Alloys under Seismic Loadings. Metals, 9(10), 1099. https://doi.org/10.3390/met9101099