Atomistic Study of the Role of Defects on α → ϵ Phase Transformations in Iron under Hydrostatic Compression
Abstract
1. Introduction
2. Materials and Methods
2.1. Interatomic Potentials
2.2. MD Simulation Setup
2.3. Monte Carlo Simulation Setup
2.4. Atomic Structure Identification
3. Results and Discussion
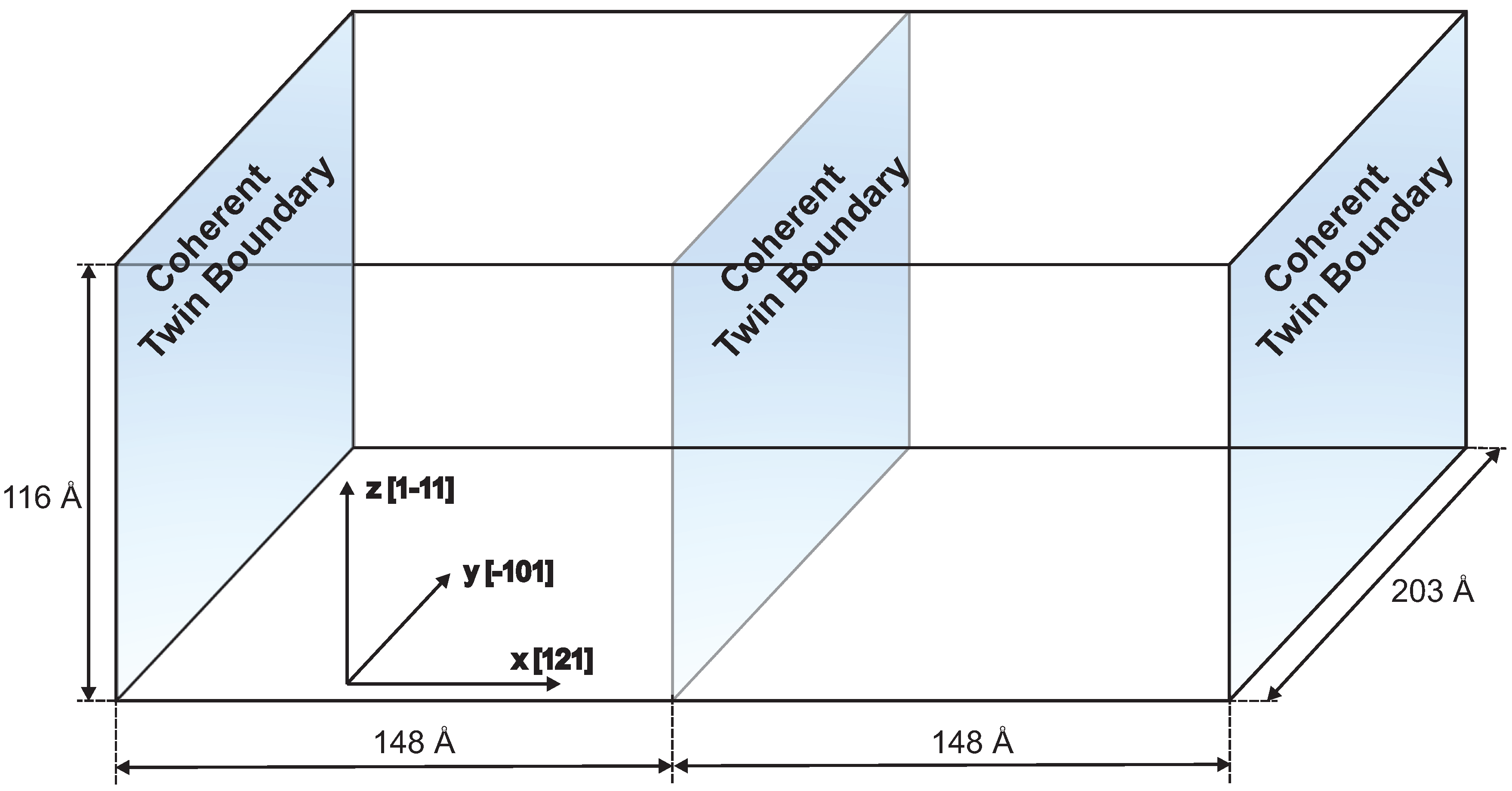
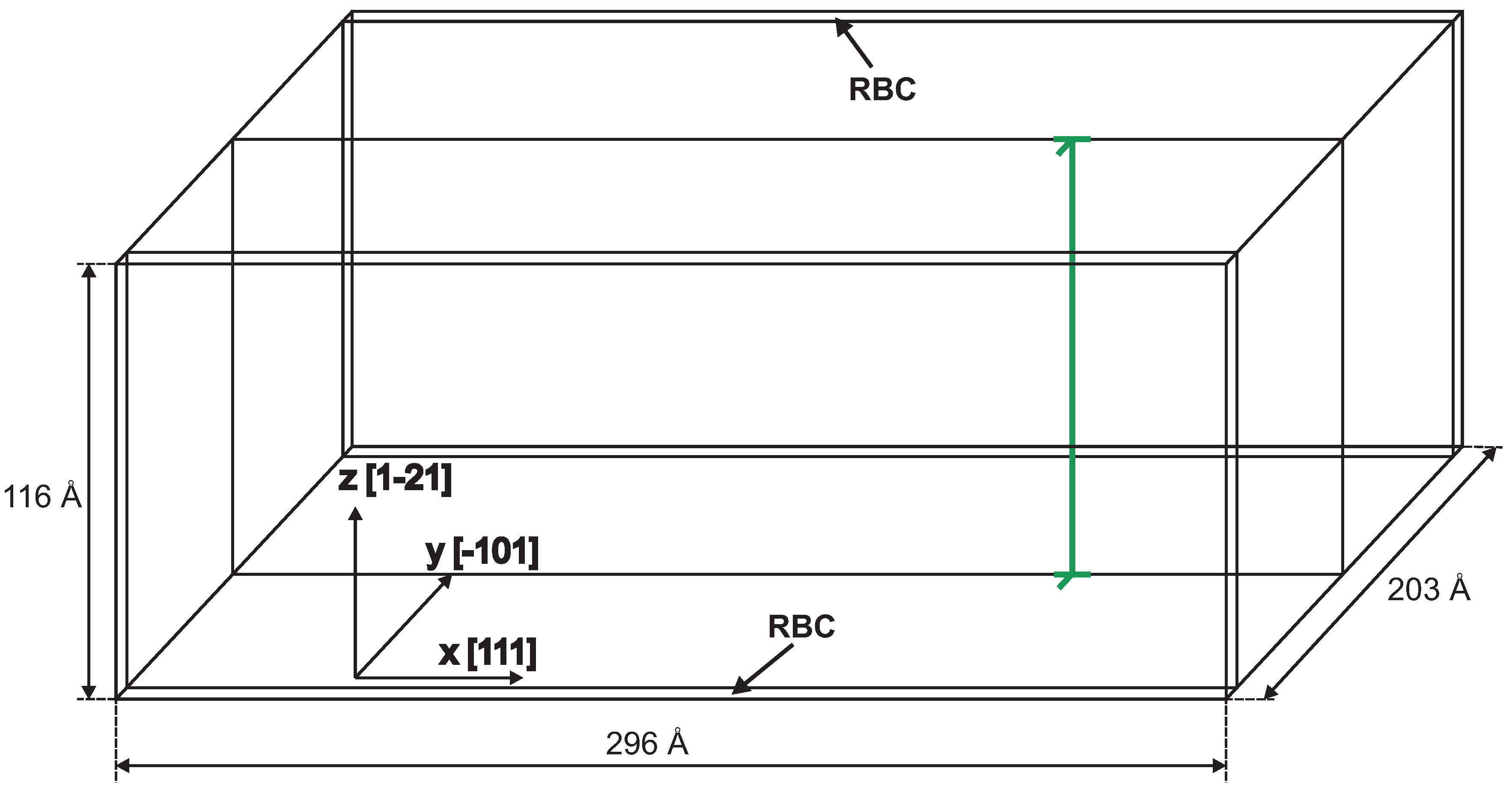
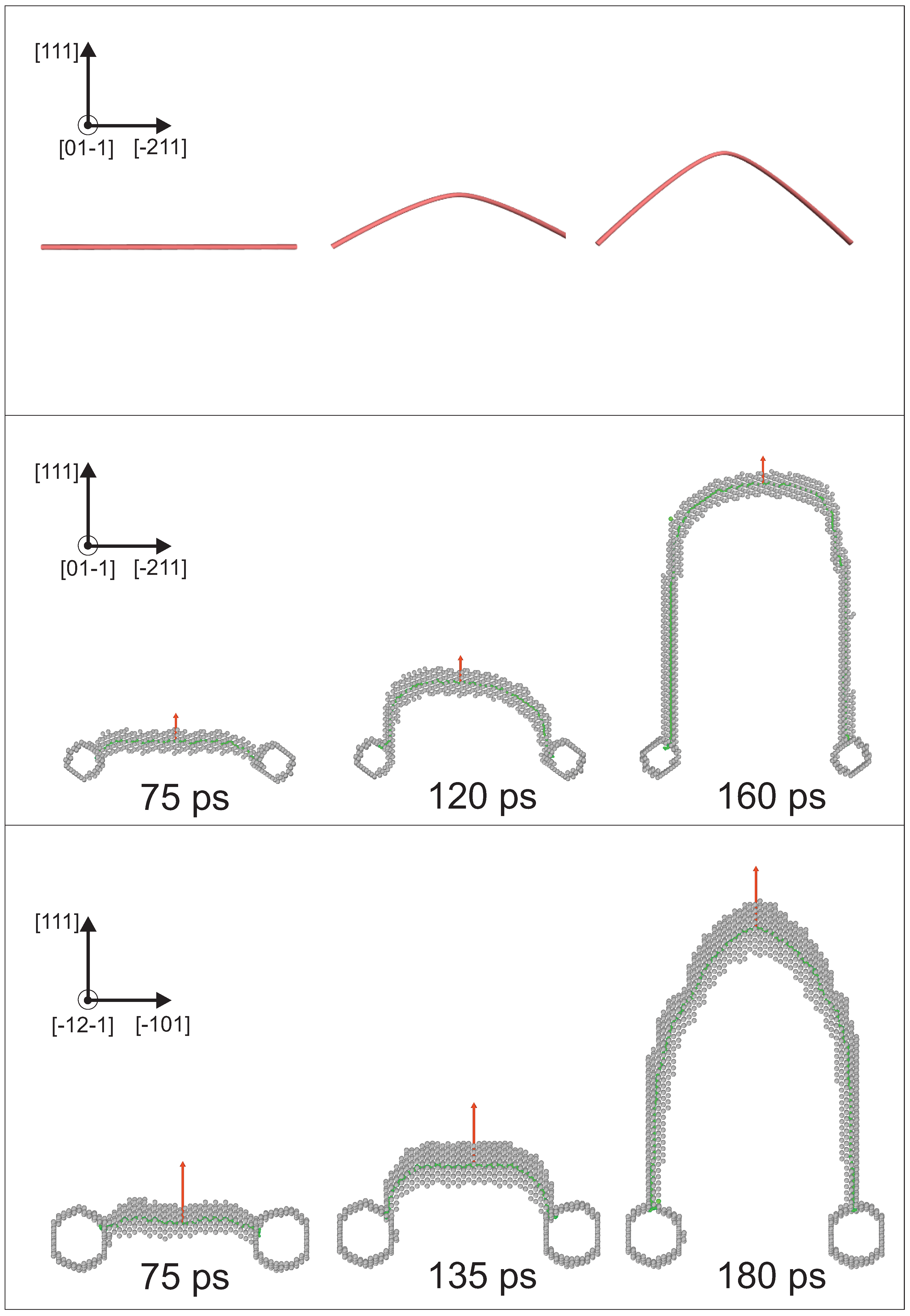
3.1. Frank–Read Source in bcc Iron
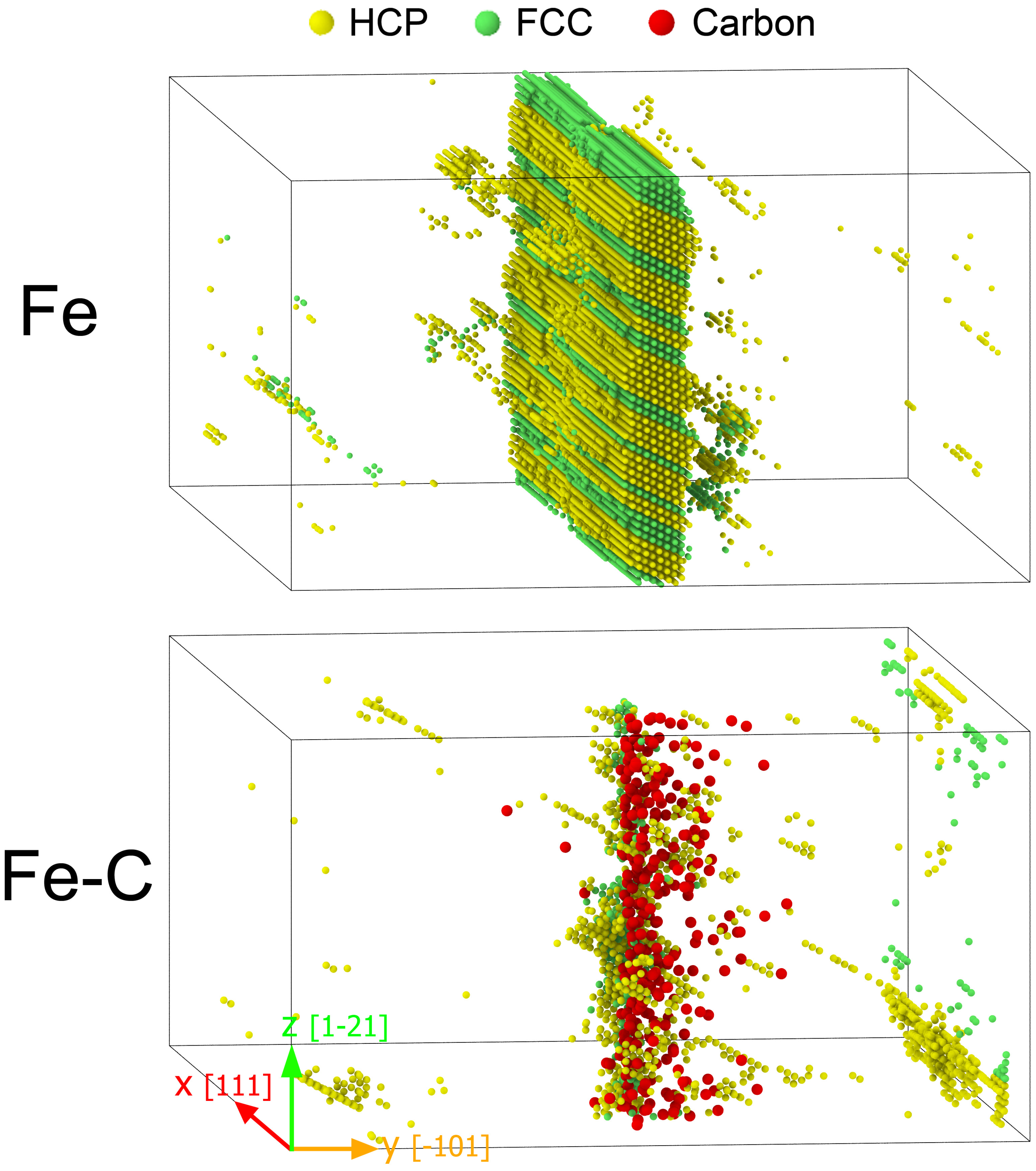
3.2. Pressure-Induced Phase Transformation
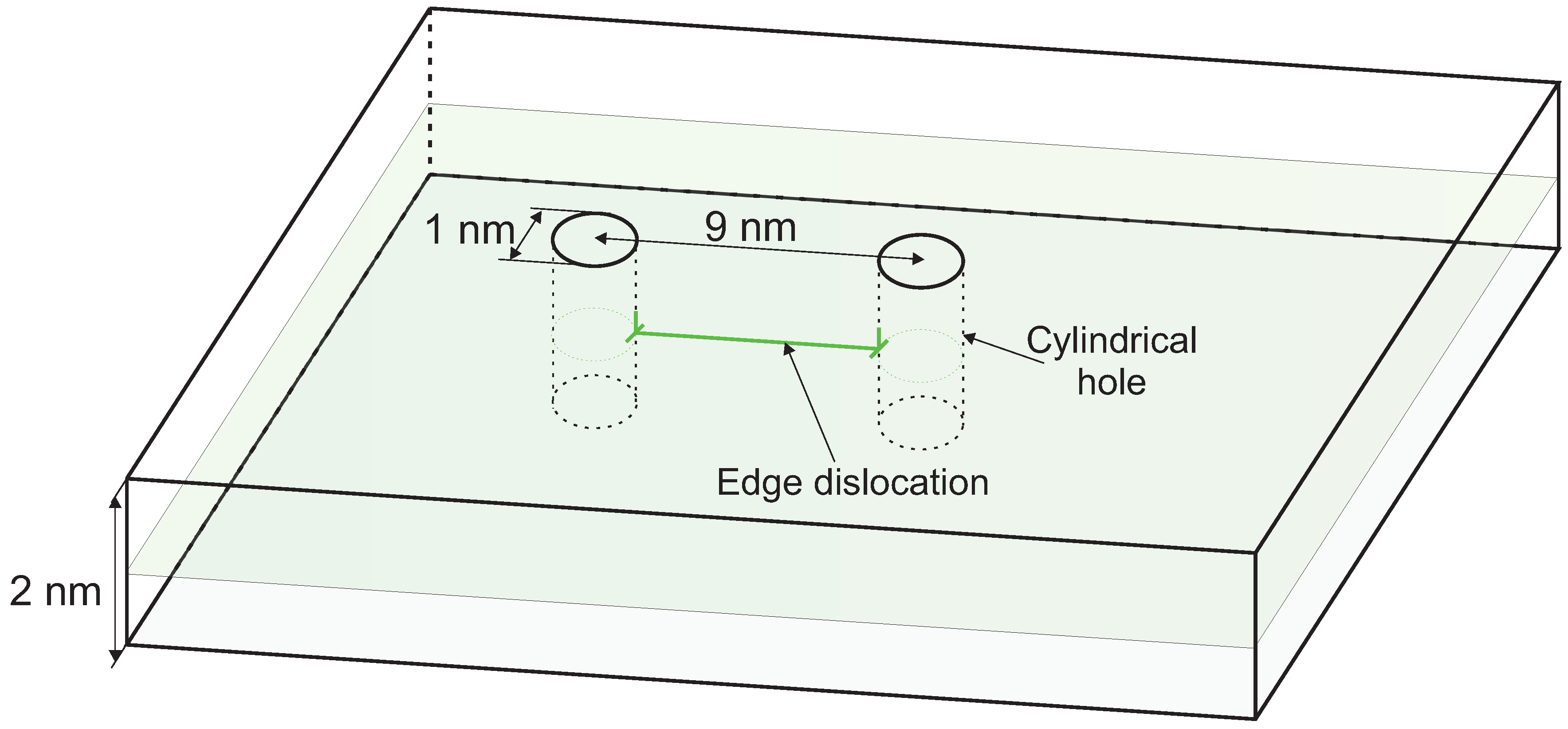
3.3. Edge Dislocation
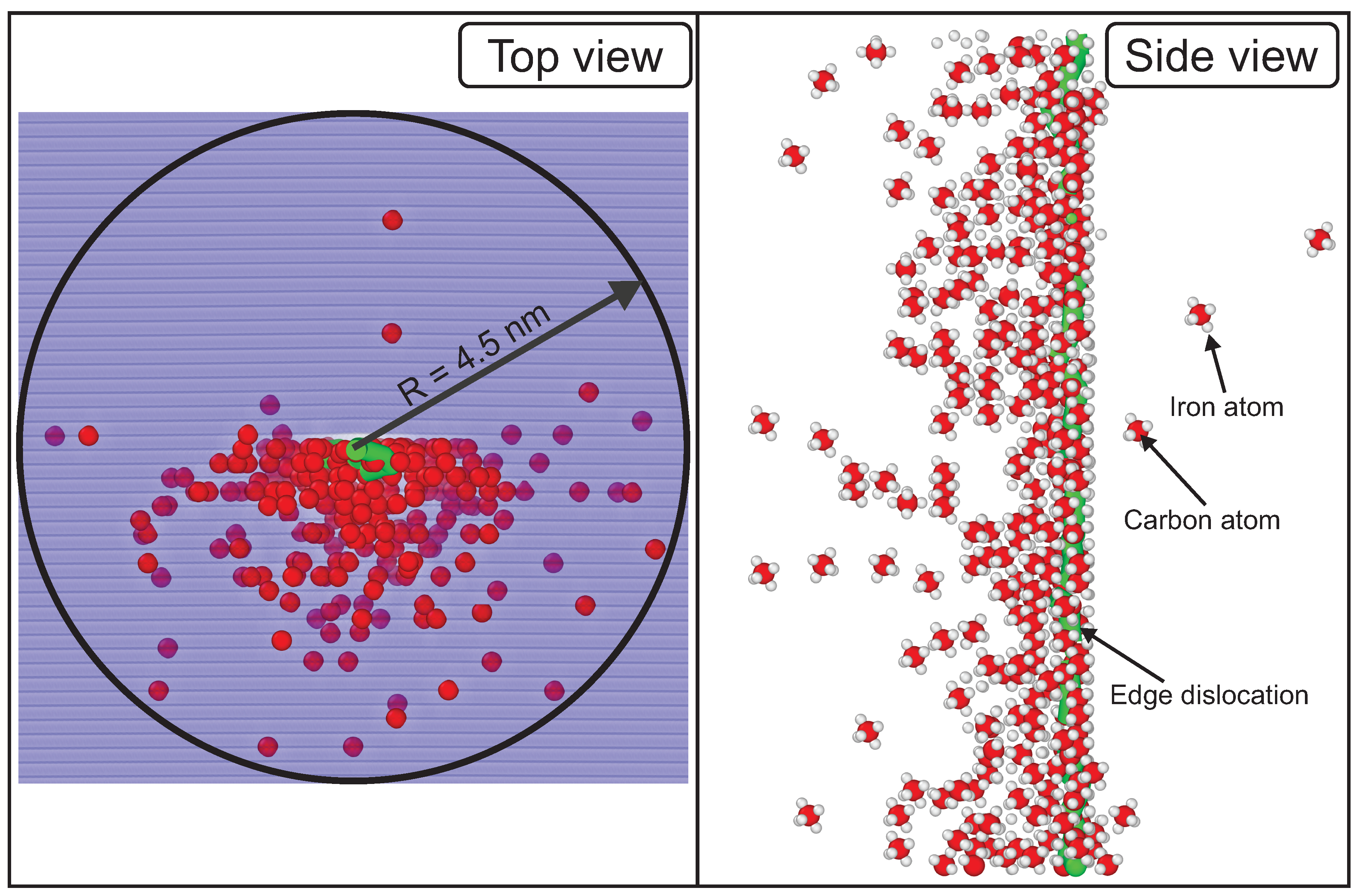
3.4. Cottrell Atmosphere
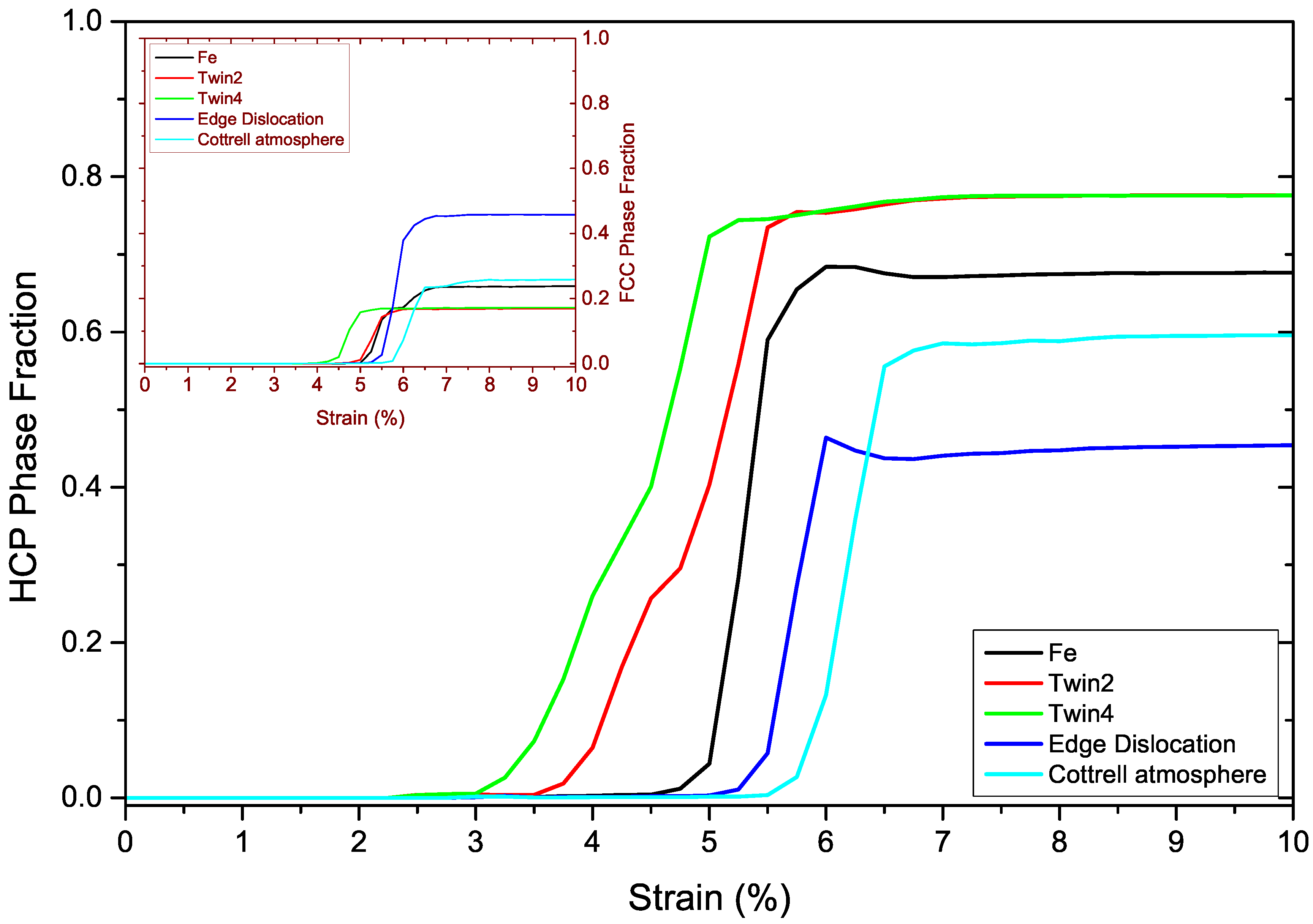
3.5. Comparison
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bancroft, D.; Peterson, E.L.; Minshall, S. Polymorphism of Iron at High Pressure. J. Appl. Phys. 1956, 27, 291–298. [Google Scholar] [CrossRef]
- Jamieson, J.C.; Lawson, A.W. X-ray Diffraction Studies in the 100 Kilobar Pressure Range. J. Appl. Phys. 1962, 33, 776–780. [Google Scholar] [CrossRef]
- Bassett, W.A.; Huang, E. Mechanism of the Body-Centered Cubic–Hexagonal Close-Packed Phase Transition in Iron. Science 1987, 238, 780–783. [Google Scholar] [CrossRef] [PubMed]
- Dewaele, A.; Denoual, C.; Anzellini, S.; Occelli, F.; Mezouar, M.; Cordier, P.; Merkel, S.; Véron, M.; Rausch, E. Mechanism of the α-ϵ phase transformation in iron. Phys. Rev. B 2015, 91, 174105. [Google Scholar] [CrossRef]
- Kadau, K. Microscopic View of Structural Phase Transitions Induced by Shock Waves. Science 2002, 296, 1681–1684. [Google Scholar] [CrossRef] [PubMed]
- Kalantar, D.H.; Belak, J.F.; Collins, G.W.; Colvin, J.D.; Davies, H.M.; Eggert, J.H.; Germann, T.C.; Hawreliak, J.; Holian, B.L.; Kadau, K.; et al. Direct Observation of the α-ϵ Transition in Shock-Compressed Iron via Nanosecond X-ray Diffraction. Phys. Rev. Lett. 2005, 95, 075502. [Google Scholar] [CrossRef] [PubMed]
- Boehler, R.; Santamaría-Pérez, D.; Errandonea, D.; Mezouar, M. Melting, density, and anisotropy of iron at core conditions: New x-ray measurements to 150 GPa. J. Phys. Conf. Ser. 2008, 121, 022018. [Google Scholar] [CrossRef]
- Sinmyo, R.; Hirose, K.; Ohishi, Y. Melting curve of iron to 290 GPa determined in a resistance-heated diamond-anvil cell. Earth Planet. Sci. Lett. 2019, 510, 45–52. [Google Scholar] [CrossRef]
- Gunkelmann, N.; Tramontina, D.R.; Bringa, E.M.; Urbassek, H.M. Morphological changes in polycrystalline Fe after compression and release. J. Appl. Phys. 2015, 117, 085901. [Google Scholar] [CrossRef]
- Ekman, M.; Sadigh, B.; Einarsdotter, K.; Blaha, P. Ab initio study of the martensitic bcc-hcp transformation in iron. Phys. Rev. B 1998, 58, 5296–5304. [Google Scholar] [CrossRef]
- Herper, H.C.; Hoffmann, E.; Entel, P. Ab initio full-potential study of the structural and magnetic phase stability of iron. Phys. Rev. B 1999, 60, 3839–3848. [Google Scholar] [CrossRef]
- Friák, M.; Šob, M. Ab initio study of the bcc-hcp transformation in iron. Phys. Rev. B 2008, 77, 174117. [Google Scholar] [CrossRef]
- Jafari, M.; Nobakhti, M.; Jamnezhad, H.; Bayati, K. Density functional theory study of the α → ω martensitic transformation in titanium induced by hydrostatic pressure. Condens. Matter Phys. 2013, 16, 33703. [Google Scholar] [CrossRef]
- Errandonea, D.; Meng, Y.; Somayazulu, M.; Häusermann, D. Pressure-induced α → ω transition in titanium metal: A systematic study of the effects of uniaxial stress. Phys. B Condens. Matter 2005, 355, 116–125. [Google Scholar] [CrossRef]
- Trinkle, D.R.; Hennig, R.G.; Srinivasan, S.G.; Hatch, D.M.; Jones, M.D.; Stokes, H.T.; Albers, R.C.; Wilkins, J.W. New Mechanism for the α to ω Martensitic Transformation in Pure Titanium. Phys. Rev. Lett. 2003, 91, 025701. [Google Scholar] [CrossRef]
- Friák, M.; Hickel, T.; Körmann, F.; Udyansky, A.; Dick, A.; von Pezold, J.; Ma, D.; Kim, O.; Counts, W.; Šob, M.; et al. Determining the Elasticity of Materials Employing Quantum-mechanical Approaches: From the Electronic Ground State to the Limits of Materials Stability. Steel Res. Int. 2011, 82, 86–100. [Google Scholar] [CrossRef]
- Fisher, J. Application of nucleation theory to isothermal martensite. Acta Metall. 1953, 1, 32–35. [Google Scholar] [CrossRef]
- Luu, H.T.; Gunkelmann, N. Pressure-induced phase transformations in Fe-C: Molecular dynamics approach. Comput. Mater. Sci. 2019, 162, 295–303. [Google Scholar] [CrossRef]
- Harrison, R.J.; Voter, A.F.; Chen, S.P. Atomistic Simulation of Materials: Beyond Pair Potentials; Number 1; A Division of Plenum Publishing Corporation: New York, NY, USA, 1994; pp. 281–286. [Google Scholar] [CrossRef]
- Gunkelmann, N.; Bringa, E.M.; Kang, K.; Ackland, G.J.; Ruestes, C.J.; Urbassek, H.M. Polycrystalline iron under compression: Plasticity and phase transitions. Phys. Rev. B 2012, 86, 144111. [Google Scholar] [CrossRef]
- Kadau, K.; Germann, T.C.; Lomdahl, P.S.; Holian, B.L. Atomistic simulations of shock-induced transformations and their orientation dependence in bcc Fe single crystals. Phys. Rev. B 2005, 72, 064120. [Google Scholar] [CrossRef]
- Kadau, K.; Germann, T.C.; Lomdahl, P.S.; Albers, R.C.; Wark, J.S.; Higginbotham, A.; Holian, B.L. Shock Waves in Polycrystalline Iron. Phys. Rev. Lett. 2007, 98, 135701. [Google Scholar] [CrossRef] [PubMed]
- Venables, J.A. The martensite transformation in stainless steel. Philos. Mag. J. Sci. 1962, 7, 35–44. [Google Scholar] [CrossRef]
- Yang, X.S.; Sun, S.; Wu, X.L.; Ma, E.; Zhang, T.Y. Dissecting the Mechanism of Martensitic Transformation via Atomic-Scale Observations. Sci. Rep. 2014, 4, 6141. [Google Scholar] [CrossRef] [PubMed]
- Veiga, R.G.A.; Perez, M.; Becquart, C.S.; Domain, C. Atomistic modeling of carbon Cottrell atmospheres in bcc iron. J. Phys. Condens. Matter 2012, 25, 025401. [Google Scholar] [CrossRef]
- Veiga, R.; Goldenstein, H.; Perez, M.; Becquart, C. Monte Carlo and molecular dynamics simulations of screw dislocation locking by Cottrell atmospheres in low carbon Fe–C alloys. Scr. Mater. 2015, 108, 19–22. [Google Scholar] [CrossRef]
- Queyreau, S.; Marian, J.; Gilbert, M.R.; Wirth, B.D. Edge dislocation mobilities in bcc Fe obtained by molecular dynamics. Phys. Rev. B 2011, 84, 064106. [Google Scholar] [CrossRef]
- Daw, M.S.; Foiles, S.M.; Baskes, M.I. The embedded-atom method: A review of theory and applications. Mater. Sci. Rep. 1993, 9, 251–310. [Google Scholar] [CrossRef]
- Gunkelmann, N.; Bringa, E.M.; Tramontina, D.R.; Ruestes, C.J.; Suggit, M.J.; Higginbotham, A.; Wark, J.S.; Urbassek, H.M. Shock waves in polycrystalline iron: Plasticity and phase transitions. Phys. Rev. B 2014, 89, 140102. [Google Scholar] [CrossRef]
- Gunkelmann, N.; Bringa, E.M.; Urbassek, H.M. Influence of phase transition on shock-induced spallation in nanocrystalline iron. J. Appl. Phys. 2015, 118, 185902. [Google Scholar] [CrossRef]
- Amadou, N.; de Resseguier, T.; Dragon, A.; Brambrink, E. Coupling between plasticity and phase transition in shock- and ramp-compressed single-crystal iron. Phys. Rev. B 2018, 98, 024104. [Google Scholar] [CrossRef]
- Hepburn, D.J.; Ackland, G.J. Metallic-covalent interatomic potential for carbon in iron. Phys. Rev. B 2008, 78, 165115. [Google Scholar] [CrossRef]
- Tschopp, M.A.; Solanki, K.N.; Gao, F.; Sun, X.; Khaleel, M.A.; Horstemeyer, M.F. Probing grain boundary sink strength at the nanoscale: Energetics and length scales of vacancy and interstitial absorption by grain boundaries in α-Fe. Phys. Rev. B 2012, 85, 064108. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Osetsky, Y.N.; Bacon, D.J. An atomic-level model for studying the dynamics of edge dislocations in metals. Model. Simul. Mater. Sci. Eng. 2003, 11, 427–446. [Google Scholar] [CrossRef]
- Bacon, D.; Osetsky, Y.; Rodney, D. Dislocation–Obstacle Interactions at the Atomic Level. In Dislocations in Solids; Elsevier: Amsterdam, The Netherlands, 2009; Chapter 88; pp. 1–90. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Vo, N.Q.; Averback, R.S.; Bellon, P.; Caro, A. Limits of hardness at the nanoscale: Molecular dynamics simulations. Phys. Rev. B 2008, 78, 241402. [Google Scholar] [CrossRef]
- Waseda, O.; Veiga, R.G.A.; Morthomas, J.; Chantrenne, P.; Becquart, C.S.; Ribeiro, F.; Jelea, A.; Goldenstein, H.; Perez, M. Formation of carbon Cottrell atmospheres and their effect on the stress field around an edge dislocation. Scr. Mat. 2016, 129, 16–19. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Nelson, D.R.; Ronchetti, M. Bond-orientational order in liquids and glasses. Phys. Rev. B 1983, 28, 784–805. [Google Scholar] [CrossRef]
- Honeycutt, J.D.; Andersen, H.C. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters. J. Phys. Chem. 1987, 91, 4950–4963. [Google Scholar] [CrossRef]
- Kelchner, C.L.; Plimpton, S.J.; Hamilton, J.C. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085–11088. [Google Scholar] [CrossRef]
- Ackland, G.J.; Jones, A.P. Applications of local crystal structure measures in experiment and simulation. Phys. Rev. B 2006, 73, 054104. [Google Scholar] [CrossRef]
- Stukowski, A. Structure identification methods for atomistic simulations of crystalline materials. Model. Simul. Mater. Sci. Eng. 2012, 20, 045021. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2009, 18, 015012. [Google Scholar] [CrossRef]
- de Koning, M.; Cai, W.; Bulatov, V.V. Anomalous Dislocation Multiplication in FCC Metals. Phys. Rev. Lett. 2003, 91, 025503. [Google Scholar] [CrossRef]
- Shimokawa, T.; Kitada, S. Dislocation Multiplication from the Frank-Read Source in Atomic Models. Mater. Trans. 2014, 55, 58–63. [Google Scholar] [CrossRef]
- Li, X.Y.; Yang, W. Atomistic simulations for the evolution of a U-shaped dislocation in fcc Al. Phys. Rev. B 2006, 74, 144108. [Google Scholar] [CrossRef]
- Tsuru, T.; Aoyagi, Y.; Kaji, Y.; Shimokawa, T. Influence of Competition between Intragranular Dislocation Nucleation and Intergranular Slip Transfer on Mechanical Properties of Ultrafine-Grained Metals. Mater. Trans. 2013, 54, 1580–1586. [Google Scholar] [CrossRef]
- Fitzgerald, S.P.; Aubry, S.; Dudarev, S.L.; Cai, W. Dislocation dynamics simulation of Frank-Read sources in anisotropic α-Fe. Model. Simul. Mater. Sci. Eng. 2012, 20, 045022. [Google Scholar] [CrossRef]
- Po, G.; Cui, Y.; Rivera, D.; Cereceda, D.; Swinburne, T.D.; Marian, J.; Ghoniem, N. A phenomenological dislocation mobility law for bcc metals. Acta Mater. 2016, 119, 123–135. [Google Scholar] [CrossRef]
- Po, G.; Ghoniem, N. A variational formulation of constrained dislocation dynamics coupled with heat and vacancy diffusion. J. Mech. Phys. Solids 2014, 66, 103–116. [Google Scholar] [CrossRef]
- Domain, C.; Monnet, G. Simulation of Screw Dislocation Motion in Iron by Molecular Dynamics Simulations. Phys. Rev. Lett. 2005, 95, 215506. [Google Scholar] [CrossRef]
- Vitek, V.; Smith, D.A.; Pond, R.C. Structure of tilt grain boundaries in b.c.c. metals. Philos. Mag. A 1980, 41, 649–663. [Google Scholar] [CrossRef]
- Hahn, E.N.; Fensin, S.J.; Germann, T.C.; Meyers, M.A. Symmetric tilt boundaries in body-centered cubic tantalum. Scr. Mater. 2016, 116, 108–111. [Google Scholar] [CrossRef]
- Forbes, J.W. Shock Wave Compression of Condensed Matter; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar] [CrossRef]
- Burgers, W. On the process of transition of the cubic-body-centered modification into the hexagonal-close-packed modification of zirconium. Physica 1934, 1, 561–586. [Google Scholar] [CrossRef]
- Wang, F.M.; Ingalls, R. Iron bcc-hcp transition: Local structure from x-ray-absorption fine structure. Phys. Rev. B 1998, 57, 5647–5654. [Google Scholar] [CrossRef]
- Meyers, M.; Jarmakani, H.; Bringa, E.; Remington, B. Chapter 89 Dislocations in Shock Compression and Release. In Dislocations in Solids; Elsevier: Amsterdam, The Netherlands, 2009; pp. 91–197. [Google Scholar] [CrossRef]
- Turneaure, S.J.; Renganathan, P.; Winey, J.; Gupta, Y. Twinning and Dislocation Evolution during Shock Compression and Release of Single Crystals: Real-Time X-ray Diffraction. Phys. Rev. Lett. 2018, 120, 265503. [Google Scholar] [CrossRef]
- Meyers, M.A.; Murr, L.E. (Eds.) Shock Waves and High-Strain-Rate Phenomena in Metals; Springer US: New York, NY, USA, 1981. [Google Scholar] [CrossRef]
- Vítek, V. Dissociation of Dislocations on {110} Planes in Anisotropie B.C.C. Metals. Phys. Status Solidi B 1966, 15, 557–566. [Google Scholar] [CrossRef]
- Kuznetsov, A.; Gornostyrev, Y.; Katsnelson, M.; Trefilov, A. Effect of the dislocations on the kinetics of a martensitic transition. Mater. Sci. Eng. A 2001, 309–310, 168–172. [Google Scholar] [CrossRef]
- Cohen, J.; Hinton, R.; Lay, K.; Sass, S. Partial dislocations on the {110} planes in the b.c.c. lattice. Acta Metall. 1962, 10, 894–895. [Google Scholar] [CrossRef]
- Clouet, E.; Garruchet, S.; Nguyen, H.; Perez, M.; Becquart, C.S. Dislocation interaction with C in α-Fe: A comparison between atomic simulations and elasticity theory. Acta Mater. 2008, 56, 3450–3460. [Google Scholar] [CrossRef]
- Wilde, J.; Cerezo, A.; Smith, G.D.W. Three-dimensional atomic-scale mapping of a Cottrell atmosphere around a dislocation in iron. Scr. Mater. 2000, 43, 39–48. [Google Scholar] [CrossRef]
- Grujicic, M.; Olson, G.B. Dynamics of Martensitic Interfaces. Interface Sci. 1998, 6, 155–164. [Google Scholar] [CrossRef]
- Smith, R.F.; Eggert, J.H.; Swift, D.C.; Wang, J.; Duffy, T.S.; Braun, D.G.; Rudd, R.E.; Reisman, D.B.; Davis, J.P.; Knudson, M.D.; et al. Time-dependence of the alpha to epsilon phase transformation in iron. J. Appl. Phys. 2013, 114, 223507. [Google Scholar] [CrossRef]
- Shao, J.L.; Wang, P.; Zhang, F.G.; He, A.M. Hcp/fcc nucleation in bcc iron under different anisotropic compressions at high strain rate: Molecular dynamics study. Sci. Rep. 2018, 8, 7650. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luu, H.-T.; Veiga, R.G.A.; Gunkelmann, N. Atomistic Study of the Role of Defects on α → ϵ Phase Transformations in Iron under Hydrostatic Compression. Metals 2019, 9, 1040. https://doi.org/10.3390/met9101040
Luu H-T, Veiga RGA, Gunkelmann N. Atomistic Study of the Role of Defects on α → ϵ Phase Transformations in Iron under Hydrostatic Compression. Metals. 2019; 9(10):1040. https://doi.org/10.3390/met9101040
Chicago/Turabian StyleLuu, Hoang-Thien, Roberto G. A. Veiga, and Nina Gunkelmann. 2019. "Atomistic Study of the Role of Defects on α → ϵ Phase Transformations in Iron under Hydrostatic Compression" Metals 9, no. 10: 1040. https://doi.org/10.3390/met9101040
APA StyleLuu, H.-T., Veiga, R. G. A., & Gunkelmann, N. (2019). Atomistic Study of the Role of Defects on α → ϵ Phase Transformations in Iron under Hydrostatic Compression. Metals, 9(10), 1040. https://doi.org/10.3390/met9101040





