Weld Seam Geometry and Electrical Resistance of Laser-Welded, Aluminum-Copper Dissimilar Joints Produced with Spatial Beam Oscillation
Abstract
:1. Introduction
- (1)
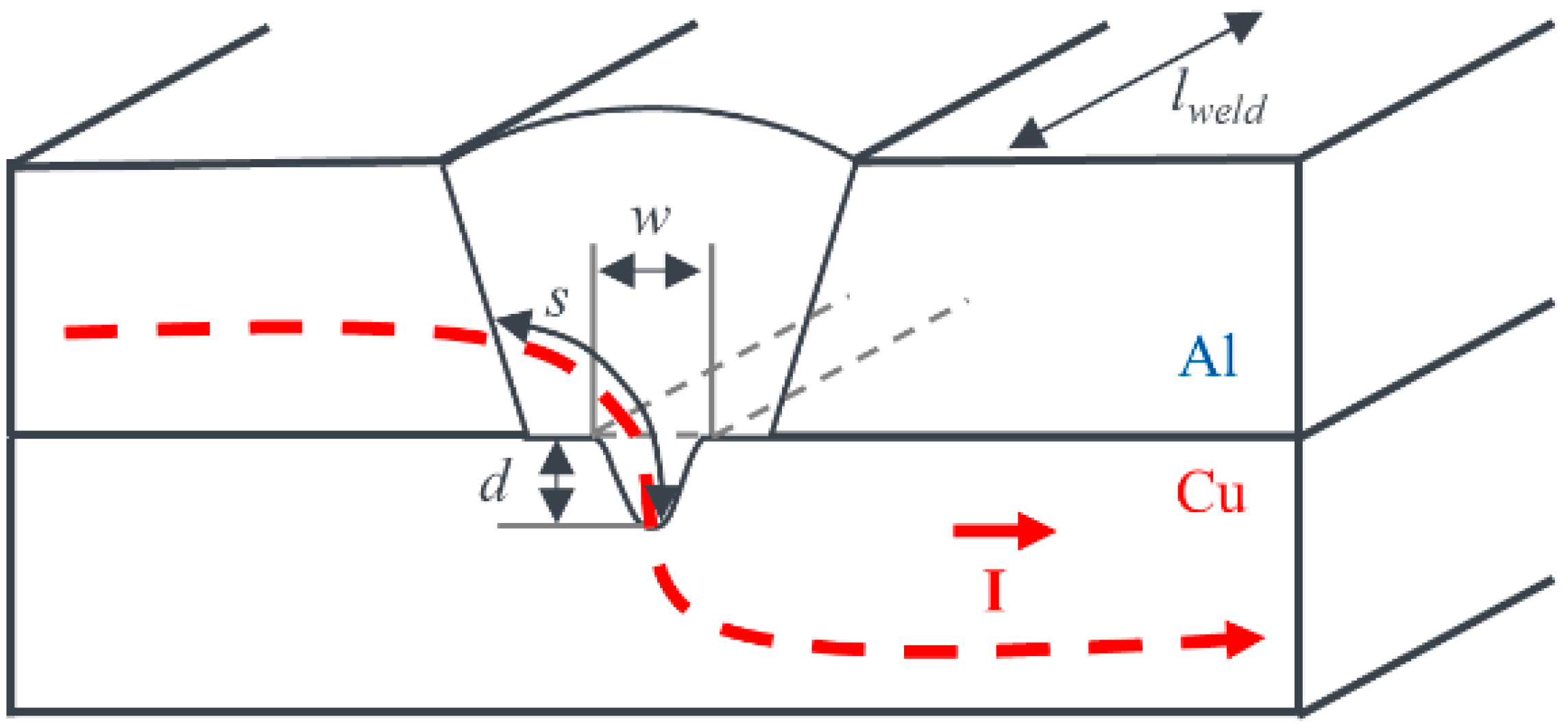
- the seam width at the interface between the sheets,
- (2)
- the metallurgical composition of the weld seam,
- (3)
- the constancy of the geometrical properties of the weld seam along the welding direction,
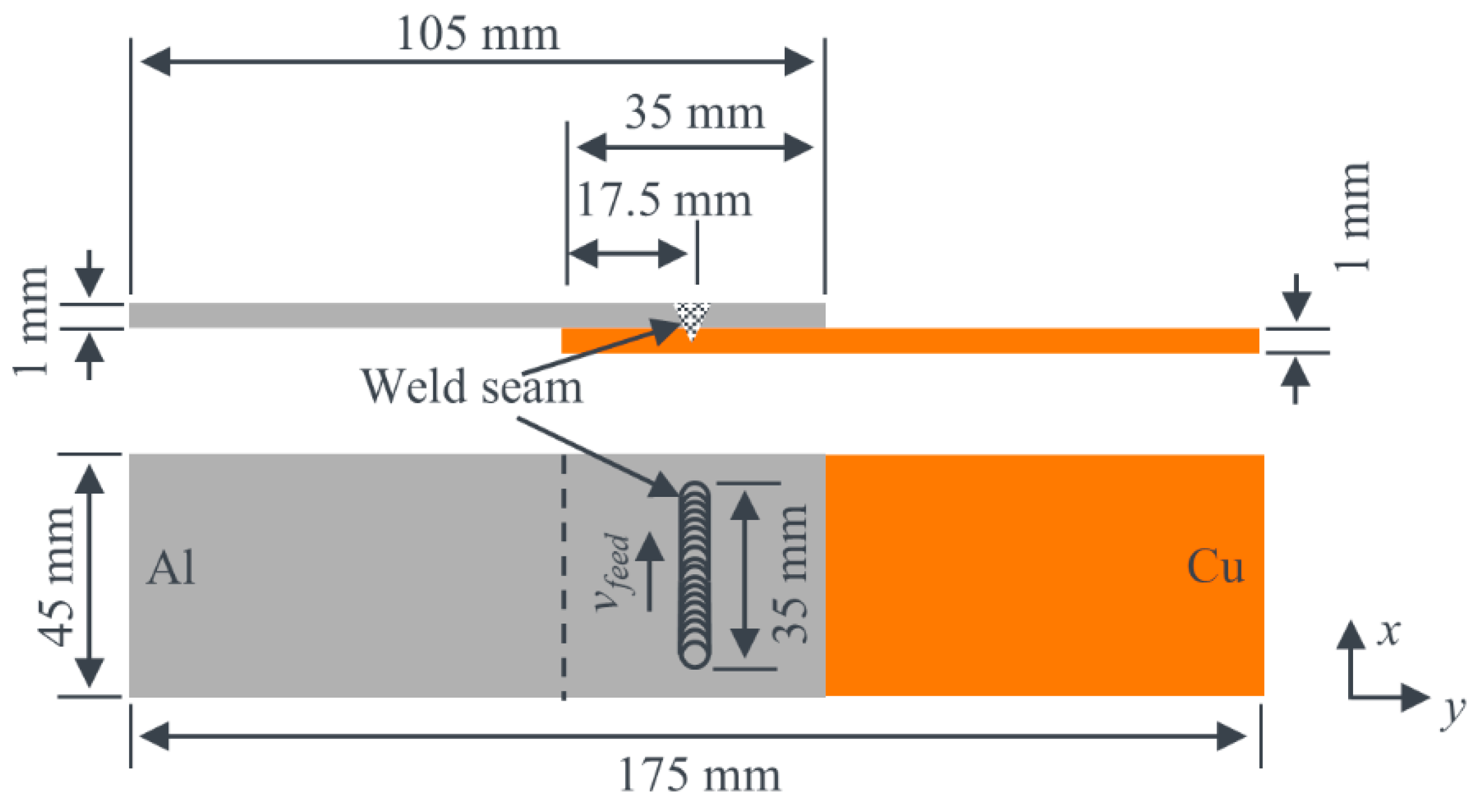
2. Materials and Methods
2.1. Experimental Setup
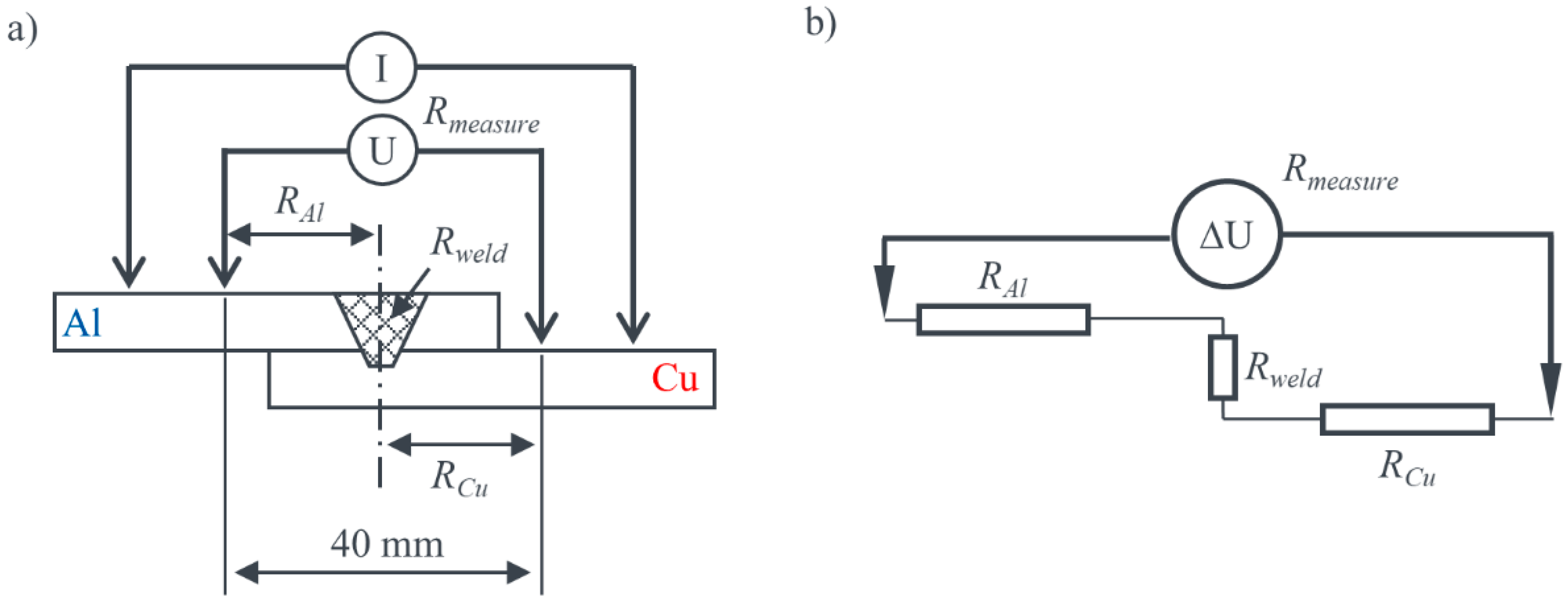
2.2. Evaluation Procedure and Basic Considerations
3. Results
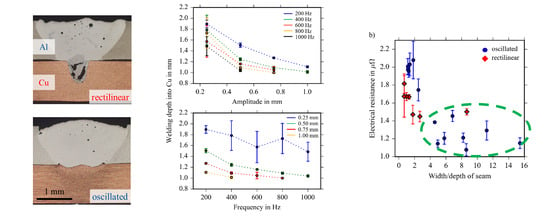
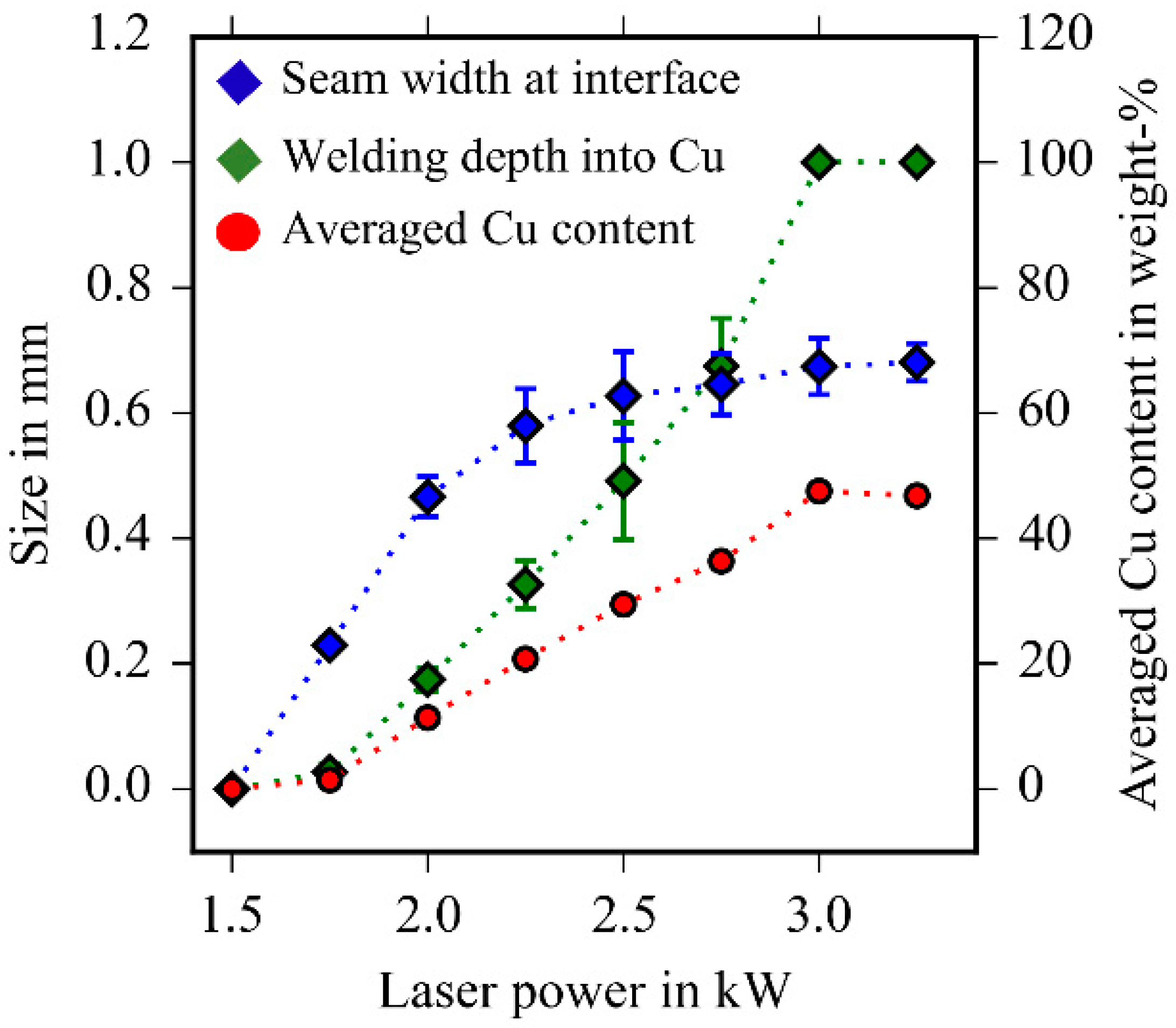
3.1. Welding Without Spatial Oscillation of the Laser Beam
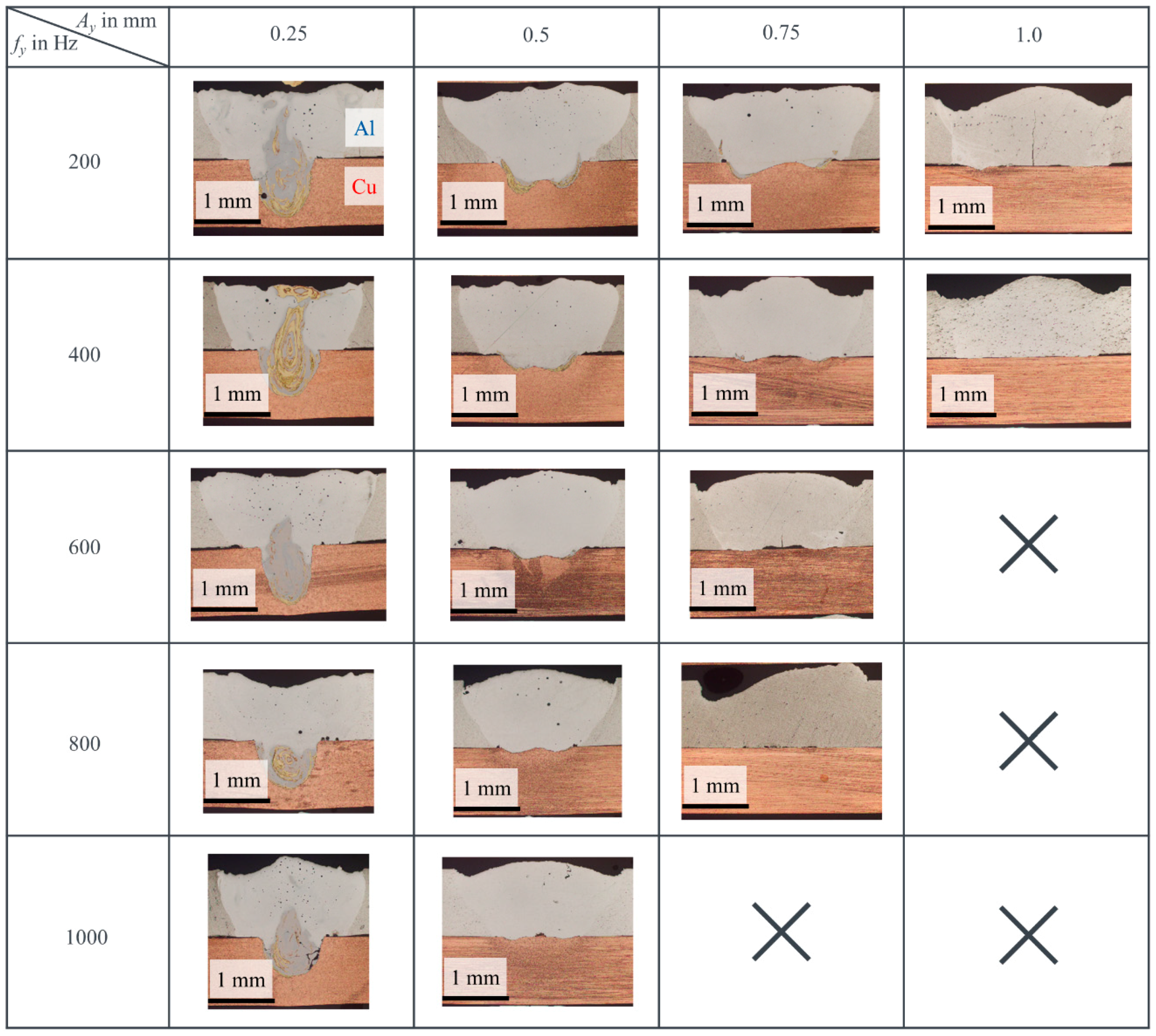
3.2. Welding with Spatial Oscillation of the Laser Beam
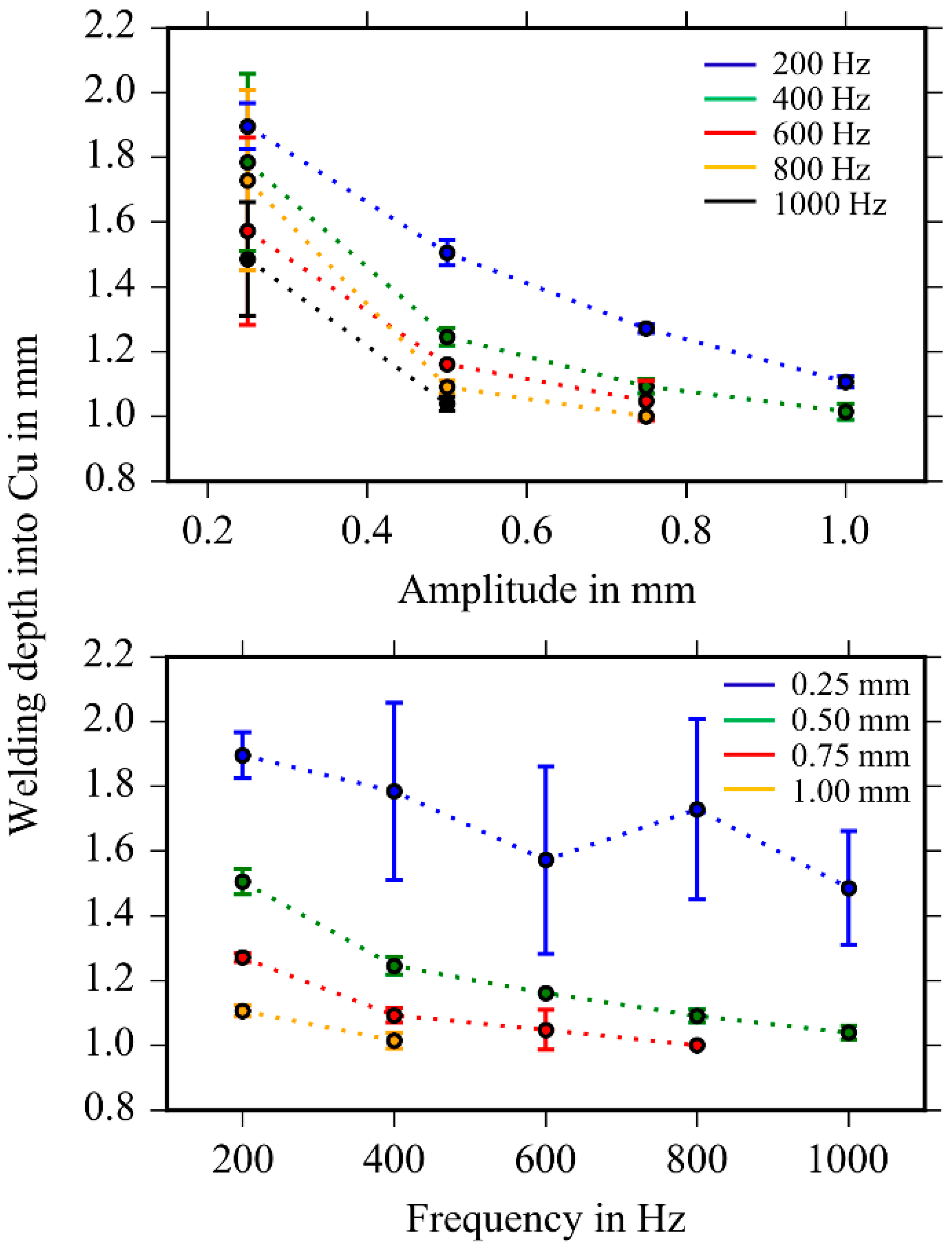
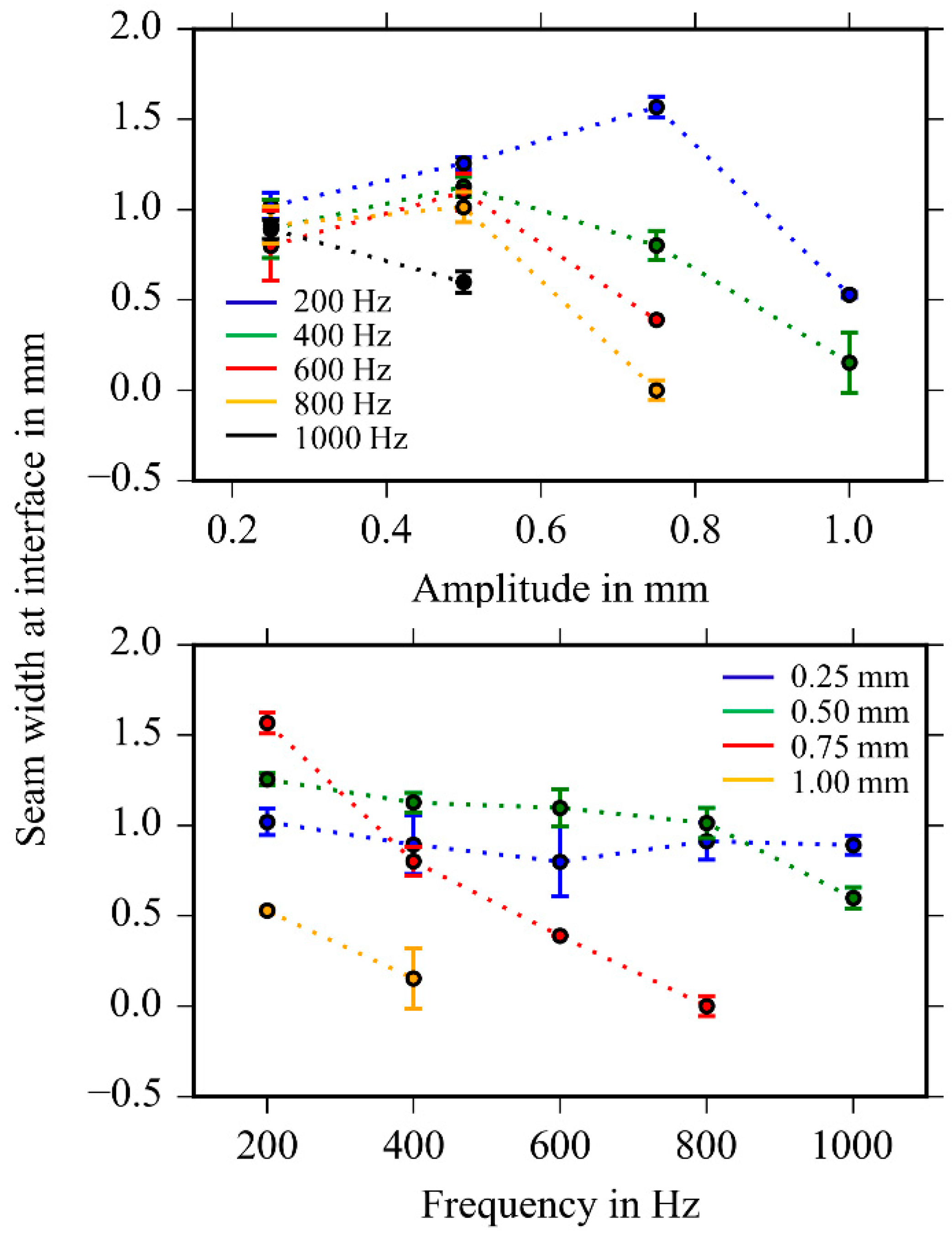
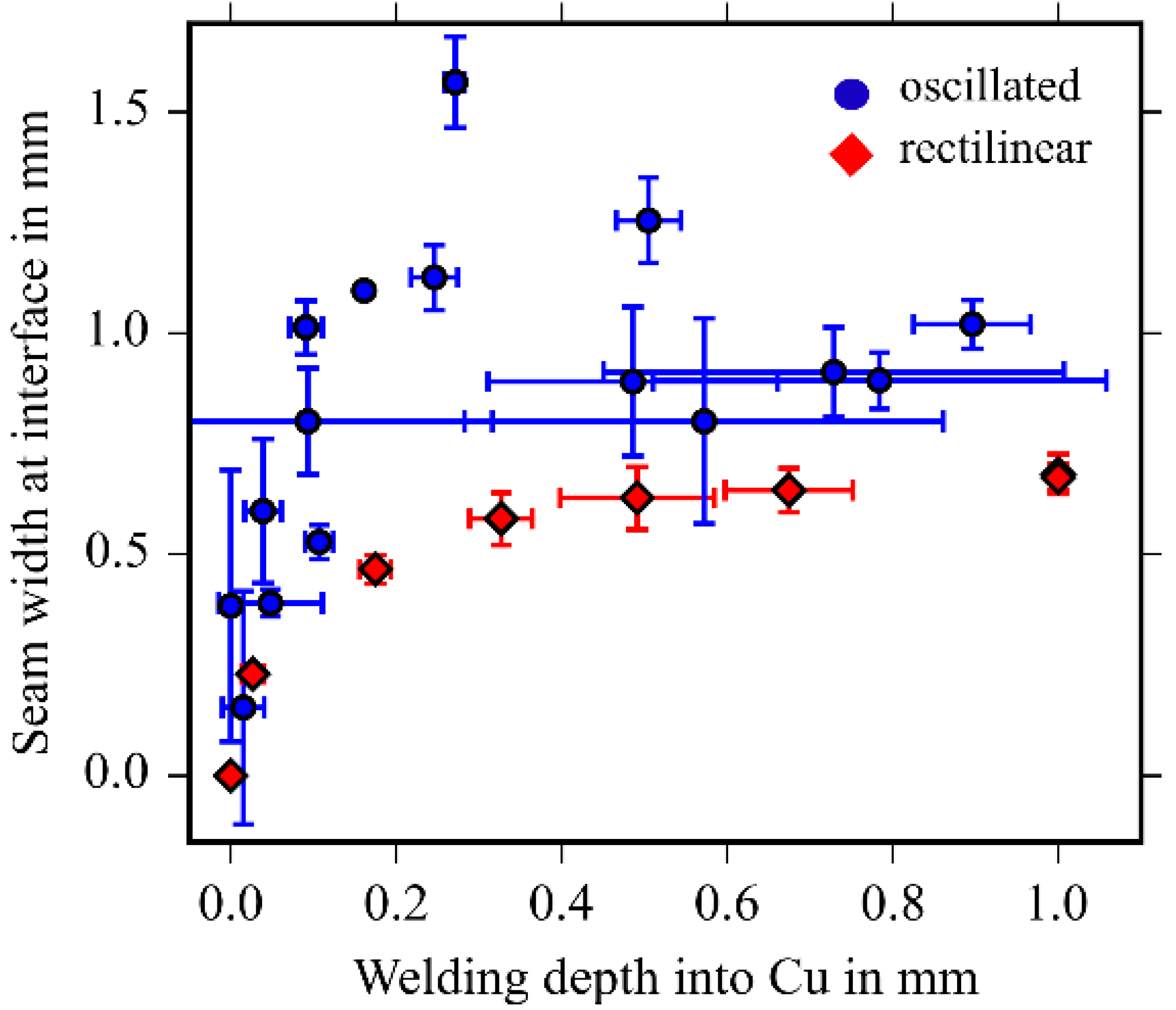
3.3. Geometry of Weld Seams as a Function of Oscillation Parameters
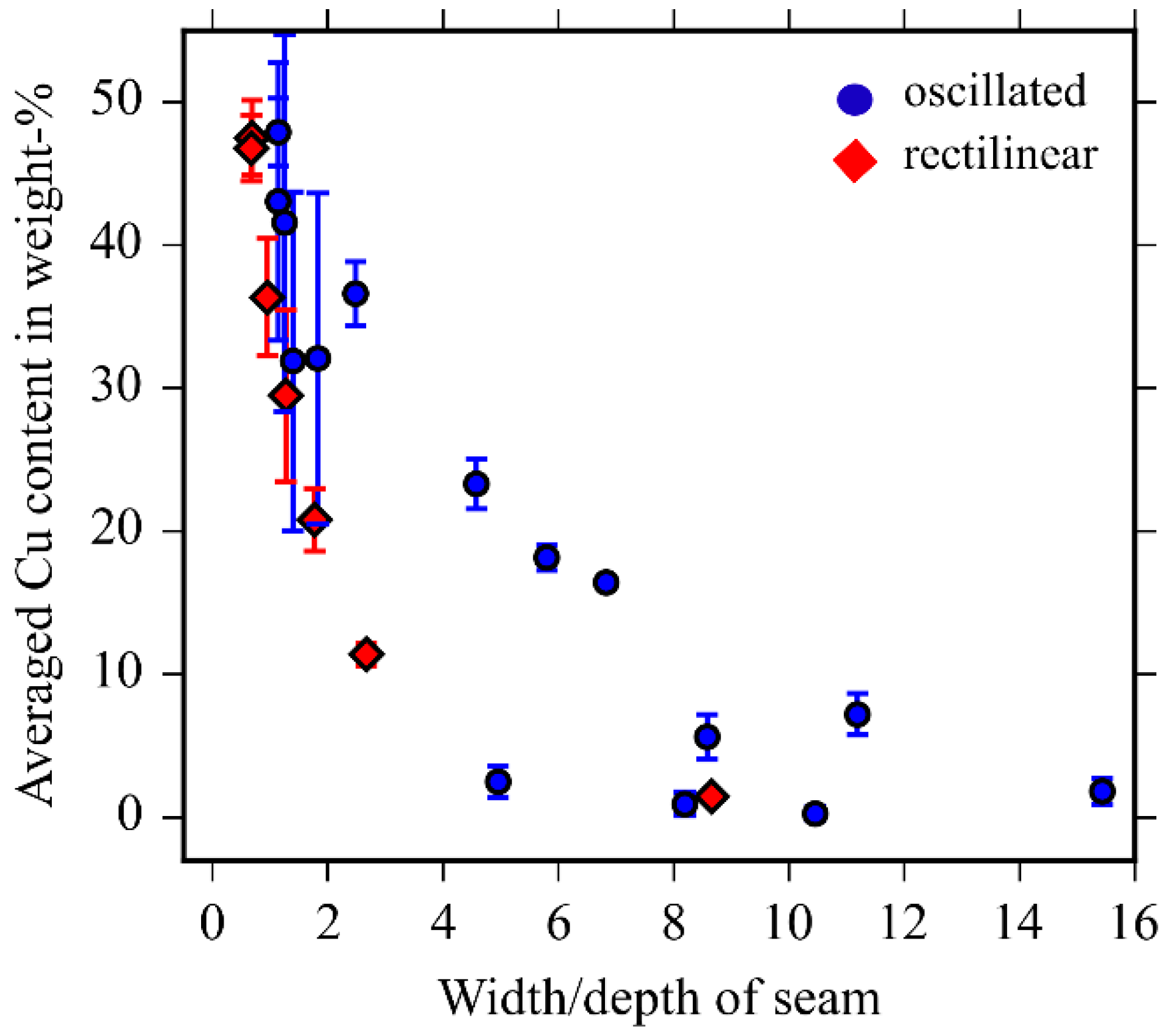
3.4. Averaged Cu Content as a Function of the Geometry of the Weld Seams
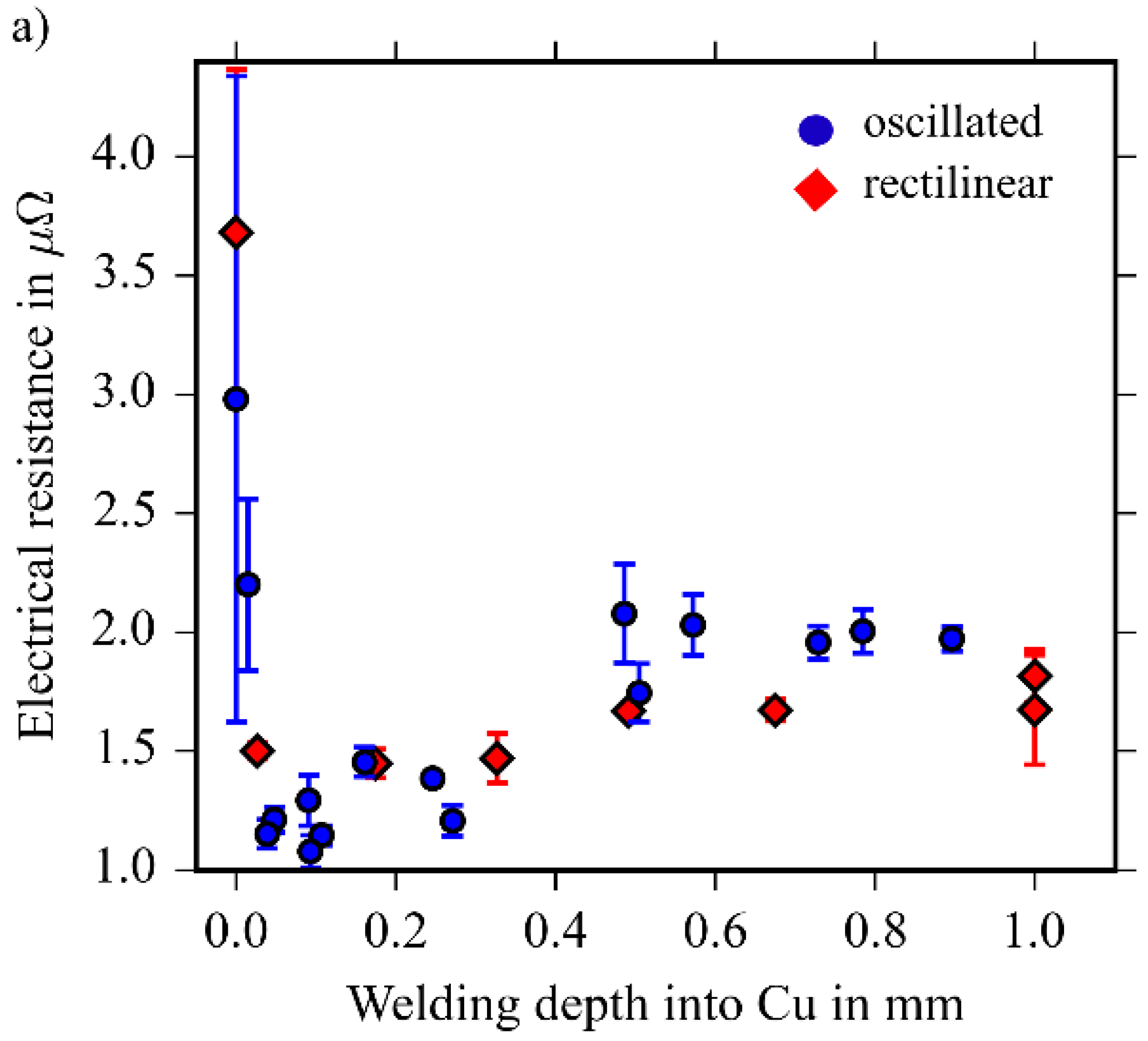
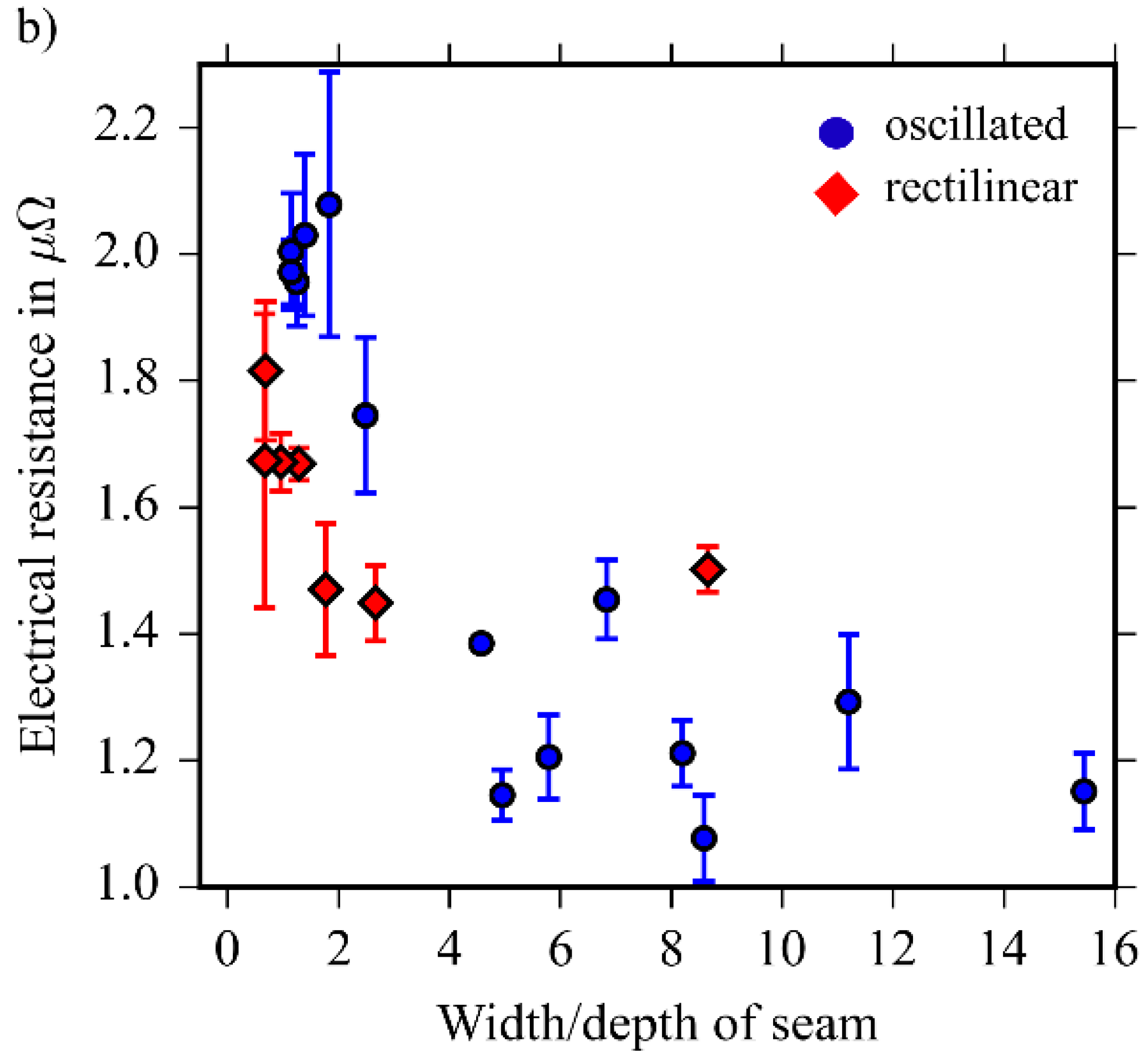
3.5. Electrical Resistance as a Function of the Geometry of the Weld Seams
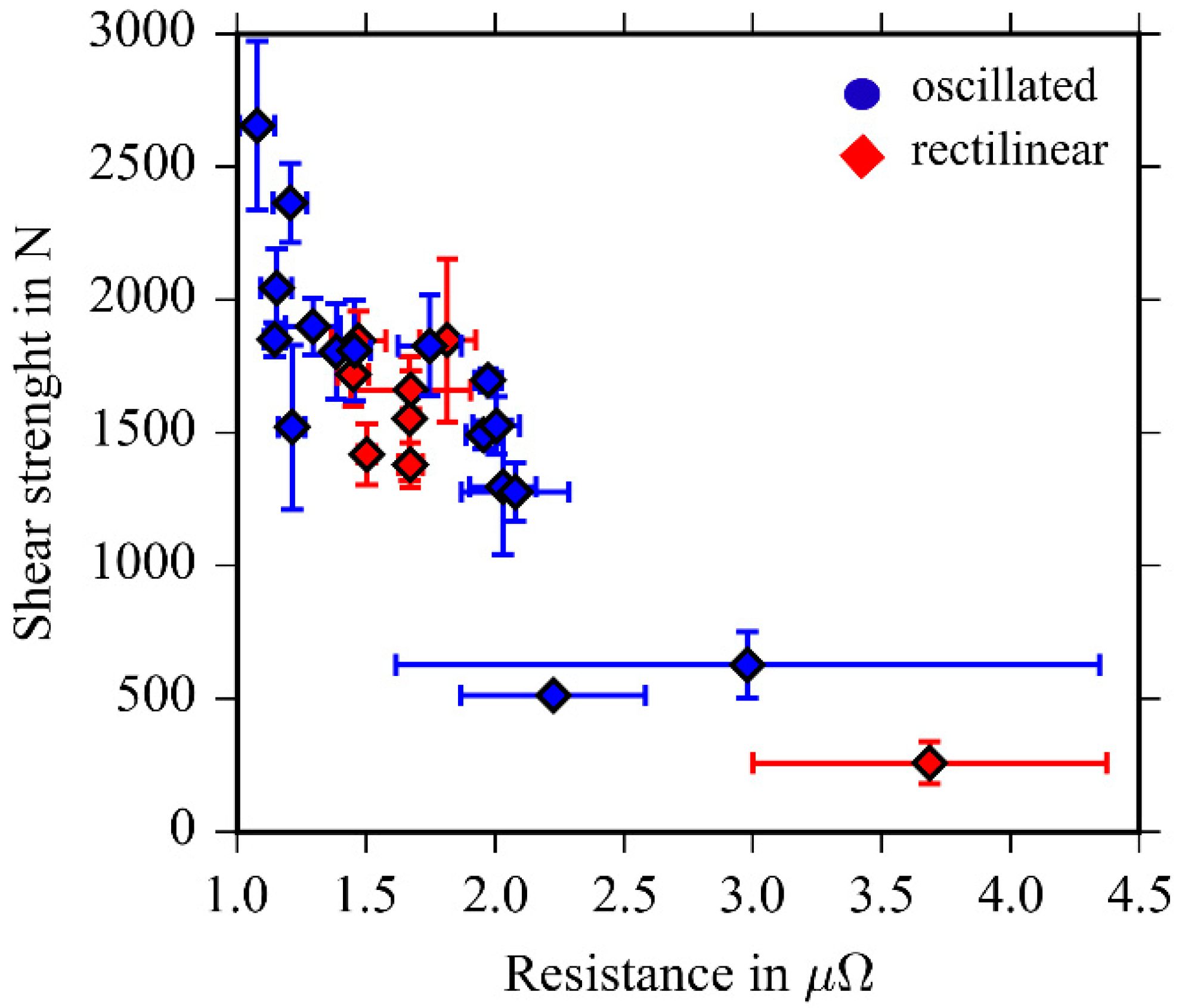
3.6. Correlation of Electrical Resistance and Mechanical Strength
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schmidt, P.A.; Schweier, M.; Zaeh, M.F. Joining of lithium-ion batteries using laser beam welding: Electrical losses of welded aluminum and copper joints. In Proceedings of the International Congress on Applications of Lasers and Electro-Optics (ICALEO 2012), Anaheim, CA, USA, 23–27 September 2012. [Google Scholar]
- Kirchhoff, M. Laser applications in battery production—From cutting foils to welding the case. In Proceedings of the 2013 3rd International Electric Drives Production Conference (EDPC), Nuremberg, Germany, 29–30 October 2013; IEEE: New York, NY, USA, 2013; pp. 1–3. [Google Scholar]
- Smith, S.; Blackburn, J.; Gittos, M.; Bono, P.D.; Hilton, P. Welding of dissimilar metallic materials using a scanned laser beam. In Proceedings of the 32nd International Congress on Applications of Lasers & Electro-Optics (ICALEO), Miami, FL, USA, 6–10 October 2013; pp. 6–10. [Google Scholar]
- Rabkin, D.M.; Ryabov, V.R.; Lozovskaya, A.V.; Dovzhenko, V.A. Preparation and properties of copper-aluminum intermetallic compounds. Powder Metall. Metal Ceram. 1970, 8, 695–700. [Google Scholar] [CrossRef]
- Solchenbach, T.; Plapper, P. Mechanical characteristics of laser braze-welded aluminium-copper connections. Opt. Laser Technol. 2013, 54, 249–256. [Google Scholar] [CrossRef]
- Sommer, M.; Weberpals, J.-P.; Müller, S.; Berger, P.; Graf, T. Advantages of laser beam oscillation for remote welding of aluminum closely above the deep-penetration welding threshold. J. Laser Appl. 2017, 29, 12001. [Google Scholar] [CrossRef]
- Thiel, C.; Weber, R.; Johannsen, J.; Graf, T. Stabilization of a laser welding process against focal shift effects using beam manipulation. Phys. Procedia 2013, 41, 209–215. [Google Scholar] [CrossRef]
- Kraetzsch, M.; Standfuss, J.; Klotzbach, A.; Kaspar, J.; Brenner, B.; Beyer, E. Laser beam welding with high-frequency beam oscillation. Welding of dissimilar materials with brilliant fiber lasers. Phys. Procedia 2011, 12, 142–149. [Google Scholar] [CrossRef]
- Gedicke, J.; Olowinsky, A.; Artal, J.; Gillner, A. Influence of temporal and spatial laser power modulation on melt pool dynamics. In Proceedings of the 26th International Congress on Applications of Laser and Electro-Optics (ICALEO 2007), Orlando, FL, USA, 29 October–1 November 2007; pp. 816–822. [Google Scholar]
- Solchenbach, T.; Plapper, P.; Wanye, C. Electrical performance of laser braze-weldedd aluminum-copper interconnects. J. Manuf. Processes 2014, 16, 183–189. [Google Scholar] [CrossRef]
- Fetzer, F.; Jarwitz, M.; Stritt, P.; Weber, R.; Graf, T. Fine-tuned remote laser welding of aluminum to copper with local beam oscillation. Phys. Procedia 2016, 83, 455–462. [Google Scholar] [CrossRef]
- Heider, A.; Sollinger, J.; Abt, F.; Boley, M.; Weber, R.; Graf, T. High-speed X-ray analysis of spatter formation in laser welding of copper. Phys. Procedia 2013, 41, 112–118. [Google Scholar] [CrossRef]
- Heider, A.; Stritt, P.; Hess, A.; Weber, R.; Graf, T. Process stabilization at welding copper by laser power modulation. Phys. Procedia 2011, 12, 81–87. [Google Scholar] [CrossRef]
- Hagenlocher, C.; Fetzer, F.; Weber, R.; Graf, T. Benefits of very high feed rates for laser beam welding of AlMgSi aluminum alloys. J. Laser Appl. 2018, 30, 12015. [Google Scholar] [CrossRef]
- Graf, T.; Berger, P.; Weber, R.; Hügel, H.; Heider, A.; Stritt, P. Analytical expressions for the threshold of deep-penetration laser welding. Laser Phys. Lett. 2015, 5, 56002. [Google Scholar] [CrossRef]
- Hügel, H.; Graf, T. Laser in der Fertigung; Vieweg + Teubner, GWV Fachverlage GmbH: Wiesbaden, Germany, 2009. [Google Scholar]




© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jarwitz, M.; Fetzer, F.; Weber, R.; Graf, T. Weld Seam Geometry and Electrical Resistance of Laser-Welded, Aluminum-Copper Dissimilar Joints Produced with Spatial Beam Oscillation. Metals 2018, 8, 510. https://doi.org/10.3390/met8070510
Jarwitz M, Fetzer F, Weber R, Graf T. Weld Seam Geometry and Electrical Resistance of Laser-Welded, Aluminum-Copper Dissimilar Joints Produced with Spatial Beam Oscillation. Metals. 2018; 8(7):510. https://doi.org/10.3390/met8070510
Chicago/Turabian StyleJarwitz, Michael, Florian Fetzer, Rudolf Weber, and Thomas Graf. 2018. "Weld Seam Geometry and Electrical Resistance of Laser-Welded, Aluminum-Copper Dissimilar Joints Produced with Spatial Beam Oscillation" Metals 8, no. 7: 510. https://doi.org/10.3390/met8070510
APA StyleJarwitz, M., Fetzer, F., Weber, R., & Graf, T. (2018). Weld Seam Geometry and Electrical Resistance of Laser-Welded, Aluminum-Copper Dissimilar Joints Produced with Spatial Beam Oscillation. Metals, 8(7), 510. https://doi.org/10.3390/met8070510