Life Prediction of Crack Growth for P92 Steel Under Strain-Controlled Creep–Fatigue Conditions Using a Sharp Notched Round Bar Specimen
Abstract
1. Introduction
2. Materials and Methods
3. Experimental Procedure
3.1. Measurement Method for Crack Growth Length
- a = crack length (mm);
- a0 = initial crack length (mm);
- D = diameter of the specimen (mm);
- y = half-distance between the output terminals;
- U = current voltage (;
- U0 = initial voltage (.
3.2. Criteria of Failure Life and Crack Initiation
3.3. Experimental Conditions
4. Experimental Results
4.1. Cycle-Sequential Characteristics of the Nominal Stress Range
4.2. Crack Growth Behavior
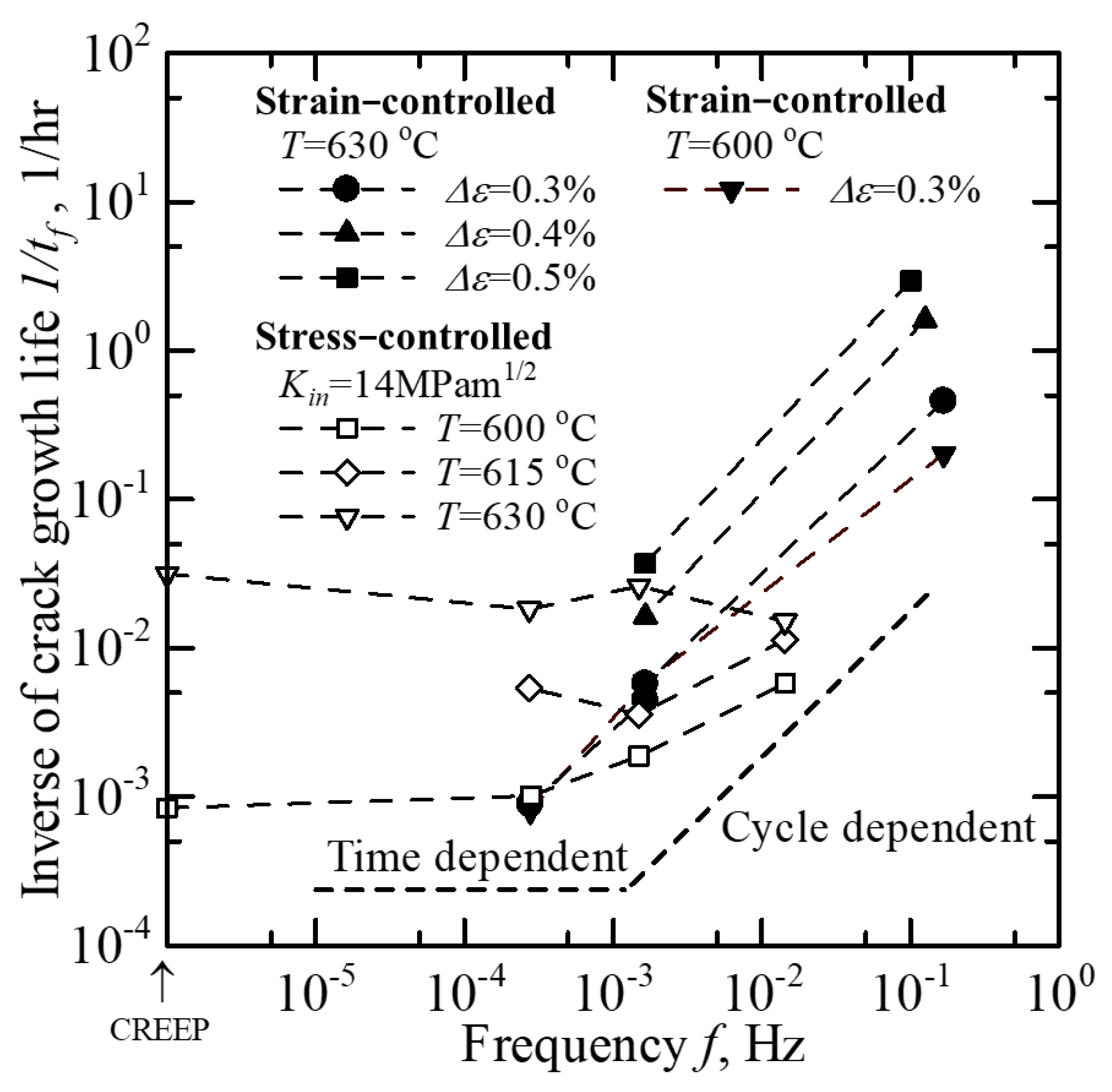
4.3. The Load Frequency Characteristics of the Inverse Value of Crack Growth Life
5. Analysis and Discussion
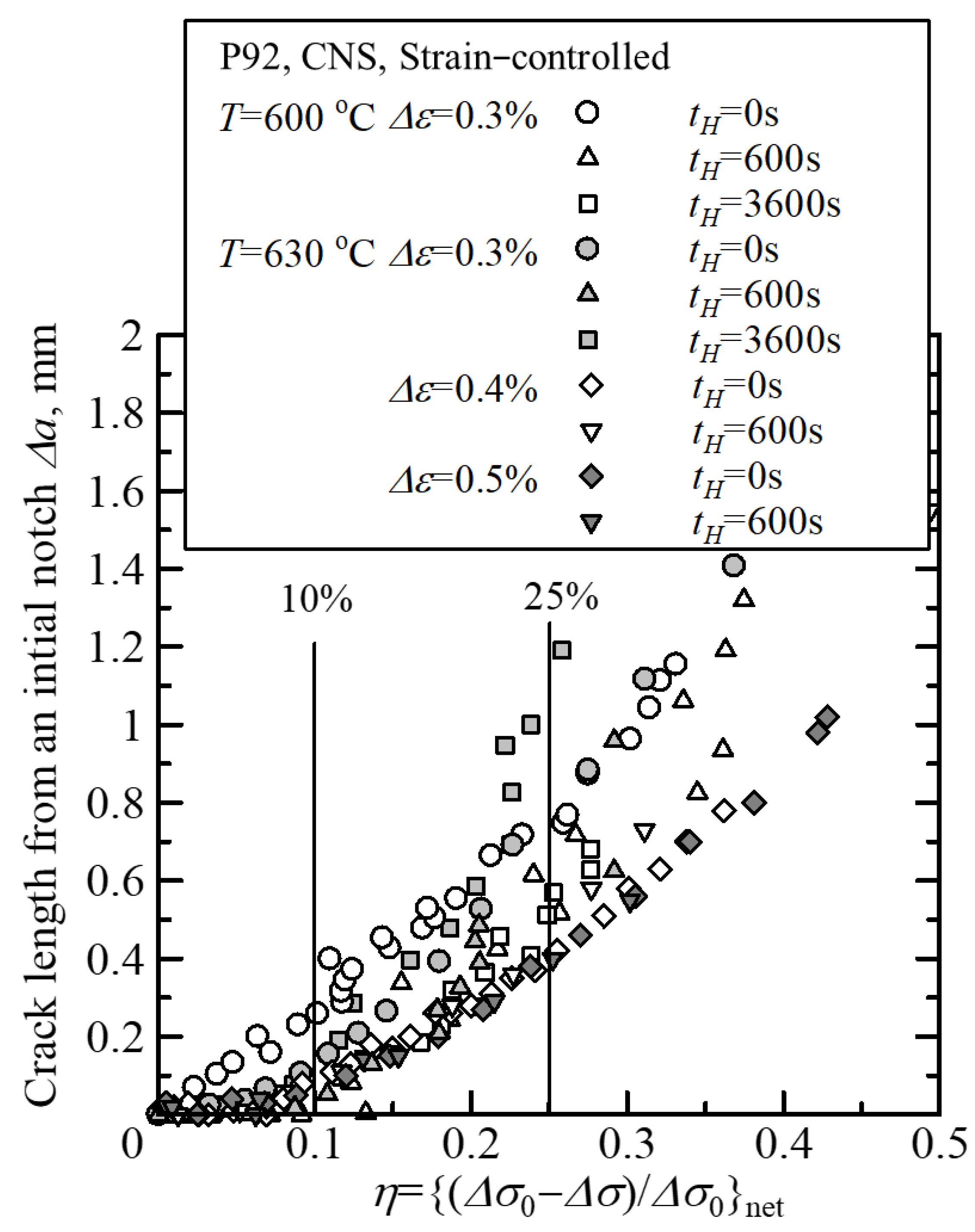
5.1. Relationship Between Crack Length and Stress Reduction Ratio
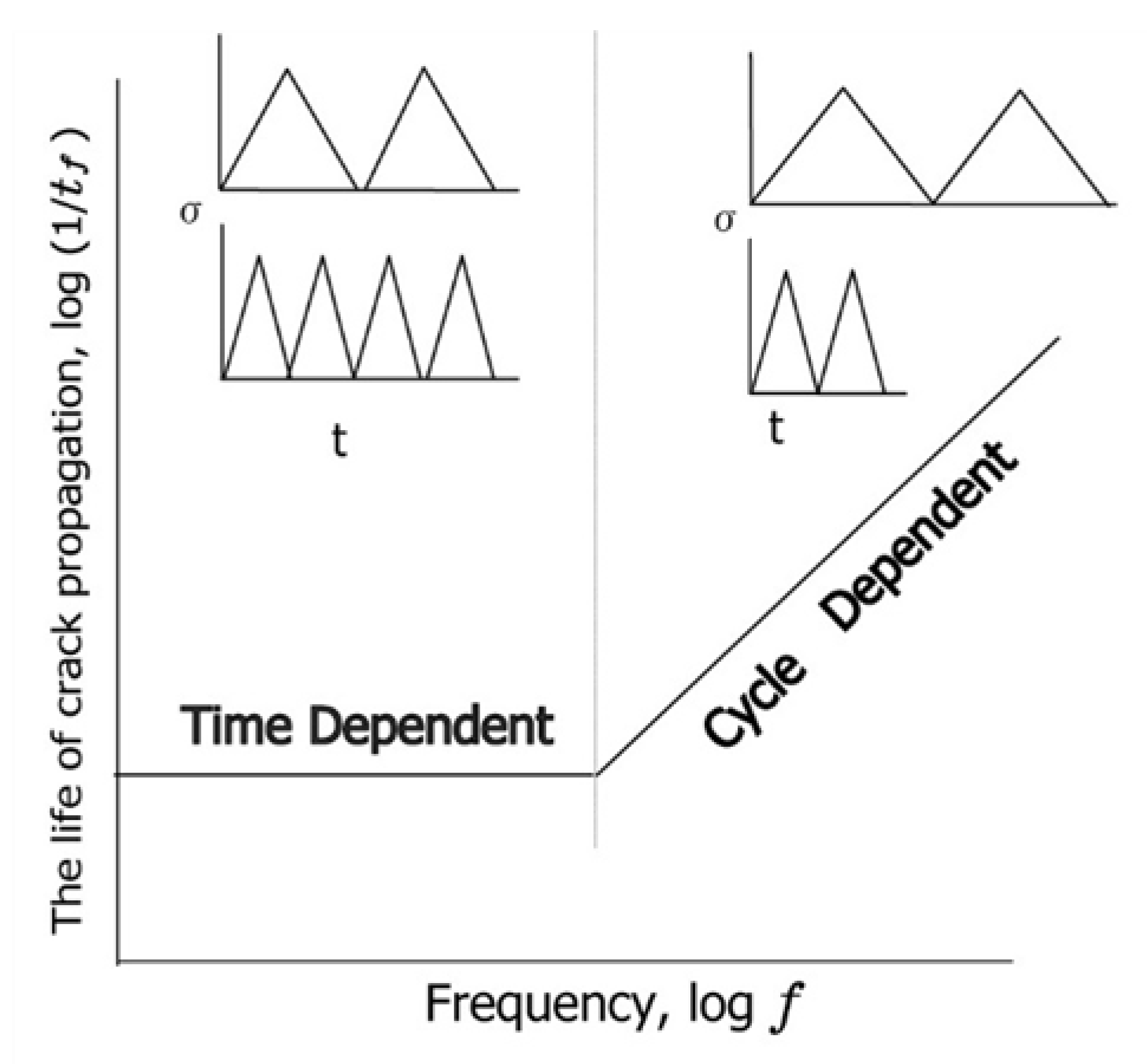
5.2. Separate Estimation Method for the Cycle-Dependent Mechanism from the Time-Dependent Mechanism for Crack Growth Life
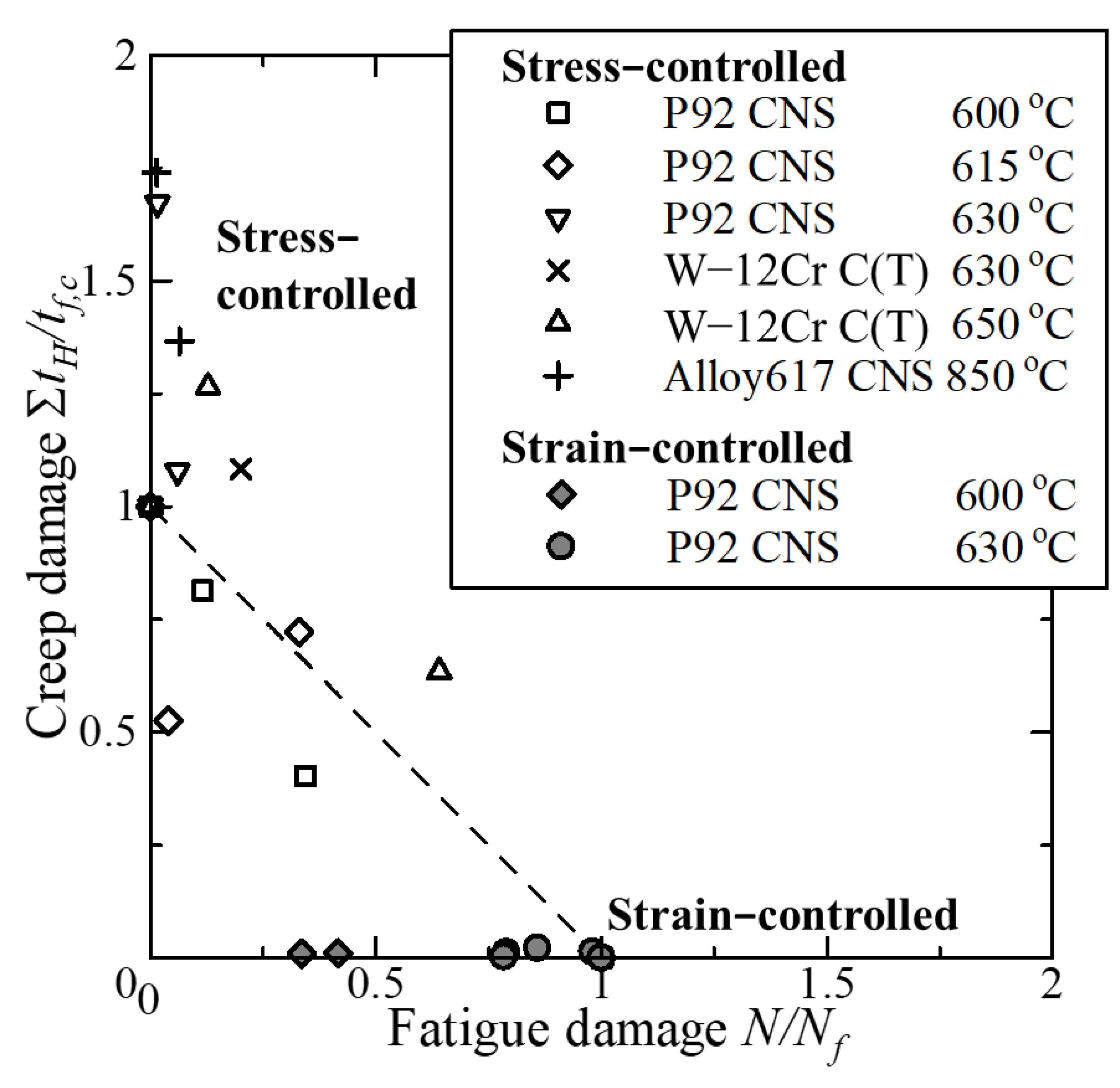
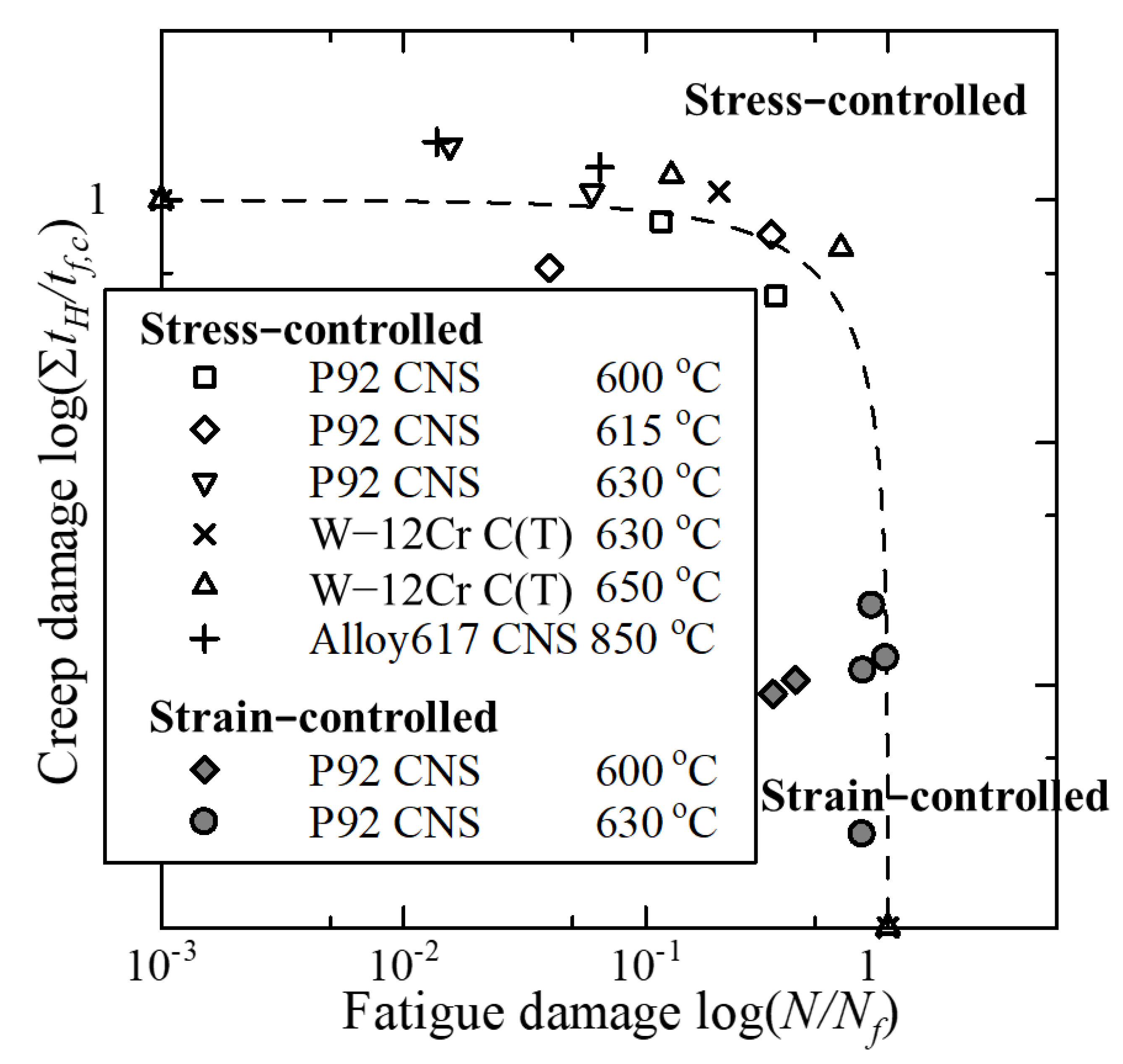
5.3. Representation of the Creep and Fatigue Accumulated Damage Law
5.4. Representation by the Manson–Coffin Law
5.5. Discussion
5.6. Limitations
6. Conclusions
- The cycle-sequential characteristics of the nominal stress range, , was found to monotonously decrease against the applied strain cycles, which verifies the previous result [1] and makes it possible to accurately determine the failure life and crack initiation using the reduction ratio of the nominal stress range, , as proposed in the previous study [1].
- The effect of specimen diameter on the crack growth curve was found to be well-controlled by the initial net section diameter Dnet, and to show good correlation between and η. This result shows that crack growth life is not dominated by the crack length but by the ratio of the crack length to the initial net section diameter of the specimen.
- The crack growth life of the CNS under strain-controlled creep–fatigue conditions for P92 steel was found to be dominated by the cycle-dependent mechanism in a strain range from 0.3% to 0.5%. By contrast, the crack growth life of the CNS under stress-controlled creep–fatigue conditions for P92 steel was mainly dominated by the time-dependent mechanism in the same temperature range.
- A unified cumulative failure law under stress- and strain-controlled conditions was investigated. The results show that, for a sharp notched specimen of P92 steel, the failure life under strain-controlled creep and fatigue conditions exists in the region of the cycle-dependent mechanism; however, the failure life under stress-controlled creep and fatigue conditions exists in the region of the time-dependent mechanism under the same temperature range as that under strain-controlled conditions. These results correspond well to the results in point 3 above.
- Under strain-controlled creep and fatigue conditions for the CNS, since the crack growth life was dominated by the cycle-dependent mechanism in a strain range from 0.3% to 0.5%, the Manson–Coffin law was found to be applicable not only to a smooth specimen under low cycle fatigue but also to the CNS under low cycle fatigue and creep–fatigue conditions with different values of α and C.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sugiura, R.; Yokobori, A.T., Jr.; Nakagawa, T.; Adachi, T.; Nonaka, I.; Tabuchi, M.; Hasegawa, Y.; Matsuzaki, T. Characterizations of creep and fatigue crack initiation and growth life for P92 using circular notched round bar specimen. In Creep and Fatigue Interactions: Test Methods and Models; Saxena, A., Dogan, B., Eds.; ASTM International: West Conshohocken, PA, USA, 2011; Volume 9, pp. 67–86. [Google Scholar]
- Ozeki, G.; Yokobori, A.T., Jr.; Tabuchi, M.; Hayakawa, M.; Nikbin, K. Testing and Estimation Methods of Crack Growth Life for Alloy 617 Under Strain-Controlled Creep and Fatigue Conditions Using Circular Sharp Notched Round bar Specimen. In Advances in Accelerated Testing and Predictive Methods in Creep, Fatigue, and Environmental Cracking; ASTM International STP1643: West Conshohocken, PA, USA, 2023; pp. 42–62. [Google Scholar] [CrossRef]
- Awaji, K.; Yokobori, A.T., Jr.; Yokobori, T. The variation of the stress singularity at the notch tip as notch angle and radius of curvature. Comput. Struct. 1986, 22, 25–30. [Google Scholar] [CrossRef]
- ASTME1457-19; Standard Test Method for Measurement of Creep Crack Growth Times in Metals. ASTM International: West Conshohocken, PA, USA, 2019. [CrossRef]
- Mehmanparast, A.; Davies, M.; Nikbin, K. Evaluation of the testing and analysis methods in ASTM E2760-10 Creep and fatigue crack growth testing standard for a range of steel. In Creep and Fatigue Interactions. Test Method and Models; Saxena, A., Dogan, B., Eds.; ASTM International: West Conshohocken, PA, USA, 2011; Volume 8, pp. 1–18. [Google Scholar]
- Yokobori, A.T., Jr.; Sugiura, R.; Kimoto, S.; Yoshino, D.; Matsuzaki, T. Law of crack growth life for P92 steel under the conditions of creep and fatigue multiplication and projection of the threshold temperature of creep crack growth based on this law. In Proceedings of the ASME Pressure Vessels and Piping Conference PVP2009, Prague, Czech Republic, 26–30 July 2009; ASME: New York, NY, USA, 2009. [Google Scholar]
- ASME. ASME Boiler & Pressure Vessel Code; Sec., III, Division 5; ASME: New York, NY, USA, 2021. [Google Scholar]
- ASTM E2714-13; Standard Test Method for Creep and Fatigue Testing. ASTM International: West Conshohockencken, PA, USA, 2020. [CrossRef]
- Robinson, E. Effect of temperature variation on the long time rupture strength of steels: Trans. ASME 1952, 74, 777–780. [Google Scholar] [CrossRef]
- Taira, S. IUTAM Colloquium; Springer: New York, NY, USA, 1962; p. 96. [Google Scholar]
- Lemaitre, J.; Plumtree, A. Application of damage concepts to predict creep damage failures. J. Eng. Mater. Technol. Trans. ASME 1979, 101, 284–292. [Google Scholar] [CrossRef]
- Bui-Quoc, T.; Biron, A. A phenomenological approach for the analysis of combined fatigue and creep. Nucl. Eng. Des. 1982, 71, 89–102. [Google Scholar] [CrossRef]
- Shimakawa, T.; Suzono, N.; Usui, Y.; Fukuda, Y.; Kasahara, N. Current status and issues on creep and fatigue life evaluation in elevated temperature design guidance. Jpn. High Press. Inst. 2001, 39, 19–31. (In Japanese) [Google Scholar]
- Koo, G.-H.; Lee, S.-Y.; Seo, J.-H.; Song, K.-H.; Choi, G.-S. A study on creep and fatigue evaluation of nuclear cladded components by ASME-III, Division. Metals 2023, 16, 2898. [Google Scholar] [CrossRef]
- Nonaka, I. Creep and fatigue life estimation of gr.91 steel and its welded joints. Metals 2023, 13, 1880. [Google Scholar] [CrossRef]
- Manson, S.S. Behavior of Materials Under Conditions of Thermal Stress; National Advisory Committee for Aeronautics: Washington, DC, USA, 1953. [Google Scholar]
- Coffin, L.F. A study of the effects of cyclic thermal stresses on a ductile metal. Trans. ASME 1954, 76, 931–950. [Google Scholar] [CrossRef]
- ISO 12106; Metallic Materials—Fatigue Testing—Axial-Strain-Controlled Method. ISO: Geneva, Switzerland, 2017.
- Johnson, H.H. Calibrating the Electric Potential Method for Studying Slow Crack Growth. Mater. Res. Stand. 1965, 5, 442–445. [Google Scholar]
- Schwalbe, K.H.; Hellmann, D. Application of the Electric Potential method to Crack Length Measurement Using Johnson’s Formula. J. Test. Eval. 1981, 9, 218–221. [Google Scholar] [CrossRef]
- Yokobori, A.T., Jr.; Kuriyama, T.; Kaji, Y.; Yokobori, T. The Effect of the Stress rate in a Cycle and the Stress Hold Time respectively on Fracture Life under High Temperature Creep and fatigue, and Creep and fatigue Multiplication Conditions. Jpn. Soc. Strength Fract. Mater. 1986, 21, 25–32. [Google Scholar]
- Yokobori, A.T., Jr.; Tabuchi, M. The Chapter of Q* Parameter for Crack Growth Prediction. In Comprehensive Structural Integrity, 2nd ed.; Ferri, M.H.A., Winston, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2023; pp. 434–452. [Google Scholar] [CrossRef]
- Wang, X.; Gong, J.; Zhao, Y.; Wang, Y.; Yu, M. Characterization of Low Cycle Fatigue of New Ferritic-Martensitic P92 Steel at High Temperature, Effect of Strain Amplitude, Steel. Res. Int. 2015, 86, 1046–1055. [Google Scholar]
- Yokobori, A.T., Jr.; Sugiura, R.; Tabuchi, M.; Fuji, A.; Adachi, T.; Yokobori, T. The Effect of Multi-Axial Stress Component on Creep Crack Growth Rate Concerning Structural Brittleness. In Proceedings of the 11th International Conference on Fracture, Turin, Italy, 20–25 March 2005; ICF: Lexington, Kentucky, 2005. CD-ROM. [Google Scholar]
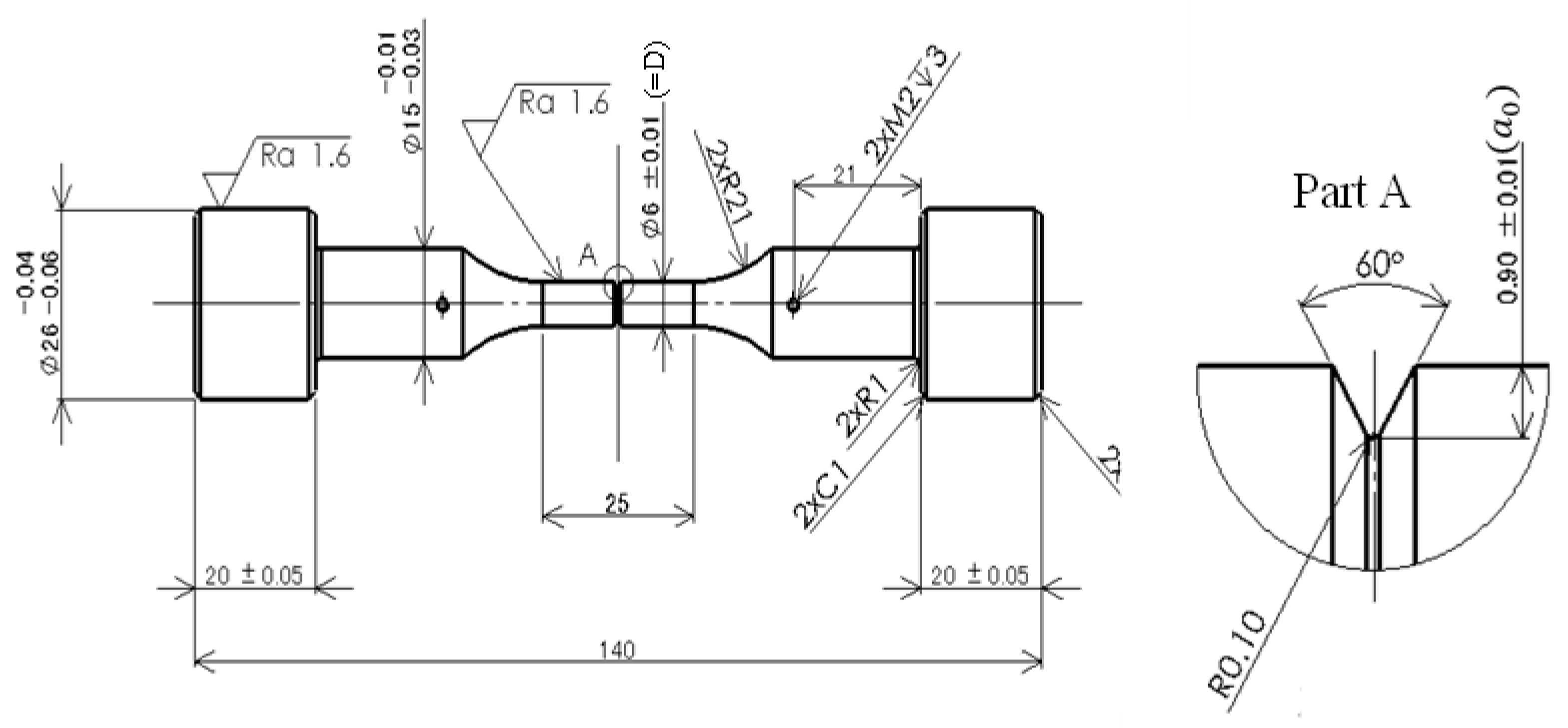
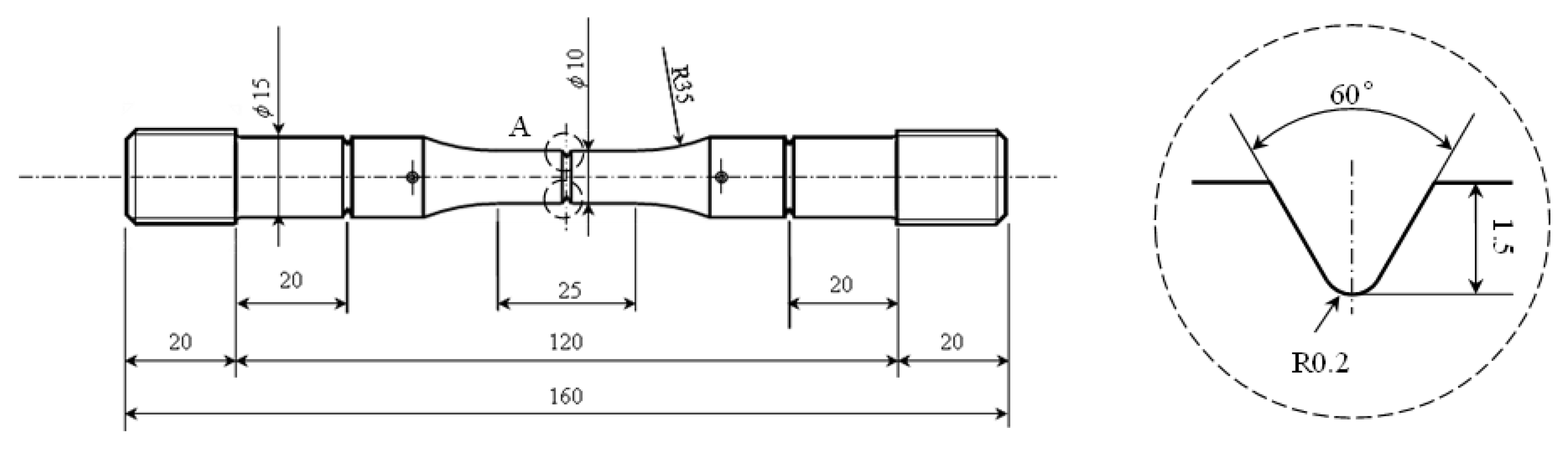
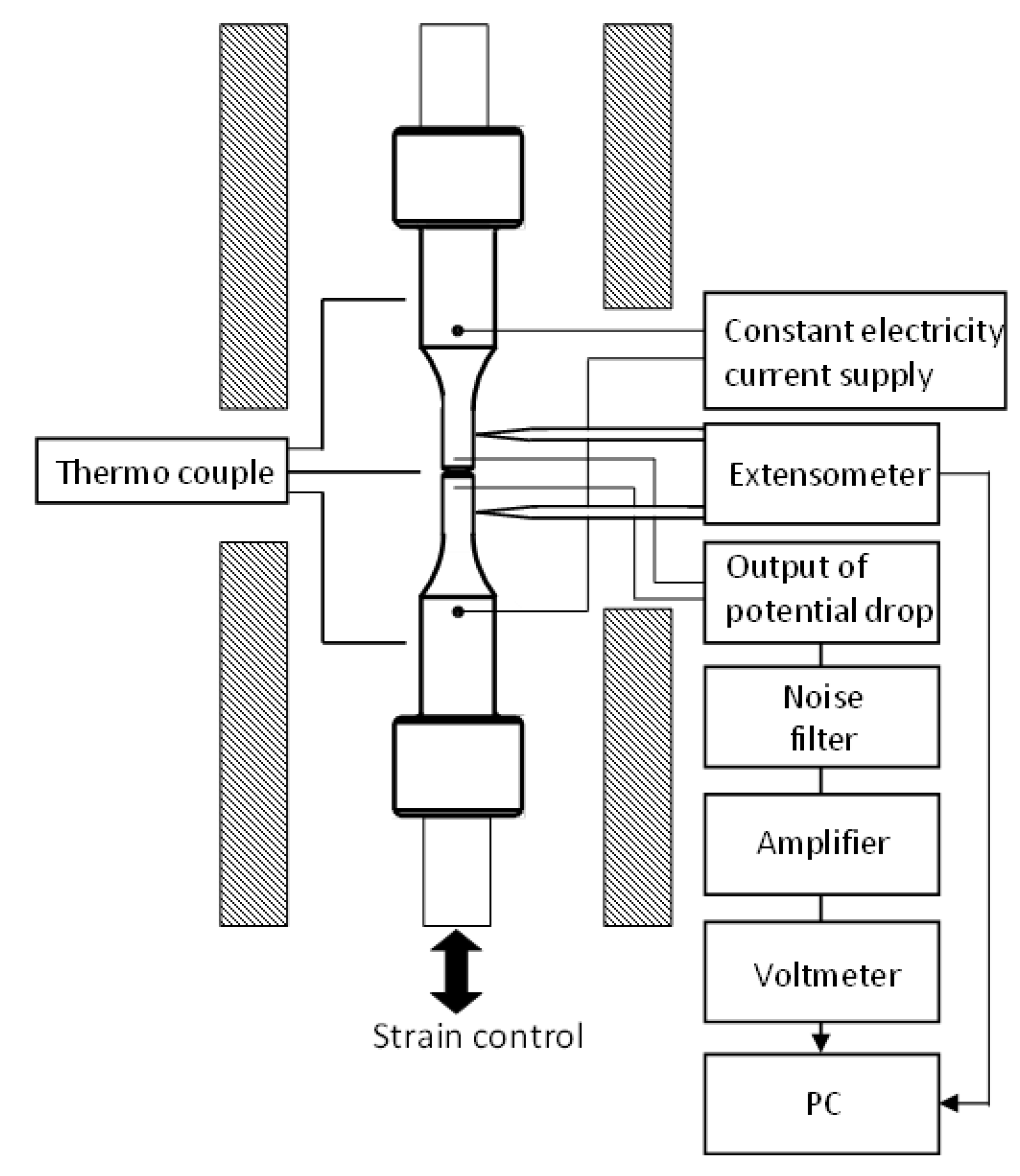





| C | Si | Mn | P | S | Cr | Mo | W | Nb | V | N | B |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.085 | 0.26 | 0.49 | 0.006 | 0.0012 | 8.85 | 0.50 | 1.80 | 0.06 | 0.20 | 0.0510 | 0.0030 |
| 0.2YS (MPa) | TS (MPa) | Uniform EL (%) | EL (%) | RA (%) |
|---|---|---|---|---|
| 583 | 731 | 2.68 | 27.6 | 74.6 |
| dε/dt [%/s] | Temp. [°C] | Diameter, D [mm] | ∆ε [%] | tH [s] | Nf [-] | 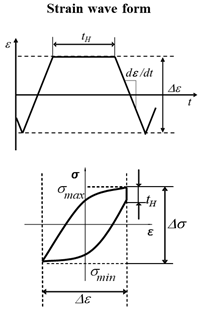 |
| 0.1 | 600 | 10 | 0.3 | 0 | 2980 | |
| 600 | 1000 | |||||
| 3600 | 1240 | |||||
| 630 | ||||||
| 0 | 1310 | |||||
| 600 | 1035 | |||||
| 3600 | 1125 | |||||
| 630 | 6 | 0.4 | 0 | 372 | ||
| 600 | 365 | |||||
| 0.5 | 0 | 168 | ||||
| 600 | 160 |
| σnet [MPa] | Kin [MPa√m] | Temp. [°C] | tR = tD [s] | tH [s] | tf [h] | 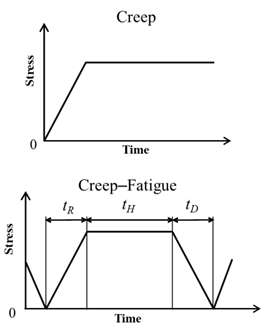 |
| 300 | 14 | 600 | 35 | 0 | 172.1 | |
| 600 | 533 | |||||
| 3600 | 985.2 | |||||
| Creep | 1189 | |||||
| 615 | 35 | 0 | 88.3 | |||
| 600 | 279.4 | |||||
| 3600 | 186.3 | |||||
| 630 | 35 | 0 | 66.3 | |||
| 600 | 38.4 | |||||
| 3600 | 54.8 | |||||
| Creep | 31.7 | |||||
| Specimen | Temp. [°C] | tH [s] | α [-] | C [-] |
|---|---|---|---|---|
| CNS | 630 | 0 | 0.594 | 1.8 |
| 600 | 0.521 | 3.2 | ||
| Smooth | 630 | 0 | 0.816 | 1.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yokobori, A.T., Jr.; Ozeki, G.; Jinno, K.; Seino, H.; Sugiura, R.; Nonaka, I. Life Prediction of Crack Growth for P92 Steel Under Strain-Controlled Creep–Fatigue Conditions Using a Sharp Notched Round Bar Specimen. Metals 2025, 15, 737. https://doi.org/10.3390/met15070737
Yokobori AT Jr., Ozeki G, Jinno K, Seino H, Sugiura R, Nonaka I. Life Prediction of Crack Growth for P92 Steel Under Strain-Controlled Creep–Fatigue Conditions Using a Sharp Notched Round Bar Specimen. Metals. 2025; 15(7):737. https://doi.org/10.3390/met15070737
Chicago/Turabian StyleYokobori, A. Toshimitsu, Jr., Go Ozeki, Kazutaka Jinno, Hiroaki Seino, Ryuji Sugiura, and Isamu Nonaka. 2025. "Life Prediction of Crack Growth for P92 Steel Under Strain-Controlled Creep–Fatigue Conditions Using a Sharp Notched Round Bar Specimen" Metals 15, no. 7: 737. https://doi.org/10.3390/met15070737
APA StyleYokobori, A. T., Jr., Ozeki, G., Jinno, K., Seino, H., Sugiura, R., & Nonaka, I. (2025). Life Prediction of Crack Growth for P92 Steel Under Strain-Controlled Creep–Fatigue Conditions Using a Sharp Notched Round Bar Specimen. Metals, 15(7), 737. https://doi.org/10.3390/met15070737








