Abstract
Body-centered cubic (BCC) metals, extensively utilized in low-alloy high-strength steels and heat-resistant alloys, exhibit a pronounced ductile–brittle transition (DBT) at cryogenic temperatures, marked by a well-defined yet narrow ductile–brittle transition temperature (DBTT) window. This paper overviews the research progress regarding the DBT mechanism of BCC metals. This mechanism was recently found to be related to the mobility of screw dislocation relative to edge dislocation, a decrease in which can induce a critical drop in the proliferation efficiency of dislocation sources. Furthermore, this paper summarizes the current research on the dilute solution softening effect of BCC metals, which has been frequently observed and studied in refractory alloys. The mechanism of this effect involves the low-temperature mobility of screw dislocations that could be promoted by specific solute atoms through kink pair nucleation. This offers a potential strategy for reducing the DBTT of low-alloy steels using a dilute solution, namely microalloying in metallurgy. However, the current understanding of the relationship between the macroscopic ductility of BCC alloys and the dilute solution softening effect is limited. This review aimed to draw attention to this relationship and strengthen related research.
1. Introduction
Metallic materials suffer from a ductile-to-brittle transition (DBT) phenomenon as temperature decreases over a critical point or range, which is called the DBT temperature (DBTT). Above the DBTT, metals or alloys fracture in a ductile mode accompanied, by large energy absorption through plastic deformation. Below the DBTT, cracks propagate rapidly without evident deformation at the crack tip, thereby inducing a brittle fracture behavior. Different from face-centered cubic (FCC) and hexagonal close-packed (HCP) metals, body-centered cubic (BCC) metals exhibit the most pronounced DBT behavior, with a distinct temperature interval over which the transition occurs [1,2,3,4,5,6]. BCC is the most common crystal structure of refractory metals and alloys, as well as iron and steels, due to its much higher ability to achieve high strength and creep resistance through processing or heat treatment. Understanding the mechanisms underlying the DBT of BCC metals and alloys is of significance for improving their low-temperature toughness and reducing their DBTT.
Compared with FCC metals, BCC metals possess a higher number of slip systems, but only a limited number of these systems (e.g., {110} <111>) can be activated at low temperatures due to their high critical shear stresses. This results in pronounced deformation anisotropy [7]. From the perspective of energy, the atomic arrangement in BCC metals is less compact than in FCC metals, leading to higher lattice resistance. Dislocations in BCC metals must overcome significant Peierls potential during motion. Thermal activation above the DBTT facilitates dislocation movement, overcoming Peierls potential and enabling ductile fracture via plastic deformation. Below the DBTT, thermal activation is insufficient, causing the Peierls potential to become insurmountable, which restricts the dislocation motion and leads to brittle fracture. From the perspective of dislocation motion and multiplication, the mobility of screw dislocations in BCC metals is more temperature-sensitive than that of edge dislocations. Below the DBTT, the screw-character ends of the Frank–Read (F-R) source have restricted mobility and cannot effectively curl back, resulting in inefficient dislocation multiplication. As a result, plastic deformation is stuck at the crack tip, leading to brittle fracture. Recent studies by Han et al. have advanced the understanding of DBT in BCC metals. In their investigation of Cr metal, they identified the ratio of screw dislocation to edge dislocation motion rates α as a key parameter controlling DBT [8]. On the basis of F-R dislocation sources, they elucidated how α influences dislocation multiplication and proposed a DBTT prediction model for BCC metals [9]. Experimental validation confirmed the role of α in regulating the proliferation efficiency of F-R dislocation sources [10]. These findings established a direct link between DBTT and the mobility of screw dislocations in BCC metals. Further, the motion of screw dislocations is fundamentally governed by the thermally activated nucleation and migration of double kinks, which are significantly temperature-dependent [11]. Nucleation barriers hinder the formation of the initial double kinks on flat screw dislocation lines due to high Peierls potential. Raising the nucleation energy barrier to inhibit the initiation of screw dislocations is significantly affected by the temperature at low temperatures. Migration barriers hinder the slipping of formed screw dislocation double kinks along the edged component of the kinematic process, and solute atoms, among other things, hinder the slipping of double kinks, which can be increased by raising the migration barriers to limit the dislocation slip rate, which is also greatly affected by the temperature at low temperatures. Ghafarollahi and Curtin discussed the nucleation and migration of double kinks in BCC alloys, as detailed in the studies in [12,13], and proposed an analytical statistical model for double-kink nucleation and migration with energy barriers under the effect of solute atoms. However, due to the discrete three-dimensional core structure of screw dislocations and the lack of proper characterization techniques, the study focuses primarily on model constructions and theoretical calculations. The lack of direct evidence makes it impossible to experimentally verify the temperature dependence of double kinks and their effect on screw dislocation mobility.
Besides temperature-dependent thermal activation, solute atoms would also exert great influences on the nucleation and migration of double kinks in BCC metals. As early as 1978, Pink and Arsenault [14] discussed the “alloy softening” effect in BCC alloys, where the solid solution of alloying elements results in a lower yield stress than that of the base metal at low temperatures. This phenomenon, known as “dilute solid solution softening”, is observed in dilute solid solution systems (alloy content < 1 at. %); this anomalous effect manifests as simultaneous strength reduction and ductility enhancement at low temperatures, countering the known “solid solution strengthening” effect. Recent molecular dynamics simulations by Lin et al. [15] revealed that Re additions in BCC-W alloys effectively decreased the DBTT while flattening the DBT slope, thereby enhancing cryogenic fracture toughness. On the basis of density functional calculations, Ghafarollahi and Curtin [12,13] reported that the yield stresses of dilute Fe–Si, W–Ta, and W–Re alloys at 0 K were remarkably lower than those of pure Fe and pure W, and suggested that solute atoms improve the low-temperature mobility of screw dislocations by lowering the nucleation energy of double kinks. Wakeda et al. [16] demonstrated that Si reduces the nucleation energy of double kinks from 150.6 meV in pure Fe to 50 meV in Fe-Si alloys, accompanied by a decrease in DBTT of approximately 50 K. Furthermore, Trinkle [17] concluded that in dilute BCC Mo alloys at low temperatures, double kinks on screw dislocations can migrate rapidly along the dislocation line, as they are at the edge, which is less temperature-sensitive. Therefore, the kink migration has a negligible barrier, and the double-kink nucleation is the rate-limiting step of screw dislocation mobility at low temperatures. Dilute solute atoms promote double-kink nucleation through their stress fields, thereby enhancing the mobility of screw dislocations at low temperatures.
Since BCC is the main crystal structure of most low-alloy steels and refractory alloys, elucidating the DBT mechanism in BCC metals and understanding/utilizing the dilute solution softening effect are of significant scientific and practical value for improving the low-temperature toughness of such materials. Therefore, this review aimed to enhance the understanding of the DBT mechanism and the dilute solid solution softening effect in BCC metals, providing new insights for further reducing the ductile-to-brittle transition temperature (DBTT) of BCC metals or alloys, and thereby advancing the development of cost-effective cryogenic-resistant alloy materials.
2. DBT of BCC Metals
The low-temperature brittleness of BCC metals stems from the competitive mechanism between hindered screw dislocation motion and cleavage fracture. At low temperatures, screw dislocations exhibit significantly diminished mobility, whereas edge dislocations maintain relatively high mobility. The velocity ratio between screw and edge dislocations (α = vs/ve, where α is the dislocation source efficiency, vs is the screw dislocation motion rate, and ve is the edge dislocation motion rate) becomes the critical parameter governing DBT. When the temperature decreases below the DBTT, α undergoes a precipitous decline, rendering F-R dislocation sources incapable of sustained multiplication. Consequently, crack tips cannot release stress through dislocation emission, ultimately resulting in brittle fracture. Fundamentally, this phenomenon arises from the dynamic competition between screw and edge dislocations, manifesting the synergistic relationship between dislocation motion and microstructural evolution.
2.1. DBT Behavior of BCC Metals
In the 1950s, Petch et al. [18,19] proposed that dissociative fracturing occurs once the stress reaches the stress required for crack extension. Thomson et al. [4] proposed a crack passivation model by calculating the dislocation emission energy at the crack tip. Samuels et al. [20] developed a dynamic crack tip passivation model. Hirsch and Roberts et al. [21] pointed out that the dislocation motion can be useful in hindering crack extension. These experiments and simulation calculations related to fracture mechanics [9,22,23,24,25,26,27,28] are important theoretical foundations for explaining the ductile–brittle transition behavior of BCC metals. Zhang et al. [29] conducted systematic numerical simulations to study the low-temperature brittle fracture behavior of BCC metals, as illustrated in Figure 1a,b. Their findings revealed that the uncertainty distribution characteristics of four distinct crack propagation pathways are closely associated with the low-temperature brittleness of BCC metals, indirectly reflecting the material’s brittle fracture behavior at low temperatures. As shown in Figure 1c [30], the transition from ductile to brittle fracture in BCC metals occurs as the temperature decreases. Its fracture behavior has remarkable features: a lack of thermal activation at low temperatures leads to the dislocation motion being hindered, and the plastic deformation ability of the material is reduced, while the stress concentration is intensified, and the rapid expansion of microcracks ultimately leads to brittle fracture. Above the DBTT, ductile fractures are dominated by slow crack propagation with a characteristic dimpled morphology; below the DBTT, brittle fractures feature rapid crack extension manifested by cleavage steps and river patterns; and in the DBT zone, a hybrid fracture morphology emerges, combining localized dimples with cleavage features, indicative of competing plastic deformation and brittle fracture mechanisms. Du et al. [31] investigated the microstructural evolution and fracture behavior of three typical BCC metals (tantalum (Ta), iron (Fe), and tungsten (W)) at low temperature using a multiscale quasi-continuum method. Their results showed that Ta exhibits ductile fracture behavior due to dislocation emission at the crack tip and energy dissipation through twinning bands, which suppresses crack propagation. Iron (Fe) undergoes plastic deformation via dislocations and twins in the early stages but transitions to brittle fracture in the later stages, showing high sensitivity to DBT. Tungsten (W) experiences delayed crack propagation due to dislocation activity and twin formation but is unable to effectively suppress brittle fracture, resulting in predominantly brittle fracture behavior. Zhao et al. [32] experimentally analyzed the impact fracture morphology of ultra-low-carbon high-strength steel with different microstructures at low temperature and found the following: in Figure 2a, the impact energy of S1 decreases sharply with decreasing temperature, while the ductility of S2/S3 decreases more gently, and the DBTT values of S1, S2, and S3 are estimated to be −39 °C, −72 °C, and −101 °C. In Figure 2b, the fracture pattern of S1 at low temperatures is a large area of cleavage river patterns without obvious traces of plastic deformation, which represents a brittle fracture. In Figure 2c, the fracture pattern of S2 is a mixture of quasi-cleavage and dimples, which is a mixed brittle–tough fracture. In Figure 2d, the fracture morphology of S3 is dominated by ductile fracturing with more dimples and a smaller quasi-cleavage region.
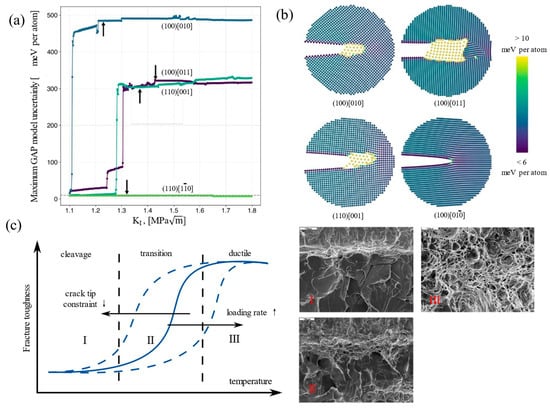
Figure 1.
Fracture predictions of Fe-GAP18 (an existing Gaussian approximation potential for ferromagnetic BCC iron) trained on Dragoni et al.’s original database (Reprinted from Ref. [29]) and fracture toughness in the DBT region (Reprinted from Ref. [30]). (a) Maximum model uncertainty during fracture simulations of four crack systems; (b) simulation snapshots colored by the model’s uncertainty; (c) fracture toughness in the DBT region.
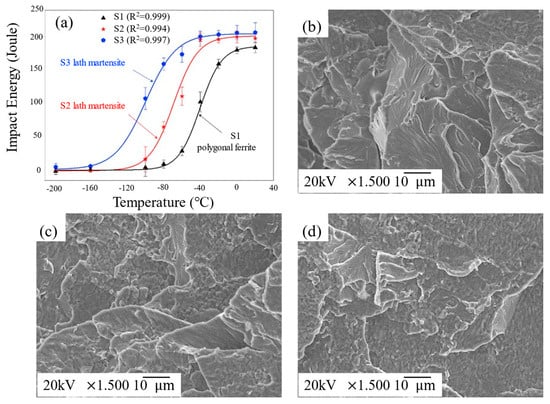
Figure 2.
(a) The impact energy vs. test temperatures along with the Boltzmann function fitting based on the experimental data (Reprinted with permission from Ref. [32], 2019, Elsevier). Typical impact fracture surfaces of steels fractured at −40 °C for (b) S1 (the rolled sample was austenitized at 900 °C for 0.5 h, followed by water quenching), (c) S2 (the other homogenization-treated ingot was forged to 55 mm thickness; the as-forged sample was rolled at 1000 °C down to 12 mm in thickness and water-quenched), and (d) S3 (the S2 steel was austenitized at 900 °C for 0.5 h, followed by water quenching).
The following are the critical factors governing low-temperature ductile/brittle fracture behavior and structural evolution in BCC metals. (1) Crystal structure and slip systems. Figure 3a [33] illustrates the DBTT curves for FCC, HCP, and BCC metals. BCC metals exhibit significant low-temperature brittleness. FCC metals with 12 independent slip systems ({111} <110>) undergo uniform plastic deformation due to the multi-slip systems and typically do not exhibit DBT. HCP metals with only three slip systems ({0001} <11–20>) have minimal plastic deformation ability and are nearly brittle at room temperature, without significant DBT variation upon cooling [34]. BCC metals have a slip direction of <111>, and slip planes such as {110}, {112}, and {123}, totaling 48 independent slip systems; however, compared with FCC metals, the effective slip systems are limited at low temperatures. The atomic arrangement is not compact enough, as shown in Figure 3b, and the Peierls potentials are high, which leads to dislocation cross-slip difficulties and exacerbates stress concentration and brittle fracture. The difficulty of screw dislocation slip requires overcoming the Peierls potential, further limiting its movability. (2) Dislocation behavior with Peierls potential: At low temperatures, screw dislocations rely on thermal activation for double-kink nucleation. Insufficient thermal activation leads to low nucleation rates, causing dislocation plugging that initiates microcracks. Solute atoms such as real earth (Re) and nickel (Ni) enhance screw dislocation mobility by lowering the Peierls potential. A representative example is provided by Raffo et al. [35], whose experimental studies on W–Re alloys demonstrated that adding 1% Re significantly reduced the DBTT. (3) Grain boundary and impurity elements: The segregation of impurities such as phosphorus (P) and sulfur (S) at the grain boundaries reduces the boundary binding energy and causes intergranular brittle fractures. Adding rare earth elements like cerium (Ce) or lanthanoids (Las) mitigates detrimental inclusions (e.g., MnS), purifies grain boundaries, and refines the grain structures, thereby significantly enhancing low-temperature impact toughness. A representative case is demonstrated by Dong et al. [36], where rare earth-modified HRB400E rebar exhibited a 117% increase in impact energy at −20 °C. (4) Temperature and strain rate: As a result of insufficient thermal activation energy at low-temperature/high-strain-rate conditions, dislocations have difficulty overcoming the Peierls potential, which can cause stress concentrations to initiate brittle fracture. A representative example is shown in the study by Riedle et al. [37], who found that pure tungsten (W) undergoes cleavage fracture at liquid nitrogen temperatures (77 K). The results of the multiscale dislocation dynamics simulations conducted by P. El. Ters et al. [38] are shown in Figure 4a, which demonstrates that small-size grains (0.5 μm) show jagged fluctuation at 300 K, manifesting as localized brittleness of the dislocations. Conversely, adequate thermal activation enhances dislocation mobility under high-temperature/low-strain-rate conditions, enabling the material to exhibit ductile behavior. Figure 4a–c shows smoother curves with increasing temperature, indicating an increase in toughness. In Figure 4d, the hardening step of 0.5 μm grains disappears at 600 K, which is higher than that at 300 K, indicating that the temperature increase weakens the dislocation plugging effect and enhances the toughness.
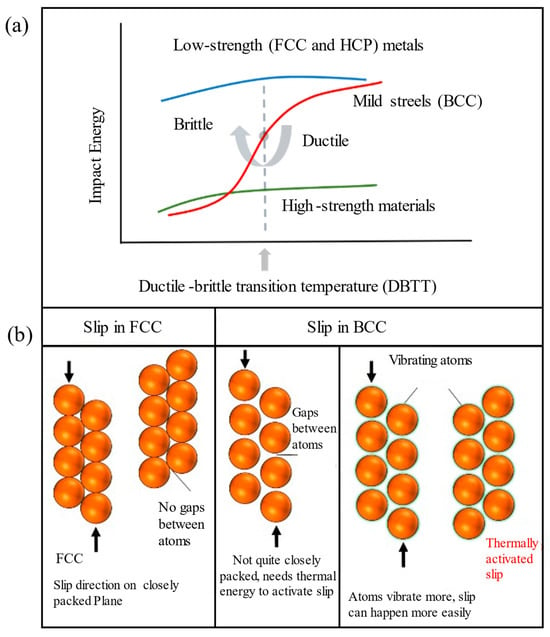
Figure 3.
(a) Schematic diagram of the ductile and brittle behavior of three crystalline structures of metals or alloys (Adapted from Ref. [33]). (b) Comparison of BCC and FCC metal slip systems (https://msestudent.com/what-is-the-difference-between-fcc-and-bcc-crystal-structure-properties-interstitial-sites-and-examples, accessed on 24 January 2020).
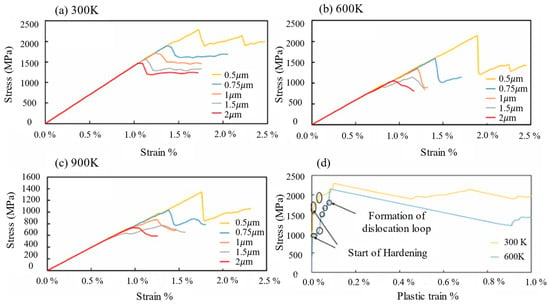
Figure 4.
Stress–strain curves at different sizes for (a) 300 K, (b) 600 K, and (c) 900 K. (d) Stress vs. plastic strain for 0.5 μm at 300 K and 600 K (Reprinted with permission from Ref. [38], 2023, Elsevier).
2.2. Dislocations in DBT of BCC Metals
Extensive computational studies [39,40,41] have established that screw dislocations in BCC metals exhibit a discrete three-dimensional core structure, which results in significant lattice friction during their movement. The slip of these dislocations is a thermally activated process that becomes increasingly hindered as the temperature decreases. A representative example is chromium (Cr) [8], in which the substantial increase in Peierls potential at low temperatures makes dislocation slips particularly difficult. The pronounced low-temperature DBT behavior observed in BCC metals is attributed to their unique crystal structures and dislocation behaviors. The deformation characteristics are closely related to the DBT mechanism, which mainly involves the coordinated effects of dislocation nucleation, dislocation motion, and the relative motion rates of screw dislocations and edge dislocations.
(1) Dislocation nucleation dominance: Research by Rice et al. [4,42,43] showed that the stress concentration at crack tips during material deformation is blunted by dislocation nucleation and motion, a process regulated by temperature and strain rate. At elevated temperatures, thermal activation facilitates rapid dislocation nucleation, forming a passivation zone that inhibits crack propagation, leading to ductile behavior. Conversely, dislocation nucleation is hindered at low temperatures, causing stress concentrations to persist and trigger brittle fractures. Thus, dislocation nucleation governs crack propagation and dominates the DBT behavior in BCC metals. (2) Dislocation motion dominance: Gumbsch et al. found that the stress concentration at the crack tip is dynamically regulated by dislocation mobility through three-point bending experiments [2], and Brunner et al. [44,45,46,47] studied tungsten (W) metal. Dislocations are highly mobile under high-temperature or low-strain-rate conditions, rapidly migrating to the crack tip to form dislocation sources and passivate the crack, resulting in ductile behavior and a lowering of the DBTT. Conversely, dislocation motion is restricted at low temperatures or high strain rates, preventing stress release and leading to brittle fracture with an elevated DBTT. This behavior reflects a dynamic equilibrium between dislocation migration rates and stress concentration accumulation rates, which determines the DBT in BCC metals through the coupling of temperature and strain rate. (3) Relative motion rate control of screw–edge dislocation: Han et al. [8,9,42,48] found that the DBT is controlled by the ratio of the relative motion rates of the screw dislocations to the edge dislocations (α = vs /ve) [8,49], which determines the plasticity capability of the material by regulating the multiplication efficiency of the F-R dislocation source; the specific mechanism is shown in Figure 5 [8,10]. When α ≥ 0.5, edge dislocations bow out beyond the semicircle, screw dislocations dominate the slip surface and efficiently proliferate the F-R dislocation source, the plastic mechanism dominates, and the material exhibits ductility. When α < 0.5, dislocations are difficult to coordinate, dislocation sources fail, and stress-concentrated brittle fractures dominate. In high-temperature nanoindentation experiments [8], the team found that the screw dislocation mobility was significantly increased with temperature, and the α value also increased with temperature, promoting the activation of dislocation sources and reducing the DBTT. In chromium (Cr), the critical α value for DBT was identified as 0.7, corresponding to a morphological transition in dislocation bow-out from semicircular configurations to fully activated F-R source geometries [8]. Quantitative theoretical modeling [10] further correlates dislocation source efficiency directly with the vs/ve mobility ratio, establishing α as a fundamental microstructural parameter for predicting ductile versus brittle failure modes.
where x and y denote the slip distances of the edge dislocation and screw dislocation, respectively; r is the radius of the dislocation source; the major axis of the ellipse is (x + r); the minor axis of the ellipse is (y + r); and the ratio of the major and minor axes of the ellipse is k.
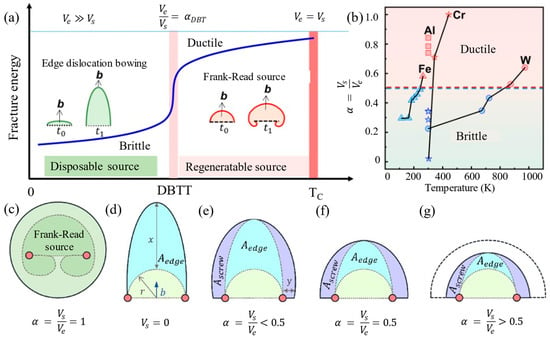
Figure 5.
Mechanism of the relative mobility of the screw versus edge dislocations controlling the DBT in metals (Reprinted from Ref. [8]. and Reprinted with permission from Ref. [10], 2025, Elsevier). (a) The relative mobility of dislocations determines the efficiency of the dislocation source (TC—critical temperature; ve—edge dislocation velocity; αDBT—the α value at DBTT; α—velocity ratio of screw dislocation and edge dislocation; t0—time before dislocation bow-out; t1—time after dislocation bow-out); (b) the relative mobility of screw versus edge dislocations with temperature for Cr, Al, W, and Fe; (c) efficient operating F-R dislocation source with α = 1; (d) disposal dislocation source with α = 0; (e) dislocation source with lower efficiency (α < 0.5); (f) dislocation source with an efficiency of α = 0.5; (g) dislocation source with higher efficiency (α > 0.5).
The DBT in BCC metals fundamentally arises from the dynamic competition between screw and edge dislocation velocities. This mechanism provides a well-defined microdynamic target for optimizing the low-temperature toughness of BCC metals [50] through controlled dislocation kinematics.
3. Role of Screw Dislocation in the DBT of BCC Metals
Screw dislocations play a pivotal role in governing the low-temperature DBT of BCC metals, exhibiting the strongest temperature dependence. This behavior primarily stems from three mechanistic origins: The first is the temperature dependence of double-kink thermal activation, in which the screw dislocation motion critically relies on thermally activated double-kink nucleation and migration processes. The second is mobility disparity with edge dislocations. At low temperatures, screw dislocations demonstrate significantly lower mobility compared with edge dislocations. This mobility deficit leads to dislocation source inactivation and brittle fracture initiation. The third is the effects of solute atoms. Specific solute atoms enhance low-temperature screw dislocation mobility by perturbing local stress fields, thereby lowering the activation energy barrier for double-kink nucleation. Crucially, double-kink dynamics serve as the pivotal mechanism constraining screw dislocation mobility at low temperatures, and they dominate the DBT behavior in BCC metals.
3.1. Double-Kink Structure in Screw Dislocation
In the plastic deformation of BCC-W, the distinct core structures and energy states of 1/2〈111〉 screw dislocations are intrinsically linked to their double-kink nucleation mechanisms [51,52,53]. In Figure 6 [39,40,54], the green arrow indicates the differential displacement vector used to quantify the degree of lattice distortion caused by dislocations along the direction of the Burr vector [111], the length of which is proportional to the magnitude of the relative displacement between neighboring columns of atoms, with the solid green symbol marking the center of the dislocation core. Screw dislocations exhibit four distinct core structures—easy core, hard core, split core, and saddle point—with significant energy disparities among them. The hard core has the highest energy, and the atomic columns are highly consistent. The saddle point is a transitional state in a dislocation slip path. The easy core energy is the lowest and stable, and the structure is compact and symmetrical. Meanwhile, the split core comes from the maximum energy of severe lattice distortion and is asymmetrically structured, close to the atomic column. This energy gradient dictates the dynamic behavior of screw dislocations, enabling slipping via the double-kink mechanism. Screw dislocations reduce slip resistance by forming a double-kink structure, which surmounts the Peierls potential; the extension of these double kinks toward both ends of the dislocation is also influenced by the Peierls valley. Figure 7a [16] shows the effects on the Peierls valley and Peierls potential of screw dislocations following the substitution of solute atoms for Fe atoms at the dislocation core. According to Cottrell’s dislocation theory [55], the restricted screw dislocation motion at low temperatures arises from a high Peierls potential that hinders thermally activated double-kink nucleation, leading to dislocation pile-ups and subsequent brittle fracture. During dislocation motion, screw dislocations predominantly reside in low-energy Peierls valleys [56] and must overcome periodic Peierls potential. When positioned in the Peierls valley, dislocations encounter minimal resistance to expansion, allowing localized kink folds to form under thermal activation. These kinks subsequently propagate along the dislocation line under shear stress, eventually forming the double-kink structure depicted in Figure 7b. The edged components at the kink steps reduce the activation energy of the extension, causing double kinks to extend to both ends, thus driving the whole screw dislocation forward; however, this structure makes the screw dislocation slip path complex, leading to increased lattice friction and difficult slips. If the double-kink nucleation is insufficient, the dislocation motion is blocked and drives the material toward brittle fracture. Consequently, the nucleation and migration of double-kink structures are dominated by thermally activated processes and exhibit the strongest temperature dependence [17,57,58,59]. The combination of limited lateral slipping of the screw dislocations and rapid movement of the edge dislocations in BCC metals leads to the destruction of the mixed dislocation structure and the formation of long straight screw dislocations [60]. At low temperatures, the disparity between fast-moving edge dislocations and slow-moving screw dislocations prevents the evolution of an effective dislocation source, insufficiently producing mobile dislocations and inducing brittleness. As the temperature increases, thermal activation facilitates double-kink nucleation [10]. For instance, the effective formation of screw dislocation double kinks in W metal is approximately 1.05 eV [49], which lies near the DBT threshold. Minor temperature reductions significantly suppress double-kink nucleation.
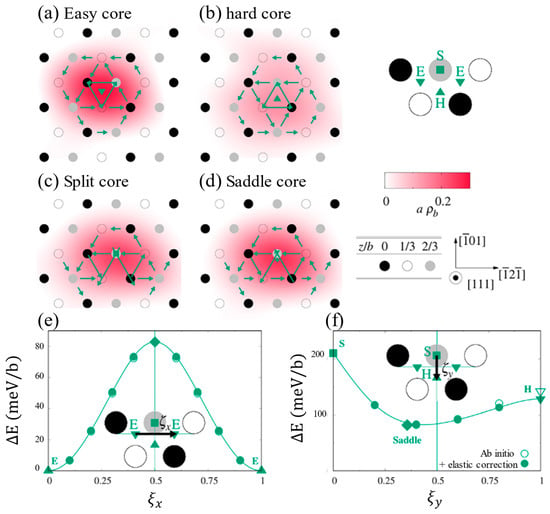
Figure 6.
Core structures of the ½ <111> screw dislocation in BCC-W and its energetic changes (Reprinted with permission from Ref. [39], 2016, Spring Nature, and Reprinted with permission from Ref. [40], 2014, APS, and Reprinted with permission from Ref. [54], 2021, Elsevier). (a) easy; (b) hard; (c) split cores; (d) saddle configuration; (e) Peierls barrier, i.e., the minimum energy path between adjacent easy cores; (f) straight path between split and hard cores, i.e., the saddle configuration.
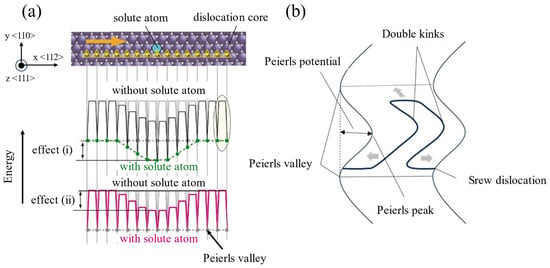
Figure 7.
(a) Schematic diagram of the influence of solute atoms on the screw dislocation slip energy barrier (Reprinted with permission from Ref. [16], 2017, Elsevier). (b) Schematic diagram of double kinks.
Trinkle et al. [12,13,17] demonstrated through first-principles calculations and experimental studies that certain solute atoms, such as Re and Pt, can effectively enhance the formation of double kinks in the screw dislocations of BCC metals. These solutes significantly reduce dislocation motion resistance by lowering the formal energy barriers associated with double-kink nucleation, thereby promoting their nucleation and growth.
Screw dislocations overcome slip resistance by forming double-kink structures, which must overcome the Peierls potential. The expansion of these double kinks toward the dislocation ends is also influenced by the Peierls valleys. The Peierls–Nabarro stress dominates the dislocation motion, with solute atoms contributing to the nucleation of the double kinks by reshaping the electronic structure of the core of the dislocation and the strain field. Wakeda et al. [16] further revealed through first-principles calculations that solute atoms can promote double-kink nucleation by reducing the energy difference (∆E) and Peierls potential associated with screw dislocations transitioning from the easy core to the hard core. For example, silicon (Si) significantly lowers the Peierls potential by reconstructing the electron cloud or inducing lattice distortion, reducing ∆E from 150.6 meV in pure iron (Fe) to approximately 50 meV. P reduces ∆E and the Peierls potential through charge transfer and bond electron cloud rearrangement, enabling screw dislocations to form double kinks even at low temperatures. Aluminum (Al), through its light atomic size effect and electronic interactions, modifies the local stress field within the dislocation core, lowering the formal energy barrier. In pure iron (Fe), aluminum (Al) reduces ∆E from 150.6 meV to approximately 80 meV, thereby facilitating double-kink nucleation. These mechanisms highlight how solute atoms promote double-kink nucleation in BCC metals by altering the core energetics and electronic configurations.
3.2. Low-Temperature Mobility of Screw Dislocations
The low-temperature mobility of screw dislocations constitutes the critical limiting factor for the low-temperature DBT in BCC metals. The F-R dislocation sources play a pivotal role in screw dislocation multiplication. Insufficient screw dislocation mobility at low temperatures reduces the number of mobile dislocations, leading to stress concentration and brittle fracture initiation. While edge dislocations can slide relatively easily, they alone cannot fulfill the extensive plastic deformation demands, particularly at low temperatures when screw dislocations are significantly less mobile than edge dislocations. This disparity hinders the effective self-proliferation of dislocations, resulting in stress concentration and brittle fracture, and causes a sudden DBT in BCC metals. The motion of screw dislocations requires the Peierls potential to be overcome through the formation of double kinks via thermal activation. Figure 8 [49] illustrates the structural evolution of rolled tungsten (W) at different temperatures, visually demonstrating the recovery of screw dislocation motion with increasing temperature. Below the DBTT, the relative motion rate ratio between screw and edge dislocations (α = vs/ve) decreases significantly. The nucleation and migration of double kinks in screw dislocations become increasingly difficult, leading to reduced motion and dislocation source failure. Consequently, the material cannot relieve stresses through plastic deformation, resulting in the dominance of brittle fractures. Near the DBTT, rising temperatures promote the thermal activation of screw dislocations, which enables some to migrate and bend. This enhances the dislocation source’s efficiency and crack tip blunting, initiating the DBT [61,62,63,64]. Above the DBTT, thermal activation facilitates rapid nucleation and migration of double kinks, allowing screw dislocations to move as bent mixed dislocations. This effectively suppresses crack nucleation and propagation, enabling significant plasticity and completing the DBT [13]. As the temperature increases further, the mobility of screw dislocations also accelerates; double kinks nucleate and migrate rapidly; and screw dislocations move as bent mixed dislocations, releasing stress and inhibiting crack propagation, thereby imparting toughness to the material. At low temperatures, the mobility of screw dislocations is limited by the nucleation rate of double kinks. Although the edged component of double kinks reduces the extension activation energy, the overall energy barrier for nucleation results in a screw dislocation mobility that is several orders of magnitude lower than that of the edge dislocations. Additionally, the elevated critical initiation stress of screw dislocations at low temperatures further restricts their mobility. Solute atoms can effectively modulate this process by perturbing the local stress field, thereby reducing the activation energy for double-kink nucleation in screw dislocations and promoting their initiation at low temperatures. Woodward et al. [17] demonstrated that Re solute atoms in Mo–Re alloys attract screw dislocation cores, lowering the energy barrier for double-kink nucleation. Below 350 K, the presence of Re solute significantly enhances the nucleation rate of double kinks and improves the mobility of screw dislocations.

Figure 8.
Evolution of dislocation structures in rolled tungsten before and after DBT (Reprinted with permission from Ref. [49], 2021, Elsevier). (b—Burgers vector). (a) Pre-existing dislocations before testing, (b) below the DBTT, (c) at the DBTT, and (d) above the DBTT.
The low-temperature ductility and DBT of BCC metals are predominantly governed by the mobility of screw dislocations at low temperatures. This dominance arises because, unlike edge dislocations, the mobility of screw dislocations is essential for activating and proliferating F-R dislocation sources, which facilitates extensive plastic deformation in BCC metals under low-temperature conditions. The low-temperature mobility of screw dislocations is closely tied to the number of double kinks on the dislocation. The edged component at the kink step allows the kink pair to expand to both ends of the screw dislocation with a smaller activation energy, thus driving the entire screw dislocation forward.
4. Dilute Solid Solution Softening Effect
The dilute solid solution softening effect refers to a unique phenomenon where low-concentration solutes (alloy content < 1 at. %) induce metal softening at low temperatures. This effect arises from solute-induced lattice distortions that reduce the Peierls potential, thereby weakening dislocation pinning and promoting the motion of screw dislocations [65,66,67]. The mechanisms include (1) solute-induced local atomic rearrangement that lowers double-kink nucleation (the Peierls mechanism); (2) kink-slip bypass pinning points; and (3) promoting cross-kink unpinning. Additionally, the attraction interaction between solutes and dislocations enhances dislocation mobility by reducing double-kink nucleation energy barriers (e.g., Re in W–Re and Mo–Re alloys), decreases critical resolved shear stress (CRSS), improves the plastic deformation capability, and delays brittle fracture. This effect is particularly pronounced in BCC metals, manifesting as a significant decrease in low-temperature flow stress.
4.1. Dilute Solid Solution System and Softening Effect
A dilute solid solution system refers to solid solutions with solute atomic concentrations (alloy content < 1 at. %) within the matrix lattice without forming ordered phases or precipitates. While solute atoms typically act as solid solution strengtheners by hindering dislocation motion, the dilute solid solution softening effect describes a unique phenomenon where specific solute additions lead to material softening at low temperatures. This effect occurs because solute atoms reduce the Peierls potential associated with screw dislocation double-kink nucleation, thereby weakening the pinning effect on dislocations. By lowering the energy barriers for kink formation and propagation, solute atoms enhance dislocation mobility, reduce CRSS, and improve plastic deformability. Additionally, this softening mechanism promotes the plastic deformation capability of the material and delays the occurrence of brittle fractures.
The dilute solid solution softening effect is a unique phenomenon caused by low-concentration solutes (alloy content < 1 at. %) enhancing dislocation mobility through mechanisms involving reduced Peierls potential and enabling mechanisms such as kink-slip and unpinning. In dilute solid solution systems, the motion of screw dislocation is governed by three primary mechanisms, as illustrated in Figure 9 [68].
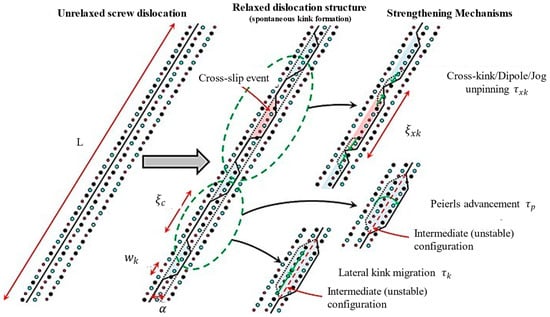
Figure 9.
Structure and motion of screw dislocations in dilute solution systems (Reprinted with permission from Ref. [68], 2020, Elsevier).
(1) Peierls mechanism [69,70,71,72]: In dilute solid solutions, solute atoms induce local lattice distortions that facilitate dislocation motion by reducing the energy required for double-kink nucleation. This directly weakens the Peierls potential, thereby promoting material softening.
(2) Kink-slip mechanism [68]: In dilute solid solution systems, where solute atom concentrations are low, dislocations are more likely to bypass pinning points via kink-slip. This reduces the pinning effect and lowers resistance to dislocation motion, enabling kinks to extend more readily and causing material softening.
(3) Cross-kink and unpinning mechanisms [68,73,74]: The formation of cross-kink mechanisms relies on solute-induced multi-slip surface kinks. In dilute solid solution systems, solute atoms promote kink formation and pinning, but the resistance to kink extension remains low. This allows dislocations to unpin and continue gliding, resulting in the softening behavior of the material.
4.2. Dilute Solid Solution Softening Mechanim
The mechanism of dilute solid solution softening appears to be the effect of solute atoms on dislocation motion, i.e., the effect of the screw dislocation’s double-kink structure. Solute atoms reduce the nucleation energy barrier of double kinks by interacting with the dislocation core, thereby promoting dislocation mobility and material softening. The study by Weertman et al. [58] demonstrated that solute atoms facilitate localized atomic rearrangements along dislocation lines, enabling double-kink nucleation at lower stress levels. The motion of screw dislocations at low temperatures depends on the nucleation and migration of double kinks. Solute atoms lower the nucleation barrier by modifying the local energy landscape of the dislocation core. In pure BCC metals (e.g., iron (Fe)), periodic energy barriers of uniform height arise from the Peierls potential [75,76,77]. In contrast, solute atoms in dilute solid solutions reduce the energy barrier for double-kink formation, particularly in regions along the dislocation line where localized solute fluctuations enhance kink nucleation. However, solute atoms increase the migration barrier for kinks, as they must overcome the maximum energy barrier along the dislocation line [13]. Figure 8 [16] illustrates that solute atoms are positioned centrally and migrate along the screw dislocation line by overcoming energy barriers. In dilute solid solution systems at low temperatures, solute additions alter the double-kink structure of screw dislocations [78,79], thereby softening the metallic matrix [17]. Additionally, attractive forces exist between solute atoms and dislocation lines. At low concentrations, these attractive solutes exert a pulling effect on the dislocation core, reducing the Peierls potential for dislocation motion. This interaction promotes dislocation mobility and ultimately leads to material softening.
The dilute solid solution softening in BCC metals is effectively promoted by certain solute atoms that enhance screw dislocation double-kink nucleation in dilute solid solution systems. Curtin et al. [12] demonstrated that in W–Re alloys, low concentrations of Re interact attractively with the screw dislocation cores, reducing the activation energy for double-kink nucleation. The local stress field perturbations caused by Re lower the resistance to kink extension, facilitating screw dislocation slip at low temperatures. Density functional theory (DFT) calculations indicate that the interactions of Re solutes with screw dislocations significantly reduce the nucleation energy barrier. Experimental data show a 30% reduction in yield stress for a W-1% Re alloy at 300 K compared with pure tungsten (W). The Wiener Process Model (WPM) predicts that Re’s addition makes double-kink nucleation the dominant mechanism by reducing energy fluctuations during migration, ultimately achieving low-temperature softening. Zhang et al. [80] found that in W–Re alloys, the hardness was the lowest when the Re content was 5 wt.%, showing solid solution softening. In Fe–Si alloys, low concentrations of silicon (Si) atoms reduce the nucleation energy barrier for double-kink nucleation through local lattice distortions. Energy fluctuations induced by silicon (Si) atoms promote double-kink nucleation, lowering the Peierls potential and enhancing the low-temperature mobility of screw dislocations. Both the Discrete Rigid-Kink Model (DRKM) and the Stochastic Rigid-Kink Model (SRKM) demonstrate that Si atoms reduce nucleation energy barriers, shifting plastic deformation from kink-controlled to migration-controlled, ultimately resulting in material softening. Trinkle [17] noted that in Mo–Re alloys, the softening effect is most pronounced at low temperatures (77 K) with an 8% Re concentration, where yield stress is reduced by about 30% compared with pure molybdenum (Mo). Double-kink deformation cores dominate this softening, confirming the solute-facilitated softening mechanism. In Mo–Pt alloys, strong attractive interactions between the concentration of platinum (Pt) solutes (alloy content ≪ 1 at. %) and dislocations significantly reduce the double-kink nucleation energy barrier, resulting in initial softening. Ghafarollahi et al. [12] studied Fe–Si alloys and found that silicon (Si) atoms reduce the energy barrier to double-kink nucleation through localized energy fluctuations, thereby promoting low-temperature softening. Wakeda et al. [16] discovered that solute atoms modify the local bonding environment in screw dislocation cores through chemical misfit (the first-principles interaction energy with the “easy core” structure correlates highly with the change in the γ-surface caused by solute atoms), thereby modulating the Peierls barrier and achieving solute softening. A strong correlation exists between chemical misfit (∆γ) and interaction energy (Eint(0)) in Figure 10c,d [16], independent of ΔEM, indicating that solute atoms significantly influence the local energy state of screw dislocations in the easy core by altering the local chemical bonding environment (e.g., the difference in the strength of Fe–solute and Fe–Fe bonds). Solute atoms (e.g., Si, Cu) exhibit negative ∆γ values by lowering the local bonding energy, stabilizing the easy core and reducing the energy difference between the transition-state hard core and M-points. This lowers the Peierls potential and promotes dislocation slip, manifesting as low-temperature softening. In addition, Sc forms strongly attractive dislocation–solute interactions through chemical misfit, creating energy valleys that reduce the activation energy for double-kink nucleation. This accelerates dislocation slip rates, enhances low-temperature dislocation mobility, decreases CRSS, and ultimately manifests as solute softening.
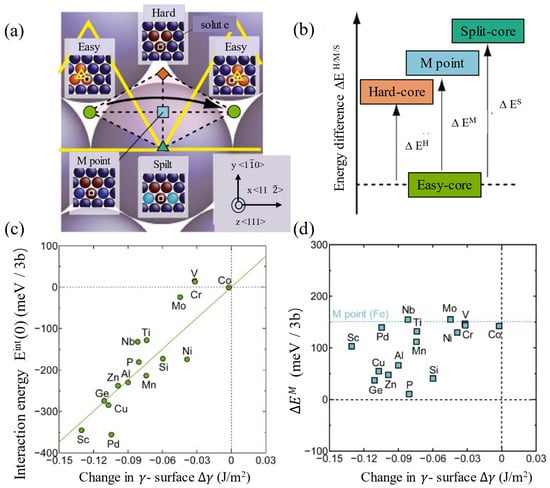
Figure 10.
The schematic of the effects of a solute atom on the energy surfaces for screw dislocation slip motion (Reprinted with permission from Ref [16], 2017, Elsevier). (a) Transformation of the dislocation core structure during the slip process; (b) energy differences in dislocation core structures; (c) the values of Eint(0) are plotted as functions of the change in the γ-surface ∆γ in the panels; (d) the values of ∆EM are also plotted as functions of the change in the γ-surface ∆γ in the panels.
The core mechanism of dilute solid solution softening in BCC metals lies in the solute atoms effectively promoting double-kink nucleation and propagation by modulating the bonding environment and energy fluctuations, and perturbing the stress field at the screw dislocations’ cores. This mechanism provides crucial theoretical guidance for the design of high-performance BCC alloys.
5. Potential of Dilute Solid Solution Softening in Lowering the DBTT
The DBTT is the critical temperature at which a metallic material transitions from a ductile to a brittle behavior, and lowering the DBTT enhances the low-temperature ductility. The dilute solid solution softening mechanism significantly lowers the DBTT through solute atom microalloying and regulation of the dislocation dynamics. The effect originates from two primary aspects: on the one hand, controlling impurities and inclusions is crucial. It is widely accepted that the low-temperature toughness of low-alloy steels after the addition of rare earth (Re) is attributed to inclusion modification and grain boundary purification. Modern research and metallurgical techniques have enabled the control of impurity elements and inclusions at very low levels. For example, Liu et al. [81] demonstrated that adding an appropriate amount of cerium (Ce) to C-Mn steel purifies the grain boundaries and suppresses the formation of large irregular sulfur (S)- or titanium (Ti)-containing inclusions. This reduces the risk of cleavage fracture in C-Mn steels at low temperatures, increases resistance to crack propagation, significantly improves low-temperature toughness, and lowers the DBTT. However, such approaches remain constrained by the inherent limitations of ferrite matrix in further reducing the DBTT. On the other hand, the dilute solid solution softening effect after the addition of rare earth solid solutions plays a significant role. Solute atoms (e.g., Ni, Mn, Si) promote low-temperature dislocation slips by reconfiguring the electron clouds in the dislocation core or inducing lattice distortions, thereby reducing the Peierls–Nabarro stress and the double-kink nucleation energy barrier. For example, Tanaka et al. [82] found that adding 2 mass% nickel (Ni) to ultra-low-carbon (C) steel decreased the DBTT from 200 K to 150 K. The yield stress was lower than that of the nickel (Ni)-free matrix, exhibiting significant solid solution softening. Wakeda et al. [16] noted that silicon (Si) in Fe–Si alloys reduced the double-kink nucleation energy barrier from 150.6 meV in pure iron (Fe) to 50 meV, leading to a DBTT reduction of about 50 K; scandium (Sc) also formed strong interactions with dislocations through chemical misfit, creating energy valleys that significantly lowered the activation energy for double-kink nucleation and promoted low-temperature dislocation slip dynamics. This solute softening effect enhances low-temperature plastic deformability by reducing the CRSS, suppressing brittle fracture tendencies, and ultimately leading to a significant reduction in the DBTT. Hu et al. [78] investigated the solute-induced softening effect of 21 alternative alloying elements (Al, Co, Cr, etc.) in BCC-W and found that aluminum (Al) and manganese (Mn) are the most promising alternative solute elements to Re for improving the low-temperature toughness of BCC-W, capable of significantly reducing the DBTT. Solute atoms (e.g., Mn, Si) enhance low-temperature toughness by reducing strain-rate sensitivity, thereby potentially lowering the DBTT. Uenishi et al. [83] observed, in interstitial-free (IF) steels, that Mn/Si additions reduce low-temperature brittleness by adjusting the dislocation thermal activation mechanism. In the models of Sato and Meshii et al. [68], Mn solute atoms inhibit brittle fracture by introducing misfit strain centers, reducing the double-kink nucleation energy barrier, and making dislocations more prone to slip at low temperatures. These findings collectively highlight the importance of solute atom interactions in enhancing low-temperature toughness and reducing the DBTT in BCC metals.
In summary, the dilute solid solution softening mechanism, combined with the unique role of solute atoms, particularly rare earth elements, overcomes the limitations of traditional inclusion modification and offers a novel approach to reducing the DBTT. By leveraging the grain boundary purification capability of rare earth elements and the electron/strain effects of solutes such as scandium (Sc) and nickel (Ni), a synergistic improvement in low-temperature toughness can be achieved. This approach not only enhances the mechanical performance of materials at low temperatures but also accelerates the development of high-strength, low-temperature-resistant materials for applications in extreme environments, such as polar engineering and aerospace.
6. Conclusions and Prospects
This paper reviews the low-temperature brittle fracture behavior and dilute solid solution softening effects of BCC metals. The DBT behavior of BCC metals is mainly governed by the low-temperature mobility of screw dislocations, whose core mechanism is the nucleation and migration of double kinks. Dilute solid solution softening reduces the nucleation activation energy of the double kinks of screw dislocations through the action of solute atoms on the double kinks of screw dislocations and weakens the Peierls potential, thus enhancing the screw dislocation mobility and lowering the DBTT. The addition of specific alloying elements, such as Ce, Re, and Ni, to BCC metals can effectively promote the dilute solid solution softening effect, reduce the DBTT, and improve the low-temperature toughness. Rare earth elements, due to their unique atomic and electronic structures, show significant potential for enhancing the properties of BCC metals. However, the mechanisms through which these elements improve low-temperature toughness remain unclear and warrant further investigation. The principal conclusions and prospects are summarized as follows.
Conclusions:
(1) BCC metals exhibit fewer effective slip systems and higher dislocation motion resistance compared with FCC metals at low temperatures, making them prone to stress concentration and eventual brittle fracture. This pronounced low-temperature brittleness is attributed to the high Peierls potential, which hinders screw dislocation motion. The resulting dislocation pile-up triggers significant DBT, leading to a distinct DBTT and brittle fracture.
(2) The DBT mechanism in BCC metals is primarily governed by the low-temperature mobility of screw dislocations, which overcome the Peierls potential through the nucleation and migration of double kinks. Their motion is thermally activated and regulated by temperature-dependent processes. When the ratio of the relative motion rates of the screw dislocations to the edge dislocations α ≥ 0.5, the screw dislocations dominate the slip surface and activate the F-R dislocation source to proliferate dislocations efficiently, which makes the material ductile. Conversely, when α < 0.5, the source of dislocations fails to proliferate, which leads to brittle fracture caused by stress concentration.
(3) The low-temperature mobility of screw dislocations in BCC metals is dominated by the nucleation rate of double kinks. Overcoming the Peierls potential involves thermally activated nucleation and migration processes. Nucleation requires the dislocation segments to surmount the energy barrier of the Peierls potential, while migration is influenced by residual potential barriers. Solute atoms reduce this energy barrier, promoting double-kink nucleation and enhancing dislocation slip rates. Insufficient thermal activation at low temperatures reduces the nucleation rates, causing dislocations to become trapped in the Peierls valleys, leading to pile-up and brittle fracture. Alloying counteracts this limitation by systematically reducing the nucleation barriers, effectively restoring dislocation mobility at low temperatures, and mitigating brittleness.
(4) The dilute solid solution softening effect describes how trace solute additions (alloy content < 1 at. %) reduce the formal energy barrier of double kinks in screw dislocations. This is achieved through localized lattice distortions at low temperatures, which increase the nucleation rate of double kinks and enhance the low-temperature mobility of screw dislocations. By promoting the dynamic expansion of double kinks, solute atoms lower the Peierls potential for dislocation slip, thereby improving the low-temperature toughness of BCC metals and significantly reducing the DBTT.
Prospects:
(1) Currently, due to the limitations of low-temperature in situ experimental techniques, research on the DBT mechanism of BCC metals remains focused on theoretical derivations and ex situ experimental validations. Further microscopic and intuitive evidence is required to substantiate the screw dislocation-controlled DBT mechanism and the effects of dilute solid solution softening. Future studies should employ multiscale approaches combining computational simulations (e.g., first-principles calculations, density functional theory, and molecular dynamics simulations) with advanced experimental characterization techniques (e.g., in situ TEM and atom probe tomography) to precisely elucidate the mechanisms by which solid-solution rare earth elements influence the low-temperature toughness and DBT of low-alloyed steels.
(2) The dilute solid solution softening effect of alloying elements serves as a crucial mechanism for enhancing the low-temperature toughness and reducing the DBTT in BCC alloys. By developing an integrated “alloy composition–low-temperature mobility of screw dislocations–low-temperature toughness” design strategy, further breakthroughs can be achieved in improving the low-temperature toughness of BCC alloys. This approach will accelerate the research and development of cost-effective cryogenic alloys, meeting the demand for such materials in applications such as polar engineering, aerospace, and cryogenic storage.
Author Contributions
J.Z. Writing—original draft, Investigation, Data curation. T.Z. Writing—review & editing, Supervision, Methodology, Funding acquisition. T.H. Writing—review & editing, Supervision, Methodology. Y.L. Writing—review & editing, Resources, Investigation. K.W. Writing—review & editing, Resources. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the National Key Research and Development Program (No. 2023YFB3710300) and the National Natural Science Foundation of China (No. 52471090).
Conflicts of Interest
The author Yan Li was employed by the company Shandong Iron and Steel Co., Ltd. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Abbreviations | Full Names | Symbols | Marginal Notes |
| DBT | Ductile-to-brittle transition | ||
| DBTT | Ductile-to-brittle transition temperature | ||
| FCC | Face-centered cubic | ||
| HCP | Hexagonal close-packed | ||
| BCC | Body-centered cubic | ||
| F-R dislocation source | Frank-Read (F-R) source | ||
| Velocity ratio between screw and edge dislocations | α = vs/ve | ||
| Screw dislocation motion rate | vs | ||
| Edge dislocation motion rate | ve | ||
| Ta | Tantalum | ||
| Fe | Iron | ||
| W | Tungsten | ||
| Ni | Nickel | ||
| P | Phosphorus | ||
| S | Sulfur | ||
| Ce | Cerium | ||
| La | Lanthanoids | ||
| Cr | Chromium | ||
| TC | critical temperature | ||
| αDBT | The α value at DBTT | ||
| t0 | Time before dislocation bow out | ||
| t1 | Time after dislocation bow out | ||
| Si | Silicon | ||
| ∆E | Reduced energy difference of solute atoms for the transition from Easy core to the Hard core | ||
| Al | Aluminum | ||
| CRSS | Critical resolved shear stress | ||
| DFT | Density functional theory | ||
| WPM | Wiener Process Model | ||
| DRKM | Discrete Rigid-Kink Model | ||
| SRKM | Stochastic Rigid Kink Model | ||
| Mo | Molybdenum | ||
| Pt | Platinum | ||
| ∆γ | Chemical misfit | ||
| Eint(0) | Interaction energy | ||
| ΔEM | Energy difference between M point and Easy-core | ||
| Re | Rare earth | ||
| Ti | Titanium | ||
| C | Carbon | ||
| Sc | Scandium | ||
| Mn | Manganese | ||
| IF steels | Interstitial-free (IF) steels |
References
- Christian, J. Some surprising features of the plastic deformation of body-centered cubic metals and alloys. Metall. Trans. A 1983, 14, 1237–1256. [Google Scholar] [CrossRef]
- Gumbsch, P.; Riedle, J.; Hartmaier, A.; Fischmeister, H.F. Controlling factors for the brittle-to-ductile transition in tungsten single crystals. Science 1998, 282, 1293–1295. [Google Scholar] [CrossRef]
- John, C.S. The brittle-to-ductile transition in pre-cleaved silicon single crystals. Philos. Mag. 1975, 32, 1193–1212. [Google Scholar] [CrossRef]
- Rice, J.R.; Thomson, R. Ductile versus brittle behaviour of crystals. Philos. Mag. 1974, 29, 73–97. [Google Scholar] [CrossRef]
- Roberts, S.G.; Booth, A.S.; Hirsch, P.B. Dislocation activity and brittle-ductile transitions in single crystals. Mater. Sci. Eng. A 1994, 176, 91–98. [Google Scholar] [CrossRef]
- Tarleton, E.; Roberts, S.G. Dislocation dynamic modelling of the brittle–ductile transition in tungsten. Philos. Mag. 2009, 89, 2759–2769. [Google Scholar] [CrossRef]
- Suzuki, T.; Takeuchi, S.; Yoshinaga, H. Dislocation Dynamics and Plasticity; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Lu, Y.; Zhang, Y.H.; Ma, E.; Han, W.Z. Relative mobility of screw versus edge dislocations controls the ductile-to-brittle transition in metals. Proc. Natl. Acad. Sci. USA 2021, 118, e2110596118. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Ma, E.; Sun, J.; Han, W.Z. A unified model for ductile-to-brittle transition in body-centered cubic metals. J. Mater. Sci. Technol. 2023, 141, 193–198. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Han, W.Z. Dislocation source efficiency as a governing factor in the ductile-to-brittle transition of metals. J. Mater. Sci. Technol. 2025, 229, 173–176. [Google Scholar] [CrossRef]
- Caillard, D.; Martin, J. Thermally Activated Mechanisms in Crystal Plasticity; University of Cambridge: Cambridge, UK, 2003. [Google Scholar]
- Ghafarollahi, A.; Curtin, W.A. Theory of kink migration in dilute BCC alloys. Acta Mater. 2021, 215, 117078. [Google Scholar] [CrossRef]
- Ghafarollahi, A.; Curtin, W.A. Theory of double-kink nucleation in dilute BCC alloys. Acta Mater. 2020, 196, 635–650. [Google Scholar] [CrossRef]
- Pink, E.; Arsenault, R.J. Low-temperature softening in body-centered cubic alloys. Prog. Mater. Sci. 1980, 24, 1–50. [Google Scholar] [CrossRef]
- Lin, P.D.; Nie, J.F.; Cui, S.G.; Lu, Y.P. Molecular dynamics study on the ductile-to-brittle transition in W-Re alloy systems. Acta Mater. 2025, 285, 120684. [Google Scholar] [CrossRef]
- Wakeda, M.; Tsuru, T.; Kohyama, M.; Ozaki, T.; Sawada, H.; Itakura, M.; Ogata, S. Chemical misfit origin of solute strengthening in iron alloys. Acta Mater. 2017, 131, 445–456. [Google Scholar] [CrossRef]
- Trinkle, D.R.; Woodward, C. The chemistry of deformation: How solutes soften pure metals. Science 2005, 310, 1665–1667. [Google Scholar] [CrossRef]
- Petch, N.J. The ductile-brittle transition in the fracture of α-iron: I. Philos. Mag. 1958, 3, 1089–1097. [Google Scholar] [CrossRef]
- Heslop, J.; Petch, N.J. The ductile-brittle transition in the fracture of α-iron: II. Philos. Mag. 1958, 3, 1128–1136. [Google Scholar] [CrossRef]
- Samuels, J.; Roberts, S.G.; Hirsch, P.B. The brittle-to-ductile transition in silicon. Mater. Sci. Eng. 1988, 105, 39–46. [Google Scholar] [CrossRef]
- Hirsch, P.B.; Roberts, S.G. The brittle-ductile transition in silicon. Philos. Mag. 1990, 64, 55–80. [Google Scholar] [CrossRef]
- Han, W.Z.; Lu, Y.; Zhang, Y.H. Mechanism of Ductile-to-Brittle transition in body-centered-cubic metals: A brief review. Acta Metall. Sin. 2023, 59, 335–348. [Google Scholar]
- Chang, S.L.; Li, W.W.; Yu, X.W.; Hui, Y.T.; Zhong, Y.C. Effect of hydrogen on the surface properties and cracking behavior of Ti-6Al-3Nb-2Zr-1Mo alloy welded joint. Corros. Sci. 2025, 249, 112837. [Google Scholar]
- Wu, X.D.; Zhao, T.L.; Hou, T.P. Effect of aging precipitation on the stress corrosion cracking behavior of Ni(Fe, Al)-maraging steel. Available online: http://ijmmm.ustb.edu.cn/article/doi/10.1007/s12613-024-3062-x (accessed on 30 May 2025).
- Seo, L.W.; Kim, J.Y.; Kim, Y.J. Combined Ductile-Brittle Fracture Simulation of API X80 Under Impact Loading. J. Pipeline Sci. Eng. 2025, 100295. [Google Scholar] [CrossRef]
- Jiao, J.S.; Fang, J.; Zhang, J.W.; Rolfe, R. Advancing fracture toughness evaluation: The Weighted Omega metric for enhanced sensitivity to Brittle-to-Ductile transitions and geometric variations. Theor. Appl. Fract. Mec. 2025, 138, 104928. [Google Scholar] [CrossRef]
- Clement, D.; Jacquemoud, C.; Chapuliot, S. A simple criterion to exclude the risk of brittle fracture in the brittle-to-ductile transition temperature range. Eng. Fract. Mech. 2025, 314, 110739. [Google Scholar] [CrossRef]
- Bharadwaja, B.; Alankar, A. Finite element implementation of Field Crack Mechanics for brittle and ductile fracture. Theor. Appl. Fract. Mec. 2024, 131, 104434. [Google Scholar] [CrossRef]
- Zhang, L.; Gabor, C.; Erik, V.D.G.; Francesco, M. Atomistic fracture in bcc iron revealed by active learning of Gaussian approximation potential. NPJ Comput. Mater. 2023, 9, 217. [Google Scholar] [CrossRef]
- Multi-Scale Simulation of Crack Propagation in the Ductile-Brittle Transition Region. Available online: https://www.researchgate.net/publication/257867878_Multi-Scale_Simulation_of_Crack_Propagation_in_the_Ductile-Brittle_Transition_Region (accessed on 1 August 2013).
- Du, H.; Ni, Y.S. Multi-scale simulation and toughness and brittleness analysis of three body-centered cubic metal cracks of tantalum, iron and tungsten. Acta Phys. Sin-Ch. Ed. 2016, 65, 196202. [Google Scholar]
- Zhao, Y.; Tong, X.; Wei, X.H.; Xu, S.S.; Lan, S.; Wang, X.L. Effects of microstructure on crack resistance and low-temperature toughness of ultra-low carbon high strength steel. Int. J. Plast. 2019, 116, 203–215. [Google Scholar] [CrossRef]
- Impact Toughness and Microstructure Characterization of Thermally Aged Alloy 52 Narrow-Gap Dissimilar Metal Weld. Available online: https://www.researchgate.net/publication/312895036_Impact_toughness_and_microstructure_characterization_of_thermally_aged_Alloy_52_narrow-gap_dissimilar_metal_weld (accessed on 1 November 2016).
- Ha, K.F. Fundamentals of Fracture Physics; Beijing Science Press: Beijing, China, 2000; p. 55. [Google Scholar]
- Raffo, P.L. Yielding and fracture in tungsten and tungsten-rhenium alloys. J. Less Common. Met. 1969, 17, 133–149. [Google Scholar] [CrossRef]
- Wei, S.H.; Lu, H.C.; Liu, T.S.; Wang, C.C.; Xie, X.; Dong, H. Effect of rare earth on low-temperature impact toughness of HRB400E rebar. Chi. Metal. 2022, 32, 16–25. [Google Scholar]
- Riedle, J.; Gumbsch, P.; Fischmeister, H.F. Cleavage anisotropy in tungsten single crystals. Phys. Rev. Lett. 1996, 76, 3594. [Google Scholar] [CrossRef] [PubMed]
- Pascale, E.T.; Mutasem, A. On the investigation of size effect in bcc α-iron under high strain rate and high temperature: Multiscale dislocations dynamics simulation. Eur. J. Mech. A-Solids 2023, 97, 104779. [Google Scholar]
- Dezerald, L.; Rodney, D.; Clouet, E.; Ventelon, L.; Willaime, F. Plastic anisotropy and dislocation trajectory in BCC metals. Nat. Commun. 2016, 7, 11695. [Google Scholar] [CrossRef] [PubMed]
- Dezerald, L.; Ventelon, L.; Clouet, E.; Denoual, C.; Rodnry, D. Ab initio modeling of the two-dimensional energy landscape of screw dislocations in bcc transition metals. Phys. Rev. B 2014, 89, 024104. [Google Scholar] [CrossRef]
- Egorov, A.; Kraych, A.; Mrovec, M.; Drautz, R. Core structure of dislocations in ordered ferromagnetic FeCo. Phys. Rev. Mater. 2024, 8, 093604. [Google Scholar] [CrossRef]
- Han, W.Z.; Lu, Y.; Zhang, Y.H. Research Progress on Tough-Brittle Transition Mechanism of Body-Centered Cubic Metals. Acta Metall. Sin. 2023, 59, 335–338. [Google Scholar]
- Kameda, J. A kinetic model for ductile-brittle fracture mode transition behavior. Acta Metall. 1986, 34, 2391–2398. [Google Scholar] [CrossRef]
- Brunner, D.; Glebovsky, V. Analysis of flow-stress measurements of high-purity tungsten single crystals. Mater. Lett. 2000, 44, 144–152. [Google Scholar] [CrossRef]
- Giannattasio, A.; Roberts, S.G. Strain-rate dependence of the brittle-to-ductile transition temperature in tungsten. Philos. Mag. 2007, 87, 2589–2598. [Google Scholar] [CrossRef]
- Giannattasio, A.; Tanaka, M.; Joseph, T.; Roberts, S. An empirical correlation between temperature and activation energy for brittle-to-ductile transitions in single-phase materials. Phys. Scr. 2007, 89, 2589–2598. [Google Scholar] [CrossRef]
- Giannattasio, A.; Yao, Z.; Tarleton, E.; Roberts, S. Brittle-ductile transitions in polycrystalline tungsten. Philos. Mag. 2010, 90, 3947–3959. [Google Scholar] [CrossRef]
- Lu, Y.; Han, W.Z. Pre-stored edge dislocations-enabled pseudo-toughness in chromium. Acta Mater. 2023, 248, 118788. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Han, W.Z. Mechanism of brittle-to-ductile transition in tungsten under small-punch testing. Acta Mater. 2021, 220, 117332. [Google Scholar] [CrossRef]
- Chen, B.; Li, S.Z.; Ding, J.; Ding, X.D.; Sun, J. Correlating dislocation mobility with local lattice distortion in refractory multi-principal element alloys. Scr. Mater. 2025, 138, 104928. [Google Scholar] [CrossRef]
- Duesbery, M.S.; Vitek, V. Plastic anisotropy in bcc transition metals. Acta Mater. 1998, 46, 1481–1492. [Google Scholar] [CrossRef]
- Mrovec, M.; Gröger, R.; Bailey, A.G. Bond-order potential for simulations of extended defects in tungsten. Phys. Rev. B 2007, 75, 104119. [Google Scholar] [CrossRef]
- Vitek, V. Core structure of screw dislocations in body-centred cubic metals: Relation to symmetry and interatomic bonding. Philos. Mag. 2004, 84, 415–428. [Google Scholar] [CrossRef]
- Screw dislocations in BCC transition metals: From ab initio modeling to yield criterion. Comptes Rendus Phys. 2021, 22, 83–116. [CrossRef]
- Cottrell, A.H. Theory of brittle fracture in steel and similar metals. Trans. Met. Soc. AIME 1958, 212, 192–203. [Google Scholar]
- Butler, B.G.; Paramore, J.D.; Ligda, J.P. Mechanisms of deformation and ductility in tungsten—A review. Int. J. Refract. Met. Hard Mater. 2018, 75, 248–261. [Google Scholar] [CrossRef]
- Shinzato, S.; Wakeda, M.; Ogata, S. An atomistically informed kinetic Monte Carlo model for predicting solid solution strengthening of body-centered cubic alloys. Int. J. Plast. 2019, 122, 319–337. [Google Scholar] [CrossRef]
- Weertman, J. Dislocation Model of Low-Temperature Creep. J. Appl. Phys. 1958, 29, 1685–1689. [Google Scholar] [CrossRef]
- Zhao, Y.; Marian, J. Direct prediction of the solute softening-to-hardening transition in W-Re alloys using stochastic simulations of screw dislocation motion. Model. Simul. Mater. Sc. 2018, 26, 045002. [Google Scholar] [CrossRef]
- Caillard, D. On the stress discrepancy at low-temperatures in pure iron. Acta Mater. 2014, 62, 267–275. [Google Scholar] [CrossRef]
- Lu, Y.; Han, W.Z. Lowering the ductile-to-brittle transition temperature to—36° C via fine-grained structures in chromium. Scr. Mater. 2024, 239, 115813. [Google Scholar] [CrossRef]
- Zheng, R.Y.; Jian, R.W.; Beyerlein, I.J.; Han, W.Z. Atomic-scale hidden point-defect complexes induce ultrahigh-irradiation hardening in tungsten. Nano Lett. 2021, 21, 5798–5804. [Google Scholar] [CrossRef]
- Pan, Q.S.; Zhang, L.X.; Feng, R.; Lu, Q.H. Gradient cell–structured high-entropy alloy with exceptional strength and ductility. Science 2021, 376, 984–989. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.J.; Fang, Y.; Cheng, P.M.; Ke, X.X.; Zhang, M.C.; Zou, J.W.; Ding, J. The origin of exceptionally large ductility in molybdenum alloys dispersed with irregular-shaped La2O3 nano-particles. Nat. Commun. 2024, 15, 4105. [Google Scholar] [CrossRef] [PubMed]
- Arsenault, R. The double-kink model for low-temperature deformation of BCC metals and solid solutions. Acta Metall. 1967, 15, 501–511. [Google Scholar] [CrossRef]
- Medvedeva, N.; Gornostyrev, Y.N.; Freeman, A.J. Solid solution softening in bcc Mo alloys: Effect of transition-metal additions on dislocation structure and mobility. Phys. Rev. B 2005, 72, 134107. [Google Scholar] [CrossRef]
- Sato, A.; Meshii, M. Solid solution softening and solid solution hardening. Acta Metall. 1973, 21, 753–768. [Google Scholar] [CrossRef]
- Maresca, F.; Curtin, W.A. Theory of screw dislocation strengthening in random BCC alloys from dilute to “High-Entropy” alloys. Acta Mater. 2020, 182, 144–162. [Google Scholar] [CrossRef]
- Luo, A.; Jacobson, D.; Shin, K. Cross-kinks control hanism of iridium and rhenium in tungsten at room temperature. Int. J. Refract. Met. Hard Mater. 1991, 10, 107–114. [Google Scholar] [CrossRef]
- Stephens, J.R.; Witzke, W.R. Alloy softening in group via metals alloyed with rhenium. J. Less. Common. Met. 1971, 23, 325–342. [Google Scholar] [CrossRef]
- Stephens, J.R.; Witzke, W.R. Alloy softening in binary iron solid solutions. J. Less. Common. Met. 1976, 48, 285–308. [Google Scholar] [CrossRef]
- Tanaka, T.; Watanabe, S. The temperature dependence of the yield stress and solid solution softening in Fe Ni and Fe Si alloys. Acta Metall. 1971, 19, 991–1000. [Google Scholar] [CrossRef]
- Kocks, U.; Argon, A.; Ashby, M. Models for macroscopic slip. Prog. Mater. Sci. 1975, 19, 171–185. [Google Scholar]
- Zhou, X.R.; He, S.C.; Marian, J. Cross-kinks control screw dislocation strength in equiatomic bcc refractory alloys. Acta Mater. 2021, 211, 116875. [Google Scholar] [CrossRef]
- Itakura, M.; Kaburaki, H.; Yamaguchi, M. First-principles study on the mobility of screw dislocations in bcc iron. Acta Metall. 2012, 60, 3698–3710. [Google Scholar] [CrossRef]
- Kinoshita, K.; Shimokawa, T.; Kinari, T. Influence of non-glide stresses on the peierls energy of screw dislocations. Trans. JSME 2014, 80, CM0018. [Google Scholar] [CrossRef][Green Version]
- Ventelon, L.; Willaime, F.; Clouet, E.; Sawada, H.; Kawakami, K. Ab initio investigation of the Peierls potential of screw dislocations in bcc Fe and W. Acta Mater. 2013, 61, 3973–3985. [Google Scholar] [CrossRef]
- Hu, Y.J.; Fellinger, M.R.; Butler, B.G.; Wang, Y.; Darling, K.A. Solute-induced solid-solution softening and hardening in bcc tungsten. Acta Mater. 2017, 141, 304–316. [Google Scholar] [CrossRef]
- Romaner, L.; Ambrosch-Draxl, C.; Pippan, R. Effect of rhenium on the dislocation core structure in tungsten. Phys. Rev. Lett. 2010, 104, 195503. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Ma, E.; Sun, J.; Han, W.Z. Unveiling the intrinsic rhenium effect in Tungsten. Acta Mater. 2024, 264, 119586. [Google Scholar] [CrossRef]
- Wu, L.P.; Liu, Y.; Zhi, J.G.; Zhang, J.S.; Liu, Q. Effect mechanism of rare earth Ce on the strength and toughness of C-Mn low-temperature steel. Rare Matal Mater. Eng. 2022, 51, 4561–4569. [Google Scholar]
- Tanaka, M.; Matsuo, K.; Yoshimura, N.; Shigesato, G.; Hoshino, M. Effects of Ni and Mn on brittle-to-ductile transition in ultralow-carbon steels. Mater. Sci. Eng. A 2017, 682, 370–375. [Google Scholar] [CrossRef]
- Uenishi, A.; Teodosiu, C. Solid solution softening at high strain rates in Si-and/or Mn-added interstitial free steels. Acta Mater. 2003, 51, 4437–4446. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).