Understanding Shock Response of Body-Centered Cubic Molybdenum from a Specific Embedded Atom Potential
Abstract
1. Introduction
2. Computational Details
2.1. EAM Potential Functions and Parametrization
2.2. Quasi-Isentropic Shock Loading Setting
2.3. Piston Shock Loading Setting
3. Results and Discussion
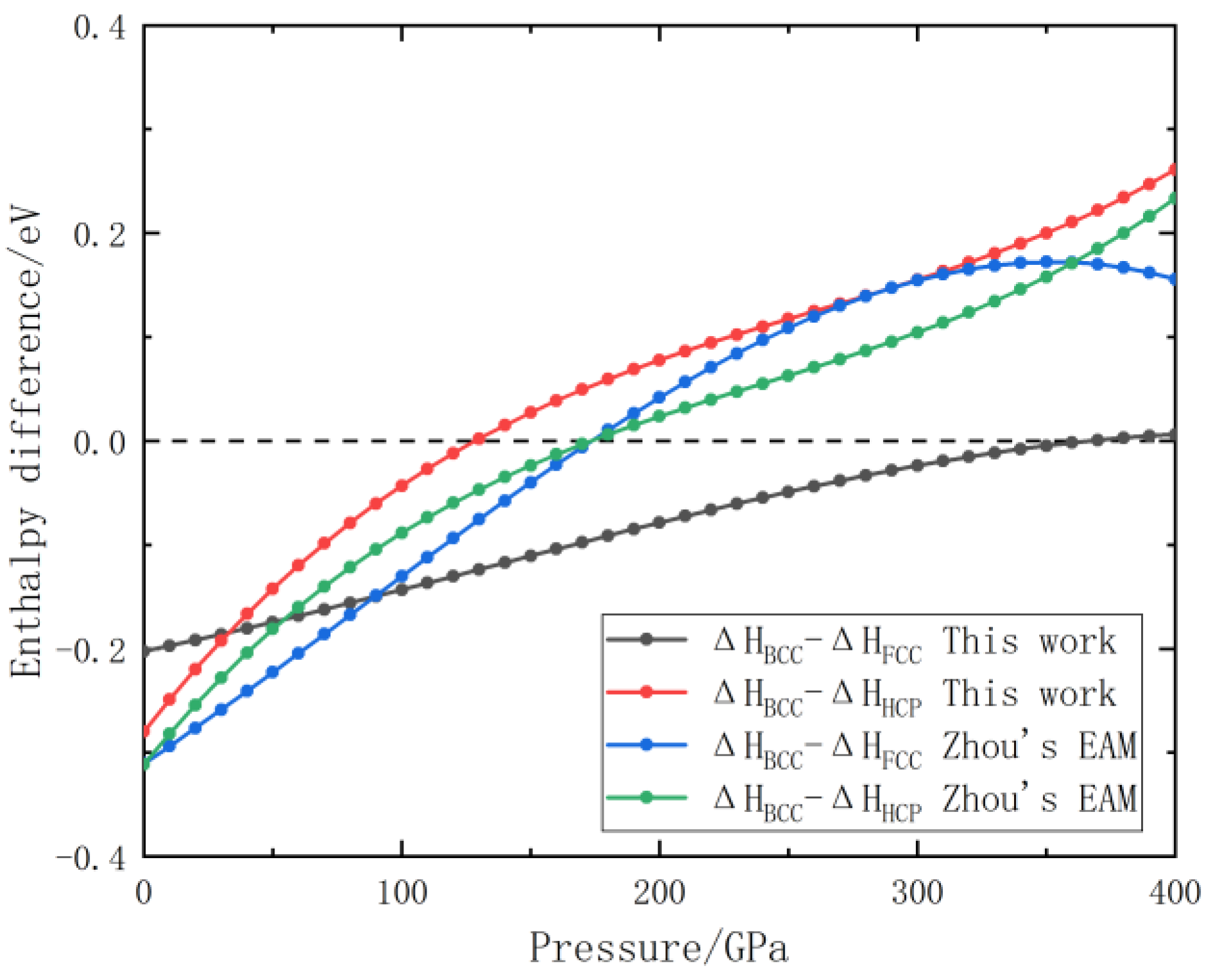
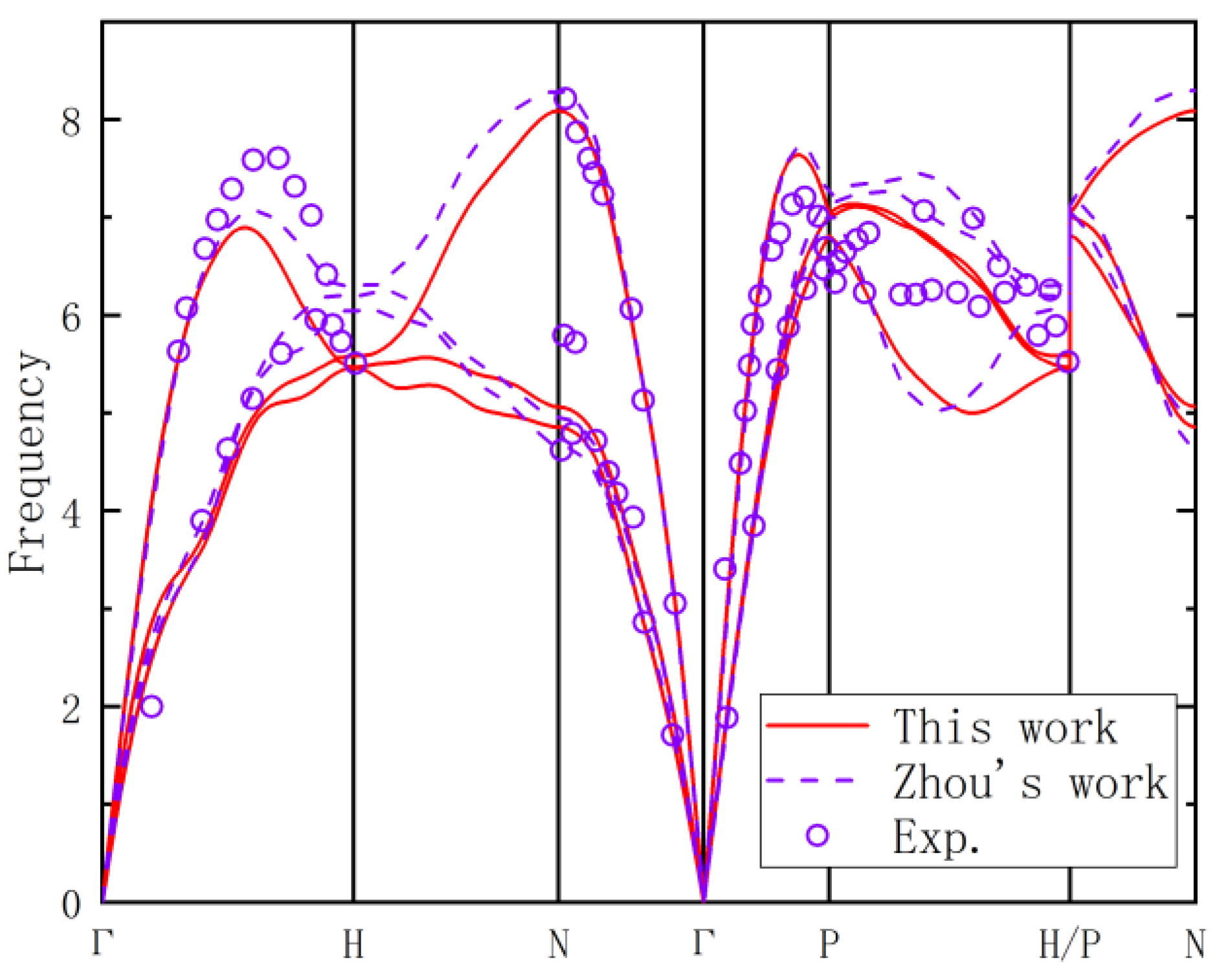
3.1. Validation of EAM Potential
3.2. Quasi-Isentropic Shock
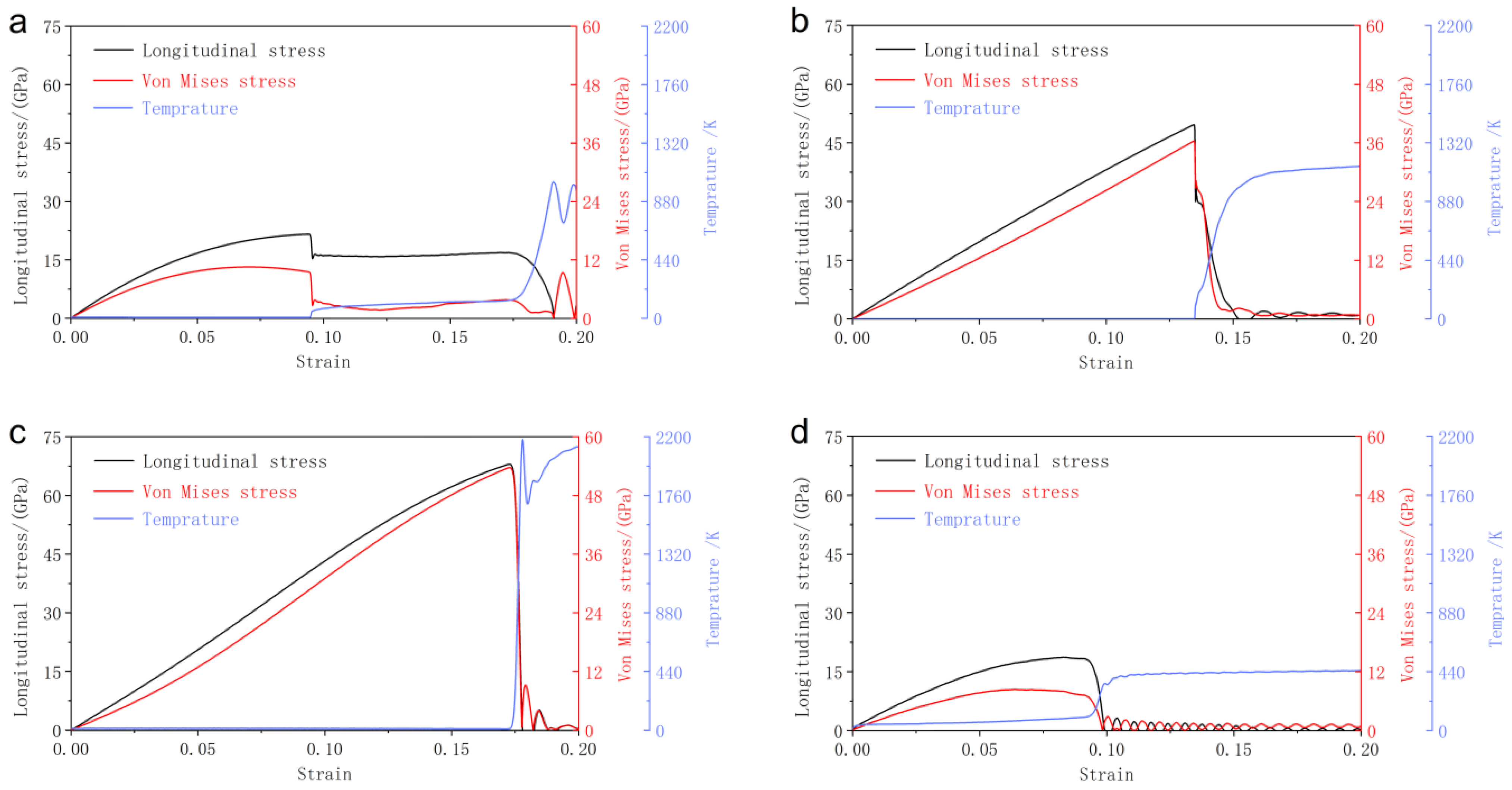
3.2.1. Mechanical Response
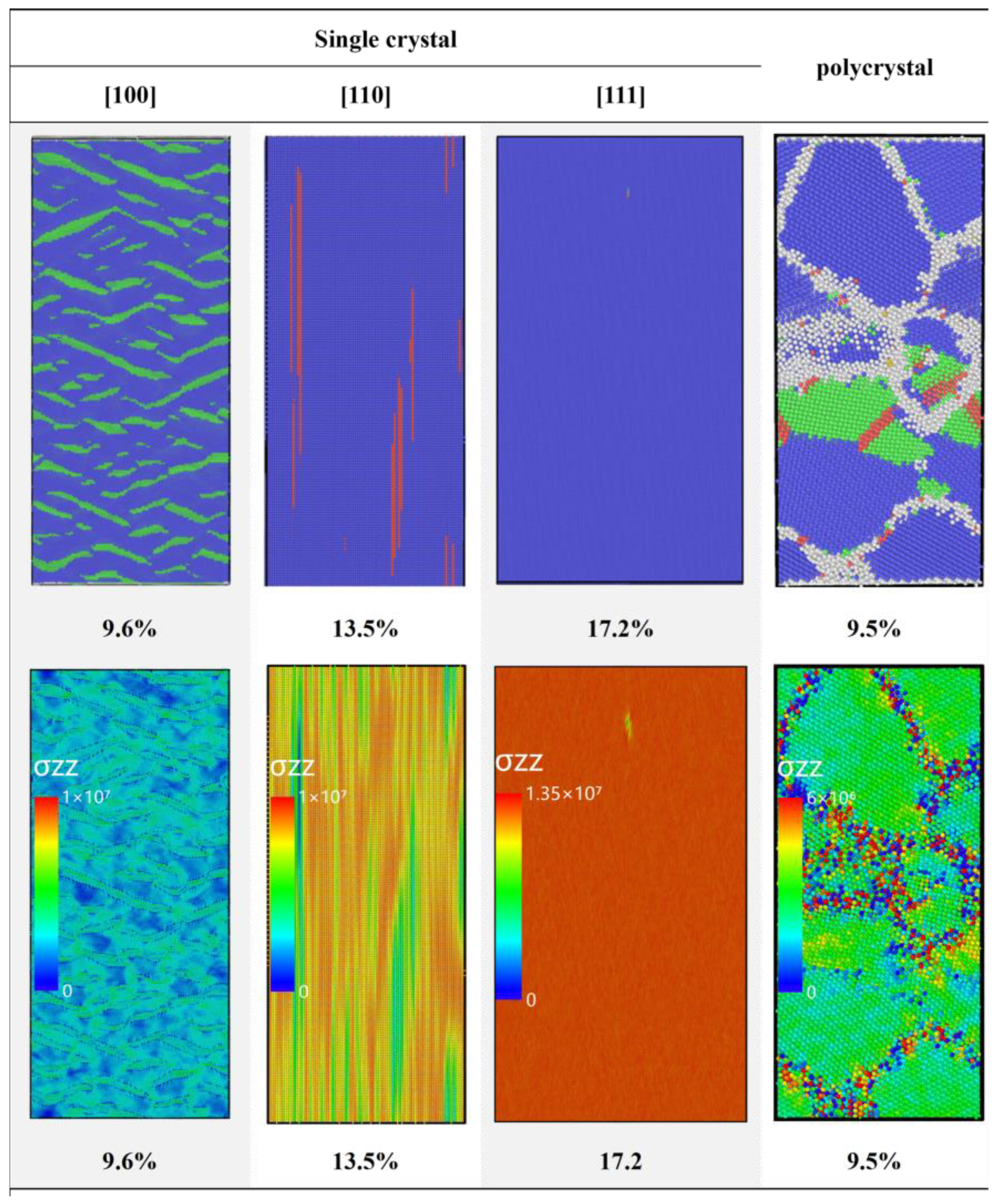
3.2.2. Plastic Behaviors and Structure Evolution
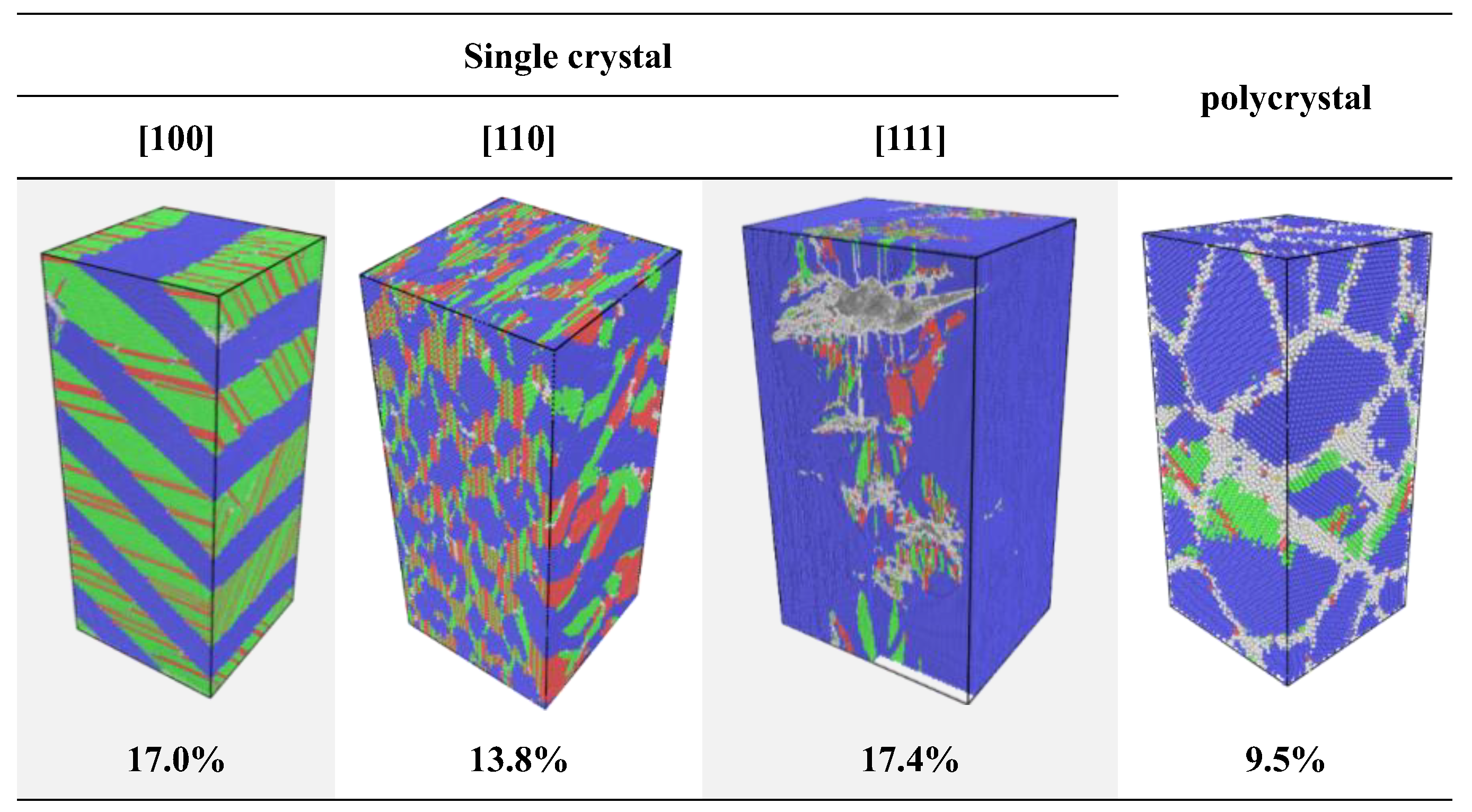
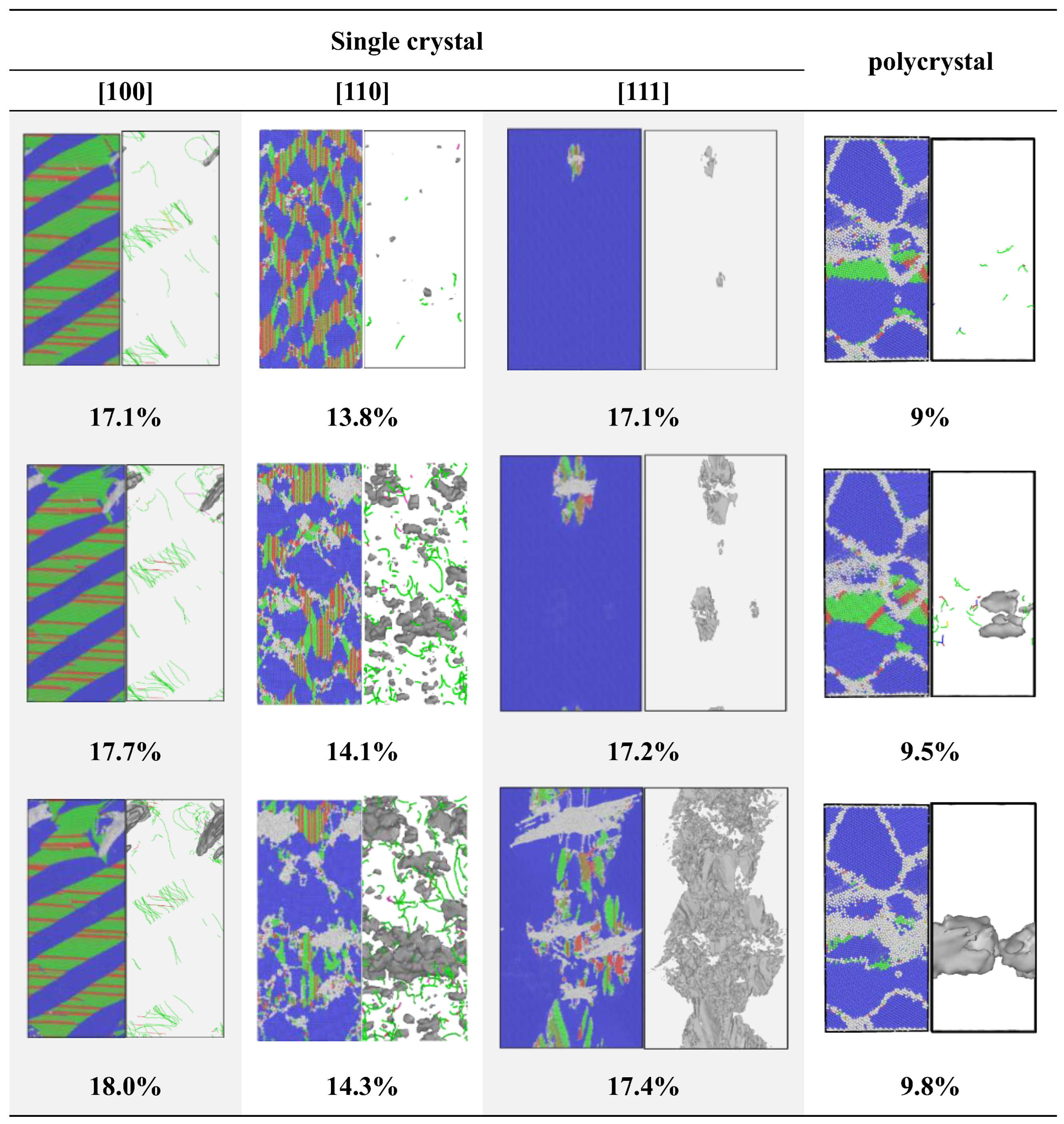
3.2.3. Void Nucleation and Growth Behavior Across Crystallographic Orientations
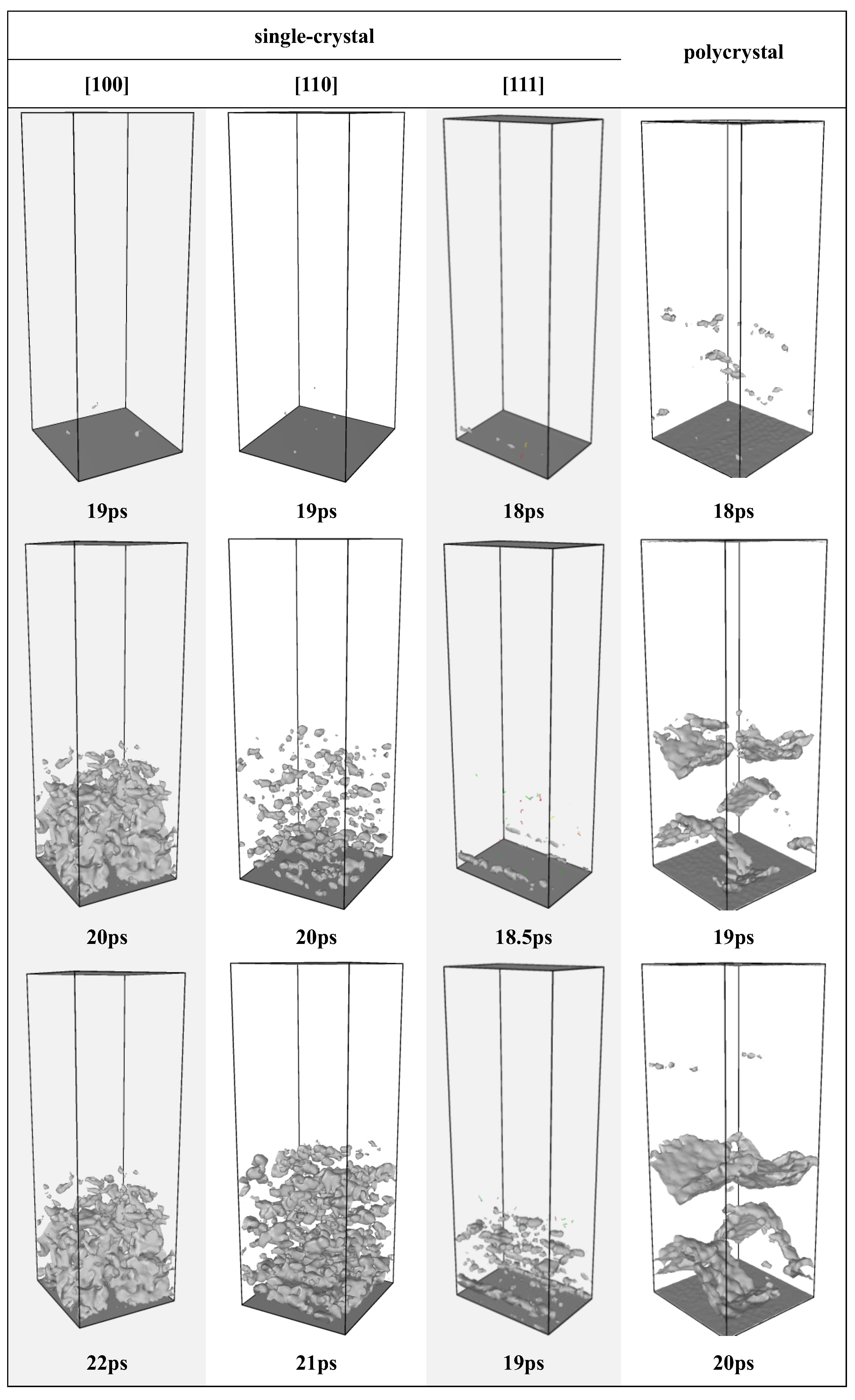
3.3. Piston-Driven Shock
4. Conclusions
- Under quasi-isentropic loading at a strain rate of 109 s−1, the critical stresses along the three principal crystallographic orientations follow the order [111] (67.9 GPa) > [110] (49.6 GPa) > [100] (21.5 GPa). This sequence is governed by the Schmid factor and subsequently influences the dominant plastic deformation mechanisms. The critical stress of polyscrystal (18.6 GPa) is lower than that of single crystals. Grain boundaries in polycrystalline Mo leads to non-uniform stress distribution and result in fast fracture failure. The resultant spall strength of Mo under piston-driven shock loading shows the same order as quasi-isentropic loading: [111] (41.08 GPa) > [110] (33.85 GPa) > [100] (18.45 GPa) > polycrystalline (17.96 GPa).
- At a strain rate of 109 s−1, phase transformation serves as the primary stress relaxation mechanism for longitudinal stress induced by high strain along the [100] and [110] loading directions. In contrast, phase transition is nearly inactive while loading along the [111] direction, where the system rapidly transitions to void nucleation and growth for stress relaxation. For polycrystalline Mo, grain boundaries induce heterogeneous stress distributions with localized concentrations, act as nucleation sites for voids, and promote their growth and coalescence along boundaries, leading to intergranular fracture as the dominant failure mode—distinct from the transgranular fracture observed in single crystals.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dudarev, S.L.; Boutard, J.L.; Lässer, R.; Caturla, M.J.; Derlet, P.M.; Fivel, M.; Fu, C.C.; Lavrentiev, M.Y.; Malerba, L.; Mrovec, M.; et al. The EU programme for modelling radiation effects in fusion reactor materials: An overview of recent advances and future goals. J. Nucl. Mater. 2009, 386–388, 1–7. [Google Scholar] [CrossRef]
- Zinkle, S.J.; Ghoniem, N.M. Operating temperature windows for fusion reactor structural materials. Fusion Eng. Des. 2000, 51–52, 55–71. [Google Scholar] [CrossRef]
- Yan, G.-Q.; Cheng, X.-L.; Zhang, H.; Zhu, Z.-Y.; Ren, D.-H. Different effects of electronic excitation on metals and semiconductors. Phys. Rev. B 2016, 93, 214302. [Google Scholar] [CrossRef]
- Sand, A.E.; Byggmästar, J.; Zitting, A.; Nordlund, K. Defect structures and statistics in overlapping cascade damage in fusion-relevant bcc metals. J. Nucl. Mater. 2018, 511, 64–74. [Google Scholar] [CrossRef]
- Gandhi, V.; Ravindran, S.; Joshi, A.; Ravichandran, G. Real-time characterization of dislocation slip and twinning of shock-compressed molybdenum single crystals. Phys. Rev. Mater. 2023, 7, 073601. [Google Scholar] [CrossRef]
- Wang, J.; Coppari, F.; Smith, R.F.; Eggert, J.H.; Lazicki, A.E.; Fratanduono, D.E.; Rygg, J.R.; Boehly, T.R.; Collins, G.W.; Duffy, T.S. X-ray diffraction of molybdenum under shock compression to 450 GPa. Phys. Rev. B 2015, 92, 174114. [Google Scholar] [CrossRef]
- Lu, C.H.; Hahn, E.N.; Remington, B.A.; Maddox, B.R.; Bringa, E.M.; Meyers, M.A. Phase Transformation in Tantalum under Extreme Laser Deformation. Sci. Rep. 2015, 5, 15064. [Google Scholar] [CrossRef]
- Belonoshko, A.B.; Burakovsky, L.; Chen, S.P.; Johansson, B.; Mikhaylushkin, A.S.; Preston, D.L.; Simak, S.I.; Swift, D.C. Molybdenum at High Pressure and Temperature: Melting from Another Solid Phase. Phys. Rev. Lett. 2008, 100, 135701. [Google Scholar] [CrossRef] [PubMed]
- Gachegova, E.; Davydov, D.; Mironov, S.; Kalinenko, A.; Ozerov, M.; Zherebtsov, S.; Plekhov, O. The Influence of Absorbing Coating Material on the Efficiency of Laser Shock Peening. Metals 2024, 14, 1045. [Google Scholar] [CrossRef]
- Akhmedov, E.N. Molybdenum lattice properties at high pressure. J. Phys. Chem. Solids 2018, 121, 62–66. [Google Scholar] [CrossRef]
- Oniyama, T.; Gupta, Y.M.; Ravichandran, G. Shock compression of molybdenum single crystals to 110 GPa: Elastic–plastic deformation and crystal anisotropy. J. Appl. Phys. 2020, 127, 205902. [Google Scholar] [CrossRef]
- Farihi, J.; Gänsicke, B.T.; Koester, D. Evidence for Water in the Rocky Debris of a Disrupted Extrasolar Minor Planet. Science 2013, 342, 218–220. [Google Scholar] [CrossRef] [PubMed]
- Mandal, A.; Gupta, Y.M. Elastic-plastic deformation of molybdenum single crystals shocked to 12.5 GPa: Crystal anisotropy effects. J. Appl. Phys. 2019, 125, 055903. [Google Scholar] [CrossRef]
- Huang, X.; Li, F.; Zhou, Q.; Meng, Y.; Litasov, K.D.; Wang, X.; Liu, B.; Cui, T. Thermal equation of state of Molybdenum determined from in situ synchrotron X-ray diffraction with laser-heated diamond anvil cells. Sci. Rep. 2016, 6, 19923. [Google Scholar] [CrossRef]
- Johanns, K.E.; Sedlmayr, A.; Phani, P.S.; Mönig, R.; Kraft, O.; George, E.P.; Pharr, G.M. In-situ tensile testing of single-crystal molybdenum-alloy fibers with various dislocation densities in a scanning electron microscope. J. Mater. Res. 2012, 27, 508–520. [Google Scholar] [CrossRef]
- Wehrenberg, C.E.; Mcgonegle, D.; Bolme, C.; Higginbotham, A.; Lazicki, A.; Lee, H.J.; Nagler, B.; Park, H.S.; Remington, B.A.; Rudd, R.E.; et al. In situ X-ray diffraction measurement of shock-wave-driven twinning and lattice dynamics. Nature 2017, 550, 496–499. [Google Scholar] [CrossRef]
- Luo, S.-N.; Germann, T.C.; Tonks, D.L. Spall damage of copper under supported and decaying shock loading. J. Appl. Phys. 2009, 106, 123518. [Google Scholar] [CrossRef]
- Hahn, E.N.; Germann, T.C.; Ravelo, R.J.; Hammerberg, J.E.; Meyers, M.A. Non-equilibrium molecular dynamics simulations of spall in single crystal tantalum. AIP Conf. Proc. 2017, 1793, 070006. [Google Scholar]
- Park, N.-Y.; Cha, P.-R.; Kim, Y.-C.; Seok, H.-K.; Han, S.-H.; Lee, S.-C.; Cho, S.; Jung, H. Radiation damage in nano-crystalline tungsten: A molecular dynamics simulation. Met. Mater. Int. 2009, 15, 447–452. [Google Scholar] [CrossRef]
- Feng, Y.; Li, J.; Yang, X. Intragranular and Intergranular Crack Propagation in Nanocrystalline Ni Under Single-Cycle Mode I Loading. Met. Mater. Int. 2022, 28, 1590–1598. [Google Scholar] [CrossRef]
- Ding, J.; Li, Z.; Wang, W.; Ma, Y.; Liu, W.; Liang, C. Evaluation of structural and mechanical strength of symmetric tilt interface in W/Fe composite laminate using molecular dynamics. J. Phys. Chem. Solids 2022, 168, 110800. [Google Scholar] [CrossRef]
- Hahn, E.N.; Fensin, S.J.; Germann, T.C.; Gray, G.T. Orientation dependent spall strength of tantalum single crystals. Acta Mater. 2018, 159, 241–248. [Google Scholar] [CrossRef]
- Derlet, P.M.; Nguyen-Manh, D.; Dudarev, S.L. Multiscale modeling of crowdion and vacancy defects in body-centered-cubic transition metals. Phys. Rev. B 2007, 76, 054107. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, W. Atomic Scale Diffusion Study in Quaternary and Quinary Alloys of Co–Cr–Fe–Mn–Ni System. Met. Mater. Int. 2024, 30, 457–468. [Google Scholar] [CrossRef]
- Ye, W.; Misra, M.; Menezes, P.; Mushongera, L.T. Influence of Grain Boundary Character on Dopants Segregation in Nanocrystalline Aluminum. Met. Mater. Int. 2023, 29, 18–26. [Google Scholar] [CrossRef]
- Jasim, S.A.; Ali, M.H.; Mahmood, Z.H.; Rudiansyah, M.; Alsultany, F.H.; Mustafa, Y.F.; Ramadan, M.F.; Surendar, A. Role of Alloying Composition on Mechanical Properties of CuZr Metallic Glasses During the Nanoindentation Process. Met. Mater. Int. 2022, 28, 2075–2082. [Google Scholar] [CrossRef]
- Zepeda-Ruiz, L.A.; Stukowski, A.; Oppelstrup, T.; Bulatov, V.V. Probing the limits of metal plasticity with molecular dynamics simulations. Nature 2017, 550, 492–495. [Google Scholar] [CrossRef]
- Chen, X.; Luo, G.; Cao, Y.; Liang, C. Effect of Atomic Ordering on Phase Stability and Elastic Properties of Pd-Ag Alloys. Metals 2024, 14, 1017. [Google Scholar] [CrossRef]
- Hu, Y.; Xu, J.; Su, L.; Zhang, Y.; Ding, S.; Shen, Y.; Xia, R. Tensile responses of polycrystalline Mo via molecular dynamics simulation: Grain size and temperature effects. Mater. Chem. Phys. 2023, 296, 127270. [Google Scholar] [CrossRef]
- Frederiksen, S.L.; Jacobsen, K.W.; Schiøtz, J. Simulations of intergranular fracture in nanocrystalline molybdenum. Acta Mater. 2004, 52, 5019–5029. [Google Scholar] [CrossRef]
- Mostafa, A.; Vu, L.; Guo, Z.; Shargh, A.K.; Dey, A.; Askari, H.; Abdolrahin, N. Phase-transformation assisted twinning in Molybdenum nanowires. Comput. Mater. Sci. 2024, 244, 113273. [Google Scholar] [CrossRef]
- Lee, B.-J.; Baskes, M.I.; Kim, H.; Koo Cho, Y. Second nearest-neighbor modified embedded atom method potentials for bcc transition metals. Phys. Rev. B 2001, 64, 184102. [Google Scholar] [CrossRef]
- Han, S.; Zepeda-Ruiz, L.A.; Ackland, G.J.; Car, R.; Srolovitz, D.J. Interatomic potential for vanadium suitable for radiation damage simulations. J. Appl. Phys. 2003, 93, 3328–3335. [Google Scholar] [CrossRef]
- Park, H.; Fellinger, M.R.; Lenosky, T.J.; Tipton, W.W.; Trinkle, D.R.; Rudin, S.P.; Woodward, C.; Wilkins, J.W.; Hennig, R.G. Ab initio based empirical potential used to study the mechanical properties of molybdenum. Phys. Rev. B 2012, 85, 214121. [Google Scholar] [CrossRef]
- Ravelo, R.; Germann, T.C.; Guerrero, O.; An, Q.; Holian, B.L. Shock-induced plasticity in tantalum single crystals: Interatomic potentials and large-scale molecular-dynamics simulations. Phys. Rev. B 2013, 88, 134101. [Google Scholar] [CrossRef]
- Rydberg, R. Graphische Darstellung einiger bandenspektroskopischer Ergebnisse. Z. Für Physik 1932, 73, 376–385. [Google Scholar] [CrossRef]
- Rose, J.H.; Smith, J.R.; Guinea, F.; Ferrante, J. Universal features of the equation of state of metals. Phys. Rev. B 1984, 29, 2963–2969. [Google Scholar] [CrossRef]
- Holian, B.L.; Voter, A.F.; Wagner, N.J.; Ravelo, R.J.; Chen, S.P.; Hoover, W.G.; Hoover, C.G.; Hammerberg, J.E.; Dontje, T.D. Effects of pairwise versus many-body forces on high-stress plastic deformation. Phys. Rev. A 1991, 43, 2655–2661. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Tsuzuki, H.; Branicio, P.S.; Rino, J.P. Structural characterization of deformed crystals by analysis of common atomic neighborhood. Comput. Phys. Commun. 2007, 177, 518–523. [Google Scholar] [CrossRef]
- Honeycutt, J.D.; Andersen, H.C. Molecular dynamics study of melting and freezing of small Lennard-Jones clusters. J. Phys. Chem. 1987, 91, 4950–4963. [Google Scholar] [CrossRef]
- Stukowski, A.; Albe, K. Extracting dislocations and non-dislocation crystal defects from atomistic simulation data. Model. Simul. Mater. Sci. Eng. 2010, 18, 085001. [Google Scholar] [CrossRef]
- Marinica, M.C.; Ventelon, L.; Gilbert, M.R.; Proville, L.; Dudarev, S.L.; Marian, J.; Bencteux, G.; Willaime, F. Interatomic potentials for modelling radiation defects and dislocations in tungsten. J. Phys. Condens. Matter 2013, 25, 395502. [Google Scholar] [CrossRef]
- Pearson, W.B.; Vineyard, G.H. A Handbook of Lattice Spacings and Structures of Metals and Alloys. Phys. Today 2009, 11, 36. [Google Scholar] [CrossRef]
- Ding, J.; Ma, Y.; Liu, W.; Liang, C. High-temperature structural stability and mechanical properties of η-carbides M6W6C, M3W3C and M2W2C from first-principles calculations. Ceram. Int. 2025, 51, 21742–21751. [Google Scholar] [CrossRef]
- Zhou, X.W.; Johnson, R.A.; Wadley, H.N.G. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers. Phys. Rev. B 2004, 69, 144113. [Google Scholar] [CrossRef]
- Kong, L.T. Phonon dispersion measured directly from molecular dynamics simulations. Comput. Phys. Commun. 2011, 182, 2201–2207. [Google Scholar] [CrossRef]
- Kong, L.T.; Bartels, G.; Campañá, C.; Dennistoon, C.; Müser, M.H. Implementation of Green’s function molecular dynamics: An extension to LAMMPS. Comput. Phys. Commun. 2009, 180, 1004–1010. [Google Scholar] [CrossRef]
- Zarestky, J.; Stassis, C.; Harmon, B.N.; Ho, K.M.; Fu, C.L. Temperature dependence of the vibrational modes of molybdenum. Phys. Rev. B 1983, 28, 697–701. [Google Scholar] [CrossRef]
- Woods, A.D.B.; Chen, S.H. Lattice dynamics of molybdenum. Solid State Commun. 1964, 2, 233–237. [Google Scholar] [CrossRef]
- Farber, D.L.; Krisch, M.; Antonangeli, D.; Beraud, A.; Badro, J.; Occelli, F.; Orlikowski, D. Lattice Dynamics of Molybdenum at High Pressure. Phys. Rev. Lett. 2006, 96, 115502. [Google Scholar] [CrossRef]
- Leng, Y.; Li, Z.; Liu, W.; Ma, Y.; Liang, C. Orientation Dependent Quasi-isentropic Tensile Behaviors of Body-Centered Cubic Tungsten Through Molecular Dynamics. Met. Mater. Int. 2024, 30, 2699–2712. [Google Scholar] [CrossRef]
- Knezevic, M.; Beyerlein, I.J.; Lovato, M.L.; Tomé, C.N.; Richards, A.W.; McCabe, R.J. A strain-rate and temperature dependent constitutive model for BCC metals incorporating non-Schmid effects: Application to tantalum–tungsten alloys. Int. J. Plast. 2014, 62, 93–104. [Google Scholar] [CrossRef]
- Wijnen, J.; Hoefnagels, J.P.M.; Geers, M.G.D.; Peerlings, R.H.J. Discrete slip plane analysis of ferrite microtensile tests: Influence of dislocation source distribution and non-Schmid effects on slip system activity. Mater. Des. 2025, 251, 113698. [Google Scholar] [CrossRef]
- Zhao, S.; Yin, S.; Liang, X.; Cao, F.; Yu, Q.; Zhang, R.; Dai, L.; Ruestes, C.J.; Ritchie, R.O.; Minor, A.M. Deformation and failure of the CrCoNi medium-entropy alloy subjected to extreme shock loading. Sci. Adv. 2023, 9, eadf8602. [Google Scholar] [CrossRef]
- Ma, B.; Rao, Q.; He, Y. Molecular dynamics simulation of temperature effect on tensile mechanical properties of single crystal tungsten nanowire. Comput. Mater. Sci. 2016, 117, 40–44. [Google Scholar] [CrossRef]
- Zhang, J.; Li, Y.; Li, X.; Zhai, Y.; Zhang, Q.; Ma, D.; Mao, S.; Deng, Q.; Li, Z.; Li, X.; et al. Timely and atomic-resolved high-temperature mechanical investigation of ductile fracture and atomistic mechanisms of tungsten. Nat. Commun. 2021, 12, 2218. [Google Scholar] [CrossRef]
- Chang, H.; Huang, Z.; Wen, S.; Chen, J.; Liu, X.; Pan, M.; Zhao, Y. The influence of crystal defects on the elastic properties of tungsten metals. Fusion Eng. Des. 2016, 109–111, 321–325. [Google Scholar] [CrossRef]
- Kanel, G.I.; Razorenov, S.V.; Utkin, A.V.; Fortov, V.E.; Baumung, K.; Karrow, H.U.; Rusch, D.; Licht, V. Spall strength of molybdenum single crystals. J. Appl. Phys. 1993, 74, 7162–7165. [Google Scholar] [CrossRef]
- Dora, T.L.; Singh, S.K.; Mishra, R.R.; Yu, H.; Rawat, N.K.; Verma, A. Exploring deformation mechanisms in a refractory high entropy alloy (MoNbTaW). Int. J. Mech. Sci. 2025, 288, 110000. [Google Scholar] [CrossRef]
- Liu, W.; Li, Z.; Bai, X.; Ma, Y.; Liang, C.P. A unified model for yield strength and plastic behavior of nanovoid evolution in tungsten based on molecular dynamics simulations. Comput. Mater. Sci. 2022, 211, 111534. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.; Ma, Y.; Liang, C. Heterogeneous nucleation of plastic defects and tension-compression asymmetry in the presence of vacancies in W single crystals. J. Nucl. Mater. 2025, 610, 155806. [Google Scholar] [CrossRef]
- Li, Z.; Liu, W.; Ma, Y.; Liang, C. Influence of crystallographic orientations and nanovoid on the plastic mechanism and damage behavior of single-crystal tungsten under shock. J. Mater. Res. Technol. 2025, 35, 714–725. [Google Scholar] [CrossRef]
- Rice, J.R.; Tracey, D.M. On the ductile enlargement of voids in triaxial stress fields∗. J. Mech. Phys. Solids 1969, 17, 201–217. [Google Scholar] [CrossRef]
- Mcveigh, C.; Vernerey, F.; Liu, W.K.; Moran, B.; Olson, G. An interactive micro-void shear localization mechanism in high strength steels. J. Mech. Phys. Solids 2007, 55, 225–244. [Google Scholar] [CrossRef]



| Loading Crystal Type | Loading Direction | Orthogonal Coordinate System Axes | Simulation System Dimensions (Å) | Number of Atoms | |
|---|---|---|---|---|---|
| Mo | Single crystal | [100] | [100] [010] [001] | 283.14 * 283.14 * 585.16 | 3,013,200 |
| [100] | [001] [10] [110] | 195.05 * 195.76 * 400.42 | 982,080 | ||
| [111] | [10] [11] [111] | 293.73 * 380.28 * 588.67 | 4,219,776 | ||
| Polycrystal | x | x, y, z | 100.24 * 100.24 * 200.48 | 128,520 |
| Loading Crystal Type | Loading Direction | Simulation System Dimensions (Å) | Number of Atoms | Impact Velocity (km/s) | Loading Time | |
|---|---|---|---|---|---|---|
| Mo | Single crystal | [100] | 201 * 201 * 503 | 1,310,720 | 0.8 | 5 ps + 5 ps + 5 ps |
| [110] | 200 * 201 * 492 | 1,290,240 | 0.8 | 5 ps + 5 ps + 5 ps | ||
| [111] | 133 * 200 * 501 | 861,120 | 0.8 | 5 ps + 5 ps + 5 ps | ||
| Polycrystal | x | 200 * 200 * 501 | 1,283,447 | 0.8 | 5 ps + 5 ps + 5 ps |
| Parameters | Mo |
|---|---|
| α | 4.9757 |
| Ec(eV) | 7.57 |
| f3 | 0.0266 |
| f4 | 0.0306 |
| U0(eV) | 0.5669 |
| r1 | 2.8366 |
| αp | 2.1431 |
| β3 | 0 |
| β4 | 0 |
| rs | 2.8388 |
| s | 5.6106 |
| rc | 4.7733 |
| a1 | −1.6319 |
| a2 | 2.1267 |
| a3 | −0.9473 |
| a4 | 0.1434 |
| p | 4.2079 |
| q | 3.3179 |
| ρ0 | 0.0826 |
| This Work | Exp. [45] | MEAM [34] | GGA-PBE [34] | |
|---|---|---|---|---|
| a0 () | 3.146 | 3.146 | 3.167 | 3.169 |
| Ec (eV/atom) | −6.805 | −6.81 | −6.82 | −6.25 |
| C11 (GPa) | 453.65 | 464.7 | 441 | 462 |
| C12 (GPa) | 161.64 | 161.5 | 158 | 163 |
| C44 (GPa) | 108.36 | 108.9 | 96 | 102 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Leng, Y.; Chen, X.; Liang, C. Understanding Shock Response of Body-Centered Cubic Molybdenum from a Specific Embedded Atom Potential. Metals 2025, 15, 685. https://doi.org/10.3390/met15060685
Jiang Y, Leng Y, Chen X, Liang C. Understanding Shock Response of Body-Centered Cubic Molybdenum from a Specific Embedded Atom Potential. Metals. 2025; 15(6):685. https://doi.org/10.3390/met15060685
Chicago/Turabian StyleJiang, Yichen, Yanchun Leng, Xiaoli Chen, and Chaoping Liang. 2025. "Understanding Shock Response of Body-Centered Cubic Molybdenum from a Specific Embedded Atom Potential" Metals 15, no. 6: 685. https://doi.org/10.3390/met15060685
APA StyleJiang, Y., Leng, Y., Chen, X., & Liang, C. (2025). Understanding Shock Response of Body-Centered Cubic Molybdenum from a Specific Embedded Atom Potential. Metals, 15(6), 685. https://doi.org/10.3390/met15060685





