Abstract
This paper primarily investigates the response and failure behavior of 6063-T5 aluminum alloy square tubes with varying outer side lengths under symmetric curvature-controlled cyclic bending in different bending directions. The response is characterized by the moment–curvature relationship and the variation in the outer side length with respect to curvature, whereas failure is characterized by the relationship between the controlled curvature and the number of cycles required to initiate buckling. The outer side lengths studied are 20 mm, 30 mm, 40 mm, and 50 mm, and the bending directions considered are 0°, 22.5°, and 45°. The moment–curvature curves exhibited cyclic hardening, and stable loops were formed for all outer side lengths and bending directions. An increase in the outer side length resulted in a higher peak bending moment, while a greater bending direction led to a slight increase in the peak bending moment. For a fixed bending direction, the curves representing the variation of the outer side length (defined as the change in length divided by the original length) with respect to curvature displayed symmetry, serrated features, and an overall increasing trend as the number of cycles increased, irrespective of the specific outer side length. In addition, increasing either the outer side length or altering the bending direction led to a larger variation in the outer side length. As for the relationship between curvature and the number of cycles required to initiate buckling, the data for each bending direction and each of the four outer side lengths formed distinct straight lines on a double-logarithmic plot. Based on the experimental observations, empirical equations were developed to characterize these relationships. These equations were then used to predict the experimental data and showed excellent agreement with the measured results.
1. Introduction
Traditional circular tubes are commonly used in piping and structural support applications. Their widespread use can be attributed to several key advantages, including uniform distribution of stress under internal pressure, high torsional rigidity, and ease of manufacturing. However, they have inherent limitations in load-bearing capacity, wear resistance, and shock absorption [1,2]. In contrast, square tubes (as depicted in Figure 1) offer several advantages over circular tubes. Under the same cross-sectional area, square tubes generally exhibit higher bending rigidity in specific directions, particularly under unidirectional or bidirectional bending loads. This advantage makes square tubes more suitable for applications such as frame structures and bridge supports. The flat surfaces of square tubes make them easier to weld, bolt, or rivet to other structures compared to circular tubes, thereby reducing the complexity of joints. Additionally, the straight edges of square tubes facilitate alignment and clamping during cutting, drilling, or machining, improving processing accuracy.

Figure 1.
Schematic diagram of a square tube.
In structural design, square tubes allow for more efficient assembly by minimizing space wastage, making them particularly suitable for applications in construction, shelving, and vehicle frames. Moreover, square tubes can be arranged or assembled more compactly, whereas circular tubes leave more gaps between them, giving square tubes an advantage in material utilization. When subjected to lateral pressure or concentrated loads (such as those in beams or supports), square tubes provide better structural support than circular tubes, as their flat surfaces can directly contact the load [2]. In contrast, circular tubes are more prone to local deformation. Due to these advantages, square tubes are widely used in buildings, machinery, and vehicle structures to ensure rigidity and load-bearing stability.
Substantial progress is made in understanding the bending behavior of smooth circular tubes. In 1987, Kyriakides and Shaw developed a mechanical apparatus capable of performing both monotonic and cyclic bending tests on circular tubes, with or without the application of external pressure. The materials studied included 1020 steel, 1018 steel, 304 stainless steel, 6061-T6 aluminum alloy, and NiTi smooth circular tubes. This body of work is well-documented in the literature (Kyriakides and Shaw [3], Corona and Kyriakides [4], Corona and Kyriakides [5], Corona et al. [6], Limam et al. [7], Limam et al. [8], Bechle and Kyriakides [9], Jiang et al. [10], Kazinakis et al. [11]).
Subsequent studies have also provided valuable insights into related phenomena. For example, Yuan and Mirmiran [12] investigated the static buckling behavior of concrete-filled fiber-reinforced polymer (FRP) tubes under single curvature bending. Results from analytical and experimental analysis reveal that such columns are more prone to buckling than steel-reinforced concrete columns, prompting proposed revisions to existing stability design equations. Elchalakani et al. [13] proposed a simplified theoretical model to predict the moment–rotation behavior of circular hollow steel tubes subjected to pure bending, incorporating ovalization and rigid-plastic behavior. The model, validated against experimental data, shows good agreement—particularly with the star-shaped plastic mechanism—and offers a closed-form solution suitable for routine design applications. Houliara and Karamanos [14] studied the structural stability and bifurcation behavior of long, pressurized, thin-walled elastic tubes under in-plane bending using nonlinear finite element analysis. It further develops a simplified analytical model that accurately predicts bifurcation characteristics by accounting for pressure, initial curvature, and ovality, with results validated for thin-walled tubes. Yazdani and Nayebi [15] analyzed the ratcheting and fatigue behavior of thin-walled tubes subjected to cyclic bending combined with constant internal pressure using Chaboche’s nonlinear hardening model and Lemaitre’s damage mechanics. A simplified method yields results consistent with experiments, showing that increasing internal pressure significantly reduces whole-life ratcheting, and the Bree diagram is used to define shakedown and ratcheting boundaries.
Elchalakani et al. [16] proposed new ductile slenderness limits for concrete-filled tubes (CFT) based on experimental strain data and a simplified energy method using the Ritz approach. The study shows that current design code limits may overestimate allowable slenderness, with the newly derived limits offering improved accuracy for plastic design by capturing the effects of post-buckling behavior and concrete confinement. Shamass et al. [17] examined the elastoplastic buckling behavior of thin circular cylindrical shells under combined axial tension and external pressure using Flugge’s shell theory and two plasticity models—flow theory and deformation theory. Results show that deformation theory predicts lower buckling pressures under over-constrained conditions, with discrepancies increasing due to geometric and material parameters; findings are validated through FEA and differential quadrature methods. Li and Wang [18] numerically investigated the seismic performance of cable-stiffened single-layer latticed shells, comparing them with conventional unstiffened shells. Through modal and time-history analyses, it is shown that cable stiffening significantly enhances seismic behavior, with key influencing factors including cable pretension and cross-sectional properties. Chegeni et al. [19] examined how corrosion depth and shape affect the structural performance of thin-walled steel pipes under internal pressure and bending. Results show that deeper corrosion significantly reduces bending capacity, and corrosion spreading in the circumferential direction has the most detrimental impact on pipe behavior.
Jin et al. [20] investigated the mechanical behavior of tubes under combined axial compression and bending through experiments and finite element simulations using ABAQUS. The study finds good agreement between experimental and numerical results, confirming the models’ reliability for analyzing local buckling modes and ultimate loads, offering valuable insights for manufacturing applications. Silveira et al. [21] explored the buckling behavior of simply supported square steel plates with centered elliptical holes under biaxial compression. Using constructal design, finite element method, and exhaustive search, optimal geometries were identified to maximize ultimate buckling stress, demonstrating that stress performance improves with geometries aligned with the Principle of Optimal Distribution of Imperfections. He et al. [22] analytically studied the deformation transition mechanism in tube free bending and introduced a correction factor to refine the relationship between die deviation and bending radius. Validated through experiments and simulations with AA5052 tubes, the proposed method enhances forming accuracy and offers valuable guidance for designing more precise and reliable bending processes.
Wang et al. [23] experimentally and numerically investigated the bending behavior of square concrete-filled steel tubes (CFSTs) reinforced with internal latticed steel angles. Results show that the steel angles improve crack resistance and delay neutral axis shift, while the steel tube’s yield strength and thickness are the most influential on bending capacity; validated FE models and proposed design equations provide reliable, conservative predictions. Liu et al. [24] investigated the flexural behavior of multicell concrete-filled round-ended steel tubes (M-CFRTs) through experiments and finite element analysis, revealing ductile failure modes and strong composite action between concrete and steel. Key factors like material strengths, cell number, steel ratio, and aspect ratio were analyzed, offering valuable insights for practical structural applications. Yang et al. [25] modified the traditional damping strain energy model using reverse off-axis transformation and validated it through vibration tests on CFRP hollow tubes. The results reveal how laminate parameters influence bending and torsional damping, offering theoretical guidance for optimizing CFRP drive shaft design. Wang et al. [26] proposed a quadratic model to analyze bending–torsion buckling (BTB) during spatial tube forming, identifying three BTB zones based on the dominance of torsion or bending. An analytical method for predicting critical lever of combined loading is developed using energy principles and validated through simulations, providing insights into the effects of geometry, material properties, and imperfections on BTB behavior.
Despite extensive studies on the bending behavior of circular tubes, a notable gap remains in the literature regarding the behavior of square tubes under bending loads. To address this gap, the present study aims to investigate the behavior of 6063-T5 aluminum alloy square tubes under cyclic bending loads. The investigation focuses on four distinct outer side lengths (20 mm, 30 mm, 40 mm, and 50 mm) and three different bending directions (0°, 22.5°, and 45°). Cyclic bending tests were conducted using a specialized experimental apparatus, with key parameters—such as bending moment, curvature, outer side length variation, and the number of cycles required to initiate buckling—measured and thoroughly analyzed.
2. Materials and Methods
Cyclic bending tests were performed on square tubes with varying outer side lengths and bending directions using a tube-bending machine in conjunction with a curvature–ovalization measurement system. The experimental setup, materials, specimen configurations, and testing procedures are described in detail in the following sections.
2.1. Bending Device
Figure 2 shows the four-point bending machine employed for the cyclic bending tests. The apparatus features two rotating sprockets mounted on supporting beams, connected by a durable chain that provides structural integrity. The system is capable of accommodating specimens up to 1 m in length. As depicted in Figure 3, square tubes were fitted with solid rod extensions at both ends to facilitate secure mounting during testing. During bending, the interaction between the tube and the rollers permitted unrestricted axial movement. Bending loads, applied in both forward and reverse directions, were introduced via two concentrated forces exerted by a pair of rollers. In forward bending, two rollers on each sprocket applied force to the solid rod extensions. In reverse bending, the alternate set of rollers on each sprocket delivered the force. The transition to forward bending was triggered by retracting either the upper or lower hydraulic cylinder, which, in turn, caused the sprockets to rotate. Reverse bending was achieved by reversing the flow direction of the hydraulic circuit [27].

Figure 2.
Schematic diagram of the tube-bending machine (reprinted from [27]).
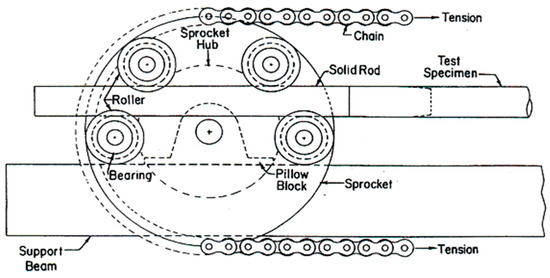
Figure 3.
Enlarged schematic diagram of the sprocket (reprinted from [27]).
Due to spatial constraints imposed by the rollers, only solid rods with circular cross-sections could be accommodated. However, directly inserting a circular rod into a square tube was not feasible. To overcome this limitation, a new solid rod configuration was developed for use with the bending apparatus, as shown in Figure 4a. Figure 4b displays the disassembled components of the square tube and the redesigned solid rod, while an exploded view of the rod is provided in Figure 5a. The redesigned rod features a square cross-section at one end and a circular cross-section at the other, joined by welding along the contact surfaces. Since the study aimed to investigate the influence of different outer side lengths, solid rods with varying square cross-section dimensions were fabricated. In contrast, the circular cross-section on the opposite end was standardized across all specimens, as illustrated in Figure 5b.

Figure 4.
(a) Schematic illustration of the newly designed solid rod installed on the tube-bending machine and (b) exploded view showing the disassembled square tube alongside the newly designed solid rod.

Figure 5.
(a) Exploded view schematic of the newly designed solid rod and (b) photograph of four solid rods.
2.2. Curvature–Ovalization Measurement Apparatus (COMA)
Figure 6 depicts the curvature–ovalization measurement apparatus (COMA) developed by Pan et al. [28], designed to measure both the curvature and cross-sectional ovalization of tubes. Ovalization is defined as the relative change in the outer diameter compared to the original diameter. This lightweight device was installed near the mid-span of the tube. Curvature was calculated based on the fixed distance between two side inclinometers and their measured angular displacements. Furthermore, the COMA is equipped with a magnetic sensor at its center to detect changes in the outer diameter of circular tubes. In the present study, the COMA was modified to monitor variations in the outer side length of square tubes.

Figure 6.
Schematic diagram of the COMA.
2.3. Square Tubes
In this study, 6063-T6 aluminum alloy square tubes were chosen as the experimental material due to their excellent machinability and consistent mechanical properties. This alloy is widely used in industry and is well-suited for experiments involving cyclic bending loads. The chemical composition by weight percentage is as follows: Mg 0.880, Si 0.652, Fe 0.118, Cu 0.180, Cr 0.071, Mn 0.013, Zn 0.010, and Ti 0.010, with the balance being aluminum.
The material properties employed in the experiments included a Young’s modulus of 68.6 GPa, a Poisson’s ratio of 0.33, an elongation at break of 9.4%, an ultimate tensile strength of 186 MPa, an ultimate compressive strength of 171 MPa, and a 0.2% offset yield strength of 160 MPa. The square tubes used had a length of 500 mm and a wall thickness of 0.7 mm. Figure 7a shows a schematic of the square tube’s cross-section. As illustrated in Figure 7b, four different outer side lengths (ℓo) were examined: 20 mm, 30 mm, 40 mm, and 50 mm

Figure 7.
(a) Schematic illustration of the cross-section of a square tube and (b) photograph of 6063-T6 aluminum alloy square tubes with four different outer side lengths (ℓo).
2.4. Test Procedures
Specimens were subjected to curvature-controlled cyclic bending at a curvature rate of 0.05 m−1·s−1. As illustrated in Figure 8, the bending moment direction was fixed along the x-axis. The orientation angle (Φ) was defined as the angle between the outer side of the square tube and the bending moment direction (i.e., the x-axis). When the outer side aligned with the x-axis, Φ was set to 0°. Three orientation angles were investigated: 0°, 22.5°, and 45°. Figure 9 presents photographs of 6063-T6 aluminum alloy square tubes undergoing cyclic bending at Φ = 0°, 22.5°, and 45°.
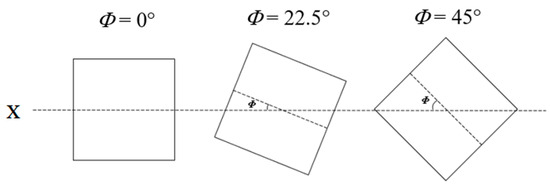
Figure 8.
Schematic illustration of the square tube cross-sections at different orientation angles (Φ).

Figure 9.
Photographs of 6063-T6 aluminum alloy square tubes subjected to cyclic bending at orientation angles Φ of (a) 0°, (b) 22.5°, and (c) 45°.
The bending moment (M) was measured using load cells integrated within the bending machine, as shown in Figure 2. Curvature (κ) and the relative variation in the outer side length (Δℓ/ℓo, where Δℓ is the change in ℓo) were measured using the COMA system depicted in Figure 6. Additionally, the number of cycles to initiate buckling (Nb) was recorded.
3. Results and Discussion
3.1. Appearance Changes of Square Tubes
Regardless of the value of Φ, the deformation process of the square tube under cyclic bending can be visually divided into four distinct stages: the initial stage, the second stage, the third stage, and the fourth stage.
In the initial stage, the square tube undergoes cyclic bending without any noticeable external changes. However, in the second stage, an indentation begins to form at the center of the vertical tube wall, perpendicular to the tube’s longitudinal axis, as shown in Figure 10a. The depth and extent of the indentation are positively correlated with ℓo. Simultaneously, the central region of the horizontal tube wall bulges outward, exhibiting a similar size-dependent relationship. Additionally, during the transition from the first stage to the second stage, the bending moment decreases by approximately 20%, which also serves as the buckling criterion defined in our experiment.

Figure 10.
Appearance changes of square tubes at different stages: (a) second stage, (b) third stage, and (c) fourth stage.
Upon reaching the third stage, buckling occurs at the corners above or below the vertical tube wall, leading to the formation of a hole approximately one-tenth of the tube’s edge length, as illustrated in Figure 10b. This causes a rapid rupture of the upper or lower tube wall within the same cycle. At this point, subsequent cracks propagate either upward or downward from the rupture hole.
In the fourth stage, cracks begin to form on the sidewalls of the square tube near the existing holes and gradually expand over time, as depicted in Figure 10c. Notably, the crack growth rate is closely related to ℓo; shorter ℓo corresponds to slower crack growth, while longer ℓo leads to faster propagation. Eventually, the crack extends to either the top or bottom of the tube.
3.2. Relationship Between the Moment (M) and Curvature (κ)
Figure 11a–d show the M–κ curves for square tubes subjected to cyclic bending with varying outer side lengths (ℓo = 20, 30, 40, and 50 mm) at a fixed orientation angle (Φ = 0°). Figure 12a–c present the M–κ curves for square tubes with a fixed ℓo of 30 mm and varying orientation angles (Φ = 0°, 22.5°, and 45°). The curvature (κ) was controlled within the range of +0.4 m−1 to −0.4 m−1.
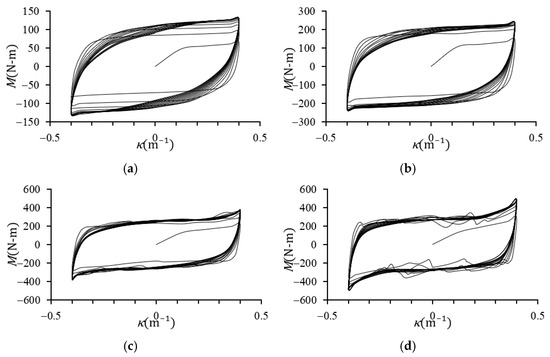
Figure 11.
Experimental M–κ curves of 6063-T5 aluminum alloy square tubes under cyclic bending with a varying ℓo ((a) 20 mm, (b) 30 mm, (c) 40 mm, and (d) 50 mm) and fixed Φ (0°)).
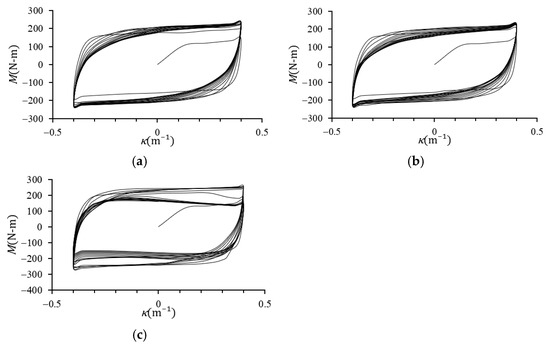
Figure 12.
Experimental M–κ curves of the 6063-T5 aluminum alloy square tubes under cyclic bending with a fixed ℓo (30 mm) and varying Φ ((a) 0°, (b) 22.5, and (c) 45°).
During the initial loading stage, the square tubes remained within the elastic regime, resulting in a linear increase in the M with respect to κ. As κ increased further, plastic deformation commenced, causing the rate of increase in M to diminish and resulting in permanent deformation. All M–κ curves exhibited cyclic hardening and stabilized after a few cycles.
For a fixed Φ, increasing ℓo led to a higher peak M value. Likewise, for a fixed ℓo, increasing Φ caused a gradual rise in the peak M. Notably, variations in κ did not alter the overall trends of the M–κ curves. Hence, additional M–κ curves for other combinations of ℓo and Φ were considered unnecessary.
3.3. Relationship Between Outer Side Length Variation (Δℓ/ℓo) and Curvature (κ)
Figure 13a–d show the Δℓ/ℓo-κ curves for square tubes subjected to cyclic bending with varying outer side lengths (ℓo = 20, 30, 40, and 50 mm) at a fixed orientation angle (Φ = 0°). Figure 14a–c illustrate the corresponding Δℓ/ℓo-κ relationship curves for square tubes with a fixed ℓo of 30 mm and varying orientation angles (Φ = 0°, 22.5°, and 45°). The curvature κ ranged from +0.4 m−1 to −0.4 m−1. In all cases, the Δℓ/ℓo-κ curves displayed nonlinear behavior, whether the deformation was elastic or plastic. As κ increased during loading, Δℓ/ℓo also increased, reaching its maximum at κ = +0.4 m−1. Upon unloading, Δℓ/ℓo decreased but did not return to zero at κ = 0 m−1, indicating residual plastic strain. With continued reverse loading, both κ and Δℓ/ℓo increased again, peaking at κ = −0.4 m−1. After returning to κ = 0 m−1, Δℓ/ℓo was slightly higher than in the previous cycle, reflecting the accumulation of plastic deformation. This progressive increase in Δℓ/ℓo continued with additional loading cycles. The Δℓ/ℓo curves also demonstrated symmetry, ratcheting behavior, and incremental growth with cycling. At a given κ, higher ℓo or Φ values resulted in larger Δℓ/ℓo. Because these trends were consistent, further testing with additional ℓo or Φ values was considered unnecessary.


Figure 13.
Experiment Δℓ/ℓo-κ relationships for 6063-T5 aluminum alloy square tubes under cyclic bending with a varying ℓo ((a) 20 mm, (b) 30 mm, (c) 40 mm, and (d) 50 mm) and fixed Φ (0°)).
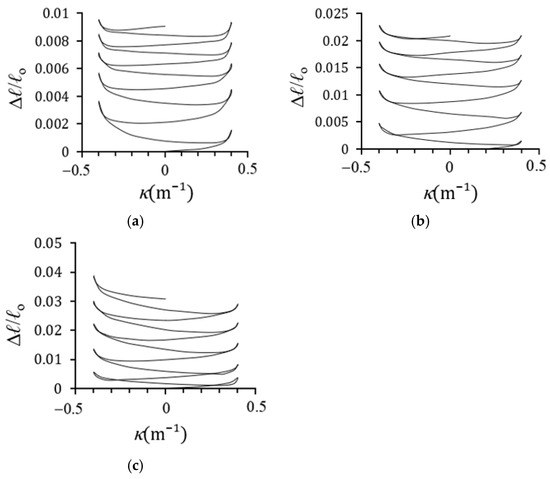
Figure 14.
Experiment Δℓ/ℓo-κ relationships for 6063-T5 aluminum alloy square tubes under cyclic bending with a fixed ℓo (30 mm) and varying Φ ((a) 0°, (b) 22.5°, and (c) 45°).
3.4. Relationship Between the Curvature (κ) and Number of Cycles Required to Initiate Buckling (Nb)
Figure 15a–c show the κc–Nb relationships of square tubes under cyclic bending for various ℓo values and bending directions (Φ = 0°, 22.5°, and 45°), plotted on double logarithmic scales. The straight lines in the plots represent least-squares regression results. For each bending direction, the four ℓo values correspond to four distinct linear trends. At fixed Φ and ℓo, the number of cycles to buckling (Nb) decreased with increasing critical curvature (κc). Similarly, for fixed Φ and κc, a larger ℓo resulted in a higher Nb. Conversely, at fixed ℓo and κc, Nb showed a slight decrease as Φ increased. It is worth noting that, for each κc value, two specimens were tested, and the resulting Nb values showed minimal variation, indicating good consistency.
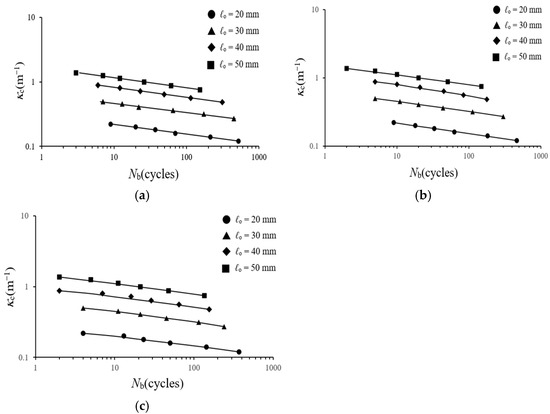
Figure 15.
Experimental κc–Nb relationships for 6063-T5 aluminum alloy square tubes under cyclic bending with varying Φ ((a) 0°, (b) 22.5°, and (c) 45°) on double logarithmic coordinates.
Since the κc–Nb relationships for square tubes under cyclic bending appear as straight lines, the following equation is proposed:
or equivalently,
κc = C(Nb)−α
logκc = logC − αlogNb.
Here, C and α are material parameters. The parameter C represents the value of κc when Nb equals 1, while α denotes the slope of the fitted straight line.
Based on the experimental results shown in Figure 15a–c and Figure 16a,b, respectively, present the logC versus ℓo/t and logα versus ℓo/t for different values of Φ. The straight lines were derived using the least-squares method and correspond to bending directions of Φ = 0°, 22.5°, and 45°. Since all the curves exhibit linear relationships, the following empirical equations are proposed:
and
logC = Co − β(ℓo/t)
logα = αo − γ(ℓo/t).
Here, Co, β, αo, and γ are material parameters.

Figure 16.
(a) Relationship between logC and ℓo/t for different Φ and (b) relationship between logα and ℓo/t for different Φ.
Figure 17a–d illustrate the relationships between the material parameters C0, β, α0, γ, and Φ. Since all of these relationships are linear, the following empirical equations are proposed to describe the dependencies of C0, β, α0, and γ, and Φ:
and
Co = a1Φ + a2
β = b1Φ + b2
αo = c1Φ + c2
γ = d1Φ + d2.
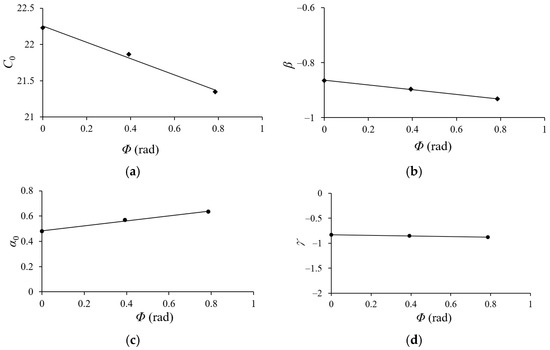
Figure 17.
(a) Relationship between Co and Φ, (b) relationship between β and Φ, (c) relationship between αo and Φ, and (d) relationship between γ and Φ.
Here, a1, a2, b1, b2, c1, c2, d1, and d2 are material parameters. According to the straight lines shown in Figure 17a–d, the values of these parameters were determined to be −1.1205, 22.254, −0.0862, −0.8639, 0.1954, 0.4847, −0.0624, and −0.8292, respectively. Then, Equations (1)–(8) were employed to describe the κc–Nb curves of 6063-T5 aluminum alloy square tubes with various ℓo values and different Φ (0°, 22.5°, and 45°). The predicted results are shown as dashed lines in Figure 18a–c. The comparison indicates that the proposed equations provide an adequate and reasonable representation of the experimental results.

Figure 18.
Experimental and descriptive κc–Nb relationships for 6063-T5 aluminum alloy square tubes under cyclic bending with varying Φ ((a) 0°, (b) 22.5°, and (c) 45°) on double logarithmic coordinates.
4. Conclusions
This study investigated the behavior of 6063-T6 aluminum alloy square tubes with four different ℓo values (20, 30, 40, and 50 mm) under cyclic bending at three bending angles (Φ = 0°, 22.5°, and 45°). Only curvature-controlled, symmetric pure bending loads were applied, meaning that the forward and reverse curvatures had equal magnitudes. Several important conclusions can be drawn from the results:
- (1)
- During the initial loading stage, the square tubes exhibited elastic behavior, resulting in a linear increase in bending moment (M) with increasing curvature (κ). As κ increased further, plastic deformation initiated, causing the M–κ curves to gradually flatten and permanent deformation to occur. All M–κ curves demonstrated cyclic hardening and stabilized after several loading cycles. At a fixed bending angle (Φ), increasing ℓo led to a higher peak M value. Similarly, for a fixed ℓo, increasing Φ resulted in a gradual increase in the peak M value.
- (2)
- The Δℓ/ℓo-κ curves exhibited nonlinear behavior, regardless of whether the square tube underwent elastic or plastic bending deformation. As the number of cyclic bending loads increased, Δℓ/ℓo continued to grow. For a fixed Φ, the Δℓ/ℓo-κ curves displayed symmetry, serrated patterns, and progressive growth with increasing cycle count. At a fixed κ, increasing ℓo or Φ led to an increase in Δℓ/ℓo.
- (3)
- The Δℓ/ℓo-κ curves exhibited nonlinear behavior regardless of whether the square tubes experienced elastic or plastic bending deformation. With increasing numbers of cyclic bending loads, Δℓ/ℓo progressively increased. For a fixed bending angle (Φ), the Δℓ/ℓo-κ curves demonstrated symmetry, serrated patterns, and incremental growth as the cycle count increased. At a constant curvature (κ), increasing either ℓo or Φ resulted in higher Δℓ/ℓo values.
- (4)
- The deformation process of square tubes under cyclic bending can be categorized into four distinct stages based on their external appearance: the initial, second, third, and fourth stages. The transition from the first to the second stage is marked by a decrease in bending moment of approximately 20%, which is used as the buckling criterion in this study.
- (5)
- The κc–Nb relationships indicated that, at a fixed Φ and ℓo, Nb decreased with increasing κc. Similarly, at a fixed Φ and κc, Nb increased as ℓo increased. For a fixed ℓo and κc, Nb slightly decreased with increasing Φ. When the κc–Nb data were plotted on double logarithmic coordinates, the four distinct ℓo values corresponded to four straight lines for each Φ, each with a unique slope and intercept.
- (6)
- Equations (1) or (2) can be used to describe the κc–Nb relationships. Experimental data revealed linear relationships between logC and ℓo/t (Figure 16a) and between logα and ℓo/t (Figure 16b), which were used to derive Equations (3) and (4), respectively. Additionally, the data in Figure 16a,b were employed to establish linear relationships between Co and Φ (Figure 17a), β and Φ (Figure 17b), αo and Φ (Figure 17c), and γ and Φ (Figure 17d), leading to Equations (5)–(8). These equations were then used to predict the κc–Nb behavior of 6063-T6 aluminum alloy square tubes under cyclic bending with various ℓo and Φ values. As illustrated in Figure 18a–c, the predicted results aligned well with the experimental data, indicating that the proposed equations effectively represent the observed behavior.
Author Contributions
Conceptualization, C.-M.L., M.-C.Y. and W.-F.P.; methodology, C.-M.L. and W.-F.P.; software, C.-M.L. and M.-C.Y.; validation, M.-C.Y. and W.-F.P.; formal analysis, C.-M.L. and M.-C.Y.; investigation, C.-M.L. and M.-C.Y.; resources, W.-F.P.; data curation, C.-M.L., M.-C.Y. and W.-F.P.; writing—original draft preparation, C.-M.L., M.-C.Y. and W.-F.P.; writing—review and editing, W.-F.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Science and Technology Council (NSTC) under grant number 112-2221-E-006-174.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jin, S.Y.; Altenhof, W. Comparison of the load/displacement and energy absorption performance of round and square AA6061-T6 extrusions under a cutting deformation mode. Int. J. Crashworthiness 2007, 12, 265–278. [Google Scholar] [CrossRef]
- Hanssen, A.G.; Langseth, M.; Hopperstad, O.S. Static and dynamic crushing of circular aluminum extrusions with aluminum foam filler. Int. J. Impact Eng. 2000, 24, 475–507. [Google Scholar] [CrossRef]
- Kyriakides, S.; Shaw, P.K. Inelastic buckling of tubes under cyclic bending. J. Press. Vessel Technol. 1987, 109, 169–178. [Google Scholar] [CrossRef]
- Corona, E.; Kyriakides, S. An experimental investigation of the degradation and buckling of circular tubes under cyclic bending and external pressure. Thin-Walled Struct. 1991, 12, 229–263. [Google Scholar] [CrossRef]
- Corona, E.; Kyriakides, S. Asymmetric collapse modes of pipes under combined bending and pressure. Int. J. Solids Struct. 2000, 24, 505–535. [Google Scholar] [CrossRef]
- Corona, E.; Lee, L.H.; Kyriakides, S. Yield anisotropic effects on buckling of circular tubes under bending. Int. J. Solids Struct. 2006, 43, 7099–7118. [Google Scholar] [CrossRef]
- Limam, A.; Lee, L.H.; Corana, E. Inelastic wrinkling and collapse of tubes under combined bending and internal pressure. Int. J. Mech. Sci. 2010, 52, 37–47. [Google Scholar] [CrossRef]
- Limam, A.; Lee, L.H.; Corona, E.; Kyriakides, S. On the collapse of dented tubes under combined bending and internal pressure. Int. J. Solids Struct. 2012, 55, 1–12. [Google Scholar] [CrossRef]
- Bechle, N.J.; Kyriakides, S. Localization of NiTi tubes under bending. Int. J. Solids Struct. 2014, 51, 967–980. [Google Scholar] [CrossRef]
- Jiang, D.; Kyriakides, S.; Bechle, N.J.; Landis, C.M. Bending of pseudoelastic NiTi tubes. Int. J. Solids Struct. 2017, 124, 192–214. [Google Scholar] [CrossRef]
- Kazinakis, K.; Kyriakides, S.; Jiang, D.; Bechle, N.J.; Landis, C.M. Buckling and collapse of pseudoelastic NiTi tubes under bending. Int. J. Solids Struct. 2021, 221, 2–17. [Google Scholar] [CrossRef]
- Yuan, W.; Mirmiran, A. Buckling analysis of concrete-filled FRP tubes. Int. J. Struct. Stab. Dyn. 2001, 1, 367–383. [Google Scholar] [CrossRef]
- Elchalakani, M.; Zhao, X.L.; Grzebieta, R.H. Plastic mechanism analysis of circular tubes under pure bending. Int. J. Mech. Sci. 2002, 44, 1117–1143. [Google Scholar] [CrossRef]
- Houliara, S.; Karamanos, S.A. Buckling and post-buckling of long pressurized elastic thin-walled tubes under in-plane bending. Int. J. Nonlinear Mech. 2006, 44, 491–511. [Google Scholar] [CrossRef]
- Yazdani, H.; Nayebi, A. Continuum damage mechanics analysis of thin-walled tube under cyclic bending and internal constant pressure. Int. J. Appl. Mech. 2013, 5, 1350038. [Google Scholar] [CrossRef]
- Elchalakani, M.; Karrech, A.; Hassanein, M.F.; Yang, B. Plastic and yield slenderness limits for circular concrete filled tubes subjected to static pure bending. Thin-Walled Struct. 2016, 109, 50–64. [Google Scholar] [CrossRef]
- Shamass, R.; Alfano, G.; Guarracino, F. On elastoplastic buckling analysis of cylinders under nonproportional loading by differential quadrature method. Int. J. Struct. Stab. Dyn. 2017, 17, 1750072. [Google Scholar] [CrossRef]
- Li, P.; Wang, L. Nonlinear stability behavior of cable-stiffened single-layer latticed shells under earthquakes. Int. J. Struct. Stab. Dyn. 2018, 18, 1850117. [Google Scholar] [CrossRef]
- Chegeni, B.; Jayasuriya, S.; Das, S. Effect of corrosion on thin-walled pipes under combined internal pressure and bending. Thin-Walled Struct. 2019, 143, 106218. [Google Scholar] [CrossRef]
- Jin, S.; Cheng, P.; Saneian, M.; Yong, B. Mechanical behavior of thin tubes under combined axial compression and bending. Thin-Walled Struct. 2021, 159, 107255. [Google Scholar] [CrossRef]
- Silveira1, T.; Pinto, V.T.; Neufeld, J.P.S.; Pavlovic, A.; Rocha, L.A.O.; Santos, E.D.; Isoldi, L.A. Applicability evidence of constructal design in structural engineering: Case study of biaxial elasto-plastic buckling of square steel plates with elliptical cutout. J. Appl. Comp. Mech. 2021, 7, 922–934. [Google Scholar]
- He, Z.R.; Li, G.J.; Yang, J.C.; Guo, X.Z.; Duan, X.Y.; Guo, W.; Liu, X.; Deng, Y.Y.; Cheng, C. Insight into the deformation transition effect in free bending of tubes. Thin-Walled Struct. 2023, 348, 134673. [Google Scholar] [CrossRef]
- Wang, J.; Li, J.R.; Li, H.; Lv, L.Y. Behaviour of square concrete-filled steel tubes reinforced with internal latticed steel angles under bending. Structures 2023, 48, 1436–1454. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, T.; Yu, W.Z.; Pan, Z.M.; Cao, G.H. Behavior of multicell concrete-filled round-ended steel tubes under bending. Structures 2024, 67, 106984. [Google Scholar] [CrossRef]
- Yang, M.; Xi, J.; Hu, H.; Qin, T.; Wang, Y. Mechanism and influence research on the bending and torsion damping of composite hollow tube. Int. J. Struct. Stab. Dyn. 2024, 24, 2450239. [Google Scholar] [CrossRef]
- Wang, H.; Wu, J.; Lin, Y.; Wu, W.; Wang, M.; Yang, Z.; Liu, L. Plastic buckling and wrinkling behavior of tubes under combined bending and torsion loads. Thin-Walled Struct. 2025, 209, 112912. [Google Scholar] [CrossRef]
- Yu, M.C.; Pan, W.F. Failure of elliptical tubes with different long–short axis ratios under cyclic bending in different directions. Metals 2023, 13, 1891. [Google Scholar] [CrossRef]
- Pan, W.F.; Wang, T.R.; Hsu, C.M. A curvature-ovalization measurement apparatus for circular tubes under cyclic bending. Exp. Mech. 1998, 38, 99–102. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).