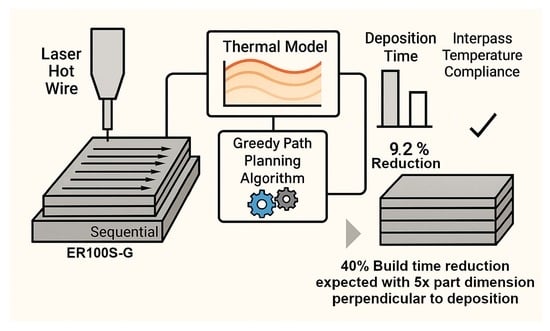
Path Planning for Rapid DEDAM Processing Subject to Interpass Temperature Constraints
Abstract
1. Introduction
2. Materials and Methods
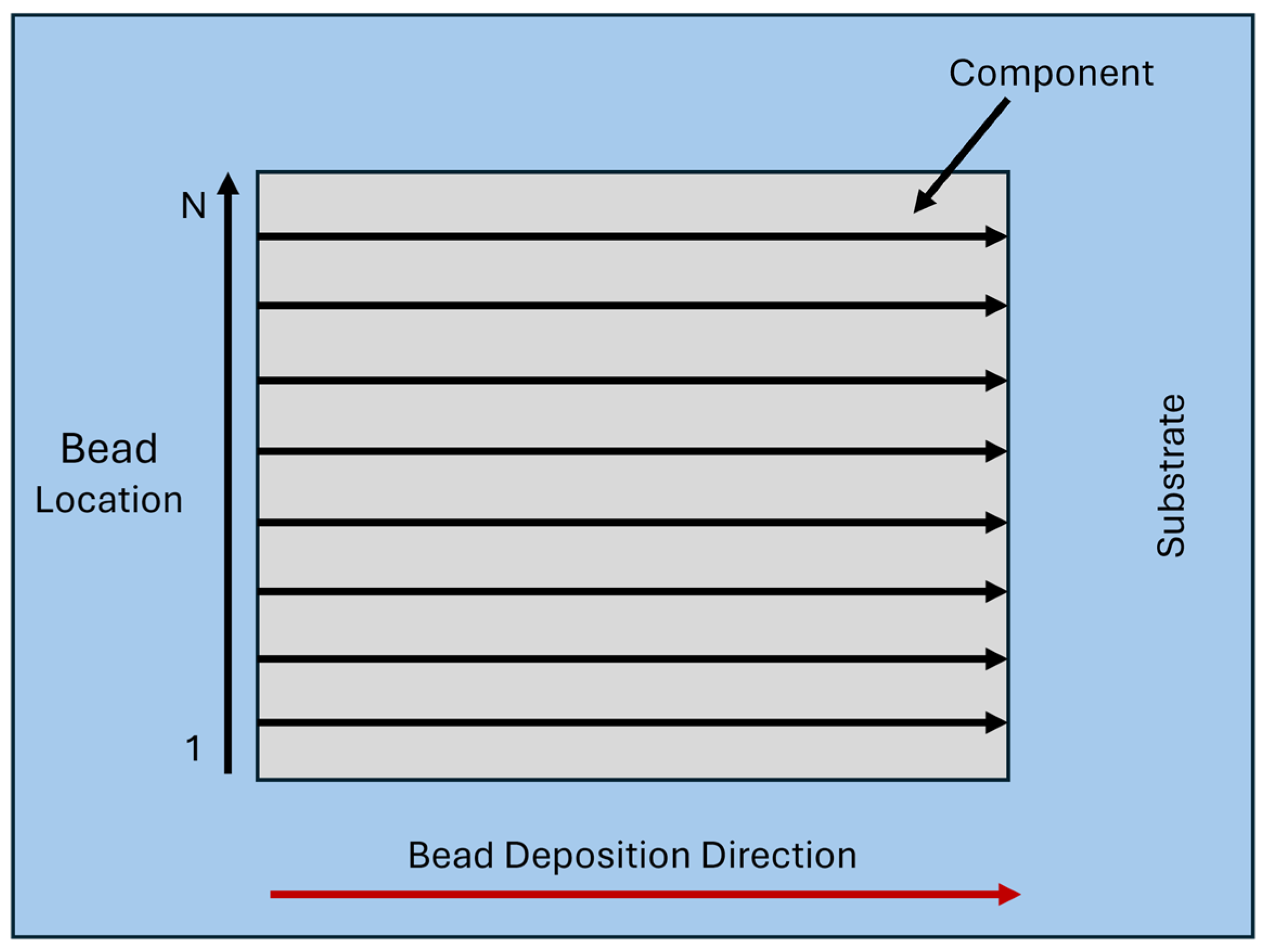
2.1. LHW-DED AM Process
2.2. Modeling and Path Planning
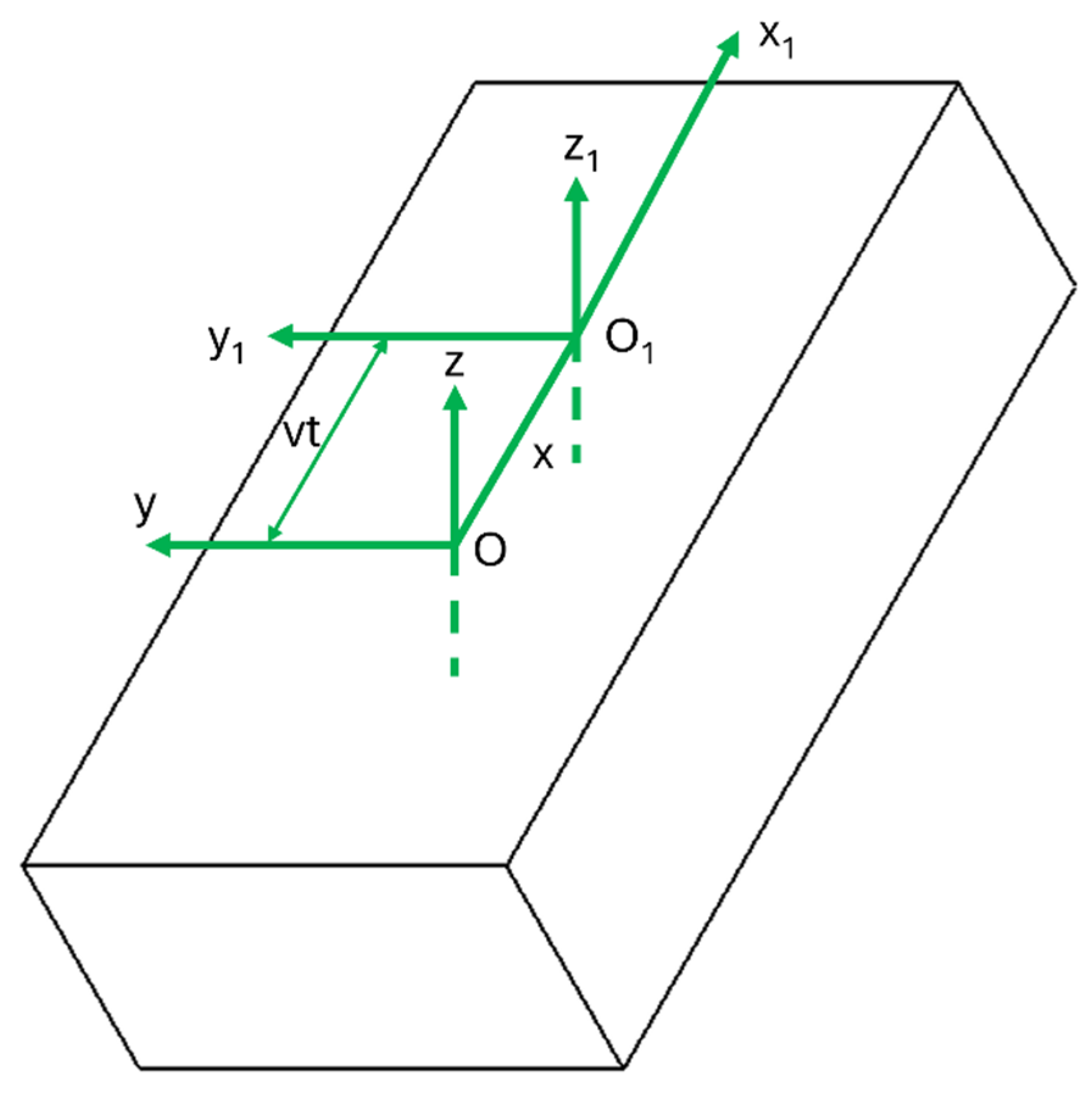
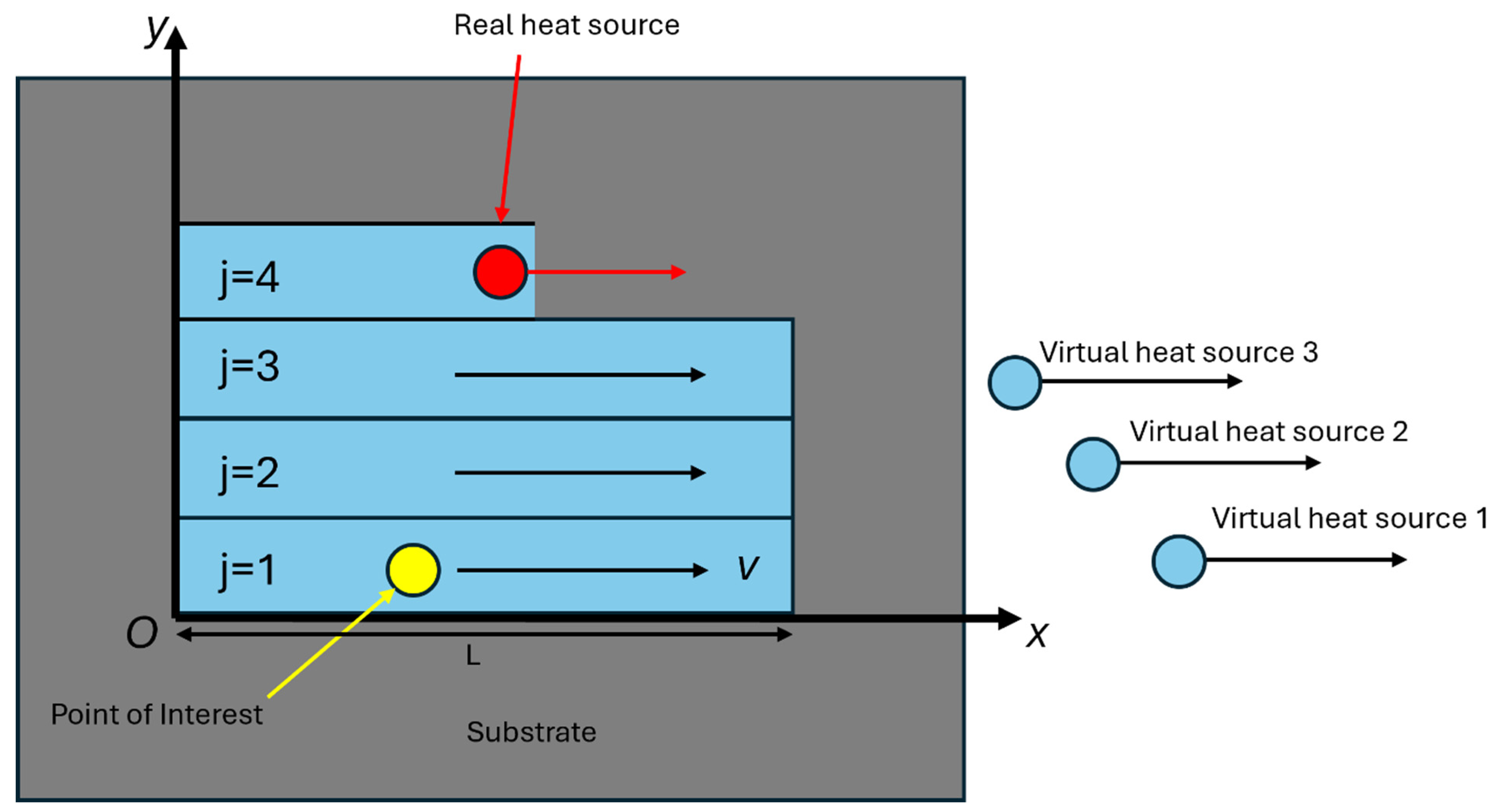
2.2.1. Analytic Model for Computing Temperature Field
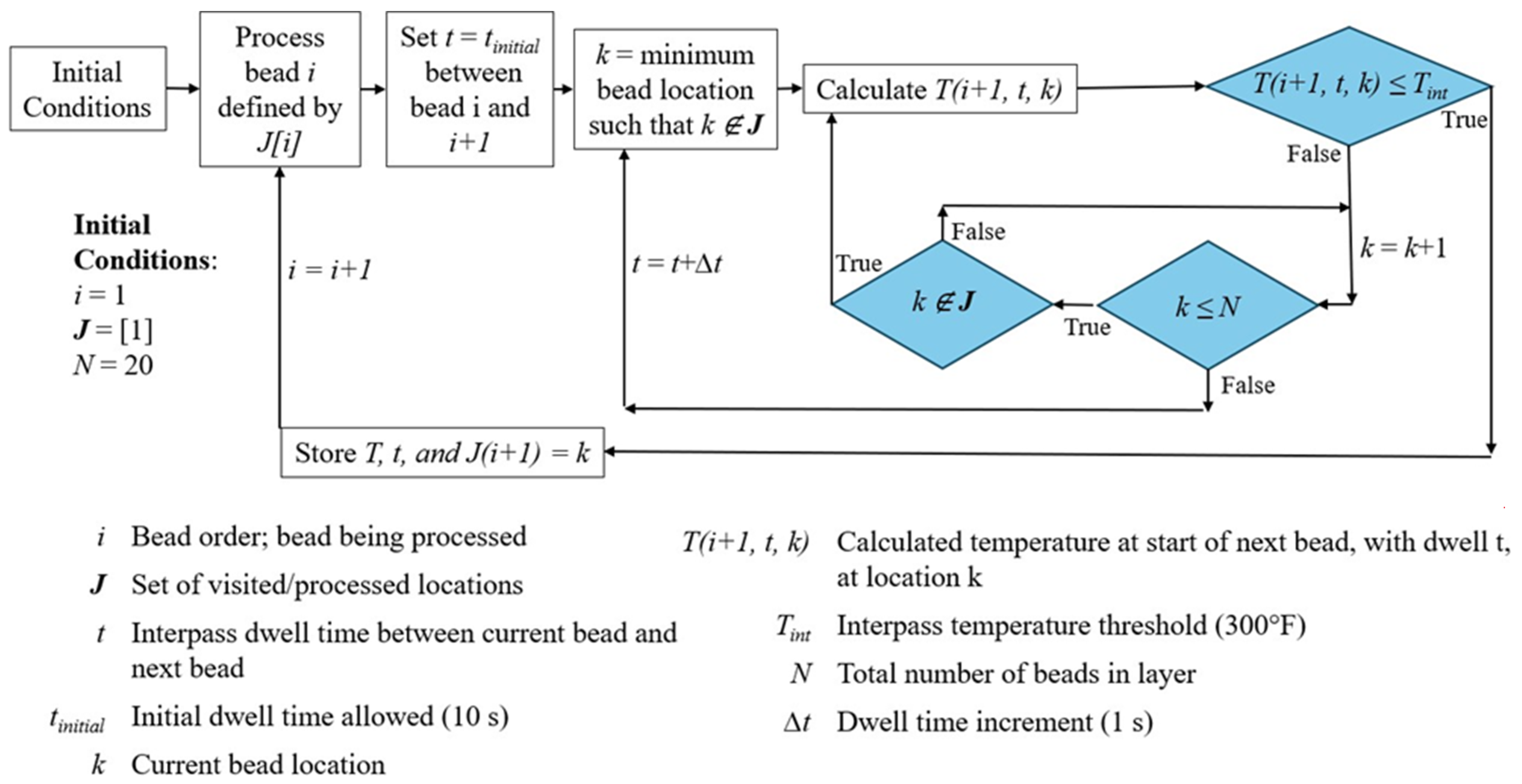
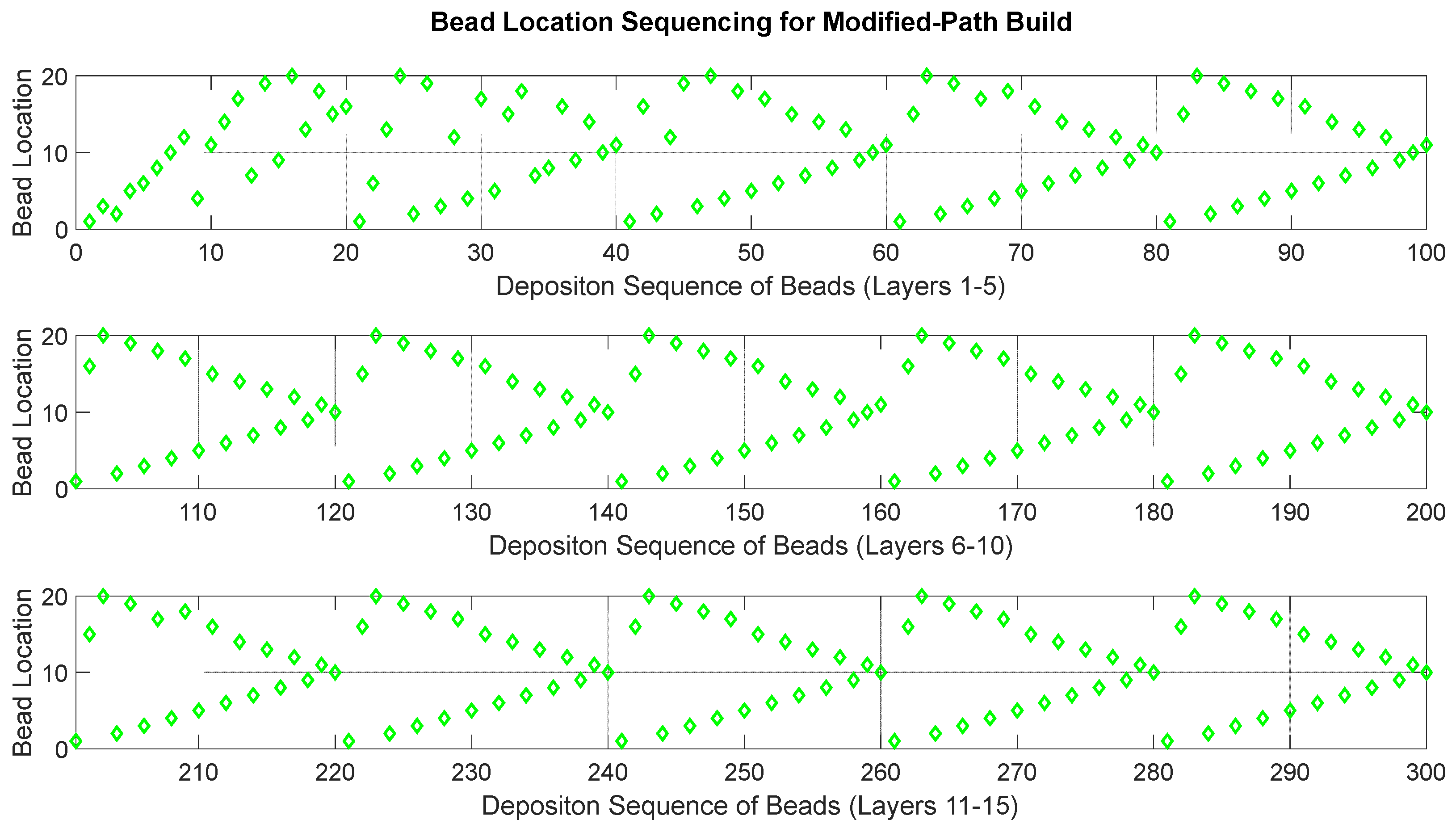
2.2.2. Algorithm for Path Planning
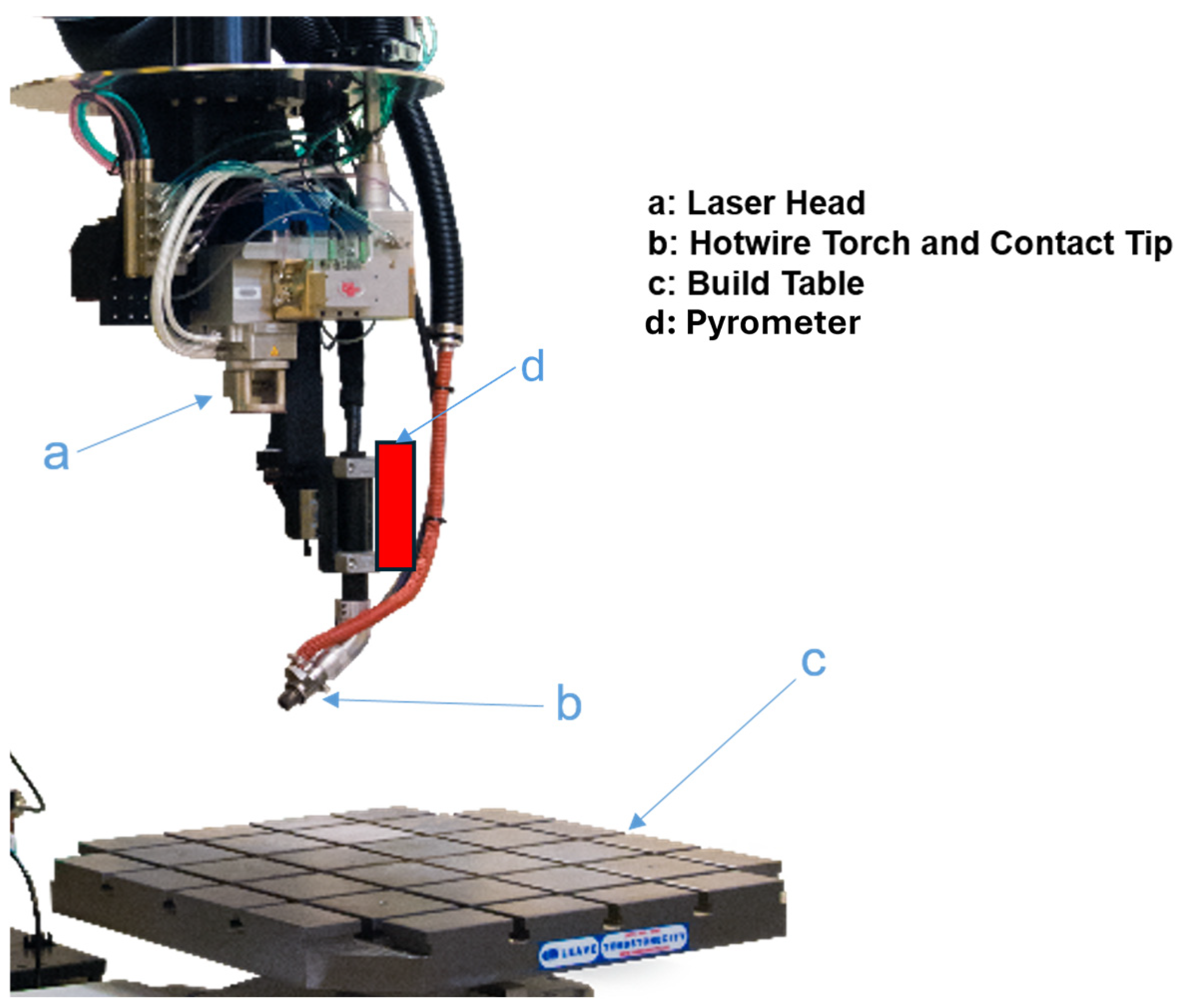
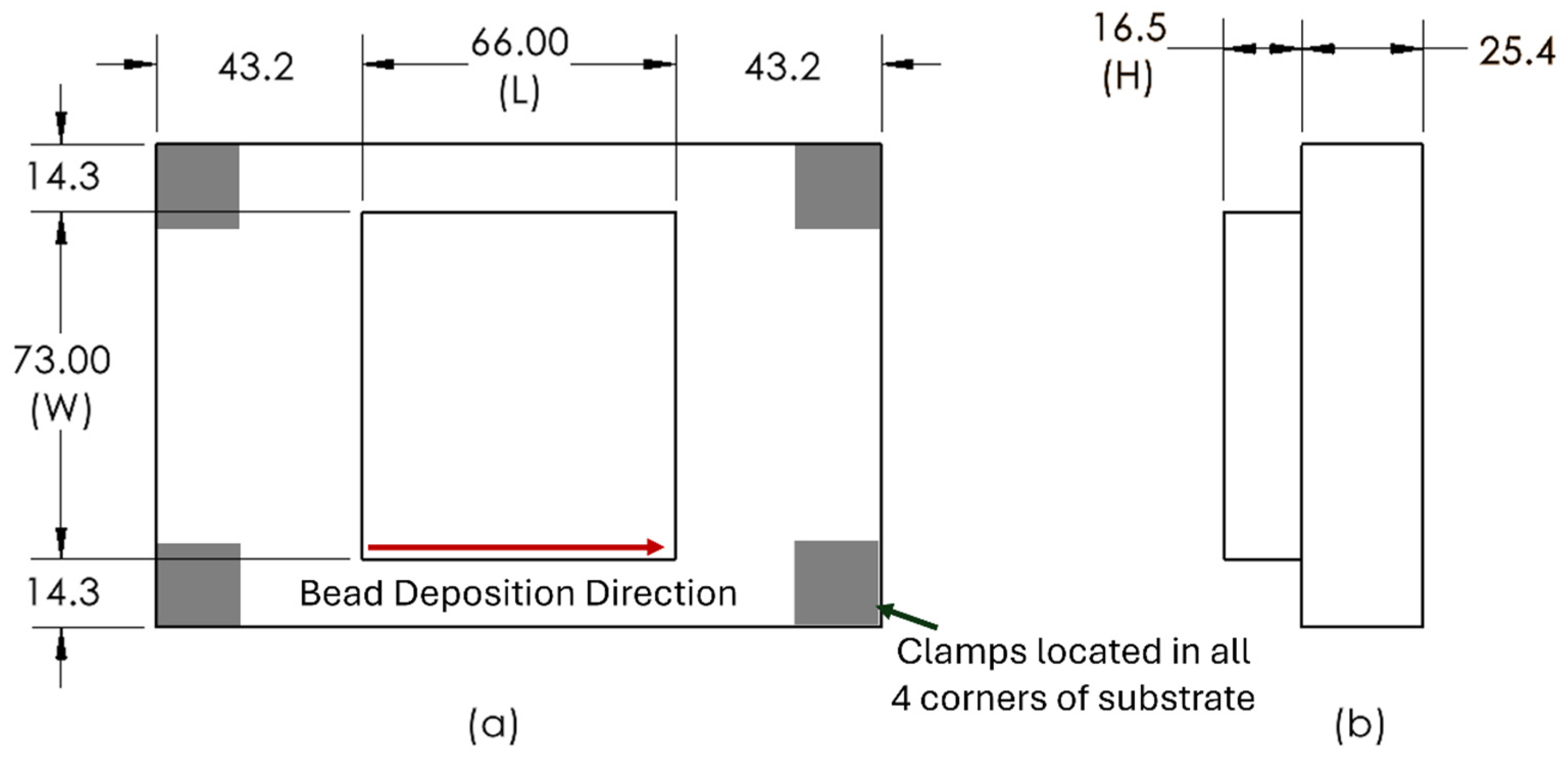
2.3. Experimental Setup
2.4. ER100S-G Wire
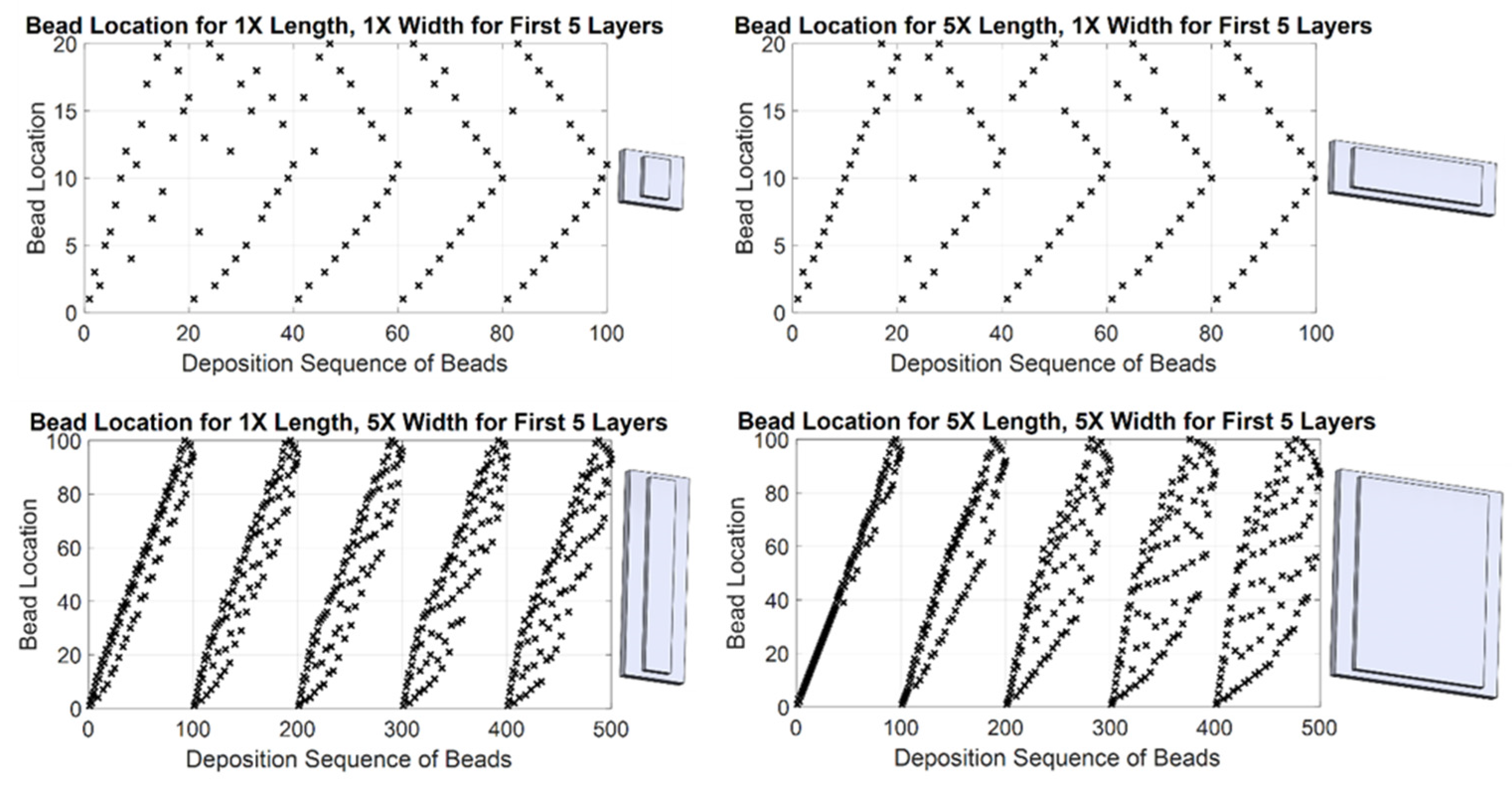
2.5. Projecting Results to Larger Components
3. Results and Discussion
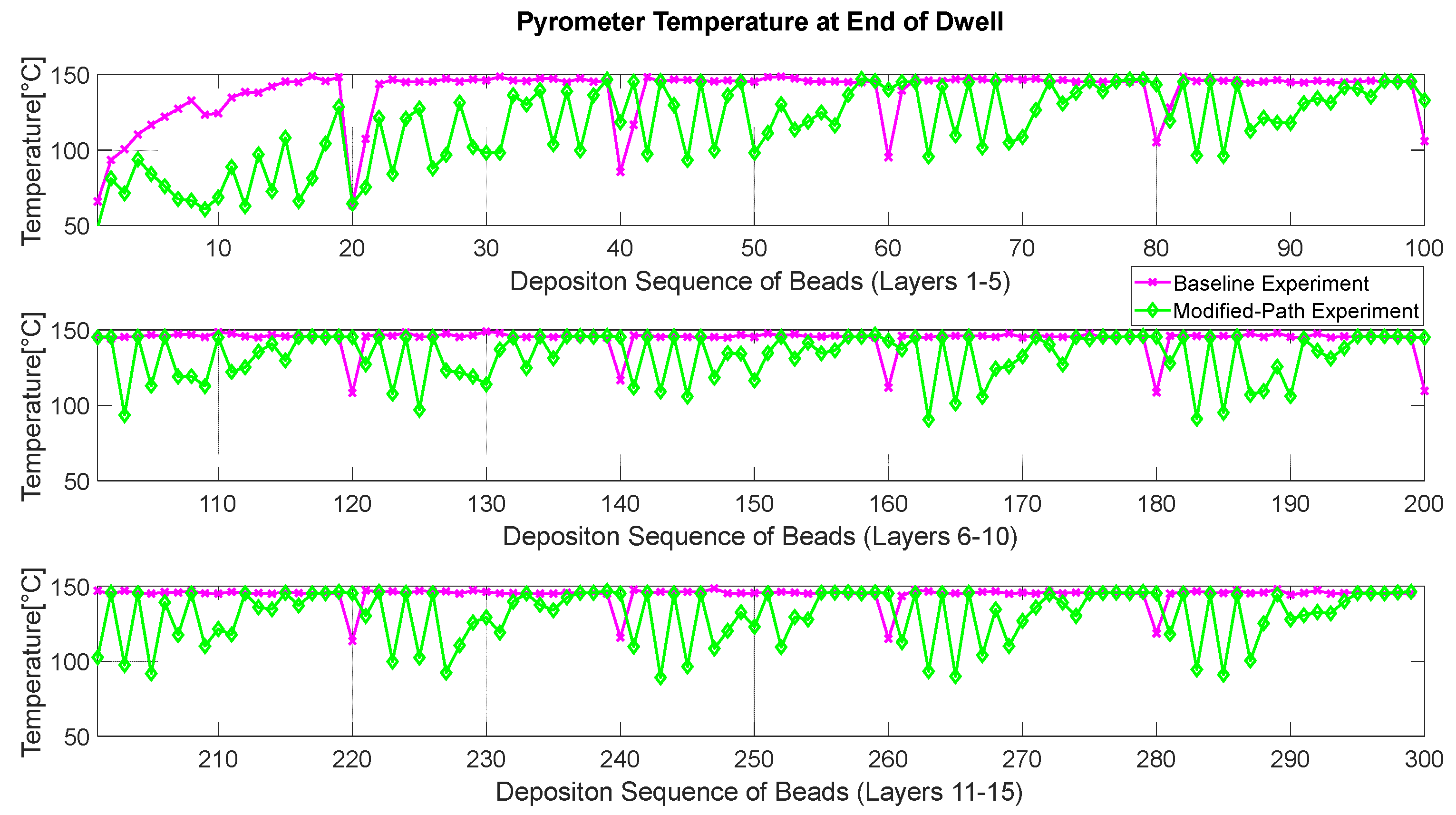
3.1. Measured Interpass Temperatures
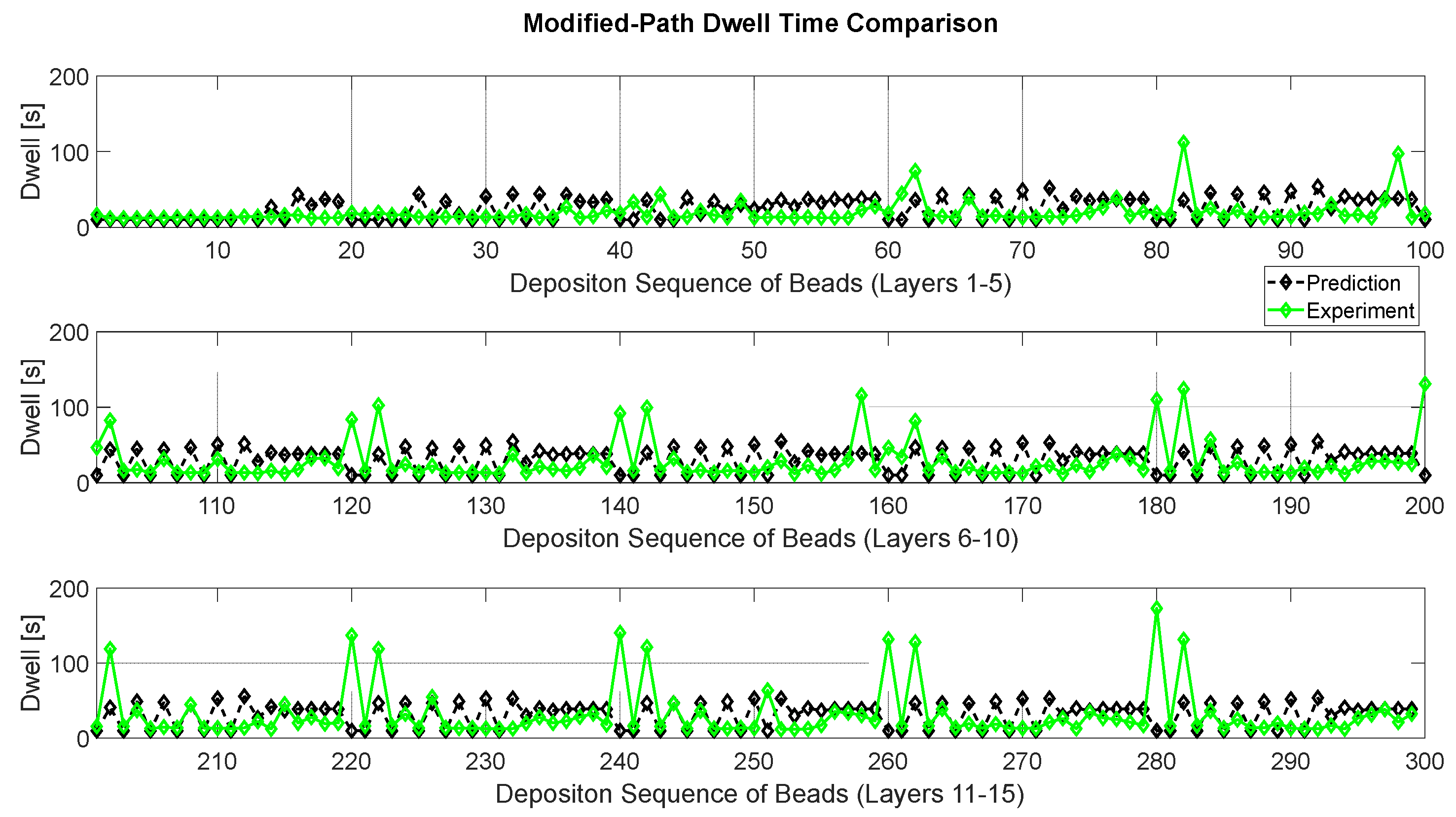
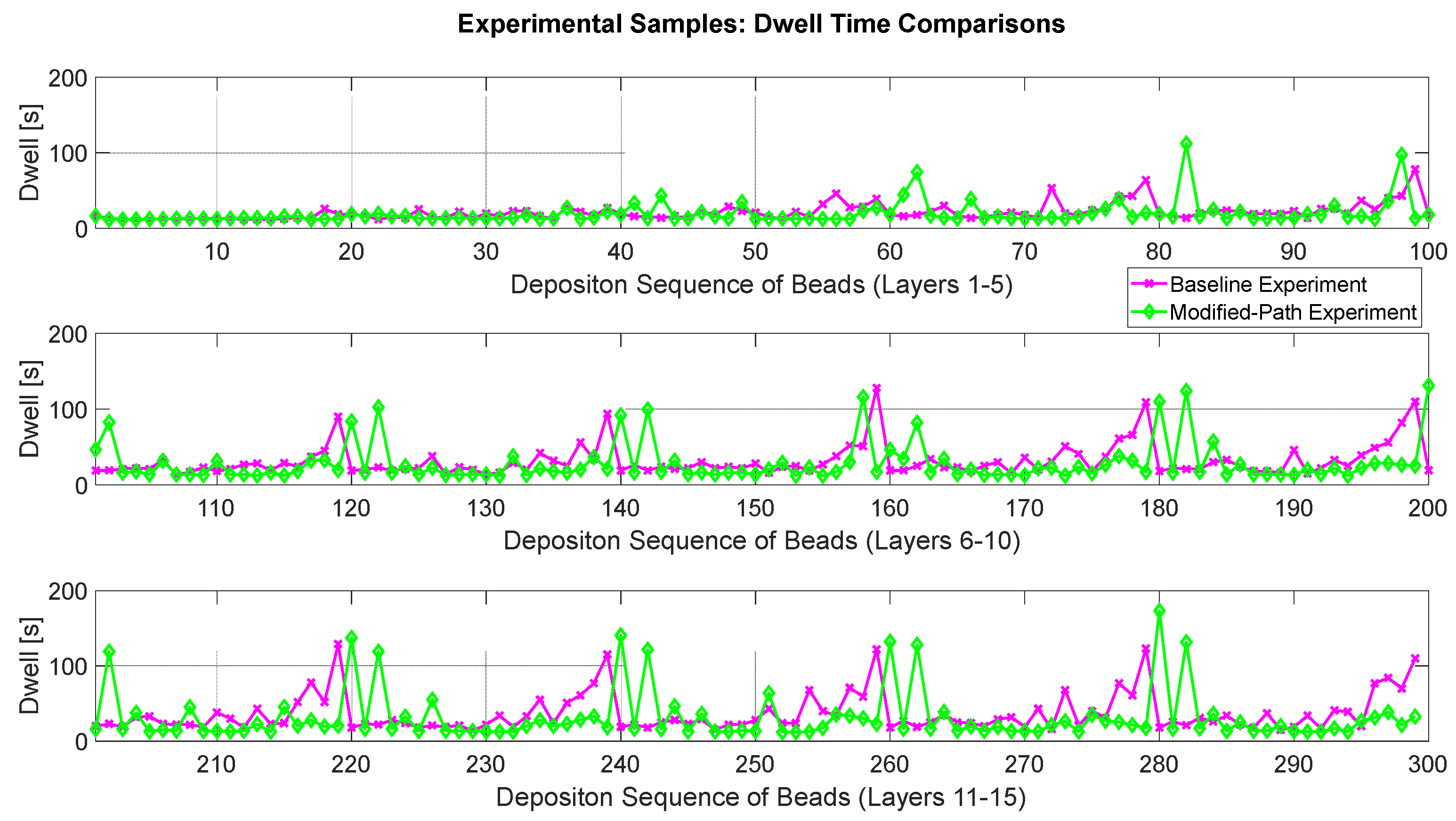
3.2. Predicted Interpass Dwell Time vs. Measurements
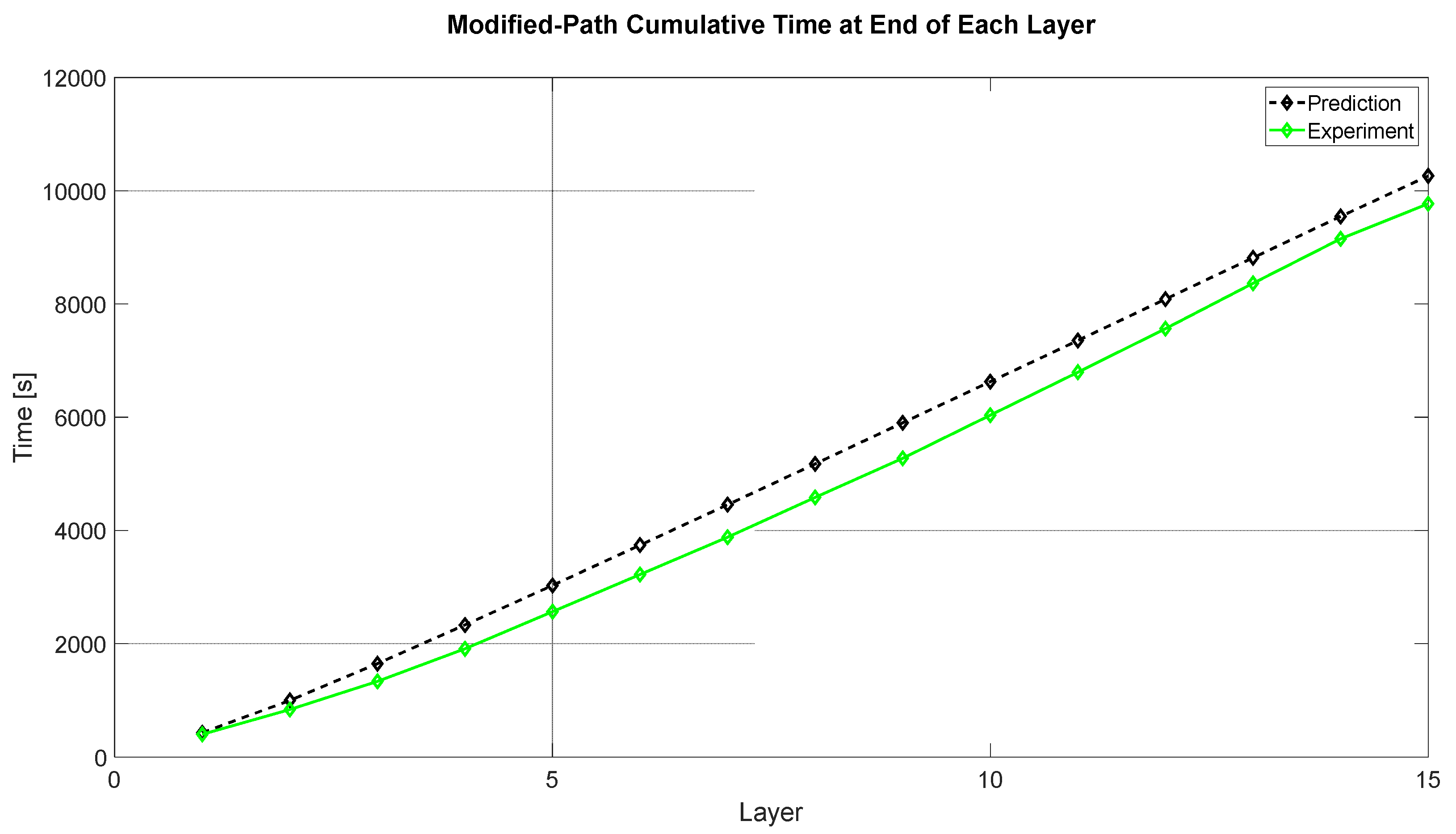
3.3. Build Time Reduction
3.4. Predicted Build Time Reduction for Larger Components
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Modified Rosenthal Derivation
References
- Bambach, M.; Sizova, I.; Silze, F.; Schnick, M. Comparison of laser metal deposition of Inconel 718 from powder, hot and cold wire. Procedia CIRP 2018, 74, 206–209. [Google Scholar] [CrossRef]
- Mao, Y.; Chen, H.; Xiong, J. Research progress in laser additive manufacturing of aluminum alloys: Microstructure, defect, and properties. J. Mater. Res. Technol. 2024, 30, 695–716. [Google Scholar] [CrossRef]
- Wen, P.; Feng, Z.; Zheng, S. Formation quality optimization of laser hot wire cladding for repairing martensite precipitation hardening stainless steel. Opt. Laser. Technol. 2015, 65, 180–188. [Google Scholar] [CrossRef]
- Wen, P.; Shan, J.; Zheng, S.; Wang, G. Control of wire transfer behaviors in hot wire laser welding. Int. J. Adv. Manuf. Technol. 2016, 83, 2091–2100. [Google Scholar] [CrossRef]
- Liu, S.; Liu, W.; Kovacevic, R. Experimental investigation of laser hot-wire cladding. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2017, 231, 1007–1020. [Google Scholar] [CrossRef]
- Liu, S.; Liu, W.; Harooni, M.; Ma, J.; Kovacevic, R. Real-time monitoring of laser hot-wire cladding of Inconel 625. Opt. Laser. Technol. 2014, 62, 124–134. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, G.; Wei, S.; Li, C.; Rong, Y. Process improvement in laser hot wire cladding for martensitic stainless steel based on the Taguchi method. Front. Mech. Eng. 2016, 11, 242–249. [Google Scholar] [CrossRef]
- Kottman, M.; Zhang, S.; McGuffin-Cawley, J.; Denney, P.; Narayanan, B.K. Laser Hot Wire Process: A Novel Process for Near-Net Shape Fabrication for High-Throughput Applications. Miner. Met. Mater. Soc. 2015, 67, 622–628. [Google Scholar] [CrossRef]
- Zhang, Z.; Kong, F.; Kovacevic, R. Laser hot-wire cladding of Co-Cr-W metal cored wire. Opt. Lasers. Eng. 2020, 128, 105998. [Google Scholar] [CrossRef]
- Budde, L.; Biester, K.; Lammers, M.; Hermsdorf, J.; Kaierle, S.; Overmeyer, L. Influence of process parameters on single weld seam geometry and process stability in Laser Hot-Wire Cladding of AISI 52100. Adv. Ind. Manuf. Eng. 2023, 7, 100122. [Google Scholar] [CrossRef]
- Stavropoulos, P.; Pastras, G.; Tzimanis, K.; Bourlesas, N. Addressing the challenge of process stability control in wire DED-LB/M process. CIRP Ann. 2024, 73, 129–132. [Google Scholar] [CrossRef]
- Funderburk, R.S. The Importance of Interpass Temperature Key Concepts in Welding Engineering. Weld. Innov. 1998, XV, 31–32. [Google Scholar]
- Wang, X.L.; Tsai, Y.T.; Yang, J.R.; Wang, Z.Q.; Li, X.C.; Shang, C.J.; Misra, R.D.K. Effect of interpass temperature on the micros tructure and mechanical properties of multi-pass weld metal in a 550-MPa-grade offshore engineering steel. Weld. World 2017, 61, 1155–1168. [Google Scholar] [CrossRef]
- Wongpanya, P.; Boellinghaus, T.; Lothongkum, G.; Kannengiesser, T. Effects of Preheating and Interpass Temperature on Stresses in S 1100 QL Mult-Pass Butt-Welds 79 Welding in the World-Research Supplement. Weld. World 2008, 52, 79–92. [Google Scholar] [CrossRef]
- Ramjaun, T.; Stone, H.J.; Karlsson, L.; Kelleher, J.; Moat, R.J.; Kornmeier, J.R.; Dalaei, K.; Bhadeshia, H.K.D.H. Effect of interpass temperature on residual stresses in multipass welds produced using low transformation temperature filler alloy. Sci. Technol. Weld. Join. 2014, 19, 44–51. [Google Scholar] [CrossRef]
- Sirin, K.; Sirin, S.Y.; Kaluc, E. Influence of the interpass temperature on t8/5 and the mechanical properties of submerged arc welded pipe. J. Mater. Process. Technol. 2016, 238, 152–159. [Google Scholar] [CrossRef]
- Geng, H.; Li, J.; Xiong, J.; Lin, X. Optimisation of interpass temperature and heat input for wire and arc additive manufacturing 5A06 aluminium alloy. Sci. Technol. Weld. Join. 2017, 22, 472–483. [Google Scholar] [CrossRef]
- Ma, Y.; Cuiuri, D.; Shen, C.; Li, H.; Pan, Z. Effect of interpass temperature on in-situ alloying and additive manufacturing of titanium aluminides using gas tungsten arc welding. Addit. Manuf. 2015, 8, 71–77. [Google Scholar] [CrossRef]
- Shen, C.; Pan, Z.; Cuiuri, D.; Ding, D.; Li, H. Influences of deposition current and interpass temperature to the Fe3Al-based iron aluminide fabricated using wire-arc additive manufacturing process. Int. J. Adv. Manuf. Technol. 2017, 88, 2009–2018. [Google Scholar] [CrossRef]
- Derekar, K.; Lawrence, J.; Melton, G.; Addison, A.; Zhang, X.; Xu, L. Influence of Interpass Temperature on Wire Arc Additive Manufacturing (WAAM) of Aluminium Alloy Components. MATEC Web Conf. 2019, 269, 5001–5006. [Google Scholar] [CrossRef]
- Poulain, P.; Wang, J.; Bouvier, S.; Williams, S.; Budnyk, S.; Gavrilovic-Wohlmuther, A. Impact of interpass temperature on the microstructure and mechanical properties of super duplex stainless steel in CW-GMA additive manufacturing. J. Manuf. Process. 2025, 146, 30–43. [Google Scholar] [CrossRef]
- Ren, K.; Liu, N.; Zhang, W.; Chew, Y.; Zhang, Y.; Fuh, J.Y.; Bi, G. Laser power planning in directed energy deposition by deep reinforcement learning. Int. J. Adv. Manuf. Technol. 2024, 135, 4683–4694. [Google Scholar] [CrossRef]
- Pinnacle Alloys. ER100S-G DATA SHEET. 2015, Volume 0117. Available online: http://www.pinnaclealloys.com/wp/wp-content/uploads/2015/11/Pinnacle-Alloys-ER100S-G-1.17.pdf (accessed on 29 January 2025).
- Weldcote Metals. ERS100S-1. 2020, Volume 54. Available online: https://weldcotemetals.com/dataFiles/specs/tech100S-1.pdf (accessed on 29 January 2025).
- American Welding Society (Committee on Filler Metals and Allied Materials). Specification for Low-Alloy Steel Electrodes and Rods for Gas Shielded Arc Welding, 5th ed.; Miami, F.L., Ed.; American Welding Society: Doral, FL, USA, 2022. [Google Scholar]
- Antonysamy, A. Microstructure, Texture and Mechanical Property Evolution During Additive Manufacturing of Ti6Al4V Alloy for Aerospace Applications. Ph.D. Dissertation, University of Manchester, Manchester, UK, 2012. [Google Scholar]
- Montevecchi, F.; Venturini, G.; Grossi, N.; Scippa, A.; Campatelli, G. Idle time selection for wire-arc additive manufacturing: A finite element-based technique. Addit. Manuf. 2018, 21, 479–486. [Google Scholar] [CrossRef]
- Vázquez, L.; Rodríguez, N.; Rodríguez, I.; Alberdi, E.; Álvarez, P. Influence of interpass cooling conditions on microstructure and tensile properties of Ti-6Al-4V parts manufactured by WAAM. Weld. World 2020, 64, 1377–1388. [Google Scholar] [CrossRef]
- Ren, K.; Chew, Y.; Fuh, J.Y.H.; Zhang, Y.F.; Bi, G.J. Thermo-mechanical analyses for optimized path planning in laser aided additive manufacturing processes. Mater. Des. 2019, 162, 80–93. [Google Scholar] [CrossRef]
- He, C.; Wood, N.; Bugdayci, N.B.; Okwudire, C. Generalized SmartScan: An Intelligent LPBF Scan Sequence Optimization Approach for Reduced Residual Stress and Distortion in Three-Dimensional Part Geometries. J. Manuf. Sci. Eng. 2025, 147, 041001. [Google Scholar] [CrossRef]
- Song, G.H.; Lee, C.M.; Kim, D.H. Investigation of path planning to reduce height errors of intersection parts in wire-arc additive manufacturing. Materials 2021, 14, 6477. [Google Scholar] [CrossRef]
- Zhao, T.; Yan, Z.; Wang, L.; Pan, R.; Wang, X.; Liu, K.; Guo, K.; Hu, Q.; Chen, S. Hybrid path planning method based on skeleton contour partitioning for robotic additive manufacturing. Robot. Comput. Integr. Manuf. 2024, 85, 102633. [Google Scholar] [CrossRef]
- Nguyen, L.; Buhl, J.; Bambach, M. Multi-bead overlapping models for tool path generation in wire-arc additive manufacturing processes. Procedia Manuf. 2020, 47, 1123–1128. [Google Scholar] [CrossRef]
- Rosenthal, D. Mathematical Theory of Heat Distribution During Welding and Cutting. Weld. J. 1941, 20, 220–234. [Google Scholar]
- Rykalin, N.N. Calculation of Heat Processes in Welding; Repositories of The University of Texas at Austin: Austin, TX, USA, 1960. [Google Scholar]
- Cohen, H.; Eisenbud, D.; Singer, M. The Greedy Algorithm. In Graphs, Networks, and Algorithms; Springer: Berlin/Heidelberg, Germany, 2008; pp. 129–153. [Google Scholar]
- Wu, S.S.Q.; Baker, B.W.; Rotter, M.D.; Rubenchik, A.M.; Wiechec, M.E.; Brown, Z.M.; Beach, R.J.; Matthews, M.J. Polarization effects associated with thermal processing of HY-80 structural steel using high-power laser diode array. Opt. Eng. 2017, 56, 124108. [Google Scholar] [CrossRef]
- LINCOLN® ER100S-1. January 2022. Available online: www.lincolnelectric.com (accessed on 29 January 2025).
- Baker, B.; McNelley, T.; Matthews, M.; Rotter, M.; Rubenchik, A.; Wu, S. Use of high-power diode laser arrays for pre- and post-weld heating during friction stir welding of steels. In Friction Stir Welding and Processing VIII; Springer International Publishing: Berlin/Heidelberg, Germany, 2016; pp. 21–36. [Google Scholar] [CrossRef]
- Cao, Z.; Dong, P.; Brust, F. Fast thermal solution procedure for analyzing 3D multi-pass welded structures. Eng. Mater. Sci. 2000, 455, 12–21. [Google Scholar]
- Perret, W.; Schwenk, C.; Rethmeier, M. Comparison of Analytical and Numerical Welding Temperature Field Calculation. Comput. Mater. Sci. 2010, 47, 1005–1015. [Google Scholar] [CrossRef]
- Li, J.; Wang, Q.; Michaleris, P. An analytical computation of temperature field evolved in directed energy deposition. J. Manuf. Sci. Eng. Trans. ASME 2018, 140, 101004. [Google Scholar] [CrossRef]
- Li, J.; Wang, Q.; Michaleris, P. Towards Computational Modeling of Temperature Field Evolution in Directed Energy Deposition Processes. 2018. Available online: http://asmedigitalcollection.asme.org/DSCC/proceedings-pdf/DSCC2018/51906/V002T23A001/2376748/v002t23a001-dscc2018-8973.pdf (accessed on 29 January 2025).


| Stage | Wire Feed Rate | Laser Power | Laser Travel Speed | Stage Duration |
|---|---|---|---|---|
| Preheat | 0 mm/s | 7.5 kW | - | 0.1 s |
| Pre-Fill | 30 mm/s | 7.5 kW | - | 0.25 s |
| Main-Deposition | 60 mm/s | 7.5 kW | 13 mm/s | Determined by bead length |
| End-Fill | 45 mm/s | 7 kW | - | 0.4 s |
| End-Delay | 0 mm/s | 2 kW | - | 0.5 s |
| Current Supplied | 99.83 A |
|---|---|
| Average Voltage | 1.80 V |
| Wire Diameter | 1.14 mm |
| Wire Length with Current Applied | 22.5 mm |
| Composition (wt-%) | C | Mn | Si | Ni | Mo | Cr | S | P | V |
|---|---|---|---|---|---|---|---|---|---|
| ER100S-G | (0.05–0.06) | (1.63–1.69) | (0.46–0.50) | (1.88–1.96) | (0.43–0.45) | (0.04–0.06) | (0.002–0.005) | (0.005–0.009) | <0.01 |
| Specific Heat | 580 |
| Density | 7700 |
| Thermal Conductivity | 35 |
| Part Number | Length [mm] | Width [mm] | Height [mm] | Predicted Build Time for Baseline [s] | Predicted Build Time for Modified Path [s] | Predicted Time Savings [%] | CPU Runtime [s] |
|---|---|---|---|---|---|---|---|
| 1 | 66 | 92.5 | 16.5 | 11,849 | 10,268 | 13.3 | 75.2 |
| 2 | 330 | 92.5 | 16.5 | 24,492 | 22,982 | 6.2 | 173.9 |
| 3 | 66 | 452.5 | 16.5 | 43,616 | 26,178 | 40.0 | 234.2 |
| 4 | 330 | 452.5 | 16.5 | 93,817 | 66,776 | 28.8 | 2091.9 |
| 5 | 66 | 92.5 | 66 | 48,466 | 42,227 | 12.9 | 1050.8 |
| 6 | 330 | 92.5 | 66 | 106,398 | 101,026 | 5.0 | 2747.9 |
| 7 | 66 | 452.5 | 66 | 169,415 | 105,839 | 37.5 | 3011.6 |
| 8 | 330 | 452.5 | 66 | 383,990 | 284,358 | 25.9 | 40,787.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatala, G.W.; Reutzel, E.W.; Wang, Q. Path Planning for Rapid DEDAM Processing Subject to Interpass Temperature Constraints. Metals 2025, 15, 570. https://doi.org/10.3390/met15060570
Hatala GW, Reutzel EW, Wang Q. Path Planning for Rapid DEDAM Processing Subject to Interpass Temperature Constraints. Metals. 2025; 15(6):570. https://doi.org/10.3390/met15060570
Chicago/Turabian StyleHatala, Glenn W., Edward W. Reutzel, and Qian Wang. 2025. "Path Planning for Rapid DEDAM Processing Subject to Interpass Temperature Constraints" Metals 15, no. 6: 570. https://doi.org/10.3390/met15060570
APA StyleHatala, G. W., Reutzel, E. W., & Wang, Q. (2025). Path Planning for Rapid DEDAM Processing Subject to Interpass Temperature Constraints. Metals, 15(6), 570. https://doi.org/10.3390/met15060570