Peculiarities of the Creep Behavior of 15Kh2NMFAA Vessel Steel at High Temperatures
Abstract
1. Introduction
2. Materials and Methods
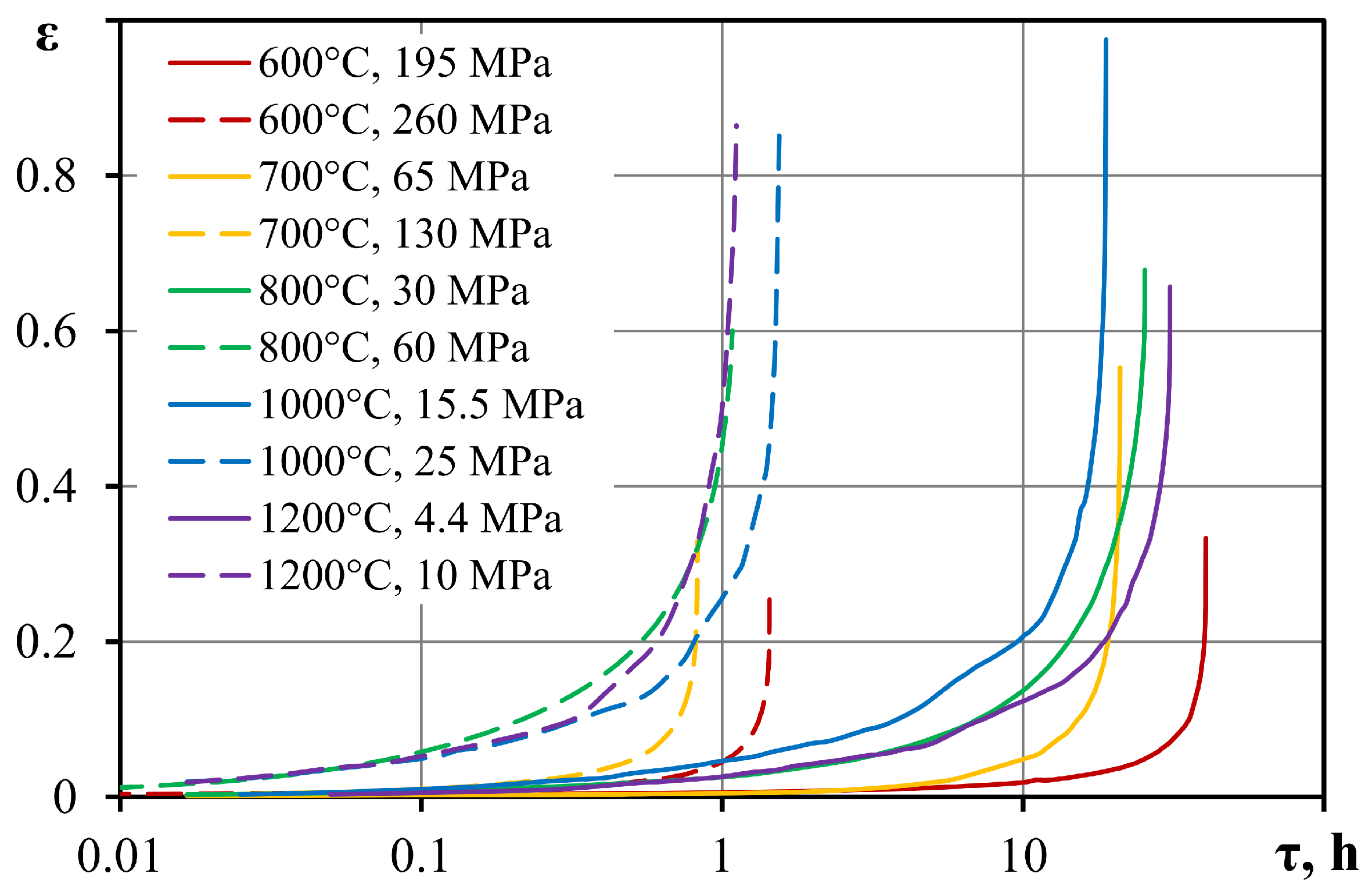
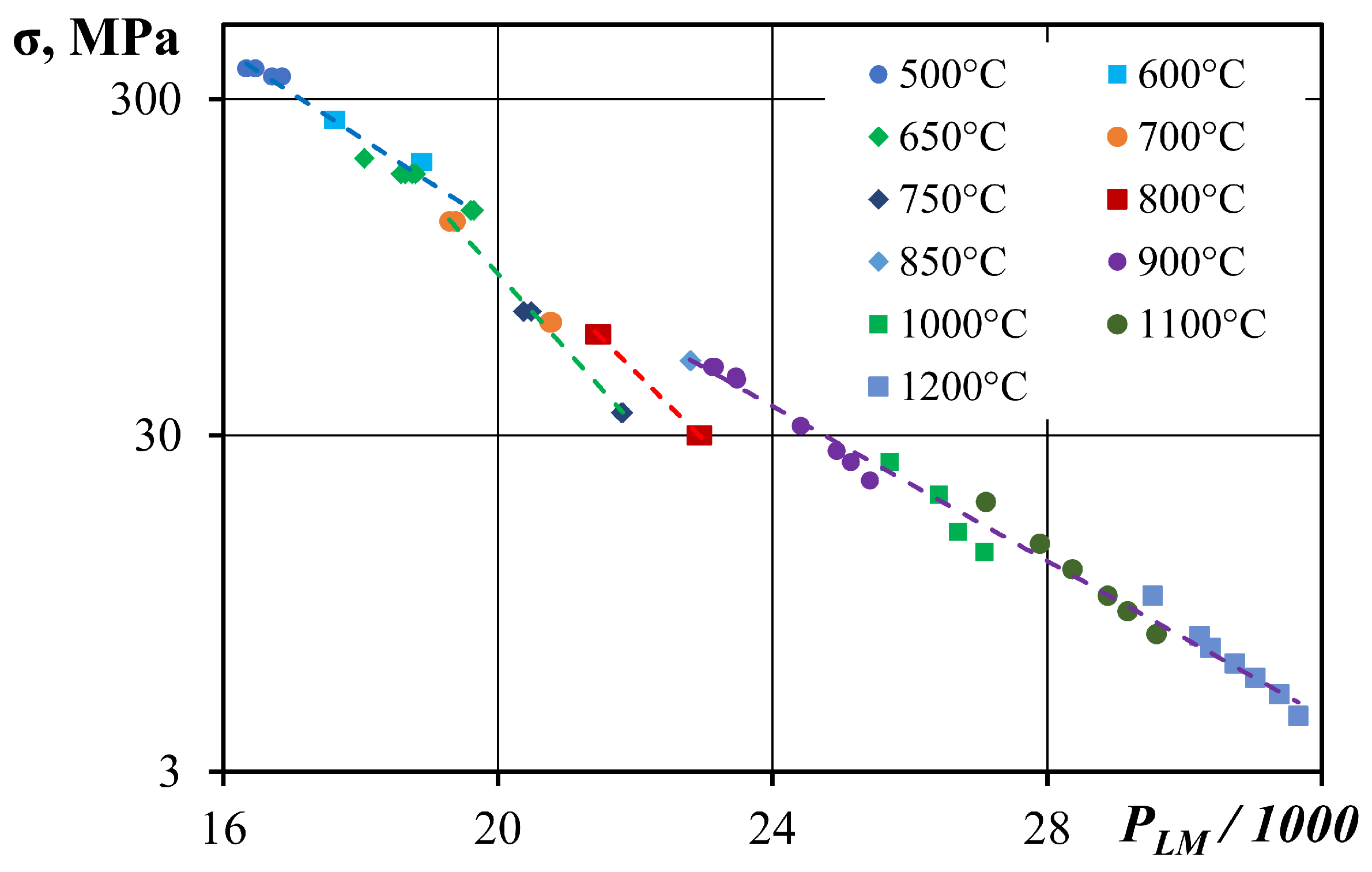
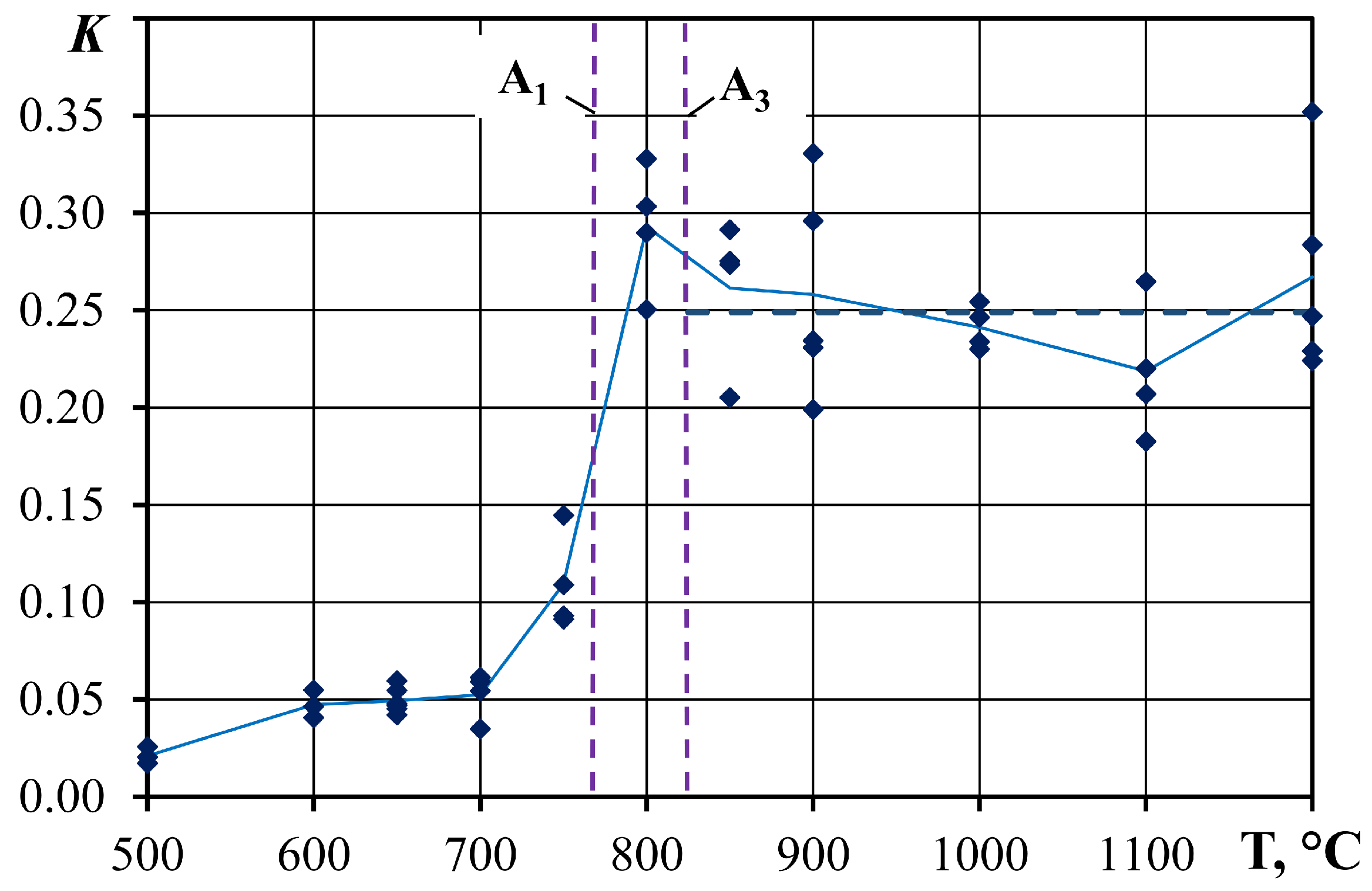
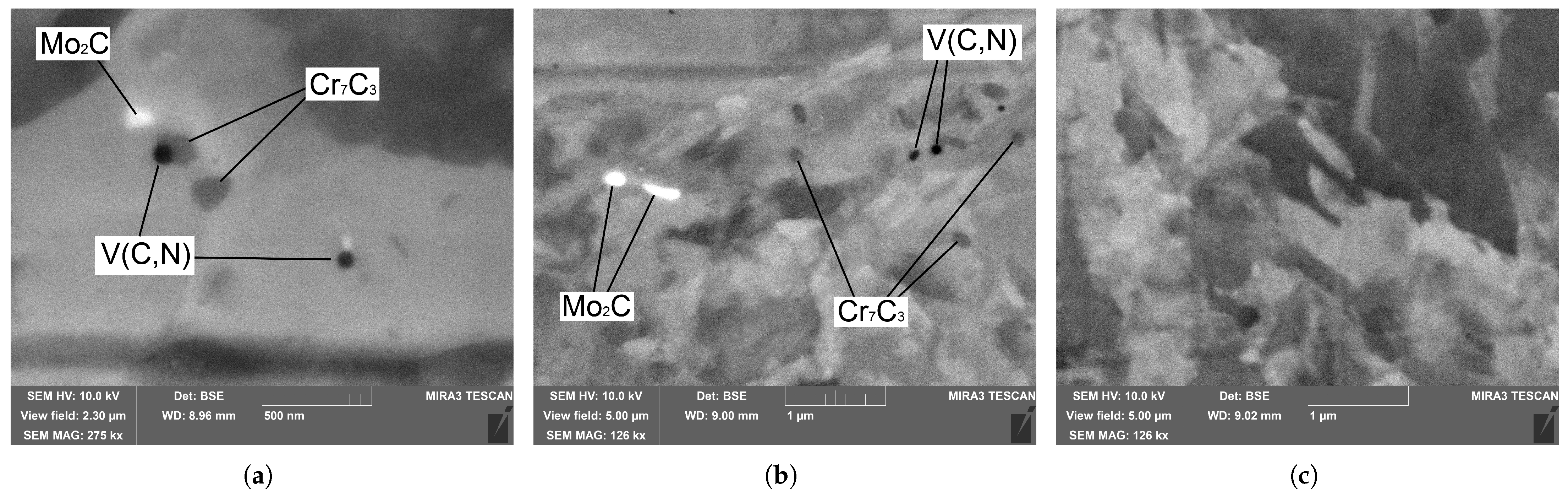
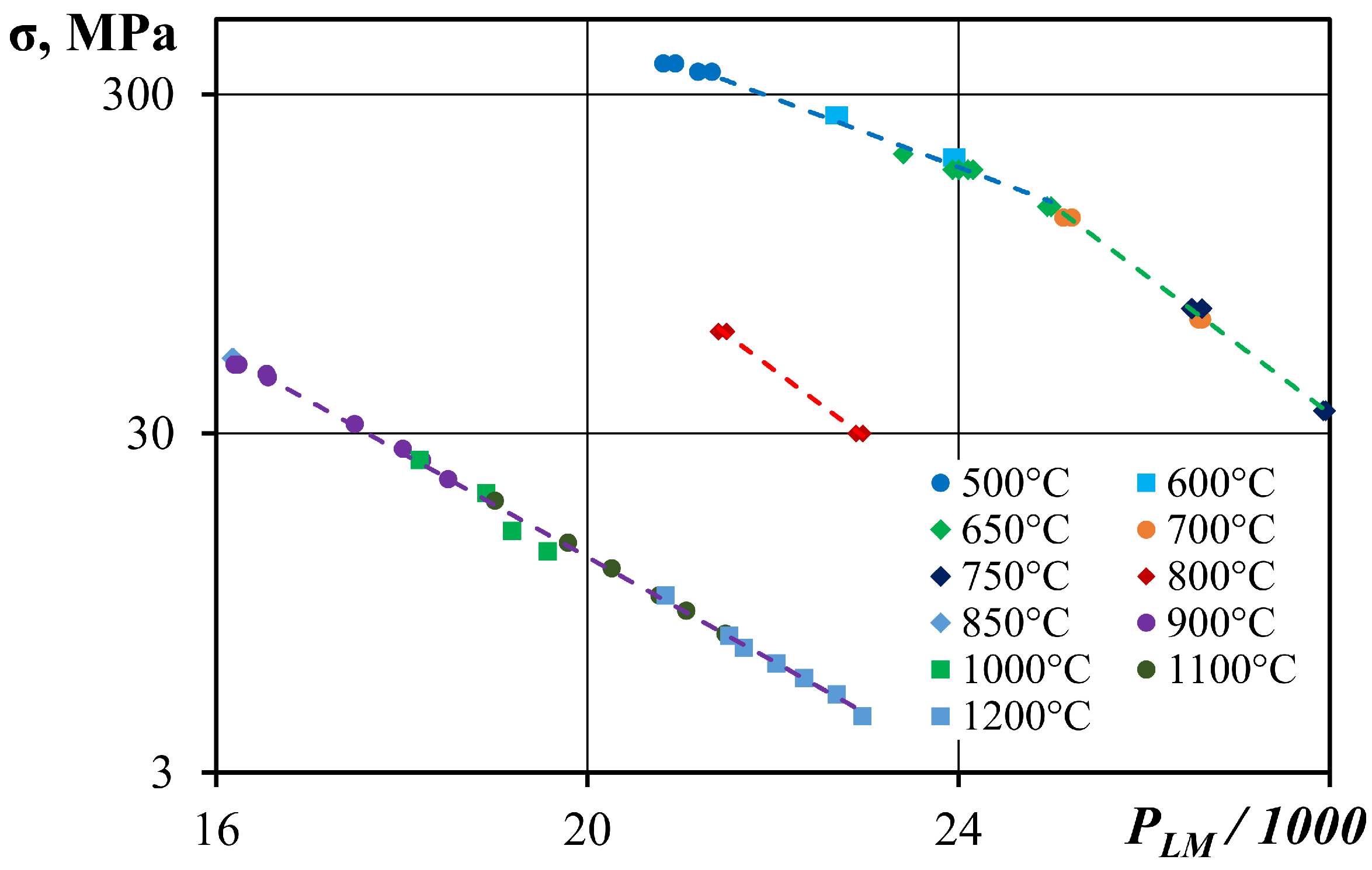
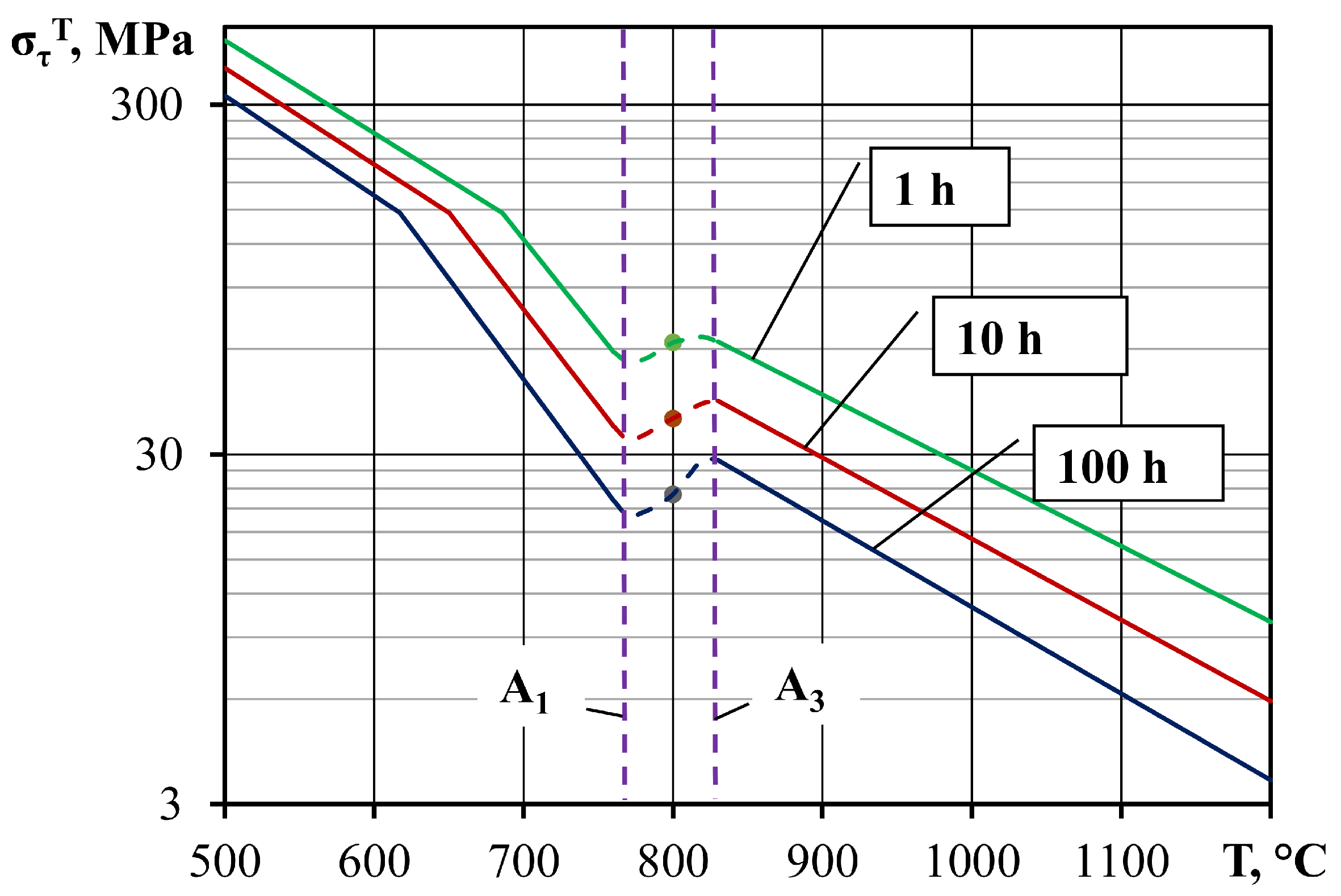
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| T, °C | Test No. | Stress , MPa | Rupture Time , h | Test Environment | T, °C | Test No. | Stress , MPa | Rupture Time , h | Test Environment |
|---|---|---|---|---|---|---|---|---|---|
| 500 | 1 | 370 | 20.0 | air | 850 | 29 | 50 | 2.1 | argon |
| 2 | 370 | 13.6 | 30 | 50 | 2.0 | ||||
| 3 | 350 | 41.0 | 31 | 48 | 0.6 | argon | |||
| 4 | 350 | 64.3 | 32 | 48 | 0.5 | ||||
| 600 | 5 | 195 | 46.1 | air | 900 | 33 | 45 | 1.0 | vacuum |
| 6 | 195 | 40.5 | 34 | 44 | 1.0 | argon | |||
| 7 | 260 | 1.4 | 35 | 32 | 6.5 | vacuum | |||
| 8 | 260 | 1.6 | 36 | 27 | 18.0 | ||||
| 650 | 9 | 140 | 19.3 | air | 37 | 25 | 27.0 | ||
| 10 | 140 | 17.3 | 38 | 22 | 46.8 | ||||
| 11 | 180 | 2.1 | 1000 | 39 | 25 | 1.6 | vacuum | ||
| 12 | 180 | 1.6 | 40 | 20 | 5.7 | ||||
| 13 | 180 | 1.4 | 41 | 15.5 | 9.4 | ||||
| 14 | 180 | 2.4 | 42 | 13.5 | 18.9 | ||||
| 15 | 200 | 0.4 | 1100 | 43 | 19 | 0.6 | vacuum | ||
| 700 | 16 | 130 | 0.8 | argon | 44 | 14.3 | 2.1 | ||
| 17 | 130 | 0.7 | 45 | 12 | 4.6 | ||||
| 18 | 65 | 21.0 | 46 | 10 | 10.7 | ||||
| 19 | 65 | 23.1 | 47 | 9 | 17.5 | ||||
| 750 | 20 | 70 | 1.1 | argon | 48 | 7.7 | 35.5 | ||
| 21 | 70 | 0.8 | 1200 | 49 | 10 | 1.1 | vacuum | ||
| 22 | 70 | 0.8 | 50 | 7.6 | 3.3 | ||||
| 23 | 35 | 21.3 | 51 | 7 | 4.2 | ||||
| 24 | 35 | 20.2 | 52 | 6.3 | 7.2 | ||||
| 800 | 25 | 60 | 0.9 | argon | 53 | 5.7 | 11.6 | ||
| 26 | 60 | 1.1 | 54 | 5.7 | 11.5 | ||||
| 27 | 30 | 25.4 | 55 | 5.1 | 20.0 | ||||
| 28 | 30 | 21.8 | 56 | 4.4 | 30.8 |
References
- Kymäläinen, O.; Tuomisto, H.; Theofanous, T.G. In-vessel retention of corium at the Loviisa plant. Nucl. Eng. Des. 1997, 169, 109–130. [Google Scholar] [CrossRef]
- Theofanous, T.G.; Maguire, M.; Angelini, S.; Salmassi, T. The first results from the ACOPO experiment. Nucl. Eng. Des. 1997, 169, 49–57. [Google Scholar] [CrossRef]
- Rempe, J.L.; Knudson, D.L.; Condie, K.G.; Suh, K.Y.; Cheung, F.-B.; Kim, S.-B. Corium retention for high power reactors by an in-vessel core catcher in combination with External Reactor Vessel Cooling. Nucl. Eng. Des. 2004, 230, 293–309. [Google Scholar] [CrossRef]
- Loktionov, V.; Mukhtarov, E.; Lyubashevskaya, I. Features of heat and deformation behavior of a VVER-600 reactor pressure vessel under conditions of inverse stratification of corium pool and worsened external vessel cooling during the severe accident. Part 1. The effect of the inverse melt stratification and in-vessel top cooling of corium pool on the thermal loads acting on VVER-600’s reactor pressure vessel during a severe accident. Nucl. Eng. Des. 2018, 326, 320–332. [Google Scholar]
- Loktionov, V.; Mukhtarov, E.; Lyubashevskaya, I. Features of heat and deformation behavior of a VVER-600 reactor pressure vessel under conditions of inverse stratification of corium pool and worsened external vessel cooling during the severe accident. Part 2. Creep deformation and failure of the reactor pressure vessel. Nucl. Eng. Des. 2018, 327, 161–171. [Google Scholar]
- Carénini, L.; Fichot, F.; Seignour, N. Modelling issues related to molten pool behaviour in case of In-Vessel Retention strategy. Ann. Nucl. Energy 2018, 118, 363–374. [Google Scholar] [CrossRef]
- Fichot, F.; Carénini, L.; Sangiorgi, M.; Hermsmeyer, S.; Miassoedov, A.; Bechta, S.; Zdarek, J.; Guenadou, D. Some considerations to improve the methodology to assess In-Vessel Retention strategy for high-power reactors. Ann. Nucl. Energy 2018, 119, 36–45. [Google Scholar] [CrossRef]
- Wang, H.; Villanueva, W. Structural behavior of an ablated reactor pressure vessel wall with external cooling. Ann. Nucl. Energy 2022, 153, 104446. [Google Scholar] [CrossRef]
- Gencheva, R.; Stefanova, A.; Groudev, P.; Chatterjee, B.; Mukhopadhyay, D. Study of invessel melt retention for VVER-1000/v320 reactor. Nucl. Eng. Des. 2016, 298, 208–217. [Google Scholar] [CrossRef]
- Mao, J.; Zhu, J.; Bao, S.; Luo, L.; Gao, Z. Investigation on Structural Behaviors of Reactor Pressure Vessel With the Effects of Critical Heat Flux and Internal Pressure. Int. J. Press. Vess. Piping 2016, 139, 139–140. [Google Scholar] [CrossRef]
- Mao, J.; Zhu, J.W.; Bao, S.; Luo, L.; Gao, Z.L. Creep Deformation and Damage Behavior of Reactor Pressure Vessel under Core Meltdown Scenario. Nucl. Eng. Des. 2018, 327, 161–171. [Google Scholar] [CrossRef]
- Matejovic, P.; Barnak, M.; Bachraty, M.; Vranka, L.; Tuma, Z. VVER-440/V213 long-term containment pressurization during severe accident. Nucl. Eng. Des. 2021, 377, 111145. [Google Scholar] [CrossRef]
- Sarkar, A.; Sunil, S.; Kumawat, B.; Reddy, G.B.; Kapoor, R.; Kumar, H.; Shrivastav, V. High temperature creep behavior of a low alloy Mn-Mo-Ni reactor pressure vessel steel. J. Nucl. Mater. 2021, 557, 153293. [Google Scholar] [CrossRef]
- Lu, C.; Wang, P.; Zheng, S.; Wu, X.; Liu, R.; He, Y.; Yang, J.; Gao, Z.; Tu, S.-T. Creep behavior and life prediction of a reactor pressure vessel steel above phase-transformation temperature via a deformation mechanism-based creep model. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 3342–3359. [Google Scholar] [CrossRef]
- Lu, C.; Wu, X.; He, Y.; Gao, Z.; Liu, R.; Chen, Z.; Zheng, W.; Yang, J. Deformation mechanism-based true-stress creep model for SA508 Gr.3 steel over the temperature range of 450–750 °C. J. Nucl. Mater. 2019, 526, 151776. [Google Scholar] [CrossRef]
- Gao, Z.; Lu, C.; He, Y.; Liu, R.; He, H.; Wang, W.; Zheng, W.; Yang, J. Influence of phase transformation on the creep deformation mechanism of SA508 Gr.3 steel for nuclear reactor pressure vessels. J. Nucl. Mater. 2019, 519, 292–301. [Google Scholar] [CrossRef]
- Xie, L.J.; Ning, D.; Yang, Y.Z. Experimental study on creep characterization and lifetime estimation of RPV material at 723–1023 K. J. Mater. Eng. Perform. 2017, 26, 644–652. [Google Scholar] [CrossRef]
- Kuleshova, E.; Fedotova, S.; Maltsev, D.A.; Potekhin, A. Trends of Structure Degradation of VVER-1000 Reactor Pressure Vessel Steels Determining Their Performance at Lifetimes of over 60 Years. Phys. At. Nucl. 2025, 87, 1138–1150. [Google Scholar] [CrossRef]
- Lobanov, L.; Kostin, V.; Makhnenko, O.; Zukov, V.; Kostenevych, O. Forecasting of Structural Transformations in Heat Affected Zone Steel Of 15KH2NMFA at Anti-Corrosion Cladding. Probl. At. Sci. Technol. 2020, 2, 89–96. [Google Scholar] [CrossRef]
- Blum, W. Mechanisms of creep deformation in steel. In Creep-Resistant Steels; Elsevier: Amsterdam, The Netherlands, 2008; pp. 365–402. [Google Scholar]
- Kucharova, K.; Sklenicka, V.; Kvapilova, M.; Svoboda, M. Creep and microstructural processes in a low-alloy 2.25%Cr1.6%W steel (ASTM Grade 23). Mat. Charact. 2015, 109, 1–8. [Google Scholar] [CrossRef]
- Sklenička, V.; Kloc, L. Creep in Boiler Materials: Mechanisms, Measurement and Modelling. In Power Plant Life Management and Performance Improvement; Woodhead Publishing: Sawston, UK, 2011; pp. 180–221. [Google Scholar]
- Whittaker, M.T.; Wilshire, B. Creep and creep fracture of 2.25 Cr–1.6 W steels (Grade 23). Mater. Sci. Eng. A 2010, 527, 4932–4938. [Google Scholar] [CrossRef]
- Radchenko, V.P.; Afanasyeva, E.A.; Saushkin, M.N. Prediction of creep and long-term strength of material by sample-leader under ductile fracture conditions. Appl. Mech. Tech. Phys. 2023, 64, 199–209. (In Russian) [Google Scholar] [CrossRef]
- Claesson, E.; Magnusson, H.; Kohlbrecher, J.; Thuvander, M.; Lindberg, F.; Andersson, M.; Hedström, P. Carbide Precipitation during Processing of Two Low-Alloyed Martensitic Tool Steels with 0.11 and 0.17 V/Mo Ratios Studied by Neutron Scattering, Electron Microscopy and Atom Probe. Metals 2022, 12, 758. [Google Scholar] [CrossRef]
- Sklenička, V.; Kuchařová, K.; Dvorak, J.; Kvapilová, M.; Král, P. Creep Damage Tolerance Factor λ of Selected Creep-Resistant Steels. Key Eng. Mater. 2017, 754, 47–50. [Google Scholar] [CrossRef]
- Kvapilová, M.; Ohanková, M.; Král, P.; Dvořák, J.; Kuchařová, K.; Čmaka, L.J.; Sklenička, V. Characterization of creep properties and the microstructure of a service-exposed low alloy CrMoV steel steam pipe. Mater. Sci. Eng. A 2022, 853, 143684. [Google Scholar] [CrossRef]
- Kloc, L. Creep of ex-service 0.5 CrMoV steel at low strain rates. Mater. Sci. Eng. A 2009, 510, 70–73. [Google Scholar] [CrossRef]
- Shigeyama, H.; Takahashi, Y.; Siefert, J.; Parker, J. Creep-Fatigue Life Evaluation for Grade 91 Steels with Various Origins and Service Histories. Metals 2024, 14, 148. [Google Scholar] [CrossRef]
- Saxena, A. A Phenomenological Model for Creep and Creep-Fatigue Crack Growth Rate Behavior in Ferritic Steels. Metals 2023, 13, 1749. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhong, W.; Bai, B.; Yang, W.; Wang, Z.; Huang, C. Research on the Fracture Behavior and Microstructure of T91 Steel at Ultrahigh Creep Temperatures. Metals 2022, 12, 2054. [Google Scholar] [CrossRef]
- Dudova, N. 9–12% Cr Heat-Resistant Martensitic Steels with Increased Boron and Decreased Nitrogen Contents. Metals 2022, 12, 1119. [Google Scholar] [CrossRef]
- Di Pompeo, V.; Santoni, A.; Santecchia, E.; Spigarelli, S. On the Short-Term Creep Response at 482 °C (900 °F) of the 17–4PH Steel Produced by Bound Metal Deposition. Metals 2022, 12, 477. [Google Scholar] [CrossRef]
- Kassner, M.E. New Developments in Understanding Harper–Dorn, Five-Power Law Creep and Power-Law Breakdown. Metals 2020, 10, 1284. [Google Scholar] [CrossRef]
- Loktionov, V.; Lyubashevskaya, I.; Terentyev, E. The regularities of creep deformation and failure of the VVER’s pressure vessel steel 15Kh2NMFA-A in air and argon at temperature range 500–900 °C. Nucl. Mater. Energy 2021, 28, 101019. [Google Scholar] [CrossRef]
- Loktionov, V.; Lyubashevskaya, I.; Terentyev, E. Regularities of the creep deformation and failure of 15Kh2NMFA-A steel within the temperature range of 900–1200 °C. Int. J. Press. Vess. Piping 2022, 199, 104745. [Google Scholar] [CrossRef]
- Terentyev, E.V.; Marchenkov, A.Y.; Loktionov, V.D.; Lyubashevskaya, I.V.; Chuprin, D.V.; Borodavkina, K.T.; Sviridov, G.B. Investigation of Creep Characteristics of Vessel Steel 15Kh2NMFA-A of WWER-type Reactor at Temperatures 500–1200 °C. Fact. Lab. Mater. Diagn. 2024, 90, 56–66. (In Russian) [Google Scholar] [CrossRef]
- Loktionov, V.; Lyubashevskaya, I.; Sosnin, O.; Terentyev, E. Short-term strength properties and features of high-temperature deformation of VVER reactor pressure vessel steel 15Kh2NMFA-A within the temperature range 20–1200 °C. Nucl. Eng. Des. 2019, 352, 110188. [Google Scholar] [CrossRef]
- Dudko, V.; Yuzbekova, D.; Gaidar, S.; Vetrova, S.; Kaibyshev, R. Tempering behavior of novel low-alloy high-strength steel. Metals 2022, 12, 2177. [Google Scholar] [CrossRef]
- Kaybyshev, R.O.; Skorobogatykh, V.N.; Shchenkova, I.A. New martensitic steels for fossil power plant: Creep resistance. Phys. Met. Metallogr. 2010, 109, 186–200. [Google Scholar] [CrossRef]
- Baker, T.N. Processes, microstructure and properties of vanadium microalloyed steels. Mater. Sci. Technol. 2009, 25, 1083–1107. [Google Scholar] [CrossRef]

| C | Mn | Si | Cr | Ni | Mo | V | P | S | |
|---|---|---|---|---|---|---|---|---|---|
| Req. | 0.13–0.18 | 0.30–0.60 | 0.17–0.37 | 1.80–2.30 | 1.00–1.50 | 0.50–0.70 | 0.10–0.12 | ≤0.012 | ≤0.015 |
| Act. | 0.15 | 0.6 | 0.32 | 2.09 | 1.2 | 0.57 | 0.1 | 0.009 | 0.002 |
| T, °C | Larson–Miller Parameter Coefficients | Difference of Experimental and Calculated Values | |||
|---|---|---|---|---|---|
| , MPa | , h | ||||
| 500–650 | 4.71440 | −0.10217 | 25.8 | 195.0/184.0 | 13.55/23.70 |
| 650–760 | 7.28976 | −0.20549 | 26.0 | 70.0/65.9 | 1.06/0.80 |
| 800 | 6.13906 | −0.20328 | 20.0 | 30.0/32.1 | 21.84/29.78 |
| 830–1200 | 4.18859 | –0.15361 | 14.1 | 13.5/15.2 | 18.88/34.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Terentyev, E.; Marchenkov, A.; Loktionov, V.; Pankina, A.; Sviridov, G.; Borodavkina, K.; Chuprin, D.; Lavrik, N. Peculiarities of the Creep Behavior of 15Kh2NMFAA Vessel Steel at High Temperatures. Metals 2025, 15, 571. https://doi.org/10.3390/met15060571
Terentyev E, Marchenkov A, Loktionov V, Pankina A, Sviridov G, Borodavkina K, Chuprin D, Lavrik N. Peculiarities of the Creep Behavior of 15Kh2NMFAA Vessel Steel at High Temperatures. Metals. 2025; 15(6):571. https://doi.org/10.3390/met15060571
Chicago/Turabian StyleTerentyev, Egor, Artem Marchenkov, Vladimir Loktionov, Anastasia Pankina, Georgy Sviridov, Ksenia Borodavkina, Danila Chuprin, and Nikita Lavrik. 2025. "Peculiarities of the Creep Behavior of 15Kh2NMFAA Vessel Steel at High Temperatures" Metals 15, no. 6: 571. https://doi.org/10.3390/met15060571
APA StyleTerentyev, E., Marchenkov, A., Loktionov, V., Pankina, A., Sviridov, G., Borodavkina, K., Chuprin, D., & Lavrik, N. (2025). Peculiarities of the Creep Behavior of 15Kh2NMFAA Vessel Steel at High Temperatures. Metals, 15(6), 571. https://doi.org/10.3390/met15060571







