Acoustic Emission During Rubber-like Deformation in Ni51Fe18Ga27Co4 Single Crystalline Shape Memory Alloys
Abstract
1. Introduction
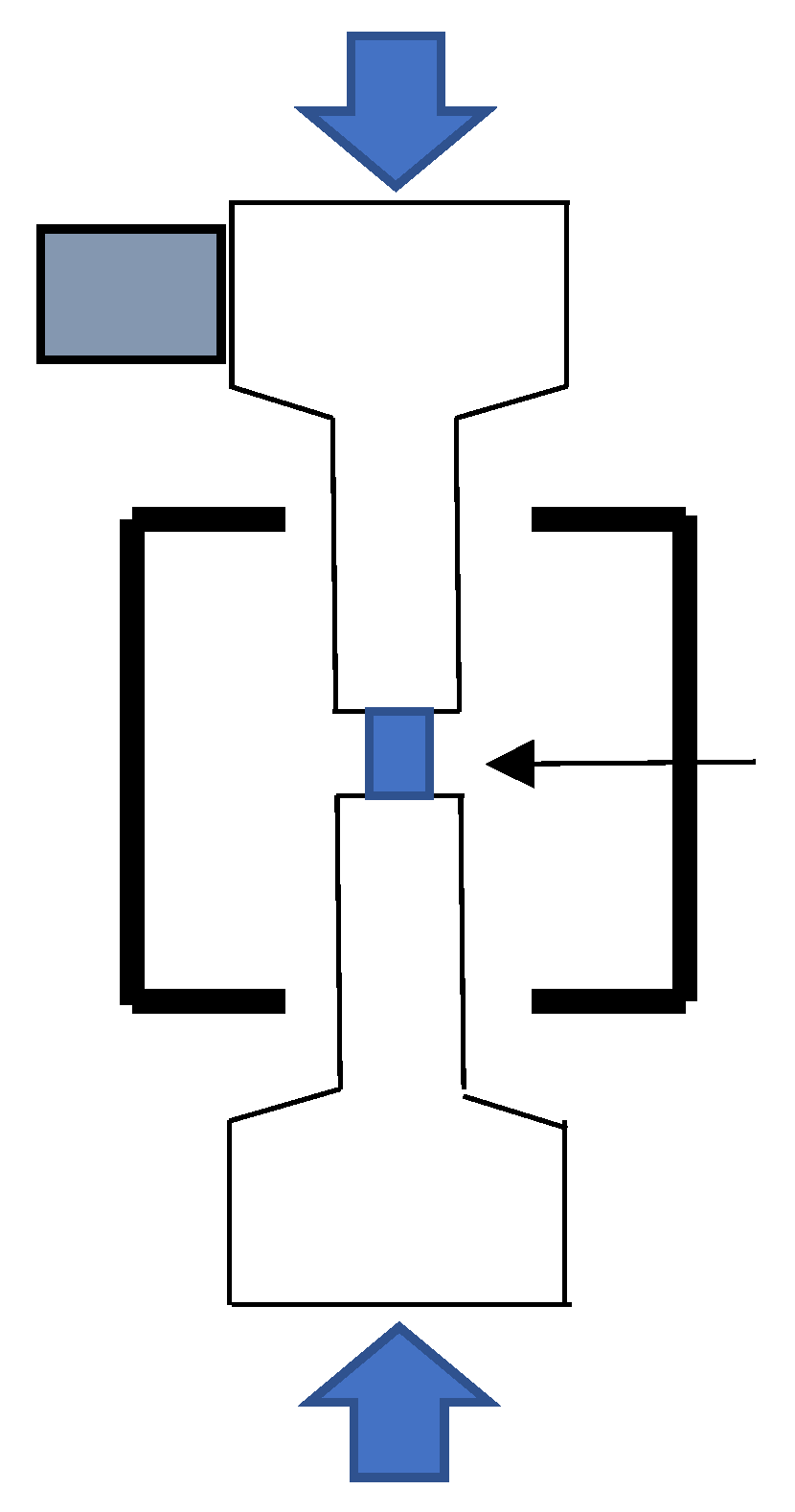
2. Experimental
3. Results
4. Discussion
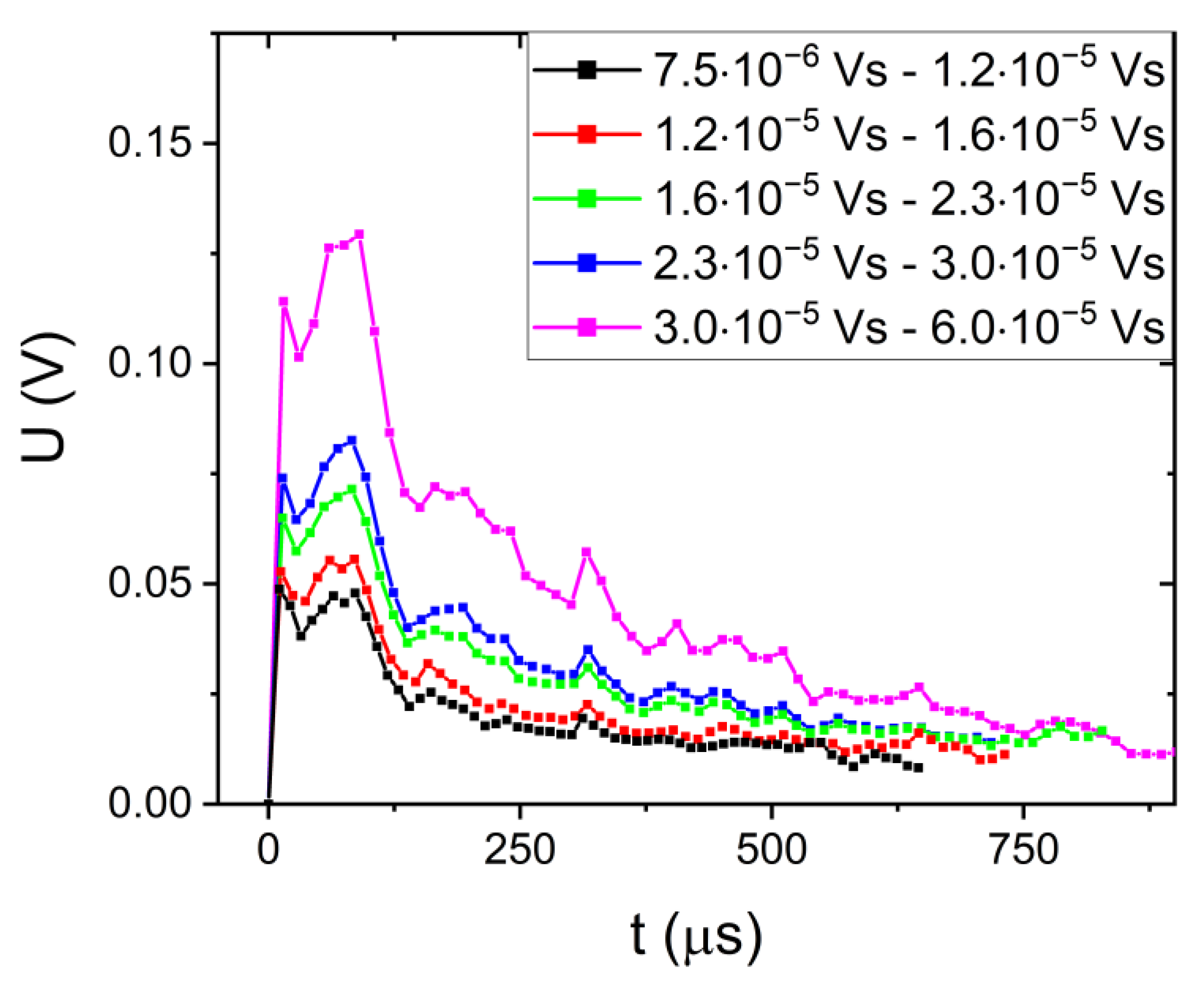
4.1. AE During Loading and Unloading
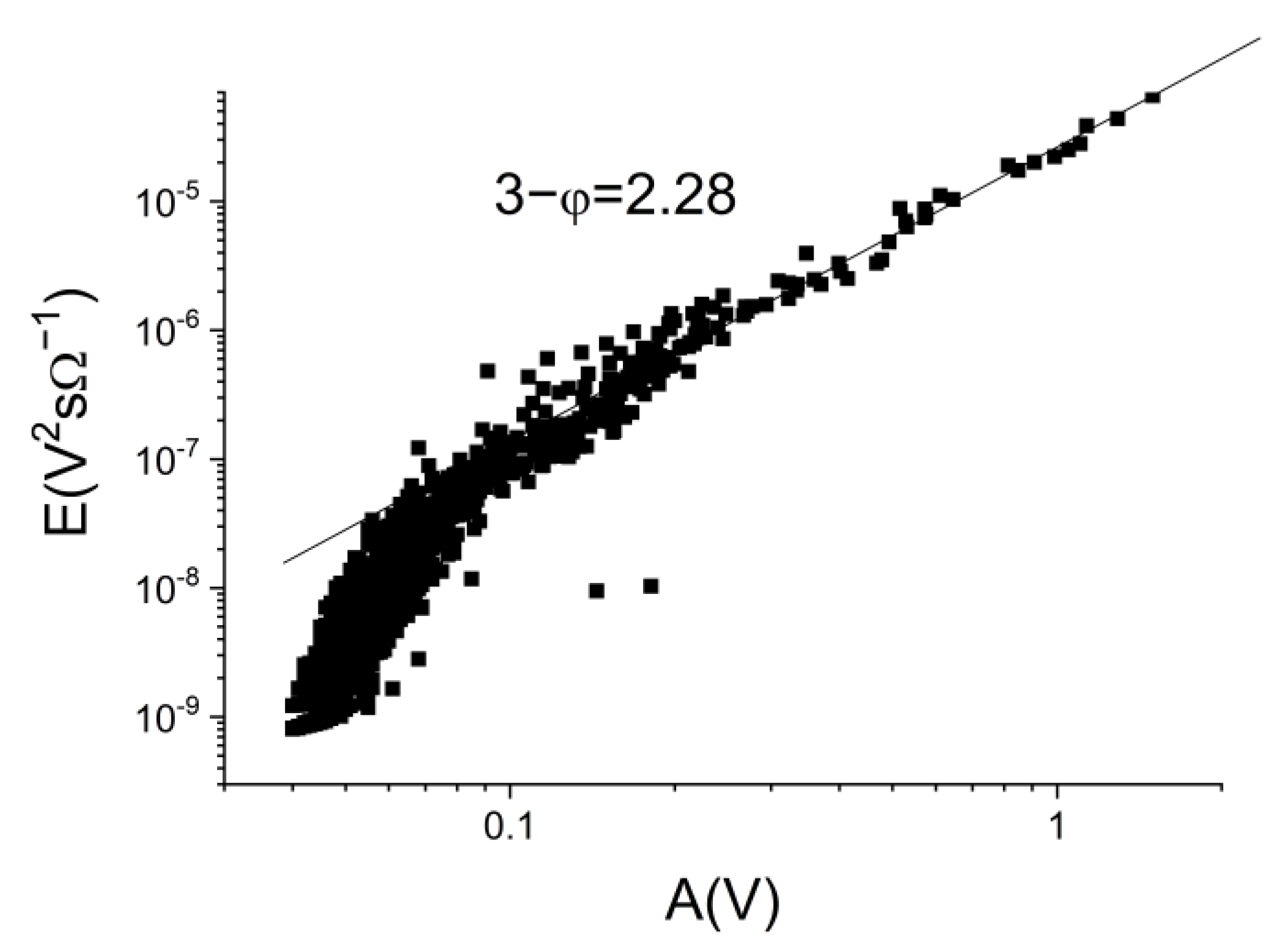
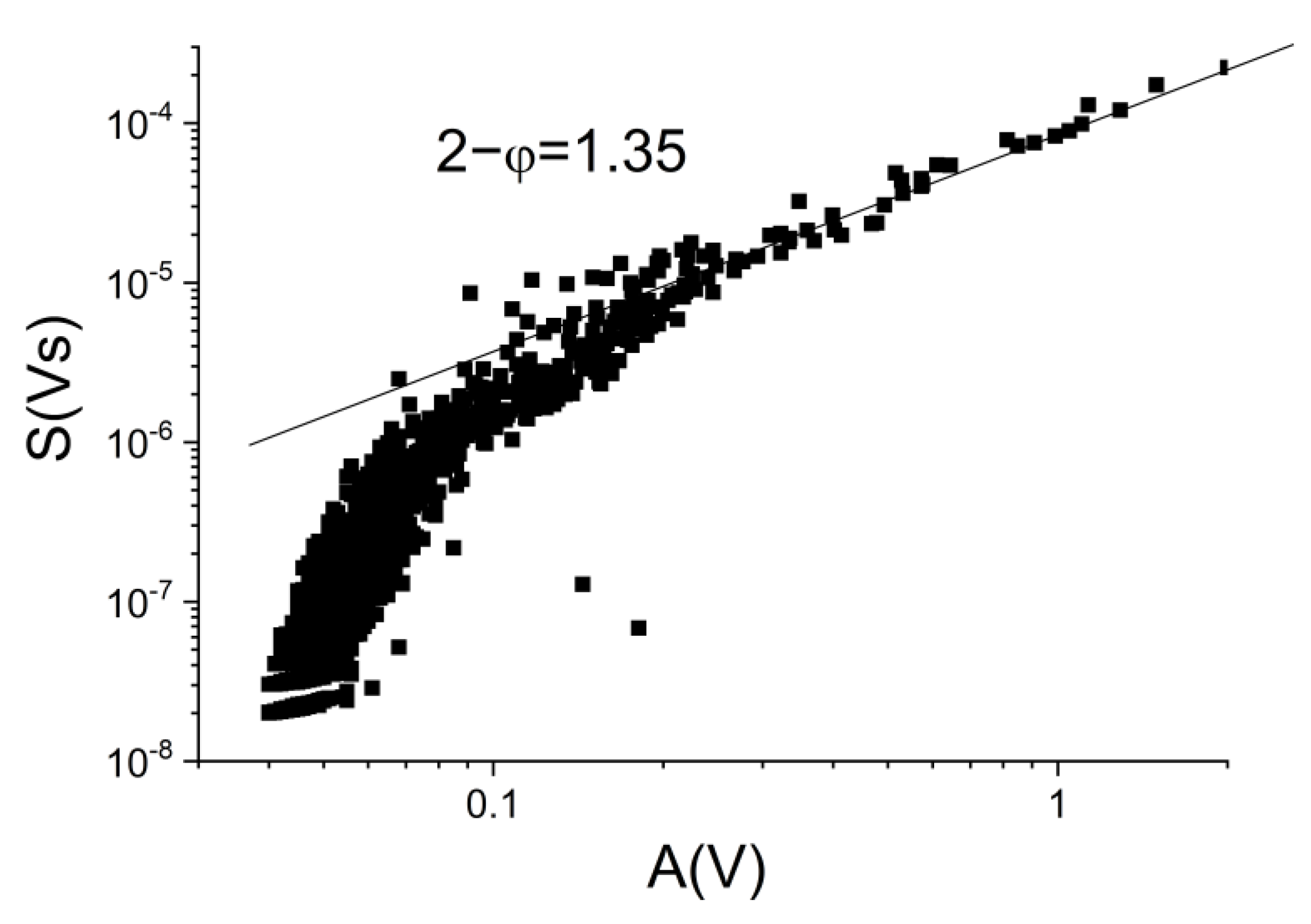
4.2. Power Exponents of the Acoustic Emission Parameters
| Single Crystal | Summary | ε | α |
|---|---|---|---|
| Ni51Fe18Ga27Co4, this work, averaged | Rubber-like, Stress-induced | 1.5 ± 0.1 | 2.3 ± 0.2 |
| Ni2MnGa [13] | Single twin boundary Type I, stress-induced | 2.3 ± 0.2 | |
| Ni2MnGa [13] | Single twin boundary Type II, stress-induced (less than one decade energy range) | 3.0 ± 0.2 | |
| Ni2MnGa [34] | Type II | 1.5 ± 0.1 | |
| Ni2MnGa [35] | Type I | 1.5 ± 0.1 | |
| Ni2MnGa [25] | Single twin boundary Type I, stress-induced | 1.5 ± 0.1 | 2.1 ± 0.1 |
| Ni2MnGa [36] | After compression along the [100] direction, magnetic field-induced | 1.5 ± 0.1 | 1.8 ± 0.2 |
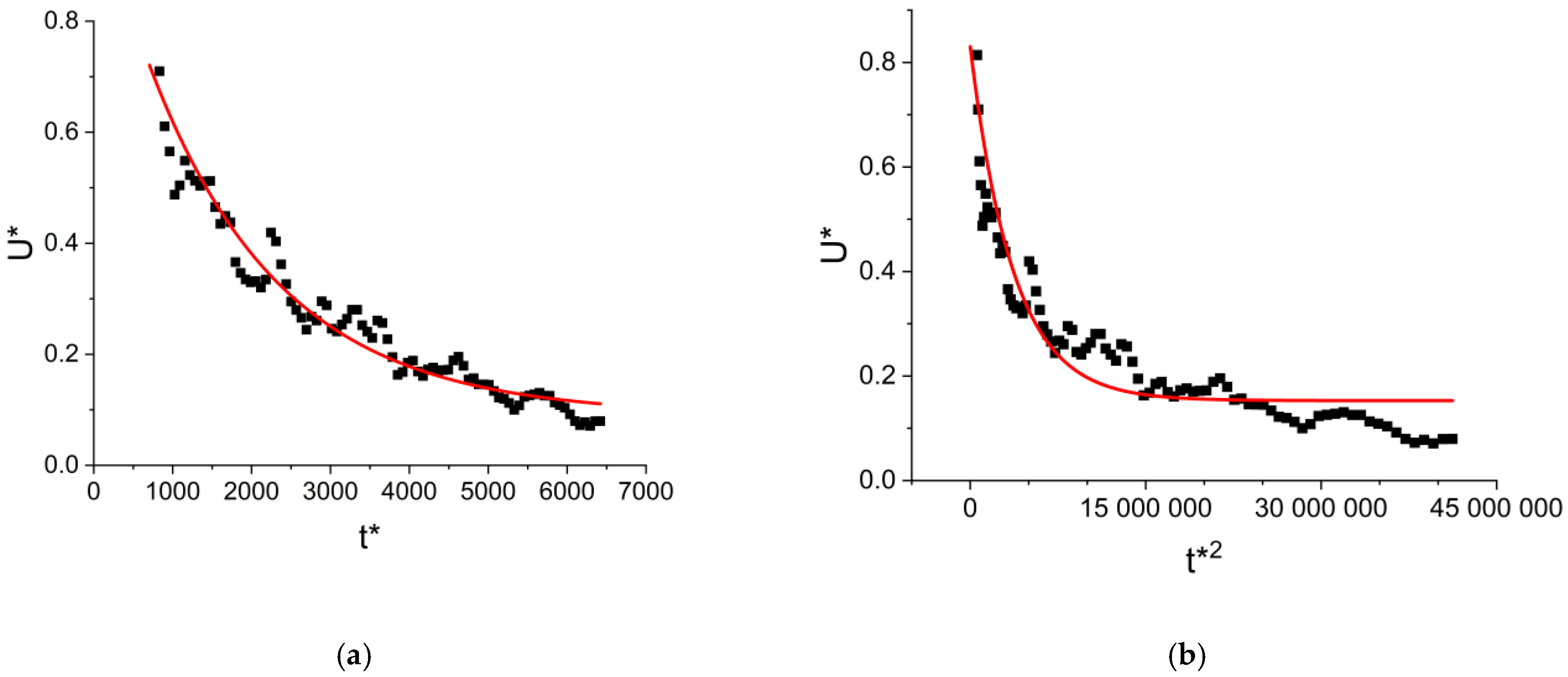
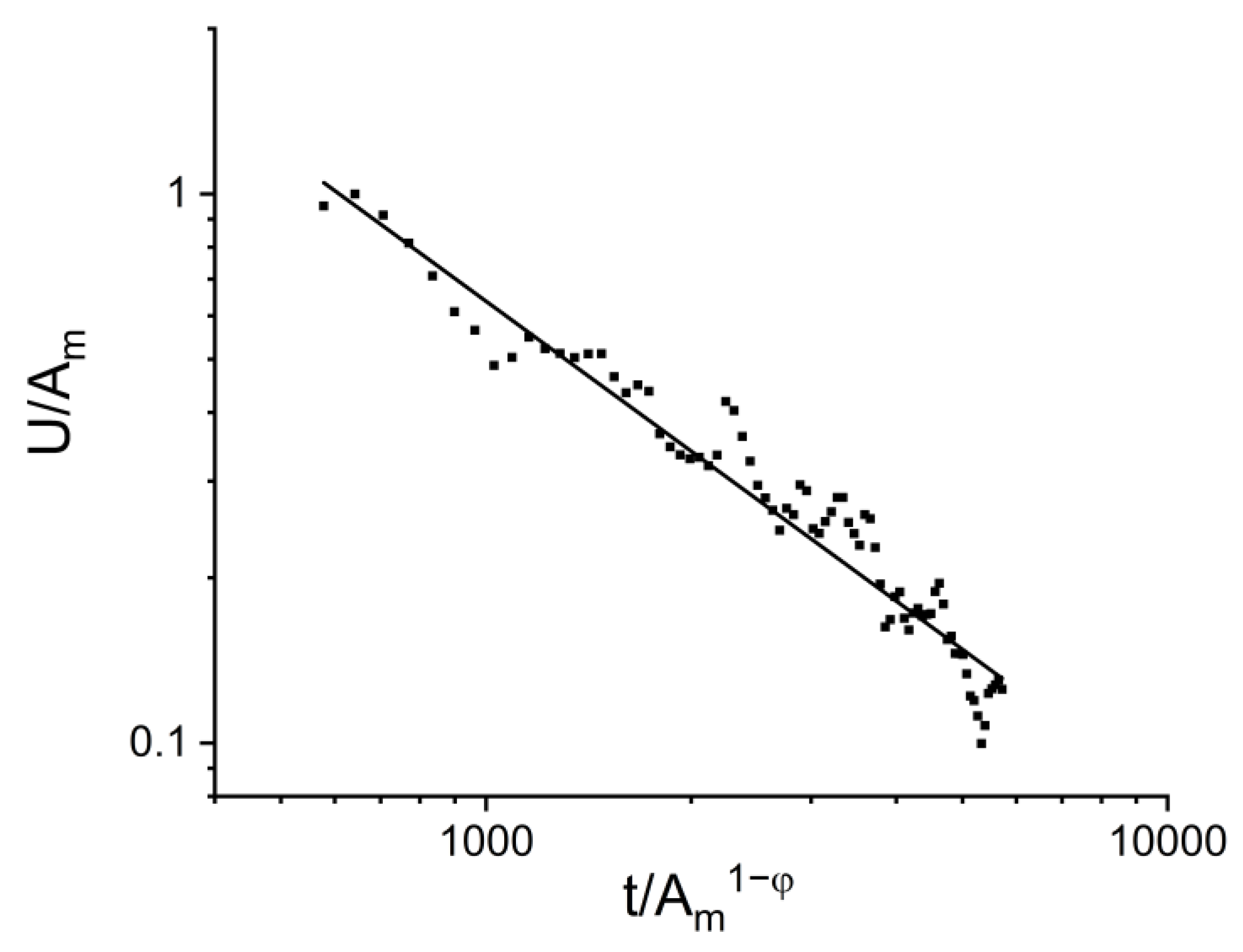
4.3. Normalized Temporal Avalanche Shapes for Fixed Duration and Area
5. Conclusions
- -
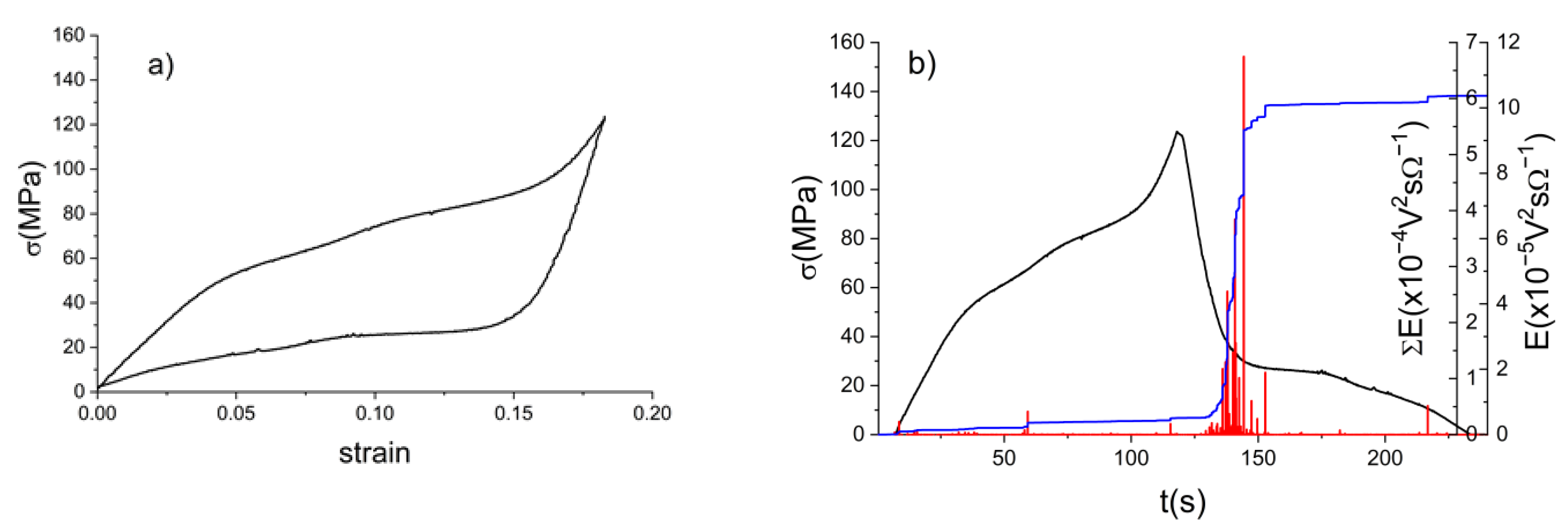
- It is shown that, after SIM aging, there is a well-detectable acoustic emission activity during the rubber-like deformation (up to about 15%) of Ni51Fe18Ga27Co4 single crystals.
- -
- The observed large AE activity at the beginning of the unloading plateau on the stress–stain curve and the observed large AE asymmetry for loading and unloading is attributed to difficulties in the re-nucleation of the SIM-aged martensite variant.
- -
- The characteristic exponents, calculated either from all of the data points, or from the separation of the two types of AE signals (belonging to re-nucleation of the SIM aged variant as well as to reorientations of the competing variants), are the same within the error bars.
- -
- The normalized universal temporal shapes of the avalanches for a fixed area, using the amplitude, A, and scaling parameters (i.e., the versus plots), were very well scaled together, with φ values obtained from the and cross-correlation exponents. The tail of this function decays slower by a smaller exponent than the theoretically predicted one, which can be attributed to either the intrinsic absorption of AE signals and/or the overlap of sub-avalanches.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Otsuka, K.; Wayman, C.M. Shape Memory Materials; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Ren, X.; Otsuka, K. Origin of rubber-like behaviour in metal alloys. Nature 1997, 389/9, 579–582. [Google Scholar] [CrossRef]
- Alaneme, K.K.; Anaele, J.U.; Okotete, E.A. Martensite aging phenomena in Cu-based alloys: Effects of structural transformation, mechanical and shape memory properties: A critical review. Sci. Afr. 2021, 12, e00760. [Google Scholar] [CrossRef]
- Ryklina, E.; Polyakova, K.; AKonopatsky, A.; Teplyakova, C.; Murygin, S.; Andreev, V.; Poletika, T.; Girsova, S.; Komarov, V.; Piskunova, P. Effect of original structure on aging-induced microstructure and transformation behavior of Ni-rich NiTi alloy using various aging modes. J. Alloys Comp. 2025, 1010, 177859. [Google Scholar] [CrossRef]
- Niendorf, T.; Krooβ, P.; Somsen, C.; Eggeler, G.; Chumlyakov, Y.I.; Maier, H.J. Martensite aging—avenue to new high temperature shape memory alloys. Acta Mater. 2015, 89, 298–304. [Google Scholar] [CrossRef]
- Panchenko, E.; Timofeeva, E.; Eftifeeva, A.; Osipovich, S.; Surikov, N.; Chumlyakov, Y.; Gerstein, G.; Maier, H.J. Giant rubber-like behavior induced by martensite aging in Ni51Fe18Ga27Co4 single crystals. Scr. Mater. 2019, 162, 387–390. [Google Scholar] [CrossRef]
- Panchenko, E.Y.; Timofeeva, E.E.; Chumlyakov, Y.I.; Osipovich, K.S.; Tagiltsev, A.I.; Gerstein, G.; Maier, H.J. Compressive shape memory actuation response of stress-induced martensite aged Ni51Fe18Ga27Co4 single crystals. Mat. Sci. Eng. 2019, A746, 448–455. [Google Scholar] [CrossRef]
- Morito, H.; Fujita, A.; Oikawa, K.; Ishida, K.; Fukamichi, K.; Kainuma, R. Stress assisted magnetic-field-induced strain in Ni-Fe-Ga-Co ferromagnetic shape memory alloys. Appl. Phys. Lett. 2007, 90, 062505. [Google Scholar] [CrossRef]
- Rajput, G.S.; Vora, J.; Prajapati, P.; Chaudhari, R. Areas of recent developments for shape memory alloy: A review. Mater. Today Proc. 2022, 62, 7194. [Google Scholar] [CrossRef]
- Lauhoff, C.; Reul, A.; Langenkämper, D.; Krooß, P.; Somsen, C.; Gutmann, M.J.; Pedersen, B.; Kireeva, I.V.; Chumlyakov, Y.I.; Eggeler, G.; et al. Effects of aging on the stress-induced martensitic transformation and cyclic superelastic properties in Co-Ni-Ga shape memory alloy single crystals under compression. Acta Mater. 2022, 226, 117623. [Google Scholar] [CrossRef]
- Reul, A.; Lauhoff, C.; Krooß, P.; Somsen, C.; Langenkämper, D.; Gutmann, M.J.; Pedersen, B.; Hofmann, M.; Gan, W.M.; Kireeva, I.; et al. On the impact of nanometric γ ’ precipitates on the tensile deformation of superelastic Co49Ni21Ga30. Acta Mater. [CrossRef]
- Bronstein, E.; Tóth, L.Z.; Daróczi, L.; Beke, D.L.; Talmon, R.; Shilo, D. Tracking Twin Boundary Jerky Motion at Nanometer and Microsecond Scales. Adv. Funct. Mater. 2021, 31, 2106573. [Google Scholar] [CrossRef]
- Perevertov, A.; Sevcik, M.; Heczko, O. Correlation between Acoustic Emission and Stress Evolution during Single Twin Boundary Motion in Ni-Mn-Ga Magnetic Shape Memory Single Crystal. Phys. Status Solidi. RRL 2022, 17, 2200245. [Google Scholar] [CrossRef]
- Weidner, A.; Vinogradov, A.; Vollmer, M.; Krooß, P.; Kriegel, M.J.; Klemm, V.; Chumlyakov, Y.; Niendorf, T.; Biermann, H. In situ characterization of the functional degradation of a [0,1] orientedFe–Mn–Al–Ni single crystal under compression using acoustic emission measurements. Acta Mater. 2021, 220, 11733. [Google Scholar] [CrossRef]
- Setna, J.P.; Dahmen, K.A.; Myers, C.R. Crackling noise. Nature 2001, 410, 242–250. [Google Scholar] [CrossRef]
- LeBlanc, M.; Angheluta, L.; Dahmen, K.; Goldenfeld, N. Universal fluctuations and extreme statistics of avalanches near the depinning transition. Phys. Rev. E 2013, 87, 022126. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Bohn, F.; Sommer, R.L.; Durin, G.; Zapperi, S.S.; Setna, J.P. Universality beyond power laws and the average avalanche shape. Nat. Phys. 2011, 7, 316–320. [Google Scholar] [CrossRef]
- Kamel, S.M.; Samy, N.M.; Tóth, L.Z.; Daróczi, L.; Beke, D.L. Denouement of the Energy-Amplitude and Size-Amplitude Enigma for Acoustic-Emission Investigations of Materials. Materials 2022, 15, 4556. [Google Scholar] [CrossRef]
- Casals, B.; Dahmen, K.A.; Gou, B.; Rooke, S.; Salje, E.K.H. The duration-energy-size enigma for acoustic emission. Sci. Rep. 2021, 11, 5590. [Google Scholar] [CrossRef] [PubMed]
- Spark, G.; Maas, R. Shapes and velocity relaxation of dislocation avalanches in Au and Nb microcrystals. Acta Mater. 2018, 152, 86–95. [Google Scholar] [CrossRef]
- Planes, A.; Manosa, L.; Vives, E. Acoustic emission in martensitic transformations. J. Alloys Compd. 2013, 577, S699–S704. [Google Scholar] [CrossRef]
- Dobrinevski, A.; Le Doussal, P.; Weise, K.J. Avalanche shape and exponents beyond mean-field theory. Europhys. Lett. 2015, 108, 66002. [Google Scholar] [CrossRef]
- Vu, C.-C.; Weiss, J. Asymmetric Damage Avalanche Shape in Quasibrittle Materials and Subavalanche (Aftershock) Clusters. Phys. Rev. Lett. 2020, 125, 105502. [Google Scholar] [CrossRef]
- Antonaglia, J.; Wright, W.J.; Gu, X.; Byer, R.R.; Hufnagel, T.C.; LeBlanc, M.; Uhl, J.T.; Dahmen, K.A. Bulk metallic glasses deform via avalanches. Phys. Rev. Lett. 2014, 112, 1555501. [Google Scholar] [CrossRef] [PubMed]
- Tóth, L.Z.; Bronstein, E.; Daróczi, L.; Shilo, D.; Beke, D.L. Scaling of average avalanche shapes for acoustic emission during jerky motion of single twin boundary in single-crystalline Ni2MnGa. Materials 2023, 16, 2089. [Google Scholar] [CrossRef]
- Kamel, S.M.; Daróczi, L.; Tóth, L.Z.; Panchenko, E.Y.; Chumlyakov, Y.I.; Samy, N.M.; Beke, D.L. Acoustic emission and DSC investigations of anomalous stress-stain curves and burst like shape recovery of Ni49Fe18Ga27Co6 shape memory single crystals. Intermetallics 2023, 159, 107932. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Beke, D.L.; Bolgar, M.K.; Toth, L.Z.; Daroczi, L. On the asymmetry of the forward and reverse martensitic transformations in shape memory alloys. J. Alloys Compd. 2018, 741, 106–115. [Google Scholar] [CrossRef]
- Otsuka, K.; Ren, X. Mechanism of martensite aging effects and new aspects. Mater. Sci. Eng. 2001, A312, 207–218. [Google Scholar] [CrossRef]
- Timofeeva, E.; Panchenko, E.Y.; Tokhmetova, A.B.; Eftifeeva, A.B.; Chumlyakov, Y.I.; Volochaev, M.N. The cyclic stability of rubber-like behaviour in stress-induced martensite aged Ni49Fe18Ga27Co6 (at.%) single crystals. Mat. Lett. 2021, 300, 130207. [Google Scholar] [CrossRef]
- Li, J.; Zhang, J.-z.; Zeng, L.-y.; Wang, S.; Song, X.-y.; Chen, N.-l.; Zuo, X.-w.; Rong, Y.-h. Revealing dislocation activity modes 980 during yielding and uniform deformation of low-temperature tempered steel by acoustic emission. J. Iron Steel Res. Int. 2024, 31, 3022–3036. [Google Scholar] [CrossRef]
- Zhao, Y.; Ding, X.; Sun, J.; Salje, E.K.H. Thermal and athermal crackling noise in ferroelastic nanaostuctures. J. Phys. Condens Matter 2014, 26, 142201. [Google Scholar] [CrossRef][Green Version]
- Nataf, G.; Salje, E.K.H. Avalanches in ferroelectric and coelastic materials: Phase transition, domain switching and propagation. Feroelectrics 2020, 569, 82–107. [Google Scholar] [CrossRef]
- Zreihan, N.; Faran, E.; Vives, E.; Planes, A.; Shilo, D. Coexistence of a well-determined kinetic law and a scale-invariant power law during the same physical process. Phys. Rev. B 2018, 97, 014103. [Google Scholar] [CrossRef]
- Zreihan, N.; Faran, E.; Vives, E.; Planes, A.; Shilo, D. Relations between stress drops and acoustic emission measured during mechanical loading. Phys. Rev. Mater 2019, 3, 043603. [Google Scholar] [CrossRef]
- Daróczi, L.; Piros, E.; Tóth, L.Z.; Beke, D.L. Magnetic field induced random pulse trains of magnetic and acoustic noises in martensitic single-crystal Ni2MnGa. Phys. Rev. B 2016, 96, 014416. [Google Scholar] [CrossRef]
- Chen, Y.; Gou, B.; Yuan, B.; Ding, X.; Sun, J.; Salje, E.K.H. Multiple Avalanche Processes in Acoustic Emission Spectroscopy: Multibranching of the Erenergy-Amplitude Scaling. Phys. Stat. Sol. B 2021, 259, 2100465. [Google Scholar] [CrossRef]
- Chen, Y.; Gou, B.; Ding, X.; Sun, J.; Salje, E.K.H. Fine structure of acoustic emission spectra: How to separate dsiclocation movements and entanglements in 316L stainless steel. Appl. Phy. Lett. 2020, 117, 262901. [Google Scholar] [CrossRef]
- Chen, Y.; Gou, B.; Ding, X.; Sun, J.; Salje, E.K.H. Real-time monitoring dislocations, martensitic transfromations and detwinning in stainless steel: Statistical analysis and mashine learning. J. Mat. Sci Technol. 2021, 92, 31–39. [Google Scholar] [CrossRef]
- Chen, Y.; Gou, B.; Xu, X.; Ding, X.; Sun, J.; Salje, E.K.H. Multibranches of acoustic emission as identifier for deformation mechanisms in additively manufactured 316L stainless steel. Addit. Manuf. 2023, 78, 103819. [Google Scholar] [CrossRef]
- McFaul, L.W.; Wright, W.J.; Sickle, J.; Dahmen, J.A. Force oscillations distort avalanche shapes. Mater. Res. Lett. 2019, 7, 456–502. [Google Scholar] [CrossRef]
- Utsu, T.; Ogata, Y.; Matsu’ura, R.S. The Centenary of the Omori Formula for a Decay Law of Aftershock Activity. J. Phys. Earth 1995, 43, 1–33. [Google Scholar] [CrossRef]



ε | α | δ | φ | φ |
|---|---|---|---|---|
| 1.5 ± 0.1 | 2.3 ± 0.2 | 1.6 ± 0.1 | 0.7 ± 0.1 | 0.7 ± 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Daróczi, L.; Kamel, S.M.; Tóth, L.Z.; Panchenko, E.Y.; Chumljakov, Y.I.; Beke, D.L. Acoustic Emission During Rubber-like Deformation in Ni51Fe18Ga27Co4 Single Crystalline Shape Memory Alloys. Metals 2025, 15, 131. https://doi.org/10.3390/met15020131
Daróczi L, Kamel SM, Tóth LZ, Panchenko EY, Chumljakov YI, Beke DL. Acoustic Emission During Rubber-like Deformation in Ni51Fe18Ga27Co4 Single Crystalline Shape Memory Alloys. Metals. 2025; 15(2):131. https://doi.org/10.3390/met15020131
Chicago/Turabian StyleDaróczi, Lajos, Sarah M. Kamel, László Z. Tóth, Elena Yu. Panchenko, Yuri I. Chumljakov, and Dezső L. Beke. 2025. "Acoustic Emission During Rubber-like Deformation in Ni51Fe18Ga27Co4 Single Crystalline Shape Memory Alloys" Metals 15, no. 2: 131. https://doi.org/10.3390/met15020131
APA StyleDaróczi, L., Kamel, S. M., Tóth, L. Z., Panchenko, E. Y., Chumljakov, Y. I., & Beke, D. L. (2025). Acoustic Emission During Rubber-like Deformation in Ni51Fe18Ga27Co4 Single Crystalline Shape Memory Alloys. Metals, 15(2), 131. https://doi.org/10.3390/met15020131








