Characterization and Modelling of Microstructure Evolution and Flow Stress of Single-Phase Austenite and Ferrite Phases in Duplex Stainless Steels
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Procedure
2.2. Parameter Identification for Microstructure Model StrucSim
3. Results and Discussion
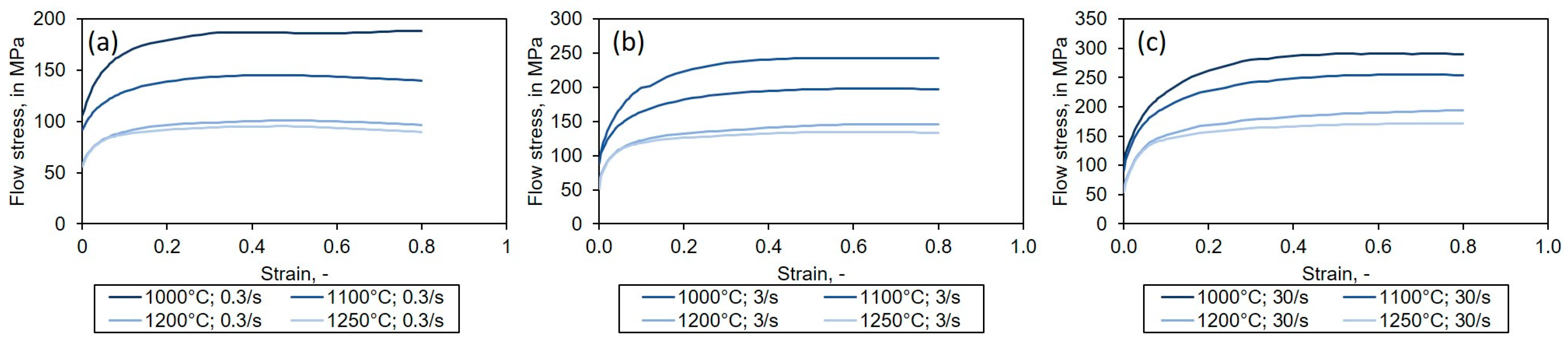
3.1. Experimental Results
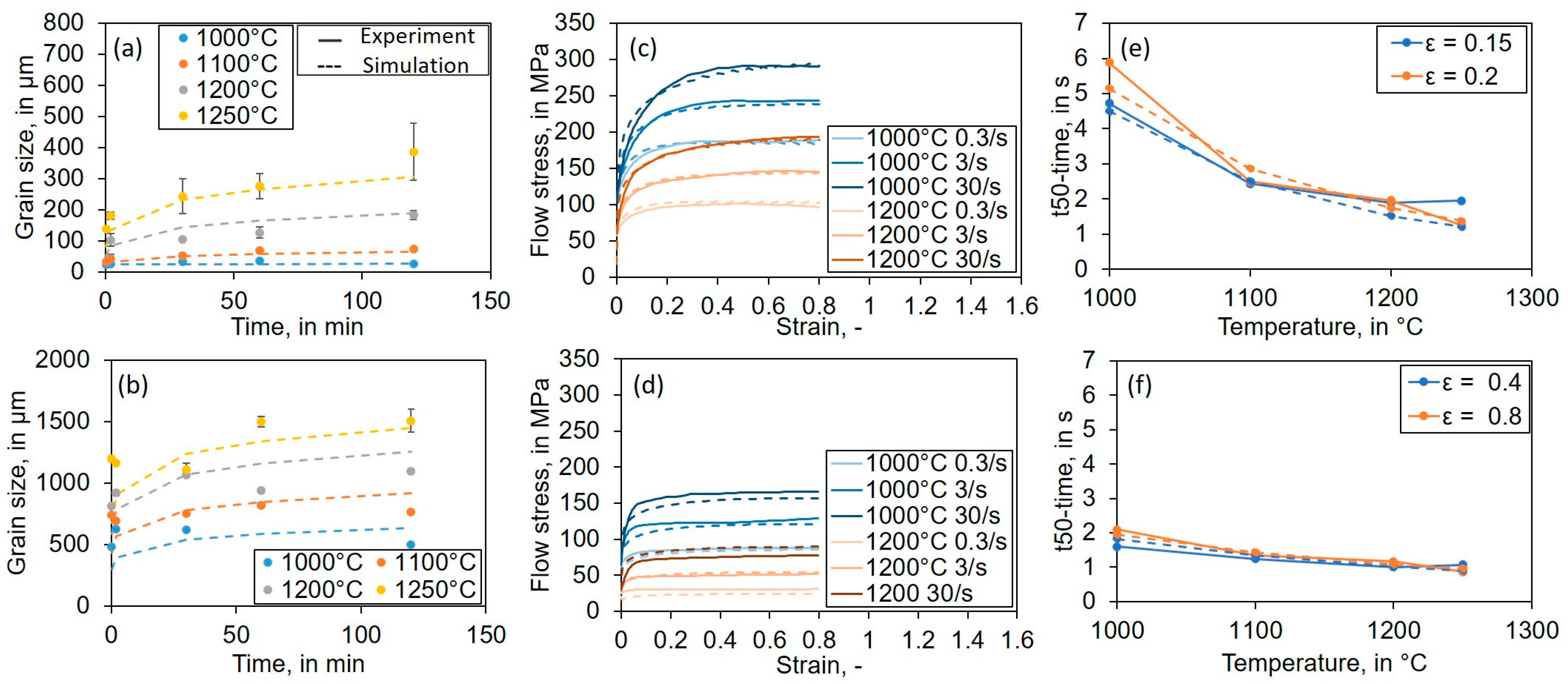
3.1.1. Grain Growth Analysis
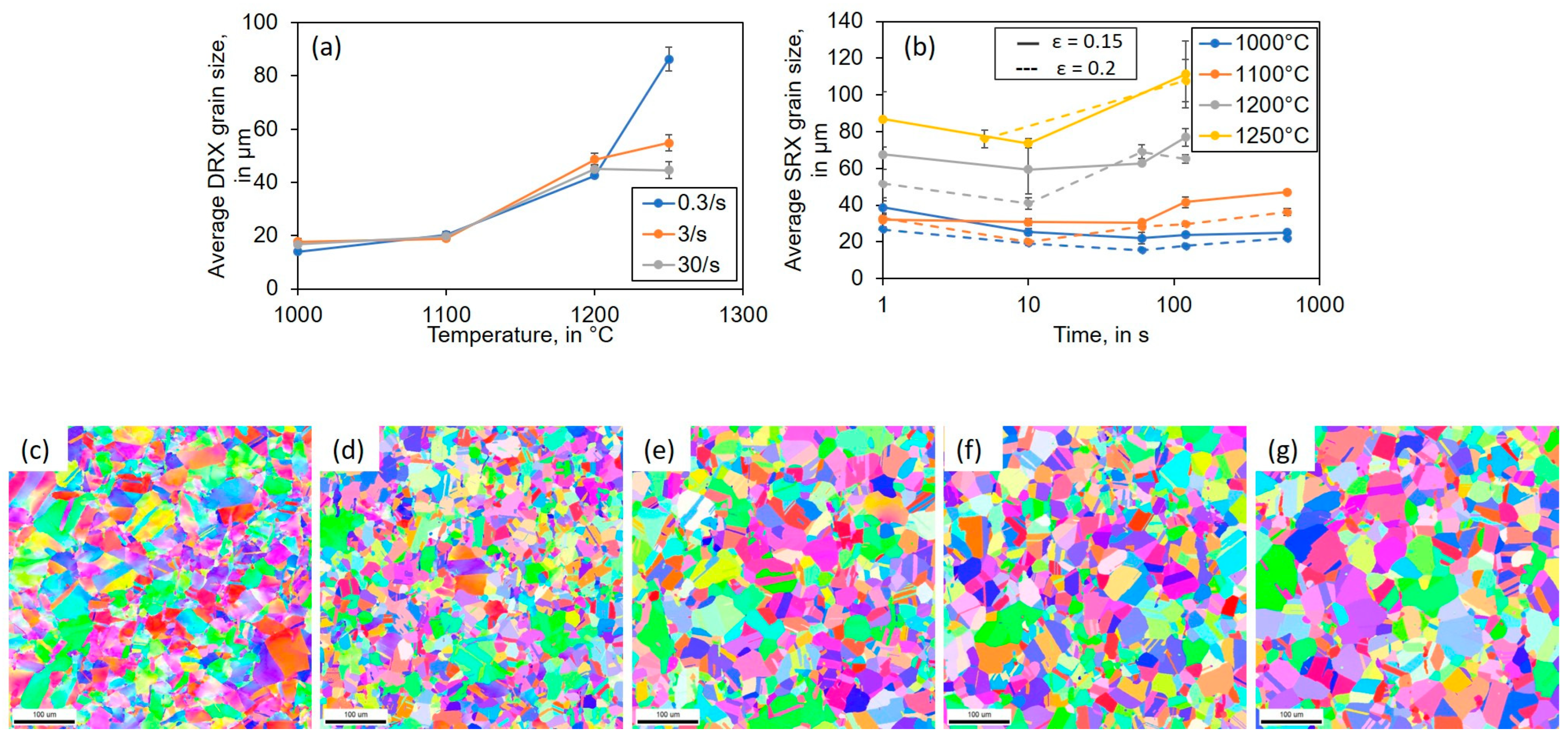
3.1.2. DRX Analysis
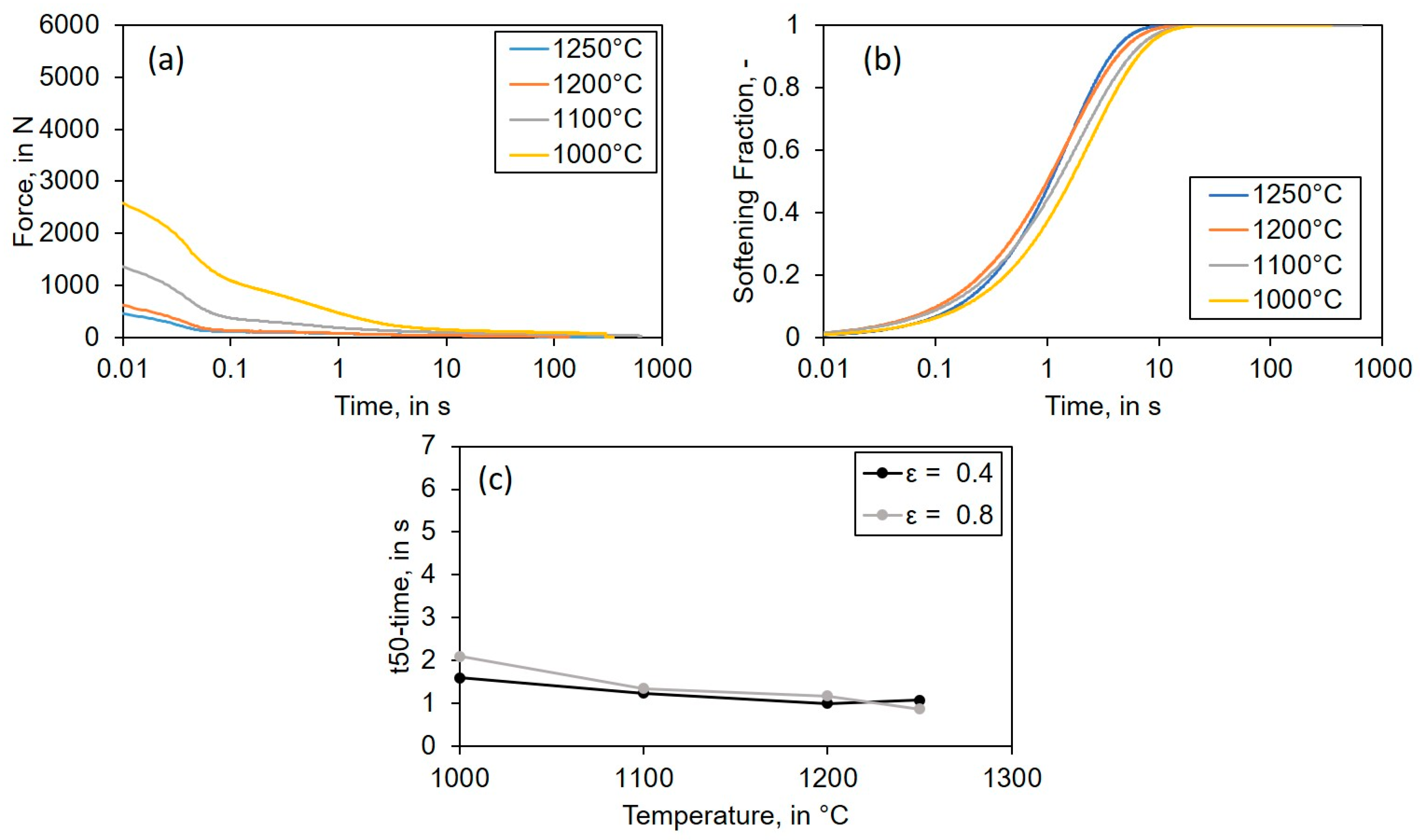
3.1.3. SRX Analysis
3.1.4. DRX and SRX Grain Size Analysis
3.2. Parameter Identification
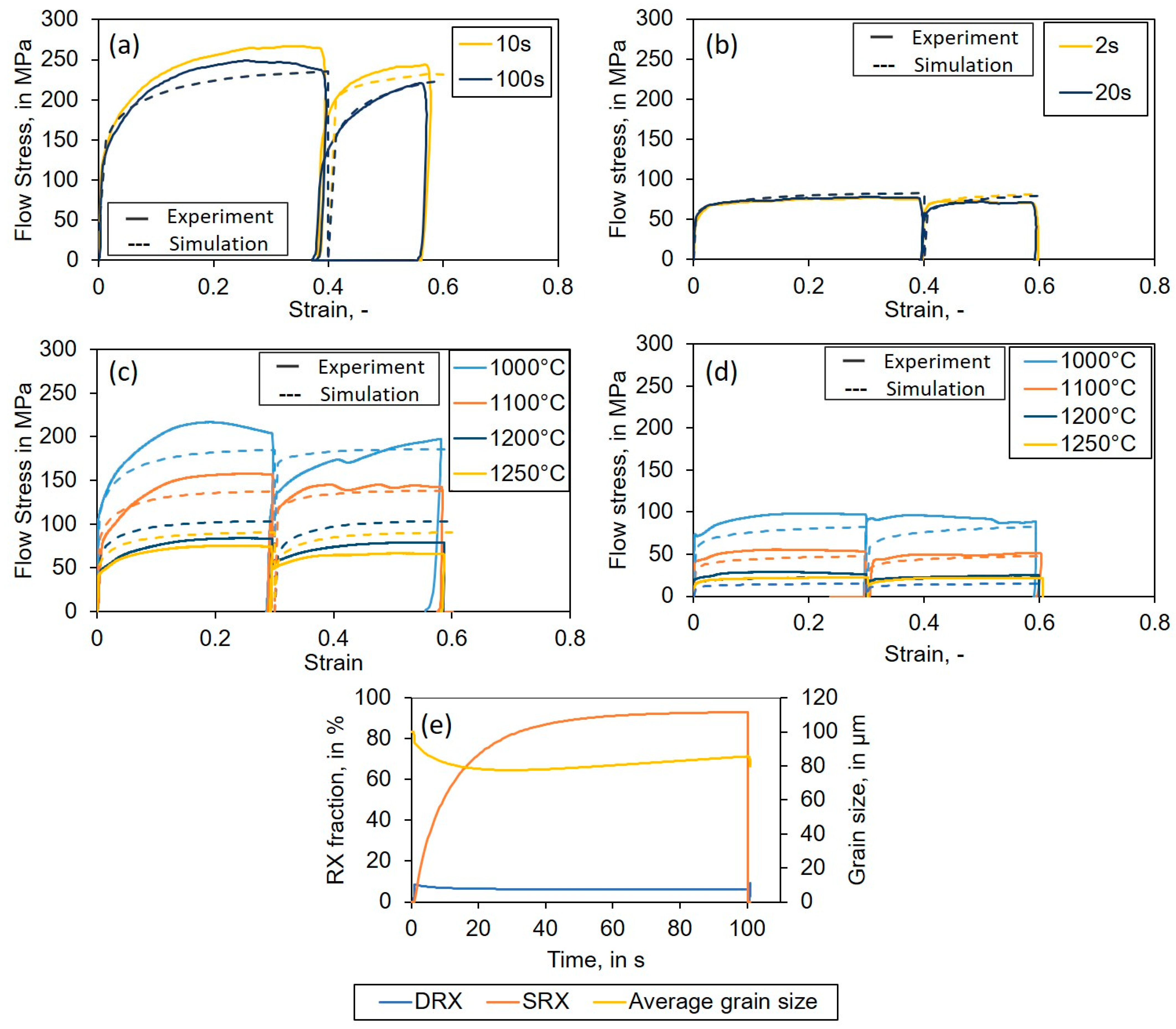
3.3. Validation Experiments
4. Conclusions
- Austenite and ferrite single-phase steels show different grain growth kinetics and recrystallization mechanisms during dynamic and static characterization experiments. While grain refinement was observed with EBSD measurements during compression and stress relaxation tests in austenite, the ferrite samples show the development of a substructure leading to new globular grains without a significant refinement in grain size.
- The parameters for StrucSim were successfully identified, and a good agreement was found between the experimental and fitted flow stress values. However, large initial grain sizes in the ferrite single-phase steels were present that could influence the results and need to be considered for future studies.
- The flow stress evolution during double compression tests calculated with StrucSim shows a good agreement with the experiments. StrucSim is able to depict the softening behavior during different pause times appropriately and a qualitative analysis of the microstructure properties DRX, SRX, and average grain size shows a realistic microstructure evolution. It should be noted, however, that, due to the experimental setup using a deformation dilatometer, friction could not be excluded from the measurements, leading to a scatter in the experimental results that it was not possible to model.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DSS | Duplex stainless steels |
| CSS | Carbon capture and storage |
| DRX | Dynamic recrystallization |
| SRX | Static recrystallization |
| MDRX | Metadynamic recrystallization |
| DDRX | Discontinuous dynamic recrystallization |
| CDRX | Continuous dynamic recrystallization |
| FSU | Flow stress utilities |
| IPF | Inverse pole figure |
References
- Liu, H.; Hua, Y.; Shi, S.; Lin, X.; Neville, A.; Wang, Y.; Sun, J. Stability of passive film and pitting susceptibility of 2205 duplex stainless steel in CO2/H2S-containing geothermal environment. Corros. Sci. 2023, 210, 110832. [Google Scholar] [CrossRef]
- Yevtushenko, O.; Bettge, D.; Bohraus, S.; Bäßler, R.; Pfennig, A.; Kranzmann, A. Corrosion behavior of steels for CO2 injection. Process Saf. Environ. Prot. 2014, 92, 108–118. [Google Scholar] [CrossRef]
- Kim, K.; Park, H.-W.; Ding, S.; Park, H.-W.; Yanagimoto, J. Flow Stress of Duplex Stainless Steel by Inverse Analysis with Dynamic Recovery and Recrystallization Model. ISIJ Int. 2021, 61, 280–291. [Google Scholar] [CrossRef]
- Kumar, A.; Gupta, A.; Khatirkar, R.K.; Bibhanshu, N.; Suwas, S. Strain Rate Sensitivity Behaviour of a Chrome-Nickel Austentic-Ferritic Stainless Steel and its Constitutive Modelling. ISIJ Int. 2018, 58, 1840–1849. [Google Scholar] [CrossRef]
- Haghdadi, N.; Cizek, P.; Beladi, H.; Hodgson, P.D. A novel high-strain-rate ferrite dynamic softening mechanism facilitated by the interphase in the austenite/ferrite microstructure. Acta Mater. 2017, 126, 44–57. [Google Scholar] [CrossRef]
- Cabrera, J.M.; Mateo, A.; Llanes, L.; Prado, J.M.; Anglada, M. Hot deformation of duplex stainless steels. J. Mater. Process. Technol. 2003, 143–144, 321–325. [Google Scholar] [CrossRef]
- Quadfasel, A.; Nietsch, J.A.; Teller, M.; Hirt, G. Modelling of Hot Flow Stress of Duplex Steel in Dependence of Microstructure Using the Rule of Mixture. Metals 2021, 11, 1285. [Google Scholar] [CrossRef]
- Sasaki, S.; Brüggemann, H.; Katsumura, T.; Hirt, G. Hot deformation behavior and microstructure evolution of each single phase in DSS. J. Mater. Process. Technol. 2023, 322, 118195. [Google Scholar] [CrossRef]
- Karjalainen, L.P. Stress relaxation method for investigation of softening kinetics in hot deformed steels. Mater. Sci. Technol. 1995, 11, 557–565. [Google Scholar] [CrossRef]
- Karhausen, K.; Kopp, R. Model for integrated process and microstructure simulation in hot forming. Steel Res. 1992, 63, 247–256. [Google Scholar] [CrossRef]
- Krämer, A.M.; Lohmar, J.; Hirt, G. Precise Prediction of Microstructural Properties with Minimal Experimental Effort for the Nickel-Base Alloy Inconel 718. Adv. Mater. Res. 2016, 1140, 43–50. [Google Scholar] [CrossRef]
- Kopp, R.; Luce, R.; Leisten, B.; Wolske, M.; Tschirnich, M.; Rehrmann, T.; Volles, R. Flow stress measuring by use of cylindrical compression test and special application to metal forming processes. Steel Res. 2001, 72, 394–401. [Google Scholar] [CrossRef]
- Huang, K.; Logé, R.E. A review of dynamic recrystallization in metallic materials. Mater. Des. 2016, 111, 548–574. [Google Scholar] [CrossRef]
- Vervynckt, S.; Verbeken, K.; Thibaux, P.; Houbaert, Y. Characterization of the Austenite Recrystallization by Comparing Double Deformation and Stress Relaxation Tests. Steel Res. Int. 2010, 81, 234–244. [Google Scholar] [CrossRef]
- Ma, M.; Ding, H.; Tang, Z.; Zhao, J.; Ziang, Z.; Li, G. Effect of strain rate and temperature on hot workability and flow behaviour of duplex stainless steel. Ironmak. Steelmak. 2016, 43, 88–96. [Google Scholar] [CrossRef]
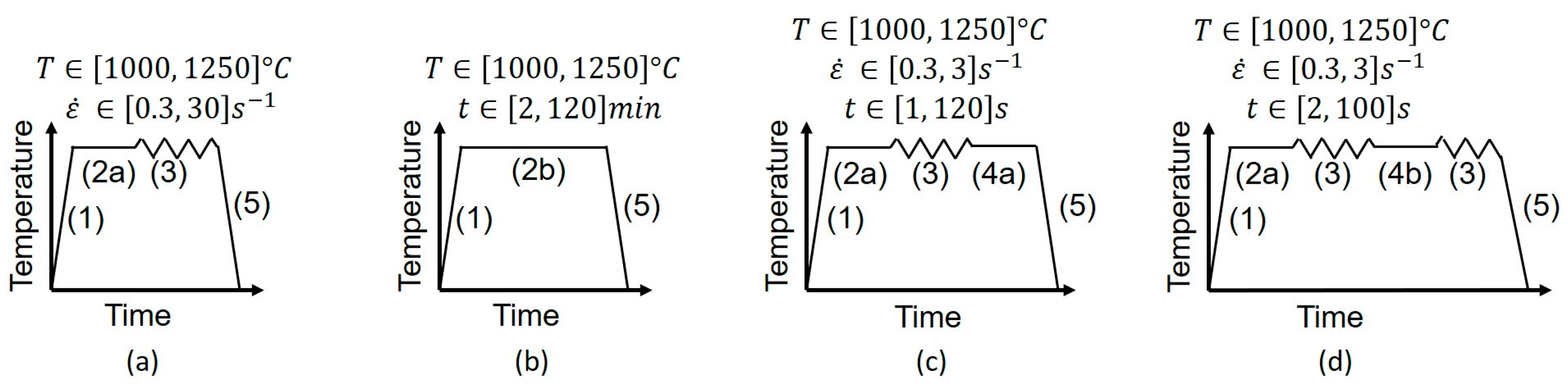






| Ferrite | Chemical Composition | Initial Grain Size | Remaining Austenite | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [°C] | Fe | Cr | Mo | Ni | Si | Mn | C | N | [µm] | [%] |
| 1000 | Balance | 29.30 | 3.80 | 5.30 | 0.30 | 0.20 | 0.003 | 0.02 | 479 | 0.0 |
| 1100 | Balance | 27.50 | 3.50 | 5.90 | 0.30 | 0.30 | 0.004 | 0.02 | 741 | 0.0 |
| 1200 | Balance | 26.20 | 3.20 | 6.70 | 0.30 | 0.30 | 0.005 | 0.05 | 815 | 0.0 |
| 1250 | Balance | 26.00 | 3.10 | 7.20 | 0.30 | 0.30 | 0.009 | 0.06 | 1200 | 0.0 |
| Austenite | Chemical Composition | Initial Grain Size | Remaining Ferrite | |||||||
| [°C] | Fe | Cr | Mo | Ni | Si | Mn | C | N | [µm] | [%] |
| 1000 | Balance | 21.90 | 2.20 | 9.90 | 0.30 | 0.40 | 0.037 | 0.16 | 25 | 7.0 |
| 1100 | Balance | 21.60 | 2.00 | 10.10 | 0.30 | 0.40 | 0.044 | 0.19 | 29 | 3.9 |
| 1200 | Balance | 22.00 | 1.90 | 10.30 | 0.30 | 0.40 | 0.056 | 0.22 | 126 | 0.1 |
| 1250 | Balance | 22.00 | 1.90 | 10.50 | 0.30 | 0.40 | 0.070 | 0.24 | 133 | 0.2 |
| Austenite | Ferrite | ||||||
|---|---|---|---|---|---|---|---|
| QGG | 8.88 × 105 | E1 | 3.08 | QGG | 4.63 × 105 | E1 | 1 |
| HD1 | 4.97 | B1 | 12,500 | HD1 | 8.68 | B1 | - |
| HD2 | 8.89 × 1038 | B2 | −0.19 | HD2 | 2.72 × 109 | B2 | - |
| Qw | 338,650 | D1 | −1.855 | Qw | 338,650 | D1 | - |
| A1 | 0.2729 | D2 | 2.347 | A1 | 0.763 | D2 | - |
| A2 | 0 | O1 | 9.31 × 10−3 | A2 | 0 | O1 | 9.16 × 10−7 |
| A3 | 0.263 | O2 | 0.164 | A3 | 0.0035 | O2 | 0.52 |
| A4 | 0.649 | O3 | 6.32 × 10−3 | A4 | 10 | O3 | 0.033 |
| A5 | 3683 | C | 0.205 | A5 | 1 | C | 0.205 |
| F1 | 2.40 × 10−3 | CS1 | 3.65 × 104 | F1 | 2.76 × 10−2 | CS1 | - |
| F2 | 0 | CS2 | 0 | F2 | 0 | CS2 | - |
| F3 | 0.46 | CS3 | 0 | F3 | 0.1 | CS3 | - |
| F4 | −0.35 | CS4 | −0.71 | F4 | 0.01 | CS4 | - |
| Qs | 2.18 × 105 | CS5 | 0.23 | Qs | 4.00 × 104 | CS5 | - |
| g1 | 0.83 | g1 | 0.86 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brüggemann, H.; Sasaki, S.; Röder, M.; Katsumura, T.; Bailly, D. Characterization and Modelling of Microstructure Evolution and Flow Stress of Single-Phase Austenite and Ferrite Phases in Duplex Stainless Steels. Metals 2025, 15, 130. https://doi.org/10.3390/met15020130
Brüggemann H, Sasaki S, Röder M, Katsumura T, Bailly D. Characterization and Modelling of Microstructure Evolution and Flow Stress of Single-Phase Austenite and Ferrite Phases in Duplex Stainless Steels. Metals. 2025; 15(2):130. https://doi.org/10.3390/met15020130
Chicago/Turabian StyleBrüggemann, Holger, Shunsuke Sasaki, Maximilian Röder, Tatsuro Katsumura, and David Bailly. 2025. "Characterization and Modelling of Microstructure Evolution and Flow Stress of Single-Phase Austenite and Ferrite Phases in Duplex Stainless Steels" Metals 15, no. 2: 130. https://doi.org/10.3390/met15020130
APA StyleBrüggemann, H., Sasaki, S., Röder, M., Katsumura, T., & Bailly, D. (2025). Characterization and Modelling of Microstructure Evolution and Flow Stress of Single-Phase Austenite and Ferrite Phases in Duplex Stainless Steels. Metals, 15(2), 130. https://doi.org/10.3390/met15020130






