Methods for Evaluating the Elastic Properties of Stainless Steel Perforated Plates
Abstract
1. Introduction
2. Materials and Methods
2.1. Stainless Steel 316L Plate Perforation
2.2. Perforated Stainless Steel 316L Plates’ Elastic Properties Determination Using Laser Vibrometry
2.3. Perforated Stainless Steel 316L Plates’ Elastic Properties Determination Using Three-Point Flexural Test
2.4. Perforated Stainless Steel 316L Plates’ Elastic Properties Determination Using the Finite Element Method (FEM)
3. Results
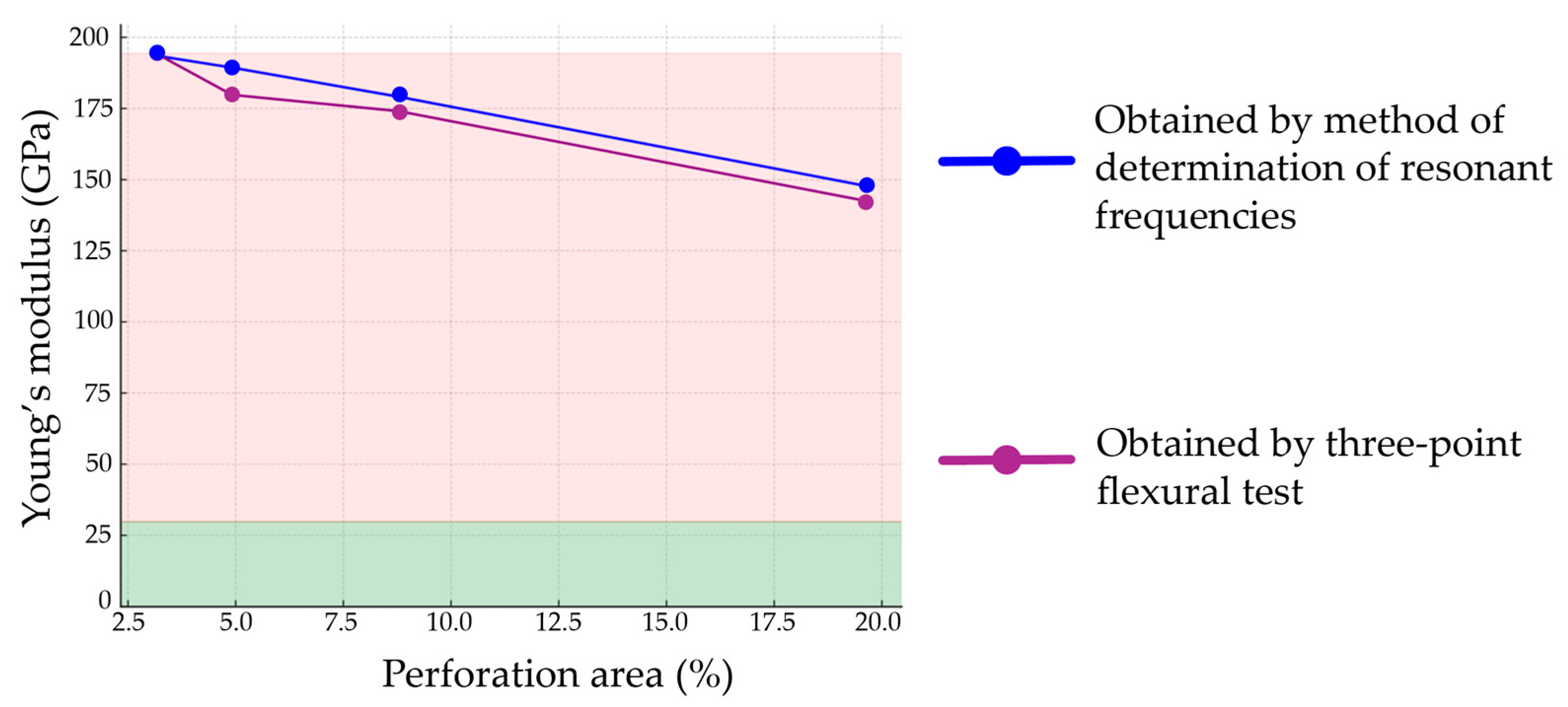
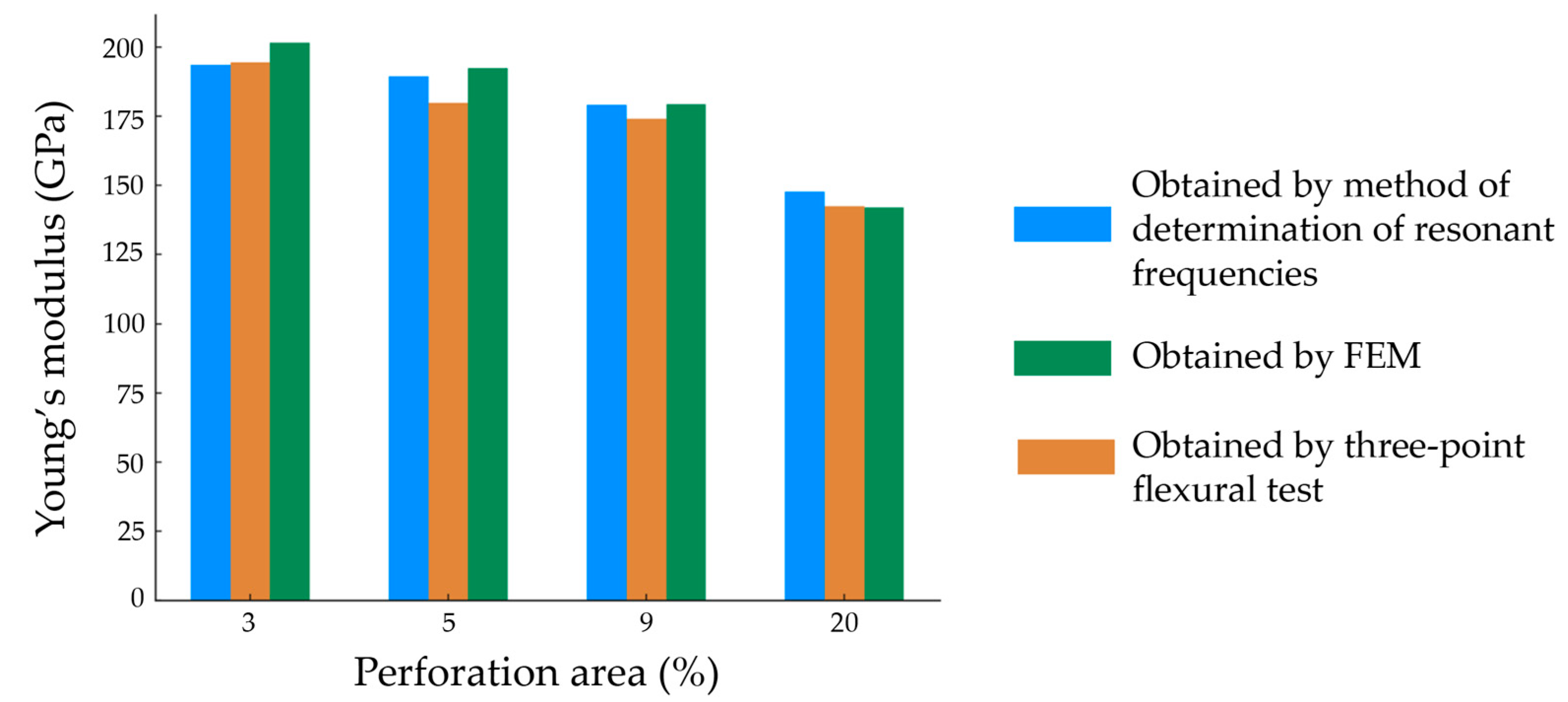
3.1. Elastic Properties of Perforated Stainless Steel 316L Plates Obtained by Method of Determination of Resonant Frequencies and by Three-Point Flexural Test
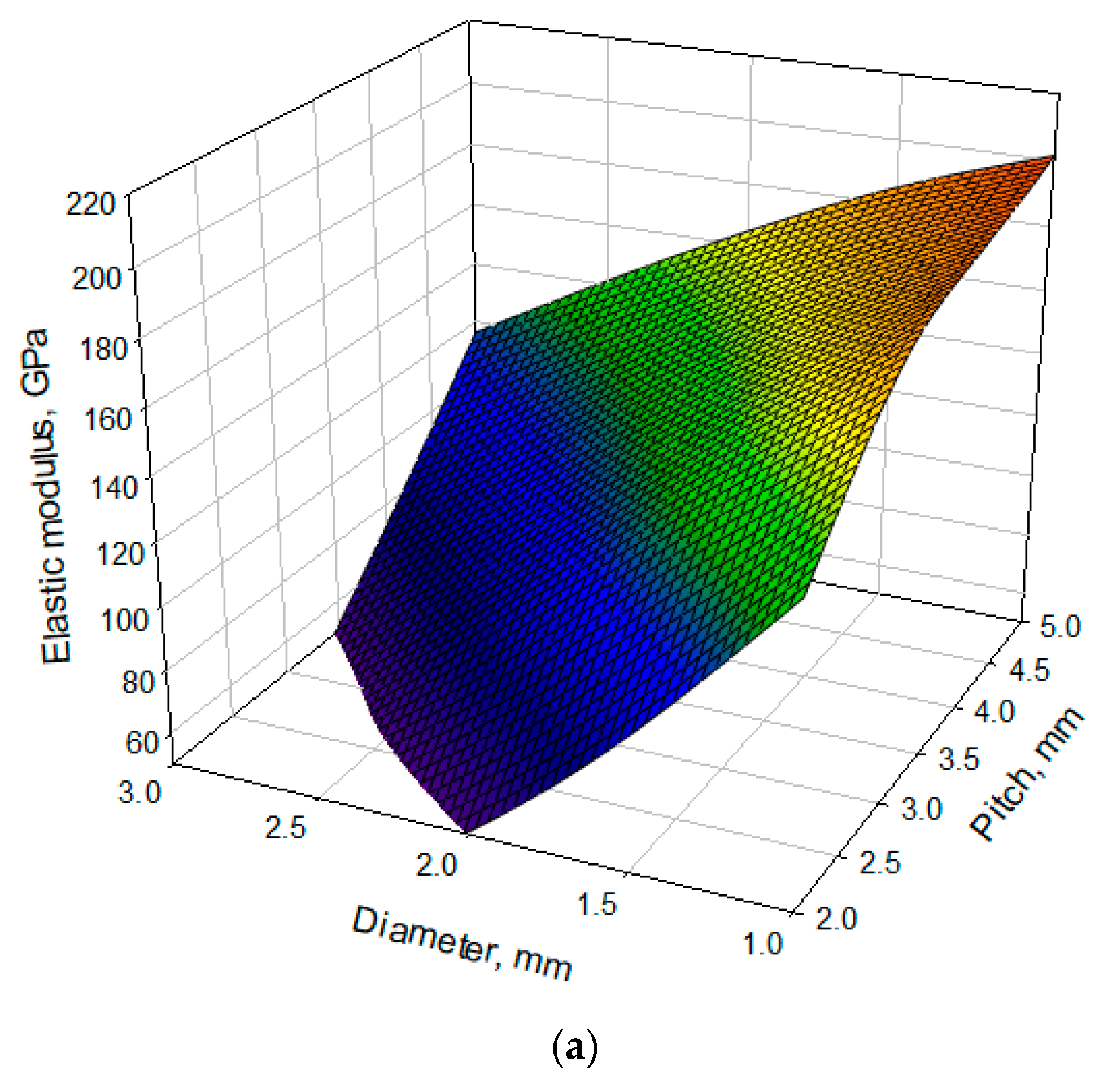
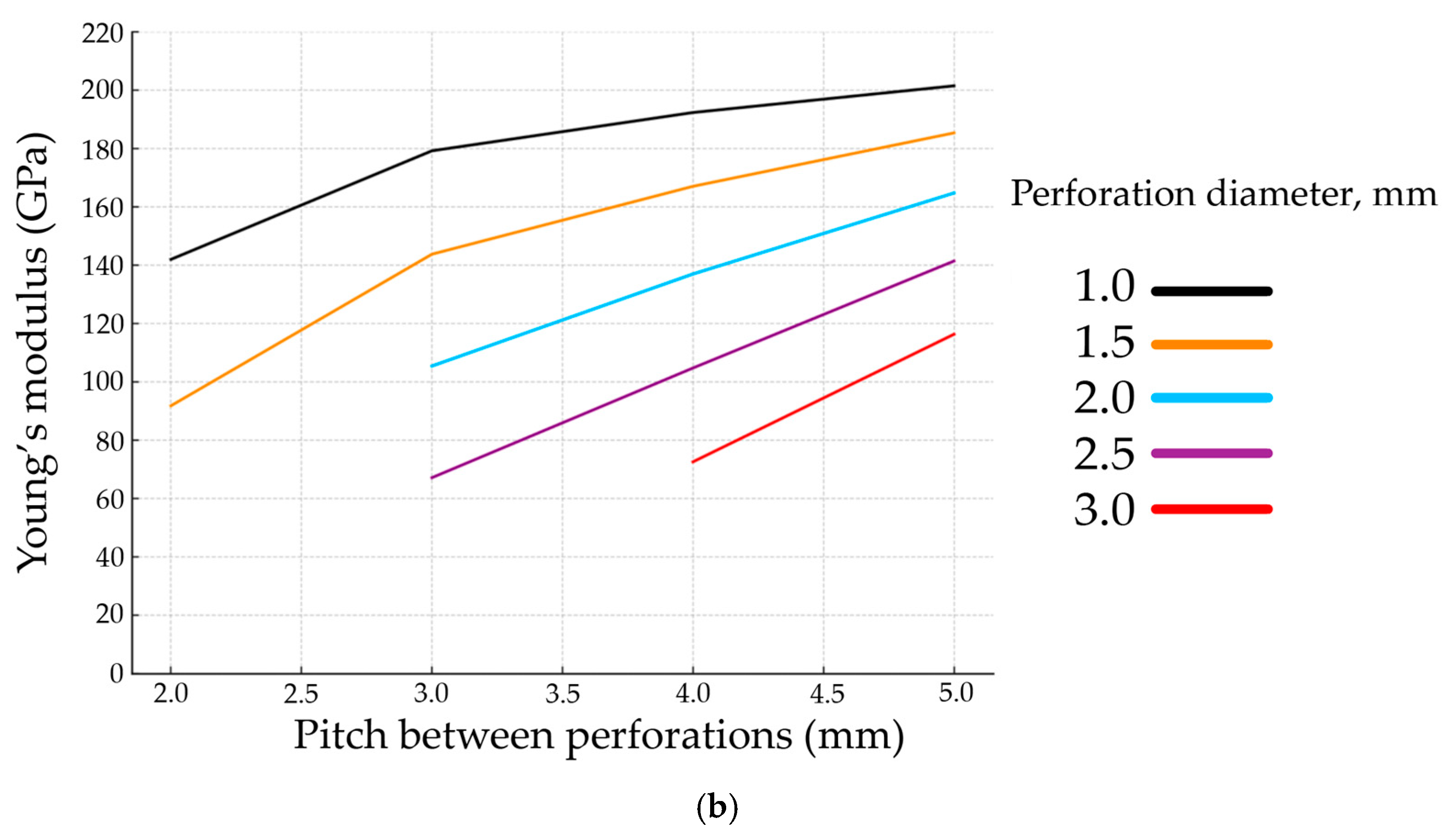
3.2. Elastic Properties of Perforated Stainless Steel 316L Plates with Variable Perforation Diameter and Pitch Between Perforations Using the Finite Element Method
4. Discussion
4.1. Methods for Reducing the Elastic Modulus
4.2. The Method of Determination of Resonant Frequencies, the Three-Point Flexural Test Method, and the Finite Element Method Obtained Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nuwirth, A.L.; Ashley, B.S.; Hardaker, W.M.; Sheth, N.P. Biomedical Applications of Metals; Rai, M., Ingle, A.P., Medici, S., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 3–95. [Google Scholar]
- Swee, H.T. Engineering Materials for Biomedical Application; World Scientific Publishing Co. Pte. Ltd.: Hackensack, NJ, USA, 2004; pp. 4–29. [Google Scholar]
- Marco Specialty Steel, Inc. Designers, Specifiers & Buyers. In Handbook for Perforated Metals; Industrial Perforators Association: Houston, TX, USA, 1993; pp. 3–14. [Google Scholar]
- Mironovs, V.; Lisicins, M. Perforated Metal Materials and Their Use Possibilities; RTU Publishing House: Riga, Latvia, 2015; pp. 15–152. [Google Scholar]
- Lisicins, M.; Serdjuks, D.; Akishin, P.; Mironovs, V.; Goremikins, V.; Lapkovskis, V. Improving the Structural Efficiency of Punched Metal-Material-Based Composites. Polymers 2024, 16, 3468. [Google Scholar] [CrossRef] [PubMed]
- Baik, S.C.; Oh, K.H.; Lee, D.N. Analysis of the Deformation of a Perforated Sheet under Uniaxial Tension. J. Mater. Process. Technol. 1996, 58, 139–144. [Google Scholar] [CrossRef]
- Xinjian, D.; Arnaud, W.; Wilkinson, D.S.; Metzger, D.R. Plastic Limit Analysis of Perforated Material Under Finite Deformation. In Proceedings of the ASME 2005 Pressure Vessels and Piping Conference, Denver, CO, USA, 17–21 July 2005; Volume 2, pp. 1–5. [Google Scholar]
- Wadley, H.N. Cellular Metals Manufacturing. Adv. Eng. Mater. 2002, 4, 726–733. [Google Scholar] [CrossRef]
- Qian, Y.J.; Kong, D.Y.; Liu, S.M.; Sun, S.M.; Zhao, Z. Investigation on micro-perforated panel absorber with ultra-micro perforations. Appl. Acoust. 2013, 74, 931–935. [Google Scholar] [CrossRef]
- Abo Dorra, H.M.; Abd-Elbasseer, M.; Mahmoud, A.E.A.; Mohamed, H.K. Effect of Orifices Distribution Pattern on the Sound Absorption Performance of Double Metal Micro-Perforated Panels. Int. J. Mech. Prod. Eng. Res. Dev. 2020, 10, 15467–15476. [Google Scholar]
- Mironovs, V.; Kuzmina, J.; Serdjuks, D.; Usherenko, Y.; Lisicins, M. Sustainable Lifecycle of Perforated Metal Materials. Materials 2023, 16, 3012. [Google Scholar] [CrossRef] [PubMed]
- Karakaya, C. Numerical Investigation on Perforated Sheet Metals under Tension Loading. Open Chem. 2022, 20, 244–253. [Google Scholar] [CrossRef]
- Reza, F.; Tamaki, Y.; Takahashi, H.; Iwasaki, N.; Miyazaki, T. Properties of a gypsum-bonded magnesia investment using a K₂SO₄ solution for titanium casting. Dent. Mater. J. 2009, 28, 4. [Google Scholar] [CrossRef][Green Version]
- Kroes, L. Creating More Efficiency and Patient Safety by Changing Processes and Contents of Instrument Trays. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2009. [Google Scholar]
- Wexler Surgical. Available online: https://www.wexlersurgical.com/wexler-metal-sterilization-tray-single-level-wsilicone-brackets-105quotx215quotx25quot-266x533x63cm-p-1464.html (accessed on 1 October 2024).
- Dewidar, M.; Khalil, A.; Lim, J.K. Processing and Mechanical Properties of Porous 316L Stainless Steel for Biomedical Applications. Trans. Nonferrous Met. Soc. 2007, 17, 468–473. [Google Scholar] [CrossRef]
- Shahzamanian, M.M.; Banerjee, R.; Dahotre, N.B.; Srinivasa, A.R.; Reddy, J.N. Analysis of stress shielding reduction in bone fracture fixation implant using functionally graded materials. Compos. Struct. 2023, 321, 117262. [Google Scholar] [CrossRef]
- Wintermantel, E.; Mayer, J.; Goehring, T.N.; Aqida, S. Composites for Biomedical Applications. Ref. Modul. Mater. Sci. Mater. Eng. 2016, 2–3. [Google Scholar] [CrossRef]
- William, D.F. Handbook of Biomaterial Properties, 2nd ed.; Murphy, W., Black, J., Hastings, G., Eds.; Springer: New York, NY, USA, 2016; pp. 153–154. [Google Scholar]
- Ratner, B.D.; Hoffman, A.S.; Schoen, F.J.; Lemons, J.E. Biomaterials Science. An Introduction to Materials in Medicine, 2nd ed.; Elsevier: London, UK, 2004; pp. 526–528. [Google Scholar]
- Follansbee, P.S. Fundamentals of Strength. Principles, Experiment, and Applications of an Internal State Variable Constituve Formulation; John Wiley & Sons: Hoboken, NJ, USA, 2014; pp. 7–8. [Google Scholar]
- Callister, W.D. Fundamentals of Materials Science and Engineering: An Integrated Approach, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 183–190. [Google Scholar]
- Callister, W.D.; Rethwisch, D.G. Fundamentals of Materials Science and Engineering: An Integrated Approach, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008; pp. 226–228. [Google Scholar]
- Ahmed, M.S. Numerical Analysis of the Perforated Steel Sheets Under Uni-Axial Tensile Force. Metals 2019, 9, 632. [Google Scholar] [CrossRef]
- Callister, W.D.; Rethwisch, D.G. Materials Science and Engineering: An Introduction, 10th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018; pp. 433–435. [Google Scholar]
- Migonney, V. Biomaterials. Bioengineering and Health Science Series; ISTE Ltd.: Hertfordshire, UK; John Wiley & Sons: Hoboken, NJ, USA, 2014; pp. 31–34. [Google Scholar]
- Ratner, B.D.; Hoffman, A.S.; Schoen, F.J.; Lemons, J.E. Biomaterials Science. An Introduction to Materials in Medicine, 1st ed.; Academic Press: Millbrae, CA, USA, 1996; pp. 37–50. [Google Scholar]
- Hanawa, T. Research and development of metals for medical devices based on clinical needs. Sci. Technol. Adv. Mater. 2012, 13, 064102. [Google Scholar] [CrossRef]
- Sáenz de Viteri, V.; Fuentes, E. Titanium and Titanium Alloys as Biomaterials. In Tribology—Fundamentals and Advancements; Gegner, J., Ed.; IntechOpen: Rijeka, Croatia, 2013; pp. 160–163. [Google Scholar]
- Krasnikovs, A.; Kononova, O.; Machanovskis, A.; Zaharevskis, V.; Akishins, P.; Ruchevskis, S. Characterization of mechanical properties by inverse technique for composite reinforced by knitted fabric. Part 2. Experimental evaluation of mechanical properties by frequency eigenvalues method. J. Vibroeng. 2012, 14, 691–698. [Google Scholar]
- Kovalovs, A.; Rucevskis, S. Identification of elastic properties of composite plate. IOP Conf. Ser. Mater. Sci. Eng. 2011, 23, 012034. [Google Scholar] [CrossRef]
- Wesolowski, M.; Barkanov, E.; Rucevskis, S.; Chate, A.; La Delfa, G. Characterisation of elastic properties of laminated composites by non-destructive techniques. In Proceedings of the ICCM International Conferences on Composite Materials, Edinburgh, UK, 27–31 July 2009; pp. 5–7. [Google Scholar]
- Rothberg, S.J.; Allen, M.S.; Castellini, P.; Di Maio, D.; Dirckx, J.J.J.; Ewins, D.J.; Halkon, B.J.; Muyshondt, P.; Paone, N.; Ryan, T.; et al. An international review of laser Doppler vibrometry: Making light work of vibration measurement. Opt. Lasers Eng. 2017, 99, 11–22. [Google Scholar] [CrossRef]
- Barkanov, E.; Wesolowski, M.; Akishin, P.; Mihovski, M. Techniques for Non-Destructive Material Properties Characterisation. In Non-Destructive Testing and Repair of Pipelines; Barkanov, E.N., Dumitrescu, A., Parinov, I.A., Eds.; Engineering Materials; Springer: Cham, Switzerland, 2018; pp. 194–203. [Google Scholar]
- Rikards, R.; Abramovich, H.; Green, T.; Auzins, J.; Chate, A. Determination of Elastic Properties of Stiffened Composite Shells by Vibration Analysis. Mech. Adv. Mater. Struct. 2003, 10, 177–180. [Google Scholar]
- Pickett, G. Equations for Computing Elastic Constants from Flexural and Torsional Resonant Frequencies of Vibration of Prisms and Cylinders. Proc. ASTM 1945, 45, 846–865. [Google Scholar]
- ASTM Standard E 1876-07; Standard Test Method for Dynamic Young’s Modulus, Shear Modulus and Poisson’s Ratio by Impulse Excitation of Vibration. ASTM International: West Conshohocken, PA, USA, 2007.
- Losertová, M.; Štamborská, M.; Lapin, J.; Mareš, V. Comparison of deformation behavior of 316L stainless steel and Ti6Al4V alloy applied in traumatology. Metalurgija 2016, 55, 667–670. [Google Scholar]
- Auzins, J.; Janushevskis, A.; Janushevskis, J.; Skukis, E. Software EDAOpt for experimental design, analysis and multiobjective robust optimization. In Proceedings of the 1st International Conference on Engineering and Applied Sciences Optimization, Kos, Greece, 4–6 June 2014; pp. 1055–1077. [Google Scholar]
- Yaqoob, K.; Amjad, I.; Awan, M.A.M.; Liaqat, U.; Zahoor, M.; Kashif, M. Novel Method for the Production of Titanium Foams to Reduce Stress Shielding in Implants. ACS Omega 2023, 8, 1876–1884. [Google Scholar] [CrossRef]
- Niinomi, M.; Nakai, M. Titanium-Based Biomaterials for Preventing Stress Shielding Between Implant Devices and Bone. Int. J. Biomater. 2011, 2011, 836587. [Google Scholar] [CrossRef] [PubMed]




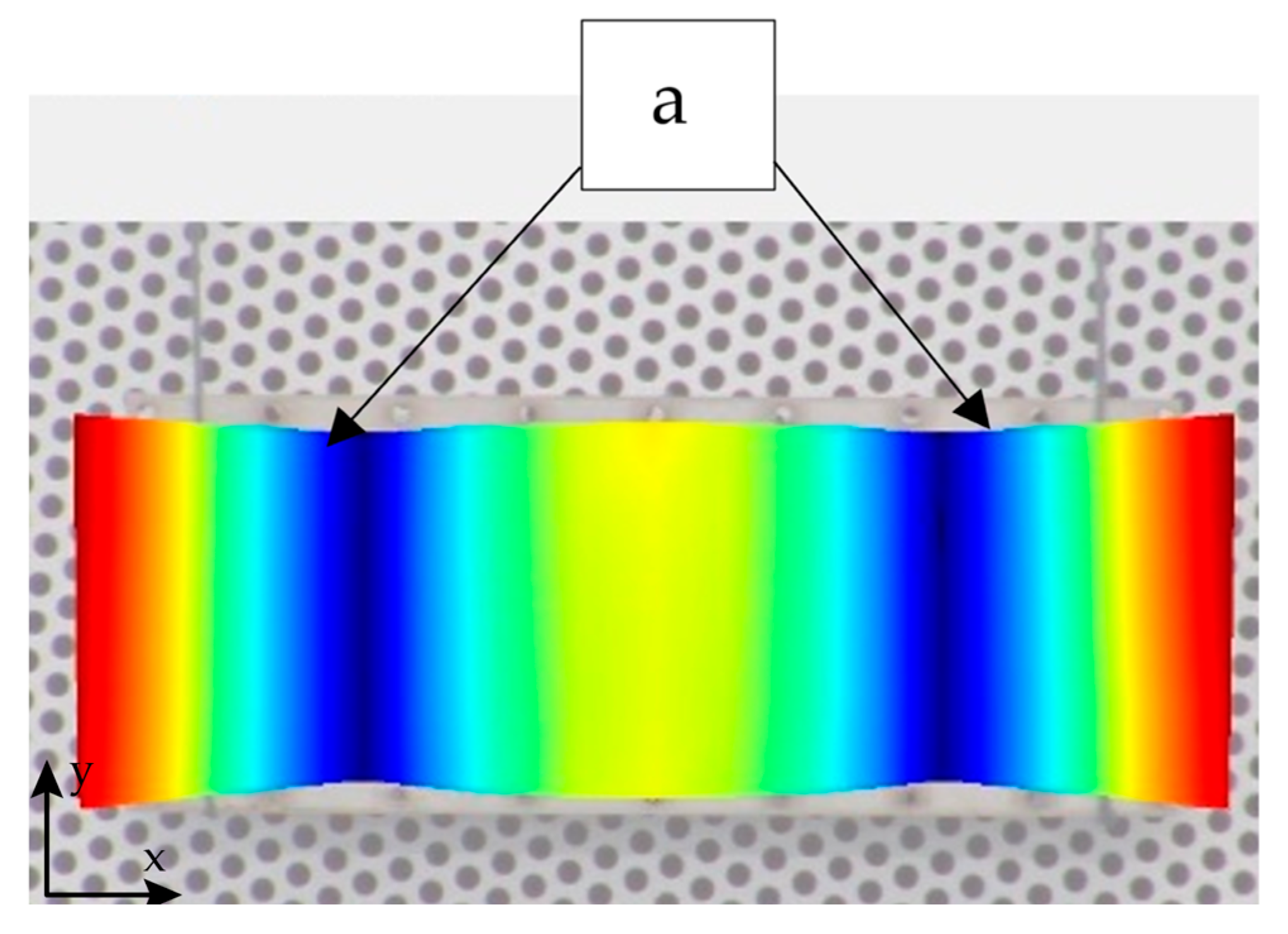



| Sample No. | Perforation Diameter (mm) | Pitch between Perforations (mm) | Perforation Area (%) |
|---|---|---|---|
| 1. | 1 | 5 | 3.14 |
| 2. | 1 | 4 | 4.91 |
| 3. | 1 | 3 | 8.78 |
| 4. | 1 | 2 | 19.63 |
| Sample No. | Weight (g) | Length (mm) | Width (mm) | Thickness (mm) | Fundamental Bending Frequency (kHz) | Correction Factor T | Perforated Plates’ Young’s Modulus (GPa) |
|---|---|---|---|---|---|---|---|
| 1. | 7.4 | 50 | 20 | 1 | 2.100 | 1.003 | 193.63 |
| 2. | 7.4 | 50 | 20 | 1 | 2.077 | 1.003 | 189.41 |
| 3. | 7.2 | 50 | 20 | 1 | 2.048 | 1.003 | 179.18 |
| 4. | 6.6 | 50 | 20 | 1 | 1.943 | 1.003 | 147.84 |
| Pitch Between Holes (mm) | Experimental 1st Eigenfrequency (kHz) | Numerical 1st Eigenfrequency (kHz) | 1st Eigenfrequency Difference (%) | Experimental Weight (g) | Numerical Weight (g) | Weight Difference (%) |
|---|---|---|---|---|---|---|
| 5 | 2.100 | 2.121 | 1.0 | 7.40 | 7.55 | 2.0 |
| 4 | 2.077 | 2.089 | 0.6 | 7.40 | 7.43 | 0.4 |
| 3 | 2.048 | 2.047 | 0.0 | 7.20 | 7.21 | 0.1 |
| 2 | 1.943 | 1.922 | −1.1 | 6.60 | 6.48 | −1.8 |
| Sample No. | Perforation Diameter (mm) | Pitch Between Perforations (mm) | Weight (g) | Fundamental Bending Frequency (kHz) | Correction Factor T | Young’s modulus of Perforated Virtual Samples (GPa) | Perforation Area (%) |
|---|---|---|---|---|---|---|---|
| V1 | 1 | 5 | 7.55 | 2.121 | 1.003 | 201.53 | 3.14 |
| V2 | 1 | 4 | 7.43 | 2.089 | 1.003 | 192.38 | 4.91 |
| V3 | 1 | 3 | 7.21 | 2.047 | 1.003 | 179.26 | 8.78 |
| V4 | 1 | 2 | 6.48 | 1.922 | 1.003 | 142.03 | 19.63 |
| V5 | 1.5 | 5 | 7.25 | 2.076 | 1.003 | 185.39 | 7.07 |
| V6 | 1.5 | 4 | 6.97 | 2.010 | 1.003 | 167.08 | 11.05 |
| V7 | 1.5 | 3 | 6.48 | 1.934 | 1.003 | 143.81 | 19.64 |
| V8 | 1.5 | 2 | 4.82 | 1.729 | 1.003 | 91.84 | 44.18 |
| V9 | 2 | 5 | 6.82 | 2.018 | 1.003 | 164.79 | 12.57 |
| V10 | 2 | 4 | 6.33 | 1.910 | 1.003 | 137.02 | 19.64 |
| V11 | 2 | 3 | 5.45 | 1.806 | 1.003 | 105.47 | 34.91 |
| V12 | 2.5 | 5 | 6.27 | 1.950 | 1.003 | 141.46 | 19.64 |
| V13 | 2.5 | 4 | 5.50 | 1.792 | 1.003 | 104.79 | 30.68 |
| V14 | 2.5 | 3 | 4.12 | 1.658 | 1.003 | 67.19 | 54.54 |
| V15 | 3 | 5 | 5.59 | 1.873 | 1.003 | 116.36 | 28.27 |
| V16 | 3 | 4 | 4.49 | 1.651 | 1.003 | 72.62 | 44.18 |
| Free Term | Linear Term | Quadratic Term | σcross, % | R2adjusted | σ, % | Standard Deviation of Expression | Maximal Relative Error, % |
|---|---|---|---|---|---|---|---|
| 51.275 | 62.22 | −6.78 | 54.39 | 0.97 | 16.32 | 20.69 | 1.27 |
| Free Term | Linear Terms | Quadratic Terms | σcross, % | R2adjusted | σ, % | Standard Deviation of Expression | Maximal Relative Error, % |
|---|---|---|---|---|---|---|---|
| 144.767 | 52.3702 −109.531 | −7.07648 −5.0348 17.2956 | 11.65 | 0.99 | 8.79 | 42.12 | 7.06 |
| Sample No. | Perforation Diameter (mm) | Pitch Between Perforations (mm) | Weight (g) | Fundamental Bending Frequency (kHz) | Correction Factor T | Young’s Modulus of Perforated Virtual Samples (GPa) | Young’s Modulus of Perforated Virtual samples Obtained Using Mathematical Model (GPa) | Difference, % | Perforation Area (%) |
|---|---|---|---|---|---|---|---|---|---|
| T1 | 1.75 | 3.5 | 6.49 | 1.960 | 1.003 | 147.93 | 140.21 | 5.21 | 19.64 |
| T2 | 2.25 | 2.5 | 3.46 | 1.631 | 1.003 | 54.61 | 56.82 | 4.05 | 63.62 |
| T3 | 2.75 | 4.5 | 5.76 | 1.895 | 1.003 | 122.73 | 111.88 | 8.85 | 29.33 |
| Methods | Pearson Correlation Coefficient |
|---|---|
| Determination of resonant frequencies and three-point bending test | 0.98 |
| Determination of resonant frequencies and finite element method | 0.99 |
| Finite element method and three-point bending test | 0.99 |
| Perforation Area (%) | Percentage Reduction in Young’s Modulus Obtained by the Method of Determination of Resonant Frequencies (%) | Percentage Reduction in Young’s Modulus Obtained by the Three-Point Flexural Test (%) | Percentage Reduction in Young’s Modulus Obtained by FEM (%) |
|---|---|---|---|
| 3.14 | 0 | 0 | 0 |
| 4.91 | 2.18 | 7.51 | 4.54 |
| 8.78 | 7.46 | 10.45 | 11.05 |
| 19.63 | 23.65 | 26.68 | 29.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mironovs, V.; Osipova, M.; Akishin, P.; Zemchenkovs, V.; Serdjuks, D. Methods for Evaluating the Elastic Properties of Stainless Steel Perforated Plates. Metals 2025, 15, 711. https://doi.org/10.3390/met15070711
Mironovs V, Osipova M, Akishin P, Zemchenkovs V, Serdjuks D. Methods for Evaluating the Elastic Properties of Stainless Steel Perforated Plates. Metals. 2025; 15(7):711. https://doi.org/10.3390/met15070711
Chicago/Turabian StyleMironovs, Viktors, Marija Osipova, Pavel Akishin, Vjcheslavs Zemchenkovs, and Dmitrijs Serdjuks. 2025. "Methods for Evaluating the Elastic Properties of Stainless Steel Perforated Plates" Metals 15, no. 7: 711. https://doi.org/10.3390/met15070711
APA StyleMironovs, V., Osipova, M., Akishin, P., Zemchenkovs, V., & Serdjuks, D. (2025). Methods for Evaluating the Elastic Properties of Stainless Steel Perforated Plates. Metals, 15(7), 711. https://doi.org/10.3390/met15070711









