Experimental and Numerical Investigation on Fracture Behavior and Energy Absorption Characteristics of Aluminum Foam in the Taylor Tests
Abstract
1. Introduction
2. Materials and Methods
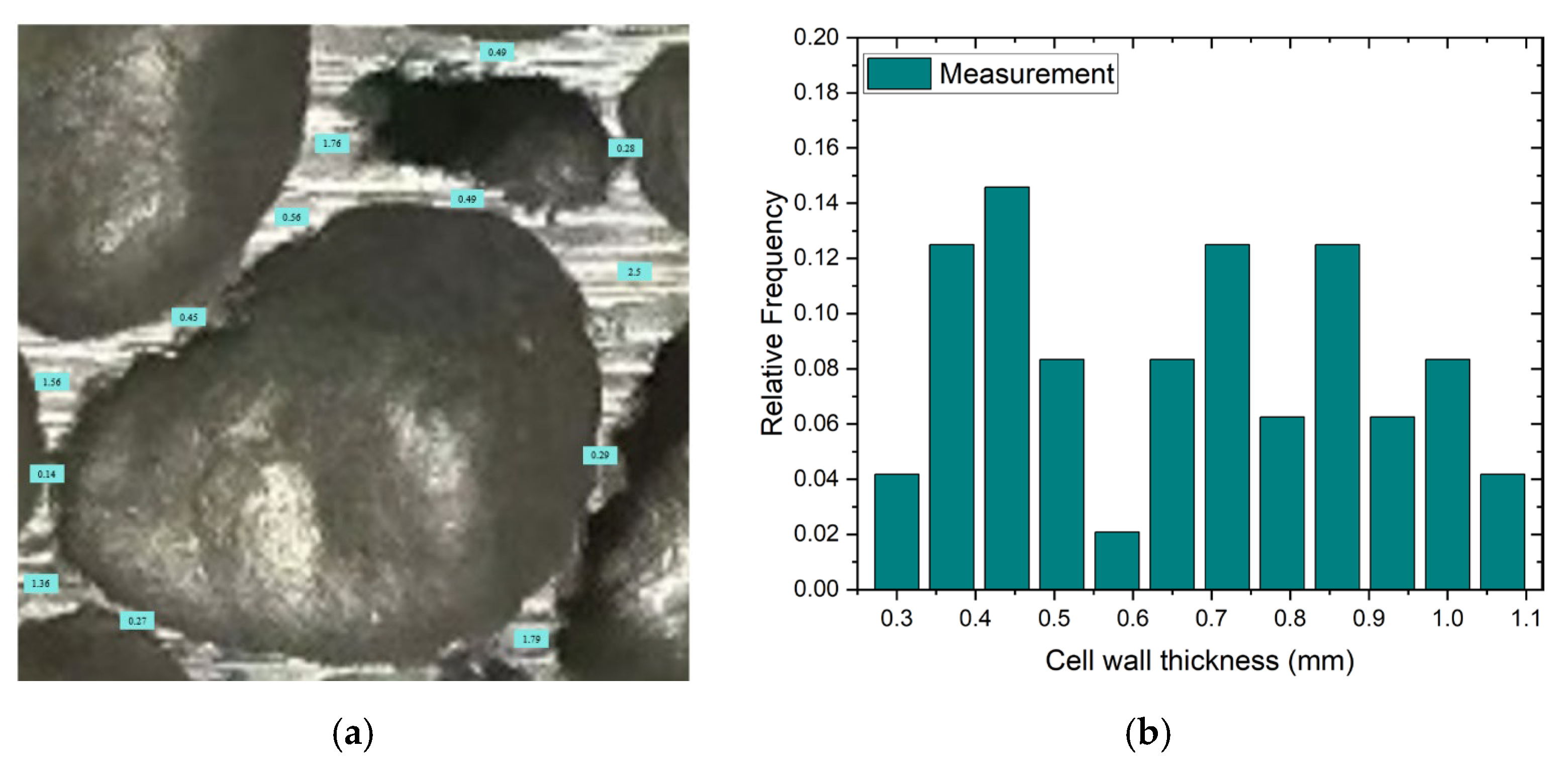
2.1. Test Materials and Preparation
2.2. Experimental System Design
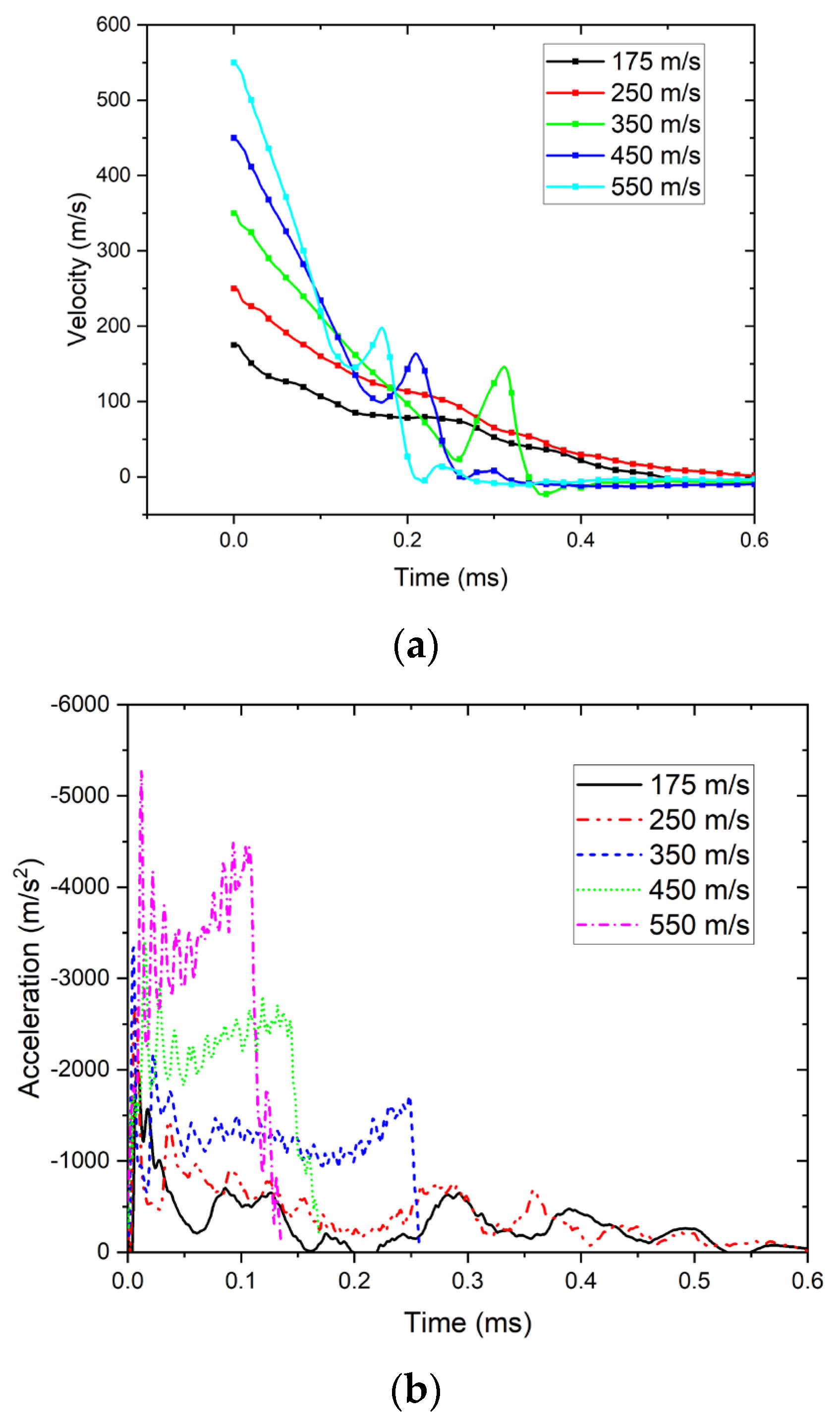
3. Experimental Results and Discussion
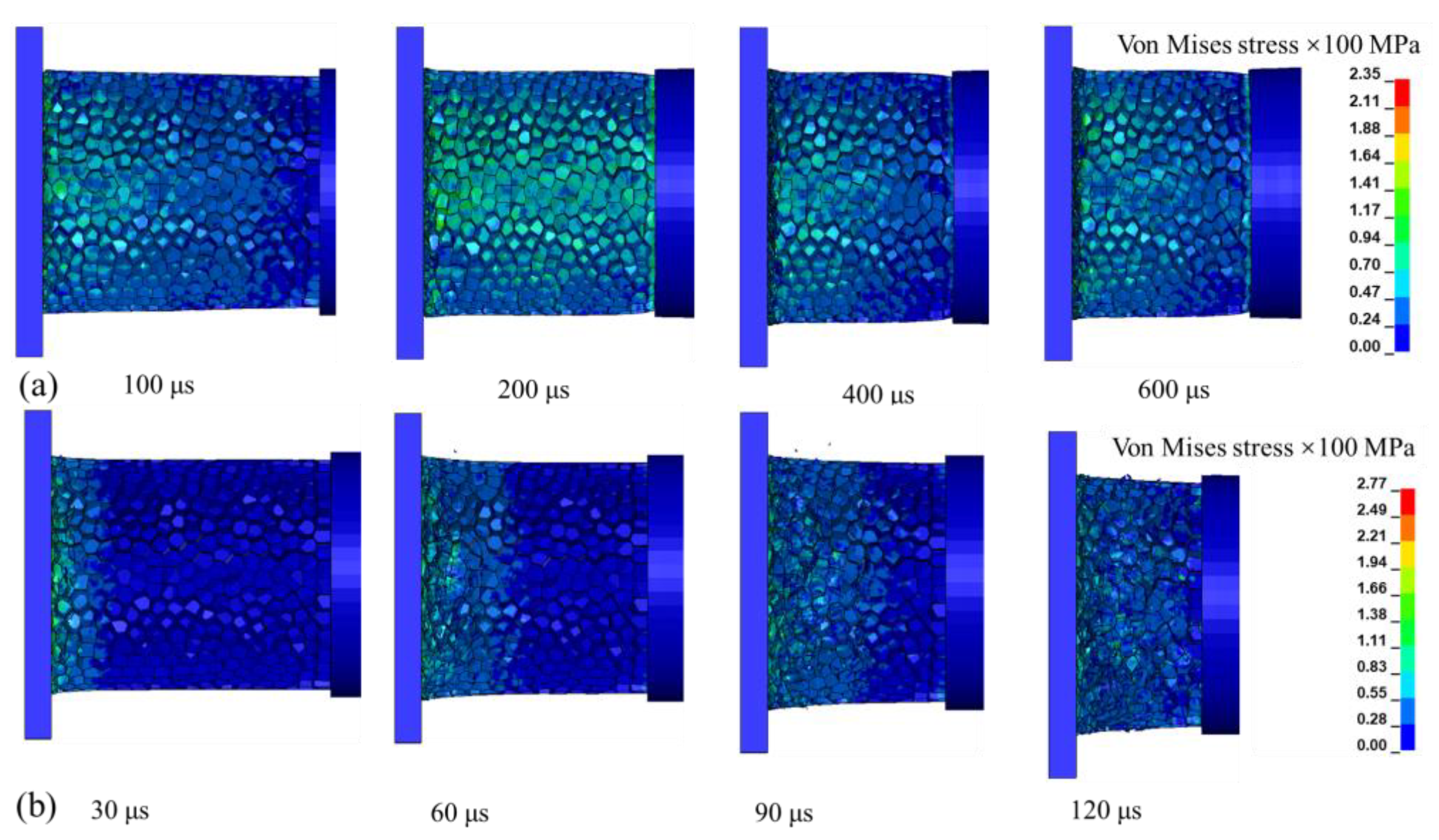
4. Numerical Results and Discussion
4.1. Numerical Simulation Method
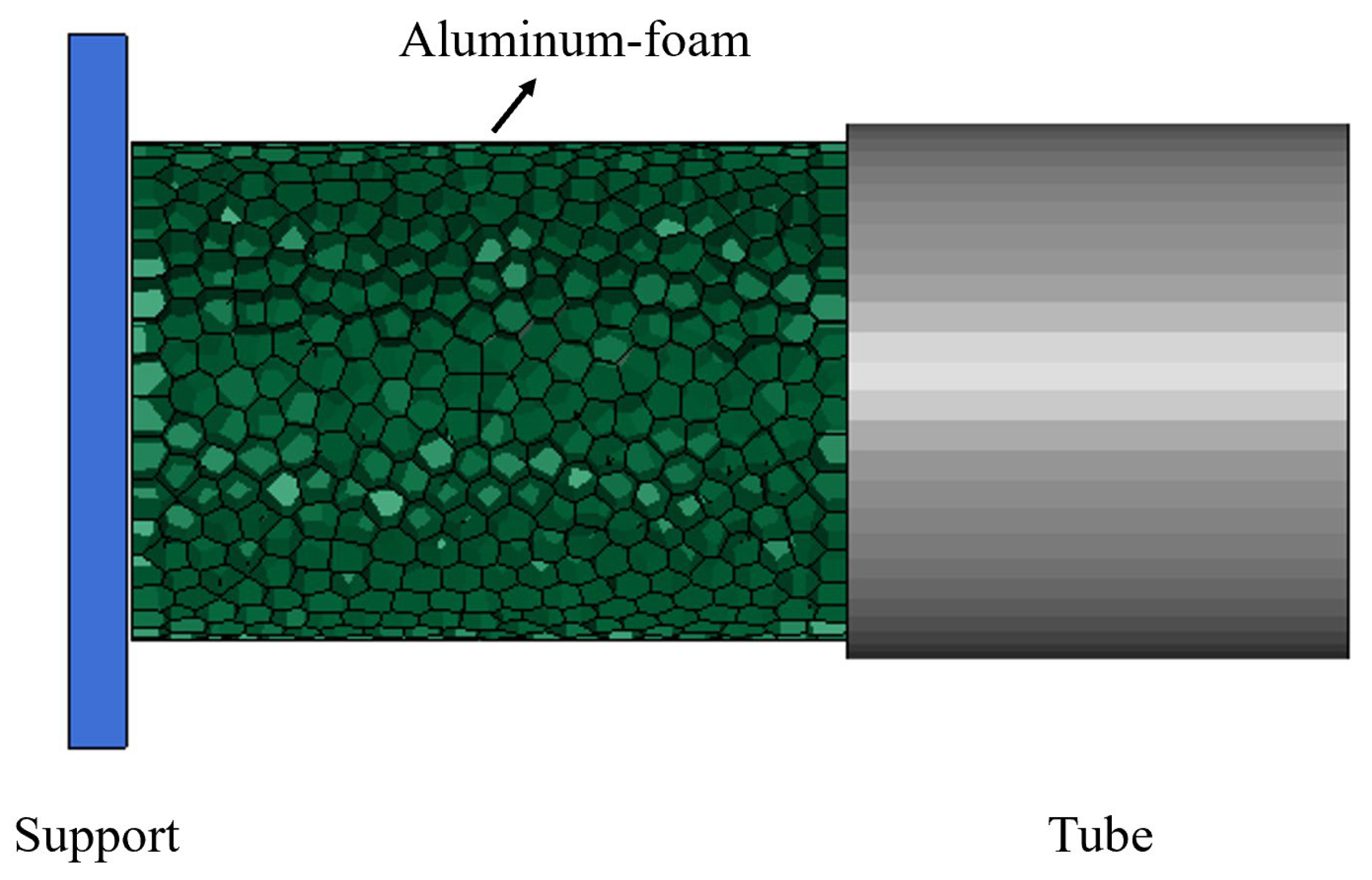
4.2. Numerical Setup
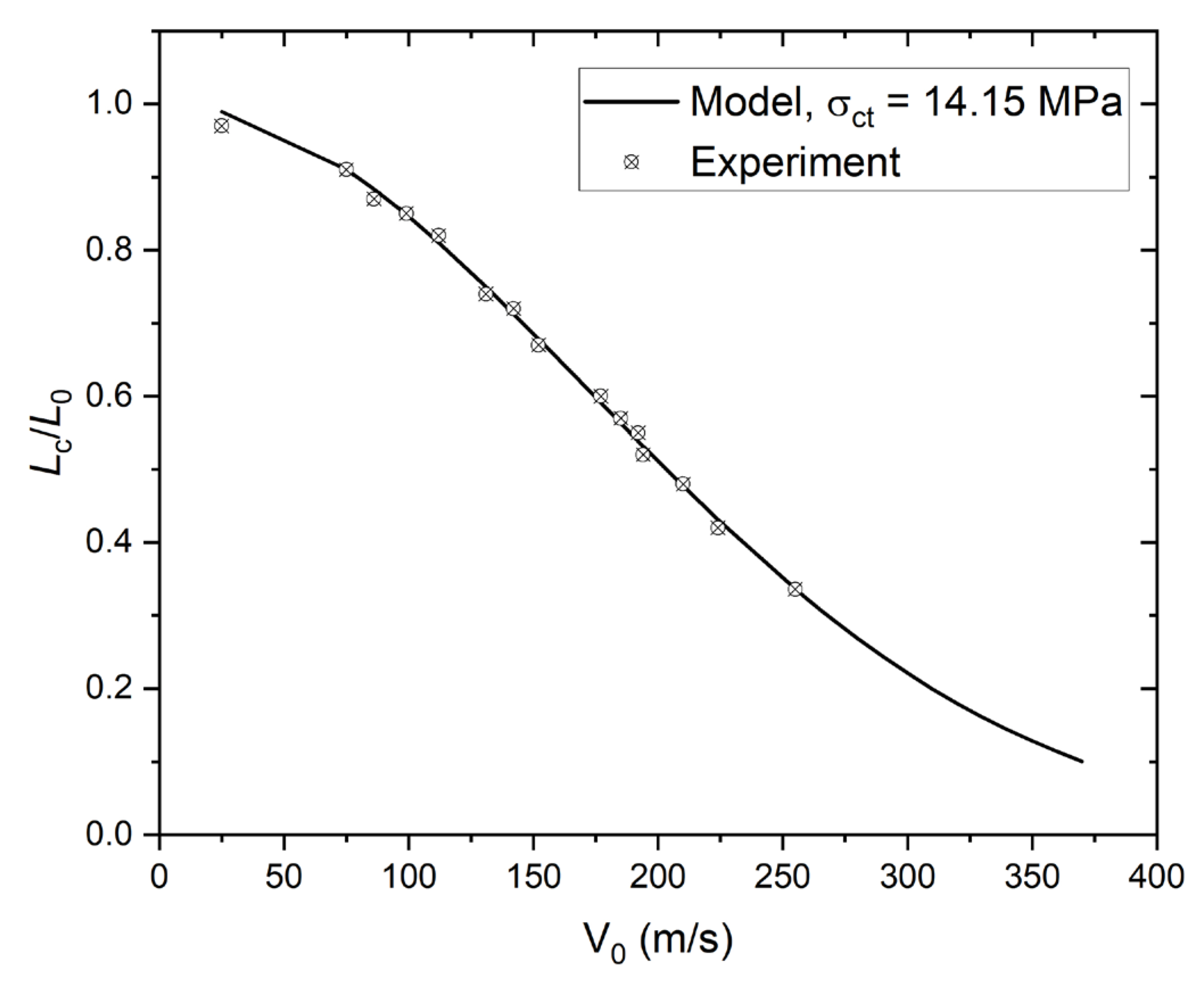
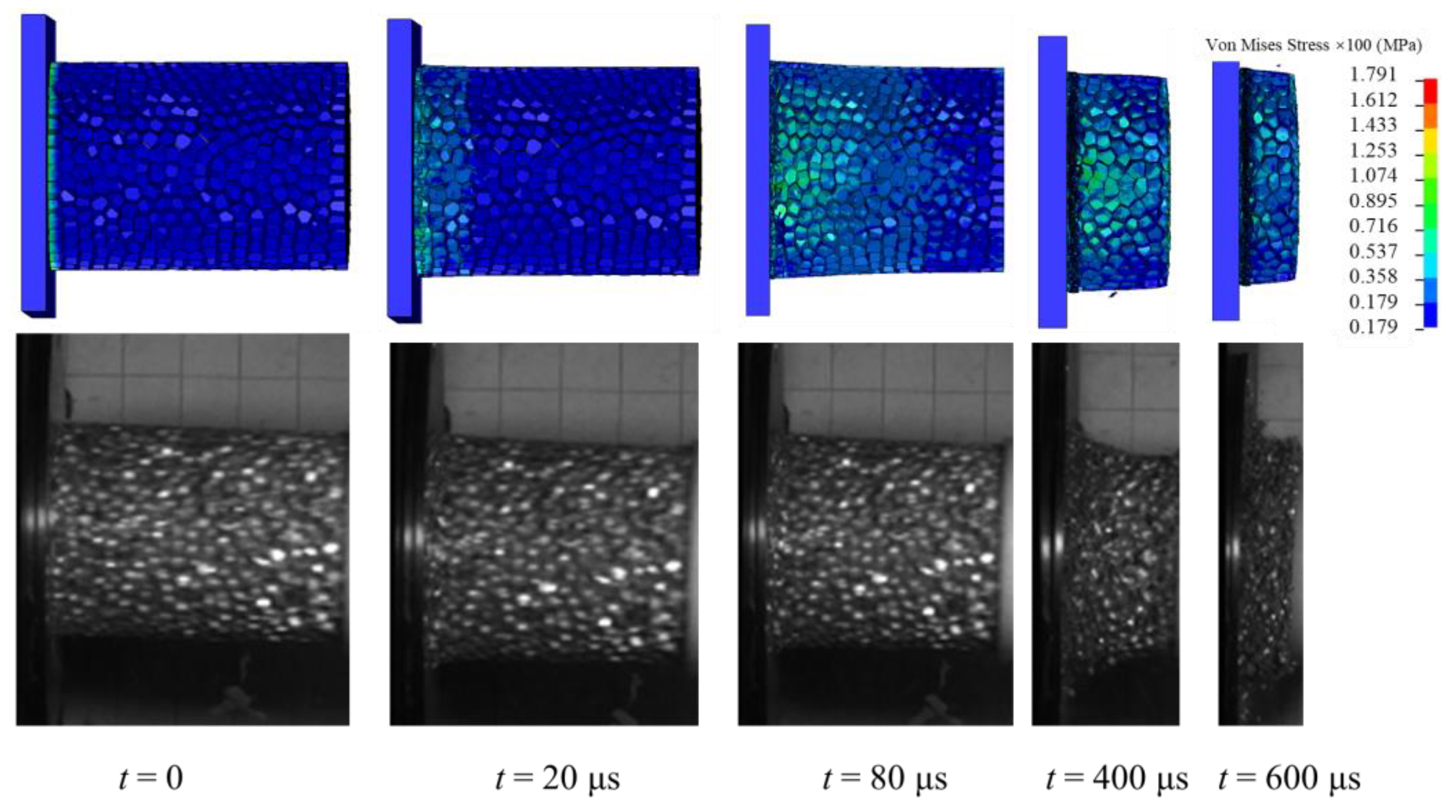
4.3. Validation of Numerical Simulations
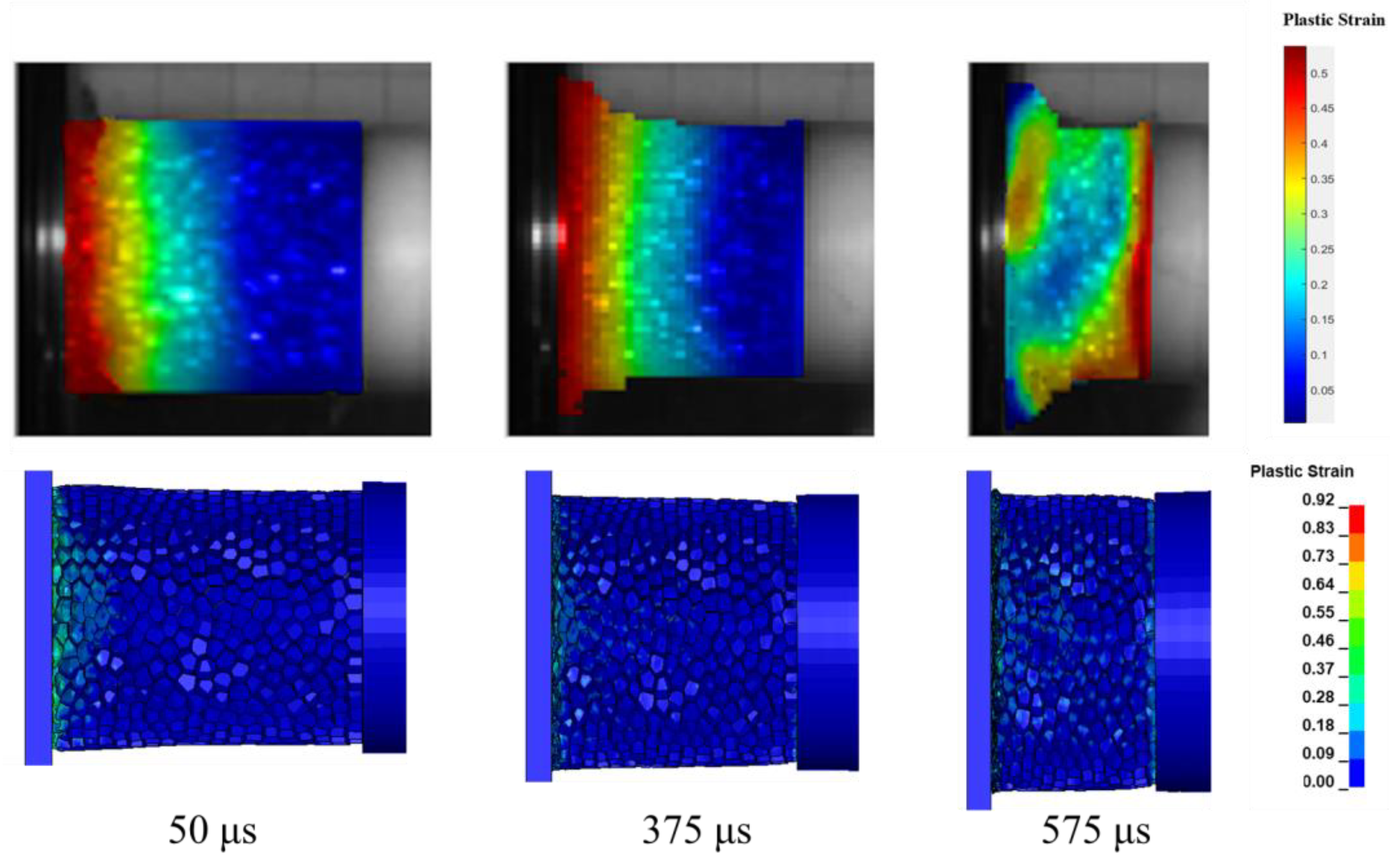
4.4. Dynamic Impact Process
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, X.W.; Zhang, J.; Zhang, J.X.; He, R.; Liu, Q.M. Low-velocity impact of square conical gradient aluminium foam-filled automobile energy-absorbing boxes. Int. J. Crashworthiness 2024, 29, 330–346. [Google Scholar] [CrossRef]
- Casaburo, A.; Petrone, G.; Meruane, V.; Franco, F.; De Rosa, S. The vibroacoustic behaviour of aluminium foam sandwich panels in similitude. J. Sandw. Struct. Mater. 2021, 23, 4170–4195. [Google Scholar] [CrossRef]
- Xia, Y.; Wu, C.Q.; Liu, Z.X.; Yuan, Y.M. Protective effect of graded density aluminium foam on RC slab under blast loading—An experimental study. Constr. Build. Mater. 2016, 111, 209–222. [Google Scholar] [CrossRef]
- Kumar, R.; Jain, H.; Sriram, S.; Chaudhary, A.; Khare, A.; Ch, V.A.N.; Mondal, D.P. Lightweight open cell aluminum foam for superior mechanical and electromagnetic interference shielding properties. Mater. Chem. Phys. 2020, 240, 122274. [Google Scholar] [CrossRef]
- Amsterdam, E.; Onck, P.R.; De Hosson, J.T.M. Fracture and microstructure of open cell aluminum foam. J. Mater. Sci. 2005, 40, 5813–5819. [Google Scholar] [CrossRef]
- Guo, Q.; Yao, W.J.; Li, W.B.; Wang, X.M.; Huang, C.Q. Mechanical Properties of Aluminium Foam and Affect Dynamic Strain-Stress Relationship. Sci. Adv. Mater. 2021, 13, 2200–2212. [Google Scholar] [CrossRef]
- Ma, C.C.; Lan, F.C.; Chen, J.Q.; Liu, J.; Zeng, F.B. Automobile crashworthiness improvement by energy-absorbing characterisation of aluminium foam porosity. Mater. Res. Innov. 2015, 19, S109–S112. [Google Scholar] [CrossRef]
- Novak, N.; Vesenjak, M.; Duarte, I.; Tanaka, S.; Hokamoto, K.; Krstulovic-Opara, L.; Guo, B.Q.; Chen, P.W.; Ren, Z.R. Compressive Behaviour of Closed-Cell Aluminium Foam at Different Strain Rates. Materials 2019, 12, 4108. [Google Scholar] [CrossRef]
- Peroni, M.; Solomos, G.; Pizzinato, V. Impact behaviour testing of aluminium foam. Int. J. Impact Eng. 2013, 53, 74–83. [Google Scholar] [CrossRef]
- Mukai, T.; Miyoshi, T.; Nakano, S.; Somekawa, H.; Higashi, K. Compressive response of a closed-cell aluminum foam at high strain rate. Scr. Mater. 2006, 54, 533–537. [Google Scholar] [CrossRef]
- Li, Z.B.; Chen, R.; Lu, F.Y. Comparative analysis of crashworthiness of empty and foam-filled thin-walled tubes. Thin Wall. Struct. 2018, 124, 343–349. [Google Scholar] [CrossRef]
- Qiu, Q.Z.; Wang, H.T.; Ma, W.T. Experimental and Analytical Study on Multiscale Cushioning and Energy Absorption of Aluminum Foam at Different Strain Rates. Appl. Sci. 2025, 15, 2638. [Google Scholar] [CrossRef]
- Shi, S.Q.; Kang, J.G.; Sui, S.B. Experimental Study of Quasi-static and Dynamic Compressive Property of Close-cell Aluminum Foam. Rare Metal Mat. Eng. 2011, 40, 150–154. [Google Scholar]
- Liu, H.; Cao, Z.K.; Luo, H.J.; Shi, J.C.; Yao, G.C. Performance of closed-cell aluminum foams subjected to impact loading. Mat. Sci. Eng. A Struct. 2013, 570, 27–31. [Google Scholar] [CrossRef]
- Bin Muhit, I.; Shim, C.S.; Yun, N.R.; Park, S.D. Effect of Strain Rate on Impact Behavior of Aluminum Foam. KSCE J. Civ. Eng. 2019, 23, 4852–4863. [Google Scholar] [CrossRef]
- Taylor, G.I. The use of flat-ended projectiles for determining dynamic yield stress I. Theoretical considerations. Proc. R. Soc. 1948, 194, 289–299. [Google Scholar]
- Lopatnikov, S.L.; Gama, B.A.; Jahirul Haque, M.; Krauthauser, C.; Gillespie, J.W.; Guden, M.; Hall, I.W. Dynamics of metal foam deformation during Taylor cylinder–Hopkinson bar impact experiment. Compos. Struct. 2003, 61, 61–71. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, J.; Lu, G. Taylor impact test for ductile porous materials—Part 2: Experiments. Int. J. Impact Eng. 2003, 28, 499–511. [Google Scholar] [CrossRef]
- Lu, G.; Wang, B.; Zhang, T. Taylor impact test for ductile porous materials—Part 1: Theory. Int. J. Impact Eng. 2001, 25, 981–991. [Google Scholar] [CrossRef]
- Lee, J. Estimation of High Speed Mechanical Properties for Metallic Materials under Impact and Blast Load Using Taylor Impact Test. Trans. KSME A 2022, 46, 859–867. [Google Scholar] [CrossRef]
- Wlodarczyk, E.; Sarzynski, M. Experimental analysis of density and compressive strain of porous metal with the use of Taylor test. Arch. Mech. 2014, 66, 245–256. [Google Scholar]
- Huang, B.; Lin, L.; Xu, T.L.; Xiao, X.K.; Wang, J.Q. A Study of the Dynamic Mechanical Properties of Q460D Steel. Metals 2023, 13, 1609. [Google Scholar] [CrossRef]
- Kovácik, J. Correlation between elastic modulus, shear modulus, Poisson’s ratio and porosity in porous materials. Adv. Eng. Mater. 2008, 10, 250–252. [Google Scholar] [CrossRef]
- Hao, G.L.; Xu, Q.P.; Wang, H.; Li, X.Y. Effect of pore structure on mechanical properties of porous TiAl. Mater. Sci. Technol. 2016, 32, 1592–1596. [Google Scholar] [CrossRef]
- Zhao, H.X.; Li, L.H.; Ding, S.; Liu, C.X.; Ai, J.Y. Effect of porous structure and pore size on mechanical strength of 3D-printed comby scaffolds. Mater. Lett. 2018, 223, 21–24. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Tang, L.Q.; Liu, Z.J.; Jiang, Z.Y.; Liu, Y.P.; Wu, Y.D. Yield properties of closed-cell aluminum foam under triaxial loadings by a 3D Voronoi model. Mech. Mater. 2017, 104, 73–84. [Google Scholar] [CrossRef]
- Wang, E.R.; Cai, J.J.; Huo, X.T.; Guo, X. Multiaxial yield behavior of transversely isotropic closed-cell aluminum foams. Int. J. Solids Struct. 2025, 314, 113322. [Google Scholar] [CrossRef]
- Jia, R.; Zhao, G.P. Influence of Cell Wall Material and Cell Numbers on Mechanical Properties of Closed-Cell Aluminum Foams. J. Mater. Eng. Perform. 2025, 34, 10378–10386. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, H.; Dong, X.; Fan, C.; Zou, Y.; Han, Y.; Sun, Y. Effect of cell diameter variations on the mechanical behavior of aluminum foams: Experiments and modeling. Mater. Today Commun. 2024, 3, 109090. [Google Scholar] [CrossRef]
- Falco, S.; Jiang, J.; De Cola, F.; Petrinic, N. Generation of 3D polycrystalline microstructures with a conditioned Laguerre-Voronoi tessellation technique. Comp. Mater. Sci. 2017, 136, 20–28. [Google Scholar] [CrossRef]
- Wejrzanowski, T.; Skibinski, J.; Szumbarski, J.; Kurzydlowski, K.J. Structure of foams modeled by Laguerre–Voronoi tessellations. Comp. Mater. Sci. 2013, 67, 216–221. [Google Scholar] [CrossRef]
- Flores-Johnson, E.A.; Shen, L.; Guiamatsia, I.; Nguyen, G.D. Numerical investigation of the impact behaviour of bioinspired nacre-like aluminium composite plates. Compos. Sci. Technol. 2014, 96, 13–22. [Google Scholar] [CrossRef]














| Sample No. | Velocity (m/s) | Maximum Pressure (MPa) | Length of the Specimen (mm) | Length of the Recovered Sample (mm) | Maximum Diameter of the Recovered Sample (mm) | Mass Loss (g) |
|---|---|---|---|---|---|---|
| 1 | 75 | 24 | 100 | 91.3 | 78.3 | 12.0 |
| 2 | 95 | 54 | 100 | 84.8 | 77.5 | 18.4 |
| 3 | 131 | 60 | 100 | 75.0 | 76.3 | 22.5 |
| 4 | 177 | 110 | 100 | 60.4 | 72.5 | 64.3 |
| 5 | 194 | 122 | 100 | 55.5 | 72.4 | 72.3 |
| 6 | 210 | 125 | 100 | 52.4 | 68.7 | 69.5 |
| 7 | 255 | 140 | 100 | 33.6 | 65.8 | 56.4 |
| Parameters | A/MPa | B/MPa | C | n | m | /s−1 | Tr/K | Tm/K |
| Value | 520 | 477 | 0.001 | 0.52 | 1 | 5 × 10−4 | 293 | 893 |
| Parameters | D1 | D2 | D3 | D4 | D5 | ρ/kg·m−3 | E/GPa | ν |
| Value | 0.096 | 0.049 | −3.465 | 0.016 | 1.099 | 2700 | 70 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, C.; Dong, X.; Xiao, Y.; Lou, W. Experimental and Numerical Investigation on Fracture Behavior and Energy Absorption Characteristics of Aluminum Foam in the Taylor Tests. Metals 2025, 15, 1313. https://doi.org/10.3390/met15121313
Fan C, Dong X, Xiao Y, Lou W. Experimental and Numerical Investigation on Fracture Behavior and Energy Absorption Characteristics of Aluminum Foam in the Taylor Tests. Metals. 2025; 15(12):1313. https://doi.org/10.3390/met15121313
Chicago/Turabian StyleFan, Chenyang, Xingyu Dong, Youcai Xiao, and Wenzhong Lou. 2025. "Experimental and Numerical Investigation on Fracture Behavior and Energy Absorption Characteristics of Aluminum Foam in the Taylor Tests" Metals 15, no. 12: 1313. https://doi.org/10.3390/met15121313
APA StyleFan, C., Dong, X., Xiao, Y., & Lou, W. (2025). Experimental and Numerical Investigation on Fracture Behavior and Energy Absorption Characteristics of Aluminum Foam in the Taylor Tests. Metals, 15(12), 1313. https://doi.org/10.3390/met15121313





