The Effect of Heavy-Duty Vehicle Crossings on the State of Stress of Buried Pipelines
Abstract
:1. Introduction
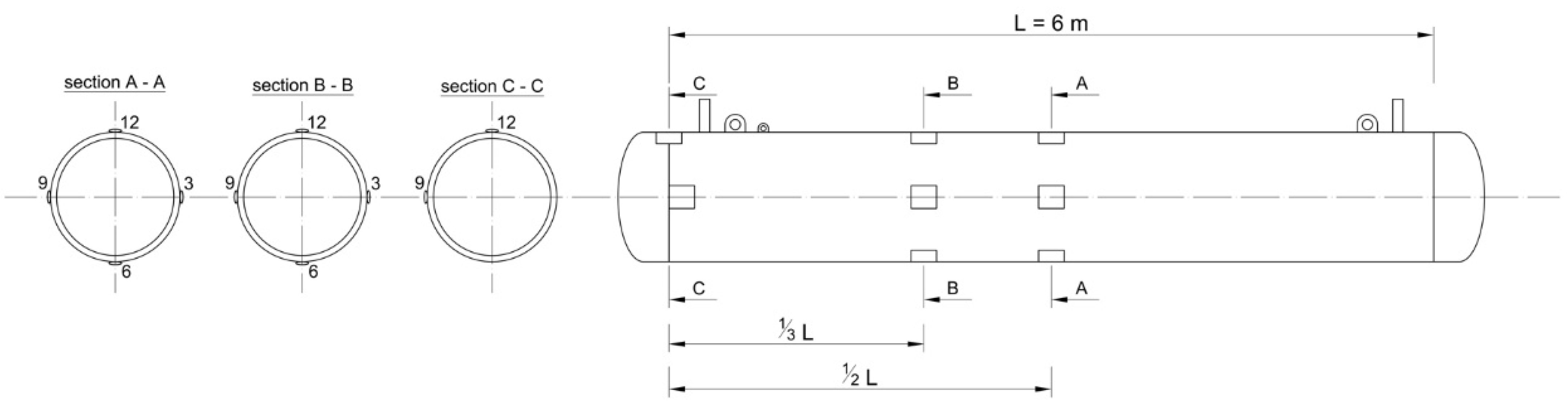
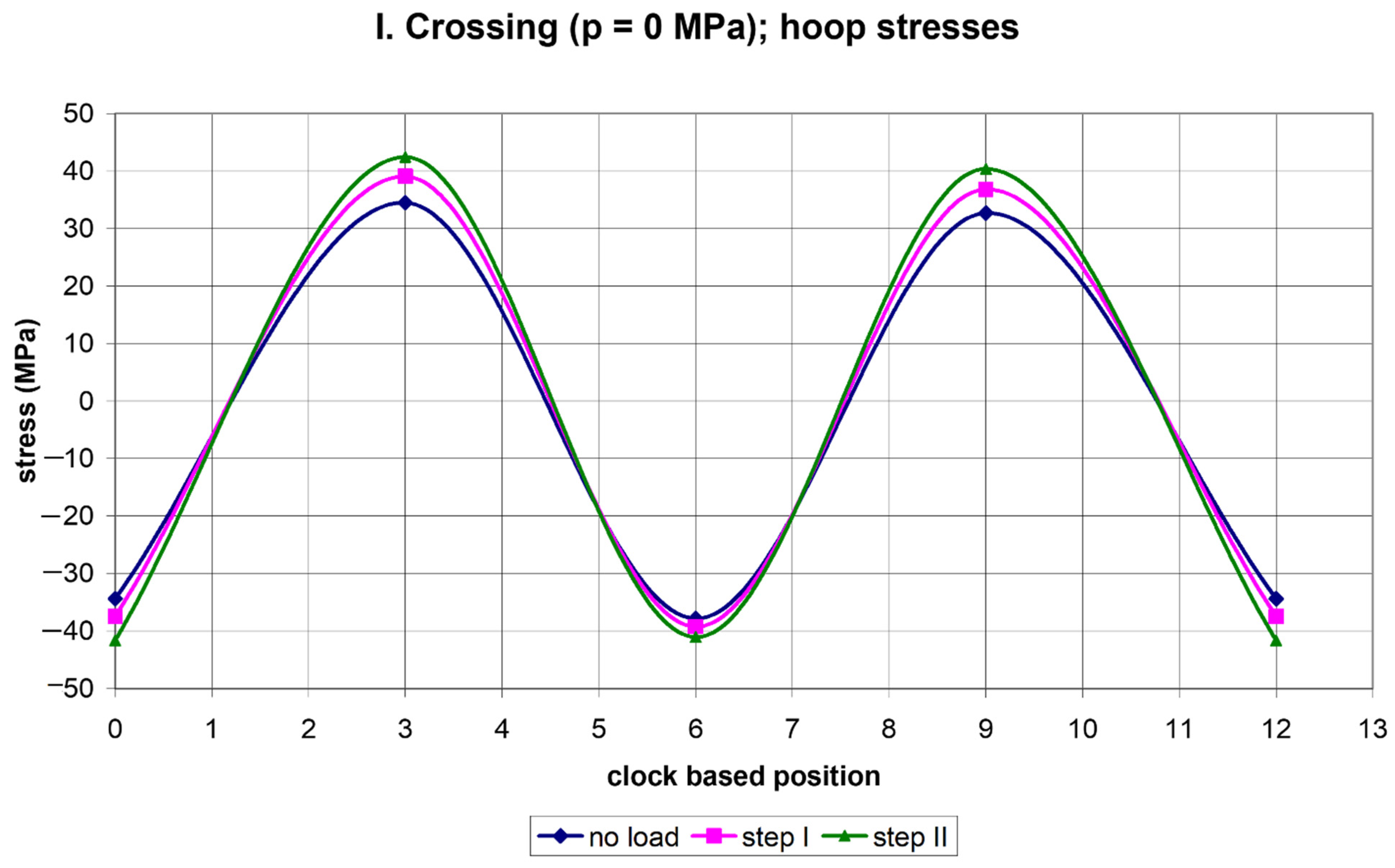
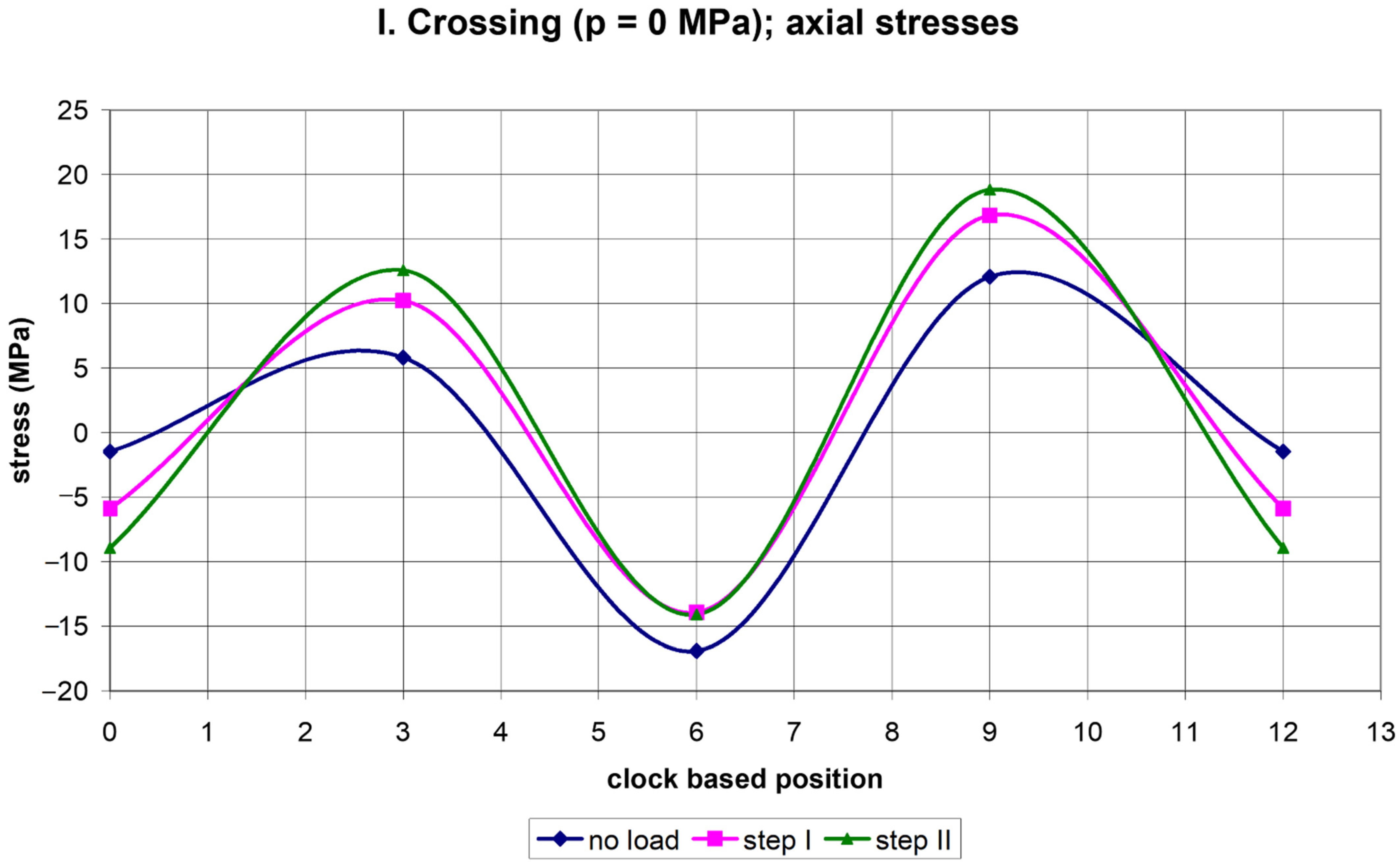
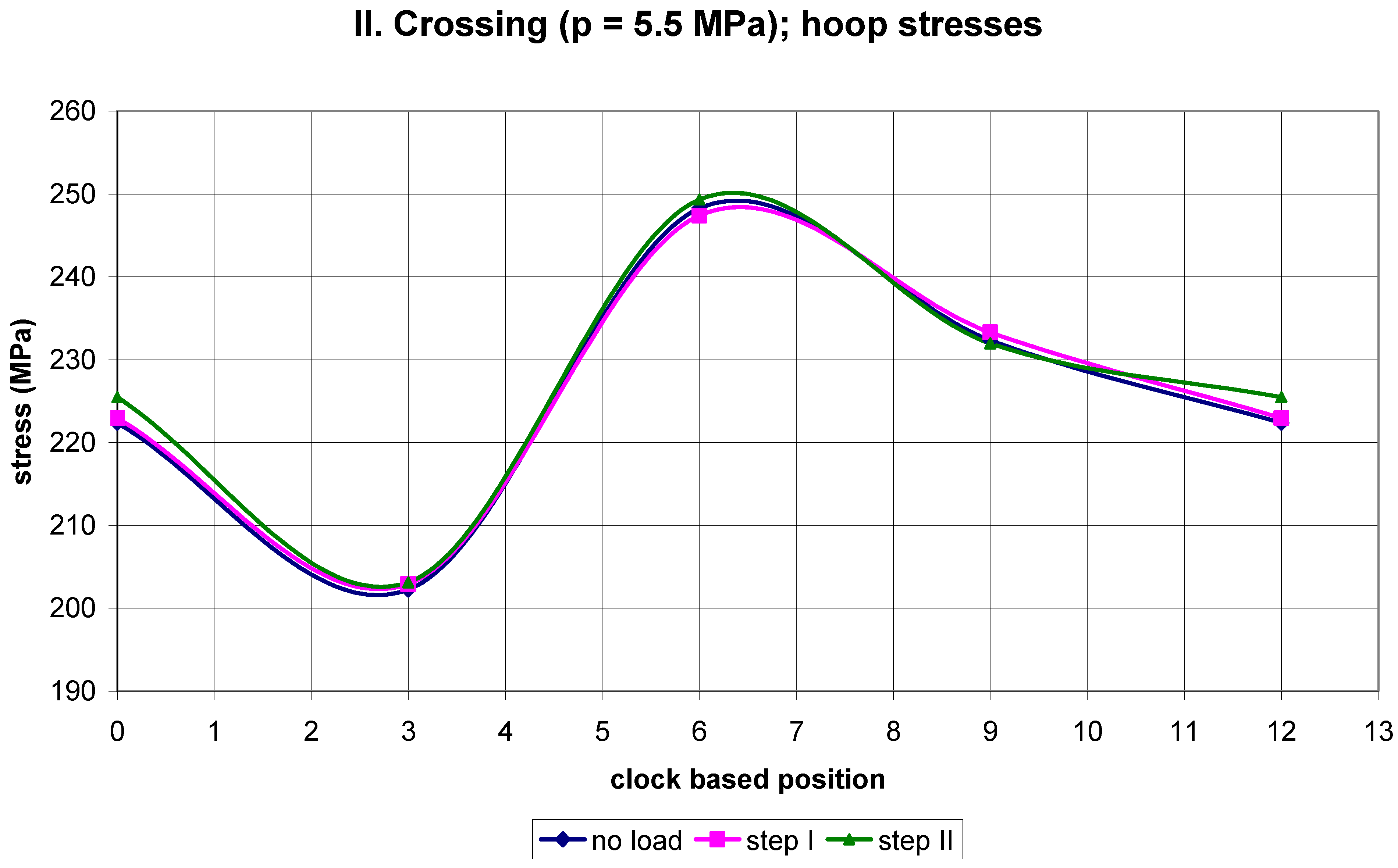
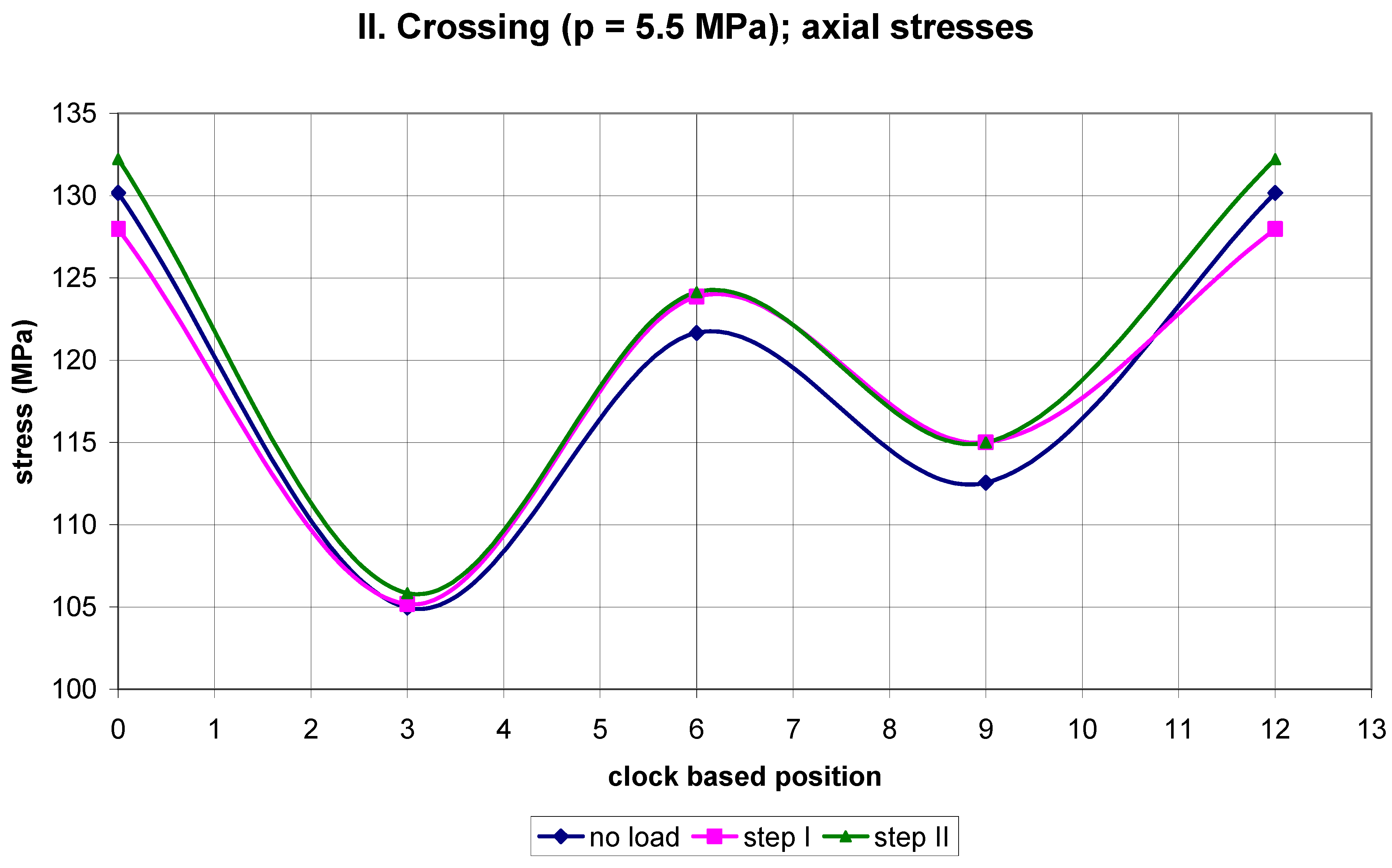
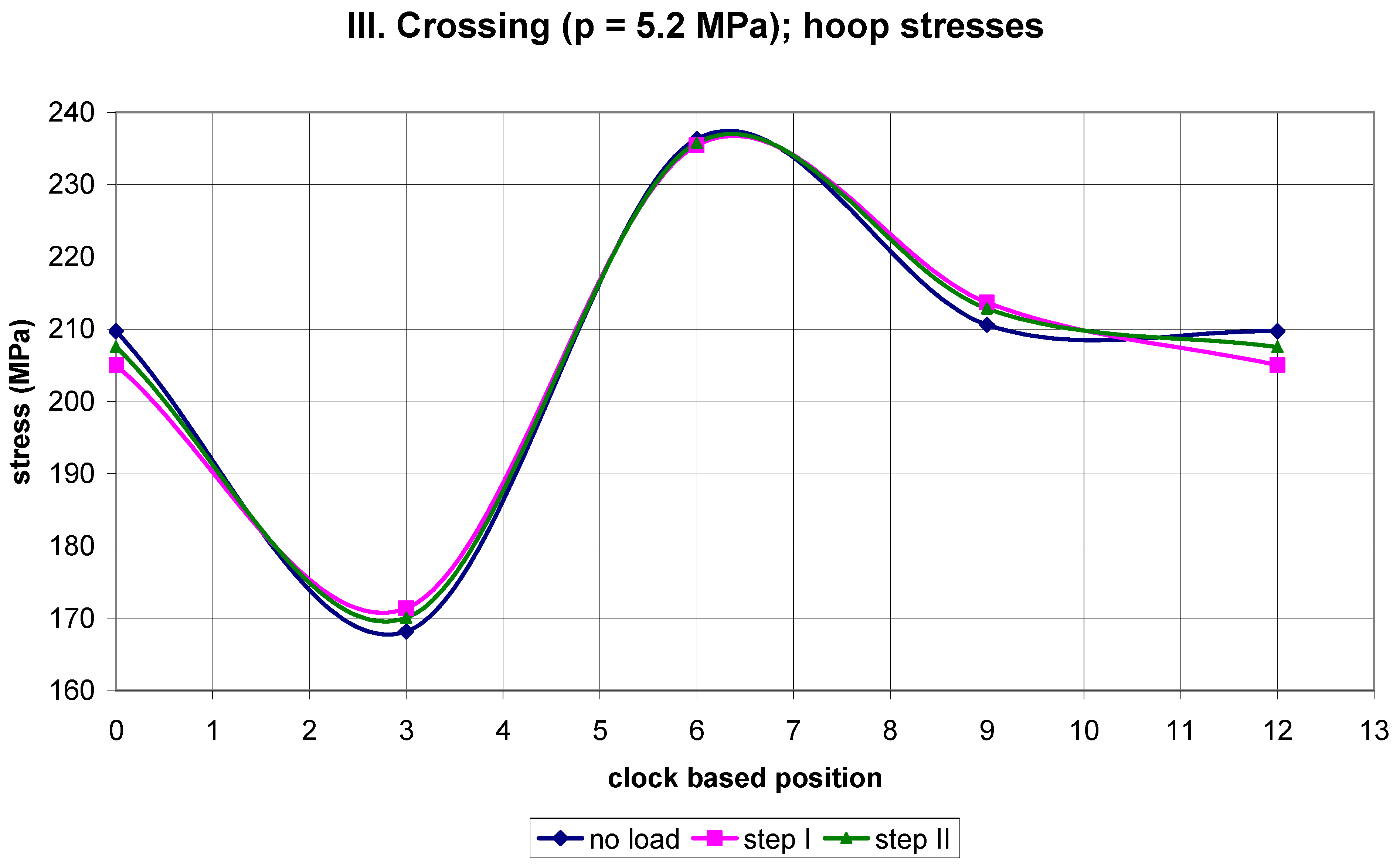
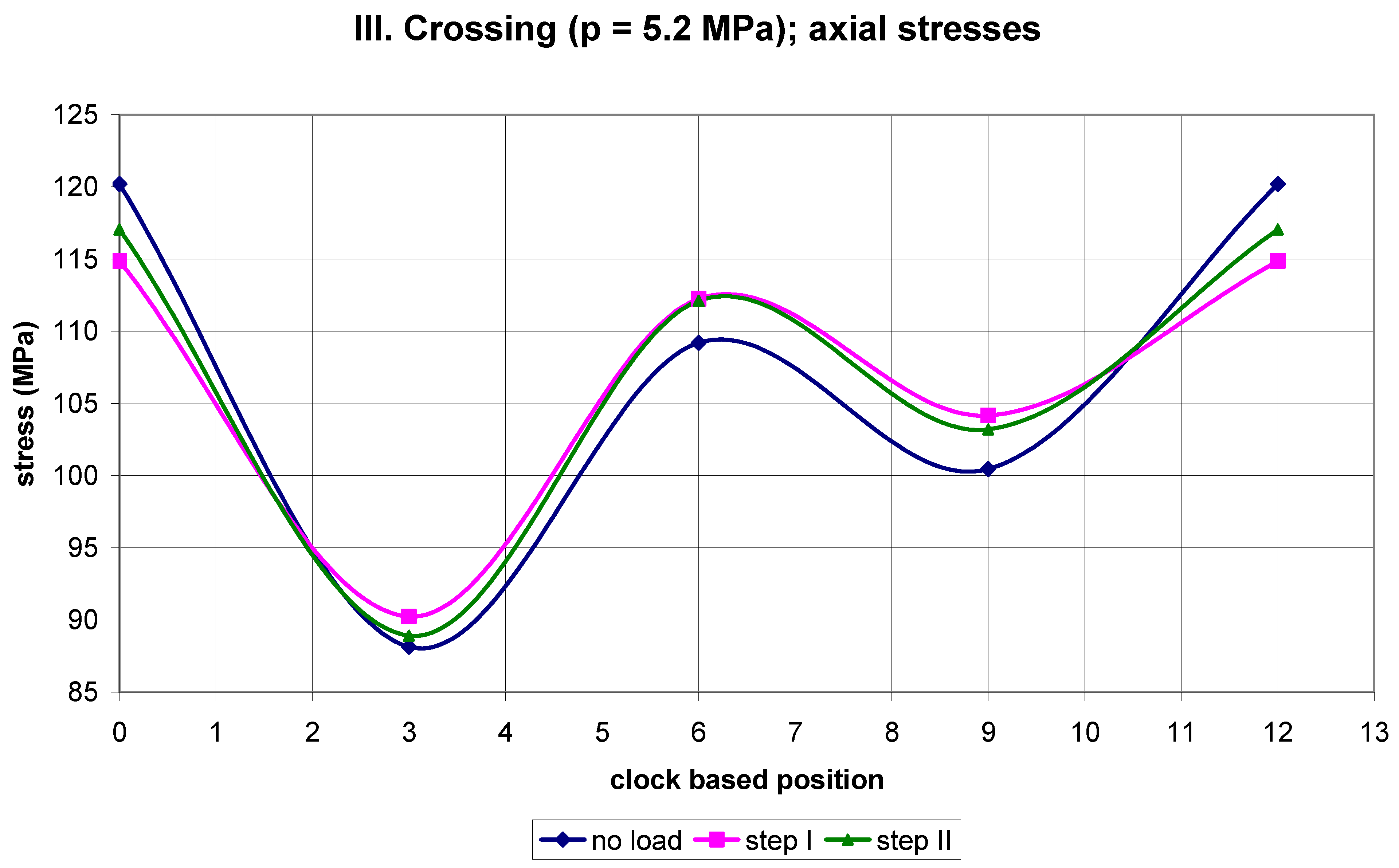
2. Results of Strain Gauge Measurements
3. Engineering Estimation of the State of Stress of a Buried Pipe
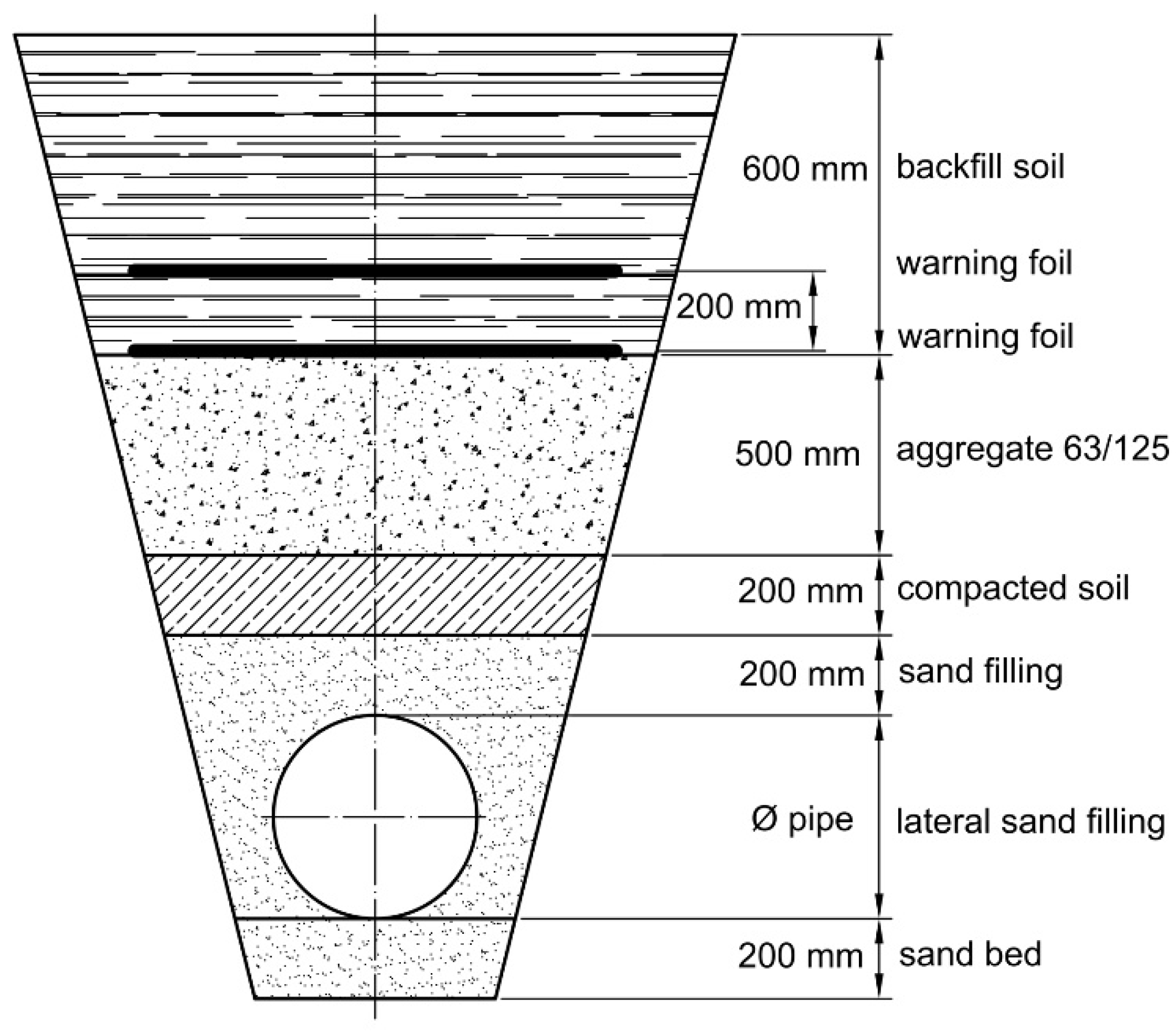
3.1. Backfilling of a Soil
- Δy = vertical deflection of pipe, (mm)
- D = pipe outside diameter, (mm)
- dl = deflection lag factor (~1.0–1.5),
- db = bedding constant (~0.1),
- pz = pressure on pipe due to soil load, (MPa)
- (EI)eq = equivalent pipe wall stiffness as composed of the stiffness of the bare pipe (EI), lining (ELIL) and coating (ECIC) per mm of pipe length, (Nmm)
- I = t3/12, [mm3]
- t = wall thickness of pipe, (mm)
- r = mean pipe radius, (mm)
- E′ = modulus of soil reaction, (MPa)
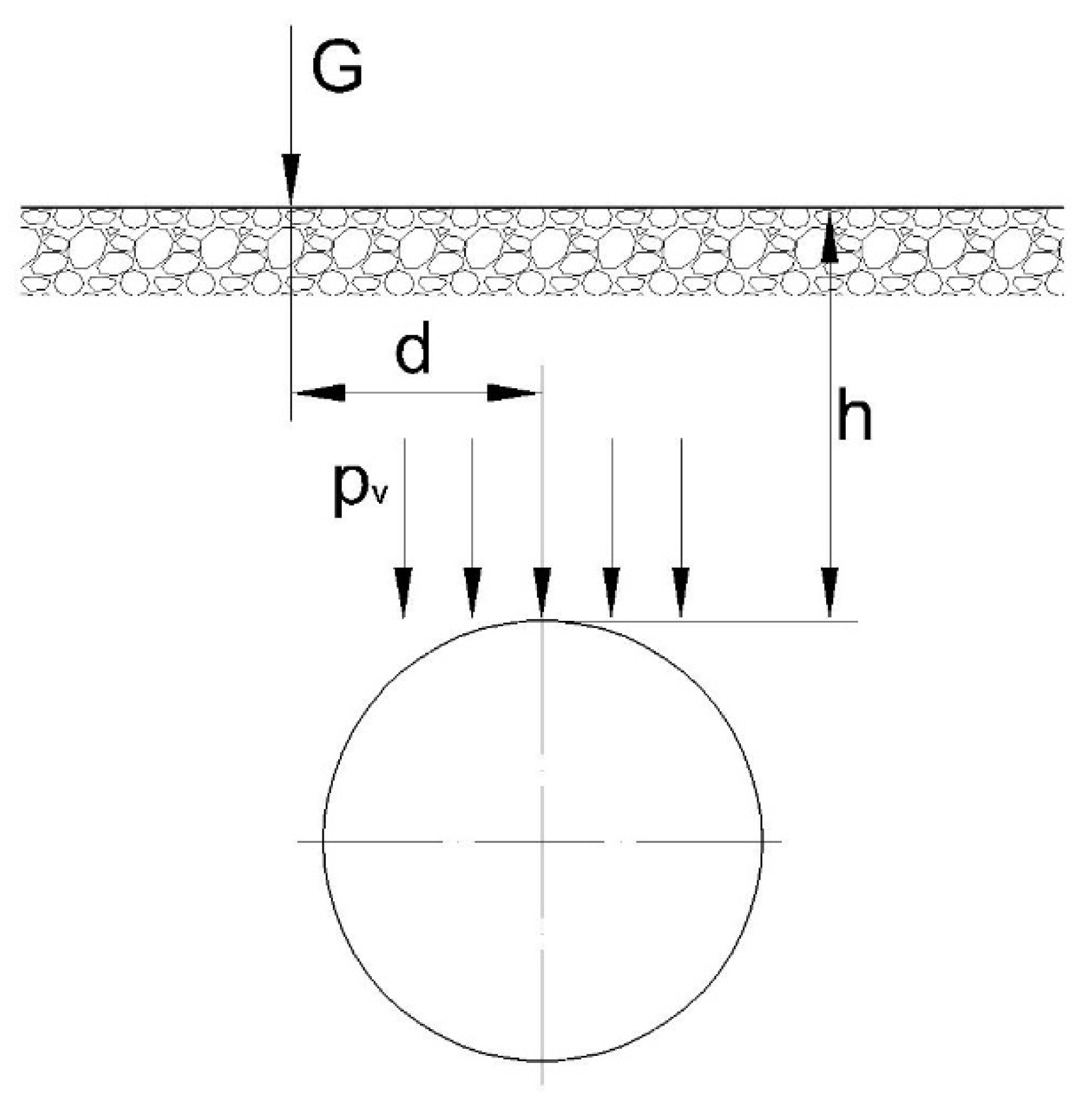
3.2. Crossing the Buried Pipe with the Vehicle
- pV pressure transmitted to the pipe, (MPa)
- G concentrated load at the surface above pipe. (N)
- h depth of soil cover above the pipe, (mm)
- d offset distance from the pipe to the line of application of the surface load, (mm)
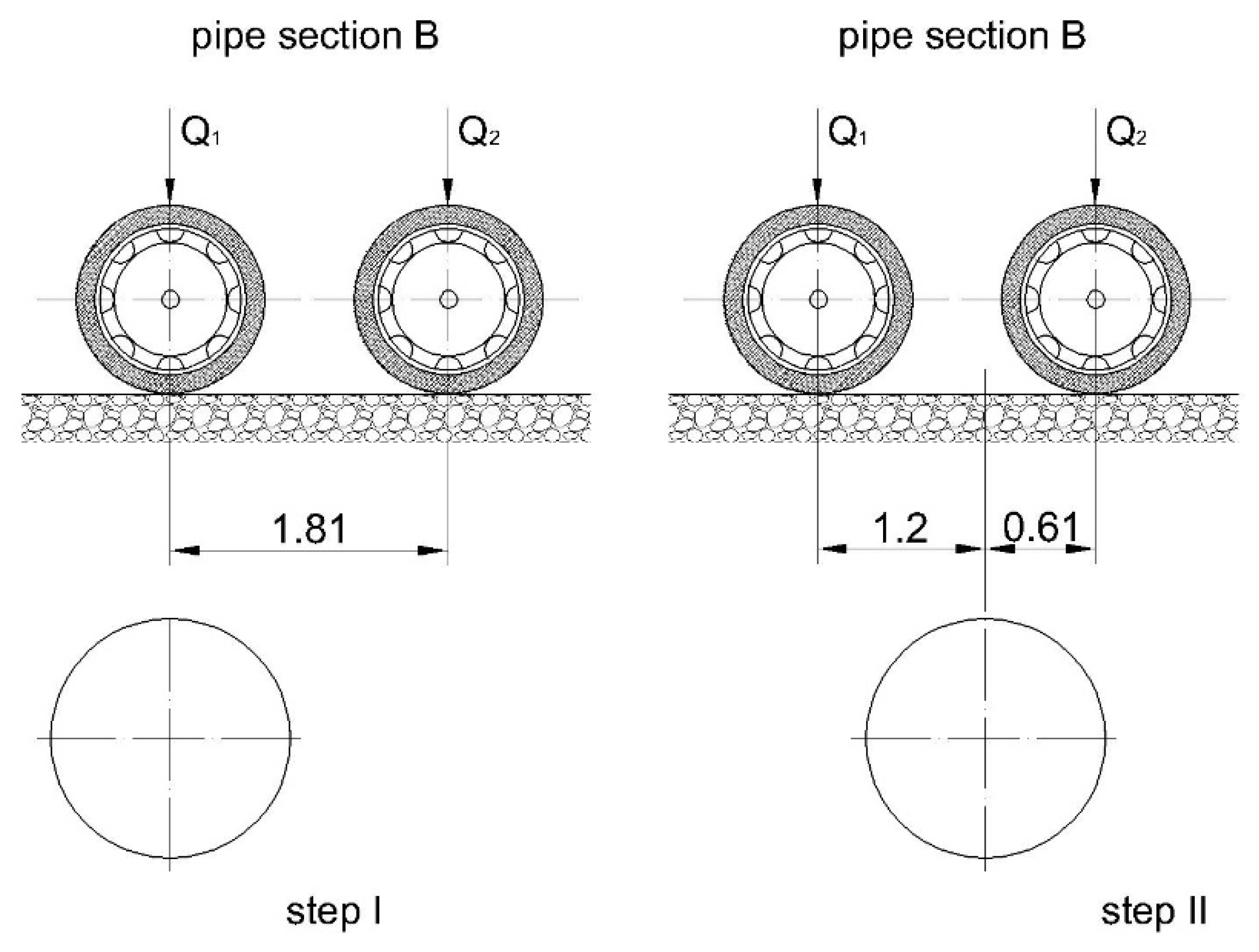
3.2.1. Step I
3.2.2. Step II
- for step I loadingfor step II loading
3.3. Summary
4. Conclusions and Observations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vilkys, T.; Rudzinskas, V.; Prentkovskis, O.; Tretjakovas, J.; Višniakov, N.; Maruschak, P. Evaluation of Failure Pressure for Gas Pipelines with Combined Defects. Metals 2018, 8, 346. [Google Scholar] [CrossRef] [Green Version]
- Rusin, A.; Stolecka-Antzak, K.; Rogoziński, K.; Rusin, K. Analysis of the Effects of Failure of a Gas Pipeline Caused by a Me- chanical Damage. Energies 2021, 14, 7686. [Google Scholar] [CrossRef]
- Koenig, R.A., Jr.; Taylor, J.P. Protection of Pipelines through Highway Roadbeds; National Cooperative Highway Research Program, Report 309; Transportation Research Board: Washington, DC, USA, 1988. [Google Scholar]
- British and European Standard BS EN 1594:2013. Gas Infrastructure. Pipelines for Maximum Operating Pressure over 16 Bar. Functional Requirements; British Standards Institution (BSI): London, UK, 2013. [Google Scholar]
- Ksenofontov, P.V.; Popov, S.N.; Fedorov, Y.Y. Development of Protective Gas Pipes Sleeves for Operation in Permafrost Soils. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1079, 032044. [Google Scholar] [CrossRef]
- McDonough, R. Highway Traffic and the Effect on Pipelines. Pipeline Gas J. 2021, 248, 48–49. [Google Scholar]
- Bahadori, A. Cathodic Corrosion Protection Systems—A Guide for Oil and Gas Industries; GPP, Elsevier, Inc.: New York, NY, USA, 2014; pp. 48–58. [Google Scholar]
- Mrázek, J. Anti-Corrosive Protection of Pipelines in Protective Sleeves. Plyn (Gas) 1998, 2, 34–35. (In Czech) [Google Scholar]
- Mrázek, J. Measurements in Protective Sleeves by Means of Smell Sensors. Plyn (Gas) 2002, 4, 85–87. (In Czech) [Google Scholar]
- Czech Standard TPG 702 04. Gas Mains and Service Pipelines for Maximum Operating Pressure up to 100 Bar Included; Czech Gas Association: Prague, Czech Republic, 2018. (In Czech) [Google Scholar]
- Šperl, M. Overall Evaluation of Key Experiments; Report TE02000162DV263; ITAM ASCR: Prague, Czech Republic, 2019. (In Czech) [Google Scholar]
- Gajdoš, Ľ.; Šperl, M.; Hračov, S. Deformations in Buried Pipe. Plyn (Gas) 2017, 1, 15–22. (In Czech) [Google Scholar]
- Guidelines for the Design of Buried Steel Pipe. American Lifelines Alliance: ASCE. July 2001, pp. 1–76. Available online: www.americanlifelinesalliance.org (accessed on 9 December 2021).
- Murthy, V.N.S. Principles and Practices of Soil Mechanics; Marcel Decker, Inc.: New York, NY, USA, 2002; pp. 173–205. [Google Scholar]
- Craig, R.F. Craig’s Soil Mechanics; Spon Press: New York, NY, USA, 2004; pp. 144–160. [Google Scholar]

| Rt0.5 (MPa) | Rm (MPa) | KV (J) |
|---|---|---|
| 400 | 578 | 72 |
| Position (h) | 12 | 3 | 6 | 9 | ||||
|---|---|---|---|---|---|---|---|---|
| Strain (10−6) | Hoop | Axial | Hoop | Axial | Hoop | Axial | Hoop | Axial |
| no load | −165 | 43 | 159 | −22 | −159 | −27 | 141 | 11 |
| step I | −173.4 | 26 | 174.6 | −7.2 | −170.2 | −10.5 | 154.1 | 28.1 |
| step II | −189.2 | 17.2 | 187.6 | −0.7 | −178.8 | −8.7 | 168.5 | 32.6 |
| Position (h) | 12 | 3 | 6 | 9 | ||||
|---|---|---|---|---|---|---|---|---|
| Strain (10−6) | Hoop | Axial | Hoop | Axial | Hoop | Axial | Hoop | Axial |
| no load | 890 | 308 | 829 | 215 | 1028 | 229 | 964 | 208 |
| step I | 896 | 296.5 | 832 | 215 | 1020.5 | 241 | 965 | 218.5 |
| step II | 902 | 313.5 | 832 | 218 | 1029.5 | 239.5 | 958.5 | 220.5 |
| Position (h) | 12 | 3 | 6 | 9 | ||||
|---|---|---|---|---|---|---|---|---|
| Strain (10−6) | Hoop | Axial | Hoop | axial | HOOP | Axial | Hoop | Axial |
| no load | 843 | 278 | 688 | 183 | 988 | 186 | 876 | 181 |
| step I | 828 | 259 | 700.5 | 188.5 | 979.5 | 202 | 885.5 | 194.5 |
| step II | 837 | 266 | 696 | 184 | 981 | 201 | 883 | 191 |
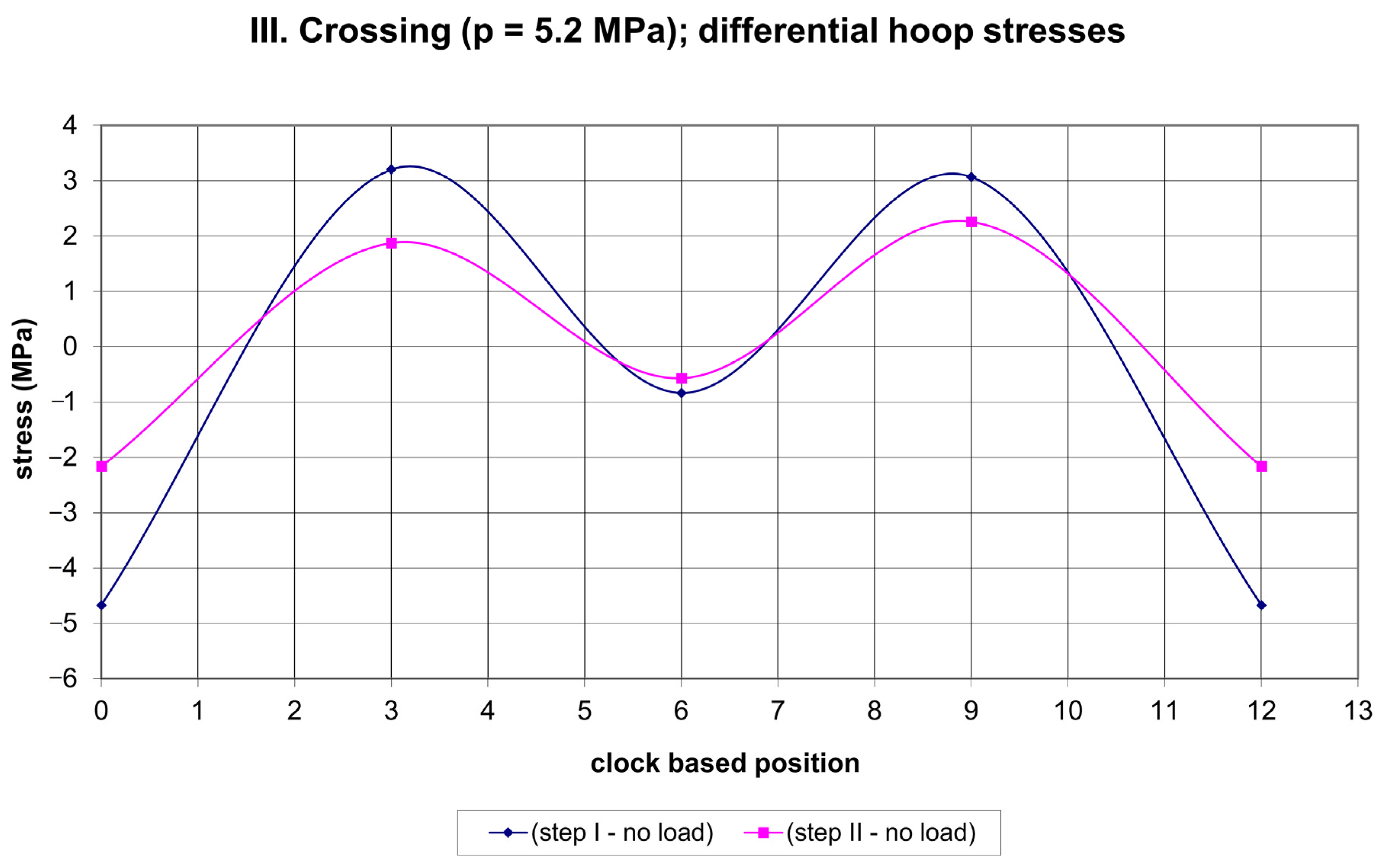
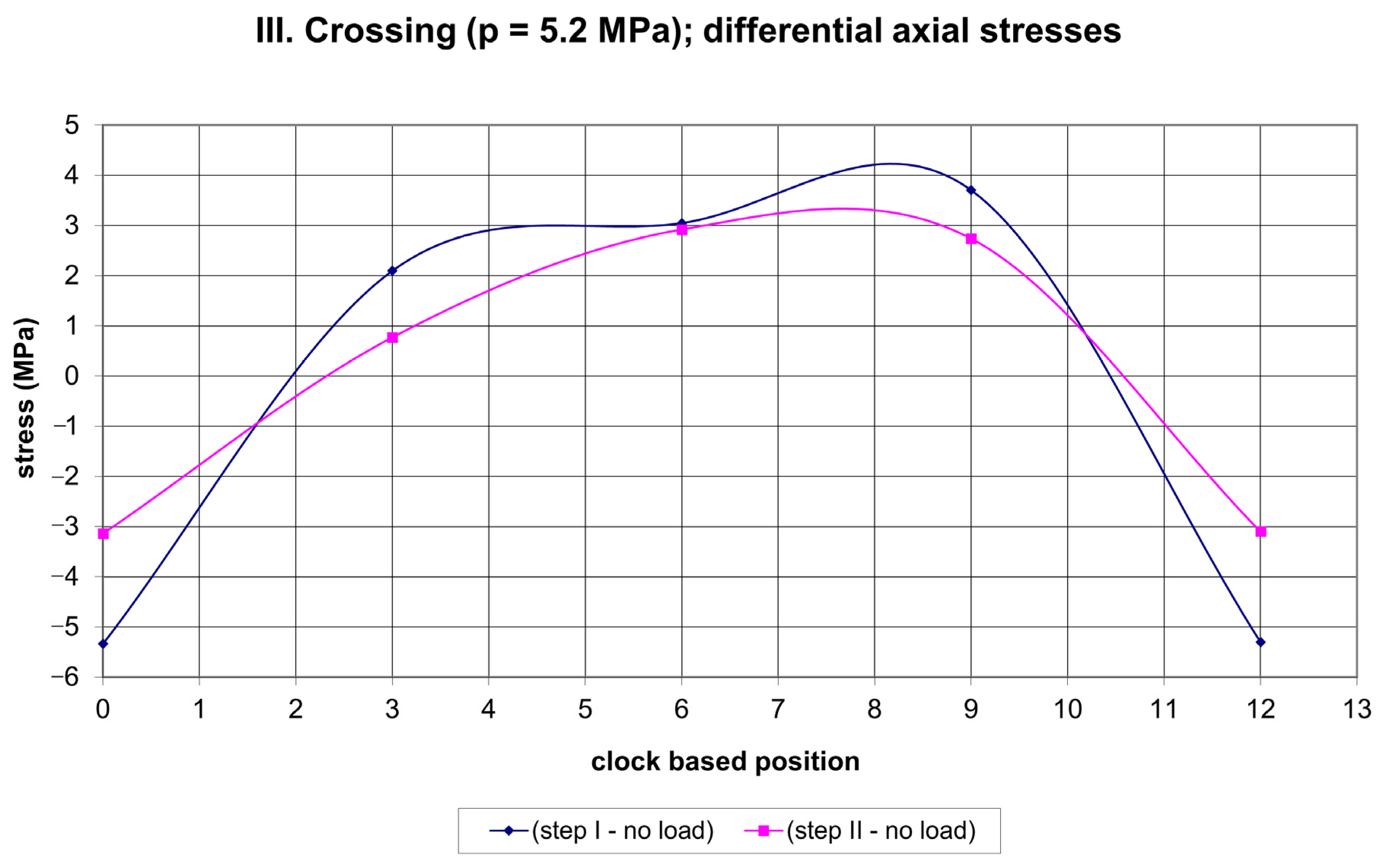
| Loading | Range of Differential Stresses | |
|---|---|---|
| Hoop Stress (MPa) | Axial Stress (MPa) | |
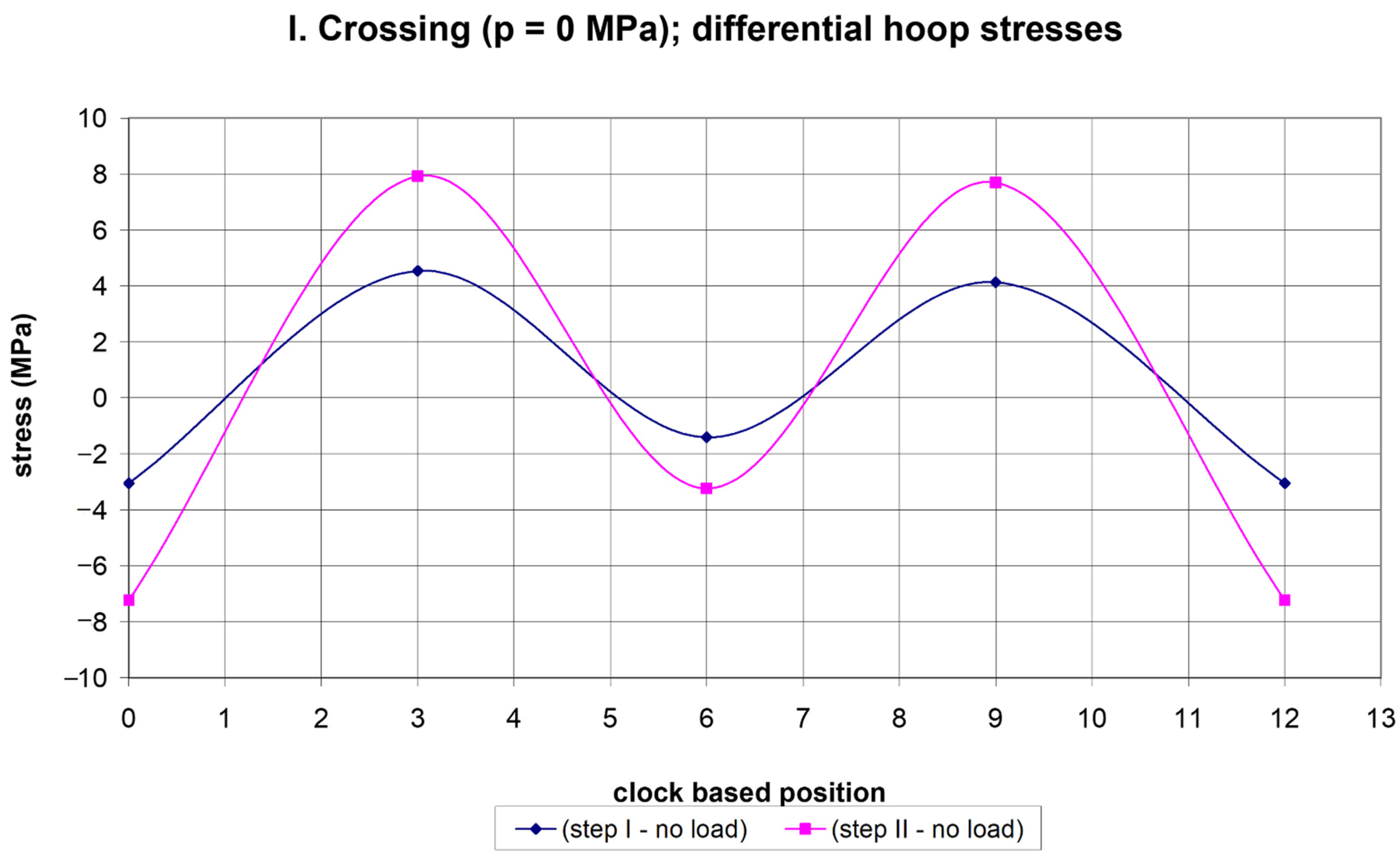
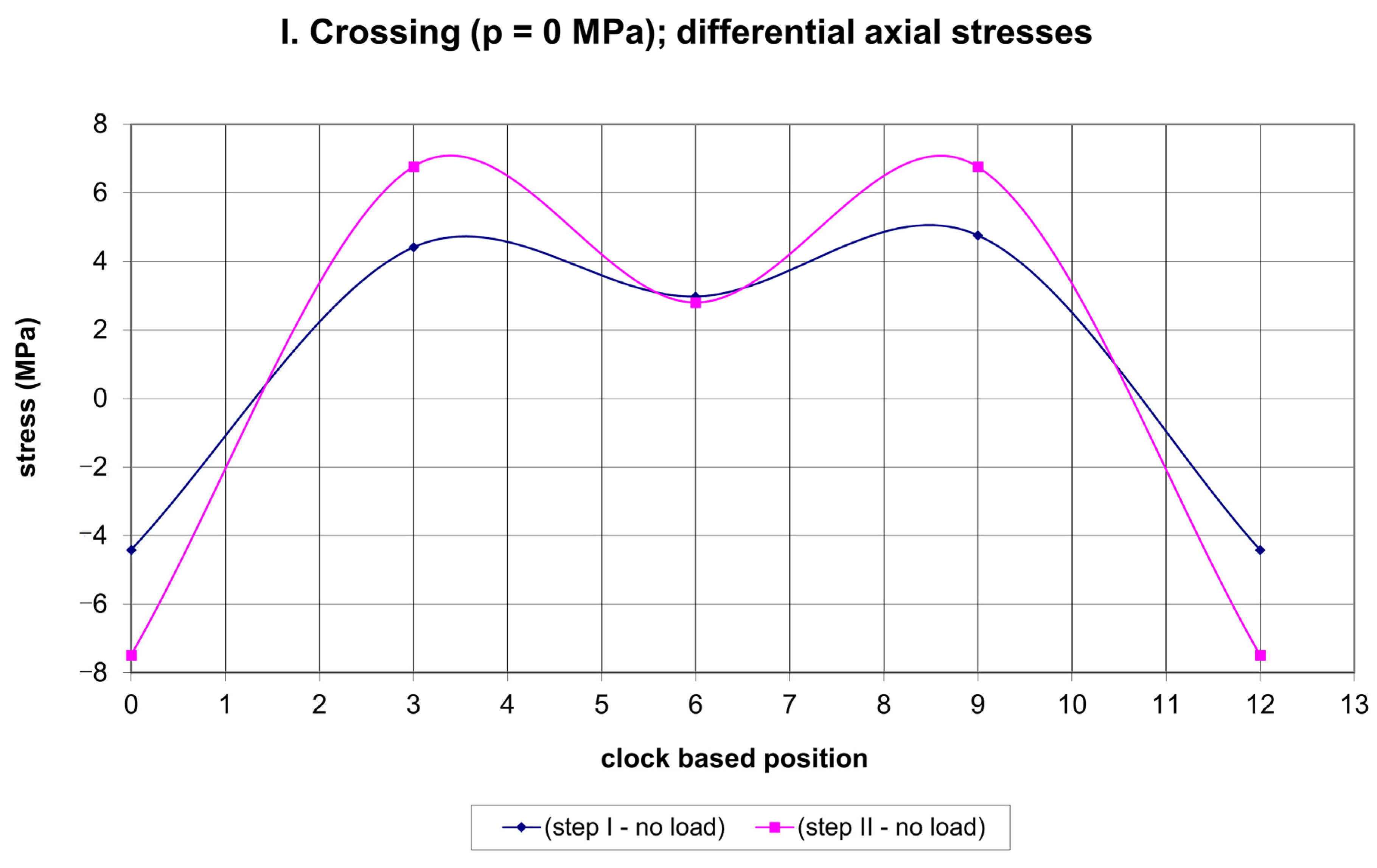
| crossing I (p = 0 MPa) | (−7; 8) | (−7.5; 7) |
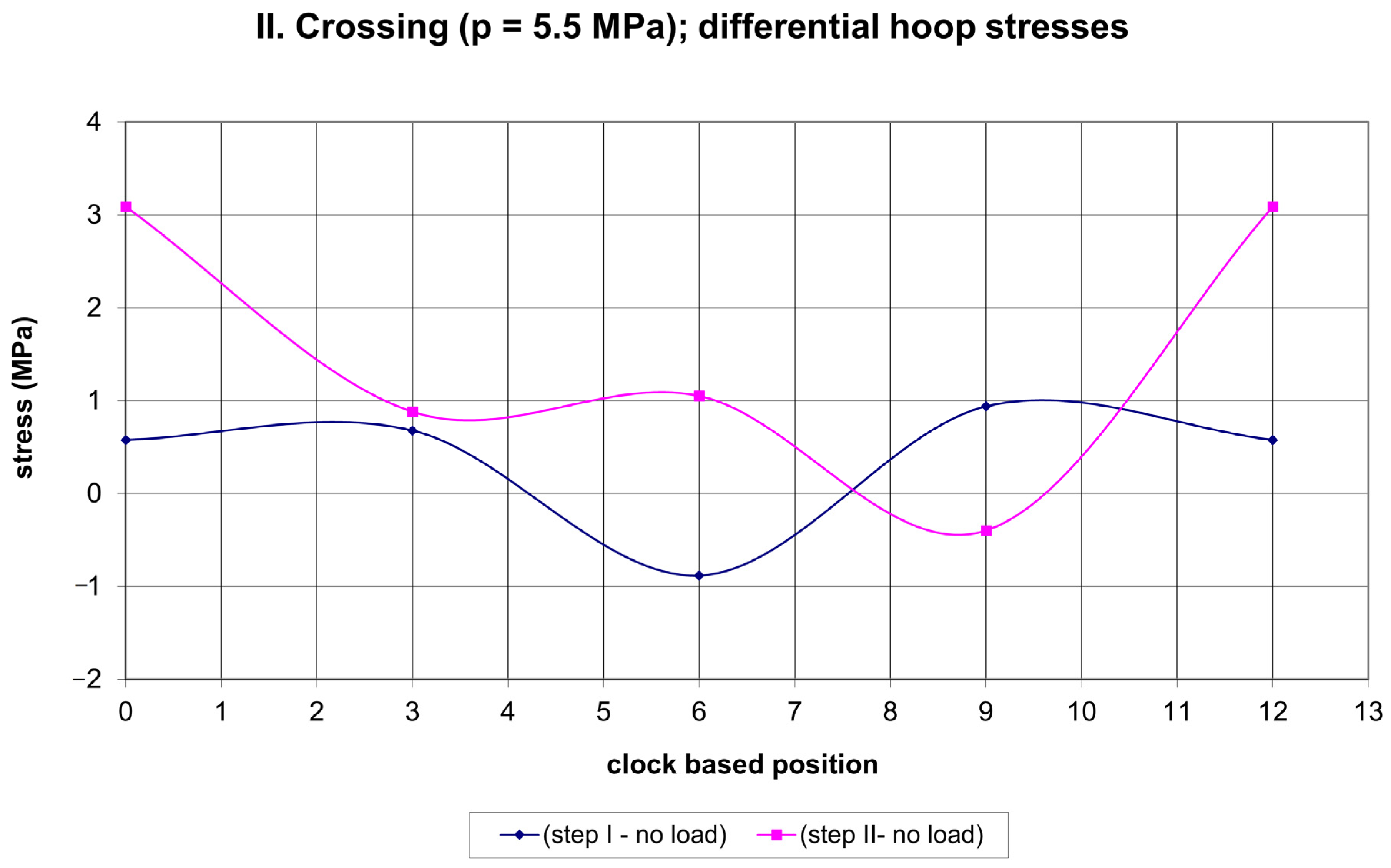
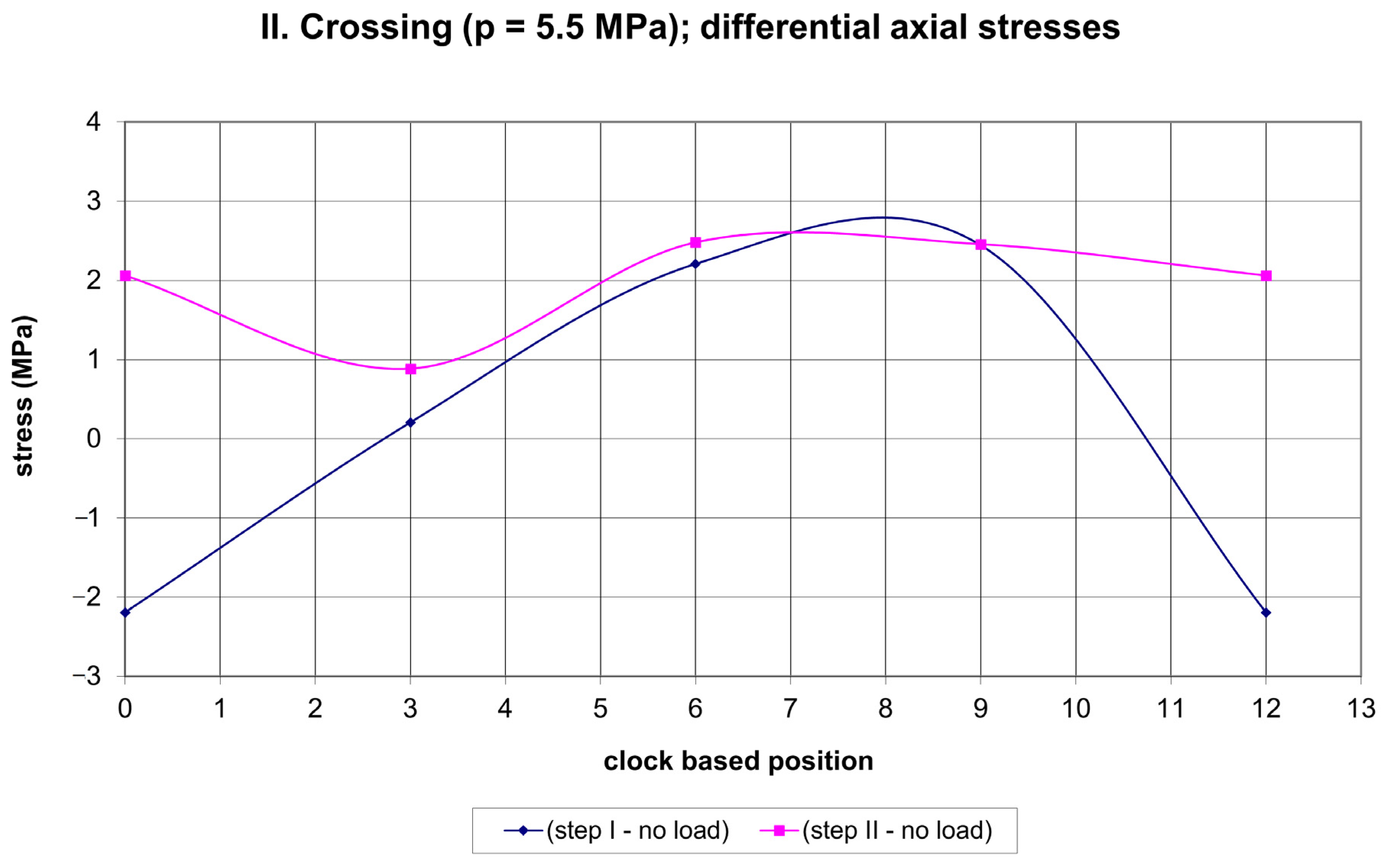
| crossing II (p = 5.5 MPa) | (−1; 3) | (−2; 2) |
| crossing III (p = 5.2 MPa) | (−4.5; 3) | (−5.5; 3.5) |
| Layer | Mass Density (kg/m3) | Height (m) |
|---|---|---|
| backfill soil | 1730 | 0.6 |
| agregate | 1900 | 0.5 |
| compacted earth | 2000 | 0.2 |
| sand | 1900 | 0.2 |
| Loading | Hoop Stresses σφ (MPa) Determined by | |
|---|---|---|
| Soil Mechanics | Strain Gauge Measurement | |
| backfill | −33.5 | −34.4 |
| step I | −9.4 | −3.1 |
| step II | −9.1 | −7.2 |
| p = 5.5 MPa | 221.7 * | 222.4 |
| p = 5.2 MPa | 209.7 * | 209.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gajdoš, Ľ.; Šperl, M.; Kec, J.; Crha, P. The Effect of Heavy-Duty Vehicle Crossings on the State of Stress of Buried Pipelines. Metals 2022, 12, 153. https://doi.org/10.3390/met12010153
Gajdoš Ľ, Šperl M, Kec J, Crha P. The Effect of Heavy-Duty Vehicle Crossings on the State of Stress of Buried Pipelines. Metals. 2022; 12(1):153. https://doi.org/10.3390/met12010153
Chicago/Turabian StyleGajdoš, Ľubomír, Martin Šperl, Jan Kec, and Petr Crha. 2022. "The Effect of Heavy-Duty Vehicle Crossings on the State of Stress of Buried Pipelines" Metals 12, no. 1: 153. https://doi.org/10.3390/met12010153
APA StyleGajdoš, Ľ., Šperl, M., Kec, J., & Crha, P. (2022). The Effect of Heavy-Duty Vehicle Crossings on the State of Stress of Buried Pipelines. Metals, 12(1), 153. https://doi.org/10.3390/met12010153







