Applying Membrane Mode Enhanced Cohesive Zone Elements on Tailored Forming Components

Abstract

Forming of hybrid bulk metal components might include severe membrane mode deformation of the joining zone. This effect is not reflected by common Traction Separation Laws used within Cohesive Zone Elements that are usually applied for the simulation of joining zones. Thus, they cannot capture possible damage of the joining zone under these conditions. Membrane Mode Enhanced Cohesive Zone Elements fix this deficiency. This novel approach can be implemented in finite elements. It can be used within commercial codes where an implementation as a material model is beneficial as this simplifies model preparation with the existing GUIs. In this contribution, the implementation of Membrane Mode Enhanced Cohesive Zone Elements as a material model is presented within MSC Marc along with simulations showing the capabilities of this approach.

1. Introduction

The requirements for technical products are rising. Fulfilling these becomes more and more difficult using mono material components. A hybrid component combines different materials and can be tailored to meet specific requirements that might not be possible with a single material. The joining process to produce hybrid components from two or more mono material parts is usually at the end of the production chain. If a forming process is included, joining is either during or after the forming process. Doing the joining process before forming allows to treat the joining zone during forming geometrically and thermomechanically. This provides more flexibility to tailor the hybrid component regarding its requirements; this process is called Tailored Forming (Figure 1).

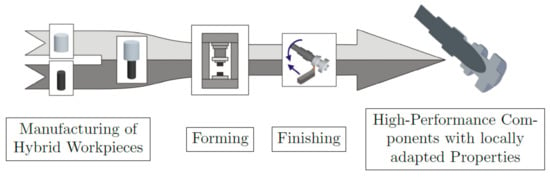
Figure 1. Tailored forming process chain [1].

The joining zone is intended to be firmly bonded. In the case of aluminium and steel, intermetallic compounds often arise. Their existence shows that a firm bond is obtained during joining. Subsequent heat treatments cause thickening of intermetallic compounds to about 2 μm [2]. Though practical investigations indicate advantages of joining zones without or with a non-measurable intermetallic compound thickness during forming [3].

Thin layers are often modelled using cohesive zone elements. Standard formulations use traction separation laws for the constitutive relation which are not sufficient here. Forming of hybrid bulk metal components might include severe membrane deformations that are additional deformation modes not describable by separations. Internal Thickness Extrapolation (InTEx) [4] and Membrane Mode Enhanced Cohesive Zone Elements (MMECZE) [5] are two novel approaches that consider additional loading directions. Internal Thickness Extrapolation aims on layers that are thin but not completely flat, reconstructs a volumetric geometry from a flat element topology and applies bulk material models. Membrane Mode Enhanced Cohesive Zone Elements are focused on flat joining zones and combine Traction Separation Laws for the separation loading directions with a bulk material capturing the damage contribution from membrane mode deformation of the joining zone. Here, the latter approach is more convenient due to the flatness of the joining zone.

2. Membrane Mode Enhanced Cohesive Zone Elements

Membrane Mode Enhanced Cohesive Zone Elements are extensively described in [5]. Here, key points are summarised that are necessary for the implementation and application.

The Continuum Damage Mechanics framework from Lemaitre [6] is a concept that can describe damage in various bulk material models. Damage ($0\le D\le 1$) reduces the effective surface area for load transmission. Stress is distributed on a smaller portion of the material; the elastic and the plastic response are affected. For Membrane Mode Enhanced Cohesive Zone Elements the framework is applied at an interface. Instead of tensorial stresses, traction vectors transmit the load through the material. Figure 2 shows the joining zone with partial defects ($\partial S_D$) that reduce the surface area for load transmission ($t$). The effective traction due to a reduction of the load transmitting surface area is

$$\tilde{t}=\frac{t}{1-D}$$

(1)

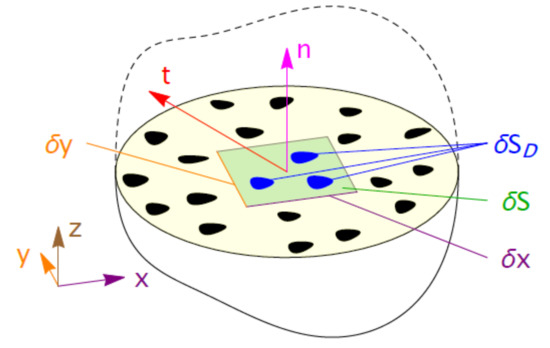
Figure 2. Damage of an interface [5].

The change of damage is related to the rate $\dot{D}$ which depends on the combination of the plastic multiplier $\dot{\lambda }$ describing the amount of deformation and the strain energy density release rate $Y$. The latter is the amount of elastic energy stored in the material that is released due to damage softening

$$\dot{D}=\dot{\lambda } \frac{1}{1-D} {\left(\frac{Y}{S}\right)}^s$$

(2)

$$\mathrm{with} Y=\frac{1}{2} \frac{1}{{\left(1-D\right)}^2} \left(\frac{t_t^2}{E}+\frac{t_s^2}{G}\right)$$

(3)

where s and S are damage related material parameters, $t_t$ and $t_s$ are the tension and shearing part of the traction, and $E$ and $G$ are the Young’s and shearing modulus.

Traction Separation Laws (TSLs) are defined on the cohesive surface (black dashed in Figure 3) that describes the midplane of the initially coincident faces of the upper and lower component

$$x_{cs}=\frac{x_u+x_l}{2}$$

(4)

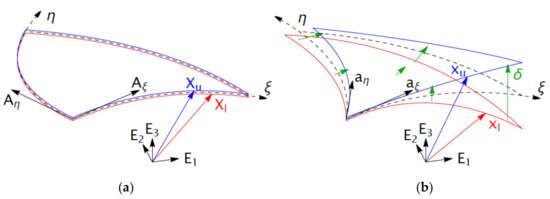
Figure 3. Separation of a joining zone; initial configuration (a) and current configuration (b) [5].

TSLs describe the traction over separation relation. They are often curves with a nonlinear load increase that levels off smoothly for a rising displacement until failure. This might be realistic for the application of modelling adhesives. Within Tailored Forming brittle failure of an infinitesimal thin joining zone has to be described. The theoretically infinitesimal stiffness with sharp load release after failure is modelled using a large but finite artificial stiffness k to circumvent numerical problems

$$t=k \delta$$

(5)

where $t$ is the traction resulting from the separation $\delta$ (see green vectors in Figure 3). This traction separation relation induces a reaction force in the direction contrary to the separation.

The membrane mode deformation can be modelled, see Figure 3, as angular and length changes of the vectors $A_{\xi }$ and $A_{\eta }$ in the initial configuration to $a_{\xi }$ and $a_{\eta }$ in the current configuration. Describing these vectors in a two-dimensional local coordinate system that follows the cohesive surface (two dimensional quantities with ˆ in the following) allows to compute a two-dimensional deformation gradient

$$\begin{array}{c}F=\frac{\partial \widehat{x}}{\partial \widehat{X}}=\frac{\partial \widehat{x}}{\partial \widehat{\xi }}\cdot \frac{\partial \widehat{\xi }}{\partial \widehat{X}}\\ \mathrm{with} \frac{\partial \widehat{x}}{\partial \widehat{\xi }}=\left(\begin{array}{cc}{\widehat{A}}_{\xi }& {\widehat{A}}_{\eta }\end{array}\right) \mathrm{and}\frac{\partial \widehat{\xi }}{\partial \widehat{X}}={\left(\begin{array}{cc}{\widehat{a}}_{\xi }& {\widehat{a}}_{\eta }\end{array}\right)}^{-1}\end{array}$$

(6)

Based on the deformation gradient a variety of material models can be applied; here the Lemaitre model is used. The plastic multiplier as amount of (plastic) deformation can be computed (right in Figure 4). Together with tractions from the traction separation relation (left) a damage rate ($\dot{D}$) results. Accumulation of the damage $D$ (or certainly high tractions $t_n$ and $t_s$) might then cause interruption of the cohesion.

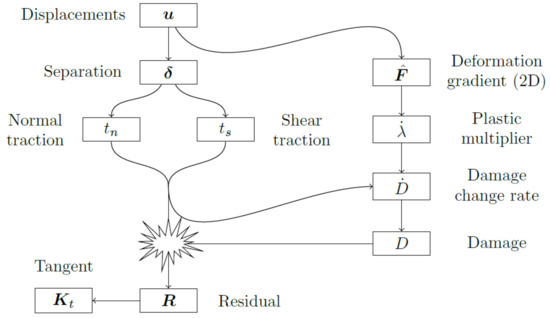
Figure 4. Merging cohesive zone modes and membrane modes [5].

The Membrane Mode Enhanced Cohesive Zone Element concept does not necessitate this, but failure is updated explicitly here. This means the load transmission is cut off in the time step after failure occurred. Such procedure is numerically very advantageous as failure induced instabilities are inhibited and the nonlinearity of the computation is limited to the nonlinearity of the forming process itself.

3. Cohesive Modelling in MSC Marc

Marc is a nonlinear finite element solver from MSC Software (MSC Marc Mentat 2019 Feature Pack 1, Newport Beach, CA, US). The pre- and postprocessor Mentat, also from MSC Software, allows to setup simulations for Marc. Linear and quadratic Cohesive Zone Elements are provided by the software package [7]. Figure 5 shows the connectivity (a) and Gauss integration points (b) of element 188. The connectivity corresponds to a brick element, though the thickness in one direction is (initially) zero so the geometry complies with a quadrilateral element. As integration is only executed in the cohesive surface (dashed midplane, Figure 5a), a Gauss integration scheme contains only $2\times 2=4$ points like a quadrilateral element. Wedge or triangle like element types and Newton Cotes integration schemes are also available. The degrees of freedom are displacements in three directions. In case of a thermomechanical analysis a weak coupling is realized with a staggered approach, i.e., a separate thermal element is used additionally to the mechanical element (e.g., the thermal element 222 corresponds to the mechanical element 188).

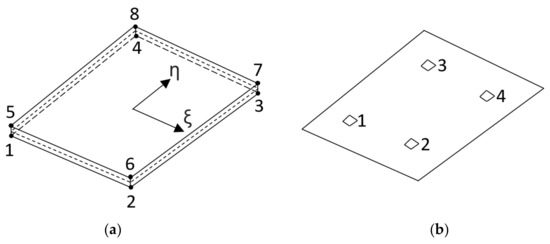
Figure 5. MSC Marc element 188: connectivity (a) and Gauss integration points (b) [7].

Modelling of cohesive zones is realised as a subsequent step of solid modelling. Existing nodes are doubled and the Cohesive Zone Element is placed. Cohesive elements can either immediately be inserted (Toolbox/General/Matching Boundaries) or when a certain load criterion is reached (Toolbox/Fracture mechanics/Delamination). Here, the direct insertion is beneficial to track membrane changes even if the load remains small. The inserted cohesive elements can use user subroutines to define the material behaviour.

Figure 6 shows the analysis path from pre- to postprocessing; element and material subroutines are drawn as sub steps of processing to discuss the implementation that interacts here. During processing, coordinates and displacements are handed over to the element subroutine. In the case of cohesive elements, separations are computed and the material subroutine is called. The material subroutine returns a tangent and stress. This is processed in the element subroutine to an element stiffness matrix and a residual.

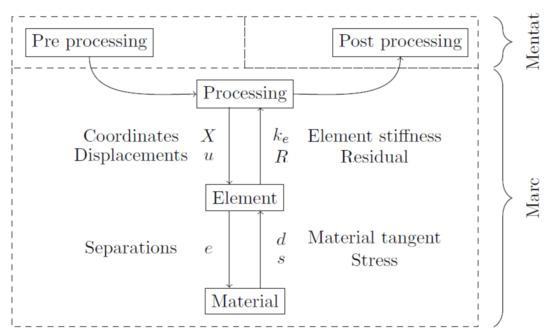
Figure 6. Processing.

4. Membrane Mode Enhanced Cohesive Zone Element Technology as a Material Subroutine

A cohesive formulation based on separations does not need to know more about the deformation than the separations. Though Membrane Mode Enhanced Cohesive Zone Elements need information about the membrane deformation. Therefore, in [5] they are implemented as a user element. To comfortably use this new technology within MSC Marc, it has to be implemented as a material model. The missing information has to be gathered and the differing output has to be discussed as well.

4.1. Gathering Information about the Membrane Deformation

For the sake of simplicity, Figure 6 only shows the separation as most important information that is transferred from the element to the material. Some further data are the external element number m(1) and the integration point number nn. However, the required information about the membrane deformation is not transferred. Though Marc provides some functions that help to gather the required information about the membrane deformation [8]. The (internal) element nodes nodes and the number of nodes num can be determined using

call elnodes(ielint(m(1)),num,nodes)

where ielint(m(1)) converts the external to an internal element number. The number of nodes is used to identify the current element type. The internal node numbers have to be converted to external node numbers

nodeid = nodext(nodes(i))

as these can be used to obtain nodal values with

call nodvar(icod,nodeid,valno,nqncomp,nqdatatype)

where, e.g., icod=0 gives coordinates and icod=1 displacements.

The requested data is returned in valno; nqncomp and nqdatatype are the size and type of the returned data. With these the initial and current cohesive surface geometry can be constructed; e.g. the corner points for a linear quad like element in initial configuration are

xs(:,1) = (xl(:,1) + xl(:,5))/2

xs(:,2) = (xl(:,2) + xl(:,6))/2

xs(:,3) = (xl(:,3) + xl(:,7))/2

xs(:,4) = (xl(:,4) + xl(:,8))/2,

where xl are the node coordinates. For the current configuration the displacements have to be added. All this happens within a material subroutine that is called in one certain integration point. The location of integration point number nn for a linear quad with Gauss integration is

select case (nn)

 case (1)

  xi = − 1.d0/dsqrt(3.d0)

  eta = − 1.d0/dsqrt(3.d0)

 case (2)

  xi = + 1.d0/dsqrt(3.d0)

  eta = − 1.d0/dsqrt(3.d0)

 case (3)

  xi = − 1.d0/dsqrt(3.d0)

  eta = + 1.d0/dsqrt(3.d0)

 case (4)

  xi = + 1.d0/dsqrt(3.d0)

  eta = + 1.d0/dsqrt(3.d0)

end select .

With standard bilinear ansatz functions and derivatives

N(1) = 0.25d0 * ( 1.d0 − xi) * ( 1.d0 − eta)

N(2) = 0.25d0 * ( 1.d0 + xi) * ( 1.d0 − eta)

N(3) = 0.25d0 * ( 1.d0 + xi) * ( 1.d0 + eta)

N(4) = 0.25d0 * ( 1.d0 − xi) * ( 1.d0 + eta)

Nxi(1) = 0.25d0 *        (−1.d0 + eta)

Nxi(2) = 0.25d0 *        ( 1.d0 − eta)

Nxi(3) = 0.25d0 *        ( 1.d0 + eta)

Nxi(4) = 0.25d0 *        (−1.d0 − eta)

Neta(1) = 0.25d0 * (−1.d0 + xi)

Neta(2) = 0.25d0 * (−1.d0 − xi)

Neta(3) = 0.25d0 * ( 1.d0 + xi)

Neta(4) = 0.25d0 * ( 1.d0 − xi)

the 3D tangential vectors in initial and current configuration can be determined. E.g. for the quadrilateral like element with the number of cohesive surface points num2 the tangential vectors in the initial configuration are

axi3Di = (/ 0.d0, 0.d0, 0.d0 /)

aet3Di = (/ 0.d0, 0.d0, 0.d0 /)

do i = 1, num2

 axi3Di(1) = axi3Di(1) + xs(1,i) * Nxi(i)

 axi3Di(2) = axi3Di(2) + xs(2,i) * Nxi(i)

 axi3Di(3) = axi3Di(3) + xs(3,i) * Nxi(i)

 aeta3Di(1) = aeta3Di(1) + xs(1,i) * Neta(i)

 aeta3Di(2) = aeta3Di(2) + xs(2,i) * Neta(i)

 aeta3Di(3) = aeta3Di(3) + xs(3,i) * Neta(i)

end do

and accordingly, in the current configuration. With the procedure in [5] the 2D tangential vectors and finally the 2D deformation gradient can be computed that describes the membrane deformation.

4.2. Returning Stress and Material Tangent

The stress returned from a standard Traction Separation Law as a material routine for interfaces contains three components: normal direction ($N$) and two shearing directions ($S1$ and $S2$)

$$s=\left(\begin{array}{c}{s}_N\\ s_{S1}\\ s_{S2}\end{array}\right)$$

(7)

The corresponding tangent considers the changes with respect to normal and (two) shearing separations

$$d=\left(\begin{array}{ccc}\partial s_N/\partial {\delta }_N& \partial s_N/\partial {\delta }_{S1}& \partial s_N/\partial {\delta }_{S2}\\ \partial s_{S1}/\partial {\delta }_N& \partial s_{S1}/\partial {\delta }_{S1}& \partial s_{S1}/\partial {\delta }_{S2}\\ \partial s_{S2}/\partial {\delta }_N& \partial s_{S2}/\partial {\delta }_{S1}& \partial s_{S2}/\partial {\delta }_{S2}\end{array}\right)$$

(8)

Taking all directions into account, two in plane stretching (IP1 and IP2) directions and the out of plane shearing direction (OPS) have to be added

$$s=\left(\begin{array}{c}{s}_N\\ s_{S1}\\ s_{S2}\\ s_{IP1}\\ s_{IP2}\\ s_{OPS}\end{array}\right)$$

(9)

$$\mathit{d}=\left(\begin{array}{cccccc}\partial s_N/\partial {\delta }_N& \partial s_N/\partial {\delta }_{S1}& \partial s_N/\partial {\delta }_{S2}& \partial s_N/\partial {\delta }_{IP1}& \partial s_N/\partial {\delta }_{IP2}& \partial s_N/\partial {\delta }_{OPS}\\ \partial s_{S1}/\partial {\delta }_N& \partial s_{S1}/\partial {\delta }_{S1}& \partial s_{S1}/\partial {\delta }_{S2}& \partial s_{S1}/\partial {\delta }_{IP1}& \partial s_{S1}/\partial {\delta }_{IP2}& \partial s_{S1}/\partial {\delta }_{OPS}\\ \partial s_{S2}/\partial {\delta }_N& \partial s_{S2}/\partial {\delta }_{S1}& \partial s_{S2}/\partial {\delta }_{S2}& \partial s_{S2}/\partial {\delta }_{IP1}& \partial s_{S2}/\partial {\delta }_{IP2}& \partial s_{S2}/\partial {\delta }_{OPS}\\ \partial s_{IP1}/\partial {\delta }_N& \partial s_{IP1}/\partial {\delta }_{S1}& \partial s_{IP1}/\partial {\delta }_{S2}& \partial s_{IP1}/\partial {\delta }_{IP1}& \partial s_{IP1}/\partial {\delta }_{IP2}& \partial s_{IP1}/\partial {\delta }_{OPS}\\ \partial s_{IP2}/\partial {\delta }_N& \partial s_{IP2}/\partial {\delta }_{S1}& \partial s_{IP2}/\partial {\delta }_{S2}& \partial s_{IP2}/\partial {\delta }_{IP1}& \partial s_{IP2}/\partial {\delta }_{IP2}& \partial s_{IP2}/\partial {\delta }_{OPS}\\ \partial s_{OPS}/\partial {\delta }_N& \partial s_{OPS}/\partial {\delta }_{S1}& \partial s_{OPS}/\partial {\delta }_{S2}& \partial s_{OPS}/\partial {\delta }_{IP1}& \partial s_{OPS}/\partial {\delta }_{IP2}& \partial s_{OPS}/\partial {\delta }_{OPS}\end{array}\right)$$

(10)

The resistance of a zero thickness surface regarding in plane stretching and out of plane shearing is assumed to be zero. This can be justified considering a very thin layer where the reaction force depends on the integral over the thickness. Without thickness, the reaction force becomes zero. Hence in-plane stretching and out-of-plane shearing are assumed not to contribute to the residual and thus Membrane Mode Enhanced Cohesive Zone Elements build their element residual solely based on the separation modes. The other directions are still considered for damage calculations but can be omitted in the stress and consequently also in the tangent

$$s=\left(\begin{array}{c}{s}_N\\ s_{S1}\\ s_{S2}\\ 0\\ 0\\ 0\end{array}\right)$$

(11)

$$\mathit{d}=\left(\begin{array}{cccccc}\partial s_N/\partial {\delta }_N& \partial s_N/\partial {\delta }_{S1}& \partial s_N/\partial {\delta }_{S2}& \partial s_N/\partial {\delta }_{IP1}& \partial s_N/\partial {\delta }_{IP2}& \partial s_N/\partial {\delta }_{OPS}\\ \partial s_{S1}/\partial {\delta }_N& \partial s_{S1}/\partial {\delta }_{S1}& \partial s_{S1}/\partial {\delta }_{S2}& \partial s_{S1}/\partial {\delta }_{IP1}& \partial s_{S1}/\partial {\delta }_{IP2}& \partial s_{S1}/\partial {\delta }_{OPS}\\ \partial s_{S2}/\partial {\delta }_N& \partial s_{S2}/\partial {\delta }_{S1}& \partial s_{S2}/\partial {\delta }_{S2}& \partial s_{S2}/\partial {\delta }_{IP1}& \partial s_{S2}/\partial {\delta }_{IP2}& \partial s_{S2}/\partial {\delta }_{OPS}\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right)$$

(12)

At this point, it can be noticed that all necessary stress components for Membrane Mode Enhanced Cohesive Zone Elements can be returned and processed in the standard Cohesive Zone Element manner. Though the influence of in plane modes in the tangent cannot be captured in this way what might have an influence on the convergence. In [5], failure is updated explicitly. For this reason, the influence of membrane mode deformations during one load step cancels out

$$d=\left(\begin{array}{cccccc}\partial s_N/\partial {\delta }_N& \partial s_N/\partial {\delta }_{S1}& \partial s_N/\partial {\delta }_{S2}& 0& 0& 0\\ \partial s_{S1}/\partial {\delta }_N& \partial s_{S1}/\partial {\delta }_{S1}& \partial s_{S1}/\partial {\delta }_{S2}& 0& 0& 0\\ \partial s_{S2}/\partial {\delta }_N& \partial s_{S2}/\partial {\delta }_{S1}& \partial s_{S2}/\partial {\delta }_{S2}& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0\end{array}\right)$$

(13)

and the tangent can also be processed in the standard Cohesive Zone Element manner.

4.3. Thermal and Mechanical Parameters

In [5], several simulations are carried out to fit parameters for the material model. The maximum allowable tensile and shear traction are determined to be $t_{t,max}=365 \mathrm{MPa}$ and $t_{s,max}=300 \mathrm{MPa}$. The Lemaitre damage parameters are $s=1.0$ and $S=0.34$.

The thermal conductivity of the joining zone considered as bulk material within an InTEx element is investigated in [9]. For undamaged ($D=0$) or fully damaged ($D=1$) material, the conductivity is

$$\kappa \left(D=0\right)=68 \frac{\mathrm{W}}{\mathrm{mK}} , \kappa \left(D=1\right)=0.01 \frac{\mathrm{W}}{\mathrm{mK}} .$$

(14)

This can be converted to a heat transfer coefficient $h$

$$h\left(D=0\right)=6800000\frac{\mathrm{W}}{{\mathrm{m}}^2\mathrm{K}} , h\left(D=1\right)=1000 \frac{\mathrm{W}}{{\mathrm{m}}^2\mathrm{K}} ,$$

(15)

with the corresponding bulk material thickness of $t=10 \mu m$. It is assumed that $h$ linearly depends on $D$

$$h\left(D\right)=\left(6800000\left(1-D\right)+1000 D\right)\frac{\mathrm{W}}{{\mathrm{m}}^2\mathrm{K}} .$$

(16)

5. Simulation of a Transverse Link

The transverse link is an advanced demonstrator component for Tailored Forming. All processes and also the final geometry are currently under development. The raw hybrid part is produced by extrusion; a forging process and afterwards machining is used to generate the final geometry. According to the current state, the raw part is an L formed steel profile (32 mm × 32 mm, width = 7 mm) that is filled with aluminium (Figure 7a). The final geometry is flattened, contains an indentation in the middle and has three holes for mounting (Figure 7b).

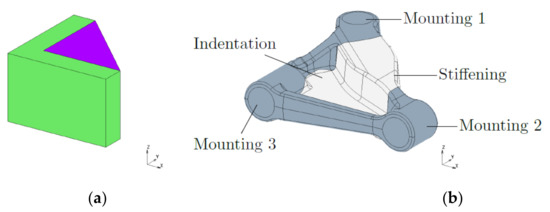
Figure 7. Transverse link; raw (a) and final geometry (b).

The forging process is simulated here to test Membrane Mode Enhanced Cohesive Zone Elements in a new load case especially with the implementation in MSC Marc. The simulations might also give an idea of the impact of forming on this specific part, though the validity is limited as no material data for this certain joining zone is available; the parameters in Section 4.3 stem from a different process. For the bulk materials temperatures of ${\Theta }_{st}=750 °\mathrm{C}$ and ${\Theta }_{al}=480 °\mathrm{C}$ and yield stresses of ${\sigma }_{y,st}=270 \mathrm{MPa}$ and ${\sigma }_{y,al}=40 \mathrm{MPa}$ [10] are assumed.

The component has a symmetry in thickness direction that is utilised during the simulations. In a first step, the forming tool is modelled by subtracting the final geometry (except for the holes) from a solid block. To prevent burr formation, the tool is extended in forming direction, see Figure 8; practically this can be realised in a closed die process. Simulations show that the indentation in the middle induces a severe loading of the joining zone; the slope at the edge of the indentation is large and coincides with the joining zone. This causes failure of the joining zone in a very early stage. Figure 9a shows a damage contour plot of the slightly formed component. Nodal averaging is activated to visualise the damage also in the bulk elements around. Even if damage ranges from 0 to 1, here 0.5 is used as upper limit as interface elements contribute a damage and bulk elements do not. In the case of a tetraeder mesh, or also if the corner here would be damaged from both sides, the averaging result can only be utilised to indicate that damage occurs. The extent is influenced as the share of damage contributing elements varies. Figure 9b only contains the interface elements, nodal averaging is deactivated and the damage can be seen directly on the interface elements using a scale from 0 to 1.

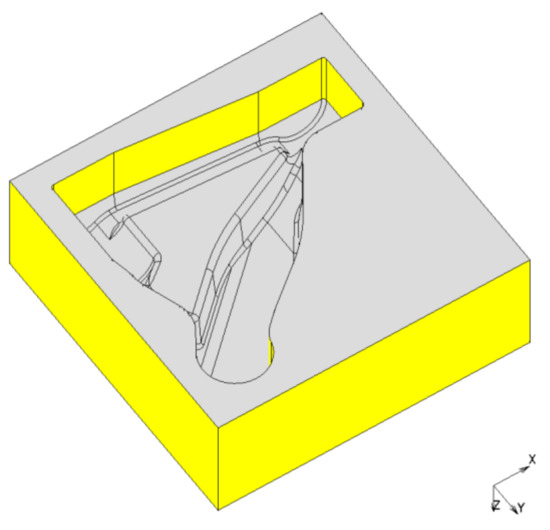
Figure 8. Forming tool.

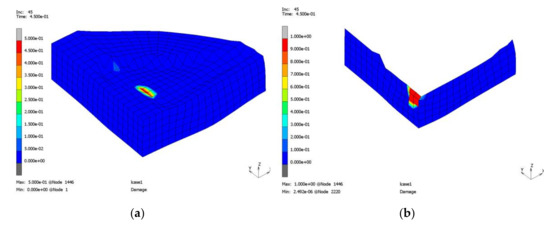
Figure 9. Forming process using the original geometry; whole geometry (a) and joining zone (b): joining zone damage.

Next, the simplified geometry in Figure 10 is used that does not contain the indentation in the middle. The results strongly depend on the starting position of the specimen in the form. In the case depicted in Figure 11a, a crack arises after the aluminium gets in contact with the radius of the form. With a slightly different position (1 mm shift in x and y direction), three positions get cracks, though later (Figure 11b). The inner corner is strongly shear loaded. On the backside (Figure 12) two shear induced cracks arise that are both close to the stiffening between mounting 1 and 2 (Figure 7b). The strong dependency on the position of the specimen in the form necessitates a holder or special geometry of the form that allows reliable and repeatable positioning. To further reduce loading, the form is again simplified by dropping the stiffening.

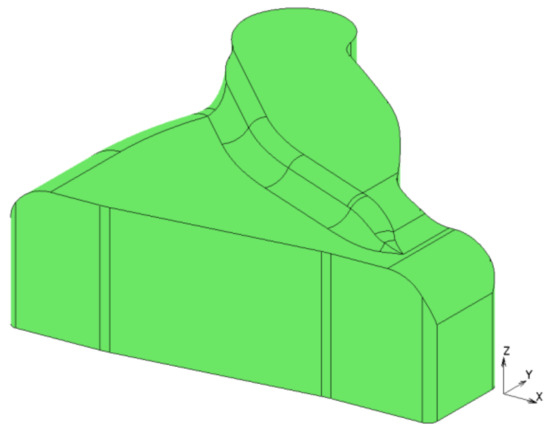
Figure 10. Simplified geometry.

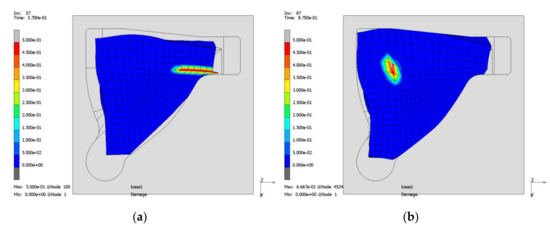
Figure 11. Forming process using a simplified geometry with two different initial positions (a) and (b) of the specimen in the form: joining zone damage.

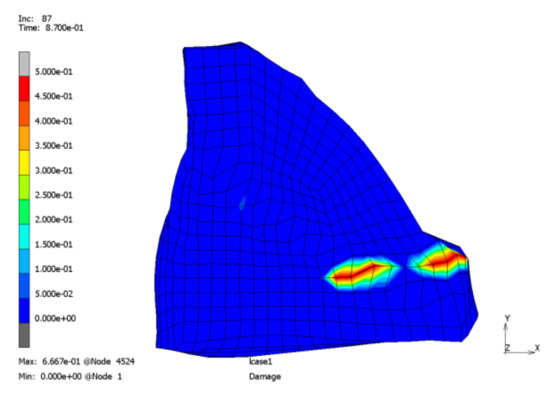
Figure 12. Forming process using a simplified geometry (backside of Figure 11b): joining zone damage.

The process can now be executed further. Though filling the edge around mounting 1 (Figure 7b) causes severe difficulties. The stronger steel and a thin portion of the weaker aluminium enter the groove and come into contact on both sides (Figure 13a). Further forming induces compression, the aluminium starts yielding normal to the compression direction and decohesion is caused by shearing (Figure 13b). The decohesion induces a reduced heat flow that results in a temperature jump, see Figure 14. Using an adapted temperature range (Figure 14b) the effect can be noticed better compared to the plot with the whole temperature range (Figure 14a).

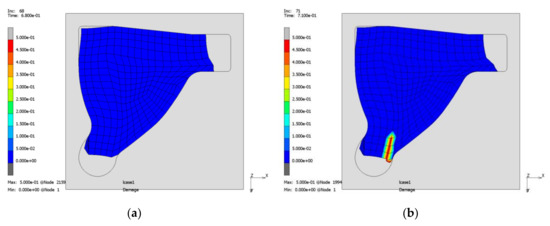
Figure 13. Forming process using a further simplified geometry; before (a) and after failure initiation (b): Joining zone damage.

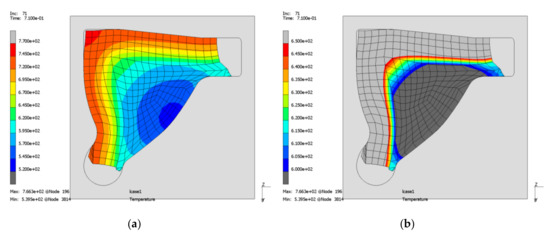
Figure 14. Forming process using a further simplified geometry; whole (a) and adapted temperature range (b): temperature distribution.

Using a tetraeder mesh (tetraeder for the bulk, triangle or wedge like elements for the interface) instead of a hexaeder mesh (hexaeder for the bulk, quadrilaterial or hexaeder like elements for the interface) leads to very similar results. Figure 15 shows the same increment as Figure 13b and the specimen exhibits failure in the same position.

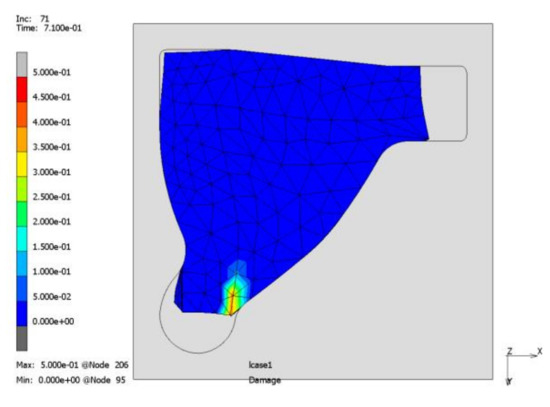
Figure 15. Forming process using tetraeder elements: joining zone damage.

6. Indentation Test

There are several standard tests for Cohesive Zone Elements, e.g. the double cantilever beam test or the end notch flexure test. However, they focus on shear or normal separation induced delamination. Therefore, an indentation test is used here that is influenced by membrane modes as well. A sandwich of 20 mm × 4 mm steel (upper part) and 20 mm × 4 mm aluminium (lower part) is compressed by a cylinder with a radius of 6 mm. The simulation is carried out in 3D but boundary conditions are applied to enforce plane strain conditions. Furthermore, symmetry conditions are utilised. The parameters for the joining zone are adopted from Section 4.3, for the bulk materials room temperature is assumed and accordingly yield stresses of ${\sigma }_{y,st}=600 \mathrm{MPa}$ and ${\sigma }_{y,al}=400 \mathrm{MPa}$ [10].

Figure 16 shows some increments of the simulation using a fine mesh. Predamaging, failure, and successive delamination can be observed. The contact algorithm adopted from [5] maintains a certain stiffness in normal direction only for compression. Therefore, penetration after failure is prevented but tangential sliding occurs.

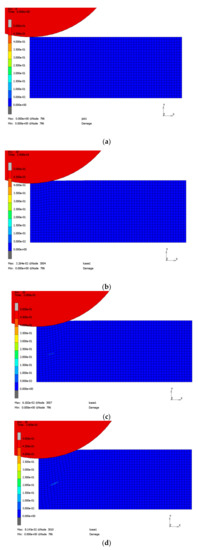
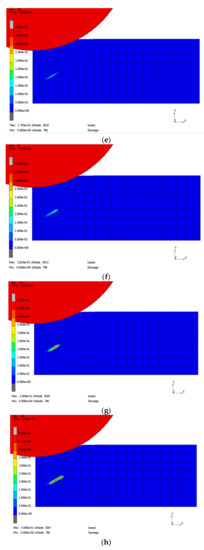
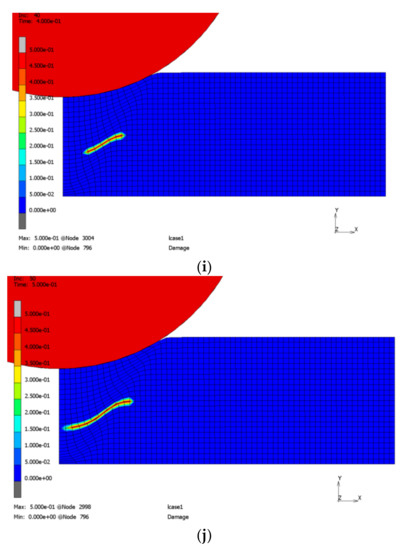
Figure 16. Indentation test: Joining zone damage: increment 0 (a), 10 (b), 20 (c), 30 (d), 36 (e), 37 (f), 38 (g), 39 (h), 40 (i), 50 (j).

The simulations are carried out with 10, 20, 30, 40, 50, and 60 elements in horizontal direction. Table 1 contains the increment and position of failure initiation for the different meshes. The three finer discretisations lead to very similar results regarding failure initiation.

Table 1. Location and increment of failure initiation.

Number of Elements in Horizontal Direction	Failure in Increment	Failure Position from Left Corner
10	59	0.21 mm
20	47	1.40 mm
30	43	0.93 mm
40	40	1.20 mm
50	39	1.16 mm
60	37	1.13 mm

7. Conclusions

Interfaces can be modelled using Cohesive Zone Elements. However, standard formulations do not consider membrane deformations that occur during forming of hybrid bulk material components. Membrane Mode Enhanced Cohesive Zone Elements capture these effects. An implementation of this technology in the nonlinear finite element solver MSC Marc is carried out. The new technology can be used for thermomechanical simulations in combination with all capabilities that Marc provides for usual Cohesive Zone Elements as it is implemented as a material subroutine in the provided standard interface element.

Simulations of a transverse link are carried out to test the technology. The material parameters stem from a different joining process and the development of the transverse link itself is not finished yet. Though some general findings might be valid:

(1)

The intended geometry contains severe deformation affecting the joining zone.

(2)

A more similar geometry of the raw component and the formed component would reduce the probability of failure initiation here.

(3)

The starting position in the form significantly influences the process and should be fixed.

(4)

A closed die process with burr prevention should be considered to prevent zones with very large deformation where a crack initiation might be triggered.

An indentation test is suited to investigate mesh dependency due to a simpler geometry. The load increment and also the position of failure initiation change from coarse to fine mesh, but are stable for further mesh refinement.