Current Trends and Applications of Machine Learning in Tribology—A Review
Abstract
:1. Introduction
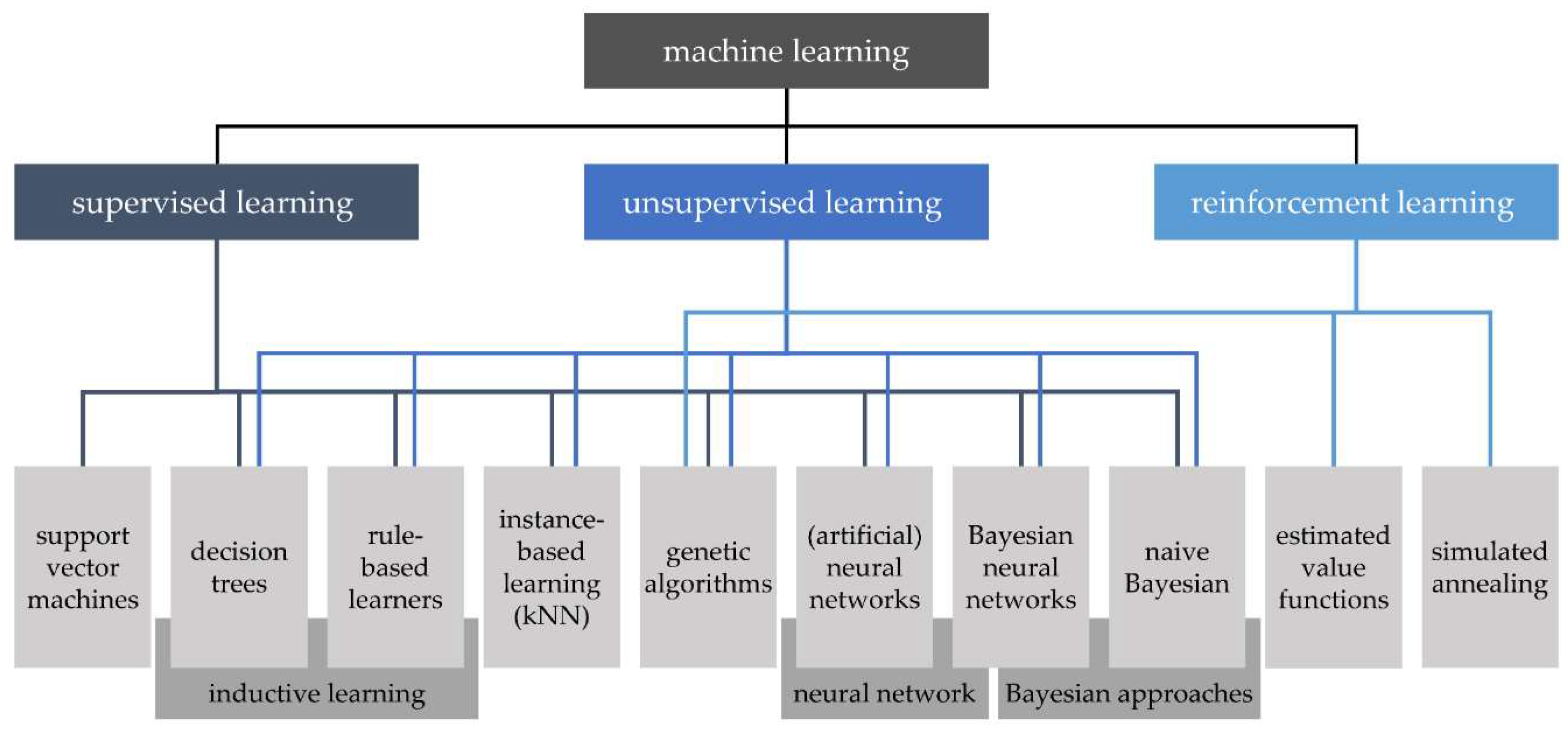
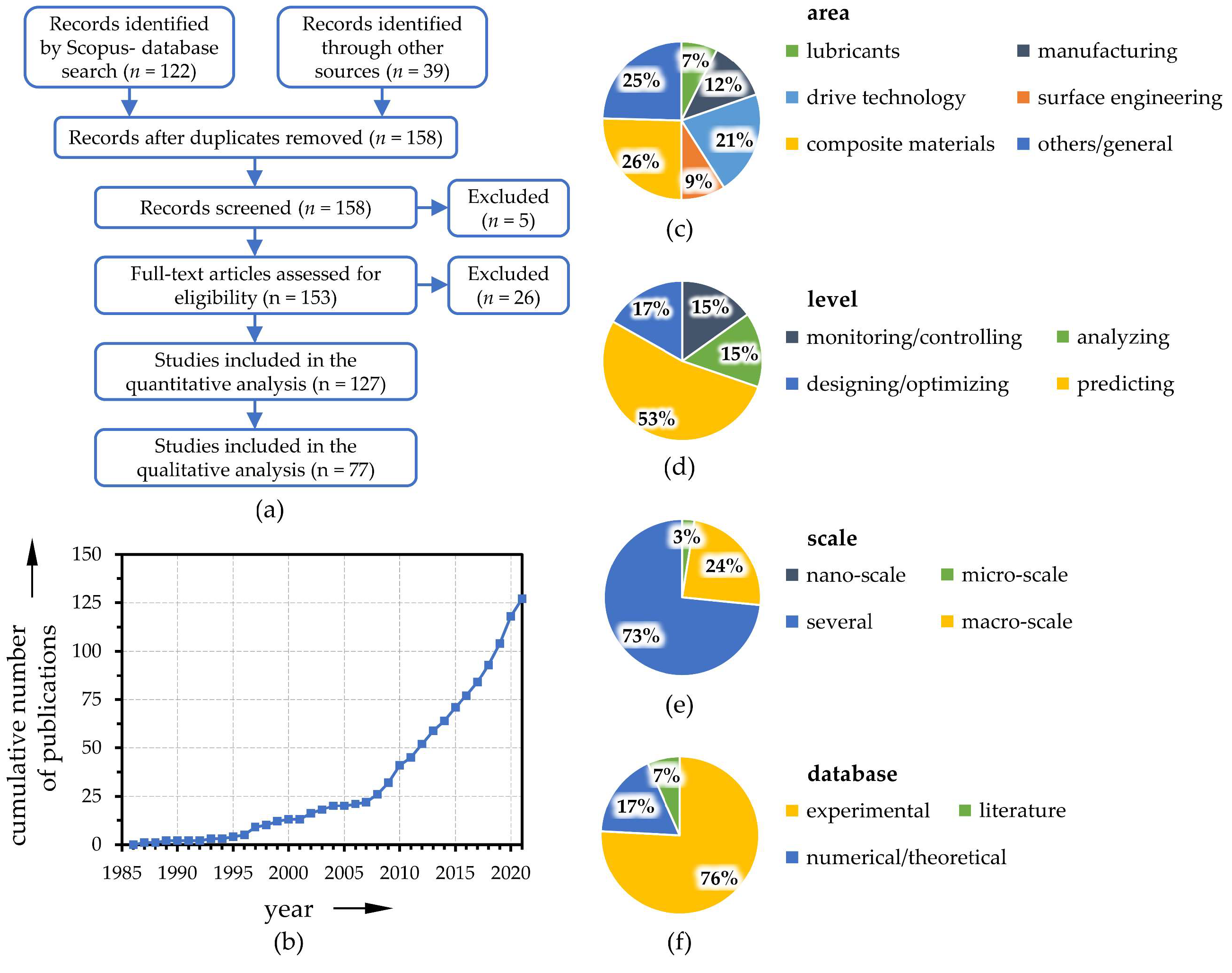
2. Background and a Quantitative Survey on Machine Learning in Tribology
3. Results
3.1. Composite Materials
3.1.1. Thermoset Matrix Composites
3.1.2. Thermoplastic Matrix Composites
3.1.3. Metal Matrix Composites
3.2. Drive Technology
3.2.1. Rolling Bearings
3.2.2. Sliding Bearings
3.2.3. Seals
3.2.4. Brakes and Clutches
3.3. Manufacturing
3.4. Surface Engineering
3.4.1. Coatings
3.4.2. Surface Texturing
3.5. Lubricants
3.6. Others/General
4. Summary and Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AE | acoustic emission |
| AI | artificial intelligence |
| ALPS | age-layered population structure |
| ANFIS | adaptive neuro-fuzzy interference system |
| ANN | artificial neural network |
| ART | adaptive resonance theory |
| BFS | blast furnaces slag |
| CCD | centrale composite design |
| CDI | cage dynamics indicator |
| CF | carbon fiber |
| CMC | ceramic matrix composite |
| CNT | carbon nanotube |
| CoD | coefficient of determination |
| COF | coefficient of friction |
| CoP | coefficient of prognosis |
| CVT | centroidal voronoi tessellation |
| DFT | density function theory |
| DoE | design of experiments |
| DT | decision tree |
| EA | evolutionary algorithm |
| EBP | error back propagation |
| EHL | elastohydrodynamic lubrication |
| ELM | extreme learning machine |
| FE | finite element |
| FFT | fast fourier transformation |
| GBM | gradient boosting machine |
| GE | grammatical evolution |
| GO | graphene oxide |
| HL | hydrodynamic lubrication |
| HVOF | high-velocity oxy-fuel |
| IBA | improved bat algorithm |
| kNN | k-nearest neighbor |
| LFM | lateral force microscopy |
| LHS | latin hypercube sampling |
| LM | levenberg-marquardt |
| MBE | model-based estimation |
| MD | molecular dynamics |
| ML | machine learning |
| MLP | multilayer perception |
References
- Holmberg, K.; Erdemir, A. Influence of tribology on global energy consumption, costs and emissions. Friction 2017, 5, 263–284. [Google Scholar] [CrossRef]
- Vakis, A.; Yastrebov, V.; Scheibert, J.; Nicola, L.; Dini, D.; Minfray, C.; Almqvist, A.; Paggi, M.; Lee, S.; Limbert, G.; et al. Modeling and simulation in tribology across scales: An overview. Tribol. Int. 2018, 125, 169–199. [Google Scholar] [CrossRef]
- Ciulli, E. Tribology and industry: From the origins to 4.0. Front. Mech. Eng. 2019, 5, 103. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Yin, N.; Chen, S.; Liu, C. Tribo-informatics: Concept, architecture, and case study. Friction 2021, 9, 642–655. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Marian, M.; Profito, F.J.; Aragon, N.; Shah, R. The use of artificial intelligence in tribology—A perspective. Lubricants 2021, 9, 2. [Google Scholar] [CrossRef]
- Wuest, T.; Weimer, D.; Irgens, C.; Thoben, K.-D. Machine learning in manufacturing: Advantages, challenges, and applications. Prod. Manuf. Res. 2016, 4, 23–45. [Google Scholar] [CrossRef] [Green Version]
- Ghoddusi, H.; Creamer, G.G.; Rafizadeh, N. Machine learning in energy economics and finance: A review. Energy Econ. 2019, 81, 709–727. [Google Scholar] [CrossRef]
- Kaieski, N.; da Costa, C.A.; Righi, R.D.R.; Lora, P.S.; Eskofier, B. Application of artificial intelligence methods in vital signs analysis of hospitalized patients: A systematic literature review. Appl. Soft Comput. 2020, 96, 106612. [Google Scholar] [CrossRef]
- Kügler, P.; Marian, M.; Schleich, B.; Tremmel, S.; Wartzack, S. tribAIn—Towards an explicit specification of shared tribological understanding. Appl. Sci. 2020, 10, 4421. [Google Scholar] [CrossRef]
- Ji, Y.; Bao, J.; Yin, Y.; Ma, C. Applications of artificial intelligence in tribology. Recent Patents Mech. Eng. 2016, 9, 193–205. [Google Scholar] [CrossRef]
- Argatov, I. Artificial Neural Networks (ANNs) as a novel modeling technique in tribology. Front. Mech. Eng. 2019, 5, 1074. [Google Scholar] [CrossRef] [Green Version]
- Bell, J. Machine Learning: Hands-On for Developers and Technical Professionals; Wiley: Hoboken, NJ, USA, 2014; ISBN 978-1-118-88906-0. [Google Scholar]
- Wittpahl, V. Künstliche Intelligenz; Springer: Berlin, Germany, 2019; ISBN 978-3-662-58041-7. [Google Scholar]
- Müller, A.C.; Guido, S. Introduction to Machine Learning with Python: A Guide for Data Scientist, 1st ed.; O’Reilly: Beijing, China, 2016; ISBN 978-1-4493-6941-5. [Google Scholar]
- Schölkopf, B.; Smola, A.J. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2002; ISBN 978-0-262-19475-4. [Google Scholar]
- Bishop, C.M. Pattern recognition and machine learning. In Information Science and Statistics; Springer: New York, NY, USA, 2006; pp. 21–24. ISBN 9780387310732. [Google Scholar]
- Freund, Y. Boosting a weak learning algorithm by majority. Inf. Comput. 1995, 121, 256–285. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef] [Green Version]
- Forsyth, D. Applied Machine Learning; Springer: Cham, Switzerland, 2019; ISBN 978-3-030-18113-0. [Google Scholar]
- Sarkar, D.; Bali, R.; Sharma, T. Practical Machine Learning with Python: A Problem-Solver’s Guide to Building Real-World Intelligent Systems; Apress L.P.: Berkeley, CA, USA, 2017; ISBN 978-1-4842-3206-4. [Google Scholar]
- Kinnebrock, W. Neuronale Netze: Grundlagen, Anwendungen, Beispiele; 2., verb. Aufl.; Oldenbourg: München, Germany, 1994; ISBN 3-486-22947-8. [Google Scholar]
- Tallian, T.E. A computerized expert system for tribological failure diagnosis. J. Tribol. 1989, 111, 238–244. [Google Scholar] [CrossRef]
- Tallian, T.E. Tribological design decisions using computerized databases. J. Tribol. 1987, 109, 381–386. [Google Scholar] [CrossRef]
- Jones, S.P.; Jansen, R.; Fusaro, R.L. Preliminary investigation of neural network techniques to predict tribological properties. Tribol. Trans. 1997, 40, 312–320. [Google Scholar] [CrossRef]
- Karkoub, M.; Elkamel, A. Modelling pressure distribution in a rectangular gas bearing using neural networks. Tribol. Int. 1997, 30, 139–150. [Google Scholar] [CrossRef]
- Santner, E. Computer support in tribology—Experiments and database. Tribotest 1996, 2, 267–280. [Google Scholar] [CrossRef]
- Myshkin, N.; Kwon, O.; Grigoriev, A.; Ahn, H.-S.; Kong, H. Classification of wear debris using a neural network. Wear 1997, 203–204, 658–662. [Google Scholar] [CrossRef]
- Umeda, A.; Sugimura, J.; Yamamoto, Y. Characterization of wear particles and their relations with sliding conditions. Wear 1998, 216, 220–228. [Google Scholar] [CrossRef]
- Chowdhury, M.A.; Nuruzzaman, D.M.; Rahaman, M.L. Tribological behavior of composite materials—A review. Recent Pat. Mech. Eng. 2010, 1, 123–128. [Google Scholar] [CrossRef]
- Tyagi, R.; Davim, J.P. Processing Techniques and Tribological Behavior of Composite Materials; Engineering Science Reference, an Imprint of IGI Global: Hershey, PA, USA, 2015; ISBN 9781466675308. [Google Scholar]
- Omrani, E.; Menezes, P.L.; Rohatgi, P.K. State of the art on tribological behavior of polymer matrix composites reinforced with natural fibers in the green materials world. Eng. Sci. Technol. Int. J. 2016, 19, 717–736. [Google Scholar] [CrossRef] [Green Version]
- Milosevic, M.; Valášek, P.; Ruggiero, A. Tribology of natural fibers composite materials: An overview. Lubricants 2020, 8, 42. [Google Scholar] [CrossRef] [Green Version]
- Nayak, S.K.; Satapathy, A. Wear analysis of waste marble dust-filled polymer composites with an integrated approach based on design of experiments and neural computation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 234, 1846–1856. [Google Scholar] [CrossRef]
- Friedrich, K.; Reinicke, R.; Zhang, Z. Wear of polymer composites. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2002, 216, 415–426. [Google Scholar] [CrossRef]
- Liujie, X.; Davim, J.P.; Cardoso, R. Prediction on tribological behaviour of composite PEEK-CF30 using artificial neural networks. J. Mater. Process. Technol. 2007, 189, 374–378. [Google Scholar] [CrossRef]
- Zhang, G.; Guessasma, S.; Liao, H.; Coddet, C.; Bordes, J.-M. Investigation of friction and wear behaviour of SiC-filled PEEK coating using artificial neural network. Surf. Coat. Technol. 2006, 200, 2610–2617. [Google Scholar] [CrossRef]
- Padhi, P.K.; Satapathy, A.; Nakka, A.M. Processing, characterization, and wear analysis of short glass fiber-reinforced polypropylene composites filled with blast furnace slag. J. Thermoplast. Compos. Mater. 2013, 28, 656–671. [Google Scholar] [CrossRef]
- Padhi, P.K.; Satapathy, A. Analysis of sliding wear characteristics of BFS filled composites using an experimental design approach integrated with ANN. Tribol. Trans. 2013, 56, 789–796. [Google Scholar] [CrossRef]
- Egala, R.; Jagadeesh, G.V.; Setti, S.G. Experimental investigation and prediction of tribological behavior of unidirectional short castor oil fiber reinforced epoxy composites. Friction 2021, 9, 250–272. [Google Scholar] [CrossRef]
- Nirmal, U. Prediction of friction coefficient of treated betelnut fibre reinforced polyester (T-BFRP) composite using artificial neural networks. Tribol. Int. 2010, 43, 1417–1429. [Google Scholar] [CrossRef]
- Nasir, T.; Yousif, B.F.; McWilliam, S.; Salih, N.D.; Hui, L.T. An artificial neural network for prediction of the friction coefficient of multi-layer polymeric composites in three different orientations. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2010, 224, 419–429. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Friedrich, K.; Velten, K. Prediction on tribological properties of short fibre composites using artificial neural networks. Wear 2002, 252, 668–675. [Google Scholar] [CrossRef]
- Velten, K.; Reinicke, R.; Friedrich, K. Wear volume prediction with artificial neural networks. Tribol. Int. 2000, 33, 731–736. [Google Scholar] [CrossRef]
- Gyurova, L.A.; Miniño-Justel, P.; Schlarb, A.K. Modeling the sliding wear and friction properties of polyphenylene sulfide composites using artificial neural networks. Wear 2010, 268, 708–714. [Google Scholar] [CrossRef]
- Jiang, Z.; Gyurova, L.A.; Schlarb, A.K.; Friedrich, K.; Zhang, Z. Study on friction and wear behavior of polyphenylene sulfide composites reinforced by short carbon fibers and sub-micro TiO2 particles. Compos. Sci. Technol. 2008, 68, 734–742. [Google Scholar] [CrossRef] [Green Version]
- Gyurova, L.A.; Friedrich, K. Artificial neural networks for predicting sliding friction and wear properties of polyphenylene sulfide composites. Tribol. Int. 2011, 44, 603–609. [Google Scholar] [CrossRef]
- Jiang, Z.; Gyurova, L.; Zhang, Z.; Friedrich, K.; Schlarb, A.K. Neural network based prediction on mechanical and wear properties of short fibers reinforced polyamide composites. Mater. Des. 2008, 29, 628–637. [Google Scholar] [CrossRef]
- Busse, M.; Schlarb, A.K. A novel neural network approach for modeling tribological properties of polyphenylene sulfide reinforced on different scales. In Tribology of Polymeric Nanocomposites; Elsevier: Cham, Switzerland, 2013; pp. 779–793. [Google Scholar] [CrossRef]
- Zhu, J.; Shi, Y.; Feng, X.; Wang, H.; Lü, X. Prediction on tribological properties of carbon fiber and TiO2 synergistic reinforced polytetrafluoroethylene composites with artificial neural networks. Mater. Des. 2009, 30, 1042–1049. [Google Scholar] [CrossRef]
- Li, S.; Shao, M.; Duan, C.; Yan, Y.; Wang, Q.; Wang, T.; Zhang, X. Tribological behavior prediction of friction materials for ultrasonic motors using Monte Carlo-based artificial neural network. J. Appl. Polym. Sci. 2019, 136, 47157. [Google Scholar] [CrossRef]
- Kurt, H.I.; Oduncuoglu, M. Application of a neural network model for prediction of wear properties of ultrahigh molecular weight polyethylene composites. Int. J. Polym. Sci. 2015, 2015, 315710. [Google Scholar] [CrossRef] [Green Version]
- Vinoth, A.; Datta, S. Design of the ultrahigh molecular weight polyethylene composites with multiple nanoparticles: An artificial intelligence approach. J. Compos. Mater. 2020, 54, 179–192. [Google Scholar] [CrossRef]
- Kordijazi, A.; Zhao, T.; Zhang, J.; Alrfou, K.; Rohatgi, P. A review of application of machine learning in design, synthesis, and characterization of metal matrix composites: Current status and emerging applications. JOM 2021, 73, 2060–2074. [Google Scholar] [CrossRef]
- Genel, K.; Kurnaz, S.; Durman, M. Modeling of tribological properties of alumina fiber reinforced zinc–aluminum composites using artificial neural network. Mater. Sci. Eng. A 2003, 363, 203–210. [Google Scholar] [CrossRef]
- Kumar, K.R.; Mohanasundaram, K.M.; Arumaikkannu, G.; Subramanian, R. Artificial neural networks based prediction of wear and frictional behaviour of aluminium (A380)–fly ash composites. Tribol. Mater. Surf. Interfaces 2012, 6, 15–19. [Google Scholar] [CrossRef]
- Saravanan, S.D.; Senthilkumar, M. Prediction of tribological behaviour of rice husk ash reinforced aluminum alloy matrix composites using artificial neural network. Russ. J. Non-Ferrous Metals 2015, 56, 97–106. [Google Scholar] [CrossRef]
- Arif, S.; Alam, T.; Ansari, A.H.; Shaikh, M.B.N.; Siddiqui, M.A. Analysis of tribological behaviour of zirconia reinforced Al-SiC hybrid composites using statistical and artificial neural network technique. Mater. Res. Express 2018, 5, 056506. [Google Scholar] [CrossRef]
- Vettivel, S.; Selvakumar, N.; Narayanasamy, R.; Leema, N. Numerical modelling, prediction of Cu–W nano powder composite in dry sliding wear condition using response surface methodology. Mater. Des. 2013, 50, 977–996. [Google Scholar] [CrossRef]
- Stojanović, B.; Vencl, A.; Bobić, I.; Miladinović, S.; Skerlić, J. Experimental optimisation of the tribological behaviour of Al/SiC/Gr hybrid composites based on Taguchi’s method and artificial neural network. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 311. [Google Scholar] [CrossRef]
- Thankachan, T.; Prakash, K.S.; Kamarthin, M. Optimizing the tribological behavior of hybrid copper surface composites using statistical and machine learning techniques. J. Tribol. 2018, 140, 031610. [Google Scholar] [CrossRef]
- Gangwar, S.; Pathak, V.K. Dry sliding wear characteristics evaluation and prediction of vacuum casted marble dust (MD) reinforced ZA-27 alloy composites using hybrid improved bat algorithm and ANN. Mater. Today Commun. 2020, 25, 101615. [Google Scholar] [CrossRef]
- Hasan, S.; Kordijazi, A.; Rohatgi, P.K.; Nosonovsky, M. Triboinformatic modeling of dry friction and wear of aluminum base alloys using machine learning algorithms. Tribol. Int. 2021, 161, 107065. [Google Scholar] [CrossRef]
- Hasan, S.; Kordijazi, A.; Rohatgi, P.K.; Nosonovsky, M. Triboinformatics Approach for friction and wear prediction of al-graphite composites using machine learning methods. J. Tribol. 2021, 144, 011701. [Google Scholar] [CrossRef]
- Kankar, P.; Sharma, S.C.; Harsha, S. Fault diagnosis of ball bearings using machine learning methods. Expert Syst. Appl. 2011, 38, 1876–1886. [Google Scholar] [CrossRef]
- Vargas-Machuca, J.; García, F.; Coronado, A.M. Detailed comparison of methods for classifying bearing failures using noisy measurements. J. Fail. Anal. Prev. 2020, 20, 744–754. [Google Scholar] [CrossRef]
- Desavale, R.G.; Venkatachalam, R.; Chavan, S.P. Antifriction bearings damage analysis using experimental data based models. J. Tribol. 2013, 135, 041105. [Google Scholar] [CrossRef]
- Gomes, G.F.; Mendez, Y.A.D.; Alexandrino, P.D.S.L.; Da Cunha, S.S.; Ancelotti, A.C. A Review of vibration based inverse methods for damage detection and identification in mechanical structures using optimization algorithms and ANN. Arch. Comput. Methods Eng. 2019, 26, 883–897. [Google Scholar] [CrossRef]
- Subrahmanyam, M.; Sujatha, C. Using neural networks for the diagnosis of localized defects in ball bearings. Tribol. Int. 1997, 30, 739–752. [Google Scholar] [CrossRef]
- Kanai, R.A.; Desavale, R.G.; Chavan, S.P. Experimental-based fault diagnosis of rolling bearings using artificial neural network. J. Tribol. 2016, 138, 031103. [Google Scholar] [CrossRef]
- Schwarz, S.; Grillenberger, H.; Tremmel, S.; Wartzack, S. Prediction of rolling bearing cage dynamics using dynamics simulations and machine learning algorithms. Tribol. Trans. 2021, 1–23. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A Decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Wirsching, S.; Marian, M.; Bartz, M.; Stahl, T.; Wartzack, S. Geometrical optimization of the EHL roller face/rib contact for energy efficiency in tapered roller bearings. Lubricants 2021, 9, 67. [Google Scholar] [CrossRef]
- Most, T.; Will, J. Metamodel of Optimal Prognosis—An Automatic Approach for Variable Reduction and Optimal Meta-Model Selection. In Proceedings of the 2008 Weimarer Optimierungs und Stochastiktage 5.0, Weimar, Germany, 20–21 November 2008. [Google Scholar] [CrossRef]
- Canbulut, F.; Yildirim, S.; Sinanoglu, C. Design of an artificial neural network for analysis of frictional power loss of hydrostatic slipper bearings. Tribol. Lett. 2004, 17, 887–899. [Google Scholar] [CrossRef]
- Ünlü, B.S.; Durmuş, H.; Meriç, C. Determination of tribological properties at CuSn10 alloy journal bearings by experimental and means of artificial neural networks method. Ind. Lubr. Tribol. 2012, 64, 258–264. [Google Scholar] [CrossRef]
- Moder, J.; Bergmann, P.; Grün, F. Lubrication regime classification of hydrodynamic journal bearings by machine learning using torque data. Lubricants 2018, 6, 108. [Google Scholar] [CrossRef] [Green Version]
- Prost, J.; Cihak-Bayr, U.; Neacșu, I.; Grundtner, R.; Pirker, F.; Vorlaufer, G. Semi-supervised classification of the state of operation in self-lubricating journal bearings using a random forest classifier. Lubricants 2021, 9, 50. [Google Scholar] [CrossRef]
- Francisco, A.; Lavie, T.; Fatu, A.; Villechaise, B. Metamodel-assisted optimization of connecting rod big-end bearings. J. Tribol. 2013, 135, 041704. [Google Scholar] [CrossRef]
- Li, X.; Fu, P.; Chen, K.; Lin, Z.; Zhang, E. The contact state monitoring for seal end faces based on acoustic emission detection. Shock Vib. 2015, 2016, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Li, X. Acoustic Emission Monitoring for Film Thickness of Mechanical Seals Based on Feature Dimension Reduction and Cascaded Decision. In Proceedings of the 2014 Sixth International Conference on Measuring Technology and Mechatronics Automation, Zhangjiajie, China, 10–11 January 2014; pp. 64–70. [Google Scholar] [CrossRef]
- Logozzo, S.; Valigi, M.C. Investigation of instabilities in mechanical face seals: Prediction of critical speed values. In Advances in Mechanism and Machine Science; Uhl, T., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 3865–3872. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, X.; Huang, W.; Liu, Y.; Hu, S. Gas face seal status estimation based on acoustic emission monitoring and support vector machine regression. Adv. Mech. Eng. 2020, 12, 168781402092132. [Google Scholar] [CrossRef]
- Yin, Y.; Bao, J.; Yang, L. Wear performance and its online monitoring of the semimetal brake lining for automobiles. Ind. Lubr. Tribol. 2014, 66, 100–105. [Google Scholar] [CrossRef]
- Xiao, G.; Zhu, Z. Friction materials development by using DOE/RSM and artificial neural network. Tribol. Int. 2010, 43, 218–227. [Google Scholar] [CrossRef]
- Aleksendrić, D.; Duboka, Č.; Mariotti, G.V. Neural modelling of friction material cold performance. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2008, 222, 1201–1209. [Google Scholar] [CrossRef]
- Aleksendrić, D.; Barton, D.C. Neural network prediction of disc brake performance. Tribol. Int. 2009, 42, 1074–1080. [Google Scholar] [CrossRef]
- Aleksendrić, D.; Barton, D.C.; Vasić, B. Prediction of brake friction materials recovery performance using artificial neural networks. Tribol. Int. 2010, 43, 2092–2099. [Google Scholar] [CrossRef]
- Aleksendric, D. Neural network prediction of brake friction materials wear. Wear 2010, 268, 117–125. [Google Scholar] [CrossRef]
- Timur, M.; Aydin, F. Anticipating the friction coefficient of friction materials used in automobiles by means of machine learning without using a test instrument. Turk. J. Electr. Eng. Comput. Sci. 2013, 21, 1440–1454. [Google Scholar] [CrossRef]
- Senatore, A.; D’Agostino, V.; Di Giuda, R.; Petrone, V. Experimental investigation and neural network prediction of brakes and clutch material frictional behaviour considering the sliding acceleration influence. Tribol. Int. 2011, 44, 1199–1207. [Google Scholar] [CrossRef]
- Grzegorzek, W.; Scieszka, S.F. Prediction on friction characteristics of industrial brakes using artificial neural networks. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2013, 228, 1025–1035. [Google Scholar] [CrossRef]
- Gupta, S.K.; Pandey, K.; Kumar, R. Artificial intelligence-based modelling and multi-objective optimization of friction stir welding of dissimilar AA5083-O and AA6063-T6 aluminium alloys. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2016, 232, 333–342. [Google Scholar] [CrossRef]
- D’Orazio, A.; Forcellese, A.; Simoncini, M. Prediction of the vertical force during FSW of AZ31 magnesium alloy sheets using an artificial neural network-based model. Neural Comput. Appl. 2018, 31, 7211–7226. [Google Scholar] [CrossRef]
- Huggett, D.J.; Liao, T.W.; Wahab, M.A.; Okeil, A. Prediction of friction stir weld quality without and with signal features. Int. J. Adv. Manuf. Technol. 2018, 95, 1989–2003. [Google Scholar] [CrossRef]
- Das, S.; Roy, R.; Chattopadhyay, A. Evaluation of wear of turning carbide inserts using neural networks. Int. J. Mach. Tools Manuf. 1996, 36, 789–797. [Google Scholar] [CrossRef]
- Sathiya, P.; Aravindan, S.; Haq, A.N.; Paneerselvam, K. Optimization of friction welding parameters using evolutionary computational techniques. J. Mater. Process. Technol. 2009, 209, 2576–2584. [Google Scholar] [CrossRef]
- Tansel, I.N.; Demetgul, M.; Okuyucu, H.; Yapici, A. Optimizations of friction stir welding of aluminum alloy by using genetically optimized neural network. Int. J. Adv. Manuf. Technol. 2010, 48, 95–101. [Google Scholar] [CrossRef] [Green Version]
- Atharifar, H. Optimum parameters design for friction stir spot welding using a genetically optimized neural network system. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2009, 224, 403–418. [Google Scholar] [CrossRef]
- Anand, K.; Shrivastava, R.; Tamilmannan, K.; Sathiya, P. A Comparative study of artificial neural network and response surface methodology for optimization of friction welding of incoloy 800 H. Acta Metall. Sin. Engl. Lett. 2015, 28, 892–902. [Google Scholar] [CrossRef] [Green Version]
- Dewan, M.W.; Huggett, D.J.; Liao, T.W.; Wahab, M.A.; Okeil, A. Prediction of tensile strength of friction stir weld joints with adaptive neuro-fuzzy inference system (ANFIS) and neural network. Mater. Des. 2016, 92, 288–299. [Google Scholar] [CrossRef] [Green Version]
- Jang, J.-S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Baraka, A.; Panoutsos, G.; Cater, S. A real-time quality monitoring framework for steel friction stir welding using computational intelligence. J. Manuf. Proc. 2015, 20, 137–148. [Google Scholar] [CrossRef]
- Das, B.; Pal, S.; Bag, S. Torque based defect detection and weld quality modelling in friction stir welding process. J. Manuf. Proc. 2017, 27, 8–17. [Google Scholar] [CrossRef]
- Fereshteh-Saniee, F.; Nourbakhsh, S.H.; Pezeshki, S.M. Estimation of flow curve and friction coefficient by means of a one-step ring test using a neural network coupled with FE simulations. J. Mech. Sci. Technol. 2012, 26, 153–160. [Google Scholar] [CrossRef]
- Bustillo, A.; Pimenov, D.; Matuszewski, M.; Mikolajczyk, T. Using artificial intelligence models for the prediction of surface wear based on surface isotropy levels. Robot. Comput. Manuf. 2018, 53, 215–227. [Google Scholar] [CrossRef]
- Hutchings, I.; Shipway, P. Surface engineering. In Tribology; Elsevier: Amsterdam, The Netherlands, 2017; pp. 237–281. ISBN 9780081009109. [Google Scholar]
- Cetinel, H. The artificial neural network based prediction of friction properties of Al2O3-TiO2 coatings. Ind. Lubr. Tribol. 2012, 64, 288–293. [Google Scholar] [CrossRef]
- Sahraoui, T.; Guessasma, S.; Fenineche, N.; Montavon, G.; Coddet, C. Friction and wear behaviour prediction of HVOF coatings and electroplated hard chromium using neural computation. Mater. Lett. 2004, 58, 654–660. [Google Scholar] [CrossRef]
- Upadhyay, R.; Kumaraswamidhas, L. Multilayer nitride coating performance optimized by an artificial neural network approach. Ciência Tecnol. Mater. 2016, 28, 47–54. [Google Scholar] [CrossRef]
- Upadhyay, R.K.; Kumaraswamidhas, L.A. Friction and wear response of nitride coating deposited through PVD magnetron sputtering. Tribol. Mater. Surf. Interfaces 2016, 10, 196–205. [Google Scholar] [CrossRef]
- Otero, J.E.; Ochoa, E.D.L.G.; Vallinot, I.B.; Tanarro, E.C. Optimising the design of textured surfaces for reducing lubricated friction coefficient. Lubr. Sci. 2016, 29, 183–199. [Google Scholar] [CrossRef] [Green Version]
- Boidi, G.; da Silva, M.R.; Profito, F.J.; Machado, I.F. Using machine learning Radial Basis Function (RBF) method for predicting lubricated friction on textured and porous surfaces. Surf. Topogr. Metrol. Prop. 2020, 8, 044002. [Google Scholar] [CrossRef]
- Mo, F.; Shen, C.; Zhou, J.; Khonsari, M.M. Statistical analysis of the influence of imperfect texture shape and dimensional uncertainty on surface texture performance. IEEE Access 2017, 5, 27023–27035. [Google Scholar] [CrossRef]
- Marian, M.; Grützmacher, P.; Rosenkranz, A.; Tremmel, S.; Mücklich, F.; Wartzack, S. Designing surface textures for EHL point-contacts—Transient 3D simulations, meta-modeling and experimental validation. Tribol. Int. 2019, 137, 152–163. [Google Scholar] [CrossRef]
- Tremmel, S.; Marian, M.; Zahner, M.; Wartzack, S.; Merklein, M. Friction reduction in EHL contacts by surface microtexturing—Tribological performance, manufacturing and tailored design. Ind. Lubr. Tribol. 2019, 71, 986–990. [Google Scholar] [CrossRef]
- Zambrano, V.; Brase, M.; Hernández-Gascón, B.; Wangenheim, M.; Gracia, L.; Viejo, I.; Izquierdo, S.; Valdés, J. a digital twin for friction prediction in dynamic rubber applications with surface textures. Lubricants 2021, 9, 57. [Google Scholar] [CrossRef]
- Shea, T.M.; Gunsel, S. Modeling base oil properties using NMR spectroscopy and neural networks. Tribol. Trans. 2003, 46, 296–302. [Google Scholar] [CrossRef]
- Dai, K.; Gao, X. Estimating antiwear properties of lubricant additives using a quantitative structure tribo-ability relationship model with back propagation neural network. Wear 2013, 306, 242–247. [Google Scholar] [CrossRef]
- Durak, E.; Salman, O.; Kurbanoglu, C. Analysis of effects of oil additive into friction coefficient variations on journal bearing using artificial neural network. Ind. Lubr. Tribol. 2008, 60, 309–316. [Google Scholar] [CrossRef]
- Humelnicu, C.; Ciortan, S.; Amortila, V. Artificial neural network-based analysis of the tribological behavior of vegetable oil–diesel fuel mixtures. Lubricants 2019, 7, 32. [Google Scholar] [CrossRef] [Green Version]
- Bhaumik, S.; Mathew, B.R.; Datta, S. Computational intelligence-based design of lubricant with vegetable oil blend and various nano friction modifiers. Fuel 2019, 241, 733–743. [Google Scholar] [CrossRef]
- Bhaumik, S.; Pathak, S.; Dey, S.; Datta, S. Artificial intelligence based design of multiple friction modifiers dispersed castor oil and evaluating its tribological properties. Tribol. Int. 2019, 140, 105813. [Google Scholar] [CrossRef]
- Mujtaba, M.; Masjuki, H.; Kalam, M.; Ong, H.C.; Gul, M.; Farooq, M.; Soudagar, M.E.M.; Ahmed, W.; Harith, M.; Yusoff, M. Ultrasound-assisted process optimization and tribological characteristics of biodiesel from palm-sesame oil via response surface methodology and extreme learning machine—Cuckoo search. Renew. Energy 2020, 158, 202–214. [Google Scholar] [CrossRef]
- Summers, A.Z.; Gilmer, J.B.; Iacovella, C.R.; Cummings, P.T.; McCabe, C. MoSDeF, a Python framework enabling large-scale computational screening of soft matter: Application to chemistry-property relationships in lubricating monolayer films. J. Chem. Theory Comput. 2020, 16, 1779–1793. [Google Scholar] [CrossRef] [PubMed]
- Baboukani, B.S.; Ye, Z.; Reyes, K.G.; Nalam, P.C. Prediction of nanoscale friction for two-dimensional materials using a machine learning approach. Tribol. Lett. 2020, 68, 1–14. [Google Scholar] [CrossRef]
- Moayedi, H.; Hayati, S. Artificial intelligence design charts for predicting friction capacity of driven pile in clay. Neural Comput. Appl. 2019, 31, 7429–7445. [Google Scholar] [CrossRef]
- Rouet-Leduc, B.; Hulbert, C.; Bolton, D.C.; Ren, C.X.; Riviere, J.; Marone, C.; Guyer, R.A.; Johnson, P.A. Estimating fault friction from seismic signals in the laboratory. Geophys. Res. Lett. 2018, 45, 1321–1329. [Google Scholar] [CrossRef] [Green Version]
- Tijani, I.; Akmeliawati, R. Support vector regression based friction modeling and compensation in motion control system. Eng. Appl. Artif. Intell. 2012, 25, 1043–1052. [Google Scholar] [CrossRef]
- Tijani, I.B.; Wahyudi, M.; Talib, H. Adaptive neuro-fuzzy inference system (ANFIS) for friction modelling and compensation in motion control system. Int. J. Model. Simul. 2011, 31, 32–41. [Google Scholar] [CrossRef]
- Ao, Y.; Wang, Q.; Chen, P. Simulating the worn surface in a wear process. Wear 2002, 252, 37–47. [Google Scholar] [CrossRef]
- Haviez, L.; Toscano, R.; El Youssef, M.; Fouvry, S.; Yantio, G.; Moreau, G. Semi-physical neural network model for fretting wear estimation. J. Intell. Fuzzy Syst. 2015, 28, 1745–1753. [Google Scholar] [CrossRef]
- Argatov, I.I.; Chai, Y.S. Artificial neural network modeling of sliding wear. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 235, 748–757. [Google Scholar] [CrossRef]
- Almqvist, A. Fundamentals of physics-informed neural networks applied to solve the Reynolds boundary value problem. Lubricants 2021, 9, 82. [Google Scholar] [CrossRef]
- Bucholz, E.W.; Kong, C.S.; Marchman, K.R.; Sawyer, W.G.; Phillpot, S.; Sinnott, S.B.; Rajan, K. Data-driven model for estimation of friction coefficient via informatics methods. Tribol. Lett. 2012, 47, 211–221. [Google Scholar] [CrossRef]
- Perčić, M.; Zelenika, S.; Mezić, I. Artificial intelligence-based predictive model of nanoscale friction using experimental data. Friction 2021, 9, 1726–1748. [Google Scholar] [CrossRef]

| Subject | Database, Number of Data Sets (If Applicable Divided in Train/Test/Validation) | Inputs | Outputs | ML Approach | Prediction | Ref. |
|---|---|---|---|---|---|---|
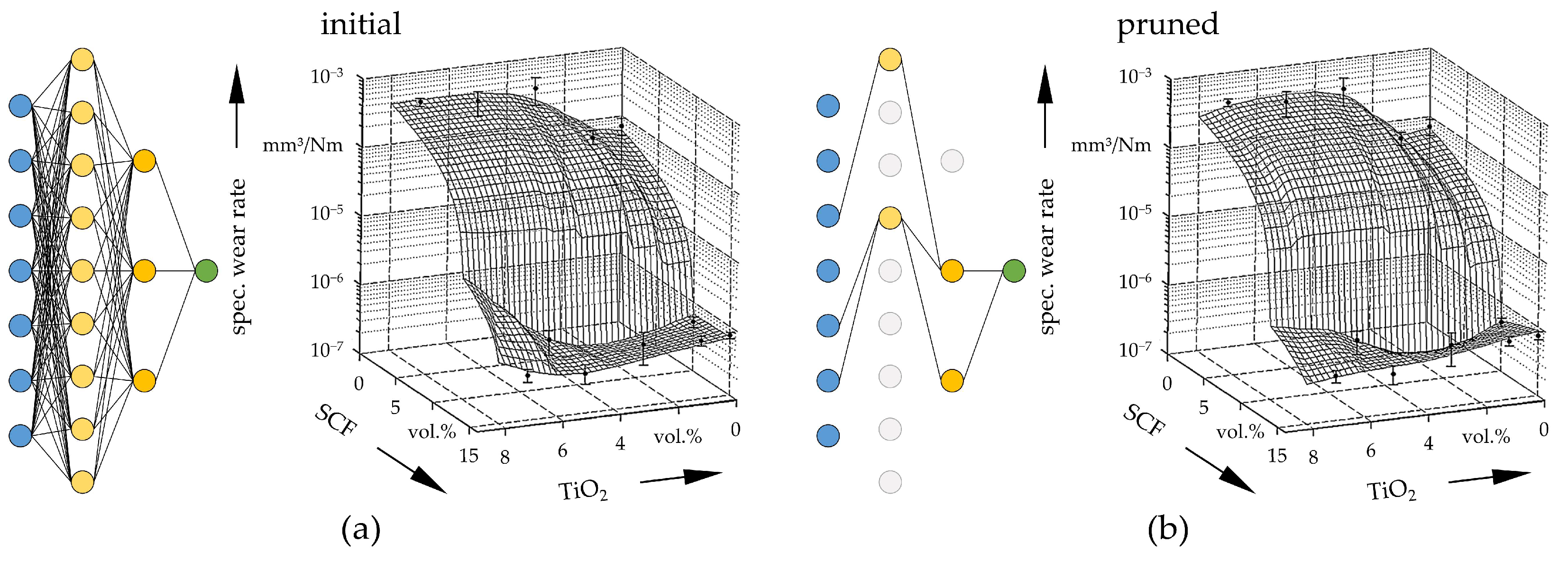
| SGF and BFS reinforced epoxy | experimental (pin-on-disk) Taguchi DoE, 16 | BFS content, sliding velocity, normal load, sliding distance | spec. wear rate | back propagation ANN (4:7:1) | Errors < 6.9% | [39] |
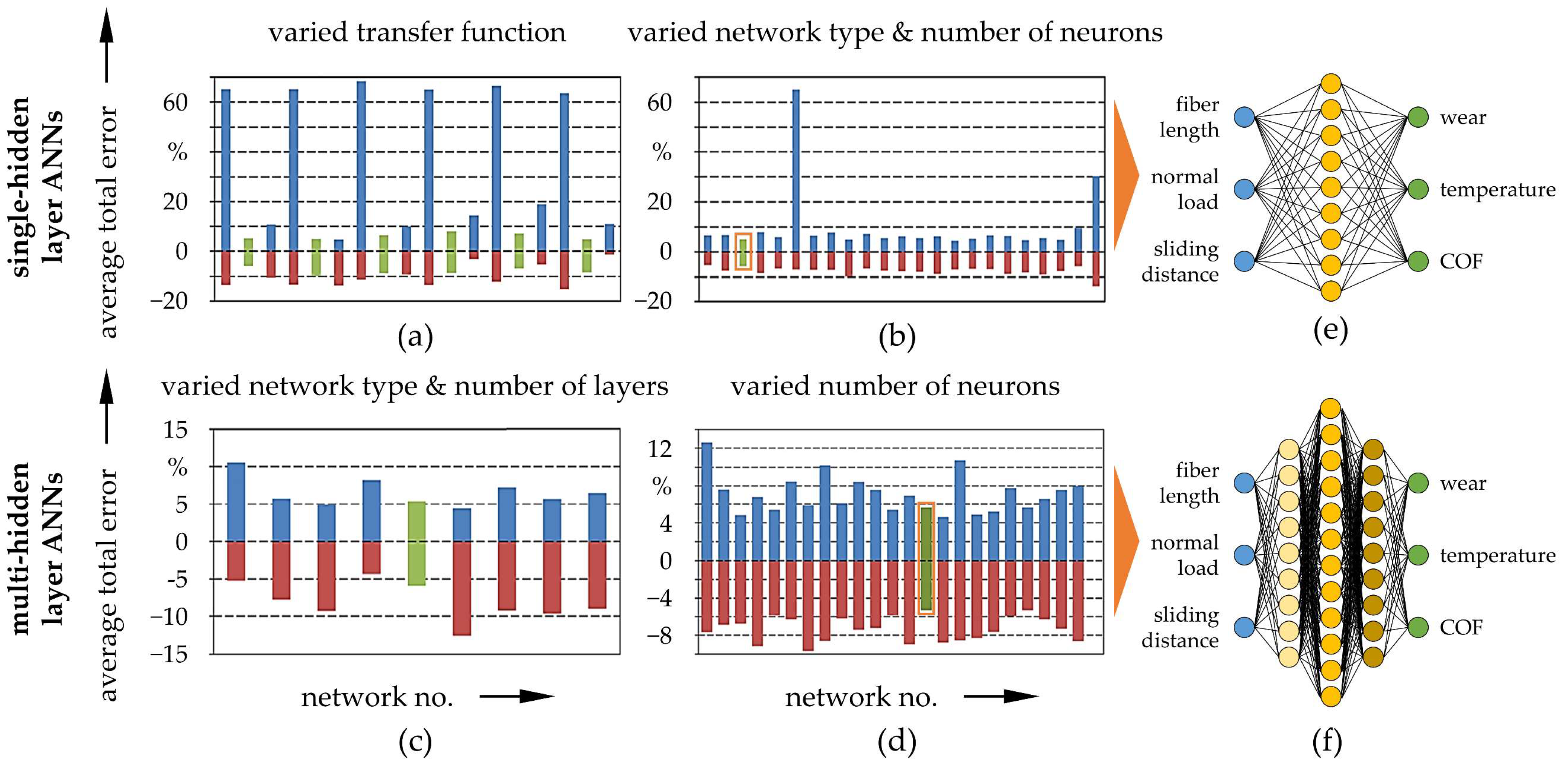
| unidirectional short castor oil fiber reinforced epoxy | experimental (pin-on-disk) full factorial DoE, 36 (60%/20%/20%) | fiber length, normal load, sliding distance | wear, temperature, COF | various ANNs, best results for back propagation ANN (3:9:3 & 3:9:12:9:3) | averaged total errors < 5% | [40] |
| treated betelnut fiber reinforced polyester | experimental (block-on-disk), 492 | fiber orientation, normal load, sliding distance | COF | ANN (3:30:20:1) | SSE < 1% | [41] |
| glass fiber reinforced polyester | experimental (disk-on-flat), 7389 | fiber orientation, rotational speed, normal load, test duration | COF | ANN (4:40:1) | SSE < 15% | [42] |
| SCF, graphite, PTFE, and TiO2 reinforced PPS | experimental (pin-on-disk), 90 (80%/20%) | matrix vol. fraction, filler, reinforcing agent and lubricant, contact pressure, sliding speed, tensile strength, compressive strength | spec. wear rate, COF | various gradient descent back propagation ANNs (7:9:3:1 for wear, 7:3:1:1 for COF) | MRE < 0.78 (wear), MRE < 0.12 (COF) | [45] |
| experimental (pin-on-disk), 124 (80%/20%) | MRE < 0.55 (wear), MRE < 0.10 (COF) | [47] | ||||
| MRE < 0.14 (wear), MRE < 0.03 (COF) | [49] | |||||
| CF and TiO2 reinforced PTFE | experimental (block-on-ring), 30–105 (10–98%/2–90%), best results for largest database | PTFE content, carbon fiber content, TiO2 content, sliding speed, normal load, hardness, compressive strength | vol. wear loss, COF | various ANNs, best results for gradient search ANN (7:15:10:5:1) | CoD > 90% | [50] |
| aramid pulp, PTW, mica, Cu, and SiO2 reinforced PTFE | experimental (rotor/stator test-rig) in orthogonal table DoE, 18 (80%/20%) | aramid pulp content, PTW content, mica content, Cu content, SiO2 content | spec. wear rate, COF | back propagation ANN | RMSE < 2.08 (wear), RMSE < 0.019 (COF) | [51] |
| Monte Carlo-based ANN | RMSE < 0.97 (wear), RMSE < 0.007 (COF) | |||||
| ZnO, zeolite, CNT, CF, GO, and wollastonite reinforced UHMWPE | experiments from literature, 125 | UHMWPE content, ZnO content, Zeolite content, CNT content, CF content, GO content, wollastonite content, normal load, sliding speed | vol. wear loss | back propagation ANN (11:12:1) | R2 > 0.8, mean total error < 4.1% | [52] |
| MWCNT and graphene reinforced UHMWPE | experiments from literature, 153 | MWCNT fiber diameter, MWCNT fiber length, MWCNT content, graphene sheet length, graphene sheet thickness, graphene content, UHMWPE molecular weight, UHMWPE tensile strength, UHMWPE Young’s modulus | Young’s modulus, tensile strength | scaled conjugate gradient back propagation ANN (7:3:1 for Young’s modulus and 7:5:1 for tensile strength) | R2 > 0.93 (Young’s modulus), R2 > 0.97 (tensile strength) | [53] |
| graphite reinforced Al-Si alloy | experimental (block-on-disk) in Taguchi’s orthogonal array DoE, 27 (70%/15%/15%) | graphene content, normal load, sliding speed | vol. wear rate, COF | back propagation ANN (3:20:30:2) | R2 > 0.98 | [60] |
| aluminum nitride and boron nitride reinforced copper | experimental (pin-on-disk) in Taguchi’s orthogonal array DoE, 27 (90%/10%) | volume fraction, normal load, sliding velocity, sliding distance | spec. wear rate | back propagation ANN (4:7:1) | errors < 3.4% | [61] |
| marble dust reinforced Zn-Al alloy | experimental (pin-on-disk) in Taguchi’s orthogonal array DoE, 25 (60%/20%/20%) | filler content, normal load, sliding velocity, sliding distance, amb. temperature | spec. wear rate | IBA trained ANN (5:7:1) | MSE < 0.26, accuracy > 97% | [62] |
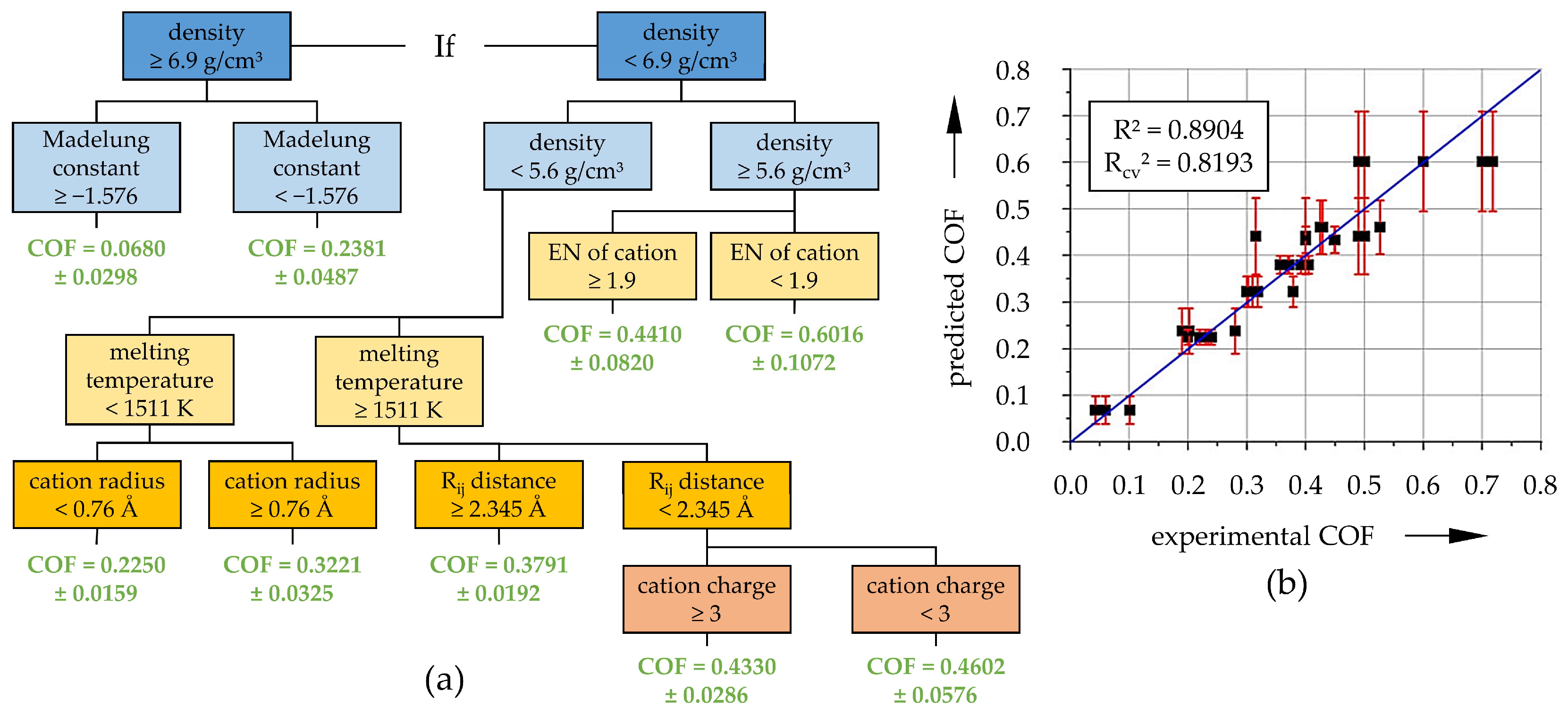
| Graphite reinforced aluminum alloy | experiments from literature, 852 | graphite content, hardness, ductility, processing procedure, heat treatment, SiC content, yield strength, tensile strength, normal load, sliding velocity, sliding distance, | vol. wear rate, COF | back propagation ANN (11:10:10:10:2) | MSE < 0.003 wear) RMSE < 0.06 (wear) R2 > 0.74 (wear) MSE < 0.004 (COF) RMSE < 0.06 (COF) R2 > 0.86 (COF) | [63,64] |
| kNN | MSE < 0.002 wear) RMSE < 0.04 (wear) R2 > 0.85 (wear) MSE < 0.007 (COF) RMSE < 0.08 (COF) R2 > 0.76 (COF) | |||||
| RF | MSE < 0.001 wear) RMSE < 0.04 (wear) R2 > 0.88 (wear) MSE < 0.004 (COF) RMSE < 0.06 (COF) R2 > 0.86 (COF) | |||||
| SVM | MSE < 0.006 (COF) RMSE < 0.08 (COF) R2 > 0.76 (COF) | |||||
| GBM | MSE < 0.002 wear) RMSE < 0.04 (wear) R2 > 0.86 (wear) MSE < 0.003 (COF) RMSE < 0.05 (COF) R2 > 0.89 (COF) |
| Subject | Database, Number of Data Sets (If Applicable Divided in Train/Test/Validation) | Inputs | Outputs | ML Approach | Prediction | Ref. |
|---|---|---|---|---|---|---|
| groove ball bearing defect diagnosis | experimental (bearing test-rig), 108 (90%/10%) | peak value of amplitude, average of top five peak values of amplitude, peak value of auto-correlation function, standard deviation, kurtosis | bearing state | EBP ANN | success rate > 95% | [69] |
| ART2 ANN | success rate = 100% | |||||
| ball bearing condition monitoring | experimental (bearing test-rig), 145 (75%/25%) | speed, load, defect volume, radial clearance, number of balls | vibration velocity | back propagation ANN (5:12:1) | errors < 14% | [70] |
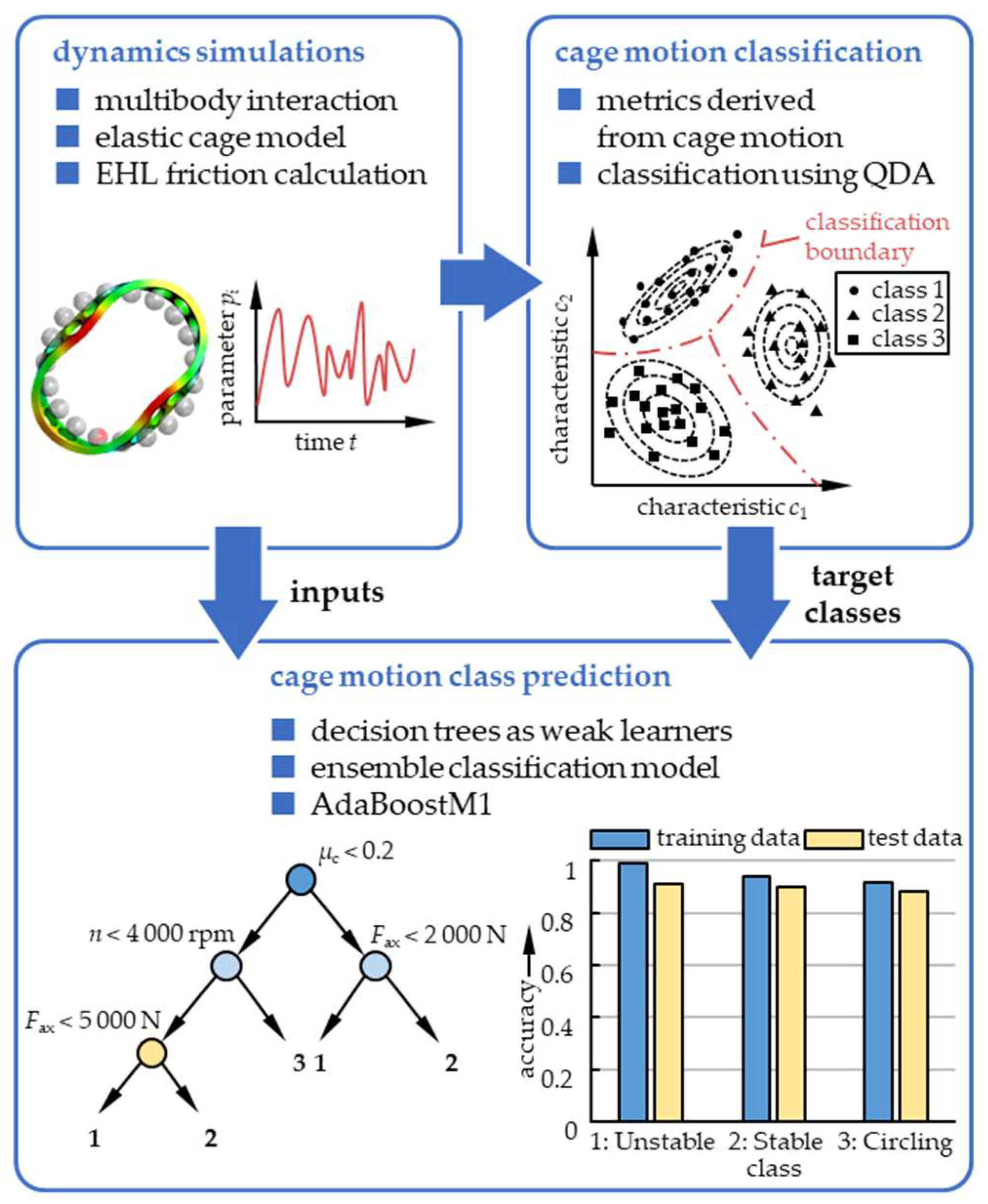
| cage motion mode classification in rolling bearings | numerical (dynamics simulation) in LHS, 4000 | cage mass, cage bending stiffness, pocket clearance, guidance clearance, bearing type, COF, axial force, radial force, bending moment, rotational speed | CDI | QDA and DT | accuracy > 91% | [71] |
| TRB roller/face rib contact geometry design | numerical (EHL simulation) in LHS, 370 (70%/30%) | roller face radius, eccentricity, rib radius | max. pressure, min. film height, COF | MOP | CoP > 90%, errors < 2% | [73] |
| frictional power losses of hydrostatic slipper bearings | experimental (hydrostatic slipper test-rig) | average roughness, relative velocity, supply pressure, hydrostatic pocket ratio, capillary tube diameter | frictional power loss | back propagation ANN | errors < 1.9% | [75] |
| dry and lubricated journal bearing behavior | experimental (journal bearing test-rig), 4 | time, load, rotational speed | COF, bearing weight loss, journal weight loss | EBP ANN (3:5:5:3 for dry and 3:4:4:3 for lubricated case) | mean errors < 4% (dry), mean errors < 5.3% (lubricated), | [76] |
| journal bearing lubrication regime prediction | experimental (journal bearing test-rig), 888 (80%/20%) | frictional torque | lubrication regime | FFT+ back propagation ANN (1:256:128:64:32:16:8:1) | accuracy > 99% | [77] |
| journal bearing operating condition classification | experimental (journal bearing test-rig), 9 (75%/25%) | time, lateral force | operating state | RFC (DT) | accuracy > 94% | [78] |
| connecting rod big-end bearing design | numerical (elastic HL simulation) in CCF DoE, 9 | oil viscosity at ref. temperature, oil viscosity at ref. pressure, oil thermo-viscosity coefficient, oil piezo-viscosity coefficient, oil piezo-viscosity index, oil supply pressure, lemon shape, shell bore relief depth, shell bore relief length, barrel shape, radial clearance | pressure times velocity product, power loss | nondominated sorting genetic algorithm | R2 > 0.99 | [79] |
| face seal friction instability prediction | numerical (dynamics simulation), 40 (90%/10%) | axial stiffness torsional stiffness | critical speed | various ANNs, best results for EBP ANN (2:10:1) | R2 > 0.97 | [82] |
| disk brake performance | experimental (inertial dynamometer), 275 (70%/10%/20%) | applied pressure, initial speed, number of braking events, phenolic resin, iron oxide, barites, calcium carbonate, brass chips, aramid, mineral fiber, vermiculite, steel fiber, glass fiber, brass powder, copper powder, graphite, friction dust, molybdenum disulphide, aluminum oxide, silica, magnesium oxide, spec. molding pressure, molding temperature, molding time, heat treatment temperature, heat treatment time | brake factor | various ANNs, best results for Bayesian ANN (26:8:4:1) | sufficient (not quantified) | [86,87] |
| brake materials | experimental (inertial dynamometer), 408 (34%/33%/33%) | sliding speed, contact pressure, temperature, binder resin, premix masterbatch, residuum | COF | EPB ANN (6:12:1) | errors < 4% | [92] |
| clutch materials | experimental (pin-on-disk), 200 (50%/25%/25%) | sliding speed, sliding acceleration, contact pressure | COF | EPB ANN (3:6:3:1) | sufficient within the data range (not quantified) | [91] |
| EPB ANN (3:6:7:1) |
| Subject | Database, Number of Data Sets (If Applicable Divided in Train/Test/Validation) | Inputs | Outputs | ML Approach | Prediction | Ref. |
|---|---|---|---|---|---|---|
| friction stir welding process optimization | experimental (friction stir welding), 14 | heating pressure, heating time, upsetting pressure, upsetting time | tensile strength, metal loss | back propagation ANN (4:9:2) | MSE < 0,01% | [97] |
| experimental (friction stir welding), 30 | RMSE < 0.98 (tensile strength), RMSE < 0.05 (tensile strength), | [100] | ||||
| experimental (friction stir welding), 73 (60%/20%/20%) | rotational speed, welding speed, plunge force, empirical force index | tensile strength | various ANNs, best results for back propagation ANN (3:5:1) | mean absolute error < 7.7% | [101] | |
| ANFIS | mean absolute error < 10.1% | |||||
| friction stir welding process monitoring | experimental (friction stir welding), 25 (80%/20%) | rotational speed, welding speed | weld threshold for downward force, weld threshold for traverse force | RBF trained ANN | accuracy > 80% | [103] |
| experimental (friction stir welding), 64 (60%/25%/15%) | rotational speed, welding speed, shoulder diameter | tensile strength | SVM | error < 0.5% | [104] | |
| back propagation ANN | error < 3% | |||||
| ring forming | numerical (FE simulation), 700 | polynomial regression factors to fit load-displacement curves | strain hardening exponent, strength coefficient, COF | ANN (8:21:3:3) | accuracy > 97% | [105] |
| Subject | Database, Number of Data Sets (If Applicable Divided in Train/Test/Validation) | Inputs | Outputs | ML Approach | Prediction | Ref. |
|---|---|---|---|---|---|---|
| thermally sprayed Al2O3-TiO2 coatings | experimental (pin-on-disk), 8 | load, environment (dry or acid) | linear wear, COF at different time steps | back propagation ANN (2:80:63) | sufficient (not quantified) | [108] |
| HVOF sprayed Cr-C-Ni-Cr and WC-Co coatings and electroplated hard chromium | experimental (pin-on-disk), 360 (50%/50%) | material type, normal load, sliding velocity, sliding distance | COF | back propagation ANN (4:6:4:1) | errors < 11% | [109] |
| multilayer nitride PVD coatings | experimental (pin-on-disk), 246 (70%/15%/15%) | time, normal load, sliding velocity, lap, bias voltage, gas flow rate | spec. wear rate, COF | back propagation ANN (6:5:5:2) | errors < 1% | [110,111] |
| surface texture design for EHL contacts | experimental (mini traction machine), 2000 (90%/5%/5%) | average velocity, slide-to-roll ratio, normal load, minor axis, major axis, texture depth, texture density | COF | various ANNs, best results for back propagation ANN (7:20:1) | MSE < 0,1%, R2 > 0.99 | [112] |
| experimental (mini traction machine), 1704 | entrainment speed, slide-to-roll ratio, surface feature ball, surface feature disk | COF | Hardy multiquadric RBF | R2 > 0.935 | [113] | |
| numerical (EHL simulation) in LHS, 70 (70%/30%) | texture diameter, texture depth texture distance | max. pressure, min. film height, COF | MOP | CoP > 83% | [115,116] | |
| surface texture design for HL contacts | numerical (HL simulation) | dimple diameter, depth, area density, and various statistical deviations | COF, load carrying capacity | various ANNs, best results for back propagation ANN (41:20:2) | accuracy > 99.7% (COF), accuracy > 97.5% (load carrying capacity) | [114] |
| Subject | Database, Number of Data Sets (If Applicable Divided in Train/Test/Validation) | Inputs | Outputs | ML Approach | Prediction | Ref. |
|---|---|---|---|---|---|---|
| PTFE-based additives in mineral oil | experimental (journal bearing test-rig), 252 (80%/20%) | load, velocity, additive concentration | COF | back propagation ANN (3:5:3:1) | accuracy > 98% | [120] |
| vegetable oil- diesel fuel mixtures | experimental (pin-on-disk), 135 | sunflower concentration, rapeseed concentration | COF | back propagation ANN (2:2:6:9:1) | RMSE < 0,1% | [121] |
| lubricant formulations with vegetable oil blends and friction modifiers (MWCNT, graphene) | literature (pin-on-disk, four-ball-tests), 200 | speed, normal load, temperature, ball/pin/disk hardness, coconut oil content, castor oil content, palm oil content, MWCNT content, MWCNT size, graphene content, graphene dimensions | COF | scaled conjugate gradient back propagation ANN | accuracy > 92% | [122,123] |
| biodiesel formulation | experimental (transesterification), 30 | time, catalyst concentration, methanol-to-oil ratio, duty cycle | biodiesel yield | RSM | R2 > 0.994, MSE < 0.023, RMSE < 0.151 | [124] |
| Cuckoo ELM | R2 > 0.996, MSE < 0.024, RMSE < 0.117 | |||||
| lubricant additives | literature and numerical (DFT and MD simulation) | lattice constant, c/a ratio, bond angle, interlayer space, M-X length, X-X length, M-radii, hexagonal width, in-plane stiffness, cohesive energy, binding energy, bandgap energy, thermal conductivity, average mass | maximum energy barrier | Bayesian model | MSE < 0.25 | [126] |
| Application Area | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Composite Materials | Drive Technology | Manufacturing | Surface Engineering | |||||||||||
| ML Approach | Thermoset Matrix | Thermoplastic Matrix | Metal Matrix | Rolling Bearings | Sliding Bearings | Seals | Brakes And Clutches | Friction Stir Welding | Forming | Machining | Coating | Texturing | Lubricants | Others |
| ANN | [39,40,41,42] | [43,44,45,46,47,48,49,50,51,52,53] | [60,61,62,63,64] | [69,70] | [75,76,77] | [82] | [86,87,88,89,91,92] | [97,98,99,100,101,103,104] | [105] | [106] | [108,109,110,111] | [112,114] | [120,121,122,123] | [131,132,133,134,136] |
| ANFIS | [101] | |||||||||||||
| Bayesian | [126] | |||||||||||||
| DT | [63,64] | [60] | [106] | [135,136] | ||||||||||
| KNN | [63,64] | |||||||||||||
| MOP | [73] | [115,116] | ||||||||||||
| QDA | [71] | |||||||||||||
| RF | [63,64] | [78] | [106] | [136] | ||||||||||
| RBF | [106] | [113] | ||||||||||||
| SVM | [63,64] | [83] | [90] | [104] | [136] | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marian, M.; Tremmel, S. Current Trends and Applications of Machine Learning in Tribology—A Review. Lubricants 2021, 9, 86. https://doi.org/10.3390/lubricants9090086
Marian M, Tremmel S. Current Trends and Applications of Machine Learning in Tribology—A Review. Lubricants. 2021; 9(9):86. https://doi.org/10.3390/lubricants9090086
Chicago/Turabian StyleMarian, Max, and Stephan Tremmel. 2021. "Current Trends and Applications of Machine Learning in Tribology—A Review" Lubricants 9, no. 9: 86. https://doi.org/10.3390/lubricants9090086
APA StyleMarian, M., & Tremmel, S. (2021). Current Trends and Applications of Machine Learning in Tribology—A Review. Lubricants, 9(9), 86. https://doi.org/10.3390/lubricants9090086







