Fundamentals of Physics-Informed Neural Networks Applied to Solve the Reynolds Boundary Value Problem
Abstract
:1. Introduction
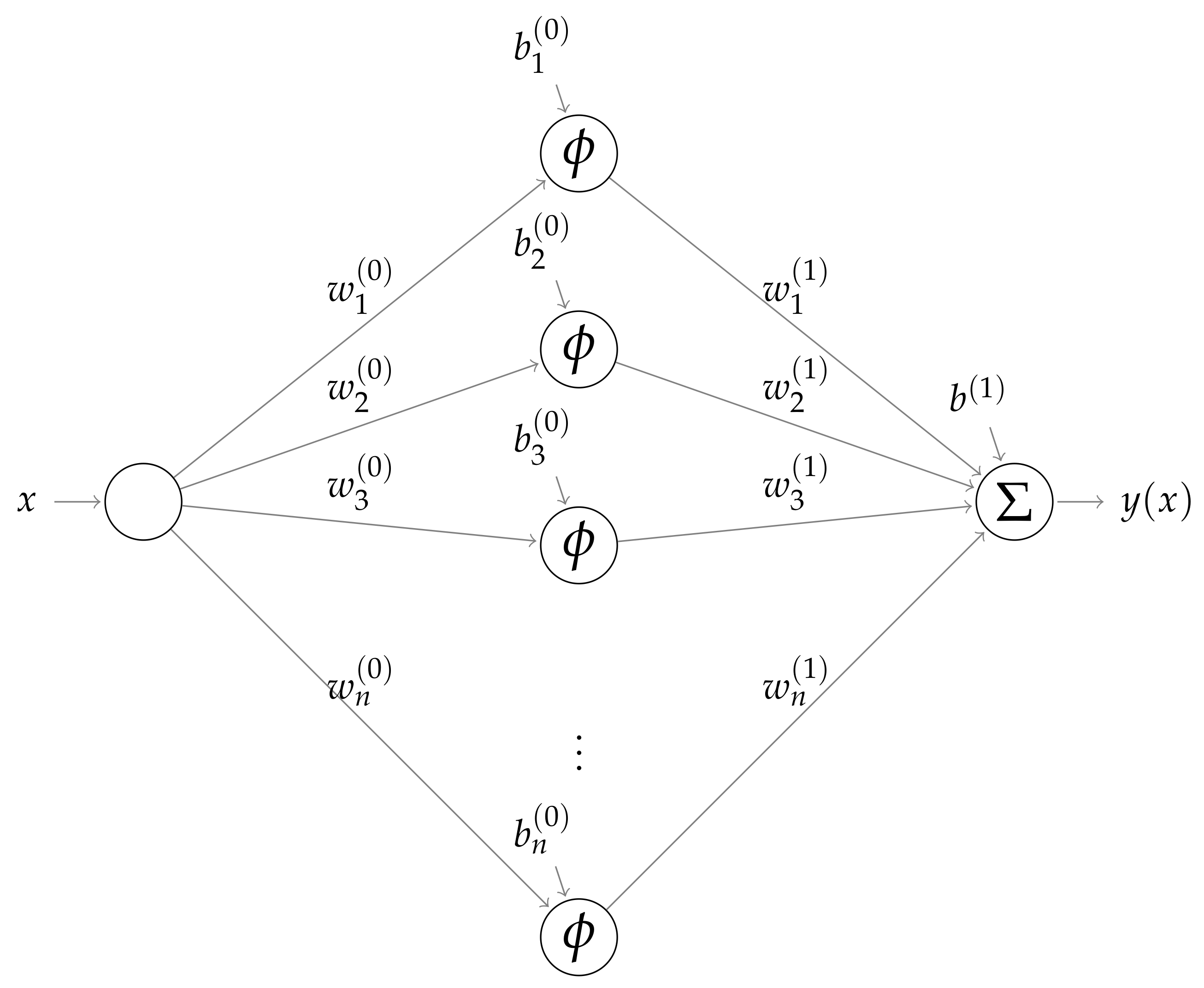
2. PINN Architecture
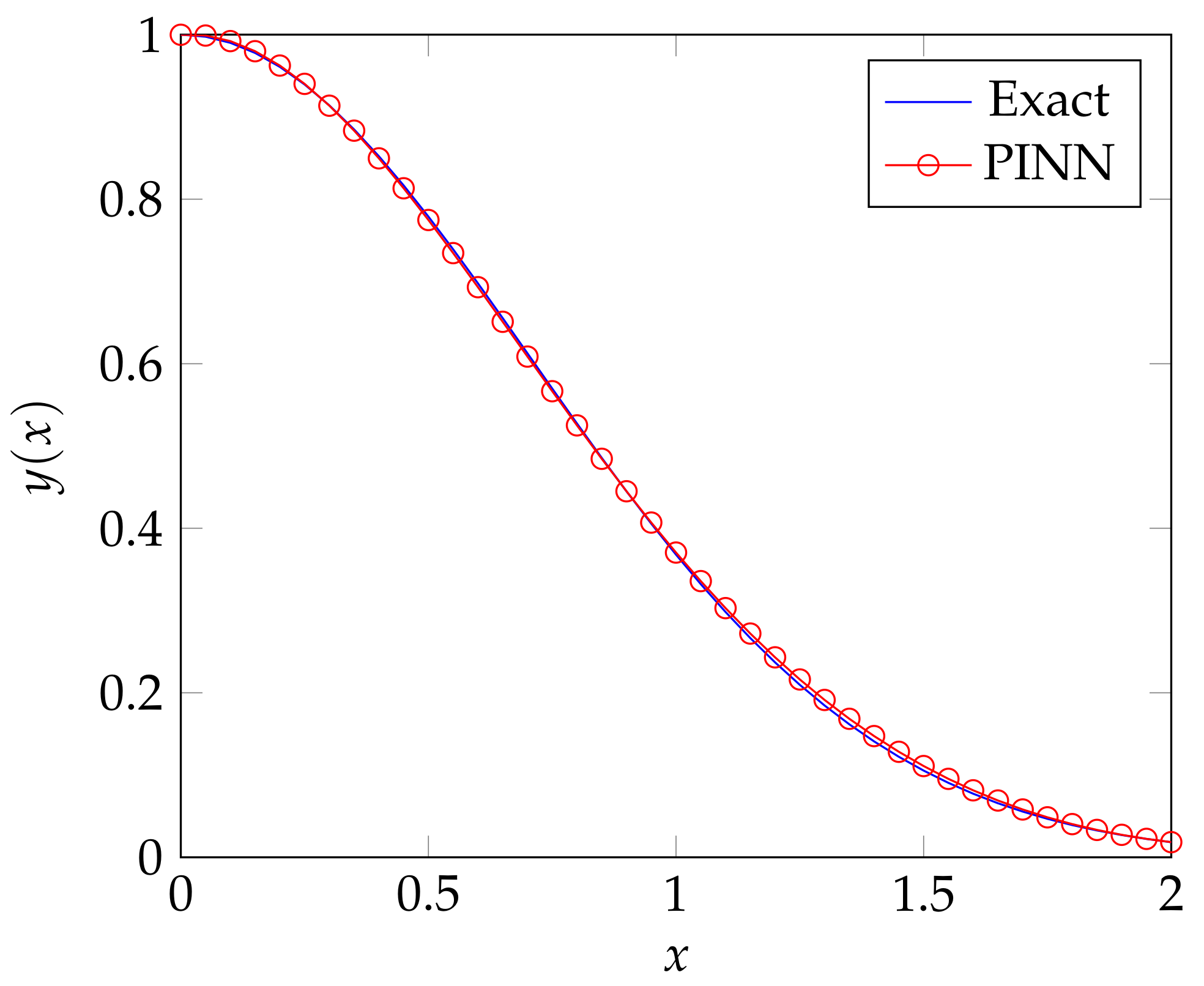
3. A First Order ODE Example
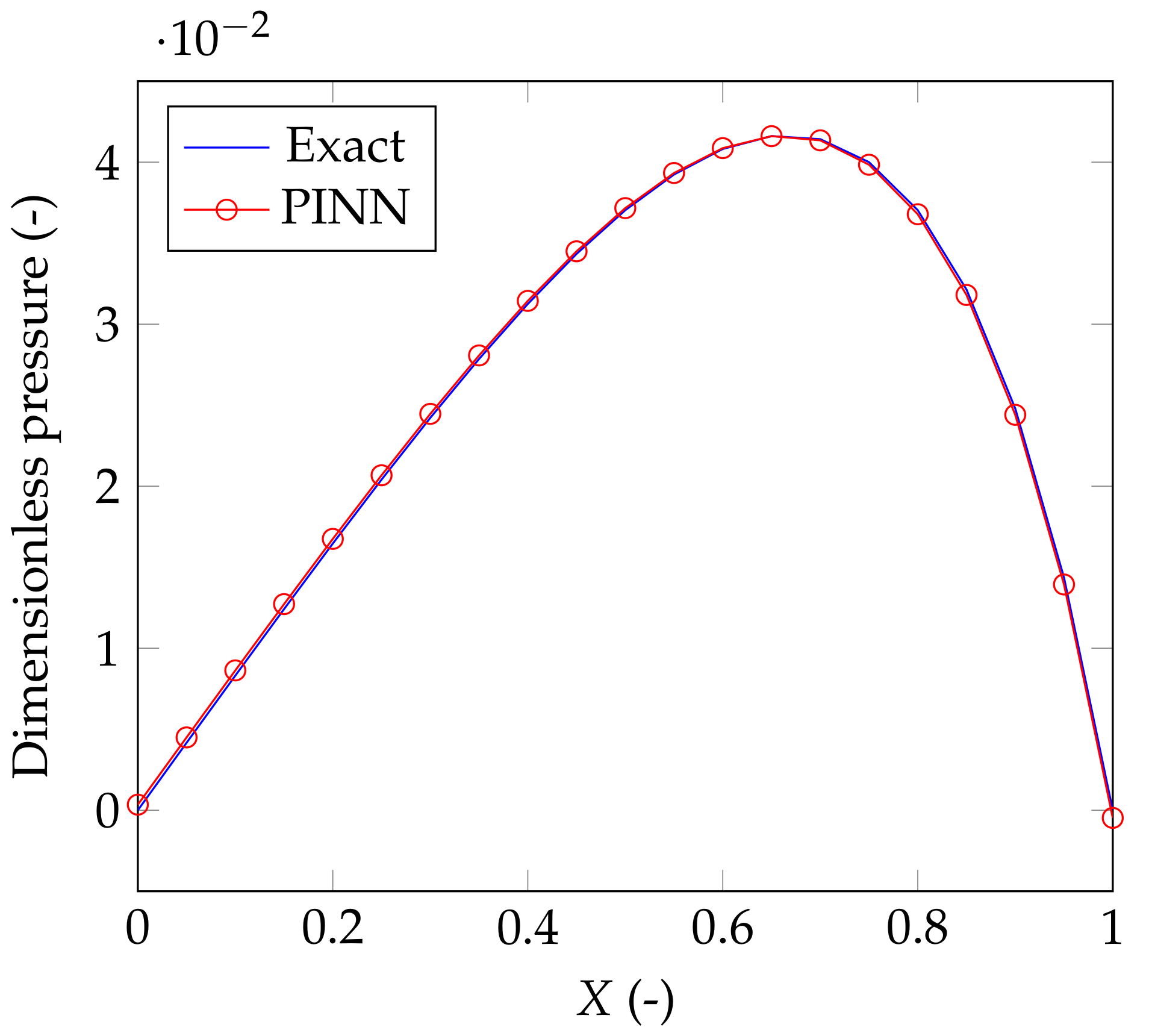
4. A PINN for the Classical Reynolds Equation
5. Concluding Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Karniadakis, G.E.; Kevrekidis, I.G.; Perdikaris, L.L.P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Bai, X.D.; Wang, Y.; Zhang, W. Applying physics informed neural network for flow data assimilation. J. Hydrodyn. 2020, 32, 1050–1058. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Liu, G.R. Mesh Free Methods: Moving beyond the Finite Element Method; Taylor & Francis: Boca Raton, FL, USA, 2003. [Google Scholar]
- Reynolds, O. On the theory of lubrication and its application to Mr. Beauchamps tower’s experiments, including an experimental determination of the viscosity of olive oil. Philos. Trans. R. Soc. Lond. A 1886, 177, 157–234. [Google Scholar]
- Almqvist, A.; Burtseva, E.; Pérez-Rà fols, F.; Wall, P. New insights on lubrication theory for compressible fluids. Int. J. Eng. Sci. 2019, 145, 103170. [Google Scholar] [CrossRef]
- Almqvist, A.; Burtseva, E.; Rajagopal, K.; Wall, P. On lower-dimensional models in lubrication, part a: Common misinterpretations and incorrect usage of the reynolds equation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 235, 1692–1702. [Google Scholar] [CrossRef]
- Almqvist, A.; Burtseva, E.; Rajagopal, K.; Wall, P. On lower-dimensional models in lubrication, part b: Derivation of a reynolds type of equation for incompressible piezo-viscous fluids. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 235, 1703–1718. [Google Scholar] [CrossRef]
- Almqvist, A. Physics-Informed Neural Network Solution of 2nd Order Ode:s. MATLAB Central File Exchange. Retrieved 31 July 2021. Available online: https://www.mathworks.com/matlabcentral/fileexchange/96852-physics-informed-neural-network-solution-of-2nd-order-ode-s (accessed on 7 July 2020).
- Neidinger, R.D. Introduction to automatic differentiation and MATLAB object-oriented programming. SIAM Rev. 2010, 52, 545–563. [Google Scholar] [CrossRef] [Green Version]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2018, 18, 1–43. [Google Scholar]
- Cauchy, A.M. Méthode générale pour la résolution des systèmes d’équations simultanées. Comp. Rend. Sci. Paris 1847, 25, 536–538. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Almqvist, A.; Pérez-Ràfols, F. Scientific Computing with Applications in Tribology: A Course Compendium. 2019. Available online: http://urn.kb.se/resolve?urn=urn:nbn:se:ltu:diva-72934 (accessed on 26 July 2021).
| Parameter | Description | Value |
|---|---|---|
| # of grid points for the solution domain | 41 | |
| # of training batches (# or corrections during 1 Epoch) | 1000 | |
| # of Epochs (1 Epoch contains training batches) | 100 | |
| Learning rate coefficient (relaxation for the update) | 0.01 | |
| N | # of nodes/neurons in the hidden layer | 10 |
| Node | ||||
|---|---|---|---|---|
| 1 | 1.8500 | −0.5946 | −3.5805 | 0.3055 |
| 2 | 1.8588 | 1.5974 | 0.9712 | |
| 3 | 0.3025 | 1.9241 | 0.8921 | |
| 4 | 1.4546 | 0.3742 | −0.9955 | |
| 5 | 0.5065 | 1.2535 | −0.1430 | |
| 6 | −1.0898 | −1.0199 | −1.1067 | |
| 7 | −0.8302 | 0.3519 | −1.1668 | |
| 8 | 0.3789 | 1.6502 | 0.1754 | |
| 9 | 2.5012 | 0.7657 | 1.2955 | |
| 10 | 2.2743 | 1.4172 | 1.2787 |
| Parameter | Description | Value |
|---|---|---|
| # of grid points for the solution domain | 21 | |
| K | Slope parameter for the Reynolds equation | 1 |
| # of training batches (# or corrections during 1 epoch) | 2000 | |
| # of Epochs (1 epoch contains training batches) | 600 | |
| Learning rate coefficient (relaxation for the update) | 0.005 | |
| N | # of nodes/neurons in the hidden layer | 10 |
| Node | ||||
|---|---|---|---|---|
| 1 | 0.0557 | 1.9808 | −0.2186 | −0.0641 |
| 2 | −6.3047 | 6.1664 | 0.1220 | |
| 3 | −9.3674 | 11.4571 | 0.3843 | |
| 4 | −4.5473 | 3.3266 | 0.0305 | |
| 5 | −2.4464 | −1.9884 | 0.1188 | |
| 6 | −0.1365 | −0.1674 | 0.4155 | |
| 7 | 0.8581 | 0.5253 | 0.5089 | |
| 8 | 1.0901 | 2.0858 | 0.3348 | |
| 9 | 0.2085 | 0.2523 | −0.2024 | |
| 10 | −3.2168 | 5.9722 | −0.9899 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almqvist, A. Fundamentals of Physics-Informed Neural Networks Applied to Solve the Reynolds Boundary Value Problem. Lubricants 2021, 9, 82. https://doi.org/10.3390/lubricants9080082
Almqvist A. Fundamentals of Physics-Informed Neural Networks Applied to Solve the Reynolds Boundary Value Problem. Lubricants. 2021; 9(8):82. https://doi.org/10.3390/lubricants9080082
Chicago/Turabian StyleAlmqvist, Andreas. 2021. "Fundamentals of Physics-Informed Neural Networks Applied to Solve the Reynolds Boundary Value Problem" Lubricants 9, no. 8: 82. https://doi.org/10.3390/lubricants9080082
APA StyleAlmqvist, A. (2021). Fundamentals of Physics-Informed Neural Networks Applied to Solve the Reynolds Boundary Value Problem. Lubricants, 9(8), 82. https://doi.org/10.3390/lubricants9080082





