Avoiding Starvation in Tribocontact Through Active Lubricant Transport in Laser Textured Surfaces
Abstract
:1. Introduction
1.1. Solution Approach
1.2. Outline of Article
2. Materials and Methods
2.1. Materials
2.2. Numerical Methods
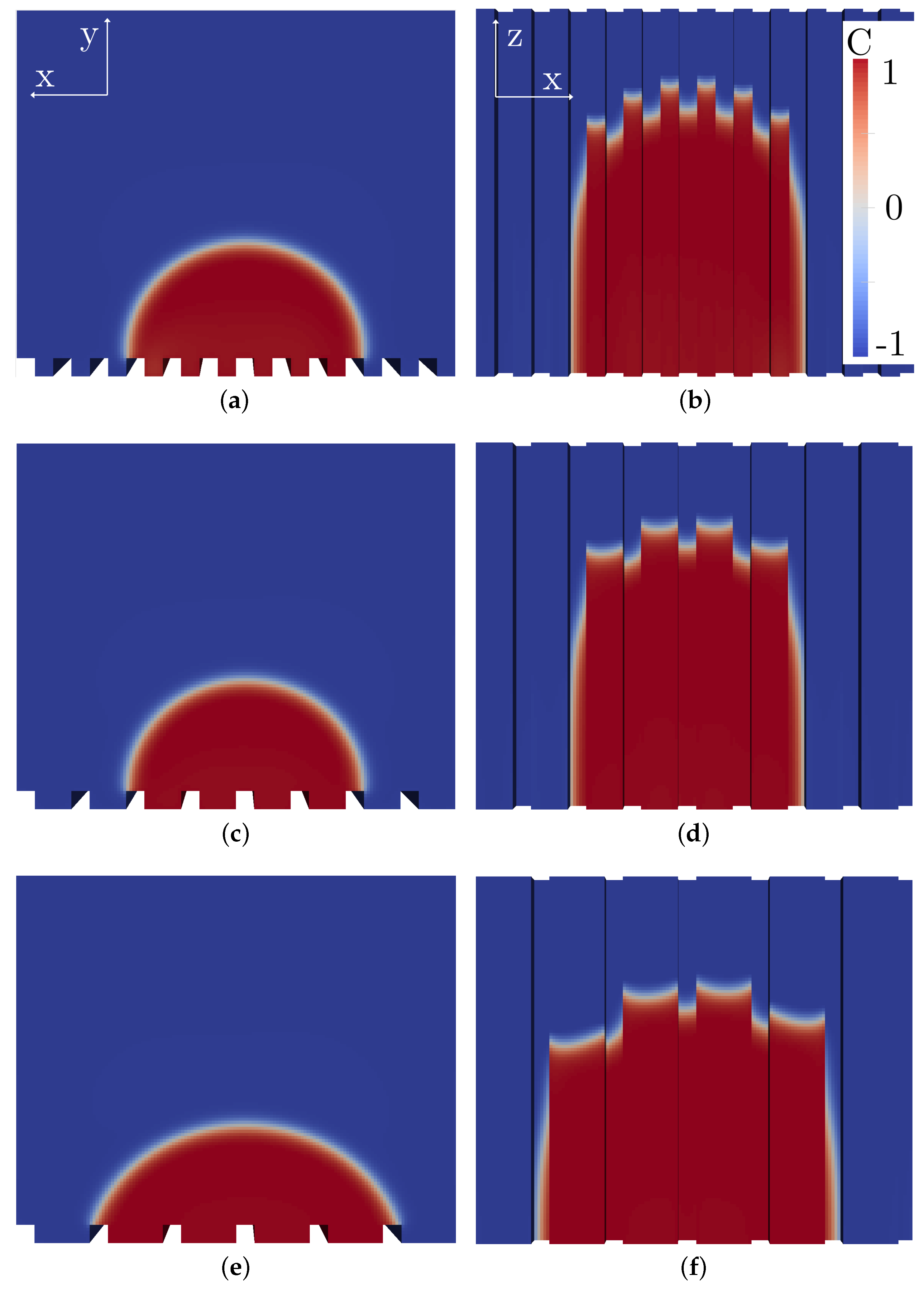
2.2.1. Phase-Field Approach for Interface Evolution
2.2.2. Governing Equations for the Fluid Flow
2.2.3. Numerical Aspects
2.3. Experimental Methods
2.3.1. Laser Surface Texturing
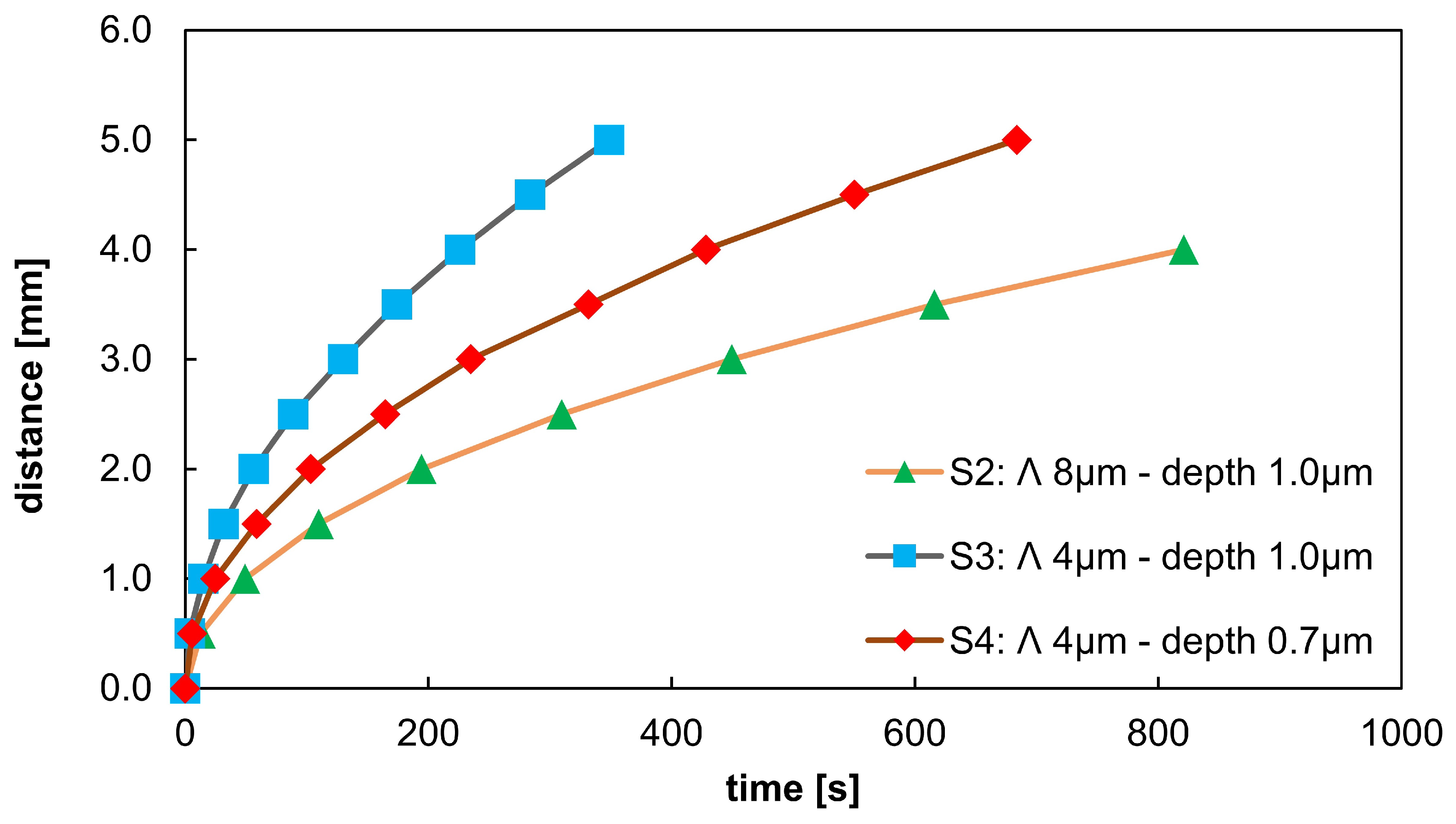
2.3.2. Fluid Transport Evaluation
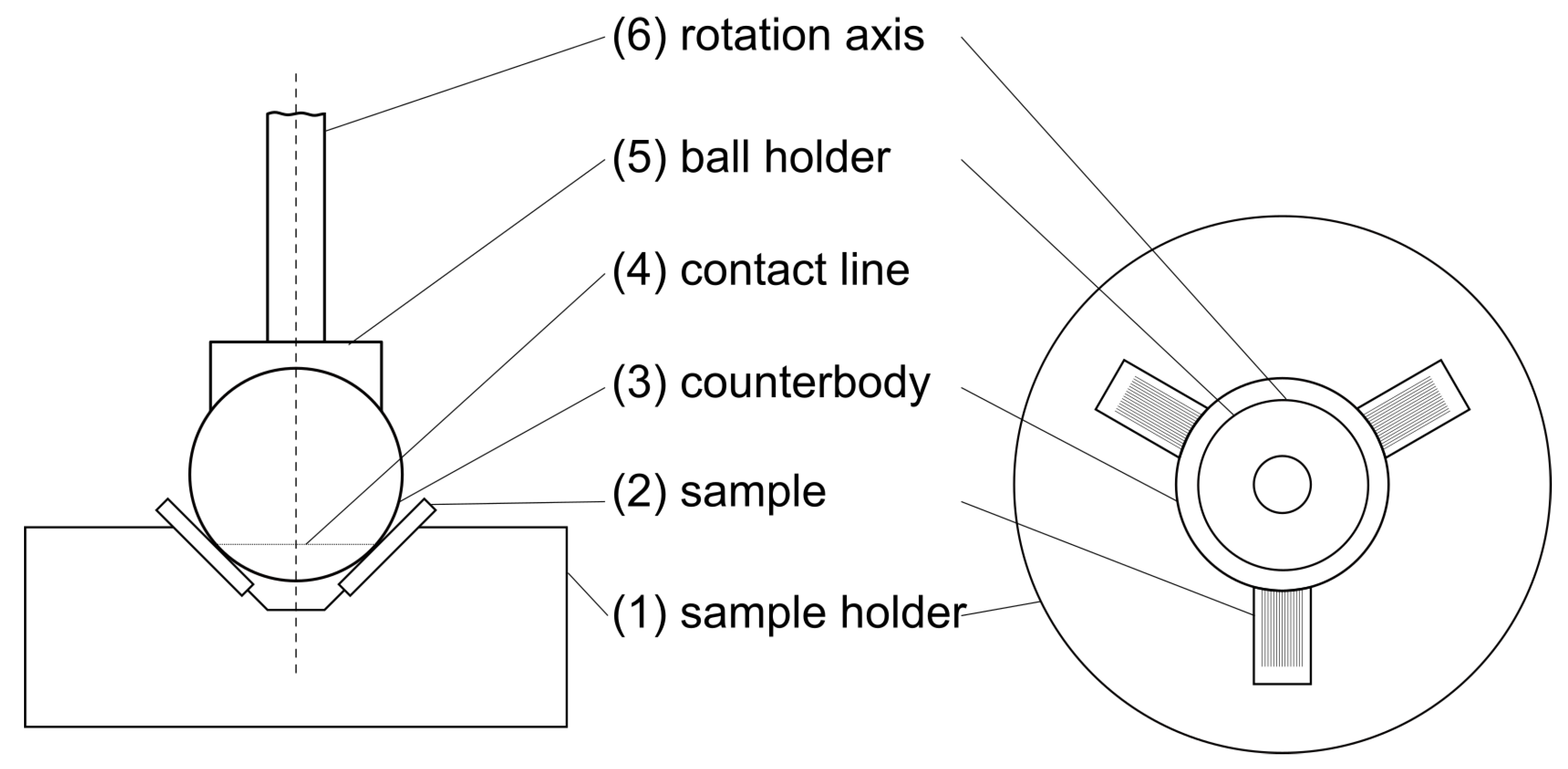
2.3.3. Characterization of Tribological Properties
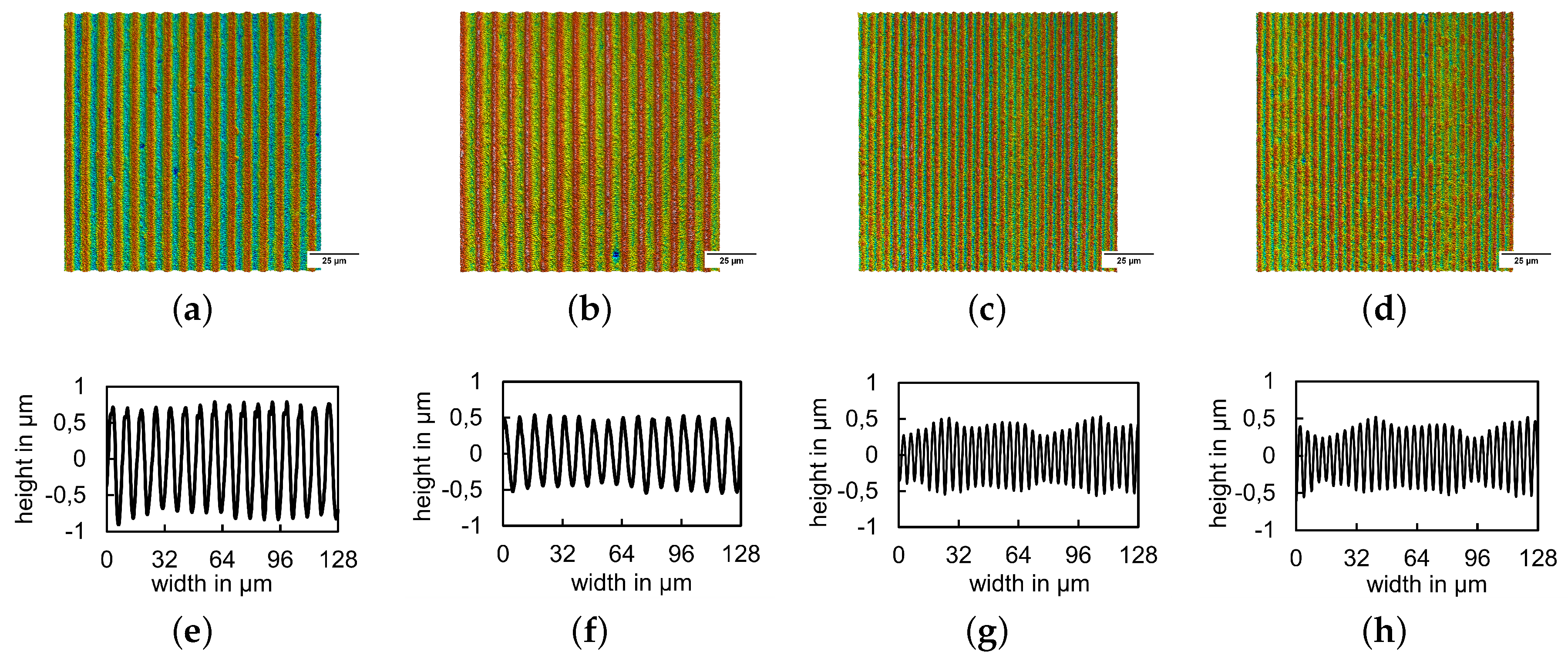
2.3.4. Surface Characterization
3. Results and Discussion
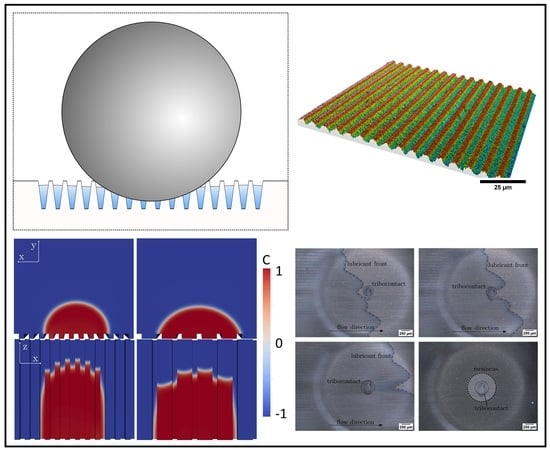
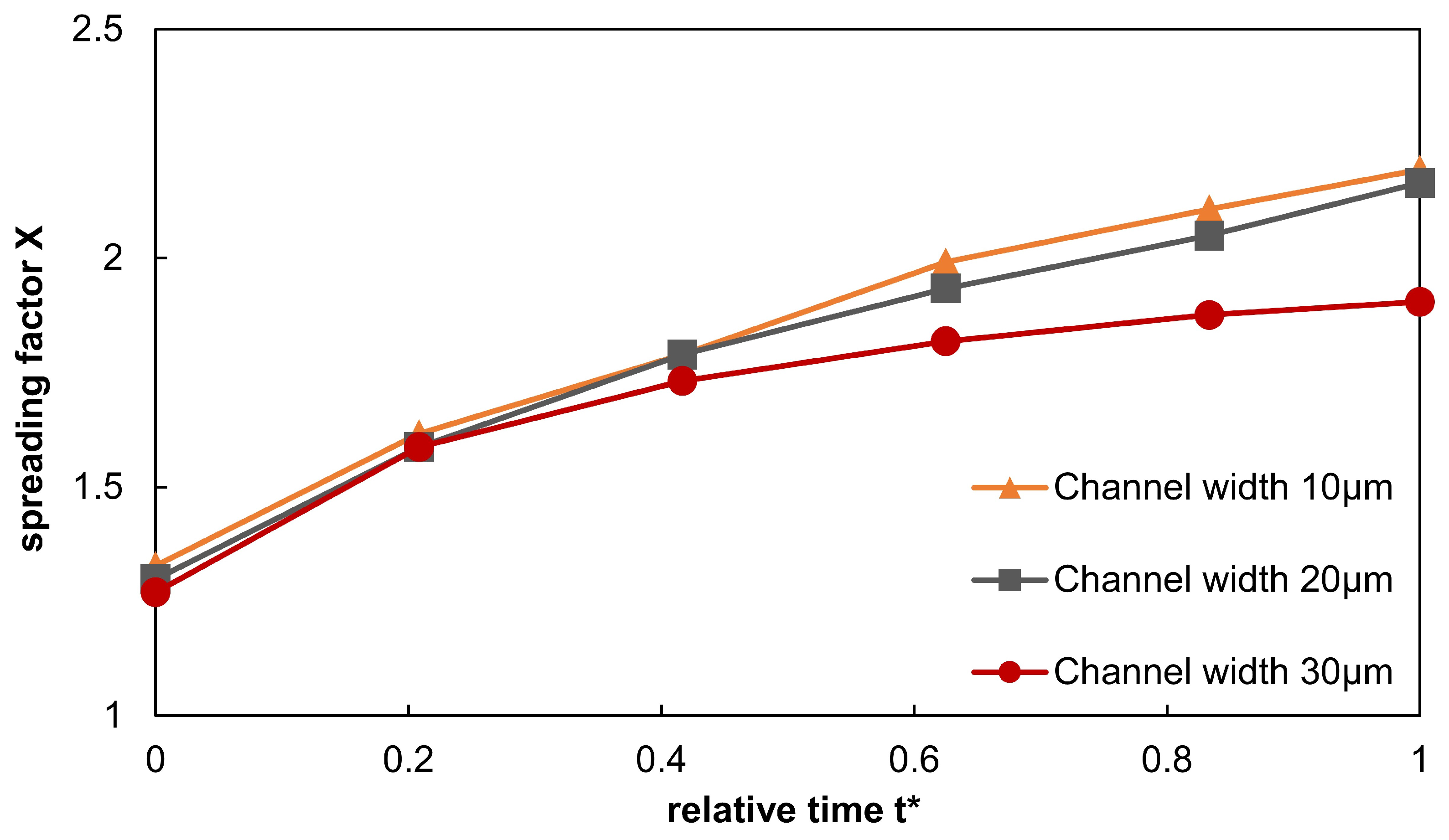
3.1. Numerical Results-Droplet Wetting on Line-Like Textures
3.2. Experimental Results
3.2.1. Fabrication of Line-Like Surface Textures Using DLIP
3.2.2. Fluid Transport Inside Laser Textured Surfaces
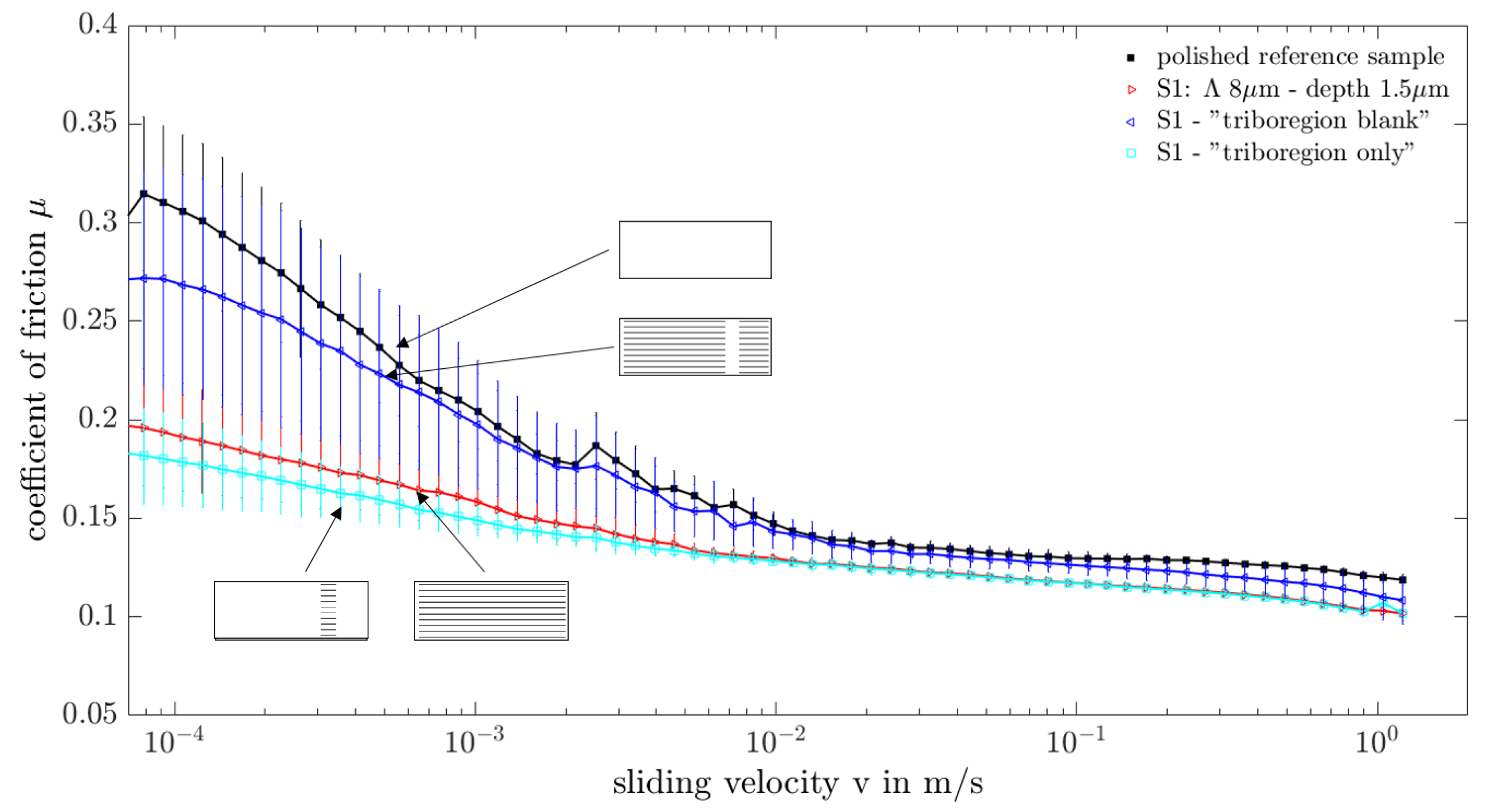
3.2.3. Evaluation of Tribological Performance
3.2.4. Transition of Fluid out of Laser Textured Surfaces into Tribocontact
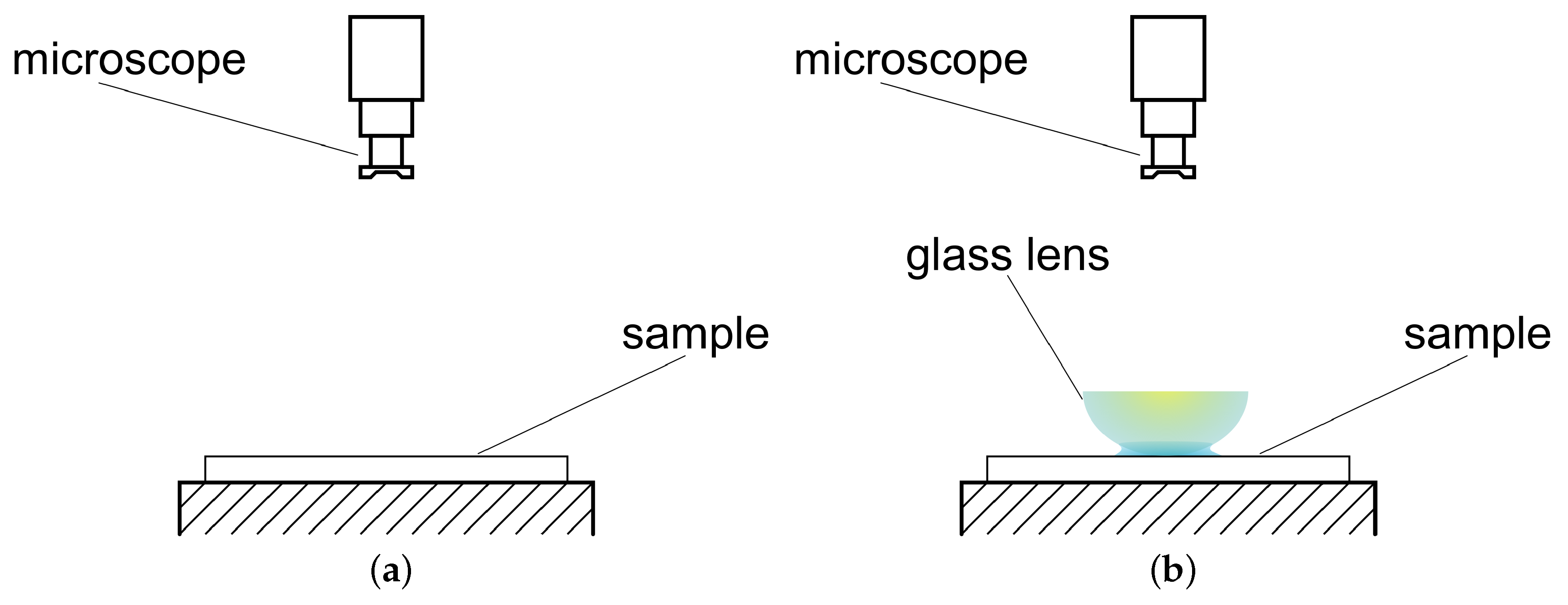
- Due to a necessary amount of light for microscopy a glass lens is used instead of the 100Cr6 ball. The lens has the same radius of curvature and similar wetting properties.
- The phenomena in the tribometer occur under dynamic conditions. In the alternative setup it is only possible to observe effects under static conditions.
- The test samples first run in the tribometer and then the transition effects with the glass lens are observed. Therefore, the tribocontact exists on the sample and the glass lens is put manually into this contact.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| LST | laser surface texturing |
| COF | coefficient of friction |
| DLW | Direct Laser Writing |
| DLIP | Direct Laser Interference Patterning |
Appendix A
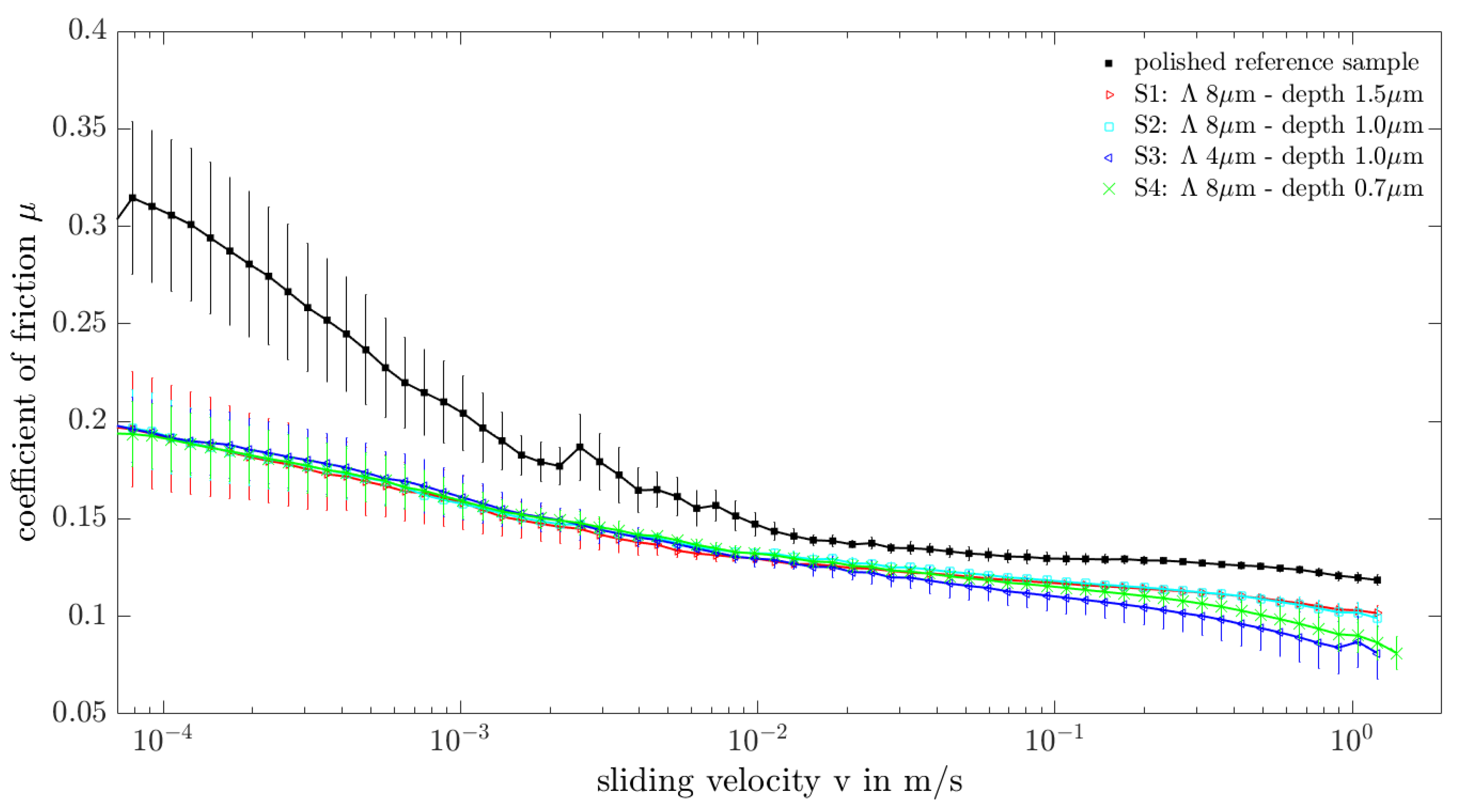
Appendix A.1. Tribological comparison of all DLIP textures introduced in this study
Appendix A.2. Numerical Parameters and Solver Settings
| Field | Solver | Preconditioner | Smoother |
|---|---|---|---|
| pd | PCG | DIC | GaussSeidel |
| U | BiCGStab | DILU | none |
| C | PBiCG | DILU | none |
| Ccoupled | GMRES | Cholesky | none |
| Operation | OpenFOAM | Scheme |
|---|---|---|
| Time derivative | ddt | Euler |
| Gradient | grad | Gauss linear |
| Divergence | div | Gauss Gamma |
| Laplacian | laplacian | Gauss linear uncorrected |
| Interpolation | interpolation | linear |
References
- Holmberg, K.; Andersson, P.; Erdemir, A. Global energy consumption due to friction in passenger cars. Tribol. Int. 2012, 47, 221–234. [Google Scholar] [CrossRef]
- Baumgartner, W.; Saxe, F.; Weth, A.; Hajas, D.; Sigumonrong, D.; Emmerlich, J.; Singheiser, M.; Böhme, W.; Schneider, J.M. The sandfish’s skin: Morphology, chemistry and reconstruction. J. Bionic Eng. 2007, 4, 1–9. [Google Scholar] [CrossRef]
- Kovalchenko, A.; Ajayi, O.; Erdemir, A.; Fenske, G. Friction and wear behavior of laser textured surface under lubricated initial point contact. Wear 2011, 271, 1719–1725. [Google Scholar] [CrossRef]
- Borghi, A.; Gualtieri, E.; Marchetto, D.; Moretti, L.; Valeri, S. Tribological effects of surface texturing on nitriding steel for high-performance engine applications. Wear 2008, 265, 1046–1051. [Google Scholar] [CrossRef]
- Blatter, A.; Maillat, M.; Pimenov, S.; Shafeev, G.; Simakin, A.; Loubnin, E. Lubricated sliding performance of laser-patterned sapphire. Wear 1999, 232, 226–230. [Google Scholar] [CrossRef]
- Andersson, P.; Koskinen, J.; Varjus, S.E.; Gerbig, Y.; Haefke, H.; Georgiou, S.; Zhmud, B.; Buss, W. Microlubrication effect by laser-textured steel surfaces. Wear 2007, 262, 369–379. [Google Scholar] [CrossRef]
- Duarte, M.; Lasagni, A.; Giovanelli, R.; Narciso, J.; Louis, E.; Mücklich, F. Increasing lubricant film lifetime by grooving periodical patterns using laser interference metallurgy. Adv. Eng. Mater. 2008, 10, 554–558. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Martin, B.; Bettscheider, S.; Gachot, C.; Kliem, H.; Mücklich, F. Correlation between solid–solid contact ratios and lubrication regimes measured by a refined electrical resistivity circuit. Wear 2014, 320, 51–61. [Google Scholar] [CrossRef]
- Etsion, I. State of the art in laser surface texturing. J. Tribol. 2005, 127, 248–253. [Google Scholar] [CrossRef]
- Braun, D. Größeneffekte bei strukturierten tribologischen Wirkflächen. Ph.D. Thesis, KIT, Karlsruhe, Germany, 2015. [Google Scholar]
- Stark, T.; Alamri, S.; Aguilar-Morales, A.I.; Kiedrowski, T.; Lasagni, A.F. Positive effect of laser structured surfaces on tribological performance. J. Laser Micro Nanoeng. 2019, 14, 13–18. [Google Scholar]
- Lasagni, A.F. Laser interference patterning methods: Possibilities for high-throughput fabrication of periodic surface patterns. Adv. Opt. Technol. 2017, 6, 265–275. [Google Scholar] [CrossRef]
- Klima, J. Lubricant Transport Towards Tribocontact in Capillary Surface Structures; KIT Scientific Publishing: Karlsruhe, Germany, 2018; ISBN 978-3-7315-0814-4. [Google Scholar]
- Lucas, R. Ueber das Zeitgesetz des kapillaren Aufstiegs von Flüssigkeiten. Kolloid Zeitschrift 1918, 23, 15–22. [Google Scholar] [CrossRef]
- Washburn, E.W. The dynamics of capillary flow. Phys. Rev. 1921, 17, 273. [Google Scholar] [CrossRef]
- Yang, D.; Krasowska, M.; Priest, C.; Popescu, M.N.; Ralston, J. Dynamics of capillary-driven flow in open microchannels. J. Phys. Chem. 2011, 115, 18761–18769. [Google Scholar] [CrossRef]
- Chen, T. Capillary Force-Driven Fluid Flow in Open Grooves with Different Sizes. J. Thermophys. Heat Transf. 2015, 29, 594–601. [Google Scholar] [CrossRef]
- Grützmacher, P.G.; Rosenkranz, A.; Gachot, C. How to guide lubricants–Tailored laser surface patterns on stainless steel. Appl. Surf. Sci. 2016, 370, 59–66. [Google Scholar] [CrossRef]
- Lambert, P. Surface Tension in Microsystems; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Jacqmin, D. Contact-line dynamics of a diffuse fluid interface. J. Fluid Mech. 2000, 402, 57–88. [Google Scholar] [CrossRef]
- Cai, X.; Marschall, H.; Wörner, M.; Deutschmann, O. Numerical Simulation of Wetting Phenomena with a Phase-Field Method Using OpenFOAM®. Chem. Eng. Technol. 2015, 38, 1985–1992. [Google Scholar] [CrossRef]
- Fink, V.; Cai, X.; Stroh, A.; Bernard, R.; Kriegseis, J.; Frohnapfel, B.; Marschall, H.; Wörner, M. Drop bouncing by micro-grooves. Int. J. Heat Fluid Flow 2018, 70, 271–278. [Google Scholar] [CrossRef]
- Zolper, T.; Li, Z.; Chen, C.; Jungk, M.; Marks, T.; Chung, Y.W.; Wang, Q. Lubrication Properties of Polyalphaolefin and Polysiloxane Lubricants: Molecular Structure—Tribology Relationships. Tribol. Lett. 2012, 48, 355–365. [Google Scholar] [CrossRef]
- Deubelbeiss, Y.; Kaus, B. Comparison of Eulerian and Lagrangian numerical techniques for the Stokes equations in the presence of strongly varying viscosity. Phys. Earth Planet. Int. 2008, 171, 92–111. [Google Scholar] [CrossRef]
- Niethammer, M.; Marschall, H.; Kunkelmann, C.; Bothe, D. A numerical stabilization framework for viscoelastic fluid flow using the finite volume method on general unstructured meshes. Int. J. Numer. Methods Fluids 2018, 86, 131–166. [Google Scholar] [CrossRef]
- Lasagni, A.; Roch, T.; Berger, J.; Kunze, T.; Lang, V.; Beyer, E. To use or not to use (direct laser interference patterning), that is the question. In Proceedings of the Laser-Based Micro-and Nanoprocessing IX, San Francisco, CA, USA, 10–12 February 2015; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9351, p. 935115. [Google Scholar]



| Period | Hatch Distance | Frequency | Pulse Energy | Fluence | Pulse Overlap | |
|---|---|---|---|---|---|---|
| S1 | 20 | / | 96.88% | |||
| S2 | 10 | / | 93.75% | |||
| S3 | 10 | / | 93.75% | |||
| S4 | / | 90.63% |
| S1 | S2 | S3 | S4 | |
|---|---|---|---|---|
| period | ||||
| depth |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stark, T.; Kiedrowski, T.; Marschall, H.; Lasagni, A.F. Avoiding Starvation in Tribocontact Through Active Lubricant Transport in Laser Textured Surfaces. Lubricants 2019, 7, 54. https://doi.org/10.3390/lubricants7060054
Stark T, Kiedrowski T, Marschall H, Lasagni AF. Avoiding Starvation in Tribocontact Through Active Lubricant Transport in Laser Textured Surfaces. Lubricants. 2019; 7(6):54. https://doi.org/10.3390/lubricants7060054
Chicago/Turabian StyleStark, Tobias, Thomas Kiedrowski, Holger Marschall, and Andrés Fabián Lasagni. 2019. "Avoiding Starvation in Tribocontact Through Active Lubricant Transport in Laser Textured Surfaces" Lubricants 7, no. 6: 54. https://doi.org/10.3390/lubricants7060054
APA StyleStark, T., Kiedrowski, T., Marschall, H., & Lasagni, A. F. (2019). Avoiding Starvation in Tribocontact Through Active Lubricant Transport in Laser Textured Surfaces. Lubricants, 7(6), 54. https://doi.org/10.3390/lubricants7060054