Numerical Simulation of a Slipper Model with Multi-Lands and Grooves for Hydraulic Piston Pumps and Motors in Mixed Lubrication
Abstract
1. Introduction
2. Theoretical Model
2.1. Basic Equations
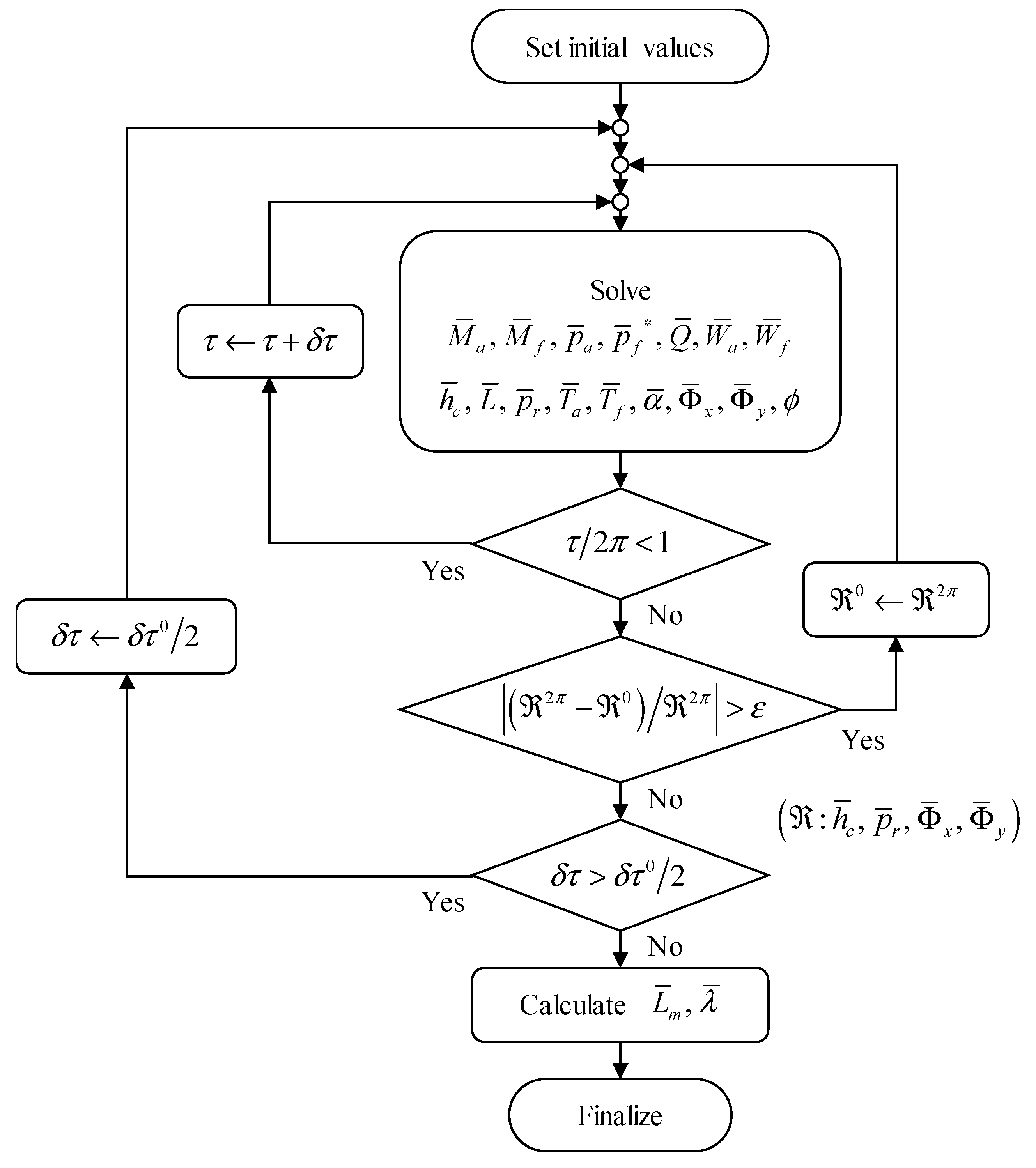
2.2. Calculation Procedure
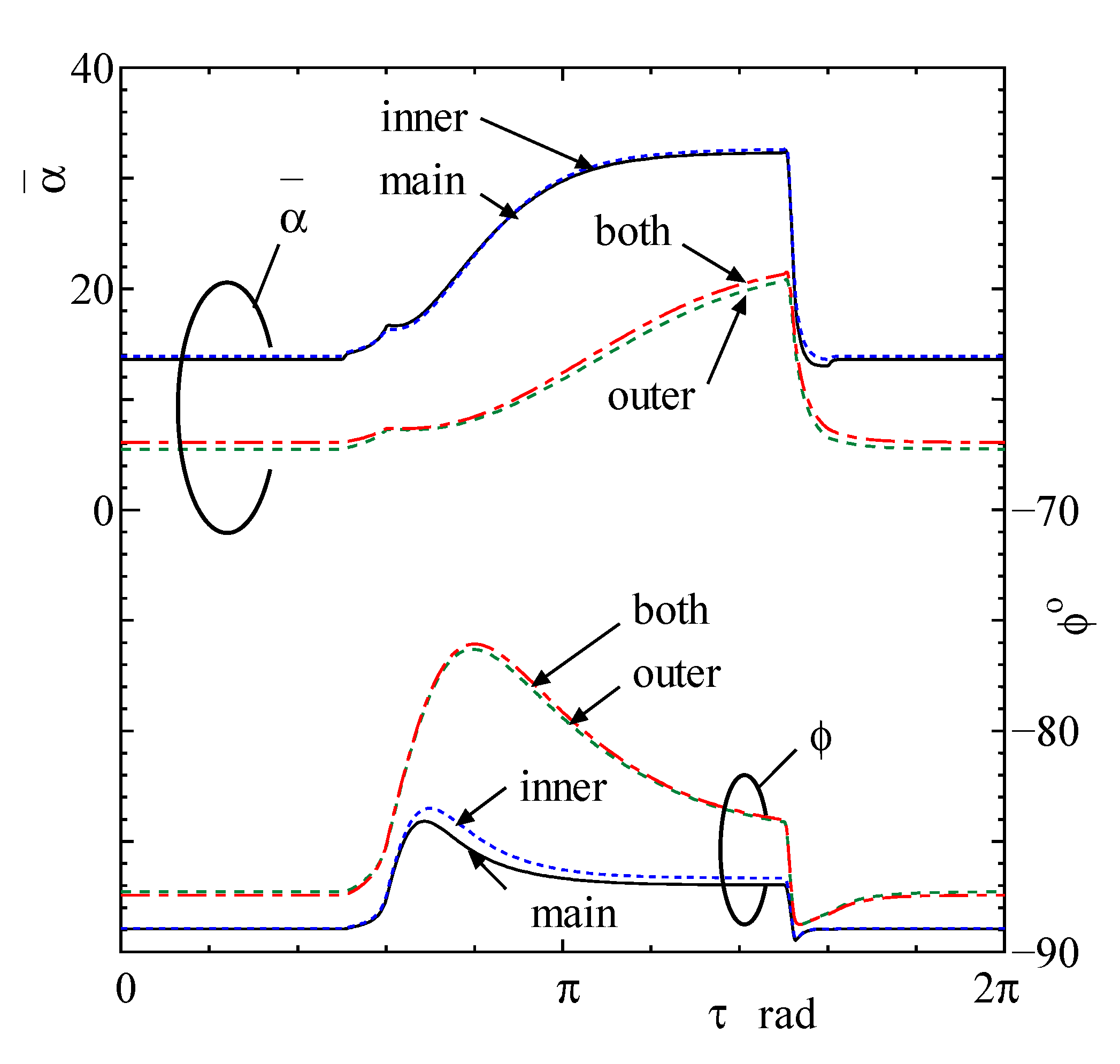
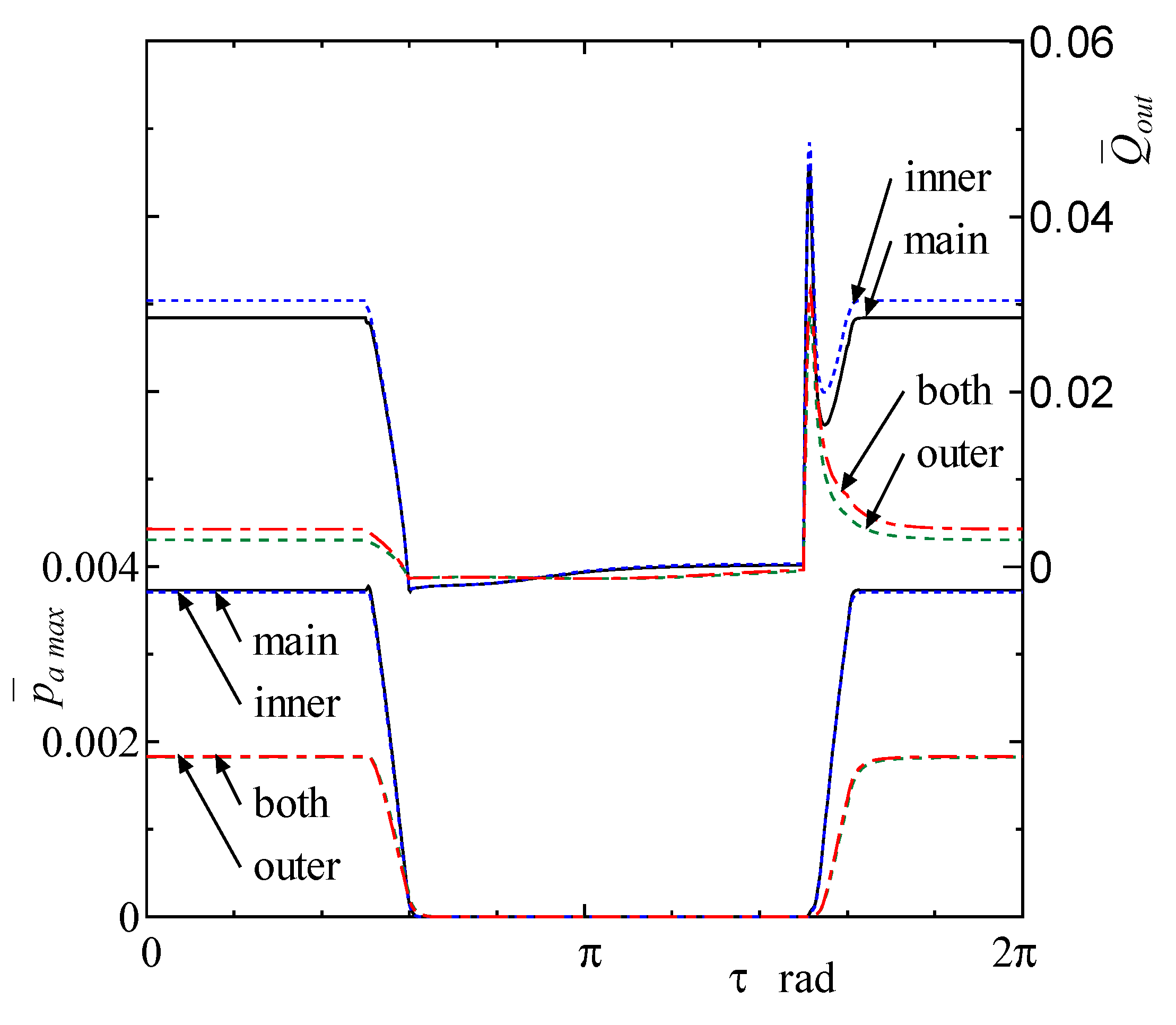
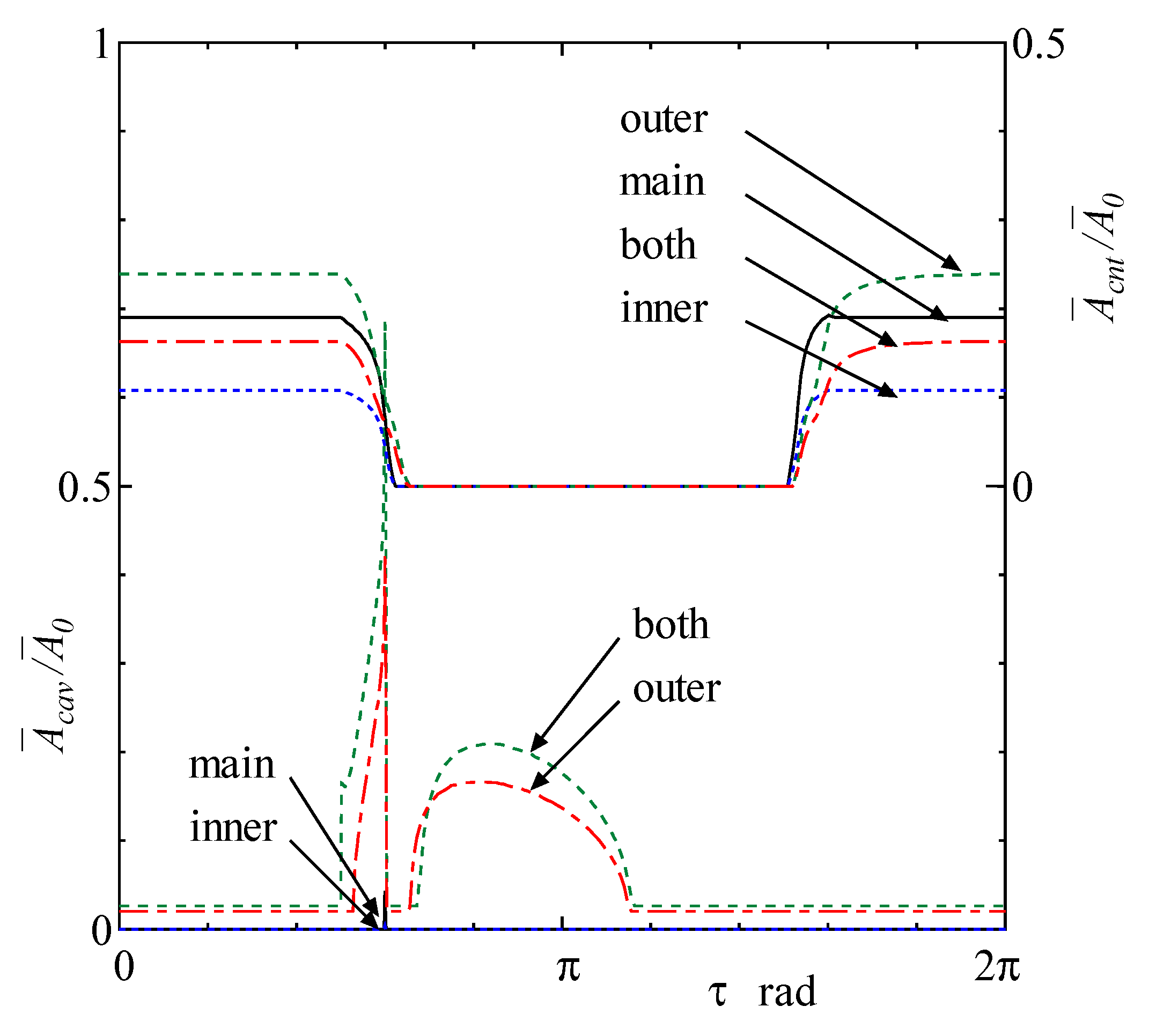
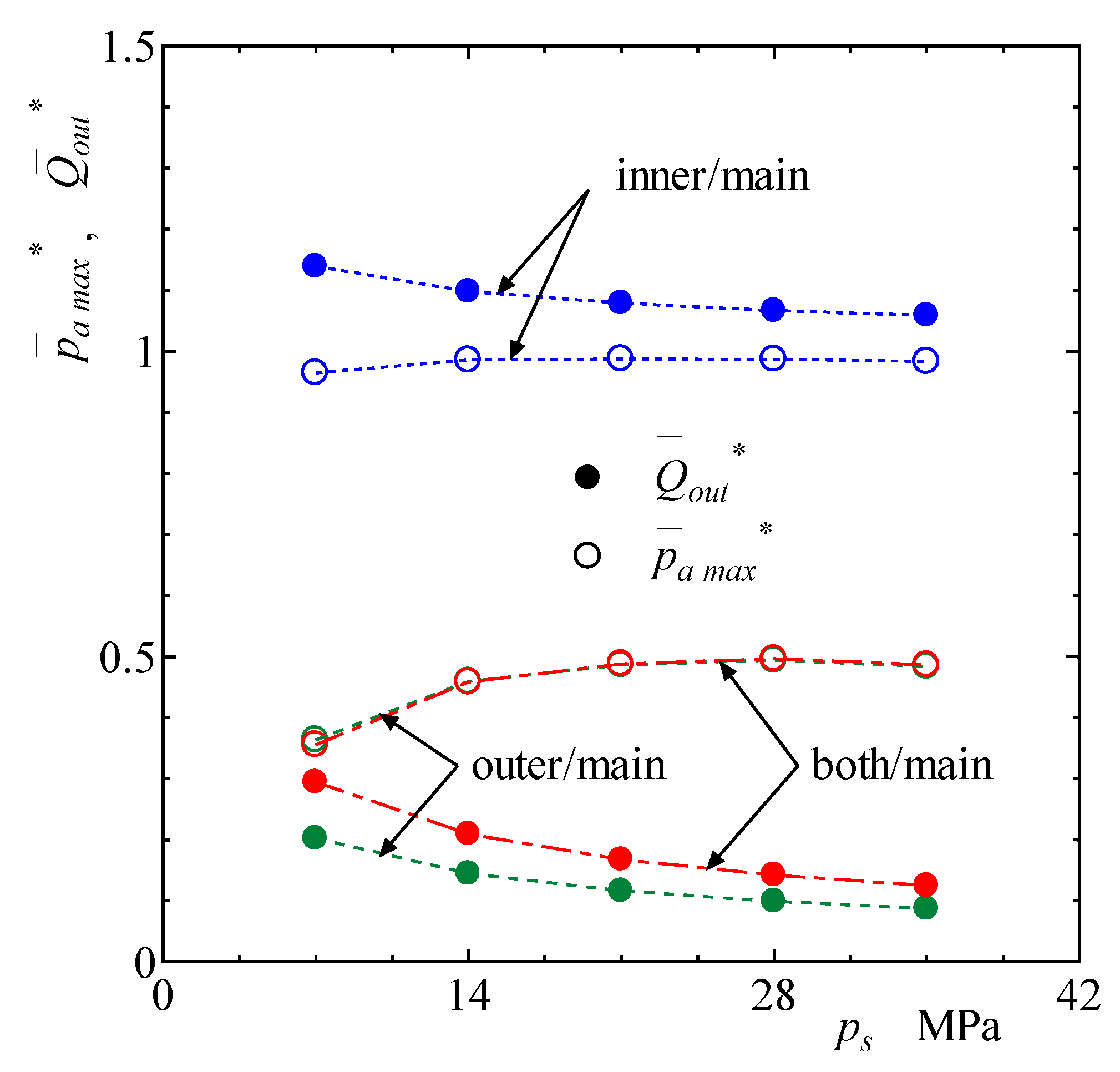
3. Results and Discussion
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
Nomenclature
| inner radius ratio of main land, = | |
| outer radius ratio of main land, = | |
| inner radius ratio of inner land, = | |
| outer radius ratio of inner land, = | |
| inner radius ratio of outer land, = | |
| outer radius ratio of outer land, = | |
| separation | |
| equivalent elastic modulus, = | |
| H | representative clearance |
| hardness, = | |
| h | clearance, = |
| center thickness | |
| mean film thickness | |
| moment inertia, = | |
| bulk modulus | |
| power loss, = | |
| moment, = | |
| mass, = | |
| pressure, = | |
| ambient pressure, = | |
| recess pressure, = | |
| supply pressure, = | |
| Q | flow rate, = |
| leaked flow rate, = | |
| revolution radius | |
| representative radius | |
| coordinates, = r/R2, θ, z/H | |
| load eccentricity | |
| parameter, = | |
| friction torque, = | |
| recess volume, = | |
| load, = | |
| plasticity index | |
| coordinates | |
| coordinates | |
| pad inclination angle, = | |
| restrictor parameter, = | |
| equivalent radius of asperity summit | |
| hydrostatic balance ratio | |
| asperity density | |
| stiffness, = | |
| viscosity | |
| surface roughness, = | |
| standard deviation of asperity summit height | |
| time, = | |
| pad azimuth | |
| representative angular velocity | |
| disk angular velocity | |
| pad angular velocity | |
| Subscripts: | |
| a | asperity, contact |
| c | center |
| f | fluid |
| gri | inner groove |
| gro | outer groove |
| in | inner land |
| m | time-average |
| max | maximum |
| min | minimum |
| mn | main land |
| out | outer land |
| r | recess |
| 0 | reference, high pressure period |
| 1 | inside |
| 2 | outside |
Appendix A
Appendix B
References
- Shute, N.A.; Turnbull, D.E. Minimum power loss of hydrostatic slipper bearings for axial piston machines. Proc. Int. Conv. Lubr. Wear 1963, 6, 3–14. [Google Scholar]
- Böinghoff, O. Untersuchen zum Reibungsverhalten der Gleitschuhe in Schrägscheiben-Axialkolbenmascinen. VDI Forsch. 1977, 584, 1–46. [Google Scholar]
- Iboshi, N.; Yamaguchi, A. Characteristics of a slipper bearing for swash plate type axial piston pumps and motors: 1st report, theoretical analysis. Bull. Jpn. Soc. Mech. Eng. 1982, 25, 1921–1930. [Google Scholar] [CrossRef][Green Version]
- Koç, E.; Hooke, C.J. Considerations in the design of partially hydrostatic slipper bearings. Tribol. Int. 1997, 30, 815–823. [Google Scholar] [CrossRef]
- Manring, N.D. The relative motion between the ball guide and slipper retainer within an axial-piston swash-plate type hydrostatic pump. J. Dyn. Syst. Meas. Control Trans. ASME 1999, 121, 518–523. [Google Scholar] [CrossRef]
- Suzuki, K.; Suzuki, M.; Sakurai, S.; Hemmi, M.; Kazama, T. Multi body dynamics of a slipper in swash plate type piston pumps and motors couples with hydrodynamic analysis of oil-film. Bull. Jpn. Soc. Mech. Eng. 2014, 80, FE0224. (In Japanese) [Google Scholar] [CrossRef]
- Schenk, A.; Ivantysynova, M.A. Transient thermoelastohydrodynamic lubrication model for the slipper/swashplate in axial piston machines. J. Tribol. Trans. ASME 2015, 137, 031701–031710. [Google Scholar] [CrossRef]
- Lin, S.; Hu, J. Tribo-dynamic model of slipper bearings. Appl. Math. Model. 2015, 39, 548–558. [Google Scholar] [CrossRef]
- Hashemi, S.; Kroker, A.; Bobach, L.; Bartel, D. Multibody dynamics of pivot slipper pad thrust bearing in axial piston machines incorporating thermal elastohydrodynamics and mixed lubrication model. Tribol. Int. 2016, 96, 57–76. [Google Scholar] [CrossRef]
- Bergada, J.M.; Watton, J.; Haynes, J.M.; Davies, D.L. The hydrostatic/hydrodynamic behaviour of an axial piston pump slipper with multiple lands. Meccanica 2010, 45, 58–602. [Google Scholar] [CrossRef]
- Chen, J.; Ma, J.; Li, J.; Fu, Y. Performance optimization of grooved slippers for aero hydraulic pumps. Chin. J. Aeronaut. 2016, 29, 814–823. [Google Scholar] [CrossRef]
- Schenk, A.T. Predicting Lubrication Performance between the Slipper and Swashplate in Axial Piston Hydraulic Machines. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2014. [Google Scholar]
- Kazama, T. Mathematical modeling of a multi-land slipper for swash-plate type axial piston pumps and motors. In Proceedings of the 5th China-Japan Joint Workshop on Fluid Power, Beijing, China, 23 July 2018; pp. 46–50. [Google Scholar]
- Tang, H.; Yin, Y.; Ren, Y.; Xiang, J.; Chen, J. Impact of the thermal effect on the load-carrying capacity of a slipper pair for an aviation axial-piston pump. Chin. J. Aeronaut. 2018, 31, 395–409. [Google Scholar] [CrossRef]
- Hashemi, S.; Friedrich, H.; Bobach, L.; Bartel, D. Validation of a thermal elastohydrodynamic multibody dynamics model of the slipper pad by friction force measurement in the axial piston pump. Tribol. Int. 2017, 115, 319–337. [Google Scholar] [CrossRef]
- Kazama, T. Thermohydrodynamic lubrication model applicable to a slipper of swashplate type axial piston pumps and motors (Effects of operating conditions). Tribol. Online 2010, 5, 250–254. [Google Scholar] [CrossRef]
- Yamaguchi, A.; Matsuoka, H. A mixed lubrication model applicable to bearing/seal parts of hydraulic equipment. J. Tribol. Trans. ASME 1992, 114, 116–121. [Google Scholar] [CrossRef]
- Kazama, T.; Yamaguchi, A. Application of a mixed lubrication model for hydrostatic thrust bearings of hydraulic equipment. J. Tribol. Trans. ASME 1993, 115, 686–691. [Google Scholar] [CrossRef]
- Greenwood, J.A.; Williamson, J.B.P. Contact of nominally flat surfaces. Proc. R. Soc. Lond. 1996, 295, 300–319. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication. J. Lubr. Technol. Trans. ASME 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. Application of average flow model to lubrication between rough sliding surfaces. J. Lubr. Technol. Trans. ASME 1979, 101, 220–230. [Google Scholar] [CrossRef]
- Kazama, T.; Yamaguchi, A. Experiment on mixed lubrication of hydrostatic thrust bearings for hydraulic equipment. J. Lubr. Technol. Trans. ASME 1995, 117, 399–402. [Google Scholar] [CrossRef]
- Kazama, T. Numerical simulation of a slipper model for water hydraulic pumps/motors in mixed lubrication. In Proceedings of the 6th JFPS International Symposium on Fluid Power, Tsukuba, Japan, 7–10 November 2005. [Google Scholar] [CrossRef]
- Kazama, T. Numerical simulation of a slipper with retainer for axial piston pumps and motors under swashplate vibration. JFPS Int. J. Fluid Power Syst. 2017, 10, 18–23. [Google Scholar] [CrossRef][Green Version]


| Parameter | Value | Unit |
|---|---|---|
| 0.5 | ||
| 0.6 | ||
| 0.7 | ||
| 0.8 | ||
| 0.9 | ||
| 1 | ||
| 1 | GPa | |
| 100 | g | |
| 2.4 | ||
| 12.5 | mm | |
| 0.3 | mm | |
| 0.08 | ||
| 1.1 | ||
| 28 | mPa·s | |
| 875 | kg/m3 | |
| 1 | μm |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kazama, T. Numerical Simulation of a Slipper Model with Multi-Lands and Grooves for Hydraulic Piston Pumps and Motors in Mixed Lubrication. Lubricants 2019, 7, 55. https://doi.org/10.3390/lubricants7070055
Kazama T. Numerical Simulation of a Slipper Model with Multi-Lands and Grooves for Hydraulic Piston Pumps and Motors in Mixed Lubrication. Lubricants. 2019; 7(7):55. https://doi.org/10.3390/lubricants7070055
Chicago/Turabian StyleKazama, Toshiharu. 2019. "Numerical Simulation of a Slipper Model with Multi-Lands and Grooves for Hydraulic Piston Pumps and Motors in Mixed Lubrication" Lubricants 7, no. 7: 55. https://doi.org/10.3390/lubricants7070055
APA StyleKazama, T. (2019). Numerical Simulation of a Slipper Model with Multi-Lands and Grooves for Hydraulic Piston Pumps and Motors in Mixed Lubrication. Lubricants, 7(7), 55. https://doi.org/10.3390/lubricants7070055




