Numerical Study of Power Loss and Lubrication of Connecting Rod Big-End
Abstract
:1. Introduction
2. Model and Procedure
- Lubricant is assumed to be Newtonian and incompressible, therefore oil density remains unchanged;
- Lubricant is treated as an iso-viscous fluid;
- Oil flow is assumed laminar;
- Hydrodynamic lubrication has been considered at connecting rod big-end and crankpin interface;
- There is no slippage at the boundaries;
- Elastic deformation of bearing surfaces has been neglected.
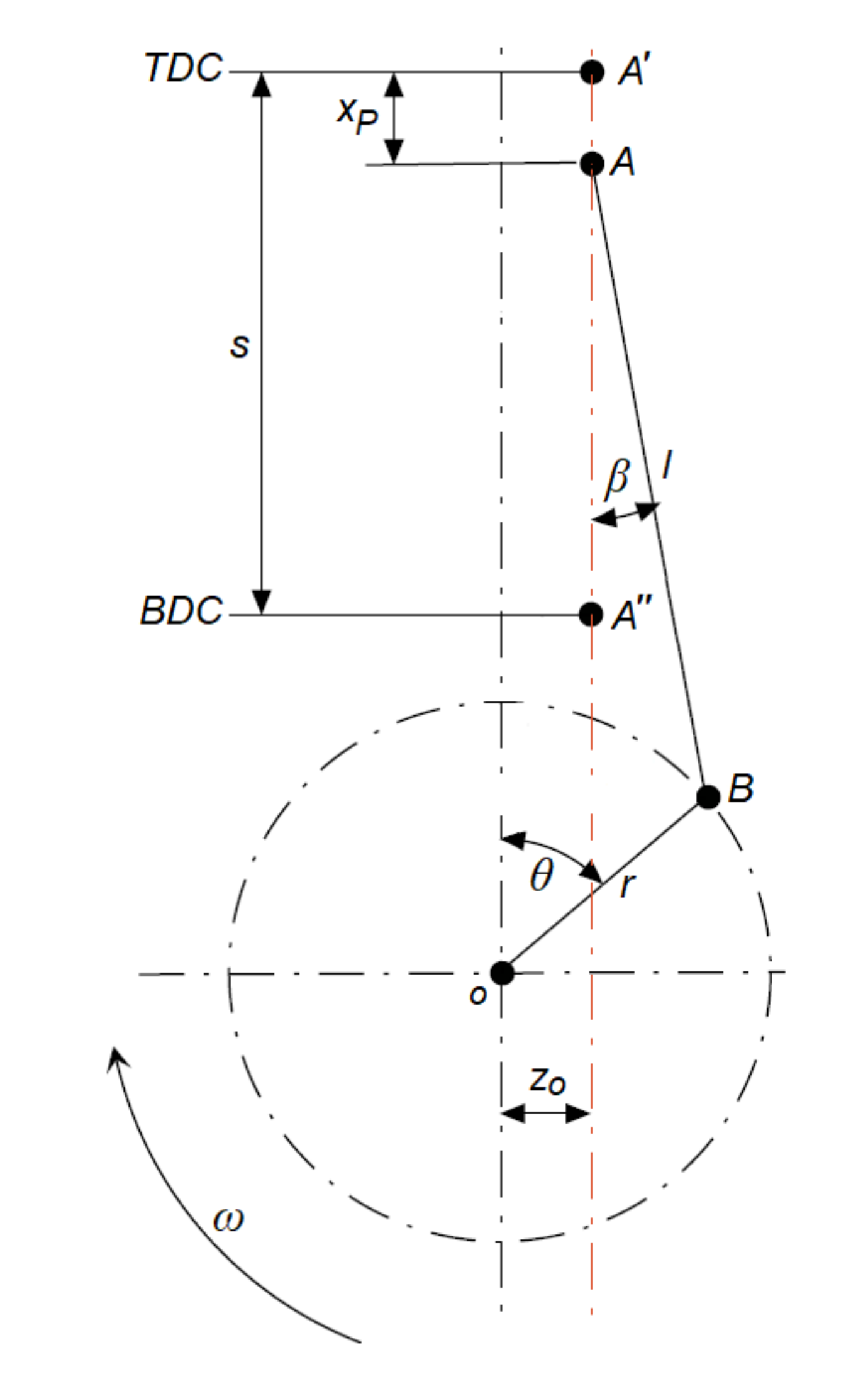
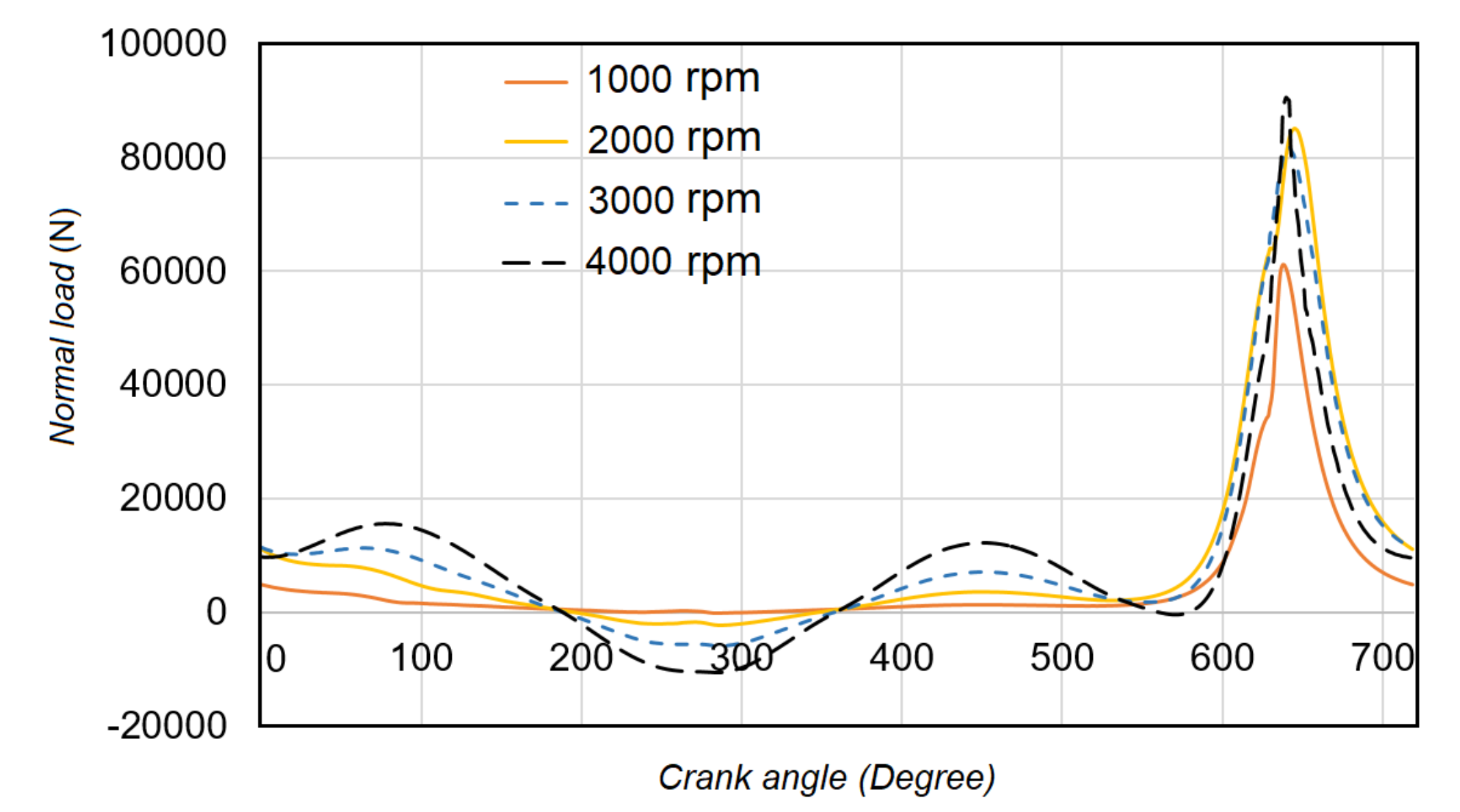
2.1. Connecting Rod Big-End Loads
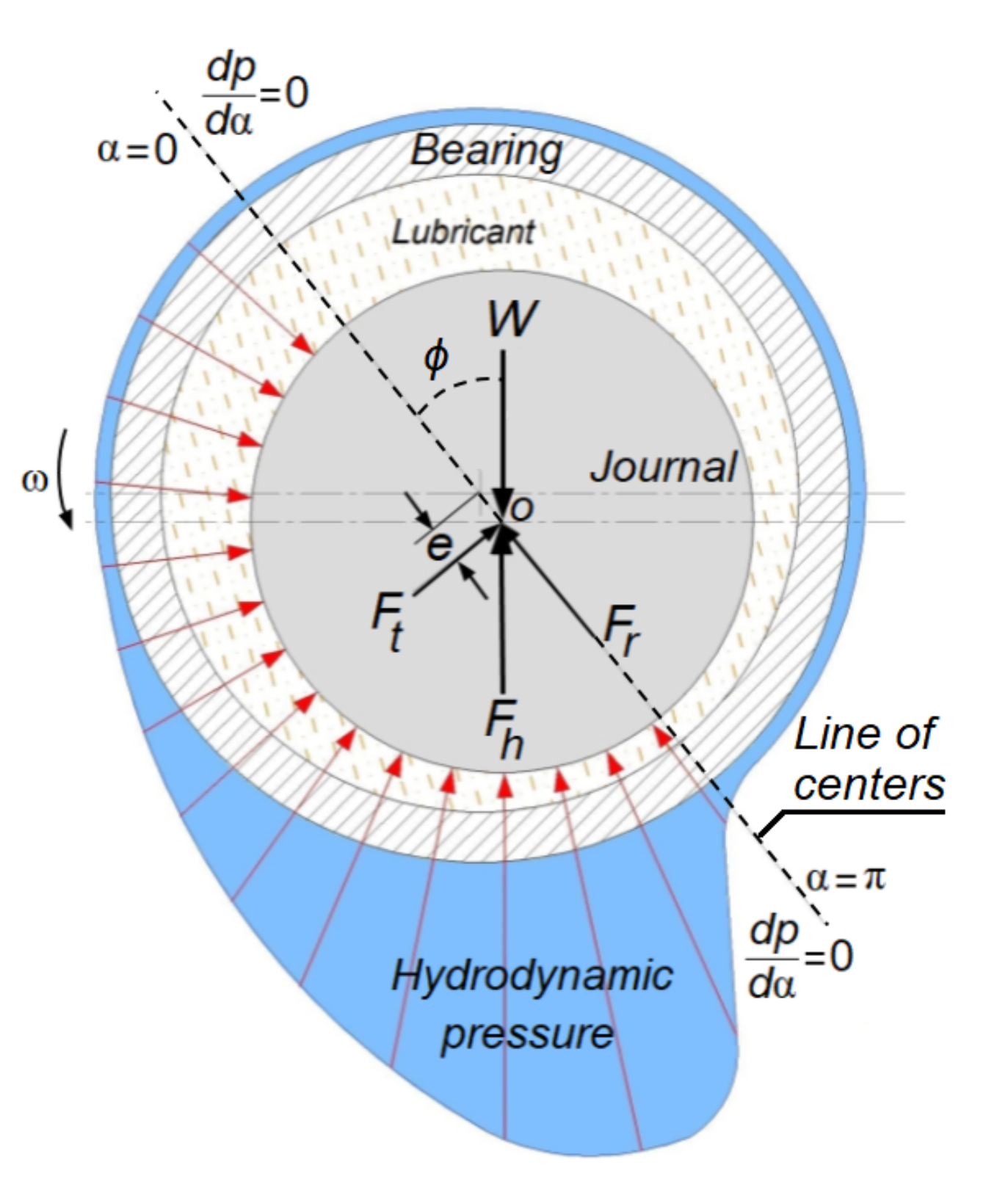
2.2. Reynolds Equation for Bearing Analysis
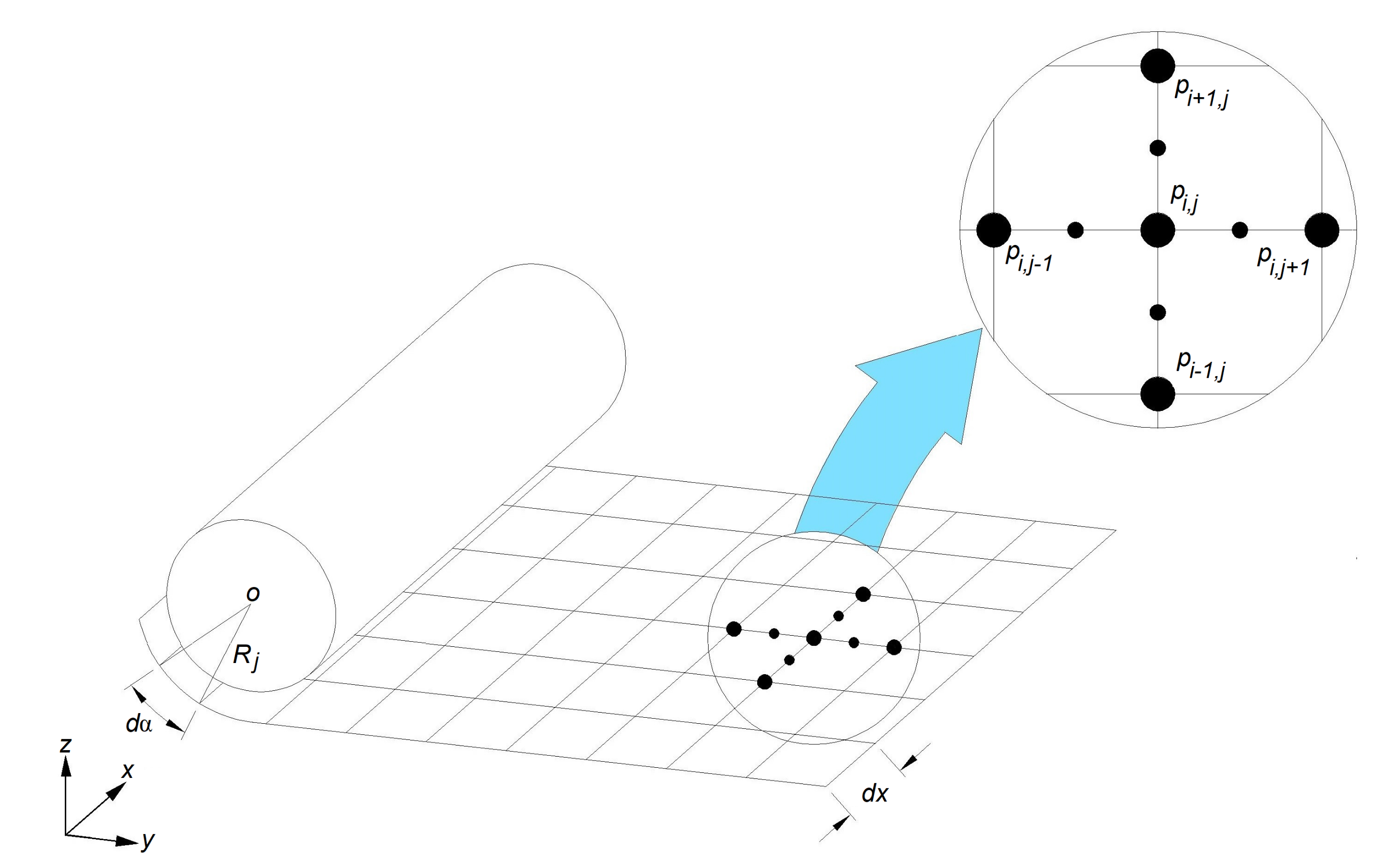
2.3. Numerical Solution
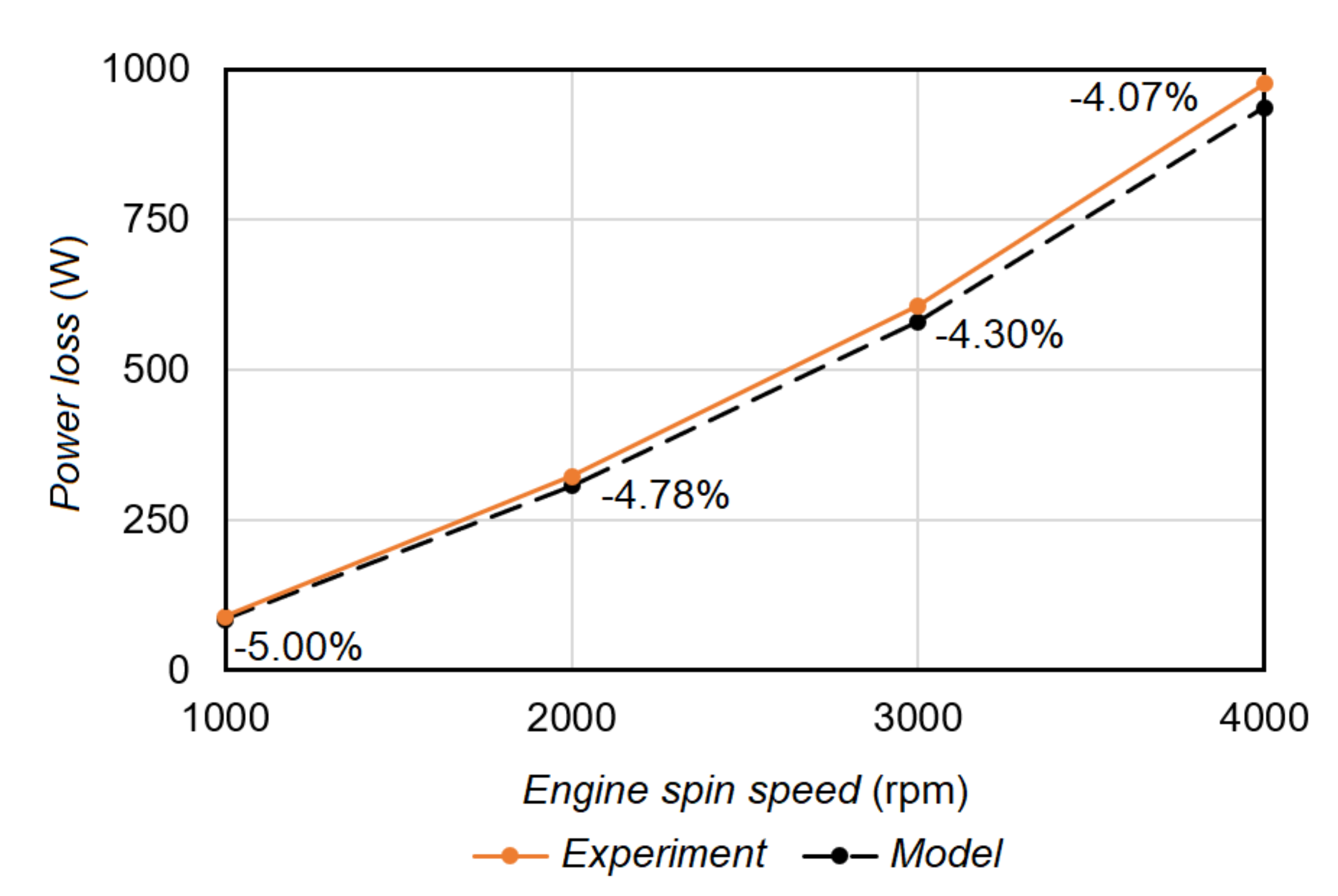
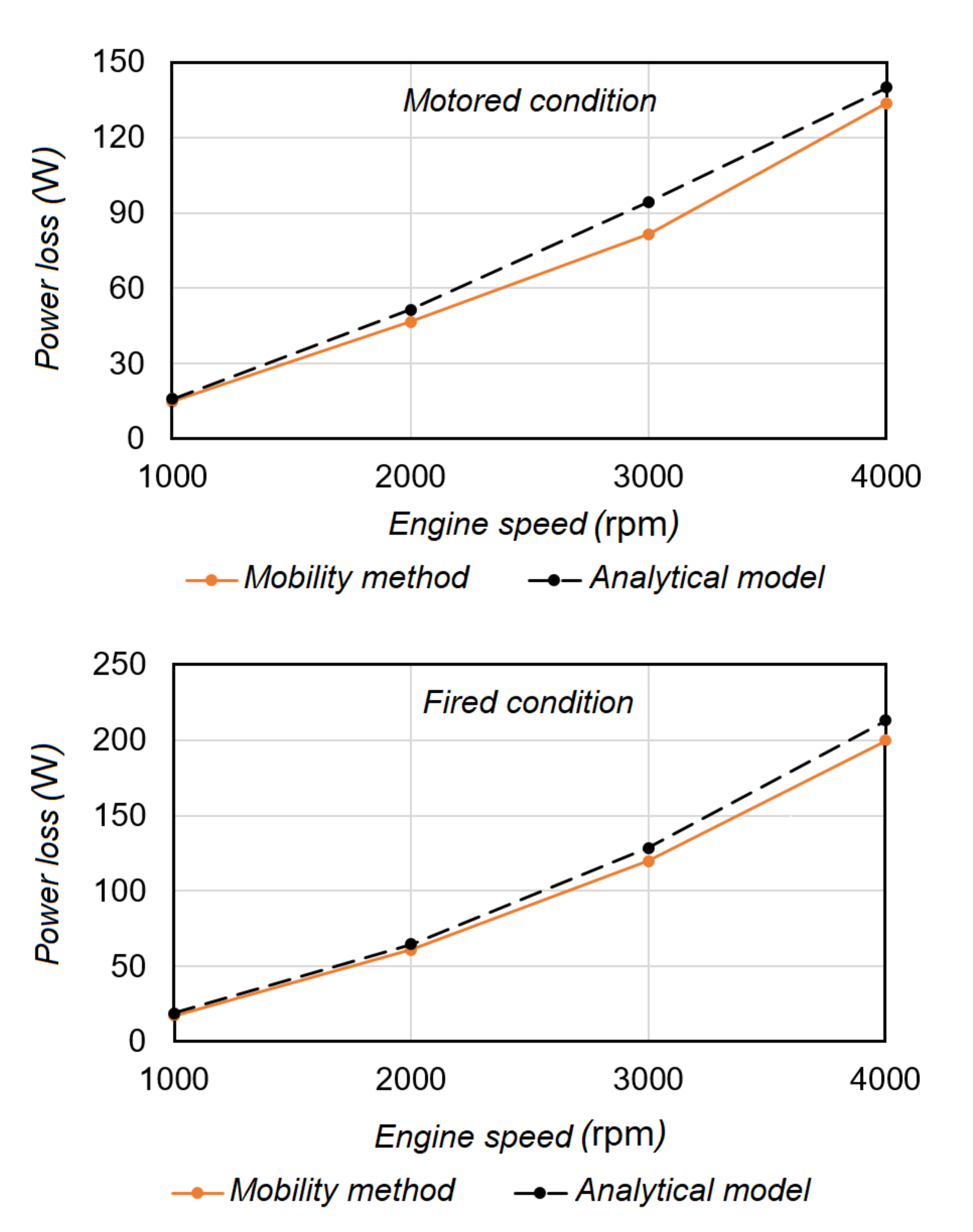
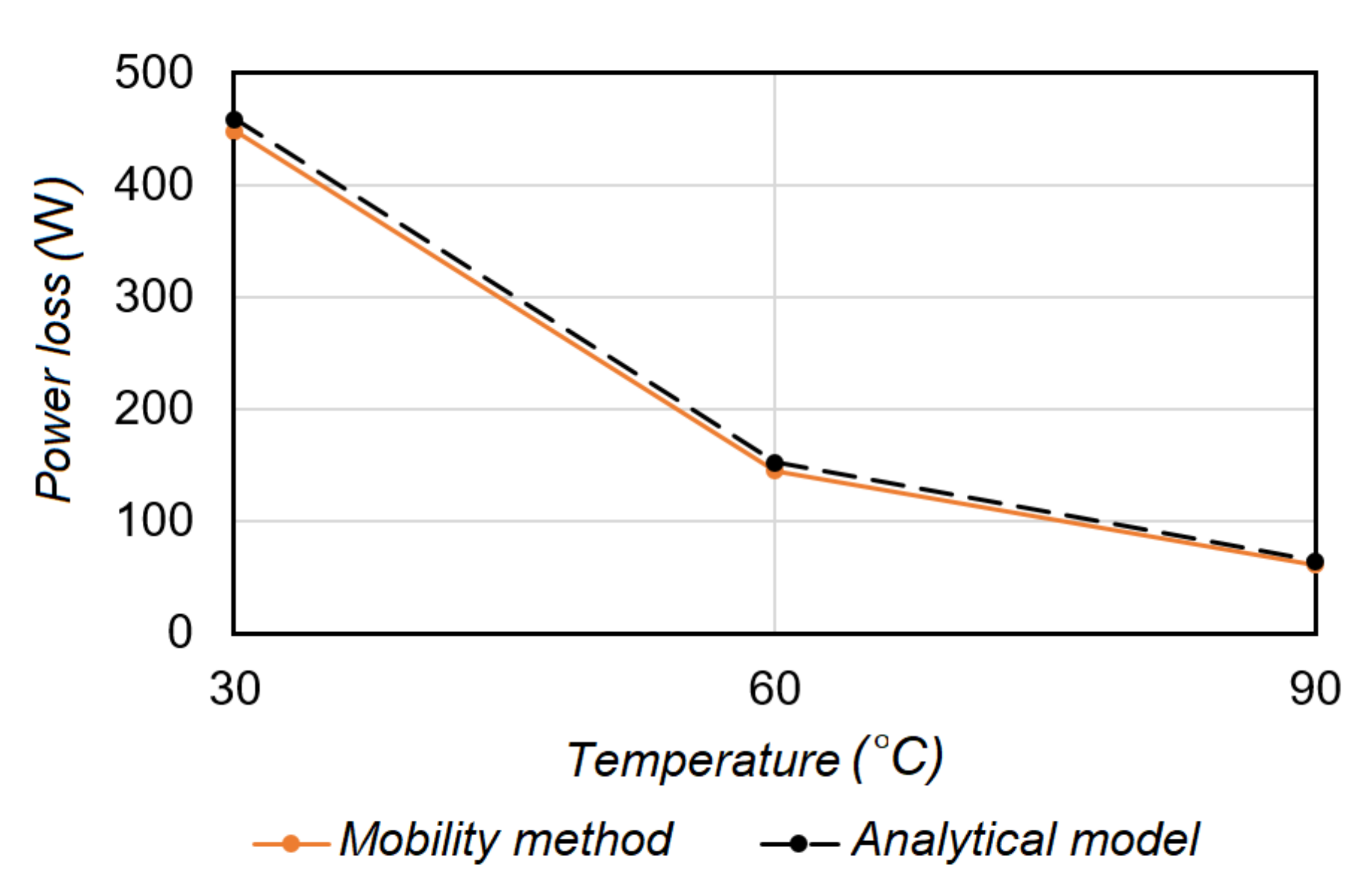
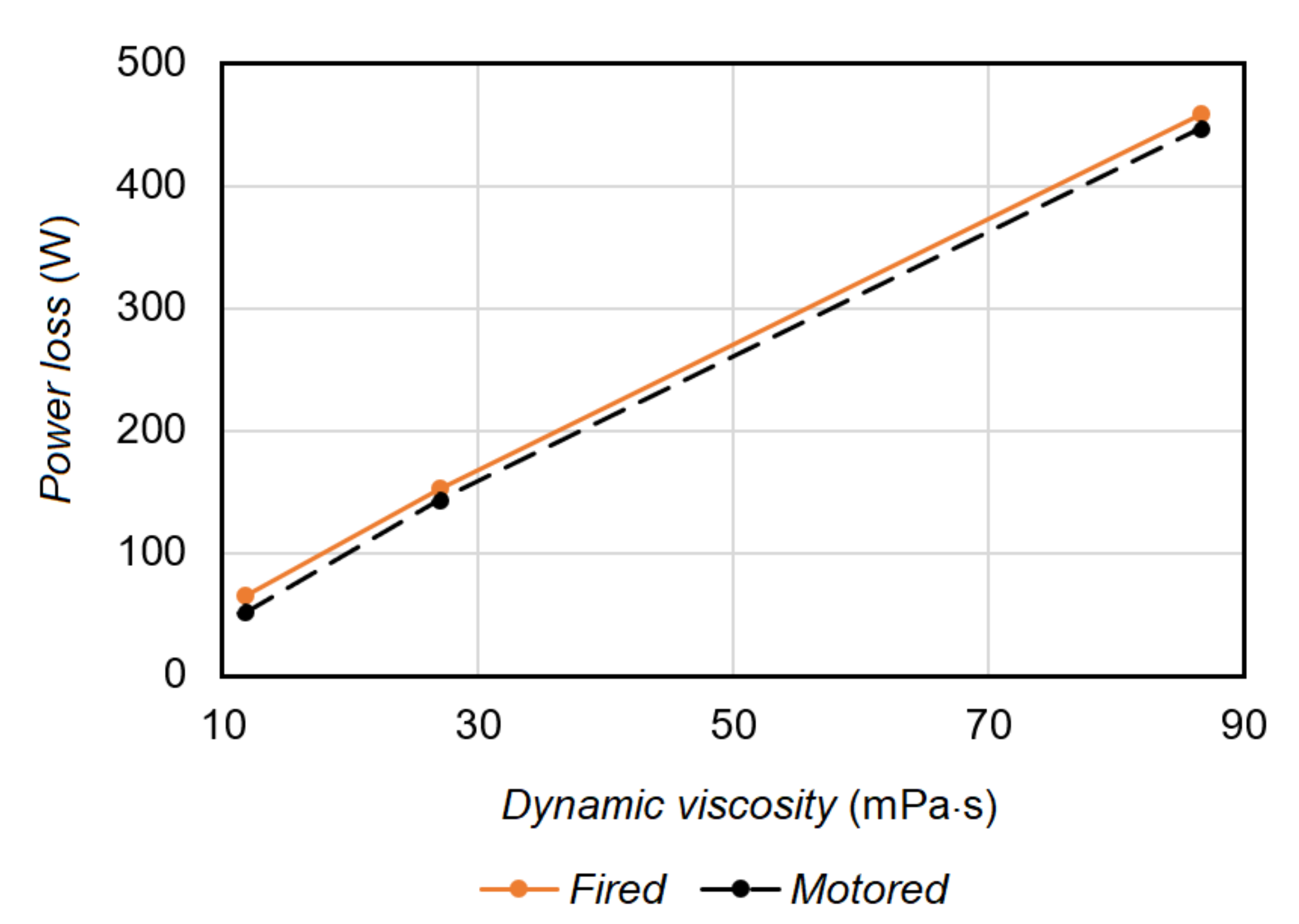
3. Model Validation
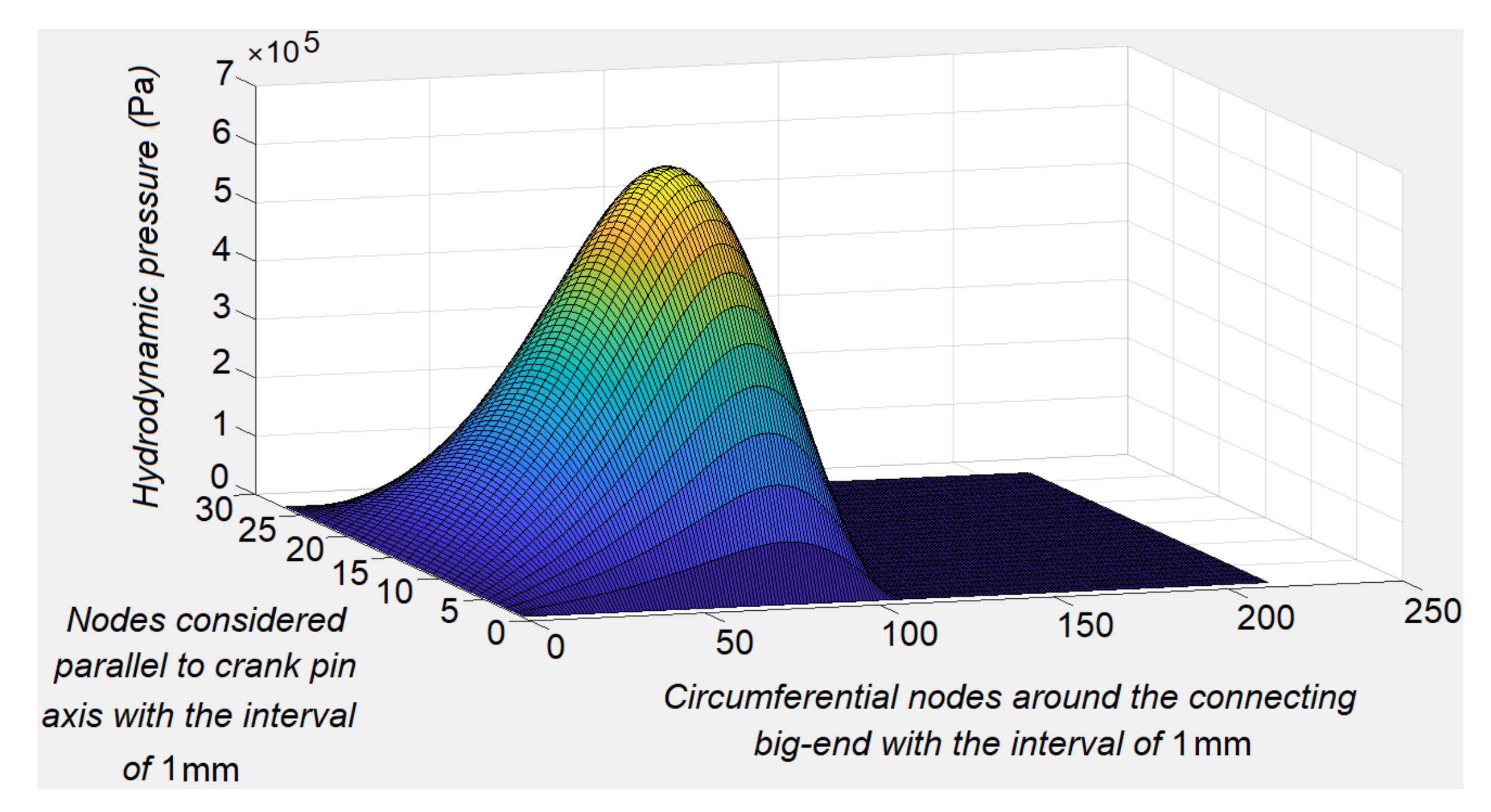
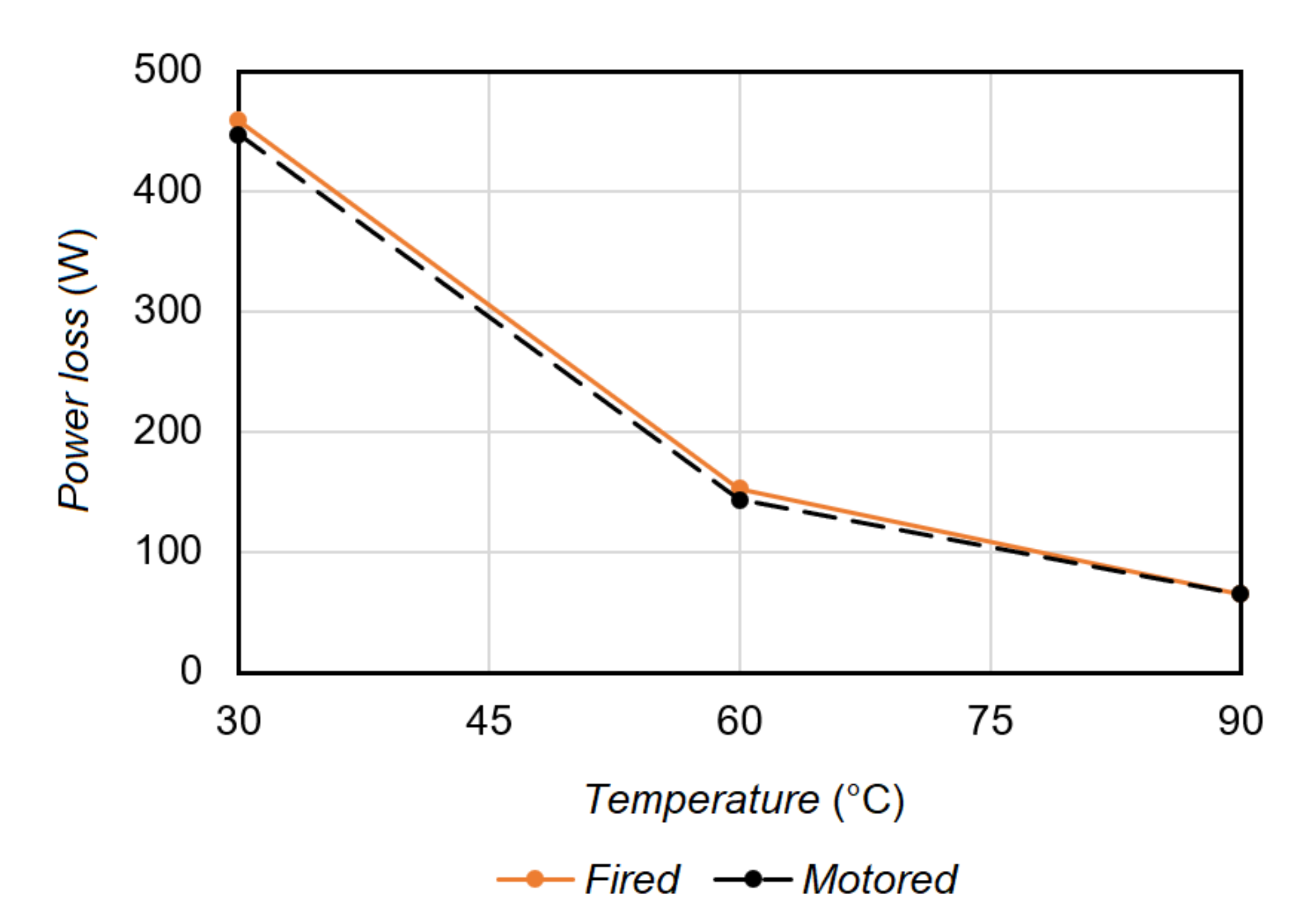
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Hydrodynamic Force Components, Fr and Ft Based on Mobility Method for π Film Lubricated Journal Bearing
References
- Rahnejat, H. (Ed.) Tribology and Dynamics of Engine and Powertrain: Fundamentals, Applications and Future Trends; Woodhead Publishing: Cambridge, UK, 2010. [Google Scholar]
- Stachowiak, G.; Batchelor, A.W. Engineering Tribology; Butterworth-Heinemann: Oxford, UK, 2013. [Google Scholar]
- Khonsari, M.M.; Booser, E.R. Applied Tribology: Bearing Design and Lubrication; John Wiley and Sons: New York, NY, USA, 2017. [Google Scholar]
- Delprete, C.; Razavykia, A. Piston dynamics, lubrication and tribological performance evaluation: A review. J. Eng. Res. 2018. [Google Scholar] [CrossRef]
- Delprete, C.; Razavykia, A. Piston ring–liner lubrication and tribological performance evaluation: A review. J. Eng. Tribol. 2018, 232, 193–209. [Google Scholar] [CrossRef]
- Booker, J.F. Dynamically loaded journal bearings: Mobility method of solution. J. Basic Eng. 1965, 87, 537–546. [Google Scholar] [CrossRef]
- Booker, J.F. Dynamically-loaded journal bearings: Numerical application of the mobility method. J. Lubr. Technol. 1971, 93, 168–174. [Google Scholar] [CrossRef]
- Goenka, P.K. Analytical curve fits for solution parameters of dynamically loaded journal bearings. J. Tribol. 1984, 106, 421–427. [Google Scholar] [CrossRef]
- Fantino, B.; Godet, M.; Frêne, J. Dynamic Behaviour of an Elastic Connecting—Rod Bearing—Theoretical Study; SAE Technical Paper; SAE International: Warrendale, PA, USA, 1983; Volume 830307. [Google Scholar]
- Fantino, B.; Frene, J. Comparison of dynamic behavior of elastic connecting-rod bearing in both petrol and diesel engines. J. Tribol. 1985, 107, 87–91. [Google Scholar] [CrossRef]
- Hirani, H.; Athre, K.; Biswas, S. Dynamically loaded finite length journal bearings: Analytical method of solution. J. Tribol. 1999, 121, 844–852. [Google Scholar] [CrossRef]
- Paranjpe, R.S. Analysis of non-Newtonian effects in dynamically loaded finite journal bearings including mass conserving cavitation. J. Tribol. 1992, 114, 736–744. [Google Scholar] [CrossRef]
- Livanos, G.; Kyrtatos, N.P. A Model of the Friction Losses in Diesel Engines; SAE Technical Paper; 2006-01-0888; SAE International: Warrendale, PA, USA, 2006. [Google Scholar]
- DuBois, G.B.; Ocvirk, F.W. Analytical Derivation and Experimental Evaluation of Short-bearing Approximation for Full Journal Bearing; NACA Report; NACA: Boston, MA, USA, 1953; Volume 1157. [Google Scholar]
- Vignolo, G.G.; Barilá, D.O.; Quinzani, L.M. Approximate analytical solution to Reynolds equation for finite length journal bearings. Tribol. Int. 2011, 44, 1089–1099. [Google Scholar] [CrossRef]
- Chasalevris, A.; Sfyris, D. Evaluation of the finite journal bearing characteristics, using the exact analytical solution of the Reynolds equation. Tribol. Int. 2013, 57, 216–234. [Google Scholar] [CrossRef]
- Abbasi, A.; Khadem, S.E.; Bab, S.; Friswell, M.I. Vibration control of a rotor supported by journal bearings and an asymmetric high-static low-dynamic stiffness suspension. Nonlinear Dyn. 2016, 85, 525–545. [Google Scholar] [CrossRef]
- Dousti, S.; Allaire, P.; Dimond, T.; Cao, J. An extended Reynold equation applicable to high reduced Reynolds number operation of journal bearings. Tribol. Int. 2016, 102, 182–197. [Google Scholar] [CrossRef]
- Booker, J.F. Basic equations for fluid films with variable properties. J. Tribol. 1989, 111, 475–479. [Google Scholar] [CrossRef]
- Martin, F.A. Friction in Internal Combustion Engine Bearings. Proc. Inst. Mech. Eng. 1985, C67/85, 1–17. [Google Scholar]
- Booker, J.F. A Table of the Journal-Bearing Integral. J. Basic Eng. 1965, 87, 533–535. [Google Scholar] [CrossRef]

| c | journal-bearing clearance (mm) | 0.026 |
| D | cylinder bore (mm) | 83.80 |
| l | connecting rod length (mm) | 153 |
| journal width (mm) | 19.5 | |
| r | crank radius (mm) | 49.5 |
| crankpin radius (mm) | 25.45 | |
| piston mass (kg) | 0.540 | |
| wrist pin mass (kg) | 0.257 | |
| connecting rod mass (kg) | 0.714 | |
| wrist pin offset (mm) | 0.5 | |
| crankshaft offset (mm) | 0 | |
| oil dynamic viscosity (mPa·s) | 11.734 | |
| combined surface roughness (m) | 0.37 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Razavykia, A.; Delprete, C.; Baldissera, P. Numerical Study of Power Loss and Lubrication of Connecting Rod Big-End. Lubricants 2019, 7, 47. https://doi.org/10.3390/lubricants7060047
Razavykia A, Delprete C, Baldissera P. Numerical Study of Power Loss and Lubrication of Connecting Rod Big-End. Lubricants. 2019; 7(6):47. https://doi.org/10.3390/lubricants7060047
Chicago/Turabian StyleRazavykia, Abbas, Cristiana Delprete, and Paolo Baldissera. 2019. "Numerical Study of Power Loss and Lubrication of Connecting Rod Big-End" Lubricants 7, no. 6: 47. https://doi.org/10.3390/lubricants7060047
APA StyleRazavykia, A., Delprete, C., & Baldissera, P. (2019). Numerical Study of Power Loss and Lubrication of Connecting Rod Big-End. Lubricants, 7(6), 47. https://doi.org/10.3390/lubricants7060047







