The Impact of Lubricant Film Thickness and Ball Bearings Failures ^†

Abstract

An effort was made to find a relationship between the lubricant thickness at the point of contact of rolling element ball bearings, and empirical equations to predict the life for bearings under constant motion. Two independent failure mechanisms were considered, fatigue failure and lubricant failure resulting in seizing of the roller bearing. A theoretical formula for both methods was established for the combined probability of failure using both failure mechanisms. Fatigue failure was modeled with the empirical equations of Lundberg and Palmgren and standardized in DIN/ISO281. The seizure failure, which this effort sought to investigate, was predicted using Greenwood and Williamson’s theories on surface roughness and asperities during lubricated contact. These two mechanisms were combined, and compared to predicted cycle lives of commercial roller bearing, and a clear correlation was demonstrated. This effort demonstrated that the Greenwood–Williams theories on the relative height of asperities versus lubricant film thickness can be used to predict the probability of a lubricant failure resulting in a roller bearing seizing during use.

1. Introduction

Ball bearings are used in countless mechanical applications to convert sliding mechanical contact into rolling contact [1,2,3], dramatically reducing friction energy losses. Sliding contact inherently has a high friction force, as random asperities can contact the surface and induce wear and damage to machined parts [4,5,6,7,8,9]. Rolling contact, however, has dramatically lower friction; the overwhelming majority of the friction loss is merely hysteresis from elastic deflections of the circular bearings.

Rolling element bearings are one of the most common configuration of ball bearings, with the bearings contained in a circular race to allow continued circular motion. As long as there is a minimum surface friction to enable the bearings to roll, there will be a dramatic reduction in circular friction for an object spinning inside or outside of the races. Bearings can be spherical, cylindrical, or a host of different configurations depending on the applications of the ball bearings.

A well built bearing can last indefinitely, however all mechanical objects have some risk of failure. Despite the previous assumptions that stresses less than half of yield have no significant risk of failure, there is always some risk of fatigue and fracture, which may manifest itself in the life of a ball bearing. The most likely bearing failure, however, is lubricant failure causing the bearings to seize. Ball bearings overwhelmingly use lubricant oils and greases to ensure there is not an excessive build-up of heat and friction between the races and the bearings. While a minimum amount of friction is necessary to ensure the bearings roll rather than slide (often specified as a minimum axial load), too much friction can cause the bearings to stick to the race and seize up, rather than allowing rolling.

Friction is inherently random and variable, as it is impacted by the different random surface asperities; as such, it is incredibly difficult to model. The usual (but not exclusive) mechanism of lubricant failure is as follows: a high enough friction will heat the lubricant, which will reduce the viscosity of the lubricant, which will increase the friction heating, and this feedback loop will continue until the friction between the bearing and the races is so great that the bearing seizes. If a bearing seizes during a critical application, the results can be catastrophic.

While it is impossible to truly know the exact nature of every bearing surface, empirical equations can be generated to determine the $L_{10}$ life from a known bearing load, lubricant cleanliness, lubricant viscosity, and continuous bearing speed. The $L_{10}$ life is defined as the number of revolutions a bearing can experience before a 10% chance of bearing failure. This effort was to study how tribological properties such as the lubricant film thickness [10,11,12] can serve to predict the change of failure after a single revolution, and thus estimate the $L_{10}$ life.

2. Empirical Equations for $L_{10}$ Life

To properly develop a numerical model for ball bearing failures, it is necessary to have empirical data on bearing failure to verify and validate it. In this aim, the $L_{10}$ empirical equations provided by Timken [13] was used as a basis for validating predictions of bearing life as a function of lubricant thickness. The world’s largest manufacturer of ball bearings is Svenska Kullagerfabriken (SKF), a Swedish company founded in 1907; they use a bearing life calculator [14,15] similar to Timken as well. Timken’s life equations were provided in easily duplicated empirical equations, versus a software life calculator; for the purpose of this analysis, Timken was used. These Timken empirical equation ultimately yield the $L_{10}$ life in revolutions before the bearings have a 10% chance of failure. The core equation for $L_{10}$ life is [13]

$$\begin{array}{ccc}\hfill L_{10}& =& A_{10}·{(\frac{C_{a1}}{P})}^{\widehat{p}}·{10}^6,\hfill \end{array}$$

(1)

where $C_{a1}$ (N) is the basic dynamic load rating, P (N) is the equivalent load, and $A_{10}$ is the life modification factor. The value of $\widehat{p}$ was found empirically, and it is 3 for spherical bearings and 10/3 for cylindrical bearings [16,17,18], based on empirical research of Lundberg and Palmgren [16,17,18].

The value of $A_{10}$ is a function of several dimensionless parameters

$$\begin{array}{ccc}\hfill A_{10}& =& a_1·a_2·C_g·C_l·C_j·C_s·C_v·C_{gr},\hfill \end{array}$$

(2)

where $a_2$ is a material factor that was treated as 1 for steel bearings; $C_g$ is a geometry factor set to 1 for spherical roller bearings; $G_{gr}$ is the grease factor that is set to 1 if not using grease and 0.79 with grease; $a_2$ is a material factor set to 1 for steel bearings; and $C_j$ ranges between 0.747 and 1.0, depending on how tapered the bearing is, and this simulation assumed $C_j=1$ for non-tapered bearings. The value of $C_l$ is inverse proportional to the equivalent load P (N)

$$\begin{array}{ccc}\hfill C_l& =& P^{-0.25},\hfill \\ \hfill P& =& F_a+1.2·F_r,\hfill \end{array}$$

(3)

where $F_a$ (N) and $F_r$ (N) are the axial and radial loads. The speed factor is proportional to the square root of the speed in revolutions per minute

$$\begin{array}{ccc}\hfill C_s& =& \sqrt{{\mathsf{\Omega }}_{RPM}},\hfill \end{array}$$

(4)

and the viscosity factor $C_v$ is proportional to the square root of the kinematic viscosity $\nu$ (cSt) in centistokes

$$\begin{array}{ccc}\hfill C_v& =& 1.6·\sqrt{\nu }.\hfill \end{array}$$

(5)

Finally, the factor $a_1$ is set to the probability of failure of interest,

$$\begin{array}{ccc}\hfill a_1& =& 4.26·{\left(log\frac{100}{R}\right)}^{2/3}+0.05,\hfill \end{array}$$

(6)

where R represents the probability of surviving the calculated number of cycles. If R = 90, to represent $L_{10}$, then the value of $a_1$ is 1.

3. Tribological Predictions of $L_{10}$ Life

Equation (1) can predict the $L_{10}$, but it gives no information as to the mechanics of the failure; it is purely based on empirical data. To better understand the mechanism of failure, a model based on the tribological properties to find the values of $L_{10}$ needs to be developed, with Equation (1) being used to verify and validate this model.

Regardless of the $L_{10}$ life, a ball bearing failure can happen; $L_{10}$ life is really a function of the probability of failure in the face of random conditions such as surface asperities. One common form of bearing failure is seizure, where excessive friction can yield increased heating, which reduces the lubricant viscosity, increasing the friction; eventually, the friction increases until it is high enough that the bearing seizes. Another potential cause of failure is a failure in fatigue; this increases exponentially with increasing load relative to fatigue life. For the purpose of the analysis, the driving cause of failure is treated as an excessively high increase in friction from the approximated average friction.

The greater the lubricant thickness is at the point of elastohydrodynamic contact, the less wear and friction can be expected. According to Greenwood and Williamson’s research [19,20,21,22,23,24], wear and friction (other than from fluid stresses, and hysteresis of rolling contact) occur due to random asperities exceeding the thickness of the lubricant film [19,20,21,22,23,24,25,26]; the thicker is the lubricant, the lower is the mean ratio of true contact area ratio [1,27]. Assuming the surface asperities height follows a normal distribution, the ratio of metal-on-metal contact $A_{real}/A$ with the lubricant thickness should roughly follow

$$\begin{array}{ccc}\hfill \frac{A_{real}}{A}& \approx & exp\left(-\frac{h}{\sigma }\right),\hfill \end{array}$$

(7)

where $A_{real}$ (m${}^2$) represents the true metal-on-metal contact area, A (m${}^2$) represents the apparent (but not true) surface contact area, h (m) represents the lubricant film thickness, and $\sigma$ (m) represents the RMS average asperities height. In addition to the fatigue life, where the failure life is proportional to the load over the fatigue load to the power of 10/3, it is expected that the $L_{10}$ probability of lubricant failure will be a function of the lubricant film thickness h (m)

$$\begin{array}{ccc}\hfill L_{10}& =& f\left(h\right)+f\left(\frac{C_{a1}}{P}\right)\hfill \end{array}$$

(8)

4. First Parametric Study

The simulation assumed a lubricant with an ISO Viscosity Grade of 46, with a kinematic viscosity of 46 cSt at 40 ${}^{\circ }$C, and kinematic viscosity of 8.5 cSt at 100 ${}^{\circ }$C, lubricant properties of a typical commercially available bearing gear oil (Mobil SHC 625). The temperature range in the simulation was varied from 20 ${}^{\circ }$C to 300 ${}^{\circ }$C (112.2355 cSt to 1.0648 cSt). A copy of the Matlab computer code for this simulation is included in the Supplementary Materials.

A parametric study was conducted, utilizing the Timken 29348 roller bearing. This has an inner bore of 240 mm, a dynamic load rating $C_{a1}$ of 2,040 kN, and an average roller diameter of 315.7 mm. While the roller diameters are not clearly specified, CAD estimation yielded a length of 49.68 mm and an average roller radius of 18.87 mm, with a total of 23 rollers. The bearing is made of steel, thus the Young’s modulus $E_Y$ is 210 GPa, and the Poisson’s ratio p is 0.3. The parametric study calculated both the $L_{10}$ life as defined in Equation (1), and compared it to the predicted lubricant film thickness [10,11,12,28,29,30,31,32,33,34,35,36,37,38,39,40], and the relative fatigue load. The parametric study was conducted for a temperature ranging between 20 ${}^{\circ }$C and 300 ${}^{\circ }$C, in increments of 10 ${}^{\circ }$C; an equivalent axial load of 1–100% (in 1% increments) of the 2,040 kN dynamic load $C_{a1}$; and a bearing speed of 1,000–15,000 RPM, in increments of 500 RPM. With each of these parameters, the $L_{10}$ life was calculated with Equation (1).

The next step was to predict the film thickness of the lubricant at the point of contact between the bearings and the rollers during elastohydrodynamic contact [1,41,42,43,44,45,46,47,48]. In 1974, empirical equations by Hamrock and Dowson [33] characterized the minimum $h_0$ (m) and central $h_c$ (m) film thickness

$$\begin{array}{ccc}\hfill h_{min}& =& 3.63R^{\prime }\left(U_n^{0.68}\right)\left(G_n^{0.49}\right)\left(W_n^{-0.073}\right)\left(1-exp[-0.68{\kappa }_{ellipse}]\right),\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill h_c& =& 2.69R^{\prime }\left(U_n^{0.67}\right)\left(G_n^{0.53}\right)\left(W_n^{-0.067}\right)\left(1-0.61·exp\left[-0.73{\kappa }_{ellipse}\right]\right),\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill U_n& =& \frac{{\mu }_{0}U}{E^{\prime }{R}^{\prime }},\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill G_n& =& {\alpha }_{PVC}{E}^{\prime },\hfill \end{array}$$

(12)

$$\begin{array}{ccc}\hfill W_n& =& \frac{W}{E^{\prime }{R}^{\prime 2}},\hfill \end{array}$$

(13)

where $h_{min}$ (m) is the minimum film thickness, $h_c$ (m) is the central film thickness, $U_n$ is the dimensionless speed parameter, $G_n$ is the dimensionless material parameter, $W_n$ is the dimensionless load parameter, ${\kappa }_{ellipse}$ is the ellipticity of the contact area, ${\mu }_0$ (Pa·s) is the dynamic viscosity of the lubricant at atmospheric pressure, and ${\alpha }_{PVC}$ (Pa${}^{-1}$) is the pressure viscosity coefficient

$$\begin{array}{ccc}\hfill {\alpha }_{PVC}& =& (0.965·lo{g}_{10}\left(\nu \right)+0.6)·{10}^{-8},\hfill \end{array}$$

(14)

where $\nu$ is the kinematic viscosity (m${}^2$/s) and U (m/s) is the velocity of contact. The reduced Young’s modulus E’ (Pa) and reduced radius R’ (m) are for Hertz contact equations for elastic deflection [1,49]. Assuming cylindrical rollers and a consistent material were used, the equations for E’ (Pa) and R’ (m) are

$$\begin{array}{ccc}\hfill R^{\prime }& =& 1/\left\{\frac{1}{R_r}+\frac{1}{R_R}\right\},\hfill \end{array}$$

(15)

$$\begin{array}{ccc}\hfill E^{\prime }& =& \frac{E_Y}{1-p^2}.\hfill \end{array}$$

(16)

where $R_r$ (m) is the radius of the cylindrical bearing roller, $R_R$ (m) is the radius of the bearing race, and $E_Y$ (Pa) and p are the Young’s modulus and Poisson’s ratio of the bearing material.

To realize the minimum $h_{min}$ and central $h_c$ elastohydrodynamic film thickness, it is necessary to determine the dynamic viscosity of the lubricant. The viscosity of the lubricant, however, is affected by temperature [2,50,51,52,53], as hotter oils are inherently less viscous. A reduction in viscosity results in a reduced minimum film thickness [33], but this reduced film thickness results in a cooler oil film [29], as there is less thermal resistance from the center of the oil film to the surface of the ball bearing. As a result of this contradiction, it is necessary to use iteration to converge on a realistic lubricant oil temperature and viscosity, so that a minimum film thickness can be determined.

The first step is to calculate the flash temperature heating of the surface of the ball bearing. This is done by first calculating the dimensionless Peclet number [1,29]

$$\begin{array}{ccc}\hfill L& =& \frac{U·b_H}{2{\alpha }_{bb}},\hfill \end{array}$$

(17)

where $b_H$ (m) is the length of contact, also defined as the Hertzian half width of the contact between the roller and the race [1]

$$\begin{array}{ccc}\hfill b_H& =& \sqrt{\frac{4·W·R^{\prime }}{\pi ·L_r·E_Y^{\prime }}},\hfill \end{array}$$

(18)

where $L_r$ (m) is the half length of the roller, and ${\alpha }_{bb}$ (m${}^2$/s) is the thermal diffusivity [54] of the ball bearing,

$$\begin{array}{ccc}\hfill {\alpha }_{bb}& =& \frac{k_{bb}}{{\rho }_{bb}·C_{P,bb}},\hfill \end{array}$$

(19)

where $k_{bb}$ ($\mathrm{W}/{\mathrm{m}}^2·{}^{\circ }\mathrm{C}$) is the thermal conductivity, ${\rho }_{bb}$ (kg/m${}^3$) is the density, and $C_{P,bb}$ ($\mathrm{J}/\mathrm{kg}·{}^{\circ }$C) is the specific heat capacity; all of these ${}_{bb}$ parameters are for the ball bearing material (steel).

Once the dimensionless Peclet number L is known, one can calculate the average flash temperature [55,56,57,58], which is defined as the temperature that results from the high-pressure and heating. For $L<0.1$, the friction heating is considered a stationary heat source, where the temperature distribution is effectively steady state, where the heat flow can be considered a flow of thermal current through a thermal resistance of the ball bearing. For $0.1<L<5.0$, the friction heating is considered a slow-moving heat source, where there is ample time for the temperature to be conducted through the ball bearing, and for $L>5.0$ the friction heating is considered a high-speed heat source [29]. In this study, consistently the Peclet number has always exceeded the value of 5.

The predictive analytical equation used by this model for average flash temperature can vary with Peclet number, but the flash heating for Peclet numbers greater than 5 is [1,29]

$$\begin{array}{ccc}\hfill \Delta T_F=& \frac{0.266{\mu }_{COF}·W·U}{k_{bb}·b_H}\sqrt{\frac{{\alpha }_{bb}}{U·b_H}}& L>5.0,\hfill \end{array}$$

(20)

where ${\mu }_{COF}$ is the dimensionless coefficient of friction (COF), $b_H$ (m) is defined with Equation (18), W (N) is the load, and $\Delta T_F$ (${}^{\circ }$C) is the surface temperature increase due to friction. The value of ${\mu }_{COF}$ is assumed to be 0.0018, which is a standard friction coefficient for the rolling resistance spherical roller bearings [13,14,15].

The friction temperature can be used to calculate the average viscosity [1,45,46,53], where

$$\begin{array}{ccc}\hfill \nu & =& \widehat{Z}-exp[-0.7487-3.295·\widehat{Z}+0.6119·{\widehat{Z}}^2-0.3193·{\widehat{Z}}^3],\hfill \\ \hfill \widehat{Z}& =& 10{}^{\wedge }\left[10{}^{\wedge }(A-B·lo{g}_{10}{T}_L)\right]-0.7\hfill \end{array}$$

(21)

where $\nu$ (mm${}^2$/s) is the kinematic viscosity, and A and B are dimensionless coefficients derived empirically. They can be found by measuring the kinematic viscosity at two temperature points, calculating the Z-value [53],

$$\begin{array}{ccc}\hfill Z& =& \nu +0.7+exp[-1.47-1.84\nu -0.51{\nu }^2],\hfill \end{array}$$

(22)

and obtaining the viscosity coefficients, where [53]

$$\begin{array}{ccc}\hfill lo{g}_{10}lo{g}_{10}Z& =& A-B·lo{g}_{10}T,\hfill \\ \hfill B& =& \frac{lo{g}_{10}lo{g}_{10}{Z}_i-lo{g}_{10}lo{g}_{10}{Z}_j}{lo{g}_{10}{T}_j-lo{g}_{10}{T}_i},\hfill \\ \hfill A& =& lo{g}_{10}lo{g}_{10}{Z}_i+B·lo{g}_{10}{T}_i,\hfill \end{array}$$

(23)

where $T_i$, $T_j$, $Z_i$, and $Z_j$ are the temperature (Kelvin) and Z-coefficients at temperature points i and j. To convert the values of kinematic viscosity from cSt to ${\mathrm{m}}^2/\mathrm{s}$, simply multiply it by ${10}^{-6}$; the kinematic viscosity (${\mathrm{m}}^2/\mathrm{s}$) can be used to calculate the dynamic viscosity $\mu$ (Pa·s) of the lubricant [59],

$$\begin{array}{ccc}\hfill \mu & =& {\rho }_{lub}·\nu ,\hfill \end{array}$$

(24)

and this value can be used to calculate the film thickness using the Hamrock–Dowson [33] empirical equations.

If there is a given friction force that will cause the bearings to seize, and the friction is affected by the ratio of the height of the surface asperities (which follow a normal distribution) over the lubricant film thickness, an accurate equation for $L_{10}$ in revolutions ${\log }_{10}$ as a function of $h_c$ (m) is realized with Equation (25)

$$\begin{array}{ccc}\hfill lo{g}_{10}(L_{10})& =& b_1+b_2·(\frac{P}{C_{a1}}{)}^{3/10}+b_3·log\left(h_c\right),\hfill \end{array}$$

(25)

where $h_c$ (m) is the central film thickness in micrometers. Equation (25) incorporates two separate failure mechanisms, where $b_2$ is a coefficient for the rolling contact fatigue failure [16,17,18], and $b_3$ is a coefficient for the lubricant seizure based on friction (originating from Greenwood–Williams theory [19,20,21,22,23,24,25,26]). The fatigue life theory is an entirely different and independent failure mechanism from lubricant seizure; Equation (25) combines both potential failures into $L_{10}$ to obtain an overall probability of bearing failure during a given revolution.

The calculated value of $L_{10}$ found with Equation (25) closely matches the value of $L_{10}$ found with Equation (1), and is observed to match in Figure 1 for a Timken 29348 roller bearing. The coefficients for this particular design are $b_1=18.7598$, $b_2=-7.6583$, and $b_3=0.3086$, and the coefficient of determination $R^2$ between Equation (1) and Equation (25) is 0.96858, showing an extremely strong match.

5. Second Parametric Study

A second parametric was conducted to see if varying the bearing size would affect the coefficients for Equation (25), for 52 different spherical roller bearings, with dimensions tabulated in

Table 1. Dimensions of Timken Spherical Roller Bearings, used in the parametric study described in Section 5. The average radius of the roller race $R_R$ (m) is the half the average of variables $d_b$, H, E, and D, where $R_R=\frac{d_b+H+E+D}{8}$.

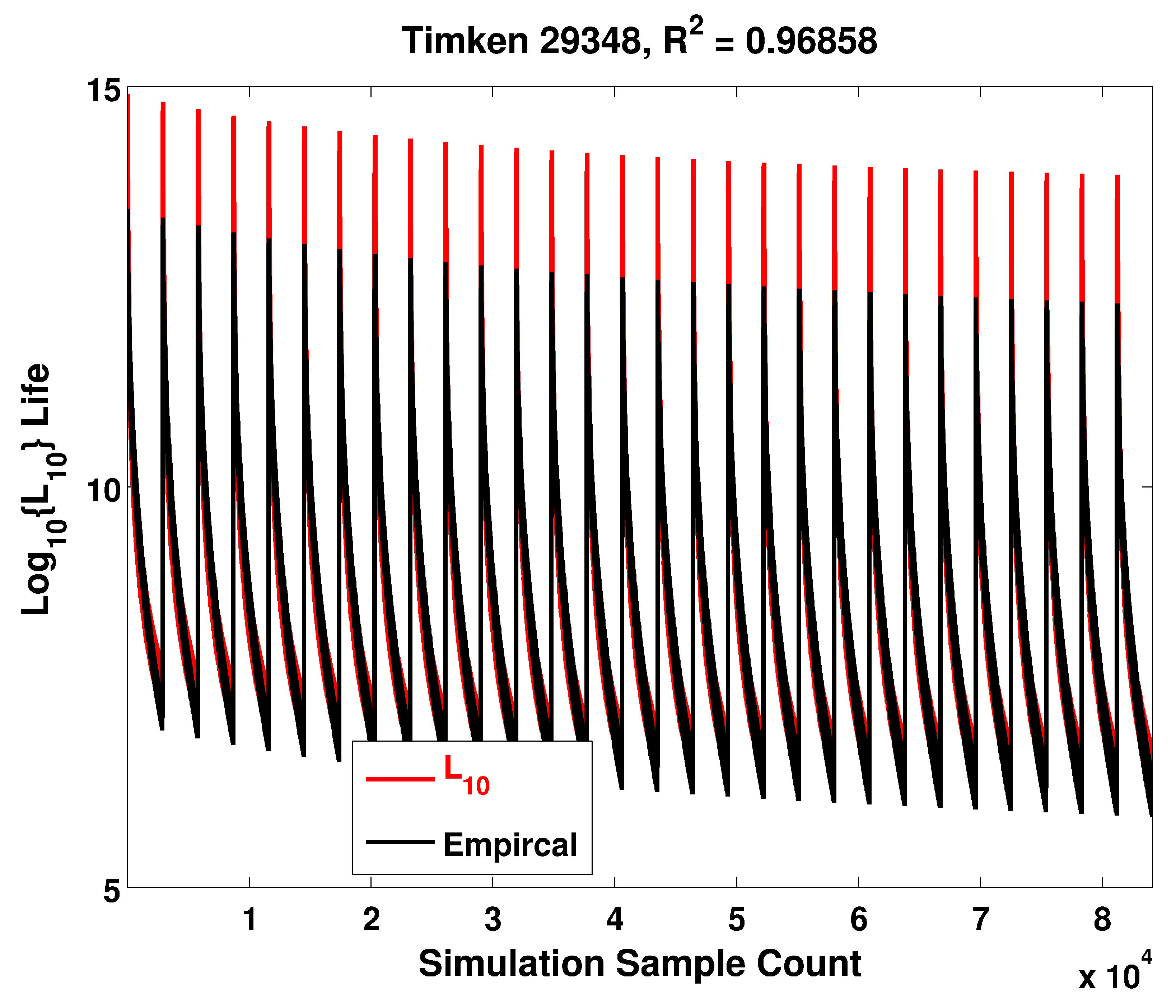
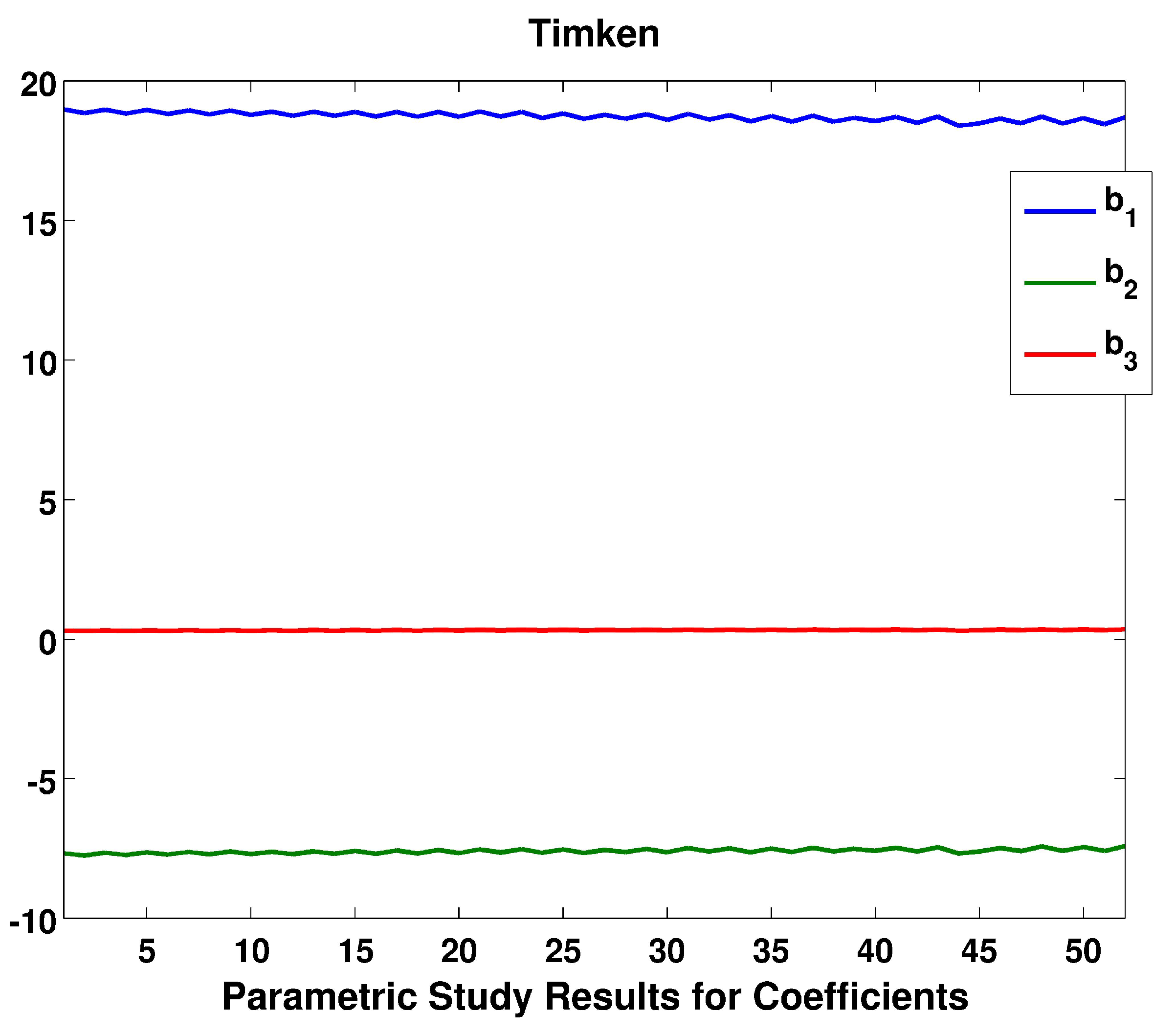
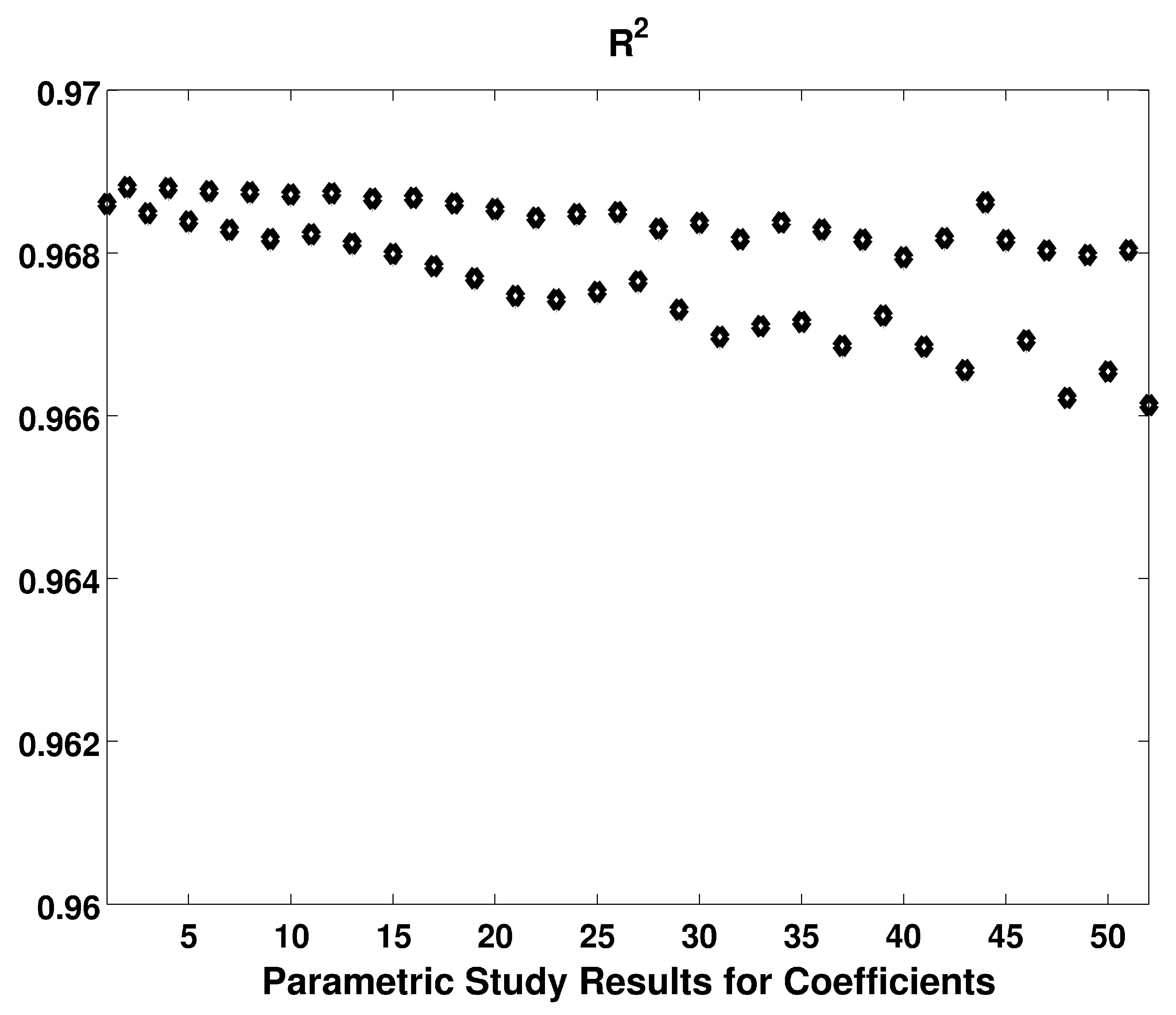
	Model	d (mm)	${\mathit{C}}_{\mathit{a}1}$ (kN)	${\mathit{d}}_{\mathit{b}}$ (mm)	H (mm)	E (mm)	D (mm)
1	29418	90	820	98.9	148	137	190
2	29320	100	462	108.1	141	134	170
3	29420	100	1020	108.8	164	151	210
4	29322	110	604	118.6	157	149	190
5	29422	110	1200	120.3	180	167	230
6	29324	120	768	128.5	172	163	210
7	29424	120	1390	131.6	197	182	250
8	29326	130	852	140.3	186	177	225
9	29426	130	1600	142.4	213	197	270
10	29328	140	970	148.9	199	188	240
11	29428	140	1640	152.8	223	207	280
12	29330	150	993	159.5	209	198	250
13	29430	150	1860	163.5	238	222	300
14	29332	160	1190	170.5	225	213	270
15	29432	160	2100	175	255	237	320
16	29334	170	1230	179.2	235	223	280
17	29434	170	2380	184.8	270	251	340
18	29336	180	1430	190.7	251	238	300
19	29436	180	2660	197.6	286	267	360
20	29338	190	1620	202.2	268	253	320
21	29438	190	3040	205.5	303	281	380
22	29340	200	1880	213.3	284	269	340
23	29440	200	3210	217	317	295	400
24	29344	220	1950	231.6	303	288	360
25	29444	220	3350	237.8	339	317	420
26	29348	240	2040	251.9	323	308	380
27	29448	240	3410	259	360	338	440
28	29352	260	2580	275.7	356	340	420
29	29452	260	4160	279.2	391	367	480
30	29356	280	2580	296.8	376	360	440
31	29456	280	4920	300.6	423	397	520
32	29360	300	3150	315.6	407	388	480
33	29460	300	4990	321.1	443	418	540
34	29364	320	2830	333.3	427	407	500
35	29464	320	5155	320	469	444	580
36	29368	340	3120	365.8	463	443	540
37	29468	340	5922	340	500	473	620
38	29372	360	3632	360	476	457	560
39	29472	360	5440	360	528	498	640
40	29376	380	4295	380	507	486	600
41	29476	380	6493	380	546.1	518	670
42	29380	400	3850	400	534	510	620
43	29480	400	7333	400	577.1	547	710
44	29284	420	2682	420	513.1	498	580
45	29384	420	4040	420	561	537	650
46	29484	420	6780	420	608	576	730
47	29388	440	4530	440	585	561	680
48	29488	440	8606	440	635	602	780
49	29392	460	4820	460	614	589	710
50	29492	460	8120	460	666	631	800
51	29396	480	4820	480	635	610	730
52	29496	480	9320	480	700	662	850

. The mean bearing radius was modeled from 90 mm to 480 mm. As observed in Figure 2, the three coefficients $b_1$, $b_2$, and $b_3$ vary slightly; the ratio of standard deviation to mean is well under 5%. The average values of the coefficients are ${\overline{b}}_1=18.73$, ${\overline{b}}_2=-7.6$, and ${\overline{b}}_3=0.32$; these values are nearly identical to the values found for the Timken 29348 described in Section 4. By plugging these values into Equation (25), a universal equation for the $L_{10}$ failure life for spherical roller bearing life could be obtained, presented as Equation (26). As observed in Figure 3, the coefficient of determination $R^2$ between this Equation (26) and the Timken equation (Equation (1)) never goes below 0.966, validating this theory of predicted lubricant thickness having a clear and calculable effect on the function life of roller bearings.

$$\begin{array}{ccc}\hfill lo{g}_{10}(L_{10})& =& 18.73-7.6·(\frac{P}{C_{a1}}{)}^{3/10}+0.32·log\left(h_c\right).\hfill \end{array}$$

(26)

As a simple test, Equation (26) was compared to both the original Timken equation (Equation (1)) [13] and the SKF calculator [14], using the the Timken and SKF 29348 spherical roller thrust bearing, with the Mobil 625 oil (with a kinematic viscosity of 46 cSt at 40 ${}^{\circ }$C, and kinematic viscosity of 8.5 cSt at 100 ${}^{\circ }$C), at a temperature of 70 ${}^{\circ }$C (kinematic viscosity of 15.5429 cSt), a speed of 1,000 RPM, and an axial load of 408 kN (20% of the dynamic fatigue load of 2,040 kN). The calculated $lo{g}_{10}\left(L_{10}\right)$ life with the Timken equation (Equation (1)) was 9.2495; the calculated $lo{g}_{10}\left(L_{10}\right)$ life with Equation (26) was 9.4348, an error of less than 2%. The SKF calculator for the same dimension bearing, with the same speed, load, oil, and temperature, and a simplified lubricant cleanliness factor of 0.6 (middle range between dirtiest of 0.2 and cleanest of 1.0) is 31,700 h, which at 1,000 RPM corresponds to 1.902 billion revolutions; the $lo{g}_{10}\left(L_{10}\right)$ of this value is 9.2792. It is clear that the Timken equation (Equation (1)) [13], the SKF calculator [14], and Equation (26) all yield comparable results, as a further validation of Equation (26).

6. Conclusions

A validated model to predict the probability of failures for roller bearings was developed. Empirical equations from Timken were developed from available data on commercial bearings to predict the $L_{10}$ life based on known bearing conditions (lubricant viscosity, bearing speed, and loads). These conditions were used, along with the roller bearing geometry, to predict the lubricant film thickness at the central point of contact. A thicker film thickness is expected to inherently have lower friction, and therefore a lower chance of lubricant failure, and a clear trend of lubricant thickness impacting the probability of bearing failure per revolution was observed. By knowing the relationship between lubricant film thickness and failure probability, more in-depth analysis of failure can be obtained, such as if one were to numerically solve the Reynolds equation for non-standard geometries, fluctuating temperatures, or rapid accelerations and decelerations. The relative load to the fatigue load is also considered; fatigue is a comparably significant influence on determining the bearing $L_{10}$ life. This model demonstrates how the lubricant film thickness can be used to obtain a reasonable approximation for the life and probability of failure in seizing of a roller bearing.