Prediction of Wear in Crosslinked Polyethylene Unicompartmental Knee Arthroplasty
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Wear Simulation of Tricompartmental Design
2.2. Computational Determination of Wear Factor
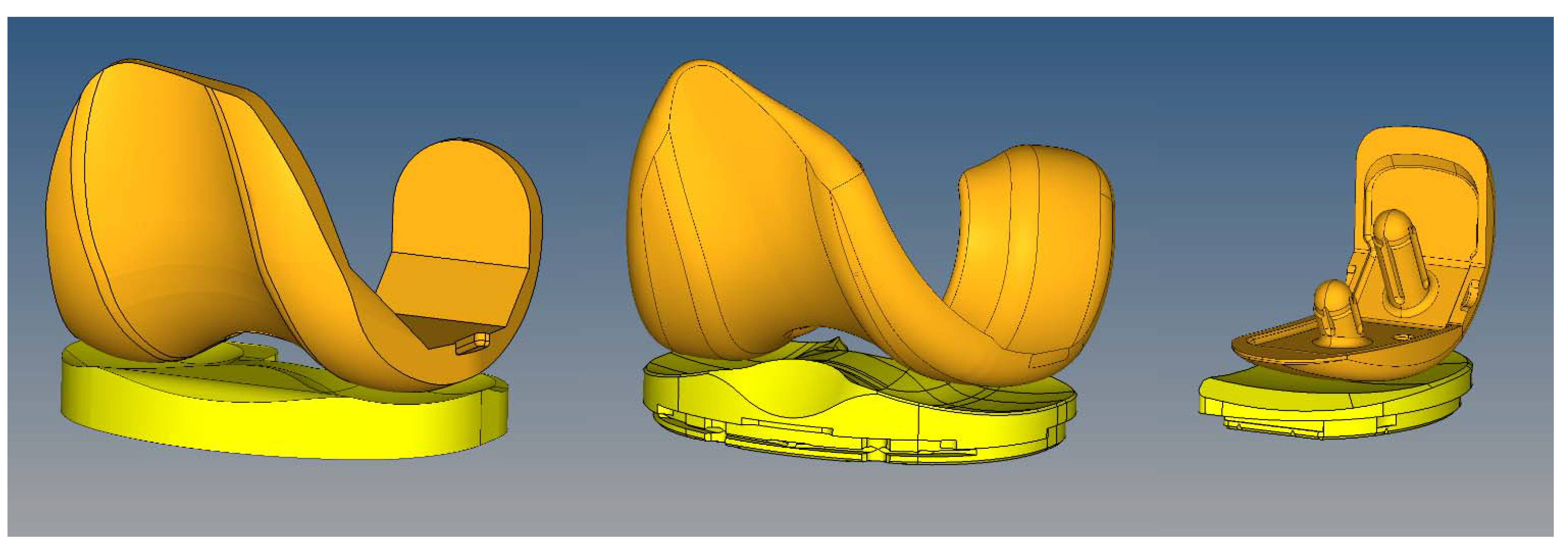
2.3. Experimental Wear Simulation of Unicompartmental Design
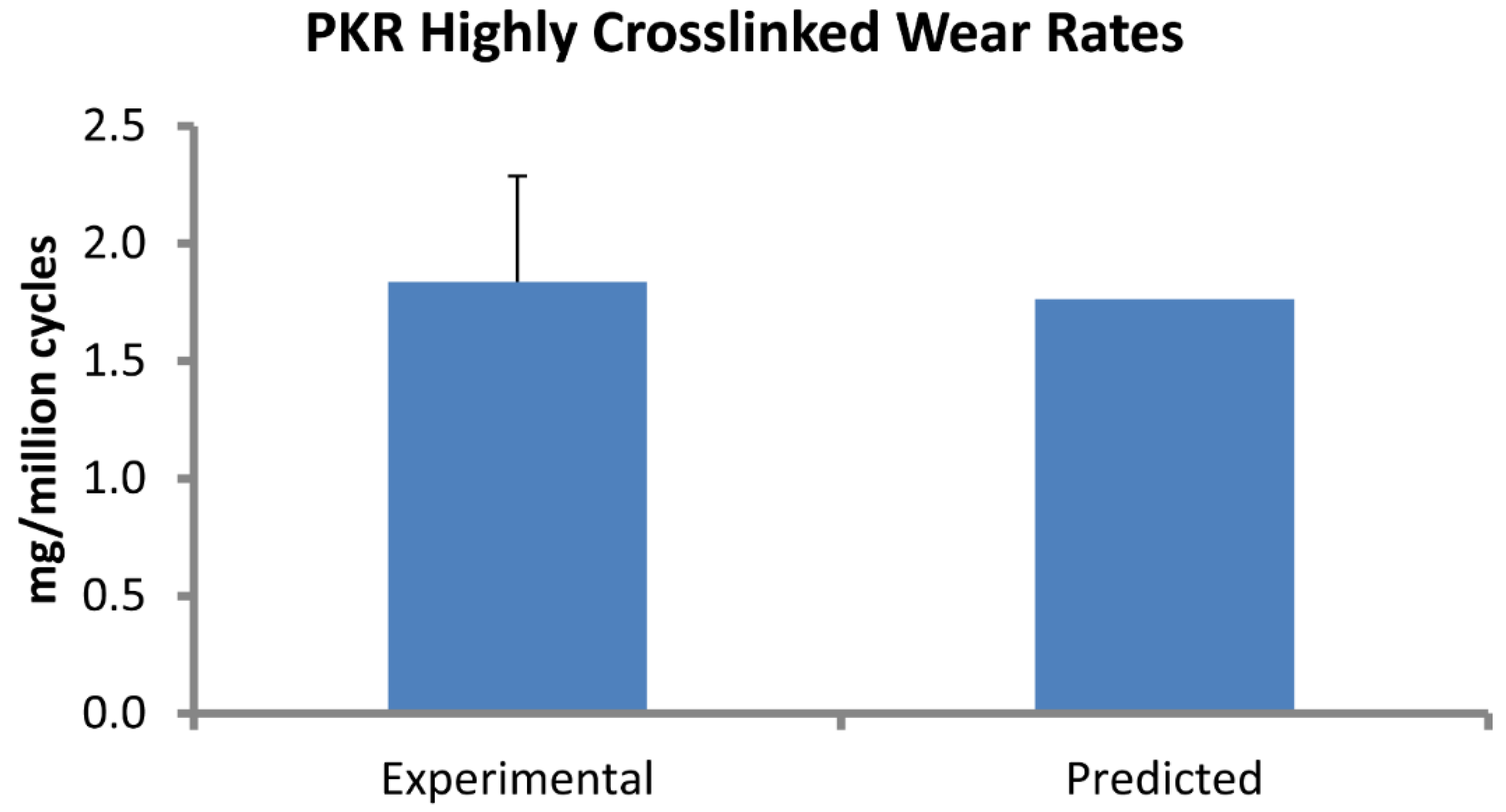
3. Results
| Standard Crosslinked PE | Highly Crosslinked PE |
|---|---|
| 1.70 × 10−10 | 5.24 × 10−11 |
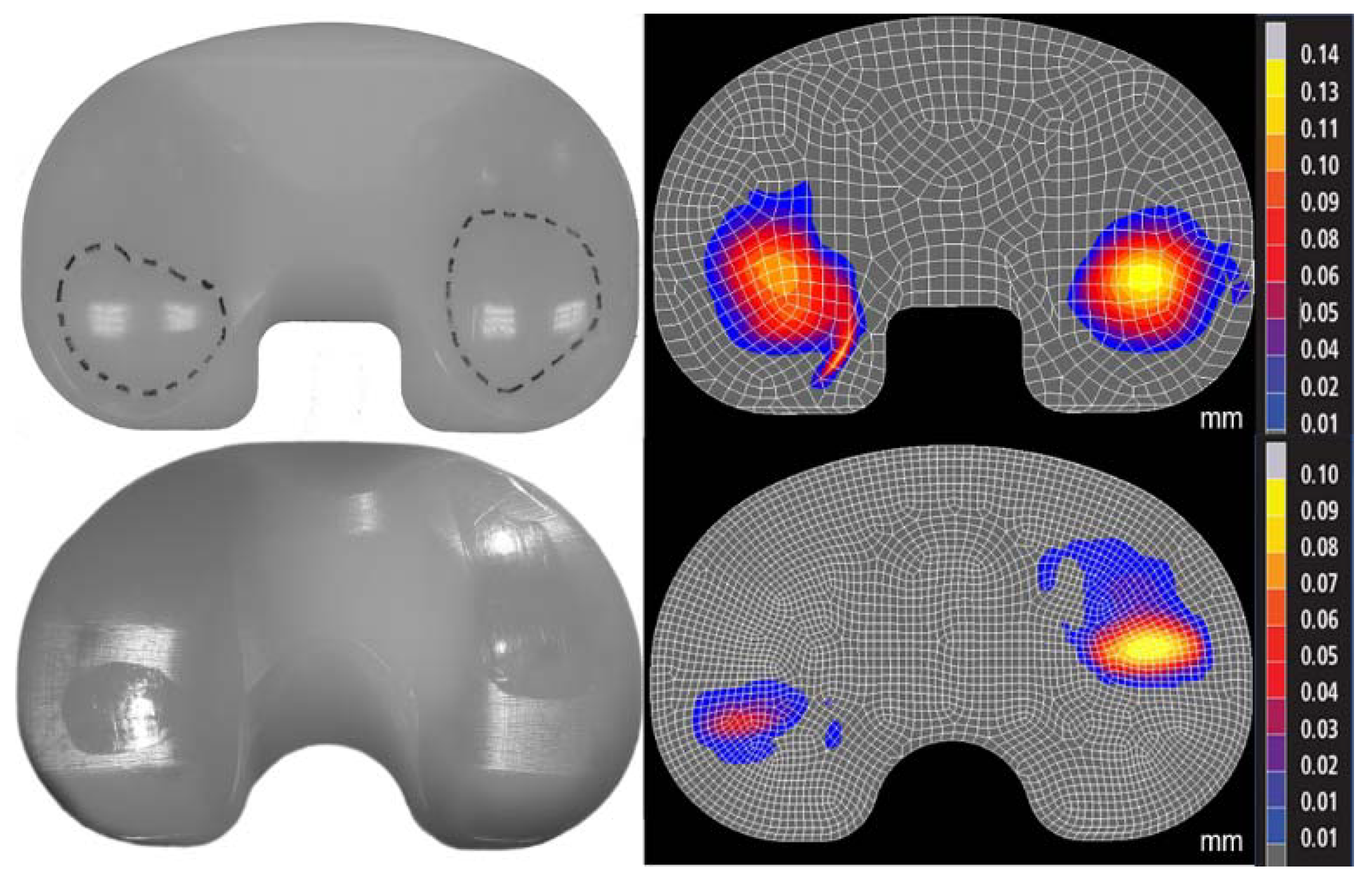
| Triathlon TKR | Triathlon PKR |
|---|---|
| 57.6 | 39.9 |
| Polyethylene type | M:L Load Distribution | Medial Penetration | Lateral Penetration |
|---|---|---|---|
| Highly Crosslinked TKA | 70:30 | 0.025 | 0.018 |
| Standard Crosslinked TKA | 60:40 | 0.045 | 0.039 |
| Standard Crosslinked TKA | 68:32 | 0.054 | 0.029 |
| Highly Crosslinked PKR | 60:40 | 0.019 |
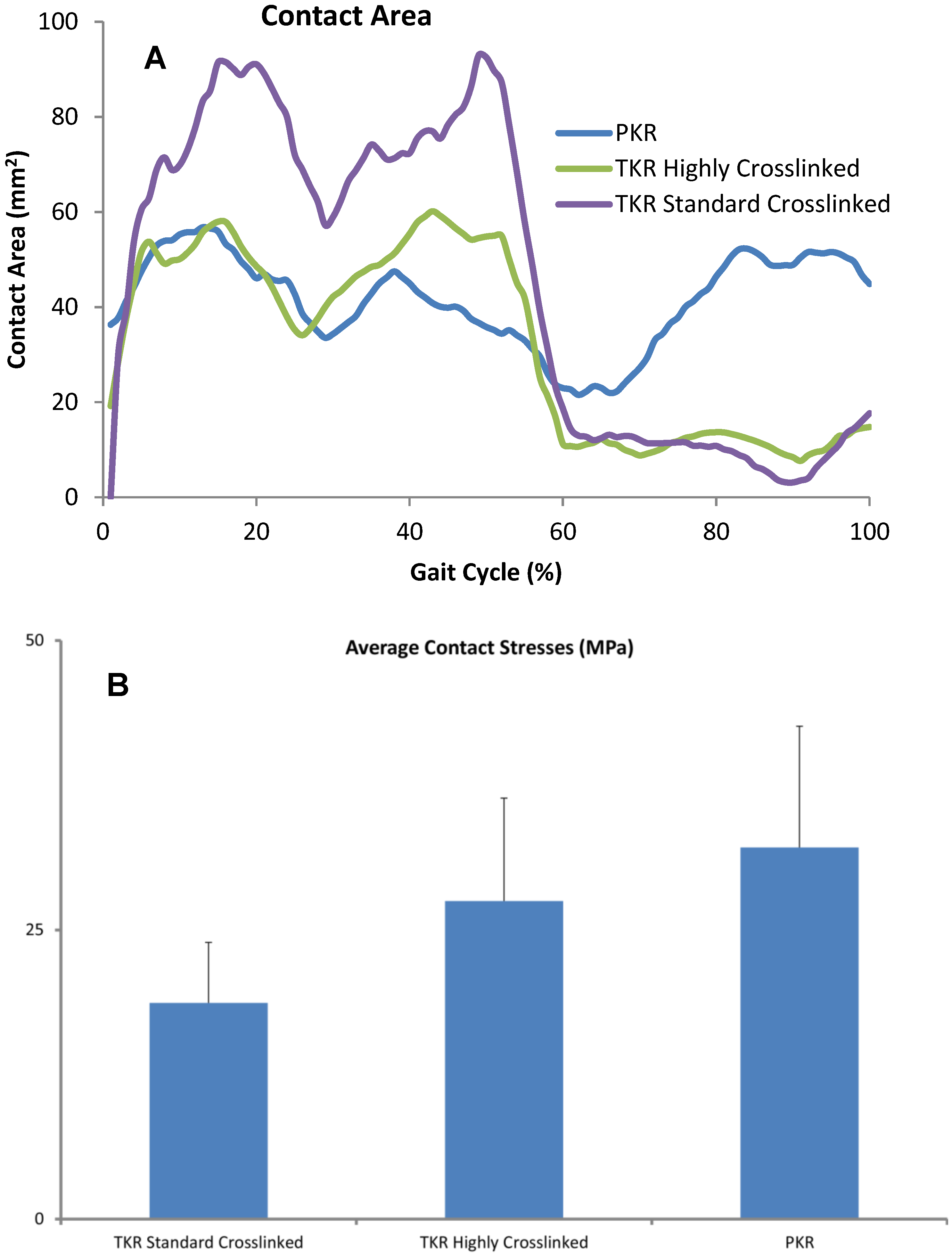
| Phase | Triathlon TKR | Triathlon PKR |
|---|---|---|
| Stance | 56 | 62 |
| Swing | 44 | 38 |
4. Discussion
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Sharkey, P.F.; Hozack, W.J.; Rothman, R.H.; Shastri, S.; Jacoby, S.M. Insall Award paper. Why are total knee arthroplasties failing today? Clin. Orthop. Relat. Res. 2002, 404, 7–13. [Google Scholar] [CrossRef] [PubMed]
- Callaghan, J.J.; O’Rourke M, R.; Saleh, K.J. Why knees fail: Lessons learned. J. Arthroplast. 2004, 19, 31–34. [Google Scholar] [CrossRef]
- Kurtz, S.M.; Gawel, H.A.; Patel, J.D. History and systematic review of wear and osteolysis outcomes for first-generation highly crosslinked polyethylene. Clin. Orthop. Relat. Res. 2011, 469, 2262–2277. [Google Scholar] [CrossRef] [PubMed]
- Hodrick, J.T.; Severson, E.P.; McAlister, D.S.; Dahl, B.; Hofmann, A.A. Highly crosslinked polyethylene is safe for use in total knee arthroplasty. Clin. Orthop. Relat. Res. 2008, 466, 2806–2812. [Google Scholar] [CrossRef] [PubMed]
- Sharkey, P.F.; Lichstein, P.M.; Shen, C.; Tokarski, A.T.; Parvizi, J. Why are total knee arthroplasties failing today—Has anything changed after 10 years? J. Arthroplast. 2014, 29, 1774–1778. [Google Scholar] [CrossRef]
- Le, D.H.; Goodman, S.B.; Maloney, W.J.; Huddleston, J.I. Current modes of failure in TKA: Infection, instability, and stiffness predominate. Clin. Orthop. Relat. Res. 2014, 472, 2197–2200. [Google Scholar] [CrossRef] [PubMed]
- Weale, A.E.; Newman, J.H. Unicompartmental arthroplasty and high tibial osteotomy for osteoarthrosis of the knee. A comparative study with a 12- to 17-year follow-up period. Clin. Orthop. Relat. Res. 1994, 302, 134–137. [Google Scholar] [PubMed]
- Hui, C.; Salmon, L.J.; Kok, A.; Williams, H.A.; Hockers, N.; van der Tempel, W.M.; Chana, R.; Pinczewski, L.A. Long-term survival of high tibial osteotomy for medial compartment osteoarthritis of the knee. Am. J. Sports Med. 2011, 39, 64–70. [Google Scholar] [CrossRef] [PubMed]
- Broughton, N.S.; Newman, J.H.; Baily, R.A. Unicompartmental replacement and high tibial osteotomy for osteoarthritis of the knee. A comparative study after 5–10 years’ follow-up. J. Bone Joint Surg. Br. 1986, 68, 447–452. [Google Scholar] [PubMed]
- Pandit, H.; Jenkins, C.; Gill, H.S.; Barker, K.; Dodd, C.A.; Murray, D.W. Minimally invasive Oxford phase 3 unicompartmental knee replacement: Results of 1000 cases. J. Bone Joint Surg. Br. 2011, 93, 198–204. [Google Scholar] [CrossRef] [PubMed]
- Patil, S.; Colwell, C.W., Jr.; Ezzet, K.A.; D’Lima, D.D. Can normal knee kinematics be restored with unicompartmental knee replacement? J. Bone Joint Surg. Am. 2005, 87, 332–338. [Google Scholar] [CrossRef] [PubMed]
- Parratte, S.; Pauly, V.; Aubaniac, J.M.; Argenson, J.N. No Long-term Difference Between Fixed and Mobile Medial Unicompartmental Arthroplasty. Clin. Orthop. Relat. Res. 2012, 470, 61–68. [Google Scholar] [CrossRef] [PubMed]
- Kuipers, B.M.; Kollen, B.J.; Bots, P.C.; Burger, B.J.; van Raay, J.J.; Tulp, N.J.; Verheyen, C.C. Factors associated with reduced early survival in the Oxford phase III medial unicompartment knee replacement. Knee 2010, 17, 48–52. [Google Scholar] [CrossRef] [PubMed]
- Lidgren, L.; Robertsson, O.; W-Dahl, A. The Swedish Knee Arthroplasty Register Annual Report. 2009. Available online: www.ort.lu.se/knee/ (accessed on 25 April 2012).
- Archard, J.F. Contact and rubbing of flat surfaces. J. Appl. Phys. 1953, 24, 981–988. [Google Scholar] [CrossRef]
- Abdelgaied, A.; Liu, F.; Brockett, C.; Jennings, L.; Fisher, J.; Jin, Z. Computational wear prediction of artificial knee joints based on a new wear law and formulation. J. Biomech. 2011, 44, 1108–1116. [Google Scholar] [CrossRef] [PubMed]
- Knight, L.A.; Pal, S.; Coleman, J.C.; Bronson, F.; Haider, H.; Levine, D.L.; Taylor, M.; Rullkoetter, P.J. Comparison of long-term numerical and experimental total knee replacement wear during simulated gait loading. J. Biomech. 2007, 40, 1550–1558. [Google Scholar] [CrossRef] [PubMed]
- Strickland, M.A.; Taylor, M. In-silico wear prediction for knee replacements—Methodology and corroboration. J. Biomech. 2009, 42, 1469–1474. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Sakoda, H.; Sawyer, W.G.; Banks, S.A.; Fregly, B.J. Predicting knee replacement damage in a simulator machine using a computational model with a consistent wear factor. J. Biomech. Eng. 2008, 130. [Google Scholar] [CrossRef]
- Kang, L.; Galvin, A.L.; Fisher, J.; Jin, Z. Enhanced computational prediction of polyethylene wear in hip joints by incorporating cross-shear and contact pressure in additional to load and sliding distance: Effect of head diameter. J. Biomech. 2009, 42, 912–918. [Google Scholar] [CrossRef] [PubMed]
- Hermida, J.; Patil, S.; Chen, P.C.; McNulty, D.; Swope, S.; Colwell, C.W.; D’Lima, D.D. Total Knee Arthroplasty Design Affects Polyethylene Wear. In Proceedings of the Annual Meeting AAOS, New Orleans, LA, USA, 5–9 February 2003; Volume 4, p. 398.
- Hermida, J.C.; Fischler, A.; Colwell, C.W., Jr.; D’Lima, D.D. The effect of oxidative aging on the wear performance of highly crosslinked polyethylene knee inserts under conditions of severe malalignment. J. Orthop. Res. 2008, 26, 1585–1590. [Google Scholar] [CrossRef] [PubMed]
- Standard Number 14243-3:2014: Implants for Surgery—Wear of Total Knee Joint Prostheses—Part 3: Loading and Displacement Parameters for Wear-Testing Machines with Displacement Control and Corresponding Environmental Conditions for Test; International Organization for Standardization (ISO): Geneva, Switzerland, 2014.
- Fischer-Cripps, A.C. Introduction to Contact Mechanics; Springer-Verlag: New York, NY, USA, 2000. [Google Scholar]
- D’Lima, D.D.; Chen, P.C.; Colwell, C.W., Jr. Polyethylene contact stresses, articular congruity, and knee alignment. Clin. Orthop. Relat. Res. 2001, 392, 232–238. [Google Scholar] [CrossRef] [PubMed]
- D’Lima, D.D.; Steklov, N.; Fregly, B.J.; Banks, S.; Colwell, C.W., Jr. In vivo contact stresses during activities of daily living after knee arthroplasty. J. Orthop. Res. 2008, 26, 1549–1555. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, M.A.; Sucec, M.C.; Fregly, B.J.; Banks, S.A.; Sawyer, W.G. Quantifying multidirectional sliding motions in total knee replacements. J. Tribol. 2005, 127, 280–286. [Google Scholar] [CrossRef]
- McKellop, H.A.; D’Lima, D. How have wear testing and joint simulator studies helped to discriminate among materials and designs? J. Am. Acad. Orthop. Surg. 2008, 16, S111–S119. [Google Scholar] [PubMed]
- D’Lima, D.D.; Patil, S.; Steklov, N.; Slamin, J.E.; Colwell, C.W., Jr. Tibial forces measured in vivo after total knee arthroplasty. J. Arthroplast. 2006, 21, 255–262. [Google Scholar] [CrossRef]
- Engh, G.A.; Zimmerman, R.L.; Parks, N.L.; Engh, C.A. Analysis of wear in retrieved mobile and fixed bearing knee inserts. J. Arthroplast. 2009, 24, 28–32. [Google Scholar] [CrossRef]
- Halder, A.; Kutzner, I.; Graichen, F.; Heinlein, B.; Beier, A.; Bergmann, G. Influence of limb alignment on mediolateral loading in total knee replacement: In vivo measurements in five patients. J. Bone Joint Surg. Am. 2012, 94, 1023–1029. [Google Scholar] [CrossRef] [PubMed]
- Berry, D.J.; Currier, J.H.; Mayor, M.B.; Collier, J.P. Knee wear measured in retrievals: A polished tray reduces insert wear. Clin. Orthop. Relat. Res. 2012, 470, 1860–1868. [Google Scholar] [CrossRef] [PubMed]
- Schmalzried, T.P.; Szuszczewicz, E.S.; Northfield, M.R.; Akizuki, K.H.; Frankel, R.E.; Belcher, G.; Amstutz, H.C. Quantitative assessment of walking activity after total hip or knee replacement. J. Bone Joint Surg. Am. 1998, 80, 54–59. [Google Scholar] [CrossRef] [PubMed]
- Lavernia, C.J.; Sierra, R.J.; Hungerford, D.S.; Krackow, K. Activity level and wear in total knee arthroplasty: A study of autopsy retrieved specimens. J. Arthroplast. 2001, 16, 446–453. [Google Scholar] [CrossRef]
- Benjamin, J.; Szivek, J.; Dersam, G.; Persselin, S.; Johnson, R. Linear and volumetric wear of tibial inserts in posterior cruciate-retaining knee arthroplasties. Clin. Orthop. Relat. Res. 2001, 392, 131–138. [Google Scholar] [CrossRef] [PubMed]
- Bragdon, C.R.; O’Connor, D.O.; Lowenstein, J.D.; Jasty, M.; Syniuta, W.D. The importance of multidirectional motion on the wear of polyethylene. Proc. Inst. Mech. Eng. H 1996, 210, 157–165. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.; Stark, C.; Dumbleton, J.H. Mechanistic and morphological origins of ultra-high molecular weight polyethylene wear debris in total joint replacement prostheses. Proc. Inst. Mech. Eng. H 1996, 210, 141–155. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Galvin, A.; Jin, Z.; Fisher, J. A new formulation for the prediction of polyethylene wear in artificial hip joints. Proc. Inst. Mech. Eng. H 2011, 225, 16–24. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A.; Lee, G.Y.; Steklov, N.; Colwell, C.W., Jr.; Ezzet, K.A.; D’Lima, D.D. Effect of tibial component varus on wear in total knee arthroplasty. Knee 2012, 19, 560–563. [Google Scholar] [CrossRef] [PubMed]
- Turell, M.; Wang, A.; Bellare, A. Quantification of the effect of cross-path motion on the wear rate of ultra-high molecular weight polyethylene. Wear 2003, 255, 1034–1039. [Google Scholar] [CrossRef]
- Kang, L.; Galvin, A.L.; Brown, T.D.; Jin, Z.; Fisher, J. Quantification of the effect of cross-shear on the wear of conventional and highly cross-linked UHMWPE. J. Biomech. 2008, 41, 340–346. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Netter, J.; Hermida, J.; Flores-Hernandez, C.; Steklov, N.; Kester, M.; D'Lima, D.D. Prediction of Wear in Crosslinked Polyethylene Unicompartmental Knee Arthroplasty. Lubricants 2015, 3, 381-393. https://doi.org/10.3390/lubricants3020381
Netter J, Hermida J, Flores-Hernandez C, Steklov N, Kester M, D'Lima DD. Prediction of Wear in Crosslinked Polyethylene Unicompartmental Knee Arthroplasty. Lubricants. 2015; 3(2):381-393. https://doi.org/10.3390/lubricants3020381
Chicago/Turabian StyleNetter, Jonathan, Juan Hermida, Cesar Flores-Hernandez, Nikolai Steklov, Mark Kester, and Darryl D. D'Lima. 2015. "Prediction of Wear in Crosslinked Polyethylene Unicompartmental Knee Arthroplasty" Lubricants 3, no. 2: 381-393. https://doi.org/10.3390/lubricants3020381
APA StyleNetter, J., Hermida, J., Flores-Hernandez, C., Steklov, N., Kester, M., & D'Lima, D. D. (2015). Prediction of Wear in Crosslinked Polyethylene Unicompartmental Knee Arthroplasty. Lubricants, 3(2), 381-393. https://doi.org/10.3390/lubricants3020381





