Monitoring and Prediction of the Real-Time Transient Thermal Mechanical Behaviors of a Motorized Spindle Tool
Abstract
1. Introduction
2. Experimental Approach
- Experimental measurement of spindle temperature rise and thermal displacement;
- Data analysis, including correlation assessment and multivariate regression to evaluate potential sensor–placement combinations;
- Prediction-model selection based on minimizing displacement error while using the fewest sensors.
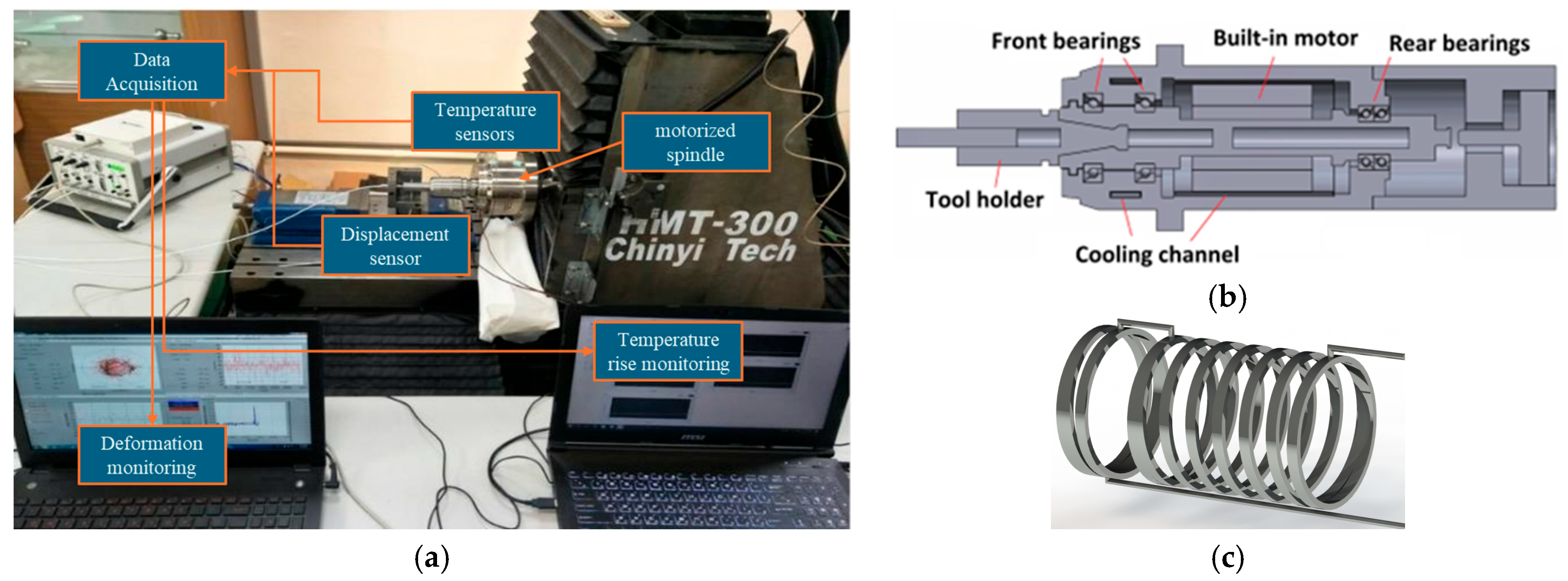
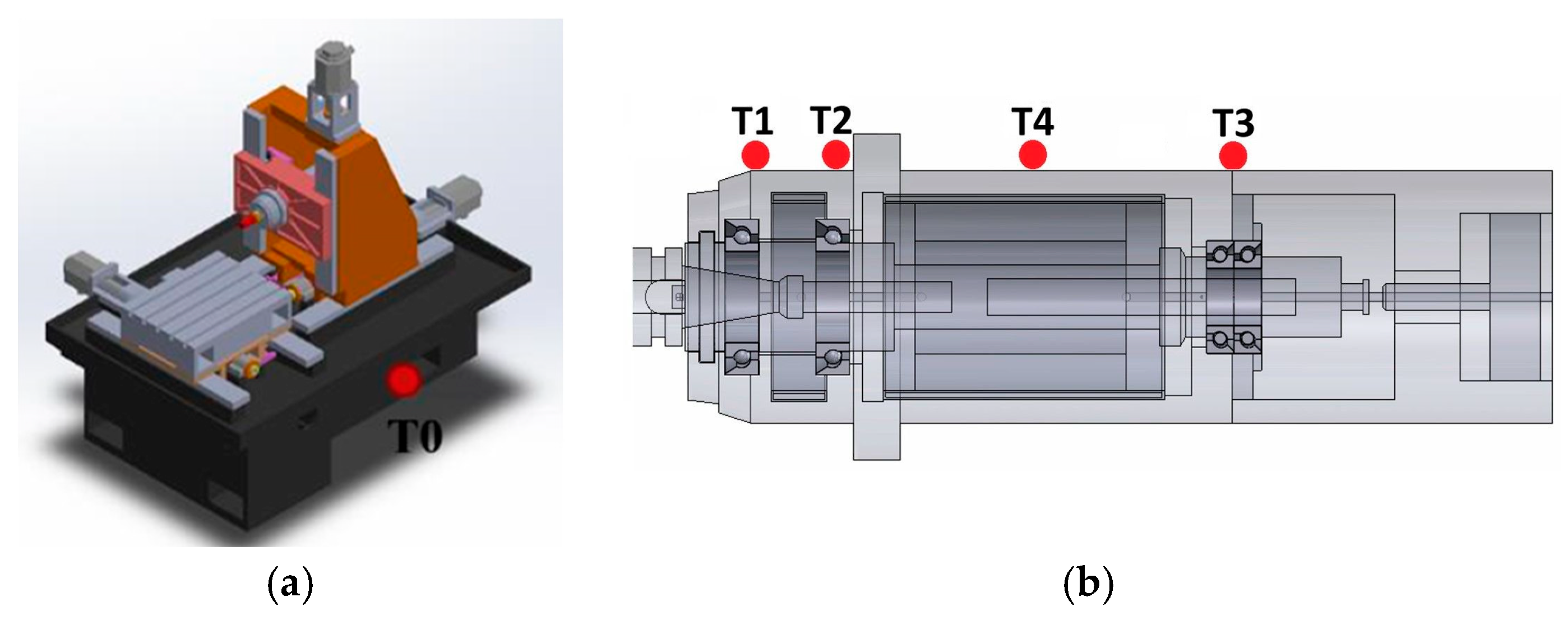
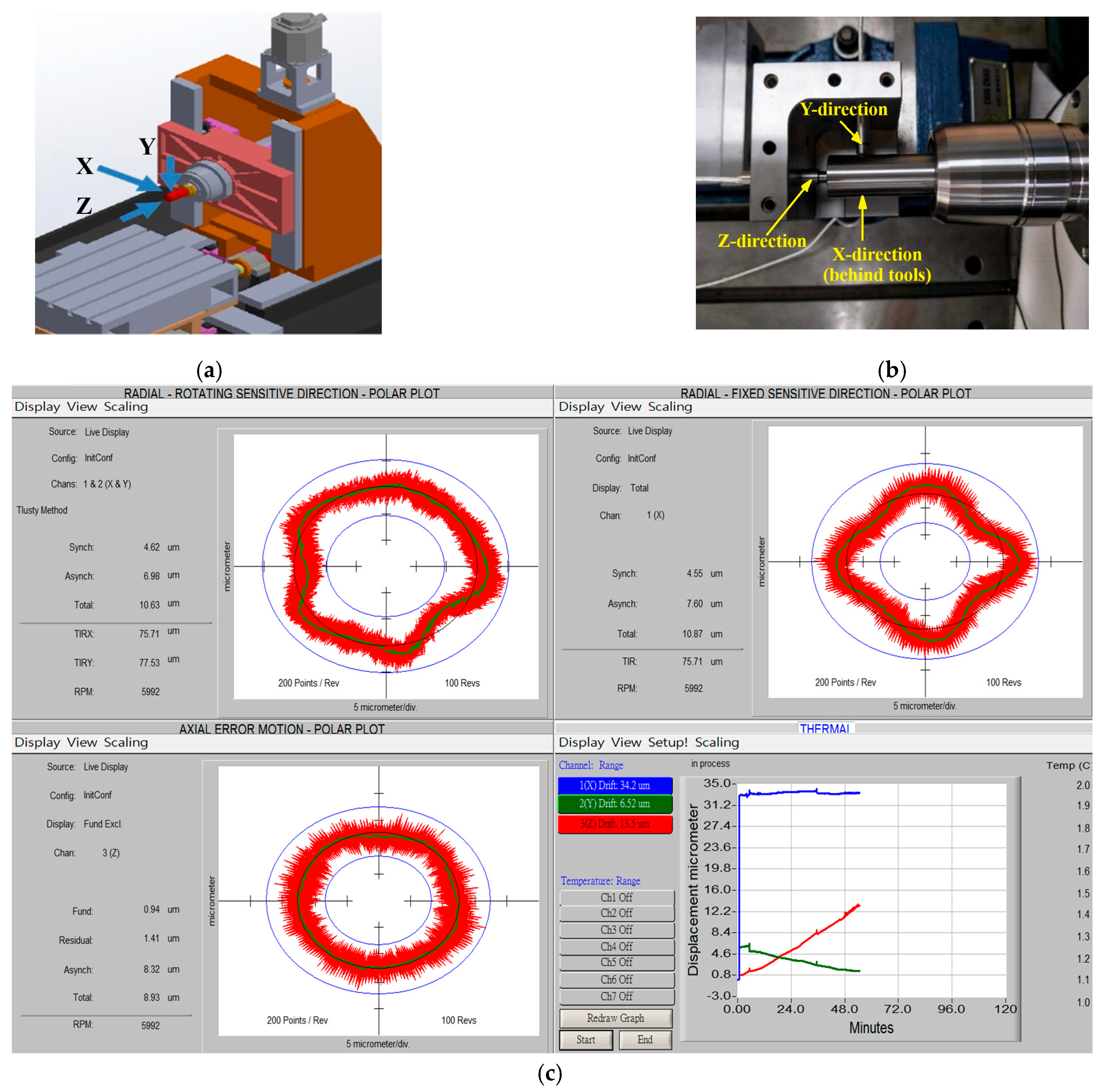
2.1. Experimental Setup
2.2. Thermal Deformation Prediction Model: Multivariate Regression Analysis
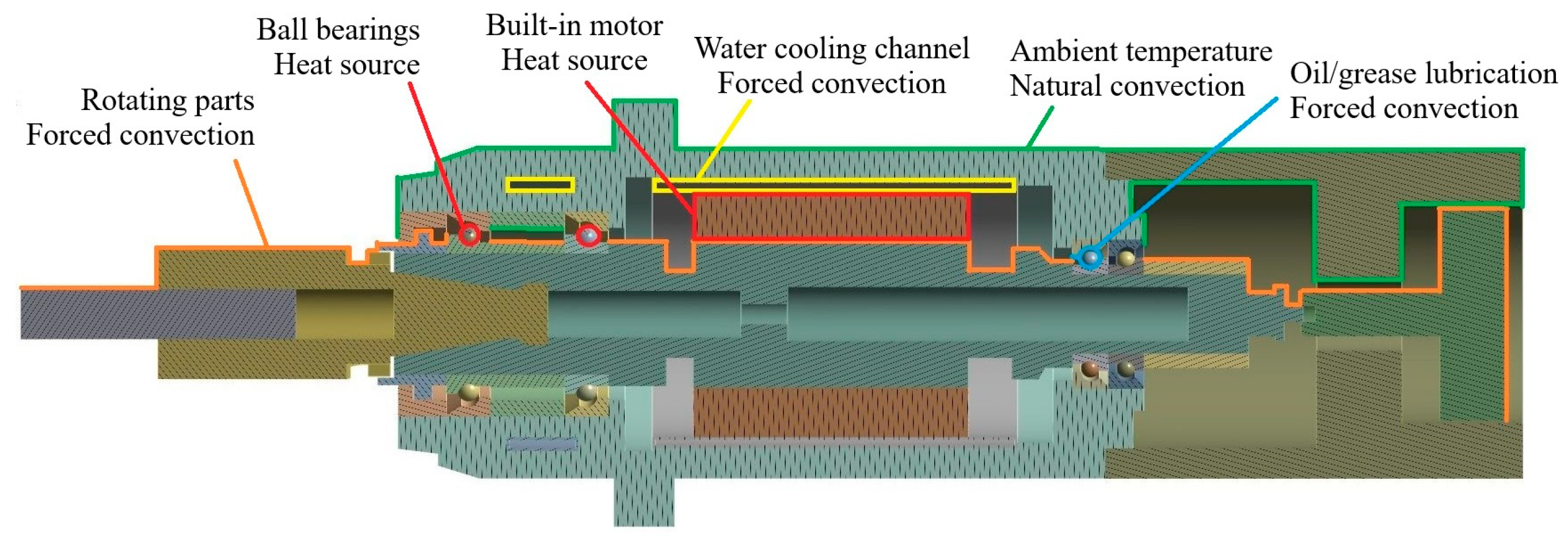
3. Finite Element Modeling Approach
3.1. Thermal–Mechanical Modeling
3.2. Heat Generation of Ball Bearing
3.3. Heat Generation of Built-In Motor
3.4. Convective Heat Transfer Coefficient
3.5. Transient Thermal–Mechanical Analysis
3.6. Thermal Analysis Parameters
4. Results and Discussion
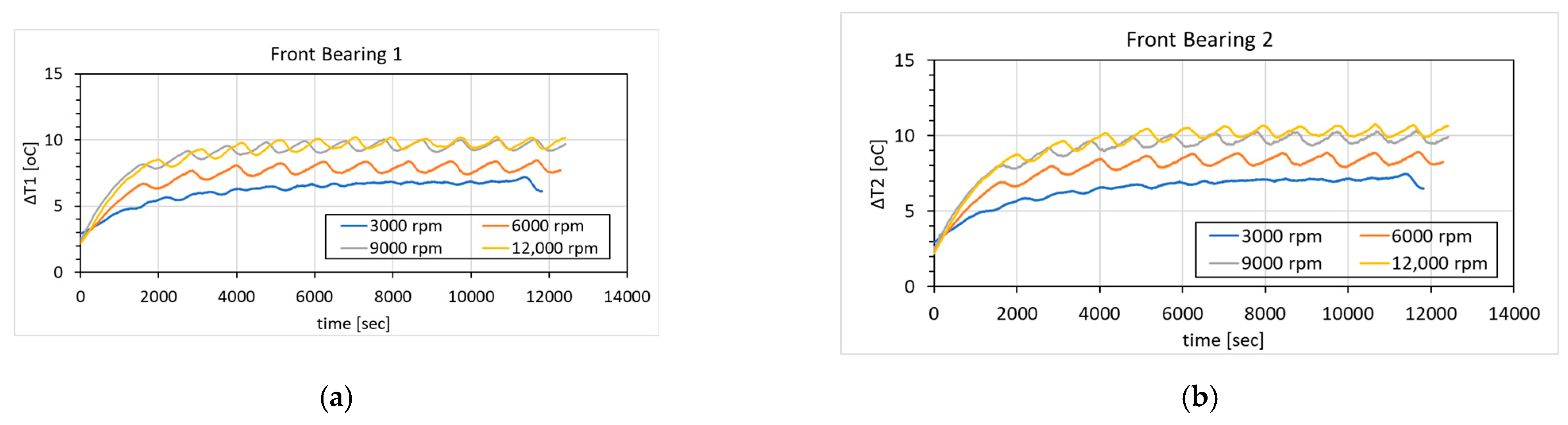
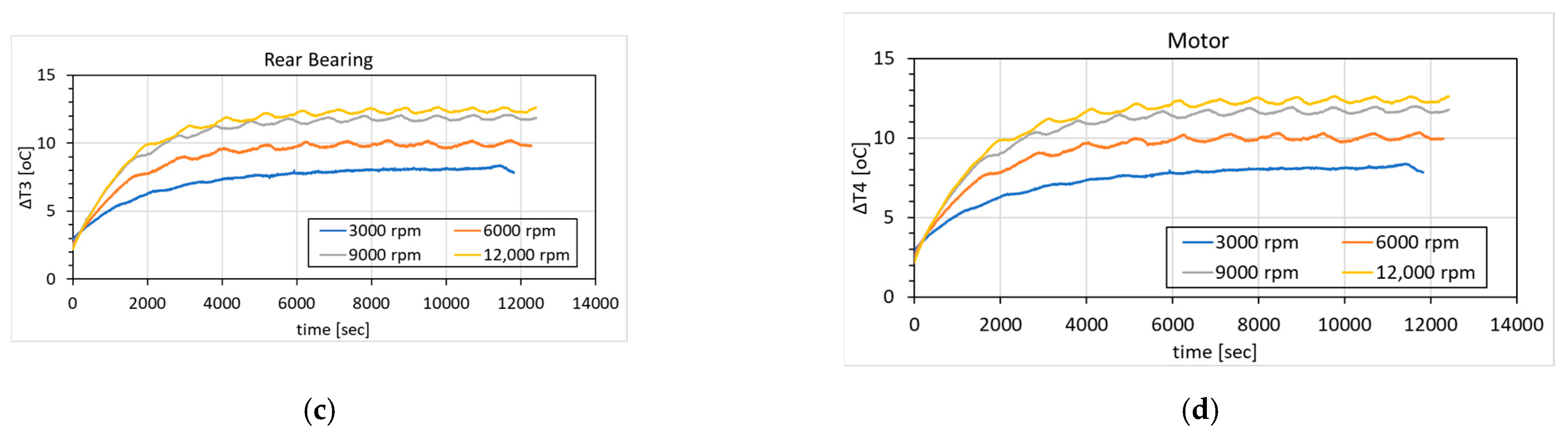
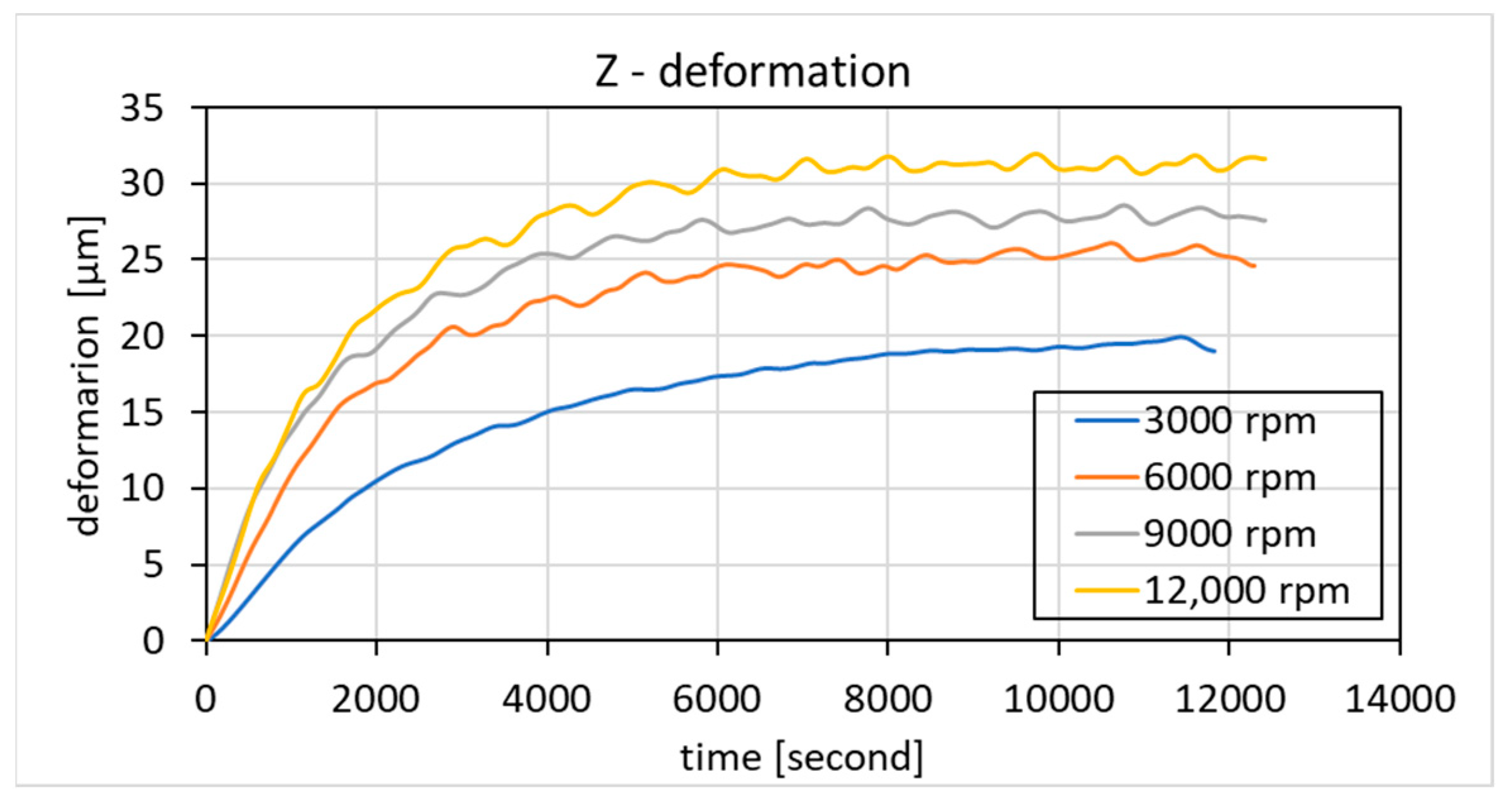
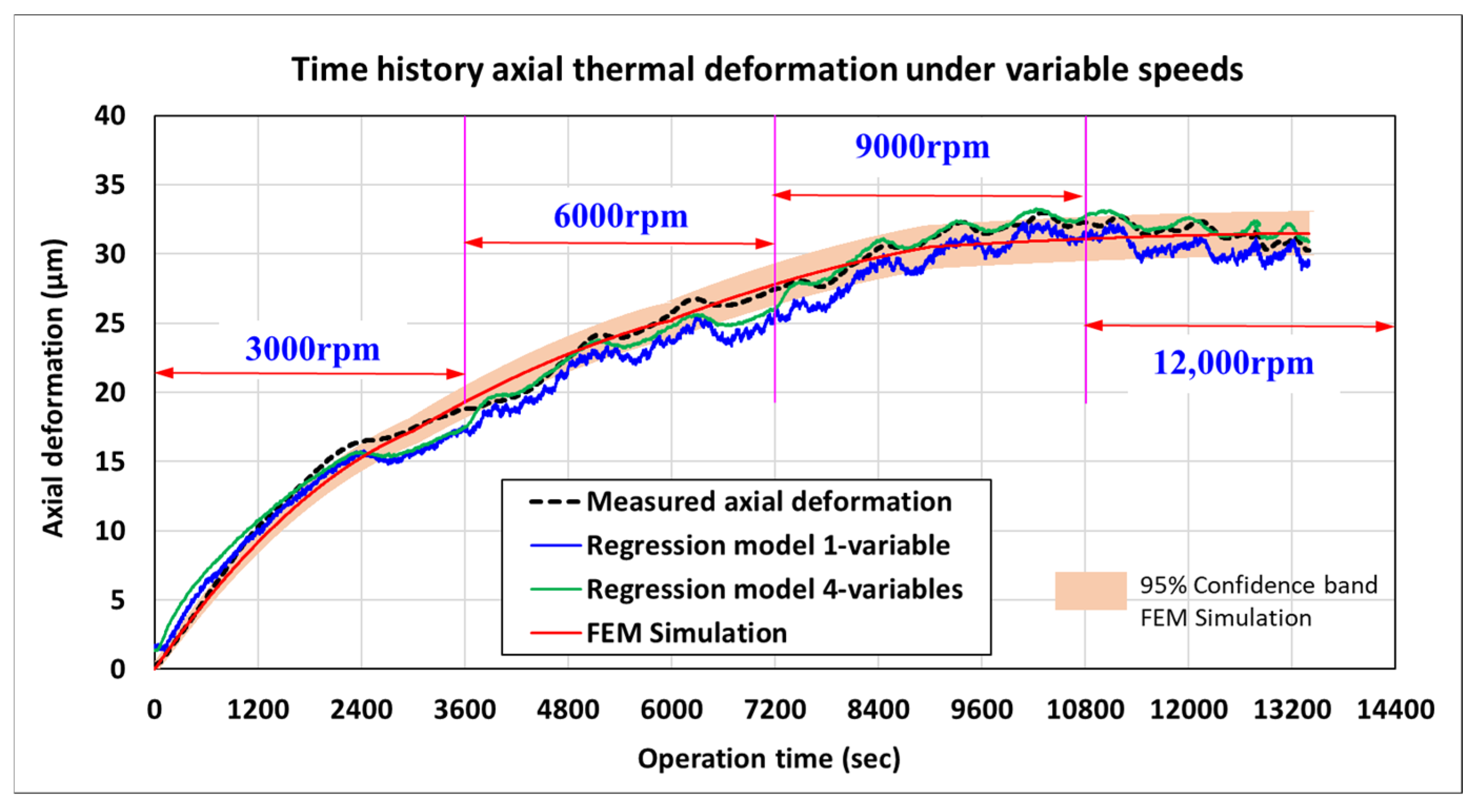
4.1. Thermal Temperature Rise and Deformation Measurement Results
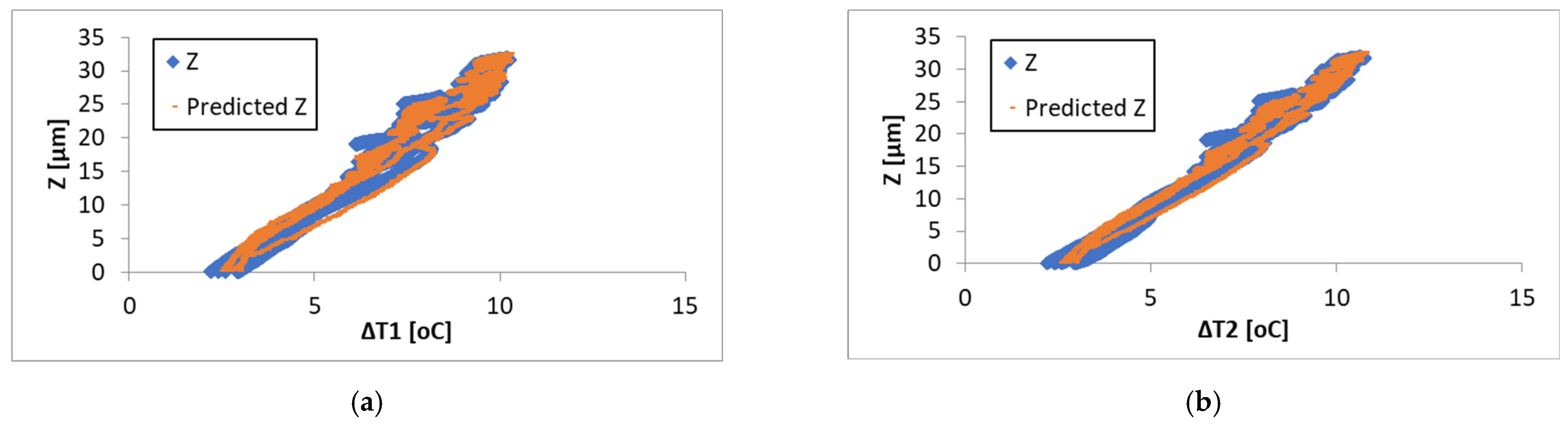
4.2. Multivariate Regression Analysis and Model Selection
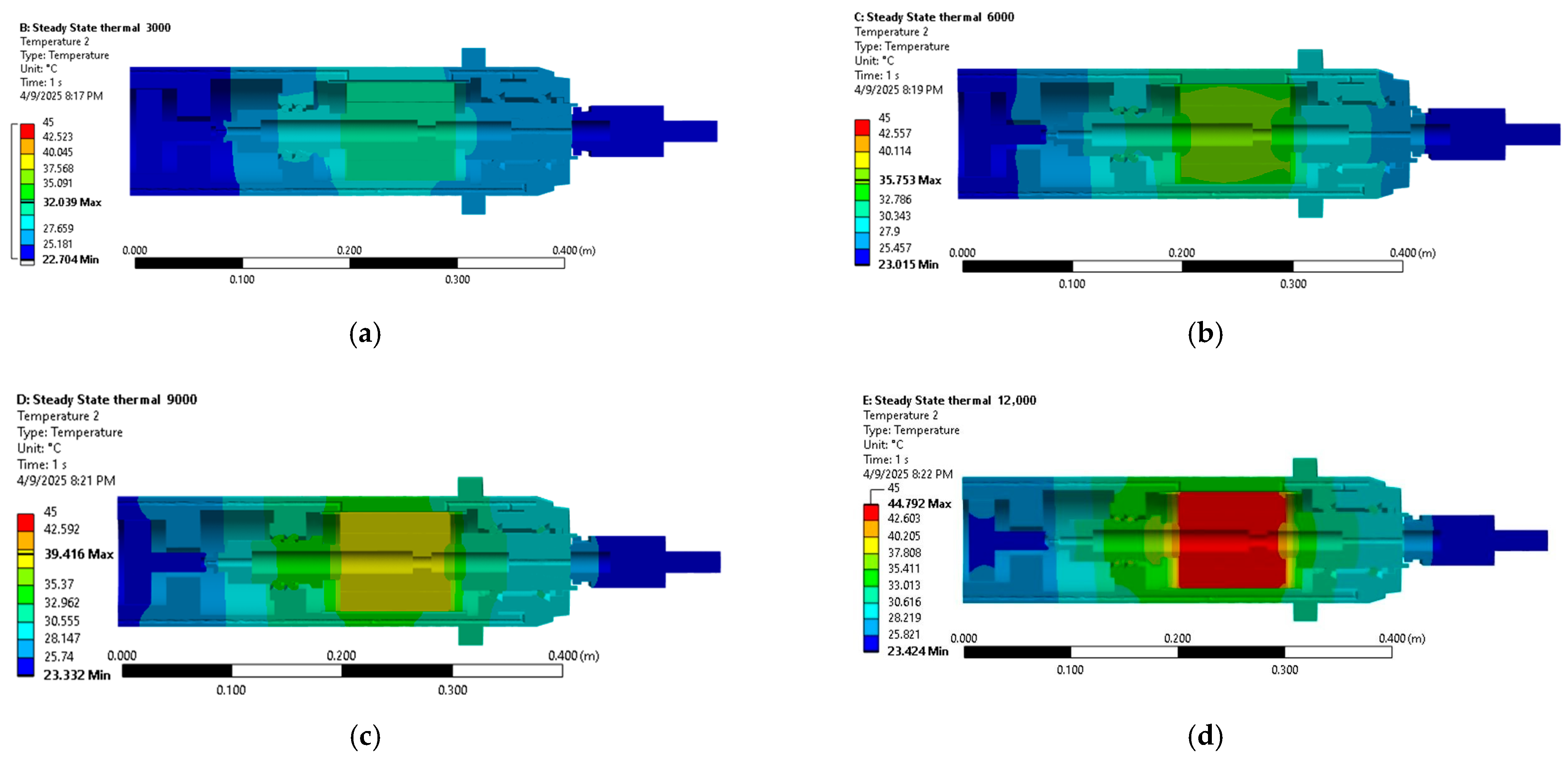
4.3. Thermal–Mechanical Behaviors
4.4. Model Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fu, Y.Q.; Gao, W.G.; Yang, J.Y.; Zhang, Q.; Zhang, D.W. Thermal Error Measurement, Modeling and Compensation for Motorized Spindle and the Research on Compensation Effect Validation. Adv. Mater. Res. 2014, 889–890, 1003–1008. [Google Scholar] [CrossRef]
- Lei, M.; Gao, F.; Li, Y.; Xia, P.; Wang, M.; Yang, J. Feedback Control–Based Active Cooling with Pre-Estimated Reliability for Stabilizing the Thermal Error of a Precision Mechanical Spindle. Int. J. Adv. Manuf. Technol. 2022, 121, 2023–2040. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, T.; Gao, W.; Tian, Y.; Qi, X.; Wang, P.; Zhang, D. Active Coolant Strategy for Thermal Balance Control of Motorized Spindle Unit. Appl. Therm. Eng. 2018, 134, 460–468. [Google Scholar] [CrossRef]
- He, S.; Tang, T.; Bao, J.; Tang, R. Research on Teaching Reform of Experimental Measurement of Temperature Field and Thermal Deformation of Machine Tool. IOP Conf. Ser. Earth Environ. Sci. 2019, 358, 042015. [Google Scholar] [CrossRef]
- Prasad, V.V.S.H.; Kamala, V. Thermal Error Compensation in High-Speed CNC Machine Feed Drives. AIP Conf. Proc. 2021, 2317, 030026. [Google Scholar] [CrossRef]
- Arief, T.M.; Liao, H.-E.; Lin, P.-Y.; Hung, J.-P. Finite Element Modeling of Milling Spindle Thermal Behavior with Variation of Bearing Preload. In Lecture Notes in Mechanical Engineering; Springer: Singapore, 2025; pp. 439–446. [Google Scholar] [CrossRef]
- Arief, T.M.; Lin, W.-Z.; Royandi, M.A.; Hung, J.-P. Development of a Digital Model for Predicting the Variation in Bearing Preload and Dynamic Characteristics of a Milling Spindle under Thermal Effects. Lubricants 2024, 12, 185. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, W.; Lan, S.; Ni, J.; Wu, W.; Lu, B. A Review on Spindle Thermal Error Compensation in Machine Tools. International J. Mach. Tools Manuf. 2015, 95, 20–38. [Google Scholar] [CrossRef]
- Liu, K.; Liu, H.; Li, T.; Liu, Y.; Wang, Y. Intelligentization of Machine Tools: Comprehensive Thermal Error Compensation of Machine-Workpiece System. Int. J. Adv. Manuf. Technol. 2019, 102, 3865–3877. [Google Scholar] [CrossRef]
- Li, Y.; Yu, M.; Bai, Y.; Hou, Z.; Wu, W. A Review of Thermal Error Modeling Methods for Machine Tools. Appl. Sci. 2021, 11, 5216. [Google Scholar] [CrossRef]
- Liu, H.; Miao, E.; Wang, J.; Zhang, L.; Zhao, S. Temperature-Sensitive Point Selection and Thermal Error Model Adaptive Update Method of CNC Machine Tools. Machines 2022, 10, 427. [Google Scholar] [CrossRef]
- Yao, X.; Hu, T.; Yin, G.; Cheng, C. Thermal Error Modeling and Prediction Analysis Based on OM Algorithm for Machine Tool’s Spindle. Int. J. Adv. Manuf. Technol. 2020, 106, 3345–3356. [Google Scholar] [CrossRef]
- Yue, H.; Guo, C.; Li, Q.; Zhao, L.; Hao, G. Thermal Error Modeling of CNC Milling Machining Spindle Based on an Adaptive Chaos Particle Swarm Optimization Algorithm. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 427. [Google Scholar] [CrossRef]
- Wei, X.; Ye, H.; Miao, E.; Pan, Q. Thermal Error Modeling and Compensation Based on Gaussian Process Regression for CNC Machine Tools. Precis. Eng. 2022, 77, 65–76. [Google Scholar] [CrossRef]
- Fu, G.; Mu, S.; Zheng, Y.; Lu, C.; Wang, X.; Wang, T. MA-CNN Based Spindle Thermal Error Modeling Using the Depth Feature Analysis with Thermal Error Mechanism. Measurement 2024, 226, 114183. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, B.; Dai, Y.; Zhu, W.; Wang, Q.; Wang, B. Research on Thermal Error Modeling of Motorized Spindle Based on BP Neural Network Optimized by Beetle Antennae Search Algorithm. Machines 2021, 9, 286. [Google Scholar] [CrossRef]
- Dai, Y.; Pang, J.; Rui, X.; Li, W.; Wang, Q.; Li, S.-Z. Thermal Error Prediction Model of High-Speed Motorized Spindle Based on Delm Network Optimized by Weighted Mean of Vectors Algorithm. Case Stud. Therm. Eng. 2023, 47, 103054. [Google Scholar] [CrossRef]
- Liu, Y.-C.; Li, K.-Y.; Tsai, Y.-C. Spindle Thermal Error Prediction Based on LSTM Deep Learning for a CNC Machine Tool. Appl. Sci. 2021, 11, 5444. [Google Scholar] [CrossRef]
- Wei, X.; Ye, H.; Wang, G.; Hu, W. Adaptive Thermal Error Prediction for CNC Machine Tool Spindle Using Online Measurement and an Improved Recursive Least Square Algorithm. Case Stud. Therm. Eng. 2024, 56, 104239. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Z.; Liu, Q.; Wang, D.; Li, X. A Comprehensive Prediction and Compensation Method of Spindle Thermal Error for a CNC Grinding Machine. Digit. Eng. 2024, 2, 100012. [Google Scholar] [CrossRef]
- Dong, Y.; Chen, F.; Lu, T.; Qiu, M. Research on Thermal Stiffness of Machine Tool Spindle Bearing under Different Initial Preload and Speed Based on FBG Sensors. Int. J. Adv. Manuf. Technol. 2022, 119, 941–951. [Google Scholar] [CrossRef]
- Sun, S.; Qiao, Y.; Gao, Z.; Wang, J.; Bian, Y. A Thermal Error Prediction Model of the Motorized Spindles Based on ABHHO-LSSVM. Int. J. Adv. Manuf. Technol. 2023, 127, 2257–2271. [Google Scholar] [CrossRef]
- Chen, Y.; Deng, X.; Lin, X.; Guo, S.; Jiang, S.; Zhou, J. Thermal Deformation Prediction for Spindle System of Machining Center Based on Multi-Source Heterogeneous Information Fusion. J. Mech. Sci. Technol. 2023, 37, 4227–4238. [Google Scholar] [CrossRef]
- Liao, C.-W.; Lee, M.-T.; Liu, Y.-C. A Thermal Deformation Estimation Method for High Precision Machine Tool Spindles Based on the Convolutional Neural Network. J. Mech. Sci. Technol. 2023, 37, 3151–3162. [Google Scholar] [CrossRef]
- Li, Y.; Wu, K.; Wang, N.; Wang, Z.; Li, W.; Lei, M. Thermal Deformation Analysis of Motorized Spindle Base on Thermo-Solid Structure Coupling Theory. Heat. Mass. Transfer 2024, 60, 1755–1771. [Google Scholar] [CrossRef]
- Huang, X.; Yu, R.; Jiang, Z.; Rong, Z. Modeling and Reliability Global Sensitivity Analysis of Motorized Spindles Considering Thermal Errors. J. Northeast. Univ. (Nat. Sci.) 2024, 45, 675. [Google Scholar] [CrossRef]
- Lu, Q.; Zhu, D.; Wang, M.; Li, M. Digital Twin-Driven Thermal Error Prediction for CNC Machine Tool Spindle. Lubricants 2023, 11, 219. [Google Scholar] [CrossRef]
- Xiao, J.; Fan, K. Research on the Digital Twin for Thermal Characteristics of Motorized Spindle. Int. J. Adv. Manuf. Technol. 2022, 119, 5107–5118. [Google Scholar] [CrossRef]
- Chang, P.-Y.; Yang, P.-Y.; Chou, F.-I.; Chen, S.-H. Hybrid Optimization Algorithm for Thermal Displacement Compensation of Computer Numerical Control Machine Tool Using Regression Analysis and Fuzzy Inference. Sci. Prog. 2023, 106, 00368504231171268. [Google Scholar] [CrossRef]
- Lee, J.-H.; Yang, S.-H. Statistical Optimization and Assessment of a Thermal Error Model for CNC Machine Tools. Int. J. Mach. Tools Manuf. 2002, 42, 147–155. [Google Scholar] [CrossRef]
- Miao, E.; Liu, Y.; Liu, H.; Gao, Z.; Li, W. Study on the Effects of Changes in Temperature-Sensitive Points on Thermal Error Compensation Model for CNC Machine Tool. Int. J. Mach. Tools Manuf. 2015, 97, 50–59. [Google Scholar] [CrossRef]
- Liu, H.; Miao, E.M.; Wei, X.Y.; Zhuang, X.D. Robust Modeling Method for Thermal Error of CNC Machine Tools Based on Ridge Regression Algorithm. Int. J. Mach. Tools Manuf. 2017, 113, 35–48. [Google Scholar] [CrossRef]
- Liu, J.; Ma, C.; Gui, H.; Wang, S. Thermally-Induced Error Compensation of Spindle System Based on Long Short Term Memory Neural Networks. Appl. Soft Comput. 2021, 102, 107094. [Google Scholar] [CrossRef]
- Yu, B.-F.; Liu, K.; Li, K.-Y. Application of Multiple Regressions to Thermal Error Compensation Technology—Experiment on Workpiece Spindle of Lathe. Int. J. Autom. Smart Technol. 2016, 6, 103–110. [Google Scholar] [CrossRef]
- Maurya, S.N.; Luo, W.-J.; Panigrahi, B.; Negi, P.; Wang, P.-T. Input Attribute Optimization for Thermal Deformation of Machine-Tool Spindles Using Artificial Intelligence. J. Intell. Manuf. 2025, 36, 2387–2408. [Google Scholar] [CrossRef]
- Haoshuo, W.; Guangsheng, C.; Yushan, S. Prediction of Thermal Errors in a Motorized Spindle in CNC Machine Tools by Applying Loads Based on Heat Flux. Proc. Inst. Mech. Eng. Part. C 2024, 238, 264–278. [Google Scholar] [CrossRef]
- Tan, F.; Deng, C.; Xiao, H.; Luo, J.; Zhao, S. A Wrapper Approach-Based Key Temperature Point Selection and Thermal Error Modeling Method. Int. J. Adv. Manuf. Technol. 2020, 106, 907–920. [Google Scholar] [CrossRef]
- Liu, Y.; Miao, E.; Liu, H.; Chen, Y. Robust Machine Tool Thermal Error Compensation Modelling Based on Temperature-Sensitive Interval Segmentation Modelling Technology. Int. J. Adv. Manuf. Technol. 2020, 106, 655–669. [Google Scholar] [CrossRef]
- Ariaga, N.; Longstaff, A.; Fletcher, S. A Method for Temperature Sensor and Model Selection for Machine Tool Thermal Error Modelling Using ANFIS and ANN. Int. J. Adv. Manuf. Technol. 2024, 135, 863–881. [Google Scholar] [CrossRef]
- Cheng, Y.; Jin, S.; Qiao, K.; Zhou, S.; Xue, J. Predictive Modeling of Thermal Displacement for High-Speed Electric Spindle. Int. J. Precis. Eng. Manuf. 2025, 26, 345–361. [Google Scholar] [CrossRef]
- Cao, L.; Khim, G.; Baek, S.G.; Chung, S.-C.; Park, C.-H. A Selection Method of Key Temperature Points for Thermal Error Modeling of Machine Tools Featuring Multiple Heat Sources. Precis. Eng. 2025, 93, 528–539. [Google Scholar] [CrossRef]
- NSK Ltd. Part 5: Technical Guides. In NSK Motion & Control Super Precision Bearings; NSK Ltd.: Tokyo, Japan, 2022. [Google Scholar]
- Alexopoulos, E.C. Introduction to Multivariate Regression Analysis. Hippokratia 2010, 14, 23–28. [Google Scholar] [PubMed]
- Liu, J.; Ma, C.; Wang, S.; Wang, S.; Yang, B.; Shi, H. Thermal-Structure Interaction Characteristics of a High-Speed Spindle- Bearing System. Int. J. Mach. Tools Manuf. 2019, 137, 42–57. [Google Scholar] [CrossRef]
- Harris, T.A.; Kotzalas, M.N. Essential Concepts of Bearing Technology: Rolling Bearing Analysis, 5th ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Harris, T.A.; Kotzalas, M.N. Advanced Concepts of Bearing Technology: Rolling Bearing Analysis, 5th ed.; CRC Press: Boca Raton, FL, USA, 2006; ISBN 978-0-8493-7182-0. [Google Scholar]
- Jiang, Z.; Huang, X.; Chang, M.; Li, C.; Ge, Y. Thermal Error Prediction and Reliability Sensitivity Analysis of Motorized Spindle Based on Kriging Model. Eng. Fail. Anal. 2021, 127, 105558. [Google Scholar] [CrossRef]
- Wu, Q.; Li, Y.; Lin, Z.; Pan, B.; Gu, D.; Luo, H. Thermal Error Prediction in High-Power Grinding Motorized Spindles for Computer Numerical Control Machining Based on Data-Driven Methods. Micromachines 2025, 16, 563. [Google Scholar] [CrossRef]
- Bossmanns, B.; Tu, J.F. A Thermal Model for High Speed Motorized Spindles. Int. J. Mach. Tools Manuf. 1999, 39, 1345–1366. [Google Scholar] [CrossRef]
- Zhang, L.; Xuan, J.; Shi, T. Obtaining More Accurate Thermal Boundary Conditions of Machine Tool Spindle Using Response Surface Model Hybrid Artificial Bee Colony Algorithm. Symmetry 2020, 12, 361. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, P.; Chen, C.; Yu, D.; Wu, Z. A Method for Thermal Performance Modeling and Simulation of Machine Tools. Int. J. Adv. Manuf. Technol. 2013, 68, 1517–1527. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, Z. Cooling Prediction of Motorized Spindle Based on Multivariate Linear Regression. J. Phys. Conf. Ser. 2021, 1820, 012196. [Google Scholar] [CrossRef]
- Dong, Y.; Ma, Y.; Qiu, M.; Chen, F.; He, K. Analysis and Experimental Research of Transient Temperature Rise Characteristics of High-Speed Cylindrical Roller Bearing. Sci. Rep. 2024, 14, 711. [Google Scholar] [CrossRef]
- Wang, S.; Naito, C.; Quiel, S.; Bravo, J.; Suleiman, M.; Romero, C.; Neti, S. Parametric Analysis of Transient Thermal and Mechanical Performance for a Thermosiphon-Concrete Thermal Energy Storage System. J. Energy Storage 2024, 104, 114176. [Google Scholar] [CrossRef]


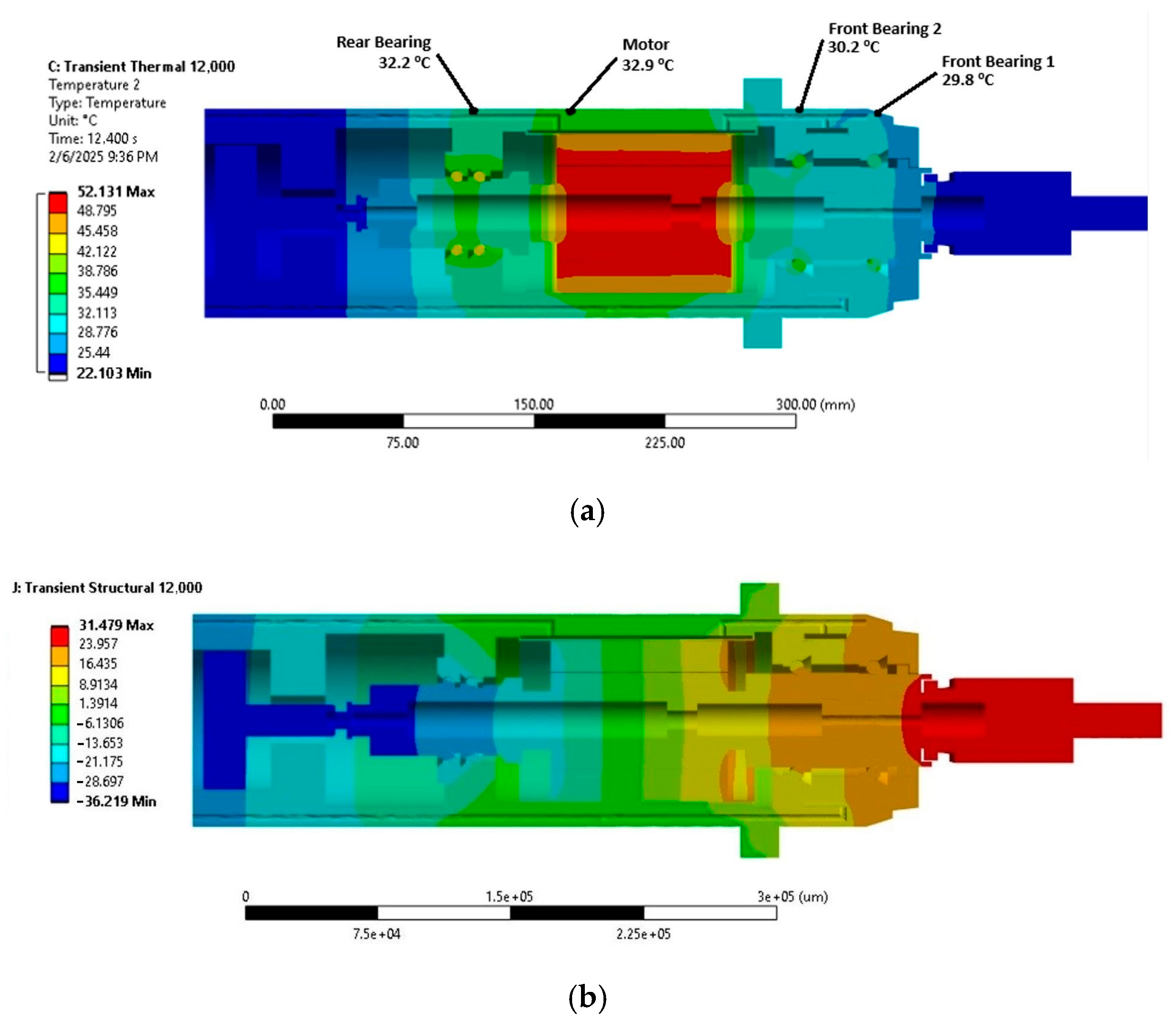
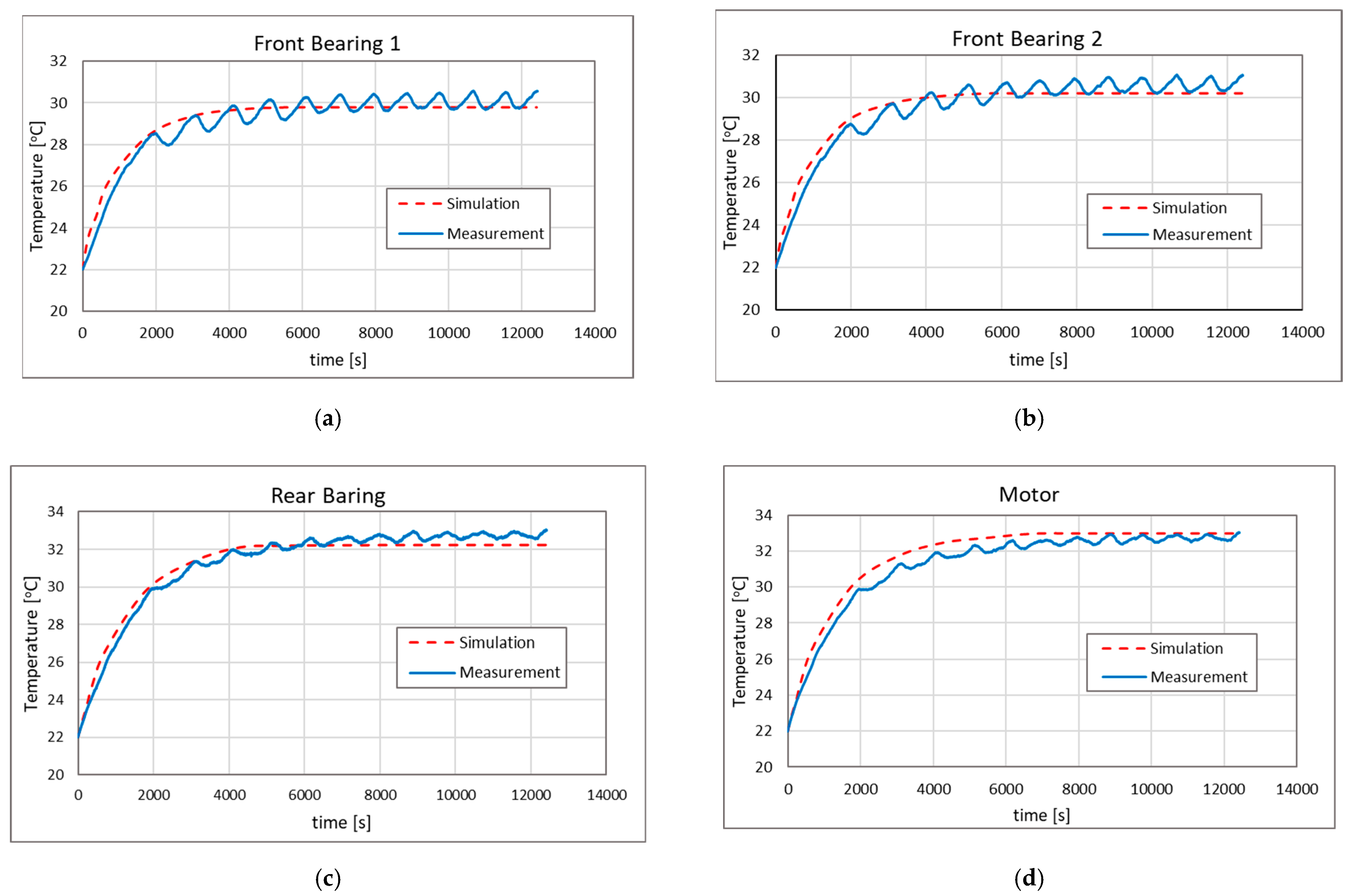
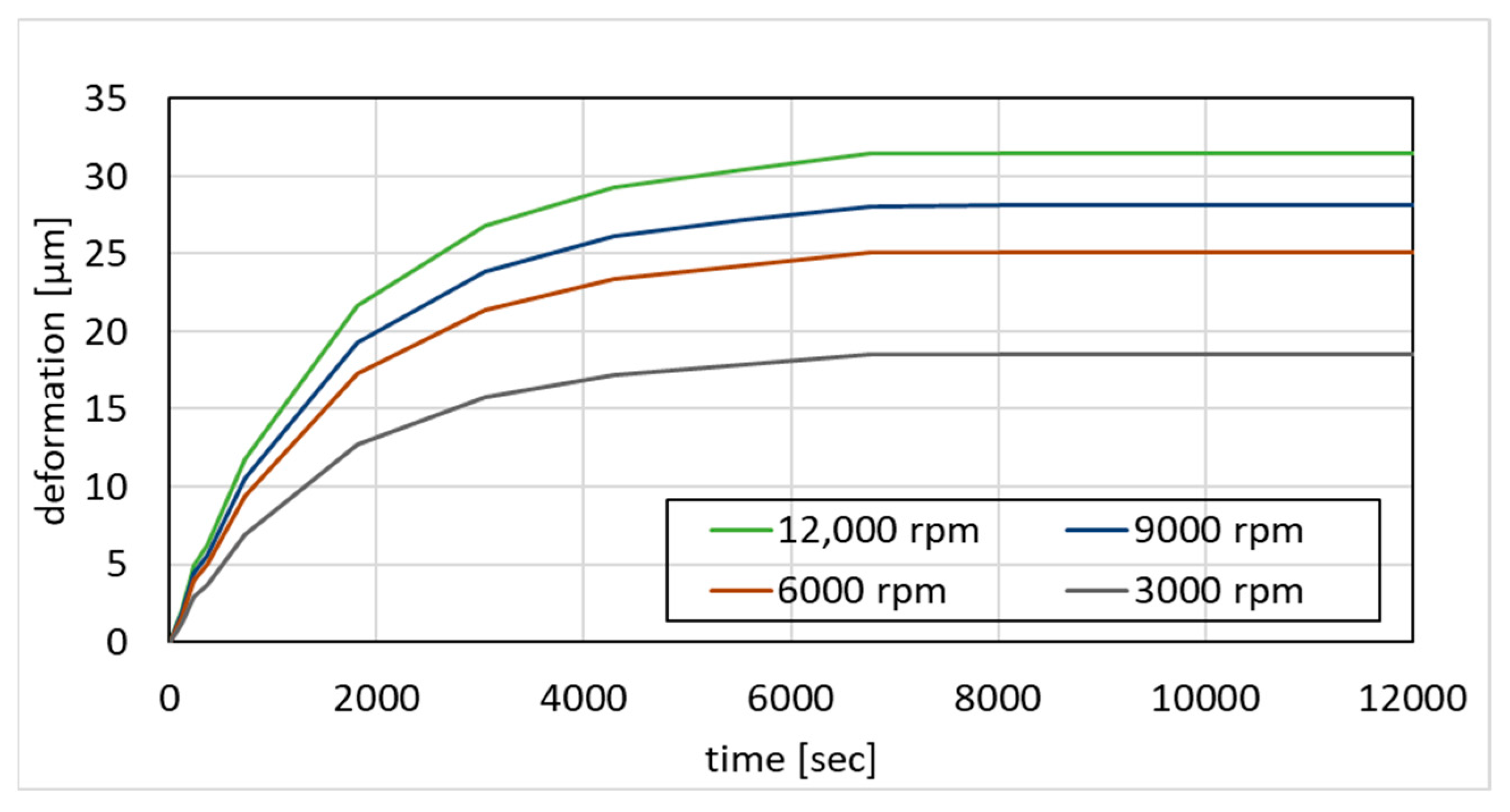
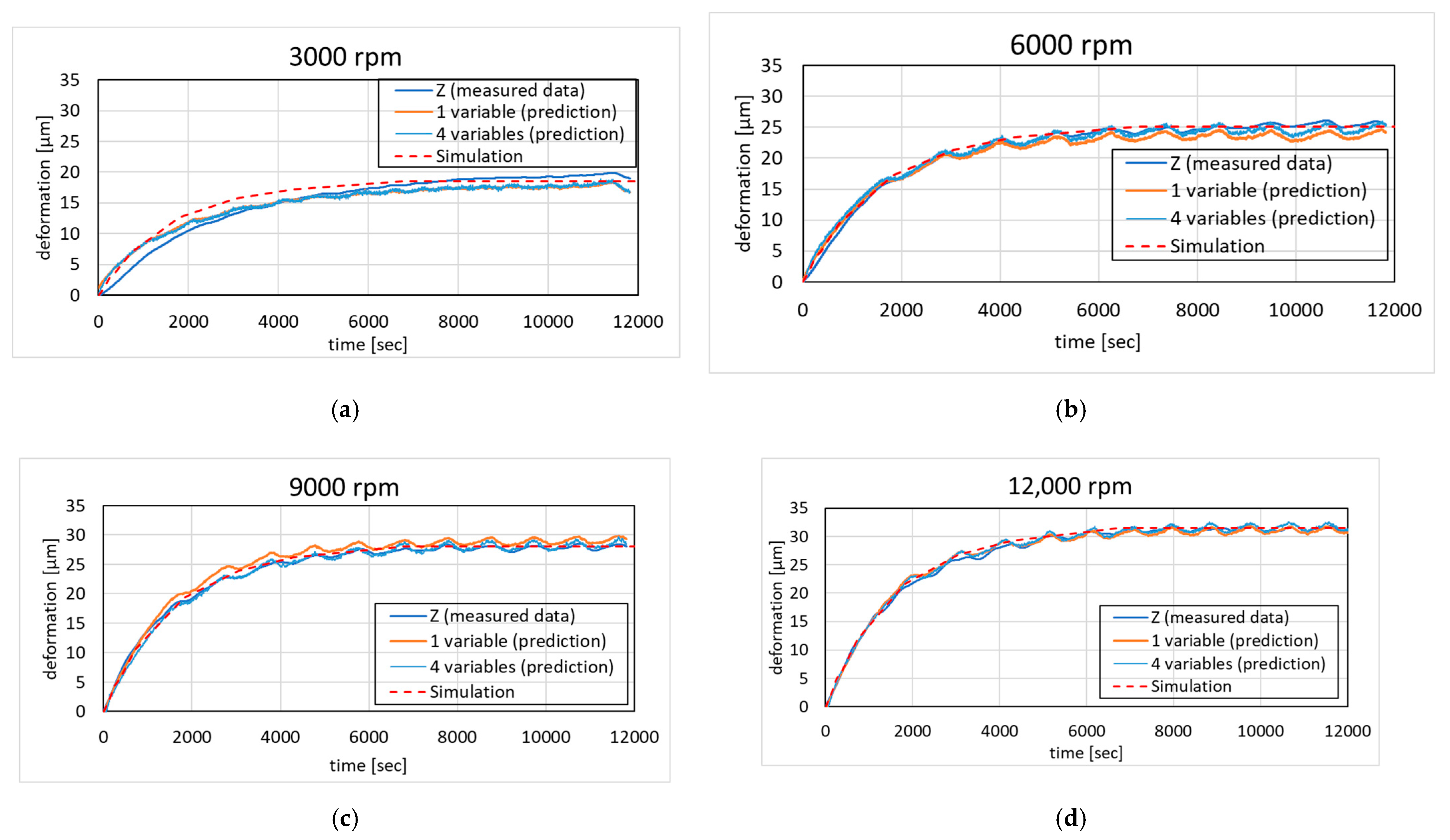

| Spindle Speed (rpm) | Front Bearing Heat Loss (W) | Rear Bearing Heat Loss (W) | Motor Power Loss (W) |
|---|---|---|---|
| 3000 | 22.4 | 9.5 | 119 |
| 6000 | 65.9 | 26.6 | 239 |
| 9000 | 125.3 | 49.3 | 359 |
| 12,000 | 198.6 | 76.9 | 479 |
| Spindle Speed (rpm) | Natural Convection (W/m2·°C) | Rotating Surfaces (W/m2·°C) | Rolling Bearing (W/m2·°C) | Cooling Channel (W/m2·°C) |
|---|---|---|---|---|
| 3000 | 9.7 | 46.7 | 17.4 | 202 |
| 6000 | 9.7 | 74.2 | 24.6 | 202 |
| 9000 | 9.7 | 97.2 | 30.2 | 202 |
| 12,000 | 9.7 | 117.8 | 34.8 | 202 |
| No. | Variable Number | Variable (s) | RMSE (µm) | R2 | MS | η (%) |
|---|---|---|---|---|---|---|
| 1 | 1 | ΔT1 | 2.00588811 | 0.926418 | 4.023915934 | 92.58 |
| 2 | 1 | ΔT2 | 1.47593211 | 0.960163 | 2.178553617 | 94.52 |
| 3 | 1 | ΔT3 | 1.29753423 | 0.97721 | 1.245920653 | 95.03 |
| 4 | 1 | ΔT4 | 1.11616526 | 0.977217 | 1.245926698 | 95.73 |
| 5 | 2 | ΔT1, ΔT2 | 0.94087558 | 0.983811 | 0.885355383 | 96.56 |
| 6 | 2 | ΔT1, ΔT3 | 1.20309184 | 0.97353 | 1.447607414 | 95.42 |
| 7 | 2 | ΔT1, ΔT4 | 1.00387463 | 0.98157 | 1.007887802 | 96.28 |
| 8 | 2 | ΔT2, ΔT3 | 1.28165607 | 0.96996 | 1.642843653 | 95.07 |
| 9 | 2 | ΔT2, ΔT4 | 1.09270177 | 0.978165 | 1.194143529 | 95.83 |
| 10 | 2 | ΔT3, ΔT4 | 0.91634349 | 0.984644 | 0.839788324 | 96.77 |
| 11 | 3 | ΔT1, ΔT2, ΔT3 | 0.8765848 | 0.985948 | 0.76852651 | 96.91 |
| 12 | 3 | ΔT1, ΔT2, ΔT4 | 0.85511587 | 0.986628 | 0.731342676 | 97.02 |
| 13 | 3 | ΔT1, ΔT3, ΔT4 | 0.88370991 | 0.985718 | 0.78107085 | 96.97 |
| 14 | 3 | ΔT2, ΔT3, ΔT4 | 0.90459135 | 0.985035 | 0.818419264 | 96.86 |
| 15 | 4 | ΔT, ΔT2, ΔT3, ΔT4 | 0.83943138 | 0.987114 | 0.704789015 | 97.11 |
| No. | Model | Method | RMSE (µm) | R2 | MS | η (%) |
|---|---|---|---|---|---|---|
| 1 | This study (1 variable) | Multivariate regression | 1.1162 | 0.97722 | 1.2459 | 95.73 |
| 2 | This study (4 variables) | Multivariate regression | 0.8394 | 0.98711 | 0.7047 | 97.11 |
| 3 | Dai et al. [17] | DELM | 1.5058 | 0.9844 | n.a. | 96.90 |
| 4 | Yue et al. [13] | ACPSO | 1.5700 | 0.8872 | n.a. | 95.53 |
| 5 | Li et al. [16] | BAS-BP | 2.0610 | 0.9500 | n.a. | 94.10 |
| Step Number | Step End Time [s] | Imported Temperature [°C] | Axial Deformation [µm] | ||||||
|---|---|---|---|---|---|---|---|---|---|
| T1 | T2 | T3 | T4 | 3000 rpm | 6000 rpm | 9000 rpm | 12,000 rpm | ||
| 1 | 0 | 22 | 22 | 22 | 22 | 0 | 0 | 0 | 0 |
| 2 | 124 | 23.32 | 23.22 | 22.93 | 23.01 | 1.20 | 1.62 | 1.81 | 2.03 |
| 3 | 244.44 | 24.05 | 23.90 | 23.77 | 23.83 | 2.90 | 3.93 | 4.40 | 4.93 |
| 4 | 364.88 | 24.53 | 24.58 | 24.68 | 24.78 | 3.66 | 4.96 | 5.56 | 6.22 |
| 5 | 726.2 | 26.27 | 26.37 | 26.61 | 26.81 | 6.93 | 9.34 | 10.52 | 11.79 |
| 6 | 1810.2 | 28.47 | 28.79 | 29.81 | 30.16 | 12.71 | 17.24 | 19.30 | 21.63 |
| 7 | 3050.2 | 29.4 | 29.72 | 31.34 | 31.74 | 15.74 | 21.34 | 23.89 | 26.77 |
| 8 | 4290.2 | 29.7 | 30.06 | 32.09 | 32.47 | 17.23 | 23.36 | 26.15 | 29.30 |
| 9 | 5530.2 | 29.8 | 30.20 | 32.18 | 32.75 | 17.90 | 24.27 | 27.17 | 30.44 |
| 10 | 6770.2 | 29.8 | 30.20 | 32.21 | 32.97 | 18.50 | 25.09 | 28.09 | 31.47 |
| 11 | 8010.2 | 29.8 | 30.21 | 32.21 | 32.98 | 18.51 | 25.10 | 28.10 | 31.48 |
| 12 | 9250.2 | 29.8 | 30.21 | 32.22 | 32.99 | 18.51 | 25.10 | 28.10 | 31.48 |
| 13 | 10,490 | 29.8 | 30.21 | 32.22 | 32.99 | 18.51 | 25.10 | 28.10 | 31.48 |
| 14 | 11,730 | 29.8 | 30.21 | 32.22 | 32.99 | 18.51 | 25.10 | 28.10 | 31.48 |
| 15 | 12,400 | 29.8 | 30.21 | 32.22 | 32.99 | 18.51 | 25.10 | 28.10 | 31.48 |
| No. | Variable (s) | RMSE (µm) | |||
|---|---|---|---|---|---|
| 3000 rpm | 6000 rpm | 9000 rpm | 12,000 rpm | ||
| 1 | ΔT4 | 1.402 | 1.177 | 1.167 | 0.531 |
| 2 | ΔT3, ΔT4 | 1.450 | 1.109 | 1.103 | 0.500 |
| 3 | ΔT1, ΔT2, ΔT4 | 1.299 | 0.785 | 0.589 | 0.586 |
| 4 | ΔT1, ΔT2, ΔT3, ΔT4 | 1.314 | 0.763 | 0.549 | 0.528 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arief, T.M.; Lin, W.-Z.; Hung, J.-P.; Royandi, M.A.; Chen, Y.-J. Monitoring and Prediction of the Real-Time Transient Thermal Mechanical Behaviors of a Motorized Spindle Tool. Lubricants 2025, 13, 269. https://doi.org/10.3390/lubricants13060269
Arief TM, Lin W-Z, Hung J-P, Royandi MA, Chen Y-J. Monitoring and Prediction of the Real-Time Transient Thermal Mechanical Behaviors of a Motorized Spindle Tool. Lubricants. 2025; 13(6):269. https://doi.org/10.3390/lubricants13060269
Chicago/Turabian StyleArief, Tria Mariz, Wei-Zhu Lin, Jui-Pin Hung, Muhamad Aditya Royandi, and Yu-Jhang Chen. 2025. "Monitoring and Prediction of the Real-Time Transient Thermal Mechanical Behaviors of a Motorized Spindle Tool" Lubricants 13, no. 6: 269. https://doi.org/10.3390/lubricants13060269
APA StyleArief, T. M., Lin, W.-Z., Hung, J.-P., Royandi, M. A., & Chen, Y.-J. (2025). Monitoring and Prediction of the Real-Time Transient Thermal Mechanical Behaviors of a Motorized Spindle Tool. Lubricants, 13(6), 269. https://doi.org/10.3390/lubricants13060269






