Abstract
Cycloidal reducers are widely used in precision drive systems due to their reduced backlash in meshing and compact design. However, their operational durability is limited by surface wear and lubricant degradation under elevated contact loads and boundary lubrication conditions. This study introduces a modified wear prediction model based on four-ball tribological testing, specifically adapted to simulate the complex tribological conditions in cycloidal gear contacts. The model incorporates the total acid number (TAN) and thermal conductivity coefficient of the lubricant as dimensionless factors, enabling a dynamic prediction of wear intensity as the lubrication degrades. This innovation allows an accurate estimation of service life and reliability in high-load, small-contact-area mechanical systems and offers a practical diagnostic tool for the predictive maintenance of gear transmissions.
1. Introduction
Cycloidal reducers are widely used components in robotics, aerospace systems and precision machinery due to their compactness, high load-bearing capacity and wear resistance. Their operational reliability depends on progressive surface wear and oil degradation during the operation of the surfaces under cyclic contact conditions. Improving the tribological efficiency of such gears requires the analysis of wear mechanisms, the behavior of oil materials and the evolution of contact pressures in real technical systems. The tribosystem of the friction components of gear drives consists of moving surfaces and the lubricant between them. Lubricating oils play an important role in ensuring that such tribosystems operate smoothly throughout their lifetime.
There is an increasing amount of research and technologies that can track the wear of lubricated joints (based on wear products, follow-up the friction between surfaces and temperature fluctuations) and provide a change in lubricants in response to this, while realizing automatic maintenance of the joint and improving its efficiency [1]. However, such technologies are expensive and can increase the price of machinery.
The simulation of sliding wear in lubricated components can provide enough information to predict the wear behavior of their surfaces and thus the possible lifetime and maintenance of the machine components. Numerical wear simulation should provide not only the model of wear, considering such parameters as normal force, hardness, surface roughness and deformations and wear volume, but also an experimental verification with a possibly high conformity to the model results [2]. Such lubricated sliding wear models are based on a numerical simulation of the lubrication mode (EHL, mixed or boundary lubrication), possible adhesion effects, the change in surface topography and data of heat generation using the finite element method (FEM) [3,4,5]. Some of the wear models are used specifically for journal bearings [6] or applied for rolling–sliding contact investigations [7,8].
The durability of cycloidal gear reducers is significantly affected by surface wear, particularly under high-load and partial lubrication conditions. Recent studies have shown that tooth profile modifications can influence the wear distribution and improve load-carrying behavior in cycloid drives [9]. Detailed contact analysis and wear calculation methods have been developed to better predict operational degradation in cycloid–pin gear mechanisms [10]. Moreover, the tooth surface wear alters the formation of the lubrication film and reduces transmission efficiency, which is particularly relevant in both cycloidal and involute gear systems [11]. Advanced studies on localized heat generation have further demonstrated the importance of accurately modeling contact temperature distributions [12]. The complexity of meshing geometry, including curved contact lines in internal gears, adds to the challenges of simulating realistic wear behavior [13]. Specific models are applied for the evaluation of the lubrication film stability of grease-lubricated cycloid drives, studying the impact of the modification of thermal conditions of elastohydrodynamic lubrication and the effect of axial modification [14]. Also investigated is the thermal stability of lubricants at cycloidal reducers, taking into consideration heat generation and its possible impact on the lubricant of the cycloidal reducer [15,16]. Numerical models are applied to the lubrication conditions of cycloidal gears. A simulation was applied for the evaluation of churning and pumping/squeezing effects during the meshing of gears [17]. Theoretical analysis of the lubrication applied for housing the rollers and pins of a cycloid reducer shows that at the boundary mixed lubrication conditions occur between contact elements. Improvements in tribological efficiency of reducers are suggested by the modification of surface roughness, lubricant type and the design of the gearbox [18]. Models of gear system dynamics analysis and evaluation include the influence of the thermal deformation of the tooth due the surface contact temperature [19]. Gear system dynamics analyses include also the tooth surface wear, geometric errors and time-varying meshing stiffness [20]. However, most of these simulations of cycloid reducers’ operation do not present comprehensive models of wear mechanisms and abrasion progress during friction pairs’ operation. Despite these advances, current models often lack the integration of lubricant degradation indicators, which are essential for long-term wear forecasting. This study addresses this gap by proposing a wear prediction model that incorporates the total acid number (TAN) and thermal conductivity of the lubricant into a dimensionless framework, offering a practical method for predicting wear progression in cycloidal transmissions.
Taken into consideration should be the models of lubricated joints, which evaluate the factors and conditions influencing the wear friction surfaces and limiting the longevity of the drive. A model has been developed based on the assumption that mild wear mainly occurs when a temporary layer disappears, formed by a chemical reaction between the base material and the additives in the lubricant. When part of this layer is removed, the chemical balance of the system is disturbed, and the system will try to restore the balance by the use of the base material [21].
Other models are based on the measurement of thermal activation promoted by the contact stress of surface asperities to determine the material loss in the contact area [22]; the models can also include consideration of the change in the dynamic viscosity of the oil and its possible impact on the wear coefficient [23]. An advanced mechano-chemical model of contact mechanics simulation has been developed, which includes the tribo-chemical reactions on the surface and considers tribo-film removal and its behavior during the friction process. This model can be used for the monitoring of tribosystems and includes a wear prediction model in boundary lubrication conditions [24].
A model that examines the transition from light wear to heavy wear in lubricated contacts highlights the importance of thermal effects. Such a transition from mild wear to severe adhesive wear occurs when the surface exceeds a predetermined critical temperature by more than 10%. The model includes a local application of Archard’s wear law and a contact pressure–temperature modeling scheme. The simulation results are in good agreement with the experimentally determined transition parameters [25].
A wear model simulating the time-dependent wear of a ball on a flat contact shows the usefulness and limitations of this type of modeling compared to experimental results obtained from reciprocating tribometer tests. These tests show the importance of adjusting the conditions of simulations and experiments to achieve an optimal match [2].
An important impact on the wear behavior of lubricated systems can be had with wear-reducing oil additives [26,27,28,29]. Such a modification of the lubricant, an important tribosystem component, should be followed by the comparison of friction prediction models [30]. Only a few of the lubricated contact models include the simulation of lubrication in four-ball test conditions [31], which are most efficient in reflecting the tribological behavior of lubricant in the contact zone [32,33].
The aim of this study is to develop a wear behavior model for lubricated contacts representative of cycloidal gearboxes, based on four-ball tribological testing results, in order to assess the impact of lubricant degradation on wear intensity.
2. Model and Methods
2.1. Wear Model and Theoretical Methods
To simulate the tribological conditions typical for cycloidal gearboxes, a four-ball tribological test method was applied. Although this method is standardized (DIN 51350/1-4) [34] and widely used for evaluating lubricants, in this study it was adapted to reflect the boundary and mixed lubrication regimes characteristic of contact interfaces in cycloidal reducers, such as the interaction between lobed discs and rolling pins.
The investigation consists of a theoretical model and the tribological tests based on model parameters. The theoretical model is based on the geometric parameters of the four-ball test scheme. During the testing, the thickness of the boundary lubricant can vary from the initial to a zero value. The nature of the tests in the circuit should contribute, to the greatest extent, to the persistence of lubrication and stability of the wear process. The four-ball scheme best satisfies the requirement of constant lubrication conditions: the operating surface of at least one contacting body is dipped into the lubricant for each cycle, and the lubrication conditions are restored. The surface with the renewed lubricant film comes into contact again, thereby ensuring constant lubrication conditions. At the same time, the pressure in the contact is so high that the main part of the lubricant is removed upon entering the contact. A certain small part remains, which ensures the constancy of the boundary lubrication test conditions. The theory for determining the parameters of wear models is developed on the basis of solving inverse wear–contact problems. At the same time the dependencies for calculating parameters are determined according to the accepted mathematical form of the wear law, geometric relationships, continuity conditions in contact, equilibrium conditions and wear test results. The more determining factors in the model, the more complex is the solution. So already two parameters (for example, pressure and speed) significantly complicate the task and require certain approximations and simplifications. Here it is proposed that the most rational test schemes be used when the contact pressure changes during testing due to a change in the contact area, which makes it possible to obtain results for a range of pressures based on the test results of one sample. Wear models obtained using a four-ball scheme are advisable to use to assess the wear resistance of joints with small contact areas (gears, cam mechanisms) where the contact is taking place along a line or at the points.
The structural scheme consists of four identical balls of radius R. Three lower balls 1–3 are motionlessly located on the plane and touch each other according to the scheme in Figure 1.
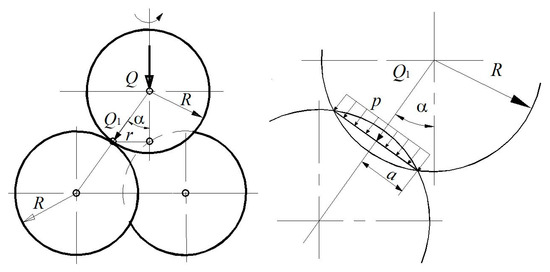
Figure 1.
The geometry of the four-ball test scheme.
The upper ball 4 rotates and is pressed in the center towards the lower balls with a force Q. The presence of the ball cage ensures the stable, stationary position of the lower balls under vertical load and rotation of the upper ball with a moment around the vertical axis. This simple stable system of four balls, the centers of which form a tetrahedron, is widely used as a scheme for tribological studies, with oils poured into the space between the balls. In the process of the friction of the upper ball on the lower ones, wear areas of a circular shape are formed on them. To determine the normal component of the force Q1 on the lower balls, it is necessary to determine the angle α:
From the geometry of the contact (Figure 1), the angle α is determined:
Taking into account (2), we obtain an expression for the normal force on the lower balls:
The friction path for the friction zones of the lower balls is as follows:
where n is the number of revolutions of the upper ball per unit of time; t is the test duration.
To describe the wear process, including in the presence of a lubricant, mathematical forms of wear regularities are used. The wear pattern is established experimentally and approximated by certain functions. The most widespread is representation of experimental patterns in the form of a dependence of wear intensity on various factors (contact pressure, sliding speed, temperature, lubrication). To determine the parameters of wear regularities, the samples with a variable contact area are tested during the wear process. During wear tests, the dimensions of the worn contact area are periodically or continuously measured depending on the friction path. Based on the test results, an approximating function is designed. Next, to determine the numerical value of the parameters of the wear model, the inverse wear–contact problem is solved for the contact of bodies of the corresponding configuration.
Traditionally, the wear model (law) is understood as the functional dependence of the wear rate (intensity) on the determining factors of the wear process: contact pressure, properties of structural and lubricant materials, sliding speed, temperature and other factors in the form [35]:
The number of determining factors and their form of presentation depend on the physical formulation of the wear problem with respect to the design of the friction pair and the conditions of testing and operation. It is convenient to represent the level of influence of determining factors on wear in the form of power dependences. In this case, the values of the parameters determine both the quantitative and qualitative effect on the wear. For practical calculations based on the wear model, it is rational to represent the determining factors in the form of dimensionless complexes [30]. In our case, to predict the wear of non-conformal joints in the presence of a lubricant and in tests using a four-ball scheme, the following form of the wear model is proposed:
where dW/dL is the wear rate;
kw is the wear coefficient;
µ is the friction coefficient;
p is the contact pressure, N/mm2;
HB is brinell hardness, N/mm2;
α is the oil temperature conductivity coefficient, m2/s;
ν is the kinematic oil viscosity, m2/s;
TAN is the total acidity number, mg KOH/g;
m, n are the parameters.
The presented wear model with known wear parameters can be used to predict the durability of tribo-pairs and to optimize the design, kinematic and power parameters of the coupling according to the criterion of minimum wear. The wear regularity can be applied in practice if the algorithm for determining the parameters of this pattern is known. It is the model parameters that quantitatively make it possible to evaluate the influence of determining factors (pressure, temperature speed). The parameters can be set only based on the results of experimental tests, which makes the model close to the real operating conditions of the friction unit.
The model is proposed in the form of two dimensionless complexes that determine the influence of contact pressures and properties of structural and lubricant materials. The principle of similarity and dimensions was used as the basis for constructing the model. To predict wear using model (6), an algorithm for determining the parameters of this model is needed. To determine the parameters kw, m, n, a solution to the inverse wear–contact problem is proposed based on the results of laboratory wear tests [36].
The geometric relationship between normal wear and the half-width of the circular area a will be written in the form (Figure 1):
Let us assume that the pressure is uniformly distributed over the contact area. Then the contact pressure through the load and the contact area are determined by the equation
Based on the results of wear tests, an approximating power function of the size of the wear spot diameter a (L) from the friction path L is determined in the form
where c, β are the parameters of the approximating function.
After substituting Equations (3) and (7)–(9) into the wear model Equation (6), we get
After integrating and transforming Equation (10), we have
From the condition of satisfaction of Equation (11) for any L, it follows:
To determine the parameter n, a series of tests is carried out at different values of the acidity number. In this case, the corresponding approximating functions of type (9) are obtained.
Here, the tasks of determining the wear parameters based on the test results of samples with a variable contact area are considered. The exponent m in expression (6) characterizes the rate of change in contact pressures during wear and is related to the exponent β of the experimental function according to (12). The acid number of the oil does not depend on the size of the wear area and therefore does not affect the parameters m and β. The acid number will only affect the dimensional coefficient c, which is confirmed experimentally.
Let two approximating functions be obtained from the test results at two values of the acid number:
Thus, we get a system of two equations:
Dividing the first equation by the second after taking the logarithm and transformations, we obtain the equation for the parameter n:
The coefficient kw is determined from one of the equations of system (14):
2.2. Tribological Tests and Surface Investigation
The semisynthetic engine oil SAE 10W40 of API CI-4 class was used for the tribological tests. The tests were performed with oils that were new and with oils that operated after a 5000 and 10,000 km run.
Tribological tests of friction torque and surface wear according to the wear scar diameter (WSD) were performed at room temperature using the four-balls testing machine of the Tribology Laboratory of Vytautas Magnus University. This setup is designed to reproduce the high contact pressures and small-scale tribo-contacts observed in cycloidal drives, making it suitable for determining wear trends under real conditions of lubricant degradation. A testing methodology according to the standard DIN 51350-3 was used [34]. The diameter of the steel balls used in the test was 12.7 mm; they were made of 100Cr6 bearing steel (E = 21.98 × 104 MPa; ν = 0.3, where ν is the Poisson ratio; E is the modulus of elasticity). According to the standard, the tests were carried out at a 150 and 300 N loading. The wear resistance of the different oils was evaluated according to the measured WSD of the worn balls.
The investigation of the viscosity and acidity of the lubricants was performed according to standard ASTM methodologies.
The surface morphology of friction surfaces was characterized by scanning electron microscopy (SEM, Hitachi S-3400N, Tokyo, Japan). The chemical composition of the samples was determined by energy-dispersive X-ray spectroscopy (EDX, Bruker Quad 5040, Hamburg, Germany).
3. Results
3.1. Tribological Testing Results
The friction torque was measured during the tests at two different loading versions for each tested oil and is presented in the graphs in Figure 2.
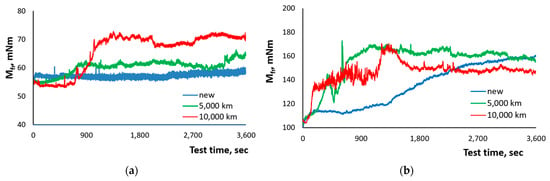
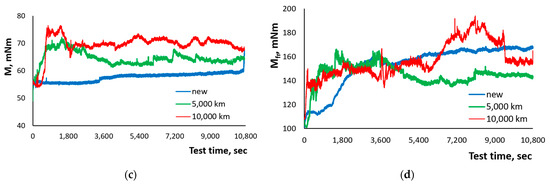
Figure 2.
Changes in friction torque during tests for different runs of engine oils, by loading and run: (a) 1 h run at 150 N loading; (b) 1 h run at 300 N loading; (c) 3 h run at 150 N loading; (d) 3 h run at 300 N loading.
These measurement results show that for a shorter test time, the lowest value and most stable friction torque are demonstrated by the new oil at a lower loading, but the increase of the loading to 300 N causes instability and higher values of friction torque in time when using the new oil (Figure 2b,d). The tests at a lower loading (150 N) show the comparably stable friction torque of all three tested versions of oil, with the highest friction value of the long-term-operated oil (Figure 2a,c) that passes the process of the loosing of lubrication properties of oil because of its aging and increasing acidity. However, at a higher loading the friction behavior of oils changes. The friction torque value of the new oil reaches the values of used oils in the short term, and during the longer tests its advantage is only in the stability of friction torque. The most unstable friction torque shows in the oil which was used the longest. The longer operation of the tested oils in total causes a higher fluctuation in friction torque at a 300 N loading, and that is related to the lower lubricity efficiency of oils at higher loading.
The results of the wear measurement after the tests (Figure 3) pass the logical scheme of factors influencing the wear resistance ability of lubricating oils.
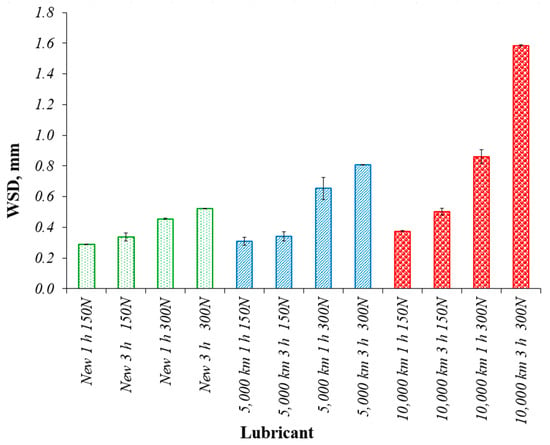
Figure 3.
Results of wear scar diameter for different runs of engine oil at 150 and 300 N loading.
A higher loading and longer operation cause higher wear in all three tested oils. The wear protection ability of long-term-operated oil is lowest because of its aging and higher acidity, which deteriorates the anti-wear properties of the oil. Compared to the new oil, the increase in wear of surfaces for longer-operated oil is much more expressed at the increased loading, because the standard anti-wear additives of oil lose their efficiency during operation, and at a higher loading their effect almost disappears.
3.2. Friction Surface Investigation
The friction surface investigation after the wear tests (Table 1) shows a clear link to the wear value measurements. Despite that the areas of wear spots seen in the selected pictures pass the wear measurements, the structure of wear traces on the ball surfaces are different for new and for used oils. The wear spot on the balls tested with new oil is more solid (especially after shorter tests), and the tests of the used oils show deeper scratches, which could be caused by additional wear particles passing into the contact zone. The formation of such wear products is much more probable in long-term-operated oils whose wear protection abilities are depleting.

Table 1.
Wear spots in the samples after the tests for different loading and operation runs.
3.3. Physical and Chemical Properties of the Oils
Analysis of the physical and chemical properties of the tested oils helps to explain the changes in the tribological properties of the oils during the longer operation period. The most important oil properties were measured and are presented in Table 2.

Table 2.
Physical and chemical properties of the tested oils.
As it was expected, the acidity of used oils increases over time. The lower viscosity of used oils could be related to the aging of the oil due the increase in the moisture in the oil from outside sources and from oil dissociation products. This lower viscosity also conduces to the lower anti-wear properties of the oil.
3.4. Identifying the Parameters of the Wear Model and Test Conformity
Wear tests in the four-ball scheme allow for the variability in the dimensions of the contact (wear) area during the tests and, accordingly, the contact pressure during the wear process. When testing one sample, it is possible to obtain a function of the dependence of wear on the friction path for the range of contact pressures. This feature is taken into account in the calculated dependencies (Equations (7)–(9)). The obtained coefficients consider the effect of changes in contact pressure on wear (external load is included in the formation of pressure).
The results of wear tests with a lubricant according to the four-ball scheme are shown in Table 3. The friction path was calculated using Equation (4) at n = 1420 rpm.

Table 3.
Wear test results used for the wear model.
Shown below (Figure 4) are approximations (via Excel) of the dependence of the wear area on the friction path at different loads and values of the acid number of the lubricant.
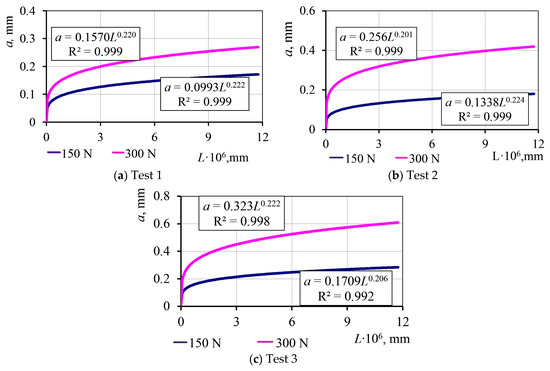
Figure 4.
Determination of the parameters of wear data at the loadings 150 N and 300 N for the approximation function of wear spot diameter: a (L) = cL^β.
The parameters of the approximation function (4) are summarized in Table 4.

Table 4.
The parameters for wear for model calculation.
As expected, the values of the β parameter for a given lubricant are approximately the same. In accordance with the data in Table 4, we take the average value of the β parameter equal to 0.2157.
Then, according to Equation (12), the parameter m = 1.32. The determination of the parameter n was carried out for tests 2 and 3 according to Equation (15):
It is accepted that n = 2.075. The coefficient kw was determined by Equation (16) for the following test parameters: HB = 200 MPa, µ = 0.05, ν = 13.6 N/mm2, α = 6.9 N/mm2, TAN = 1.7 mg KOH/g, R = 12.7 mm.
Thus, the law of wear (6) after identifying the parameters takes the form
4. Discussion
The evaluation of friction and wear tests shows the correlation of friction torque stability with the value of the wear scar. That relation is especially clear at a higher loading and longer operation of the friction pair. The test results show the efficiency of oil additives in the beginning of lubricants’ operation at a lower loading of a new oil (Figure 2), but an increased loading reduces their efficiency, limiting their ability to create a stable surface protection layer and accordingly a lubrication film. It increases the friction torque value, but the stability of friction is still higher than that of the oils that operated for a longer period. This stability has a direct correlation with the wear protection ability of new oils with a full set additives, as is shown in Figure 3. The higher fluctuation in friction for older oils shows that the protective surface layer and lubrication film is constantly appearing and vanishing, what is caused by the lack of additives efficiency. The clear and deeper surface scratches created with the old films (see Table 1) confirm that the rest of the additives in such oils are already not able to form a uniform protective layer, and that causes higher values of total wear.
The wear model considered the main parameters of friction and wear dependencies, and the identification of the parameters of the wear model for test conformity (Table 4) shows that the degree index of the approximate function (parameter β) in all cases (new oil, after 5000 km and after 10,000 km runs; loading with 150 N and 300 N) remains close to constant (0.20–0.22). It shows a good test conformity.
However, the changes in lubrication conditions during the operation caused by the lubricant aging can have a direct impact on the c parameter of the approximate function of the model. This c parameter function increases as the condition of the lubricant deteriorates: a) with a load of 150 N after a 5000 km run, the parameter increases by about 34% compared to a new lubricant and by 70% after 10,000 km run; b) at a 300 N load, the increase in the parameter is significantly higher—after a 5000 km run, about 63%, and after a 10,000 km run, over 100%.
Our modeling of the wear of the lubricated contact surfaces of cycloidal gear transmissions is based on high localized contact pressures and boundary lubrication. The model presented in Equation (6) integrates a broad set of parameters: it includes Brinell hardness (HB) to reflect material characteristics and lubricant-specific properties such as kinematic viscosity (ν), thermal conductivity coefficient (α) and total acid number (TAN), along with mechanical conditions such as contact pressure (p) and friction coefficient (μ). This holistic approach allows us to account for the interactive effects of materials, mechanical loading and lubricant degradation, which are collectively responsible for wear in cycloidal reducers. Although high-performance steels such as 100Cr6 or case-hardened alloys like 16MnCr5 are commonly used in cycloidal transmissions due to their high fatigue and wear resistance, our findings confirm that even optimal materials are susceptible to increased wear when lubricant degradation occurs.
The dimensionless wear rate equation (Equation (17)) enables a quantitative assessment of the influence of contact pressure, the mechanical properties of materials, frictional conditions and lubricant characteristics on wear. This model is particularly suitable for evaluating the wear resistance of components in cycloidal gearboxes, where highly localized contacts are subjected to elevated specific loads under boundary lubrication. These contacts, such as those between rolling pins and internal disc profiles, are characterized by the intermittent formation and breakdown of the lubricating film. The proposed model allows the prediction of wear intensity in such interfaces by incorporating changes in the physicochemical condition of the lubricant, which is critical for estimating the service life and operational reliability of cycloidal transmissions, especially under prolonged use or limited maintenance intervals.
In future research on lubricating materials and studying the patterns of wear of lubricated friction surfaces, it is appropriate to evaluate the wear of the balls not by the diameter of the spot but by calculating the volume of the worn material [40]. This more objectively evaluates the ability of the lubricant to protect the friction surfaces from wear.
It is also important to pay attention to oil acidity changes during operation for the long-term operation modeling of engine oils’ wear behavior. A monitoring of acidity indicators could be applied for this [40]. Another important factor to be considered in future—the influence of the lubricant additives aging on the lubricant efficiency. The performed investigations show that the additive’s capability to modify the surface is most efficient for fresh lubricants, and with the aging of lubricants the surface saturation with active components is reduced [41].
Further investigations are planned to enhance the model by incorporating volumetric wear analysis, integrating thermomechanical coupling and exploring the interaction between wear progression and system-level dynamic instability. The inclusion of real transmission system testing and online health monitoring data will further strengthen the applicability and robustness of the model in predictive maintenance scenarios.
5. Conclusions
The lubricating properties of oils degrade during service due to oxidation and the depletion of active additives, leading to changes in their physicochemical characteristics. Among these, the total acid number (TAN) is a key indicator strongly correlated with the loss of lubricating effectiveness and increased wear intensity.
The wear modeling of lubricated surfaces has demonstrated that the exponent in the wear function remains stable across different lubricant conditions, while the scaling parameter increases significantly as the lubricant ages. This confirms the model’s responsiveness to lubricant degradation and its applicability for evaluating wear processes under boundary lubrication conditions.
Considering the kinematic and structural features of cycloidal gearboxes, particularly the presence of concentrated contact zones with high specific pressures and intermittent lubrication, the proposed model is especially suitable for analyzing the wear resistance of their load-bearing elements. Enhancing the model through a volumetric wear estimation and monitoring of TAN allows for a more accurate prediction of the reducer’s service life and wear behavior during extended operation.
The model can therefore be effectively applied to forecast surface degradation in cycloidal gear systems, providing valuable input for maintenance planning, the selection of lubricants and evaluation of durability under real-world operating conditions.
Author Contributions
Conceptualization, J.P., O.D. and R.R.; methodology, O.D., J.P. and D.V.; validation, J.P., O.D. and R.R.; formal analysis, J.P., O.D., G.A. and R.R.; investigation, O.D., J.P. and D.V.; resources, O.D., J.P. and D.V.; data curation, O.D., D.V., J.I. and R.M.; writing—original draft preparation, J.P., O.D. and D.V.; writing—review and editing, J.P. and R.R.; visualization, D.V., O.D. and R.R.; supervision, J.P. and O.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Desai, P.S.; Granja, V.; Higgs, C.F., III. Lifetime Prediction Using a Tribology-Aware, Deep Learning-Based Digital Twin of Ball Bearing-Like Tribosystems in Oil and Gas. Processes 2021, 9, 922. [Google Scholar] [CrossRef]
- Andersson, J.; Almqvist, A.; Larsson, R. Numerical simulation of a wear experiment. Wear 2011, 271, 2947–2952. [Google Scholar] [CrossRef]
- Zhu, D.; Martini, A.; Wang, W.; Hu, Y.; Lisowsky, B.; Wang, Q.J. Simulation of Sliding Wear in Mixed Lubrication. J. Tribol. 2007, 129, 544–552. [Google Scholar] [CrossRef]
- Patel, R.; Khan, Z.A.; Saeed, A.; Bakolas, V. A Review of Mixed Lubrication Modelling and Simulation. Tribol. Ind. 2022, 44, 150–168. [Google Scholar] [CrossRef]
- Winkler, A.; Bartz, M.; Wartzack, S. Numerical Wear Modeling in the Mixed and Boundary Lubrication Regime. Lubricants 2022, 10, 334. [Google Scholar] [CrossRef]
- Jia, H.; Li, J.; Wang, J.; Xiao, K.; Han, Y. A lubricated wear model for determining wear surface geometry on journal-bearing surfaces. Surf. Topogr. Metrol. Prop. 2020, 8, 17. [Google Scholar] [CrossRef]
- Pei, X.; Pu, W.; Zhang, Y.; Huang, L. Surface topography and friction coefficient evolution during sliding wear in a mixed lubricated rolling-sliding contact. Tribol. Int. 2019, 137, 303–312. [Google Scholar] [CrossRef]
- Beheshti, A.; Khonsari, M.M. An engineering approach for the prediction of wear in mixed lubricated contacts. Wear 2013, 308, 121–131. [Google Scholar] [CrossRef]
- Li, X.; Yang, H.; Niu, W.; Guo, R.; Sun, L. Investigation on Tooth Surface Wear of Cycloid Drives Considering Tooth Profile Modifications. Lubricants 2023, 11, 323. [Google Scholar] [CrossRef]
- Wang, Y.; Wei, B.; Wang, Z.; Yang, J.; Xu, J. Research on Loaded Contact Analysis and Tooth Wear Calculation Method of Cycloid–Pin Gear Reducer. Lubricants 2023, 11, 445. [Google Scholar] [CrossRef]
- Yin, Z.; Wang, H.; Fu, X.; Fan, Z.; Ma, Q. Study on the influence of tooth surface wear on the lubrication performance of double involute gear transmission. Sci. Rep. 2025, 15, 7612. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Guo, Q.; Xu, B.; Gou, X. Tooth surface contact temperature of spur-face gear drive in point contact considering heat flow distribution. Int. J. Heat Fluid Flow 2025, 112, 109759. [Google Scholar] [CrossRef]
- Jia, C.; Zhang, G.; Li, G. Numerical Analysis of Tooth Contact and Wear Characteristics of Internal Cylindrical Gears with Curved Meshing Line. Appl. Sci. 2024, 14, 5399. [Google Scholar] [CrossRef]
- Gong, J.; Yan, H.; Meng, F.; Jing, X. Thermal-elastohydrodynamic lubrication study of axial-modified greased cycloid drive in rotate vector reducer. Tribol. Int. 2023, 185, 4–17. [Google Scholar] [CrossRef]
- Vasić, M.; Blagojević, M.; Dragoi, M.V. Thermal stability of lubricants in cycloidal reducers. Eng. Today 2022, 1, 7–17. [Google Scholar] [CrossRef]
- Vasić, M.; Blagojević, M.; Banić, M.; Maccioni, L.; Concli, F. Theoretical and experimental investigation of the thermal stability of a cycloid speed reducer. Lubricants 2025, 13, 70. [Google Scholar] [CrossRef]
- Concli, F.; Maccioni, L.; Gorla, C. Lubrication of gearboxes: CFD analysis of a cycloidal gear set. WIT Trans. Eng. Sci. 2019, 123, 101–112. [Google Scholar]
- Mačkić, T.; Blagojevic, M.; Babić, Ž.; Jotić, G.; Škundrić, J. An analysis of lubrication regime between the contact elements of cycloid reducer. In Proceedings of the 11th International Conference on Accomplishments in Electrical and Mechanical Engineering and Information Technology DEMI 2013, Banja Luka, Bosnia and Herzegovina, 30 May–1 June 2013; pp. 77–82. [Google Scholar]
- Shi, J.-F.; Gou, X.-F.; Zhu, L.-Y. Five-state engaging model and dynamics of gear-rotor-bearing system based on time-varying contact analysis considering gear temperature and lubrication. Appl. Math. Model. 2022, 112, 47–77. [Google Scholar] [CrossRef]
- Liu, C.; Tang, M.; Yang, X.; Ying, J. Influence of Tooth Surface Wear on Dynamic Characteristics of Gear Systems Considering Three-Dimensional Tooth Surface Geometric Errors. Shock. Vib. 2025, 2539671, 18. [Google Scholar] [CrossRef]
- Bosman, R.; Schipper, D.J. Mild Wear Prediction of Boundary-Lubricated Contacts. Tribol. Lett. 2011, 42, 169–178. [Google Scholar] [CrossRef]
- Pei, X.; Pu, W.; Yang, J.; Zhang, Y. Wear law in mixed lubrication based on stress-promoted thermal activation. Friction 2021, 9, 710–722. [Google Scholar] [CrossRef]
- Qin, W.; Zhang, Y.; Li, C. Determination of wear coefficient in mixed lubrication using FEM. Appl. Math. Model. 2018, 59, 629–639. [Google Scholar] [CrossRef]
- Ghanbarzadeh, A.; Wilson, M.; Morina, A.; Dowson, D.; Neville, A. Development of a new mechano-chemical model in boundary lubrication. Tribol. Int. 2016, 93, 573–582. [Google Scholar] [CrossRef]
- Bosman, R.; Schipper, D.J. On the transition from mild to severe wear of lubricated, concentrated contacts: The IRG (OECD) transition diagram. Wear 2010, 269, 581–589. [Google Scholar] [CrossRef]
- Padgurskas, J.; Rukuiža, R.; Prosyčevas, I.; Kreivaitis, R. Tribological properties of lubricant additives of Fe, Cu and Co nanoparticles. Tribol. Int. 2013, 60, 224–232. [Google Scholar] [CrossRef]
- Liehpao, O.F. Ashless Antiwear and Extreme-Pressure Additives. In Lubricant Additives: Chemistry and Applications, 2nd ed.; Leslie, R., Rudnick, L.R., Eds.; CRC Press: Boca Raton, FL, USA, 2009; Chapter 8; pp. 214–249. [Google Scholar]
- Farng, L.O.; Deckman, D.E.; Givens, W.A. Ashless Anti-wear additives for Future Engine Oils. In Proceedings of the 14th International Colloquium Tribology, Stuttgart, Germany, 13–15 January 2004. [Google Scholar]
- Farng, L.O.; Deckman, D.E. Novel Anti-Wear Additives for Future Lubricants, Additives 2007. In Proceedings of the Conference Applications for Future Transport, London, UK, 17–19 April 2007. [Google Scholar]
- Zhang, J.; Yamaguchi, E.; Spikes, H. Comparison of Three Laboratory Tests to Quantify Mild Wear Rate. Tribol. Trans. 2013, 56, 919–928. [Google Scholar] [CrossRef]
- Marko, M.D.; Kyle, J.P.; Wang, Y.S.; Terrell, E.J. Tribological investigations of the load, temperature, and time dependence of wear in sliding contact. PLoS ONE 2017, 12, e0175198. [Google Scholar] [CrossRef]
- Totten, G.E.; Westbrook, S.R.; Shah, R.J. Fuels and Lubricants Handbook: Technology, Properties, Performance, and Testing; ASTM International: West Conshohocken, PA, USA, 2003. [Google Scholar]
- Mang, T.; Dresel, W. Lubricants and Lubrication; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2007. [Google Scholar]
- DIN 51350-3; Testing of Lubricants—Testing in the Four-Ball Tester—Part 3: Determination of Wearing Characteristics of Liquid Lubricants. Deutsches Institut für Normung e.V.: Berlin, Germany, 1977. (In Germany)
- Dykha, A.; Sorokatyi, R.; Makovkin, O.; Babak, O. Calculation-experimental modeling of wear of cylindrical sliding bearings. East. Eur. J. Enterp. Technol. 2017, 5, 51–59. [Google Scholar] [CrossRef][Green Version]
- Dykha, A.V.; Marchenko, D.D.; Dytynyuk, V.A. Determination of the Parameters of the Wear Law Based on the Results of Laboratory Tests. J. Frict. Wear 2020, 41, 153–159. [Google Scholar] [CrossRef]
- ASTM D445; Standard Test Method for Kinematic Viscosity of Transparent and Opaque Liquids (the Calculation of Dynamic Viscosity). ASTM: West Conshohocken, PA, USA, 2024.
- ASTM D2270; Standard Practice for Calculating Viscosity Index from Kinematic Viscosity at 40 °C and 100 °C. ASTM: West Conshohocken, PA, USA, 2024.
- ASTM D664; Standard Test Method for Acid Number of Petroleum Products by Potentiometric Titration. ASTM: West Conshohocken, PA, USA, 2024.
- Padgurskas, J.; Volskis, D.; Rukuiža, R.; Kupčinskas, A.; Basheleishvili, N.; Tučkutė, S. Limitary State of Heavy-Duty Engine Oils and Their Evaluation According to the Change of Tribological Properties during Operation. Lubricants 2023, 11, 236. [Google Scholar] [CrossRef]
- Fernandes, W.; Tomanik, E.; Moreira, H.; Cousseau, T.; Pintaude, G. Effect of Aged Oils on Ring-Liner Wear. SAE Int. J. Fuels Lubr. 2020, 13, 167–176. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).











