Abstract
This study aims to investigate the dynamic behavior of water-lubricated stern bearings during service. A transient rotor dynamics numerical model is developed to research the effects of operating conditions and critical structural parameters on the variation patterns of the dynamic characteristic coefficients and journal orbit of WLBs. The main stiffness and damping formulas for dimensionless bearings are fitted based on numerical results. Additionally, the accuracy of the model calculations is experimentally verified on a water-lubricated bearing test rig. The results demonstrate that the variation trends of the main stiffness and main damping coefficients in the horizontal and vertical directions of the bearings are proportional to the external load and inversely proportional to the rotational speed. Under eccentric excitation, the dynamic characteristic coefficients of the bearings change periodically with time as an approximately sinusoidal function. With the increase in the bearing length-to-diameter ratio or the decrease in the radial clearance-to-radius ratio, the main stiffness and the main damping coefficients in the horizontal direction increase, while the main stiffness coefficient in the vertical direction decreases. This study provides theoretical support for modeling the transient transverse vibration of a propulsion shaft system.
1. Introduction
Acoustic stealth is a critical performance metric that significantly influences underwater vehicles’ operational safety and tactical advantage. The radiated noise from these vehicles primarily comprises hydrodynamic noise, mechanical equipment noise, and marine propulsion shaft system–hull structure coupling noise [1]. With the improvement of hydrodynamic performance and the development of vibration isolation technology, the impact of structural coupling noise on the acoustic stealth of underwater vehicles has become increasingly prominent. As an essential component of the marine propulsion shaft system, water-lubricated stern bearings are mainly used to support the propeller shaft. However, seawater’s low viscosity substantially diminishes the load-bearing capacity of stern bearings. Under the influence of low speed, heavy load, and shaft system misalignment [2,3], the dynamic performance of water-lubricated stern bearings exhibits significant nonlinearity [4,5]. This makes it highly susceptible to abnormal vibration and noise, which are key determinants of the acoustic stealth capability of marine propulsion shaft systems.
In recent years, an increasing number of scholars have focused on the influence of external excitation on the dynamic characteristics of water-lubricated bearings [4,5,6,7]; Ye et al. [8] analyzed the influence laws of the radial clearance, length-to-diameter ratio, and rotational speed on the journal orbit and circumferential pressure distribution of the shaft through water-lubricated bearing experiments. Tang et al. [9] proposed an optimization method for slat water-lubricated bearings based on the friction dynamics mechanism. They established a dynamic model of water-lubricated bearings considering mass conservation cavitation, determined the optimal slat structure under specific operating conditions through numerical simulation, and analyzed the effects of key parameters such as rotational speed, radial clearance, and surface roughness. Additionally, they investigated the effects of the width and number of slats on the tribo-dynamic characteristics and proposed a comprehensive optimization scheme. Cai et al. [10] investigated the influence of the journal shape error and wear on the lubrication performance and dynamic behavior of water-lubricated bearings under nonlinear excitation caused by propellers; the results revealed that the nonlinear excitation significantly increased the journal orbit, and the influence of shaft shape error on the performance of the bearings was considerably more significant than that of the wear. Tang et al. [11] analyzed the influence law of the microgroove parameter on the tribo-dynamic performance of coupled microgroove bearings under the condition of mass-conserving cavitation and identified optimal groove parameters that enhance the bearing performance under these conditions. Cha et al. [12] compared the difference between the journal orbits solved by the linear method based on stiffness and damping coefficients and the transient nonlinear method; the results indicated that the linear method can only deliver accurate prediction results when the eccentricity distance is less than 37% of the radial clearance.
The dynamic characteristic coefficients of water-lubricated stern bearings are crucial indicators reflecting their operational state. Zhang et al. [13] derived the coefficients of the dynamic characteristics of the water film whilst considering the dynamic deformation of the bearing bush and found that the stiffness and damping coefficients under dynamic deformation at high eccentricity were significantly different from those obtained when only static deformation was considered. Wang et al. [14] used CFD to analyze the dynamic characteristics of sliding bearings numerically. They found that the stiffness damping coefficient of the bearing changed significantly with the increase in rotational speed, which is consistent with the traditional calculation method. Liu et al. [15] calculated the water film stiffness coefficient of water-lubricated rubber bearings using an elastohydrodynamic lubrication model. They determined the comprehensive stiffness coefficient of the bearing by using a weighted average of the water film stiffness coefficient and the structural stiffness of the rubber material. Chen et al. [16] established a support model for stern bearings whilst considering the effect of discrete distributions and analyzed the impact of the rotational speed, load, and bush elastic moduli on the stiffness damping coefficients of the bearings. Feng and Jiang et al. [17] analyzed the dynamic performances of a motorized spindle supported on water-lubricated bearings. They found that the tilt angle of the thrust bearing leads to an uneven distribution of stiffness and damping in the motor spindle system and affects system stability. Leng et al. [18] derived the Reynolds equation of the perturbation pressure, taking the elastic deformation of the bush and roughness contact effect into account, and investigated the influences of the roughness peak height and radial inclination angle of the axial journal on the stiffness and damping coefficients. Ouyang et al. [19] developed a dynamic analysis model for water-lubricated stern bearings considering journal deflection. The results demonstrated that the journal deflection significantly affects the bearing’s horizontal and vertical stiffness and damping.
Although the above research has obtained many valuable conclusions, research on the change rule of the time-varying characteristic parameters of water-lubricated stern bearing under the action of external excitation is still relatively limited. Most of the aforementioned studies take the stiffness and damping coefficients as static parameters, analyzing the trend of how the operating condition parameters and structural parameters of stern bearings influence the dynamic characteristic coefficients under steady-state conditions, neglecting the effect of time-dependent changes in the dynamic characteristics of bearings resulting from variations in the journal position under external excitations. Therefore, this paper establishes a transient dynamics model of a water-lubricated bearing system considering external excitation, studies the influence law of working condition parameters and structural parameters on its dynamics behavior, fits the empirical formula of time-varying characteristic coefficients accordingly, and carries out a validation of the model in a water-lubricated transom bearing comprehensive performance test rig. This paper is organized as follows: Section 1 reviews the current development of the dynamic characteristics of a plain bearing rotor system. Section 2 proposes a new rotor system dynamics model and proves the correctness of the present model by comparing it with published numerical calculations. Section 3 conducts a series of parametric studies to evaluate the effects of the external load, rotational speed, eccentric excitation distance, length-to-diameter ratio, and radial clearance-to-radius ratio on the transient dynamics of the bearings, and empirical formulas for the main stiffness and damping coefficients of the dimensionless bearings are fitted based on numerical calculations. The model’s accuracy is validated in Section 4 through water-lubricated bearing tests. The primary findings and conclusions of this research are summarized in Section 5.
2. Mathematical Model
2.1. Rotor System Dynamic Model
Figure 1 shows a force diagram of the rotor system dynamic model. In Figure 1a, x and y represent the horizontal and vertical directions, respectively; OB and OJ, respectively, represent the geometric centers of the bearing and journal, and the eccentric distance between the geometric center of journal OJ and the center of mass Om is Qe. θ is the circumferential angle, φ is the attitude angle of the journal, e is the journal eccentricity, Fh and Ff represent hydrodynamic forces and water film shear forces, respectively, mj is the mass of the journal, and W is the external load on the journal. Figure 1b presents a schematic diagram of the bearing’s main stiffness and main damping coefficients in the horizontal and vertical directions. Kxx and Kyy represent the main stiffness coefficients in the horizontal and vertical directions, respectively. Cxx and Cyy represent the main damping coefficients in the horizontal and vertical directions, respectively.
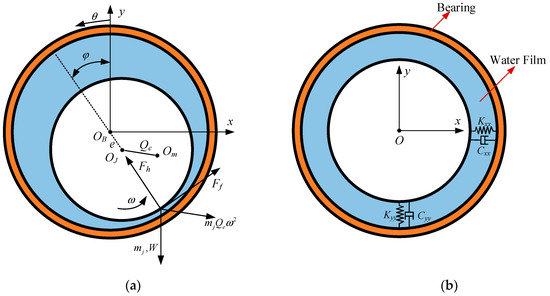
Figure 1.
Schematic diagram of the dynamic model of a water-lubricated stern bearing: (a) dynamic force balance; (b) schematic of stiffness and damping.
When the stern bearing reaches the “take-off” speed, a hydrodynamic pressure effect is generated, and the hydrodynamic force primarily supports the bearing load. However, due to manufacturing and installation errors, rotor imbalance occurs, leading to eccentric excitation effects. The combined influence of hydrodynamic forces, external loads, and eccentric excitation mainly determines the journal’s motion. Considering the eccentric excitation of the rotor motion, the equation can be described as follows:
where mj is the mass of the journal, x” and y” represent the acceleration in the horizontal and vertical directions, respectively, Fhx and Fhy represent the hydrodynamic component force in the horizontal and vertical directions, respectively, Ffx and Ffy represent the hydrodynamic shear resistance in the horizontal and vertical directions respectively, W is the external load on the journal, and the distance of the eccentric excitation of the journal can be calculated according to the following formula:
where λ is the journal unbalanced eccentricity ratio, and c represents the radial clearance.
The rotor dynamics equations are solved numerically using the fourth-order Runge–Kutta method, and the following first-order differential equations can be derived according to Equation (1):
where x’ and y’ represent the horizontal and vertical velocities, respectively.
Subsequently, displacements and velocities in the x and y directions can be calculated iteratively:
The coefficients kij can be calculated by the following formula:
2.2. Transient Hydrodynamic Model
This paper employs the elastohydrodynamic lubrication (EHL) model [20] to calculate the transient hydrodynamic pressure. The expression of the Reynolds equation, derived from the continuity condition and the force equilibrium condition of the micro metamorphic body, is given by:
where h is the thickness of the water film; ρ is the density of the lubricant; η is the viscosity of the lubricant; ph is the pressure of the water film; U is the relative velocity component between the bearing and rotor surfaces in the x direction; and V is the relative velocity component between the two surfaces in the y direction.
The polar coordinate form of the Reynolds equation corresponding to Equation (6) is expressed as [21]:
where θ and z are the circumferential and axial directions, respectively; RB and ω are the inner radius of the bearing and angular velocity of the journal, respectively.
When the journal rotates normally, the bearing water film thickness is uniformly distributed along the axial direction. However, the influence of the hydrodynamic pressure will lead to the deformation of the bearing liner layer. Therefore, it is necessary to add the liner deformation to the water film thickness calculation. The final expression for the water film thickness is given by:
where ε is the bearing eccentricity ratio, and δ is the liner deformation matrix. In this paper, the Winkler algorithm [22] is employed to calculate the elastic deformation of the bearing liner:
where Eb is the modulus of elasticity of the bearing lining material, vb is the Poisson’s ratio of the bearing lining, ph is the hydrodynamic pressure, and T is the thickness of the bearing lining.
Integrating the hydrodynamic pressure distribution over the film area can derive the hydrodynamic forces in the horizontal and vertical directions [21]:
The shear resistance of the water film can be calculated according to the following equation [21]:
Based on obtaining the horizontal and vertical hydrodynamic component forces, the dynamic characteristic coefficients of the liquid film can be obtained by the finite difference method. These coefficients encompass the main stiffness and damping in the horizontal direction (Kxx, Cxx) and the vertical direction (Kyy, Cyy). The following formulas give calculations for these coefficients [14]:
2.3. Calculation Procedure
The computational flow of the support dynamics considering vibration coupling is shown in Figure 2. The vibration response of the journal is simplified as changes in the spatial coordinates of the journal. Under the influence of eccentric excitation, the coordinates of the journal continuously change over time, implying that the eccentricity and eccentric angle of the bearing differ at each time step. Therefore, this program calculates the parameters such as hydrodynamic force, friction force, and eccentric excitation of the bearing at the current time step. These parameters are then substituted into the rotor system dynamics model to obtain the spatial position of the journal at the next time step. By iterating this process, the program generates the temporal change curves of each performance parameter of the bearing throughout the entire calculation period. Additionally, at each time step, the model synchronizes the differential solution method to obtain the dynamic coefficients of the bearing water film.
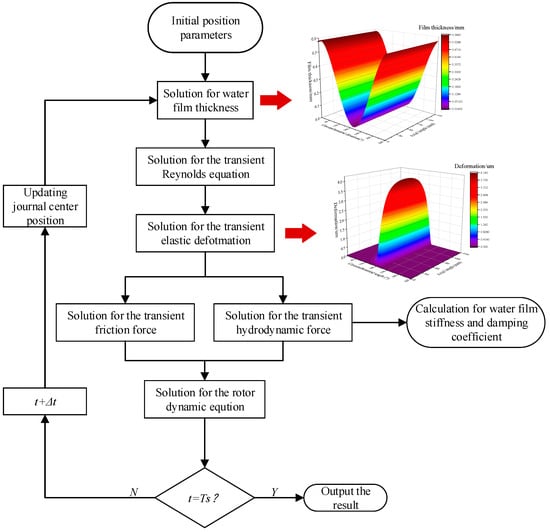
Figure 2.
Transient calculation flow.
2.4. Model Validation
2.4.1. Dynamic Model Validation
To validate the correctness of the existing model, this study refers to the literature [12] for model validation. The main bearing parameters are shown in Table 1, and the amount of unbalanced distance set at different speeds is detailed in Table 2. The comparison results of the journal orbit under different rotational speeds are shown in Figure 3, which shows that the calculation results of the model in this paper are more consistent with the results of the reference, thereby validating the accuracy of the proposed model to a certain extent.

Table 1.
Main calculation parameters [12].

Table 2.
Eccentric excitation distance of rotor at different rotational speeds [12].
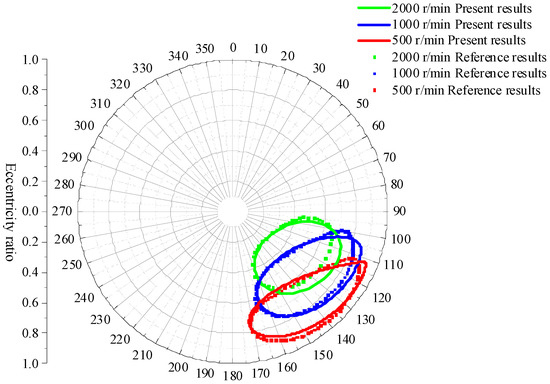
Figure 3.
Comparison of journal orbits at different speeds.
2.4.2. Validation of the Dynamic Characteristic Coefficient Differential Solution Model
To validate the accuracy of the dynamic characteristic coefficient calculation of this model, the basic parameters of the bearing in the literature [21] were used to calculate the dynamic characteristic coefficients. The resulting values were compared against those reported in the literature, serving as a reference benchmark. The comparative analysis is illustrated in Figure 4. As shown in Figure 4, it can be observed that the trend of the main stiffness and main damping coefficients in both the horizontal and vertical directions calculated by the existing model was consistent with that of the reference, and the maximum error observed did not exceed 10%. This consistency substantiates the reliability of the dynamic-characteristic-solving model employed in this study. It is worth noting that the coefficients of the dynamic characteristics calculated in the reference were dimensionless numbers. Moreover, the lubrication method adopted in the reference was oil lubrication. Still, in the numerical calculation of fluids, the non-Newtonian fluid and laminar flow assumptions for oil lubrication also apply to water-lubricated bearings. Consequently, the high degree of agreement between the calculation results of the existing model and those of the reference supports the correctness of the dynamic characteristic solution model adopted in this study.
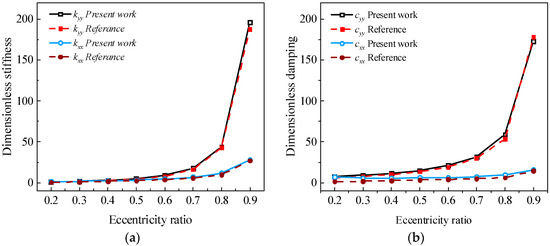
Figure 4.
Comparison of stiffness and damping at different eccentricities: (a) dimensionless stiffness verification; (b) dimensionless damping verification.
3. Results and Discussion
Due to the low viscosity of water, there is often local contact between the stern bearing and the journal under low-speed and heavy load conditions. Under these circumstances, the displacement changes in the journal are typically in the order of micrometers, at which point the stiffness and damping characteristics of the bearing are mainly determined by the properties of the lining material. Therefore, this section focuses on the dynamic behavior of water-lubricated bearings under elastohydrodynamic lubrication. It analyzes the influences of the external load, rotational speed, eccentric excitation distance, length-to-diameter ratio, and radial clearance-to-radius ratio on the eccentricity ratio, attitude angle, journal orbits, and dynamic parameters of water-lubricated bearings. The main structural parameters of the rotor system and the operating condition parameters are summarized in Table 3.

Table 3.
Basic bearing parameters.
3.1. Effects of External Loads
Since the cross-dynamic characteristic coefficients of the bearings have minimal influence on the vibration of the shaft system, this section focuses on extracting and analyzing the main stiffness and damping coefficients of the bearings in both the horizontal and vertical directions. Under the influence of eccentric excitation, the dynamic characteristic coefficients of the bearings change over time under various external loads, as illustrated in Figure 5. These curves demonstrate that the dynamic characteristic coefficients exhibit approximately sinusoidal cyclic changes. Additionally, it is observed that the main stiffness (Kxx) and main damping (Cxx) coefficients of the bearings in the horizontal direction, as well as the main stiffness (Kyy) and main damping (Cyy) coefficients in the vertical direction, increase with the rise in the external load. When the external load increases from 500 N to 1250 N, the average values of Kxx and Cxx increase by 77.59% and 42.85%, respectively, while the increase ratios of the average values of Kyy and Cyy reach 193.14% and 115.07%. It is evident that the increase ratios of the dynamic characteristic coefficients in the vertical direction are significantly larger than those in the horizontal direction. Combined with Figure 6, it can be seen that under the influence of external load and journal gravity, the vertical offset of the center point of the journal orbit is much larger than that in the horizontal direction. With the increase in the external load, the eccentricity ratio increases. At the same time, the attitude angle decreases, which increases the hydrodynamic component forces in the vertical direction, thereby enhancing the sensitivity of the hydrodynamic force response to displacement perturbations in this direction.
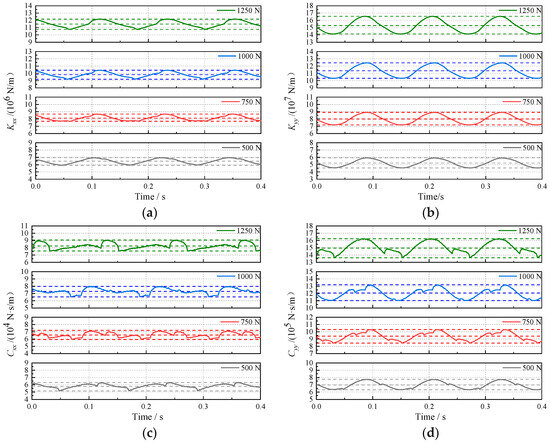
Figure 5.
Effect of external bearing load on dynamic characteristic coefficients: (a) Kxx; (b) Kyy; (c) Cxx; (d) Cyy.
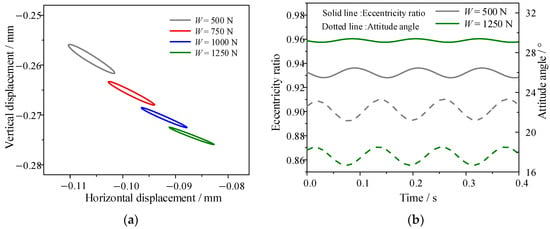
Figure 6.
Effect of external load on journal spatial state: (a) journal orbits; (b) eccentricity and attitude angle.
In order to further investigate the effect of the external load, parameters such as the peak-to-peak value and standard deviation are introduced to analyze the time-varying characteristic coefficients. With the increase in the external load, the peak-to-peak value and standard deviation of these dynamic characteristic coefficients for the stern bearing exhibit corresponding increases. As illustrated in Figure 5a, the peak-to-peak value of Kxx increases from 1.05 × 106 N/m to 1.42 × 106 N/m, and the standard deviation increases from 3.27 × 105 N/m to 4.34 × 105 N/m. Importantly, the ratio of the peak-to-peak value to the average value of Kxx under the corresponding operating conditions decreases from 16.26% to 12.35%. Comparing with Figure 5b–d, it can be observed that Kyy, Cxx, and Cyy all show a trend of an increase in the peak-to-peak value and a decrease in the ratio to their average values. with decreasing rates of 10.55%, 1.51%, and 3.11%, respectively. Notably, the change in amplitude for the main stiffness and main damping coefficients in the vertical direction is more obvious, corresponding to the fact that, as shown in Figure 6, the range of the journal orbit decreases with the increase in the external load, leading to reductions in both the eccentricity and attitude angle from the center point of the journal orbit. Combining the above analyses, it is evident that changes in external load have the most significant effect on Kyy, followed by Cyy, while the impact on Cxx is the least pronounced.
3.2. Effect of Rotational Speed
The curves depicting the time-varying dynamic characteristic coefficients of the bearings at different rotational speeds are shown in Figure 7, which indicates that the frequency of dynamic characteristic coefficients change is consistent with the rotational frequency of the journal. With the increase in rotational speed, the bearing’s main stiffness and main damping coefficients in both horizontal and vertical directions are reduced. When the rotational speed increases from 300 r/min to 600 r/min, the average values of Kxx decrease by 3.24%, while those of Cxx decrease by 33.53%. In contrast, the decrease ratio of the average values of Kyy and Cyy reaches 47.02% and 61.43%, respectively. These results indicate that an increase in the rotational speed significantly weakens the dynamic characteristic coefficients in the vertical direction compared to the horizontal direction.
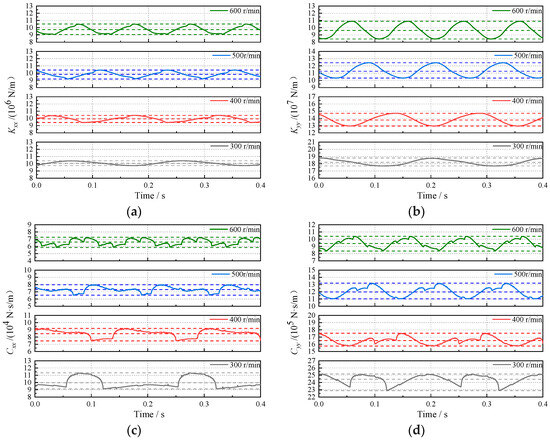
Figure 7.
Effect of rotational speed on dynamic characteristic coefficients: (a) Kxx; (b) Kyy; (c) Cxx; (d) Cyy.
Figure 8 shows the effect of the rotational speed on the spatial state of the journal; with the increase in the rotational speed, the position of the center point of the journal orbit gradually becomes closer to the center point of the bearing, and the minimum thickness of the water film increases, which implies that the hydrodynamic pressure effect of the rotor system is enhanced. In addition, since the minimum thickness of the water film usually occurs at the bottom of the bearing, it directly determines the support stiffness characteristics of the bearing. Consequently, the effect of the rotational speed on the main stiffness (Kyy) and damping (Cyy) coefficients in the vertical direction is much more pronounced than that in the horizontal direction. This finding aligns with the conclusion derived from the analysis of Figure 7.
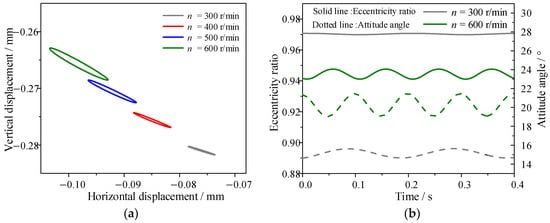
Figure 8.
Effect of rotational speed on journal spatial state: (a) journal orbits; (b) eccentricity and attitude angle.
From Figure 7a–d, it can be observed that both the peak-to-peak values and standard deviations of the main stiffness coefficients of the bearing increase with the increase in therotational speed. Conversely, the main damping coefficients’ peak-to-peak values and standard deviations decrease with the increase in the rotational speed. When the rotational speed increases from 300 r/min to 600 r/min, the ratios of the peak-to-peak values to the corresponding average values of Kxx and Kyy increase from 6.65% and 6.05%, respectively, to 14.89% and 25.39%, and the ratio of the peak-to-peak value to the corresponding average value of Cxx decreases marginally from 22.18% to 21.52% In contrast, that of Cyy increases from 9.48% to 21.84%. In summary, Kyy exhibits the highest sensitivity to changes in the rotational speed, followed by Cyy, while the change in the rotational speed has the least impact on Cxx.
3.3. Effect of Eccentric Excitation
In this section, the influence of different degrees of eccentric excitation is simulated by changing the distance of eccentric excitation. Figure 9 shows the influence of eccentric excitation on the dynamic characteristic coefficients of the bearings; it can be observed that the peaks of the main stiffness and main damping of the bearing in both the horizontal and vertical directions increase with the rise in eccentric excitation. Correspondingly, the standard deviation of the coefficients of the dynamic characteristics also increases to a certain extent. This trend corresponds to the observation in Figure 10, which shows that the range of the change in the journal orbit expands as the eccentric excitation increases. It is worth noting that when the unbalanced eccentricity ratio is larger than 1, Cxx and Cyy produce more abrupt changes during the cycle, leading to a significant difference in the variation law of damping under large eccentricity excitation compared with that when the unbalanced eccentricity ratio is smaller than 1. This can likely be attributed to the nonlinear relationship between the eccentricity change resulting from the expanded range of the journal orbit and the corresponding changes in the hydrodynamic force. Moreover, since Cxx and Cyy are of a smaller order of magnitude than the stiffness coefficients, variations in the journal orbit range have a more pronounced effect on the damping characteristics.
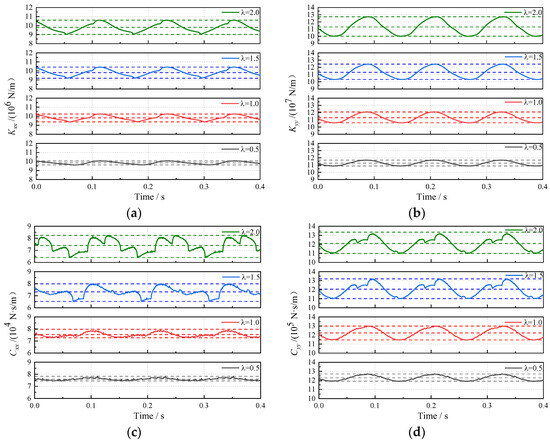
Figure 9.
Effect of eccentric excitation on dynamic characteristic coefficients: (a) Kxx; (b) Kyy; (c) Cxx; (d) Cyy.
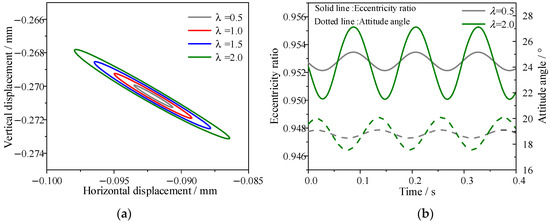
Figure 10.
Effect of eccentricity excitation on journal spatial state: (a) journal orbits; (b) eccentricity and attitude angle.
3.4. Effect of the Length-to-Diameter Ratio
Figure 11 shows the effect of the length-to-diameter ratio on the change rule of the dynamic characteristic coefficients with time; it can be observed that as the length-to-diameter ratio increases, the main stiffness and main damping coefficient of the bearing in the horizontal direction increase, while the main stiffness and main damping coefficient in the vertical direction decrease. When the bearing length-to-diameter ratio increases from 0.8 to 1.4, the average values of Kxx and Cxx increase by 9.77% and 61.63%, respectively, while the average values of Kyy and Cyy decrease by 55.10% and 28.75%, respectively. Combined with the effect of the length-to-diameter ratio on the spatial state of the journal (as shown in Figure 12), this indicates that an increase in the length-to-diameter ratio leads to an increase in the attitude angle of the center of the journal orbit. Therefore, under the same degree of external perturbation, the response in the horizontal direction increases along with the bearing dynamic characteristic coefficient, and the opposite effect is observed in the vertical direction.
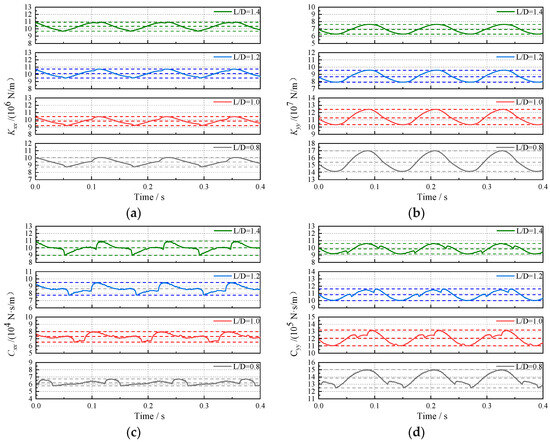
Figure 11.
Effect of length-to-diameter ratio on dynamic characteristic coefficients: (a) Kxx; (b) Kyy; (c) Cxx; (d) Cyy.
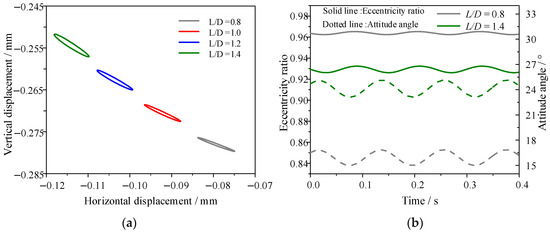
Figure 12.
Effect of length-to-diameter ratio on journal spatial state: (a) journal orbits; (b) eccentricity and attitude angle.
From Figure 11a–d, it can be observed that the peak-to-peak values of Kxx, Kyy, and Cyy decrease with the increase in the length-to-diameter ratio. Conversely, the peak-to-peak value of Cxx increases with the increase in the length-to-diameter ratio. When the bearing length-to-diameter ratio increases from 0.8 to 1.4, the ratios of the peak-to-peak values of Kxx and Cyy to the corresponding average values decrease from 13.79% and 18.28% to 11.96% and 14.58%, respectively, while the ratios of the peak-to-peak values of Kyy and Cxx to the corresponding average values increase from 18.50% and 15.59% to 19.37% and 19.60%, respectively. Changes in the length-to-diameter ratio have a more pronounced effect on the magnitude of the fluctuations in the damping coefficients. Combined with Figure 12, it can be seen that the range of the journal orbit increases to a certain extent with the increase in the length-to-diameter ratio. However, the increase in the attitude angle leads to an increase in the degree of inclination of the journal orbit, and the range of the displacement change in the horizontal direction decreases, reducing the amplitude of the fluctuation of the main damping and the main stiffness in the horizontal direction; however, as the thickness of the water film in the vertical direction increases, the response to the external perturbation decreases. Integrating the findings from Figure 11 and Figure 12 reveals that Cxx is the most sensitive to changes in the length-to-diameter ratio, Kyy is the second most sensitive, and changes in length-to-diameter ratio have the least effect on Kxx.
3.5. Effect of Radial Clearance-to-Radius Ratio
To analyze the effect of the radial clearance-to-radius ratio on the stern bearing in the case of the same eccentric excitation, the ratio of the distance to the radial clearance for eccentric excitation under different radial clearance-to-radius ratios is changed in this section. The curves depicting the dynamic characteristic coefficients of the bearings over time under different radial clearance-to-radius ratios are shown in Figure 13, which show that Kxx, Cxx, and Cyy decrease as the radial clearance-to-radius ratio increases, while Kyy increases with the increase in the radial clearance-to-radius ratio; additionally, the peak-to-peak values and standard deviations of Kxx and Cxx decrease with increasing the radial clearance-to-radius ratio, whereas the peak-to-peak values and standard deviations of Kyy and Cyy increase with increasing the radial clearance-to-radius ratio. As shown in Figure 14, as the radial clearance-to-radius ratio increases, the carrying capacity of the water film decreases, and the range of the journal orbit decreases; however, the thickness of the water film in the vertical direction decreases, thereby increasing the sensitivity of the water film to displacement perturbations in the vertical direction, as the increased sensitivity offsets the weakening effect of the reduced vertical position change.
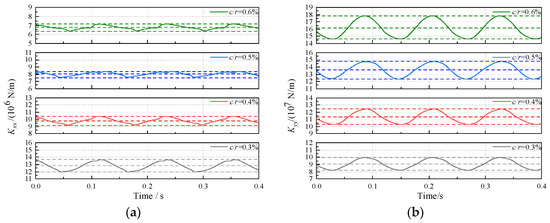
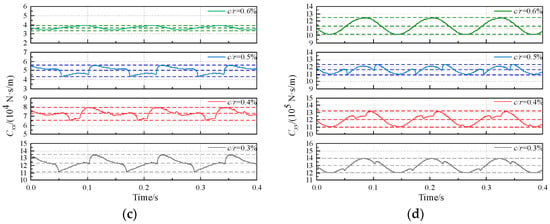
Figure 13.
Effect of radial clearance-to-radius ratio on dynamic characteristic coefficients: (a) Kxx; (b) Kyy; (c) Cxx; (d) Cyy.
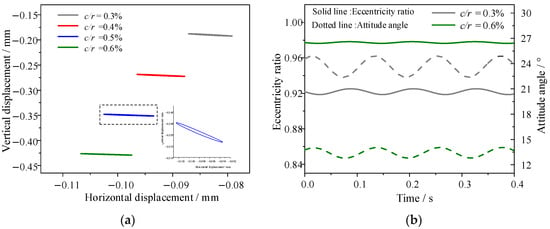
Figure 14.
Effect of radial clearance-to-radius ratio on journal spatial state: (a) journal orbits; (b) eccentricity and attitude angle.
3.6. Equation Fitting and Verification
Based on the above analysis, it is known that the time-varying characteristic coefficients of the bearings are affected by the coupling effects of the external load, rotational speed, eccentric excitation distance, length-to-diameter ratio, and radial clearance-to-radius ratio. While the numerical calculation is time-consuming, improving the efficiency of the dynamic performance evaluation for actual bearings in operation can be achieved through formula fitting of the stiffness and damping curves. According to the similarity principle, the equation fitting with dimensionless parameters still applies to full-size bearings under the same conditions. Therefore, the dimensionless stiffness and damping coefficients are used in this section for analysis. The dimensionless coefficients of each parameter are defined as follows:
where F0 is the dimensionless unit of the load, which can be calculated according to , and k0 and c0 are the dimensionless units of the stiffness and damping coefficients, respectively.
Since the dynamic characteristic coefficients of the bearings under the action of eccentric excitation show a cyclic variation with an approximate sinusoidal function, this section employs the Fourier series to fit the main stiffness and damping of the bearings in the horizontal and vertical directions. It should be noted that the dynamic characteristic parameters fitted in this section are based on the following working condition ranges: the dimensionless external load ranges from 14 to 34, the dimensionless eccentric excitation distance is in the range of 0.2% to 0.8%, the length-to-diameter ratio is in the range of 0.8 to 1.4, and the radial clearance-to-radius ratio is in the range of 0.3% to 0.7%. The previous analysis showed that the curves of the main stiffness of the bearing in the horizontal and vertical directions as a function of time are relatively smooth and can be fitted with a low-order Fourier series. The final fitting equations for kxx and kyy are:
The enhancement in the fitting accuracy for the main damping coefficient becomes increasingly limited as the order of the Fourier series increases. For example, when the fitting function for cxx is set to a two-order Fourier level, the coefficient of determination (R2) reaches 0.9614, which meets the fitting requirements; under the premise of ensuring the fitting accuracy, the fitting equations of cxx and cyy are:
To verify the validity of Equations (14)–(17), the bearing’s dimensionless main stiffness and main damping in the horizontal and vertical directions were calculated using numerical computation and fitting formula method, with the bearing parameters specified in Table 4. The comparison of the results from the different methods is shown in Figure 15, which shows that the results from the numerical computation and the formula computation were relatively similar, with the maximum relative error of not exceeding 9.63%. Notably, the relative errors of kxx and kyy were less than 2%, proving that the time-varying characteristic coefficient formulas fitted in this study essentially meet the required standards.

Table 4.
Main calculation parameters.

Figure 15.
Comparison of the results of numerical calculations and formula calculations (a) kxx; (b) kyy; (c) cxx; (d) cyy.
4. Test Validation
4.1. Design of Test Rig
This chapter employs a water-lubricated bearing shrinkage test rig to further verify the accuracy of the model proposed in this paper, which can be used for scaled-down bearing tests with journal diameters of 100 mm and a bearing length-to-diameter ratio of 1. The rated power of the test bench is 30 kW, with a rated speed of 1175 r/min. A sketch of the bench structure is shown in Figure 16, which is mainly composed of the drive system, loading system, lubrication system, data acquisition system, and test bearings, as well as the console input inlet and outlet water flow, load, speed, and other test parameters. Hydraulic loading is used to apply an external load to the test bearing, and a force sensor is set up between the loading device and the bearing housing to monitor the load size; water inlet and outlet ports are provided above and below the bearing housing to provide lubrication medium for the test bearing. Two eddy current displacement sensors are arranged perpendicularly to each other in the shaft section of the test bearing for obtaining the journal orbit.
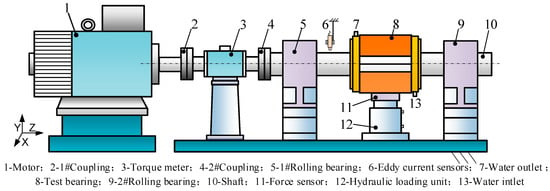
Figure 16.
Schematic diagram of the test rig.
The water-lubricated bearing test rig adopted in this study is a specialized experimental apparatus designed to evaluate the performance of marine water-lubricated bearings. Based on hydrodynamic lubrication technology and the linear velocity approximation principle, the rig simulates the actual service operational speeds and specific pressure conditions of marine stern bearings. By employing signal acquisition and analysis systems, it enables the real-time monitoring of critical tribological and dynamic parameters during bearing operation, including the frictional moment, vibration magnitude, and journal motion trajectory. These measurements are systematically analyzed to comprehensively assess the dynamic and acoustic performance of the bearings, thereby providing critical insights into their operational stability, wear resistance, and noise generation mechanisms under simulated marine propulsion environments.
The main parameters of the test bearing are shown in Table 5. The bearing housings are mainly made of stainless steel, and the bearing liner material utilized in this test is PEEK 450FC30, a carbon fiber-reinforced composite developed by Victrex, UK. This material exhibits high tensile strength and rigidity, making it suitable for the low-speed, heavy-load conditions typical of marine propulsion shaft systems. The incorporation of carbon fibers reduces thermal expansion and enhances wear resistance. The high elastic modulus ensures minimal deformation of the bearing liner under heavy loads, thereby improving the water film’s load-carrying capacity. This minimizes localized contact between the journal and the bearing liner surface. When considering the stiffness of the bearing material, the integrated stiffness can be calculated using the following formula:
where K represents the comprehensive stiffness of the bearing, and Kw and Kl represent the water film stiffness and liner material stiffness respectively.

Table 5.
Basic parameters of test bearing.
4.2. Journal Orbit Acquisition Method
The eddy current sensor is used to measure the journal orbits, with the sensor arrangement scheme shown in Figure 17, where an eddy current sensor is arranged in the horizontal and vertical directions to collect the displacement signals in both directions, respectively. It should be emphasized that the sensors must be located in the same cross-section and aligned with the shaft center, and the sensors are connected to the acquisition card through the preamplifier to realize the signal acquisition. Firstly, the initial displacement of the journal is collected in the static loading state, and then after the speed is stabilized, the journal orbit at each speed is collected. The final journal orbit results are obtained by subtracting the initial displacement of the journal from the journal orbit data collected at different speeds.
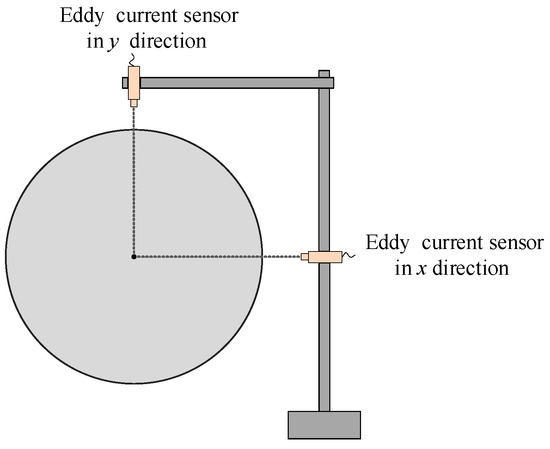
Figure 17.
Eddy current sensors arrangement.
4.3. Analysis of Test Results
At the beginning of the test, the console is started, the lubrication water system is turned on, a radial load of 600 N is applied to the bearing seat, and then the motor is turned on and the rotational speed range is set from 400 to 600 r/min. The journal orbit is collected at different speeds. The test orbit is processed, as shown in Figure 18.
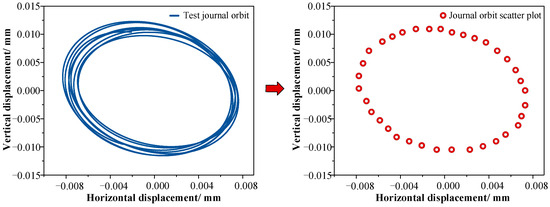
Figure 18.
Journal orbit test data processing.
In this test, the method of reference [23] is employed to determine the eccentricity distance of the rotor. By comparing the numerical computation results at a rotational speed of 500 r/min with the experimental data, the offset was determined to be 0.3 mm. This value served as a reference for other rotational speeds, and an imbalance of 0.3 mm was preset. The test journal orbits were then collected, and the test data were processed. A comparison of the experimental journal orbit and the predicted journal orbit of the numerical computation was obtained. As shown in Figure 19, it is noted that the range of the journal orbit increases with the increase in the rotational speed, which indicates that an increase in the rotational speed makes the rotor system unstable. The numerical magnitude and the trend of the test orbit and the numerical computation predicted trajectory are roughly in line with each other, which further illustrates the accuracy of the nonlinear dynamics model in this paper.
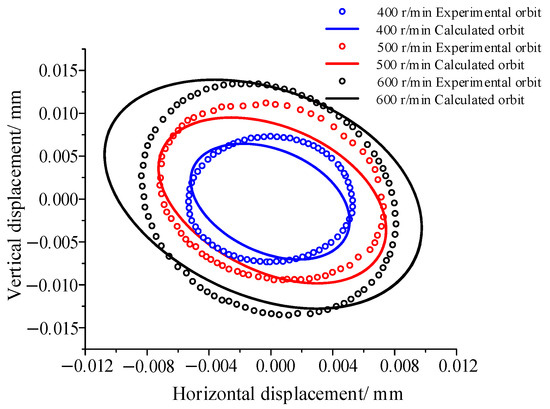
Figure 19.
Comparison of test journal orbit and numerical calculation results.
5. Conclusions
This paper establishes a transient dynamic model of a water-lubricated stern bearing system, and the model’s accuracy is verified by both simulation and testing. The effects of the external load, rotational speed, eccentric excitation distance, length-to-diameter ratio, and radial clearance-to-radius ratio on the main dynamic parameters of the bearing and the spatial state of the journal are systematically investigated. Based on the results of the parametric analysis, the dimensionless time-varying characteristic coefficient characterization formulas of vibration coupling are fitted, and the formulas are verified; the following conclusions can be drawn:
- (1)
- The dynamic characteristic coefficients display approximately sinusoidal periodic changes under the action of eccentric excitation. The fluctuation amplitude of the journal orbit range and the dynamic characteristic coefficients increase with the increase in the eccentric excitation. Notably, the damping coefficients are significantly influenced by the eccentric excitation.
- (2)
- The main stiffness and main damping coefficients of the bearing in both the horizontal and vertical directions are proportional to the external load and inversely proportional to the rotational speed; the external load significantly influences the degree of fluctuation of the main stiffness and main damping coefficients in the vertical direction, and as the rotational speed rises, the peak-to-peak value of the main stiffness coefficient of the bearing increases, while the peak-to-peak value of the main damping coefficient decreases.
- (3)
- With the increase in the length-to-diameter ratio or the decrease in the radial clearance-to-radius ratio, the main stiffness and main damping in the horizontal direction increase, while the main stiffness in the vertical direction decreases. The reasonable design of the structure of the water-lubricated stern bearings is crucial to the influence of their dynamic behavior.
- (4)
- Based on the simulation data, the formulae for calculating the main stiffness and main damping coefficients of the dimensionless bearing were fitted, and the predictive ability of the fitted formulae was verified; the results showed that the maximum relative error of the dynamic characteristic coefficients was less than 10%.
- (5)
- In this paper, a detailed parametric study of the dynamic behavior of water-lubricated bearings under eccentric excitation was conducted to provide new insights into the transient transverse vibration modeling of marine propulsion shaft systems. Despite these contributions, this study acknowledges certain limitations. Future research should focus on improving the lining deformation model to achieve more realistic dynamic simulations of water-lubricated bearings. Additionally, further exploration of the mixed lubrication dynamics behavior of water-lubricated bearings under low-speed and heavy-load conditions is necessary to optimize the structural parameters of the bearings and improve their service capability.
Author Contributions
Conceptualization, H.Z. and Q.L.; data curation, H.Z.; formal analysis, H.Z.; funding acquisition, Y.J.; investigation, H.Z. and Y.J.; methodology, H.Z.; project administration, Y.J.; resources, Y.J.; software, H.Z.; supervision, T.H.; validation, H.Z. and Q.L.; visualization, W.O.; writing—original draft, H.Z.; writing—review and editing, H.Z. and Q.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was financially supported by the National Natural Science Foundation of China under grant no. 52241102.
Data Availability Statement
The data that support the results of this study are available from the authors upon reasonable request.
Acknowledgments
The authors are so grateful for the valuable suggestions from Ziyang Yan during this study.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| x | Horizontal direction |
| y | Vertical direction |
| OB | Bearing center |
| OJ | Journal geometric center |
| Om | Journal center of mass |
| Qe | Eccentric excitation distance, mm |
| e | Journal eccentricity, mm |
| θ | Circumferential angle, rad |
| φ | Attitude angle, rad |
| Fh | Hydrodynamic force, N |
| Ff | Shearing friction force, N |
| Kxx | Horizontal stiffness coefficient, N/m |
| Kyy | Vertical stiffness coefficient, N/m |
| Cxx | Horizontal damping coefficient N·s/m |
| Cyy | Vertical damping coefficient, N·s/m |
| Horizontal acceleration, m/s2 | |
| Vertical acceleration, m/s2 | |
| mj | Journal mass, kg |
| ω | Angular velocity, rad/s |
| W | External load, N |
| λ | Unbalanced eccentricity ratio |
| c | Radial clearance, mm |
| x′ | Horizontal velocity |
| y′ | Vertical velocity |
| kij (i,j = 1~4) | Iteration coefficients for different time steps |
| Δt | Iteration timestep, s |
| η | Lubricant viscosity, Pa·s |
| ρ | Lubricant density, kg/m3 |
| ph | Hydrodynamic pressure, Pa |
| h | Water film thickness, mm |
| U | Horizontal relative velocity component, m/s |
| V | Vertical relative velocity component, m/s |
| RB | Bearing radius, mm |
| z | Axial direction |
| ε | Eccentricity ratio |
| δ | Liner deformation matrix |
| T | Lining thickness, mm |
| Eb | Bearing elastic modulus, MPa |
| vb | Bearing Poisson’s ratio |
| ΔFhx | Horizontal hydrodynamic force increments, N |
| ΔFhy | Vertical hydrodynamic force increments, N |
| Δx | Horizontal displacement disturbances, mm |
| Δy | Vertical displacement disturbances, mm |
| Horizontal velocity disturbances, m/s | |
| Vertical velocity disturbances, m/s | |
| L | Bearing length, mm |
| D | Bearing inner diameter, mm |
| n | Rotational speed, r/min |
| Ts | Computation time, s |
| F0 | Dimensionless units of force |
| Dimensionless external load | |
| r | Journal radius, mm |
| Dimensionless eccentric excitation distance | |
| L/D | Length-to-diameter ratio |
| c/r | Radial clearance-to-radius ratio |
| kxx | Horizontal dimensionless stiffness coefficient |
| kyy | Vertical dimensionless stiffness coefficient |
| cxx | Horizontal dimensionless damping coefficient |
| cyy | Vertical dimensionless damping coefficient |
| k0 | Dimensionless units of stiffness coefficients |
| c0 | Dimensionless units of the damping coefficient |
| K | Comprehensive stiffness of the bearing, N/m |
| Kw | Water film stiffness, N/m |
| Kl | Liner material stiffness, N/m |
| σt | Tensile stress of the bearing liner material, MPa |
| σf | Flexural stress of the bearing liner material, MPa |
| σc | Compressive stress of the bearing liner material, MPa |
References
- Song, Y.; Wen, J.; Yu, D.; Liu, Y.; Wen, X. Reduction of vibration and noise radiation of an underwater vehicle due to propeller forces using periodically layered isolators. J. Sound Vib. 2014, 333, 3031–3043. [Google Scholar] [CrossRef]
- Yang, T.; Han, Y.; Wang, Y.; Xiang, G. Numerical analysis of the transient wear and lubrication behaviors of misaligned journal bearings caused by linear shaft misalignment. J. Tribol. 2022, 144, 051801. [Google Scholar] [CrossRef]
- Xie, Z.; Jiao, J.; Zhao, B.; Zhang, J.; Xu, F. Theoretical and experimental research on the effect of bi-directional misalignment on the static and dynamic characteristics of a novel bearing. Mech. Syst. Signal Process. 2024, 208, 111041. [Google Scholar] [CrossRef]
- Xiang, G.; Wang, J.; Han, Y.; Yang, T.; Dai, H.; Yao, B.; Zhou, C.; Wang, L. Investigation on the nonlinear dynamic behaviors of water-lubricated bearings considering mixed thermoelastohydrodynamic performances. Mech. Syst. Signal Process. 2022, 169, 108627. [Google Scholar] [CrossRef]
- Chang-Jian, C.-W. Nonlinear simulation of rotor dynamics coupled with journal and thrust bearing dynamics under nonlinear suspension. Tribol. Trans. 2010, 53, 897–908. [Google Scholar] [CrossRef]
- Yang, T.; Xiao, K.; Xiang, G.; Wang, L.; Cai, J.; Wang, J. Effects of rotating microgroove on tribo-dynamic performance of coupled bearings. Int. J. Mech. Sci 2024, 279, 109629. [Google Scholar] [CrossRef]
- Xiang, G.; Wang, C.; Wang, Y.; Han, Y.; Wang, J.; Lv, Z. Dynamic mixed lubrication investigation of water-lubricated bearing with unbalanced rotor during start-up. Tribol. Trans. 2021, 64, 764–776. [Google Scholar] [CrossRef]
- Ye, X.; Wang, J.; Zhang, D.; Hu, L.; She, X. Experimental Research of Journal Orbit for Water-Lubricated Bearing. Math. Probl. Eng. 2016, 2016, 8361596. [Google Scholar] [CrossRef]
- Tang, D.; Xiang, G.; Guo, J.; Cai, J.; Yang, T.; Wang, J.; Han, Y. On the optimal design of staved water-lubricated bearings driven by tribo-dynamic mechanism. Phys. Fluids 2023, 35, 093611. [Google Scholar] [CrossRef]
- Cai, J.; Han, Y.; Xiang, G.; Wang, J.; Wang, L. Effects of wear and shaft-shape error defects on the tribo-dynamic response of water-lubricated bearings under propeller disturbance. Phys. Fluids 2022, 34, 077118. [Google Scholar] [CrossRef]
- Tang, D.; Xiao, K.; Xiang, G.; Cai, J.; Fillon, M.; Wang, D.; Su, Z. On the nonlinear time-varying mixed lubrication for coupled spiral microgroove water-lubricated bearings with mass conservation cavitation. Tribol. Int. 2024, 193, 109381. [Google Scholar] [CrossRef]
- Cha, M.; Kuznetsov, E.; Glavatskih, S. A comparative linear and nonlinear dynamic analysis of compliant cylindrical journal bearings. Mech. Mach. Theory 2013, 64, 80–92. [Google Scholar] [CrossRef]
- Zhang, Z.; Mao, Q.; Xu, H. Paper XI (iv) The effect of dynamic deformation on dynamic properties and stability of cylindrical journal bearings. In Tribology Series; Elsevier: Amsterdam, The Netherlands, 1987; Volume 11, pp. 363–366. [Google Scholar]
- Wang, K.; Wu, J.; Zhao, G. Numerical analysis of sliding bearing dynamic characteristics based on CFD. J. Phys. Conf. Ser. 2017, 916, 012025. [Google Scholar] [CrossRef]
- Liu, S.; Yang, B. Modeling and analysis of flexible multistage rotor systems with water-lubricated rubber bearings. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Montreal, QC, Canada, 14–20 November 2014; p. V04BT04A078. [Google Scholar]
- Chen, Z.; Wang, J.; Li, R.; Liu, Y. A novel 4-DOF marine stern bearing support model considering discrete distribution effects. Ocean Eng. 2024, 312, 119072. [Google Scholar] [CrossRef]
- Feng, H.; Jiang, S. Dynamic analysis of water-lubricated motorized spindle considering tilting effect of thrust bearing. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 3780–3790. [Google Scholar] [CrossRef]
- Leng, Z.; Lv, F.; Zhang, J.; Jiao, C.; Gao, G.; Ta, N.; Rao, Z. Study of dynamic coefficients of water film in marine stern tube bearing considering roughness and deformation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2021, 235, 2257–2271. [Google Scholar] [CrossRef]
- Ouyang, W.; Cheng, Q.; Jin, Y.; Liu, Q.; Wang, B.; Wang, L. Lubrication performance distribution of large aspect ratio water-lubricated bearings considering deformation and shaft bending. Tribol. Trans. 2021, 64, 730–743. [Google Scholar] [CrossRef]
- Wen, S.; Huang, P. Principles of Tribology; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Zhang, Z.; Zhang, Y.; Xie, Y. Fluid Dynamic Lubrication Theory of Sliding Bearings; Higher Education Press: Beijing, China, 1986. [Google Scholar]
- Jain, S.; Sinhasan, R.; Singh, D. A study of EHD lubrication in a journal bearing with piezoviscous lubricants. ASLE Trans. 1984, 27, 168–176. [Google Scholar] [CrossRef]
- Xiang, G.; Wang, J.; Zhou, C.; Shi, Y.; Wang, Y.; Cai, J.; Wang, C.; Jin, D.; Han, Y. A tribo-dynamic model of coupled journal-thrust water-lubricated bearings under propeller disturbance. Tribol. Int. 2021, 160, 107008. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).