Intelligent Tool Wear Prediction Using CNN-BiLSTM-AM Based on Chaotic Particle Swarm Optimization (CPSO) Hyperparameter Optimization
Abstract
1. Introduction
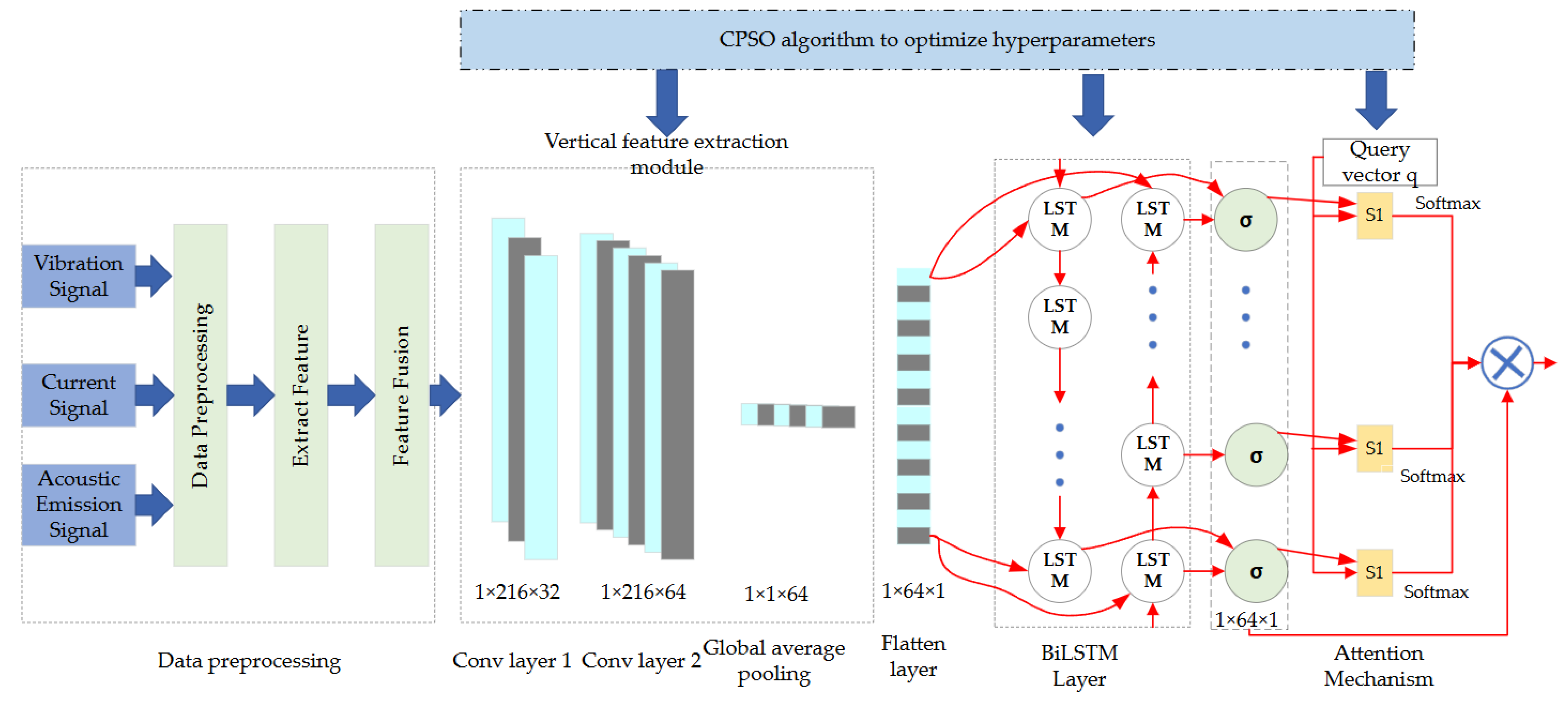
2. CPSO-CNN-BiLSTM-AM Model
2.1. Model Structure Diagram
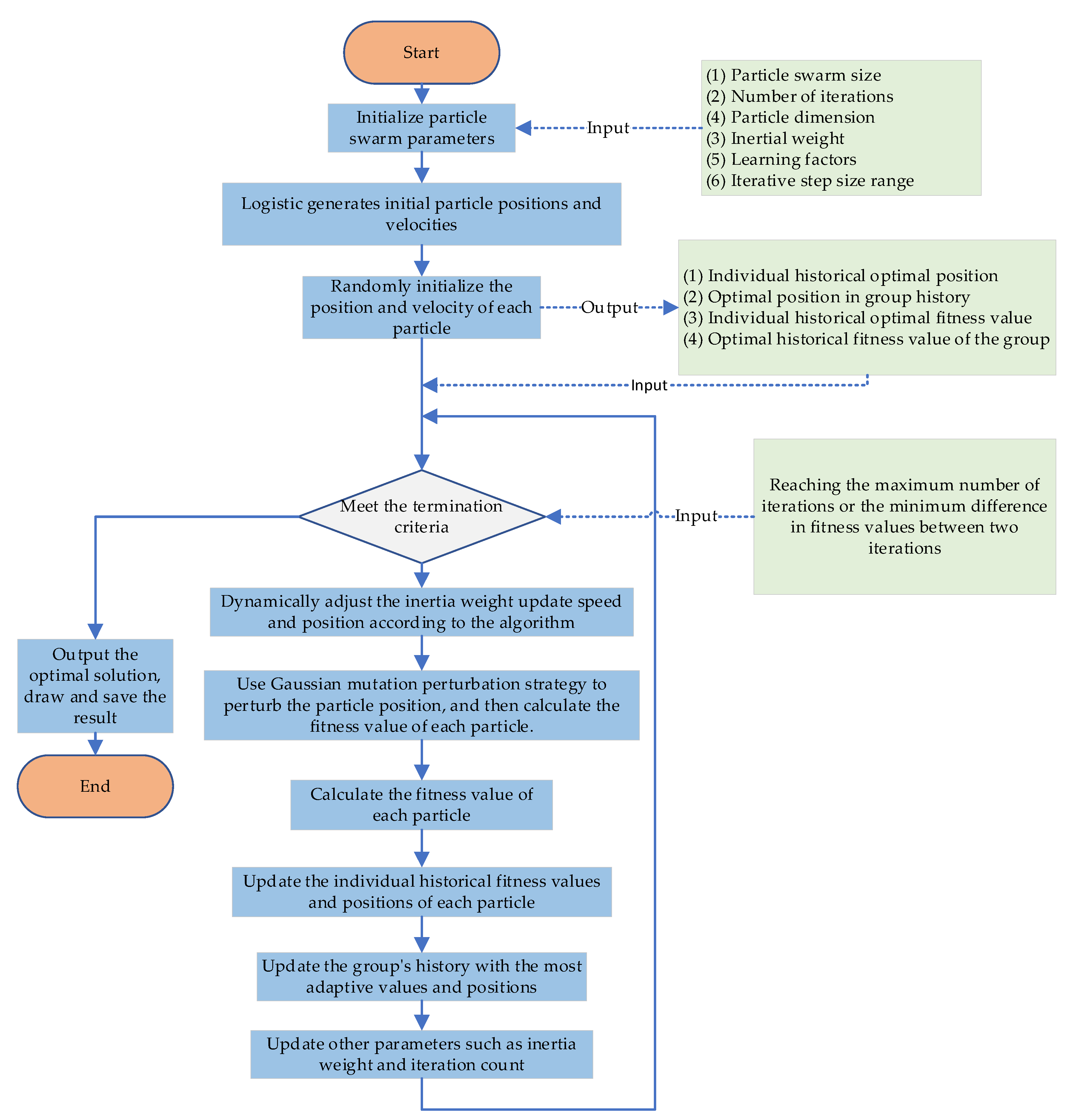
2.2. Improved Chaotic Particle Swarm Optimization
2.2.1. CPSO
| Algorithm 1. CPSO algorithm (pseudocode) |
| @startuml -start : Initialize the particle swarm (positions, velocities); : Calculate the particle fitness value; : Update the individual optimal position ( ) and the global optimal position ( ); while (Maximum number of iterations not reached) : Update particle positions using Logistic chaotic mapping; : Adaptive inertia weight adjusts velocity; : Gaussian mutation disturbs the particle position; : Calculate the particle fitness value; : Update and ; endwhile : Output the global optimal position ( ); -stop @enduml |
2.2.2. Improved CPSO
2.3. CNN-BiLSTM-AM Model
2.3.1. CNN
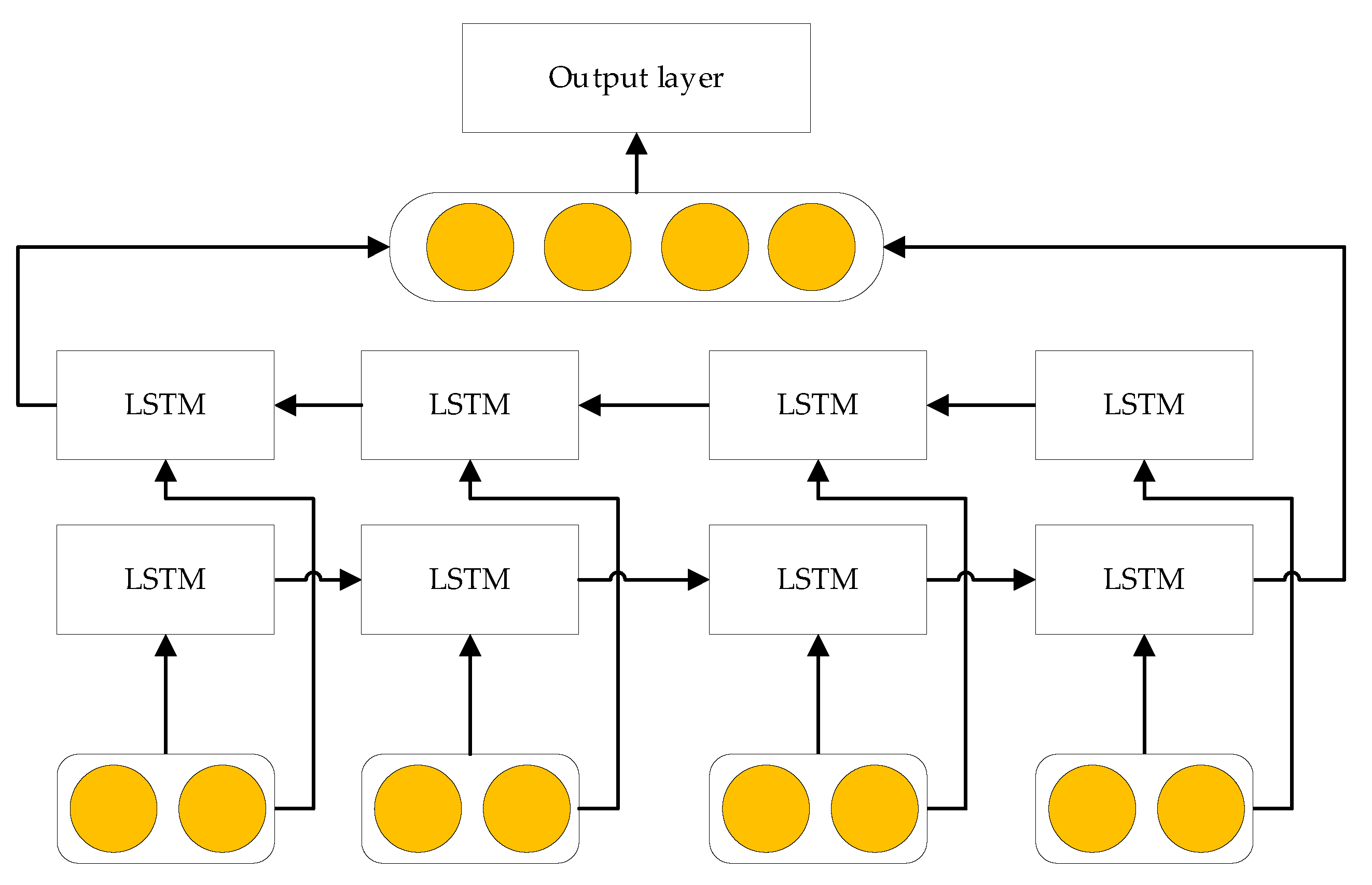
2.3.2. BiLSTM Algorithm
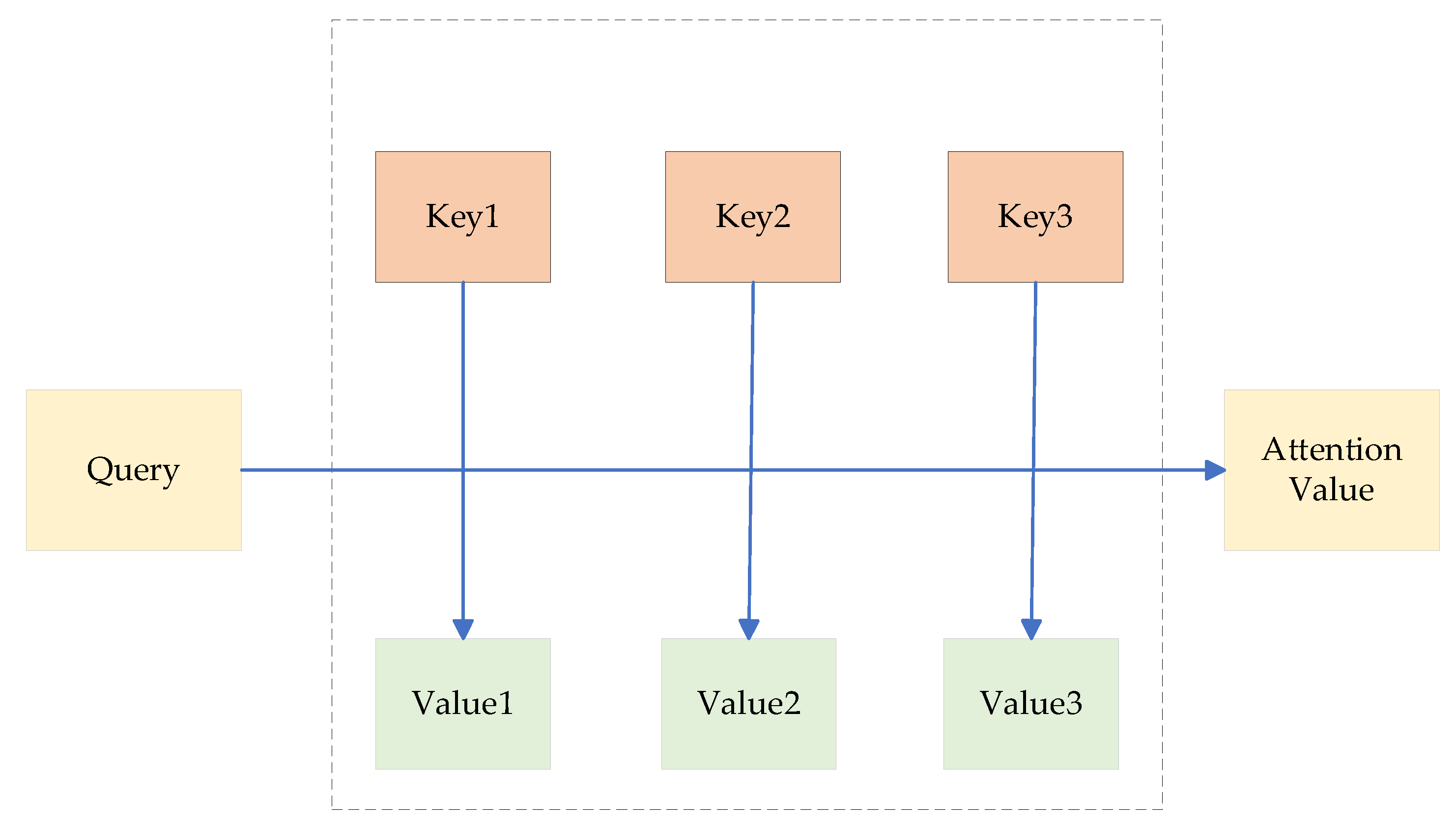
2.3.3. Attention Mechanism
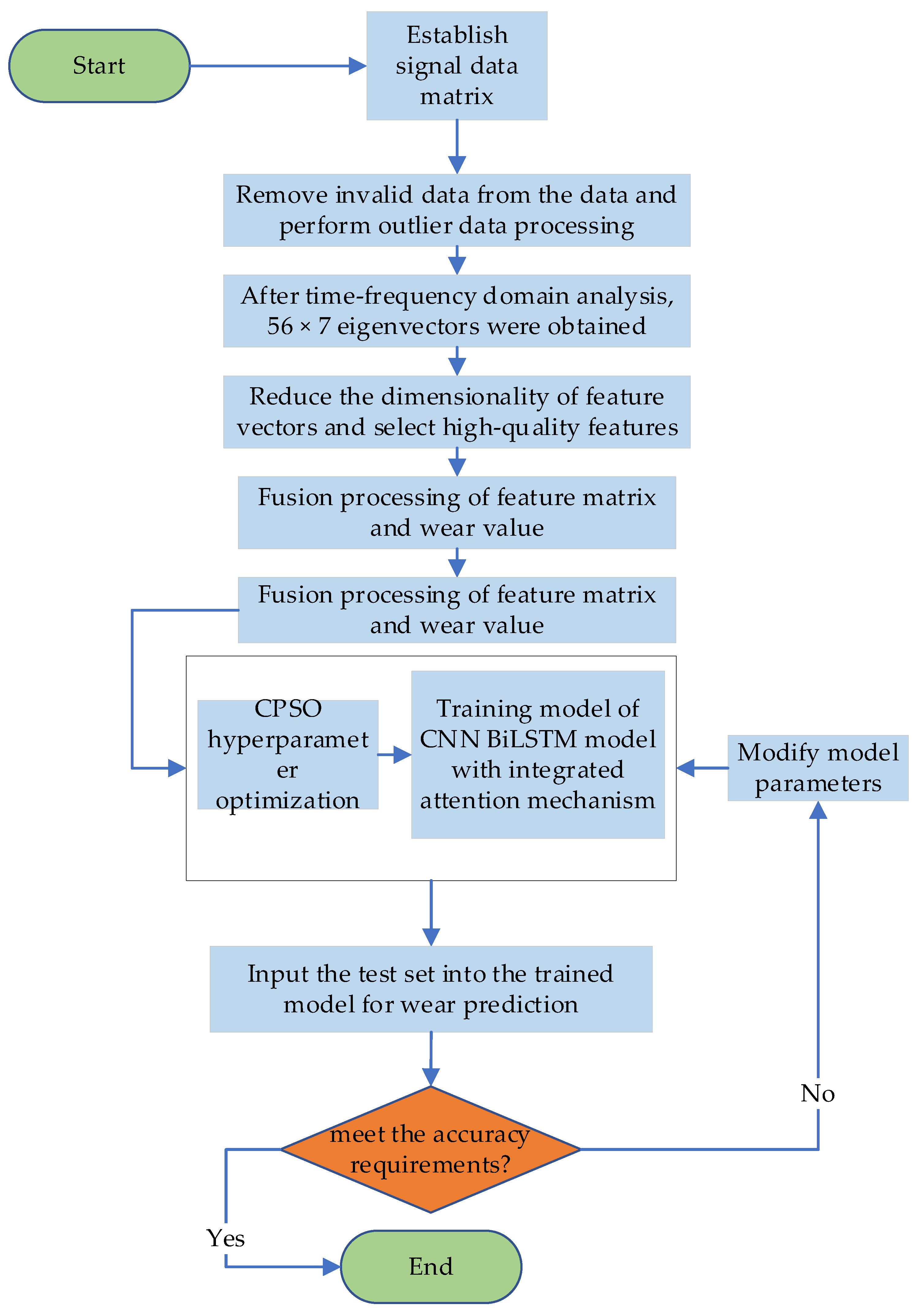
2.4. Tool Monitoring Process Based on the CPSO-CNN-BiLSTM-AM Model
2.4.1. Monitoring Process
2.4.2. Model Parameter Settings
3. Materials and Methods
3.1. Introduction to the PHM2010 Dataset
3.2. Introduction to the Self-Built Dataset
- (a)
- Initial wear stage: At this stage, the tool flank wear width (VB value) is less than 0.1 mm. The cutting edge is slightly worn due to initial contact with the workpiece material (45 steel).
- (b)
- As the cutting process continues, the tool edge gradually loses its sharpness, and the friction between the tool and workpiece intensifies.
- (c)
- Late wear stage: The tool edge is severely worn, and local micro-chipping may occur. This feature directly indicates that the tool is about to reach the end of its service life.
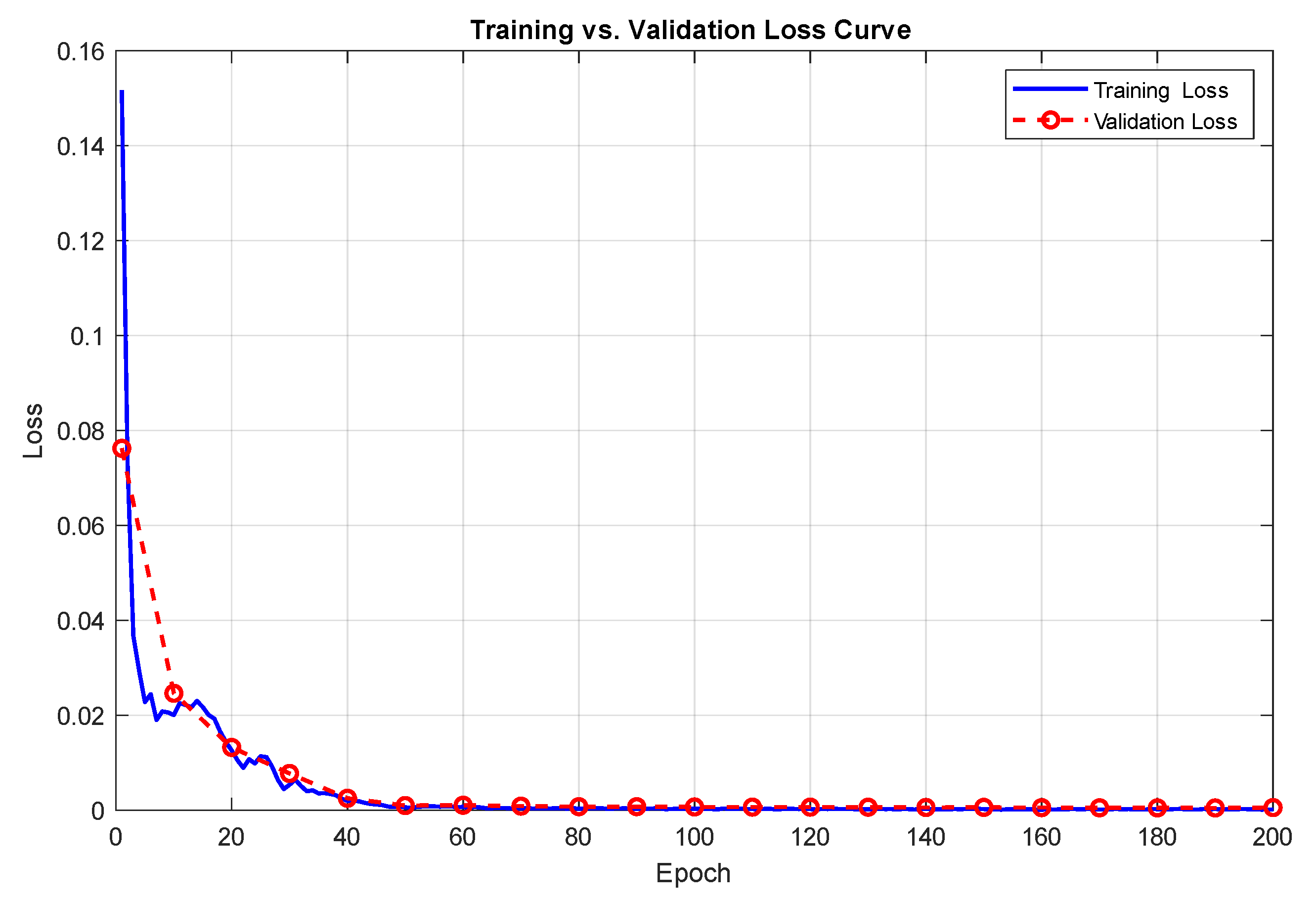
4. Results
4.1. Experimental Environment Configuration
4.2. Data Preprocessing
4.3. Hyperparameter Settings
4.4. Model Evaluation Metrics
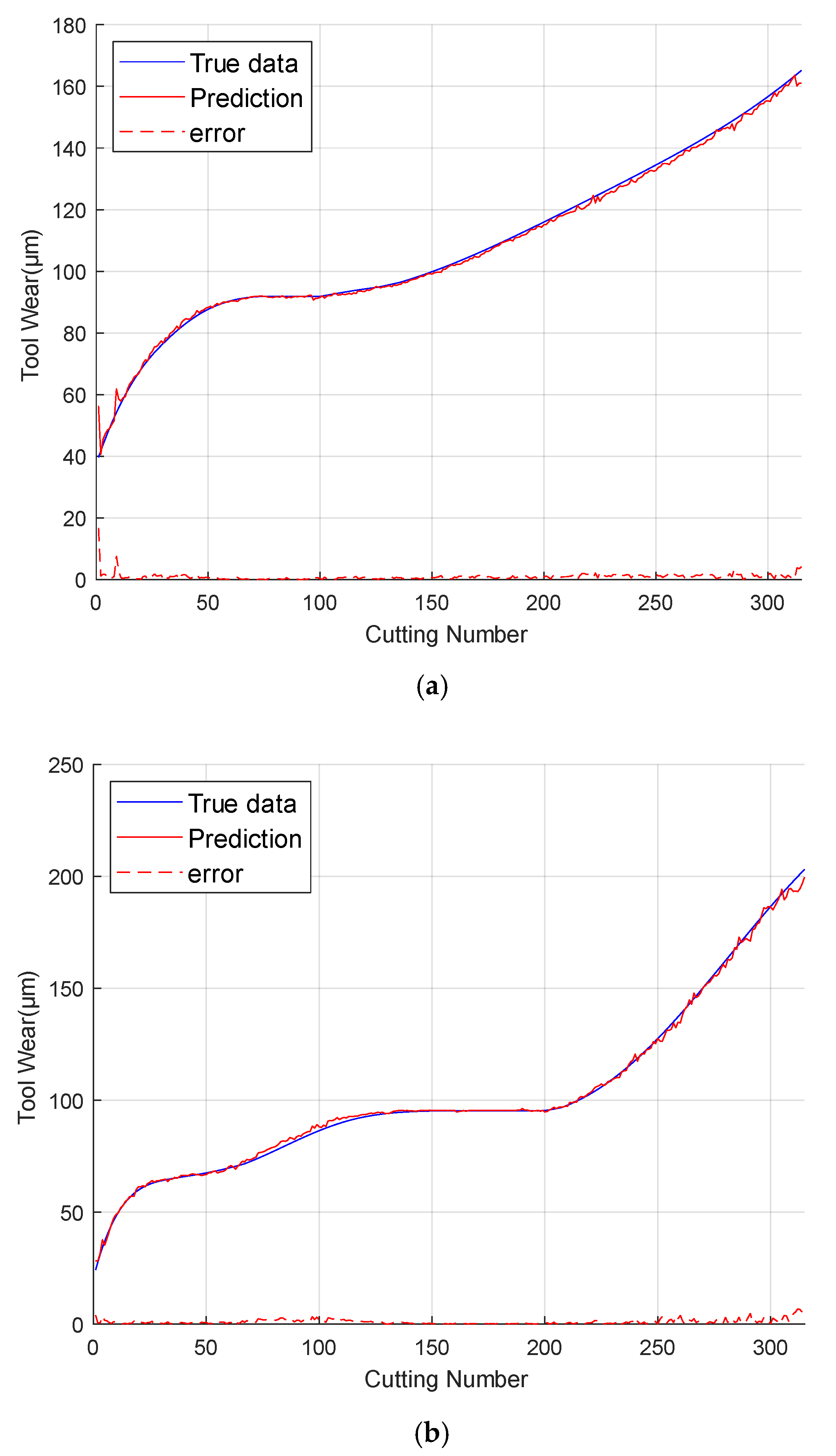
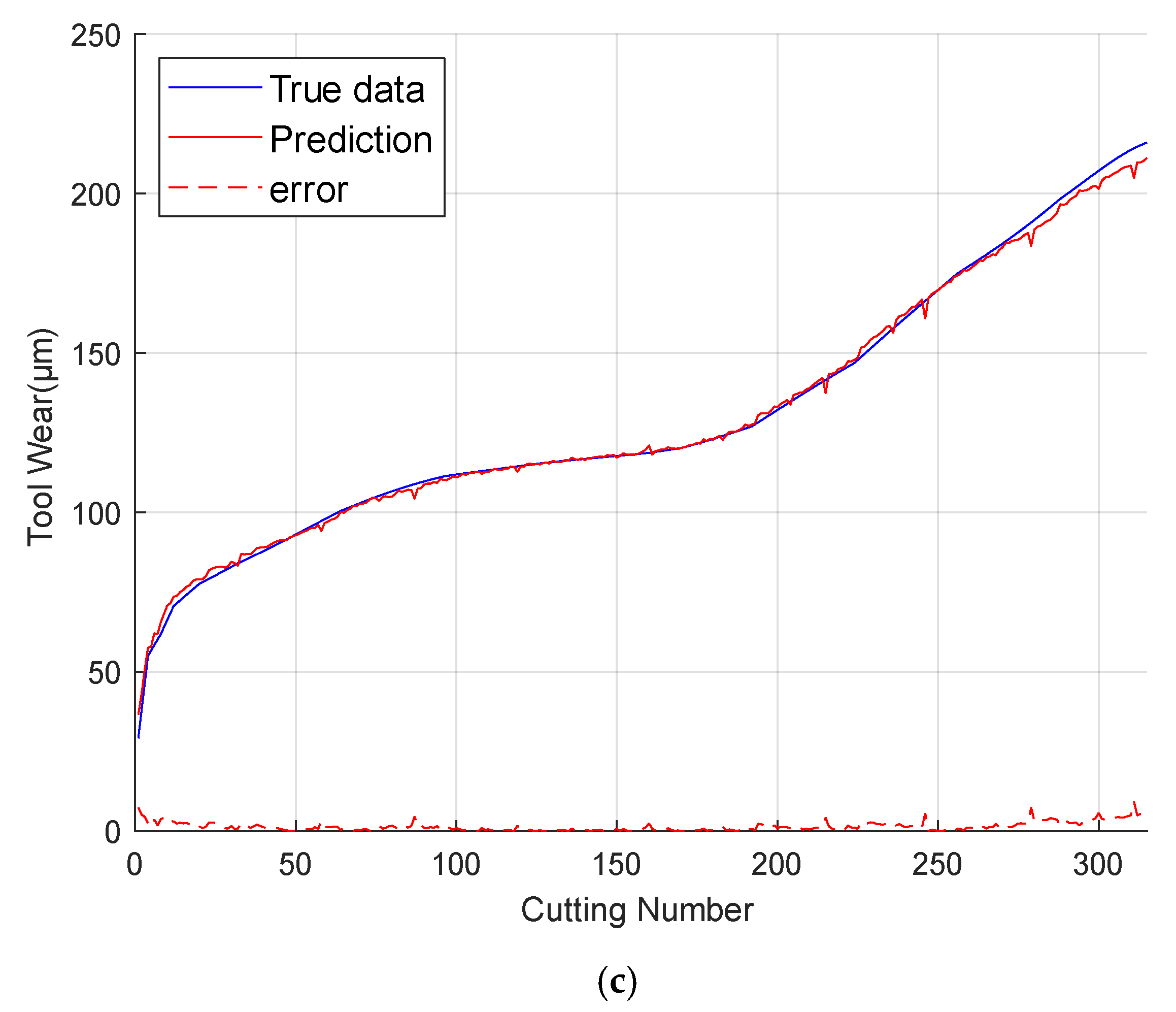
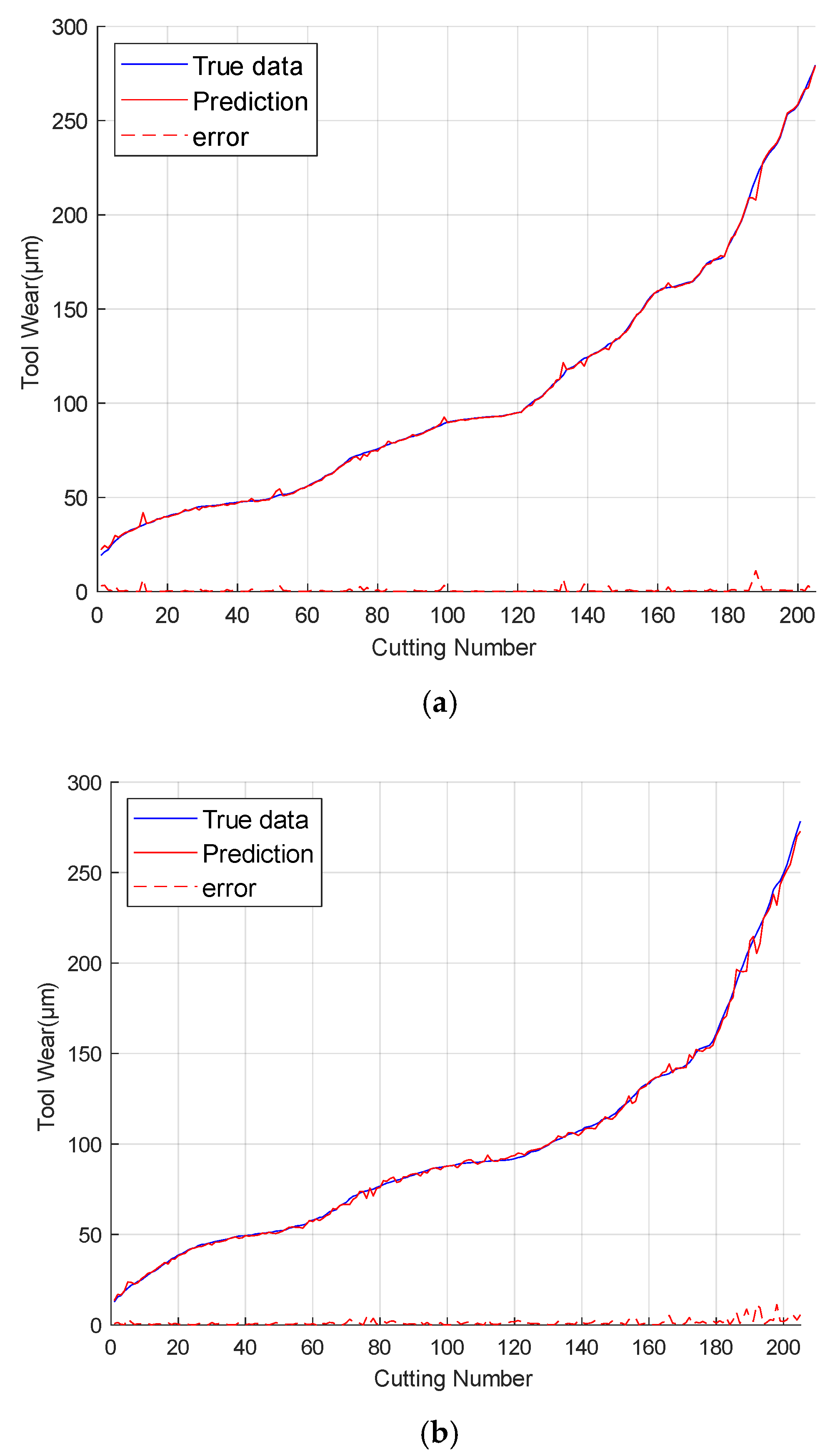
4.5. Result Analysis Based on the Public Dataset PHM2010
4.6. Result Analysis Based on Self-Built Dataset
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jia, R.; Yue, C.; Liu, Q.; Xia, W.; Qin, Y.; Zhao, M. Tool wear condition monitoring method based on relevance vector machine. Int. J. Adv. Manuf. Technol. 2023, 128, 4721–4734. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, J.; Qian, Q.; Qin, Y. A comprehensive survey of machine remaining useful life prediction approaches based on pattern recognition: Taxonomy and challenges. Meas. Sci. Technol. 2024, 35, 062001. [Google Scholar] [CrossRef]
- Lin, G.; Shi, H.; Liu, X.; Wang, Z.; Zhang, H.; Zhang, J. Tool wear on machining of difficult-to-machine materials: A review. Int. J. Adv. Manuf. Technol. 2024, 134, 989–1014. [Google Scholar] [CrossRef]
- Gao, J.; Qiao, H.; Zhang, Y. Intelligent Recognition of Tool Wear with Artificial Intelligence Agent. Coatings 2024, 14, 827. [Google Scholar] [CrossRef]
- Yao, X. Lstm Model Enhanced By Kolmogorov-Arnold Network: Improving Stock Price Prediction Accuracy. Trends Soc. Sci. Humanit. Res. 2024, 4, 19. [Google Scholar]
- Karnehm, D.; Samanta, A.; Rosenmüller, C.; Neve, A.; Williamson, S. Core Temperature Estimation of Lithium-Ion Batteries Using Long Short-Term Memory (LSTM) Network and Kolmogorov-Arnold Network (KAN). IEEE Trans. Transp. Electrif. 2024, 11, 10391–10401. [Google Scholar] [CrossRef]
- Cai, W.; Zhang, W.; Hu, X.; Liu, Y. A hybrid information model based on long short-term memory network for tool condition monitoring. J. Intell. Manuf. 2020, 31, 1497–1510. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, B.; Liu, B.; Peng, C. Milling Cutter Wear State Identification Method Based on Improved ResNet-34 Algorithm. Appl. Sci. 2024, 14, 8951. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, H.; Hou, L.; Yi, S. Overview of Tool Wear Monitoring Methods Based on Convolutional Neural Network. Appl. Sci. 2021, 11, 12041. [Google Scholar] [CrossRef]
- De Barrena, T.; Ferrando, J.; García, A.; Badiola, X.; de Buruaga, M.; Vicente, J. Tool remaining useful life prediction using bidirectional recurrent neural networks (BRNN). Int. J. Adv. Manuf. Technol. 2023, 125, 4027–4045. [Google Scholar] [CrossRef]
- Guan, R.; Cheng, Y.; Zhou, S.; Gai, X.; Lu, M.; Xue, J. Research on tool wear classification of milling 508III steel based on chip spectrum feature. Int. J. Adv. Manuf. Technol. 2024, 133, 1531–1547. [Google Scholar] [CrossRef]
- Sharma, P.; Thulasi, H.; Mishra, S.; Ramkumar, J. Identification of parameter-dependent machine learning models for tool flank wear prediction in dry titanium machining. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2024, 12, 09544089241304236. [Google Scholar] [CrossRef]
- Cheng, Y.N.; Gai, X.Y.; Jin, Y.B.; Guan, R.; Lu, M.D.; Ding, Y. A new method based on a WOA-optimized support vector machine to predict the tool wear. Int. J. Adv. Manuf. Technol. 2022, 121, 6439–6452. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, J.; Feng, P.; Zhang, X.; Yu, D.; Zhang, J. A genetic particle swarm optimization algorithm for feature fusion and hyperparameter optimization for tool wear monitoring. Expert Syst. Appl. 2025, 285, 127975. [Google Scholar] [CrossRef]
- Niu, M.; Liu, K.; Wang, Y. A semi-supervised learning method combining tool wear laws for machining tool wear states monitoring. Mech. Syst. Signal Process. 2025, 224, 112032. [Google Scholar] [CrossRef]
- He, Z.; Shi, T.; Chen, X. An Innovative Study for Tool Wear Prediction Based on Stacked Sparse Autoencoder and Ensemble Learning Strategy. Sensors 2025, 25, 2391. [Google Scholar] [CrossRef]
- Zhu, K.; Guo, H.; Li, S.; Lin, X. Physics-Informed Deep Learning for Tool Wear Monitoring. IEEE Trans. Ind. Inform. 2024, 20, 524–533. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, J.; Wang, W.; Du, J.; Yang, X. A novel method based on deep transfer learning for tool wear state prediction under cross-dataset. Int. J. Adv. Manuf. Technol. 2024, 131, 171–182. [Google Scholar] [CrossRef]
- Gao, H.; Xie, A.; Shen, H.; Yu, L.; Wang, Y.; Hu, Y.; Gao, Y.; Xu, J.; Wu, W. Tool Wear Monitoring Algorithm Based on SWT-DCNN and SST-DCNN. Sci. Program. 2022, 2022, 6441066. [Google Scholar] [CrossRef]
- Chang, H.; Ho, P.; Chen, J. Tool wear monitoring in microdrilling through the fusion of features obtained from acoustic and vibration signals. Int. J. Adv. Manuf. Technol. 2024, 134, 3587–3598. [Google Scholar] [CrossRef]
- Kurek, J.; Swiderska, E.; Szymanowski, K. Tool Wear Classification in Chipboard Milling Processes Using 1-D CNN and LSTM Based on Sequential Features. Appl. Sci. 2024, 14, 4730. [Google Scholar] [CrossRef]
- Zhang, W.C.; Cui, E.M. Study on wear state of ultrasonic-assisted grinding of glass-ceramics with diamond tools based on DBO-BiLSTM. J. Vib. Control. 2024, 10, 10775463241292703. [Google Scholar] [CrossRef]
- Che, Z.Y.; Peng, C.; Liao, T.; Wang, J.K. Improving milling tool wear prediction through a hybrid NCA-SMA-GRU deep learning model. Expert Syst. Appl. 2024, 255, 124556. [Google Scholar] [CrossRef]
- Wang, B.; Lei, Y.; Li, N.; Wang, W. Multiscale Convolutional Attention Network for Predicting Remaining Useful Life of Machinery. IEEE Trans. Ind. Electron. 2021, 68, 7496–7504. [Google Scholar] [CrossRef]
- Rehman, A.; Nishat, T.; Ahmed, M.; Begum, S.; Ranjan, A. Chip Analysis for Tool Wear Monitoring in Machining: A Deep Learning Approach. IEEE Access 2024, 12, 112672–112689. [Google Scholar] [CrossRef]
- Abdeltawab, A.; Zhang, X.; Zhang, L. Enhanced tool condition monitoring using wavelet transform-based hybrid deep learning based on sensor signal and vision system. Int. J. Adv. Manuf. Technol. 2024, 132, 5111–5140. [Google Scholar] [CrossRef]
- Abdeltawab, A.; Xi, Z.; Zhang, L. Tool wear classification based on maximal overlap discrete wavelet transform and hybrid deep learning model. Int. J. Adv. Manuf. Technol. 2024, 130, 2443–2456. [Google Scholar] [CrossRef]
- Dong, W.H.; Xiong, X.Q.; Ma, Y.; Yue, X.Y. Woodworking Tool Wear Condition Monitoring during Milling Based on Power Signals and a Particle Swarm Optimization-Back Propagation Neural Network. Appl. Sci. 2021, 11, 9026. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Y.; Mao, Y. Establishment and Solution Test of Wear Prediction Model Based on Particle Swarm Optimization Least Squares Support Vector Machine. Machines 2025, 13, 290. [Google Scholar] [CrossRef]
- Ativor, G.; Temeng, V.; Ziggah, Y. Optimisation of multilayer perceptron neural network using five novel metaheuristic algorithms for the prediction of wear of excavator bucket teeth. Knowl. Based Syst. 2025, 321, 113753. [Google Scholar] [CrossRef]
- Nargundkar, A.; Kumar, S.; Bongale, A. Multi-Objective Optimization of Friction Stir Processing Tool with Composite Material Parameters. Lubricants 2024, 12, 428. [Google Scholar] [CrossRef]
- He, J.; Xu, Y.; Pan, Y.; Wang, Y. Adaptie weighted generative adversarial network with attention mechanism: A transfer data augmentation method for tool wear prediction. Mech. Syst. Signal Process. 2024, 212, 111288. [Google Scholar] [CrossRef]
- Zhu, K.; Huang, C.; Li, S.; Lin, X. Physics-informed Gaussian process for tool wear prediction. ISA Trans. 2023, 143, 548–556. [Google Scholar] [CrossRef]
- Wu, X.; Zhang, C.; Li, Y.; Huang, W.Z.; Zeng, K.; Shen, J.Y.; Zhu, L.F. Researches on tool wear progress in mill-grinding based on the cutting force and acceleration signal. Measurement 2023, 218, 12. [Google Scholar] [CrossRef]
- Hao, Z.; Zhang, H.; Fan, Y. Tool wear mathematical model of PCD during ultrasonic elliptic vibration cutting SiCp/Al composite. Int. J. Refract. Met. Hard Mater. 2025, 126, 106967. [Google Scholar] [CrossRef]
- Liang, Y.; Feng, P.; Song, Z.; Zhu, S.; Wang, T.; Xu, J.; Yue, Q.; Jiang, E.; Ma, Y.; Song, G.; et al. Wear mechanisms of straight blade tool by dual-periodic impact platform. Int. J. Mech. Sci. 2025, 288, 110031. [Google Scholar] [CrossRef]
- Lin, Z.; Fan, Y.; Tan, J.; Li, Z.; Yang, P.; Wang, H.; Duan, W. Tool wear prediction based on XGBoost feature selection combined with PSO-BP network. Sci. Rep. 2025, 15, 3096. [Google Scholar] [CrossRef]
- Song, C.; Xiang, D.; Yuan, Z.; Zhang, Z.; Yang, S.; Gao, G.; Tong, J.; Wang, X.; Cui, X. Two-dimensional ultrasonic-assisted variable cutting depth scratch force model considering tool wear and experimental verification. Tribol. Int. 2025, 204, 110510. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, S.; Zhang, P.; Long, H.; Sun, Y.; Zhao, N.; Yang, X. The pin tool wear identification with vibration signal of friction stir lap welding based on a new pin tool wear division model. Measurement 2025, 242, 116131. [Google Scholar] [CrossRef]
- Wang, S.; Yu, Z.; Xu, G.; Zhao, F. Research on Tool Remaining Life Prediction Method Based on CNN-LSTM-PSO. IEEE Access 2023, 11, 80448–80464. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, C.; Huang, X.; Ding, P.; Li, Y. Cutting tool remaining useful life prediction based on robust empirical mode decomposition and Capsule-BiLSTM network. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2023, 237, 3308–3323. [Google Scholar] [CrossRef]
- Yang, Z.; Li, L.; Zhang, Y.; Jiang, Z.; Liu, X. Tool Wear State Monitoring in Titanium Alloy Milling Based on Wavelet Packet and TTAO-CNN-BiLSTM-AM. Processes 2025, 13, 13. [Google Scholar] [CrossRef]
- Demetgul, M.; Zheng, Q.; Tansel, I.; Fleischer, J. Monitoring the misalignment of machine tools with autoencoders after they are trained with transfer learning data. Int. J. Adv. Manuf. Technol. 2023, 128, 3357–3373. [Google Scholar] [CrossRef]







| Parameter | Settings | Initial Value/Range |
|---|---|---|
| CNN Part | Size of the first layer filter | [3, 3] (the spatial scale for capturing local features) |
| Number of first-layer filters | 16 (extracting 16 types of local features) | |
| First layer stride | 1 (controlling the sliding step size of the convolution kernel) | |
| First layer padding mode | ‘same’ (keeping the size of the feature map unchanged) | |
| Size of the second-layer filter | [5, 5] (capturing spatial features in a larger range) | |
| Number of second-layer filters | 32 (extracting 32 types of local features with higher feature dimensions) | |
| Second-layer stride | 1 | |
| Second-layer padding mode | ‘same’ | |
| BiLSTM Part | Pooling layer type | MaxPooling1D (dimensionality reduction and extraction of main features) |
| Pooling kernel size | 2 | |
| Pooling layer stride | 2 | |
| Number of neurons in the first layer | initial 30, optimization range [32, 128] | |
| First layer dropout rate | 0.2 (suppressing overfitting) | |
| First-layer recurrent dropout rate | 0.2 (dropout in recurrent connections) | |
| Number of neurons in the second layer | initial 30, optimization range [64, 256] | |
| Second-layer dropout rate | 0.2 | |
| Second-layer recurrent dropout rate | 0.2 | |
| Number of neurons in the third layer | initial 30, optimization range [64, 256] | |
| Third-layer dropout rate | 0.2 | |
| Third-layer recurrent dropout rate | 0.2 | |
| AM | Number of attention heads | initial 4, optimization range [2, 8] (number of parallel feature interaction groups) |
| Attention dimension | initial 128, optimization range [64, 256] (feature mapping dimension) | |
| Attention calculation method | Scaled Dot-Product Attention | |
| Attention weight initialization | Xavier initialization | |
| Normalization layer | Normalization type | Layer Normalization (accelerates training stability) |
| Normalization parameter | (prevents numerical instability) | |
| Output layer | Activation function | Linear activation (predicting continuous values for regression tasks) |
| Output dimension | 1 (predicting tool wear amount with a single value) |
| Parameter | Value |
|---|---|
| Spindle | 10,400 (r/min) |
| Feed rate | 1555 (mm/min) |
| Depth of cut (y direction, radial) | 0.125 (mm) |
| Depth of cut (z direction, axial) | 0.2 (mm) |
| Sampling rate | 50 (kHz) |
| Workpiece material | Stainless steel (HRC52) |
| Equipment Name | Equipment Model | Equipment Parameters |
|---|---|---|
| Data Acquisition Card | INV3062C (Beijing Orient Vibration and Noise Technology Institute, Beijing, China) | Frequency range: 0~20 KHz; Resolution: 24 bits; Number of channels: 8 |
| Three-axis Vibration Sensor | INV9832 (Beijing Orient Vibration and Noise Technology Institute, Beijing, China) | Frequency range: 1–10 KHz; Sensitivity: 100 mV/g |
| Hall Current Sensor | CHK-100R1 (Changzhou Huaguan Sensor Co., Ltd., Changzhou, China) | Frequency range: 20 Hz~20 KHz; Sensitivity: 50 mV/g |
| Acoustic Emission Sensor | PXR 15RMH (Physical Acoustics Corporation, Princeton, NJ, USA) | Frequency range: 0~20 KHz |
| Cutting Tool | Stabila 4-flute End Mill(Stabila GmbH, Bremen, Germany) | Material: Tungsten steel |
| Cutting Material | 45 Steel | Dimensions:15 cm × 10 cm × 10 cm |
| Equipment Name | Equipment Model |
|---|---|
| Feed Rate | 1200 (mm/min) |
| Tool Rotational Speed | 8000 (r/min) |
| Axial Depth of Cut | 5 mm |
| Radial Depth of Cut | 0.5 mm |
| Sampling Frequency | 20 kHz |
| Single Sampling Time | 17 s |
| Channel | Signal |
|---|---|
| Channel 1 | Fx: Vibration signal in X-axis (g) |
| Channel 2 | Fy: Vibration signal in Y-axis (g) |
| Channel 3 | Fz: Vibration signal in Z-axis (g) |
| Channel 4 | Current in U direction (A) |
| Channel 5 | Current in V direction (A) |
| Channel 6 | A3: Current in W direction (A) |
| Channel 7 | AE(N) AE: Acoustic emission signal AE (N) |
| Configuration | Information |
|---|---|
| CPU | 11th Gen Intel(R) Core(TM) i7-11800H @ 2.30GHz (2.30 GHz) |
| Graphics card | NVIDIA GeForce RTX 3060 Laptop GPU |
| Operating system | 64 bit Windows 11 |
| Development environment | Pytorch 2.10 |
| python | Version = 3.10 |
| CUDA | 12.0 |
| Configuration | Information |
| Training Set | Test Set |
|---|---|
| C1 + C4 | C6 |
| C1 + C6 | C4 |
| Parameter | Parameter Name | Value |
|---|---|---|
| Optimization algorithm parameters | Learning rate | 0.01/[0.001, 0.1] |
| Number of CPSO particles | 30 | |
| Inertia weight | 0.1 | |
| Training parameters | Number of model iterations | 200 |
| Regularization parameters | Regularization coefficient | 0.01/[0.001, 0.01] |
| Attention mechanism | Number of attention heads | 4/[2, 8] |
| Module | C1 | C4 | C6 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | |
| LSTM [5] | 13.32 | 12.89 | 13.52 | 12.52 | 13.11 | 12.09 | 14.40 | 15.01 | 15.76 |
| PSO-CNN [40] | 11.46 | 11.31 | 11.58 | 11.21 | 11.92 | 11.67 | 12.09 | 12.81 | 13.57 |
| PSO-BiLSTM [41] | 9.21 | 9.82 | 9.41 | 9.29 | 8.16 | 9.37 | 9.47 | 9.51 | 8.04 |
| CNN-BiLSTM-AM [42] | 5.41 | 5.58 | 4.28 | 5.81 | 4.84 | 5.53 | 4.25 | 5.17 | 5.75 |
| VAE-CNN-LSTM [43] | 1.39 | 1.96 | 1.56 | 2.01 | 2.37 | 2.11 | 2.01 | 1.90 | 1.83 |
| PSO-CNN–BiLSTM-AM | 3.13 | 3.41 | 3.94 | 3.52 | 2.96 | 3.47 | 2.47 | 3.71 | 3.54 |
| CPSO-CNN-BiLSTM-AM | 0.83 | 0.99 | 0.95 | 1.01 | 1.79 | 1.41 | 1.34 | 0.88 | 1.01 |
| Module | A1 | A2 | A3 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | |
| LSTM [5] | 16.31 | 16.42 | 16.49 | 16.33 | 17.85 | 16.35 | 18.58 | 18.31 | 16.51 |
| PSO-CNN [40] | 14.31 | 14.29 | 14.90 | 14.31 | 15.85 | 14.27 | 14.79 | 14.26 | 14.61 |
| PSO-BiLSTM [41] | 10.51 | 10.81 | 10.51 | 10.85 | 10.65 | 10.25 | 11.57 | 11.18 | 10.39 |
| CNN-BiLSTM-AM [42] | 4.14 | 4.47 | 4.25 | 4.61 | 4.82 | 4.68 | 4.49 | 6.48 | 5.21 |
| VAE-CNN-LSTM [43] | 4.01 | 4.64 | 4.27 | 5.41 | 4.26 | 4.18 | 4.68 | 6.01 | 4.85 |
| PSO-CNN–BiLSTM-AM | 2.46 | 3.13 | 2.79 | 3.14 | 3.51 | 3.52 | 3.25 | 2.59 | 3.01 |
| CPSO-CNN-BiLSTM-AM | 1.35 | 1.41 | 1.67 | 1.19 | 1.98 | 1.55 | 1.83 | 1.90 | 1.81 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, F.; Yang, Z.; Zhang, H.; Sun, W. Intelligent Tool Wear Prediction Using CNN-BiLSTM-AM Based on Chaotic Particle Swarm Optimization (CPSO) Hyperparameter Optimization. Lubricants 2025, 13, 500. https://doi.org/10.3390/lubricants13110500
Ma F, Yang Z, Zhang H, Sun W. Intelligent Tool Wear Prediction Using CNN-BiLSTM-AM Based on Chaotic Particle Swarm Optimization (CPSO) Hyperparameter Optimization. Lubricants. 2025; 13(11):500. https://doi.org/10.3390/lubricants13110500
Chicago/Turabian StyleMa, Fei, Zhengze Yang, Hepeng Zhang, and Weiwei Sun. 2025. "Intelligent Tool Wear Prediction Using CNN-BiLSTM-AM Based on Chaotic Particle Swarm Optimization (CPSO) Hyperparameter Optimization" Lubricants 13, no. 11: 500. https://doi.org/10.3390/lubricants13110500
APA StyleMa, F., Yang, Z., Zhang, H., & Sun, W. (2025). Intelligent Tool Wear Prediction Using CNN-BiLSTM-AM Based on Chaotic Particle Swarm Optimization (CPSO) Hyperparameter Optimization. Lubricants, 13(11), 500. https://doi.org/10.3390/lubricants13110500





