Thermal Tribo-Dynamic Behaviors of Water-Lubricated Bearings during Start-Up with Journal Shape Error
Abstract
1. Introduction
2. Mathematic Model
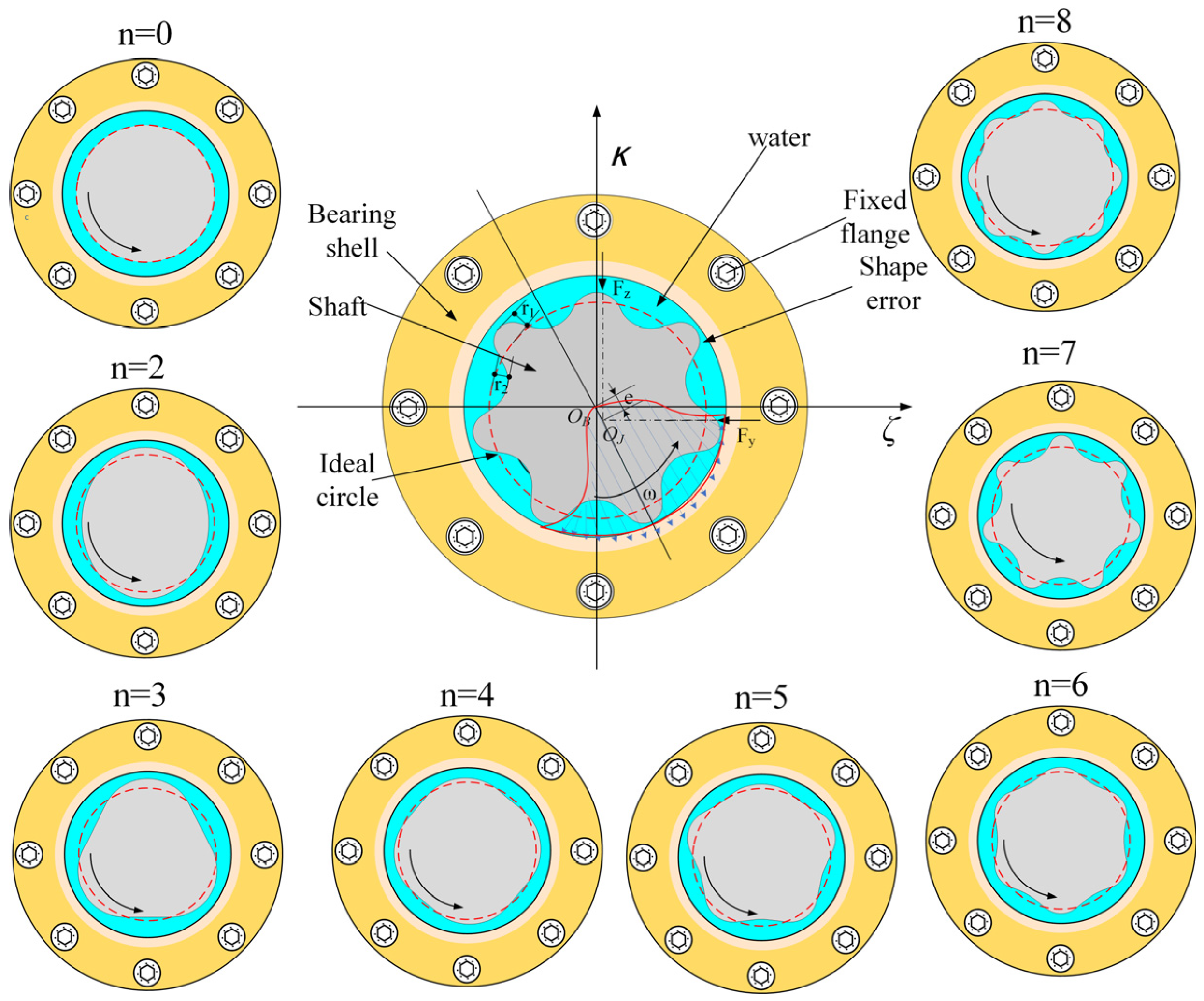
2.1. Transient Lubrication Gap
2.2. Dynamic Equations
2.3. Transient Hydrodynamic Model
2.3.1. Transient Reynolds Equation
2.3.2. Hydrodynamic Forces
2.4. 3D Thermal Model
2.5. Transient Contact Model
2.5.1. Transient Asperity Contact
2.5.2. Contact Forces
2.6. Transient Deformation
2.7. Transient Friction Forces
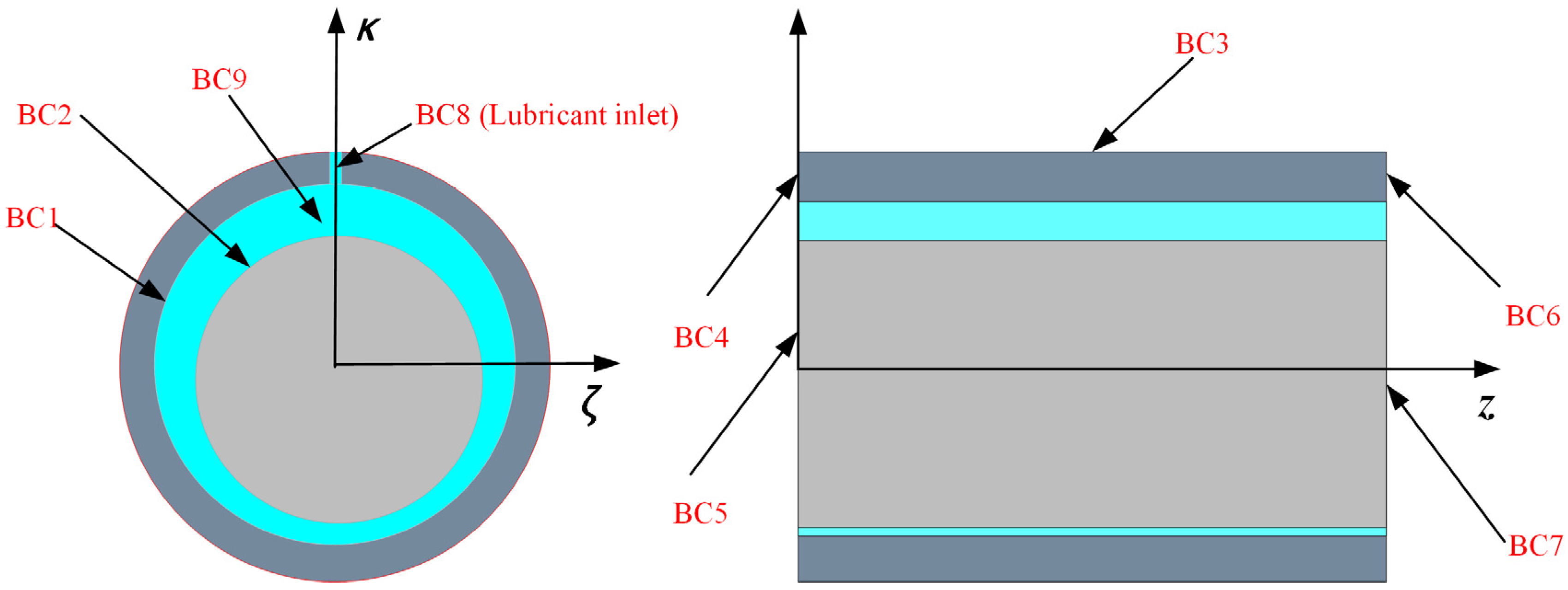
2.8. Boundary Conditions
2.8.1. Thermal Boundary
- (a)
- Internal heat exchange boundary conditions (BC1-BC2);
- (b)
- External heat exchange boundary conditions (BC3-BC8);
- (c)
- Cavitation boundary conditions.
2.8.2. Cavitation Boundary
3. Numerical Schemes
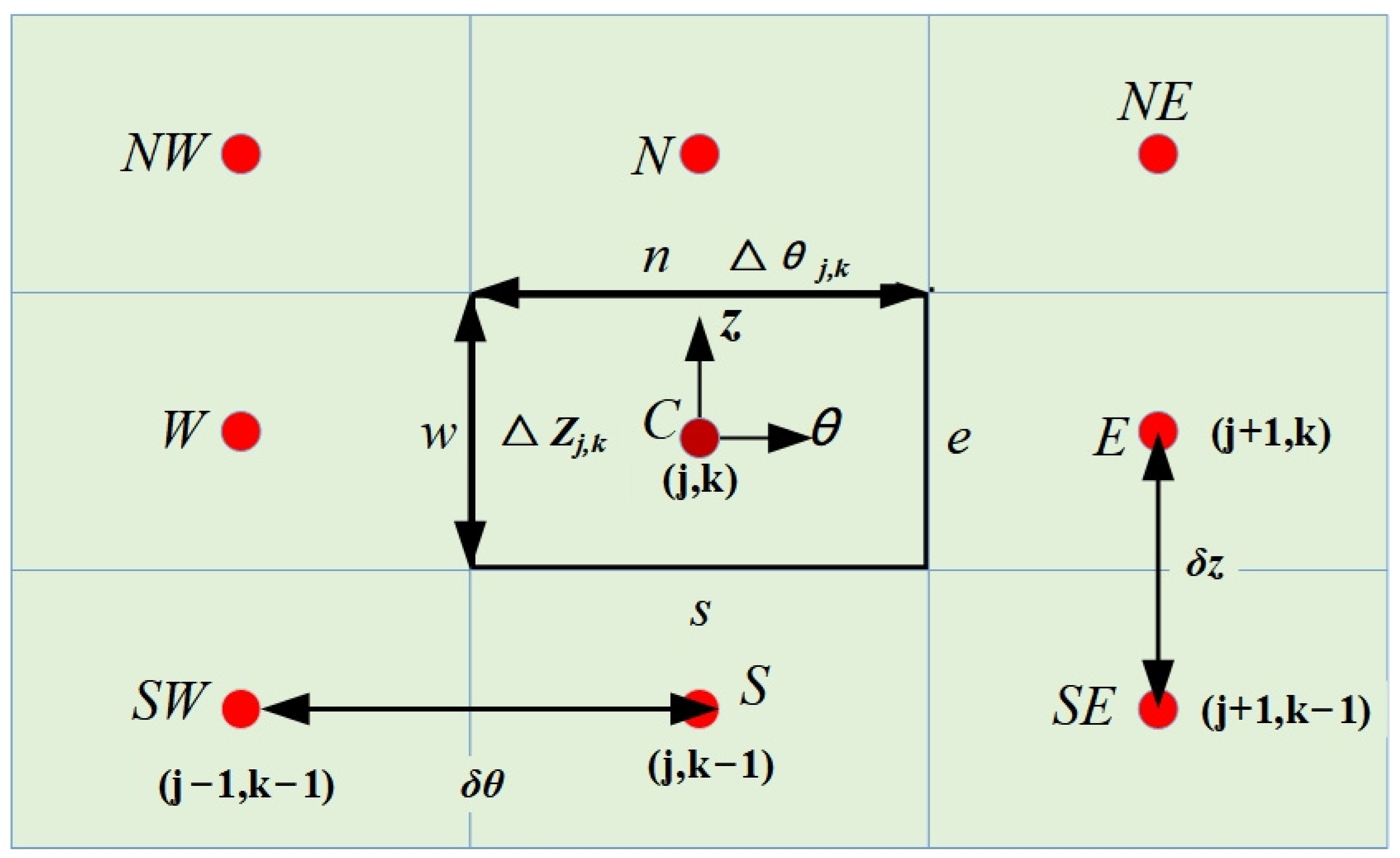
3.1. Numerical Scheme of the Reynolds Equation
3.2. Numerical Scheme of the Dynamic Equation
4. Results and Discussion
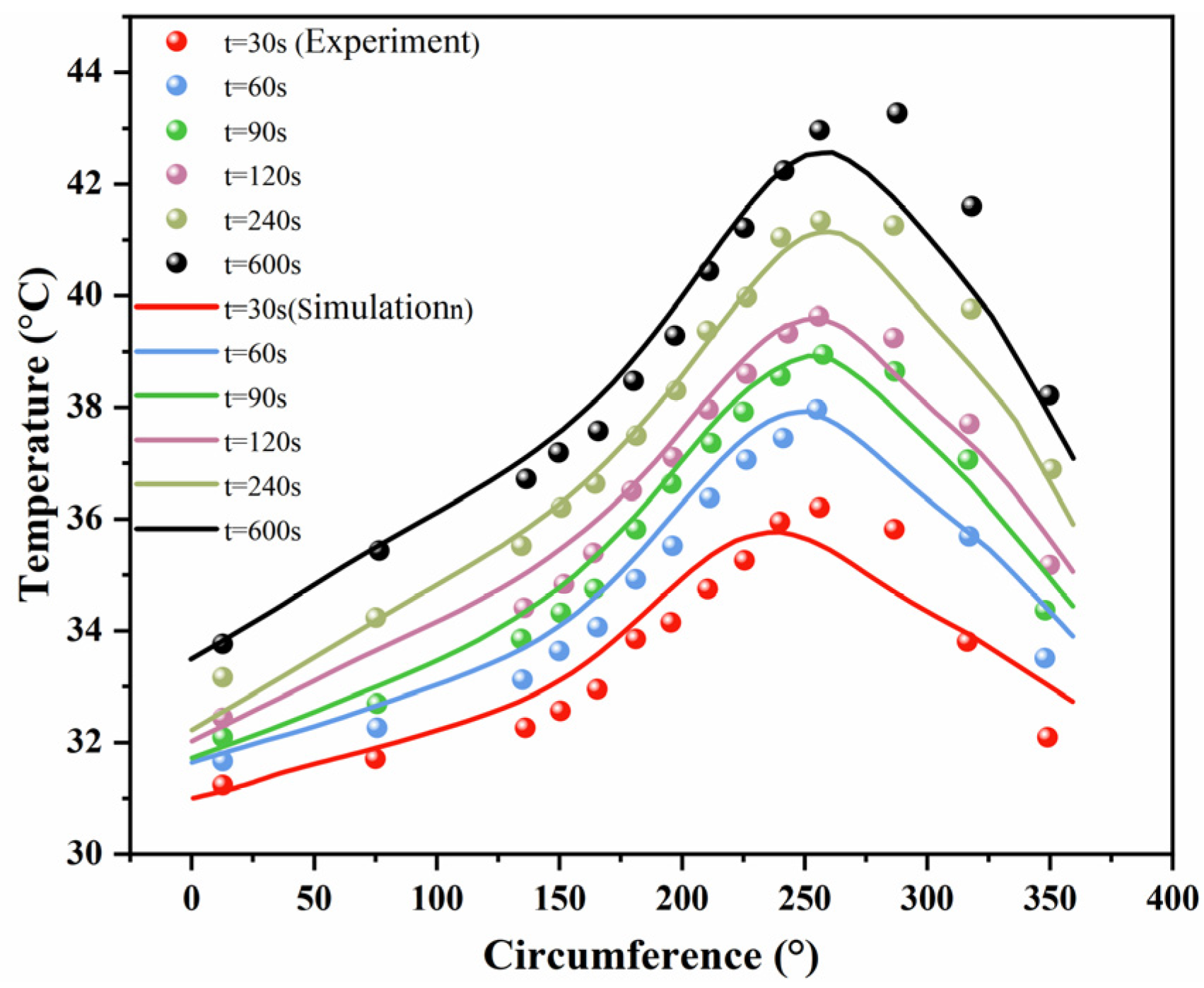
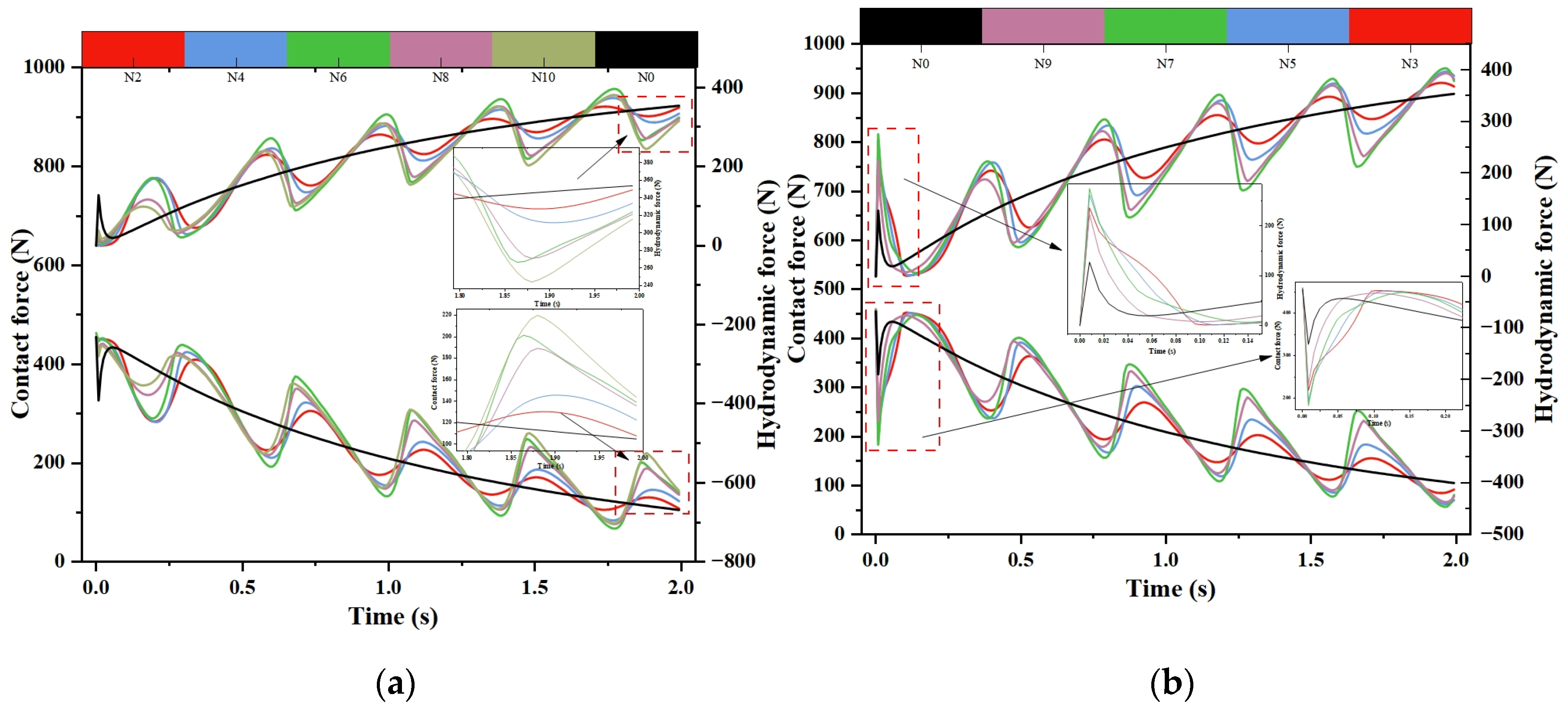
4.1. Verification of Present Model
4.2. Setting of Simulation Parameters
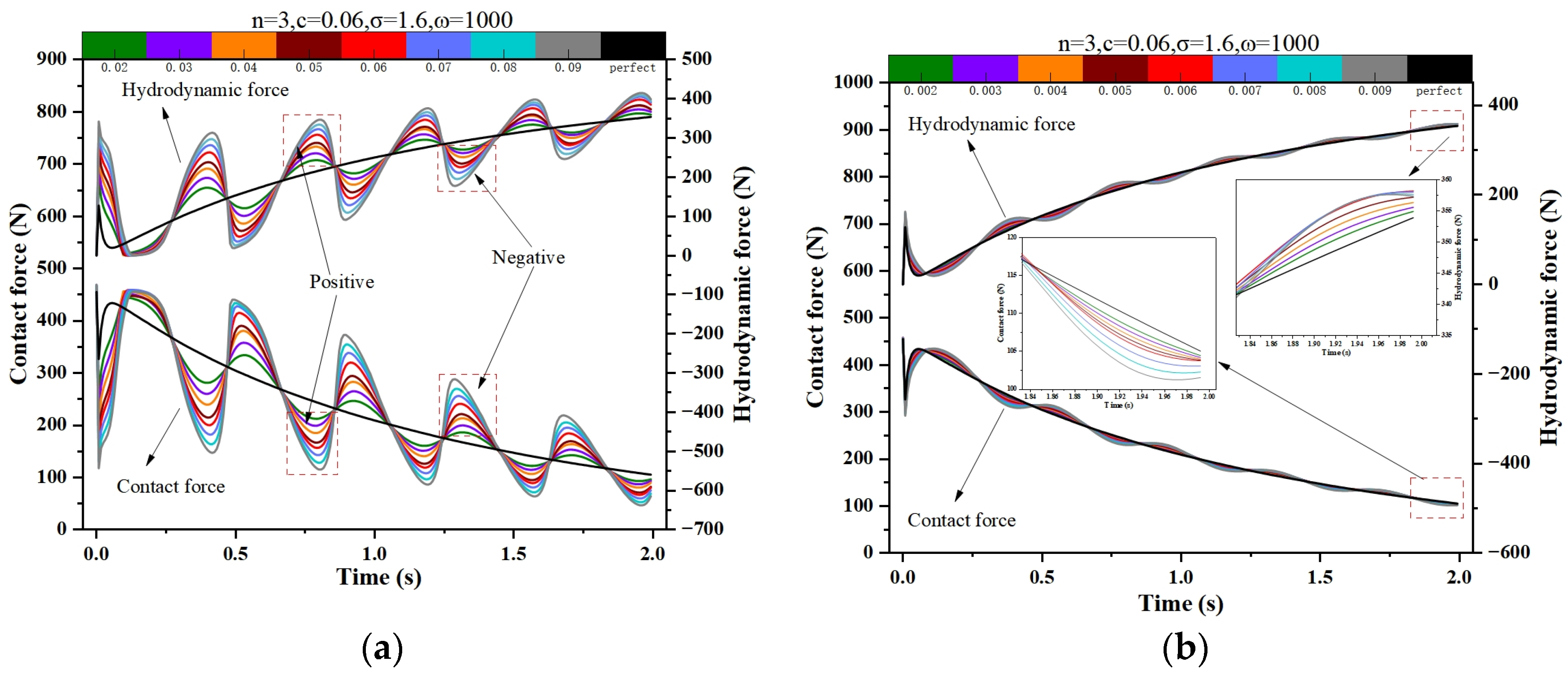
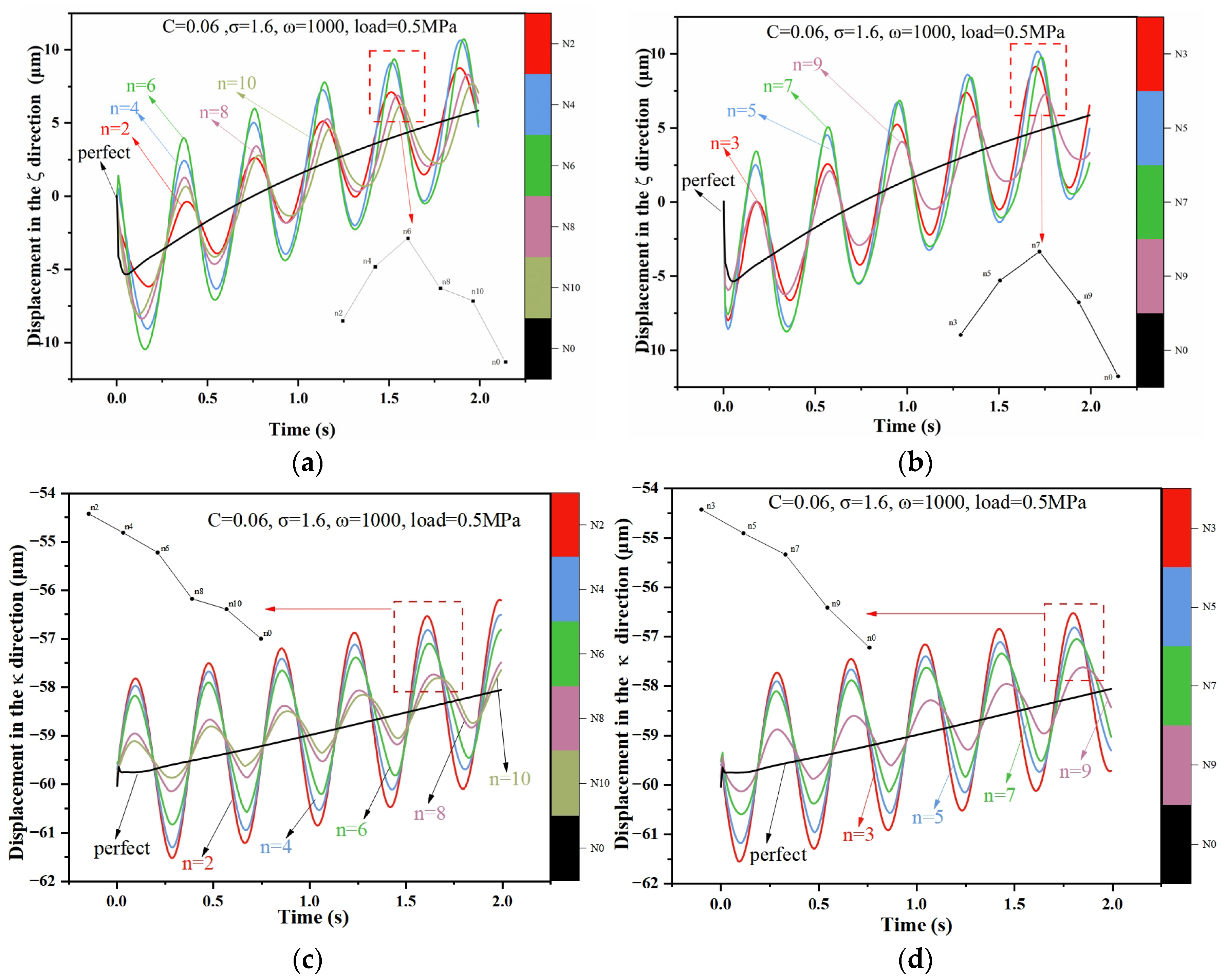
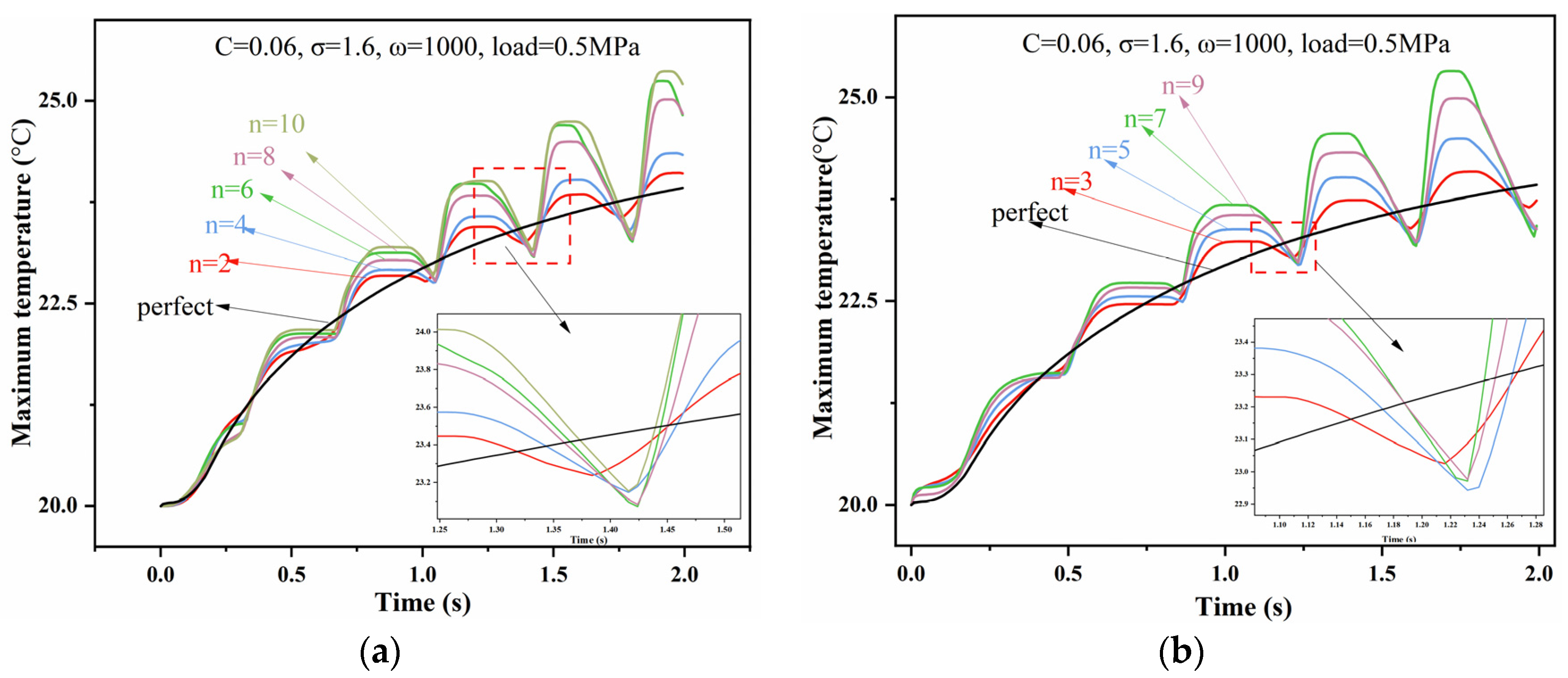
4.3. Effect of Different Journal Shape Error Amplitude
4.4. Effect of Different Journal Shape Error Waviness Orders
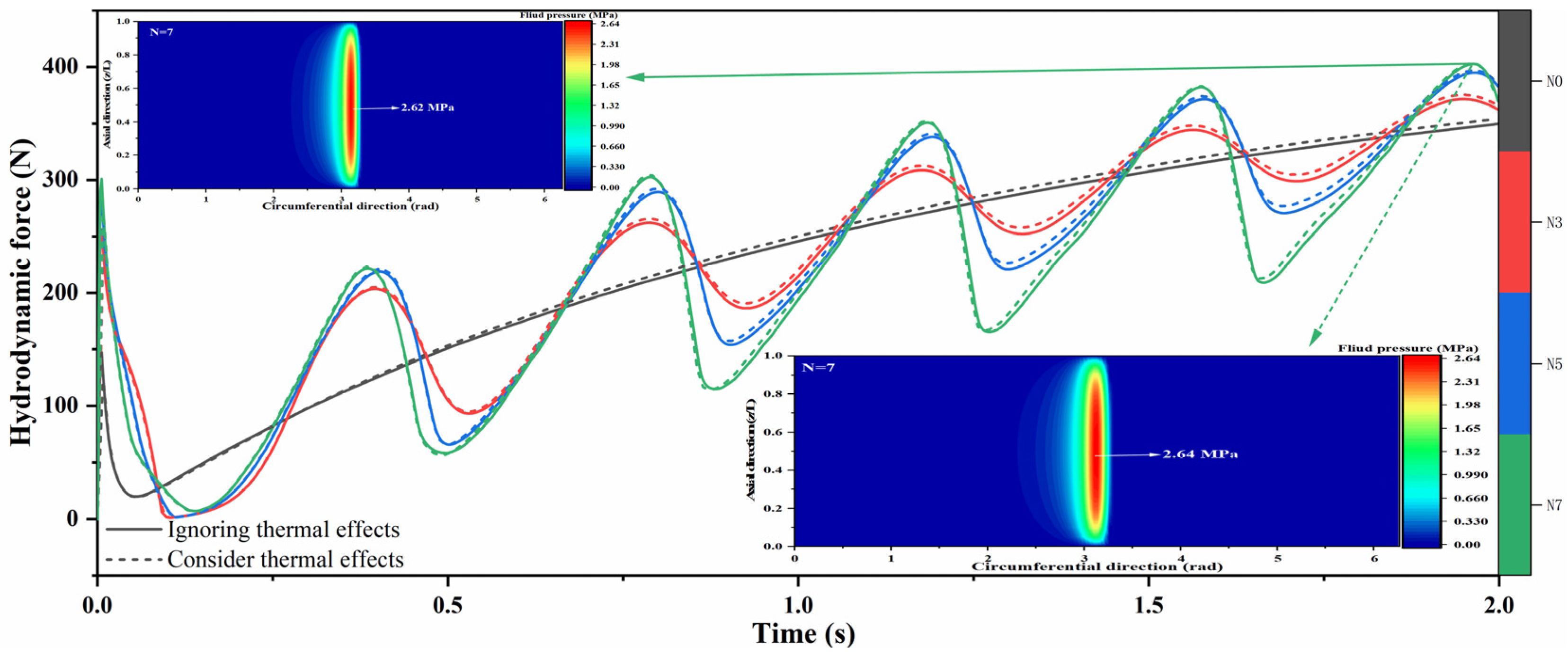
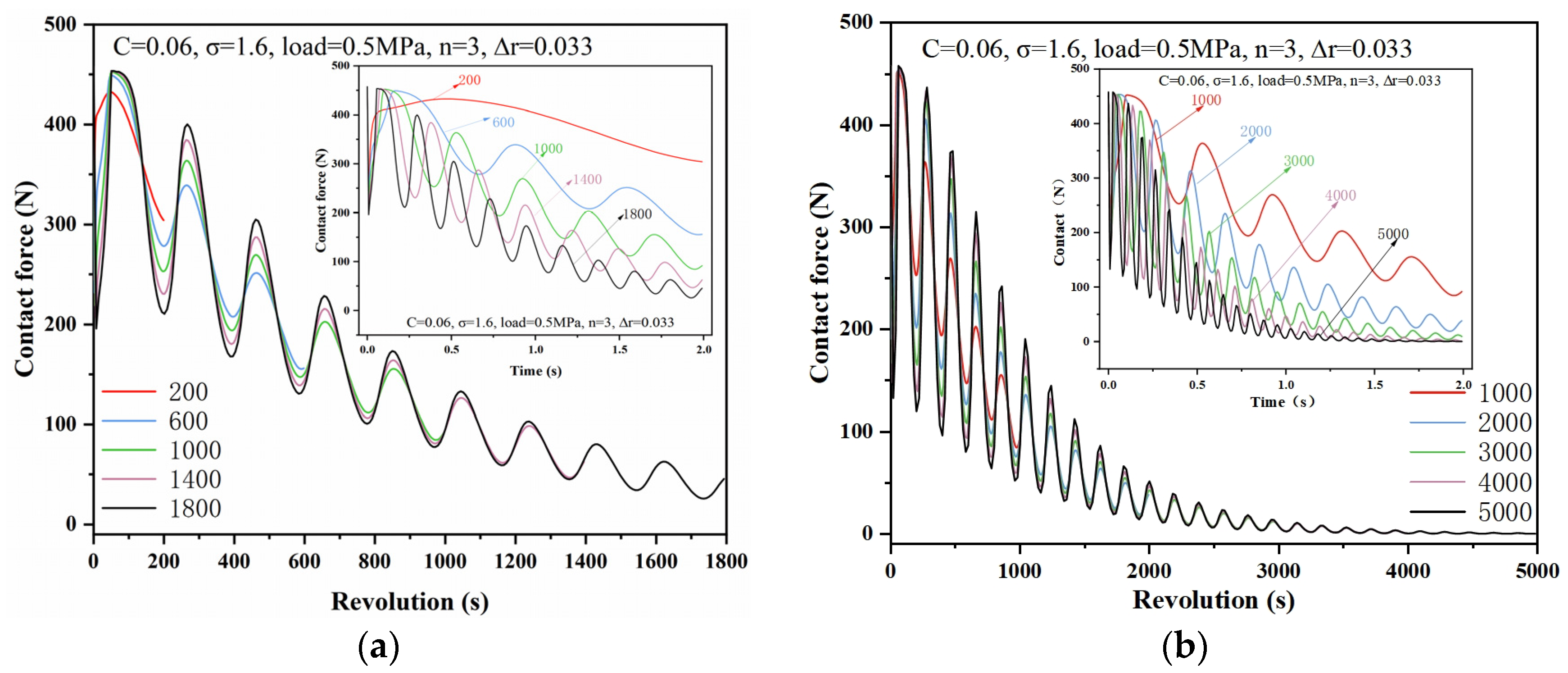
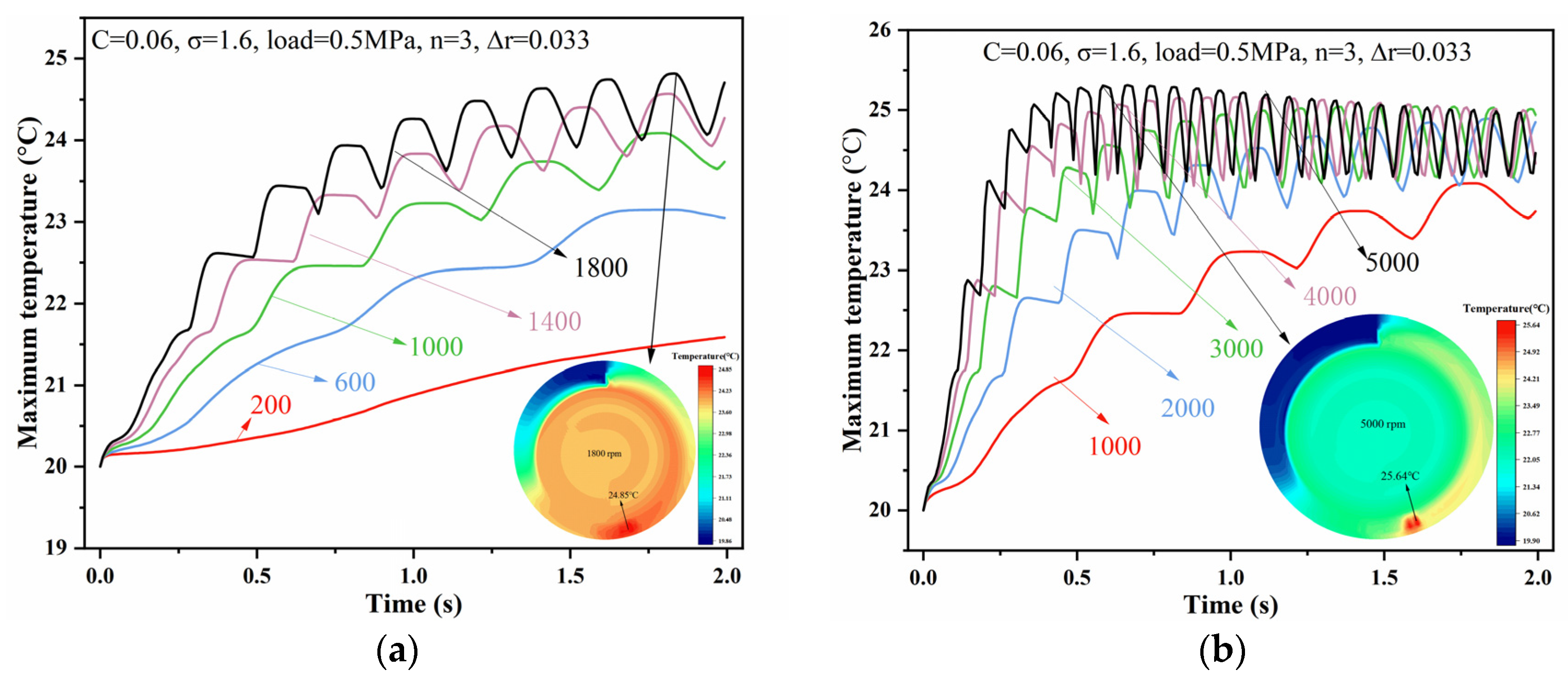
4.5. Effect of Different Starting Speeds on Bearing Performance
5. Conclusions
- (1)
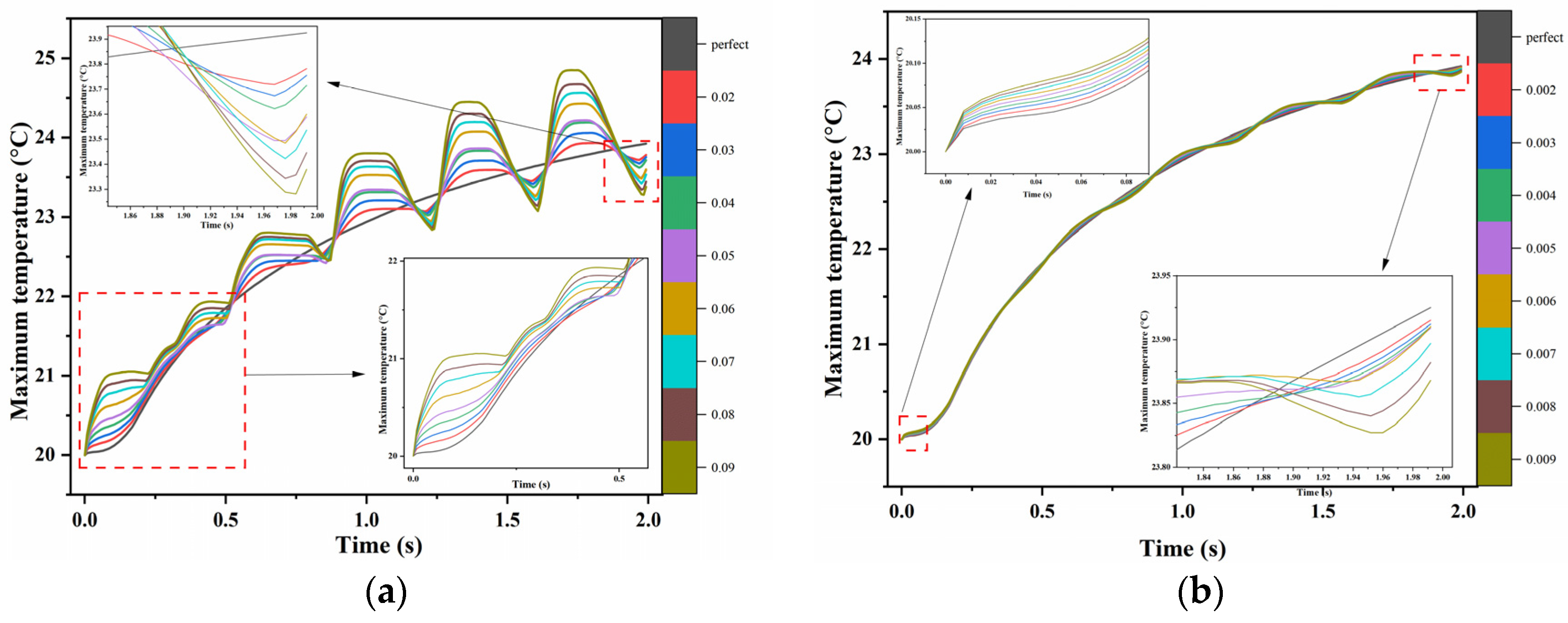
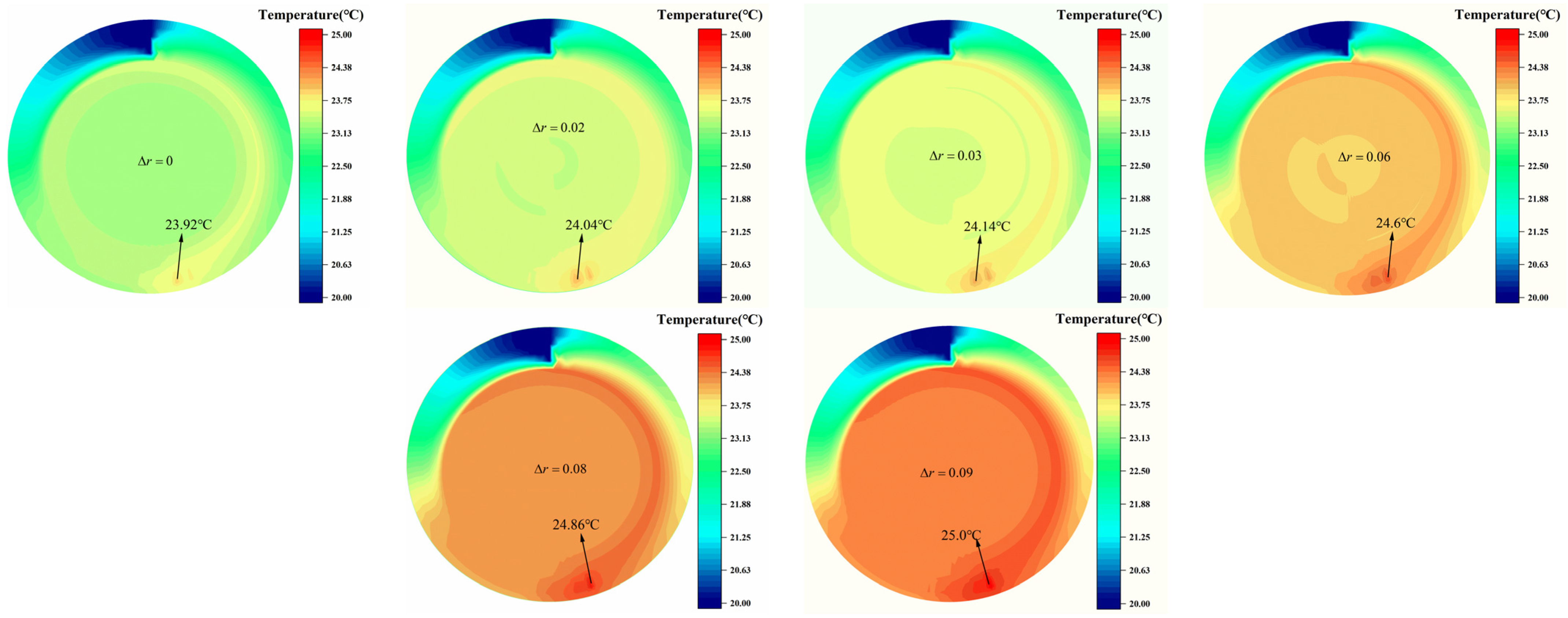
- The greater the amplitude of the journal shape error, the more pronounced the temperature increase during start-up and the greater the fluctuation in lubrication performance. The location of the maximum temperature during the bearing’s start-up state remains unaffected by changes in error amplitude. Temperature changes are not significant when the amplitude of the shape error is less than 9‰ of the bearing radius clearance.
- (2)
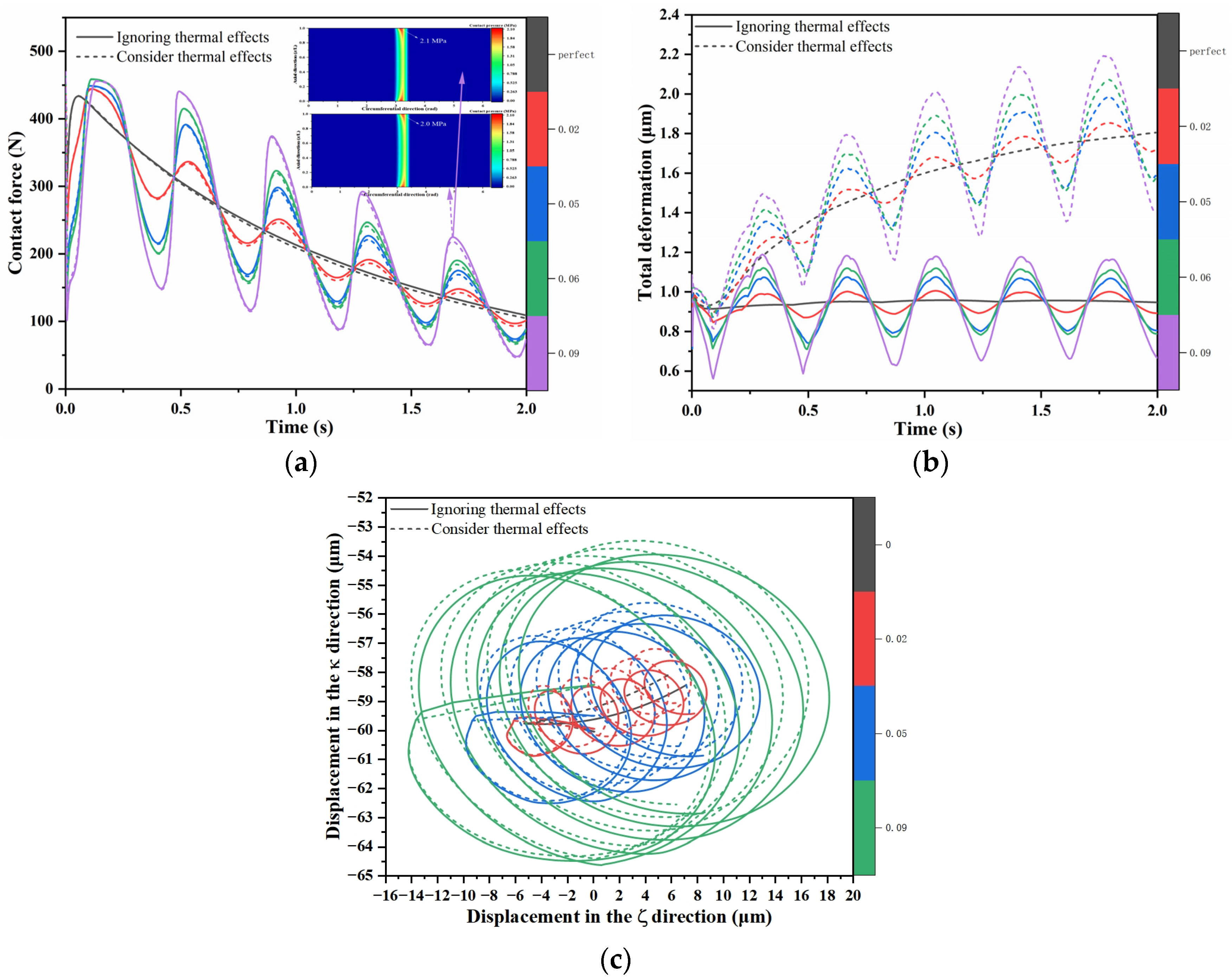
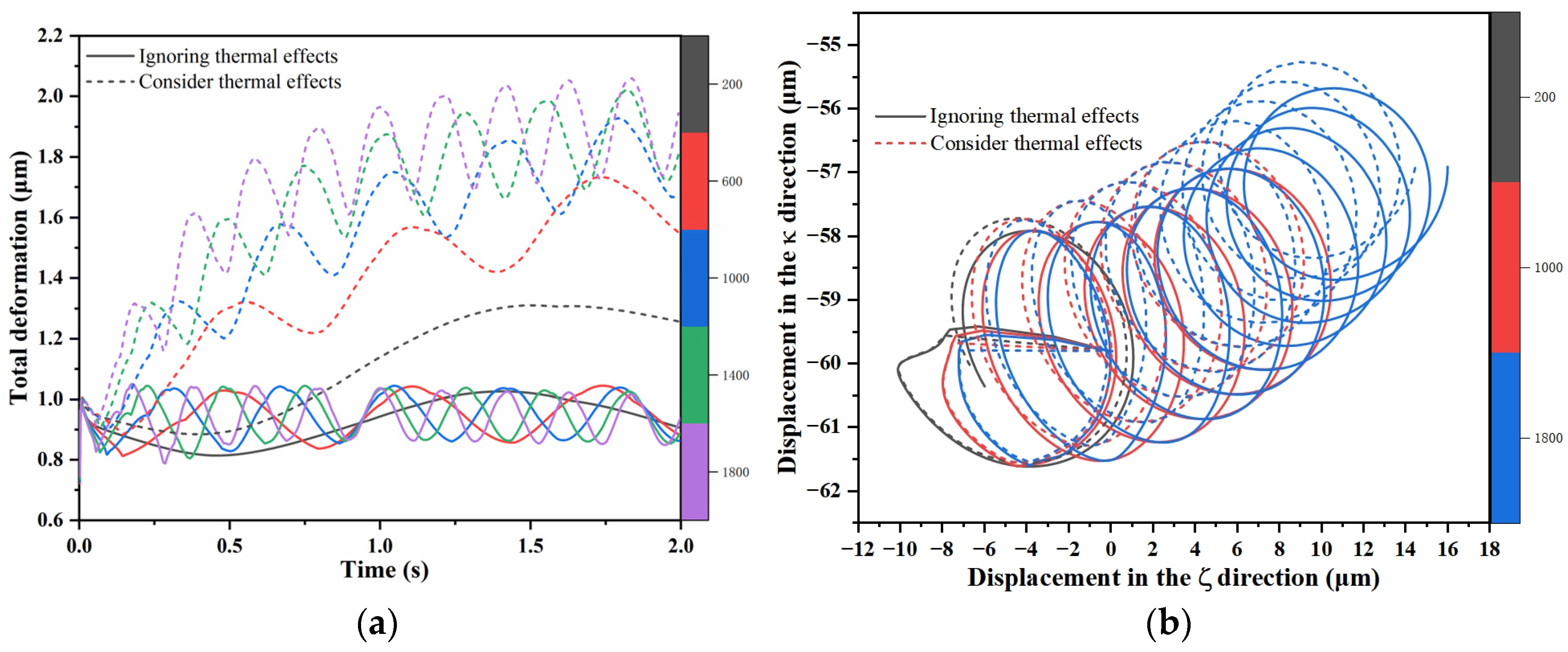
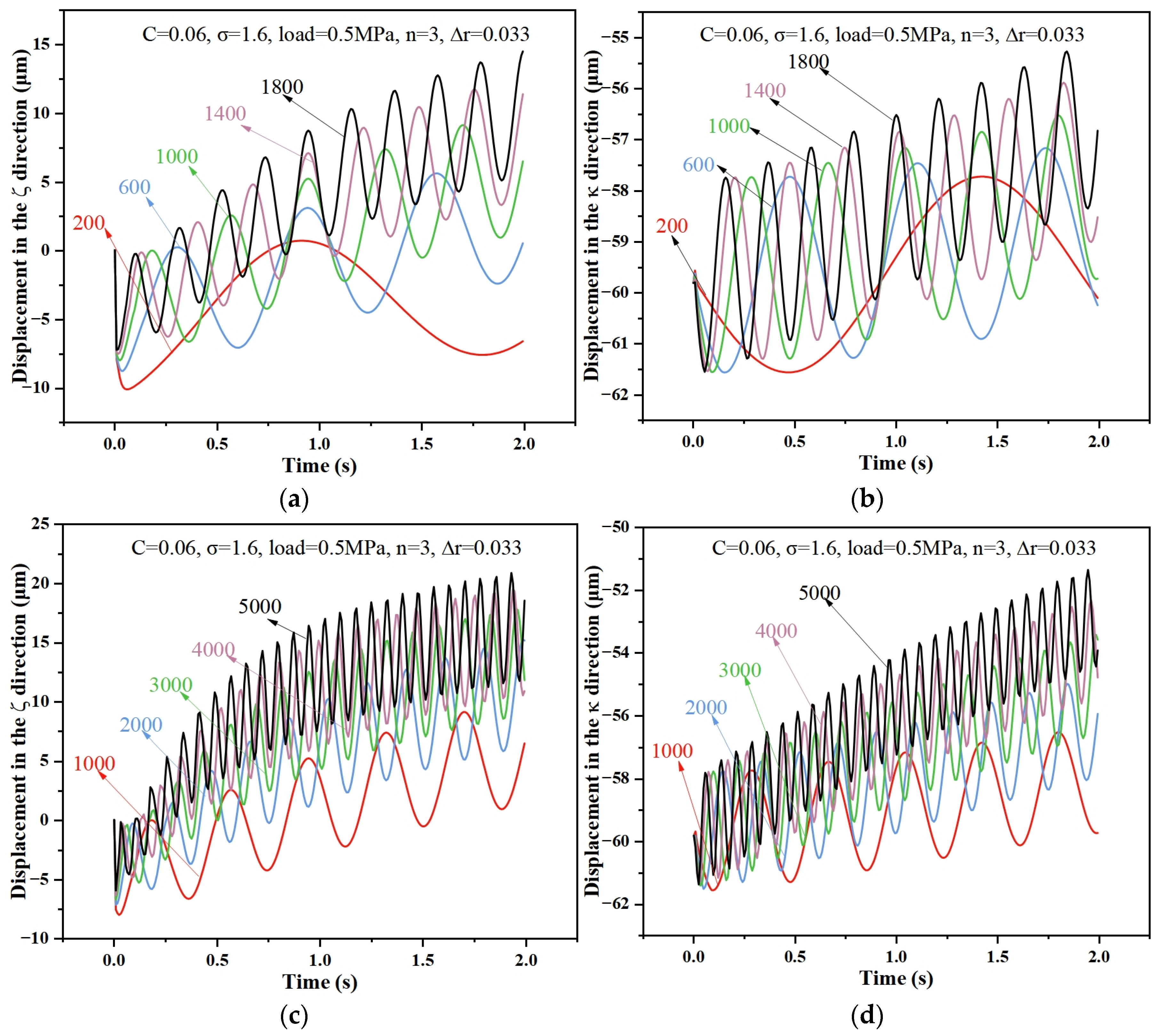
- The temperature effect reduces the displacement in the vertical direction during the start-up state of the WLB, which is more significant at higher waviness orders of journal shape error.
- (3)
- The higher the starting speed of the bearing, the easier it is to reach the EHL state, but the temperature rise becomes faster and the shaft track becomes larger. And when the speed is lower, although the temperature is lower, the friction and contact force are greater, so one must be careful when choosing the starting speed.
- (4)
- The neglect of thermal effects leads to an underestimation of the hydrodynamic effect during the startup of WLBs with journal shape errors, resulting in errors in the prediction of the friction dynamics behavior.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Z.H.; Wang, F.; Wu, X.Y.; Li, C.P. The Influence of Structure Parameters on the Dynamic Pressure Effect of Water-lubricated Journal Bearing. Hydraul. Pneum. Seal. 2019, 39, 9–14. [Google Scholar]
- Xiang, G.; Han, Y.F. Study on the tribo-dynamic performances of water-lubricated microgroove bearings during start-up. Tribol. Int. 2020, 151, 106395. [Google Scholar] [CrossRef]
- Du, Y.Y.; Li, M. Effects on lubrication characteristics of water-lubricated rubber bearings with journal tilting and surface roughness. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2020, 234, 161–171. [Google Scholar] [CrossRef]
- Xie, Z.L.; Jiao, J.; Yang, K.; Zhang, H. A state-of-art review on the water-lubricated bearing. Tribol. Int. 2023, 180, 108276. [Google Scholar] [CrossRef]
- Mokhtar, M.O.A.; Howarth, R.B.; Davies, P.B. Wear characteristics of plain hydrodynamic journal bearings during repeated starting and stopping. Tribol. Trans. 1977, 20, 191–194. [Google Scholar] [CrossRef]
- Mokhtar, M.O.A.; Howarth, R.B.; Davies, P.B. The behavior of plain hydrodynamic journal bearings during starting and stopping. Tribol. Trans. 1977, 20, 183–190. [Google Scholar] [CrossRef]
- Monmousseau, P.; Fillon, M. Transient thermoelastohydrodynamic analysis for safe operating conditions of a tilting-pad journal bearing during start-up. Tribol. Int. 2000, 33, 225–231. [Google Scholar] [CrossRef]
- Cristea, A.F.; Bouyer, J.; Fillon, M. Transient pressure and temperature field measurements in a lightly loaded circumferential groove journal bearing from startup to steady-state thermal stabilization. Tribol. Trans. 2017, 60, 988–1010. [Google Scholar] [CrossRef]
- Krupka, I.; Svoboda, P.; Hartl, M. Effect of surface topography on mixed lubrication film formation during start up under rolling/sliding conditions. Tribol. Int. 2010, 43, 1035–1042. [Google Scholar] [CrossRef]
- Cui, S.H.; Gu, L.; Fillon, M. The effects of surface roughness on the transient characteristics of hydrodynamic cylindrical bearings during startup. Tribol. Int. 2018, 128, 421–428. [Google Scholar] [CrossRef]
- Cui, S.H.; Gu, L.; Wang, L.Q. Numerical analysis on the dynamic contact behavior of hydrodynamic journal bearings during start-up. Tribol. Int. 2018, 121, 260–268. [Google Scholar] [CrossRef]
- Patir, N.; Cheng, H.S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication. J Tribol. 1978, 100, 12–17. [Google Scholar] [CrossRef]
- Greenwood, J.; Tripp, J. The contact of two nominally flat rough surfaces. Proc. Inst. Mech. Eng. 1970, 185, 625–633. [Google Scholar] [CrossRef]
- Xiang, G.; Han, Y.F.; He, T.; Wang, J.X.; Xiao, K.; Li, J.Y. Transient tribo-dynamic model for journal bearings during start-up considering 3D thermal characteristic. Tribol. Int. 2020, 144, 106123. [Google Scholar] [CrossRef]
- Xiang, G.; Wang, C.; Wang, Y.J.; Han, Y.F.; Wang, J.X.; Lv, Z.L. Dynamic Mixed Lubrication Investigation of Water lubricated Bearing with Unbalance Rotor During Start-up. Tribol. Trans. 2021, 64, 764–776. [Google Scholar] [CrossRef]
- Xiang, G.; Yang, T.Y.; Guo, J.; Wang, J.X. Optimization transient wear and contact performances of water-lubricated bearings under fluid-solid-thermal coupling condition using profile modification. Wear 2022, 502–503, 204379. [Google Scholar] [CrossRef]
- Song, M.; Azam, S.; Jang, J.; Park, S.S. Effect of Shape Errors on the Stability of Externally Pressurized Air Journal Bearings Using Semi-Implicit Scheme. Tribol. Int. 2017, 115, 580–590. [Google Scholar] [CrossRef]
- Zhang, H.; Ding, J.G.; Peng, C.; Chang, Y.; Zeng, X.Y.; Yang, H.; Liu, X.B.; Wei, W. Effect of Surface Waviness on the Performances of an Aerostatic Thrust Bearing with Orifice-Type Restrictor. Int. J. Precis. Eng. Manuf. 2021, 22, 1735–1759. [Google Scholar] [CrossRef]
- Cui, H.L.; Wang, Y.; Yue, X.B.; Huang, M.; Wang, W. Effects of Manufacturing Errors on the Static Characteristics of Aerostatic Journal Bearings with Porous Restrictor. Tribol. Int. 2017, 115, 246–260. [Google Scholar] [CrossRef]
- Lee, S.M.; Lee, D.W.; Ha, Y.H.; Lee, S.J.; Hwang, J.H.; Choi, Y.H. A Study on the Influence of Waviness Error to a Hydrostatic Bearing for a Crankshaft Pin Turner. Tribol. Trans. 2013, 56, 1077–1087. [Google Scholar] [CrossRef]
- Rajput, A.K.; Sharma, S.C. Combined Influence of Geometric Imperfections and Misalignment of Journal on the Performance of Four Pocket Hybrid Journal Bearing. Tribol. Int. 2016, 97, 59–70. [Google Scholar] [CrossRef]
- Luboš, S.; Michal, H.; Byrtus, M. Investigation of bearing clearance effects in dynamics of turbochargers. Int. J. Mech. Sci. 2017, 127, 62–72. [Google Scholar]
- Wang, X.; Xu, Q.; Wang, B.; Zhang, L.; Peng, Z. Effect of surface waviness on the static performance of aerostatic journal bearings. Tribol. Int. 2016, 103, 394–405. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Q.; Huang, M.; Zhang, L.; Peng, Z. Effects of journal rotation and surface waviness on the dynamic performance of aerostatic journal bearings. Tribol. Int. 2017, 112, 1–9. [Google Scholar] [CrossRef]
- Cai, J.L.; Hang, Y.F.; Xiang, G.; Wang, J.X.; Wang, L.W. Effects of wear and shaft-shape error defects on the tribo-dynamic response of water-lubricated bearings under propeller disturbance. Phys. Fluids 2022, 34, 077118. [Google Scholar] [CrossRef]
- Pasichnyi, O.O.; Lavrinenko, V.I. The Influence of Circumferential Waviness of the Diamond Wheel Working Surface on the Machined Surface Roughness. J. Superhard Mater. 2019, 41, 278–280. [Google Scholar] [CrossRef]
- Nikolakopoulos, P.; Papadopoulos, C. A study of friction in worn misaligned journal bearings under severe hydrodynamic lubrication. Tribol. Int. 2008, 41, 461–472. [Google Scholar] [CrossRef]
- Tang, D.X.; Xiang, G.; Guo, J.; Cai, J.L.; Yang, T.Y.; Wang, J.X.; Han, Y.F. On the optimal design of staved water-lubricated bearings driven by tribo-dynamic mechanism. Phys. Fluids 2023, 35, 093611. [Google Scholar] [CrossRef]
- Guo, J.; Ding, B.; Wang, Y.F.; Han, Y.F. Co-optimization for hydrodynamic lubrication and leakage of V-shape textured bearings via linear weighting summation. Phys. Scr. 2023, 98, 125218. [Google Scholar] [CrossRef]
- Sun, F.; Zhang, X.; Wang, Z.; Sun, Z.; Wang, D. Effects of shaft shape errors on the dynamic characteristics of a rotor-bearing system. J. Tribol. 2019, 141, 101701. [Google Scholar] [CrossRef]
- Chen, S.A.; Xiang, G.; Fillon, M.; Guo, J.; Wang, J.X.; Cai, J.L. On the tribo-dynamic behaviors during start-up of water lubricated bearing considering imperfect journal. Tribol. Int. 2022, 174, 107685. [Google Scholar] [CrossRef]
- Khonsari, M.M.; Booser, E.R. Proper film thickness key to bearing survival. Mach. Des. 2006, 78, 100–105. [Google Scholar]
- Yang, T.Y.; Xiang, G.; Cai, J.L.; Wang, L.W.; Lin, X.; Wang, J.X.; Zhou, G.W. Five-DOF nonlinear tribo-dynamic analysis for coupled bearings during start-up. Int. J. Mech. Sci. 2024, 269, 109068. [Google Scholar] [CrossRef]
- Song, Y.K.; Xiao, K.; Xiang, G. Entropy-based fluid–solid–thermal coupled wear prediction of journal bearing during repeated starting and stopping. Wear 2024, 536–537, 205157. [Google Scholar] [CrossRef]
- Kogut, L.; Etsion, I. A finite element based elastic-plastic model for the contact of rough surfaces. Tribol. Trans. 2003, 46, 383–390. [Google Scholar] [CrossRef]
- Tang, D.X.; Xiao, K.; Xiang, G.; Cai, J.L.; Fillon, M.; Wang, D.F.; Su, Z.L. On the nonlinear time-varying mixed lubrication for coupled spiral microgroove water-lubricated bearings with mass conservation cavitation. Tribol. Int. 2024, 193, 109381. [Google Scholar] [CrossRef]
- Beheshti, A.; Khonsari, M. An Engineering Approach for the Prediction of Wear in Mixed Lubricated Contacts. Wear 2013, 308, 121–131. [Google Scholar] [CrossRef]
- Han, Y.F.; Chan, C.; Wang, Z. Effects of Shaft Axial Motion and Misalignment on the Lubrication Performance of Journal Bearings Via a Fast Mixed EHL Computing Technology. Tribol. Trans. 2015, 58, 247–259. [Google Scholar] [CrossRef]
- Wang, Q.; Shi, F.H.; Lee, S.C. A Mixed-TEHD Model for Journal-Bearing Conformal Contact—Part II: Contact, Film Thickness, and Performance Analyses. J. Tribol. 1998, 120, 206–213. [Google Scholar] [CrossRef]
- Vincent, B.; Maspeyrot, P.; Frene, J. Cavitation in Noncircular Journal Bearings. Wear 1997, 207, 122–127. [Google Scholar] [CrossRef]
- Kucinschi, B.R.; Fillon, M.; Fr^ene, J.; Pascovici, M.D. A Transient Thermoelastohydrodynamic Study of Steadily Loaded Plain Journal Bearings Using Finite Element Method Analysis. J. Tribol. 2000, 122, 219–226. [Google Scholar] [CrossRef]
- Cha, M.; Kuznetsov, E.; Glavatskih, S. A comparative linear and nonlinear dynamic analysis of compliant cylindrical journal bearings. Mech. Mach. Theory 2013, 64, 80–92. [Google Scholar] [CrossRef]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Bearing radius | 50 mm | Bearing width | 80 mm |
| Bearing specific heat capacity | 380 J/(kg·K) | Journal specific heat capacity | 490 J/(kg·K) |
| Radius clearance | 0.123 mm | Lubricant specific heatcapacity | 2000 J/(kg·K) |
| Journal thermal expansivity | 12 μm/(m·K) | Bearing thermal expansivity | 17 μm/(m·K) |
| Bearing Poisson ratio | 0.3 | Bearing elastic modulus | 120 GPa |
| Journal elastic modulus | 210 GPa | lubricating temperature | 30 °C |
| Journal Poisson ratio | 0.33 | Lubricant viscosity (30 °C) | 0.05 Pa·s |
| Bearing thermal conductivity | 65 W/m·K | Journal thermal conductivity | 50 W/m·K |
| Bearing density | 8940 kg/m3 | Journal density | 7700 kg/m3 |
| Lubricant thermal conductivity | 0.13 W/m·K | Lubricant density | 870 kg/m3 |
| Start-up time | 7 s |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Inner radius/RB | 22.5 mm | Water specific heat capacity/CPW | 4200 J/(kg·K) |
| Outer radius/RO | 24 mm | Journal density ρJ | 7800 kg/m3 |
| Bearing width/L | 20 mm | Journal elastic modulus/EJ | 210 GPa |
| Radius clearance/C | 0.06 mm | Journal Poisson ratio/νJ | 0.3 |
| Bearing elastic modulus/EB | 3.89 GPa | Journal thermal conductivity/kJ | 50 W/(m·K) |
| Bearing Poisson ratio/νB | 0.4 | Journal specific heat capacity/CPJ | 460 J/(kg·K) |
| Bearing density/ρB | 1300 kg/m3 | Journal thermal expansivity | 11.9 μm/(m·K) |
| Bearing thermal conductivity/kB | 11 W/(m·K) | Convection heat transfercoefficient/hh | 80 W/(m·K) |
| Bearing specific heat capacity/CPJ | 1005 J/(kg·K) | Inlet temperature/Tinlet | 20 °C |
| Bearing thermal expansivity | 50 μm/(m·K) | Water thermal conductivity/kW | 0.599 W/(m·K) |
| Water density/ρW | 1000 kg/m3 | Journal surface roughness/σJ | 0.2 μm |
| Water viscosity/ηW | 0.001 Pa·s | Bearing surface roughness/σB | 1.6 μm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Cai, J.; Zhang, J.; Liu, Z. Thermal Tribo-Dynamic Behaviors of Water-Lubricated Bearings during Start-Up with Journal Shape Error. Lubricants 2024, 12, 106. https://doi.org/10.3390/lubricants12040106
Chen S, Cai J, Zhang J, Liu Z. Thermal Tribo-Dynamic Behaviors of Water-Lubricated Bearings during Start-Up with Journal Shape Error. Lubricants. 2024; 12(4):106. https://doi.org/10.3390/lubricants12040106
Chicago/Turabian StyleChen, Shouan, Jianlin Cai, Junfu Zhang, and Zaixin Liu. 2024. "Thermal Tribo-Dynamic Behaviors of Water-Lubricated Bearings during Start-Up with Journal Shape Error" Lubricants 12, no. 4: 106. https://doi.org/10.3390/lubricants12040106
APA StyleChen, S., Cai, J., Zhang, J., & Liu, Z. (2024). Thermal Tribo-Dynamic Behaviors of Water-Lubricated Bearings during Start-Up with Journal Shape Error. Lubricants, 12(4), 106. https://doi.org/10.3390/lubricants12040106




