1. Introduction
One of the ways to improve the tribological properties of friction units is an application of various coatings on the surfaces of contacting bodies. The presence of such coatings, which leads to heterogeneity of the mechanical characteristics of contacting pair materials, should be taken into account in contact problem formulations and in analyses of the processes of friction and wear of tribojunctions. Simultaneously, the geometric heterogeneity of the surfaces of contacting bodies should also be taken into account, since the presence of the surface microrelief in the form of roughness and waviness leads to the concentration of contact and internal stresses near the contacting surfaces.
Therefore, it is necessary to develop contact models that take into account the heterogeneity of the contacting bodies, both geometric and mechanical. Contact problems of this kind are quite complex, and numerical methods are often used to solve them. To obtain analytical solutions, it is necessary to use any assumptions and simplifications regarding the shape and size of bodies, and their mechanical properties. For example, it is common to assume the thinness of these coatings relative to the size of the bodies in contact and the size of the contact region. Depending on the ratio of the elastic modulus of the coating and the substrate, various analytical approximations are used in this case. A number of models are developed for thin soft coatings. In [
1], an approximate analytical solution for the problem of contact between two spheres with thin soft coatings was constructed, with assumptions of elliptical form of the contact pressure distribution. Another approximate solution of the problem of normal contact of an axisymmetric punch with a multilayer elastic base is given in [
2]. The authors present the pressure distribution in the form of two parts, one of which corresponds to the case of a homogeneous half–space, and the other being the perturbing term, which is approximated by a series of base functions. A more accurate solution to the problem of indenting a coated body is obtained, for example, in [
3], where the Hankel transform and numerical integration methods and assumptions of a specified type of contact pressure distribution (proportional to
, where
a is the contact radius) are used. The authors investigated not only the contact characteristics, but also the stress state of the bodies. A fairly accurate solution to the problem of indenting a sphere into an elastic layer perfectly bonded to an elastic half-space was obtained in [
4] by solving an infinite system of equations with the expression of contact pressure as a series that contains Tchebycheff polynomials. Using a similar method, the authors then solved the problem for a larger number of elastic layers bonded to an elastic half-space [
5]. A simple analytical solution to the problem of indenting a spherical punch into an elastic layer perfectly bonded to an elastic half-space was obtained in [
6]. The authors have shown that their solution has a sufficiently high accuracy for thin and thick coatings, as well as for coatings of arbitrary thickness in the case of a relatively small difference in the elastic modulus of the coating and the substrate. A large number of contact problems for elastic and viscoelastic bodies with coatings and analytical approaches to their solution can be found in the book [
7]. However, due to the great difficulty of obtaining analytical solutions for the contact problems for layered bodies, various numerical methods are also developed. In [
8], a general algorithm, which is based on dividing the contact region into annular areas, for solving such problem for the axisymmetric punch is presented. In [
9], the boundary element method is used to validate an approximate solution of the contact problem of indenting an almost axisymmetric punch into layered elastic materials. The finite element method is also very popular, since it makes it possible to investigate a wide range of effects that occur during the contact of bodies with coatings [
10].
A separate area is the study of the contact of deformable bodies, taking into account their surface roughness. Among the first research in this field, one can note the approach of Shtaerman [
11], who proposed to take into account roughness in the form of an additional compliant layer deformed according to the Winkler model. Another approach is presented in [
12], where the Greenwood–Williamson statistical model of roughness [
13] is taken as a base. The authors have built the numerical solution according to an iterative scheme, which included first the deformations of the asperities, and then moved to deformations of the entire sphere. The solution of the contact problem for a smooth elastic sphere and a rigid rough base is presented in [
14]. The authors also used the Greenwood–Williamson model, taking into account both the elastic deformations of the asperities and the bulk substrate. In [
15], the contact of a rigid rough sphere with an elastic half-space was studied using the finite element method based on a fractal description of roughness. An analytical formula for the dependence of the contact stiffness on the load applied to the sphere was proposed there. The dependence of the real contact area on the load in contact interaction has been studied by many researchers. In [
16], in addition to the numerical solution of the rough contact problem, the authors proposed an analytical formula for the real contact area in almost the entire range of applied loads. This formula was refined in [
17], which made it possible to more accurately determine the area of the contactless region at large loads. Another analytical expression for the relationship between the real contact area and the applied load was obtained in [
18], based on interpolation of numerical results obtained from the finite element analysis. A numerical model of contact of two rough elastic spheres is presented in [
19]. Two contact regimes corresponding to very low loads (only one asperity in contact) and moderate loads (multiple asperities in contact) were studied, and some analytical expression for the transition load between these two regimes was derived there.
To study the effect of roughness on nominal contact characteristics (contact pressures, contact area size), an approach with the introduction of additional compliance due to roughness has been suggested in [
11,
20]. To describe the additional compliance due to roughness, the contact problem at the microscale is solved, and the resulting function of the additional displacement due to roughness is derived and used for the contact problem formulation at the macroscale [
21,
22]. The method to solve contact problems at the macroscale using the power dependence of the additional displacement on the nominal pressure was developed in [
20,
23,
24]. The solution in this case can be obtained using the method of successive approximations for both cases of known or unknown in advance contact regions. A more accurate representation of the additional compliance function was obtained in [
22] on the basis of the 3-D periodic contact problem solution. Using the approach of the additional compliance, the possibility of the full contact (equality of real and nominal contact areas) in the indentation of an axisymmetric punch into an elastic half-space with a rough surface was investigated in [
25]. Another approach to take into account the effect of roughness on the distribution of the nominal contact pressures is given in [
26]. The authors present the deformations as the sum of deformations of asperities and bulk deformations using the Persson’s rough contact theory for determination of the first ones. Numerical methods are also used to calculate the distribution of the nominal contact pressure in the contact of rough bodies. For example, in [
27], the finite element method was applied for the analysis of the nominal contact characteristics for the given microgeometry parameters.
Thus, taking into account the presence of coatings on contacting bodies or their surface roughness significantly complicates the formulation and solution of contact problems. There are a few papers where the attempts to take into account both of these factors were made. For example, the contact problem for two half-spaces, one of which is rigid with a rough surface and another one is modeled by the layer bonded to the elastic base and has a smooth surface, was considered in [
28]. The author used the Greenwood–Williamson roughness model and approximate solution of Chen and Engel [
2] for a multilayer elastic half-space. Numerical results are presented there for the given values of the layer thickness, the ratio of the elastic modulus of the layer and the base, and the roughness parameters. A numerical solution for the contact of cylindrical punch with real roughness (which was determined based on profilogram data) and layered elastic half-plane was obtained for 2D contact problem formulation in [
29]. The effect of specific roughness parameters on the distribution of contact pressures in the presence and absence of the layer of a given thickness was investigated. A numerical approximate solution of the contact problem for a rough sphere and a layered elastic base using the boundary element method and the Hankel transform, as well as the additional compliance function [
22] due to the presence of microgeometry on the indenter surface, is presented in [
30]. Thus, it can be concluded that, until now, only the numerical solutions were developed to study the contact problems for the layered elastic bodies, taking into account their macroshape and surface roughness parameters. Moreover, the study of the influence of roughness parameters on contact characteristics (both nominal and real) in the case of layered bodies is also incomplete.
In this paper, the solution of the contact problem for a rough spherical punch and an elastic half-space covered by a thin soft elastic layer is developed. The use of approximation of a relatively thin soft layer lying without friction or perfectly bonded to an elastic half-space makes it possible to reduce the problem to the analysis of an integral equation with a nonlinear non-integral term, depending both on the parameters of the punch microgeometry and the mechanical and geometric characteristics of the surface layer. The numerical-analytical solution of the problem is developed, and allows us to draw some general conclusions about the influence of both the roughness parameters (size and location density of asperities) and the mechanical and geometric parameters of the surface layer on the contact characteristics (nominal and real contact area, nominal and real contact pressure distributions, approach of the contacting bodies under loading, etc.). The complete (in comparison with the previous results) analysis of roughness parameters on the characteristics of contact interaction at both macro and microlevels is performed. Moreover, the main integral equation, obtained in analytical form, makes it possible to evaluate the nature of the surface parameters effect on the nominal contact characteristics.
The manuscript is organized as follows:
Section 2 presents a problem statement in general form and the derivation of the main integral equation to solve the problem.
Section 3 includes a consideration of the contact at the microscale and the determination of the additional displacement function. In
Section 4, a general scheme to solve the main integral equation and to calculate the contact characteristics at macro and microscale is presented; and also the analysis of the surface layer on the real and nominal contact characteristics (pressure distribution, contact area, etc.) is given there. In
Section 5, the effect of the punch roughness on the nominal and real contact characteristics by comparing the results obtained for the rough and smooth punches indenting into the layered and homogeneous elastic base is analyzed. In
Section 6, the influence of the roughness parameters on the contact characteristics for the layered elastic half-space is investigated. Finally, in
Section 7, some conclusions about the effects of the surface roughness and coatings in the indentation process are made.
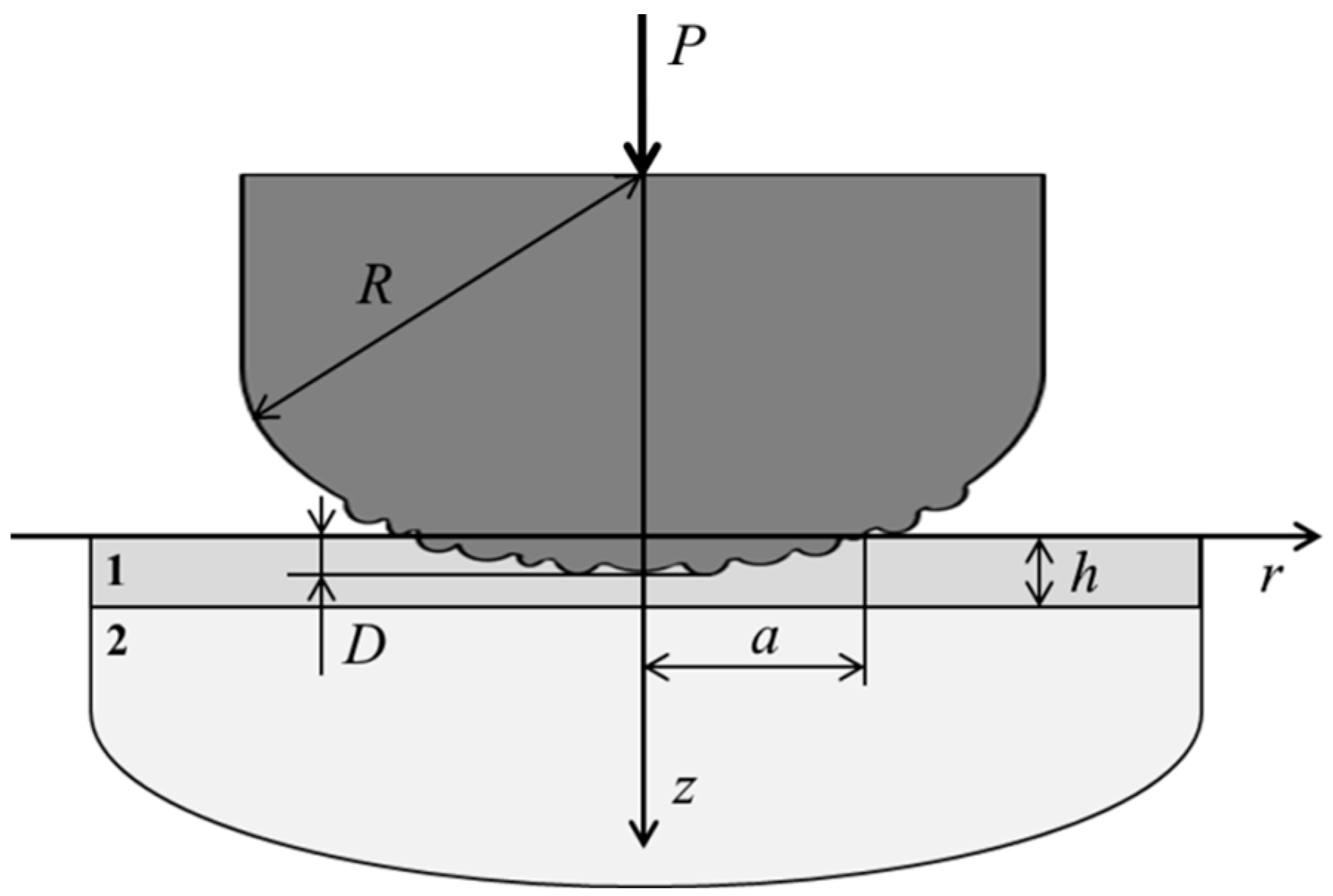
2. Problem Statement
Let us consider the indentation of an axisymmetric punch, whose macroshape is described by the function
(
R is the curvature of the punch contacting surface), into an elastic layer (1) of thickness
h, lying on an elastic half-space (2) (
Figure 1). It is assumed that there are no shear stresses between the punch and the layer that takes place at a negligible friction coefficient. The punch surface has a roughness determined by the shape of asperities, the characteristic size of which is much smaller than the punch size, and by the density of the asperities distribution on the punch surface.
The problem under consideration has axial symmetry, so the nominal contact area is a circle region of radius a.
It is shown in [
31] that in the case of a thin surface layer (practically at
), the main integral equation for determining the distribution of the contact pressure
in the problem of indenting an axisymmetric smooth punch into a two-layer elastic base can be reduced to the form
where
is the is the complete elliptic integral of the first kind,
,
,
E1 and
are the Young’s modulus and Poisson’s ratio of the surface layer,
D is the indentation depth, and coefficients
A1 and
A2 depend on the relative mechanical characteristics of the layer and the half-space and the boundary condition between them (no friction or complete adhesion). In the case of equality of the Poisson’s ratios of the layer and the half-space (
)
, where
,
E2 and
are the Young’s modulus and Poisson’s ratio of the half-space. The coefficient
A2 is 0.5 for the no-friction condition between the layer and the half-space, and in the case of the complete adhesion, it is determined as [
31]:
We consider only the case when the layer is softer than the half-space, that is
. Then, the coefficient
A2 is always positive, since
. If
, that is
, then, based on (2), the coefficient
A2 is equal to zero, and Equation (1) goes into the equation of the axisymmetric contact problem for an elastic half-space [
32]. Note that in the case of an incompressible thin surface elastic layer (
) bonded to an elastic half-space, the main Equation (1) is not applicable.
The presence of roughness on the punch contacting surface leads to a change in contact characteristics at the macroscale. It is shown in [
22] that, due to roughness, an additional displacement of the layer boundary takes place at each point of the contact surface, which is determined by the distribution of the nominal contact pressure
within the nominal contact area. In general, this dependence can be written as
, where
A is some operator determined by solving the contact problem at the microscale. Note that the additional compliance due to roughness in the form of a linear function on contact pressure was first proposed in [
11]. So, taking into account the roughness of the punch contacting surface, the integral Equation (3) takes the form
The radius of the contact area
a is not known in advance, but it can be found from the condition
(due to smoothness of the punch shape at the macroscale). Taking into account the considered punch shape at the macroscale, this condition allows us to reduce Equation (3) to (for
):
If
, Equation (4) corresponds to the indentation of the rough spherical punch into a thin layer lying without friction or bonded (compressible material) to a rigid base [
33].
It is also necessary to add the following equilibrium condition to Equation (4):
where
P is the load applied to the punch (
Figure 1).
Equations (4) and (5) allow us to calculate the nominal contact pressure distribution and the nominal contact radius at macroscale if the function is known.
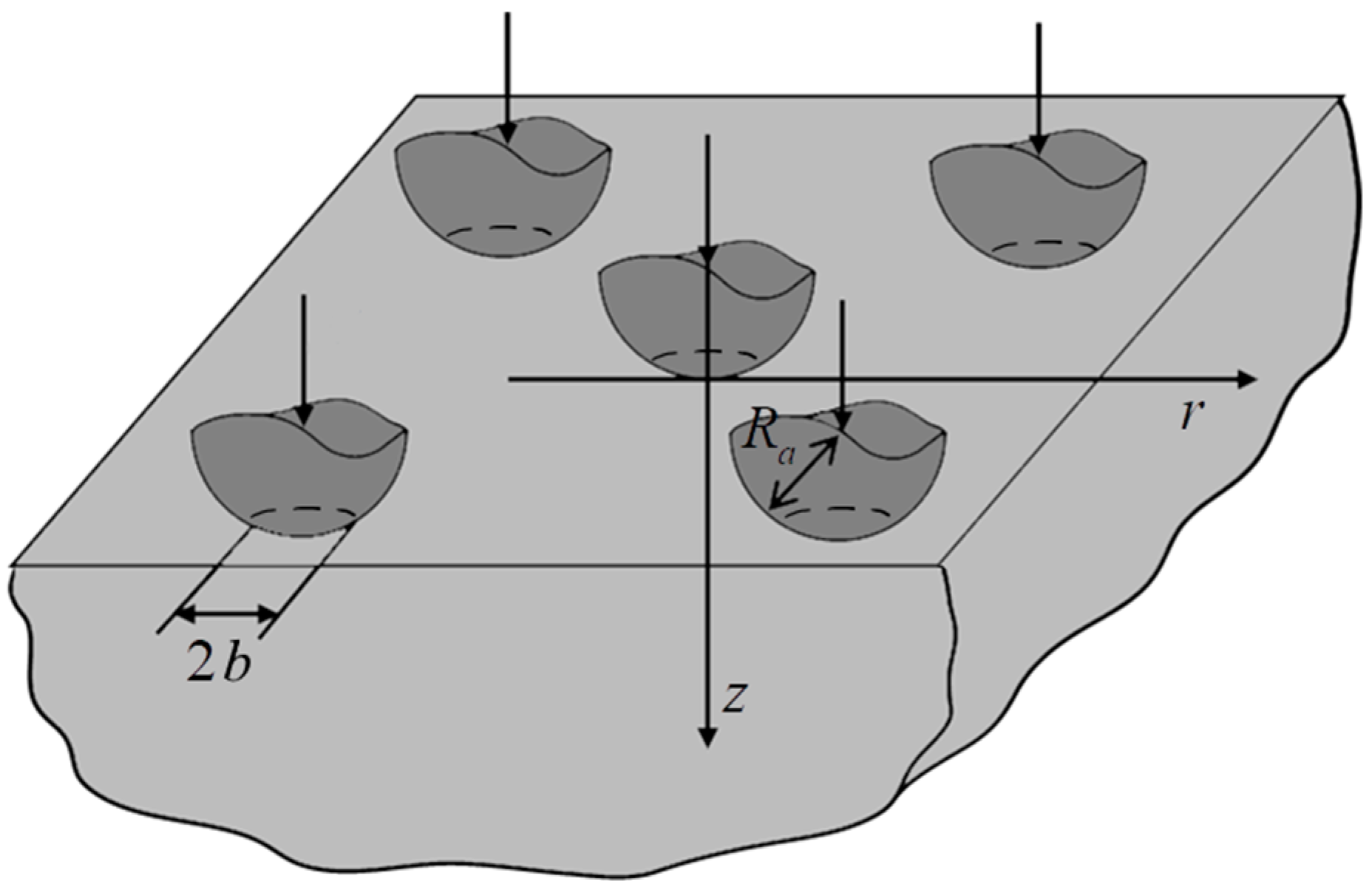
3. Calculation of the Additional Displacement Function
It is assumed that the characteristic size of the asperity, for example, the curvature radius
Ra is much smaller than the radius
a of the circular nominal contact area at the macroscale, and the number of contacting asperities inside the nominal contact area is quite large. Moreover, it is assumed that the spot radius is much smaller than the surface layer thickness
h. Then, as shown in [
21], the additional displacement function
can be determined from the solution of the contact problem for two half-spaces loaded by the nominal pressure
p: a rigid one with a rough surface and an elastic one with a smooth surface (
Figure 2). Let us describe the roughness as a set of regularly spaced identical asperities with the curvature radius
Ra and the location density
(the number of asperities per unit area). To simplify the calculations, it is assumed that all asperities have the same height and spherical shape of the contacting surface, which is described by the function
.
A general approach to solving periodic contact problems in a spatial formulation is presented in [
34]. In the case of a periodic single-level system of punches modeling the surface roughness, the additional displacement of the layer boundary
due to surface roughness can be defined as the difference between the indentation depth
d of the punches and the displacement
of the layer boundary, everywhere loaded with the constant nominal pressure. The expression for this function for spherical asperities has the form [
35]:
Here
, and the radius
b of the contact spot is found from the relation [
35]
Note that for a random distribution of asperities in height, the similar approach can be used for the calculation of the additional displacement function, taking into account the mutual influence of asperities.
5. Comparative Analysis of Contact Characteristics in Indentation of the Rough and Smooth Punches into the Coated and Homogeneous Elastic Half-Space
To analyze the punch roughness effect, in this section, we compare the results resulting from the model developed in this study with the contact characteristics calculated for the smooth punch penetrating in the coated or uncoated elastic half-space. For the smooth punch, the contact pressure in the case of the coated half-space is calculated numerically from Equation (3), where the term
is zero, using the iteration scheme (8) with
and
. In the case of the uncoated half-space, the contact pressure is determined using the Hertz theory [
33].
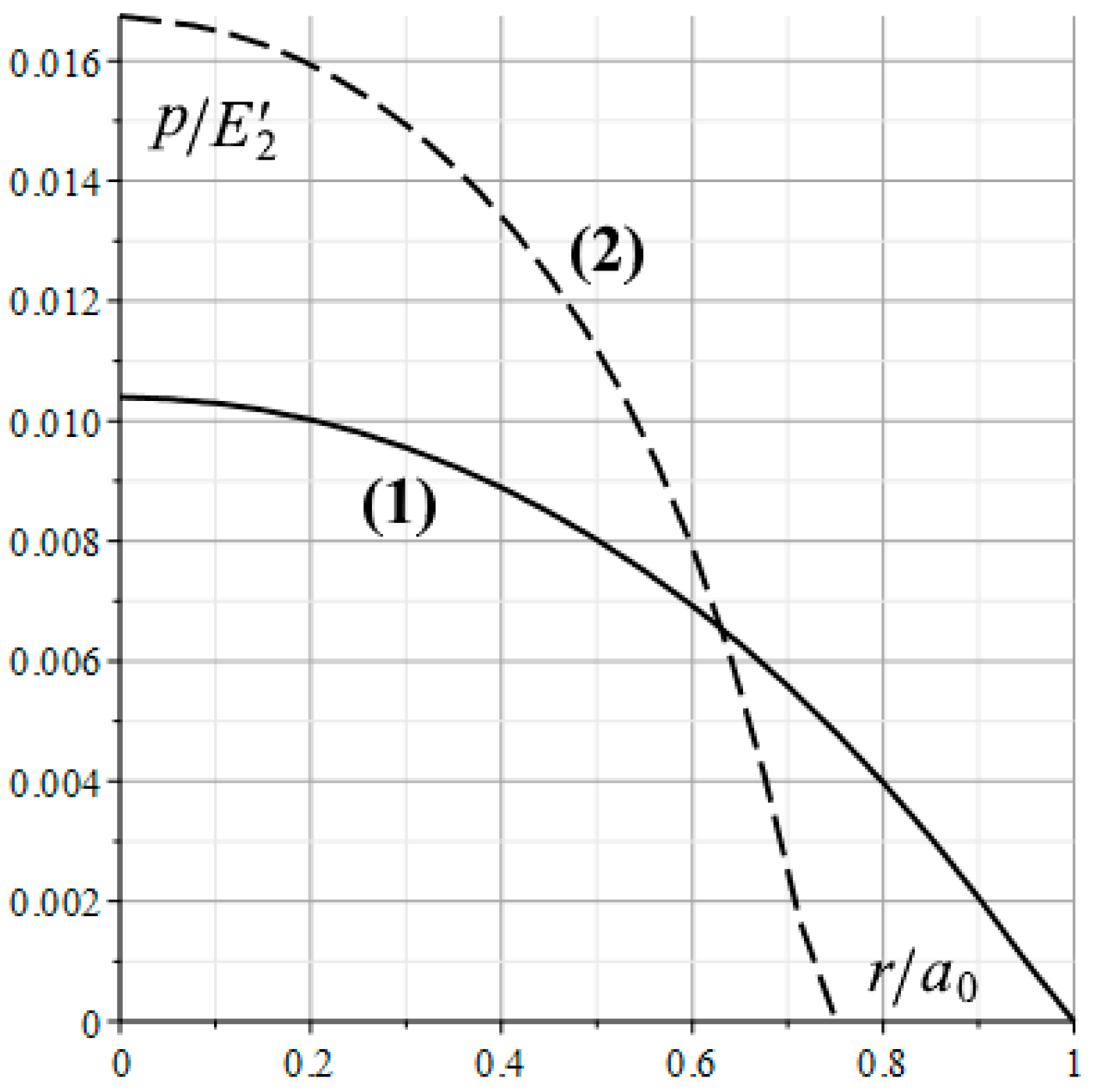
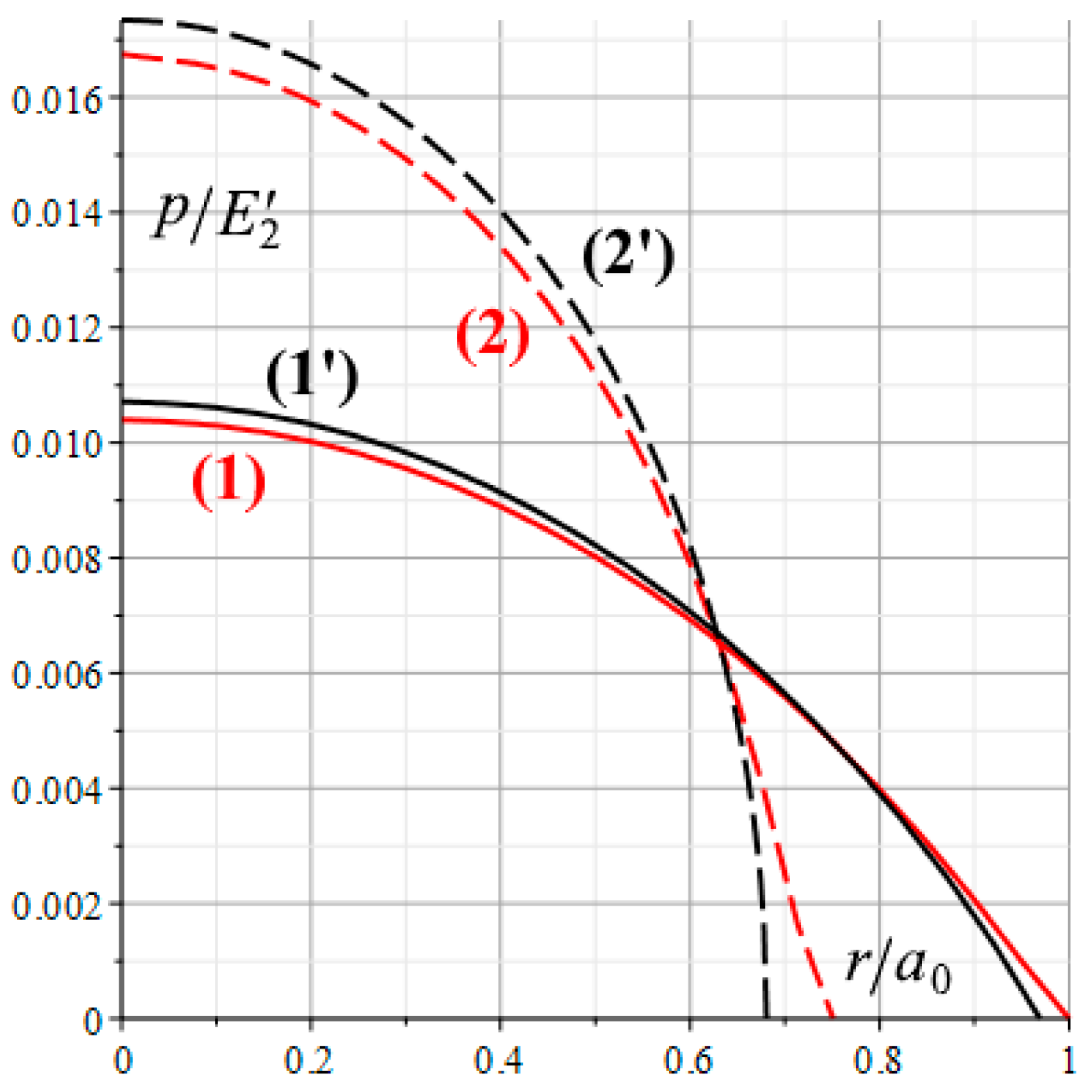
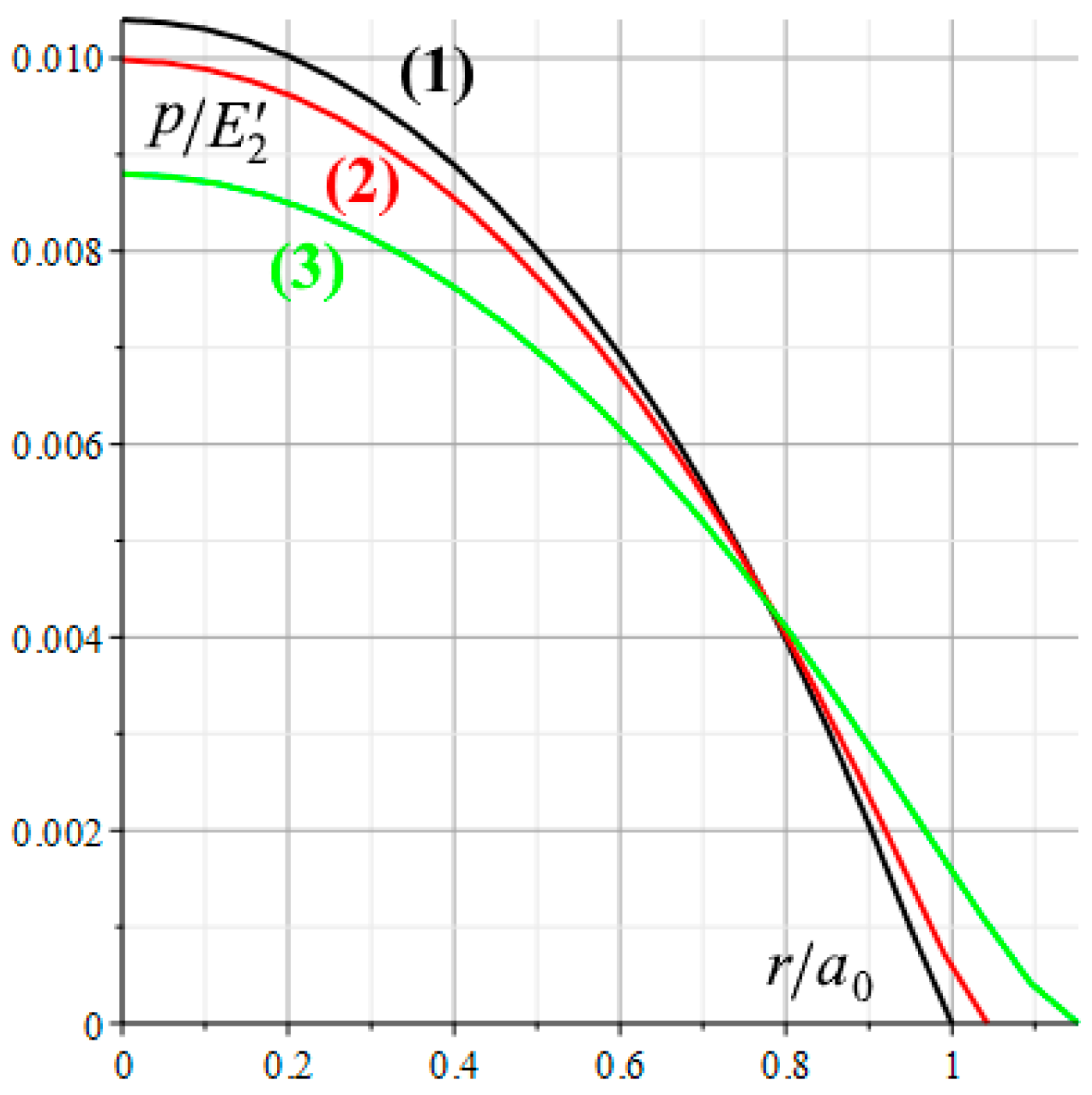
Figure 7 illustrates the distributions of the nominal contact pressures for two cases under consideration. The radial coordinate is dimensioned by the radius of the contact area
, corresponding to the indentation of the rough punch into the layered elastic base. In each case, the radius of the contact area was selected in such a way that the load
P applied to the punch was constant and equal to
. The results indicate that, both for the rough and smooth punches indenting into the homogeneous elastic half-space, the radius of the nominal contact area is smaller and the nominal contact pressure in the central part is higher than they indent into the layered base. The presence of the roughness on the punch surface leads to an increase in the size of the nominal contact area, to a decrease in the nominal contact pressure under the central part of the punch and to a zero tangent of the function
at the boundary of the nominal contact area (lines 1 and 2). This fact for an elastic thick strip was proved in [
21].
Figure 8 illustrates the dependence of the indentation depth on the load applied to the rough (1,2) and smooth (1′,2′) punches. The punch roughness parameters, the thickness, and mechanical properties of the surface layer under consideration are described in
Section 4.2.2. The depth of indentation of the smooth punch into the layered elastic half-space is equal to
, and into the homogeneous elastic half-space it is equal to
at the fixed load
. Comparison with the results of
Section 4.5, where the indentation of the rough punch into the homogeneous and layered bases is studied, shows that the presence of the roughness leads to an increase in the indentation depth under the fixed load.
6. Influence of Roughness Parameters on Contact Characteristics
In
Section 3, it was shown that in the case of modeling the punch surface roughness by the periodic system of identical asperities, the additional displacement function
depends on two parameters. They are the curvature radius of asperities
Ra and the density of their location
(the number of asperities per unit area). As shown in
Section 4.1, the parameters
B and
of the power function
approximated the additional compliance of the layer depend only on the product
. For instance, for
, the parameter values
and
were obtained.
To analyze the influence of the roughness parameters on the contact characteristics, two more values of the product
are considered:
and
(
Table 1). Using the approximation procedure described in
Section 4.1, we obtain
and
for
,
and
for
. The discrepancies in the results calculated from Equations (6) and (7) and based on the approximating function in these cases do not exceed 5% for the nominal pressures in the range from
to
, with the exception of a small region near zero value of pressure. Note that the values of the parameter
B presented in
Table 1 are obtained in units
. So they are different for different curvature radii of asperities.
Let us consider three values of the curvature radii of asperities
Ra and three values of their distribution density
(
Table 1). The procedure for determining the parameters
B and
presented in
Table 1 is described in
Section 4.1. Note that the first line of the table corresponds to the roughness parameters used in the numerical calculations of
Section 4 (
and
).
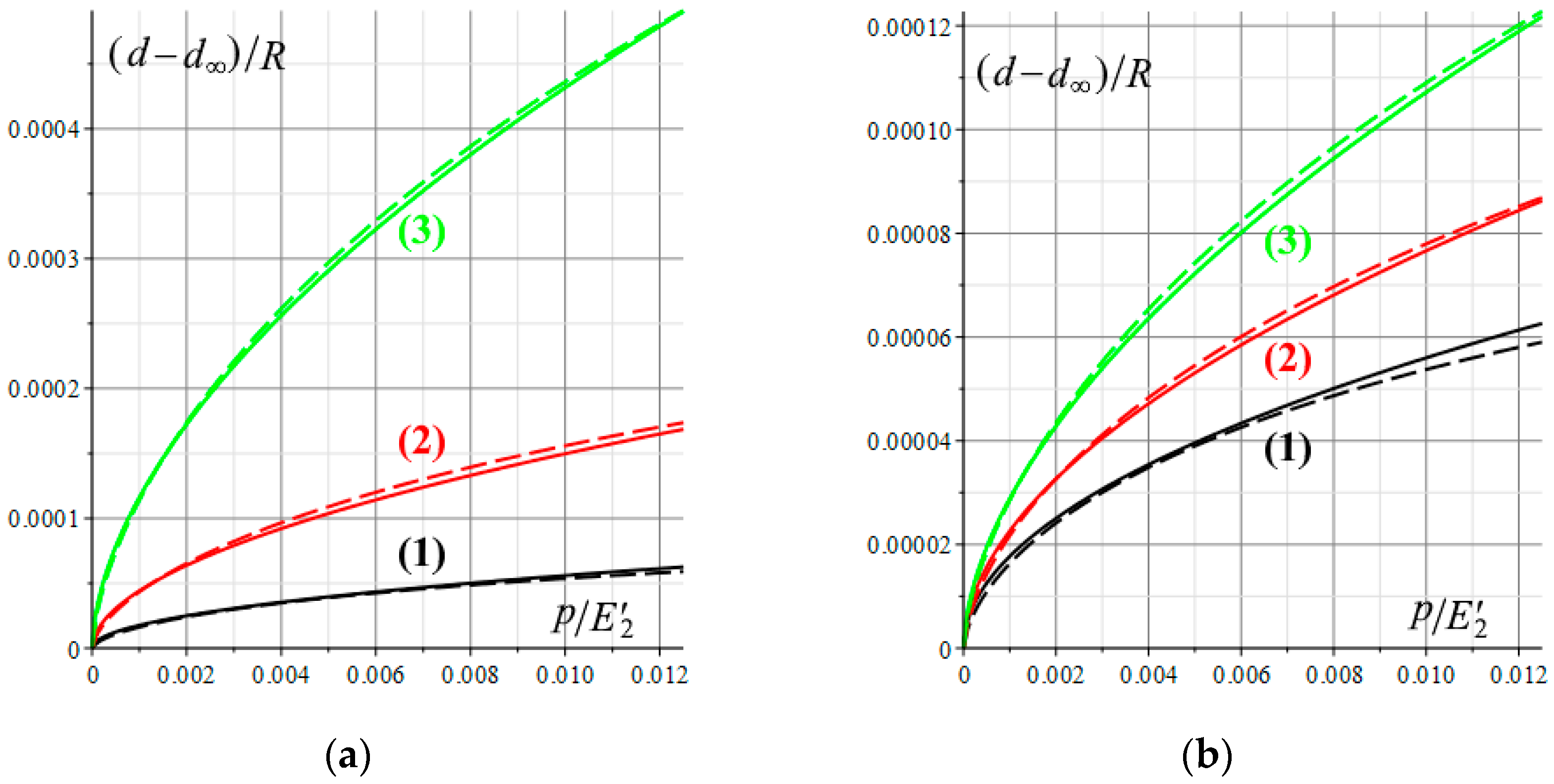
Figure 9 illustrates the dependences of the additional displacement function on the nominal pressure
p for different values of the roughness parameters
(a) and
Ra (b). It follows from the results that a decrease in both the location density of asperities and the radius of their curvature leads to an increase in the additional displacement at a constant value of the nominal pressure. However, variation of the parameter
, which is equivalent to changing the distance between asperities, has a greater influence on the additional displacement due to roughness, as follows from
Figure 9a. The calculation results also show that the approximating function gives the values of the additional displacement function closed to the values obtained from Equations (6) and (7).
The analysis of the surface roughness effect on the nominal pressure distribution in the contact of the spherical punch with the layered base has been performed based on the iterative scheme (8) with and .
Figure 10 illustrates the distribution of the nominal contact pressures for the rough punches with different values of the asperities density. The radial coordinate in
Figure 10 is dimensioned by the radius
a0 of the nominal contact area corresponding to the rough punch with
. As follows from the results, a decrease in the density
of asperities leads to a decrease in the value of the nominal contact pressure in the center of the nominal contact area and an increase in the radius of the contact area itself. As calculations show, a decrease in the curvature radius of asperities
Ra leads to a similar result, but less noticeable. Numerical calculations also show that a decrease in the values of the roughness parameters
and
Ra also leads to a decrease in the relative contact area
and an increase in the indentation depth
D and the local maximum
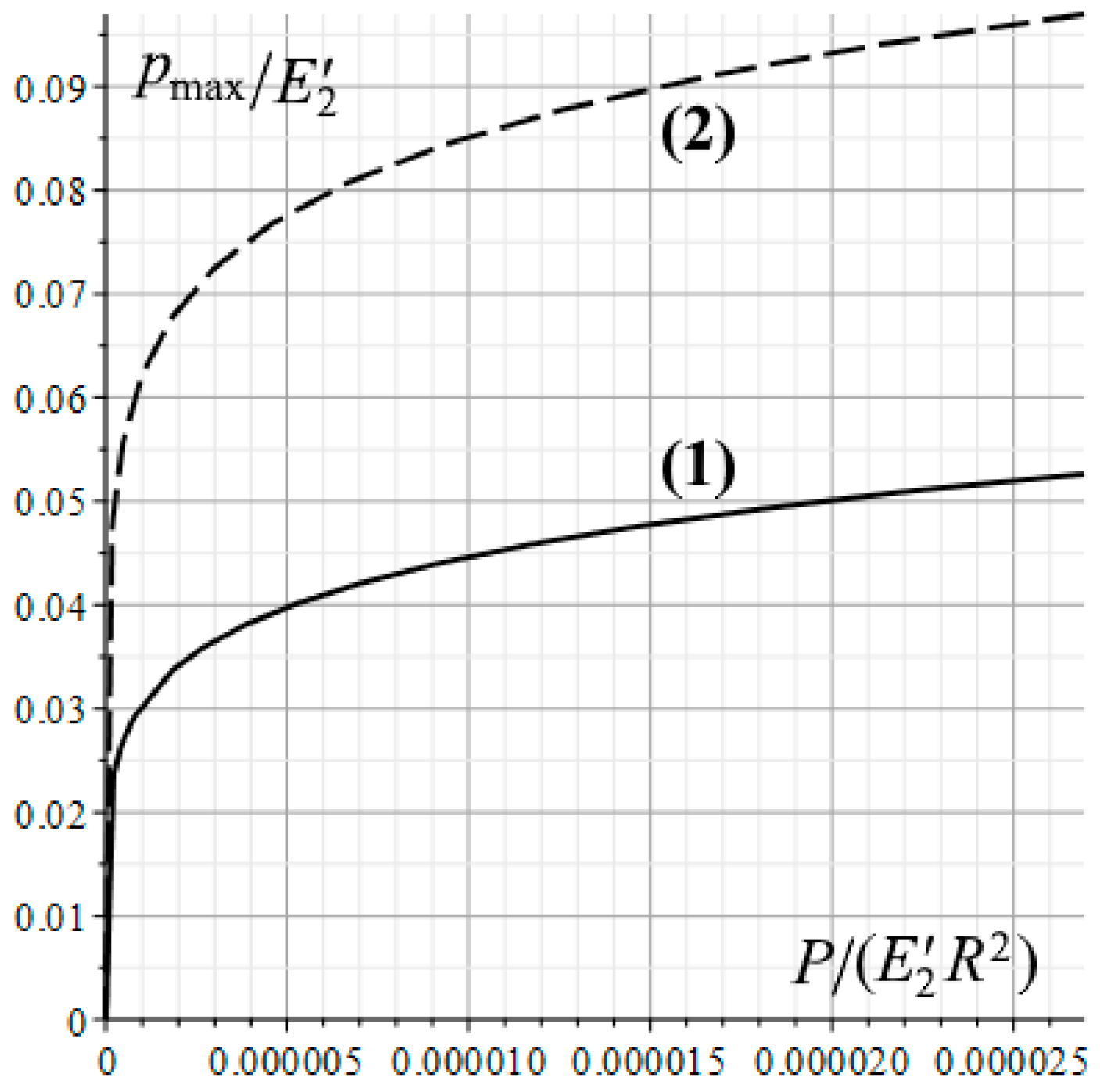
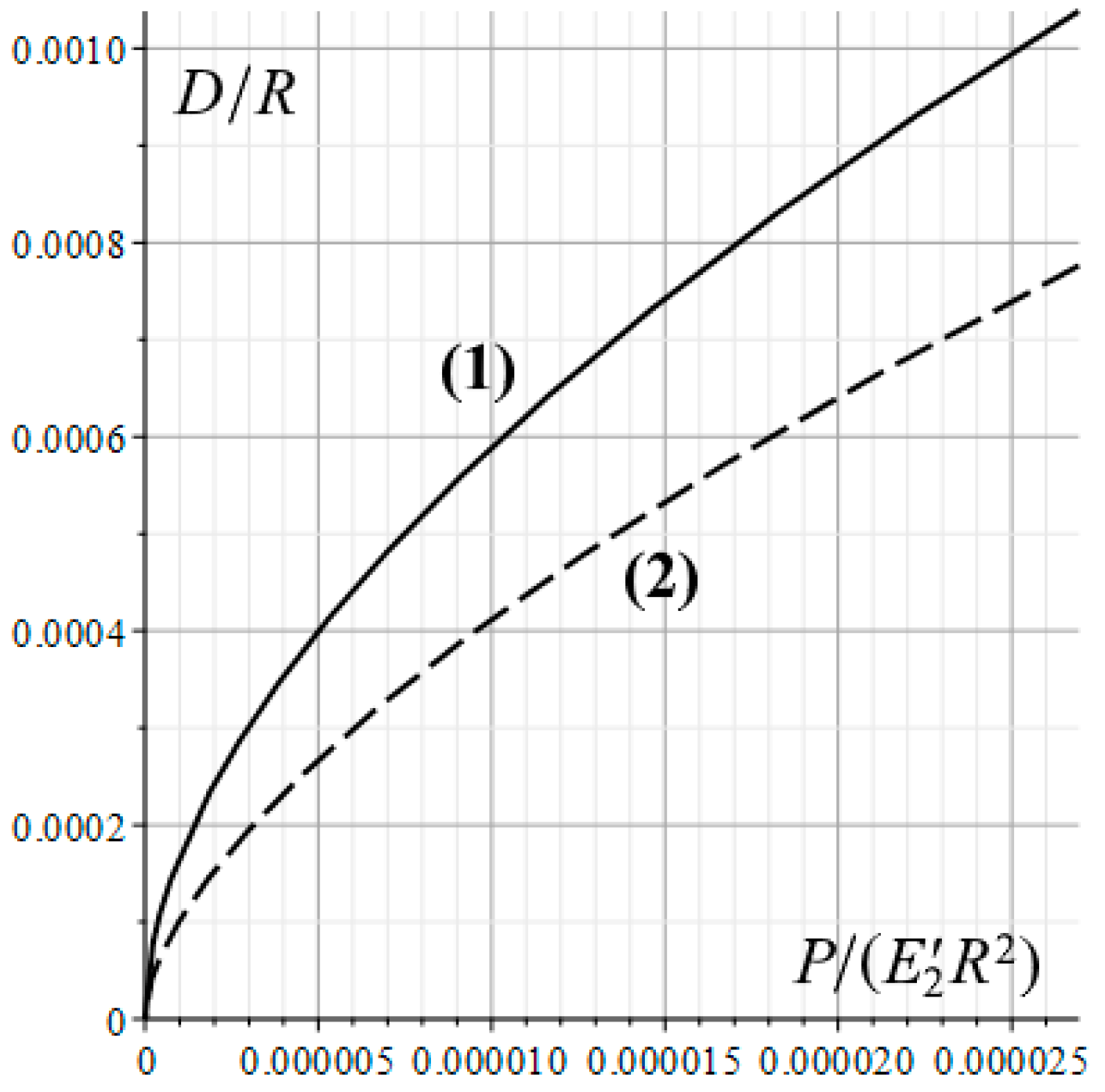
pmax of the real contact pressure. Thus, by changing the microgeometry of the punch surface, it is possible to control the additional compliance of the deformable base, and therefore to achieve the required values of the contact characteristics both at macro and microscale.
The presented dependencies illustrating the roughness parameters effect on the nominal and real contact characteristics are in good qualitative consistency with the results of the real and nominal contact characteristics analysis in indentation of rough punches into a homogeneous elastic half-space [
22,
24], and also demonstrate the surface layer thickness and mechanical properties influence on the nominal and real contact characteristics under consideration.
7. Conclusions
A numerical-analytical solution of the contact problem for an axisymmetric rough punch indenting into a thin elastic layer lying on an elastic half-space is proposed. It is assumed that the elastic modulus of the layer is less than the elastic modulus of the base. To solve the problem, a two-scale approach is used. In the frame of this approach, the solution to the contact problem at the microscale (the scale of the asperities radius and contact density) obtained with the localization principle is used to construct an integral equation to determine the nominal contact pressure and nominal contact area, taking into account the punch roughness effect.
Analysis of the contact problem solution makes it possible to conclude that the presence of a thin elastic surface layer leads to a change in both nominal and real contact characteristics. So, at the macroscale, the presence of a thin soft layer leads to an increase in the nominal contact area, to a noticeable decrease in the maximum values of the nominal contact pressures and an increase in the indentation depth. At the microscale, the existence of the thin soft surface layer leads to a decrease in the maximum real contact pressures concentrated on individual contact spots (under asperities) and to an increase in the real contact area.
The punch roughness effect (in comparison with the case of the smooth punch) consists of an increase in the nominal contact area and decrease in the nominal contact pressures. Moreover, a decrease in the asperities density (number of asperities at the unit area) or the radius of their curvature results in an increase in the nominal contact area and a decrease in the value of the nominal contact pressure in the central part of the nominal contact region of the punch and the two-layer deformable base.
The resulting solution allows us to study the combined effect of the presence of microrelief and soft coatings on the surface of contact bodies in a contact interaction. Moreover, the presented analysis of the influence of roughness parameters on the additional compliance of bodies can be used to select a microrelief and coating mechanical and geometrical characteristics in order to achieve the necessary indentation values, and also to control the stress distribution near the contact area.
Note that in this study, the materials of deformable bodies were considered to be linearly elastic and isotropic, which imposes restrictions on the magnitude of deformations. As a further development of the presented results, the plastic deformations will be included in the model, which are of great importance in determining the contact characteristics at macro and microscales [
36].