Time-Frequency Fusion Features-Based GSWOA-KELM Model for Gear Fault Diagnosis
Abstract
:1. Introduction
- (1)
- This study proposes the GSWOA-KELM model for the first time. In the new model, the GSWOA is used to find the optimal parameters of the KELM, and the results show that compared with the existing model, the proposed GSWOA-KELM model has higher diagnostic accuracy, faster convergence speed, and stronger global search capability;
- (2)
- The time-domain and frequency-domain features are extracted and fused in this study, which overcomes the limitations of single-domain features and improves the fault diagnosis ability of the model. Meanwhile, the superiority of multi-domain features in representing information ability is examined in this study, which provides a reference basis for the application of feature extraction work in other aspects.
2. Time-Frequency Features Extraction
2.1. Time-Domain Features
2.2. Frequency-Domain Features
2.3. Fusion Features
3. GSWOA-KELM Fault Diagnosis Model
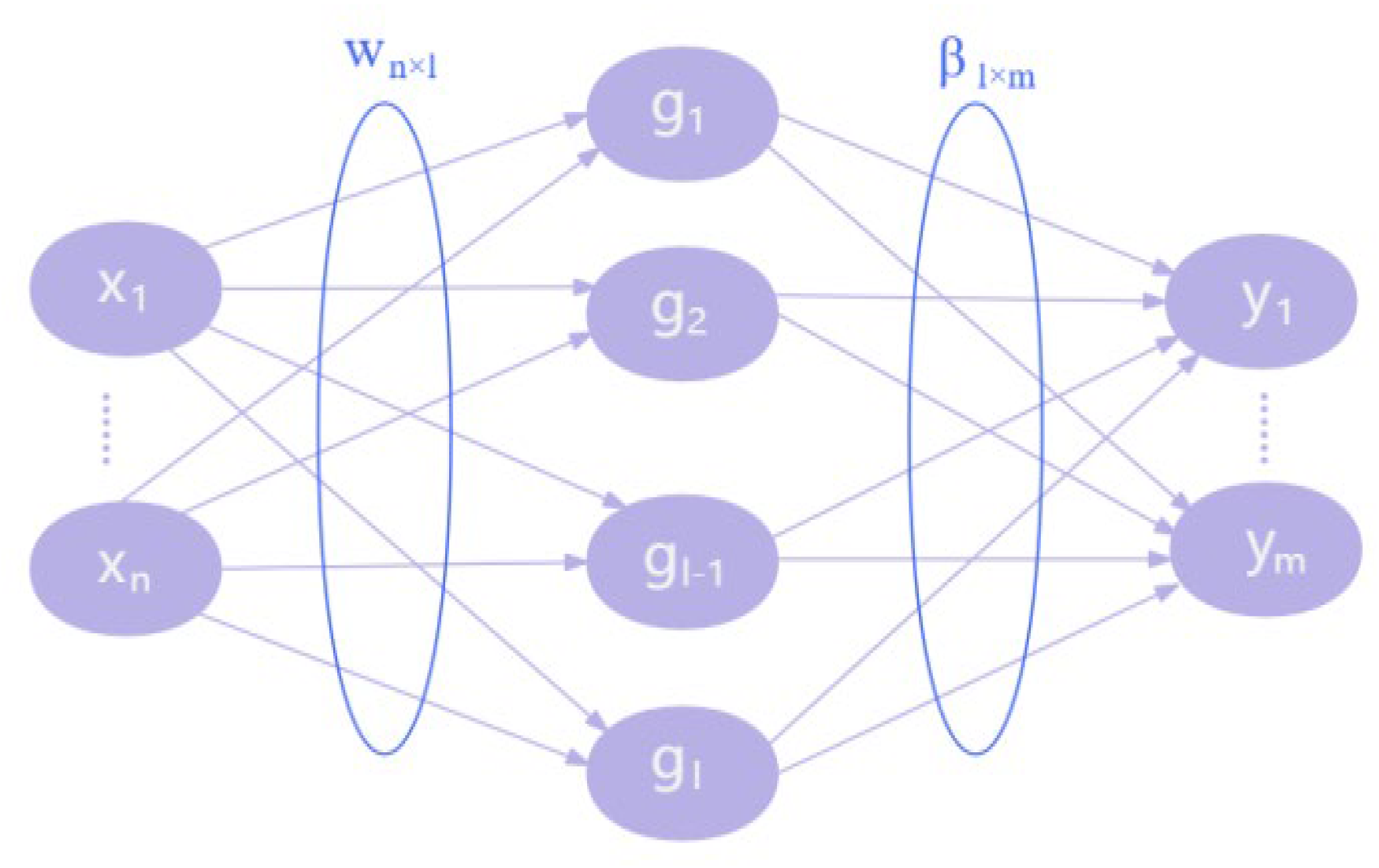
3.1. Kernel Extreme Learning Machine
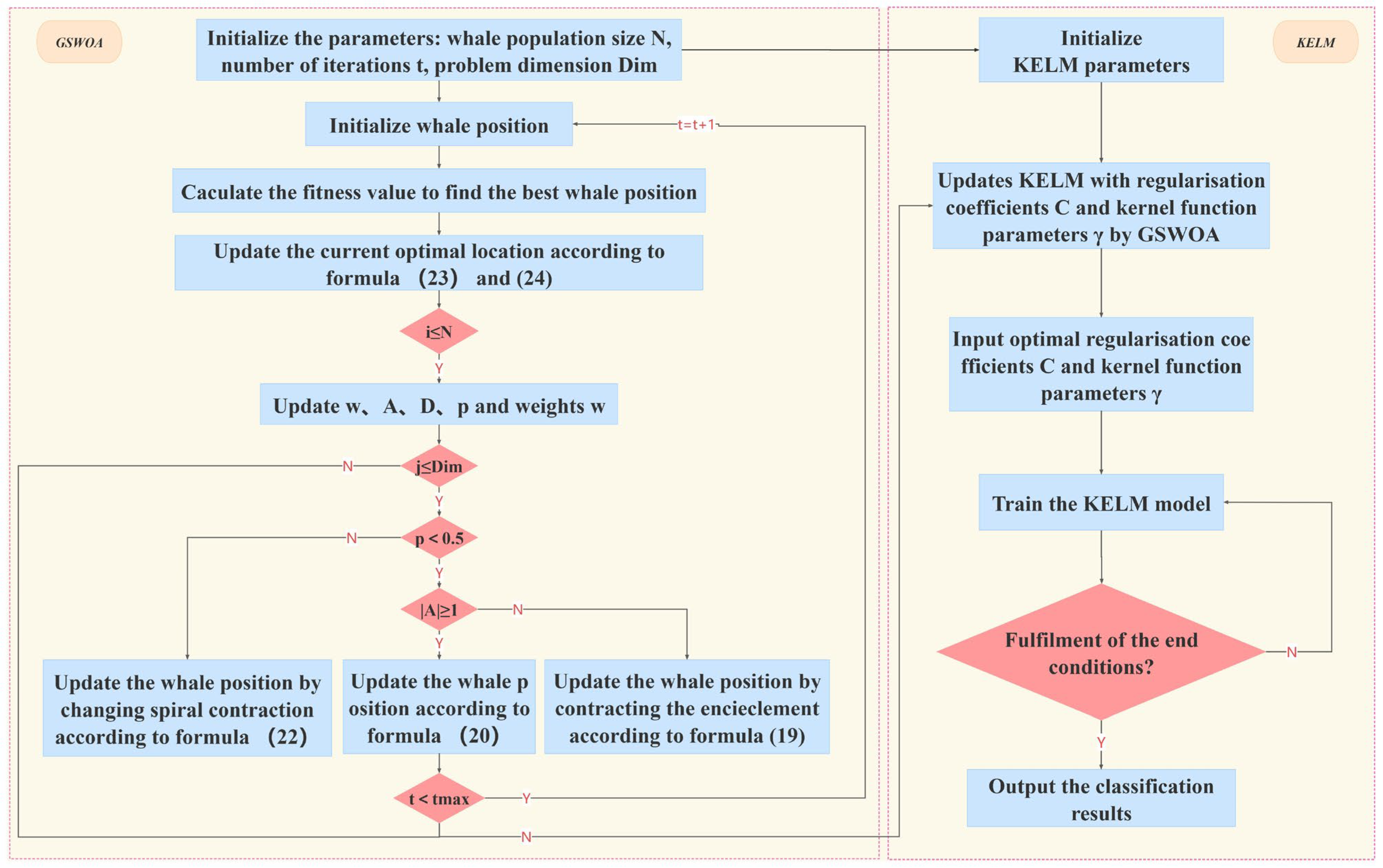
3.2. Whale Optimization Algorithm
3.3. Global Search Whale Optimization Algorithm
3.4. Kernel Extreme Learning Machine Optimized Using the Global Search Whale Optimization Algorithm
4. Experimental Verification and Result Analysis
4.1. Data Acquisition and Preprocessing
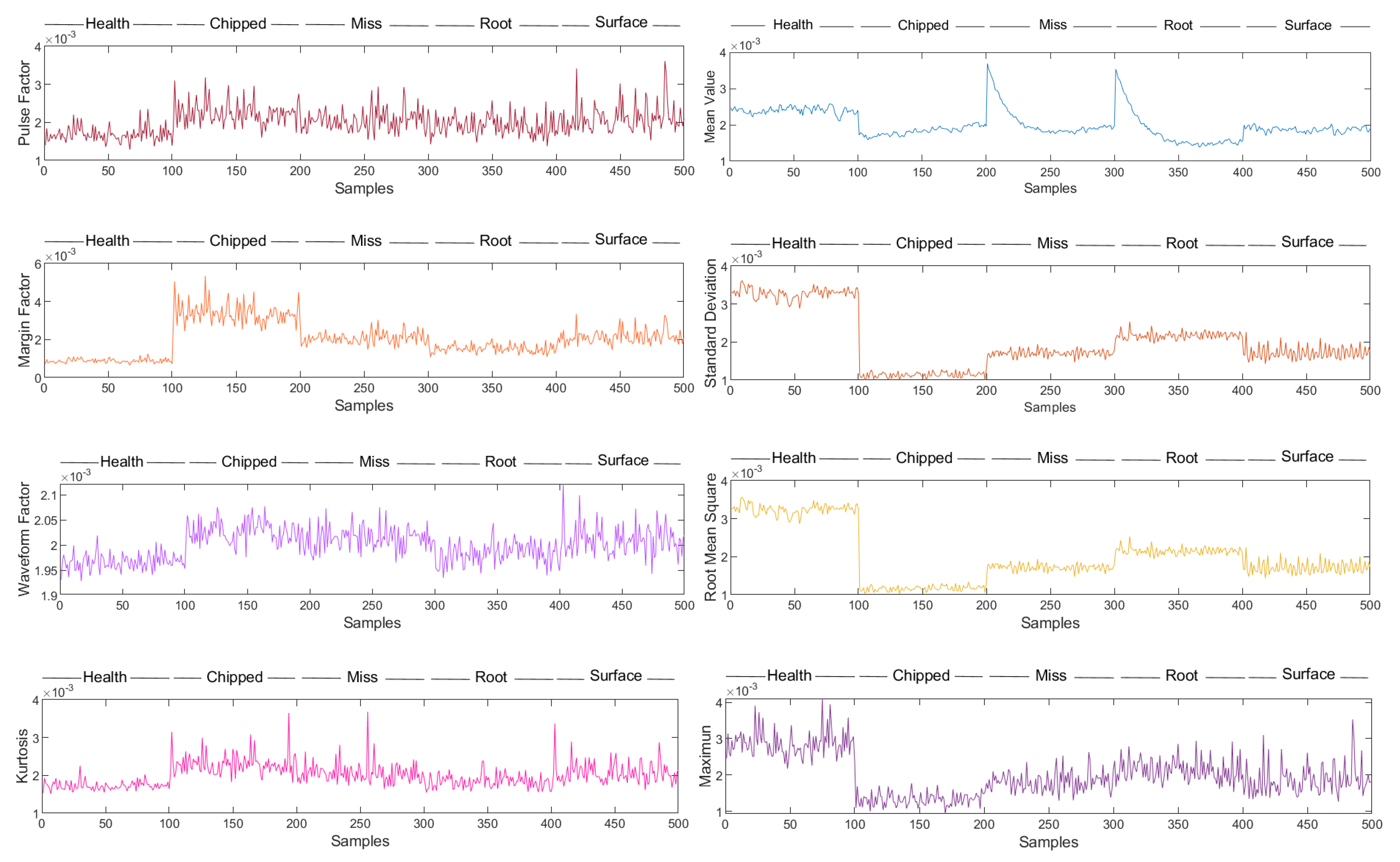
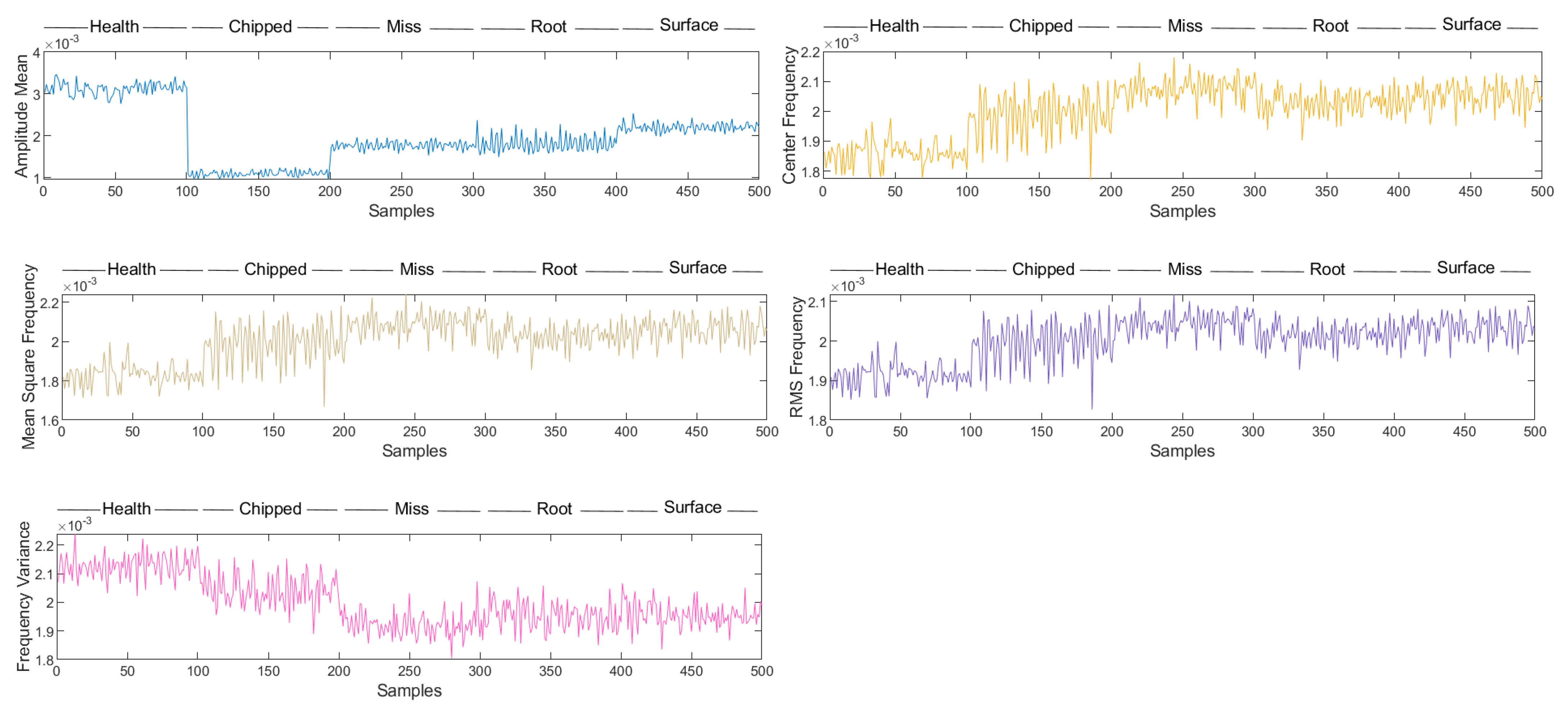
4.2. Time-Frequency Features Extraction
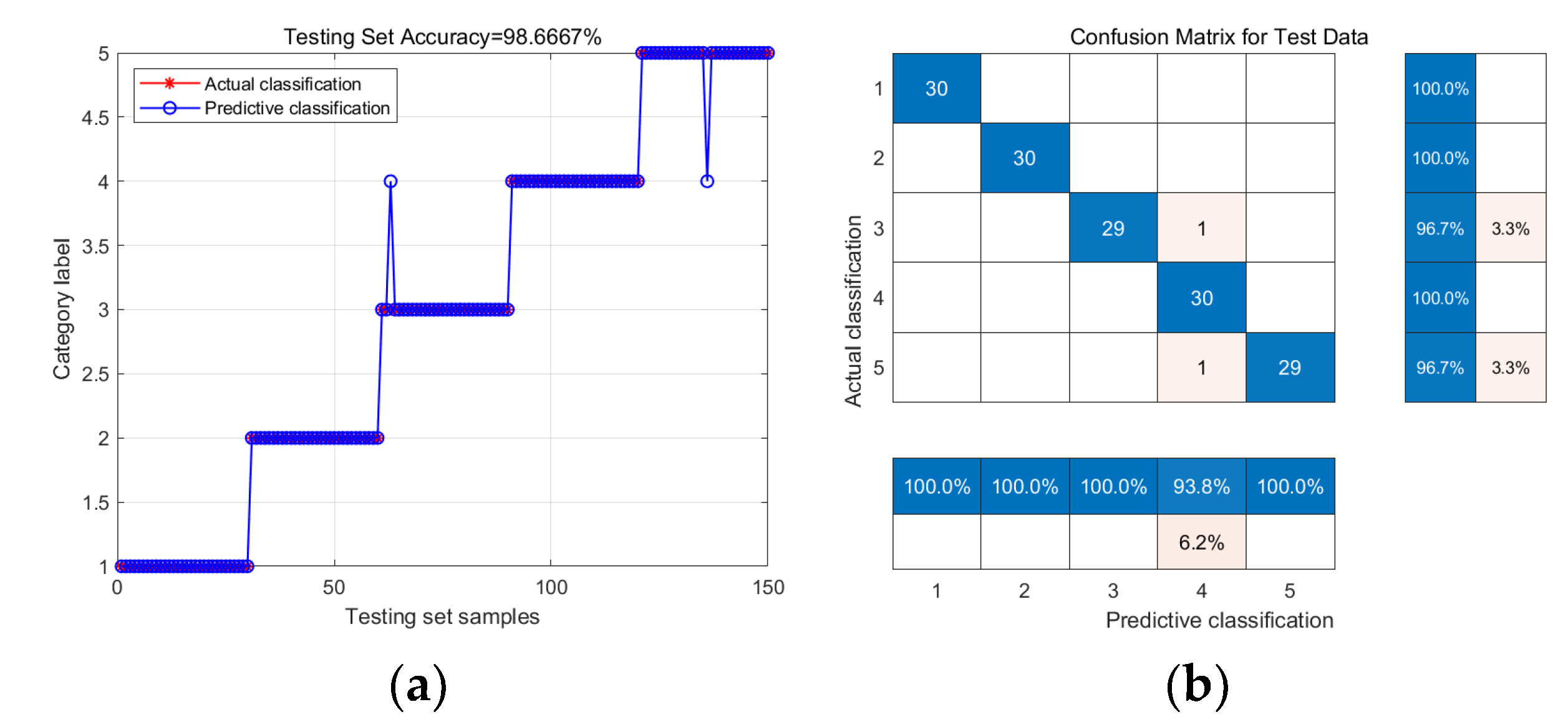
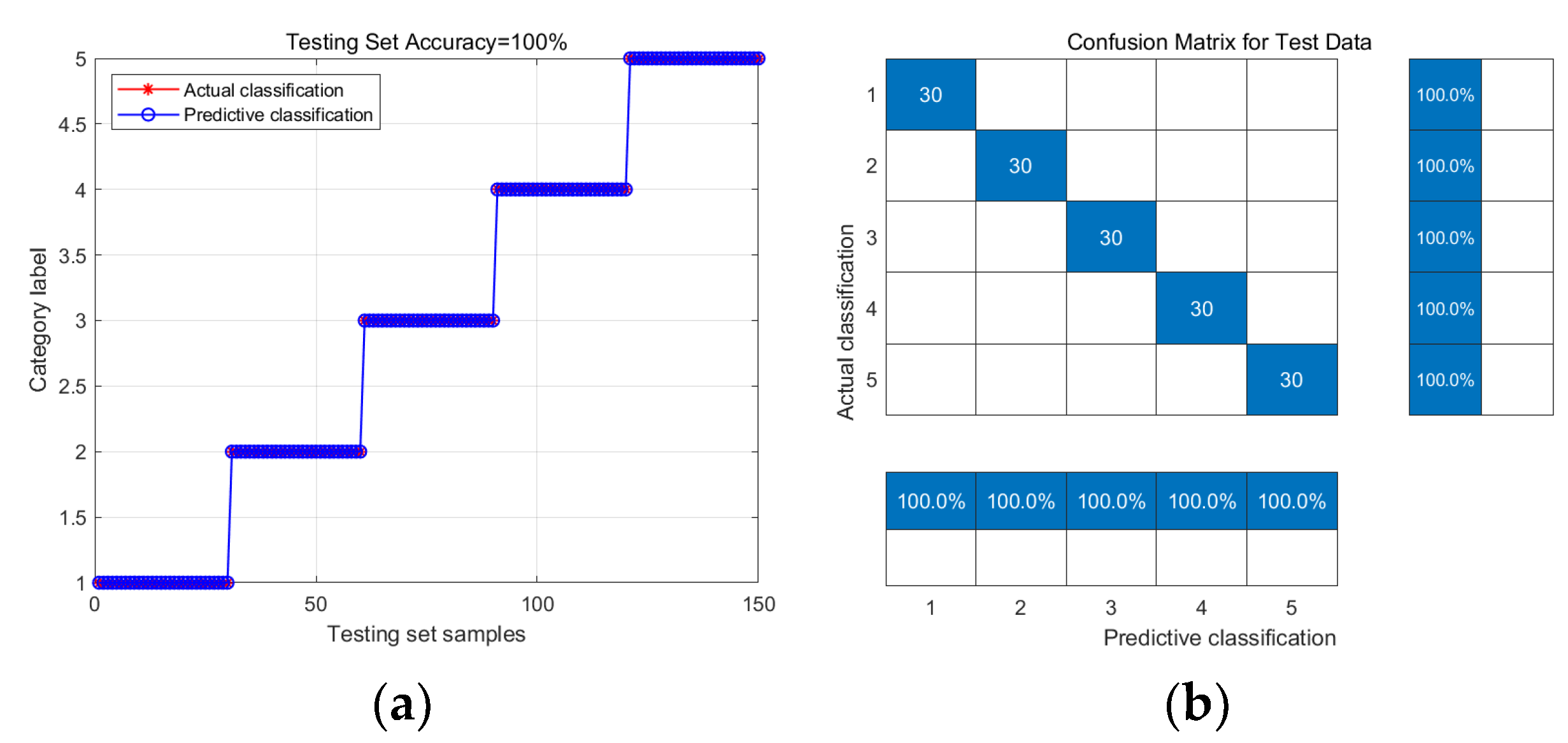
4.3. Fault Diagnosis and Result Analysis
4.3.1. Fault Diagnosis and Result Analysis without Feature Fusion
4.3.2. Fault Diagnosis and Result Analysis with Feature Fusion
5. Conclusions
- (1)
- Compared with KELM, SSA-KELM, and WOA-KELM, the GSWOA-KELM has faster convergence speed, stronger global search capability, and higher recognition accuracy;
- (2)
- When constructing a GSWOA-KELM model for gear fault diagnosis, the GSWOA-KELM performance can be improved by considering the fusion features rather than the single time-domain or frequency-domain features;
- (3)
- Compared to KELM, SSA-KELM, and WOA-KELM, the GSWOA-KELM model proposed in this study improved the fault diagnosis accuracy by 11.33%, 8.67%, and 1.33%, respectively.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hagemann, T.; Ding, H.; Radtke, E.; Schwarze, H. Operating Behavior of Sliding Planet Gear Bearings for Wind Turbine Gearbox Applications—Part II: Impact of Structure Deformation. Lubricants 2021, 9, 98. [Google Scholar] [CrossRef]
- Issaadi, I.; Hemsas, K.E.; Soualhi, A. Wind Turbine Gearbox Diagnosis Based on Stator Current. Energies 2023, 16, 5286. [Google Scholar] [CrossRef]
- Shi, Z.; Liu, S.; Yue, H.; Wu, X. Noise Analysis and Optimization of the Gear Transmission System for Two-Speed Automatic Transmission of Pure Electric Vehicles. Mech. Sci. 2023, 14, 333–345. [Google Scholar] [CrossRef]
- Vasić, M.P.; Stojanović, B.; Blagojević, M. Fault Analysis of Gearboxes in Open Pit Mine. Appl. Eng. Lett. 2020, 5, 50–61. [Google Scholar] [CrossRef]
- Bai, Z.; Ning, Z. Dynamic Responses of the Planetary Gear Mechanism Considering Dynamic Wear Effects. Lubricants 2023, 11, 255. [Google Scholar] [CrossRef]
- De las Morenas, J.; Moya-Fernández, F.; López-Gómez, J.A. The Edge Application of Machine Learning Techniques for Fault Diagnosis in Electrical Machines. Sensors 2023, 23, 2649. [Google Scholar] [CrossRef] [PubMed]
- Ma, G.; Yue, X.; Zhu, J.; Liu, Z.; Lu, S. Deep Learning Network Based on Improved Sparrow Search Algorithm Optimization for Rolling Bearing Fault Diagnosis. Mathematics 2023, 11, 4634. [Google Scholar] [CrossRef]
- Liu, H.; Song, X.; Zhang, F. Fault diagnosis of new energy vehicles based on improved machine learning. Soft Comput. 2021, 25, 12091–12106. [Google Scholar] [CrossRef]
- Zhang, C.; Peng, Z.; Chen, S.; Li, Z.; Wang, J. A Gearbox Fault Diagnosis Method Based on Frequency-Modulated Empirical Mode Decomposition and Support Vector Machine. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 369–380. [Google Scholar] [CrossRef]
- Wang, H.; Yu, Z.; Guo, L. Real-Time Online Fault Diagnosis of Rolling Bearings Based on KNN Algorithm. J. Phys. Conf. Ser. 2020, 1486, 032019. [Google Scholar] [CrossRef]
- Yuan, L.; Lian, D.; Kang, X.; Chen, Y.; Zhai, K. Rolling Bearing Fault Diagnosis Based on Convolutional Neural Network and Support Vector Machine. IEEE Access 2020, 8, 137395–137406. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, Y.; Wu, W.; Cheng, Z.; Su, X.; Lin, A. A Diagnosis Method for the Compound Fault of Gearboxes Based on Multi-Feature and BP-AdaBoost. Symmetry 2020, 12, 461. [Google Scholar] [CrossRef]
- Zhang, W.; Lu, H.; Zhang, Y.; Li, Z.; Wang, Y.; Zhou, J.; Mei, J.; Wei, Y. A Fault Diagnosis Scheme for Gearbox Based on Improved Entropy and Optimized Regularized Extreme Learning Machine. Mathematics 2022, 10, 4585. [Google Scholar] [CrossRef]
- Bai, X.; Ma, Z.; Chen, W.; Wang, S.; Fu, Y. Fault Diagnosis Research of Laser Gyroscope Based on Optimized-Kernel Extreme Learning Machine. Comput. Electr. Eng. 2023, 111, 108956. [Google Scholar] [CrossRef]
- Liang, R.; Chen, Y.; Zhu, R. A Novel Fault Diagnosis Method Based on the KELM Optimized by Whale Optimization Algorithm. Machines 2022, 10, 93. [Google Scholar] [CrossRef]
- Li, X.; Fang, Y.; Liu, L. Kernel Extreme Learning Machine for Flatness Pattern Recognition in Cold Rolling Mill Based on Particle Swarm Optimization. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 270. [Google Scholar] [CrossRef]
- Song, C.; Yao, L.; Hua, C.; Ni, Q. Comprehensive Water Quality Evaluation Based on Kernel Extreme Learning Machine Optimized with the Sparrow Search Algorithm in Luoyang River Basin, China. Environ. Earth Sci. 2021, 80, 521. [Google Scholar] [CrossRef]
- Zhou, F.; Gong, J.; Yang, X.; Han, T.; Yu, Z. A New Gear Intelligent Fault Diagnosis Method Based on Refined Composite Hierarchical Fluctuation Dispersion Entropy and Manifold Learning. Measurement 2021, 186, 110136. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, B.; Xu, S.; Han, T. Fault Diagnosis of Permanent Magnet Synchronous Motor of Coal Mine Belt Conveyor Based on Digital Twin and ISSA-RF. Processes 2022, 10, 1679. [Google Scholar] [CrossRef]
- Li, X.; Zhao, H. Performance Prediction of Rolling Bearing Using EEMD and WCDPSO-KELM Methods. Appl. Sci. 2022, 12, 4676. [Google Scholar] [CrossRef]
- Yuan, X.; Miao, Z.; Liu, Z.; Yan, Z.; Zhou, F. Multi-Strategy Ensemble Whale Optimization Algorithm and Its Application to Analog Circuits Intelligent Fault Diagnosis. Appl. Sci. 2020, 10, 3667. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, G.; Jiao, S.; Wang, J. Bearing Fault Diagnosis Based on Stochastic Resonance and Improved Whale Optimization Algorithm. Electronics 2022, 11, 2185. [Google Scholar] [CrossRef]
- Yang, T.; Li, W.; Huang, Z.; Huang, Z.; Peng, L.; Yang, J. Short-term prediction of wind power generation based on VMD-GSWOA-LSTM model. AIP Adv. 2023, 13, 085215. [Google Scholar] [CrossRef]
- Qi, J.; He, Q.; Jiang, Y.; Xu, Y. Mechanical Fault Diagnosis of Circuit Breakers Based on XGBoost and Time-Domain Features. J. Phys. Conf. Ser. 2020, 1616, 012105. [Google Scholar] [CrossRef]
- Wang, J.; Li, S.; Xin, Y.; An, Z. Gear Fault Intelligent Diagnosis Based on Frequency-Domain Feature Extraction. J. Vib. Eng. Technol. 2019, 7, 159–166. [Google Scholar] [CrossRef]
- Yan, X.; Jia, M. A novel optimized SVM classification algorithm with multi-domain feature and its application to fault diagnosis of rolling bearing. Neurocomputing 2018, 313, 47–64. [Google Scholar] [CrossRef]
- He, Z.; Li, Q.; Chu, M.; Liu, G. Dynamic Weighing Algorithm for Dairy Cows Based on Time Domain Features and Error Compensation. Comput. Electron. Agric. 2023, 212, 108077. [Google Scholar] [CrossRef]
- Zhang, Q.; Huo, R.; Zheng, H.; Huang, T.; Zhao, J. A Fault Diagnosis Method With Bitask-Based Time- and Frequency-Domain Feature Learning. IEEE Trans. Instrum. Meas. 2023, 72, 1–11. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.B.; Wang, D.H.; Lan, Y. Extreme Learning Machines: A Survey. Int. J. Mach. Learn. Cybern. 2011, 2, 107–122. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Wu, Z.; Lu, X. Microgrid Fault Diagnosis Based on Whale Algorithm Optimizing Extreme Learning Machine. J. Electr. Eng. Technol. 2023, 1–10. [Google Scholar] [CrossRef]





| Dimensional | Formula | Dimensionless | Formula |
|---|---|---|---|
| Mean Value | Pulse Factor | ||
| Standard Deviation | Margin Factor | ||
| Root-Mean-Square Value | Waveform Factor | ||
| Maximum Value | Kurtosis | ||
| Minimum Value | Skewness | ||
| Peak-peak Value | Amplitude Factor | ||
| Energy |
| Frequency Domain Characteristic Parameters | Formula |
|---|---|
| Amplitude Mean | |
| Center Frequency | |
| Mean Square Frequency | |
| Root-Mean-Square Frequency | |
| Frequency Variance |
| Fault Type | Fault Description | Classification Label | Sample Number | Total Sample Number | |
|---|---|---|---|---|---|
| Train Set | Test Set | ||||
| Health | Healthy gear. | 1 | 70 | 30 | 100 |
| Chipped | The gear is cracked or even broken. | 2 | 70 | 30 | 100 |
| Miss | Gear defect. | 3 | 70 | 30 | 100 |
| Root | There is a crack at the root of the gear. | 4 | 70 | 30 | 100 |
| Surface | Gear surface wear. | 5 | 70 | 30 | 100 |
| Input | Accuracy Rate |
|---|---|
| T | 86.67% |
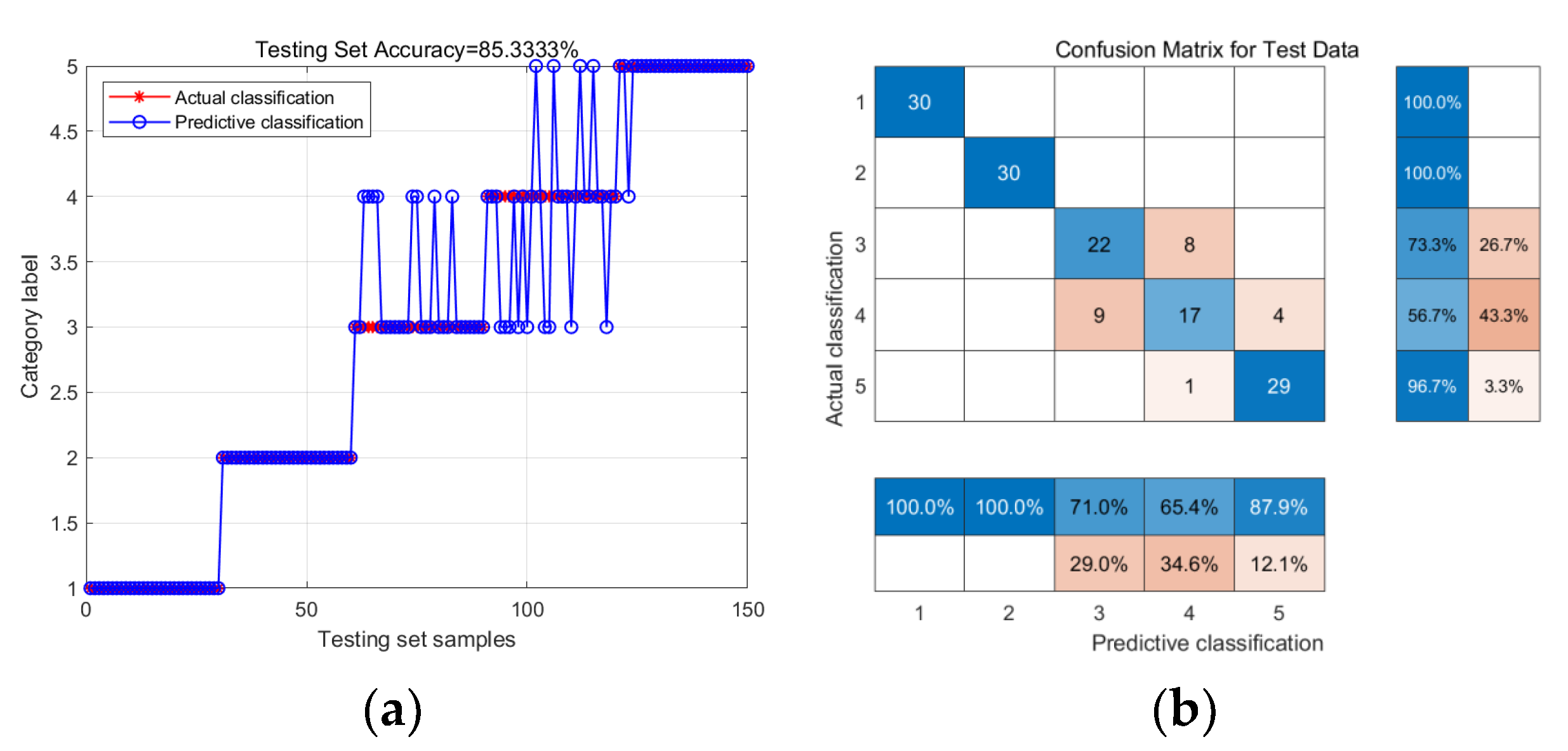
| F | 85.33% |
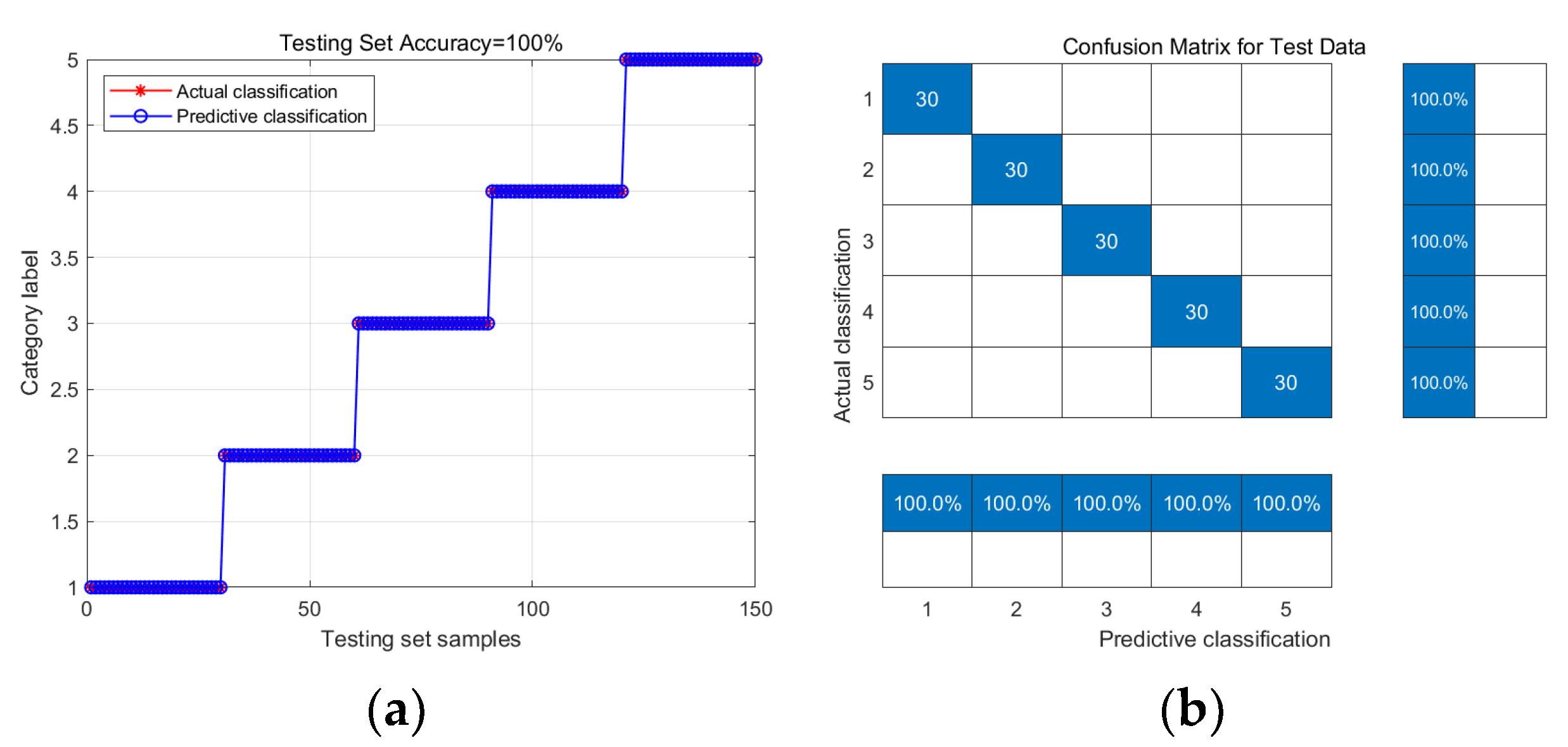
| TF | 100% |
| Fault Diagnosis Model | Fault Type | Accuracy Rate | Overall Accuracy |
|---|---|---|---|
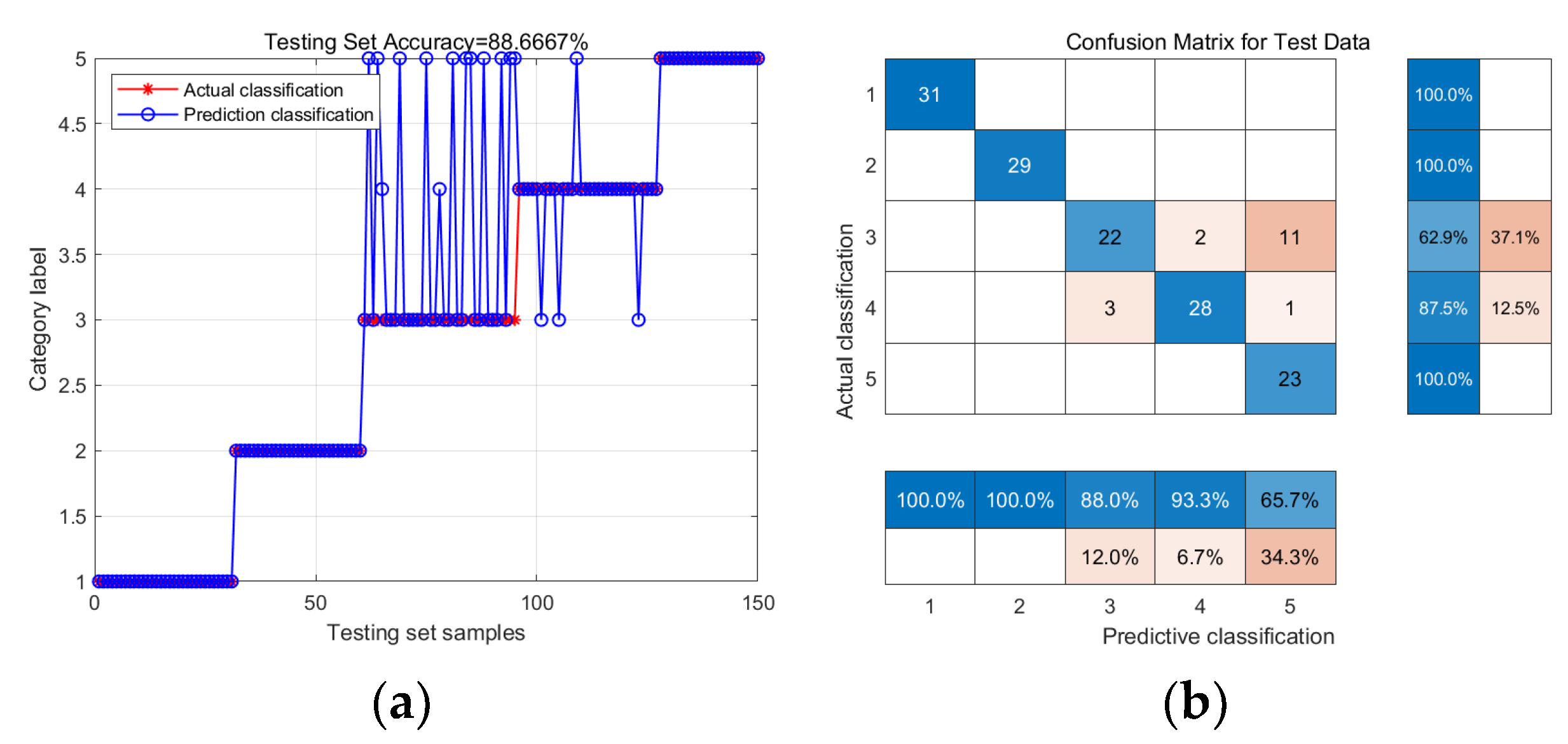
| KELM | Health | 100% | 88.67% |
| Chipped | 100% | ||
| Miss | 88.0% | ||
| Root | 93.3% | ||
| Surface | 65.7% | ||
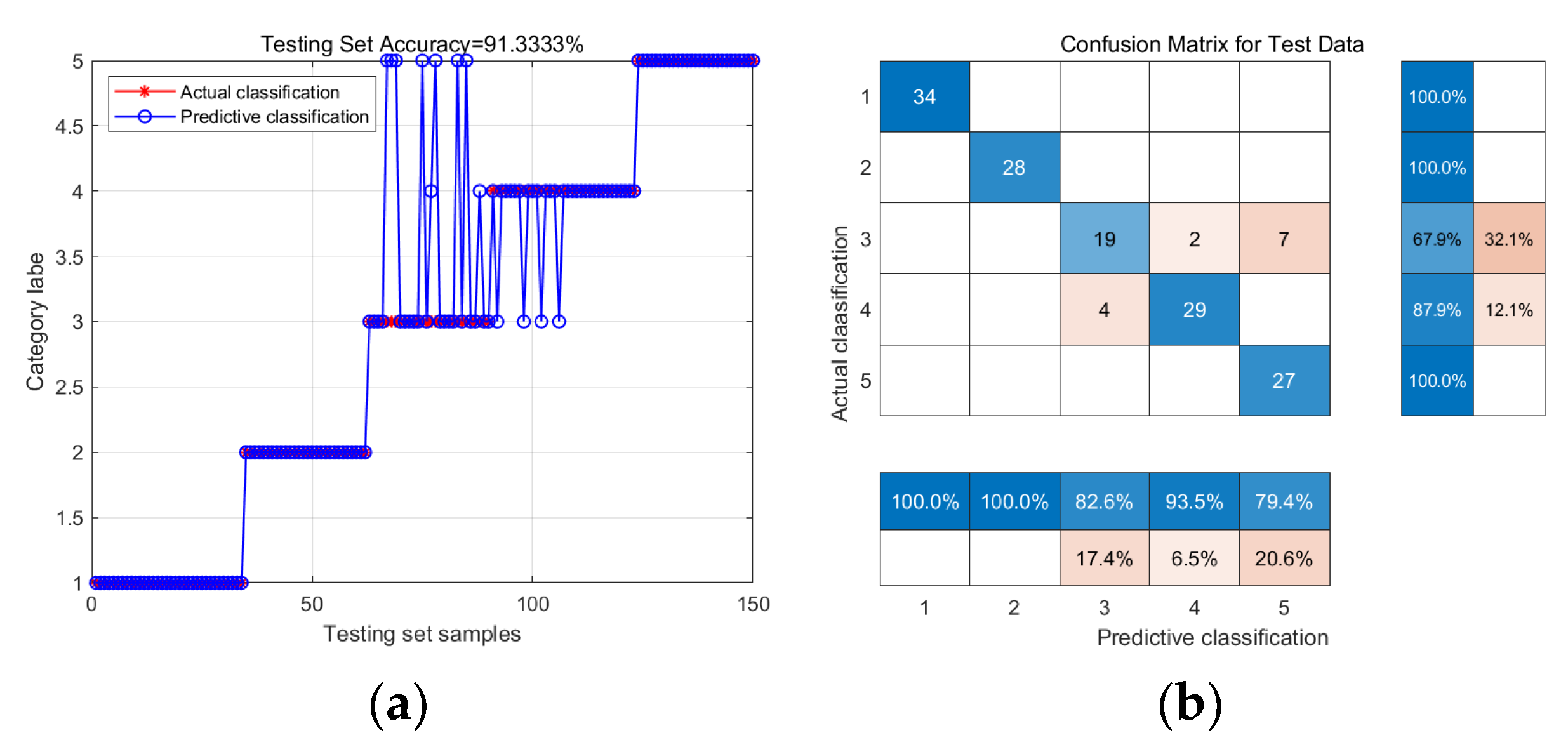
| SSA-KELM | Health | 100% | 91.33% |
| Chipped | 100% | ||
| Miss | 82.6% | ||
| Root | 83.5% | ||
| Surface | 79.4% | ||
| WOA-KELM | Health | 100% | 98.67% |
| Chipped | 100% | ||
| Miss | 100% | ||
| Root | 100% | ||
| Surface | 96.8% | ||
| GSWOA-KELM | Health | 100% | 100% |
| Chipped | 100% | ||
| Miss | 100% | ||
| Root | 100% | ||
| Surface | 100% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Zhou, H.; Wang, C.; Zhu, C.; Shen, J.; He, P. Time-Frequency Fusion Features-Based GSWOA-KELM Model for Gear Fault Diagnosis. Lubricants 2024, 12, 10. https://doi.org/10.3390/lubricants12010010
Hu Q, Zhou H, Wang C, Zhu C, Shen J, He P. Time-Frequency Fusion Features-Based GSWOA-KELM Model for Gear Fault Diagnosis. Lubricants. 2024; 12(1):10. https://doi.org/10.3390/lubricants12010010
Chicago/Turabian StyleHu, Qin, Haiting Zhou, Chengcheng Wang, Chenxi Zhu, Jiaping Shen, and Peng He. 2024. "Time-Frequency Fusion Features-Based GSWOA-KELM Model for Gear Fault Diagnosis" Lubricants 12, no. 1: 10. https://doi.org/10.3390/lubricants12010010
APA StyleHu, Q., Zhou, H., Wang, C., Zhu, C., Shen, J., & He, P. (2024). Time-Frequency Fusion Features-Based GSWOA-KELM Model for Gear Fault Diagnosis. Lubricants, 12(1), 10. https://doi.org/10.3390/lubricants12010010





