Abstract
In this study, we developed the electrical impedance method which simultaneously measures the thickness and breakdown ratio of oil films in elastohydrodynamic (EHD) line contacts within thrust needle roller bearings. Initially, we theoretically demonstrated that the oil film thickness and breakdown ratio can be simultaneously measured using the complex impedance that is produced when an AC voltage is applied to EHD line contacts. To verify the measurement accuracy of the electrical method, we monitored the oil film thickness of a thrust needle roller bearing and compared it with the theoretical value. The results revealed that the oil film thickness was thinner than the theoretical value immediately after starting the test, with the breakdown ratio being greater than 0 (indicating mixed lubrication); however, the breakdown ratio decreased over time, and the oil film thickness nearly matched the theoretical value one hour after starting the test, when it is believed that running-in wear is complete (i.e., breakdown ratio ≈ 0). Furthermore, following the test, after examining the race surface, we confirmed that running-in wear had indeed occurred. These results suggest that the developed method can monitor the lubrication conditions in EHD line contacts, such as those in thrust needle roller bearings, in detail.
1. Introduction
In recent years, due to the growing concern over global warming [], roller bearings that are used in the sliding components of various machines have been required to produce even lower torque. To reduce bearing torque, measures such as decreasing the viscosity of lubricants or reducing the lubricant fill amount have been taken. However, this may promote oil film breakdown in elastohydrodynamic (EHD) contacts [] that use roller bearings, thus leading to various types of surface damage [,,]. Consequently, ideal theoretical lubrication conditions for further reducing the torque of roller bearings may involve thinning the oil film within a contact area as much as possible without causing breakdown. Notably, the thickness and breakdown ratio of oil films in EHD contacts are crucial indices for lubrication conditions. Furthermore, as the impact between the rolling elements and the cage also affect the oil film thickness [], visualization techniques are needed to clarify the actual lubrication conditions of the roller bearings. Numerous studies have explored methods for monitoring the lubrication conditions of EHD contacts. Optical interferometry [,,,,,,,] is particularly popular, as it can accurately measure oil film thickness in EHD contacts. However, it requires the use of light-transmitting materials, and therefore, it cannot determine the lubrication conditions of actual ball bearings. Electrical methods [,,,,,,,,,,,,,,,,,,] can be a potential solution for monitoring the lubrication conditions of non-light-transmitting materials. There are three main types of electrical methods: the electrical resistance method [,,,,], electrical capacitance method [,,,,,,], and electrical impedance method [,,,,,].
First, the electrical resistance method measures the breakdown ratio of oil films by examining the electrical resistance generated in EHD contacts. This method has primarily been employed in research to identify friction and wear mechanisms under mixed lubrication conditions. Lugt et al. [] and Load et al. [] reported on the relationship between test piece surface roughness and the oil film breakdown ratio.
Furthermore, the electrical capacitance method treats the space between two sliding surfaces as a capacitor, and it measures oil film thickness in EHD contacts based on the measured capacitance. Jablonka et al. [,] not only considers the EHD point contacts, but also their surroundings as a capacitor, thus confirming that the oil film measurement accuracy of this method is equivalent to that of optical interferometry. Additionally, other studies have applied these methods to practical deep groove ball bearings to measure oil film thickness in elliptical EHD contacts [,,].
In recent years, the electrical impedance method has been proposed, wherein AC voltage is applied to a contact area, and the thickness and breakdown ratio of oil films are simultaneously measured based on the complex impedance. The authors [] also applied optical interferometry, along with the electrical impedance method, to a ball-on-disc-type apparatus (i.e., point contact), thus confirming that the oil film measurement accuracy of the electrical impedance method matches that of the optical interferometry method. Moreover, we improved the method so that it could be applied to practical ball bearings (i.e., elliptical contacts) with curvatures on rolling surfaces and multiple contact areas []. However, although this method may be applied to point or elliptical contacts, no electrical impedance methods appropriate for EHD line contacts, such as thrust needle roller bearings, have been reported.
Therefore, in this study, we developed an electrical impedance method that could be applicable to EHD line contacts; then, we applied it to actual thrust needle roller bearings and measured the oil film thickness and breakdown ratio simultaneously. This method can accurately monitor the lubrication conditions of actual roller bearings, and it may become a crucial technique for further reducing torque and extending the life of bearings.
2. Measurement Principle
2.1. Outline
In the proposed method, a sinusoidal voltage is applied to EHD line contacts, and the complex impedance of the contacts is measured. Using the modulus and phase of the measured impedance, the oil film thickness and breakdown ratio are quantified. For these quantifications, two types of models (i.e., a “geometrical model” and an “electrical model”) of the contact are required. In this study, the EHD line contacts of practical thrust needle roller bearings are targeted.
2.2. Geometrical Model
Figure 1 depicts a geometrical model of an EHD line contact area and its surroundings under mixed lubrication conditions with a thrust needle roller bearing. Furthermore, the h axis is the axis in the oil film thickness direction, the x axis is the axis in the rolling direction, and the y axis is the axis that is perpendicular to it. Additionally, h1 is the oil film thickness in the oil film-forming part of the contact area, b denotes the contact half-width, r denotes the roller radius, L denotes the straight part of the roller’s length, S1 denotes the apparent contact area, S2 denotes the roller surface area surrounding the contact area (note that S2 in Figure 1 represents the projected area on the xy plane), and α denotes the breakdown ratio (i.e., 0 ≤ α ≤ 1). Consequently, the surface upon which the breakdown (that is, h = 0) occurs in the EHD line contact is represented by αS1, as shown in Figure 1.
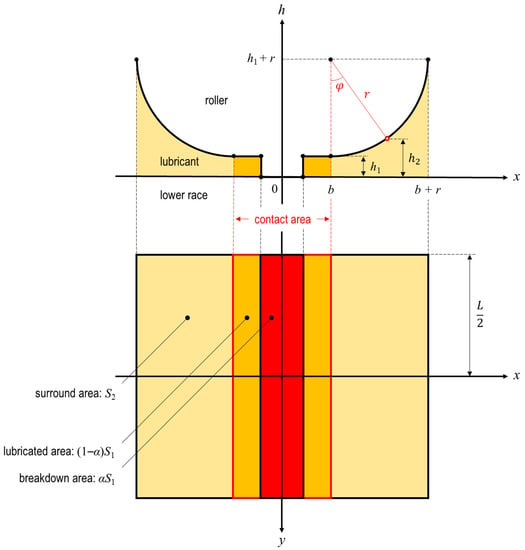
Figure 1.
Geometrical model of a thrust needle roller bearing.
Additionally, h2 in Figure 1 is a function representing the height of a roller surface around a contact area (that is, b ≤ x ≤ b + r), and we use argument , as shown in the figure, to express it in Equation , as follows:
Based on the above equation, in this study, the elastic deformation that occurs when a load is applied is ignored. Additionally, for the sake of the calculation, a model in which the roller’s center is shifted by b in the x-axis direction, as shown in Figure 1 (generally, b + r ≈ r from b ≪ r), is adopted, and it is assumed that it is completely filled with lubricant, at least in the area of x = b + r. Here, our past study [] confirmed that even if starved lubrication occurs in an area around a contact area that is not sufficiently filled with lubricant [,,], then the effect on the accuracy of the oil film measurement is negligible.
2.3. Electrical Model
Subsequently, Figure 2 shows the equivalent electric circuit of the thrust needle roller bearing. More specifically, R1 in Figure 2 denotes the electrical resistance in areas wherein oil film is breaking down, C1 denotes the capacitance in the oil film formed area within an EHD line contact, and C2 denotes the capacitance in the straight part of the roller around an EHD line contact, respectively. As shown in Figure 2, in this study, it is assumed that all contact areas are represented by the same equivalent circuit. The contact areas in the upper and lower races are connected in their respective series circuits, and these are joined by parallel circuits, which are equal in number to the rolling elements. This implies that this method determines the average value of the oil film thickness and breakdown ratio in all contact areas. In Figure 2, R1, C1, and C2 are each represented by their respective equations, as follows:
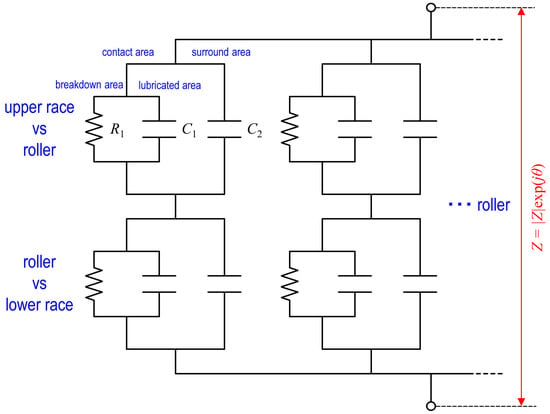
Figure 2.
Electrical model of a thrust needle roller bearing. R1: resistance in breakdown area; C1: capacitance in lubricated area within EHD line contact; and C2: capacitance in the straight area of the roller surrounding the EHD line contact.
Here, ε represents the dielectric constant of the lubricating oil, and R10 denotes the electrical resistance under a stationary contact (i.e., α = 1). Generally, h1 ≪ r; hence, Equation can be approximated as shown in Equation below.
2.4. Complex Impedance Analysis
The alternating voltage V = V(t) (as the input) and alternating current I = I(t) (as the output) can be expressed, respectively, in the following complex forms:
where j denotes the imaginary unit and t denotes time. Equations and imply that by applying the alternating voltage to the angular frequency ω and amplitude |V|, we obtain the alternating current with the amplitude |I| and phase θ operating at the same angular frequency ω. Then, the complex impedance Z can be expressed as follows:
It should be noted that the modulus |Z| (= |V|/|I|) and phase θ of the complex impedance Z are obtained from the electrical impedance measurement. Additionally, the complex impedance Z of the entire equivalent circuit shown in Figure 2 is determined by Equation , shown below, if n is the number of rolling elements in a thrust needle roller bearing.
More specifically, Equations and are obtained from Equations and .
Accordingly, using Equations , Equations and can be expressed as the equations below.
Based on Equation , the oil film breakdown ratio α can be expressed as follows:
Furthermore, based on Equation , h1 can be obtained from the following equation.
Here, the dimensionless number in Equation , shown above, can be obtained from the following equation.
In this study, we determined the average oil film thickness of the EHD line contacts; hence, if an oil film breakdown occurs in part of a contact area, then can be obtained from Equation using α and h1.
As shown above, the oil film thickness and oil film breakdown ratio in the EHD line contacts of a thrust needle roller bearing can be theoretically obtained from Equations and .
3. Experimental Details
3.1. Apparatus
We verified the measurement accuracy of the electrical impedance method using the bearing tester depicted in Figure 3. The test bearing was a thrust needle roller bearing, and we employed a spring to apply an axial load Fa. To apply the electrical impedance method to this bearing, a carbon brush pressed against the rotating shaft was used to introduce an AC voltage from a LCR meter between the upper and lower races. Additionally, by using a rubber timing belt for the rotating shaft, power was transmitted in an insulated state from the motor. A ceramic ball was set between the spring and the lower race, thus applying the axial load to the test bearing. The use of a ceramic ball allowed the AC voltage to be applied only to the test bearing, and it also prevented the lower race from tilting against the rollers. This tester was not only capable of simultaneously measuring the average oil film thickness and oil film breakdown ratio α, but also the lower race temperature T and bearing torque M. T was measured by attaching a thermocouple to the lower race, whereas M was measured using a torque meter.
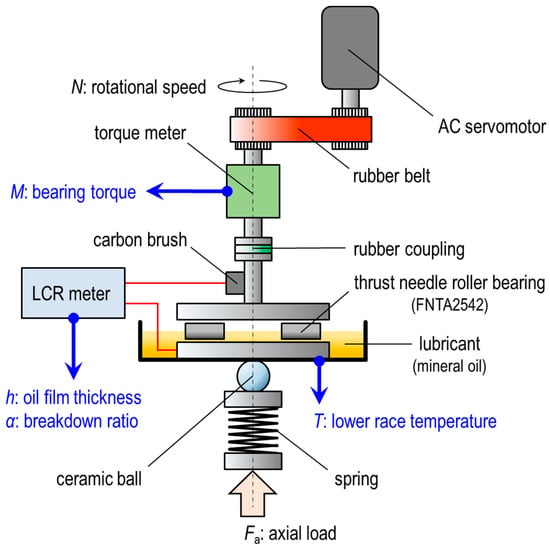
Figure 3.
Schematic diagram of the experimental apparatus.
3.2. Materials
Figure 4 shows an image of the external appearance of the test bearing used in this study. The test bearing was a thrust needle roller bearing FNTA2542 (inner diameter: 25 mm, outer diameter: 42 mm), n = 30, roller radius r = 1.0 mm, length of the roller’s straight part L = 4.6 mm, roller’s total length Lt = 5.6 mm, and roller end face chamfer curvature rc = 0.5 mm. Additionally, the roller material was SUJ2 (Young’s modulus: 208 GPa, Poisson’s ratio: 0.3). Furthermore, the material of the upper and lower races used in this test (inner diameter: 25 mm, outer diameter: 42 mm, thickness: 1.0 mm) was SK5 (Young’s modulus: 206 GPa, Poisson’s ratio: 0.3), and the material of the cage was SPCC (Young’s modulus: 205 GPa, Poisson’s ratio: 0.3). Additionally, the root-mean-square roughness, Rq1 and Rq2, of the rollers and upper and lower races are Rq1 = 0.15 μm and Rq2 = 0.12 μm, respectively. As the test bearing is an actual product and the manufacturing errors of the rollers and races (roundness, waviness, etc.) vary within their respective tolerances, the experimental results are affected by these factors; however, the developed method measures the average value of the total contact area when an axial load is applied, which mitigates the effects of the variation.

Figure 4.
Photograph of a thrust needle roller bearing (FNTA2542) and the upper and lower races.
The lubricant used in the test was mineral oil (kinematic viscosity at 40 °C: ν = 32 mm2/s), and the test was conducted using oil lubrication. The relative permittivity εoil of the mineral oil was εoil ≈ 2.1 in the AC frequency range f = 20 Hz to 1.0 MHz, so the oil film thickness was calculated by assuming that ε = εoilε0 = 2.1ε0 F/m. Note that the dielectric constant of vacuum ε0 = 8.85 × 10−12 F/m.
3.3. Procedure
In this study, the test bearing was first ultrasonically cleaned using heptane and ethanol, then, the upper race was pressed into the rotating shaft of the tester to set the test bearing. After pouring mineral oil into an oil bath, we applied a sinusoidal voltage (RMS amplitude: Ve = 1.1 V, AC frequency: f = 10 kHz) while loading an axial load Fa = 1.5 kN onto the test bearing. Before rotating the bearing, we first measured the initial complex impedance Z0 using stationary contacts (i.e., α = 1). Based on the value of Z0, the electrical resistance R10 in Equation can be obtained using the following equation.
Provided that |Z0| and θ0 in Equation are the magnitude and phase of Z0, we found that by substituting Equation into Equation , α is not affected by n. Subsequently, the upper race of the test bearing was rotated at a speed of N = 3000 min−1 for 5 h, and |Z|, θ, T, and M, using dynamic contacts, were simultaneously measured (sampling rate: 0.5 Hz). The average oil film thickness obtained using the electrical impedance method was compared with the theoretical central oil film thickness measurement that was derived using the Ertel–Grubin equation [] in order to verify the oil film measurement accuracy. Here, the theoretical oil film thickness was calculated using the viscosity of the lubricant obtained from the lower race temperature T; this varied over time. The wear track formed on the lower race after the test was observed using an optical microscope, and the surface roughness was measured using an optical interference microscope.
4. Experimental Results
4.1. Measurements of |Z| and θ
With an axial load of Fa = 1.5 kN, in a practical thrust needle roller bearing, Figure 5 shows the measured values of the modulus |Z| (upper) and phase θ (lower) of the complex impedance Z at a rotational speed of N = 3000 min−1. |Z| varied from 0.03 kΩ to 30 kΩ, approximately, and θ varied from 0° to –85°, approximately, under experimental conditions. In the following section, the average oil film thickness and breakdown ratio α will be quantified using |Z| and θ.
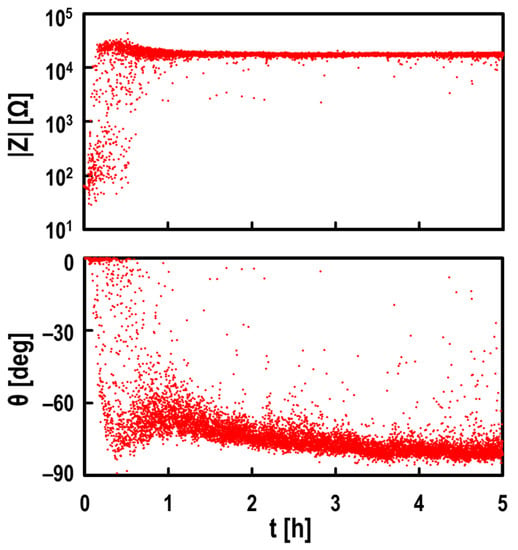
Figure 5.
Time evolution of the measured modulus |Z| (top) and phase θ (bottom); bearing: FNTA2542, lubricant: mineral oil, rotational speed: N = 3000 min−1, axial load: Fa = 1.5 kN, RMS amplitude: Ve = 1.1 V and frequency: f = 10 kHz; red plots in graphs: measured values by LCR meter.
4.2. Measurements of h, α, T, and M
Figure 6 shows the results of measuring the average oil film thickness , oil film breakdown ratio α, lower race temperature T, and bearing torque M using the test bearing. Based on Figure 6, it can be determined that the that was obtained using this method is in good agreement with the theoretical central oil film thickness T (black dashed line in the figure, derived from the Ertel–Grubin equation []). However, in the first hour after the start of the test, there was a large variation in , with many values indicating a thinner oil film thickness than the theoretical oil film thickness; nevertheless, these values approached the theoretical value. On the other hand, from the first hour α ≈ 0, α decreased over time. At this point, T and M also reached almost constant values. Hence, it appears that the running-in wear was completed in approximately an hour under these test conditions.
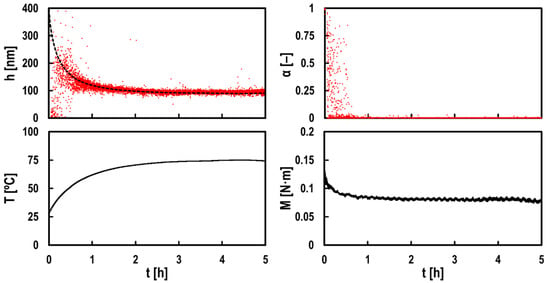
Figure 6.
Time evolution of the measured oil film thickness h (top left), breakdown ratio α (top right), lower race temperature T (bottom left), and bearing torque M (bottom right); bearing: FNTA2542, lubricant: mineral oil, rotational speed: N = 3000 min−1 and axial load: Fa = 1.5 kN; red plots in graphs: measured values using the electrical impedance method; black broken line in top left graph: theoretical prediction at T using the Ertel–Grubin equation [].
4.3. Observations of Tested Bearing
Figure 7a shows the results of observing a wear track using an optical microscope, and Figure 7b shows the results of measuring the surface roughness profile near the wear track boundary using an optical interference microscope. Asperities of 100 nm or more, observed in the undamaged area (right half of Figure 7b), could not be confirmed as being inside of the wear track (left half of Figure 7b). In addition, the surface roughness in the wear track was less than that in the undamaged part (Rq2 = 0.12 μm to 0.08 μm). Figure 6 shows that the value of after one hour was also approximately 100 nm with no breakdown area; thus, it is thought that the asperities that were greater than the oil film thickness were worn, and running-in wear was completed.
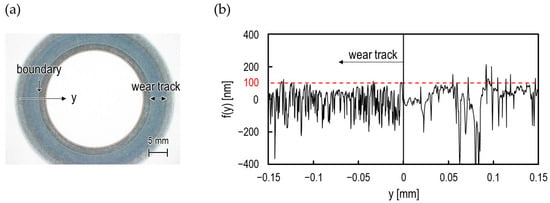
Figure 7.
Observations of the lower race surface after the experiment; (a) photograph of the wear track and (b) surface roughness profile around the boundary of the wear track; black vertical line at y = 0 in (b): boundary of the wear track; red broken line in (b): f(y) = 100 nm.
5. Discussion
5.1. Validation of Measured h-Values
In this study, as shown in Figure 1 and Figure 2, the capacitance C2c generated in the chamfer of the roller end face was ignored, and oil film thickness was determined using the capacitance C2 generated only in the straight part of the roller. However, to be precise, the oil film thickness should be calculated using the total capacitance C2t, which reflects the actual roller shape, including the chamfer of the roller end face. Therefore, we calculated C2t using the finite element method (FEM) [], and we compared it with the C2 obtained from Equation . The simulations were performed using COMSOL® Multiphysics (version 6.0), employing the AC/DC module. More specifically, the simulations were performed by assuming that the roller and race were made of steel and filled with test oil (mineral oil). The race and analytical boundary were grounded, and a potential of 1 V was applied to the roller. Figure 8 shows the triangular mesh that was automatically assigned by the software to the roller and race geometry that was used in the simulations. Furthermore, in this simulation, we did not consider elastic deformation (i.e., Fa = 0 N). Hence, given that this FEM analysis does not consider C1 occurring in the EHD line contact, it implies that it can simply be compared with C2, as obtained from Equation .
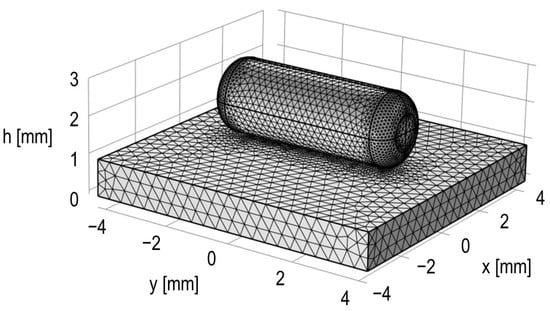
Figure 8.
Triangular mesh used for simulations; radius of roller: r = 1.0 mm, length of roller straight area: L = 4.6 mm, chamfer curvature at roller edge: rc = 0.5 mm and total length of roller: Lt = 5.6 mm.
Figure 9 shows the results of comparing C2 and C2t when changing the oil film thickness h1 (see Figure 1) under hydrodynamic lubrication (i.e., α = 0) conditions, assuming that the roller’s surroundings are sufficiently filled with the mineral oil used in this test. In accordance with Figure 9, it was found that C2 closely agrees with C2t in the range of h1 < 1 μm, even though C2 only calculates the capacitance in the straight part of the roller. However, in the range where h1 > 1 μm, C2t is slightly larger than C2. Furthermore, we found that this difference gradually widens as h1 thickens. For reference, C1 at Fa = 1.5 kN, obtained using Equation , is also shown in Figure 9. In the range of h1 < 30 nm, C1 is larger than C2; despite this, C2 significantly affects the accuracy of the oil film measurement.
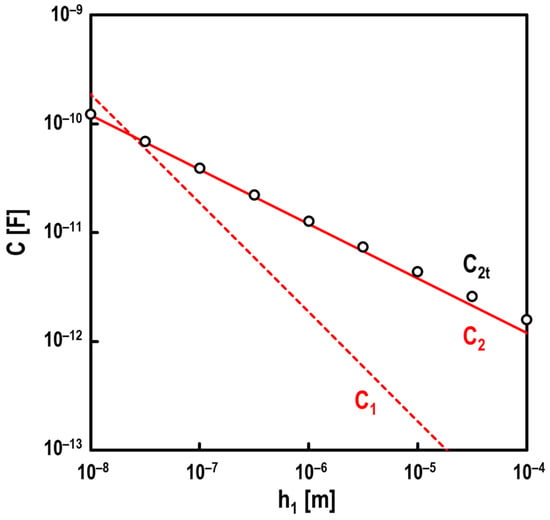
Figure 9.
Effect of a chamfer at the roller edge on capacitance between the roller and race for varying oil film thickness h1 with no breakdown area (i.e., α = 0); lubricant: mineral oil and Fa = 0 N; red line in graph: theoretical prediction C2 using Equation ; black open circles in graph: simulated values C2t using COMSOL® Multiphysics; red broken line in graph: theoretical prediction C1 at Fa = 1.5 kN using Equation .
Figure 10 shows the results of analyzing the electric field distribution at h1 = 100 μm. In Figure 10, it is determined that the electric field generated at the chamfer of the roller end face cannot be ignored when h1 is thick. In other words, the thicker h1 is, the more C2c cannot be ignored, which is thought to have led to the results shown in Figure 9. However, the oil film thickness in EHD line contacts is generally less than 1 μm, thus suggesting that ignoring C2c does not significantly affect oil film measurement accuracy (see Figure 6).
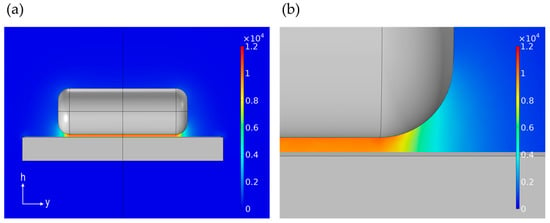
Figure 10.
Electric field distribution in the yh plane at x = 0; (a) the entire view of simulation and (b) the enlarged view of the chamfer at the roller edge; oil film thickness: h1 = 100 μm, lubricant: mineral oil and Fa = 0 N; color bar in simulated results: electric field strength: E [V/m].
Next, we discuss the length of the roller’s straight part L, for which C2c cannot be ignored. Figure 11 shows the results of the calculating relationship between h1 and C2/C2t for varying L/Lt at r = 1.0 mm and rc = 0.5 mm. From Figure 11, we found that as L/Lt increases, C2/C2t increases (i.e., the effects of C2c become smaller). However, we also found that even if L/Lt is relatively small, and the lower h1 is, the more C2c can be ignored. Given that L/Lt ≈ 0.82 for the rollers used in the bearing test, it is thought that the electrical impedance method developed in this study has a sufficient oil film measurement accuracy within the range of h1 < 1 μm, as shown in Figure 11.
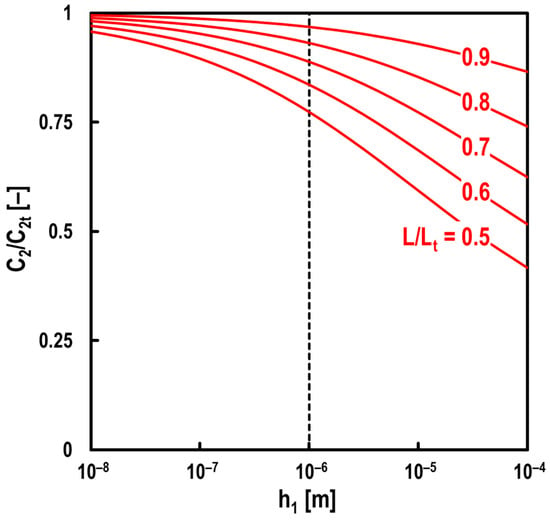
Figure 11.
Relationship between the oil film thickness h1 and ratio of C2/C2t for the varying ratio of L/Lt with no breakdown area (i.e., α = 0); lubricant: mineral oil, Fa = 0 N, radius of roller: r = 1.0 mm and chamfer curvature at roller edge: rc = 0.5 mm; red lines in graph: theoretical prediction using Equation and COMSOL® Multiphysics; black broken line in graph: h1 = 1 μm.
5.2. Validation of Measured α-Values
To confirm the validity of α, which was obtained using the electrical impedance method developed in this study, the oil film parameter Λ was calculated, which is the ratio of the measured oil film thickness and surface roughness, and we examined its relationship with breakdown ratio α. More specifically, Λ is determined using the following equation [].
Provided that in Equation is the mean oil film thickness that was measured using the developed method, and Rq1 and Rq2 denote the root-mean-square roughness of the roller and lower race before the test, Figure 12 shows the relationship between Λ and α. From Figure 12, we can determine that when Λ < 3, α increases as Λ decreases, although the variation is large. Johnson et al. [] predicted that the number of asperity contacts within the EHD contact was given by a Poisson distribution, and they pointed out that theoretically, the oil film breaks at Λ < 3. Hence, Figure 12 suggests that this method can quantitatively evaluate and α simultaneously. Furthermore, the reason for the large variation in the test results shown in Figure 12 is that the test conditions are accompanied by running-in wear, as shown in Figure 7. Additionally, Figure 6 shows that α, as well as , decreased with time, except immediately after starting the test, finally reaching α ≈ 0 and ≈ 100 nm. This result is also expected to support the idea of progressive running-in wear in EHD line contacts.
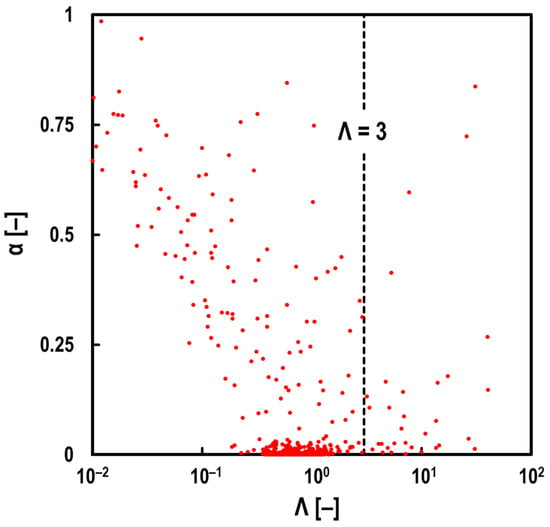
Figure 12.
Relationship between film parameter Λ and breakdown ratio α; bearing: FNTA2542, lubricant: mineral oil, rotational speed: N = 3000 min−1 and axial load: Fa = 1.5 kN; red plots in graph: measured values using the electrical impedance method; black broken line in graph: Λ = 3.
6. Conclusions
In this study, we developed an electrical impedance method that can be applied to EHD line contacts. Furthermore, we applied this method to an actual thrust needle roller bearing to simultaneously measure the thickness and breakdown ratio of oil films; then, we verified the measurement accuracy. The findings obtained in this study are as follows:
- We theoretically demonstrated that the thickness and breakdown ratio of oil films can be simultaneously measured using the complex impedance generated when a sinusoidal voltage is applied to EHD line contacts.
- We applied the developed method to an actual thrust needle bearing, and we simultaneously measured the oil film thickness and breakdown ratio. The oil film thickness and breakdown ratio fluctuated significantly immediately after starting the test, but the breakdown ratio decreased over time. Furthermore, the oil film thickness after one hour was thought to be completed when the running-in wear was found to almost match the theoretical value. It was also confirmed that the lower race temperature and bearing torque were both constant values at that time, thus indicating that the lubricated condition was stable.
- Based on the results of measuring the surface roughness of the lower race after the test, asperities of 100 nm or more, observed in the undamaged part, were not found in the wear track. One hour after the start of the test, the oil film thickness was also approximately 100 nm, and there was no breakdown area; it is thought that running-in wear was almost completed at this time.
- When using this method, the oil film thickness in the EHD line contacts is determined by ignoring the capacitance generated in the chamfer of the roller end face. As a result of calculating the capacitance in the actual roller shape using FEM, we confirmed that there is generally no problem in ignoring the capacitance that occurs in the chamfer of the roller end face. However, this suggests that when the length of the roller’s straight part is relatively short compared with the total length of roller, the capacitance occurring in the chamfer part of the roller end face cannot be ignored.
- We clarified the relationship between the oil film parameter Λ and breakdown ratio α in EHD line contacts. When Λ < 3, we found that α tended to increase as Λ decreased. The reason for the large variation in the obtained test results is that running-in wear occurred in this study.
This developed method can simultaneously monitor the thickness and breakdown ratio of oil films in EHD line contacts, and thus, it may become a very important technique for further lowering the torque and extending the life of thrust needle roller bearings. Additionally, it is considered to be very effective as a lubrication condition monitoring technique, and it can be applied to actual rolling bearings.
7. Patents
The patents related to this study are shown below.
Method for Diagnosing Rolling Device, WO-2018128062-A1, https://app.dimensions.ai/details/patent/WO-2018128062-A1 (accessed on 14 May 2023).
Bearing Device State Detecting Method, Detecting Device, and Program, WO-2022250060-A1, https://app.dimensions.ai/details/patent/WO-2022250060-A1 (accessed on 14 May 2023).
Author Contributions
Conceptualization, T.M., M.M. and K.N.; methodology, T.M. and K.N.; software, T.M.; validation, T.M., F.R., T.S., S.I. and M.M.; formal analysis, T.M.; investigation, T.M. and F.R.; resources, T.M., F.R. and T.S.; data curation, T.M., F.R. and T.S.; writing—original draft preparation, T.M.; writing—review and editing, F.R. and K.N.; visualization, T.M.; supervision, K.N.; project administration, T.M. and K.N.; funding acquisition, T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Acknowledgments
In writing this paper, I received much advice through discussions conducted with Fumihiro Itoigawa and Satoru Maegawa of Nagoya Institute of Technology. Furthermore, Guajardo Duenas Guillermo Andres, Fumiaki Aikawa, Satoshi Momozono, Michita Hokao and Nobuaki Mitamura of NSK Ltd. provided much support for this work. I would like to express my gratitude to these people.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Hertzian halfwidth | [m] | |
| f | AC frequency | [Hz] |
| f(y) | height of surface roughness in y-axis direction | [m] |
| h | coordinate perpendicular to the xy plane | [m] |
| h1 | oil film thickness in lubricated area | [m] |
| h2 | oil film thickness in surrounding area expressed as | [m] |
| mean oil film thickness expressed as | [m] | |
| j | imaginary unit | [–] |
| n | number of rollers per bearing | [–] |
| radius of roller | [m] | |
| chamfer curvature at roller edge | [m] | |
| t | time | [s] |
| x | coordinate in rolling direction | [m] |
| y | coordinate across rolling direction | [m] |
| C1 | capacitance in lubricated area within EHD line contact | [F] |
| C2 | capacitance in roller straight area surrounding EHD line contact | [F] |
| C2c | capacitance in chamfer area | [F] |
| C2t | total capacitance between roller and race reflecting actual geometry | [F] |
| E | electric field strength | [V/m] |
| Fa | axial load | [N] |
| I | alternating current expressed as | [A] |
| |I| | amplitude of alternating current | [A] |
| L | length of roller straight area | [m] |
| Lt | total length of roller | [m] |
| M | bearing torque | [N·m] |
| N | rotational speed of upper race | [s−1] |
| R1 | resistance in breakdown area under a dynamic contact | [Ω] |
| R10 | resistance of the breakdown area under a stationary contact (i.e., α = 1) | [Ω] |
| root mean square roughness of roller | [m] | |
| root mean square roughness of lower race | [m] | |
| S1 | Hertzian contact area | [m2] |
| S2 | roller surface area surrounding EHD line contact | [m2] |
| T | lower race temperature | [°C] |
| V | sinusoidal voltage expressed as | [V] |
| |V| | amplitude of sinusoidal voltage | [V] |
| Ve | RMS amplitude of sinusoidal voltage expressed as | [V] |
| Z | complex impedance expressed as | [Ω] |
| |Z| | modulus of complex impedance under dynamic contacts | [Ω] |
| |Z0| | modulus of complex impedance under stationary contacts | [Ω] |
| α | breakdown ratio of oil films | [–] |
| ε | dielectric constant of lubricant expressed as | [F/m] |
| ε0 | dielectric constant of vacuum | [F/m] |
| εoil | relative permittivity of lubricant | [–] |
| θ | phase of complex impedance under dynamic contacts | [deg] |
| θ0 | phase of complex impedance under stationary contacts | [deg] |
| ν | kinematic viscosity of lubricant | [m2/s] |
| φ | polar angle | [rad] |
| ω | angular frequency of AC voltage expressed as | [rad/s] |
| Λ | film parameter expressed as | [–] |
| dimensionless number expressed as | [–] |
References
- Yin, J.; Overpeck, J.; Peyser, C.; Stouffer, R. Big Jump of Record Warm Global Mean Surface Temperature in 2014–2016 Related to Unusually Large Oceanic Heat Releases. Geophys. Res. Lett. 2018, 45, 1069–1078. [Google Scholar] [CrossRef]
- Gohar, R.; Cameron, A. The Mapping of Elastohydrodynamic Contacts. ASLE Trans. 1967, 10, 215–225. [Google Scholar] [CrossRef]
- Tallian, T.E. On Competing Failure Modes in Rolling Contact. ASLE Trans. 1967, 10, 418–439. [Google Scholar] [CrossRef]
- Maruyama, T.; Saitoh, T.; Yokouchi, A. Differences in Mechanisms for Fretting Wear Reduction between Oil and Grease Lubrication. Tribol. Trans. 2017, 60, 497–505. [Google Scholar] [CrossRef]
- Schneider, V.; Behrendt, C.; Höltje, P.; Cornel, D.; Becker-Dombrowsky, F.M.; Puchtler, S.; Gutiérrez Guzmán, F.; Ponick, B.; Jacobs, G.; Kirchner, E. Electrical Bearing Damage, A Problem in the Nano- and Macro-Range. Lubricants 2022, 10, 194. [Google Scholar] [CrossRef]
- Liu, J.; Ni, H.; Zhou, R.; Li, X.; Xing, Q.; Pan, G. A Simulation Analysis of Ball Bearing Lubrication Characteristics Considering the Cage Clearance. ASME J. Tribol. 2023, 145, 044301. [Google Scholar] [CrossRef]
- Johnston, G.J.; Wayte, R.; Spikes, H.A. The Measurement and Study of Very Thin Lubricant Films in Concentrated Contacts. Tribol. Trans. 1991, 34, 187–194. [Google Scholar] [CrossRef]
- Kaneta, M.; Sakai, T.; Nishikawa, H. Effects of Surface Roughness on Point Contact EHL. Tribol. Trans. 1993, 36, 605–612. [Google Scholar] [CrossRef]
- Sugimura, J.; Jones, W.R.; Spikes, H.A. EHD Film Thickness in Non-steady State Contacts. ASME J. Tribol. 1998, 120, 442–452. [Google Scholar] [CrossRef]
- Kaneta, M.; Ozaki, S.; Nishikawa, H.; Guo, F. Effects of Impact Loads on Point Contact Elastohydrodynamic Lubrication Films. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2007, 221, 271–278. [Google Scholar] [CrossRef]
- Maruyama, T.; Saitoh, T. Oil Film Behavior under Minute Vibrating Conditions in EHL Point Contacts. Tribol. Int. 2010, 43, 1279–1286. [Google Scholar] [CrossRef]
- Kaneta, M.; Nishikawa, H.; Kanada, T.; Matsuda, K. Abnormal Phenomena Appearing in EHL Contacts. ASME J. Tribol. 1996, 118, 886–892. [Google Scholar] [CrossRef]
- Yagi, K.; Vergne, P. Abnormal Film Shapes in Sliding Elastohydrodynamic Contacts Lubricated by Fatty Alcohols. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2007, 221, 287–300. [Google Scholar] [CrossRef]
- Nakano, K.; Spikes, H.A. Process of Boundary Film Formation from Fatty Acid Solution. Tribology Online 2012, 7, 1–7. [Google Scholar] [CrossRef]
- Spikes, H.A. Triboelectrochemistry: Influence of Applied Electrical Potentials on Friction and Wear of Lubricated Contacts. Tribol. Lett. 2020, 68, 90. [Google Scholar] [CrossRef]
- Furey, M.J. Metallic Contact and Friction between Sliding Surfaces. ASLE Trans. 1961, 4, 1–11. [Google Scholar] [CrossRef]
- Chu, P.S.Y.; Cameron, A. Flow of Electric Current Through Lubricated Contacts. ASLE Trans. 1967, 10, 226–234. [Google Scholar] [CrossRef]
- Lugt, P.M.; Severt, R.W.M.; Fogelström, J.; Tripp, J.H. Influence of Surface Topography on Friction, Film Breakdown and Running-in in the Mixed Lubrication Regime. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2001, 215, 519–533. [Google Scholar] [CrossRef]
- Lord, J.; Larsson, R. Film-forming Capability in Rough Surface EHL Investigated Using Contact Resistance. Tribol. Int. 2008, 41, 831–838. [Google Scholar] [CrossRef]
- Clarke, A.; Weeks, I.J.J.; Evans, H.P.; Snidle, R.W. An Investigation into Mixed Lubrication Conditions Using Electrical Contact Resistance Techniques. Tribol. Int. 2016, 93, 709–716. [Google Scholar] [CrossRef]
- Crook, A.W. Elastohydrodynamic Lubrication of Rollers. Nature 1961, 190, 1182–1183. [Google Scholar] [CrossRef]
- Prashada, H. Theoretical Evaluation of Impedance, Capacitance and Charge Accumulation on Roller Bearing Operated under Electrical Fields. Wear 1988, 125, 223–239. [Google Scholar] [CrossRef]
- Jablonka, K.; Glovnea, R.; Bongaerts, J. Evaluation of EHD Films by Electrical Capacitance. J. Phys. D: Appl. Phys. 2012, 45, 385301. [Google Scholar] [CrossRef]
- Jablonka, K.; Glovnea, R.; Bongaerts, J.; Morales-Espejel, G. The Effect of the Polarity of the Lubricant upon Capacitance Measurements of EHD Contacts. Tribol. Int. 2013, 61, 95–101. [Google Scholar] [CrossRef]
- Jablonka, K.; Glovnea, R.; Bongaerts, J. Quantitative Measurements of Film Thickness in a Radially Loaded Deep-Groove Ball Bearing. Tribol. Int. 2018, 119, 239–249. [Google Scholar] [CrossRef]
- Shetty, P.; Meijer, R.J.; Osara, J.A.; Lugt, P.M. Measuring Film Thickness in Starved Grease-Lubricated Ball Bearings: An Improved Electrical Capacitance Method. Tribol. Trans. 2022, 65, 869–879. [Google Scholar] [CrossRef]
- Schneider, V.; Bader, N.; Liu, H.; Poll, G. Method for in Situ Film Thickness Measurement of Ball Bearings under Combined Loading using Capacitance Measurements. Tribol. Int. 2022, 171, 107524. [Google Scholar] [CrossRef]
- Nakano, K.; Akiyama, Y. Simultaneous Measurement of Film Thickness and Coverage of Loaded Boundary Films with Complex Impedance Analysis. Tribol. Lett. 2006, 22, 27–134. [Google Scholar] [CrossRef]
- Manabe, K.; Nakano, K. Breakdown of Oil Films and Formation of Residual Films. Tribol. Int. 2008, 41, 1103–1113. [Google Scholar] [CrossRef]
- Schnabel, A.; Marklund, P.; Minami, I.; Larsson, R. Monitoring of Running-in of an EHL Contact Using Contact Impedance. Tribol. Lett. 2016, 63, 35. [Google Scholar] [CrossRef]
- Nihira, T.; Manabe, K.; Tadokoro, C.; Ozaki, S.; Nakano, K. Complex Impedance Measurement Applied to Short-Time Contact Between Colliding Steel Surfaces. Tribol. Lett. 2015, 57, 29. [Google Scholar] [CrossRef]
- Maruyama, T.; Nakano, K. In Situ Quantification of Oil Film Formation and Breakdown in EHD Contacts. Tribol. Trans. 2018, 61, 1057–1066. [Google Scholar] [CrossRef]
- Maruyama, T.; Maeda, M.; Nakano, K. Lubrication Condition Monitoring of Practical Ball Bearings by Electrical Impedance Method. Tribol. Online 2019, 14, 327–338. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Isothermal Elastohydrodynamic Lubrication of Point Contacts: Part IV—Starvation Results. ASME J. Lubr. Technol. 1977, 99, 15–23. [Google Scholar] [CrossRef]
- Cann, P.M. The Transition between Fully Flooded and Starved Regimes in EHL. Tribol. Int. 2004, 37, 859–864. [Google Scholar] [CrossRef]
- Maruyama, T.; Saitoh, T. Relationship between Supplied Oil Flow Rates and Oil Film Thicknesses under Starved Elastohydrodynamic Lubrication. Lubricants 2015, 3, 365–380. [Google Scholar] [CrossRef]
- Dowson, D. Elastohydrodynamic and Micro-elastohydrodynamic Lubrication. Wear 1995, 190, 125–138. [Google Scholar] [CrossRef]
- Puchtler, S.; Schirra, T.; Kirchner, E.; Späck-Leigsnering, Y.; De Gersem, H. Capacitance Calculation of Unloaded Rolling Elements—Comparison of Analytical and Numerical Methods. Tribol. Int. 2022, 176, 107882. [Google Scholar] [CrossRef]
- Johnson, K.L.; Greenwood, J.A.; Poon, S.Y. A Simple Theory of Asperity Contact in Elastohydrodynamic Lubrication. Wear 1972, 19, 91–108. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).