Unbalance Response Analysis of a Spindle Supported on Gas Bearings: A Comparison between Different Approaches
Abstract
:1. Introduction
2. Materials and Methods
2.1. Nonlinear Model
2.2. Linearized Model
3. Results
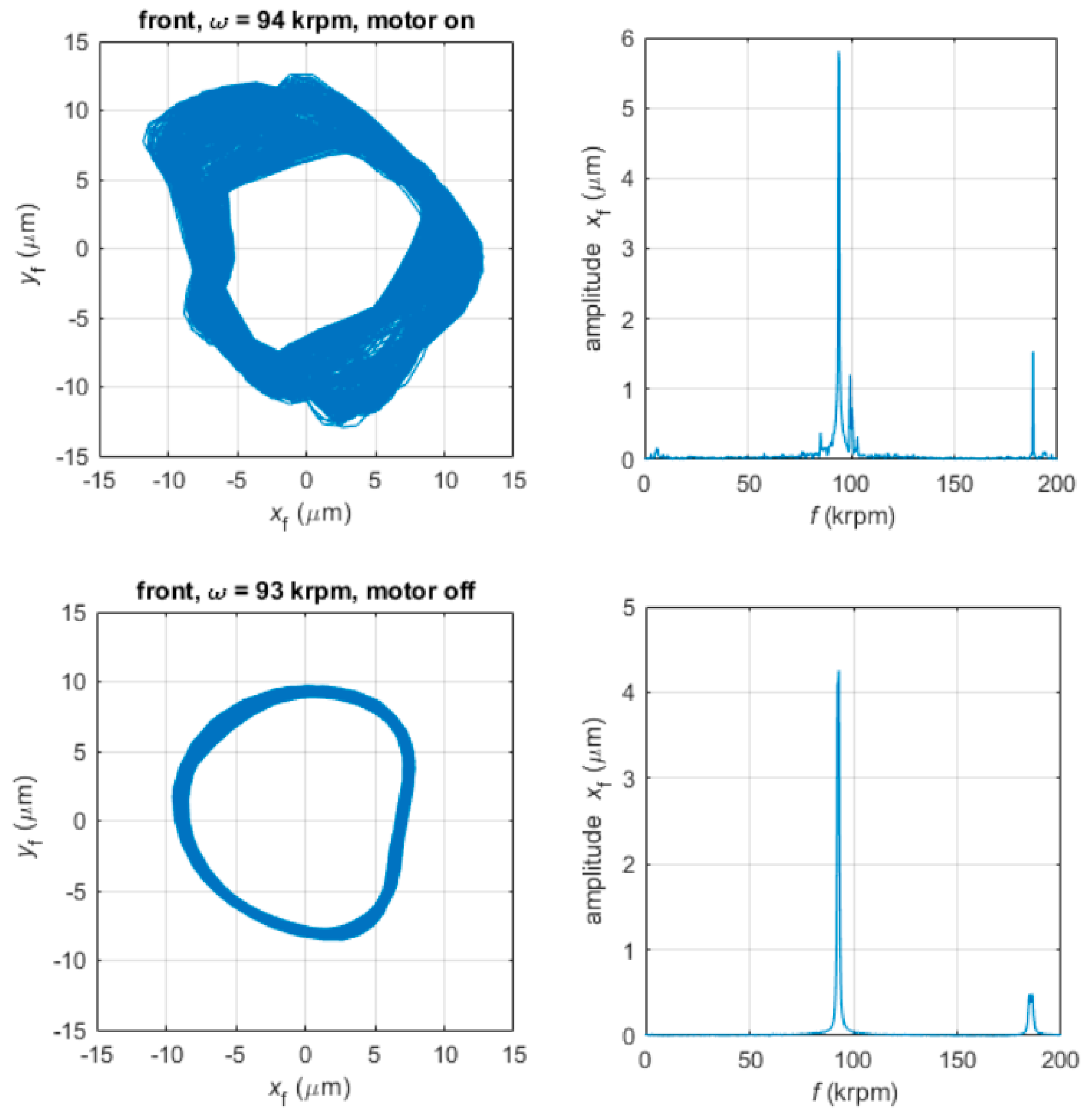
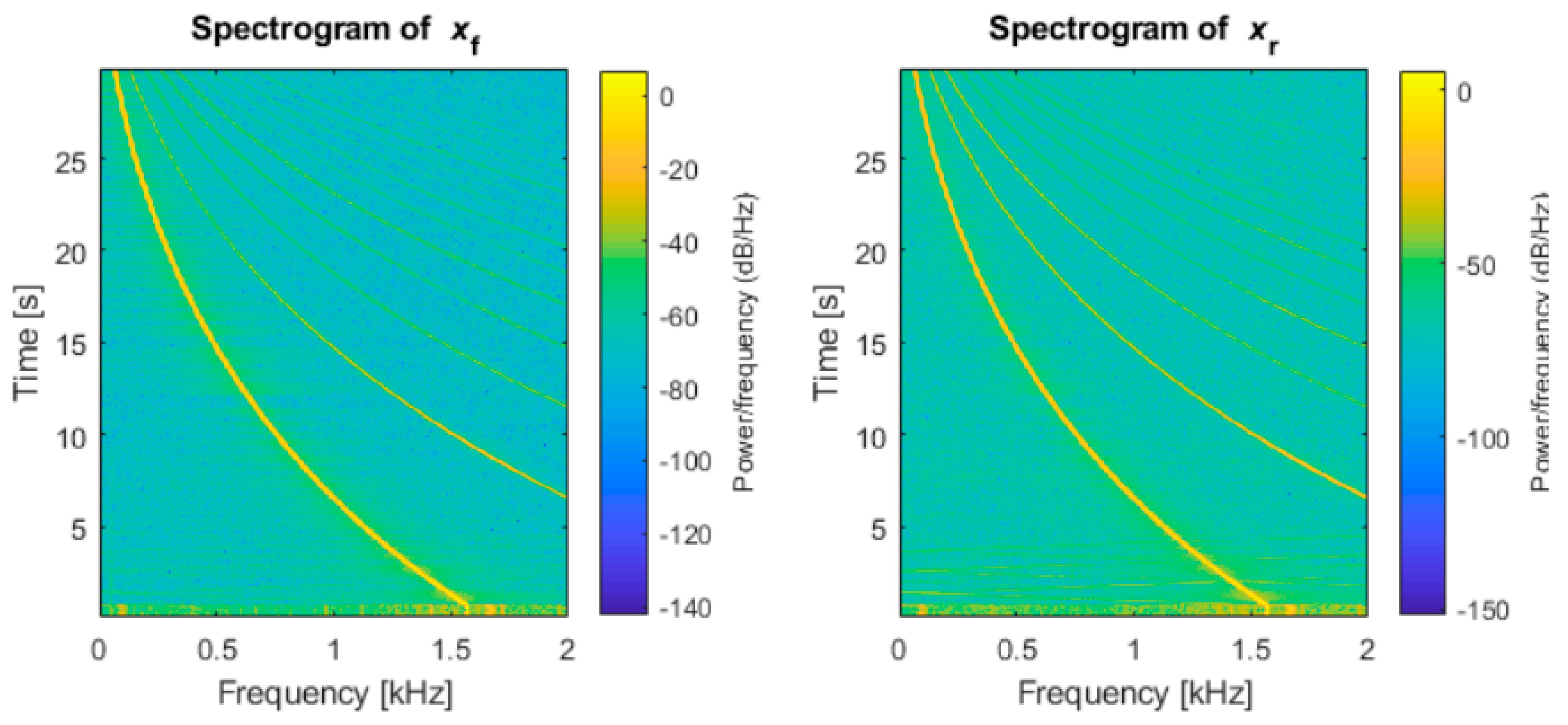
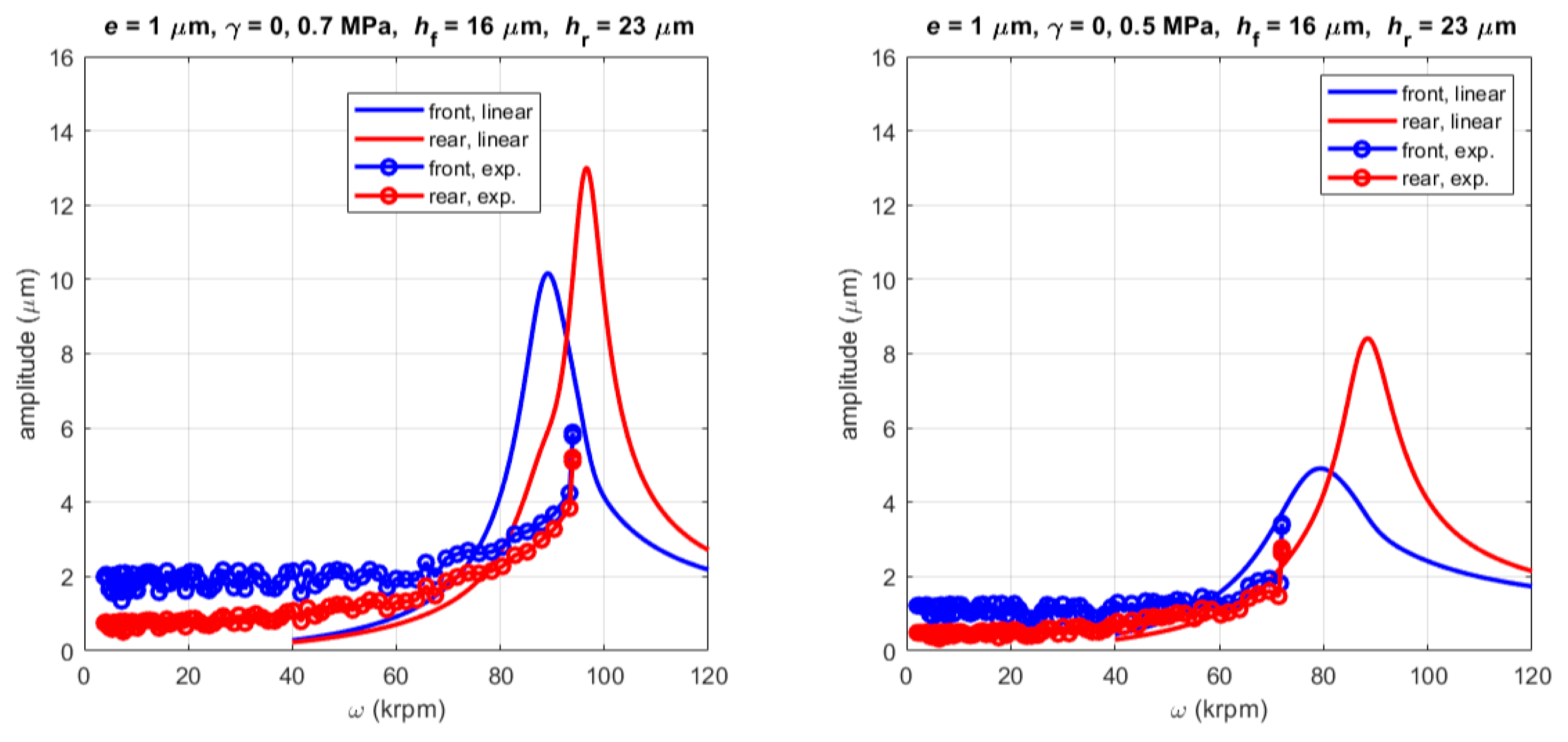
3.1. Experimental Tests
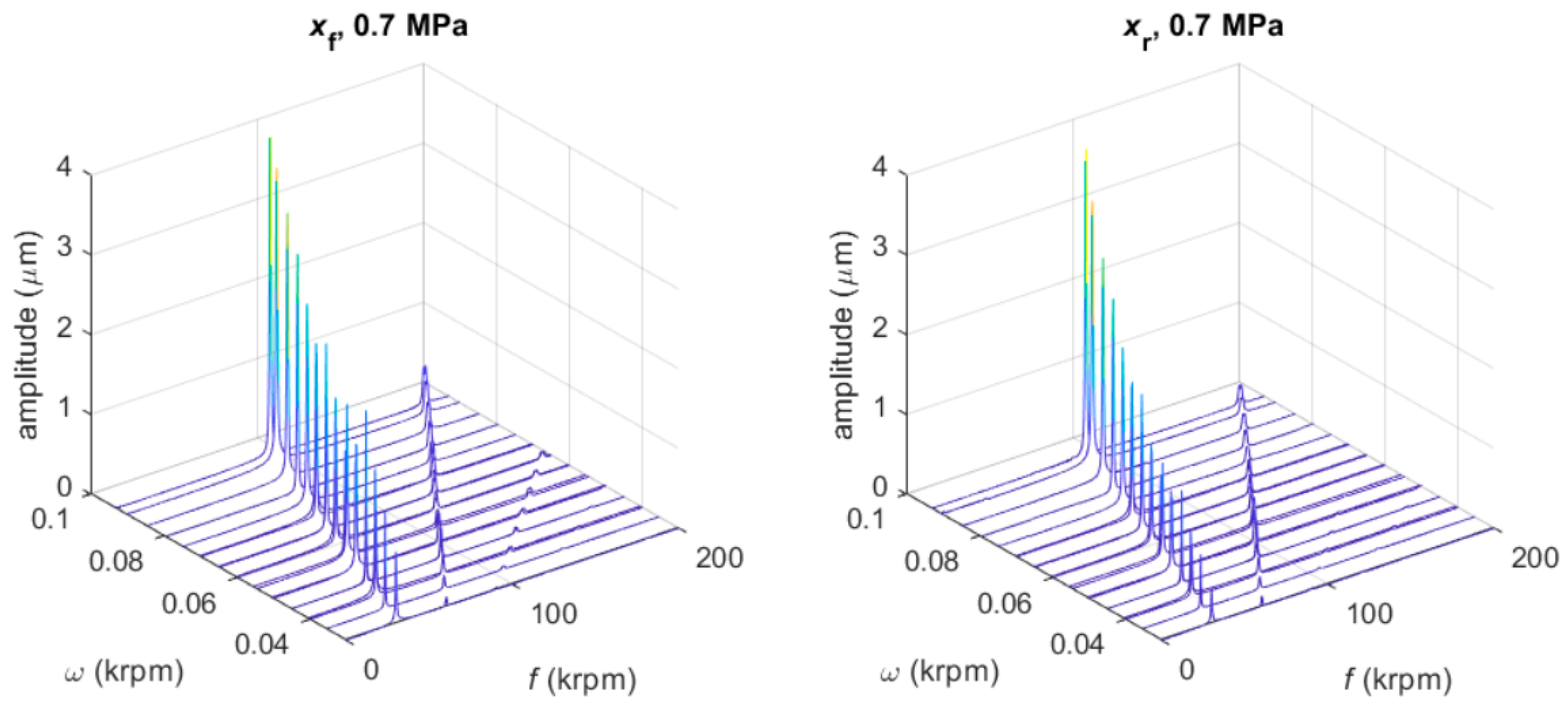
3.2. Nonlinear Model
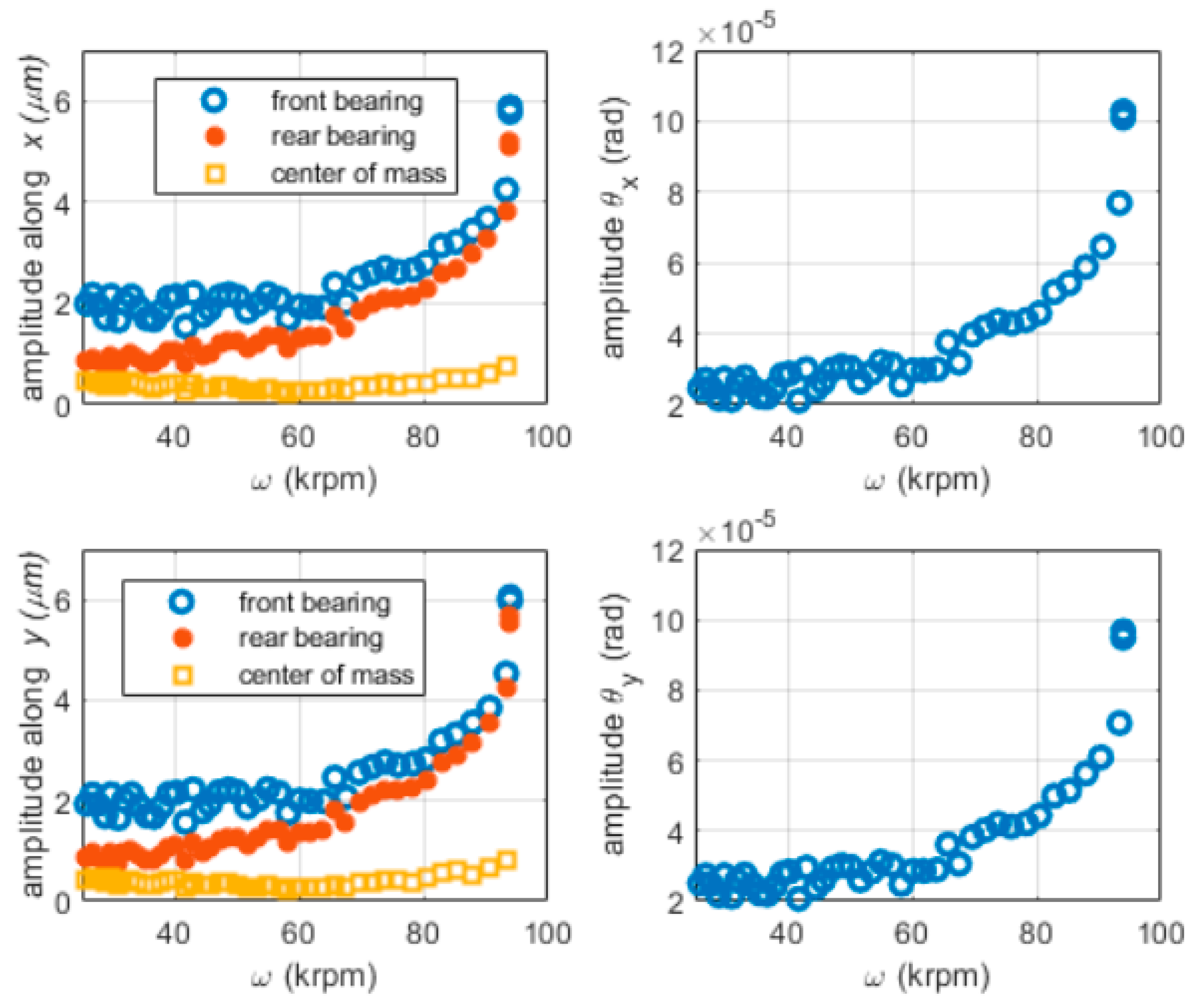
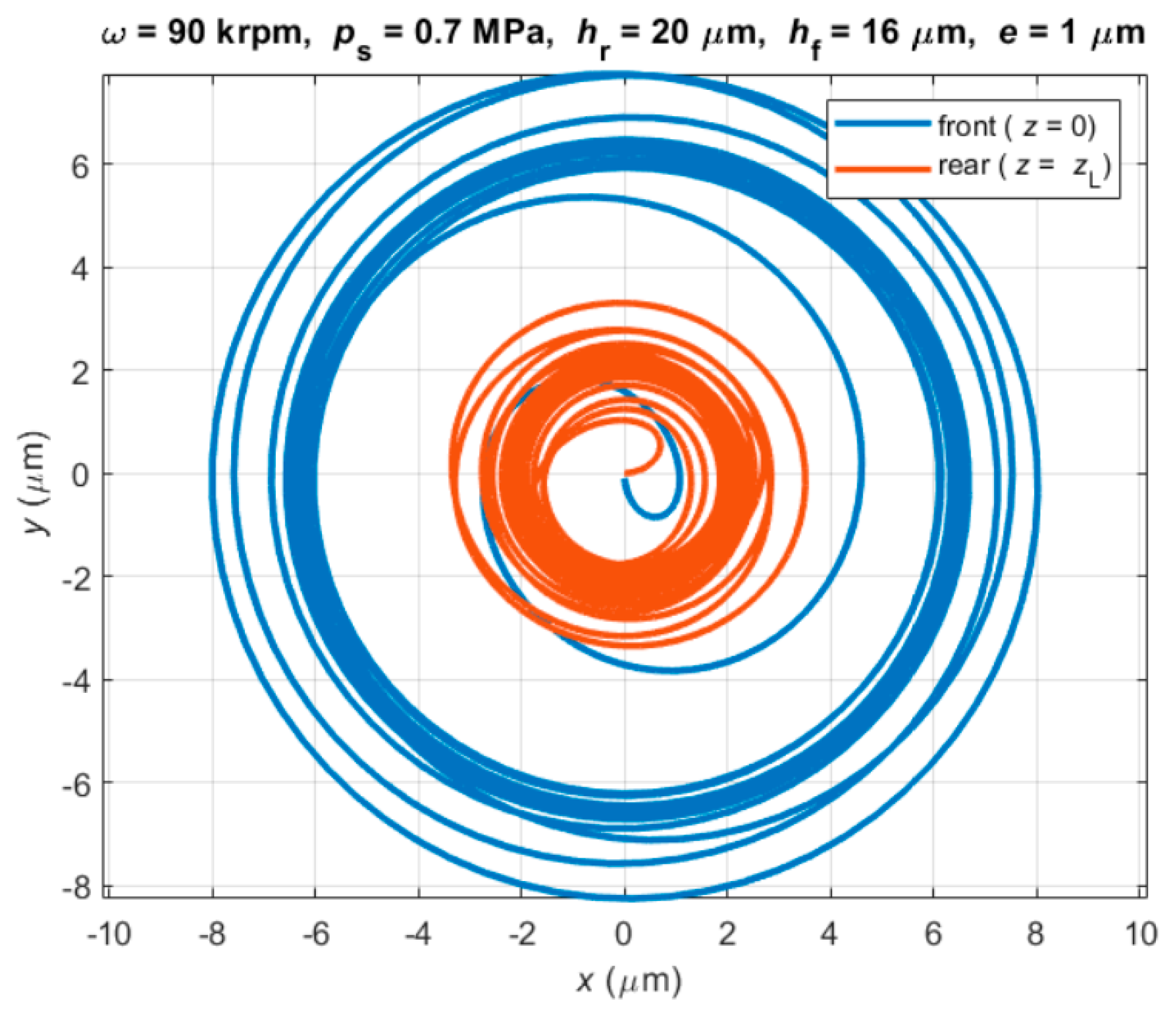
- The front bearing is the most critical one, due to the asymmetrical JB configuration with respect to the rotor center of mass.
- Although the spindle is stable in the experimental tests at all the operating speeds, the presence of a subsynchronous whirl at high speeds in the numerical results indicates that the front bearing is near the unstable whirl onset speed when the spindle is rotated at its maximum speed (about 100 krpm).
3.3. Linearized Model
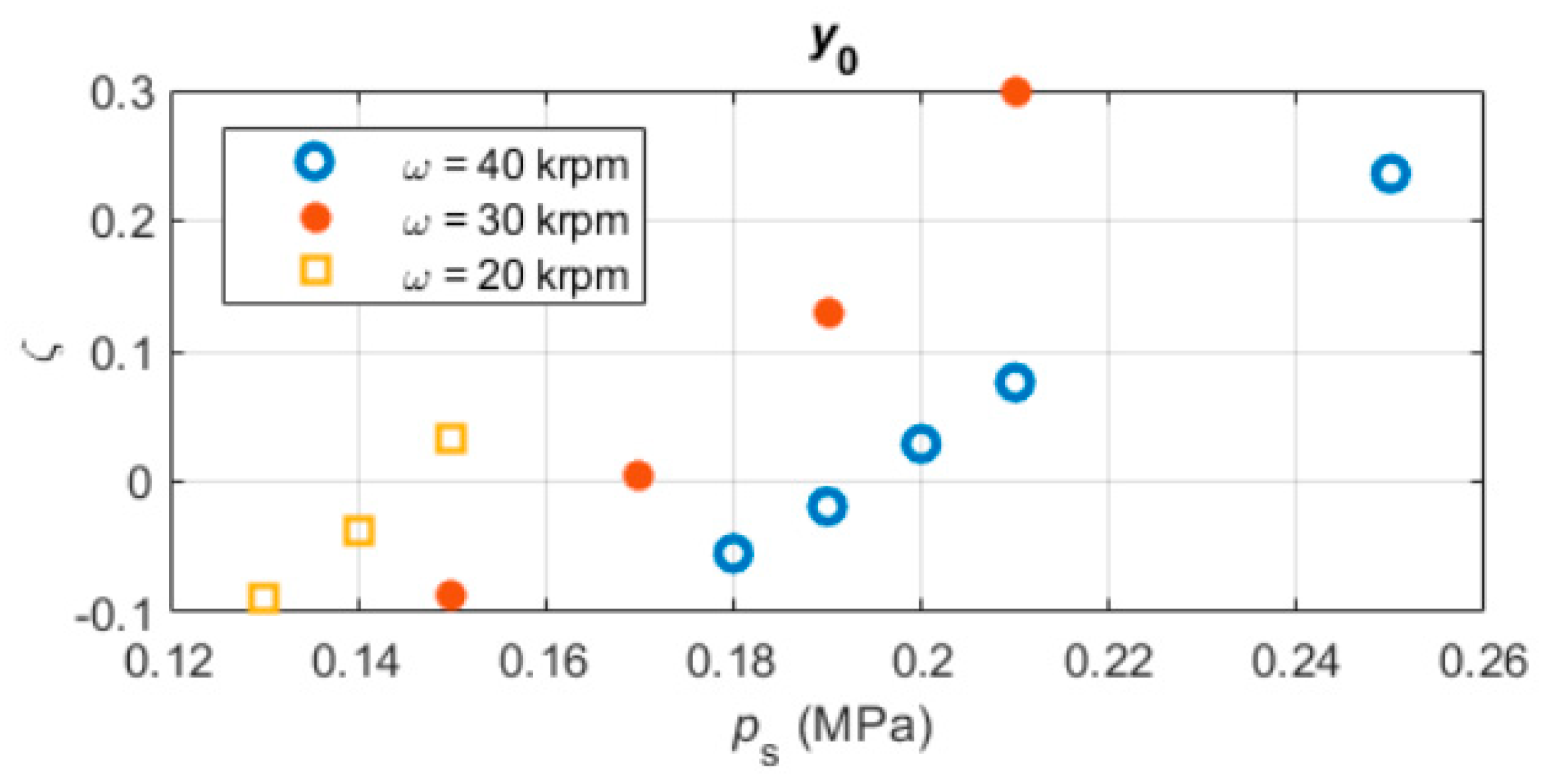
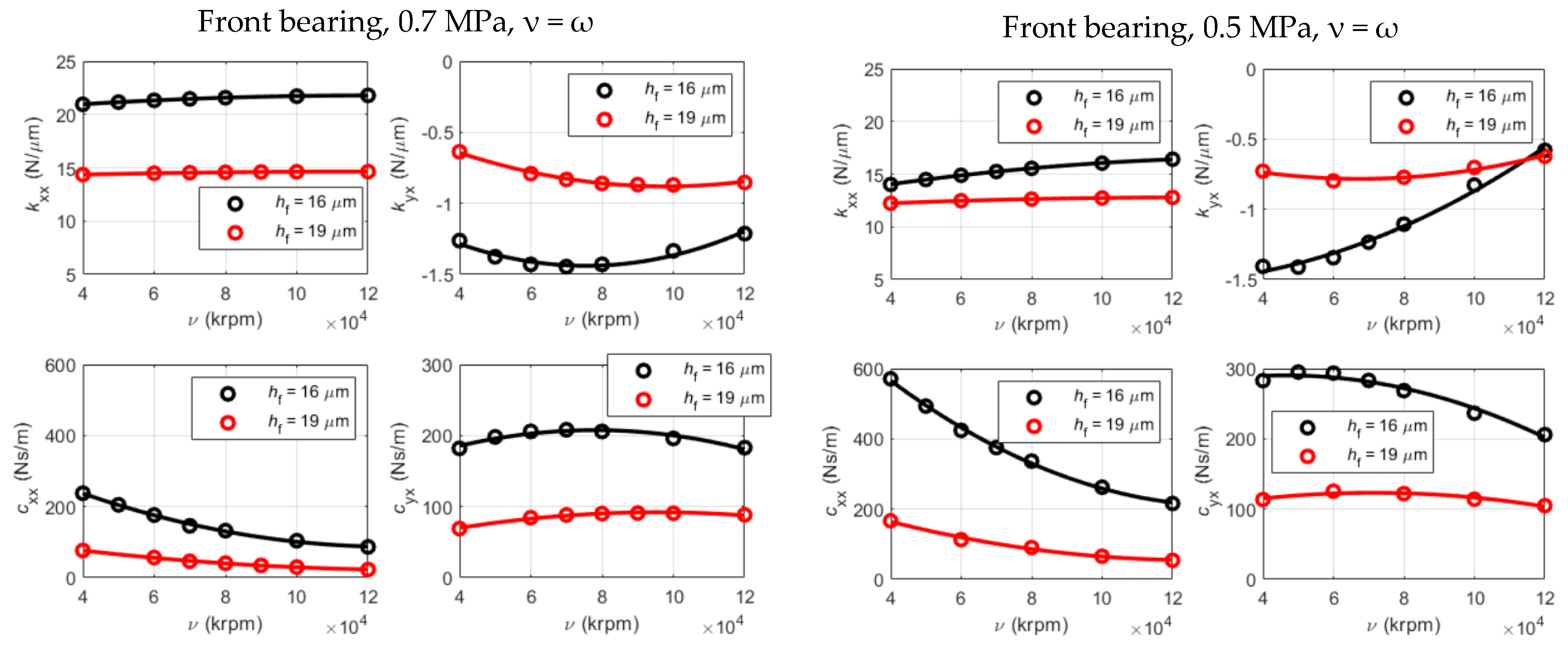
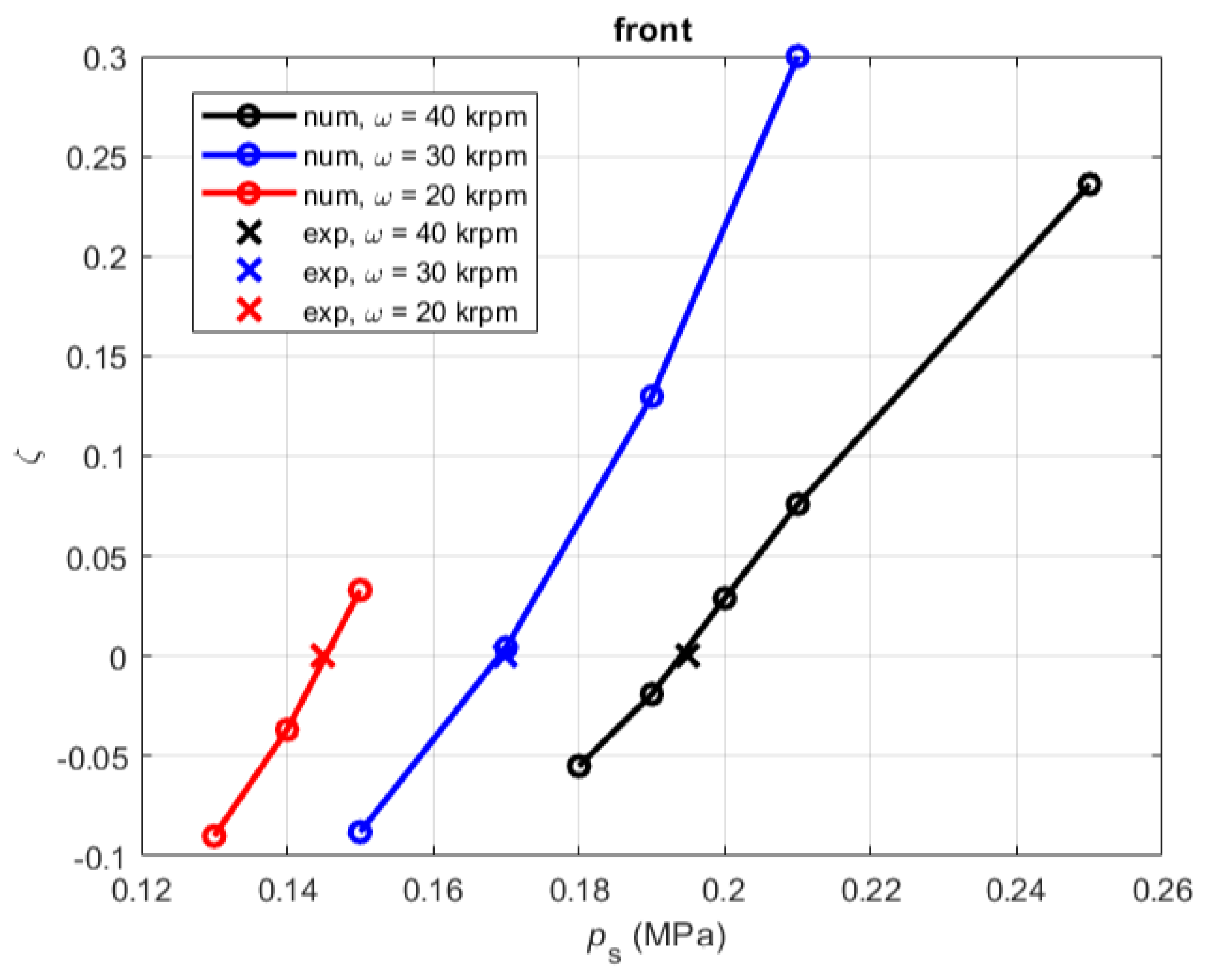
3.3.1. Air Film Dynamic Coefficients Determination
- Synchronous excitation (ν = ω);
- Small shaft eccentricity (x0 = 1 µm);
- 0.5 and 0.7 MPa absolute supply pressure;
- Minima and maxima air film thicknesses (to take into account the manufacturing tolerances and the centrifugal expansion of the shaft).
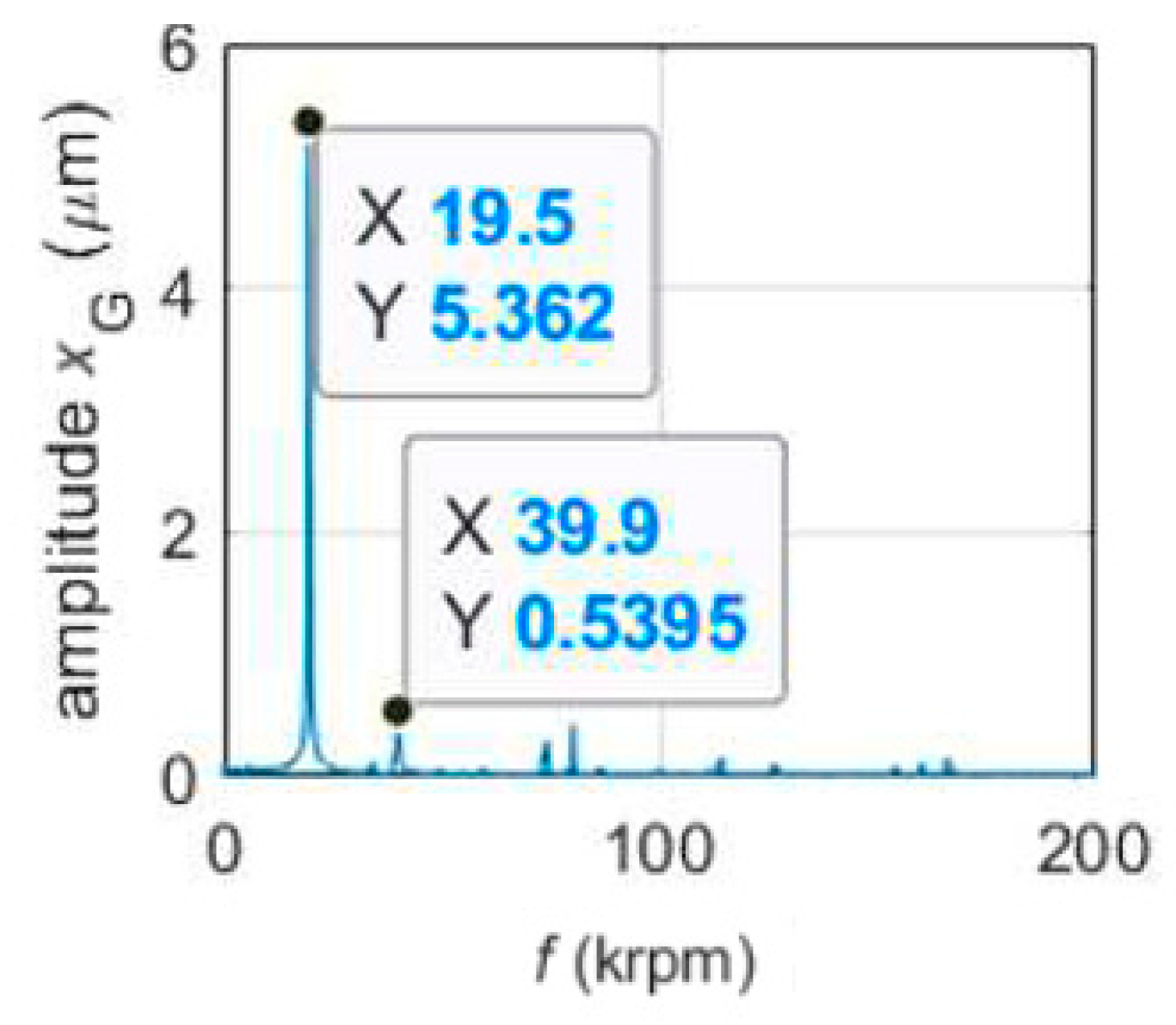
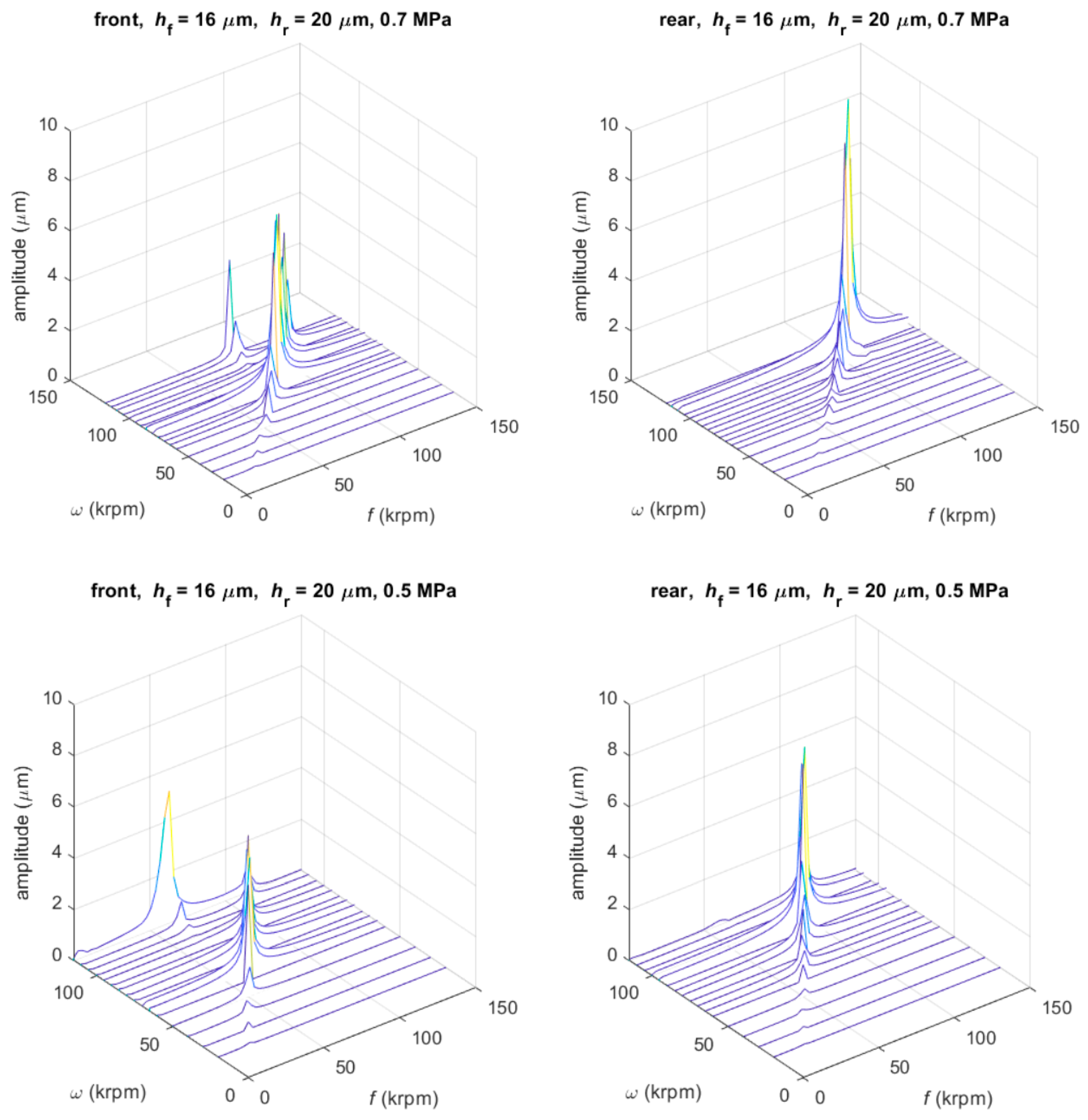
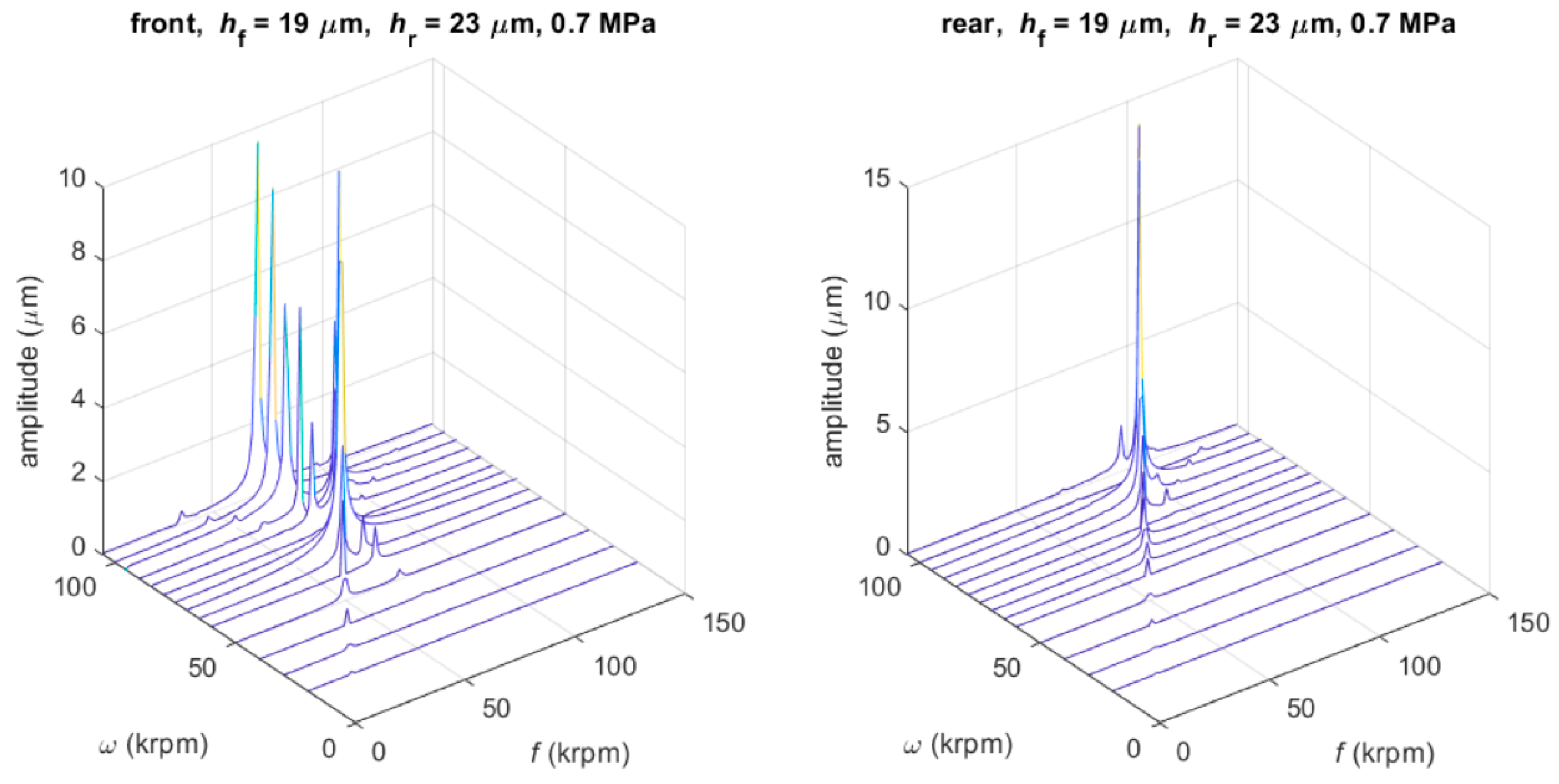
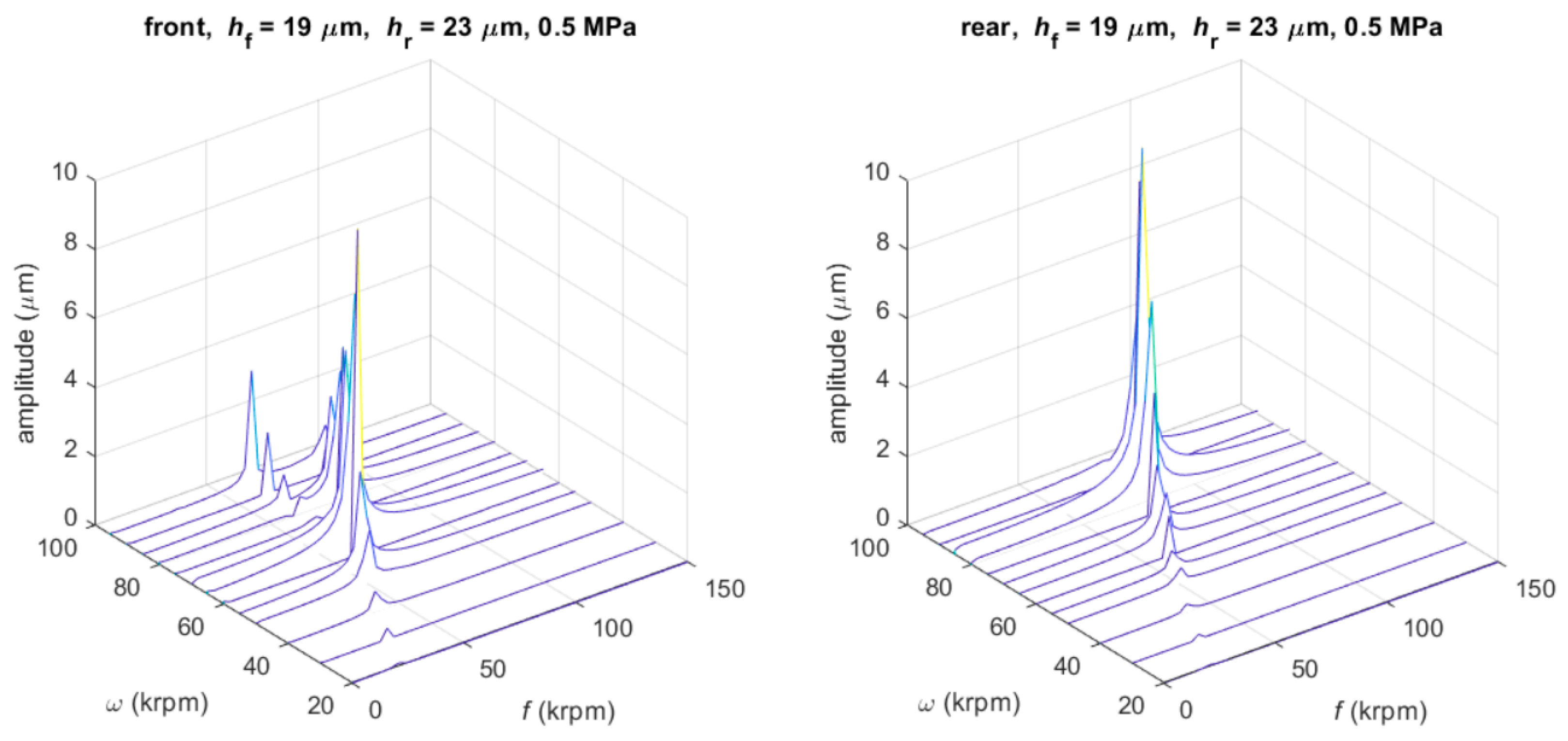
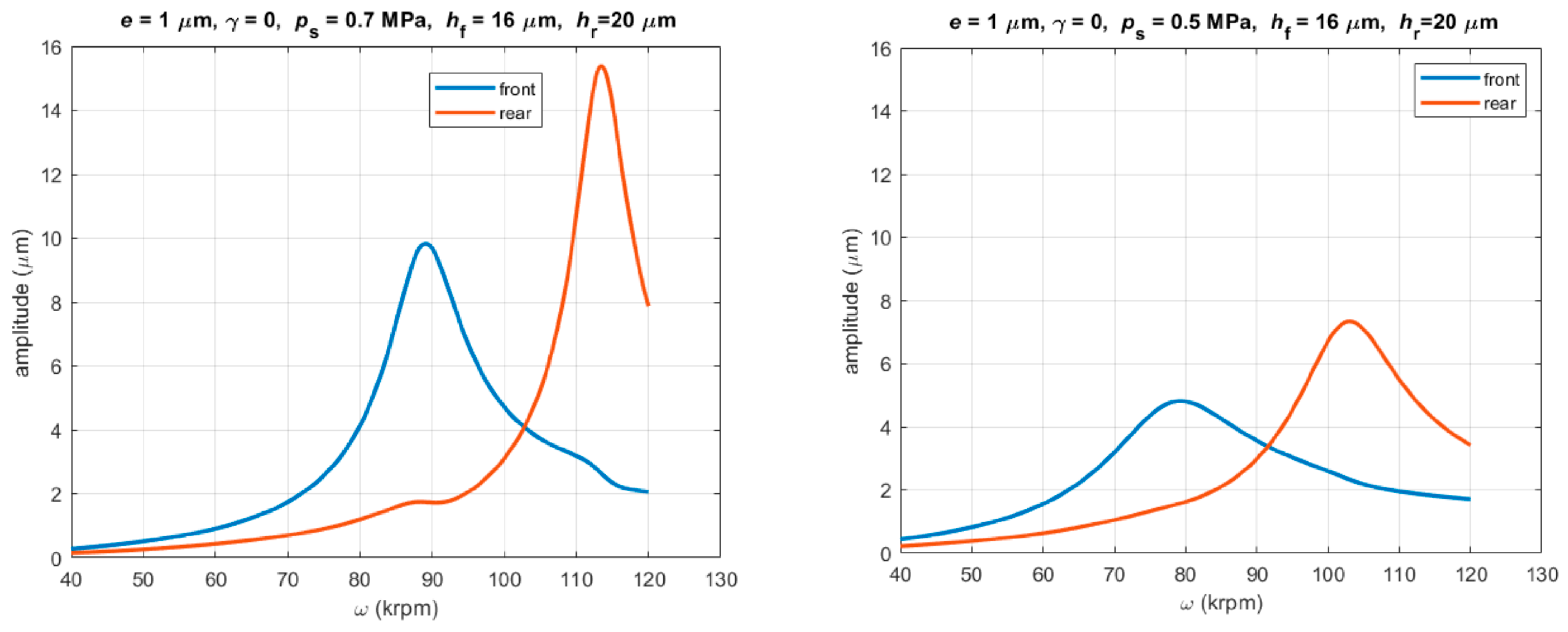
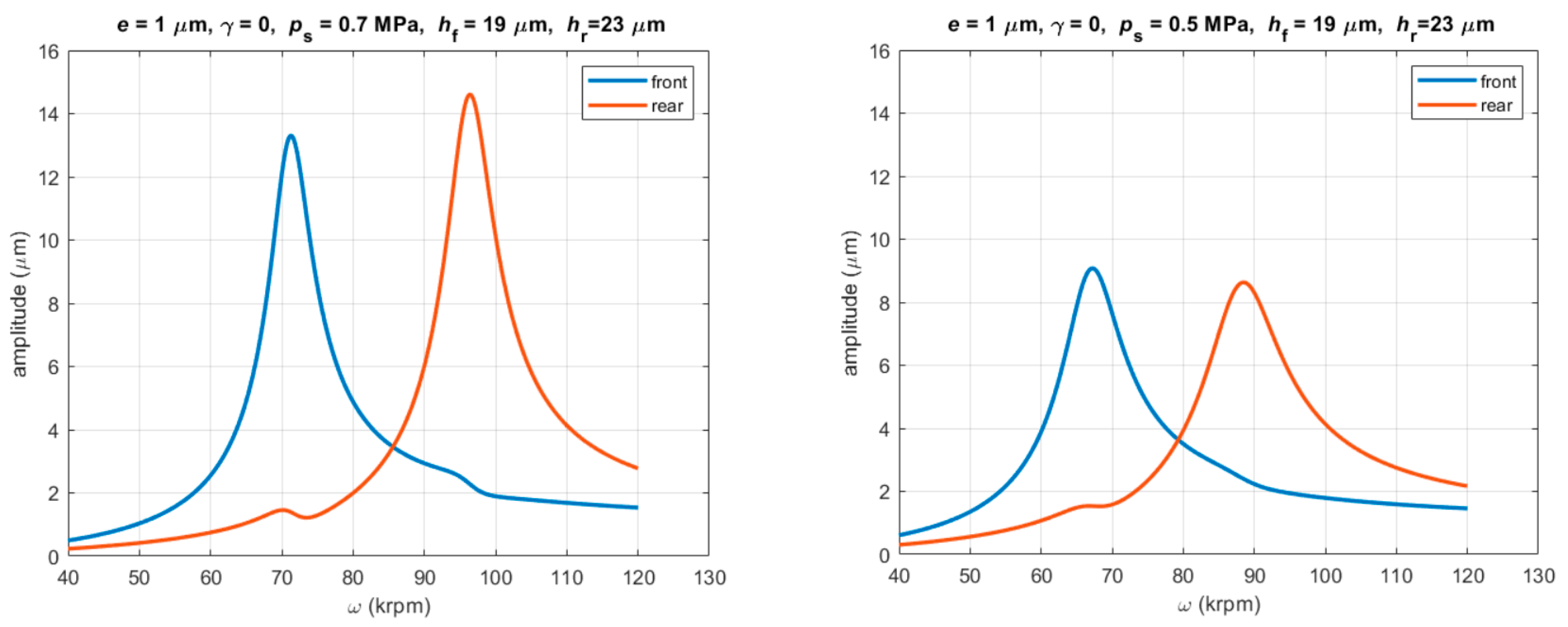
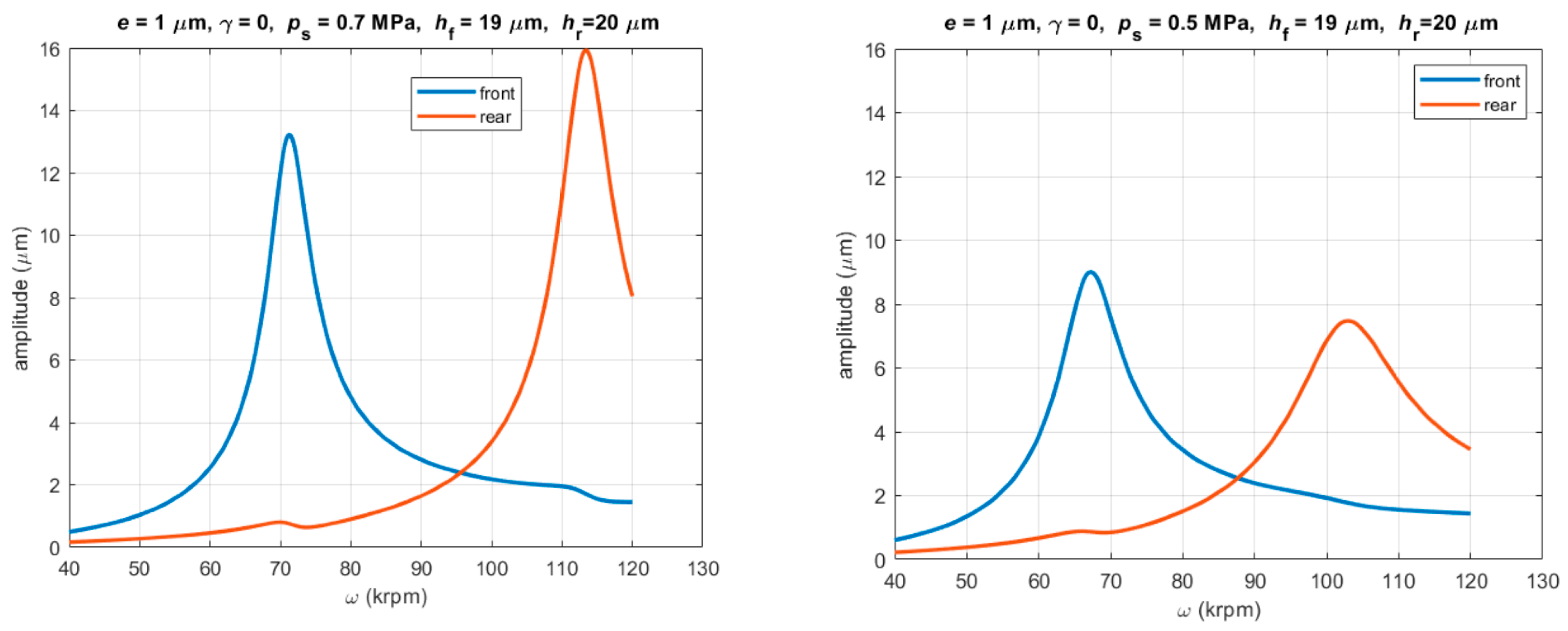
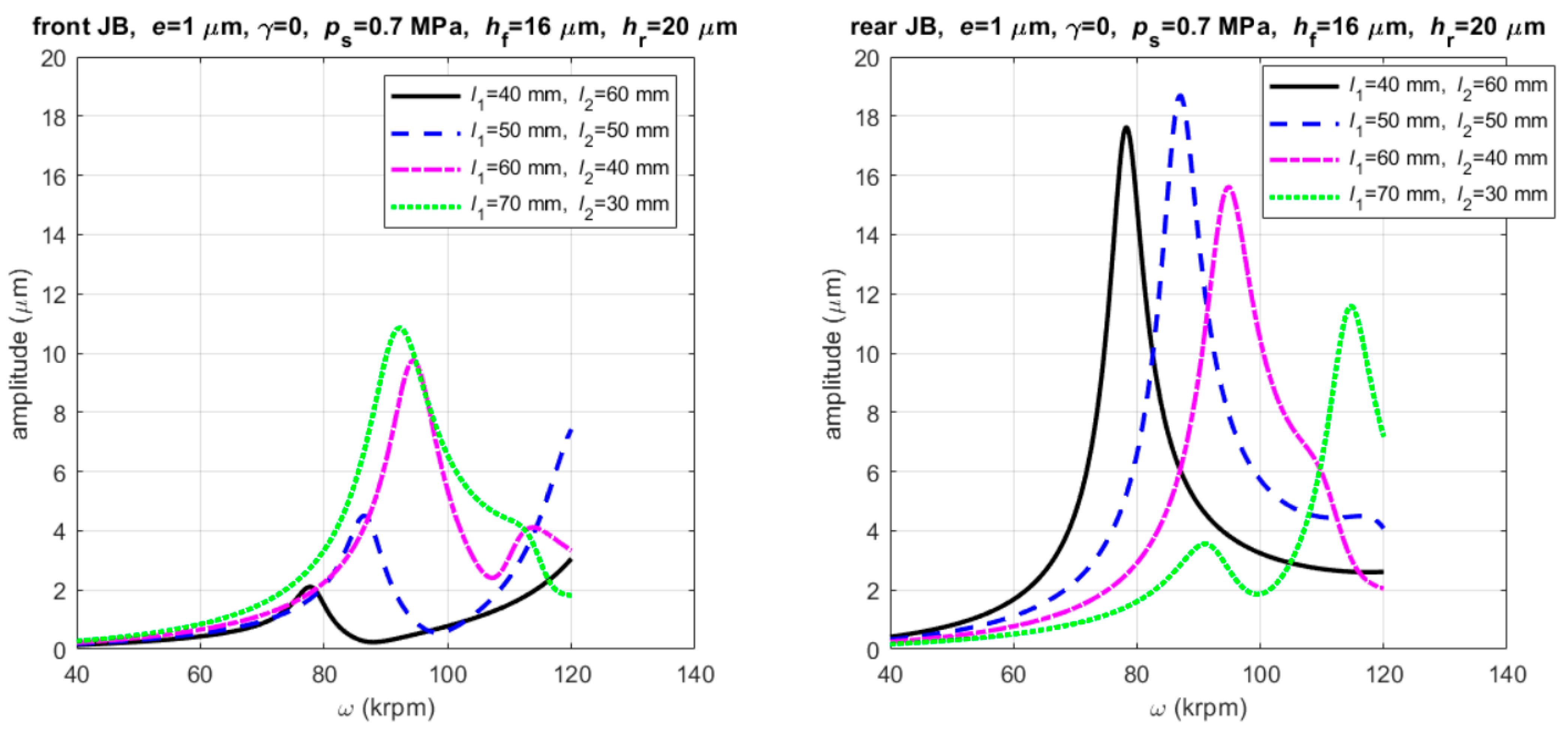
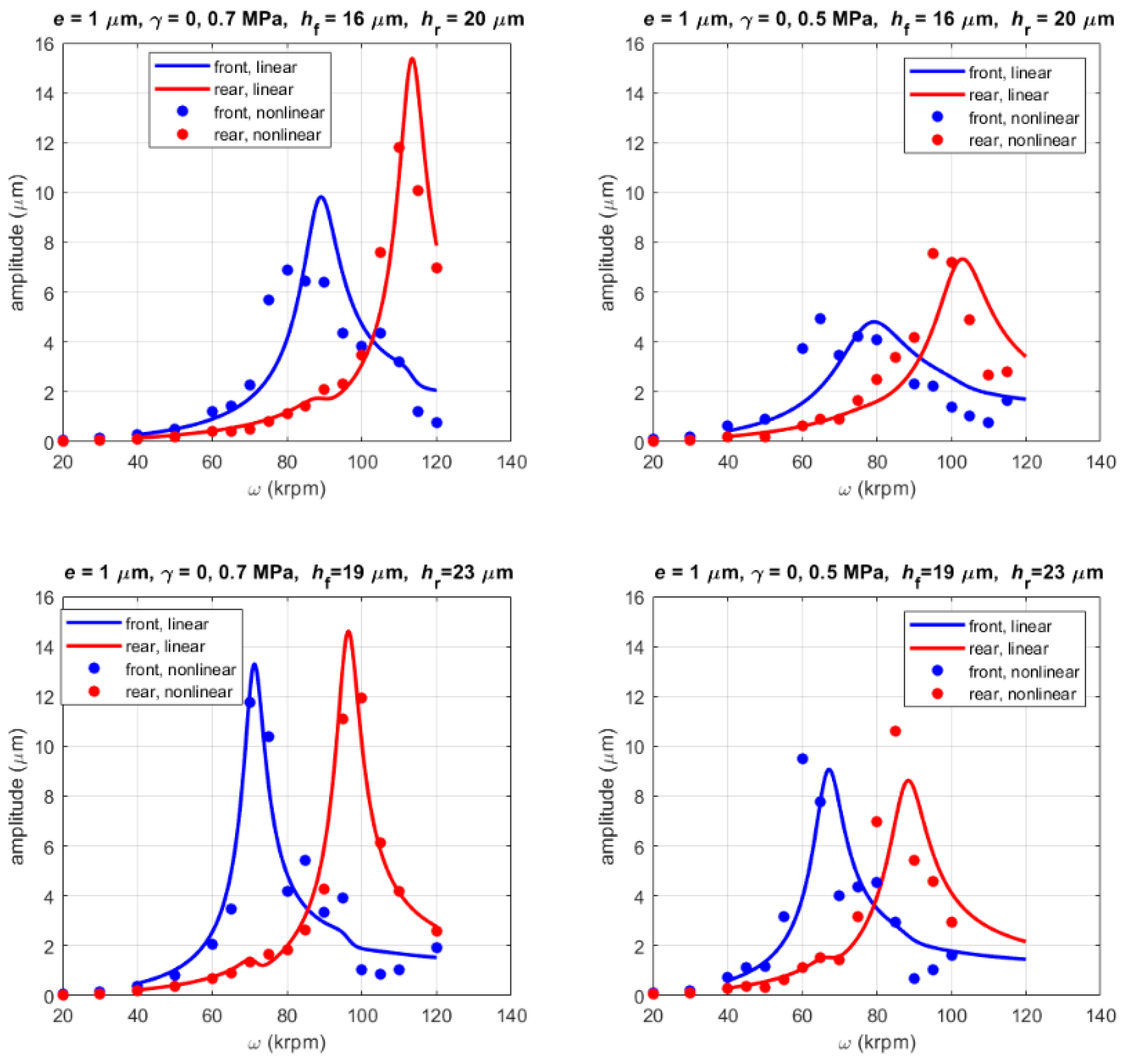
3.3.2. Unbalance Response
4. Discussion
5. Conclusions
- The results of the nonlinear and linearized models are in good agreement, especially regarding the critical speeds.
- The critical speeds are very sensitive with respect to film thickness; an increase in film thickness of one bearing involves a decrease in the corresponding critical speed, but has little effect on the other bearing.
- The position of the rotor center of mass strongly influences the unbalance response on bearings; in particular, the dynamic runout of the prototype measured on the front bearing can be reduced by moving the center of mass towards the rear bearing.
- The direct stiffness coefficients of the bearings decrease as the supply pressure is decreased; conversely, the direct damping coefficients increase.
- The direct stiffness coefficients of the bearings increase as the rotational speed is increased; conversely, the direct damping coefficients decrease.
- At high speeds, the front bearing is near the instability threshold because a subsynchronous frequency appears in the nonlinear model results (see Section 3.2).
- The difference between the experimental and numerical first critical speed is about 10% and it could be acceptable, considering that other parameters besides the film thickness may influence it, such as the orifices diameter and their discharge coefficient.
- The difference in the amplitude of the dynamic runout may be due to the fact that in numerical simulations, only the static unbalance eccentricity has been considered, while the experimental results can also be affected by a residual dynamic unbalance of the rotor.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, C.-H.; Tsai, T.-H.; Yang, D.-W.; Kang, Y.; Chen, J.-H. The comparison in stability of rotor-aerostatic bearing system compensated by orifices and inherences. Tribol. Int. 2010, 43, 1360–1373. [Google Scholar] [CrossRef]
- Miyatake, M.; Yoshimoto, S. Numerical investigation of static and dynamic characteristics of aerostatic thrust bearings with small feed holes. Tribol. Int. 2010, 43, 1353–1359. [Google Scholar] [CrossRef]
- Otsu, Y.; Miyatake, M.; Yoshimoto, S. Dynamic Characteristics of Aerostatic Porous Journal Bearings With a Surface-Restricted Layer. J. Tribol. Trans. Asme 2011, 133, 011701. [Google Scholar] [CrossRef]
- Otsu, Y.; Somaya, K.; Yoshimoto, S. High-speed stability of a rigid rotor supported by aerostatic journal bearings with compound restrictors. Tribol. Int. 2011, 44, 9–17. [Google Scholar] [CrossRef]
- Park, J.-K.; Kim, K.-W. Stability analyses and experiments of spindle system using new type of slot-restricted gas journal bearings. Tribol. Int. 2004, 37, 451–462. [Google Scholar] [CrossRef]
- Belforte, G.; Raparelli, T.; Viktorov, V.; Trivella, A. Metal woven wire cloth feeding system for gas bearings. Tribol. Int. 2009, 42, 600–608. [Google Scholar] [CrossRef]
- Belforte, G.; Colombo, F.; Raparelli, T.; Trivella, A.; Viktorov, V. Experimental analysis of air pads with micro holes. Tribol. Trans. 2013, 56, 169–177. [Google Scholar] [CrossRef]
- Bättig, P.; Schiffmann, J. Data-driven model for the dynamic characteristics of o-rings for gas bearing supported rotors. J. Appl. Mech. 2019, 86, 081003. [Google Scholar] [CrossRef]
- Al-Bender, F.; Colombo, F.; Reynaerts, D.; Villavicencio, R.; Waumans, T. Dynamic characterization of rubber o-rings: Squeeze and size effects. Adv. Tribol. 2017, 2017, 2509879. [Google Scholar] [CrossRef] [Green Version]
- Czolczynski, K. Rotordynamics of Gas-Lubricated Journal Bearing Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Czolczynski, K.; Kapitaniak, T.; Marynowski, K. Stability of rotors supported in gas bearings with bushes mounted in air rings. Wear 1996, 199, 100–112. [Google Scholar] [CrossRef]
- Hoffmann, R.; Liebich, R. Characterisation and calculation of nonlinear vibrations in gas foil bearing systems–An experimental and numerical investigation. J. Sound Vib. 2018, 412, 389–409. [Google Scholar] [CrossRef]
- Hoffmann, R.; Liebich, R. Experimental and numerical analysis of the dynamic behaviour of a foil bearing structure affected by metal shims. Tribol. Int. 2017, 115, 378–388. [Google Scholar] [CrossRef]
- Liebich, R.; Scholz, A.; Wieschalla, M. Rotors supported by elastomer-ring-dampers: Experimental and numerical investigations. In Proceedings of the 10th International Conference on Vibrations in Rotating Machinery, London, UK, 11–13 September 2012; pp. 443–453. [Google Scholar]
- Belforte, G.; Raparelli, T.; Viktorov, V. Theoretical Investigation of Fluid Inertia Effects and Stability of Self-Acting Gas Journal Bearings. J. Tribol. 1999, 121, 836–843. [Google Scholar] [CrossRef]
- Belforte, G.; Colombo, F.; Raparelli, T.; Viktorov, V. High-speed rotor with air bearings mounted on flexible supports: Test bench and experimental results. J. Tribol. 2008, 130, 21103. [Google Scholar] [CrossRef]
- Belforte, G.; Colombo, F.; Raparelli, T.; Trivella, A.; Viktorov, V. High-speed electrospindle running on air bearings: Design and experimental verification. Meccanica 2008, 43, 591–600. [Google Scholar] [CrossRef]
- Liu, W.; Bättig, P.; Wagner, P.H.; Schiffmann, J. Nonlinear study on a rigid rotor supported by herringbone grooved gas bearings: Theory and validation. Mech. Syst. Signal Processing 2021, 146, 106983. [Google Scholar] [CrossRef]
- Lund, J.W. A Theoretical Analysis of Whirl Instability and Pneumatic Hammer for a Rigid Rotor in Pressurized Gas Journal Bearings. J. Lubr. Technol. 1967, 89, 154–165. [Google Scholar] [CrossRef]
- Lund, J.W. Calculation of Stiffness and Damping Properties of Gas Bearings. J. Lubr. Technol. 1968, 90, 793–803. [Google Scholar] [CrossRef]
- Waumans, T.; Vleugels, P.; Peirs, J.; Al-Bender, F.; Reynaerts, D. Rotordynamic behaviour of a micro-turbine rotor on air bearings: Modelling techniques and experimental verification. In Proceedings of the ISMA, Leuven, Belgium, 18–20 September 2006; pp. 181–198. [Google Scholar]
- Colombo, F.; Lentini, L.; Trivella, A.; Raparelli, T.; Viktorov, V. Experimental and Numerical Dynamic Identification of an Aerostatic Electro-Spindle. Appl. Sci. 2021, 11, 11462. [Google Scholar] [CrossRef]
- Al-Bender, F. Air Bearings: Theory, Design and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]

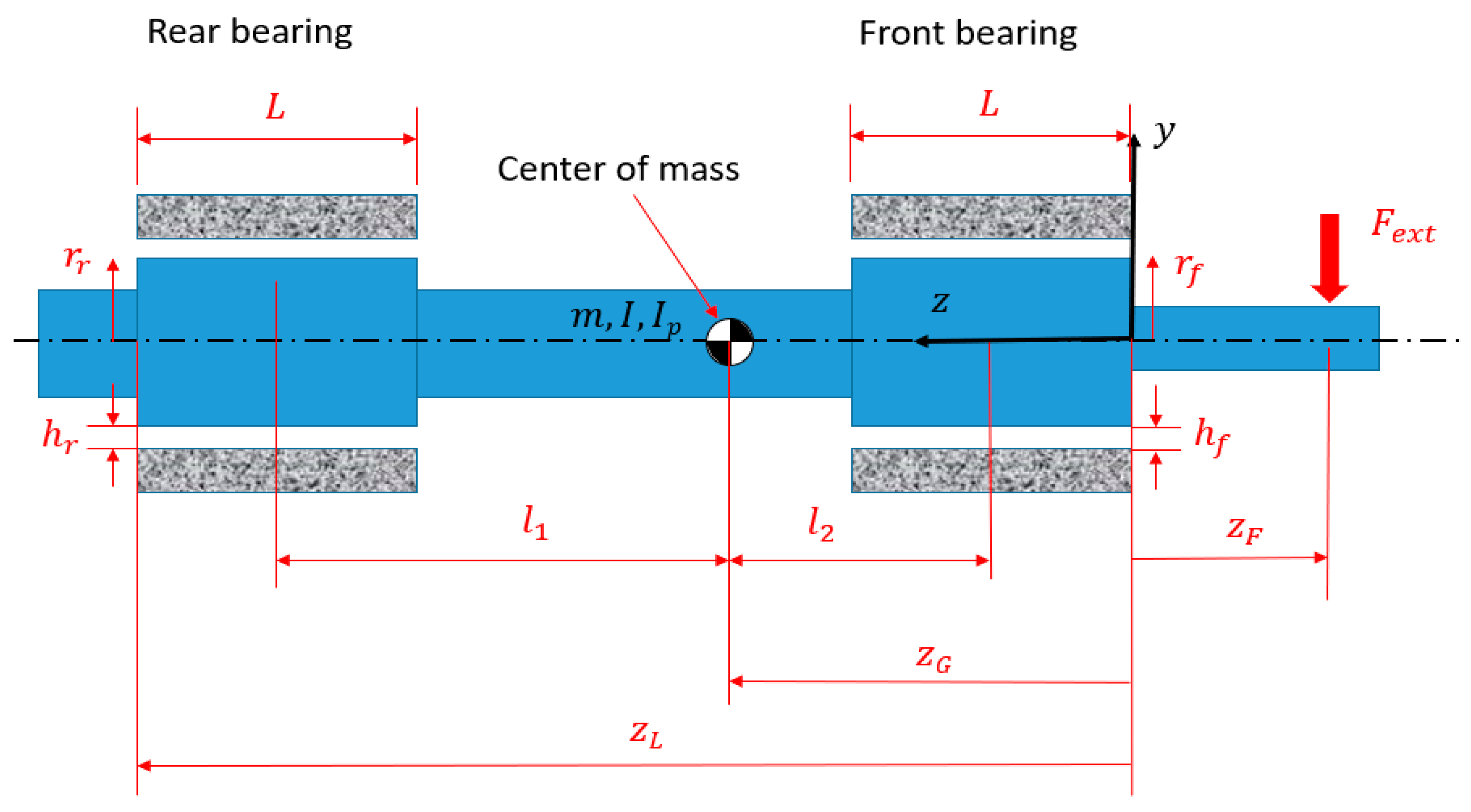
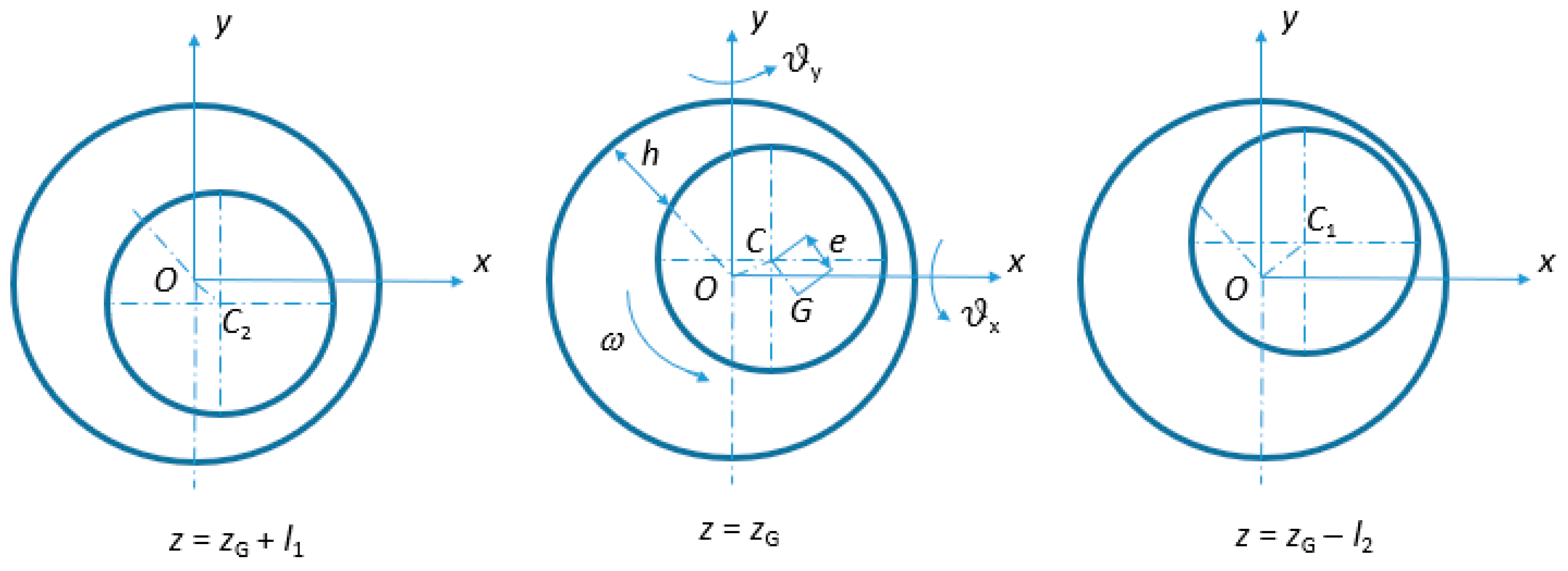



| Variable | Description | Value |
|---|---|---|
| Supply hole diameter | 0.15 mm | |
| Radial clearance on front JB | 17.5 ± 1.5 μm | |
| Radial clearance on rear JB | 21.5 ± 1.5 μm | |
| Axial distance | 70 mm | |
| Axial distance | 26 mm | |
| Journal bearing axial length | 30 mm | |
| Radius of front JB | 12.5 mm | |
| Radius of rear JB | 11 mm |
| Variable | Description | Value |
|---|---|---|
| Mass | 382 g | |
| Transverse moment of inertia | 667 kg∙mm2 | |
| Polar moment of inertia | 31 kg∙mm2 |
| Method | Time (s) |
|---|---|
| Linearized method (1000 points) | 0.5 |
| Nonlinear method (16 points) | 38,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Colombo, F.; Lentini, L.; Raparelli, T.; Trivella, A.; Viktorov, V. Unbalance Response Analysis of a Spindle Supported on Gas Bearings: A Comparison between Different Approaches. Lubricants 2022, 10, 127. https://doi.org/10.3390/lubricants10060127
Colombo F, Lentini L, Raparelli T, Trivella A, Viktorov V. Unbalance Response Analysis of a Spindle Supported on Gas Bearings: A Comparison between Different Approaches. Lubricants. 2022; 10(6):127. https://doi.org/10.3390/lubricants10060127
Chicago/Turabian StyleColombo, Federico, Luigi Lentini, Terenziano Raparelli, Andrea Trivella, and Vladimir Viktorov. 2022. "Unbalance Response Analysis of a Spindle Supported on Gas Bearings: A Comparison between Different Approaches" Lubricants 10, no. 6: 127. https://doi.org/10.3390/lubricants10060127
APA StyleColombo, F., Lentini, L., Raparelli, T., Trivella, A., & Viktorov, V. (2022). Unbalance Response Analysis of a Spindle Supported on Gas Bearings: A Comparison between Different Approaches. Lubricants, 10(6), 127. https://doi.org/10.3390/lubricants10060127









