A New Approach for the Load Calculation of the Most-Loaded Rolling Element of the Rolling Bearing with Internal Radial Clearance—A Case Study

Abstract

One of the most important factors influencing the study of the tribological behaviour of a rolling bearing is the calculation of the loads transmitted by individual rolling elements of the bearing. However, the calculation of the internal load distribution of rolling bearings is quite complicated. It is a nonlinear, statically indeterminate problem, which can only be solved numerically, through a number of iterations. This is often a problem in analysis because it complicates the mathematical model. This paper is presenting a case study with the goal to show the benefits of the application of a new approach for the calculation of the load of the most-loaded rolling element in the rolling bearing with the internal radial clearance. The calculation is based on the so-called load factors. By multiplying the load factors with the value of the external radial load, the load that is transferred by the most-loaded rolling element of the bearing is obtained. The accuracy of the results largely depends on the correct choice of the load factor. The case study aims to define guidelines for the correct choice of load factors. The case study is made for two types of bearings: the ball bearing and the roller bearing. Obtained results were compared with the results obtained based on the calculation using some of the most commonly used methods so far. The analysis showed greater precision of the considered model with the same or much simpler use. For this reason, the proposed model is considered very suitable for practical application.

1. Introduction

The calculation of the load transmitted by the most-loaded rolling element has attracted the interest of researchers since the beginning of the use of rolling bearings in machines. This is one very important characteristic of the rolling bearing, especially for the calculation of the static load capacity and the rating life, but also the overall load distribution on the rolling elements inside the bearing. However, due to the complexity of the bearing construction, the way of functioning, and many other influential factors, this problem has not yet been explicitly resolved. So far, Stribeck’s method has been the most commonly used for the calculation of this load [1].

The calculation based on the Stribeck numbers is the most commonly used method for the calculation of the load that transfers the most-loaded rolling element. Stribeck’s expressions are still in use today to calculate the static load capacity of a rolling bearing [2,3]. However, Stribeck’s method has one essential drawback: it does not take into account the influence of the size of the internal clearance on the load distribution within the bearing.

In this regard, this paper presents and tests a new mathematical model for the calculation of the load that is transferred by the most-loaded rolling element of the rolling bearing with internal radial clearance. The model is elaborated in detail in the paper [4,5] and purposed for the radially loaded rolling bearing, with balls or rollers. Based on the papers of Mitrovic et al. [6,7], the model is based on the so-called load factors, showing which part of the external load is transferred by the most-loaded rolling element of the bearing. By simple multiplication of the load factor with the value of the external radial load, the load that is transferred by the most-loaded rolling element of the bearing is obtained:

$$F_{max}=k_{max}\cdot Q,$$

(1)

where is: F_max—the load that is transferred by the most-loaded rolling element of the bearing, k_max—the load factor of the most-loaded rolling element, Q—the total external radial load.

The values of the load factor for the boundary position of support (k_maxq) were derived from the literature [4,5]. These values are shown in Tables 1 and 2 in reference [5]. These values correspond to the boundary values of the bearing deflection and the boundary external radial loads, which are defined in the papers [8,9].

If the right side of the Equation (1) is multiplied and divided by the total number of the rolling elements (z) of the bearing and the product k_max·z is marked with the S, it can be obtained:

$$F_{max}=k_{max}\cdot z\cdot \frac{Q_{}}{z}=S\cdot \frac{Q_{}}{z}.$$

(2)

The factor S shows how many times the greater load is transferred by the most-loaded rolling element relative to the case when the load would be even, i.e., when every ball would transfer the load of the size Q/z. In the literature, this factor is often called the factor of the non-uniformity load distribution [10].

Stribeck determined that with an increase in the total number of balls in the bearing with zero clearance, the factor of the non-uniformity load distribution asymptotically strives to constant S = 4.37 [1]. This number is called the Stribeck number (S) and in the literature is taken as a relevant value for the calculation of the load of the most-loaded ball at the bearings with zero clearance, i.e., at the calculation of the static load rating of the bearing [11]. Palmgren later proposed that in the bearings with the rollers, the Stribeck number amounts to S = 4.08 [12]. For the bearings with radial clearance greater than zero, the impact of the clearance on the load distribution is approximated by increasing the value of the Stribeck number on the value S = 5, independently of the size of the clearance. This applies to every type of ball and roller bearing with internal radial clearance. However, this kind of approach has justification for only orientational calculations because it takes into consideration only whether or not the clearance is present in the bearing, and the influence of the clearance size is not taken into account. Even the influence of the type of bearing on the load distribution is not taken into account. Still, the calculation based on the Stribeck numbers is the most commonly used method for the calculation of the load that transfers the most-loaded rolling element. Stribeck’s expressions are still in use today to calculate the static load capacity of a rolling bearing [2,3].

The model that is proposed in this paper takes into account the impact of the internal radial clearance and the type of bearing on the internal load distribution. The impact of the clearance is taken through the number of active rolling elements in the bearing. By its simplicity, the proposed model can be compared to the Stribeck method. The proposed model, like the Stribeck one, is based on simple mathematical operations, does not require the usage of the computer and it can be very useable for fast calculations and work in the field.

The aim of this study is to propose the guidelines to correctly choose the load factors for the new mathematical model that is developed in [5]. For this purpose, a load calculation of the most-loaded rolling element was carried out for the two different types of radial rolling bearings: the ball bearing 6206 and the bearing with the cylindrical rollers, NU 2205 EC. For both bearing types, the analysis was conducted for different values of the internal radial clearance. The obtained results were compared with results obtained based on Stribeck coefficients. Additionally, both methods were compared with the results obtained by solving the system of static equilibrium equations [4,9].

The precision of the results obtained by solving the system of static equations solely depends on the precision of the numerical procedure for solving them. In this regard, these results were considered accurate, and compared to them the calculation error according to the proposed method and the Stribeck method were analyzed. Furthermore, the coefficients of Stribeck refer to only the boundary position of support on an odd number of rolling elements (BSO position) [13], and the analysis was performed only in relation to this position of the rolling elements set, which is shown in Figure 1. This is justified because from the aspect of load distribution this is the most unfavorable position of the rolling bearing support. Then, the most-loaded rolling element transfers the largest part of the external load [14]. For these reasons, so far, almost all published studies have limited their analysis to only this position of support [15,16,17,18,19,20].

The analysis conducted showed that by correct selection of the load factor, the new model provides much more precise results compared to the Stribeck method. Based on this, in the conclusion, guidelines for the efficient selection of load factors are proposed.

2. The Static Equilibrium Equations for the BSO Position of Support

The problem of calculating the internal load distribution is a statically indeterminate problem. Therefore, the system of static equilibrium equations needs to be extended with additional equations, which are based on the relationship between contact stresses and deformations. A detailed description of the calculation is presented in the references [4,8,9].

In Figure 1, the scheme of the internal load distribution for the BSO position of support for the rolling bearing with internal radial clearance is presented. The force equilibrium condition for this position can be set as:

$$Q=F_0+2\cdot {\displaystyle \sum _{i=1}^{\frac{q-1}{2}}{F}_i\cdot \cos \left(i\gamma \right)}.$$

(3)

where: Q—the external radial load, F₀—the load of the most-loaded rolling element, Fi—the load of i-th rolling element, γ—the angular spacing between rolling bearing elements, q—the number of active rolling elements.

Equation (3) is a statically indeterminate equation. Unknown values are loads that transfer through the rolling elements of the bearing (F_i). By taking into account the symmetry of the problem, the number of unknown values is equal to (q + 1)/2. So, besides the equilibrium Equation (3), it is necessary to set up (q − 1)/2 additional equations, based on the relationship between the contact stresses and the deformations of the coupled parts of the bearing.

According to [4,8], the total deflection of the bearing is equal to the sum of the boundary deflection until the entry of the i-th rolling element into contact with the bearing rings and the projection of the total contact deformation of the i-th rolling element on the direction of the action of external load, i.e.,:

$$w_o=a_{2i+1}+\frac{{\delta }_i}{\cos (i\gamma )}.$$

(4)

where is a_2i+1—the necessary bearing deflection for the entry of the i-th rolling element in contact with rings, δ_i—the contact deformations on the place of the i-th rolling element.

The necessary bearing deflection (a_2i+1) is directly dependent on the bearing type and the internal radial clearance size. For necessary bearing deflection, study [8] adopted the term “boundary-bearing deflection” and presented a procedure for its simple determination. According to this procedure, the boundary-bearing deflection is calculated as:

$$a_q=t_q^{}\cdot \frac{e}{2}.$$

(5)

where: e—internal radial clearance, q = 2i + 1—number of rolling elements on which the inner bearing ring is supported, and t_q—coefficient of boundary-bearing deflection that can be obtained from the tables shown in the literature [4,8].

Taking into account Equation (4), the system of equations for the calculation of the internal load distribution for the BSO position can be written as:

$$\begin{array}{c}Q=F_0+2\cdot {\displaystyle \sum _{i=1}^{\frac{q-1}{2}}{F}_i\cdot \cos \left(i\gamma \right)}\\ w_0=a_3+\frac{{\delta }_1}{\cos \gamma }\\ w_0=a_5+\frac{{\delta }_2}{\cos \left(2\gamma \right)}\\ ---\\ w_0=a_{2i+1}+\frac{{\delta }_i}{\cos (i\gamma )}\\ ---\\ w_0=a_q+\frac{{\delta }_{(q-1)/2}}{\cos (\frac{q-1}{2}\gamma )}\end{array}$$

(6)

According to the Hertz theory [11], the size of the contact deformations (δ_i) can be calculated based on the equation:

$${\delta }_i={\left(\frac{F_i}{K}\right)}^{\frac{1}{n}}.$$

(7)

where is K—the effective coefficient of the bearing stiffness, and n—exponent that is dependent on the type of the bearing (n = 3/2 for a ball bearing and n = 10/9 for a bearing with the rollers).

Based on Figure 1b, it is clear that the total deflection of the bearing is equal to the contact deformation at the place of the most-loaded rolling element, i.e., w_o = δ₀. Based on that and Equation (7), the total deflection of the bearing can be written as:

$$w_o={\left(\frac{F_0}{K}\right)}^{\frac{1}{n}}.$$

(8)

That is, taking into account Equations (6)–(8), the system of equations for the calculation of the internal load distribution for the BSO position of the rolling bearing can be written as:

$$\begin{array}{c}Q=F_0+2\cdot {\displaystyle \sum _{i=1}^{\frac{q-1}{2}}{F}_i\cdot \cos \left(i\gamma \right)}\\ {\left(\frac{F_0}{K}\right)}^{\frac{1}{n}}=a_3+\frac{1}{\cos \gamma }{\left(\frac{F_1}{K}\right)}^{\frac{1}{n}}\\ {\left(\frac{F_0}{K}\right)}^{\frac{1}{n}}=a_5+\frac{1}{\cos 2\gamma }{\left(\frac{F_2}{K}\right)}^{\frac{1}{n}}\\ ---\\ {\left(\frac{F_0}{K}\right)}^{\frac{1}{n}}=a_{2i+1}+\frac{1}{\cos (i\gamma )}{\left(\frac{F_i}{K}\right)}^{\frac{1}{n}}\\ ---\\ {\left(\frac{F_0}{K}\right)}^{\frac{1}{n}}=a_q+\frac{1}{\cos (\frac{q-1}{2}\gamma )}{\left(\frac{F_{{}_{(q-1)/2}}}{K}\right)}^{\frac{1}{n}}\end{array}$$

(9)

The system of Equation (9) consists of (q + 1)/2 non-linear equations. By solving this system, it is possible to obtain the loads that transfer the individual rolling elements. Since the system is non-linear, it can be only solved numerically. The total number of active rolling elements of the bearing (q) can be easily determined based on the procedure shown in [9].

3. Case Study of the Load Calculation That Transfers the Most-Loaded Rolling Element of the Rolling Bearing

3.1. Case Study of the Ball Bearing

The radial ball bearing 6206 was taken as an example for the calculation. The effective coefficient of the bearing stiffness is K = 3.41·10⁵ N/mm^3/2. The total number of rolling elements is z = 9, and the maximum possible number of active rolling elements is z_s = 5 [8]. The values of the coefficient of boundary-bearing deflection (t_q) and the coefficient of boundary external radial load (s_q) were determined from the tables, which are presented in references [8,9] and shown in

Table 1. The coefficient of boundary-bearing deflection (t_q) and boundary external radial load (s_q) and the load factor of the most-loaded rolling element (k_maxq) for ball bearing 6206.

	q = 3	q = 4	q = 5
tq	0.3054	0.9358	4.7588
sq	0.1688	1.5498	20.0348
kmaxq	1.0000	0.5321	0.5182

. The values of the load factor for the most-loaded rolling element k_maxq are also shown in Table 1. These values were determined based on Table 1 from the literature [5].

The load that transfers the most-loaded rolling element of bearing is possibly obtained by the multiplication of factors k_maxq with the external radial load (Q), according to Equation (1). The results of the calculation for the 6206 ball bearing are shown in

Table A1. The load of the most-loaded rolling element of bearing 6206 with radial clearance e = 0 µm.

Q	5.0	8.0	10.0	20.0	50.0	80.0	100.0	200.0	500.0	800.0	1000.0	2000.0	5000.0	8000.0	10,000.0
exact result	2.9	4.4	5.4	10.5	25.4	40.3	50.1	99.2	246.0	392.6	490.3	978.3	2441.4	3904.0	4879.0
q3	5.0	8.0	10.0	20.0	50.0	80.0	100.0	200.0	500.0	800.0	1000.0	2000.0	5000.0	8000.0	10,000.0
%	75.4	82.2	84.5	91.0	96.6	98.8	99.6	101.6	103.2	103.8	104.0	104.4	104.8	104.9	105.0
q4	2.7	4.3	5.3	10.6	26.6	42.6	53.2	106.4	266.1	425.7	532.1	1064.2	2660.5	4256.8	5321.0
%	−6.6	−3.0	−1.8	1.6	4.6	5.8	6.2	7.3	8.1	8.4	8.5	8.8	9.0	9.0	9.1
q5	2.6	4.1	5.2	10.4	25.9	41.5	51.8	103.6	259.1	414.6	518.2	1036.4	2591.0	4145.6	5182.0
%	−9.1	−5.6	−4.4	−1.0	1.9	3.0	3.4	4.5	5.3	5.6	5.7	5.9	6.1	6.2	6.2
Stribek	2.4	3.9	4.9	9.7	24.3	38.8	48.6	97.1	242.8	388.4	485.6	971.1	2427.8	3884.4	4855.6
%	−14.8	−11.5	−10.4	−7.2	−4.5	−3.5	−3.1	−2.1	−1.3	−1.1	−1.0	−0.7	−0.6	−0.5	−0.5

,

Table A2. The load of the most-loaded rolling element of bearing 6206 with radial clearance e = 5 µm.

Q	5.0	7.2	10.0	50.0	66.1	80.0	100.0	200.0	500.0	800.0	854.8	1000.0	5000.0	8000.0	10,000.0
exact result	5.0	7.2	9.4	32.9	41.6	49.1	59.7	111.7	264.4	415.4	442.9	515.5	2487.2	3957.9	4937.2
q3	5.0	7.2	10.0	50.0	66.1	80.0	100.0	200.0	500.0	800.0	854.8	1000.0	5000.0	8000.0	10,000.0
%	0.0	0.0	6.6	52.2	58.8	63.0	67.5	79.0	89.1	92.6	93.0	94.0	101.0	102.1	102.5
q4	2.7	3.8	5.3	26.6	35.2	42.6	53.2	106.4	266.1	425.7	454.8	532.1	2660.5	4256.8	5321.0
%	−46.8	−46.8	−43.3	−19.0	−15.5	−13.3	−10.9	−4.8	0.6	2.5	2.7	3.2	7.0	7.6	7.8
q5	2.6	3.7	5.2	25.9	34.3	41.5	51.8	103.6	259.1	414.6	442.9	518.2	2591.0	4145.6	5182.0
%	−48.2	−48.2	−44.8	−21.2	−17.7	−15.5	−13.2	−7.2	−2.0	−0.2	0.0	0.5	4.2	4.7	5.0
Stribek	2.8	4.0	5.6	27.8	36.7	44.4	55.6	111.1	277.8	444.4	474.9	555.6	2777.8	4444.4	5555.6
%	−44.4	−44.4	−40.8	−15.5	−11.8	−9.4	−6.9	−0.6	5.1	7.0	7.2	7.8	11.7	12.3	12.5

,

Table A3. The load of the most-loaded rolling element of bearing 6206 with radial clearance e = 10 µm.

Q	10.0	20.0	20.4	50.0	100.0	187.1	200.0	500.0	800.0	1000.0	2000.0	2417.6	5000.0	8000.0	10,000.0
exact result	10.0	20.0	20.4	40.6	69.9	117.8	124.8	282.2	436.2	538.1	1043.0	1252.7	2535.7	4016.0	5000.2
q3	10.0	20.0	20.4	50.0	100.0	187.1	200.0	500.0	800.0	1000.0	2000.0	2417.6	5000.0	8000.0	10,000.0
%	0.0	0.0	0.0	23.0	43.1	58.8	60.3	77.2	83.4	85.8	91.8	93.0	97.2	99.2	100.0
q4	5.3	10.6	10.8	26.6	53.2	99.6	106.4	266.1	425.7	532.1	1064.2	1286.4	2660.5	4256.8	5321.0
%	−46.8	−46.8	−46.8	−34.5	−23.9	−15.5	−14.7	−5.7	−2.4	−1.1	2.0	2.7	4.9	6.0	6.4
q5	5.2	10.4	10.6	25.9	51.8	97.0	103.6	259.1	414.6	518.2	1036.4	1252.8	2591.0	4145.6	5182.0
%	−48.2	−48.2	−48.2	−36.2	−25.8	−17.7	−16.9	−8.2	−5.0	−3.7	−0.6	0.0	2.2	3.2	3.6
Stribek	5.6	11.1	11.3	27.8	55.6	103.9	111.1	277.8	444.4	555.6	1111.1	1343.1	2777.8	4444.4	5555.6
%	−44.4	−44.4	−44.4	−31.6	−20.5	−11.8	−10.9	−1.6	1.9	3.2	6.5	7.2	9.5	10.7	11.1

,

Table A4. The load of the most-loaded rolling element of bearing 6206 with radial clearance e = 15 µm.

Q	10.0	20.0	37.4	50.0	100.0	200.0	343.6	500.0	800.0	1000.0	2000.0	4441.4	5000.0	8000.0	10,000.0
exact result	10.0	20.0	37.4	47.3	79.6	137.6	216.3	299.8	456.9	560.4	1071.2	2301.3	2580.7	4071.6	5061.1
q3	10.0	20.0	37.4	50.0	100.0	200.0	343.6	500.0	800.0	1000.0	2000.0	4441.4	5000.0	8000.0	10,000.0
%	0.0	0.0	0.0	5.7	25.6	45.4	58.8	66.8	75.1	78.4	86.7	93.0	93.7	96.5	97.6
q4	5.3	10.6	19.9	26.6	53.2	106.4	182.8	266.1	425.7	532.1	1064.2	2363.3	2660.5	4256.8	5321.0
%	−46.8	−46.8	−46.8	−43.8	−33.2	−22.6	−15.5	−11.3	−6.8	−5.1	−0.7	2.7	3.1	4.5	5.1
q5	5.2	10.4	19.4	25.9	51.8	103.6	178.0	259.1	414.6	518.2	1036.4	2301.5	2591.0	4145.6	5182.0
%	−48.2	−48.2	−48.2	−45.2	−34.9	−24.7	−17.7	−13.6	−9.3	−7.5	−3.2	0.0	0.4	1.8	2.4
Stribek	5.6	11.1	20.8	27.8	55.6	111.1	190.9	277.8	444.4	555.6	1111.1	2467.5	2777.8	4444.4	5555.6
%	−44.4	−44.4	−44.4	−41.3	−30.2	−19.2	−11.8	−7.4	−2.7	−0.9	3.7	7.2	7.6	9.2	9.8

,

Table A5. The load of the most-loaded rolling element of bearing 6206 with radial clearance e = 20 µm.

Q	10.0	20.0	50.0	57.6	100.0	200.0	500.0	529.0	800.0	1000.0	2000.0	5000.0	6838.0	8000.0	10,000.0
exact result	10.0	20.0	50.0	57.6	88.6	150.1	317.4	333.1	477.6	582.7	1099.4	2619.6	3543.1	4123.9	5119.3
q3	10.0	20.0	50.0	57.6	100.0	200.0	500.0	529.0	800.0	1000.0	2000.0	5000.0	6838.0	8000.0	10,000.0
%	0.0	0.0	0.0	0.0	12.8	33.3	57.5	58.8	67.5	71.6	81.9	90.9	93.0	94.0	95.3
q4	5.3	10.6	26.6	30.7	53.2	106.4	266.1	281.5	425.7	532.1	1064.2	2660.5	3638.5	4256.8	5321.0
%	−46.8	−46.8	−46.8	−46.8	−40.0	−29.1	−16.2	−15.5	−10.9	−8.7	−3.2	1.6	2.7	3.2	3.9
q5	5.2	10.4	25.9	29.9	51.8	103.6	259.1	274.1	414.6	518.2	1036.4	2591.0	3543.5	4145.6	5182.0
%	−48.2	−48.2	−48.2	−48.2	−41.5	−30.9	−18.4	−17.7	−13.2	−11.1	−5.7	−1.1	0.0	0.5	1.2
Stribek	5.6	11.1	27.8	32.0	55.6	111.1	277.8	293.9	444.4	555.6	1111.1	2777.8	3798.9	4444.4	5555.6
%	−44.4	−44.4	−44.4	−44.4	−37.3	−26.0	−12.5	−11.8	−6.9	−4.7	1.1	6.0	7.2	7.8	8.5

,

Table A6. The load of the most-loaded rolling element of bearing 6206 with radial clearance e = 30 µm.

Q	10.0	20.0	50.0	80.0	100.0	105.8	200.0	500.0	800.0	971.8	1000.0	2000.0	5000.0	8000.0	10,000.0
exact result	10.0	20.0	50.0	80.0	100.0	105.8	173.5	352.0	518.6	611.9	627.1	1155.6	2696.1	4215.0	5222.3
q3	10.0	20.0	50.0	80.0	100.0	105.8	200.0	500.0	800.0	971.8	1000.0	2000.0	5000.0	8000.0	10,000.0
%	0.0	0.0	0.0	0.0	0.0	0.0	15.3	42.0	54.3	58.8	59.5	73.1	85.5	89.8	91.5
q4	5.3	10.6	26.6	42.6	53.2	56.3	106.4	266.1	425.7	517.1	532.1	1064.2	2660.5	4256.8	5321.0
%	−46.8	−46.8	−46.8	−46.8	−46.8	−46.8	−38.7	−24.4	−17.9	−15.5	−15.1	−7.9	−1.3	1.0	1.9
q5	5.2	10.4	25.9	41.5	51.8	54.8	103.6	259.1	414.6	503.6	518.2	1036.4	2591.0	4145.6	5182.0
%	−48.2	−48.2	−48.2	−48.2	−48.2	−48.2	−40.3	−26.4	−20.1	−17.7	−17.4	−10.3	−3.9	−1.6	−0.8
Stribek	5.6	11.1	27.8	44.4	55.6	58.8	111.1	277.8	444.4	539.9	555.6	1111.1	2777.8	4444.4	5555.6
%	−44.4	−44.4	−44.5	−44.4	−44.4	−44.4	−36.0	−21.1	−14.3	−11.8	−11.4	−3.9	3.0	5.4	6.4

,

Table A7. The load of the most-loaded rolling element of bearing 6206 with radial clearance e = 40 µm.

Q	10.0	20.0	50.0	80.0	100.0	163.0	200.0	500.0	800.0	1000.0	1496.1	2000.0	5000.0	8000.0	10,000.0
exact result	10.0	20.0	50.0	80.0	100.0	163.0	193.1	385.6	559.1	671.0	942.0	1211.7	2772.6	4304.5	5318.8
q3	10.0	20.0	50.0	80.0	100.0	163.0	200.0	500.0	800.0	1000.0	1496.1	2000.0	5000.0	8000.0	10,000.0
%	0.0	0.0	0.0	0.0	0.0	0.0	3.6	29.7	43.1	49.0	58.8	65.1	80.3	85.9	88.0
q4	5.3	10.6	26.6	42.6	53.2	86.7	106.4	266.1	425.7	532.1	796.1	1064.2	2660.5	4256.8	5321.0
%	−46.8	−46.8	−46.8	−46.8	−46.8	−46.8	−44.9	−31.0	−23.9	−20.7	−15.5	−12.2	−4.0	−1.1	0.0
q5	5.2	10.4	25.9	41.5	51.8	84.4	103.6	259.1	414.6	518.2	775.3	1036.4	2591.0	4145.6	5182.0
%	−48.2	−48.2	−48.2	−48.2	−48.2	−48.2	−46.3	−32.8	−25.8	−22.8	−17.7	−14.5	−6.5	−3.7	−2.6
Stribek	5.6	11.1	27.8	44.4	55.6	90.5	111.1	277.8	444.4	555.6	831.2	1111.1	2777.8	4444.4	5555.6
%	−44.4	−44.4	−44.5	−44.4	−44.4	−44.4	−42.5	−28.0	−20.5	−17.2	−11.8	−8.3	0.2	3.3	4.5

and

Table A8. The load of the most-loaded rolling element of bearing 6206 with radial clearance e = 50 µm.

Q	10.0	20.0	50.0	80.0	100.0	200.0	227.7	500.0	800.0	1000.0	2000.0	2090.9	5000.0	8000.0	10,000.0
exact result	10.0	20.0	50.0	80.0	100.0	200.0	227.7	417.7	598.7	714.2	1267.4	1316.5	2849.0	4394.0	5415.2
q3	10.0	20.0	50.0	80.0	100.0	200.0	227.7	500.0	800.0	1000.0	2000.0	2090.9	5000.0	8000.0	10,000.0
%	0.1	0.0	0.0	0.0	0.0	0.0	0.0	19.7	33.6	40.0	57.8	58.8	75.5	82.1	84.7
q4	5.3	10.6	26.6	42.6	53.2	106.4	121.2	266.1	425.7	532.1	1064.2	1112.6	2660.5	4256.8	5321.0
%	−46.7	−46.8	−46.8	−46.8	−46.8	−46.8	−46.8	−36.3	−28.9	−25.5	−16.0	−15.5	−6.6	−3.1	−1.7
q5	5.2	10.4	25.9	41.5	51.8	103.6	118.0	259.1	414.6	518.2	1036.4	1083.5	2591.0	4145.6	5182.0
%	−48.1	−48.2	−48.2	−48.2	−48.2	−48.2	−48.2	−38.0	−30.8	−27.4	−18.2	−17.7	−9.1	−5.7	−4.3
Stribek	5.6	11.1	27.8	44.4	55.6	111.1	126.5	277.8	444.4	555.6	1111.1	1161.6	2777.8	4444.4	5555.6
%	−44.4	−44.4	−44.4	−44.5	−44.4	−44.4	−44.4	−33.5	−25.8	−22.2	−12.3	−11.8	−2.5	1.1	2.6

, which are shown in Appendix A. The results are shown for different values of the internal radial clearance, which were varied in the full range of standard recommended values of the internal radial clearance for the 6206 bearings (from 0 to 50 µm) [21].

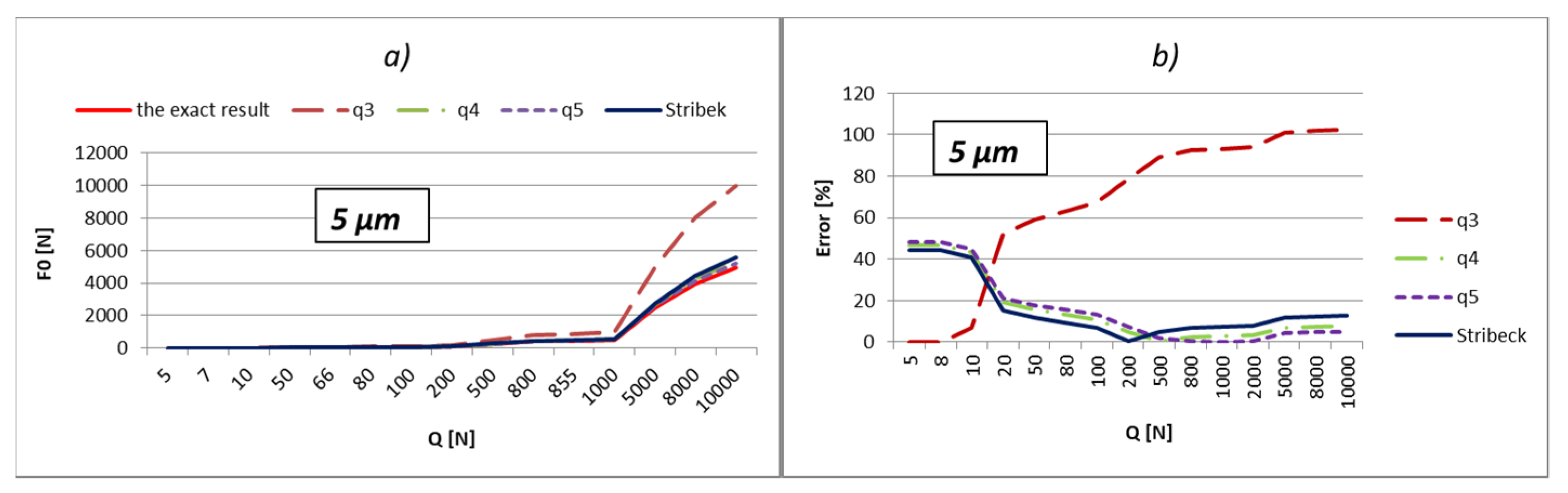
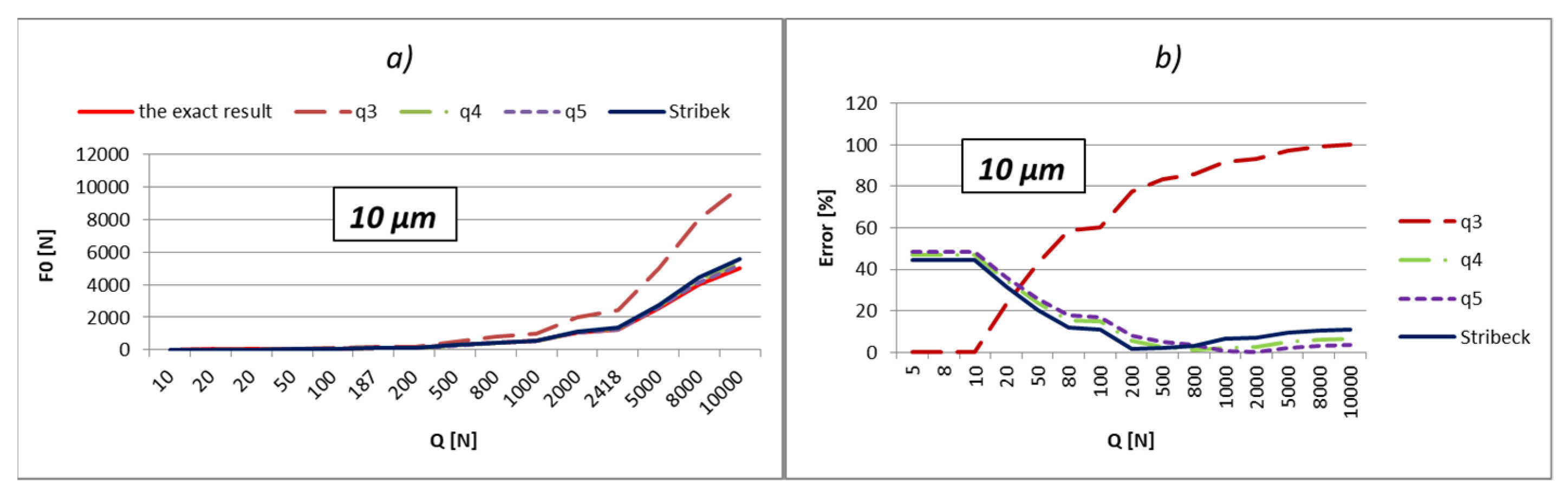
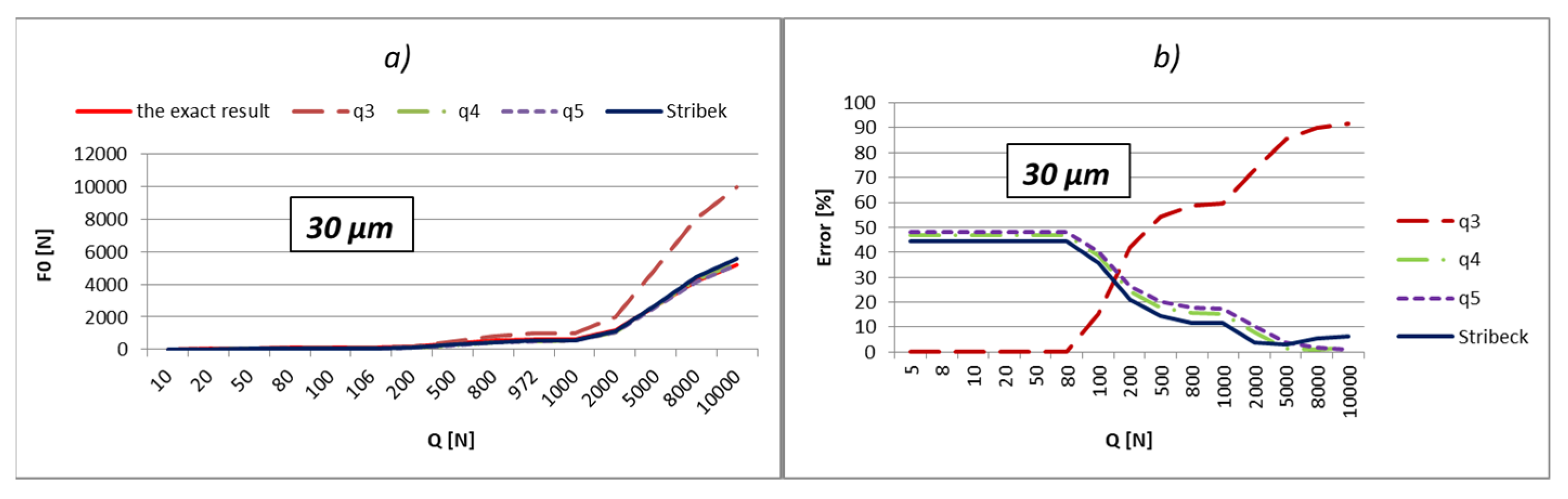
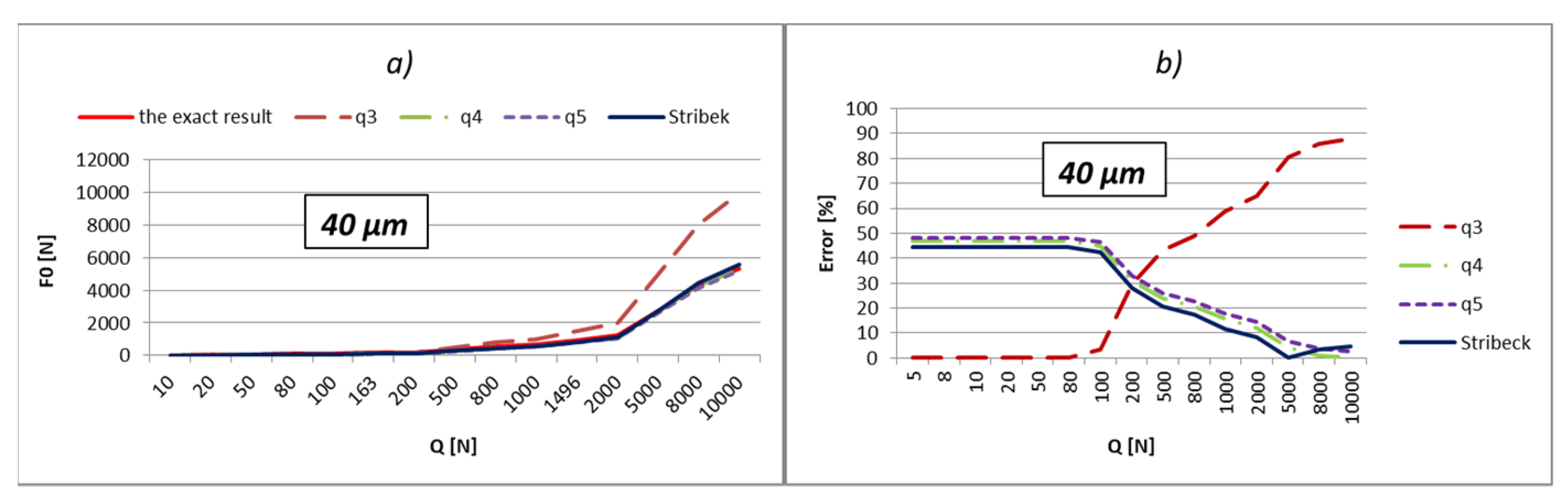
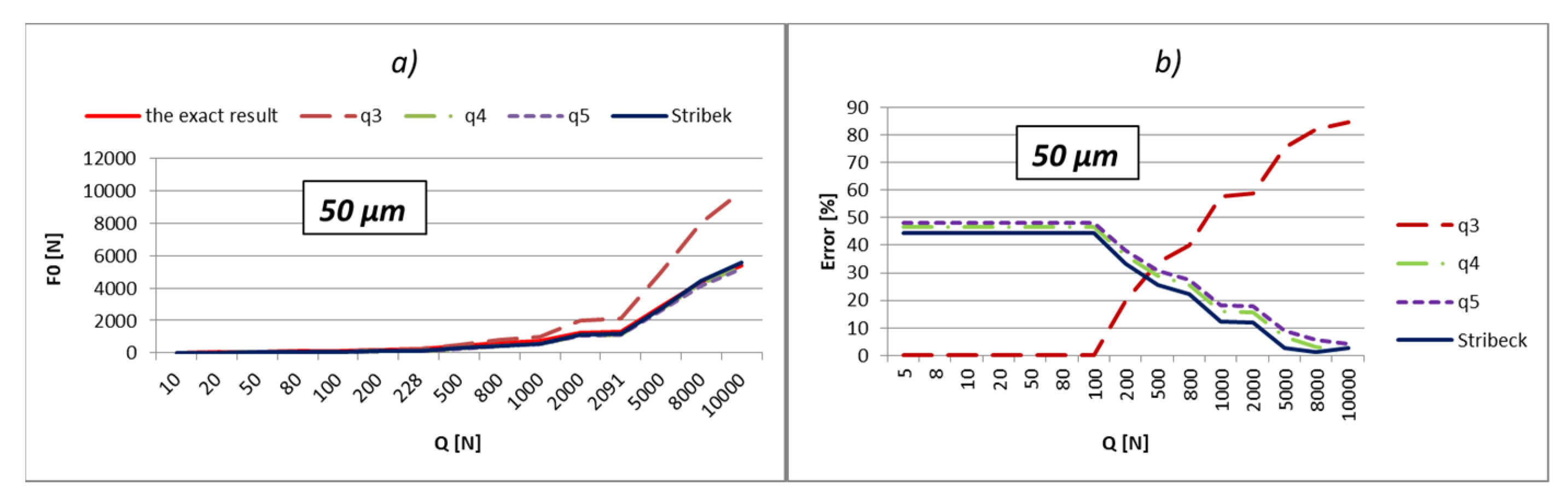
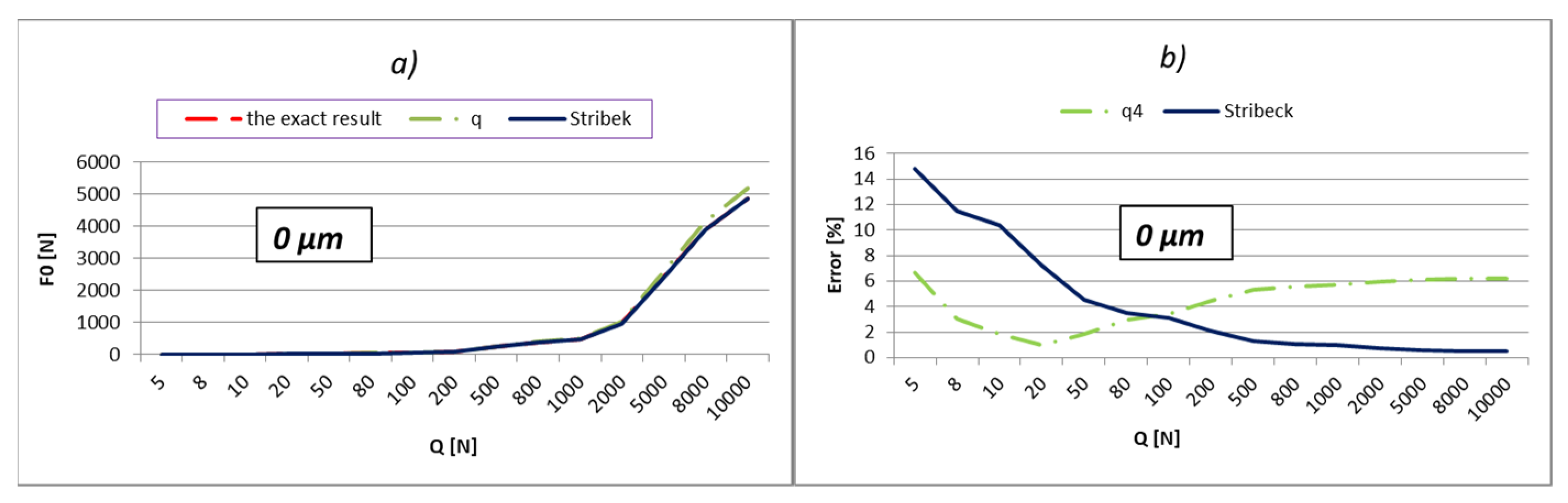
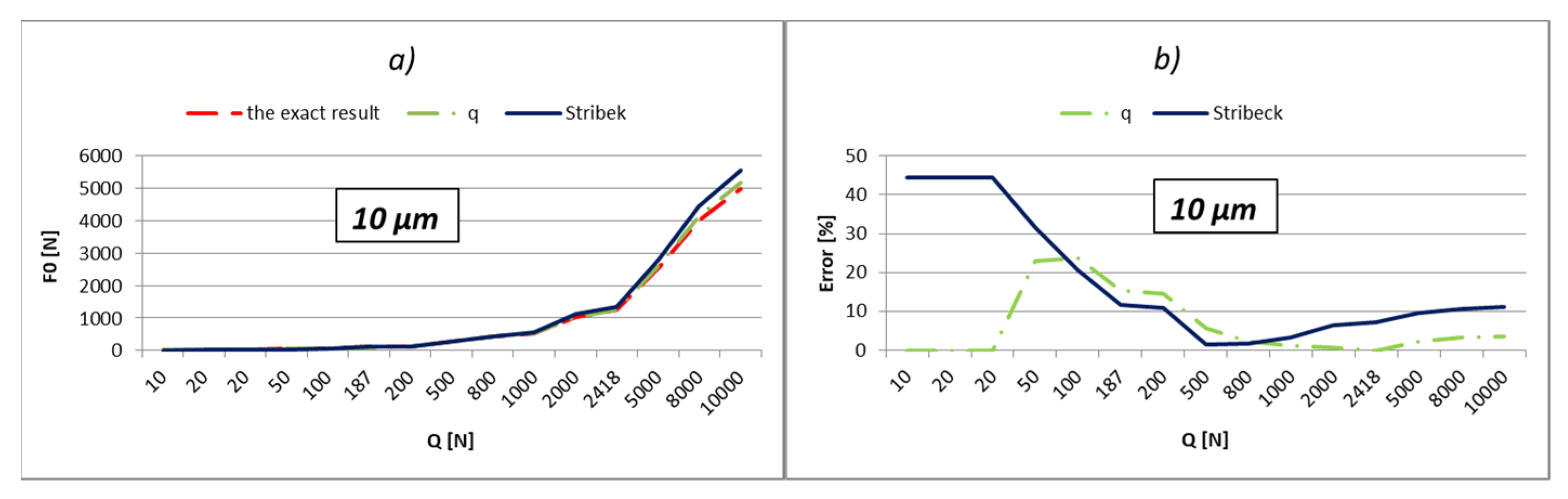
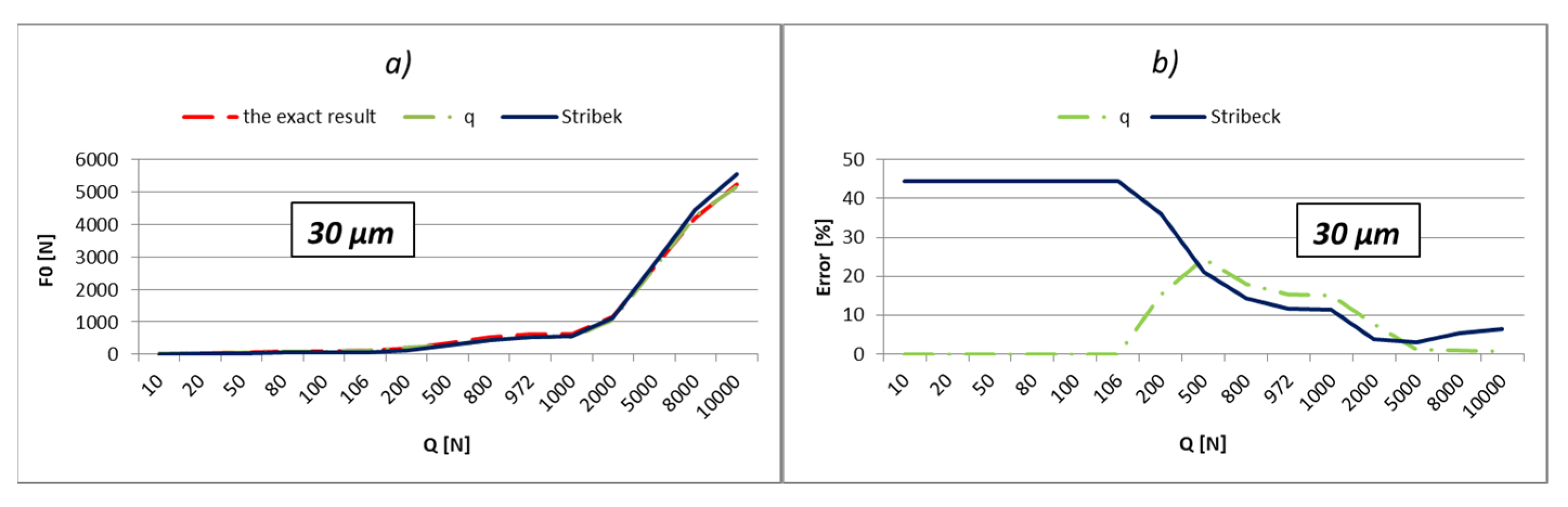
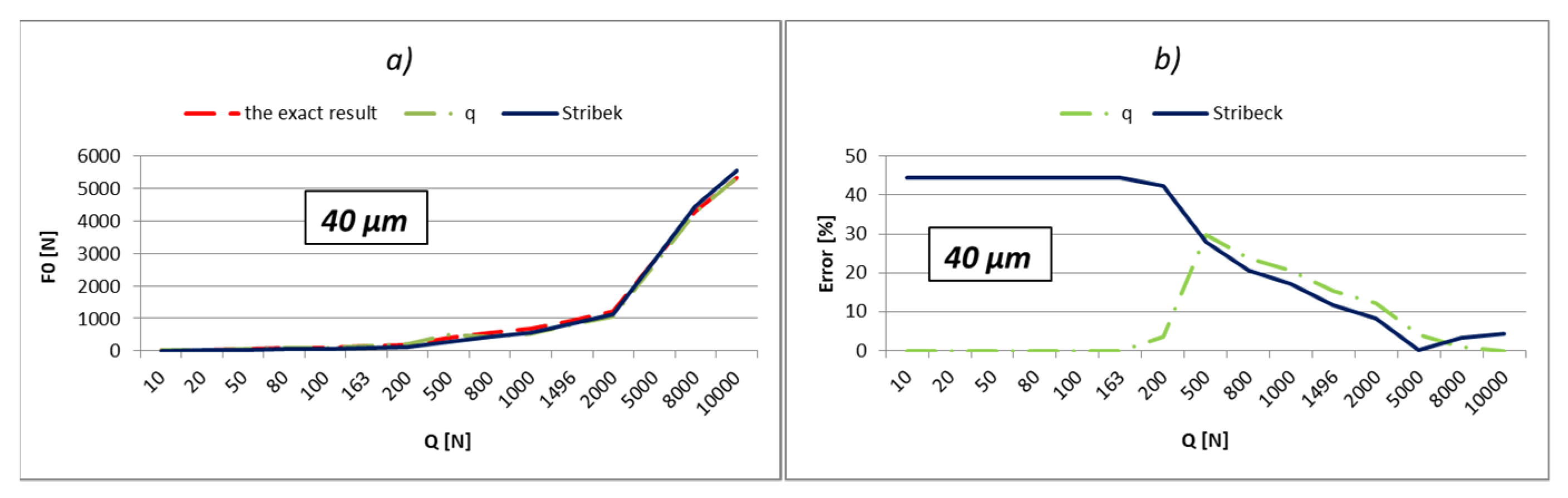
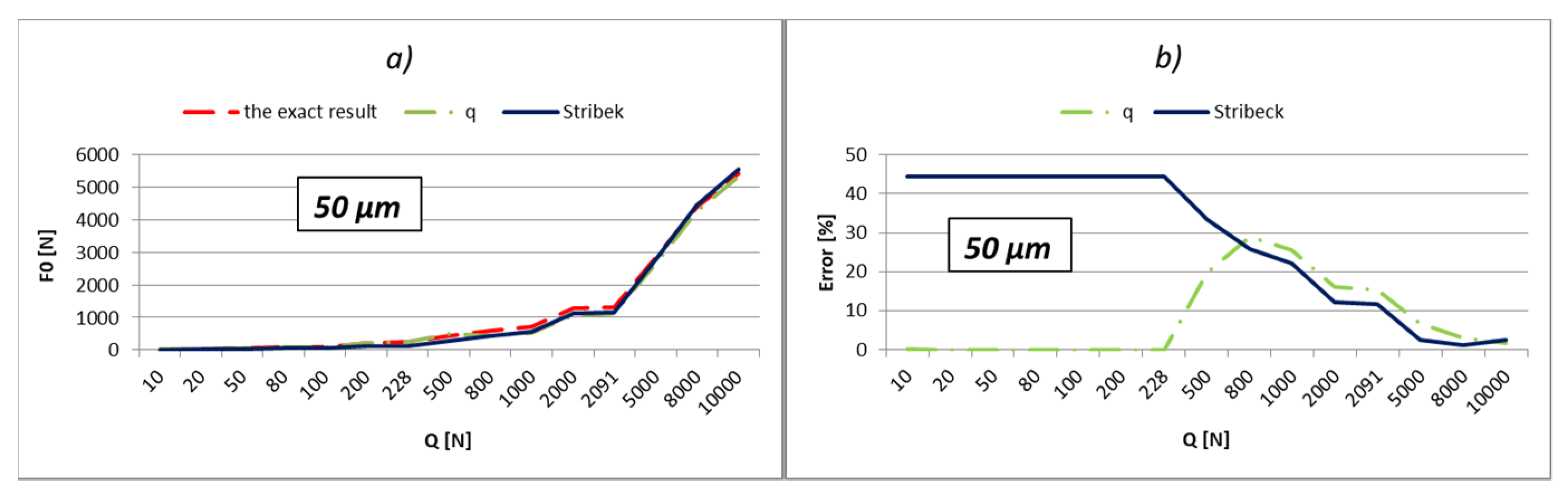
The load values for the most-loaded rolling element were calculated and shown in relation to three different methods:

• By solving the systems of nonlinear equations (Equation (9)). In Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7 and Table A8—exact value;
• Using Stribeck’s number, according to Equation (2);
• By applying the load factor of the most-loaded rolling element, according to Equation (1).

To obtain an effective analysis, the calculation was performed by using the load factors, especially for all three values of factors k_maxq shown in Table 1. The errors of calculation in percentages are shown below the results. The errors were obtained by comparing obtained results with the exact value. The external load values were varied in the range from 10 to 10,000 N, which is very close to the static load rating of the bearing, which is 11,200 N. In addition, the calculation was performed also with respect to the boundary values of external load (Q_q). These values in the tables are bold. The boundary values of the external load were calculated in relation to the following Equation [9]:

$$Q_q=K\cdot s_q\cdot {\left(\frac{e}{2}\right)}^n.$$

(10)

The results shown in Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7 and Table A8 are graphically presented in Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. The calculation results of the load of the most-loaded rolling element are shown on the left side (a), and the errors in a percentage are shown on the right side (b) of Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9.

3.2. Case Study of Bearing with Rollers

As an example for the calculation, a radial roller bearing with cylindrical rollers (NU 2205 EC) was taken. The effective coefficient of the stiffness of this bearing is K = 3.14·10⁵ N/mm^10/9. The total number of rolling elements is z = 13, and the maximal possible number of active rolling elements is z_s = 7 [8]. The values of the coefficient of boundary-bearing deflection (t_q) and the coefficient of boundary external radial load (s_q) for this bearing are shown in

Table 2. The coefficient of boundary-bearing deflection (t_q) and boundary external radial load (s_q) and the load factor of the most-loaded rolling element (k_maxq) for roller bearing NU 2205 EC.

	q = 3	q = 4	q = 5	q = 6	q = 7
t q	0.1294	0.3061	0.7604	1.7901	7.2962
s q	0.1031	0.5043	1.6650	5.2715	27.7786
kmaxq	1.0000	0.5150	0.4430	0.3506	0.3276

, and they are determined from the tables that are presented in the literature [8,9]. The values of the load factor of the most-loaded rolling element k_maxq are also shown in Table 2. These values are determined according to Table 2 from the literature [5].

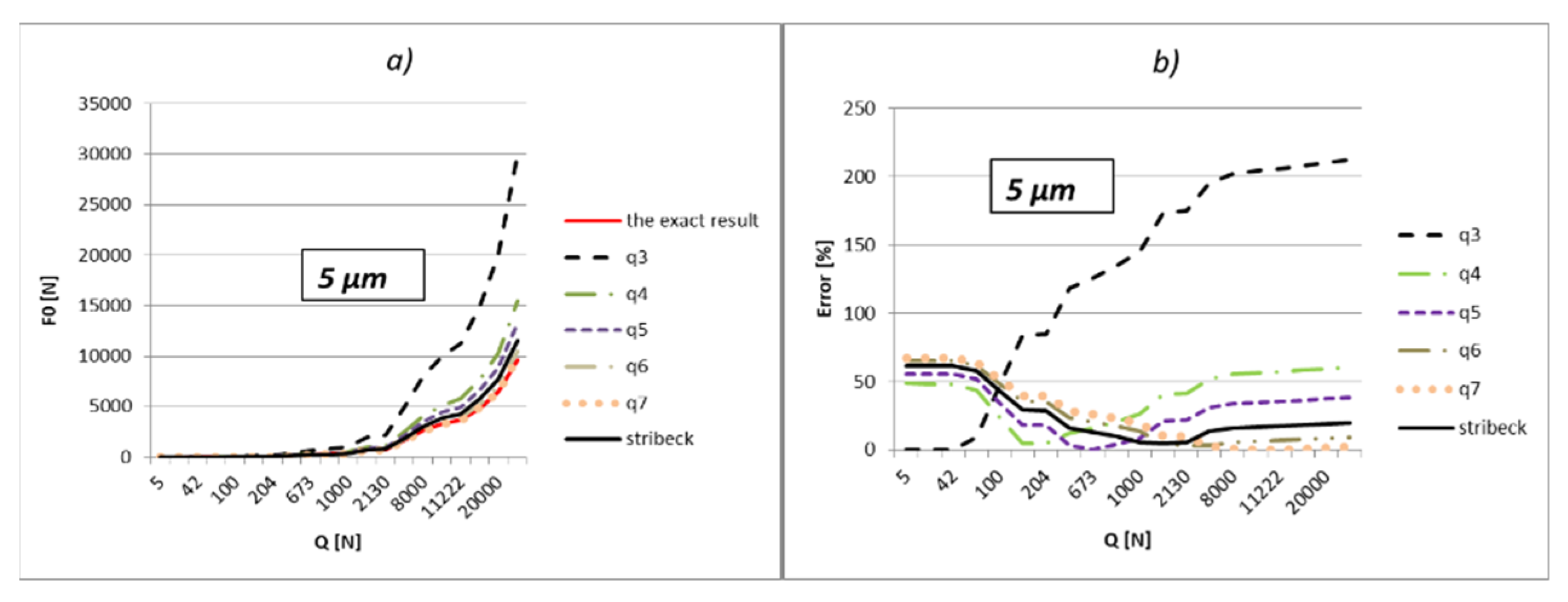
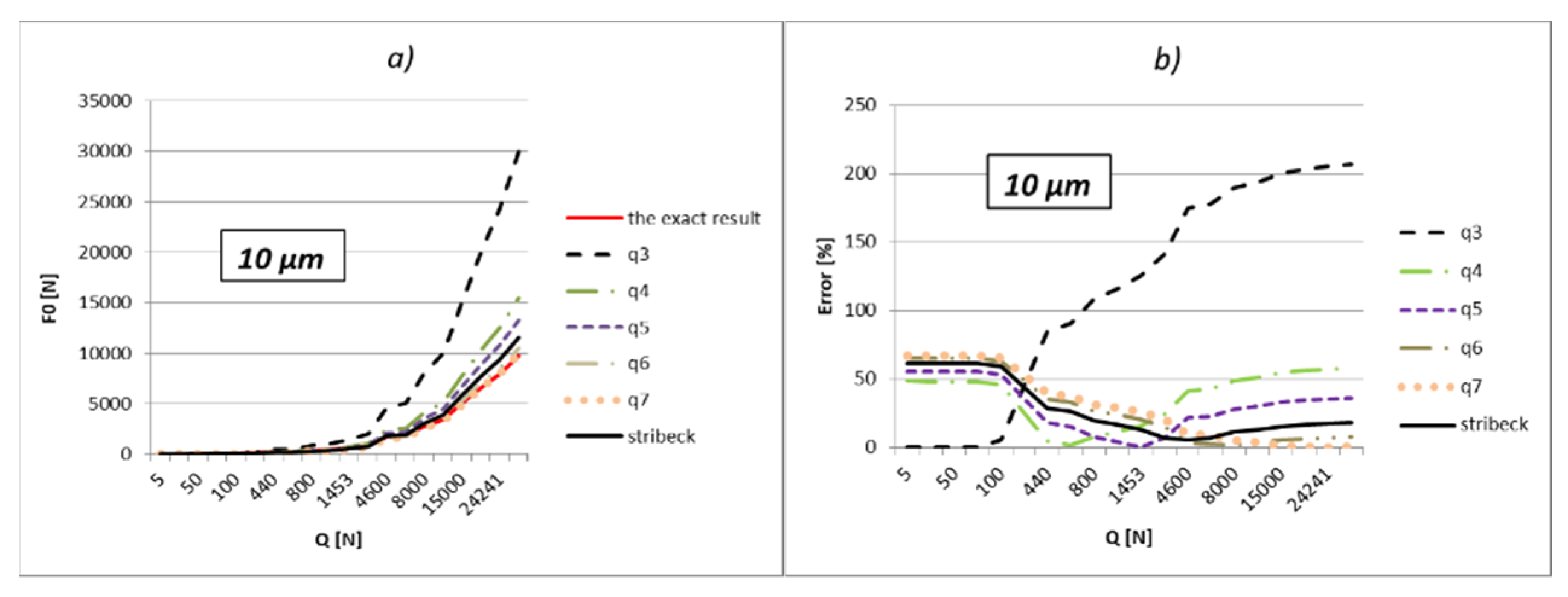
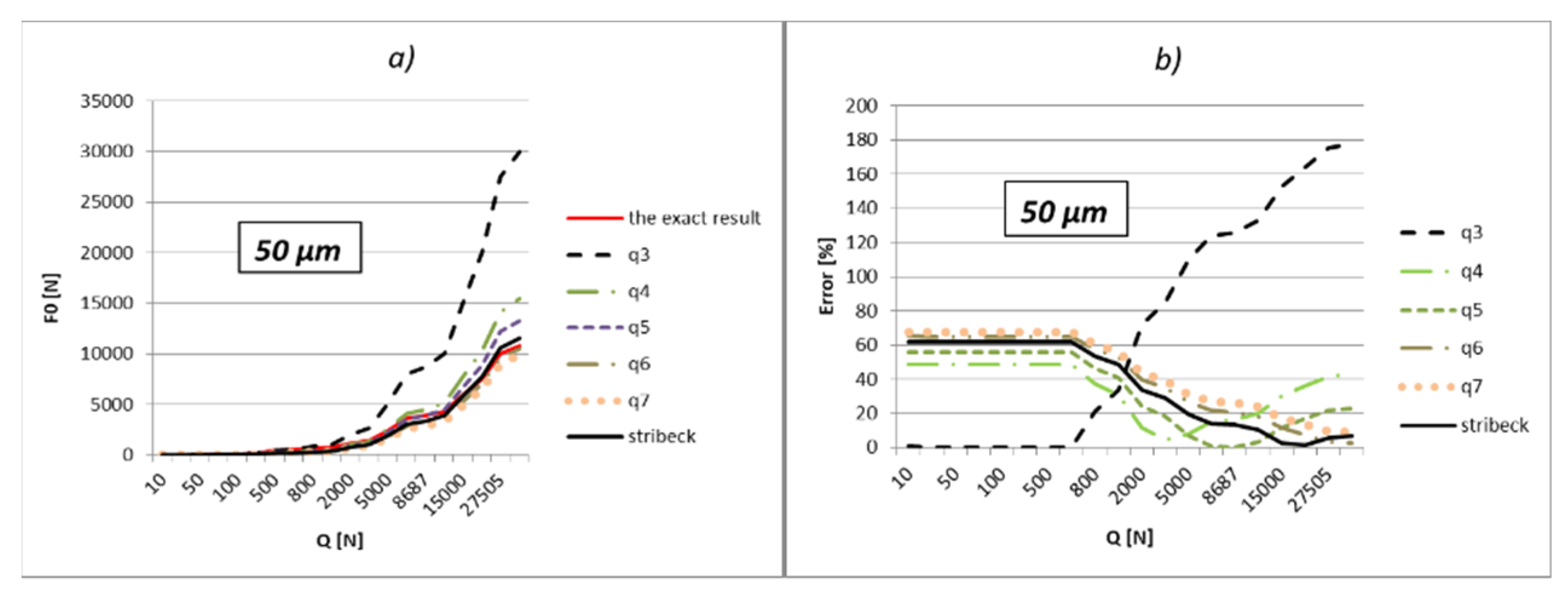
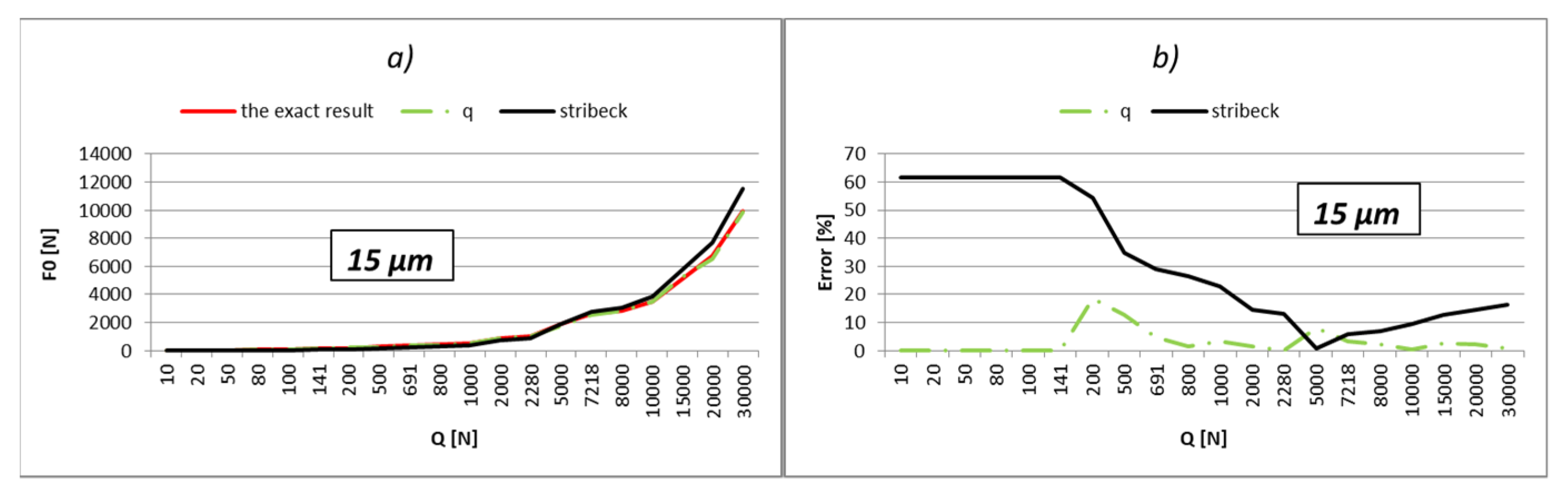
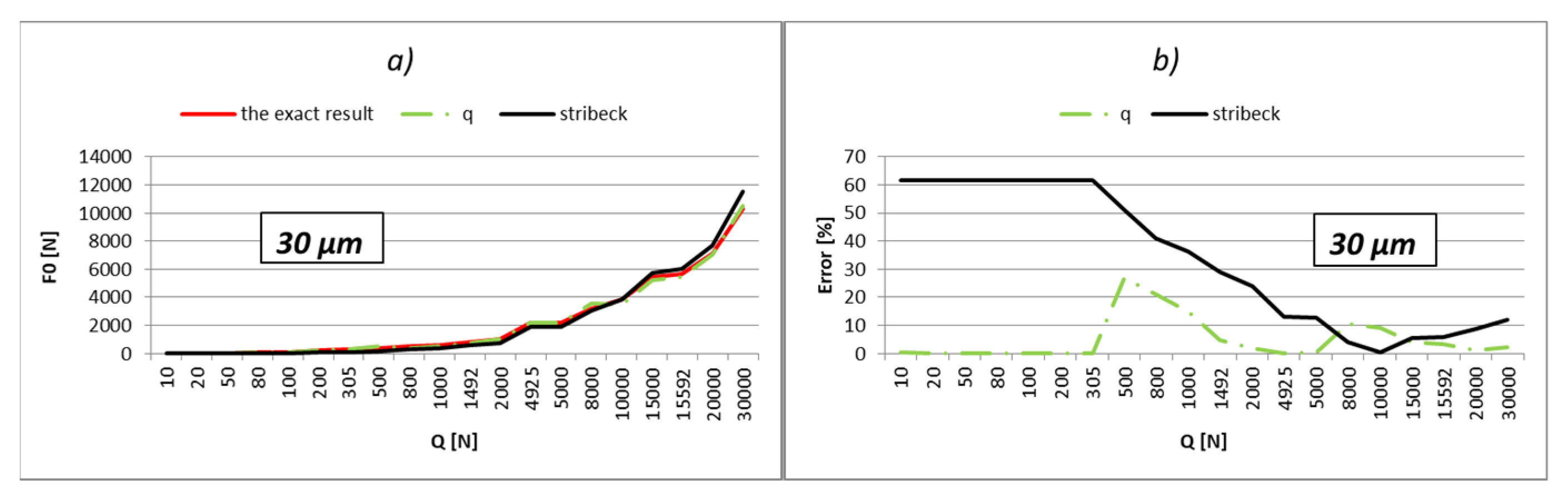
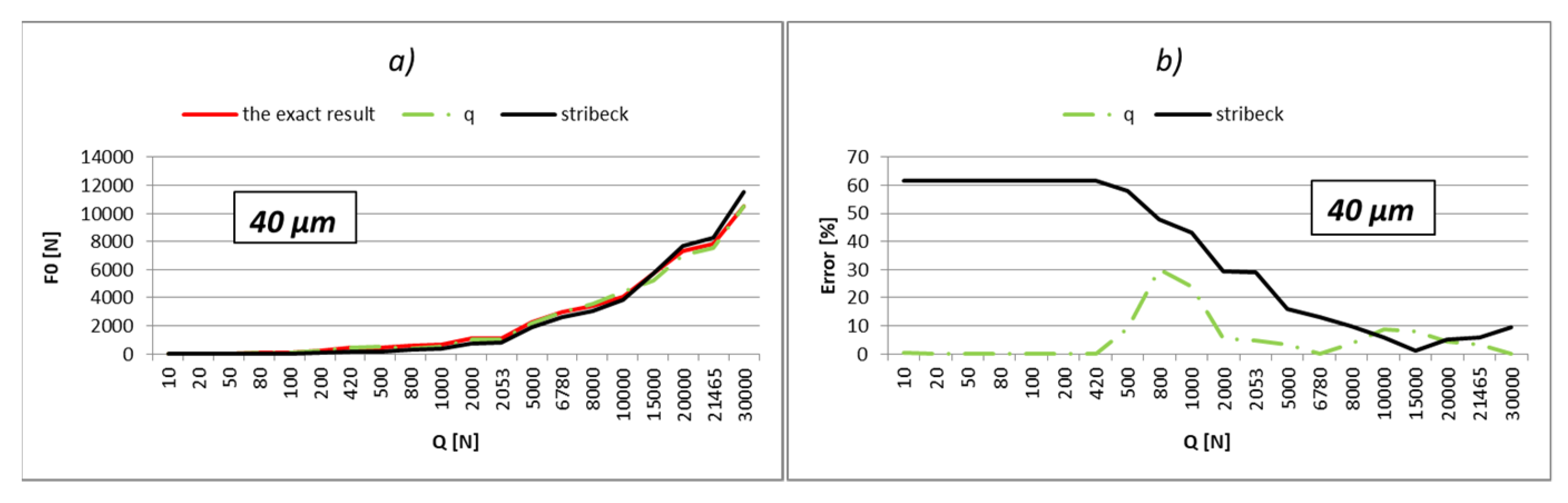
The results of the calculation are shown in

Table A9. The load of the most-loaded rolling element of roller bearing NU 2205 with clearance e = 0 µm.

Q	10.0	20.0	50.0	80.0	100.0	200.0	500.0	800.0	1000.0	2000.0	5000.0	8000.0	10,000.0	15,000.0	20,000.0	30,000.0
exact result	6.2	10.2	22.2	32.4	38.9	71.2	167.1	262.7	326.1	641.9	1587.7	2532.9	3162.9	4737.8	6312.5	9461.7
q3	10.0	20.0	50.0	80.0	100.0	200.0	500.0	800.0	1000.0	2000.0	5000.0	8000.0	10,000.0	15,000.0	20,000.0	30,000.0
%	62.3	95.3	124.8	147.1	156.9	180.9	199.2	204.5	206.6	211.6	214.9	215.8	216.2	216.6	216.8	217.1
q4	5.2	10.3	25.8	41.2	51.5	103.0	257.5	412.0	515.0	1030.0	2575.0	4120.0	5150.0	7725.0	10,300.0	15,450.0
%	−16.4	0.6	15.8	27.2	32.3	44.6	54.1	56.8	57.9	60.5	62.2	62.7	62.8	63.1	63.2	63.3
q5	4.4	8.9	22.2	35.4	44.3	88.6	221.5	354.4	443.0	886.0	2215.0	3544.0	4430.0	6645.0	8860.0	13,290.0
%	−28.1	−13.5	−0.4	9.5	13.8	24.4	32.5	34.9	35.8	38.0	39.5	39.9	40.1	40.3	40.4	40.5
q6	3.5	7.0	17.5	28.0	35.1	70.1	175.3	280.5	350.6	701.2	1753.0	2804.8	3506.0	5259.0	7012.0	10,518.0
%	−43.1	−31.5	−21.2	−13.4	−9.9	−1.5	4.9	6.8	7.5	9.2	10.4	10.7	10.8	11.0	11.1	11.2
q7	3.3	6.6	16.4	26.2	32.8	65.5	163.8	262.1	327.6	655.2	1638.0	2620.8	3276.0	4914.0	6552.0	9828.0
%	−46.8	−36.0	−26.3	−19.1	−15.8	−8.0	−2.0	−0.2	0.5	2.1	3.2	3.5	3.6	3.7	3.8	3.9
Stribek	3.1	6.3	15.7	25.1	31.4	62.8	156.9	251.1	313.8	627.7	1569.2	2510.8	3138.5	4707.7	6276.9	9415.4
%	−49.1	−38.7	−29.4	−22.5	−19.4	−11.9	−6.1	−4.4	−3.8	−2.2	−1.2	−0.9	−0.8	−0.6	−0.6	−0.5

,

Table A10. The load of the most-loaded rolling element of roller bearing NU 2205 with clearance e = 5 µm.

Q	10.0	41.7	100.0	200.0	203.7	500.0	672.6	1000.0	2000.0	2129.6	5000.0	8000.0	10,000.0	11222.1	20,000.0	30,000.0
exact result	10.0	41.7	67.4	108.6	110.1	229.2	298.0	407.3	732.0	773.8	1693.3	2650.1	3287.0	3675.9	6449.9	9605.3
q3	10.0	41.7	100.0	200.0	203.7	500.0	672.6	1000.0	2000.0	2129.6	5000.0	8000.0	10,000.0	11222.1	20,000.0	30,000.0
%	0.0	0.0	48.4	84.1	85.0	118.1	125.7	145.5	173.2	175.2	195.3	201.9	204.2	205.3	210.1	212.3
q4	5.2	21.4	51.5	103.0	104.9	257.5	346.4	515.0	1030.0	1096.7	2575.0	4120.0	5150.0	5779.4	10,300.0	15,450.0
%	−48.5	−48.5	−23.6	−5.2	−4.7	12.3	16.3	26.4	40.7	41.7	52.1	55.5	56.7	57.2	59.7	60.8
q5	4.4	18.5	44.3	88.6	90.3	221.5	298.0	443.0	886.0	943.4	2215.0	3544.0	4430.0	4971.4	8860.0	13,290.0
%	−55.7	−55.7	−34.3	−18.4	−18.0	−3.4	0.0	8.8	21.0	21.9	30.8	33.7	34.8	35.2	37.4	38.4
q6	3.5	14.6	35.1	70.1	71.4	175.3	235.8	350.6	701.2	746.6	1753.0	2804.8	3506.0	3934.5	7012.0	10,518.0
%	−64.9	−64.9	−48.0	−35.4	−35.1	−23.5	−20.9	−13.9	−4.2	−3.5	3.5	5.8	6.7	7.0	8.7	9.5
q7	3.3	13.6	32.8	65.5	66.7	163.8	220.4	327.6	655.2	697.7	1638.0	2620.8	3276.0	3676.4	6552.0	9828.0
%	−67.2	−67.2	−51.4	−39.7	−39.4	−28.5	−26.0	−19.6	−10.5	−9.8	−3.3	−1.1	−0.3	0.0	1.6	2.3
Stribek	3.8	16.0	38.5	76.9	78.4	192.3	258.7	384.6	769.2	819.1	1923.1	3076.9	3846.2	4316.2	7692.3	11,538.5
%	−61.5	−61.5	−42.9	−29.2	−28.8	−16.1	−13.2	−5.6	5.1	5.9	13.6	16.1	17.0	17.4	19.3	20.1

,

Table A11. The load of the most-loaded rolling element of roller bearing NU 2205 with clearance e = 10 µm.

Q	50.0	89.97	100.0	200.0	440.1	500.0	800.0	1000.0	1453.0	2000.0	4600.2	5000.0	8000.0	20,000.0	24,241.1	30,000.0
exact result	50.0	89.96	95.0	138.8	237.9	262.2	383.1	463.2	643.6	827.1	1671.5	1800.2	2762.5	6590.4	7940.4	9762.4
q3	50.0	89.97	100.0	200.0	440.1	500.0	800.0	1000.0	1453.0	2000.0	4600.2	5000.0	8000.0	20,000.0	24,241.1	30,000.0
%	0.0	0.01	5.3	44.1	85.0	90.7	108.8	115.9	125.7	141.8	175.2	177.8	189.6	203.5	205.3	207.3
q4	25.8	46.33	51.5	103.0	226.6	257.5	412.0	515.0	748.3	1030.0	2369.1	2575.0	4120.0	10,300.0	12,484.2	15,450.0
%	−48.5	−48.49	−45.8	−25.8	−4.7	−1.8	7.5	11.2	16.3	24.5	41.7	43.0	49.1	56.3	57.2	58.3
q5	22.2	39.86	44.3	88.6	195.0	221.5	354.4	443.0	643.7	886.0	2037.9	2215.0	3544.0	8860.0	10,738.8	13,290.0
%	−55.7	−55.70	−53.4	−36.2	−18.0	−15.5	−7.5	−4.4	0.0	7.1	21.9	23.0	28.3	34.4	35.2	36.1
q6	17.5	31.54	35.1	70.1	154.3	175.3	280.5	350.6	509.4	701.2	1612.8	1753.0	2804.8	7012.0	8498.9	10,518.0
%	−64.9	−64.94	−63.1	−49.5	−35.1	−33.2	−26.8	−24.3	−20.9	−15.2	−3.5	−2.6	1.5	6.4	7.0	7.7
q7	16.4	29.47	32.8	65.5	144.2	163.8	262.1	327.6	476.0	655.2	1507.0	1638.0	2620.8	6552.0	7941.4	9828.0
%	−67.2	−67.24	−65.5	−52.8	−39.4	−37.5	−31.6	−29.3	−26.0	−20.8	−9.8	−9.0	−5.1	−0.6	0.0	0.7
Stribek	19.2	34.60	38.5	76.9	169.3	192.3	307.7	384.6	558.8	769.2	1769.3	1923.1	3076.9	7692.3	9323.5	11,538.5
%	−61.5	−61.53	−59.5	−44.6	−28.8	−26.7	−19.7	−17.0	−13.2	−7.0	5.9	6.8	11.4	16.7	17.4	18.2

,

Table A12. The load of the most-loaded rolling element of roller bearing NU 2205 with clearance e = 15 µm.

Q	100.0	141.2	200.0	500.0	690.5	800.0	1000.0	2000.0	2279.9	5000.0	7218.3	8000.0	10,000.0	15,000.0	20,000.0	30,000.0
exact result	100.0	141.2	168.7	295.3	373.3	417.7	498.5	898.6	1009.9	1905.9	2622.7	2874.3	3516.7	5117.3	6713.9	9901.0
q3	100.0	141.2	200.0	500.0	690.5	800.0	1000.0	2000.0	2279.9	5000.0	7218.3	8000.0	10,000.0	15,000.0	20,000.0	30,000.0
%	0.0	0.0	18.6	69.3	85.0	91.5	100.6	122.6	125.7	162.3	175.2	178.3	184.4	193.1	197.9	203.0
q4	51.5	72.7	103.0	257.5	355.6	412.0	515.0	1030.0	1174.1	2575.0	3717.4	4120.0	5150.0	7725.0	10,300.0	15,450.0
%	−48.5	−48.5	−38.9	−12.8	−4.7	−1.4	3.3	14.6	16.3	35.1	41.7	43.3	46.4	51.0	53.4	56.0
q5	44.3	62.5	88.6	221.5	305.9	354.4	443.0	886.0	1010.0	2215.0	3197.7	3544.0	4430.0	6645.0	8860.0	13,290.0
%	−55.7	−55.7	−47.5	−25.0	−18.0	−15.2	−11.1	−1.4	0.0	16.2	21.9	23.3	26.0	29.9	32.0	34.2
q6	35.1	49.5	70.1	175.3	242.1	280.5	350.6	701.2	799.3	1753.0	2530.7	2804.8	3506.0	5259.0	7012.0	10,518.0
%	−64.9	−64.9	−58.4	−40.6	−35.1	−32.9	−29.7	−22.0	−20.9	−8.0	−3.5	−2.4	−0.3	2.8	4.4	6.2
q7	32.8	46.3	65.5	163.8	226.2	262.1	327.6	655.2	746.9	1638.0	2364.7	2620.8	3276.0	4914.0	6552.0	9828.0
%	−67.2	−67.2	−61.2	−44.5	−39.4	−37.3	−34.3	−27.1	−26.0	−14.1	−9.8	−8.8	−6.8	−4.0	−2.4	−0.7
Stribek	38.5	54.3	76.9	192.3	265.6	307.7	384.6	769.2	876.9	1923.1	2776.3	3076.9	3846.2	5769.2	7692.3	11,538.5
%	−61.5	−61.5	−54.4	−34.9	−28.8	−26.3	−22.9	−14.4	−13.2	0.9	5.9	7.0	9.4	12.7	14.6	16.5

,

Table A13. The load of the most-loaded rolling element of roller bearing NU 2205 with clearance e = 20 µm.

Q	100.0	194.4	200.0	500.0	800.0	950.4	1000.0	2000.0	3138.6	5000.0	8000.0	9937.0	10,000.0	15,000.0	20,000.0	30,000.0
exact result	100.0	194.3	197.4	328.4	452.4	513.8	534.0	936.4	1390.3	2010.2	2985.5	3610.5	3630.8	5236.8	6837.1	10,029.6
q3	100.0	194.4	200.0	500.0	800.0	950.4	1000.0	2000.0	3138.6	5000.0	8000.0	9937.0	10,000.0	15,000.0	20,000.0	30,000.0
%	0.0	0.0	1.3	52.3	76.8	85.0	87.3	113.6	125.7	148.7	168.0	175.2	175.4	186.4	192.5	199.1
q4	51.5	100.1	103.0	257.5	412.0	489.4	515.0	1030.0	1616.4	2575.0	4120.0	5117.5	5150.0	7725.0	10,300.0	15,450.0
%	−48.5	−48.5	−47.8	−21.6	−8.9	−4.7	−3.5	10.0	16.3	28.1	38.0	41.7	41.8	47.5	50.6	54.0
q5	44.3	86.1	88.6	221.5	354.4	421.0	443.0	886.0	1390.4	2215.0	3544.0	4402.1	4430.0	6645.0	8860.0	13,290.0
%	−55.7	−55.7	−55.1	−32.5	−21.7	−18.1	−17.0	−5.4	0.0	10.2	18.7	21.9	22.0	26.9	29.6	32.5
q6	35.1	68.1	70.1	175.3	280.5	333.2	350.6	701.2	1100.4	1753.0	2804.8	3483.9	3506.0	5259.0	7012.0	10,518.0
%	−64.9	−64.9	−64.5	−46.6	−38.0	−35.1	−34.3	−25.1	−20.9	−12.8	−6.1	−3.5	−3.4	0.4	2.6	4.9
q7	32.8	63.7	65.5	163.8	262.1	311.3	327.6	655.2	1028.2	1638.0	2620.8	3255.4	3276.0	4914.0	6552.0	9828.0
%	−67.2	−67.2	−66.8	−50.1	−42.1	−39.4	−38.6	−30.0	−26.0	−18.5	−12.2	−9.8	−9.8	−6.2	−4.2	−2.0
Stribek	38.5	74.8	76.9	192.3	307.7	365.5	384.6	769.2	1207.2	1923.1	3076.9	3821.9	3846.2	5769.2	7692.3	11,538.5
%	−61.5	−61.5	−61.0	−41.4	−32.0	−28.9	−28.0	−17.9	−13.2	−4.3	3.1	5.9	5.9	10.2	12.5	15.0

,

Table A14. The load of the most-loaded rolling element of roller bearing NU 2205 with clearance e = 30 µm.

Q	100.0	200.0	305.0	500.0	800.0	1000.0	1491.7	2000.0	4924.8	5000.0	8000.0	10,000.0	15,000.0	15,592.4	20,000.0	30,000.0
exact result	100.0	200.0	304.9	394.2	521.8	604.9	806.3	1012.3	2181.6	2208.0	3204.8	3857.1	5474.5	5665.4	7082.7	10,286.2
q3	100.0	200.0	305.0	500.0	800.0	1000.0	1491.7	2000.0	4924.8	5000.0	8000.0	10,000.0	15,000.0	15,592.4	20,000.0	30,000.0
%	0.0	0.0	0.0	26.8	53.3	65.3	85.0	97.6	125.7	126.5	149.6	159.3	174.0	175.2	182.4	191.7
q4	51.5	103.0	157.1	257.5	412.0	515.0	768.2	1030.0	2536.3	2575.0	4120.0	5150.0	7725.0	8030.1	10,300.0	15,450.0
%	−48.5	−48.5	−48.5	−34.7	−21.0	−14.9	−4.7	1.7	16.3	16.6	28.6	33.5	41.1	41.7	45.4	50.2
q5	44.3	88.6	135.1	221.5	354.4	443.0	660.8	886.0	2181.7	2215.0	3544.0	4430.0	6645.0	6907.4	8860.0	13,290.0
%	−55.7	−55.7	−55.7	−43.8	−32.1	−26.8	−18.0	−12.5	0.0	0.3	10.6	14.9	21.4	21.9	25.1	29.2
q6	35.1	70.1	106.9	175.3	280.5	350.6	523.0	701.2	1726.6	1753.0	2804.8	3506.0	5259.0	5466.7	7012.0	10,518.0
%	−64.9	−64.9	−64.9	−55.5	−46.2	−42.0	−35.1	−30.7	−20.9	−20.6	−12.5	−9.1	−3.9	−3.5	−1.0	2.3
q7	32.8	65.5	99.9	163.8	262.1	327.6	488.7	655.2	1613.4	1638.0	2620.8	3276.0	4914.0	5108.1	6552.0	9828.0
%	−67.2	−67.2	−67.2	−58.5	−49.8	−45.8	−39.4	−35.3	−26.0	−25.8	−18.2	−15.1	−10.2	−9.8	−7.5	−4.5
Stribek	38.5	76.9	117.3	192.3	307.7	384.6	573.7	769.2	1894.2	1923.1	3076.9	3846.2	5769.2	5997.1	7692.3	11,538.5
%	−61.5	−61.5	−61.5	−51.2	−41.0	−36.4	−28.8	−24.0	−13.2	−12.9	−4.0	−0.3	5.4	5.9	8.6	12.2

,

Table A15. The load of the most-loaded rolling element of roller bearing NU 2205 with clearance e = 40 µm.

Q	100.0	200.0	419.8	500.0	800.0	1000.0	2000.0	2053.5	5000.0	6779.7	8000.0	10,000.0	15,000.0	20,000.0	21,465.1	30,000.0
exact result	100.0	200.0	419.8	458.8	590.9	675.8	1088.3	1110.0	2294.4	3003.2	3417.4	4079.4	5710.4	7327.0	7799.3	10,542.0
q3	100.0	200.0	419.8	500.0	800.0	1000.0	2000.0	2053.5	5000.0	6779.7	8000.0	10,000.0	15,000.0	20,000.0	21,465.1	30,000.0
%	0.0	0.0	0.0	9.0	35.4	48.0	83.8	85.0	117.9	125.7	134.1	145.1	162.7	173.0	175.2	184.6
q4	51.5	103.0	216.2	257.5	412.0	515.0	1030.0	1057.5	2575.0	3491.6	4120.0	5150.0	7725.0	10,300.0	11,054.5	15,450.0
%	−48.5	−48.5	−48.5	−43.9	−30.3	−23.8	−5.4	−4.7	12.2	16.3	20.6	26.2	35.3	40.6	41.7	46.6
q5	44.3	88.6	186.0	221.5	354.4	443.0	886.0	909.7	2215.0	3003.4	3544.0	4430.0	6645.0	8860.0	9509.0	13,290.0
%	−55.7	−55.7	−55.7	−51.7	−40.0	−34.4	−18.6	−18.0	−3.5	0.0	3.7	8.6	16.4	20.9	21.9	26.1
q6	35.1	70.1	147.2	175.3	280.5	350.6	701.2	719.9	1753.0	2377.0	2804.8	3506.0	5259.0	7012.0	7525.7	10,518.0
%	−64.9	−64.9	−64.9	−61.8	−52.5	−48.1	−35.6	−35.1	−23.6	−20.9	−17.9	−14.1	−7.9	−4.3	−3.5	−0.2
q7	32.8	65.5	137.5	163.8	262.1	327.6	655.2	672.7	1638.0	2221.0	2620.8	3276.0	4914.0	6552.0	7032.0	9828.0
%	−67.2	−67.2	−67.2	−64.3	−55.6	−51.5	−39.8	−39.4	−28.6	−26.0	−23.3	−19.7	−13.9	−10.6	−9.8	−6.8
Stribek	38.5	76.9	161.5	192.3	307.7	384.6	769.2	789.8	1923.1	2607.6	3076.9	3846.2	5769.2	7692.3	8255.8	11,538.5
%	−61.5	−61.5	−61.5	−58.1	−47.9	−43.1	−29.3	−28.8	−16.2	−13.2	−10.0	−5.7	1.0	5.0	5.9	9.5

and

Table A16. The load of the most-loaded rolling element of roller bearing NU 2205 with clearance e = 50 µm.

Q	100.0	200.0	500.0	537.9	800.0	1000.0	2000.0	2631.3	5000.0	8000.0	8687.4	10,000.0	15,000.0	20,000.0	27,504.9	30,000.0
exact result	100.0	200.1	500.0	537.9	659.6	746.5	1164.3	1422.4	2377.5	3574.9	3848.3	4294.9	5943.7	7569.8	9993.8	10,797.0
q3	100.0	200.0	500.0	537.9	800.0	1000.0	2000.0	2631.3	5000.0	8000.0	8687.4	10,000.0	15,000.0	20,000.0	27,504.9	30,000.0
%	0.0	0.0	0.0	0.0	21.3	34.0	71.8	85.0	110.3	123.8	125.7	132.8	152.4	164.2	175.2	177.9
q4	51.5	103.0	257.5	277.0	412.0	515.0	1030.0	1355.1	2575.0	4120.0	4474.0	5150.0	7725.0	10,300.0	14,165.0	15,450.0
%	−48.5	−48.5	−48.5	−48.5	−37.5	−31.0	−11.5	−4.7	8.3	15.2	16.3	19.9	30.0	36.1	41.7	43.1
q5	44.3	88.6	221.5	238.3	354.4	443.0	886.0	1165.7	2215.0	3544.0	3848.5	4430.0	6645.0	8860.0	12,184.7	13,290.0
%	−55.7	−55.7	−55.7	−55.7	−46.3	−40.7	−23.9	−18.0	−6.8	−0.9	0.0	3.1	11.8	17.0	21.9	23.1
q6	35.1	70.1	175.3	188.6	280.5	350.6	701.2	922.5	1753.0	2804.8	3045.8	3506.0	5259.0	7012.0	9643.2	10,518.0
%	−64.9	−65.0	−64.9	−64.9	−57.5	−53.0	−39.8	−35.1	−26.3	−21.5	−20.9	−18.4	−11.5	−7.4	−3.5	−2.6
q7	32.8	65.5	163.8	176.2	262.1	327.6	655.2	862.0	1638.0	2620.8	2846.0	3276.0	4914.0	6552.0	9010.6	9828.0
%	−67.2	−67.3	−67.2	−67.2	−60.3	−56.1	−43.7	−39.4	−31.1	−26.7	−26.0	−23.7	−17.3	−13.4	−9.8	−9.0
Stribek	38.5	76.9	192.3	206.9	307.7	384.6	769.2	1012.0	1923.1	3076.9	3341.3	3846.2	5769.2	7692.3	10,578.8	11,538.5
%	−61.5	−61.6	−61.5	−61.5	−53.3	−48.5	−33.9	−28.8	−19.1	−13.9	−13.2	−10.4	−2.9	1.6	5.9	6.9

(Appendix B). The analysis is performed for different values of the internal radial clearance, which were varied between 0 and 50 µm. For this example too, the values of the load were calculated and shown regarding the three above-mentioned methods. The values of the external load were varied in the range from 10 to 30,000 N, which is close to the static load rating of this bearing, which is 34,100 N. Additionally, the results acquired in relation to the values of the boundary external load (Q_q) are bold in the tables. Results from Table A9, Table A10, Table A11, Table A12, Table A13, Table A14, Table A15 and Table A16 are graphically shown in Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17.

3.3. Discussion of the Results

The part of the load that transfers the most-loaded rolling element of the rolling bearing is possible to obtain simply by the multiplication of load factor k_maxq with the value of the external radial load. On the level of the load of the most-loaded rolling element, the largest influence is the number of active rolling elements. On the other hand, what the number of active rolling elements in the bearing will be is primarily dependent on the size of internal radial clearance and applied external load. The larger external load will cause a greater number of active rolling elements, and at low values of the external load, the number of active rolling elements will be smaller and will be in an interval q = 1÷3. It implies that for the lower values of the external load, the calculation with the factor of load k_max3 will give more accurate results. This is also shown by the results presented in the previous subchapter. The factor k_max3 corresponds to supporting the three active rolling elements of the bearing.

On the other side, for larger values of external loads, more accurate results are obtained with k_maxq factors, which correspond to the larger number of active rolling elements.

The internal radial clearance negatively affects the number of active rolling elements. The larger values of internal radial clearance, then as a consequence have a smaller number of active rolling elements in the bearing. In this regard, larger values of internal clearance will increase the zones in which the calculation with coefficient k_max3 provides the best results. By reducing the value of the internal clearance, the size of this zone will be proportionally narrower. For example, for a relatively small clearance of e = 5 µm and bearing 6206, the length of the zone in which factor k_max3 provides the best results reaches up to about 10 N, and up to 40 N for bearing NU 2205. On the other side, for clearance e = 50 µm, this zone increases up to 200 N for bearing 6206, or 900 N for bearing NU 2205 EC.

So, the larger the value of the external load and the smaller the size of the internal clearance, the calculation with load factor k_maxq provides more accurate results compared to the calculation recommended by Stribeck. This is especially expressed in the bearings with rollers. For loads that allow supporting with the maximum possible number of rolling elements, the calculation using the load factor provides much more accurate results compared to Stribeck’s method.

The calculation provides accurate results for the boundary values of external load (Q_q), which correspond to the boundary-bearing deflection (a_q). In those situations, the support system of the inner ring switches from q − 1 on q active rolling elements. Extremely high accuracy of the results is obtained also in the areas that are relatively close to the boundary values of the external load. Furthermore, a higher total number of active rolling elements in the bearing increases the accuracy and width of high-accuracy zones.

The calculation results for the boundary loads are highlighted in bold. Until the first bold load, the inner bearing ring will support according to support systems 1–2 [4,13]. At higher loads, the third rolling element engages the ring of the bearing and becomes active. The next bold column corresponds to the load when the inner ring begins to support four rolling elements, etc.

By analyzing the results shown in the pictures (Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17), it can be concluded that a much greater precision of results can be acquired by the proper selection of load factors that will give the best accuracy for a given bearing and applied external load. In doing so, it is good to keep the following recommendations and conclusions:

• The calculation provides the most accurate results in areas that are close to the boundary values of external load;
• For relatively low loads, which are expected to cause support on the maximum of three active rolling elements, the best results are obtained by calculation using the coefficient k_max3;
• For support on the maximum possible number of active rolling elements (z_s), the best results are obtained using the coefficient corresponding to that number (k_maxzs).

4. The Calculation by Applying a Selection of Coefficients

In order to properly verify the above recommendations, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28, Figure 29, Figure 30, Figure 31, Figure 32 and Figure 33 show the results of the calculation by applying the selection of coefficients. The previously discussed bearings, 6206 and NU 2205, were again taken as an example. The load distribution factors were selected according to the above recommendations. Here again, the diagrams on the right show loads of the most-loaded rolling element, while the left shows the error according to the proposed method and the Stribeck method.

Discussion of the Results

The calculation results presented in Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28, Figure 29, Figure 30, Figure 31, Figure 32 and Figure 33 show the much greater accuracy of the method proposed in this paper than the method of Stribeck.

This is especially expressed at the roller bearing NU 2205. For this bearing, Stribeck’s expressions show higher accuracy only at bearings with zero internal clearance and at high external loads (over 30,000 N), as well as in narrow zones in which the inner ring is supported according to support systems 4–5 (on four rolling elements for a BSE support system, and five rolling elements for a BSO support system) [13]. BSE is the boundary position of support on an even number of rolling elements. In other cases, with bearing NU 2205, the calculation by the proposed method provides much more accurate results, compared to Stribeck’s numbers.

On the dash-dot line, for the error of calculation on the proposed method, we can notice a higher number of peaks—one peak in each zone with a different support system of the inner ring. For the boundary values of external radial load at which a new rolling element comes into contact with rings, the error of calculation decreases to zero. By further increase of the load, it reaches a maximum value, so again it is lowered to zero in the new boundary zone when new rolling elements engage the rings. Accordingly, the peaks on the dash-dot line are occurring in the zones that are farthest from the zones of boundary-bearing deflection, that is, boundary-bearing load. Furthermore, we can notice that the height of peaks on the dot-dash lines decreases with the increase of external load.

The precision of the proposed method for the ball 6206 bearings is somewhat less. However, for the normal values of clearance (5–20 µm) [21], which are the most commonly encountered in practice, the zone of the more precise results for the proposed method is much wider compared to Stribeck’s method. From Figure 21, Figure 22, Figure 23, Figure 24 and Figure 25, it can be seen that Stribeck’s method provides more precise results in the zones where the support systems 3–4 occur. Above these zones, and up until the static load rating of the bearing, which is 11,200 N, the calculation by application of the recommended method provides more accurate results. For the bearings in which internal clearance is higher than 40 µm, Stribeck’s method is more recommendable. Those clearances fall under class C5 according to ISO 5753-1 [21].

5. Conclusions

• The aim of the research presented in this paper is the verification of a new model for calculating the load carried by the most-loaded rolling element in rolling bearings with internal radial clearance. The proposed model was verified on the example of the two different bearing types: the radial ball bearing 6206 and the roller bearing NU 2205 EC;
• By analysis of obtained results, the following can be concluded:

  -

  For the boundary values of the external load, which correspond to the boundary deflection of the bearing, the calculation by application of load factors provides accurate results;

  -

  The results show extremely high accuracy in the zones that are relatively close to the boundary values of the external load;

  -

  The higher the number of active rolling elements, the greater the accuracy of the results. Additionally, an increase in the number of active rolling elements in the bearing expands the zones with high-precision results;

  -

  The proposed calculation provides more accurate results in the bearings with a larger total number of rolling elements because in these bearings it is easier to achieve a higher number of active rolling elements.

3.

The proposed model was compared to a calculation based on Stribeck’s numbers. Both calculations are based on simple mathematical operations, do not require the usage of computers, and are very useful for fast calculations and fieldwork;

4.

As opposed to Stribeck, the model proposed in this paper takes into account the influence of internal clearance size on the load distribution within the bearing;

5.

The analysis performed in this paper has shown that by correct selection of the load factor, the new model provides much more precise results compared to the Stribeck method;

6.

When selecting a load factor, it is good to follow the next recommendations:

-

Select the values of the load factor in relation to the number of active rolling elements and the boundary positions of the supports. The method of linear interpolation can be used to specify the load factor, although the dependence between load and deflection is not linear;

-

For relatively low loads, where the support is expected on a maximum of three active rolling elements, the best results are given by the calculation using the coefficient k_max3;

-

When supporting bearings on the maximum possible number of active rolling elements (z_s), the calculation with the coefficient corresponding to that number (k_maxzs) provides the best results.

7.

The calculation performed by selecting the load factors is subjective (nonobjective) because it depends on how much the person who performs the calculation will correctly select the load factors. Yet, the application of the above recommendations can ensure high accuracy of the obtained results.